Laboration 1: Linjär algebra
|
|
|
- Adam Olofsson
- för 7 år sedan
- Visningar:
Transkript
1 MALMÖ HÖGSKOLA Centrum för teknikstudier MA119A VT 2010, Yuanji Cheng Viktigt information om labb Vid laborationen gäller följande: 1. Labben görs i grupp av två studenter, och redovisningsuppgifterna skall vara gjorda innan man kommer till labblektionen. Vid problem kan man fråga under övningslektionen. 2. Obligatorisk närvaro. 3. Under laborationslektion skall alla redovisningsuppgifter redovisas. 4. Vid redovisning ska två dokument redovisas: en Matlab m-l som visar kommando för varje uppgifter, och en Word-dokument som innehåller båda kommando och resultat. 5. Vara redo på att svara på frågor kring hur har du löst uppgifter. Laboration 1: Linjär algebra Syftet med denna labb är att lära vissa beräkningsverktyg i datorprogram Matlab för olika uppgifter som uppkommer i kursdelen av linjär algebra. Matlab är ett interaktivt program för numeriska beräkningar och visualisering. Det är också ett programeringsspråk med instruktionsrepertoar liknande den som nns i många andra program. Matlab nns på esta slags datorer, och till fördelarna med programmet hör att det ser i stort sett likadant ut oberoende av på vilket sorts dator man kör det. Börja med att logga in på ditt vanligt konto. Starta sedan Matlab genom att klicka på Matlab-ikonen. Programmet avslutas med kommandot exit. Till att börja med kan man tänka på Matlab som en avancerad räknedosa som beräknar uttryck. Man skriver in vad man vill ha gjort och Matlab svarar. > > Variabler tilldelas värden med tecknet = och nns sedan kvar i minnet. Prova på att tilldela några variabler värden. > > a = 1; En variabel, t ex a, kan raderas ur minnet med kommandot clear a. Läggs ett semikolon ; till efter en kommandorad, skrivs resultatet inte ut på skärmen. Inom Matlab nns det fem aritmetiska operatorer och dessa utföras i olika prioritetsordningar potens som har den högsta prioriteringen, dvs, prioritet 1. * / multiplikation och division är prioritet 2 + addition och subtraktion har prioritet 3. > > 3*52/4; 18.75
2 Vid utskrift till skärmen visas tal normalt i så kallad kort decimalform med fyra decimaler, med kommandot format long kan man få att utskriftet blir 14 decimaler. > > 5/ > > format long > > b Det nns också funktion för att skriva i bråktal > > format rat > > sqrt(49/16) 7/4 I) För att genera en radvektor skriver man t ex > > x = [ ] x = För att skriva ut en kolonnvektor i Matlab, använder man tecken ; t ex, > > y = [2; 1; 8] y = II) För att genera en matris i Matlab skriver man, t ex, > > A = [ ; ; ] A = Addition och substraktion beräknas som vanligt, t ex > > x = [ ]; > > y = [ ]; > > x +y > > x -y III) Skalärprodukt x y kan skrivas med kommandot > > dot(x, y) 35 IV) Längden av vektorer beräknas med hjälp av formeln x = x x varför blir det i Matlab > > sqrt(dot(x, x))
3 V) För kryssprodukt kan man göra för vektorer i rymden, t ex > > w = [0-2 5]; > > z = [-1 3 7]; > > cross(w, z) Eftersom kryssprodukt nns endast för vektorer i rymden, då får man varning om dimension av vektorer inte är 3, t ex > > cross(x, y)??? Error using ==> cross at 37 A and B must have at least one dimension of length 3. VI) Matris multiplikation kan beräknas också som vanligt, t ex > > A = [0-2 5; 3 0 4] > > B = [-1 3; 2 7; 1-6] > > C= A*B C = > > D=B*A D = VII) Beräkning av determinant av kvadratiska matriser, t ex > > det(c) 29 > > det(d) 0 VIII) Beräkning av invers av kvadratisk matris, t ex > > inv(c) 15/29 44/29 1/29 1/29 Eftersom inversen nns bara för inverterbar matris, därför inversen av D existerar ej och får en varning vid > > inv(d) Warning: Matrix is singular to working precision IX) Linjära ekvationssytem. För att lösa följande linjärt ekvationssystem, t ex, x + 2y 3z = 4 3x 5y + z = 9 2x + 3y 5z = 7 skriver man först detta på matris form AX = B sedan erhåller lösningen X = A 1 B. > > A =[ 1 2-3; 3-5 1; 2 3 5] > > B =[4; -9; 7]
4 > > X =inv(a)*b X = 32/ /111 10/111 PS: Lösningen kan även fås genom kommandot > > X = A\B. Testa detta! OBS: Lösbarhet hos ett linjärt ekvationssystem kan vara: i) lösning saknas, ii) en entydig lösning, iii) oändligt många lösningar. Dessa system av typ iii) kan inte hanteras av Matlab, och vid fallet i) löser Matlab detta med minsta-kvadrat metod, dvs, löser A T AX = A T B, och ger en lösning som är bästa i denna mening AX B 2 blir minsta för alla vektor X. Följande ekvationssystemet saknar lösningen x + y x 2y = 2 3x + 4y = 1 = 4 Om man löser detta system i Matlab, får man > > M = [ 1 2; 1-2 ; 3 4]; > > N = [-4; 2; 1]; > > S = M\N S = Anm. Vinkel beräkning arccos(x) > > acos (1/13) i radian Exempel: Vinkeln mellan vektorerna u = (1, 2, 3) och v = (4, 1, 0). > > u = [1-2 3] > > v = [4 1 0] > > a = dot(u, v) a = 2 > > sqrt(dot(u, u)) > > c = sqrt(dot(v, v)) c = > > vinkeln = acos(a/(b*c)) vinkeln = i radian X) m-l. För redovisnings ändamål kan man skappa en m-l för varje uppgift, sedan kan man återkomma till dessa uppgifter när man vill.
5 XI) Redovisninguppgifter 1) Finn vinkeln mellan vektorerna s = (2, 1) och t = (3, 4). 2) Beräkna volymen till denna parallepipped som spänns upp av vektorerna u = (1, 2, 3), v = (4, 1, 0) och w = (2, 7, 3). 3) Beräkna arean till denna triangel med hörn i punkterna P : (1, 1, 2), Q : (3, 1, 0) och R : ( 5, 4, 1). 4) Lös följande ekvationssystem x + y + 2z + 2w = 1 3x + 4y + 7z + 12w = 2 2x + 4y + 3z 2w = 12 5x + y + 3z 31w = 20 Är din lösning en riktig lösning eller en minsta-kvadrat lösning? 5) Lös matrisekvationen 2AX + 3B = 5C, där A = , B = Ange lösningen bådda i decimaltal och bråktal., C =
SF1900 Sannolikhetsteori och statistik, HT 2017 Laboration 1 för CINEK2
 Matematisk Statistik SF1900 Sannolikhetsteori och statistik, HT 2017 Laboration 1 för CINEK2 1 Introduktion Denna laboration är inte poänggivande utan är till för den som vill bekanta sig med MATLAB. Fokusera
Matematisk Statistik SF1900 Sannolikhetsteori och statistik, HT 2017 Laboration 1 för CINEK2 1 Introduktion Denna laboration är inte poänggivande utan är till för den som vill bekanta sig med MATLAB. Fokusera
Laboration: Vektorer och matriser
 Laboration: Vektorer och matriser Grundläggande om matriser Begreppet matris är en utvidgning av vektorbegreppet, och det används bl a när man löser linjära ekvationssystem. Namnet Matlab står för MATrix
Laboration: Vektorer och matriser Grundläggande om matriser Begreppet matris är en utvidgning av vektorbegreppet, och det används bl a när man löser linjära ekvationssystem. Namnet Matlab står för MATrix
TMV166 Linjär algebra för M. Datorlaboration 2: Matrisalgebra och en mekanisk tillämpning
 MATEMATISKA VETENSKAPER TMV66 07 Chalmers tekniska högskola Datorlaboration Examinator: Tony Stillfjord TMV66 Linjär algebra för M Datorlaboration : Matrisalgebra och en mekanisk tillämpning Allmänt Den
MATEMATISKA VETENSKAPER TMV66 07 Chalmers tekniska högskola Datorlaboration Examinator: Tony Stillfjord TMV66 Linjär algebra för M Datorlaboration : Matrisalgebra och en mekanisk tillämpning Allmänt Den
Linjär algebra med tillämpningar, lab 1
 Linjär algebra med tillämpningar, lab 1 Innehåll Per Jönsson Fakulteten för Teknik och Samhälle, 2013 Uppgifterna i denna laboration täcker kapitel 1-3 i läroboken. Läs igenom motsvarande kapitel. Sitt
Linjär algebra med tillämpningar, lab 1 Innehåll Per Jönsson Fakulteten för Teknik och Samhälle, 2013 Uppgifterna i denna laboration täcker kapitel 1-3 i läroboken. Läs igenom motsvarande kapitel. Sitt
15 september, Föreläsning 5. Tillämpad linjär algebra
 5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
x = som är resultatet av en omskrivning av ett ekvationssystemet som ursprungligen kunde ha varit 2x y+z = 3 2z y = 4 11x 3y = 5 Vi får y z
 Ett nytt försök med att ta fram inversen till en matris Innan vi startar med att bestämma inversen till en matris måste vi veta varför vi skulle kunna behöva den. Vi har A x b som är resultatet av en omskrivning
Ett nytt försök med att ta fram inversen till en matris Innan vi startar med att bestämma inversen till en matris måste vi veta varför vi skulle kunna behöva den. Vi har A x b som är resultatet av en omskrivning
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 016 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 016 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1.
Matriser och linjära ekvationssystem
 Linjär algebra, AT3 211/212 Matematiska vetenskaper Matriser och linjära ekvationssystem Matriser En matris är som ni redan vet ett rektangulärt talschema: a 11 a 1n A = a m1 a mn Matrisen ovan har m rader
Linjär algebra, AT3 211/212 Matematiska vetenskaper Matriser och linjära ekvationssystem Matriser En matris är som ni redan vet ett rektangulärt talschema: a 11 a 1n A = a m1 a mn Matrisen ovan har m rader
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
SKRIVNING I VEKTORGEOMETRI Delkurs
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
14 september, Föreläsning 5. Tillämpad linjär algebra
 14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Linjär Algebra M/TD Läsvecka 2
 Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser. 2.2-2.3 Matrisinvers, karakterisering
Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser. 2.2-2.3 Matrisinvers, karakterisering
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Matriser och linjära ekvationssystem
 Linjär algebra, I1 2011/2012 Matematiska vetenskaper Matriser och linjära ekvationssystem Matriser En matris är som ni vet ett rektangulärt talschema: a 11 a 1n A = a m1 a mn Matrisen ovan har m rader
Linjär algebra, I1 2011/2012 Matematiska vetenskaper Matriser och linjära ekvationssystem Matriser En matris är som ni vet ett rektangulärt talschema: a 11 a 1n A = a m1 a mn Matrisen ovan har m rader
LÖSNINGAR TILL LINJÄR ALGEBRA kl LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2017-08-24 kl 14 19 1. Vi får ū = 1 2 + 1 2 + 0 2 = 2, v = 1 2 + 2 2 + 2 2 = 3 och ū v = 1 1+1 2+0 2 = 3. Om φ är vinkeln mellan ū och v
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2017-08-24 kl 14 19 1. Vi får ū = 1 2 + 1 2 + 0 2 = 2, v = 1 2 + 2 2 + 2 2 = 3 och ū v = 1 1+1 2+0 2 = 3. Om φ är vinkeln mellan ū och v
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Kapitel 4. Programmet MATLAB
 Kapitel 4. Programmet MATLAB MATLAB (namnet härlett ur MATrix LABoratory) är ett matematikprogram baserat på matrisalgebra, som blivit mycket använt för fysikaliska och tekniska tillämpningar. Den ursprungliga
Kapitel 4. Programmet MATLAB MATLAB (namnet härlett ur MATrix LABoratory) är ett matematikprogram baserat på matrisalgebra, som blivit mycket använt för fysikaliska och tekniska tillämpningar. Den ursprungliga
MATLAB the Matrix Laboratory. Introduktion till MATLAB. Martin Nilsson. Enkel användning: Variabler i MATLAB. utvecklat av MathWorks, Inc.
 Introduktion till MATLAB Martin Nilsson Avdelningen för teknisk databehandling Institutionen för informationsteknologi Uppsala universitet MATLAB the Matrix Laboratory utvecklat av MathWorks, Inc. Matematisk
Introduktion till MATLAB Martin Nilsson Avdelningen för teknisk databehandling Institutionen för informationsteknologi Uppsala universitet MATLAB the Matrix Laboratory utvecklat av MathWorks, Inc. Matematisk
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
6.4. Linjära ekvationssytem och matriser
 5 6 MATRISER 6.4. Linjära ekvationssytem och matriser Vi har tidigare sett att linjära ekvationssytem kan skrivas om med hjälp av matriser, så visst finns det ett samband mellan dessa. Nedan ska vi studera
5 6 MATRISER 6.4. Linjära ekvationssytem och matriser Vi har tidigare sett att linjära ekvationssytem kan skrivas om med hjälp av matriser, så visst finns det ett samband mellan dessa. Nedan ska vi studera
TANA17 Matematiska beräkningar med MATLAB för M, DPU. Fredrik Berntsson, Linköpings Universitet. 9 november 2015 Sida 1 / 28
 TANA17 Matematiska beräkningar med MATLAB för M, DPU Fredrik Berntsson, Linköpings Universitet 9 november 2015 Sida 1 / 28 Föreläsning 3 Linjära ekvationssystem. Invers. Rotationsmatriser. Tillämpning:
TANA17 Matematiska beräkningar med MATLAB för M, DPU Fredrik Berntsson, Linköpings Universitet 9 november 2015 Sida 1 / 28 Föreläsning 3 Linjära ekvationssystem. Invers. Rotationsmatriser. Tillämpning:
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
ax + y + 2z = 3 ay = b 3 (b 3) z = 0 har (a) entydig lösning, (b) oändligt många lösningar och (c) ingen lösning.
 UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
Linjär algebra. 1 Inledning. 2 Matriser. Analys och Linjär Algebra, del B, K1/Kf1/Bt1. CTH/GU STUDIO 1 TMV036b /2013 Matematiska vetenskaper
 CTH/GU STUDIO 1 TMV06b - 2012/201 Matematiska vetenskaper Linjär algebra Analys och Linjär Algebra, del B, K1/Kf1/Bt1 1 Inledning Vi fortsätter även denna läsperiod att arbete med Matlab i matematikkurserna
CTH/GU STUDIO 1 TMV06b - 2012/201 Matematiska vetenskaper Linjär algebra Analys och Linjär Algebra, del B, K1/Kf1/Bt1 1 Inledning Vi fortsätter även denna läsperiod att arbete med Matlab i matematikkurserna
Inför tentamen i Linjär algebra TNA002.
 Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Uppsala Universitet Matematiska Institutionen Bo Styf. Svar till tentan. Del A. Prov i matematik Linj. alg. o geom
 Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
SF1624 Algebra och geometri
 SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
Introduktion till MATLAB
 29 augusti 2017 Introduktion till MATLAB 1 Inledning MATLAB är ett interaktivt program för numeriska beräkningar med matriser. Med enkla kommandon kan man till exempel utföra matrismultiplikation, beräkna
29 augusti 2017 Introduktion till MATLAB 1 Inledning MATLAB är ett interaktivt program för numeriska beräkningar med matriser. Med enkla kommandon kan man till exempel utföra matrismultiplikation, beräkna
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem.
 Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
MVE520 Linjär algebra LMA515 Matematik, del C
 MATEMATIK Chalmers tekniska högskola Tentamen MVE52 Linjär algebra LMA55 Matematik, del C Hjälpmedel: inga Datum: 28-8-29 kl 8 2 Telefonvakt: Sebastian Jobjörnsson ankn 6457 Examinator: Håkon Hoel Tentan
MATEMATIK Chalmers tekniska högskola Tentamen MVE52 Linjär algebra LMA55 Matematik, del C Hjälpmedel: inga Datum: 28-8-29 kl 8 2 Telefonvakt: Sebastian Jobjörnsson ankn 6457 Examinator: Håkon Hoel Tentan
(a) Bestäm för vilka värden på den reella konstanten c som ekvationssystemet är lösbart. (b) Lös ekvationssystemet för dessa värden på c.
 UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
Linjära ekvationssystem i Matlab
 CTH/GU LABORATION 2 MVE11-212/213 Matematiska vetenskaper Linjära ekvationssystem i Matlab 1 Inledning Först skall vi se lite på matriser, vilket är den grundläggande datatypen i Matlab, sedan skall vi
CTH/GU LABORATION 2 MVE11-212/213 Matematiska vetenskaper Linjära ekvationssystem i Matlab 1 Inledning Först skall vi se lite på matriser, vilket är den grundläggande datatypen i Matlab, sedan skall vi
Matriser och vektorer i Matlab
 CTH/GU LABORATION 2 TMV157-2014/2015 Matematiska vetenskaper Matriser och vektorer i Matlab 1 Inledning Först skall vi se lite på matriser, vilket är den grundläggande datatypen i Matlab, sedan skall vi
CTH/GU LABORATION 2 TMV157-2014/2015 Matematiska vetenskaper Matriser och vektorer i Matlab 1 Inledning Först skall vi se lite på matriser, vilket är den grundläggande datatypen i Matlab, sedan skall vi
En vektor är mängden av alla sträckor med samma längd och riktning.
 En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition. Räkning med vektorer. Bas och koordinater. En vektor är mängden av alla sträckor med samma längd och riktning.
 Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Linjär Algebra M/TD Läsvecka 1
 Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Innehåll. Vad är MATLAB? Grunderna i MATLAB. Informationsteknologi. Informationsteknologi.
 Grunderna i MATLAB eva@it.uu.se Innehåll Vad är MATLAB? Användningsområden MATLAB-miljön Variabler i MATLAB Funktioner i MATLAB Eempel och smakprov: Grafik Beräkningar Bilder GUI Vad är MATLAB? Utvecklat
Grunderna i MATLAB eva@it.uu.se Innehåll Vad är MATLAB? Användningsområden MATLAB-miljön Variabler i MATLAB Funktioner i MATLAB Eempel och smakprov: Grafik Beräkningar Bilder GUI Vad är MATLAB? Utvecklat
Algebraiska egenskaper hos R n i)u + v = v + U
 Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Beräkningsverktyg HT07
 Beräkningsverktyg HT07 Föreläsning 1, Kapitel 1 6 1.Introduktion till MATLAB 2.Tal och matematiska funktioner 3.Datatyper och variabler 4.Vektorer och matriser 5.Grafik och plottar 6.Programmering Introduktion
Beräkningsverktyg HT07 Föreläsning 1, Kapitel 1 6 1.Introduktion till MATLAB 2.Tal och matematiska funktioner 3.Datatyper och variabler 4.Vektorer och matriser 5.Grafik och plottar 6.Programmering Introduktion
Linjär algebra med MATLAB
 INGENJÖRSHÖGSKOLAN Matematik Fredrik Abrahamsson, Anders Andersson Innehåll Linjär algebra med MATLAB 1 Grundläggande begrepp 1 1.1 Introduktion...................................... 1 1.2 Genomförande
INGENJÖRSHÖGSKOLAN Matematik Fredrik Abrahamsson, Anders Andersson Innehåll Linjär algebra med MATLAB 1 Grundläggande begrepp 1 1.1 Introduktion...................................... 1 1.2 Genomförande
Eftersom ON-koordinatsystem förutsätts så ges vektorernas volymprodukt av:
 MATA15 Algebra, delprov, 6 hp Lördagen den 8:e december 01 Skrivtid: 800 100 Matematikcentrum Matematik NF Lösningsförslag 1 Ligger punkterna P 1 = (0, 1, 1), P = (1,, 0), P = (, 1, 1) och P 4 = (, 6,
MATA15 Algebra, delprov, 6 hp Lördagen den 8:e december 01 Skrivtid: 800 100 Matematikcentrum Matematik NF Lösningsförslag 1 Ligger punkterna P 1 = (0, 1, 1), P = (1,, 0), P = (, 1, 1) och P 4 = (, 6,
4x az = 0 2ax + y = 0 ax + y + z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
Minsta kvadratmetoden
 Minsta kvadratmetoden där Överbestämda ekvationssystem Det är lämpligt att uppfatta matrisen A som bestående av n kolonnvektorer: A a a a n a a a n a n a n a nn a j a j a nj a a a n j n Då kan vi skriva
Minsta kvadratmetoden där Överbestämda ekvationssystem Det är lämpligt att uppfatta matrisen A som bestående av n kolonnvektorer: A a a a n a a a n a n a n a nn a j a j a nj a a a n j n Då kan vi skriva
Linjär Algebra F14 Determinanter
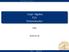 Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
November 17, 2015 (1) en enda lsg. Obs det A = 1 0. (2) k-parameter lsg. Obs det A = 0. k-kolonner efter sista ledande ettan
 Fö 9: November 7, 5 Determinanter och ekvationssystem Betrakta ett linjärt ekvssystem A X = B, där A är en kvadratisk n n)-matris och X, B n )-matriser. Låt C = [A B] utökad matris ). Gausselimination
Fö 9: November 7, 5 Determinanter och ekvationssystem Betrakta ett linjärt ekvssystem A X = B, där A är en kvadratisk n n)-matris och X, B n )-matriser. Låt C = [A B] utökad matris ). Gausselimination
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
linjära ekvationssystem.
 CTH/GU LABORATION 2 TMV216/MMGD20-2017/2018 Matematiska vetenskaper 1 Inledning Linjära ekvationssystem Denna laboration börjar med att vi påminner oss om matriser i Matlab samtidigt som vi börjar se på
CTH/GU LABORATION 2 TMV216/MMGD20-2017/2018 Matematiska vetenskaper 1 Inledning Linjära ekvationssystem Denna laboration börjar med att vi påminner oss om matriser i Matlab samtidigt som vi börjar se på
TANA17 Matematiska beräkningar med MATLAB för M, DPU. Fredrik Berntsson, Linköpings Universitet. 27 oktober 2015 Sida 1 / 31
 TANA17 Matematiska beräkningar med MATLAB för M, DPU Fredrik Berntsson, Linköpings Universitet 27 oktober 2015 Sida 1 / 31 TANA17 Kursmål och Innehåll Målet med kursen är att Ge grundläggande färdighet
TANA17 Matematiska beräkningar med MATLAB för M, DPU Fredrik Berntsson, Linköpings Universitet 27 oktober 2015 Sida 1 / 31 TANA17 Kursmål och Innehåll Målet med kursen är att Ge grundläggande färdighet
Matlabföreläsningen. Lite mer och lite mindre!
 Inmatning: Här är lite exempel på inmatning i Matlab: >> pi 3.1416 >> format long >> ans 3.141592653589793 Matlabföreläsningen Lite mer och lite mindre! >> format %återställer format (%- tecknet gör att
Inmatning: Här är lite exempel på inmatning i Matlab: >> pi 3.1416 >> format long >> ans 3.141592653589793 Matlabföreläsningen Lite mer och lite mindre! >> format %återställer format (%- tecknet gör att
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
TENTAMEN. Matematik 1 Kurskod HF1903 Skrivtid 13:15-17:15 Onsdagen 25 september 2013 Tentamen består av 3 sidor
 TENTAMEN Matematik Kurskod HF903 Skrivtid 3:5-7:5 Onsdagen 5 september 03 Tentamen består av 3 sidor Hjälpmedel: Utdelat formelblad. Räknedosa ej tillåten. Tentamen består av 3 uppgifter som totalt kan
TENTAMEN Matematik Kurskod HF903 Skrivtid 3:5-7:5 Onsdagen 5 september 03 Tentamen består av 3 sidor Hjälpmedel: Utdelat formelblad. Räknedosa ej tillåten. Tentamen består av 3 uppgifter som totalt kan
M = c c M = 1 3 1
 N-institutionen Mikael Forsberg Prov i matematik Matematik med datalogi, mfl. Linjär algebra ma4a Deadline :: 8 9 4 Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på ny
N-institutionen Mikael Forsberg Prov i matematik Matematik med datalogi, mfl. Linjär algebra ma4a Deadline :: 8 9 4 Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på ny
x 1 x 2 x 3 x 4 mera allmänt, om A är en (m n)-matris, då ger matrismultiplikationen en avbildning T A : R n R m.
 Fredagen 006 Avbildningar Låt A vara matrisen () = 0 0 Till varje vektor X i R får vi vid matrismultiplikationen AX en vektor i R Mera explicit, om X = x x x x är en given punkt i R, då får vi punkten
Fredagen 006 Avbildningar Låt A vara matrisen () = 0 0 Till varje vektor X i R får vi vid matrismultiplikationen AX en vektor i R Mera explicit, om X = x x x x är en given punkt i R, då får vi punkten
= ( 1) ( 1) = 4 0.
 MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
Uppgift 1 - programmet, Uppg6.m, visade jag på föreläsning 1. Luftmotståndet på ett objekt som färdas genom luft ges av formeln
 Matlab-föreläsning (4), 10 september, 015 Innehåll m-filer (script) - fortsättning från föreläsning 1 In- och utmatning Sekvenser, vektorer och matriser Upprepning med for-slingor (inledning) Matlab-script
Matlab-föreläsning (4), 10 september, 015 Innehåll m-filer (script) - fortsättning från föreläsning 1 In- och utmatning Sekvenser, vektorer och matriser Upprepning med for-slingor (inledning) Matlab-script
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
2x + y + 3z = 4 x + y = 1 x 2y z = 3
 ATM-Matematik Pär Hemström 7 6572 Sören Hector 7 4686 Mikael Forsberg 74 42 För studerande i linjär algebra Linjär algebra ma4a 225 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga
ATM-Matematik Pär Hemström 7 6572 Sören Hector 7 4686 Mikael Forsberg 74 42 För studerande i linjär algebra Linjär algebra ma4a 225 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga
x + y z = 2 2x + 3y + z = 9 x + 3y + 5z = Gauss-Jordan elemination ger: Area = 1 2 AB AC = 4. Span(1, 1 + x, x + x 2 ) = P 2.
 1 Matematiska Institutionen KTH Exam for the course Linjär algebra, 5B1307, Januari 14, 008, 14:00-19:00 Kursexaminator: Sandra Di Rocco Minst 15 poäng ger betyg 3, minst poäng ger betyg 4 och mins 8 poäng
1 Matematiska Institutionen KTH Exam for the course Linjär algebra, 5B1307, Januari 14, 008, 14:00-19:00 Kursexaminator: Sandra Di Rocco Minst 15 poäng ger betyg 3, minst poäng ger betyg 4 och mins 8 poäng
MMA132: Laboration 2 Matriser i MATLAB
 MMA132: Laboration 2 Matriser i MATLAB Introduktion I den här labben skall vi lära oss hur man använder matriser och vektorer i MATLAB. Det är rekommerad att du ser till att ha laborationshandledningen
MMA132: Laboration 2 Matriser i MATLAB Introduktion I den här labben skall vi lära oss hur man använder matriser och vektorer i MATLAB. Det är rekommerad att du ser till att ha laborationshandledningen
TMV166 Linjär Algebra för M. Tentamen
 MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 8 kl 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Olof Giselsson, ankn
MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 8 kl 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Olof Giselsson, ankn
Tentamen i Beräkningsvetenskap I och KF, 5.0 hp,
 Uppsala universitet Institutionen för informationsteknologi Avdelningen för beräkningsvetenskap Tentamen i Beräkningsvetenskap I och KF, 5.0 hp, 2015-12-17 Skrivtid: 14 00 17 00 (OBS! Tre timmars skrivtid!)
Uppsala universitet Institutionen för informationsteknologi Avdelningen för beräkningsvetenskap Tentamen i Beräkningsvetenskap I och KF, 5.0 hp, 2015-12-17 Skrivtid: 14 00 17 00 (OBS! Tre timmars skrivtid!)
SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 1 Måndagen den 29 november, 2010
 SF624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning Måndagen den 29 november, 200 UPPGIFT () Betrakta det linjära ekvationssystemet x + x 2 + x 3 = 7, x x 3 + x 4
SF624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning Måndagen den 29 november, 200 UPPGIFT () Betrakta det linjära ekvationssystemet x + x 2 + x 3 = 7, x x 3 + x 4
1.1 MATLABs kommandon för matriser
 MATLABs kommandon för matriser Det finns en mängd kommandon för att hantera vektorer, matriser och linjära ekvationssystem Vi ger här en kort sammanfattning av dessa kommandon För en mera detaljerad diskussion
MATLABs kommandon för matriser Det finns en mängd kommandon för att hantera vektorer, matriser och linjära ekvationssystem Vi ger här en kort sammanfattning av dessa kommandon För en mera detaljerad diskussion
1. (a) Bestäm alla värden på c som gör att matrisen A(c) saknar invers: 1 0 1. 1 c 1
 ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
Subtraktion. Räkneregler
 Matriser En matris är en rektangulär tabell av tal, 1 3 17 4 3 2 14 4 0 6 100 2 Om matrisen har m rader och n kolumner så säger vi att matrisen har storlek m n Index Vi indexerar elementen i matrisen genom
Matriser En matris är en rektangulär tabell av tal, 1 3 17 4 3 2 14 4 0 6 100 2 Om matrisen har m rader och n kolumner så säger vi att matrisen har storlek m n Index Vi indexerar elementen i matrisen genom
TAIU07 Matematiska beräkningar med MATLAB för MI. Fredrik Berntsson, Linköpings Universitet. 15 januari 2016 Sida 1 / 26
 TAIU07 Matematiska beräkningar med MATLAB för MI Fredrik Berntsson, Linköpings Universitet 15 januari 2016 Sida 1 / 26 TAIU07 Kursmål och Innehåll Målet med kursen är att Ge grundläggande färdighet i att
TAIU07 Matematiska beräkningar med MATLAB för MI Fredrik Berntsson, Linköpings Universitet 15 januari 2016 Sida 1 / 26 TAIU07 Kursmål och Innehåll Målet med kursen är att Ge grundläggande färdighet i att
Beräkningsvetenskap föreläsning 2
 Beräkningsvetenskap föreläsning 2 19/01 2010 - Per Wahlund if-satser if x > 0 y = 2 + log(x); else y = -1 If-satsen skall alltid ha ett villkor, samt en då det som skall hända är skrivet. Mellan dessa
Beräkningsvetenskap föreläsning 2 19/01 2010 - Per Wahlund if-satser if x > 0 y = 2 + log(x); else y = -1 If-satsen skall alltid ha ett villkor, samt en då det som skall hända är skrivet. Mellan dessa
Matriser. En m n-matris A har följande form. Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. 0 1, 0 0. Exempel 1
 Matriser En m n-matris A har följande form a 11... a 1n A =.., a ij R. a m1... a mn Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. Exempel 1 1 0 0 1, 0 0 ( 1 3 ) 2, ( 7 1 2 3 2, 1 3, 2 1
Matriser En m n-matris A har följande form a 11... a 1n A =.., a ij R. a m1... a mn Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. Exempel 1 1 0 0 1, 0 0 ( 1 3 ) 2, ( 7 1 2 3 2, 1 3, 2 1
MYSTERIER SOM ÅTERSTÅR
 Matematiska institutionen Stockholms universitet C.G. Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 6 MYSTERIER SOM ÅTERSTÅR Mysteriet med matrisinversen. Det
Matematiska institutionen Stockholms universitet C.G. Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 6 MYSTERIER SOM ÅTERSTÅR Mysteriet med matrisinversen. Det
KPP053, HT2016 MATLAB, Föreläsning 1. Introduktion till MATLAB Skript Inläsning och utskrift av variabler Ekvationssystem Anonyma funktioner
 KPP053, HT2016 MATLAB, Föreläsning 1 Introduktion till MATLAB Skript Inläsning och utskrift av variabler Ekvationssystem Anonyma funktioner MATLAB Väletablerat Mycket omfattande program GNU OCTAVE Öppen
KPP053, HT2016 MATLAB, Föreläsning 1 Introduktion till MATLAB Skript Inläsning och utskrift av variabler Ekvationssystem Anonyma funktioner MATLAB Väletablerat Mycket omfattande program GNU OCTAVE Öppen
KPP053, HT2015 MATLAB, Föreläsning 1. Introduktion till MATLAB Skript Inläsning och utskrift av variabler Ekvationssystem Anonyma funktioner
 KPP053, HT2015 MATLAB, Föreläsning 1 Introduktion till MATLAB Skript Inläsning och utskrift av variabler Ekvationssystem Anonyma funktioner MATLAB Väletablerat Mycket omfattande program GNU OCTAVE Öppen
KPP053, HT2015 MATLAB, Föreläsning 1 Introduktion till MATLAB Skript Inläsning och utskrift av variabler Ekvationssystem Anonyma funktioner MATLAB Väletablerat Mycket omfattande program GNU OCTAVE Öppen
LÖSNINGAR TILL LINJÄR ALGEBRA kl 8 13 LUNDS TEKNISKA HÖGSKOLA MATEMATIK. 1. Volymen med tecken ges av determinanten.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
Extramaterial till Matematik Y
 LIBER PROGRAMMERING OCH DIGITAL KOMPETENS Extramaterial till Matematik Y NIVÅ TVÅ Taluppfattning och tals användning ELEV Det finns många olika programmeringsspråk. I den här uppgiften ska du få bekanta
LIBER PROGRAMMERING OCH DIGITAL KOMPETENS Extramaterial till Matematik Y NIVÅ TVÅ Taluppfattning och tals användning ELEV Det finns många olika programmeringsspråk. I den här uppgiften ska du få bekanta
TMV142/186 Linjär algebra Z/TD
 MATEMATIK Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Chalmers tekniska högskola Datum: 2018-08-27 kl 1400 1800 Tentamen Telefonvakt: Anders Hildeman ank 5325 TMV142/186 Linjär algebra Z/TD Skriv
MATEMATIK Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Chalmers tekniska högskola Datum: 2018-08-27 kl 1400 1800 Tentamen Telefonvakt: Anders Hildeman ank 5325 TMV142/186 Linjär algebra Z/TD Skriv
Stöd inför omtentamen i Linjär algebra TNA002.
 LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna 1-4.
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna -. Föreläsningarna, 6/9 /9 : I sammanfattningen kommer en del av det vi tagit
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna -. Föreläsningarna, 6/9 /9 : I sammanfattningen kommer en del av det vi tagit
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng. Använd bifogat formulär för dessa 6 frågor.
 TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
5 Linjär algebra. 5.1 Addition av matriser 5 LINJÄR ALGEBRA
 5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
Betygsgränser: För betyg. Vem som har. Hjälpmedel: av papperet. Uppgift. 1. (4p) 0. (2p) 3 (2p) Uppgift. 2. (4p) B-2C om. vektor A (1p) b) Bestäm k så
 Kurs: HF90 Matematik, Moment TEN (Linjär Algebra) ) Datum: 4 augusti 08 Skrivtid 08:00 :000 Examinator: Armin Halilovic För godkänt betyg krävss 0 av maxx 4 poäng. Betygsgränser: För betyg A, B, C, D,
Kurs: HF90 Matematik, Moment TEN (Linjär Algebra) ) Datum: 4 augusti 08 Skrivtid 08:00 :000 Examinator: Armin Halilovic För godkänt betyg krävss 0 av maxx 4 poäng. Betygsgränser: För betyg A, B, C, D,
TMV166 Linjär Algebra för M. Tentamen
 MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 3 6 kl. 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Tony Stillfjord,
MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 3 6 kl. 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Tony Stillfjord,
Pre-Test 1: M0030M - Linear Algebra.
 Pre-Test : M3M - Linear Algebra. Test your knowledge on Linear Algebra for the course M3M by solving the problems in this test. It should not take you longer than 9 minutes. M3M Problem : Betrakta fyra
Pre-Test : M3M - Linear Algebra. Test your knowledge on Linear Algebra for the course M3M by solving the problems in this test. It should not take you longer than 9 minutes. M3M Problem : Betrakta fyra
P Q = ( 2, 1, 1), P R = (0, 1, 0) och QR = (2, 2, 1). arean = 1 2 P Q P R
 1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET MED MATRISINVERSER = = =
 Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
STOCKHOLMS UNIVERSITET VT 2011 Avd. Matematisk statistik GB DATORLABORATION 1: TIDSSERIER.
 MATEMATISKA INSTITUTIONEN Tillämpad statistisk analys, GN STOCKHOLMS UNIVERSITET VT 2011 Avd. Matematisk statistik GB 2011-03-24 DATORLABORATION 1: TIDSSERIER. I Tarfala har man under en lång följd av
MATEMATISKA INSTITUTIONEN Tillämpad statistisk analys, GN STOCKHOLMS UNIVERSITET VT 2011 Avd. Matematisk statistik GB 2011-03-24 DATORLABORATION 1: TIDSSERIER. I Tarfala har man under en lång följd av
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Föreläsning 2 David Rydh Institutionen för matematik KTH 28 augusti 2018 Detta gjorde vi igår Punkter Vektorer och skalärer, multiplikation med skalär Linjärkombinationer, spannet
SF1624 Algebra och geometri Föreläsning 2 David Rydh Institutionen för matematik KTH 28 augusti 2018 Detta gjorde vi igår Punkter Vektorer och skalärer, multiplikation med skalär Linjärkombinationer, spannet
NUMPROG, 2D1212, vt Föreläsning 1, Numme-delen. Linjära ekvationssystem Interpolation, Minstakvadratmetoden
 NUMPROG, D, vt 006 Föreläsning, Numme-delen Linjära ekvationssystem Interpolation, Minstakvadratmetoden En av de vanligaste numeriska beräkningar som görs i ingenjörsmässiga tillämpningar är att lösa ett
NUMPROG, D, vt 006 Föreläsning, Numme-delen Linjära ekvationssystem Interpolation, Minstakvadratmetoden En av de vanligaste numeriska beräkningar som görs i ingenjörsmässiga tillämpningar är att lösa ett
Läsanvisningar och övningsuppgifter i MAA150, period vt Erik Darpö
 Läsanvisningar och övningsuppgifter i MAA150, period vt1 2015 Erik Darpö ii 0. Förberedelser Nedanstående uppgifter är avsedda att användas som ett självdiagnostiskt test. Om du har problem med att lösa
Läsanvisningar och övningsuppgifter i MAA150, period vt1 2015 Erik Darpö ii 0. Förberedelser Nedanstående uppgifter är avsedda att användas som ett självdiagnostiskt test. Om du har problem med att lösa
ax + y + 4z = a x + y + (a 1)z = 1. 2x + 2y + az = 2 Ange dessutom samtliga lösningar då det finns oändligt många.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas

