1 Diagonalisering av matriser
|
|
|
- Per-Olof Jonasson
- för 6 år sedan
- Visningar:
Transkript
1 1 Diagonalisering av matriser Kan alla matriser diagonaliseras? Nej, det kan de inte. Exempel: ẋ 1 = x 1 + 2x 2, Integrerande faktor: e t x 2 = x 2 x 2 (t) = c 2 e t och ẋ 1 x 1 = 2c 2 e t. e t x 1 e t x 1 = d dt (e t x 1 ) = 2c 2 x 1 (t) = (c 1 + 2c 2 t)e t. Vi försöker lösa ekvationssystemet på samma sätt som i kapitel 3, genom att diagonalisera A. A = 1 2 har endast ett egenvärde λ = 1 och egenvektorer x = s 1, s 0 0. Matrisen gick inte att diagonalisera, men ekvationssystemet har ändå en lösning. Vi måste alltså lära oss att hantera icke diagonaliserbara matriser. ẋ = Ax x(t) = e At x löser differentialekvationen x(0) = x = 0 Detta bevisas med oändliga summor i kapitel 5. (At) n n=0 n! 1
2 Sats Diagonaliserbar matris A är av typenn n alla egenvärden till A är olika A är diagonaliserbar (1) Bevis (för n=3): Vi ska visa att A har tre linjärt oberoende egenvektorer. Till varje egenvärde kan man välja en egenvektor, så låt oss bilda Q = a 1 S 1 + a 2 S 2 + a 3 S 3, en linjärkombination av dessa som är lika med nollvektorn 0. Vi skall visa att detta bara inträffar om koefficienterna a 1, a 2, a 3 alla är lika med noll. Q = 0 (λ 1 I A)(λ 2 I A)Q = 0 a 3 (λ 1 λ 3 )(λ 2 λ 3 )S 3 = 0 Detta kräver att a 3 = 0. På motsvarande sätt bevisas att även a 1, a 2 är noll. 2
3 Det som alla studenter i världshistoriens historia har haft stora problem med är omvändningen av sats 3.9. Vad händer om jag misslyckas med att hitta n-st olika egenvärden? Svar: Vi vet inte. 1. Matrisen kan vara diagonaliserbar ändå, ex. identitetsmatrisen har 1 egenvärde men n-st egenvektorer. 2. Behöver inte vara diagonaliserbar, ex. 1 1 Kom ihåg: Olika egenvärden diagonaliserbar. Multipla egenvärden inget kan fastställas. < n st egenvektorer ej diagonaliserbar. Vissa matriser som till exempel 1 0 kan diagonaliseras medan andra som 1 2 inte kan det, men de har ändå samma egenvärde och karakteristiska polynom! Exempel Lös ekvationen: ẋ = 2 1 x 1 2 Lösning: det(λi A) = (λ 2) λ 1,2 = 2 ± i. λ 1,2 är inte reell, skillnad? Ingen. Fortsätt som vanligt. 3
4 Eftersom matrisen är på formen 2 2 och vi har två olika egenvärden så är den diagonaliserbar med egenvektorer S 1 = 1 c, c 0 i Notera att AS 1 = λ 1 S 1 = AS 1 = λ 2 S 1 Det vill säga att: S 2 = S 1 = 1 i Därmed är x(t) = c 1 e (2+i)t S 1 + c 2 e (2 i)t S 2. För alla egenvektorer (speciellt komplexa) så gäller att om S 1 är en egenvektor så är S 2 = S 1 Komponentvis fås: x 1 (t) = e 2t (C cos t + D sin t) och x 2 (t) = e 2t (D cos t C sin t) 2 Olika användbara matrisegenskaper Sats 3.12 B = S 1 AS p B (λ) = p A (λ). 4
5 Bevis: p B (λ) = det(λi B) = = det(λi S 1 AS) = = det(λs 1 S S 1 AS) = = det(s 1 (λi A)S) = = det(s 1 det(λi A) det(s) = = p A (λ). Följdsatser: n det(a) = λ i (2) i=1 n tr(a) = λ i (3) i=1 5
6 Övning 3.6: Az = λz z är egenvektor av (ai + ba), vad är egenvärden? (ai + ba)z = aiz + baz = (a + bλ)z. Övning 3.7 a) Az = λz A 2 z = λ 2 z Bevis: A 2 z = A(Az) = A(λz) = λaz = λ 2 z Men detta fungerar inte åt andra hållet om A är en elak matris. Övning 3.7 b) 1 1 A = 2, A2 = S 1 = (1, 0, 0) A 2 har egenvärden 0, 1 och egenvärden: 1 S 2 = (1, 1, 0), S 3 = ( 1, 0, 1) 0 S 1 = (1, 0, 0) A har egenvärden 0, 1, 1 och egenvärden: 1 S 2 = (1, 1, 0) 1 S 3 = (0, 1, 1) Övning Vi har en matris A sådan att A. = n. A har (n 1) linjärt oberoende 1 1 egenvektorer med egenvärde noll. Låt y vara en vektor sådan att: y z = 0 Det vill säga y 1 + y y n = 0 6
7 Jag har (n 1) vektorer av den typ som uppfyller detta. Jag vet inte vad Ay är, men jag vet att: Ay = c 1 X 1 + c 2 X c n z (Ay)z = yc n Här tappade han bort sig och bestämde han sig för att A är symmetrisk. 7
Egenvärden och egenvektorer. Linjär Algebra F15. Pelle
 Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Lösningar till utvalda uppgifter i kapitel 8
 Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Repetera hur man nner bas för rum som spänns upp av några vektorer Reptetera hur man nner bas för summa och snitt av delrum. Reptetera
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Repetera hur man nner bas för rum som spänns upp av några vektorer Reptetera hur man nner bas för summa och snitt av delrum. Reptetera
Föreläsning 8. Reglerteknik AK. c Bo Wahlberg. 27 september Avdelningen för reglerteknik Skolan för elektro- och systemteknik
 Föreläsning 8 Reglerteknik AK c Bo Wahlberg Avdelningen för reglerteknik Skolan för elektro- och systemteknik 27 september 2013 Introduktion Förra gången: Tillståndsmodell: ẋ(t) = Ax(t) + Bu(t), x(0) =
Föreläsning 8 Reglerteknik AK c Bo Wahlberg Avdelningen för reglerteknik Skolan för elektro- och systemteknik 27 september 2013 Introduktion Förra gången: Tillståndsmodell: ẋ(t) = Ax(t) + Bu(t), x(0) =
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
Multiplicera 7med A λ 1 I från vänster: c 1 (Av 1 λ 1 v 1 )+c 2 (Av 2 λ 1 v 2 )+c 3 (Av 3 λ 1 v 3 ) = 0
 Diagonalisering Anm. Begreppet diagonaliserbarhet är relevant endast för linjära avbildningar mellan rum av samma dimension, d.v.s. sådana som representeras av kvadratiska matriser. När vi i fortsättningen
Diagonalisering Anm. Begreppet diagonaliserbarhet är relevant endast för linjära avbildningar mellan rum av samma dimension, d.v.s. sådana som representeras av kvadratiska matriser. När vi i fortsättningen
Dagens teman. Linjära ODE-system av ordning 1:
 Dagens teman Linjära ODE-system av ordning 1: Egenvärdesmetoden. Lösning av homogena system x 1 (t) = a 11 x 1 (t) + + a 1n x n (t) x 2 (t) = a 21 x 1 (t) + + a 2n x n (t) x n (t) = a n1 x 1 (t) + + a
Dagens teman Linjära ODE-system av ordning 1: Egenvärdesmetoden. Lösning av homogena system x 1 (t) = a 11 x 1 (t) + + a 1n x n (t) x 2 (t) = a 21 x 1 (t) + + a 2n x n (t) x n (t) = a n1 x 1 (t) + + a
LÖSNINGAR LINJÄR ALGEBRA LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
1 Repetition - Övning 3.8
 Repetition - Övning 38 Spåret av en matris definieras som: T r(a) = n i= a ii = n i= y z = y + y 2 + + y n = A y = Vi vill definiera när ett system kan ta emot input och leverera output utan att systemet
Repetition - Övning 38 Spåret av en matris definieras som: T r(a) = n i= a ii = n i= y z = y + y 2 + + y n = A y = Vi vill definiera när ett system kan ta emot input och leverera output utan att systemet
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
Egenvärden, egenvektorer
 Egenvärden, egenvektorer Om en matris är kvadratisk (dvs n n) kan vi beräkna egenvärden och egenvektorer till matrisen. Polynomet p(λ) = det(a λi) kallas det karakterisktiska polynomet för A. Ett nollställe
Egenvärden, egenvektorer Om en matris är kvadratisk (dvs n n) kan vi beräkna egenvärden och egenvektorer till matrisen. Polynomet p(λ) = det(a λi) kallas det karakterisktiska polynomet för A. Ett nollställe
Linjär algebra Föreläsning 10
 Linjär algebra Föreläsning 10 IT-programmet, Chalmers 2006 Samuel Bengmark Repetition Handlade om kvadratiska matriser. Kvadratiska ekvationssystem har: Unik lösning omm Det(A) 0. Har oändligt antal lösningar
Linjär algebra Föreläsning 10 IT-programmet, Chalmers 2006 Samuel Bengmark Repetition Handlade om kvadratiska matriser. Kvadratiska ekvationssystem har: Unik lösning omm Det(A) 0. Har oändligt antal lösningar
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner. 2? Det är komplicerat att
 Egensystem Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner Potens av matris 2 6 Ex Givet matrisen A =, vad är A 2? Det är komplicerat att beräkna högre
Egensystem Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner Potens av matris 2 6 Ex Givet matrisen A =, vad är A 2? Det är komplicerat att beräkna högre
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
LÖSNINGAR TILL LINJÄR ALGEBRA kl 8 13 LUNDS TEKNISKA HÖGSKOLA MATEMATIK. 1. Volymen med tecken ges av determinanten.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
DIAGONALISERING AV EN MATRIS
 DIAGONALISERING AV EN MATRIS Definition ( Diagonaliserbar matris ) Låt A vara en kvadratisk matris dvs en matris av typ n n. Matrisen A är diagonaliserbar om det finns en inverterbar matris P och en diagonalmatris
DIAGONALISERING AV EN MATRIS Definition ( Diagonaliserbar matris ) Låt A vara en kvadratisk matris dvs en matris av typ n n. Matrisen A är diagonaliserbar om det finns en inverterbar matris P och en diagonalmatris
SF1624 Algebra och geometri Lösningsförsag till modelltentamen
 SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
November 24, Egenvärde och egenvektor. (en likformig expansion med faktor 2) (en rotation 30 grader moturs)
 Fö : November 4, 7 Egenvärde och egenvektor Definition s 9: Låt A resp T : R n R n vara en n n-matris resp en linjär avbildning En icke-trivial vektor v R n kallas en egenvektor till A resp till T med
Fö : November 4, 7 Egenvärde och egenvektor Definition s 9: Låt A resp T : R n R n vara en n n-matris resp en linjär avbildning En icke-trivial vektor v R n kallas en egenvektor till A resp till T med
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
x + y z = 2 2x + 3y + z = 9 x + 3y + 5z = Gauss-Jordan elemination ger: Area = 1 2 AB AC = 4. Span(1, 1 + x, x + x 2 ) = P 2.
 1 Matematiska Institutionen KTH Exam for the course Linjär algebra, 5B1307, Januari 14, 008, 14:00-19:00 Kursexaminator: Sandra Di Rocco Minst 15 poäng ger betyg 3, minst poäng ger betyg 4 och mins 8 poäng
1 Matematiska Institutionen KTH Exam for the course Linjär algebra, 5B1307, Januari 14, 008, 14:00-19:00 Kursexaminator: Sandra Di Rocco Minst 15 poäng ger betyg 3, minst poäng ger betyg 4 och mins 8 poäng
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Egenvärden och egenvektorer
 Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
A = v 2 B = = (λ 1) 2 16 = λ 2 2λ 15 = (λ 5)(λ+3). E 5 = Span C =
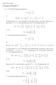 KTH Matematik Lösningar till Kapitel 7 A a Karakteristiska polynomet av detλi A det A λ λ λ b Egenvdena av A nollställen till karakteristiska polynomet alltså har A egenvdet λ c Motsvarande egenrum E lösningsrummet
KTH Matematik Lösningar till Kapitel 7 A a Karakteristiska polynomet av detλi A det A λ λ λ b Egenvdena av A nollställen till karakteristiska polynomet alltså har A egenvdet λ c Motsvarande egenrum E lösningsrummet
Diagonalisering och linjära system ODE med konstanta koe cienter.
 Diagonalisering och linjära system ODE med konstanta koe cienter. Variabelbyte i linjära system di erentialekvationer. Målet med det kapitlet i kursen är att lösa linjära system di erentialekvationer på
Diagonalisering och linjära system ODE med konstanta koe cienter. Variabelbyte i linjära system di erentialekvationer. Målet med det kapitlet i kursen är att lösa linjära system di erentialekvationer på
Chalmers tekniska högskola Datum: Våren MVE021 Linjär algebra I
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: Våren 6 Övningstentamen Telefonvakt: Thomas Bäckdahl ankn 8 MVE Linjär algebra I Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: Våren 6 Övningstentamen Telefonvakt: Thomas Bäckdahl ankn 8 MVE Linjär algebra I Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng.
 ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
Crash Course Algebra och geometri. Ambjörn Karlsson c januari 2016
 Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
19. Spektralsatsen Spektralsatsen SPEKTRALSATSEN
 9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)
![A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p) A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)](/thumbs/93/112249032.jpg) SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
Gripenberg. Mat Grundkurs i matematik 1 Tentamen och mellanförhörsomtagning,
 Mat-. Grundkurs i matematik Tentamen och mellanförhörsomtagning,..23 Skriv ditt namn, nummer och övriga uppgifter på varje papper! Räknare eller tabeller får inte användas i detta prov! Gripenberg. Skriv
Mat-. Grundkurs i matematik Tentamen och mellanförhörsomtagning,..23 Skriv ditt namn, nummer och övriga uppgifter på varje papper! Räknare eller tabeller får inte användas i detta prov! Gripenberg. Skriv
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
Lite Linjär Algebra 2017
 Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
Determinanter, egenvectorer, egenvärden.
 Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Inför tentamen i Linjär algebra TNA002.
 Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Lösningsforslag till tentamen i SF1624 den 22/ e x e y e z = 5e x 10e z = 5(1, 0, 2). 1 1 a a + 2 2a 4
 Institutionen för matematik, KTH Serguei Shimorin Lösningsforslag till tentamen i SF64 den /0 007 Eftersom planet går genom punkten (,, 0, det har ekvation a(x + b(y + + cz = 0, där a, b, c är koefficienter
Institutionen för matematik, KTH Serguei Shimorin Lösningsforslag till tentamen i SF64 den /0 007 Eftersom planet går genom punkten (,, 0, det har ekvation a(x + b(y + + cz = 0, där a, b, c är koefficienter
6.1 Skalärprodukt, norm och ortogonalitet. TMV141 Linjär algebra E VT 2011 Vecka 6. Lärmål 6.1. Skalärprodukt. Viktiga begrepp
 6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
Lösningar kommer att läggas ut på kurshemsidan första arbetsdagen efter tentamenstillfället. Resultat meddelas via epost från LADOK.
 Matematik Chalmers tekniska högskola 8-8-7 Tentamen Linjär algebra D (TMV6), Linjär algebra GU (MMGD) Telefonvakt: Carl Lundholm, ankn 679 Plats och tid: Johanneberg, 4:-8: Inga hjälpmedel. Kalkylator
Matematik Chalmers tekniska högskola 8-8-7 Tentamen Linjär algebra D (TMV6), Linjär algebra GU (MMGD) Telefonvakt: Carl Lundholm, ankn 679 Plats och tid: Johanneberg, 4:-8: Inga hjälpmedel. Kalkylator
Lösningar till MVE021 Linjär algebra för I
 Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
3 1 = t 2 2 = ( 1) ( 2) 1 2 = A(t) = t 1 10 t
 SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
x 2y + z = 1 (1) 2x + y 2z = 3 (2) x + 3y z = 4 (3)
 TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 74-4 kurser:: Linjär Algebra ma4a Matematik för ingenjörer maa 8 5 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta
TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 74-4 kurser:: Linjär Algebra ma4a Matematik för ingenjörer maa 8 5 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta
SF1624 Algebra och geometri Tentamen Torsdag, 9 juni 2016
 SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
Facit/lösningsförslag
 Facit/lösningsförslag 06-08- Låt l vara linjen med parameterform x, y, z 0 s, mellan planet x y z och planet z 0 och låt l vara skärningslinjen a) Skriv l på parameterform b) Beräkna avståndet mellan l
Facit/lösningsförslag 06-08- Låt l vara linjen med parameterform x, y, z 0 s, mellan planet x y z och planet z 0 och låt l vara skärningslinjen a) Skriv l på parameterform b) Beräkna avståndet mellan l
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng. Använd bifogat formulär för dessa 6 frågor.
 TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
0 Allmänt. Följande delar behöver man kunna utöver avsnitten som beskrivs senare i dokumentet.
 Linja r algebra TATA (del) Allmänt Följande delar behöver man kunna utöver avsnitten som beskrivs senare i dokumentet. Matrisekvationer och Gauss-elimination o Parameterform Allmänt om vektorer o Räknelagar
Linja r algebra TATA (del) Allmänt Följande delar behöver man kunna utöver avsnitten som beskrivs senare i dokumentet. Matrisekvationer och Gauss-elimination o Parameterform Allmänt om vektorer o Räknelagar
TMV142/186 Linjär algebra Z/TD
 MATEMATIK Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Chalmers tekniska högskola Datum: 2018-08-27 kl 1400 1800 Tentamen Telefonvakt: Anders Hildeman ank 5325 TMV142/186 Linjär algebra Z/TD Skriv
MATEMATIK Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Chalmers tekniska högskola Datum: 2018-08-27 kl 1400 1800 Tentamen Telefonvakt: Anders Hildeman ank 5325 TMV142/186 Linjär algebra Z/TD Skriv
Prov i matematik F2, X2, ES3, KandFys2, Lärare, Frist, W2, KandMat1, Q2 LINJÄR ALGEBRA II
 UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Bo Styf Prov i matematik F, X, ES, KandFys, Lärare, Frist, W, KandMat1, Q LINJÄR ALGEBRA II 010 08 4 Skrivtid: 1400 1900 Tillåtna hjälpmedel:
UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Bo Styf Prov i matematik F, X, ES, KandFys, Lärare, Frist, W, KandMat1, Q LINJÄR ALGEBRA II 010 08 4 Skrivtid: 1400 1900 Tillåtna hjälpmedel:
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
x 1(t) = x 2 (t) x 2(t) = x 1 (t)
 Differentialekvationer II Modellsvar till räkneövning 4 16.4. 218 (kl 12-14 B222) 1. Lös det linjära homogena DE-systemet x 1(t) = x 2 (t) x 2(t) = x 1 (t) med matrismetoden. Påminnelse: egenvärden och
Differentialekvationer II Modellsvar till räkneövning 4 16.4. 218 (kl 12-14 B222) 1. Lös det linjära homogena DE-systemet x 1(t) = x 2 (t) x 2(t) = x 1 (t) med matrismetoden. Påminnelse: egenvärden och
2s + 3t + 5u = 1 5s + 3t + 2u = 1 3s 3u = 1
 ATM-Matematik Mikael Forsberg 074-4 För studenter på distans och campus Linjär algebra ma04a 04 0 5 Skrivtid: 09:00-4:00. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja
ATM-Matematik Mikael Forsberg 074-4 För studenter på distans och campus Linjär algebra ma04a 04 0 5 Skrivtid: 09:00-4:00. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja
1. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x 1 = (2, 3, 5), x 2 = (3, 1, 1) och x 3 = (1, 3, 0).
 N-institutionen Mikael Forsberg 06-64 89 6 Prov i matematik Matematik med datalogi, mfl. Linjär algebra mk06a Testtenta. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x = (,, 5),
N-institutionen Mikael Forsberg 06-64 89 6 Prov i matematik Matematik med datalogi, mfl. Linjär algebra mk06a Testtenta. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x = (,, 5),
Lösningar till utvalda uppgifter i kapitel 1
 Lösningar till utvalda uppgifter i kapitel.3 Vi utnyttjar definitionen av skalärprodukt som ger att cos α = u v u v, där α är (minsta vinkeln mellan u och v. I vårt fall så får vi cos α = 7 4 4 =. Alltså
Lösningar till utvalda uppgifter i kapitel.3 Vi utnyttjar definitionen av skalärprodukt som ger att cos α = u v u v, där α är (minsta vinkeln mellan u och v. I vårt fall så får vi cos α = 7 4 4 =. Alltså
Stöd inför omtentamen i Linjär algebra TNA002.
 LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
Egenvektorer och egenvärden
 Egenvektorer och egenvärden Diagonalmatriser Tidigare (Sparr, kap.8) har vi bestämt avbildningsmatriser för givna linjära avbildningar. Ofta förekommer det omvända problemet (om än i diverse förklädnader):
Egenvektorer och egenvärden Diagonalmatriser Tidigare (Sparr, kap.8) har vi bestämt avbildningsmatriser för givna linjära avbildningar. Ofta förekommer det omvända problemet (om än i diverse förklädnader):
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
1. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x 1 = (2, 3, 5), x 2 = (3, 1, 1) och x 3 = (1, 3, 0).
 TM-Matematik Mikael Forsberg Linjär algebra mk4a Övningstenta LA-. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x = (,, ), x = (,, ) och x = (,, ).. För alla värden på parametern
TM-Matematik Mikael Forsberg Linjär algebra mk4a Övningstenta LA-. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x = (,, ), x = (,, ) och x = (,, ).. För alla värden på parametern
SF1624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 2010 DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
A = x
 Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Chalmers tekniska högskola Datum: kl Telefonvakt: Linnea Hietala MVE480 Linjär algebra S
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
SF1624 Algebra och geometri Tentamen Torsdag, 17 mars 2016
 SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
kvivalenta. Ange rangen för A samt en bas för kolonnrummet för A. och U =
 MATEMATIK Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola Datum: 9-- kl 8 Tentamen Telefonvakt: Aron Lagerberg tel 76-786 Linjär Algebra Z (tmv4) Skriv tentamenskod tydligt på samtliga
MATEMATIK Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola Datum: 9-- kl 8 Tentamen Telefonvakt: Aron Lagerberg tel 76-786 Linjär Algebra Z (tmv4) Skriv tentamenskod tydligt på samtliga
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
Exempelsamling :: Diagonalisering
 Exempelsamling :: Diagonalisering Mikael Forsberg :: 8 oktober Uppgifter om diagonalisering. Hitta en matris som diagonaliserar matrisen A = ( Vad blir diagonalmatrisen D? Vad betder D geometriskt? Vad
Exempelsamling :: Diagonalisering Mikael Forsberg :: 8 oktober Uppgifter om diagonalisering. Hitta en matris som diagonaliserar matrisen A = ( Vad blir diagonalmatrisen D? Vad betder D geometriskt? Vad
UPPSALA UNIVERSITET Matematiska institutionen Styf. Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 2004
 UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
2x + y + 3z = 1 x 2y z = 2 x + y + 2z = 1
 ATM-Matematik Sören Hector 7 46686 Mikael Forsberg 734 433 Matematik med datalogi, mfl. Linjär algebra ma4a 3 5 Skrivtid: :-5:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa.
ATM-Matematik Sören Hector 7 46686 Mikael Forsberg 734 433 Matematik med datalogi, mfl. Linjär algebra ma4a 3 5 Skrivtid: :-5:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa.
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Första föreläsningen Mats Boij Institutionen för matematik KTH 26 oktober, 2009 Översikt Kurspresentation Komplexa tal Kursmålen Efter genomgången kurs ska studenten vara förtrogen
SF1624 Algebra och geometri Första föreläsningen Mats Boij Institutionen för matematik KTH 26 oktober, 2009 Översikt Kurspresentation Komplexa tal Kursmålen Efter genomgången kurs ska studenten vara förtrogen
Veckans teman. Repetition av ordinära differentialekvationer ZC 1, 2.1-3, 4.1-6, 7.4-6, 8.1-3
 Veckans teman Repetition av ordinära differentialekvationer ZC 1, 2.1-3, 4.1-6, 7.4-6, 8.1-3 Ekvationstyper Första ordningen Separabla Högre ordning System Autonoma Linjära med konstanta koefficienter
Veckans teman Repetition av ordinära differentialekvationer ZC 1, 2.1-3, 4.1-6, 7.4-6, 8.1-3 Ekvationstyper Första ordningen Separabla Högre ordning System Autonoma Linjära med konstanta koefficienter
ax + y + 4z = a x + y + (a 1)z = 1. 2x + 2y + az = 2 Ange dessutom samtliga lösningar då det finns oändligt många.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
Norm och QR-faktorisering
 Norm och QR-faktorisering Skalärprodukten på C n (R n ) hänger ihop med några viktiga klasser av matriser. För en komplex matris A betecknar vi med A H det Hermitiska konjugatet till A, dvs A H = A T.
Norm och QR-faktorisering Skalärprodukten på C n (R n ) hänger ihop med några viktiga klasser av matriser. För en komplex matris A betecknar vi med A H det Hermitiska konjugatet till A, dvs A H = A T.
Del 1: Godkäntdelen. TMV142 Linjär algebra Z
 MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 130313 kl 0830 1230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV142 Linjär algebra Z Tentan
MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 130313 kl 0830 1230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV142 Linjär algebra Z Tentan
SF1624 Algebra och geometri Lösningsförslag till tentamen Tisdagen den 15 december, 2009 DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen Tisdagen den 15 december, 2009 DEL A 1 a Bestäm de komplexa koefficienterna a, b och c så att polynomet Pz z 3 + az 2 + bz + c har nollställena
SF1624 Algebra och geometri Lösningsförslag till tentamen Tisdagen den 15 december, 2009 DEL A 1 a Bestäm de komplexa koefficienterna a, b och c så att polynomet Pz z 3 + az 2 + bz + c har nollställena
Vi skall här studera första ordningens homogena system av linjära dierentialekvationer
 Kapitel System av ordinära dierentialekvationer Vi skall här studera första ordningens homogena system av linjära dierentialekvationer med konstanta koecienter. Huvudvikten läggs vid fallet att systemets
Kapitel System av ordinära dierentialekvationer Vi skall här studera första ordningens homogena system av linjära dierentialekvationer med konstanta koecienter. Huvudvikten läggs vid fallet att systemets
3x + y z = 0 4x + y 2z = 0 2x + y = Lös det överbestämda systemet nedan på bästa sätt i minsta kvadratmening. x = 1 x + y = 1 x + 2y = 2
 TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 734-433 kurser:: Linjär Algebra ma4a Matematik för ingenjörer ma3a 3 7 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och
TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 734-433 kurser:: Linjär Algebra ma4a Matematik för ingenjörer ma3a 3 7 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och
4x az = 0 2ax + y = 0 ax + y + z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
Tentamen i Linjär algebra (TATA31/TEN1) ,
 Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra TATA/TEN) 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra TATA/TEN) 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
1 dy. vilken kan skrivas (y + 3)(y 3) dx =1. Partialbråksuppdelning ger y y 3
 Lösningsförslag till tentamensskrivning i Differentialekvationer och transformer III, SF137 Tisdagen den 11 januari 211, kl 14-19 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant
Lösningsförslag till tentamensskrivning i Differentialekvationer och transformer III, SF137 Tisdagen den 11 januari 211, kl 14-19 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant
Uppgifter, 2015 Tillämpad linjär algebra
 Geometri. Uppgifter, 25 Tillämpad linjär algebra. Uppgift. Låt (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av linjära
Geometri. Uppgifter, 25 Tillämpad linjär algebra. Uppgift. Låt (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av linjära
12. SINGULÄRA VÄRDEN. (u Av) u v
 . SINGULÄRA VÄRDEN Vårt huvudresultat sen tidigare är Sats.. Varje n n matris A kan jordaniseras, dvs det finns en inverterbar matris S sån att S AS J där J är en jordanmatris. Om u och v är två kolonnvektorer
. SINGULÄRA VÄRDEN Vårt huvudresultat sen tidigare är Sats.. Varje n n matris A kan jordaniseras, dvs det finns en inverterbar matris S sån att S AS J där J är en jordanmatris. Om u och v är två kolonnvektorer
x (t) = 2 1 u = Beräkna riktnings derivatan av f i punkten a i riktningen u, dvs.
 MATEMATIK Chalmers tekniska högskola Tentamen -8-8, kl. 4.-8. TMV6 Analys och linjär algebra K Kf Bt, del C Telefonvakt: Adam Andersson, telefon: 7-884 Hjälpmedel: Inga, bara papper och penna. För full
MATEMATIK Chalmers tekniska högskola Tentamen -8-8, kl. 4.-8. TMV6 Analys och linjär algebra K Kf Bt, del C Telefonvakt: Adam Andersson, telefon: 7-884 Hjälpmedel: Inga, bara papper och penna. För full
ALA-c Innehåll. 1 Linearization and Stability Uppgift Uppgift Egenvärdesproblemet Uppgift
 Vecka ALA-c 6 Innehåll Linearization and Stability RÄKNEÖVNING VECKA. Uppgift 9........................................ Uppgift 9.5...................................... 5 Egenvärdesproblemet 9. Uppgift
Vecka ALA-c 6 Innehåll Linearization and Stability RÄKNEÖVNING VECKA. Uppgift 9........................................ Uppgift 9.5...................................... 5 Egenvärdesproblemet 9. Uppgift
SF1624 Algebra och geometri Bedömningskriterier till tentamen Tisdagen den 15 december, 2009
 SF1624 Algebra och geometri Bedömningskriterier till tentamen Tisdagen den 15 december, 2009 Allmänt gäller följande: Om lösningen helt saknar förklarande text till beräkningar och formler ges högst två
SF1624 Algebra och geometri Bedömningskriterier till tentamen Tisdagen den 15 december, 2009 Allmänt gäller följande: Om lösningen helt saknar förklarande text till beräkningar och formler ges högst två
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
