EXAMENSARBETE. Bergspänningsmätningar på litet djup
|
|
|
- Oliver Åström
- för 9 år sedan
- Visningar:
Transkript
1 EXAMENSARBETE 25:246 CIV Bergspänningsmätningar på litet djup Sofi Berg Luleå tekniska universitet Civilingenjörsprogrammet Väg- och vattenbyggnadsteknik Institutionen för Samhällsbyggnad Avdelningen för Bergmekanik 25:246 CIV - ISSN: ISRN: LTU-EX--5/246--SE
2 Förord Som en avslutande del i civilingenjörsutbildningen Väg- och vattenbyggnadsteknik vid Luleå tekniska universitet ingår att göra ett examensarbete omfattande 2 högskolepoäng. Denna rapport är resultatet av mitt examensarbete. Arbetet har utförts för att öka kunskaperna om ytliga bergspänningar och bergspänningsmätningar. Examensarbetet har genomförts på uppdrag av Banverket HK i Borlänge och har utförts under 24 och 25 på Avdelningen för bergmekanik vid Institutionen för Samhällsbyggnad. Jag vill härmed tacka Peter Lundmark, Banverket för att jag fick förtroendet att genomföra examensarbetet. Jag vill också tacka Jonny Sjöberg, SwedPower, som har handlett mig med stort engagemang och för all granskning av rapporten. Tack även till Professor Erling Nordlund som har varit examinator och tack alla ni andra på bergmekanikavdelningen för hjälp jag fått. Jag vill också tacka alla andra som på ett eller annat sätt har bidragit till mitt arbete. Slutligen vill jag ge en stor kram till min sambo för allt stöd och uppmuntran jag fått. Luleå, augusti 25 Sofi Berg i
3 Sammanfattning Vid dimensionering av underjordskonstruktioner och vid stabilitetsberäkningar är det viktigt att veta det primära spänningstillståndet eftersom det påverkar spänningsfördelningen och storleken på spänningarna runt den underjordiska öppningen. Det vanligaste sättet att mäta spänningar är genom borrhål från markytan med metoderna överborrning eller hydraulisk spräckning. Dessa metoder är relativt dyra att utföra samtidigt som det inte är klarlagt om resultaten är representativa vid ytlig bergtäckning. Syftet med det här examensarbetet har därför varit att öka kunskaperna om ytliga bergspänningar och om alternativa metoder att mäta dessa med. Målen med examensarbetet har varit att (i) utvärdera ytliga bergspänningsmätningar från tidigare utförda överborrningar i Sverige, (ii) beskriva olika typer av avlastningsmetoder, (iii) göra en analys av ytliga bergmassor med avseende på mätbarhet för att kunna avgöra om metoderna är representativa för ytliga bergspänningsmätningar, (iv) ta fram detaljerade instruktioner för ett framtida fältförsök med den avlastningsmetod som anses lämpligast baserat på denna studie. Arbetet inkluderade en litteraturstudie av olika ytliga avlastningsmetoder för att mäta bergspänningar, varav ett antal metoder valdes ut för ytterligare studier. Metodernas lämplighet för att användas på ett typiskt svenskt berg analyserades. Resultatet från överborrningar i Sverige sammanställdes och utvärderades för att bedöma vilka spänningar som är typiska för ytliga djup och om de skiljer sig markant från de på större djup. Vidare analyserades ett antal faktorer med numerisk analys i dataprogrammet UDEC för att se hur dessa påverkade spänningarna i olika modeller. Med detta som grund togs ett förslag fram till detaljerade instruktioner för ett eventuellt fältförsök med en ytlig avlastningsmetod. Baserat på denna studie har följande slutsatser kunnat dras: Det finns ett ökat behov av att utföra bergspänningsmätningar vid ytliga bergmassor. Sammanställningen av resultat från överborrningsmätningarna visar att en approximering utifrån den regressionslinje som beskrivits av Stephansson (1993) inte ger ett gott resultat. Det är representativt att mäta på markytan för spänningar på litet djup då berget består av enstaka horisontella sprickor eller bankningsplan enligt de numeriska analyserna som utförts i UDEC. Vid helt söndersprucket berg är mätningar på markytan svåra att utföra eftersom spänningarna i sådant fall är noll eller mycket nära noll. Styvhetsskillnader i berget påverkar spänningarna och har större betydelse än enskilda sprickor för resultatet. ii
4 Block- och slitssågning anses vara lämpliga metoder för ytliga bergspänningsmätningar eftersom dessa är enkla att utföra praktiskt. Töjningarna som uppstår vid friläggning av blocket beräknas enkelt om till spänningar i horisontalplanet. För fortsatta studier rekommenderas ett fältförsök med blocksågningsmetoden, kombinerat med slitssågning. iii
5 Abstract When designing underground constructions and assessing stability it is important to know the primary stress since it affects the stress redistribution around underground excavations. The most common way to measure stress is through boreholes on the surface using the overcoring or hydraulic fracturing measurement methods. These methods are relatively expensive, at the same time as it may be questioned whether the results are representative for shallow-seated constructions. The purpose of this thesis was to increase the knowledge on stresses at shallow depths and alternative methods for measuring them. The objectives of this thesis was to (i) evaluate shallow rock stress measurements from previously made overcoring in Sweden, (ii) describe different types of surface relief methods, (iii) analyse the stress state for near surface rock masses to assess the measurability and representativity of shallow stress measurements, and (iv) develop detailed instructions for a future field test using the relief method found most suitable in this thesis. The work included a literature study of different types of relief methods for measuring rock stresses, out of which a number of methods were chosen for further studies. An analysis of the methods suitable for typical Swedish rock was made. Results from overcoring measurements in Sweden were compiled and evaluated to determine which stresses are typical for shallow surface rock and if they significantly differ from those at larger depths. Furthermore, a number of factors were analysed using numerical analysis and the computer code UDEC to study how these affected stress in different models. Using this as a basis a proposal with detailed instructions for a possible field test with a surface relief method was developed. Based on this study the following conclusions could be drawn: There is a growing need to carry out measurements of rock stresses at shallow depths. The compilation of results from the overcoring data showed that an approximation based on the line of regression described by Stephansson (1993) may lead to highly erroneous results. Measurement of stresses at shallow depths or on the ground surface may produce representative results for the case when the rock comprise a few horizontal joints, as verified by the numerical analysis conducted using UDEC. For the case when the rock is heavily jointed, measurements from the surface are difficult to perform and evaluate since the stresses in those cases are zero or close to zero. Variations in stiffness of the rock have a greater effect on the result and affect the stress magnitudes more extensively than the presence of single joints in the rock mass. iv
6 Block tests (isolation of a square block from it surroundings) or slotting is considered to be suitable methods for measuring shallow stresses since these are easy to carry out from a practical point of view. Deformations that arise from the relieved section can simply be recalculated to the stress state in the horizontal plane. For future studies, a field test using the isolation of a square block method in combination with one slot is recommended. v
7 Innehållsförteckning Förord Sammanfattning Abstract Innehållsförteckning i ii iv vi 1 INLEDNING Bakgrund Syfte och mål Utförande och begränsningar BERGSPÄNNINGAR OCH MÄTMETODER Bergspänningar Bergspänningsmätningar Överborrning Avlastningsmetoder Blocksågning Avlastning med centrumhål Jacking -metoder Beräkning av töjningen vid blocksågning Beräkning av töjningen vid enkel slitssågning För- och nackdelar med de olika metoderna SAMMANSTÄLLNING OCH UTVÄRDERING AV SPÄNNINGSDATA Inledning Sammanställning av mätdata Resultat och slutsats ANALYS AV YTLIGA BERGMASSOR MED AVSEENDE PÅ MÄTBARHET Inledning Beräkningsmetod Modellbeskrivning, modellstorlek, randvillkor sprickor etc Geometri och randvillkor Indata och beräkningsfall Resultat Modell Modell Modell Diskussion REKOMMENDATIONER FÖR GENOMFÖRANDE AV FÄLTFÖRSÖK Val av metod vi
8 5.2 Mätteknik Val av mätplats Utförande, testprogram Diskussion SLUTSATSER 58 REFERENSER 59 vii
9 1 INLEDNING 1.1 Bakgrund I Sverige finns idag ett ökat behov i främst storstadsområden att använda underjordskonstruktioner till väg- och järnvägstunnlar, parkeringshus och andra typer av förvaringsutrymmen. För att finna praktiska lösningar då flertalet äldre tunnlar och underjordskonstruktioner tar upp mycket av utrymmet blir det ofta aktuellt att bygga de nya konstruktionerna nära markytan och med liten bergtäckning. Vid dimensionering av underjordskonstruktioner och vid stabilitetsberäkningar är det viktigt att veta det primära spänningstillståndet eftersom det påverkar spänningsfördelningen och storleken på spänningarna runt den underjordiska öppningen. Med kännedom om spänningarna som råder i berget innan brytningen kan en så gynnsam layout som möjligt väljas för att minska stabilitetsproblem och för att minimera eventuella förstärkningsåtgärder. Spänningstillståndet som råder nära markytan är ofta inte lika känt som det som råder på större djup. Spänningar nära markytan uppskattas ofta genom att mätdata från stora djup extrapoleras och uppskattningen av de ytliga spänningarna kan därmed bli mycket grov. Det kan i sin tur leda till stora omkostnader vid byggprojekt då exempelvis förstärkningskostnaderna kan bli mycket högre om spänningarna inte alls motsvarar de uppskattade som användes under projekteringen. Det vanligaste sättet att mäta spänningar är genom borrhål från markytan med metoderna överborrning eller hydraulisk spräckning. Dessa metoder är relativt dyra att utföra samtidigt som det inte är klarlagt om resultaten är representativa vid ytlig bergtäckning. Under tidigt 19-tal gjordes flera försök med olika ytliga avlastningsmetoder runt om i världen, dock inte i någon större utsträckning i Sverige. De ytliga avlastningsmetoderna kallas i Sverige enbart för avlastningsmetoder och är en typ av metoder där spänningsmätningen sker mot en fri yta, antingen markytan eller exempelvis en tunnelvägg. Det kan finnas praktiska fördelar med att använda en avlastningsmetod och utförandet är antagligen mindre kostsamt. Det är dock inte fastställt huruvida dessa metoder fungerar på uppsprucket, ytnära berg och om de uppmätta värdena är representativa för spänningsfältet i en större volym. 1
10 1.2 Syfte och mål Syftet med examensarbetet är att öka kunskaperna om ytliga bergspänningar och om alternativa metoder att mäta dessa med. Målen med examensarbetet är att: Sammanställa och utvärdera ytliga bergspänningsmätningar från tidigare utförda överborrningar i Sverige. Beskriva olika typer av avlastningsmetoder och deras begränsningar och möjliga tillämpningsområden. Metodernas för- och nackdelar ska också beskrivas. Göra en analys av ytliga bergmassor med avseende på mätbarhet för att kunna avgöra om metoderna är lämpliga i detta fall. Detta utförs med hjälp av dataprogrammet UDEC. Ta fram detaljerade instruktioner för ett framtida fältförsök med den metod som anses lämpligast baserat på denna studie. 1.3 Utförande och begränsningar Arbetet inkluderade en litteraturstudie av olika ytliga avlastningsmetoder för att mäta bergspänningar. Ett antal metoder valdes ut för ytterligare studier, vilka beskrivs i kapitel 2. Metodernas lämplighet för att användas på ett typiskt svenskt berg analyserades. Examensarbetet begränsades till att undersöka de mätmetoder som finns för att mäta det absoluta spänningstillståndet. Liknande metoder kan användas för att övervaka och mäta spänningsskillnader (de relativa spänningarna) men det ligger inte inom ramen för denna studie. Resultatet från överborrningar i Sverige sammanställdes och utvärderades för att bedöma vilka spänningar som är typiska för ytliga djup och om de skiljer sig markant från de på större djup. Sammanställningen begränsades till spänningsdata från överborrningsmätningar som är gjorda i Sverige och sammanställningen presenteras i kapitel 3. De mätningar som är utförda från markytan är gjorda med den s.k. Borre-cellen. Ytligt djup har definierats som c:a 5 m. Vidare analyserades ett antal faktorer med numerisk analys för att se hur dessa påverkade spänningarna i olika modeller. Analysen utfördes i dataprogrammet UDEC och begränsades till tre modeller där några olika, typiska, svenska bergförhållanden simulerades, vilka presenteras i kapitel 4. 2
11 Med detta som grund togs ett förslag fram till detaljerade instruktioner för ett eventuellt fältförsök med en ytlig avlastningsmetod, vilket presenteras i kapitel 5. Arbetet avslutades med att slutsatser drogs och rekommendationer för fortsatta studier i ämnet gavs, vilka presenteras i kapitel 6. 3
12 2 BERGSPÄNNINGAR OCH MÄTMETODER 2.1. Bergspänningar De spänningar som existerar naturligt i en orörd bergmassa benämns primärspänningar och de som finns i en störd bergmassa, från exempelvis ett tunnelbygge, kallas sekundärspänningar. In situ-spänningar är en generell benämning på spänningarna som finns i bergmassan (Nordlund et al. 1998), och kan således vara såväl primär- som sekundärspänningar beroende på aktuella förhållanden. Primärspänningarna kan i princip ha vilken riktning som helst i bergmassan, men beskrivs vanligen med en vertikal och två horisontella spänningar eftersom de största spänningarna ofta är orienterade horisontellt-vertikalt. De brukar betecknas σ v, σ h respektive σ H, där den vertikala är rent gravitativ medan σ h och σ H betecknar den minsta respektive den största spänningen i horisontalplanet. Spänningar i berg orsakas av faktorer såsom topografi, geologiska strukturer som sprickor och förkastningar, erosion, glaciala processer och tektoniska processer. Spänningsfördelningen kan vara så komplex att den lokala spänningen kan skilja sig avsevärt från medelspänningen i området. En oregelbunden topografi påverkar in situ-spänningarnas storlek och riktning så att de inte är orienterade vertikalt respektive horisontellt. Topografins påverkan är som störst nära markytan och minskar med djupet. En grov uppskattning kan göras genom att betrakta berg och dalar som tryck- respektive dragbelastningar på en slät markyta, se figur 1 och 2. a) b) Figur 1: Effekten av en oregelbunden topografi på in situ-spänningarna kan uppskattas genom att ersätta berg och dalar med linjärt varierande belastning, efter Amadei & Stephansson (1997). 4
13 Figur 2: Topografins inverkan på primärspänningarna, efter Amadei & Stephansson (1997). Bergmassor är sällan helt homogena vilket påverkar in situ-spänningarnas riktning och storlek. Det kan också vara orsaken till de spridningar av spänningsdata som ofta erhålls från ytliga bergspänningsmätningar. Geologiska strukturer är speciellt av betydelse för spänningstillståndet på litet djup. En öppen diskontinuitet eller förkastning ovanför en tunnel kan orsaka en avlastad zon i taket vilket gör att en bärande båge inte kan formas (Töyrä, 24). Vidare har jordskopan varit utsatt för tryck från inlandsisar, sedimentära bergarter och lager med sediment ofta flera kilometer tjocka. Jordskorpan har då deformerats plastiskt och anpassat sig till det rådande belastningstillståndet. När isarna smälte och berggrunden utsattes för erodering minskade de vertikala och horisontella spänningarna. De minskade dock inte lika mycket vilket resulterade i att σ H är större än σ v. Enligt plattektoniken består jordskorpan av ett antal stora plattor. Plattornas samverkan med varandra och med jordens mantel ger upphov till krafter mellan plattorna som antingen driver eller motverkar plattrörelser. De tektoniska krafterna delas in i två grupper: (i) krafter som uppkommer på grund av geodynamiska processer och (ii) termoelastiska krafter orsakade av avsvalning av oceanplattorna, se figur 3. 5
14 Figur 3: Processer som ger upphov till tektoniska spänningar, efter Zoback et al. (1989). De tektoniska spänningarna är konstanta över områden där längden och bredden är flera gånger större än tjockleken på den elastiska litosfären. I Skandinavien är det i huvudsak de påskjutande krafterna från spridningszonen, Mittatlantiska ryggen, som bidrar till de horisontella spänningarna. I World Stress Map (WSM) Project (Reinecker et al., 24), finns spänningsdata samlat från: jordbävningsmekanismer ( earthquake focal mechanisms ), tryckbrott i borrhål och borrningsinducerade sprickor ( well bore breakouts and drilling induced fractures ), in situ-spänningsmätningar ( in-situ stress measurements ) som t.ex. överborrning och hydraulisk spräckning, geologisk information ( young geologic data ). Ur WSM kan regionala spänningar utläsas och den visar den maximala spänningen σ H och dess orientering, se figur 4. 6
15 Figur 4: Spänningsdata från Word Stress Map för Skandinavien. Längden på spänningssymbolen indikerar kvaliteten på spänningsdatan och A är av bästa sort (Reinecker et al., 24). I de flesta fall i Sverige finns ett spänningsfält motsvarande en reversförkastning (σ H > σ h > σ v ) eller en horisontalförkastning (σ H > σ v > σ h ). Den typiska riktningen på största horisontalspänningen är NV SÖ, vilket anses härröra från trycket av Mittatlantiska ryggen och från den afrikanska plattans kollision med Fennoskandia. För Skandinavien beskrivs ofta spänningstillståndet enligt Stephansson (1993), se ekvation (2.1) (2.6). Dessa ekvationer baseras på regressionsanalyser från spänningsdata erhållet från hydraulisk spräckning respektive överborrning med den s.k. Leeman-metoden där z är 7
16 djupet i meter under markytan. Vertikalspänningen uttrycks som den överliggande lasten, densiteten (ρ) gånger gravitation (g) och antal meters djup (z) under markytan. Hydraulisk spräckning (HF): σ Η = 2,8+,399z [MPa] (2.1) σ h = 2,2+,24z [MPa] (2.2) σ v =ρ g z [MPa] (2.3) Överborrning (OC): σ H = 6,7+,444z [MPa] (2.4) σ h =,8+,329z [MPa] (2.5) σ v =ρ g z [MPa] (2.6) Uppskattning av spänningstillståndet utförs ofta utifrån mätdata som kommer från större djup. Spänningstillståndet som råder nära markytan är mer sällan mätt och rapporterat jämfört med från större djup. Spänningstillståndet som råder nära markytan är ofta komplext med antingen höga eller låga horisontalspänningar (Amadei & Stephansson 1997). Brown & Hoek (1978) har presenterat en översikt av spänningsvariationen med djupet från spänningsmätningar gjorda med hydraulisk spräckning i olika delar av världen, se figur 5. Tendensen i figur 5 är att förhållandet mellan horisontalspänningen och vertikalspänningen minskar på större djup. Förhållandet beror delvis på att de tektoniska spänningarna på litet djup utgör mer av de totala spänningarna än vad den gravitativa spänningspåverkan gör. Erosion och smältningen av landis har också haft mer påverkan närmare markytan. 8
17 Figur 5: Bilden till vänster visar variationen av vertikalspänningen med djupet och bilden till höger visar förhållandet mellan medelhorisontalspänningen och vertikalspänningen med djupet (Brown & Hoek 1978) Bergspänningsmätningar Spänningstillståndet är viktigt att veta på en plats för att kunna förutsäga hur den blivande underjordskonstruktionen kommer att bete sig. Spänningarna är med andra ord en viktig ingångsparameter vid dimensionering av konstruktionen och vid stabilitetsberäkningar. För att veta vilka spänningar som finns i berget används idag flera olika typer av mätmetoder som kan delas in i borrhålsmetoder och ytliga metoder, se tabell 1. Som namnen antyder sker mätningen i ett borrhål respektive på en yta. Till de ytliga metoderna hör avlastningsmetoder och jacking -metoder medan hydraulisk spräckning är en borrhålsmetod. Det finns också två andra typer av borrhålsmetoder vilka är Strain recovery methods och Borehole breakout. Dessa används dock mestadels på mycket stora djup och tas därför inte med i tabellen. Tabell 1: Olika mätmetoder indelat utifrån mätprincip, efter Amadei & Stephansson (1997). Mätmetodens namn Mätprincip Typ av metod Hydraulisk spräckning Hydraulisk metod Borrhålsmetod Blocksågning/Slitssågning Avlastningsmetod Ytlig metod Avlastning med centrumhål Avlastningsmetod Ytlig metod Överborrning Avlastningsmetod Borrhålsmetod Flat jack Jacking -metod Ytlig metod Curved jack Jacking -metod Ytlig metod 9
18 I jämförelse med andra bergsparametrar är bergspänningar en svår kvantitet att mäta, eftersom spänningen inte kan mätas direkt. Generellt innebär alla in situspänningsmätningsmetoder att berget störs på något sätt. Bergets respons på störningen mäts och analyseras. En förutsättning vid mätning av primärspänningar är att störningsprocessen av berget måste mätas på ställen långt ifrån naturliga eller artificiella öppningar. Amadei & Stephansson (1997) rekommenderar 1,5 2 gånger av öppningens storlek i avstånd från den underjordiska öppningen, förkastning eller från större bergmassor med heterogeniteter där störningen kommer att ske. I en del fall kan dock det störda spänningsfältet, d.v.s. sekundärspänningarna, vara av intresse, varför mätningar kan göras närmare befintliga underjordsutrymmen eller geologiska strukturer. Från ett slumpmässigt urval av mätdata från spänningsmätningar är standardavvikelsen av mätfelet enligt Leijon (1989) ± 2 MPa eller mindre. Detta är ofta tillfredställande vid bergsingenjörstillämpningar på stora djup men spänningsmagnituden på ytligt djup är ofta låg och det relativa mätfelet kan då bli mycket stort. 2.3 Överborrning Utvecklingen av överborrningsmetoderna har varit relativt omfattande och det är idag den kanske vanligaste metoden som används för att mäta bergspänningar. Överborrningsmetoderna innebär att en fullständig avlastning av berget åstadkoms genom borrning av ett stort hål över ett pilothål. Metoderna baseras på antagandet om ett kontinuerligt, homogent, isotropt och linjärelastiskt material. Anisotropa material kan dessutom tas hänsyn till vid utvärderingen. Det finns flera typer av överborrningsmetoder såsom: Överborrning med förtryckta celler (eng: Overcoring of prestressed cells) Överborrning med deformationsmätceller, USBM. (eng: Overcoring of deformation-type gages such as the USBM gage) Överborrning med en mätcell fäst vid den släta botten av borrhålet. (eng: Overcoring of a gage attached to the flat end of a borehole: Doorstopper and photoelastic disks) Överborrning med en CSIR triaxiell töjningscell. (eng: Overcoring of CSIR-type triaxial strain cell) Överborrning med en CSIR triaxiell töjningscell fäst vid botten av borrhålet. (eng: Overcoring of CSIR-type triaxial strain cell attached to the end of a borehole [spherical or conical cells]) Överborrning med en styv, solid eller ihålig inklusionsmätcell. (eng: Overcoring of stiff, solid or hollow inclusion-type gages.), (Amadei & Stephansson 1997). 1
19 Amadei & Stephansson (1997) beskriver principen som dessa olika metoder baseras på, med hjälp av tre grundläggande steg, se figur 6. Figur 6: De tre grundläggande stegen vid överborrning, efter Amadei & Stephansson (1997). Det första steget innebär att ett stort hål borras i berget där spänningarna sedan ska bestämmas. Håldiametern varierar mellan 6 och 2 mm beroende på var i världen testet utförs och vilken utrustning som finns tillgänglig. I Sverige är det ofta en 76 mm borrkrona som används. Det andra steget är att borra ett litet, vanligen 3 5 mm långt, pilothål i botten av det stora hålet. Pilothålet måste vara så långt att effekten av ändarna är försumbara och störningen av berget som det stora hålet orsakar minimeras. Pilothålet och det stora hålet måste vara så koncentriska som möjligt d.v.s. de ska helst ha samma mittpunkt. För att åstadkomma detta slätas oftast botten på det stora hålet ut innan borrningen av pilothålet och pilothålet centreras i hålet med hjälp av styranordningar. Pilothålet har vanligen en diameter på mm. Därefter förs ett instrument, som kan mäta små töjningar och förskjutningar, ned i pilothålet. Det tredje steget är att överborra med den större borrhålsdiametern så att en ihålig cylinder bildas och därmed avlastas spänningarna och töjningarna i berget. Förändringar av töjningar 11
20 eller förskjutningar registreras av instrumentet i pilothålet allt eftersom överborrningen sker, alternativt före och efter avslutad överborrning. En av överborrningsmetoderna, vilken även har utvecklats i Sverige, är med instrumentet Borre-cellen. Installation och mätprocedur vid överborrning med Borre-cellen visas i figur Figur 7: Principskiss över överborrning med Borre-cellen (Sjöberg & Klasson, 23) 1. Borrhål, φ76 mm, renspolas efter borrning. Planslipning av borrhålsbotten. 2. Pilothål, φ36 mm, borras och renspolas. Pilothålskärnan tas till ytan för inspektion och förutsättningen för mätning bedöms. 3. Mätcellen, monterad i ett installationsverktyg, sänks ned mot pilothålet. (Cellen hålls centrerad i grovhålet m h a styranordningar på installationsverktyget.) 4. Mätcellens främre ände med trådtöjningsgivare monterade förs in i pilothålet. Cellen frigörs från installationsverktyget via en utlösningsmekanism och de limbestrukna töjningsgivarna pressas mot pilothålets vägg m h a toppkonen. Den skyddskon som skyddar givarna under transport i borrhålet frigörs och faller ned till pilothålets botten. Utlösningsmekanismen låser samtidigt kompassen som finns i installationsverktyget så att cellens orientering i hålet registreras. 5. Limmet tillåts härda (normalt ca 8-12 timmar under natten). Installationsverktyget återtas ur borrhålet. 6. Överborrning/friborrning av mätcellen sker (φ76 mm) under fortlöpande registrering av töjningsvärden i en datalogger inbyggd i Borre. Knäckning av kärnan och upptagning till ytan. De under friborrningen avlästa töjningsvärdena överförs från mätcellens datalogger till en extern PC för utvärdering. I denna metod kan borrhålen vara torra eller vattenfyllda och mätningarna göras djupare än 5 meter. Mätningar har hittills gjorts ned till 64 meters djup från markytan. Idag är det endast denna metod som klarar att mäta i vertikala, vattenfyllda hål från markytan. För en fullständig bestämning av det tredimensionella spänningstillståndet krävs mätning i sex av varandra oberoende riktningar. Data från en överborrning med Borre-cellen innefattar nio 12
21 töjningsdifferenser i sju oberoende riktningar. Dessa har uppkommit i och med att töjningsgivarna är fastlimmade på den borrkärnan som avlastats från allt omgivande bergtryck i och med överborrningen. En linjär regressionsanalys nyttjas för att hitta den lösning som bäst passar alla uppmätta töjningar. Borre-cellen är sedan 23 också utrustad med en datalogger som registrerar töjningarna både under inlimning och överborrning (Sjöberg & Klasson 23). Efter avslutad överborrning utförs sedan ett biaxialtest på borrkärnan för att bestämma bergets elastiska parametrar. Spänningarna beräknas utifrån töjningsdifferenserna och de elastiska konstanterna för berget. Beräkningarna av spänningarna baseras på den klassiska teorin av Leeman och är detaljerat beskriven i t.ex. Amadei & Stephansson (1997). 2.4 Avlastningsmetoder I detta avsnitt ges en detaljerad beskrivning av ett par olika avlastningsmetoder. Såväl fördelar som nackdelar och begränsningar vad gäller mätbarheten hos dessa beskrivs. De olika metoderna som kommer att beskrivas är: block- och slitssågning, avlastning med centrumhål och slitssågning med installation av en flatjack eller curvedjack. Merill (1964) definierar avlastningsmetoder som metoder eller processer som helt eller delvis isolerar en bit berg från spänningsfältet i omgivningen. Avlastningsmetoderna har utvecklats från tidigt 19- tal och framåt men utvecklingen stagnerade i mitten av seklet då överborrningsmetoden tog över. Avlastningsmetoderna används för att kunna bestämma in situ-spänningarna i berg genom att mäta bergets respons vid avlastning genom borrning eller sågning. De ursprungliga måtten i mätmetodernas geometrier angavs i tum men har sedan omräknats till SI-enheter Blocksågning Blocksågning är en avlastningsmetod där mätdubbar eller töjningsgivare placeras på berget för att kunna mäta bergets förskjutning vid en avlastning. Med kännedom om bergets elasticitetsmodul och Poissons tal kan dessa förskjutningar och töjningar sedan användas för att beräkna de tvådimensionella spänningarna i berget. Lieurance (1939) var en av de första som utförde tester av blocksågning på 193-talet. Det var i och med byggandet av Hoover dam i Nevada i USA som det blev aktualiserat och nödvändigt att veta vilka spänningar som rådde i berget för att kunna bestämma behovet av förstärkning. Om spänningarna i dammens grundläggning skulle vara för låga i kanalens riktning fanns risken att botten skulle spricka upp när dammen fylldes med vatten. Därför bestämdes att spänningarna i grundläggningen skulle undersökas genom att mäta in situspänningarna vid dammen. 13
22 Lieurance genomförde mätningarna i en torrlagd tunnel av dammen och tunnelns tvärsektion var 1,5 x 1,8 m. Metoden innebar att mätdubbar placerades på tunnelväggen på ett flertal mätpunkter som låg med 15 meters mellanrum i tunneln. Geometrin vid en av punkterna ses i figur 8. Åtta mätdubbar placerades på en tänkt cirkels omkrets med diametern,58 meter. Avståndet mellan dessa mättes och därefter frilades ett 1,22 m 2 block genom att,762 m djupa hål borrades omlott. Under tiden som blocket borrades mättes skillnaden i avstånd mellan mätdubbarna, d.v.s. bergets töjning. En borrkärna från det avlastade berget studerades sedan i ett laboratorium i Denver för bestämning av elasticitetsmodulen. Figur 8: Avlastad sektion av berget och mätdubbarnas placering som Lieurance använde (Merrill, 1964). Konventionella töjningsrosettsformler användes sedan för att beräkna spänningen i berget (Merrill, 1964). Spänningen parallell med tunnelväggen bestämdes först (Amadei och Stephansson 1997). I Olsen (1957) finns en förfinad blocksågningsmetod beskriven. Kortfattat gick metoden ut på att ett rutmönster ritades upp på bergytan som referens för det tvådimensionella spänningsfältet. En 153 mm ring borrades upp i rutmönstret och en viss töjning av berget uppstod, se figur 9. Olsen visade via beräkningar att ringen skulle borras ned till ett djup av 127 mm för att en fullständig avlastning av berget skulle ske. För att mäta töjningen när borrningen runt givarna genomfördes användes elektriska töjningsgivare. Dessa 14
23 töjningsgivare var vattentäta/skyddade. För att ta fram elasticitetsmodulen och Poissons tal testades berget i ett laboratorium. Uppmärkt bergyta Borrad ring Figur 9: Testgeometri som Olsen (1957) använde. Den plana bergytan är uppmärkt i ett rutmönster och en ring i berget är konstruerad genom att borrhål borrats omlott. Olsen (1957) ansåg att det var viktigt att tiden mellan den första och andra avläsningen minimerades och ansåg att två timmar var maximalt. Han menade också att upprepade avläsningar skulle göras, direkta och omvända, för att kontrollera att eventuella fel kunde korrigeras innan mätningarna fortsatte. Summan av de direkta och omvända avläsningarna skulle vara konstanta för dessa typer av instrument. Det klassiska tvådimensionella töjning-spänningsambandet användes för att bestämma spänningarna-magnituden och riktningen på in situ-spänningarna och den maximala skjuvspänningen. Töjningsrosetten bestod av fyra individuella givare/mätare orienterade i olika riktningar. Den fjärde givaren gjorde det möjligt att beräkna standardfelet av mätningen genom minsta kvadratmetoden (Olsen, 1957). Olsen testade sin metod i två tunnelprojekt och verifierade resultaten genom att i laboratorium avlasta ett stort block som var utsatt för högt tryck. Resultatet från detta laboratorietest visade en god överensstämmelse mellan den beräknade och påförda spänningen (Merrill, 1964). 15
24 Eftersom mätningarna Olsen (1957) gjorde utfördes inne i tunnlar var inte temperaturen något problem. Om mätningarna däremot hade utförts utomhus hade temperaturförändringar, vilka introducerar termiska spänningar, varit tvungna att minimeras. Olsen beskrev tillvägagångssättet med sin metod genom sex steg som skulle följas: 1) Val av lämplig placering för testet. 2) Förbered ytan. 3) Fäst och vattenskydda lämpliga givare. 4) Avläs töjningarna två gånger, före och efter avlastningen. 5) Mät spännings-töjningsförhållandet för materialet från borrkärnor. Olsen (1957) anser att metoden är enkel och en fullt praktiskt metod för att bestämma spänningarna i berget i och med utvecklingen av verktygen som används. Olsen använde samma sätt som Lieurance hade gjort för att beräkna spänningarna (Merrill, 1964). Sipprelle och Teichman (195) beskriver också en blocksågningsmetod som testades i Bureau of Mines testgruva i Colorado, USA. En specialtillverkad diamantsåg användes vid sågningen. En plats fri från några större sprängskador valdes. Området som sågades ur var 76 x 17 mm och innefattade töjningsgivarna. Avläsningen av givarna gjordes före och efter sågning. Bergets elastiska egenskaper bestämdes via laboratorietester och sedan beräknades spänningarna. Det gjordes ett flertal mätningar under 1949 både då berget var utsatt för drag och tryck. Alla mätningar som gjordes under drag misslyckades eftersom spänningarna avlastades som sprickor i blocket. De andra mätningarna lyckades och resultaten var tillförlitliga enligt Sipprelle och Teichman (195). Mätningarna var inom 1 15 % av de teoretiskt beräknade spänningarna Avlastning med centrumhål Duvall (1974) presenterade en annan metod för att mäta spänningstillståndet på en öppen yta. Bakgrunden till metoden är att mäta den radiella förskjutningen av punkter runt ett hål som borras. Geometrin av testet visas i figur 1. Metoden består av två steg. Först installeras sex stycken mätdubbar, som är 9,5 mm i diameter och 6,3 mm långa, med 6 graders mellanrum i en tänkt cirkel med radien 254 mm. Duvall fäste mätpinnarna med epoxy. Diameteravståndet mellan mätdubbarna mättes. Det andra steget bestod i att ett hål med diameter 152 mm borrades i mitten av dubbarna. Därefter mättes avståndet mellan pinnarna igen. Från de tre uppmätta förskjutningarna kunde den sekundära principiella spänningen och dess orientering i berget bestämmas. Förskjutningen mättes ofta med en mikrometer med noggrannheten,1 mm. (Amadei & Stephansson 1997) 16
25 Figur 1: Avlastning med centrumhål, efter Duvall (1974). Mätdubbarna är markerade med små ringar och betecknas pin. Det stora hålet, avlastningshålet, i mitten borras vid avlastningen. Ivanov (1983) föreslog en liknande metod men 12 mätdubbar användes istället för sex. Detta för att förskjutningen då kunde mätas i fler riktningar än tre. De använde också en specialgjord mikrometer för att mäta förskjutningen under avlastningen med en noggrannhet på,1 mm. Avståndet mellan mätdubbarna mättes före och efter avlastningen. Problemet analyserades som ett plant spänningstillstånd i ett elastiskt isotropt material. Spänningen bestämdes utifrån tio diagonala diametrar istället för Duvalls tre. Tsur-Lavie & Van Ham (1974) beskriver i en artikel noggrannheten vid mätning med Avlastning med centrumhål. Ett viktigt konstaterande är att resultaten från mätningar endast är korrekt och exakt då berget beter sig som ett linjär-elastiskt material. Andra antaganden som görs är att berget är isotropt och homogent. Fyra möjliga felkällor har lyfts fram: (i) fel som uppstår i avläsningen av mätdubbarnas förskjutning, (ii) fel som uppstår för att det borrade avlastningshålet i mitten inte är placerat koncentriskt, (iii) en eller flera mätdubbars placering avviker från den tänkta cirkelomkretsen, (iv) avlastningshålet är inte helt cirkulärt utan en aning elliptiskt. Dessa antaganden och möjliga felkällor gäller inte bara för metoden Avlastning med centrumhål utan för alla avlastningsmetoder Jacking -metoder Flatjackmetoden representerar en av de allra första metoderna som användes i bergmekaniken för att mäta in situ-spänningar i berg. Till en början var den ämnad för att karaktärisera bergets deformerbarhet men metoden blev på 195- och 196-talet populär även för att mäta spänningar. 17
26 Jacking -metoder kallas ibland för spänningskompenseringsmetoder. En bergmassas jämvikt störs genom att slitsar sågas på ytan av berget, antingen vid markytan eller på ytan av bergrummet eller tunneln. Sågningen skapar i sin tur deformationer som mäts med mätdubbar eller töjningsgivare på båda sidor om slitsen. Slutligen återställs jämvikten genom att en apparat, en s.k. jack, sätts in i slitsen, vilken trycksätts tills dess att deformationerna försvunnit/återbildats. Den vanligaste förekommande använda jacking - metoden är flatjackmetoden. Då består jacken av två tunna och relativt mjuka ihopsvetsade metallplattor. I figur 11 visas en schematisk bild över hur en uppställning av flatjacksmätning kan se ut. Figur 11: Uppställningen vid flatjacksförsök enligt Merill (Amadei & Stephansson 1997). Generellt är jacking -metoderna avsedda för bestämning av ytliga eller nära ytan (5 7 meter) förekommande spänningar. I många avseenden kan metoden klassificeras som en ytlig avlastningsmetod (Amadei & Stephansson 1997). I figur 12 visas bergets rörelser ur bergmekanisk synvinkel. Här antas att berget är elastiskt (linjärt eller icke-linjärt) och trycksatt vinkelrätt mot flatjackens yta. Det initiala avståndet mellan två mätdubbar kallas d och den okända normalspänningen σ. Som ett resultat av att slitsen sågas reduceras σ till noll och avståndet mellan mätdubbarna reduceras med 2 d. Trycksättningen av flatjacken görs till utjämningstrycket p c där mätdubbarna är tillbaka i ursprungsläget. 18
27 Figur 12: Bergets rörelser vid ett jackförsök, (Amadei & Stephansson 1997) Bowling (1976) föreslog att istället för en flatjack använda en cylindrisk jack för att bestämma spänningarna vinkelrätt mot en bergyta. Jacken består då av en fast stålkärna som är fäst i en gummihylsa. Åtta referensstavar fästs först runt en cirkels omkrets med diametern 25 mm på en bergyta. Stavarna bildar fyra referensavstånd med 45º från varandra. Sen borras ett hål som är 15 mm i diameter och 5 mm djupt i mitten av den stora cirkeln, såsom i Duvalls metod, Avlastning med centrumhål, se figur 1. De fyra diameterförändringarna mäts. Slutligen placeras en cylindrisk jack i borrhålet och trycksätts varefter stavarnas rörelse mäts. Huvudspänningarna och deras orientering i planet parallellt med bergytan och elasticitetsmodul, bestäms från responskurvan av referensstavarna som fås under borrning och trycksättning. Curved jacks föreslogs också av Jaeger och Cook (1964) för mätning av spänningar i borrhål, på avstånd 3 6 meter in i bergmassor för att eliminera de huvudsakliga nackdelarna som flatjackmetoden innebär. Flera par av jackar måste då användas. Metoden är enligt Amadei och Stephansson (1997) komplex och kräver en kombination av uppsprickning, trycksättning, avlastning och tryckåterbildning. Den har dock fördelen att kunna bestämma de sekundära spänningarna riktade vinkelrätt mot borrhålet. Flatjacken fungerar med trycksättning upp till flera tusen psi vilket motsvarar tiotals MPa. Slitsen där jacken ska sitta kan antingen göras genom överlappande borrhål eller med en stor diamantsåg som ger en slät yta. Överlappande hål är mest lämpat för djupa slitsar, mer än 1,5 meter, medan sågen lämpar sig för slitsar grundare än 1,5 meter. Jacken sätts på plats med exempelvis cement/murbruk, epoxyharts eller gips. Murbruket måste ha liknade hållfasthet 19
28 och deformerbarhet/styvhet som det intilliggande berget. Om slitsen är gjord med en stor såg är inte gjutning av jacken nödvändig (Rocha, Lopes och Silva 1966). Bergytans deformationer och töjningar måste mätas i närheten av slitsen annars är deformationen och töjningen alldeles för liten för att vara mätbar med tillräcklig noggrannhet. Rocha, Lopes och Silva (1966) föreslog ett avstånd mindre än 3 mm mellan slits och dubb. Dubbarna placeras vinkelrätt mot den tänkta slitsen, på mittlinjen av normalen till flatjacken. Förskjutningarna mäts med en noggrannhet av,1 mm. Generellt så har flatjackmetoden flera nackdelar som påverkar utvärderingen av resultaten enligt Amadei och Stephansson (1997). Resultatet påverkas av atmosfäriska förhållanden såsom fukt, temperatur och damm. Krypdeformationer kan uppstå efter att slitsen är sågad vilket kan ge en överskattning av de tangentiella spänningarna. Trycket sprids inte alltid helt över hela jackens yta, vilket leder till att skillnaden mellan påfört tryck och verkligt tryck på berget blir stort. 2.5 Beräkning av töjningen vid blocksågning För att veta med vilken noggrannhet töjningar eller deformationer måste kunna registreras vid användandet av en avlastningsmetod har ett antal beräkningar utförts. Rådande in situspänningar och bergmassans elastiska konstanter har antagits till typiska värden för svensk berggrund. Vidare har antagits att plant spänningstillstånd råder samt att berget kan antas bete sig linjärt elastiskt och isotropt. I figur 13 visas riktningarna x, y och vinkeln ϕ. y ϕ x Figur 13: Riktningarna x, y och ϕ. Mohrs töjningscirkel ger att töjningen i en godtycklig riktning kan beräknas ur: ε 2 2 ( ϕ) ε cos ( ϕ) + ε sin ( ϕ) γ cos( ϕ) sin( ϕ) = (2.7) x y + xy där ε x = töjningen i x-led, ε y = töjningen i y-led, γ xy = skjuvtöjningen i xy-planet. 2
29 Vidare ger plant spänningstillstånd ε ε x y [ σ νσ ] = 1 x y, (2.8) Ε [ σ νσ ] = 1 y x, (2.9) Ε där σ x = spänningen i x-led, σ y = spänningen i y-led, Ε= elasticitetsmodul och ν= Poissons tal. Eftersom plant spänningstillstånd råder, d.v.s. en av huvudspänningsriktningarna är noll kan ett förenklat antagande göras vilket är att τ =. xy (2.1) Detta ger att σ x och σ y är huvudspänningar i horisontalplanet, d.v.s. σ x = σ H, σ y = σ h vilket ger ε ε x y [ σ νσ ] = 1 H h, (2.11) Ε [ σ νσ ] = 1 h H, (2.12) Ε γ 1 xy = xy G τ, (2.13) Ε G =. (2.14) 2(1 + ν ) Eftersom skjuvspänningen har antagits till noll ger (2.13) inte heller någon skjuvtöjning. Normaltöjningen kan då beräknas genom att (2.11) och (2.12) kombineras med (2.7), d.v.s. ε 1 1 = H h h H (2.15) Ε Ε 2 2 ( ϕ ) [ σ νσ ] cos ( ϕ ) + [ σ νσ ] sin ( ϕ ) Töjningen i olika riktningar (φ) har beräknats för antagna värden på σ H, σ h, E och υ motsvarande ytliga förhållanden (jmf. ekvation (2.1) t.o.m. (2.6)). Resultatet redovisas i tabell 2. 21
30 Tabell 2: Indata och resultat för töjningen vid olika förhållanden. Spänningarna är hämtade från Stephansson (1993) och övriga värden från Töyrä (24). σ H [MPa] σ h [MPa] E [GPa] ν ϕ [ ] ε [µstrain] 2,8 2,2 17,8, ,8 2,2 17,8, ,8 2,2 17,8, ,7,8 17,8, ,7,8 17,8, ,7,8 17,8, ,8 2,2 8,9, ,8 2,2 8,9, ,8 2,2 8,9, ,7,8 8,9, ,7,8 8,9, ,7,8 8,9, ,8 2,2 75,25 3 2,8 2,2 75, ,8 2,2 75, ,7,8 75, ,7,8 75, ,7,8 75,
31 2.6 Beräkning av töjningen vid enkel slitssågning Ett enkelt sätt att bestämma spänningar via avlastning vore att mäta töjningen i en dimension, d.v.s. bara i en enda riktning. Detta skulle kunna göras genom en förenklad variant av blocksågning där enbart en slits sågas upp och töjningen mäts med hjälp av mätdubbar, se figur 14. σ y σ y2 = σ 1 σ x σ x Hålrum σx2 = σ2 Infinitesimalt element Figur 14: Figur a) visar slitsen och mätdubbarna och in situ-spänningarna. Figur b) visar ett infinitesimalt element efter att slitsen blivit sågad. För att beräkna töjningen av berget vid sågningen antas att in situ-spänningarna är orienterade parallellt och vinkelrätt slitsen samt att plant spänningstillstånd antas råda, d.v.s. σ = (2.16) z Slitsens bredd a) b) ε x1 [ σ νσ ] 1 = x1 y1, (2.17) Ε där ε x1 = töjningen i x-led före slitsen har sågats, σ x1 = spänning i x-led före slitsen har sågats, σ y1 = spänning i y-led före slitsen har sågats, E= elasticitetsmodul och ν= Poissons tal. Efter slitsen har sågats så gäller: 23
32 σ x ( νσ ) 1 = ε x2 = y2 (2.18) Ε där ε x2 = töjningen i x-led efter att slitsen har sågats och σ y2 = spänning i y-led efter att slitsen har sågats. Skillnad i töjningen ges av ( σ νσ ( νσ ) 1 ε x = ε x2 ε x1 = x1 y1 y2 (2.19) Ε σ y1 1 σ y2 ε x = σ x1. (2.2) Ε I tabell 3 kombineras ovanstående ekvationer med spänningarna från Stephansson (1993) regressionsanalys, varvid töjning för några olika primärspänningar och E-moduler beräknats. Tabell 3: Indata och resultat för beräkningen av töjningen vid enkel slitssågning. σ x [MPa] E [GPa] ε [µstrain] 2,8 17, ,7 17, ,8 8, ,7 8, , , För att mäta minsta antagna horisontalspänningen för ett relativt styvt berg måste en töjning på ca 4 µstrain kunna registreras. Detta gäller vid ett mätavstånd på 1 mm. Det betyder att mätnoggrannheten är ± 2,8 MPa vilket inte är tillfredställande. Det vore önskvärt att kunna mäta med en upplösning på <1MPa. Om man kan registrera töjningar på c:a 1 µstrain så motsvarar det,7 1 MPa. Enligt Fahlesson (25) finns en typ av mätdubbar som placeras på ett visst avstånd från varandra och förskjutningen mäts med en s.k. Staegermätare. 24
33 2.7 För- och nackdelar med de olika metoderna En sammanställning av de olika metodernas för- och nackdelar presenteras i tabell 4. Tabell 4: Fördelar och nackdelar med de olika metoderna Metod Fördelar Nackdelar Blocksågning Enkel att utföra praktiskt. Ε och ν måste vara kända. Utförs direkt på en slät bergytan. Mätdubbar och töjningsgivare kan påverkas av fukt och damm. Spänningarna mäts i 2 D Sällan använd metod, liten erfarenhet. Slitssågning Enkel att utföra Spänningen mäts endast i 1 D Avlastning Enkel att utföra praktiskt. E och ν måste vara kända. med centrumhål Kan användas direkt på bergytan. Mätdubbarnas förmåga kan påverkas av fukt och damm. Flat och curved jacks ν behöver inte vara känd. Mjukt eller spjälkat berg kan mjukas upp ytterligare av limmet som används. Flatjackmetoden används direkt på en ytan. Överskattning av de tangentiella spänningarna p.g.a. krypdeformationer som Utrustningen som används är robust och stabil. Mindre påverkan på bergmassans mekaniska egenskaperna eftersom störningen av berget är relativt liten. Den mätta spänningen är medelspänningen över området. Spänningarna mäts direkt. Relativt stora bergvolymer kan testas (.5-2 m). kan uppstå efter att slitsen. Resultatet kan påverkas av atmosfäriska förhållanden som fukt, temperatur och damm. Flertalet flatjackförsök är nödvändiga för att kunna bestämma den fullständiga in situspänningen. Bergmassan måste därför ha samma mekaniska egenskaper i volymen för att omfatta dessa mätningar. Speciell utrustning krävs. 25
34 3 SAMMANSTÄLLNING OCH UTVÄRDERING AV SPÄNNINGSDATA 3.1 Inledning Spänningstillståndet som råder på litet djup är, generellt sett, inte lika känt som det som råder på stort djup. När spänningarna på litet djup uppskattas görs detta ofta genom att använda spänningarna beskrivna av Stephansson (1993). Frågan är då om detta är en tillfredställande uppskattning? Genom att sammanställa och utvärdera resultat från tidigare genomförda spänningsmätningar kan ett svar på detta ges. Värden från ett antal överborrningar som har gjorts i Sverige har sammanställts. Ur dessa data har ett konfidensintervall beräknats för att kontrollera spridningen av spänningsmätningsresultaten på varje mätnivå. Ett konfidensintervall är den vanligaste formen att uttrycka ett osäkerhetsintervall. Om man i en undersökning inte kan bestämma svaret exakt kan man i stället ge två gränser, som innesluter rätt värde med en i förväg bestämd sannolikhet, konfidensgraden. I detta fall har ett 9 % intervall valts. Detta innebär att 9 % av mätdata ligger inom intervallet (σ min < σ < σ max ). Resultaten från de sammanställda överborrningsmätningarna har jämförts med regionala data som erhölls från WSM (Reinecker et al., 24). Diagrammen med konfidensintervallen har jämförts med den regressionslinje som Stephansson (1993) beskrivit för att se om detta är en bra eller tillfredställande metod att uppskatta spänningarna med. 3.2 Sammanställning av mätdata Sammanställningen har kunnat göras genom att SwedPowers databas över resultat från bergspänningsmätningar nyttjats. Data har valts från några platser i Sverige där spänningsmätningar har utförts med överborrningsmetoden. En av de utvalda platserna för sammanställningen är Forsmark eftersom spänningsmätningarna där har utförts både på ytligt och stort djup och i två olika borrhål. Data från Forsmark är därför väl lämpad för att kunna göra en jämförelse av spänningarna på olika djup och sedan bedöma om dessa skiljer sig markant från varandra. En separat indelning av de ytliga spänningarna, från markytan till 6 meters djup, har gjorts för att dessa ska kunna jämföras med ytliga spänningar från andra mätplatser. Tre olika platser med data från mätningar som gjorts på ytligt djup har valts för att bedöma vilka spänningar som är typiska för ytliga djup. I tabell 5 visas de valda platsernas namn och dess borrhålsbeteckning. De platser där mätresultaten är konfidentiella betecknas A och B och borrhålen BH1 respektive BH2. 26
35 Tabell 5: Plats och borrhålsbeteckning Plats Borrhål Forsmark Forsmark Clab 2 A B DBT-1 DBT-3 KSI32 BH1 BH2 Beräkningar av konfidensintervallen har utförts för mätresultaten med hjälp av datorkoden som finns beskriven i Lindfors et al. (24). I figur 15, 17, 19, 21 och 23 presenteras de uppmätta värdena på σ H, σ h, σ v och riktningen på σ H för respektive mätplats. I figur 16, 18, 2, 22 och 24 presenteras 9% - konfidensintervall för olika mätnivåer för respektive mätplats. I figur presenteras mätdata från Forsmark på stort djup från Sjöberg et al. (25). I figur 29 presenteras spänningsdata från ytligt djup för samtliga platser och en regressionslinje, baserad på överborrningsdata, beskriven av Stephansson (1993). Resultaten från de sammanställda överborrningsmätningarna har också jämförts med regionala data som erhållits från WSM (Reinecker et al., 24). 27
Angående skjuvbuckling
 Sidan 1 av 6 Angående skjuvbuckling Man kan misstänka att liven i en sandwich med invändiga balkar kan haverera genom skjuvbuckling. Att skjuvbuckling kan uppstå kan man förklara med att en skjuvlast kan
Sidan 1 av 6 Angående skjuvbuckling Man kan misstänka att liven i en sandwich med invändiga balkar kan haverera genom skjuvbuckling. Att skjuvbuckling kan uppstå kan man förklara med att en skjuvlast kan
GJUTNING AV VÄGG PÅ PLATTA
 GJUTNING AV VÄGG PÅ PLATTA Studier av sprickrisker orsakat av temperaturförloppet vid härdningen Jan-Erik Jonasson Kjell Wallin Martin Nilsson Abstrakt Försök med gjutning av konstruktionen vägg på platta
GJUTNING AV VÄGG PÅ PLATTA Studier av sprickrisker orsakat av temperaturförloppet vid härdningen Jan-Erik Jonasson Kjell Wallin Martin Nilsson Abstrakt Försök med gjutning av konstruktionen vägg på platta
Tentamen i Hållfasthetslära gkmpt, gkbd, gkbi, gkipi (4C1010, 4C1012, 4C1035, 4C1020) den 13 december 2006
 KTH - HÅFASTHETSÄRA Tentamen i Hållfasthetslära gkmpt, gkbd, gkbi, gkipi (4C1010, 4C1012, 4C1035, 4C1020) den 13 december 2006 Resultat anslås senast den 8 januari 2007 kl. 13 på institutionens anslagstavla,
KTH - HÅFASTHETSÄRA Tentamen i Hållfasthetslära gkmpt, gkbd, gkbi, gkipi (4C1010, 4C1012, 4C1035, 4C1020) den 13 december 2006 Resultat anslås senast den 8 januari 2007 kl. 13 på institutionens anslagstavla,
Föreläsningsdel 3: Spänningar i jord (motsvarande Kap 3 i kompendiet, dock ej mätavsnittet 3.6)
 Föreläsningsdel 3: Spänningar i jord (motsvarande Kap 3 i kompendiet, dock ej mätavsnittet 3.6) Spänningar i jord Olika spänningstillstånd Krafter och spänningar i ett kornskelett Torrt kornskelett Vattenmättat
Föreläsningsdel 3: Spänningar i jord (motsvarande Kap 3 i kompendiet, dock ej mätavsnittet 3.6) Spänningar i jord Olika spänningstillstånd Krafter och spänningar i ett kornskelett Torrt kornskelett Vattenmättat
= 1 E {σ ν(σ +σ z x y. )} + α T. ε y. ε z. = τ yz G och γ = τ zx. = τ xy G. γ xy. γ yz
 Tekniska Högskolan i Linköping, IKP /Tore Dahlberg LÖSNINGAR TENTAMEN i Hållfasthetslära - Dimensioneringmetoder, TMHL09, 060601 kl -12 DEL 1 - (Teoridel utan hjälpmedel) 1. Spänningarna i en punkt i ett
Tekniska Högskolan i Linköping, IKP /Tore Dahlberg LÖSNINGAR TENTAMEN i Hållfasthetslära - Dimensioneringmetoder, TMHL09, 060601 kl -12 DEL 1 - (Teoridel utan hjälpmedel) 1. Spänningarna i en punkt i ett
Ingjuten sensor för mätning av uttorkningsförlopp beräkning av inverkan av sensorns dimension och orientering. Sensobyg delprojekt D4
 LUNDS TEKNISKA HÖGSKOLA LUNDS UNIVERSITET Avd Byggnadsmaterial Ingjuten sensor för mätning av uttorkningsförlopp beräkning av inverkan av sensorns dimension och orientering Sensobyg delprojekt D4 Lars-Olof
LUNDS TEKNISKA HÖGSKOLA LUNDS UNIVERSITET Avd Byggnadsmaterial Ingjuten sensor för mätning av uttorkningsförlopp beräkning av inverkan av sensorns dimension och orientering Sensobyg delprojekt D4 Lars-Olof
Material, form och kraft, F4
 Material, form och kraft, F4 Repetition Kedjekurvor, trycklinjer Material Linjärt elastiskt material Isotropi, ortotropi Mikro/makro, cellstrukturer xempel på materialegenskaper Repetition, kedjekurvan
Material, form och kraft, F4 Repetition Kedjekurvor, trycklinjer Material Linjärt elastiskt material Isotropi, ortotropi Mikro/makro, cellstrukturer xempel på materialegenskaper Repetition, kedjekurvan
Deformationsmätning av Oskarshamn 3s reaktorinneslutning i samband med täthetsprovning Kraftindustrins betongdag 2019 Ulrik Brandin Erik Hansson
 Deformationsmätning av Oskarshamn 3s reaktorinneslutning i samband med täthetsprovning Kraftindustrins betongdag 2019 Ulrik Brandin Erik Hansson Ulrik Brandin och Erik Hansson OKG 1 Agenda Orientering
Deformationsmätning av Oskarshamn 3s reaktorinneslutning i samband med täthetsprovning Kraftindustrins betongdag 2019 Ulrik Brandin Erik Hansson Ulrik Brandin och Erik Hansson OKG 1 Agenda Orientering
Deformationsberäkning runt tunnlar under Sabbatsberg 18
 Svenska Bostäder Deformationsberäkning runt tunnlar under Sabbatsberg 18 Luleå 2015-09-17 Deformationsberäkning runt tunnlar under Sabbatsberg 18 Datum 2015-09-17 Uppdragsnummer 1320007726/1320016324 Ivan
Svenska Bostäder Deformationsberäkning runt tunnlar under Sabbatsberg 18 Luleå 2015-09-17 Deformationsberäkning runt tunnlar under Sabbatsberg 18 Datum 2015-09-17 Uppdragsnummer 1320007726/1320016324 Ivan
Skillnaden mellan olika sätt att understödja en kaross. (Utvärdering av olika koncept för chassin till en kompositcontainer för godstransport på väg.
 Projektnummer Kund Rapportnummer D4.089.00 Lätta karossmoduler TR08-007 Datum Referens Revision 2008-10-27 Registrerad Utfärdad av Granskad av Godkänd av Klassificering Rolf Lundström Open Skillnaden mellan
Projektnummer Kund Rapportnummer D4.089.00 Lätta karossmoduler TR08-007 Datum Referens Revision 2008-10-27 Registrerad Utfärdad av Granskad av Godkänd av Klassificering Rolf Lundström Open Skillnaden mellan
Lösningsförslag, Inlämningsuppgift 2, PPU203 VT16.
 Lösningsförslag, Inlämningsuppgift 2, PPU203 VT16. Deluppgift 1: En segelbåt med vinden rakt i ryggen har hissat spinnakern. Anta att segelbåtens mast är ledad i botten, spinnakern drar masttoppen snett
Lösningsförslag, Inlämningsuppgift 2, PPU203 VT16. Deluppgift 1: En segelbåt med vinden rakt i ryggen har hissat spinnakern. Anta att segelbåtens mast är ledad i botten, spinnakern drar masttoppen snett
BeFo-projekt #350. Tunneldrivning i heterogena förhållanden. Översiktlig studie av styrande egenskaper avseende deformationer
 BeFo-projekt #350 Tunneldrivning i heterogena förhållanden Översiktlig studie av styrande egenskaper avseende deformationer Magnus Eriksson, SGI (nuv. Trafikverket) Rebecca Bertilsson, SGI Jonny Sjöberg,
BeFo-projekt #350 Tunneldrivning i heterogena förhållanden Översiktlig studie av styrande egenskaper avseende deformationer Magnus Eriksson, SGI (nuv. Trafikverket) Rebecca Bertilsson, SGI Jonny Sjöberg,
Lösningsskisser till Tentamen 0i Hållfasthetslära 1 för 0 Z2 (TME017), = @ verkar 8 (enbart) skjuvspänningen xy =1.5MPa. med, i detta fall,
 Huvudspänningar oc uvudspänningsriktningar n från: Huvudtöjningar oc uvudtöjningsriktningar n från: (S I)n = 0 ) det(s I) =0 ösningsskisser till där S är spänningsmatrisen Tentamen 0i Hållfastetslära för
Huvudspänningar oc uvudspänningsriktningar n från: Huvudtöjningar oc uvudtöjningsriktningar n från: (S I)n = 0 ) det(s I) =0 ösningsskisser till där S är spänningsmatrisen Tentamen 0i Hållfastetslära för
Hållfasthetslära. Böjning och vridning av provstav. Laboration 2. Utförs av:
 Hållfasthetslära Böjning och vridning av provstav Laboration 2 Utförs av: Habre Henrik Bergman Martin Book Mauritz Edlund Muzammil Kamaly William Sjöström Uppsala 2015 10 08 Innehållsförteckning 0. Förord
Hållfasthetslära Böjning och vridning av provstav Laboration 2 Utförs av: Habre Henrik Bergman Martin Book Mauritz Edlund Muzammil Kamaly William Sjöström Uppsala 2015 10 08 Innehållsförteckning 0. Förord
Spänning och töjning (kap 4) Stång
 Föreläsning 3 Spänning och töjning Spänning och töjning (kap 4) Stång Fackverk Strukturmekanik FM60 Materialmekanik SMA10 Avdelningen för Bggnadskonstruktion TH Campus Helsingborg Balk Ram Spänning (kraftmått)
Föreläsning 3 Spänning och töjning Spänning och töjning (kap 4) Stång Fackverk Strukturmekanik FM60 Materialmekanik SMA10 Avdelningen för Bggnadskonstruktion TH Campus Helsingborg Balk Ram Spänning (kraftmått)
kv Trollhättan, Stockholm PM angående bergspänningar vid ombyggnad
 kv Trollhättan, Stockholm PM angående bergspänningar vid ombyggnad Uppdrag Uppdraget att utföra denna utredning har erhållits av AMF Fastigheter. Syftet är undersöka inverkan på spänningar i jord och berg
kv Trollhättan, Stockholm PM angående bergspänningar vid ombyggnad Uppdrag Uppdraget att utföra denna utredning har erhållits av AMF Fastigheter. Syftet är undersöka inverkan på spänningar i jord och berg
Effektiv användning av bergförstärkning vid tunnelbyggande genom förbättrade analysmetoder för samverkan mellan berg och sprutbetong
 Effektiv användning av bergförstärkning vid tunnelbyggande genom förbättrade analysmetoder för samverkan mellan berg och sprutbetong Författare: Andreas Sjölander KTH Handledare: Anders Ansell KTH Richard
Effektiv användning av bergförstärkning vid tunnelbyggande genom förbättrade analysmetoder för samverkan mellan berg och sprutbetong Författare: Andreas Sjölander KTH Handledare: Anders Ansell KTH Richard
SVÄNGNINGSTIDEN FÖR EN PENDEL
 Institutionen för fysik 2012-05-21 Umeå universitet SVÄNGNINGSTIDEN FÖR EN PENDEL SAMMANFATTNING Ändamålet med experimentet är att undersöka den matematiska modellen för en fysikalisk pendel. Vi har mätt
Institutionen för fysik 2012-05-21 Umeå universitet SVÄNGNINGSTIDEN FÖR EN PENDEL SAMMANFATTNING Ändamålet med experimentet är att undersöka den matematiska modellen för en fysikalisk pendel. Vi har mätt
Laboration 1 Mekanik baskurs
 Laboration 1 Mekanik baskurs Utförs av: Henrik Bergman Mubarak Ali Uppsala 2015 01 19 Introduktion Gravitationen är en självklarhet i vår vardag, de är den som håller oss kvar på jorden. Gravitationen
Laboration 1 Mekanik baskurs Utförs av: Henrik Bergman Mubarak Ali Uppsala 2015 01 19 Introduktion Gravitationen är en självklarhet i vår vardag, de är den som håller oss kvar på jorden. Gravitationen
Tentamen i Hållfasthetslära AK
 Avdelningen för Hållfasthetslära Lunds Tekniska Högskola, LTH Tentamen i Hållfasthetslära AK1 2017-04-18 Tentand är skyldig att visa upp fotolegitimation. Om sådan inte medförts till tentamen skall den
Avdelningen för Hållfasthetslära Lunds Tekniska Högskola, LTH Tentamen i Hållfasthetslära AK1 2017-04-18 Tentand är skyldig att visa upp fotolegitimation. Om sådan inte medförts till tentamen skall den
VSMA01 - Mekanik ERIK SERRANO
 VSMA01 - Mekanik ERIK SERRANO Innehåll Material Spänning, töjning, styvhet Dragning, tryck, skjuvning, böjning Stång, balk styvhet och bärförmåga Knäckning Exempel: Spänning i en stång x F A Töjning Normaltöjning
VSMA01 - Mekanik ERIK SERRANO Innehåll Material Spänning, töjning, styvhet Dragning, tryck, skjuvning, böjning Stång, balk styvhet och bärförmåga Knäckning Exempel: Spänning i en stång x F A Töjning Normaltöjning
Toleranser och gränsvärden För borrning och sågning i betong
 Toleranser och gränsvärden För borrning och sågning i betong Final SE August 2002 / revision 4, april 2004 HiB:s kansli: Lars Sandström Box 7835 103 98 Stockholm Tel: + 46 8 698 58 00 Fax: + 46 8 698 59
Toleranser och gränsvärden För borrning och sågning i betong Final SE August 2002 / revision 4, april 2004 HiB:s kansli: Lars Sandström Box 7835 103 98 Stockholm Tel: + 46 8 698 58 00 Fax: + 46 8 698 59
LABORATION 1 AVBILDNING OCH FÖRSTORING
 LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
Avancerade metoder för planering och uppföljning av betongkonstruktioner
 Avancerade metoder 1(7) Avancerade metoder för planering och uppföljning av betongkonstruktioner Slutrapportering av SBUF-projekt nr 11015 med rubricerad titel. Sammanfattning Aktuellt forskningsprojekt
Avancerade metoder 1(7) Avancerade metoder för planering och uppföljning av betongkonstruktioner Slutrapportering av SBUF-projekt nr 11015 med rubricerad titel. Sammanfattning Aktuellt forskningsprojekt
KB Hålstenen 2. Nobelberget Nacka. PM Bergteknik Upprättat av: Stefan Bognar Granskad av: Tomas Karlberg Godkänd av: Michael Lindberg
 KB Hålstenen 2 Nobelberget Nacka PM Bergteknik 2011-08-15 Upprättat av: Stefan Bognar Granskad av: Tomas Karlberg Godkänd av: Michael Lindberg PM Bergteknik 2011-08-15 Kund KB Hålstenen 2 David Johansson
KB Hålstenen 2 Nobelberget Nacka PM Bergteknik 2011-08-15 Upprättat av: Stefan Bognar Granskad av: Tomas Karlberg Godkänd av: Michael Lindberg PM Bergteknik 2011-08-15 Kund KB Hålstenen 2 David Johansson
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER
 EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
Material, form och kraft, F2
 Material, form och kraft, 2 Repetition Genomgång av orcepd uppgift 1 Spänning Töjning Huvudspänning Stvhet Krafter Krafter Vektorstorhet: storlek, riktning, angreppspunkt Kontaktkraft, kraft som verkar
Material, form och kraft, 2 Repetition Genomgång av orcepd uppgift 1 Spänning Töjning Huvudspänning Stvhet Krafter Krafter Vektorstorhet: storlek, riktning, angreppspunkt Kontaktkraft, kraft som verkar
1. Ett material har dragprovkurva enligt figuren.
 1. Ett material har dragprovkurva enligt figuren. a) Vad kallas ett sådant materialuppträdande? b) Rita i figuren in vad som händer vid avlastning till spänning = 0 från det markerade tillståndet ( 1,
1. Ett material har dragprovkurva enligt figuren. a) Vad kallas ett sådant materialuppträdande? b) Rita i figuren in vad som händer vid avlastning till spänning = 0 från det markerade tillståndet ( 1,
Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum:
 Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum: 00-06-0 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar kan
Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum: 00-06-0 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar kan
Bedömning Kastlängder och evakueringsområde, Cementas kalkbrott Skövde.
 Cementa AB Att: Fredric Cullberg Er ref.: FC Vår ref.: MJ Dok.nr.:1231 2033 R 03 Datum: 2011-12-08. Bedömning Kastlängder och evakueringsområde, Cementas kalkbrott Skövde. Allmänt om stenkastning I samband
Cementa AB Att: Fredric Cullberg Er ref.: FC Vår ref.: MJ Dok.nr.:1231 2033 R 03 Datum: 2011-12-08. Bedömning Kastlängder och evakueringsområde, Cementas kalkbrott Skövde. Allmänt om stenkastning I samband
Tentamen i Hållfasthetslära AK2 för M Torsdag , kl
 Avdelningen för Hållfasthetslära Lunds Tekniska Högskola, LTH Tentamen i Hållfasthetslära AK2 för M Torsdag 2015-06-04, kl. 8.00-13.00 Tentand är skyldig att visa upp fotolegitimation. Om sådan inte medförts
Avdelningen för Hållfasthetslära Lunds Tekniska Högskola, LTH Tentamen i Hållfasthetslära AK2 för M Torsdag 2015-06-04, kl. 8.00-13.00 Tentand är skyldig att visa upp fotolegitimation. Om sådan inte medförts
KOHESIVA LAGAR I SKJUVNING EN EXPERIMENTELL METOD MED PLASTICERANDE ADHERENDER
 KOHESIVA LAGAR I SKJUVNING EN EXPERIMENTELL METOD MED PLASTICERANDE ADHERENDER Tomas Walander 1 1 Materialmekanik, Högskolan i Skövde, Box 408, 541 28 Skövde, e-post: tomas.walander@his.se Bild 1 END NOTCH
KOHESIVA LAGAR I SKJUVNING EN EXPERIMENTELL METOD MED PLASTICERANDE ADHERENDER Tomas Walander 1 1 Materialmekanik, Högskolan i Skövde, Box 408, 541 28 Skövde, e-post: tomas.walander@his.se Bild 1 END NOTCH
Lathund fo r rapportskrivning: LATEX-mall. F orfattare Institutionen f or teknikvetenskap och matematik
 Lathund fo r rapportskrivning: LATEX-mall F orfattare forfattare@student.ltu.se Institutionen f or teknikvetenskap och matematik 31 maj 2017 1 Sammanfattning Sammanfattningen är fristående från rapporten
Lathund fo r rapportskrivning: LATEX-mall F orfattare forfattare@student.ltu.se Institutionen f or teknikvetenskap och matematik 31 maj 2017 1 Sammanfattning Sammanfattningen är fristående från rapporten
Betongprovning Hårdnad betong Elasticitetsmodul vid tryckprovning. Concrete testing Hardened concrete Modulus of elasticity in compression
 SVENSK STANDARD Fastställd 2005-02-18 Utgåva 2 Betongprovning Hårdnad betong Elasticitetsmodul vid tryckprovning Concrete testing Hardened concrete Modulus of elasticity in compression ICS 91.100.30 Språk:
SVENSK STANDARD Fastställd 2005-02-18 Utgåva 2 Betongprovning Hårdnad betong Elasticitetsmodul vid tryckprovning Concrete testing Hardened concrete Modulus of elasticity in compression ICS 91.100.30 Språk:
Inverkan från skala och passning på skjuvhållfastheten för bergsprickor
 Inverkan från skala och passning på skjuvhållfastheten för bergsprickor BeFo rapport nr. 128, 2013 Fredrik Johansson, Tekn Dr. KTH Jord och Bergmekanik / SWECO Grasselli G. Shear strength of rock joints
Inverkan från skala och passning på skjuvhållfastheten för bergsprickor BeFo rapport nr. 128, 2013 Fredrik Johansson, Tekn Dr. KTH Jord och Bergmekanik / SWECO Grasselli G. Shear strength of rock joints
Collaborative Product Development:
 Collaborative Product Development: a Purchasing Strategy for Small Industrialized House-building Companies Opponent: Erik Sandberg, LiU Institutionen för ekonomisk och industriell utveckling Vad är egentligen
Collaborative Product Development: a Purchasing Strategy for Small Industrialized House-building Companies Opponent: Erik Sandberg, LiU Institutionen för ekonomisk och industriell utveckling Vad är egentligen
OBS I Finland användes namnet Gilsonite för Uintaite
 NVF/Finska avdelningen Utskott 33 - asfaltbeläggningar FÖRBUNDSUTSKOTTSMÖTET 17. JUNI 22 PÅ NÅDENDAL SPA Jari Pihlajamäki Den eviga asfaltbeläggningen mot utmattningen? - erfarenheter från testsektioner
NVF/Finska avdelningen Utskott 33 - asfaltbeläggningar FÖRBUNDSUTSKOTTSMÖTET 17. JUNI 22 PÅ NÅDENDAL SPA Jari Pihlajamäki Den eviga asfaltbeläggningen mot utmattningen? - erfarenheter från testsektioner
Hållfasthetslära. HT1 7,5 hp halvfart Janne Carlsson
 Hållfasthetslära HT1 7,5 hp halvfart Janne Carlsson tisdag 11 september 8:15 10:00 Föreläsning 3 PPU203 Hållfasthetslära Förmiddagens agenda Fortsättning av föreläsning 2 Paus Föreläsning 3: Kapitel 4,
Hållfasthetslära HT1 7,5 hp halvfart Janne Carlsson tisdag 11 september 8:15 10:00 Föreläsning 3 PPU203 Hållfasthetslära Förmiddagens agenda Fortsättning av föreläsning 2 Paus Föreläsning 3: Kapitel 4,
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Tisdagen den 17 juni 2008 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 1,5 högskolepoäng, FK49 Tisdagen den 17 juni 28 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 1,5 högskolepoäng, FK49 Tisdagen den 17 juni 28 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare
Att planera bort störningar
 ISRN-UTH-INGUTB-EX-B-2014/08-SE Examensarbete 15 hp Juni 2014 Att planera bort störningar Verktyg för smartare tidplanering inom grundläggning Louise Johansson ATT PLANERA BORT STÖRNINGAR Verktyg för smartare
ISRN-UTH-INGUTB-EX-B-2014/08-SE Examensarbete 15 hp Juni 2014 Att planera bort störningar Verktyg för smartare tidplanering inom grundläggning Louise Johansson ATT PLANERA BORT STÖRNINGAR Verktyg för smartare
Maria Fransson. Handledare: Daniel Jönsson, Odont. Dr
 Klassificering av allvarlig kronisk parodontit: En jämförelse av fem olika klassificeringar utifrån prevalensen av allvarlig kronisk parodontit i en population från Kalmar län Maria Fransson Handledare:
Klassificering av allvarlig kronisk parodontit: En jämförelse av fem olika klassificeringar utifrån prevalensen av allvarlig kronisk parodontit i en population från Kalmar län Maria Fransson Handledare:
Kundts rör - ljudhastigheten i luft
 Kundts rör - ljudhastigheten i luft Laboration 4, FyL VT00 Sten Hellman FyL 3 00-03-1 Laborationen utförd 00-03-0 i par med Sune Svensson Assisten: Jörgen Sjölin 1. Inledning Syftet med försöket är att
Kundts rör - ljudhastigheten i luft Laboration 4, FyL VT00 Sten Hellman FyL 3 00-03-1 Laborationen utförd 00-03-0 i par med Sune Svensson Assisten: Jörgen Sjölin 1. Inledning Syftet med försöket är att
Analys av två timmerredens påverkan på lastbilsram
 EXAMENSARBETE 2008:167 CIV Analys av två timmerredens påverkan på lastbilsram Gustav Nordström CIVILINGENJÖRSPROGRAMMET Maskinteknik Luleå tekniska universitet Institutionen för Tillämpad fysik, maskin-
EXAMENSARBETE 2008:167 CIV Analys av två timmerredens påverkan på lastbilsram Gustav Nordström CIVILINGENJÖRSPROGRAMMET Maskinteknik Luleå tekniska universitet Institutionen för Tillämpad fysik, maskin-
Belastningsanalys, 5 poäng Töjning Materialegenskaper - Hookes lag
 Töjning - Strain Töjning har med en kropps deformation att göra. Genom ett materials elasticitet ändras dess dimensioner när det belastas En lång kropp förlängs mer än en kort kropp om tvärsnitt och belastning
Töjning - Strain Töjning har med en kropps deformation att göra. Genom ett materials elasticitet ändras dess dimensioner när det belastas En lång kropp förlängs mer än en kort kropp om tvärsnitt och belastning
Linköpings Universitet 2010-12-14 IFM - Kemi Yt- och Kolloidkemi - NKEC21 NOP/Kontaktvinkel_10.doc. Lab. 1 Mätning av ytspänning och kontaktvinkel
 Linköpings Universitet 2010-12-14 IFM - Kemi Yt- och Kolloidkemi - NKEC21 NOP/Kontaktvinkel_10.doc Lab. 1 Mätning av ytspänning och kontaktvinkel Mätning av ytspänning. Många olika metoder finns för att
Linköpings Universitet 2010-12-14 IFM - Kemi Yt- och Kolloidkemi - NKEC21 NOP/Kontaktvinkel_10.doc Lab. 1 Mätning av ytspänning och kontaktvinkel Mätning av ytspänning. Många olika metoder finns för att
Eurokod 3 del 1-2 Brandteknisk dimensionering av stålkonstruktioner
 Eurokod 3 del 1-2 Brandteknisk dimensionering av stålkonstruktioner Peter Karlström, Konkret Rådgivande Ingenjörer i Stockholm AB Allmänt EN 1993-1-2 (Eurokod 3 del 1-2) är en av totalt 20 delar som handlar
Eurokod 3 del 1-2 Brandteknisk dimensionering av stålkonstruktioner Peter Karlström, Konkret Rådgivande Ingenjörer i Stockholm AB Allmänt EN 1993-1-2 (Eurokod 3 del 1-2) är en av totalt 20 delar som handlar
96 Påverkar de beräknade avsänkningarna på ett betydande sätt Natura 2000-området Storskäret?
 2017-10-24 1 96 Påverkar de beräknade avsänkningarna på ett betydande sätt Natura 2000-området Storskäret? 2017-10-24 2 Skulle de beräknade avsänkningarna på ett betydande sätt kunna påverka Natura 2000-området
2017-10-24 1 96 Påverkar de beräknade avsänkningarna på ett betydande sätt Natura 2000-området Storskäret? 2017-10-24 2 Skulle de beräknade avsänkningarna på ett betydande sätt kunna påverka Natura 2000-området
EXAMINATION KVANTITATIV METOD vt-11 (110204)
 ÖREBRO UNIVERSITET Hälsoakademin Idrott B Vetenskaplig metod EXAMINATION KVANTITATIV METOD vt-11 (110204) Examinationen består av 11 frågor, flera med tillhörande följdfrågor. Besvara alla frågor i direkt
ÖREBRO UNIVERSITET Hälsoakademin Idrott B Vetenskaplig metod EXAMINATION KVANTITATIV METOD vt-11 (110204) Examinationen består av 11 frågor, flera med tillhörande följdfrågor. Besvara alla frågor i direkt
Tentamen i matematik. f(x) = ln(ln(x)),
 Lösningsförslag Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA52G Matematisk Analys MA23G Matematisk analys för ingenjörer Tentamensdag: 203-05- kl 4.30-9.30 Hjälpmedel : Inga hjälpmedel utöver
Lösningsförslag Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA52G Matematisk Analys MA23G Matematisk analys för ingenjörer Tentamensdag: 203-05- kl 4.30-9.30 Hjälpmedel : Inga hjälpmedel utöver
Biomekanik Belastningsanalys
 Biomekanik Belastningsanalys Skillnad? Biomekanik Belastningsanalys Yttre krafter och moment Hastigheter och accelerationer Inre spänningar, töjningar och deformationer (Dynamiska påkänningar) I de delar
Biomekanik Belastningsanalys Skillnad? Biomekanik Belastningsanalys Yttre krafter och moment Hastigheter och accelerationer Inre spänningar, töjningar och deformationer (Dynamiska påkänningar) I de delar
Experimentella metoder, FK3001. Datorövning: Finn ett samband
 Experimentella metoder, FK3001 Datorövning: Finn ett samband 1 Inledning Den här övningen går ut på att belysa hur man kan utnyttja dimensionsanalys tillsammans med mätningar för att bestämma fysikaliska
Experimentella metoder, FK3001 Datorövning: Finn ett samband 1 Inledning Den här övningen går ut på att belysa hur man kan utnyttja dimensionsanalys tillsammans med mätningar för att bestämma fysikaliska
Vinjetter TDDC91 Datastrukturer och algoritmer
 Vinjetter TDDC91 Datastrukturer och algoritmer 17 augusti 2015 2 Scenario 1 Man har inom Posten Logistik AB skrivit programvara för sortering av kundinformation och vill standardisera användningen av sorteringsalgoritmer.
Vinjetter TDDC91 Datastrukturer och algoritmer 17 augusti 2015 2 Scenario 1 Man har inom Posten Logistik AB skrivit programvara för sortering av kundinformation och vill standardisera användningen av sorteringsalgoritmer.
Värmdöpumpen AB. TEKNISK MANUAL -- Robit Casing System ROX -- TOPPHAMMARE ROX-DTH -- SÄNKHAMMARE
 Värmdöpumpen AB TEKNISK MANUAL -- Robit Casing System ROX -- TOPPHAMMARE ROX-DTH -- SÄNKHAMMARE Värmdöpumpen AB www.varmdopumpen.se Box 2101 Tel: 08-978037.971915 127 02 Skärholmen Fax:08-881344 1. INTRODUKTION
Värmdöpumpen AB TEKNISK MANUAL -- Robit Casing System ROX -- TOPPHAMMARE ROX-DTH -- SÄNKHAMMARE Värmdöpumpen AB www.varmdopumpen.se Box 2101 Tel: 08-978037.971915 127 02 Skärholmen Fax:08-881344 1. INTRODUKTION
TEORETISKA BERÄKNINGAR PÅ EFFEKTEN AV BORRHÅLSBOOSTER
 UPPDRAG LiV Optimering bergvärmeanlägg UPPDRAGSNUMMER 0000 UPPDRAGSLEDARE Sten Bäckström UPPRÄTTAD AV Michael Hägg DATUM TEORETISKA BERÄKNINGAR PÅ EFFEKTEN AV BORRHÅLSBOOSTER BAKGRUND Energiutbytet mellan
UPPDRAG LiV Optimering bergvärmeanlägg UPPDRAGSNUMMER 0000 UPPDRAGSLEDARE Sten Bäckström UPPRÄTTAD AV Michael Hägg DATUM TEORETISKA BERÄKNINGAR PÅ EFFEKTEN AV BORRHÅLSBOOSTER BAKGRUND Energiutbytet mellan
Möjligheter och begränsningar hos höghållfasta stål
 Möjligheter och begränsningar hos höghållfasta stål Användning av höghållfasta stål har möjliggjort nya typer av konstruktionslösningar. Kunskap om deras möjligheter och begränsningar kan därmed bidra
Möjligheter och begränsningar hos höghållfasta stål Användning av höghållfasta stål har möjliggjort nya typer av konstruktionslösningar. Kunskap om deras möjligheter och begränsningar kan därmed bidra
Geoenergi REGEOCITIES i Karlstad. Jessica Benson & Oskar Räftegård Karlstad 2014-09-30
 Geoenergi REGEOCITIES i Karlstad Jessica Benson & Oskar Räftegård SP Karlstad 2014-09-30 Grundläggande om geoenergi Byggnadens värmebehov Fastighetsgräns KÖPT ENERGI Användning Återvinning Behov Energiförlust
Geoenergi REGEOCITIES i Karlstad Jessica Benson & Oskar Räftegård SP Karlstad 2014-09-30 Grundläggande om geoenergi Byggnadens värmebehov Fastighetsgräns KÖPT ENERGI Användning Återvinning Behov Energiförlust
Sensorer, effektorer och fysik. Mätning av töjning, kraft, tryck, förflyttning, hastighet, vinkelhastighet, acceleration
 Sensorer, effektorer och fysik Mätning av töjning, kraft, tryck, förflyttning, hastighet, vinkelhastighet, acceleration Töjning Betrakta en stav med längden L som under inverkan av en kraft F töjs ut en
Sensorer, effektorer och fysik Mätning av töjning, kraft, tryck, förflyttning, hastighet, vinkelhastighet, acceleration Töjning Betrakta en stav med längden L som under inverkan av en kraft F töjs ut en
Optimering av isoleringstjocklek på ackumulatortank
 Optimering av isoleringstjocklek på ackumulatortank Projektarbete i kursen Simulering och optimering av energisystem, 5p Handledare: Lars Bäckström Tillämpad fysik och elektronik 005-05-7 Bakgrund Umeå
Optimering av isoleringstjocklek på ackumulatortank Projektarbete i kursen Simulering och optimering av energisystem, 5p Handledare: Lars Bäckström Tillämpad fysik och elektronik 005-05-7 Bakgrund Umeå
Bostäder vid Vällkullevägen inom Kullbäckstorp 2:2 mfl. Bahatin Gündüz 010 505 47 81 bahatin.gunduz@afconsult.com
 Härryda kommun Bostäder vid Vällkullevägen inom Kullbäckstorp 2:2 mfl. Teknisk PM Geoteknik Underlag för detaljplan 2012-06-29 Handläggare: i samråd med: Bahatin Gündüz 010 505 47 81 bahatin.gunduz@afconsult.com
Härryda kommun Bostäder vid Vällkullevägen inom Kullbäckstorp 2:2 mfl. Teknisk PM Geoteknik Underlag för detaljplan 2012-06-29 Handläggare: i samråd med: Bahatin Gündüz 010 505 47 81 bahatin.gunduz@afconsult.com
Final i Wallenbergs Fysikpris
 Final i Wallenbergs Fysikpris 26-27 mars 2010. Teoriprov Lösningsförslag 1. a) Vattens värmekapacitivitet: Isens värmekapacitivitet: Smältvärmet: Kylmaskinen drivs med spänningen och strömmen. Kylmaskinens
Final i Wallenbergs Fysikpris 26-27 mars 2010. Teoriprov Lösningsförslag 1. a) Vattens värmekapacitivitet: Isens värmekapacitivitet: Smältvärmet: Kylmaskinen drivs med spänningen och strömmen. Kylmaskinens
Module 6: Integrals and applications
 Department of Mathematics SF65 Calculus Year 5/6 Module 6: Integrals and applications Sections 6. and 6.5 and Chapter 7 in Calculus by Adams and Essex. Three lectures, two tutorials and one seminar. Important
Department of Mathematics SF65 Calculus Year 5/6 Module 6: Integrals and applications Sections 6. and 6.5 and Chapter 7 in Calculus by Adams and Essex. Three lectures, two tutorials and one seminar. Important
Luddborttagning. Institutionen för produkt- och produktionsutveckling. Chalmers tekniska högskola Göteborg. Grupp E3.
 Luddborttagning Institutionen för produkt- och produktionsutveckling Chalmers tekniska högskola Göteborg Grupp E3 Jens Ekman 79009 Christoffer Routledge 8700 Ola Karlsson 860426 Axel Brown 860930 Jonny
Luddborttagning Institutionen för produkt- och produktionsutveckling Chalmers tekniska högskola Göteborg Grupp E3 Jens Ekman 79009 Christoffer Routledge 8700 Ola Karlsson 860426 Axel Brown 860930 Jonny
Hållfasthetslära Lektion 2. Hookes lag Materialdata - Dragprov
 Hållfasthetslära Lektion 2 Hookes lag Materialdata - Dragprov Dagens lektion Mål med dagens lektion Sammanfattning av förra lektionen Vad har vi lärt oss hittills? Hookes lag Hur förhåller sig normalspänning
Hållfasthetslära Lektion 2 Hookes lag Materialdata - Dragprov Dagens lektion Mål med dagens lektion Sammanfattning av förra lektionen Vad har vi lärt oss hittills? Hookes lag Hur förhåller sig normalspänning
VSMA01 - Mekanik ERIK SERRANO
 VSMA01 - Mekanik ERIK SERRANO Repetition Krafter Representation, komposanter Friläggning och jämvikt Friktion Element och upplag stång, lina, balk Spänning och töjning Böjning Knäckning Newtons lagar Lag
VSMA01 - Mekanik ERIK SERRANO Repetition Krafter Representation, komposanter Friläggning och jämvikt Friktion Element och upplag stång, lina, balk Spänning och töjning Böjning Knäckning Newtons lagar Lag
Kurskod: TAIU06 MATEMATISK STATISTIK Provkod: TENA 31 May 2016, 8:00-12:00. English Version
 Kurskod: TAIU06 MATEMATISK STATISTIK Provkod: TENA 31 May 2016, 8:00-12:00 Examiner: Xiangfeng Yang (Tel: 070 0896661). Please answer in ENGLISH if you can. a. Allowed to use: a calculator, Formelsamling
Kurskod: TAIU06 MATEMATISK STATISTIK Provkod: TENA 31 May 2016, 8:00-12:00 Examiner: Xiangfeng Yang (Tel: 070 0896661). Please answer in ENGLISH if you can. a. Allowed to use: a calculator, Formelsamling
Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum:
 Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum: 2004-08-21 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar
Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum: 2004-08-21 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar
Solar cells. 2.0 Inledning. Utrustning som används i detta experiment visas i Fig. 2.1.
 Solar cells 2.0 Inledning Utrustning som används i detta experiment visas i Fig. 2.1. Figure 2.1 Utrustning som används i experiment E2. Utrustningslista (se Fig. 2.1): A, B: Två solceller C: Svart plastlåda
Solar cells 2.0 Inledning Utrustning som används i detta experiment visas i Fig. 2.1. Figure 2.1 Utrustning som används i experiment E2. Utrustningslista (se Fig. 2.1): A, B: Två solceller C: Svart plastlåda
Tentamen i Matematik 2: M0030M.
 Tentamen i Matematik 2: M0030M. Datum: 2010-01-12 Skrivtid: 09:00 14:00 Antal uppgifter: 6 ( 30 poäng ). Jourhavande lärare: Norbert Euler Telefon: 0920-492878 Tillåtna hjälpmedel: Inga Till alla uppgifterna
Tentamen i Matematik 2: M0030M. Datum: 2010-01-12 Skrivtid: 09:00 14:00 Antal uppgifter: 6 ( 30 poäng ). Jourhavande lärare: Norbert Euler Telefon: 0920-492878 Tillåtna hjälpmedel: Inga Till alla uppgifterna
P650 - Takscreen. Installationsguide EN
 P650 - Takscreen Installationsguide 1309-150507EN V650-Tallinn Installation manual Montera främre linhjul 12 13 Placera linan över linhjulet och skruva tillbaka täcklocket på linhjulhuset (7). Öppna linhjulshuset
P650 - Takscreen Installationsguide 1309-150507EN V650-Tallinn Installation manual Montera främre linhjul 12 13 Placera linan över linhjulet och skruva tillbaka täcklocket på linhjulhuset (7). Öppna linhjulshuset
Matrismetod för analys av stångbärverk
 KTH Hållfasthetslära, J aleskog, September 010 1 Inledning Matrismetod för analys av stångbärverk Vid analys av stångbärverk är målet att bestämma belastningen i varje stång samt att beräkna deformationen
KTH Hållfasthetslära, J aleskog, September 010 1 Inledning Matrismetod för analys av stångbärverk Vid analys av stångbärverk är målet att bestämma belastningen i varje stång samt att beräkna deformationen
Tektonik (plattektonikens resultat)
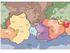 Tektonik (plattektonikens resultat) Tektonik: strukturell byggnad av jordens yttre delar i alla skalor Strukturgeologi: bergartrenas strukturer insamling av mätdata och analys (Kapitel 10 Crustal deformation)
Tektonik (plattektonikens resultat) Tektonik: strukturell byggnad av jordens yttre delar i alla skalor Strukturgeologi: bergartrenas strukturer insamling av mätdata och analys (Kapitel 10 Crustal deformation)
3 Fackverk. Stabil Instabil Stabil. Figur 3.2 Jämviktskrav för ett fackverk
 3 Fackverk 3.1 Inledning En struktur som består av ett antal stänger eller balkar och som kopplats ihop med mer eller mindre ledade knutpunkter kallas för fackverk. Exempel på fackverkskonstruktioner är
3 Fackverk 3.1 Inledning En struktur som består av ett antal stänger eller balkar och som kopplats ihop med mer eller mindre ledade knutpunkter kallas för fackverk. Exempel på fackverkskonstruktioner är
Bestämning av hängarkrafter i några av hängarna på Höga Kusten-bron
 Bestämning av hängarkrafter i några av hängarna på Höga Kusten-bron HÅKAN SUNDQUIST RAID KAROUMI CLAES KULLBERG STEFAN TRILLKOTT TRITA-BKN Teknisk Rapport 2005:12 Brobyggnad 2005 ISSN 1103-4289 ISRN Brobyggnad
Bestämning av hängarkrafter i några av hängarna på Höga Kusten-bron HÅKAN SUNDQUIST RAID KAROUMI CLAES KULLBERG STEFAN TRILLKOTT TRITA-BKN Teknisk Rapport 2005:12 Brobyggnad 2005 ISSN 1103-4289 ISRN Brobyggnad
INLEDNING... 2 MÅLSÄTTNING, EXPRIMENTPLATS OCH MÄTUTRUSTNING...
 Sidan 1 av 7 Innehåll INLEDNING... MÅLSÄTTNING, EXPRIMENTPLATS OCH MÄTUTRUSTNING... TEST LOKALISERING OCH MÅLSÄTTNING... TEORI OCH RESULTAT... TEORI... RESULTAT... 3 UTVÄRDERING... 6 APPENDIX... 6 APPENDIX
Sidan 1 av 7 Innehåll INLEDNING... MÅLSÄTTNING, EXPRIMENTPLATS OCH MÄTUTRUSTNING... TEST LOKALISERING OCH MÅLSÄTTNING... TEORI OCH RESULTAT... TEORI... RESULTAT... 3 UTVÄRDERING... 6 APPENDIX... 6 APPENDIX
Självkörande bilar. Alvin Karlsson TE14A 9/3-2015
 Självkörande bilar Alvin Karlsson TE14A 9/3-2015 Abstract This report is about driverless cars and if they would make the traffic safer in the future. Google is currently working on their driverless car
Självkörande bilar Alvin Karlsson TE14A 9/3-2015 Abstract This report is about driverless cars and if they would make the traffic safer in the future. Google is currently working on their driverless car
FALLSKYDDSSYSTEM STANDARD
 ANVÄNDARMANUAL FALLSKYDDSSYSTEM STANDARD INSTRUKTION ENLIGT EN 13374 www.safetyrespect.se info@safetyrespect.se Tel 063-130400 INNEHÅLLSFÖRTECKNING 3. Säkerhetsföreskrifter 4. Infästningar 5. Bultfot 6.
ANVÄNDARMANUAL FALLSKYDDSSYSTEM STANDARD INSTRUKTION ENLIGT EN 13374 www.safetyrespect.se info@safetyrespect.se Tel 063-130400 INNEHÅLLSFÖRTECKNING 3. Säkerhetsföreskrifter 4. Infästningar 5. Bultfot 6.
Material, form och kraft, F9
 Material, form och kraft, F9 Repetition Skivor, membran, plattor, skal Dimensionering Hållfasthet Styvhet/Deformationer Skivor Skiva: Strukturelement som är tunt i förhållande till utsträckningen i planet
Material, form och kraft, F9 Repetition Skivor, membran, plattor, skal Dimensionering Hållfasthet Styvhet/Deformationer Skivor Skiva: Strukturelement som är tunt i förhållande till utsträckningen i planet
E-II. Diffraktion på grund av ytspänningsvågor på vatten
 Q Sida 1 av 6 Diffraktion på grund av ytspänningsvågor på vatten Inledning Hur vågor bildas och utbreder sig på en vätskeyta är ett viktigt och välstuderat fenomen. Den återförande kraften på den oscillerande
Q Sida 1 av 6 Diffraktion på grund av ytspänningsvågor på vatten Inledning Hur vågor bildas och utbreder sig på en vätskeyta är ett viktigt och välstuderat fenomen. Den återförande kraften på den oscillerande
Linjär algebra förel. 10 Minsta kvadratmetoden
 Linjär algebra förel. 10 Minsta kvadratmetoden Niels Chr. Overgaard 015-09- c N. Chr. Overgaard Förel. 9 015-09- logoonly 1 / 17 Data från 1 vuxna män vikt (kg) längd (m) 58 1,69 83 1,77 80 1,79 77 1,80
Linjär algebra förel. 10 Minsta kvadratmetoden Niels Chr. Overgaard 015-09- c N. Chr. Overgaard Förel. 9 015-09- logoonly 1 / 17 Data från 1 vuxna män vikt (kg) längd (m) 58 1,69 83 1,77 80 1,79 77 1,80
MätKart Kvalitet i mätning med God mätsed
 MätKart 2017 Kvalitet i mätning med God mätsed Trimble Optical, Scanning and Imaging Trimble: Robert Jung, Teknisk produkt chef Trimble AB, Danderyd Dåtid och Nutid.. Principen har inte ändrats nämnvärt
MätKart 2017 Kvalitet i mätning med God mätsed Trimble Optical, Scanning and Imaging Trimble: Robert Jung, Teknisk produkt chef Trimble AB, Danderyd Dåtid och Nutid.. Principen har inte ändrats nämnvärt
Mätning av fokallängd hos okänd lins
 Mätning av fokallängd hos okänd lins Syfte Labbens syfte är i första hand att lära sig hantera mätfel och uppnå god noggrannhet, även med systematiska fel. I andra hand är syftet att hantera linser och
Mätning av fokallängd hos okänd lins Syfte Labbens syfte är i första hand att lära sig hantera mätfel och uppnå god noggrannhet, även med systematiska fel. I andra hand är syftet att hantera linser och
Bestämning av friktion
 Publikation 1987:142 Bestämning av friktion Metodbeskrivning 82:1983 1. ORIENTERING... 3 2. SAMMANFATTNING... 3 3. UTRUSTNING... 3 4.MÄTNING... 3 4.1 Alternativ l. Friktionspendel TRRL (figur 1)... 4 4.2
Publikation 1987:142 Bestämning av friktion Metodbeskrivning 82:1983 1. ORIENTERING... 3 2. SAMMANFATTNING... 3 3. UTRUSTNING... 3 4.MÄTNING... 3 4.1 Alternativ l. Friktionspendel TRRL (figur 1)... 4 4.2
Experimentella metoder 2013, Räkneövning 3
 Experimentella metoder 2013, Räkneövning 3 Problem 1: Fem studenter mätte längden av ett rum, deras resultat blev 3,30 m, 2,90 m, 3,70 m, 3,50 m, och 3,10 m. Inga uppgifter om mätnoggrannheten är kända.
Experimentella metoder 2013, Räkneövning 3 Problem 1: Fem studenter mätte längden av ett rum, deras resultat blev 3,30 m, 2,90 m, 3,70 m, 3,50 m, och 3,10 m. Inga uppgifter om mätnoggrannheten är kända.
Kurvlängd och geometri på en sfärisk yta
 325 Kurvlängd och geometri på en sfärisk yta Peter Sjögren Göteborgs Universitet 1. Inledning. Geometrin på en sfärisk yta liknar planets geometri, med flera intressanta skillnader. Som vi skall se nedan,
325 Kurvlängd och geometri på en sfärisk yta Peter Sjögren Göteborgs Universitet 1. Inledning. Geometrin på en sfärisk yta liknar planets geometri, med flera intressanta skillnader. Som vi skall se nedan,
VFA 5.4: Utrymningsbredd
 VFA 5.4: Utrymningsbredd VFA 5.4: UTRYMNINGSBREDD Syfte: Indata: Resultat: Att vid dimensionering av lokaler för över 150 pers. möjliggöra byte av en (1) utrymningsväg av bredden 1,2 meter mot två (2)
VFA 5.4: Utrymningsbredd VFA 5.4: UTRYMNINGSBREDD Syfte: Indata: Resultat: Att vid dimensionering av lokaler för över 150 pers. möjliggöra byte av en (1) utrymningsväg av bredden 1,2 meter mot två (2)
SKB anger i det följande när svar på delfrågorna 1-4 kommer att lämnas. För delfråga 5 ges svar i form av kompletterande information till ansökan.
 Strålsäkerhetsmyndigheten Att: Ansi Gerhardsson 171 16 Stockholm DokumentID 1385067 Ärende Handläggare Patrik Sellin Er referens SSM2011-2426-81 Kvalitetssäkrad av Olle Olsson Saida Engström Godkänd av
Strålsäkerhetsmyndigheten Att: Ansi Gerhardsson 171 16 Stockholm DokumentID 1385067 Ärende Handläggare Patrik Sellin Er referens SSM2011-2426-81 Kvalitetssäkrad av Olle Olsson Saida Engström Godkänd av
Livens inverkan på styvheten
 Livens inverkan på styvheten Sidan 1 av 9 Golv förstärkta med liv är tänkta att användas så att belastningen ligger i samma riktning som liven. Då ger liven en avsevärd förstyvning jämfört med en sandwich
Livens inverkan på styvheten Sidan 1 av 9 Golv förstärkta med liv är tänkta att användas så att belastningen ligger i samma riktning som liven. Då ger liven en avsevärd förstyvning jämfört med en sandwich
Mekanisk liggkomfort hos sängar/madrasser
 Mekanisk liggkomfort Man hör ofta att en säng är skön att ligga i - att den ger god komfort. Med detta underförstås, att sängen är mjuk och att den därmed har förmåga att fördela kroppstyngden så, att
Mekanisk liggkomfort Man hör ofta att en säng är skön att ligga i - att den ger god komfort. Med detta underförstås, att sängen är mjuk och att den därmed har förmåga att fördela kroppstyngden så, att
Strålningsfält och fotoner. Våren 2013
 Strålningsfält och fotoner Våren 2013 1. Fält i rymden Vi har lärt oss att beräkna elektriska fält utgående från laddningarna som orsakar dem Kan vi härleda nånting åt andra hållet? 2 1.1 Gauss lag Låt
Strålningsfält och fotoner Våren 2013 1. Fält i rymden Vi har lärt oss att beräkna elektriska fält utgående från laddningarna som orsakar dem Kan vi härleda nånting åt andra hållet? 2 1.1 Gauss lag Låt
Injektering i teori och praktik Fördelning av bergmassans hydrauliska egenskaper, bergmassans respons vid injektering och inläckage i tunnlar.
 Injektering i teori och praktik Fördelning av bergmassans hydrauliska egenskaper, bergmassans respons vid injektering och inläckage i tunnlar. Björn Stille Lic / Department of Civil and Environmental Engineering,
Injektering i teori och praktik Fördelning av bergmassans hydrauliska egenskaper, bergmassans respons vid injektering och inläckage i tunnlar. Björn Stille Lic / Department of Civil and Environmental Engineering,
Solowheel. Namn: Jesper Edqvist. Klass: TE14A. Datum: 2015-03-09
 Solowheel Namn: Jesper Edqvist Klass: TE14A Datum: 2015-03-09 Abstract We got an assignment that we should do an essay about something we wanted to dig deeper into. In my case I dug deeper into what a
Solowheel Namn: Jesper Edqvist Klass: TE14A Datum: 2015-03-09 Abstract We got an assignment that we should do an essay about something we wanted to dig deeper into. In my case I dug deeper into what a
Vejdimensionering som bygger på observationsmetodik
 Vejdimensionering som bygger på observationsmetodik Ulf Ekdahl Ekdahl GeoDesign AB NCHRP Project 21-09 Intelligent Soil Compaction Systems FoU arbete sommaren 2008 i Dynapacs forskningshall Analytisk vägdimensionering
Vejdimensionering som bygger på observationsmetodik Ulf Ekdahl Ekdahl GeoDesign AB NCHRP Project 21-09 Intelligent Soil Compaction Systems FoU arbete sommaren 2008 i Dynapacs forskningshall Analytisk vägdimensionering
1. Compute the following matrix: (2 p) 2. Compute the determinant of the following matrix: (2 p)
 UMEÅ UNIVERSITY Department of Mathematics and Mathematical Statistics Pre-exam in mathematics Linear algebra 2012-02-07 1. Compute the following matrix: (2 p 3 1 2 3 2 2 7 ( 4 3 5 2 2. Compute the determinant
UMEÅ UNIVERSITY Department of Mathematics and Mathematical Statistics Pre-exam in mathematics Linear algebra 2012-02-07 1. Compute the following matrix: (2 p 3 1 2 3 2 2 7 ( 4 3 5 2 2. Compute the determinant
TENTAMEN MTGC12, MATERIALTEKNIK II / MTGC10 MATERIALVAL
 Materialteknik, Jens Bergström 2016-01-21 TENTAMEN MTGC12, MATERIALTEKNIK II / MTGC10 MATERIALVAL Tid: Måndagen 25 januari, 2016 Tentamen omfattar genomgånget kursmaterial. Hjälpmedel: Kalkylator Poängsättning:
Materialteknik, Jens Bergström 2016-01-21 TENTAMEN MTGC12, MATERIALTEKNIK II / MTGC10 MATERIALVAL Tid: Måndagen 25 januari, 2016 Tentamen omfattar genomgånget kursmaterial. Hjälpmedel: Kalkylator Poängsättning:
Bromallar Eurocode. Bromall: Omlottskarvning. Innehåll. Minimimått vid omlottskarvning av armeringsstänger samt beräkning av skarvlängd.
 Bromallar Eurocode Bromall: Omlottskarvning Minimimått vid omlottskarvning av armeringsstänger samt beräkning av skarvlängd. Rev: A EN 1992-1-1: 2004 Innehåll 1 Allmänt 2 2 Omlottskarvar 4 3 Skarvlängd
Bromallar Eurocode Bromall: Omlottskarvning Minimimått vid omlottskarvning av armeringsstänger samt beräkning av skarvlängd. Rev: A EN 1992-1-1: 2004 Innehåll 1 Allmänt 2 2 Omlottskarvar 4 3 Skarvlängd
Avstånd vad är det? PC-DMIS dagar 2016
 Avstånd vad är det? PC-DMIS dagar 2016 Avstånd - vad är det? Fråga: Finns det något enklare än ett avstånd en siffra som visar hur långt det är från A till B? Svar: Nästan allting är enklare än avstånd!
Avstånd vad är det? PC-DMIS dagar 2016 Avstånd - vad är det? Fråga: Finns det något enklare än ett avstånd en siffra som visar hur långt det är från A till B? Svar: Nästan allting är enklare än avstånd!
Belastningsanalys, 5 poäng Tvärkontraktion Temp. inverkan Statiskt obestämd belastning
 Tvärkontraktion När en kropp belastas med en axiell last i en riktning förändras längden inte bara i den lastens riktning Det sker en samtidig kontraktion (sammandragning) i riktningar tvärs dragriktningen.
Tvärkontraktion När en kropp belastas med en axiell last i en riktning förändras längden inte bara i den lastens riktning Det sker en samtidig kontraktion (sammandragning) i riktningar tvärs dragriktningen.
Karta över Jorden - viktigt exempel. Sfär i (x, y, z) koordinater Funktionen som beskriver detta ser ut till att vara
 Föreläsning 1 Jag hettar Thomas Kragh och detta är kursen: Flervariabelanalys 1MA016/1MA183. E-post: thomas.kragh@math.uu.se Kursplan finns i studentportalens hemsida för denna kurs. Där är två spår: Spår
Föreläsning 1 Jag hettar Thomas Kragh och detta är kursen: Flervariabelanalys 1MA016/1MA183. E-post: thomas.kragh@math.uu.se Kursplan finns i studentportalens hemsida för denna kurs. Där är två spår: Spår
Forma komprimerat trä
 Forma komprimerat trä - maskinell bearbetning av fria former Peter Conradsson MÖBELSNICKERI Carl Malmsten Centrum för Träteknik & Design REG NR: LiU-IEI-TEK-G 07/0025 SE Oktober 2007 Omslagsbild: Stol
Forma komprimerat trä - maskinell bearbetning av fria former Peter Conradsson MÖBELSNICKERI Carl Malmsten Centrum för Träteknik & Design REG NR: LiU-IEI-TEK-G 07/0025 SE Oktober 2007 Omslagsbild: Stol
Projektmodell med kunskapshantering anpassad för Svenska Mässan Koncernen
 Examensarbete Projektmodell med kunskapshantering anpassad för Svenska Mässan Koncernen Malin Carlström, Sandra Mårtensson 2010-05-21 Ämne: Informationslogistik Nivå: Kandidat Kurskod: 2IL00E Projektmodell
Examensarbete Projektmodell med kunskapshantering anpassad för Svenska Mässan Koncernen Malin Carlström, Sandra Mårtensson 2010-05-21 Ämne: Informationslogistik Nivå: Kandidat Kurskod: 2IL00E Projektmodell
