Lathund fo r rapportskrivning: LATEX-mall. F orfattare Institutionen f or teknikvetenskap och matematik
|
|
|
- Tobias Jonasson
- för 8 år sedan
- Visningar:
Transkript
1 Lathund fo r rapportskrivning: LATEX-mall F orfattare forfattare@student.ltu.se Institutionen f or teknikvetenskap och matematik 31 maj
2 Sammanfattning Sammanfattningen är fristående från rapporten i övrigt. Man skall kunna läsa sammanfattningen utan att ha läst rapporten, och tvärtom. I sammanfattningen skall det finnas en kort beskrivning av problem, metod och de viktigaste resultaten samt vad de medför. Den skall vara komplett, objektiv och lätt att förstå. Sammanfattningen skall sammanfatta arbetet och någon extra information, som inte finns i rapporten, får inte skrivas in i sammanfattningen. Sammanfattningen skall vara kort och bör maximalt innehålla ord. Abstract Sammanfattning på engelska. 2
3 Innehåll 1 Inledning 5 2 Teori Litteraturstudie Metod Experimentell uppställning Resultat Underrubrik vid behov Fler underrubriker om så behövs Diskussion och slutsatser 6 3
4 Beteckningar ρ Densitet (kg/m 3 ) A Area (m 2 ) 4
5 1 Inledning Inledningen introducerar läsaren till problemställningen och ger bakgrunden till problemet. Inledningen är viktig för det är här som läsaren skall ledas in i hur författaren tänkt. Hela avsnittet bör skrivas så att läsaren logiskt och motiverat leds fram till den problemställning som rapporten behandlar. I inledningen skall det finnas en översikt över närliggande tidigare arbeten inom ämnet. Även här gäller att göra läsaren intresserad så att hen läser vidare i rapporten. Slutklämmen i inledningen bör göras så att det blir en mjuk övergång från Inledning till nästa kapitel. Här kan vara exempel med numrerade referenser: kan beskrivas enligt [1]. Ge syftet med arbetet dvs vad som vill åstadkommas med arbetet, frågeställningar och vilka avgränsningar som finns. Målen skall vara specifikt klarlagda samt i rapportens slutsatser ska det tydligt framgå hur målen uppnåtts. 2 Teori Beskriv teori, antaganden och annat som ligger till grund för den metod och det arbetssätt som valts. Teorin ska belysa/diskutera/sammanfatta och koppla till problemställningen. Samtliga ekvationer, figurer och tabeller ska numreras i löpande ordning. Figurer och tabeller ska ha en kortfattad text som klart och tydligt anger vad de visar. Alla figurer och tabeller ska hänvisas till i löpande text. Exempelvis beskrivs en potensfunktion som y = Cx k (1) där exponenten k bestäms genom att logaritmera ekvation (1) ln y = ln C + k ln x z = m + kw (2) z = ln y plottas mot w = ln x och lutningen på grafen ger exponenten k ifall mätdata kan beskrivas som en potensfunktion. 2.1 Litteraturstudie 3 Metod Kan i vissa fall delas upp i metodbeskrivning, experimentell uppställning och arbetsgång. Att redogöra för sin metod är viktigt bland annat för att förklara varför den valda metoden ger ett tillförlitligt resultat. Alla antaganden och förenklingar måste anges och motiveras. Definiera matematiska modeller så att andra ingenjörer och forskare kan förstå vad du gjort. Exempelvis utnyttjades Microsoft Excel 2013 för att analysera mätresultaten och plotta mätdata. 5
6 3.1 Experimentell uppställning Alla eventuella försöksuppställningar beskrivs på ett sådant sätt att andra kan upprepa samma försök och verifiera dina resultat. Utnyttja figurer som förenklar din beskrivning. 4 Resultat Detta är förmodligen den största delen av rapporten. Här redovisas resultaten rakt på sak på ett objektivt/neutralt sätt. Ofta är det lämpligt att dela upp texten i ett antal underrubriker. Materialet måste presenteras i logisk ordning, vilket inte behöver vara den ordning i vilken försöket/arbetet har utförts. Läsaren skall kunna läsa rapporten utan att behöva bläddra fram och tillbaka. Det ska vara tydligt vad som är data respektive analys av data. Visas resultat i tabell- eller figurform så måste kortfattat beskrivas vad man ser i figurerna/tabellerna. De placeras i närheten (efter) där de först refererades. Som exempel visas fyra mätningar där variabel, 1, varierades. Resultat visas i tabell 1 nedan. variabel 1 (s) variabel 2 (m) variabel 3 (J) 0,351 0, ,457 1, ,873 2, ,10 3, Tabell 1: Förklarande text Med hjälp av mätvärdena i tabell 1 skapas en produktansats av typen potensfunktion t = CL α θ β m γ g δ (3) där C, α,..., δ är konstanter som ska bestämmas experimentellt. Avgiven värmemängd från brödrosten (variabel 3) som funktion av tiden variabel 1 visas i figur 1. Den linjära anpassningen i figuren visar att (variabel 3) = 351, 8 (variabel 1) 0, 3 (4) och tillförd värmeeffekt till brödrosten bestäms då till 351,8 W. 4.1 Underrubrik vid behov Fler underrubriker om så behövs 5 Diskussion och slutsatser Här diskuteras (vad betyder/medför) resultaten utifrån ett vidare perspektiv och ställs i relation exempelvis till tidigare arbeten, referera i sådant fall till 6
7 Figur 1: Exempelfigur som visar variabel 3 som funktion av variabel 1. dessa. Utgående härifrån dras nödvändiga slutsatser som ska svara på de mål som angivits och vad resultaten har för relevans. Koppla slutsatser till uppställda mål. Diskutera felkällor och osäkerheter. Det är även lämpligt att i denna del avsluta med förslag och rekommendationer på fortsatta studier och undersökningar i ämnet. Man kan dela upp diskussion, slutsatser och framtida studier i fristående kapitel. Referenser [1] Johan Sterte m. fl. Application of the seed-film method for the preparation of structured molecular sieve catalysts. I: Catalysis Today (2001), s
TENTAPLUGG.NU AV STUDENTER FÖR STUDENTER. Kursnamn Fysik 1. Datum LP Laboration Balkböjning. Kursexaminator. Betygsgränser.
 TENTAPLUGG.NU AV STUDENTER FÖR STUDENTER Kurskod F0004T Kursnamn Fysik 1 Datum LP2 10-11 Material Laboration Balkböjning Kursexaminator Betygsgränser Tentamenspoäng Övrig kommentar Sammanfattning Denna
TENTAPLUGG.NU AV STUDENTER FÖR STUDENTER Kurskod F0004T Kursnamn Fysik 1 Datum LP2 10-11 Material Laboration Balkböjning Kursexaminator Betygsgränser Tentamenspoäng Övrig kommentar Sammanfattning Denna
Examensarbete, Högskoleingenjör energiteknik, 15 hp Grundnivå
 Examensarbete, Högskoleingenjör energiteknik, 15 hp Grundnivå Studenten ska tillämpa kunskaper och färdigheter förvärvade inom utbildningsprogrammet genom att på ett självständigt och vetenskapligt sätt
Examensarbete, Högskoleingenjör energiteknik, 15 hp Grundnivå Studenten ska tillämpa kunskaper och färdigheter förvärvade inom utbildningsprogrammet genom att på ett självständigt och vetenskapligt sätt
Experimentella metoder, FK3001. Datorövning: Finn ett samband
 Experimentella metoder, FK3001 Datorövning: Finn ett samband 1 Inledning Den här övningen går ut på att belysa hur man kan utnyttja dimensionsanalys tillsammans med mätningar för att bestämma fysikaliska
Experimentella metoder, FK3001 Datorövning: Finn ett samband 1 Inledning Den här övningen går ut på att belysa hur man kan utnyttja dimensionsanalys tillsammans med mätningar för att bestämma fysikaliska
MINIMIKRAV VID RAPPORTSKRIVNING
 MINIMIKRAV VID RAPPORTSKRIVNING Denna kortfattade beskrivning består av två delar. En allmän del kring formatering etc och en del som tar upp viktiga aspekter i respektive rapportavsnitt. För en fylligare
MINIMIKRAV VID RAPPORTSKRIVNING Denna kortfattade beskrivning består av två delar. En allmän del kring formatering etc och en del som tar upp viktiga aspekter i respektive rapportavsnitt. För en fylligare
En pendels svängningstid
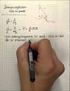 Använd denna exempelrapport som mall för din rapport. Mer detaljer hittar du i Lathund för rapportskrivning av Merkel, Andersson, Lundquist och Önnegren. Notera att denna exempelrapport beskriver ett mycket
Använd denna exempelrapport som mall för din rapport. Mer detaljer hittar du i Lathund för rapportskrivning av Merkel, Andersson, Lundquist och Önnegren. Notera att denna exempelrapport beskriver ett mycket
Att skriva teknisk ra r p a port r
 Att skriva teknisk rapport Innan du börjar, fråga: Varför skriver jag rapporten: syfte, avsikt vad vill du uppnå? Vilka ska läsa den, omfattning, språk? Vad behöver de veta? Disposition Titelsida Inledande
Att skriva teknisk rapport Innan du börjar, fråga: Varför skriver jag rapporten: syfte, avsikt vad vill du uppnå? Vilka ska läsa den, omfattning, språk? Vad behöver de veta? Disposition Titelsida Inledande
Mall för en kortare rapport/uppsats
 Mall för en kortare rapport/uppsats Detta dokument beskriver vad som ska ingå i en kortare vetenskaplig rapport. Du kommer att skriva rapporter på denna form i ett antal kurser under din utbildning, t.ex.
Mall för en kortare rapport/uppsats Detta dokument beskriver vad som ska ingå i en kortare vetenskaplig rapport. Du kommer att skriva rapporter på denna form i ett antal kurser under din utbildning, t.ex.
Labbrapport svängande skivor
 Labbrapport svängande skivor Erik Andersson Johan Schött Olof Berglund 11th October 008 Sammanfattning Grunden för att finna matematiska samband i fysiken kan vara lite svårt att förstå och hur man kan
Labbrapport svängande skivor Erik Andersson Johan Schött Olof Berglund 11th October 008 Sammanfattning Grunden för att finna matematiska samband i fysiken kan vara lite svårt att förstå och hur man kan
Fysikaliska modeller. Skapa modeller av en fysikalisk verklighet med hjälp av experiment. Peter Andersson IFM fysik, adjunkt
 Fysikaliska modeller Skapa modeller av en fysikalisk verklighet med hjälp av experiment Peter Andersson IFM fysik, adjunkt På denna föreläsning Vad är en fysikalisk modell? Linjärisering med hjälp av logaritmer
Fysikaliska modeller Skapa modeller av en fysikalisk verklighet med hjälp av experiment Peter Andersson IFM fysik, adjunkt På denna föreläsning Vad är en fysikalisk modell? Linjärisering med hjälp av logaritmer
Titel: Undertitel: Författarens namn och e-postadress. Framsidans utseende kan variera mellan olika institutioner
 Linköping Universitet, Campus Norrköping Inst/ Kurs Termin/år Titel: Undertitel: Författarens namn och e-postadress Framsidans utseende kan variera mellan olika institutioner Handledares namn Sammanfattning
Linköping Universitet, Campus Norrköping Inst/ Kurs Termin/år Titel: Undertitel: Författarens namn och e-postadress Framsidans utseende kan variera mellan olika institutioner Handledares namn Sammanfattning
Gymnasiearbete/ Naturvetenskaplig specialisering NA AGY. Redovisning
 Gymnasiearbete/ Naturvetenskaplig specialisering NA AGY Redovisning Redovisning av projekten Skriftligt i form av en slutrapport ( till handledaren via Urkund senast 11/4 (veckan innan påsklovet) Alla
Gymnasiearbete/ Naturvetenskaplig specialisering NA AGY Redovisning Redovisning av projekten Skriftligt i form av en slutrapport ( till handledaren via Urkund senast 11/4 (veckan innan påsklovet) Alla
Termodynamik, våglära och atomfysik (eller rätt och slätt inledande fysikkursen för n1)
 Termodynamik, våglära och atomfysik (eller rätt och slätt inledande fysikkursen för n1) Svängande stavar och fjädrar höstterminen 2007 Fysiska institutionen kurslaboratoriet LTH Svängande stavar och fjädrar
Termodynamik, våglära och atomfysik (eller rätt och slätt inledande fysikkursen för n1) Svängande stavar och fjädrar höstterminen 2007 Fysiska institutionen kurslaboratoriet LTH Svängande stavar och fjädrar
EXPERIMENTELLA METODER LABORATION 2 UPPTÄCK ETT SAMBAND BALKEN
 FYSIKUM Fysikum 21 mars 2005 Stockholms universitet EXPERIMENTELLA METODER LABORATION 2 UPPTÄCK ETT SAMBAND BALKEN FYSIKLINJEN ÅK1 Vårterminen 2005 Mål I den här laborationen skall du börja med att ställa
FYSIKUM Fysikum 21 mars 2005 Stockholms universitet EXPERIMENTELLA METODER LABORATION 2 UPPTÄCK ETT SAMBAND BALKEN FYSIKLINJEN ÅK1 Vårterminen 2005 Mål I den här laborationen skall du börja med att ställa
LABORATION 2 UPPTÄCK ETT SAMBAND
 Fysikum FK2002 - Fysikexperiment FK2004 - Exp. fysik för lärare Laborationsinstruktion (28 september 2010) LABORATION 2 UPPTÄCK ETT SAMBAND TÖMNING Mål Idenhärlaborationenskalldubörjamedattställauppenhypotes
Fysikum FK2002 - Fysikexperiment FK2004 - Exp. fysik för lärare Laborationsinstruktion (28 september 2010) LABORATION 2 UPPTÄCK ETT SAMBAND TÖMNING Mål Idenhärlaborationenskalldubörjamedattställauppenhypotes
Kursnamn XX poäng 2013-10-15. Rapportmall. Författare: (Skrivs i bokstavsordning om flera) Handledare:
 Kursnamn XX poäng 2013-10-15 Rapportmall Författare: (Skrivs i bokstavsordning om flera) Handledare: Innehållsförteckning En innehållsförteckning görs i Word när hela arbetet är klart. (Referenser, Innehållsförteckning,
Kursnamn XX poäng 2013-10-15 Rapportmall Författare: (Skrivs i bokstavsordning om flera) Handledare: Innehållsförteckning En innehållsförteckning görs i Word när hela arbetet är klart. (Referenser, Innehållsförteckning,
Gymnasiearbetets titel (huvudrubrik)
 Risbergska skolan Program Gymnasiearbetets titel (huvudrubrik) Underrubrik Titeln på rapporten måste givetvis motsvara innehållet. En kort överrubrik kan förtydligas med en underrubrik. Knut Knutsson BetvetA10
Risbergska skolan Program Gymnasiearbetets titel (huvudrubrik) Underrubrik Titeln på rapporten måste givetvis motsvara innehållet. En kort överrubrik kan förtydligas med en underrubrik. Knut Knutsson BetvetA10
Introduktion till Word och Excel
 Introduktion till Word och Excel HT 2006 Detta dokument baseras på Introduktion till datoranvändning för ingenjörsprogrammen skrivet av Stefan Pålsson 2005. Omarbetningen av detta dokument är gjord av
Introduktion till Word och Excel HT 2006 Detta dokument baseras på Introduktion till datoranvändning för ingenjörsprogrammen skrivet av Stefan Pålsson 2005. Omarbetningen av detta dokument är gjord av
Appendix i instruktionen
 Appendix i instruktionen Läs även Appendix A och Appendix B i instruktionerna till laboration 2 2010-10-05 Fysikexperiment, 7.5 hp 1 1 Linearisering genom logaritmering Ofta förekommer samband av typen:
Appendix i instruktionen Läs även Appendix A och Appendix B i instruktionerna till laboration 2 2010-10-05 Fysikexperiment, 7.5 hp 1 1 Linearisering genom logaritmering Ofta förekommer samband av typen:
Projektet. EDAA35 Föreläsning 7. Krav på uppgiften. Ert projektförslag. Inlämning av förslag. Egna idéer är välkomna!
 EDAA35 Föreläsning 7 OM PROJEKTET Projektet Genomförs i läsperiod 4, grupper om 3 studenter Information finns på kursens hemsida Målet är att ni ska använda den kunskap ni fått och omsätta den praktiskt
EDAA35 Föreläsning 7 OM PROJEKTET Projektet Genomförs i läsperiod 4, grupper om 3 studenter Information finns på kursens hemsida Målet är att ni ska använda den kunskap ni fått och omsätta den praktiskt
Skriftlig presentation
 Skriftlig presentation Målgruppsanpassat Syfte - informera - redovisa resultat - påverka/övertyga Rapportmall Struktur Löpsedelsteknik Kronologisk ordning Logisk ordning Alfabetisk ordning Rumlig indelning
Skriftlig presentation Målgruppsanpassat Syfte - informera - redovisa resultat - påverka/övertyga Rapportmall Struktur Löpsedelsteknik Kronologisk ordning Logisk ordning Alfabetisk ordning Rumlig indelning
Experimentella metoder 2013, Räkneövning 3
 Experimentella metoder 2013, Räkneövning 3 Problem 1: Fem studenter mätte längden av ett rum, deras resultat blev 3,30 m, 2,90 m, 3,70 m, 3,50 m, och 3,10 m. Inga uppgifter om mätnoggrannheten är kända.
Experimentella metoder 2013, Räkneövning 3 Problem 1: Fem studenter mätte längden av ett rum, deras resultat blev 3,30 m, 2,90 m, 3,70 m, 3,50 m, och 3,10 m. Inga uppgifter om mätnoggrannheten är kända.
Björn Åstrand
 HÖGSKOLAN I HALMSTAD Examensarbete Instruktioner Halvtidseminarium 2014 HT Björn Åstrand 2014-10-08 Björn Åstrand 2014 1 Halvtidsseminarium Vid halvtidsseminariet presenteras hittills uppnådda resultat
HÖGSKOLAN I HALMSTAD Examensarbete Instruktioner Halvtidseminarium 2014 HT Björn Åstrand 2014-10-08 Björn Åstrand 2014 1 Halvtidsseminarium Vid halvtidsseminariet presenteras hittills uppnådda resultat
Examensmål för gymnasieprogrammen http://www.skolverket.se/laroplaner-amnen-ochkurser/gymnasieutbildning/gymnasieskola/programstruktur-ochexamensmal
 Examensmål för gymnasieprogrammen http://www.skolverket.se/laroplaner-amnen-ochkurser/gymnasieutbildning/gymnasieskola/programstruktur-ochexamensmal Gymnasiearbetet Yrkesprogram: I målen för yrkesprogrammen
Examensmål för gymnasieprogrammen http://www.skolverket.se/laroplaner-amnen-ochkurser/gymnasieutbildning/gymnasieskola/programstruktur-ochexamensmal Gymnasiearbetet Yrkesprogram: I målen för yrkesprogrammen
4 Fler deriveringsregler
 4 Fler deriveringsregler 4. Dagens Teori Derivatan av potensfunktioner. Potensfunktioner med heltalsexponenter, som du redan kan derivera, kallas polynomfunktioner, som till exempel: f(x) = 2x4 x3 + 2x
4 Fler deriveringsregler 4. Dagens Teori Derivatan av potensfunktioner. Potensfunktioner med heltalsexponenter, som du redan kan derivera, kallas polynomfunktioner, som till exempel: f(x) = 2x4 x3 + 2x
Titel Mall för Examensarbeten (Arial 28/30 point size, bold)
 Titel Mall för Examensarbeten (Arial 28/30 point size, bold) SUBTITLE - Arial 16 / 19 pt FÖRFATTARE FÖRNAMN OCH EFTERNAMN - Arial 16 / 19 pt KTH ROYAL INSTITUTE OF TECHNOLOGY ELEKTROTEKNIK OCH DATAVETENSKAP
Titel Mall för Examensarbeten (Arial 28/30 point size, bold) SUBTITLE - Arial 16 / 19 pt FÖRFATTARE FÖRNAMN OCH EFTERNAMN - Arial 16 / 19 pt KTH ROYAL INSTITUTE OF TECHNOLOGY ELEKTROTEKNIK OCH DATAVETENSKAP
Att skriva rapporten för examensarbetet & sammanfattning av IMRAD. Ville Jalkanen TFE, UmU
 Att skriva rapporten för examensarbetet & sammanfattning av IMRAD Ville Jalkanen TFE, UmU 2017-04-20 1 Att skriva och presentera rapporter http://www.teknat.umu.se/digitalassets/50/50357_att_skriva_rapport_umth_klar.pdf
Att skriva rapporten för examensarbetet & sammanfattning av IMRAD Ville Jalkanen TFE, UmU 2017-04-20 1 Att skriva och presentera rapporter http://www.teknat.umu.se/digitalassets/50/50357_att_skriva_rapport_umth_klar.pdf
Chalmers Tekniska Högskola och Mars 2003 Göteborgs Universitet Fysik och teknisk fysik Kristian Gustafsson Maj Hanson. Svängningar
 Chalmers Tekniska Högskola och Mars 003 Göteborgs Universitet Fysik och teknisk fysik Kristian Gustafsson Maj Hanson Svängningar Introduktion I mekanikkurserna arbetar vi parallellt med flera olika metoder
Chalmers Tekniska Högskola och Mars 003 Göteborgs Universitet Fysik och teknisk fysik Kristian Gustafsson Maj Hanson Svängningar Introduktion I mekanikkurserna arbetar vi parallellt med flera olika metoder
Laboration 1 Mekanik baskurs
 Laboration 1 Mekanik baskurs Utförs av: Henrik Bergman Mubarak Ali Uppsala 2015 01 19 Introduktion Gravitationen är en självklarhet i vår vardag, de är den som håller oss kvar på jorden. Gravitationen
Laboration 1 Mekanik baskurs Utförs av: Henrik Bergman Mubarak Ali Uppsala 2015 01 19 Introduktion Gravitationen är en självklarhet i vår vardag, de är den som håller oss kvar på jorden. Gravitationen
Laborationsrapport för laboration 2 i ESS010 Elektronik. Olle Ollesson 29 september 2012 Handledare: Sven Svensson
 Laborationsrapport för laboration 2 i ESS010 Elektronik Olle Ollesson E-mail: olle.ollesson@dmail.com 29 september 2012 Handledare: Sven Svensson 1 Innehållsförteckning Sida Laborationens syfte 3 Utrustning
Laborationsrapport för laboration 2 i ESS010 Elektronik Olle Ollesson E-mail: olle.ollesson@dmail.com 29 september 2012 Handledare: Sven Svensson 1 Innehållsförteckning Sida Laborationens syfte 3 Utrustning
14. Minsta kvadratmetoden
 58 MINSTA KVADRATMETODEN. Minsta kvadratmetoden Eempel.. Det är inte så svårt att komma åt en trasig lampa på golvet för att byta den. Det är bara att gå fram till den. Hur är det om lampan hänger i taket?
58 MINSTA KVADRATMETODEN. Minsta kvadratmetoden Eempel.. Det är inte så svårt att komma åt en trasig lampa på golvet för att byta den. Det är bara att gå fram till den. Hur är det om lampan hänger i taket?
Densitet Tabellen nedan visar massan och volymen för olika mängder kopparnubb.
 Tid Vi har inte en entydig definition av tid. Tid knytas ofta till förändringar och rörelse. Vi koncentrerar på hur vi mäter tiden. Vi brukar använda enheten sekund för att mäta tiden. Enheten för tid
Tid Vi har inte en entydig definition av tid. Tid knytas ofta till förändringar och rörelse. Vi koncentrerar på hur vi mäter tiden. Vi brukar använda enheten sekund för att mäta tiden. Enheten för tid
Etappmål 1 Etappmål 2 Etappmål 3 Examensmål
 Etappmål 1 Etappmål 2 Etappmål 3 Examensmål Element/objekt, begrepp identifiera, beskriva och klassificera grundläggande element/objekt inom ämnet förklara och använda grundläggande nomenklatur inom ämnet
Etappmål 1 Etappmål 2 Etappmål 3 Examensmål Element/objekt, begrepp identifiera, beskriva och klassificera grundläggande element/objekt inom ämnet förklara och använda grundläggande nomenklatur inom ämnet
Kap Inversfunktion, arcusfunktioner.
 Kap 3. 3.5. Inversfunktion, arcusfunktioner. 30. (A) Förenkla uttrycken så långt som möjligt a. ln 8 ln + ln 8 ln + ln b. ln 3 log 0 3 log 0 e + 3 ln 3 log 3 e 30. (A) Lös ekvationerna a. e x = e x b.
Kap 3. 3.5. Inversfunktion, arcusfunktioner. 30. (A) Förenkla uttrycken så långt som möjligt a. ln 8 ln + ln 8 ln + ln b. ln 3 log 0 3 log 0 e + 3 ln 3 log 3 e 30. (A) Lös ekvationerna a. e x = e x b.
Komponentfysik ESS030. Den bipolära transistorn
 Komponentfysik ESS030 Den bipolära transistorn T- 2016 Syfte Syftet med denna laboration är att studenten ska bekanta sig med den grundläggande fysiken i en bipolär transistor. Det fundamentala byggblocket
Komponentfysik ESS030 Den bipolära transistorn T- 2016 Syfte Syftet med denna laboration är att studenten ska bekanta sig med den grundläggande fysiken i en bipolär transistor. Det fundamentala byggblocket
Rapportmall för Skogsmästarskolan 2018
 SKOGSMÄSTARPROGRAMMET Examensarbete 2018:xx Rapportmall för Skogsmästarskolan 2018 Report template School of Forest Management 2018 Back Tomas Ersson Johan Törnblom Examensarbete i skogshushållning, 15
SKOGSMÄSTARPROGRAMMET Examensarbete 2018:xx Rapportmall för Skogsmästarskolan 2018 Report template School of Forest Management 2018 Back Tomas Ersson Johan Törnblom Examensarbete i skogshushållning, 15
Övningar till datorintroduktion
 Institutionen för Fysik Umeå Universitet Ylva Lindgren Sammanfattning En samling uppgifter att göra i MATLAB, vilka ska utföras enskilt eller i grupp om två. Datorintroduktion Handledare: (it@tekniskfysik.se)
Institutionen för Fysik Umeå Universitet Ylva Lindgren Sammanfattning En samling uppgifter att göra i MATLAB, vilka ska utföras enskilt eller i grupp om två. Datorintroduktion Handledare: (it@tekniskfysik.se)
Rotationsrörelse laboration Mekanik II
 Rotationsrörelse laboration Mekanik II Utförs av: William Sjöström Oskar Keskitalo Uppsala 2015 04 19 Sida 1 av 10 Sammanfattning För att förändra en kropps rotationshastighet så krävs ett vridmoment,
Rotationsrörelse laboration Mekanik II Utförs av: William Sjöström Oskar Keskitalo Uppsala 2015 04 19 Sida 1 av 10 Sammanfattning För att förändra en kropps rotationshastighet så krävs ett vridmoment,
Ekvationer & Funktioner Ekvationer
 Ekvationer & Funktioner Ekvationer Ekvationstyp : Ekvationer av första graden När vi löser ekvationer av första graden använder vi oss av de fyra grundläggande räknesätten för att beräkna x. Vid minus
Ekvationer & Funktioner Ekvationer Ekvationstyp : Ekvationer av första graden När vi löser ekvationer av första graden använder vi oss av de fyra grundläggande räknesätten för att beräkna x. Vid minus
Hur länge ska fisken vara i dammen?
 Hur länge ska fisken vara i dammen? Frågeställning Uppgift 10 fiskodling Uppgiften går ut på att ta reda på hur länge ett stim fisk ska växa upp i en fiskodling för att få den maximala vikten tillsammans.
Hur länge ska fisken vara i dammen? Frågeställning Uppgift 10 fiskodling Uppgiften går ut på att ta reda på hur länge ett stim fisk ska växa upp i en fiskodling för att få den maximala vikten tillsammans.
2012-01-12 FÖRSLAG TILL KURSPLAN INOM KOMMUNAL VUXENUTBILDNING GRUNDLÄGGANDE NIVÅ
 Matematik, 600 verksamhetspoäng Ämnet handlar bland annat om mängder, tal och geometriska figurer. Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl ur praktiska
Matematik, 600 verksamhetspoäng Ämnet handlar bland annat om mängder, tal och geometriska figurer. Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl ur praktiska
SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 2015 Skrivtid: 08:00-13:00 Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 2015 Skrivtid: 08:00-13:00 Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera
Övningsuppgifter till Originintroduktion
 UMEÅ UNIVERSITET 05-08-01 Institutionen för fysik Ylva Lindgren Övningsuppgifter till Originintroduktion Uppgift 1. I ett experiment vill man bestämma fjäderkonstanten k för en viss fjäder. Med olika kraft
UMEÅ UNIVERSITET 05-08-01 Institutionen för fysik Ylva Lindgren Övningsuppgifter till Originintroduktion Uppgift 1. I ett experiment vill man bestämma fjäderkonstanten k för en viss fjäder. Med olika kraft
De fysikaliska parametrar som avgör periodtiden för en fjäder
 De fysikaliska parametrar som avgör periodtiden för en fjäder Teknisk Fysik, Chalmers tekniska högskola, Sverige Robin Andersson Email: robiand@student.chalmers.se Alexander Grabowski Email: alegra@student.chalmers.se
De fysikaliska parametrar som avgör periodtiden för en fjäder Teknisk Fysik, Chalmers tekniska högskola, Sverige Robin Andersson Email: robiand@student.chalmers.se Alexander Grabowski Email: alegra@student.chalmers.se
Något om Dimensionsanalys och Mathematica. Assume period T Cm Α g Β L Γ s 1 kg Α m Β m Γ s 1 kg Α m Β. Identify exponents VL HL kg 0 Α m 0 Β Γ s 1 2 Β
 HH/ITE/BN Dimensionsanalys och Mathematica 1 Något om Dimensionsanalys och Mathematica Bertil Nilsson 2016-08-15 Assume period T Cm Α g Β Γ s 1 kg Α m Β m Γ s 2 s 1 kg Α m Β s 2Β m Γ Identify exponents
HH/ITE/BN Dimensionsanalys och Mathematica 1 Något om Dimensionsanalys och Mathematica Bertil Nilsson 2016-08-15 Assume period T Cm Α g Β Γ s 1 kg Α m Β m Γ s 2 s 1 kg Α m Β s 2Β m Γ Identify exponents
Titel. Undertitel (Titel och undertitel får vara på max 250 st tecken. Kom ihåg att titeln på ditt arbete syns i ditt slutbetyg/examensbevis)
 Titel Undertitel (Titel och undertitel får vara på max 250 st tecken. Kom ihåg att titeln på ditt arbete syns i ditt slutbetyg/examensbevis) Författare: Kurs: Gymnasiearbete & Lärare: Program: Datum: Abstract
Titel Undertitel (Titel och undertitel får vara på max 250 st tecken. Kom ihåg att titeln på ditt arbete syns i ditt slutbetyg/examensbevis) Författare: Kurs: Gymnasiearbete & Lärare: Program: Datum: Abstract
ANVISNING FÖR UTARBETANDE AV TEKNISK/VETENSKAPLIGA ARTIKLAR OCH LABORATIONSRAPPORTER
 1 MÄLARDALENS HÖGSKOLA Institutionen för biologi och kemiteknik Box 325, 631 05 Eskilstuna ANVISNING FÖR UTARBETANDE AV TEKNISK/VETENSKAPLIGA ARTIKLAR OCH LABORATIONSRAPPORTER ALLMÄNT Nedan följer anvisningar
1 MÄLARDALENS HÖGSKOLA Institutionen för biologi och kemiteknik Box 325, 631 05 Eskilstuna ANVISNING FÖR UTARBETANDE AV TEKNISK/VETENSKAPLIGA ARTIKLAR OCH LABORATIONSRAPPORTER ALLMÄNT Nedan följer anvisningar
Laboration 1: Gravitation
 Laboration 1: Gravitation Inledning Försöket avser att påvisa gravitationskraften och att bestämma ett ungefärligt värde på gravitationskonstanten G i Newtons gravitationslag, m1 m F = G r Lagen beskriver
Laboration 1: Gravitation Inledning Försöket avser att påvisa gravitationskraften och att bestämma ett ungefärligt värde på gravitationskonstanten G i Newtons gravitationslag, m1 m F = G r Lagen beskriver
Matematik D (MA1204)
 Matematik D (MA104) 100 p Betygskriterier med eempeluppgifter Värmdö Gymnasium Betygskriterier enligt Skolverket Kriterier för betyget Godkänd Eleven använder lämpliga matematiska begrepp, metoder och
Matematik D (MA104) 100 p Betygskriterier med eempeluppgifter Värmdö Gymnasium Betygskriterier enligt Skolverket Kriterier för betyget Godkänd Eleven använder lämpliga matematiska begrepp, metoder och
Titel på examensarbetet. Dittnamn Efternamn. Examensarbete 2013 Programmet
 Titel på examensarbetet på två rader Dittnamn Efternamn Examensarbete 2013 Programmet Titel på examensarbetet på två rader English title on one row Dittnamn Efternamn Detta examensarbete är utfört vid
Titel på examensarbetet på två rader Dittnamn Efternamn Examensarbete 2013 Programmet Titel på examensarbetet på två rader English title on one row Dittnamn Efternamn Detta examensarbete är utfört vid
Laboration 1: Gravitation
 Laboration 1: Gravitation Inledning Försöket avser att påvisa gravitationskraften och att bestämma ett ungefärligt värde på gravitationskonstanten G i Newtons gravitationslag, m1 m F = G r Lagen beskriver
Laboration 1: Gravitation Inledning Försöket avser att påvisa gravitationskraften och att bestämma ett ungefärligt värde på gravitationskonstanten G i Newtons gravitationslag, m1 m F = G r Lagen beskriver
Lokal pedagogisk planering i matematik för årskurs 9
 Lokal pedagogisk planering i matematik för årskurs 9 Arbetsområde 4. Samband och förändring Syfte formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder. reflektera
Lokal pedagogisk planering i matematik för årskurs 9 Arbetsområde 4. Samband och förändring Syfte formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder. reflektera
Sekantmetoden Beräkningsmatematik TANA21 Linköpings universitet Caroline Cornelius, Anja Hellander Ht 2018
 Sekantmetoden Beräkningsmatematik TANA21 Linköpings universitet Caroline Cornelius, Anja Hellander Ht 2018 1. Inledning Inom matematiken är det ofta intressant att finna nollställen till en ekvation f(x),
Sekantmetoden Beräkningsmatematik TANA21 Linköpings universitet Caroline Cornelius, Anja Hellander Ht 2018 1. Inledning Inom matematiken är det ofta intressant att finna nollställen till en ekvation f(x),
Rapportinstruktioner för examensarbete på avancerad nivå inom kemi, kemisk biologi eller teknisk biologi vid Linköpings universitet
 Rapportinstruktioner för examensarbete på avancerad nivå inom kemi, kemisk biologi eller teknisk biologi vid Linköpings universitet Denna instruktion är tänkt som ett stöd vid rapportskrivningen till alla
Rapportinstruktioner för examensarbete på avancerad nivå inom kemi, kemisk biologi eller teknisk biologi vid Linköpings universitet Denna instruktion är tänkt som ett stöd vid rapportskrivningen till alla
Tryckfel i K. Vännman, Matematisk Statistik, upplaga 2:13
 Tryckfel i K. Vännman, Matematisk Statistik, upplaga 2:13 Kasper K. S. Andersen 11 oktober 2018 s. 10, b, l. 8: 1 4 17.62 1 5 17.62 s. 25, Tabell 1.13, linje 1, kolonn 7: 11 111 s. 26, Figur 1.19 b, l.
Tryckfel i K. Vännman, Matematisk Statistik, upplaga 2:13 Kasper K. S. Andersen 11 oktober 2018 s. 10, b, l. 8: 1 4 17.62 1 5 17.62 s. 25, Tabell 1.13, linje 1, kolonn 7: 11 111 s. 26, Figur 1.19 b, l.
Mälardalens högskola
 Teknisk rapportskrivning - en kortfattad handledning (Version 1.2) Mälardalens högskola Institutionen för datateknik (IDt) Thomas Larsson 10 september 1998 Västerås Sammanfattning En mycket viktig del
Teknisk rapportskrivning - en kortfattad handledning (Version 1.2) Mälardalens högskola Institutionen för datateknik (IDt) Thomas Larsson 10 september 1998 Västerås Sammanfattning En mycket viktig del
Att beräkna t i l l v ä x t takter i Excel
 Att beräkna t i l l v ä x t takter i Excel Detta kapitel är en liten matematisk vägledning om att beräkna tillväxttakten i Excel. Här visas exempel på potenser och logaritmer och hur dessa funktioner beräknas
Att beräkna t i l l v ä x t takter i Excel Detta kapitel är en liten matematisk vägledning om att beräkna tillväxttakten i Excel. Här visas exempel på potenser och logaritmer och hur dessa funktioner beräknas
Kan du det här? o o. o o o o. Derivera potensfunktioner, exponentialfunktioner och summor av funktioner. Använda dig av derivatan i problemlösning.
 Kan du det här? o o o o o o Vad innebär det att x går mot noll? Vad händer då x går mot oändligheten? Vad betyder sekant, tangent och ändringskvot och vad har dessa begrepp med derivatan att göra? Derivera
Kan du det här? o o o o o o Vad innebär det att x går mot noll? Vad händer då x går mot oändligheten? Vad betyder sekant, tangent och ändringskvot och vad har dessa begrepp med derivatan att göra? Derivera
LABORATION 2 UPPTÄCK ETT SAMBAND
 Fysikum FK2002 - Fysikexperiment FK2004 - Exp. fysik för lärare Laborationsinstruktion (28 september 2010) LABORATION 2 UPPTÄCK ETT SAMBAND FJÄDERN Mål Idenhärlaborationenskalldubörjamedattställauppenhypotes
Fysikum FK2002 - Fysikexperiment FK2004 - Exp. fysik för lärare Laborationsinstruktion (28 september 2010) LABORATION 2 UPPTÄCK ETT SAMBAND FJÄDERN Mål Idenhärlaborationenskalldubörjamedattställauppenhypotes
Lösningsförslag till Tentamen i 5B1118 Diskret matematik 5p 22 augusti, 2001
 Institutionen för matematik, KTH Mats Boij Lösningsförslag till Tentamen i 5B1118 Diskret matematik 5p 22 augusti, 2001 1. Ange kvot och rest vid division av 5BE med 1F där båda talen är angivna i hexadecimal
Institutionen för matematik, KTH Mats Boij Lösningsförslag till Tentamen i 5B1118 Diskret matematik 5p 22 augusti, 2001 1. Ange kvot och rest vid division av 5BE med 1F där båda talen är angivna i hexadecimal
Ökad dämpning genom rätt design av utloppsstrypningen
 Ökad dämpning genom rätt design av utloppsstrypningen Mikael Axin Fluida och mekatroniska system, Institutionen för ekonomisk och industriell utveckling, Linköpings universitet E-mail: mikael.axin@liu.se
Ökad dämpning genom rätt design av utloppsstrypningen Mikael Axin Fluida och mekatroniska system, Institutionen för ekonomisk och industriell utveckling, Linköpings universitet E-mail: mikael.axin@liu.se
Kovarians och kriging
 Kovarians och kriging Bengt Ringnér November 2, 2007 Inledning Detta är föreläsningsmanus på lantmätarprogrammet vid LTH. 2 Kovarianser Sedan tidigare har vi, för oberoende X och Y, att VX + Y ) = VX)
Kovarians och kriging Bengt Ringnér November 2, 2007 Inledning Detta är föreläsningsmanus på lantmätarprogrammet vid LTH. 2 Kovarianser Sedan tidigare har vi, för oberoende X och Y, att VX + Y ) = VX)
Rapportinstruktion för examensarbete på avancerad nivå inom kemi, kemisk biologi eller teknisk biologi vid Linköpings universitet
 Rapportinstruktion för examensarbete på avancerad nivå inom kemi, kemisk biologi eller teknisk biologi vid Linköpings universitet Denna instruktion är sammanställd av programnämnden för kemi, biologi och
Rapportinstruktion för examensarbete på avancerad nivå inom kemi, kemisk biologi eller teknisk biologi vid Linköpings universitet Denna instruktion är sammanställd av programnämnden för kemi, biologi och
LABORATION 3 - Regressionsanalys
 Institutionen för teknikvetenskap och matematik S0001M Matematisk statistik LABORATION 3 - Regressionsanalys I denna laboration ska du lösa ett antal uppgifter i regressionsanalys med hjälp av statistik-programmet
Institutionen för teknikvetenskap och matematik S0001M Matematisk statistik LABORATION 3 - Regressionsanalys I denna laboration ska du lösa ett antal uppgifter i regressionsanalys med hjälp av statistik-programmet
Introduktion. Torsionspendel
 Chalmers Tekniska Högskola och Göteborgs Universitet November 00 Fysik och teknisk fysik Kristian Gustafsson och Maj Hanson (Anpassat för I1 av Göran Niklasson) Svängningar Introduktion I mekanikkursen
Chalmers Tekniska Högskola och Göteborgs Universitet November 00 Fysik och teknisk fysik Kristian Gustafsson och Maj Hanson (Anpassat för I1 av Göran Niklasson) Svängningar Introduktion I mekanikkursen
Undersökande arbetssätt i matematik 1 och 2
 Matematik Gymnasieskola Modul: Matematikundervisning med digitala verktyg Del 6: Undersökande arbetssätt med matematisk programvara Undersökande arbetssätt i matematik 1 och 2 I texten Undersökande arbetssätt
Matematik Gymnasieskola Modul: Matematikundervisning med digitala verktyg Del 6: Undersökande arbetssätt med matematisk programvara Undersökande arbetssätt i matematik 1 och 2 I texten Undersökande arbetssätt
TATM79: Föreläsning 6 Logaritmer och exponentialfunktioner
 TATM79: Föreläsning 6 Logaritmer och eponentialfunktioner Johan Thim augusti 06 Den naturliga logaritmen Vi börjar med att introducera den naturliga logaritmen. Definition. Den naturliga logaritmen ln
TATM79: Föreläsning 6 Logaritmer och eponentialfunktioner Johan Thim augusti 06 Den naturliga logaritmen Vi börjar med att introducera den naturliga logaritmen. Definition. Den naturliga logaritmen ln
LABORATION 2 UPPTÄCK ETT SAMBAND BALKEN
 Fysikum FK2002 - Fysikexperiment FK2004 - Exp. fysik för lärare Laborationsinstruktion (28 september 2010) LABORATION 2 UPPTÄCK ETT SAMBAND BALKEN Mål Idenhärlaborationenskalldubörjamedattställauppenhypotes
Fysikum FK2002 - Fysikexperiment FK2004 - Exp. fysik för lärare Laborationsinstruktion (28 september 2010) LABORATION 2 UPPTÄCK ETT SAMBAND BALKEN Mål Idenhärlaborationenskalldubörjamedattställauppenhypotes
Laboration 2 Mekanik baskurs
 Laboration 2 Mekanik baskurs Utförs av: Henrik Bergman Mubarak Ali Uppsala 2015 01 19 Introduktion Friktionskraft är en förutsättning för att våra liv ska fungera på ett mindre omständigt sätt. Om friktionskraften
Laboration 2 Mekanik baskurs Utförs av: Henrik Bergman Mubarak Ali Uppsala 2015 01 19 Introduktion Friktionskraft är en förutsättning för att våra liv ska fungera på ett mindre omständigt sätt. Om friktionskraften
Tentamen i matematik. f(x) = ln(ln(x)),
 Lösningsförslag Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA52G Matematisk Analys MA23G Matematisk analys för ingenjörer Tentamensdag: 203-05- kl 4.30-9.30 Hjälpmedel : Inga hjälpmedel utöver
Lösningsförslag Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA52G Matematisk Analys MA23G Matematisk analys för ingenjörer Tentamensdag: 203-05- kl 4.30-9.30 Hjälpmedel : Inga hjälpmedel utöver
Planering för matematik 2a OBS: Provdatumen är endast förslag, kontakta läraren innan du kommer och vill ha prov
 År Startvecka 2013 2 Planering för matematik 2a OBS: Provdatumen är endast förslag, kontakta läraren innan du kommer och vill ha prov Vecka Lektion (2h) Datum Kapitel Avsnitt 2 Ti 08-jan Kap 1: Räta linjen
År Startvecka 2013 2 Planering för matematik 2a OBS: Provdatumen är endast förslag, kontakta läraren innan du kommer och vill ha prov Vecka Lektion (2h) Datum Kapitel Avsnitt 2 Ti 08-jan Kap 1: Räta linjen
GYMNASIEARBETET - ATT SKRIVA VETENSKAPLIGT
 GYMNASIEARBETET - ATT SKRIVA VETENSKAPLIGT Ditt gymnasiearbete ska bygga kring den frågeställning du kommit fram till i slutet av vårterminen i årskurs 2 och du ska i ditt arbete besvara din frågeställning
GYMNASIEARBETET - ATT SKRIVA VETENSKAPLIGT Ditt gymnasiearbete ska bygga kring den frågeställning du kommit fram till i slutet av vårterminen i årskurs 2 och du ska i ditt arbete besvara din frågeställning
Föreläsning 8, Matematisk statistik 7.5 hp för E Punktskattningar
 Föreläsning 8, Matematisk statistik 7.5 hp för E Punktskattningar Stas Volkov Stanislav Volkov s.volkov@maths.lth.se FMSF20 F8: Statistikteori 1/20 Översikt Exempel Repetition Exempel Matematisk statistik
Föreläsning 8, Matematisk statistik 7.5 hp för E Punktskattningar Stas Volkov Stanislav Volkov s.volkov@maths.lth.se FMSF20 F8: Statistikteori 1/20 Översikt Exempel Repetition Exempel Matematisk statistik
Kunskapsprofil Resultat på ämnesprovet
 Kunskapsprofil Resultat på ämnesprovet Här fylls i om eleven nått kravnivån på delproven. N = nått kravnivån, EN = ej nått kravnivån. Elevens namn: Förmågor som prövas Kunskapskrav Uppnått kravnivån (N
Kunskapsprofil Resultat på ämnesprovet Här fylls i om eleven nått kravnivån på delproven. N = nått kravnivån, EN = ej nått kravnivån. Elevens namn: Förmågor som prövas Kunskapskrav Uppnått kravnivån (N
Bestämning av hastighetskonstant för reaktionen mellan väteperoxid och jodidjon
 Bestämning av hastighetskonstant för reaktionen mellan väteperoxid och jodidjon Jesper Hagberg Simon Pedersen 28 november 2011 Chalmers Tekniska Högskola Institutionen för Kemi och Bioteknik Fysikalisk
Bestämning av hastighetskonstant för reaktionen mellan väteperoxid och jodidjon Jesper Hagberg Simon Pedersen 28 november 2011 Chalmers Tekniska Högskola Institutionen för Kemi och Bioteknik Fysikalisk
En uppsats bedömningsgrunder Struktur Innehåll Stil: språk Stil: layout
 En kandidatuppsats bedöms utifrån sin struktur, sitt innehåll och sin stil. Med struktur avses den logiska följden. Med innehåll avses textens relevans och djup. Med stil avses elegans och väckande av
En kandidatuppsats bedöms utifrån sin struktur, sitt innehåll och sin stil. Med struktur avses den logiska följden. Med innehåll avses textens relevans och djup. Med stil avses elegans och väckande av
Gymnasiearbetet för det naturvetenskapliga programmet
 Gymnasiearbetet för det naturvetenskapliga programmet Pär Leijonhufvud 2017-08-29 Innehåll Syfte.................................... 2 Arbetsformer............................... 2 Rapporten.................................
Gymnasiearbetet för det naturvetenskapliga programmet Pär Leijonhufvud 2017-08-29 Innehåll Syfte.................................... 2 Arbetsformer............................... 2 Rapporten.................................
Planering Matematik åk 8 Samband, vecka
 Planering Matematik åk 8 Samband, vecka 4 2016 Syfte Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med
Planering Matematik åk 8 Samband, vecka 4 2016 Syfte Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med
ämnesområden. Funktioner och räta linjens ekvation. Hur funktioner kan användas för att undersöka förändring, förändringstakt och andra samband.
 MATEMATIK Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl ur praktiska behov som ur människans nyfikenhet och lust att utforska matematiken som sådan. Matematisk
MATEMATIK Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl ur praktiska behov som ur människans nyfikenhet och lust att utforska matematiken som sådan. Matematisk
Gränsvärden. Joakim Östlund Patrik Lindegrén Pontus Nyrén 4 december 2003
 Gränsvärden Joakim Östlund Patrik Lindegrén Pontus Nyrén 4 december 2003 Innehåll Introduktion 3 2 Gränsvärden 4 2. Gränsvärden då går mot.................... 4 2.2 Gränsvärden då går mot a.....................
Gränsvärden Joakim Östlund Patrik Lindegrén Pontus Nyrén 4 december 2003 Innehåll Introduktion 3 2 Gränsvärden 4 2. Gränsvärden då går mot.................... 4 2.2 Gränsvärden då går mot a.....................
Anvisningar till rapporter i psykologi på B-nivå
 Anvisningar till rapporter i psykologi på B-nivå En rapport i psykologi är det enklaste formatet för att rapportera en vetenskaplig undersökning inom psykologins forskningsfält. Något som kännetecknar
Anvisningar till rapporter i psykologi på B-nivå En rapport i psykologi är det enklaste formatet för att rapportera en vetenskaplig undersökning inom psykologins forskningsfält. Något som kännetecknar
Anvisningar för rapportskrivning och muntlig redovisning
 MDH Anvisningar för rapportskrivning och muntlig redovisning Fredrik Starfelt och Elena Tomas Aparicio 2013-05-20 1 Rapporten Använd rapportmallen som kan hämtas på: http://www.mdh.se/student/minastudier/examensarbete/omraden/energiteknikrapportskrivning-och-examensarbeten
MDH Anvisningar för rapportskrivning och muntlig redovisning Fredrik Starfelt och Elena Tomas Aparicio 2013-05-20 1 Rapporten Använd rapportmallen som kan hämtas på: http://www.mdh.se/student/minastudier/examensarbete/omraden/energiteknikrapportskrivning-och-examensarbeten
Ballistisk pendel laboration Mekanik II
 Ballistisk pendel laboration Mekanik II Utförs av: William Sjöström 19940404 6956 Philip Sandell 19950512 3456 Uppsala 2015 05 09 Sammanfattning Ett sätt att mäta en gevärkulas hastighet är att låta den
Ballistisk pendel laboration Mekanik II Utförs av: William Sjöström 19940404 6956 Philip Sandell 19950512 3456 Uppsala 2015 05 09 Sammanfattning Ett sätt att mäta en gevärkulas hastighet är att låta den
Ma7-Per: Algebra. Det andra arbetsområdet handlar om algebra och samband.
 Ma7-Per: Algebra Det andra arbetsområdet handlar om algebra och samband. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera
Ma7-Per: Algebra Det andra arbetsområdet handlar om algebra och samband. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera
Matematisk statistik 9 hp, HT-16 Föreläsning 10: Punktskattningar
 Matematisk statistik 9 hp, HT-16 Föreläsning 10: Punktskattningar Anna Lindgren (Stanislav Volkov) 31 oktober + 1 november 2016 Anna Lindgren anna@maths.lth.se FMS012/MASB03 F10: Punktskattning 1/18 Matematisk
Matematisk statistik 9 hp, HT-16 Föreläsning 10: Punktskattningar Anna Lindgren (Stanislav Volkov) 31 oktober + 1 november 2016 Anna Lindgren anna@maths.lth.se FMS012/MASB03 F10: Punktskattning 1/18 Matematisk
Kurskod: GRNMAT2 Verksamhetspoäng: 600
 Kurs: Matematik Kurskod: GRNMAT2 Verksamhetspoäng: 600 lust att utforska matematiken som sådan. Matematisk verksamhet är till sin lad till den samhälleliga, sociala och tekniska utvecklingen. Kunskaper
Kurs: Matematik Kurskod: GRNMAT2 Verksamhetspoäng: 600 lust att utforska matematiken som sådan. Matematisk verksamhet är till sin lad till den samhälleliga, sociala och tekniska utvecklingen. Kunskaper
Förslag den 25 september Matematik
 Matematik Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl ur praktiska behov som ur människans nyfikenhet och lust att utforska matematiken som sådan. Matematisk
Matematik Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas såväl ur praktiska behov som ur människans nyfikenhet och lust att utforska matematiken som sådan. Matematisk
Lösandet av ekvationer utgör ett centralt område inom matematiken, kanske främst den tillämpade.
 1.1 Ekvationslösning Lösandet av ekvationer utgör ett centralt område inom matematiken, kanske främst den tillämpade. 1.1.1 Polynomekvationer Ett polynom i en variabel x är som bekant en summa av termer
1.1 Ekvationslösning Lösandet av ekvationer utgör ett centralt område inom matematiken, kanske främst den tillämpade. 1.1.1 Polynomekvationer Ett polynom i en variabel x är som bekant en summa av termer
a5 bc 3 5 a4 b 2 c 4 a3 bc 3 a2 b 4 c
 MMA11 Matematisk grundkurs TEN Datum: 15 augusti 01 Skrivtid: timmar Hjälpmedel: Penna, linjal och radermedel Denna tentamen TEN består av nio stycken om varannat slumpmässigt ordnade uppgifter som vardera
MMA11 Matematisk grundkurs TEN Datum: 15 augusti 01 Skrivtid: timmar Hjälpmedel: Penna, linjal och radermedel Denna tentamen TEN består av nio stycken om varannat slumpmässigt ordnade uppgifter som vardera
TMA226 datorlaboration
 TMA226 Matematisk fördjupning, Kf 2019 Tobias Gebäck Matematiska vetenskaper, Calmers & GU Syfte TMA226 datorlaboration Syftet med denna laboration är att du skall öva formuleringen av en Finita element-metod,
TMA226 Matematisk fördjupning, Kf 2019 Tobias Gebäck Matematiska vetenskaper, Calmers & GU Syfte TMA226 datorlaboration Syftet med denna laboration är att du skall öva formuleringen av en Finita element-metod,
Temperaturreglering. En jämförelse mellan en P- och en PI-regulator. θ (t) Innehåll Målsättning sid 2
 2008-02-12 UmU TFE/Bo Tannfors Temperaturreglering En jämförelse mellan en P- och en PI-regulator θ i w θ θ u θ Innehåll Målsättning sid 2 Teori 2 Förberedelseuppgifter 2 Förutsättningar och uppdrag 3
2008-02-12 UmU TFE/Bo Tannfors Temperaturreglering En jämförelse mellan en P- och en PI-regulator θ i w θ θ u θ Innehåll Målsättning sid 2 Teori 2 Förberedelseuppgifter 2 Förutsättningar och uppdrag 3
Kursinformation och studiehandledning, M0038M Matematik I Differentialkalkyl, Lp I 2012.
 Kursinformation och studiehandledning, M0038M Matematik I Differentialkalkyl, Lp I 2012. Kursansvarig och examinator: Staffan Lundberg, TVM. Telefon: 0920-49 18 69. Rum: E 882. E-post: lund@ltu.se Lärare
Kursinformation och studiehandledning, M0038M Matematik I Differentialkalkyl, Lp I 2012. Kursansvarig och examinator: Staffan Lundberg, TVM. Telefon: 0920-49 18 69. Rum: E 882. E-post: lund@ltu.se Lärare
M0038M Differentialkalkyl, Lekt 14, H15
 M0038M Differentialkalkyl, Lekt 14, H15 Staffan Lundberg Luleå Tekniska Universitet Staffan Lundberg M0038M H15 1/ 18 Repetition Lekt 13 En funktion f definieras som { 1 + ax x 2 om x < 2 f (x) = 1 ax
M0038M Differentialkalkyl, Lekt 14, H15 Staffan Lundberg Luleå Tekniska Universitet Staffan Lundberg M0038M H15 1/ 18 Repetition Lekt 13 En funktion f definieras som { 1 + ax x 2 om x < 2 f (x) = 1 ax
INSTRUKTIONER OCH TIPS Fördjupningsarbete Receptarier (15 hp) och Apotekare (30 hp)
 1 INSTRUKTIONER OCH TIPS Fördjupningsarbete Receptarier (15 hp) och Apotekare (30 hp) 1. Försöksplan Syftet med försöksplanen är att du ska få projektets (begränsade) målsättning helt klar för dig innan
1 INSTRUKTIONER OCH TIPS Fördjupningsarbete Receptarier (15 hp) och Apotekare (30 hp) 1. Försöksplan Syftet med försöksplanen är att du ska få projektets (begränsade) målsättning helt klar för dig innan
Att skriva en ekonomisk, humanistisk eller samhällsvetenskaplig rapport
 Att skriva en ekonomisk, humanistisk eller samhällsvetenskaplig rapport Eventuell underrubrik Förnamn Efternamn Klass Skola Kurs/ämnen Termin Handledare Abstract/Sammanfattning Du skall skriva en kort
Att skriva en ekonomisk, humanistisk eller samhällsvetenskaplig rapport Eventuell underrubrik Förnamn Efternamn Klass Skola Kurs/ämnen Termin Handledare Abstract/Sammanfattning Du skall skriva en kort
Rapport för framställande av produkt eller tjänst
 Rapport för framställande av produkt eller tjänst PA 1201 Det här är en vägledning för er som arbetat enskilt eller i en projektgrupp för framställande av produkt eller tjänst och ska skriva en projektrapport
Rapport för framställande av produkt eller tjänst PA 1201 Det här är en vägledning för er som arbetat enskilt eller i en projektgrupp för framställande av produkt eller tjänst och ska skriva en projektrapport
INSTITUTIONEN FÖR FYSIK OCH ASTRONOMI. Mekanik baskurs, Laboration 2. Friktionskraft och snörkraft
 INSTITUTIONEN FÖR FYSIK OCH ASTRONOMI Mekanik baskurs, Laboration 2 Krafter och Newtons lagar Friktionskraft och snörkraft Uppsala 2015-09-29 Instruktioner Om laborationen: Innan ni lämnar labbet: Arbeta
INSTITUTIONEN FÖR FYSIK OCH ASTRONOMI Mekanik baskurs, Laboration 2 Krafter och Newtons lagar Friktionskraft och snörkraft Uppsala 2015-09-29 Instruktioner Om laborationen: Innan ni lämnar labbet: Arbeta
Hållfasthetslära. Böjning och vridning av provstav. Laboration 2. Utförs av:
 Hållfasthetslära Böjning och vridning av provstav Laboration 2 Utförs av: Habre Henrik Bergman Martin Book Mauritz Edlund Muzammil Kamaly William Sjöström Uppsala 2015 10 08 Innehållsförteckning 0. Förord
Hållfasthetslära Böjning och vridning av provstav Laboration 2 Utförs av: Habre Henrik Bergman Martin Book Mauritz Edlund Muzammil Kamaly William Sjöström Uppsala 2015 10 08 Innehållsförteckning 0. Förord
y y 1 = k(x x 1 ) f(x) = 3 x
 Räta linjen på olika former Här ska vi bara påpeka att förutom k-form, den som vi är mest vana vid y = k y + m finns också allmän form: ax + by + c = 0 där a och b är konstanter, som inte någon står för
Räta linjen på olika former Här ska vi bara påpeka att förutom k-form, den som vi är mest vana vid y = k y + m finns också allmän form: ax + by + c = 0 där a och b är konstanter, som inte någon står för
Rapport och artikel. Får det se ut hur som helst? Förord
 Rapport och artikel Får det se ut hur som helst? 7:1 Förord Förordet kan ha en personlig prägel. Det skall vara kort (ca en halv sida) och ge fakta om rapportens tillkomst som inte berör det tekniska innehållet.
Rapport och artikel Får det se ut hur som helst? 7:1 Förord Förordet kan ha en personlig prägel. Det skall vara kort (ca en halv sida) och ge fakta om rapportens tillkomst som inte berör det tekniska innehållet.
Håkan L. (Skriv som en produkt. Gör uppdelningen i faktorer så långt det går.) 1. Faktorisera 25x Faktorisera 1. 3.
 Övningsuppgifter för att stödja repetition av gymnasiets matematik Har sammanställt ett antal övningsuppgifter som hjälp att repetera några väsentliga delar av gymnasiets matematik På slutet finns uppgifter
Övningsuppgifter för att stödja repetition av gymnasiets matematik Har sammanställt ett antal övningsuppgifter som hjälp att repetera några väsentliga delar av gymnasiets matematik På slutet finns uppgifter
