Maurice Karnaugh. Karnaugh-diagrammet gör det enkelt att minimera Boolska uttryck! William Sandqvist
|
|
|
- Stefan Hermansson
- för 7 år sedan
- Visningar:
Transkript
1 Maurice Karnaugh Karnaugh-diagrammet gör det enkelt att minimera Boolska uttryck!
2 En funktion av fyra variabler a b c d Sanningstabellen till höger innehåller 11 st 1:or och 5 st 0:or. Funktionen kan uttryckas på SP-form med 11 st mintermer eller på PSform med 5 st maxtermer. Den som använt Booles algebra vet att det därefter följer ett mödosamt arbete för att ta fram enklare uttryck. Mintermerna kan kombineras på många olika sätt som alla resulterar i olika förenklade uttryck - hur vet man om man har funnit det enklaste?
3 Ett diagram med enhetsavstånd Karnaughdiagrammet är sanningstabellen men med en annan ordning. Lägg märke till numreringen! Rutorna är ordnade så att endast en bit ändras mellan två vertikala eller horisontella rutor. Denna ordning kallas för Gray-kod.
4 Två grannar Rutorna "5" och "13" är "grannar" i Karnaughdiagrammet ( fast det är långt mellan dem i sanningstabellen ). De svarar mot två mintermer med fyra variabler, och i figuren visas hur de med Booles algebra, kan reduceras till en term med tre variabler. Det de två rutorna har gemensamt är att b=1, c=0 och d=1, och den reducerade termen uttrycker precis detta. Överallt i Karnaughdiagrammet där man hittar två ettor som är "grannar" ( vertikalt eller horisontellt ) kan man reducera de mintermerna till det som är gemensamt för de två rutorna. Detta kallas för en hoptagning.
5 Fyra grannar Rutorna "1" "3" "5" "7" är en grupp av fyra rutor med ettor som ligger som "grannar" till varandra. Även här går de fyra mintermerna att reducera till en term som uttrycker det som är gemensamt för rutorna, nämligen att a=0 och d=1. Överallt i Karnaughdiagrammet där man hittar sådana grupper av fyra ettor kan man göra sådana förenklingar, hoptagningar.
6 Åtta grannar Alla grupper av 2, 4, 8, (... 2 N dvs. med jämna 2-potenser ) rutor som innehåller ettor kan reduceras till en term, med "det som är gemensamt", en hoptagning.
7 Karnaugh - toroid Egentligen bör man avbilda Karnaughdiagrammet på en toroid ( en donut ). Når man en kant, så börjar diagrammet om från den motsatta sidan! Ruta 0 är således "granne" med ruta 2, men även "granne" med ruta 8 som är granne med ruta 10. De fyra ettorna i hörnen har b=0 och d=0 gemensamt och kan därför bilda en hoptagning.
8 Bästa hoptagningar? Man söker efter så stora hoptagningar som möjligt. I exemplet finns det en hoptagning med åtta ettor ( rutorna 0,1,3,2,4,5,7,6 ). Hörnen ( 0,2,8,10 ) är en hoptagning av fyra ettor. Två av rutorna ( 0,10 ) har redan tagits med i den första hoptagningen, men inget hindrar att en ruta bir medtagen flera gånger. Alla ettor måste med i funktionen, antingen i en hoptagning, eller som en minterm. Ettan i ruta 13 kan bilda en hoptagning med ettan i ruta 5, någon större hoptagning finns tyvärr inte för denna etta. Jämför den resulterande funktionen med de ursprungliga 11 mintermerna!
9 Felaktiga hoptagningar? Finns det några felaktiga hoptagningar i detta Karnaugh-diagram?
10 Felaktiga hoptagningar? Finns det några felaktiga hoptagningar i detta Karnaugh-diagram? Hoptagningar ska vara 2, 4, 8 (= tvåpotenser) grannar vertikalt eller horisontellt, ej diagonalt.
11 ÖH 6.1 Karnaughdiagrammet
12 ÖH 6.1 Karnaughdiagrammet bd
13 ÖH 6.1 Karnaughdiagrammet bd abd
14 ÖH 6.1 Karnaughdiagrammet bd acd abd
15 ÖH 6.1 Karnaughdiagrammet bd acd abd f = bd + acd + abd
16 (ÖH 6.2 Karnaughdiagrammet)
17 (ÖH 6.2 Karnaughdiagrammet) bd
18 (ÖH 6.2 Karnaughdiagrammet) bd abd
19 (ÖH 6.2 Karnaughdiagrammet) bd abd abc
20 (ÖH 6.2 Karnaughdiagrammet) bd abd abc f = bd + abd + abc
21 Hoptagningar av 0:or Karnaughdiagrammet är också användbart för hoptagning av 0:or. Hoptagningarna kan omfatta samma antal rutor som i fallet med hoptagning av 1:or. I detta exempel kan 0:orna tas ihop i par med sina "grannar". Maxtermerna förenklas till det som är gemensamt för rutorna.
22 De Morgan Tips! Tar man ihop 0:or som om de vore 1:or får man funktionens invers! (det vill säga helt fel) Med De Morgans lag kan man därefter ta fram den icke-inverterade funktionen. (nu helt rätt)
23 Andra variabelantal 6 Karnaughdiagram med tre och två variabler är också användbara. Metoden kan med lite möda även användas för 5 och 6 variabler men enklare är att använda något av de generella minimeringsprogram som finns.
24 ÖH 6.4 Byt från NOR till NAND?
25 ÖH 6.4 = NOR-NOR till OR-AND byt rakt av!
26 ÖH 6.4 = f ( a, b, c) = ( a + c) ( b + c)
27 ÖH 6.4 = f ( a, b, c) = ( a + c) ( b + c)
28 ÖH 6.4
29 ÖH 6.4 f ( a, b, c) = c + a b
30 ÖH 6.4 f ( a, b, c) = c + a b
31 ÖH 6.4 f ( a, b, c) = c + a b = AND-OR NAND-NAND Byt grindar rakt av
32 ÖH 6.4 f ( a, b, c) = c + a b Grind saknas på denna nivå! =
33 ÖH 6.4 f ( a, b, c) = c + a b Eller algebraiskt: Dubbelinvertera = standardknep De Morgan c + a b = c + a b = c a b
34
35 PLD-kretsar har utgångsinverterare PLD-kretsar har ofta en XORgrind på utgången så att man vid behov skall kunna invertera funktionen. Man kan då välja mellan att ta ihop 0:or eller 1:or efter vad som är fördelaktigast. När styrsignalen a är 1 blir utgången lika med b:s invers, när a är 0 blir utgången lika med b.
36 ÖH 6.5 Minimera med K-map f x3, x2, x1, x ) = m(0, 2, 4, 8, 10, 12) f =? f = ( 0?
37 ÖH 6.5 Minimera med K-map f x3, x2, x1, x ) = m(0, 2, 4, 8, 10, 12) f =? f = ( 0?
38 ÖH 6.5 Minimera med K-map f x3, x2, x1, x ) = m(0, 2, 4, 8, 10, 12) f =? f = ( 0?
39 ÖH 6.5 Minimera med K-map f x3, x2, x1, x ) = m(0, 2, 4, 8, 10, 12) f =? f = ( 0?
40 f ÖH 6.5 x3, x2, x1, x ) = m(0, 2, 4, 8, 10, 12) f =? f = ( 0? Hoptagning av ettor Hoptagning av nollor
41 f ÖH 6.5 x3, x2, x1, x ) = m(0, 2, 4, 8, 10, 12) f =? f = ( 0? Hoptagning av ettor Hoptagning av nollor f = x + 1 x 0 x 2 x 0
42 f ÖH 6.5 x3, x2, x1, x ) = m(0, 2, 4, 8, 10, 12) f =? f = ( 0? Hoptagning av ettor Hoptagning av nollor f = x + 1 x 0 x 2 x 0
43 f ÖH 6.5 x3, x2, x1, x ) = m(0, 2, 4, 8, 10, 12) f =? f = ( 0? Hoptagning av ettor Hoptagning av nollor f + f = { 0 : or som1: or } = x + x x = x1 x 0 x 2 x
44 f ÖH 6.5 x3, x2, x1, x ) = m(0, 2, 4, 8, 10, 12) f =? f = ( 0? Hoptagning av ettor Hoptagning av nollor f + = x1 x 0 x 2 x f = { 0 : or som1: or } = x + x x Denna gång var det förmånligast att ta ihop 0:or och invertera utgången!
45 ÖH 6.8 Don t Care termer Ibland kan problemställningen vara sådan att vissa ingångskombinationer är omöjliga och därför inte kan inträffa. Sådana mintermer (eller maxtermer) betecknar man med d ( don t care ) och använder dom som ettor eller nollor allt efter vad som passar bäst för att få så stora hoptagningar som möjligt. f x3, x2, x1, x ) = m(3, 5, 7, 11) + d(6, 15) f =? f = ( 0? (En risk kan vara att det som är omöjligt trots allt ändå händer! Därför kan det ofta vara bättre att ta om hand alla kombinationer.)
46 f ÖH 6.8 x3, x2, x1, x ) = m(3, 5, 7, 11) + d(6, 15) f =? f = ( 0 Hoptagning av ettor. Hoptagning av nollor.?
47 f ÖH 6.8 x3, x2, x1, x ) = m(3, 5, 7, 11) + d(6, 15) f =? f = ( 0 Hoptagning av ettor. Hoptagning av nollor.? f = x + 1 x0 x3 x2 x0
48 f ÖH 6.8 x3, x2, x1, x ) = m(3, 5, 7, 11) + d(6, 15) f =? f = ( 0 Hoptagning av ettor. Hoptagning av nollor.? f = x + 1 x0 x3 x2 x0
49 f ÖH 6.8 x3, x2, x1, x ) = m(3, 5, 7, 11) + d(6, 15) f =? f = ( 0 Hoptagning av ettor. Hoptagning av nollor.? f = x + 1 x0 x3 x2 x0 f = x x2 x1 x3 x1
50 Larm för vattentank
51 ÖH 8.2
52 8.2
53 8.2 Endast in-koderna X 0, 1, 3, 7, 15 kan förekomma. Övriga in-koder kan användas som don t care. Vi kan direkt se i tabellen att u 2 och x 3 är lika varför u 2 kan anslutas direkt till x 3. u 2 = x 3. De övriga uttrycken fås med hjälp av deras Karnaughdiagram.
54 8.2 Endast in-koderna X 0, 1, 3, 7, 15 kan förekomma. Övriga in-koder kan användas som don t care. Vi kan direkt se i tabellen att u 2 och x 3 är lika varför u 2 kan anslutas direkt till x 3. u 2 = x 3. De övriga uttrycken fås med hjälp av deras Karnaughdiagram.
55 8.2
56 8.2
57 P och N MOS-transistorer
58 ÖH 7.3 CMOS-grind?
59 ÖH 7.3 A=0 B=
60 ÖH 7.3 A=0 B=0
61 ÖH 7.3 A=0 B=0
62 ÖH 7.3 A=0 B=0
63 ÖH 7.3 A=0 B=0
64 ÖH 7.3 A=0 B= Y =
65 ÖH 7.3 A=1 B= Y =
66 7.3 A B Y OR-grind
67 ÖH 7.3 CMOS-grind? Y Inverterare!
68 ÖH 7.3 CMOS-grind? PUN Y = A B Y = A B = A + B Y Y = A + PUD B
69 ÖH 7.3 CMOS-grind! Y = A + B
70 ÖH 7.4 CMOS-grind?
71 7.4 EN = 1 Y = A När EN = 1 har vi en inverterare.
72 7.4 EN = 0 När EN = 0 är utgången helt bortkopplad från matningsspänning och jord. A kan inte längre påverka utgången. Detta är ett tredje utgångstillstånd, Threestate. Om många utgångar kopplas ihop till samma tråd ( buss ) så kan ju bara en av utgångarna åt gången få vara aktiv. De övriga är i Threestate-tillståndet.
73 Utgångar från tre olika enheter är anslutna till en gemensam buss (BUS). Datorn väljer ut (Enablar, EN) en i taget som kopplas in på bussen. De övriga två förblir urkopplade, (Three state).
74 ÖH 7.5 CMOS-grind? Tillverka Pull-up -nätet med P- transistorerna för denna CMOS grind.
75 7.5 B C A B C A B C A Y B C A Y + = = + = + = ) ( B C A Y + = = Pull-down nätet ger funktionens invers. Pull-up nätet realiserar funktionen oinverterad:
76 7.5 Y = A C + B Y = A C + B = A C B = ( A + C) B ( A + C) B Pull-up-nätet skall således bestå av A och C i parallellkoppling (+) sedan seriekopplade ( ) med B. Användandet av PMOS-transistorer inverterar variablerna A, B och C.
IE1204 Digital Design
 IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM
IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM
IE1205 Digital Design: F4 : Karnaugh-diagrammet, två- och fler-nivå minimering
 IE25 Digital Design: F4 : Karnaugh-diagrammet, två- och fler-nivå minimering Mintermer 2 3 OR f En minterm är en produktterm som innehåller alla variabler och som anger den kombination av :or och :or som
IE25 Digital Design: F4 : Karnaugh-diagrammet, två- och fler-nivå minimering Mintermer 2 3 OR f En minterm är en produktterm som innehåller alla variabler och som anger den kombination av :or och :or som
Mintermer. SP-form med tre mintermer. William Sandqvist
 Mintermer OR f 2 3 En minterm är en produktterm som innehåller alla variabler och som anger den kombination av :or och :or som tillsammans gör att termen antar värdet. SP-form med tre mintermer. f = m
Mintermer OR f 2 3 En minterm är en produktterm som innehåller alla variabler och som anger den kombination av :or och :or som tillsammans gör att termen antar värdet. SP-form med tre mintermer. f = m
Digital Design IE1204
 Digital Design IE24 F4 Karnaugh-diagrammet, två- och fler-nivå minimering william@kth.se IE24 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB
Digital Design IE24 F4 Karnaugh-diagrammet, två- och fler-nivå minimering william@kth.se IE24 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB
Definition av kombinatorisk logik Olika sätt att representera kombinatorisk logik Minimering av logiska uttryck
 KOMBINATORISK LOGIK Innehåll Definition av kombinatorisk logik Olika sätt att representera kombinatorisk logik Minimering av logiska uttryck Boolesk algebra Karnaugh-diagram Realisering av logiska funktioner
KOMBINATORISK LOGIK Innehåll Definition av kombinatorisk logik Olika sätt att representera kombinatorisk logik Minimering av logiska uttryck Boolesk algebra Karnaugh-diagram Realisering av logiska funktioner
Digital elektronik CL0090
 Digital elektronik CL0090 Föreläsning 2 2007-0-25 08.5 2.00 Naos De logiska unktionerna implementeras i grindar. Här visas de vanligaste. Svenska IEC standard SS IEC 87-2 Amerikanska ANSI/IEEE Std.9.984
Digital elektronik CL0090 Föreläsning 2 2007-0-25 08.5 2.00 Naos De logiska unktionerna implementeras i grindar. Här visas de vanligaste. Svenska IEC standard SS IEC 87-2 Amerikanska ANSI/IEEE Std.9.984
Grundläggande digitalteknik
 Grundläggande digitalteknik Jan Carlsson Inledning I den verkliga världen vet vi att vi kan få vilka värden som helst när vi mäter på något. En varm sommardag visar termometern kanske 6, 7 C. Men när det
Grundläggande digitalteknik Jan Carlsson Inledning I den verkliga världen vet vi att vi kan få vilka värden som helst när vi mäter på något. En varm sommardag visar termometern kanske 6, 7 C. Men när det
EDA Digital och Datorteknik 2009/2010
 EDA45 - Digital och Datorteknik 29/2 EDA 45 - Digital och Datorteknik 29/2, lärobokens kapitel 3 Ur innehållet: Satslogik och Boolesk algebra Grindar Funktionstabell Binär evaluering Normal orm/förenklad
EDA45 - Digital och Datorteknik 29/2 EDA 45 - Digital och Datorteknik 29/2, lärobokens kapitel 3 Ur innehållet: Satslogik och Boolesk algebra Grindar Funktionstabell Binär evaluering Normal orm/förenklad
IE1204 Digital Design
 IE204 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM F0 F
IE204 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM F0 F
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #3 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Logikgrindar Från data till digitala byggblock: Kursens
Digital- och datorteknik Föreläsning #3 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Logikgrindar Från data till digitala byggblock: Kursens
EDA Digital och Datorteknik 2010/2011
 EDA45 - Digital och Datorteknik 2/2 EDA 45 - Digital och Datorteknik 2/2, lärobokens kapitel 3 Ur innehållet: Satslogik och Boolesk algebra Grindar Funktionstabell Binär evaluering Normal orm/förenklad
EDA45 - Digital och Datorteknik 2/2 EDA 45 - Digital och Datorteknik 2/2, lärobokens kapitel 3 Ur innehållet: Satslogik och Boolesk algebra Grindar Funktionstabell Binär evaluering Normal orm/förenklad
Digitalteknik syntes Arne Linde 2012
 Digitalteknik, fortsättningskurs Föreläsning 3 Kombinatoriska nät 202 VHDL repetition + Strukturell VHDL Lite repetition + Karnaughdiagram(4-6var), flera utgångar + Quine-McCluskey + intro tid 2 Entity
Digitalteknik, fortsättningskurs Föreläsning 3 Kombinatoriska nät 202 VHDL repetition + Strukturell VHDL Lite repetition + Karnaughdiagram(4-6var), flera utgångar + Quine-McCluskey + intro tid 2 Entity
Switchnätsalgebra. Negation, ICKE NOT-grind (Inverterare) Konjunktion, OCH AND-grind. Disjunktion, ELLER OR-grind
 Dagens öreläsning behandlar: Läroboken kapitel 3 Arbetsboken kapitel,3 Ur innehållet: Satslogik och Grindar Funktionstabell Binär evaluering Normal orm/förenklad orm/ Minimal orm Karnaughdiagram Negation,
Dagens öreläsning behandlar: Läroboken kapitel 3 Arbetsboken kapitel,3 Ur innehållet: Satslogik och Grindar Funktionstabell Binär evaluering Normal orm/förenklad orm/ Minimal orm Karnaughdiagram Negation,
Tentamen i IE1204/5 Digital Design onsdagen den 5/
 Tentamen i IE1204/5 Digital Design onsdagen den 5/6 2013 9.00-13.00 Tentamensfrågor med lösningsförslag Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista
Tentamen i IE1204/5 Digital Design onsdagen den 5/6 2013 9.00-13.00 Tentamensfrågor med lösningsförslag Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista
Digital Design IE1204
 Digital Design IE1204 F10 Tillståndsautomater del II william@kth.se IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska
Digital Design IE1204 F10 Tillståndsautomater del II william@kth.se IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska
Digitalteknik F2. Digitalteknik F2 bild 1
 igitalteknik F2 igitalteknik F2 bild Återblick från F: Kombinatoriska och sekventiella kretsar Funktionstabeller ooleska funktioner Logiksymboler esignspråk igitalteknik F2 bild 2 Förenkling av komb. funkt.
igitalteknik F2 igitalteknik F2 bild Återblick från F: Kombinatoriska och sekventiella kretsar Funktionstabeller ooleska funktioner Logiksymboler esignspråk igitalteknik F2 bild 2 Förenkling av komb. funkt.
Tentamen med lösningar i IE1204/5 Digital Design Måndag 27/
 Tentamen med lösningar i IE04/5 Digital Design Måndag 7/0 04 9.00-3.00 Allmän information Examinator: Ingo Sander. Ansvarig lärare: Elena Dubrova /William Sandvist, tel 08-7904487 Tentamensuppgifterna
Tentamen med lösningar i IE04/5 Digital Design Måndag 7/0 04 9.00-3.00 Allmän information Examinator: Ingo Sander. Ansvarig lärare: Elena Dubrova /William Sandvist, tel 08-7904487 Tentamensuppgifterna
Laboration D181. ELEKTRONIK Digitalteknik. Kombinatoriska kretsar, HCMOS. 2008-01-24 v 2.1
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Christer Ardlin/Lars Wållberg/ Dan Weinehall/Håkan Joëlson 2008-01-24 v 2.1 ELEKTRONIK Digitalteknik Laboration D181 Kombinatoriska kretsar,
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Christer Ardlin/Lars Wållberg/ Dan Weinehall/Håkan Joëlson 2008-01-24 v 2.1 ELEKTRONIK Digitalteknik Laboration D181 Kombinatoriska kretsar,
Tentamen med lösningar för IE1204/5 Digital Design Torsdag 15/
 Tentamen med lösningar för IE4/5 Digital Design Torsdag 5/ 5 9.-. Allmän information Eaminator: Ingo Sander. Ansvarig lärare: Kista, William Sandqvist, tel 8-79 44 87. KTH Valhallavägen, Fredrik Jonsson,
Tentamen med lösningar för IE4/5 Digital Design Torsdag 5/ 5 9.-. Allmän information Eaminator: Ingo Sander. Ansvarig lärare: Kista, William Sandqvist, tel 8-79 44 87. KTH Valhallavägen, Fredrik Jonsson,
Grundläggande Datorteknik Digital- och datorteknik
 Grundläggande Datorteknik Digital- och datorteknik Kursens mål: Fatta hur en dator är uppbggd (HDW) Fatta hur du du programmerar den (SW) Fatta hur HDW o SW samverkar Digital teknik Dator teknik Grundläggande
Grundläggande Datorteknik Digital- och datorteknik Kursens mål: Fatta hur en dator är uppbggd (HDW) Fatta hur du du programmerar den (SW) Fatta hur HDW o SW samverkar Digital teknik Dator teknik Grundläggande
Digital Design IE1204
 Digital Design IE24 F3 CMOS-kretsen, Implementeringsteknologier william@kth.se IE24 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska
Digital Design IE24 F3 CMOS-kretsen, Implementeringsteknologier william@kth.se IE24 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska
Digital Design IE1204
 Digital Design IE1204 F3 CMOS-kretsen, Implementeringsteknologier william@kth.se IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska
Digital Design IE1204 F3 CMOS-kretsen, Implementeringsteknologier william@kth.se IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska
Omtentamen med lösningar i IE1204/5 Digital Design Fredag 10/
 Omtentamen med lösningar i IE24/5 Digital Design Fredag /4 25 8.-2. Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandvist, tel 8-794487 / Fredrik Jonsson Tentamensuppgifterna behöver
Omtentamen med lösningar i IE24/5 Digital Design Fredag /4 25 8.-2. Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandvist, tel 8-794487 / Fredrik Jonsson Tentamensuppgifterna behöver
Tentamen i IE1204/5 Digital Design onsdagen den 5/
 Tentamen i IE1204/5 Digital Design onsdagen den 5/6 2013 9.00-13.00 Allmän information Exaator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista IE1204) Tentamensuppgifterna behöver
Tentamen i IE1204/5 Digital Design onsdagen den 5/6 2013 9.00-13.00 Allmän information Exaator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista IE1204) Tentamensuppgifterna behöver
DIGITALTEKNIK I. Laboration DE1. Kombinatoriska nät och kretsar
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Björne Lindberg/Håkan Joëlson John Berge 2013 DIGITALTEKNIK I Laboration DE1 Kombinatoriska nät och kretsar Namn... Personnummer... Epost-adress...
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Björne Lindberg/Håkan Joëlson John Berge 2013 DIGITALTEKNIK I Laboration DE1 Kombinatoriska nät och kretsar Namn... Personnummer... Epost-adress...
T1-modulen Lektionerna 10-12. Radioamatörkurs OH6AG - 2011 OH6AG. Bearbetning och översättning: Thomas Anderssén, OH6NT Heikki Lahtivirta, OH2LH
 T1-modulen Lektionerna 10-12 Radioamatörkurs OH6AG - 2011 Bearbetning och översättning: Thomas Anderssén, OH6NT Original: Heikki Lahtivirta, OH2LH 1 Logikkretsar Logikkretsarna är digitala mikrokretsar.
T1-modulen Lektionerna 10-12 Radioamatörkurs OH6AG - 2011 Bearbetning och översättning: Thomas Anderssén, OH6NT Original: Heikki Lahtivirta, OH2LH 1 Logikkretsar Logikkretsarna är digitala mikrokretsar.
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #5 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Vad är ett bra grindnät? De egenskaper som betraktas som
Digital- och datorteknik Föreläsning #5 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Vad är ett bra grindnät? De egenskaper som betraktas som
Hambley avsnitt 12.7 (7.3 för den som vill läsa lite mer om grindar) sann 1 falsk 0
 1 Föreläsning 2 ht2 Hambley avsnitt 12.7 (7.3 för den som vill läsa lite mer om grindar) Lite om logiska operationer Logiska variabler är storheter som kan anta två värden; sann 1 falsk 0 De logiska variabler
1 Föreläsning 2 ht2 Hambley avsnitt 12.7 (7.3 för den som vill läsa lite mer om grindar) Lite om logiska operationer Logiska variabler är storheter som kan anta två värden; sann 1 falsk 0 De logiska variabler
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #3 Biträdande professor Jan Jonsson Instittionen för data- och informationsteknik Chalmers tekniska högskola Från data till digitala byggblock: Krsens inledande föreläsningarna
Digital- och datorteknik Föreläsning #3 Biträdande professor Jan Jonsson Instittionen för data- och informationsteknik Chalmers tekniska högskola Från data till digitala byggblock: Krsens inledande föreläsningarna
Laboration D151. Kombinatoriska kretsar, HCMOS. Namn: Datum: Epostadr: Kurs:
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Christer Ardlin/Lars Wållberg/ Håkan Joëlson 2000-01-28 v 2.3 ELEKTRONIK Digitalteknik Laboration D151 Kombinatoriska kretsar, HCMOS Namn:
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Christer Ardlin/Lars Wållberg/ Håkan Joëlson 2000-01-28 v 2.3 ELEKTRONIK Digitalteknik Laboration D151 Kombinatoriska kretsar, HCMOS Namn:
Föreläsning 4/11. Lite om logiska operationer. Hambley avsnitt 12.7, 14.1 (7.3 för den som vill läsa lite mer om grindar)
 1 Föreläsning 4/11 Hambley avsnitt 12.7, 14.1 (7.3 för den som vill läsa lite mer om grindar) Lite om logiska operationer Logiska variabler är storheter som kan anta två värden; sann 1 falsk 0 De logiska
1 Föreläsning 4/11 Hambley avsnitt 12.7, 14.1 (7.3 för den som vill läsa lite mer om grindar) Lite om logiska operationer Logiska variabler är storheter som kan anta två värden; sann 1 falsk 0 De logiska
Digital Design IE1204
 Digital Design IE24 F2 : Logiska Grindar och Kretsar, Boolesk Algebra william@kth.se IE24 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska
Digital Design IE24 F2 : Logiska Grindar och Kretsar, Boolesk Algebra william@kth.se IE24 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska
Sanningstabell. En logisk funktion kan också beskrivas genom en sanningstabell (truth table) 1 står för sann (true) 0 står för falsk (false)
 Sanningstabell En logisk funktion kan också beskrivas genom en sanningstabell (truth table) 1 står för sann (true) 0 står för falsk (false) ND OR Logiska grindar ND-grinden (OCH) IEC Symbol (International
Sanningstabell En logisk funktion kan också beskrivas genom en sanningstabell (truth table) 1 står för sann (true) 0 står för falsk (false) ND OR Logiska grindar ND-grinden (OCH) IEC Symbol (International
IE1205 Digital Design. F2 : Logiska Grindar och Kretsar, Boolesk Algebra. Fredrik Jonsson KTH/ICT/ES
 IE1205 Digital Design F2 : Logiska Grindar och Kretsar, oolesk Algebra Fredrik Jonsson KTH/ICT/ES fjon@kth.se Switch En switch har två lägen Sluten/Till (Closed/On) Öppen/Från (Open/Off) Sluten Öppen x
IE1205 Digital Design F2 : Logiska Grindar och Kretsar, oolesk Algebra Fredrik Jonsson KTH/ICT/ES fjon@kth.se Switch En switch har två lägen Sluten/Till (Closed/On) Öppen/Från (Open/Off) Sluten Öppen x
Styrteknik: Grundläggande logiska funktioner D2:1
 Styrteknik: Grundläggande logiska funktioner D2:1 Digitala kursmoment D1 Boolesk algebra D2 Grundläggande logiska funktioner D3 Binära tal, talsystem och koder Styrteknik: Grundläggande logiska funktioner
Styrteknik: Grundläggande logiska funktioner D2:1 Digitala kursmoment D1 Boolesk algebra D2 Grundläggande logiska funktioner D3 Binära tal, talsystem och koder Styrteknik: Grundläggande logiska funktioner
Kortlaboration DIK. Digitalteknik, kombinatorik.
 MMK, KTH Kortlaborationer 1 Kortlaboration DIK Digitalteknik, kombinatorik. I denna laboration bekantar vi oss med datorprogrammet LabVIEW. Programmet har blivit något av en industristandard för att automatisera
MMK, KTH Kortlaborationer 1 Kortlaboration DIK Digitalteknik, kombinatorik. I denna laboration bekantar vi oss med datorprogrammet LabVIEW. Programmet har blivit något av en industristandard för att automatisera
Tentamen i Grundläggande ellära och digitalteknik ETA 013 för D
 Lars-Erik ederlöf Per Liljas Tentamen i Grundläggande ellära och digitalteknik ET 03 för D 200-08-20 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet hjälpmedel
Lars-Erik ederlöf Per Liljas Tentamen i Grundläggande ellära och digitalteknik ET 03 för D 200-08-20 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet hjälpmedel
Transistorn en omkopplare utan rörliga delar
 Transistorn en omkopplare utan rörliga delar Gate Source Drain Principskiss för SiGe transistor (KTH) Varför CMOS? CMOS-Transistorer är enkla att tillverka CMOS-Transistorer är gjorda av vanlig sand =>
Transistorn en omkopplare utan rörliga delar Gate Source Drain Principskiss för SiGe transistor (KTH) Varför CMOS? CMOS-Transistorer är enkla att tillverka CMOS-Transistorer är gjorda av vanlig sand =>
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #4 Biträdande professor Jan Jonsson Instittionen för data- och informationsteknik Chalmers tekniska högskola SP- och PS-form: Boolesk algebra Vid förra föreläsningen
Digital- och datorteknik Föreläsning #4 Biträdande professor Jan Jonsson Instittionen för data- och informationsteknik Chalmers tekniska högskola SP- och PS-form: Boolesk algebra Vid förra föreläsningen
Quine McCluskys algoritm
 Quine McCluskys algoritm Tabellmetod för att systematiskt finna alla primimplikatorer ƒ(a,b,c,d) = m(4,5,6,8,9,0,3) + d(0,7,5) Moment : Finn alla primimplikatorer Steg: Fyll i alla mintermer i kolumn.
Quine McCluskys algoritm Tabellmetod för att systematiskt finna alla primimplikatorer ƒ(a,b,c,d) = m(4,5,6,8,9,0,3) + d(0,7,5) Moment : Finn alla primimplikatorer Steg: Fyll i alla mintermer i kolumn.
Tentamen i IE1204/5 Digital Design Torsdag 29/
 Tentamen i IE1204/5 Digital Design Torsdag 29/10 2015 9.00-13.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist
Tentamen i IE1204/5 Digital Design Torsdag 29/10 2015 9.00-13.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist
Digital- och datorteknik
 LEU Digital- och datorteknik, Chalmers, /6 Föreläsning # Uppdaterad 6 september, Digital- och datorteknik Föreläsning # Biträdande professor Jan Jonsson SP- och PS-form: Vid förra föreläsningen konstaterade
LEU Digital- och datorteknik, Chalmers, /6 Föreläsning # Uppdaterad 6 september, Digital- och datorteknik Föreläsning # Biträdande professor Jan Jonsson SP- och PS-form: Vid förra föreläsningen konstaterade
Tentamen IE Digital Design Fredag 15/
 Tentamen IE204-5 Digital Design Fredag 5/ 206 4.00-8.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: Kista, William Sandqvist
Tentamen IE204-5 Digital Design Fredag 5/ 206 4.00-8.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: Kista, William Sandqvist
Digital elektronik CL0090
 Digital elektronik CL9 Föreläsning 5 27-2-2 8.5 2. Naxos Demonstration av uartus programvara. Genomgång av uartus flödesschema. Detta dokument finns på kurshemsidan. http://www.idt.mdh.se/kurser/cl9/ VHDL-kod
Digital elektronik CL9 Föreläsning 5 27-2-2 8.5 2. Naxos Demonstration av uartus programvara. Genomgång av uartus flödesschema. Detta dokument finns på kurshemsidan. http://www.idt.mdh.se/kurser/cl9/ VHDL-kod
Omtentamen IE Digital Design Måndag 14/
 Omtentamen IE204-5 Digital Design Måndag 4/3 206 4.00-8.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: Kista, William Sandqvist
Omtentamen IE204-5 Digital Design Måndag 4/3 206 4.00-8.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: Kista, William Sandqvist
Tentamen i IE1204/5 Digital Design måndagen den 15/
 Tentamen i IE1204/5 Digital Design måndagen den 15/10 2012 9.00-13.00 Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista IE1204), Tentamensuppgifterna
Tentamen i IE1204/5 Digital Design måndagen den 15/10 2012 9.00-13.00 Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista IE1204), Tentamensuppgifterna
Tentamen med lösningar i IE Digital Design Fredag 15/
 Tentamen med lösningar i IE4-5 Digital Design Fredag 5/ 6 4.-8. Allmän information (TCOMK, Ask for an english version of this exam if needed Examinator: Ingo Sander. Ansvarig lärare: Kista, William Sandvist
Tentamen med lösningar i IE4-5 Digital Design Fredag 5/ 6 4.-8. Allmän information (TCOMK, Ask for an english version of this exam if needed Examinator: Ingo Sander. Ansvarig lärare: Kista, William Sandvist
Tentamen i Grundläggande ellära och digitalteknik ETA 013 för D
 Lars-Erik Cederlöf Tentamen i Grundläggande ellära och digitalteknik ETA 03 för D 2000-05-03 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet hjälpmedel är
Lars-Erik Cederlöf Tentamen i Grundläggande ellära och digitalteknik ETA 03 för D 2000-05-03 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet hjälpmedel är
Kombinationskretsar. Föreläsning 4 Digitalteknik Mattias Krysander Institutionen för systemteknik
 Kombinationskretsar Föreläsning 4 Digitalteknik Mattias Krysander Institutionen för systemteknik Dagens föreläsning Laboration 1 Adderare Konstruktion med minne 3 Laborationsinformation TSEA51/52: Deadline
Kombinationskretsar Föreläsning 4 Digitalteknik Mattias Krysander Institutionen för systemteknik Dagens föreläsning Laboration 1 Adderare Konstruktion med minne 3 Laborationsinformation TSEA51/52: Deadline
Tenta i Digitalteknik
 Tenta i Digitalteknik Kurskod D0011E Tentamensdatum 2011-08-26 Skrivtid 9.00-14.00 Maximalt resultat 50 poäng Godkänt resultat 25 poäng Jourhavande lärare Per Lindgren Tel 070 376 8150 Tillåtna hjälpmedel
Tenta i Digitalteknik Kurskod D0011E Tentamensdatum 2011-08-26 Skrivtid 9.00-14.00 Maximalt resultat 50 poäng Godkänt resultat 25 poäng Jourhavande lärare Per Lindgren Tel 070 376 8150 Tillåtna hjälpmedel
Institutionen för systemteknik, ISY, LiTH. Tentamen i. Tid: kl
 Institutionen för systemteknik, ISY, LiTH Tentamen i Digitalteknik TSIU05/TEN1 Tid: 2016 10 26 kl. 14 18 Lokal : TER3 TER4 Ansvarig lärare: Michael Josefsson. Besöker lokalen kl 16. Tel.: 013-28 12 64
Institutionen för systemteknik, ISY, LiTH Tentamen i Digitalteknik TSIU05/TEN1 Tid: 2016 10 26 kl. 14 18 Lokal : TER3 TER4 Ansvarig lärare: Michael Josefsson. Besöker lokalen kl 16. Tel.: 013-28 12 64
Tentamen IE Digital Design Måndag 23/
 Tentamen IE104-5 Digital Design Måndag 3/10 017 14.00-18.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: Kista, William Sandqvist
Tentamen IE104-5 Digital Design Måndag 3/10 017 14.00-18.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: Kista, William Sandqvist
Försättsblad till skriftlig tentamen vid Linköpings universitet
 Försättsblad till skriftlig tentamen vid Linköpings universitet Datum för tentamen 08-03-3 Sal (5) Tid 8- Kurskod TSEA Provkod TEN Kursnamn/benämning Provnamn/benämning Institution Antal uppgifter som
Försättsblad till skriftlig tentamen vid Linköpings universitet Datum för tentamen 08-03-3 Sal (5) Tid 8- Kurskod TSEA Provkod TEN Kursnamn/benämning Provnamn/benämning Institution Antal uppgifter som
Laboration 6. A/D- och D/A-omvandling. Lunds universitet / Fakultet / Institution / Enhet / Dokument / Datum
 Laboration 6 A/D- och D/A-omvandling A/D-omvandlare Digitala Utgång V fs 3R/2 Analog Sample R R D E C O D E R P/S Skiftregister R/2 2 N-1 Komparatorer Digital elektronik Halvledare, Logiska grindar Digital
Laboration 6 A/D- och D/A-omvandling A/D-omvandlare Digitala Utgång V fs 3R/2 Analog Sample R R D E C O D E R P/S Skiftregister R/2 2 N-1 Komparatorer Digital elektronik Halvledare, Logiska grindar Digital
Facit till övningsuppgifter Kapitel 4 Kombinatoriska nät Rita in funktionen i ett Karnaughdiagram och minimera
 Facit till övningsuppgiter Kapitel 4 Kombinatoriska nät 4-4. Rita in unktionen i ett Karnaughdiagram och minimera ör disjunktiv orm z w ör konjunktiv orm z w a) ='z'+w c) = ( + z')(w + ') = (de Morgan)
Facit till övningsuppgiter Kapitel 4 Kombinatoriska nät 4-4. Rita in unktionen i ett Karnaughdiagram och minimera ör disjunktiv orm z w ör konjunktiv orm z w a) ='z'+w c) = ( + z')(w + ') = (de Morgan)
Switch. En switch har två lägen. Sluten/Till (Closed/On) Öppen/Från (Open/Off) Sluten. Öppen. Symbol. William Sandqvist
 Switch En switch har två lägen Sluten/Till (Closed/On) Öppen/Från (Open/Off) Sluten Öppen = = Symbol S Implementering av logiska funktioner Switchen kan användas för att implentera logiska funktioner Power
Switch En switch har två lägen Sluten/Till (Closed/On) Öppen/Från (Open/Off) Sluten Öppen = = Symbol S Implementering av logiska funktioner Switchen kan användas för att implentera logiska funktioner Power
Digitalteknik EIT020. Lecture 15: Design av digitala kretsar
 Digitalteknik EIT020 Lecture 15: Design av digitala kretsar November 3, 2014 Digitalteknikens kopplingar mot andra områden Mjukvara Hårdvara Datorteknik Kretskonstruktion Digitalteknik Elektronik Figure:,
Digitalteknik EIT020 Lecture 15: Design av digitala kretsar November 3, 2014 Digitalteknikens kopplingar mot andra områden Mjukvara Hårdvara Datorteknik Kretskonstruktion Digitalteknik Elektronik Figure:,
Följddiagram för händelsestyrda rörelser
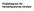 Följddiagram för händelsestyrda rörelser 2 STYROBJEKT UNIKA FASER Två arbetscylindrar ska röra sig i följande ordning. När man ger startkommando ska kolvstången i cylinder gå ut. När den har nått sitt
Följddiagram för händelsestyrda rörelser 2 STYROBJEKT UNIKA FASER Två arbetscylindrar ska röra sig i följande ordning. När man ger startkommando ska kolvstången i cylinder gå ut. När den har nått sitt
Grindar och transistorer
 Föreläsningsanteckningar Föreläsning 17 - Digitalteknik I boken: nns ej med Grindar och transistorer Vi ska kort beskriva lite om hur vi kan bygga upp olika typer av grindar med hjälp av transistorer.
Föreläsningsanteckningar Föreläsning 17 - Digitalteknik I boken: nns ej med Grindar och transistorer Vi ska kort beskriva lite om hur vi kan bygga upp olika typer av grindar med hjälp av transistorer.
Laboration Kombinatoriska kretsar
 Laboration Kombinatoriska kretsar Digital Design IE1204/5 Observera! För att få laborera måste Du ha: bokat en laborationstid i bokningssystemet (Daisy). löst ditt personliga web-häfte med förkunskapsuppgifter
Laboration Kombinatoriska kretsar Digital Design IE1204/5 Observera! För att få laborera måste Du ha: bokat en laborationstid i bokningssystemet (Daisy). löst ditt personliga web-häfte med förkunskapsuppgifter
F1: Introduktion Digitalkonstruktion II, 4p. Digital IC konstruktion. Integrerad krets. System. Algorithm - Architecture. Arithmetic X 2.
 1 X2 IN Vdd OUT GND Översikt: F1: Introduktion Digitalkonstruktion II, 4p - Föreläsare: Bengt Oelmann - Kurslitteratur: "Principles of CMOS VLSI Design - A systems Perspective" - Föreläsningar: 16 - Räkneövningar:
1 X2 IN Vdd OUT GND Översikt: F1: Introduktion Digitalkonstruktion II, 4p - Föreläsare: Bengt Oelmann - Kurslitteratur: "Principles of CMOS VLSI Design - A systems Perspective" - Föreläsningar: 16 - Räkneövningar:
Tentamen med lösningar i IE1204/5 Digital Design Torsdag 29/
 Tentamen med lösningar i IE4/5 Digital Design Torsdag 9/ 5 9.-. Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandvist tel 8-794487 Tentamensuppgifterna behöver inte återlämnas när
Tentamen med lösningar i IE4/5 Digital Design Torsdag 9/ 5 9.-. Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandvist tel 8-794487 Tentamensuppgifterna behöver inte återlämnas när
Digitalteknik. Talsystem Grindlogik Koder Booles algebra Tillämpningar Karnaughdiagram. A.Lövdahl
 Digitalteknik Talsystem Grindlogik Koder ooles algebra Tillämpningar Karnaughdiagram.Lövdahl 1001001100101100000001011010010 TLSYSTEM Talsystem är en angivelse på en viss position. De vanligaste talsystemen
Digitalteknik Talsystem Grindlogik Koder ooles algebra Tillämpningar Karnaughdiagram.Lövdahl 1001001100101100000001011010010 TLSYSTEM Talsystem är en angivelse på en viss position. De vanligaste talsystemen
SMD033 Digitalteknik. Digitalteknik F1 bild 1
 SMD033 Digitalteknik Digitalteknik F1 bild 1 Vi som undervisar Anders Hansson A3209 91 230 aha@sm.luth.se Digitalteknik F1 bild 2 Registrering Registrering via email till diglabs@luth.se Digitalteknik
SMD033 Digitalteknik Digitalteknik F1 bild 1 Vi som undervisar Anders Hansson A3209 91 230 aha@sm.luth.se Digitalteknik F1 bild 2 Registrering Registrering via email till diglabs@luth.se Digitalteknik
Lösningförslag till Exempel på tentamensfrågor Digitalteknik I.
 Lösningförslag till Exempel på tentamensfrågor Digitalteknik I.. Uttryckt i decimal form: A=28+32+8 + 2 =70 B=59 C=7 A+B+C=246 2. Jag låter A' betyda "icke A" A'B'C'D'+ABC'D'+A'BCD'+AB'CD'=D'(A'(B'C'+BC)+A(BC'+B'C))=
Lösningförslag till Exempel på tentamensfrågor Digitalteknik I.. Uttryckt i decimal form: A=28+32+8 + 2 =70 B=59 C=7 A+B+C=246 2. Jag låter A' betyda "icke A" A'B'C'D'+ABC'D'+A'BCD'+AB'CD'=D'(A'(B'C'+BC)+A(BC'+B'C))=
Moment 2 - Digital elektronik. Föreläsning 1 Binära tal och logiska grindar
 Moment 2 - Digital elektronik Föreläsning 1 Binära tal och logiska grindar Jan Thim 1 F1: Binära tal och logiska grindar Innehåll: Introduktion Talsystem och koder Räkna binärt Logiska grindar Boolesk
Moment 2 - Digital elektronik Föreläsning 1 Binära tal och logiska grindar Jan Thim 1 F1: Binära tal och logiska grindar Innehåll: Introduktion Talsystem och koder Räkna binärt Logiska grindar Boolesk
2.1 Disjunktiv och konjunktiv normalform
 Kapitel 2 Booleska funktioner 2. Disjunktiv och konjunktiv normalform Låt x,..., x n vara booleska variabler. En boolesk funktion f(x,..., x n ) är då en funktion av variablerna x,..., x n som antar något
Kapitel 2 Booleska funktioner 2. Disjunktiv och konjunktiv normalform Låt x,..., x n vara booleska variabler. En boolesk funktion f(x,..., x n ) är då en funktion av variablerna x,..., x n som antar något
Tenta i Digitalteknik
 Tenta i Digitalteknik Kurskod D0011E Tentamensdatum 2010-08-27 Skrivtid 9.00-14.00 Maximalt resultat 50 poäng Godkänt resultat 25 poäng inkl bonus Jourhavande lärare Per Lindgren Tel 070 376 8150 Tillåtna
Tenta i Digitalteknik Kurskod D0011E Tentamensdatum 2010-08-27 Skrivtid 9.00-14.00 Maximalt resultat 50 poäng Godkänt resultat 25 poäng inkl bonus Jourhavande lärare Per Lindgren Tel 070 376 8150 Tillåtna
Tentamen med lösningar IE Digital Design Måndag 23/
 Tentamen med lösningar IE04-5 Digital Design Måndag 3/0 07 4.00-8.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: Kista, William
Tentamen med lösningar IE04-5 Digital Design Måndag 3/0 07 4.00-8.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: Kista, William
Digital och Datorteknik
 Digital och Datorteknik Dig o Dat = DoD LEU43 LP-LP2 Mekatronik Digital och Datorteknik OH LV Kursens mål: Fatta hur en dator är uppbyggd (HDW) Fatta hur du du programmerar den (SW) Fatta hur HDW o SW
Digital och Datorteknik Dig o Dat = DoD LEU43 LP-LP2 Mekatronik Digital och Datorteknik OH LV Kursens mål: Fatta hur en dator är uppbyggd (HDW) Fatta hur du du programmerar den (SW) Fatta hur HDW o SW
IE1205 Digital Design: F3 : CMOS-kretsen, Implementeringsteknologier. Fredrik Jonsson KTH/ICT/ES
 IE1205 Digital Design: F3 : CMOS-kretsen, Implementeringsteknologier Fredrik Jonsson KTH/ICT/ES fjon@kth.se Transistorn en omkopplare utan rörliga delar Gate Source Drain Principskiss för SiGe ( KTH )
IE1205 Digital Design: F3 : CMOS-kretsen, Implementeringsteknologier Fredrik Jonsson KTH/ICT/ES fjon@kth.se Transistorn en omkopplare utan rörliga delar Gate Source Drain Principskiss för SiGe ( KTH )
DIGITALTEKNIK. Laboration D173. Grundläggande digital logik
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Håkan Joëlson 2007-11-19 v 1.1 DIGITALTEKNIK Laboration D173 Grundläggande digital logik Innehåll Mål. Material.... Uppgift 1...Sanningstabell
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Håkan Joëlson 2007-11-19 v 1.1 DIGITALTEKNIK Laboration D173 Grundläggande digital logik Innehåll Mål. Material.... Uppgift 1...Sanningstabell
Digital Design IE1204
 Digital Design IE204 F3 Asynkrona sekvensnät del 2 william@kth.se IE204 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska kretsar
Digital Design IE204 F3 Asynkrona sekvensnät del 2 william@kth.se IE204 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska kretsar
Vad är elektricitet?
 Vad är elektricitet? Vad är elektricitet? Grundämnenas elektriska egenskaper avgörs av antalet elektroner i det yttersta skalet - valenselektronerna! Skol-modellen av en Kiselatom. Kisel med atomnumret
Vad är elektricitet? Vad är elektricitet? Grundämnenas elektriska egenskaper avgörs av antalet elektroner i det yttersta skalet - valenselektronerna! Skol-modellen av en Kiselatom. Kisel med atomnumret
Digital Design IE1204
 Digital Design IE204 Kursomgång för Högskoleingenjörsinriktningarna: Datateknik, Elektronik och Datorteknik. Kandidatinriktningen: Informations- och Kommunikationsteknik F3 Asynkrona sekvensnät del 2 william@kth.se
Digital Design IE204 Kursomgång för Högskoleingenjörsinriktningarna: Datateknik, Elektronik och Datorteknik. Kandidatinriktningen: Informations- och Kommunikationsteknik F3 Asynkrona sekvensnät del 2 william@kth.se
Sekvensnät Som Du kommer ihåg
 Sekvensnät Som Du kommer ihåg Designmetodik Grundläggande designmetodik för tillståndsmaskiner. 1. Analysera specifikationen för kretsen 2. Skapa tillståndsdiagram 3. Ställ upp tillståndstabellen 4. Minimera
Sekvensnät Som Du kommer ihåg Designmetodik Grundläggande designmetodik för tillståndsmaskiner. 1. Analysera specifikationen för kretsen 2. Skapa tillståndsdiagram 3. Ställ upp tillståndstabellen 4. Minimera
Laboration Kombinatoriska kretsar
 Laboration Kombinatoriska kretsar Digital Design IE1204/5 Observera! För att få laborera måste Du ha: en bokad laborationstid i bokningssystemet (Daisy). löst ditt personliga web-häfte med förkunskapsuppgifter
Laboration Kombinatoriska kretsar Digital Design IE1204/5 Observera! För att få laborera måste Du ha: en bokad laborationstid i bokningssystemet (Daisy). löst ditt personliga web-häfte med förkunskapsuppgifter
Asynkrona sekvensmaskiner
 Asynkrona sekvensmaskiner En asynkron sekvensmaskin är en sekvensmaskin utan vippor Asynkrona sekvensmaskiner bygger på återkopplade kombinatoriska grindnätverk Vid analys antar man: Endast EN signal i
Asynkrona sekvensmaskiner En asynkron sekvensmaskin är en sekvensmaskin utan vippor Asynkrona sekvensmaskiner bygger på återkopplade kombinatoriska grindnätverk Vid analys antar man: Endast EN signal i
TSEA22 Digitalteknik 2019!
 1(45) 2019 Mattias Krysander Ingemar Ragnemalm D D 1(45) Föreläsning 4. Komb2. Denna föreläsning: Labb 1 Adderare Lite mer om kombinationskretsar 2(45)2(45) Förra föreläsningen: Några kombinationskretsar.
1(45) 2019 Mattias Krysander Ingemar Ragnemalm D D 1(45) Föreläsning 4. Komb2. Denna föreläsning: Labb 1 Adderare Lite mer om kombinationskretsar 2(45)2(45) Förra föreläsningen: Några kombinationskretsar.
Digital Design IE1204
 Digital Design IE204 F2 Asynkrona sekvensnät del william@kth.se IE204 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska kretsar F7
Digital Design IE204 F2 Asynkrona sekvensnät del william@kth.se IE204 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska kretsar F7
Tentamen i Digital Design
 Kungliga Tekniska Högskolan Tentamen i Digital Design Kursnummer : Kursansvarig: 2B56 :e fo ingenjör Lars Hellberg tel 79 7795 Datum: 27-5-25 Tid: Kl 4. - 9. Tentamen rättad 27-6-5 Klagotiden utgår: 27-6-29
Kungliga Tekniska Högskolan Tentamen i Digital Design Kursnummer : Kursansvarig: 2B56 :e fo ingenjör Lars Hellberg tel 79 7795 Datum: 27-5-25 Tid: Kl 4. - 9. Tentamen rättad 27-6-5 Klagotiden utgår: 27-6-29
Digital Design IE1204
 Digital Design IE204 F2 Asynkrona sekvensnät del william@kth.se IE204 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska kretsar F7
Digital Design IE204 F2 Asynkrona sekvensnät del william@kth.se IE204 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska kretsar F7
Digital Design IE1204
 Digital Design IE1204 F9 Tillståndsautomater del1 william@kth.se IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska kretsar
Digital Design IE1204 F9 Tillståndsautomater del1 william@kth.se IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska kretsar
IE1205 Digital Design: F9: Synkrona tillståndsautomater
 IE25 Digital Design: F9: Synkrona tillståndsautomater Moore och Mealy automater F8 introducerade vippor och vi konstruerade räknare, skift-register etc. F9-F skall vi titta på hur generella tillståndsmaskiner
IE25 Digital Design: F9: Synkrona tillståndsautomater Moore och Mealy automater F8 introducerade vippor och vi konstruerade räknare, skift-register etc. F9-F skall vi titta på hur generella tillståndsmaskiner
Tentamen i IE Digital Design Fredag 21/
 Tentamen i IE204-5 Digital Design Fredag 2/0 206 09.00-3.00 Allmän information (TCOMK, Ask for an english version of this exam if needed) Examinator: Ingo Sander. Ansvarig lärare: Kista, William Sandqvist
Tentamen i IE204-5 Digital Design Fredag 2/0 206 09.00-3.00 Allmän information (TCOMK, Ask for an english version of this exam if needed) Examinator: Ingo Sander. Ansvarig lärare: Kista, William Sandqvist
Omtentamen med lösningar IE Digital Design Måndag 14/
 Omtentamen med lösningar IE204-5 Digital Design Måndag 4/3 26 4.-8. Allmän information ( TCOMK, Ask for an english version of this exam if needed Examinator: Ingo Sander. Ansvarig lärare: Kista, William
Omtentamen med lösningar IE204-5 Digital Design Måndag 4/3 26 4.-8. Allmän information ( TCOMK, Ask for an english version of this exam if needed Examinator: Ingo Sander. Ansvarig lärare: Kista, William
Lösningsföslag till Exempel på tentamensuppgifter i Digitalteknik I
 Lösningsföslag till Exempel på tentamensuppgifter i Digitalteknik I Flervalsfrågor. A 2. C 3. B 4. D 5. A 6. B 7. C 8. D 9. C 0. B. B 2. C 3. A 4. C 5. A Problemuppgifter. Uttryckt i decimal form: A=28+32+8
Lösningsföslag till Exempel på tentamensuppgifter i Digitalteknik I Flervalsfrågor. A 2. C 3. B 4. D 5. A 6. B 7. C 8. D 9. C 0. B. B 2. C 3. A 4. C 5. A Problemuppgifter. Uttryckt i decimal form: A=28+32+8
F5 Introduktion till digitalteknik
 Exklusiv eller XOR F5 Introduktion till digitalteknik EDAA05 Roger Henriksson Jonas Wisbrant På övning 2 stötte ni på uttrycket x = (a b) ( a b) som kan utläsas antingen a eller b, men inte både a och
Exklusiv eller XOR F5 Introduktion till digitalteknik EDAA05 Roger Henriksson Jonas Wisbrant På övning 2 stötte ni på uttrycket x = (a b) ( a b) som kan utläsas antingen a eller b, men inte både a och
Laboration i digitalteknik Introduktion till digitalteknik
 Linköpings universitet Institutionen för systemteknik Laborationer i digitalteknik Datorteknik 6 Laboration i digitalteknik Introduktion till digitalteknik TSEA Digitalteknik D TSEA5 Digitalteknik Y TDDC75
Linköpings universitet Institutionen för systemteknik Laborationer i digitalteknik Datorteknik 6 Laboration i digitalteknik Introduktion till digitalteknik TSEA Digitalteknik D TSEA5 Digitalteknik Y TDDC75
IE1205 Digital Design: F10: Synkrona tillståndsautomater del 2
 IE1205 Digital Design: F10: Synkrona tillståndsautomater del 2 Sekvensnät Om en och samma insignal kan ge upphov till olika utsignal, är logiknätet ett sekvensnät. Det måste då ha ett inre minne som gör
IE1205 Digital Design: F10: Synkrona tillståndsautomater del 2 Sekvensnät Om en och samma insignal kan ge upphov till olika utsignal, är logiknätet ett sekvensnät. Det måste då ha ett inre minne som gör
Digitalteknik 7.5 hp distans: 5.1 Generella sekvenskretsar 5.1.1
 Digitalteknik 7.5 hp distans: 5.1 Generella sekvenskretsar 5.1.1 Från Wikipedia: Sekvensnät Ett sekvensnäts utgångsvärde beror inte bara på indata, utan även i vilken ordning datan kommer (dess sekvens).
Digitalteknik 7.5 hp distans: 5.1 Generella sekvenskretsar 5.1.1 Från Wikipedia: Sekvensnät Ett sekvensnäts utgångsvärde beror inte bara på indata, utan även i vilken ordning datan kommer (dess sekvens).
Exempel på tentamensfrågor Digitalteknik
 Exempel på tentamensfrågor Digitalteknik Till dessa frågor (som kommer från lite olika tidgare tentor) gällde förutsättningen: Hjälpmedel: Kurslitteratur, föreläsningsantecknigar lab. med mätresultat,
Exempel på tentamensfrågor Digitalteknik Till dessa frågor (som kommer från lite olika tidgare tentor) gällde förutsättningen: Hjälpmedel: Kurslitteratur, föreläsningsantecknigar lab. med mätresultat,
Tentamensskrivning 11 januari 2016
 Lunds Universitet LTH Ingenjörshögskolan IDA IEA Helsingborg Tentamensskrivning 11 januari 2016 EDI 610 Digitala system 15 poäng, varav tentamen 4,5 p Kursansvarig: Bernt-Arne Jönsson och Bertil Larsson
Lunds Universitet LTH Ingenjörshögskolan IDA IEA Helsingborg Tentamensskrivning 11 januari 2016 EDI 610 Digitala system 15 poäng, varav tentamen 4,5 p Kursansvarig: Bernt-Arne Jönsson och Bertil Larsson
IE1204/IE1205 Digital Design
 TENTAMEN IE1204/IE1205 Digital Design 2012-12-13, 09.00-13.00 Inga hjälpmedel är tillåtna! Hjälpmedel Tentamen består av tre delar med sammanlagd tolv uppgifter, och totalt 30 poäng. Del A1 (Analys) innehåller
TENTAMEN IE1204/IE1205 Digital Design 2012-12-13, 09.00-13.00 Inga hjälpmedel är tillåtna! Hjälpmedel Tentamen består av tre delar med sammanlagd tolv uppgifter, och totalt 30 poäng. Del A1 (Analys) innehåller
Tentamen i Digitalteknik TSEA22
 Tentamen i Digitalteknik TSEA22 Datum för tentamen 100601 Sal TERC,TER2 Tid 14-18 Kurskod TSEA22 Provkod TEN 1 Kursnamn Digitalteknik Institution ISY Antal uppgifter 5 Antal sidor 5 Jour/Kursansvarig Olle
Tentamen i Digitalteknik TSEA22 Datum för tentamen 100601 Sal TERC,TER2 Tid 14-18 Kurskod TSEA22 Provkod TEN 1 Kursnamn Digitalteknik Institution ISY Antal uppgifter 5 Antal sidor 5 Jour/Kursansvarig Olle
Tenta i Digitalteknik
 Tenta i Digitalteknik Kurskod D0011E Tentamensdatum 2009-08-28 Skrivtid 9.00-13.00 Maximalt resultat 50 poäng Godkänt resultat 25 poäng inkl bonus Jourhavande lärare Per Lindgren Tel 070 376 8150 Tillåtna
Tenta i Digitalteknik Kurskod D0011E Tentamensdatum 2009-08-28 Skrivtid 9.00-13.00 Maximalt resultat 50 poäng Godkänt resultat 25 poäng inkl bonus Jourhavande lärare Per Lindgren Tel 070 376 8150 Tillåtna
F5 Introduktion till digitalteknik
 George Boole och paraplyet F5 Introduktion till digitalteknik EDAA05 Roger Henriksson Jonas Wisbrant p = b! (s " r) George Boole (1815-1864) Professor i Matematik, Queens College, Cork, Irland 2 Exklusiv
George Boole och paraplyet F5 Introduktion till digitalteknik EDAA05 Roger Henriksson Jonas Wisbrant p = b! (s " r) George Boole (1815-1864) Professor i Matematik, Queens College, Cork, Irland 2 Exklusiv
Vad är elektricitet?
 Vad är elektricitet? Vad är elektricitet? Grundämnenas elektriska egenskaper avgörs av antalet elektroner i det yttersta skalet - valenselektronerna! Skol-modellen av en Kiselatom. Kisel med atomnumret
Vad är elektricitet? Vad är elektricitet? Grundämnenas elektriska egenskaper avgörs av antalet elektroner i det yttersta skalet - valenselektronerna! Skol-modellen av en Kiselatom. Kisel med atomnumret
Repetition TSIU05 Digitalteknik Di/EL. Michael Josefsson
 Repetition TSIU05 Digitalteknik Di/EL Michael Josefsson Här kommer några frågeställningar och uppgifter du kan använda för att använda som egenkontroll på om du förstått huvudinnehållet i respektive föreläsning.
Repetition TSIU05 Digitalteknik Di/EL Michael Josefsson Här kommer några frågeställningar och uppgifter du kan använda för att använda som egenkontroll på om du förstått huvudinnehållet i respektive föreläsning.
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #23 Översikt När flera smoduler placeras i processorns adressrum ansluts modulernas adressingångar till motsvarande ledningar i en. Övriga adressledningar i bussen
Digital- och datorteknik Föreläsning #23 Översikt När flera smoduler placeras i processorns adressrum ansluts modulernas adressingångar till motsvarande ledningar i en. Övriga adressledningar i bussen
