STUDENTERS VAL AV REPRESENTATIONER OCH PROBLEMLÖSNINGSSTRATEGIER UNDER GRUPPDISKUSSIONER OM VÅGFYSIK
|
|
|
- Mattias Olofsson
- för 8 år sedan
- Visningar:
Transkript
1 2:a Högskolepedagogiska utvecklingskonferensen i Karlstad 11 maj 2012 STUDENTERS VAL AV REPRESENTATIONER OCH PROBLEMLÖSNINGSSTRATEGIER UNDER GRUPPDISKUSSIONER OM VÅGFYSIK M. Enghag och K.M. Carling Avdelningen för Fysik och elektroteknik, Karlstads universitet E-post: karin.carling@kau.se, margareta.enghag@mnd.su.se Abstrakt: Denna studie genomfördes på en universitetskurs i vågfysik i syfte att följa studenters val av representationer och problemlösningsstrategier under gruppdiskussioner om vågfysik. Studenterna fick byta ut ett lektionstillfälle med övningsräkning mot att istället gruppvis diskutera lösningen av två kontextuella fysikproblem som handlade om brytning av ljus- och ljudvågor. Studien följde hur studenterna valde att representera fysikaliska fenomen under gruppdiskussionerna hur de i ord, bild ekvationer och beräkningsuttryck visar hur de uppfattar problemen. Vissa studenter utvecklade begreppsberättelser och de hade ofta förmåga till modellering med variabler och beräkningar (discoursive fluency). Andra studenter klarar vissa delar tex att sätta in värden på variabler i formler, eller lösa vissa typuppgifter (discoursive imitation). Vidare visar studien att studenterna använder visuella representationer, bilder, för att kommunicera med varandra i mycket stor utsträckning. Att de i stor utsträckning refererar till sina personliga vardagserfarenheter kunde verifieras, men detta gällde i högre utsträckning för brytning av ljud, där de saknade typexempel från lärobok och formelsamling.. Studenternas angrep först fysikuppgifter med typlösningar, men kunde till viss del genom gruppdiskussionerna upptäcka fallgropar och då justera sina resonemang. Nyckelord: fysikundervisning, representationer, kvalitativ problemlösning, kontextuella problem, brytningsfenomen för ljus och ljud INTRODUKTION Denna kvalitativa undersökning genomfördes på en universitetskurs i vågfysik i syfte att följa studenters val av representationer och problemlösningsstrategier under gruppdiskussioner om vågfysik. Fysiken är en ämnespraktik som inkluderar begrepp, modeller, tabeller, diagram, ekvationer och bilder (dvs. olika semiotiska resurser (Kress, 2010)) som studenten måste lära sig att hantera, för att kommunicera flytande (discilpinary discoursive fluency) (Airey & Linder, 2009). Gruppdiskussioner är ett sätt att ge studenter möjlighet att uppleva de samtal om fysikfenomen som de behöver för att fördjupa sina kunskaper och inte fastna i en ytligt problemlösning som bygger på att lösa typexempel (Heller & Hollabaugh,1992; Heller, Keith & Anderson, 1992). Den kurs vi följde gavs med upplägget åtta föreläsningar och fyra pass övningsräkning. För att kunna erbjuda studenterna mer av dialog för att gå djupare in i förståelsen av fysiska problem, använde vi två kontextuella problem med ljud- och ljusbrytning som krävde noggrann analys snarare än beräkningar med formler för att lösa problemen. Studenter startar från sina personliga erfarenheter i gruppdiskussioner när de försöker att bekanta sig med ett problem som kan uttryckas fysikaliskt (Enghag, Gustafsson, & Jonsson, 2007). I gruppdiskussioner försöker de hitta ett sätt att uttrycka sina vardagliga erfarenheter som leder dem in i den fysik som kan användas för att beskriva problemet. När olika semiotiska resurser används i fysik undervisningen är det ofta så att fysikläraren använder sig av de verktyg, representationer och aktiviteter som pågår. Brist på tid för studenten att använda semiotiska resurser kan resultera i att studenterna hamnar i passivt lyssnande istället för att aktivt ta del intellektuellt och praktiskt. Wells (1999, p.157) diskuterar relationen mellan text, tal och utredande förklaringar, och hur eleverna som "semiotiska lärlingar" behöver råd och stöd och "möjligheter att prata och skriva vetenskapen själva, för andra som är intresserade av, och lyhörda för, deras
2 bidrag " (vår översättning). Gruppdiskussionerna har video-filmats, samtalen transkriberats och analyserats med kategoriseringar av representationer och semiotiska resurser samt jämförelse av lösningsstrategier för de olika problemen. a) Var måste fisken befinna sig för att se ljuset från brasan, alldeles under ytan eller djupt ner? Förklara hur ni tänker. b) Bestäm det största eller minsta avstånd från vattenytan fisken ska vara på för att kunna se ljuset från brasan. SYFTE OCH FRÅGESTÄLLNINGAR Syftet är att följa studenters val av representationer och problemlösningsstrategier under gruppdiskussioner och problemlösning av två kvalitativt olika uppgifter om ljus- och ljudbrytning. Frågeställningar: 1. Hur väljer studenterna att representera de olika fysikaliska brytningsfenomenen av ljus och ljud? 2. Vilken ansats används för att lösa problemen? 3. Hur hänvisar grupperna till sina erfarenheter? 4. Vilka dialogiska mönster kan ses? DESIGN OCH METOD Tre grupper videofilmades, och och deras samtal under problemlösningstillfället transkriberades. Teckningar gjorda på grupprummets white-board fotograferades. Ett teoretiskt raster utvecklades (se Tabell 1), där representationer delades upp i aktiviteter, verktyg och semiotiska resurser (Airey & Linder, 2009) och användes för att belysa intressanta episoder i transkripten. Tabell 1: Kategorier av Representationer (Utveckling baserad på Airey & Linder, 2009) Aktiviteter (analysenhet verb som beskriver aktiviteten ) skriver ritar samtalar berättar frågar experimenterar beräknar påstår modellerar Representationer (analysenhet uttalanden ) Erfarenheter : vardag - tidigare lektioner Modell: - ekvationer - begreppsberättelser Begrepp Beräkningar: - exempel - test av specialfall Verktyg (analysenhet använda objekt ) Text Bild Mätutrustning Dator Räknedosa With- board Vi jämför likheter och skillnader mellan det kontextuella problemet med ljusbrytning, Uppgift 1, och det mer kontextuella problemet om ljudbrytning, Uppgift 2. Uppgift 1: Ljusbrytning problem 53) Fisk och ljus (Se Knight 2nd edition, s.736, En fisk befinner sig 20 m från land i en sjö. En majbrasa brinner vid kanten av sjön på stranden närmast fisken Uppgift 2: Ljudbrytning ( Egen problemkonstruktion) Fisk och ljud a) Fiskare säger ofta att man ska vara tyst när man fiskar för att ljudet skrämmer bort fiskarna. Kan ljud från sjökanten nå fiskar som befinner sig i sjön? Motivera ditt svar. Rita en bild som visar den väg du antar att ljudet tar när det breder ut sig, för några olika situationer. b) Kan totalreflektion uppstå för ljudvågor vid ett gränssnitt mellan olika ämnen? Motivera ditt svar så utförligt som möjligt. Jämför situationen med totalreflektion för ljus. RESULTAT OCH ANALYS Hur väljer studenterna att representera de olika fysikaliska brytningsfenomenen av ljus och ljud? Studenterna använder i samtliga grupper ritade bilder för att kommunicera sina resonemang i gruppen. Den första uppgiften lockade studenterna att använda en standardlösning de tidigare tränat på. Två grupper valde att låta en stråle, godtyckligt vald, nå vattnet, och använde sen direkt Snell s lag för att räkna ut brytningsvinkel, och sen avståndet till fiskens placering för att nås av strålen, se figurerna 1-2. Bilden av en ljusstråle som bryts i vattnet är ju en av de vanligaste representationerna inom optik, och finns i samtliga läromedel från grundskola till universitetskurser i fysik. En grupp tvekade efter att ha försökt löst uppgiften så, och resonerade sig fram till att någon stråle alltid måste nå fisken. Här kom denna grupp längre i sitt lösningsförslag än den lösningsanvisning som läroboken angett. Fig. 1. Studentbild 1 av ljusbrytning från en brasa vid strandkanten
3 Fig. 2. Studentbild av ljusbrytning från brasan, val av en konstruktionsstråle (av alla möjliga) När det gäller lösning av uppgift 2 fanns inga numeriska värden, och läroboken behandlade inte ljudets brytning med någon bild. Studenterna var osäkra på om Snell s lag gäller för ljud, och hade svårt att föreställa sig tredimensionell utbredning av vågor. korrekt, och då gör förbättrade ansatser. När beräkningar är möjliga är det oftast en student som genomför beräkningrna, och de andra får tid att reflektera. Hur hänvisar grupperna till sina erfarenheter? Det är i Uppgift 2, som studenterna refererar till sina personliga vardagserfarenheter, som dykning, se Tabell 2., medan man i Uppgift 1 oftare refererar till sina lektionserfarenheter. Tabell 2: Studenternas referens till vardagserfarenheter Fig.3 Studentbild av ljudbrytning från en fiskare på stranden vars röst ger ljudvågor som bryts i vattenytan. En grupp överförde problemet till ljud från en båt ner i vattnet, och undvek därmed att ta ställning till om riktningen påverkas när ljudet når vattnet. 1. Jag, som är en dykare, vet att du kan höra även om du har en utombordsmotor, och det hörs mycket bättre där nere än vad som hörs på land. 2. Jag tänkte som vågor som slår en strand. 3. Ja, tsunamier och sådant Jo det finns rum med saker som tak-rör (halv-rör?, Svåra att höra) som gör ljudet studsar, tar bort det ljud. 5. Men jag tänkte, det finns akustiska mattor och liknande. Fig. 4 Studentbild av ljudbrytning från en båt som ger ljudvågor. 6. Men du kan väl tänka en kyrka, där du brukar säga att det är bra akustik, där ljudet studsar så att du hör är mycket tydligare. 7. men ja det gör det, du har ett eko och en sådan! 8. Jag tänker att strängen, när du gör så här (visar hur du gör en puls på strängen) och när vågen träffar en solid vägg det vänder. 9. Sonar. Fig.5 Studentbild av ljudbrytning. Varianter av strålmodeller och vågmodeller förekom. 10. ja, men fiskarna kan känna hela stim av fisk och sådant, ja när du sätter det så, men varför kunde det inte vara så. 11. När vi talar om ekolod, då en gammal fiskare inom mig säger att det kommer att bli total reflektion. 12. Det material i dessa väggar är väl tar upp det ljud som vi talar nu. Fig.6 Studentbild av ljudbrytning. Vilken ansats används för att lösa problemen? Studenternas angriper först fysikuppgifter med de typlösningar de tidigare tränat på, men kunde till viss del genom gruppdiskussionerna upptäcka fallgropar och då justera sina resonemang. Det är påfallande att man påbörjar sin problemlösning med beräkningar, och senare genom reflektioner inser att något inte blev Många av studenternas erfarenheter kan hänföras till embodied knowledge eller bodily experiences (Lakoff & Johnson, 1999). Vilka dialogiska mönster kan ses? De tre grupperna fungerar väl, och alla kommer till tals, även om det är en eller två personer som driver resonemanget framåt. Det förekommer rikligt med
4 sonderande samtal (Barnes & Todd, 1995), när man prövar ut idéer, och ser om resonemangen är fruktbara. En grupp nöjer sig med en lösning de inser är felaktig, och vill hellre gå vidare för att hinna med båda problemen. I följande excerpt bestämmer sig studenterna för att välja en godtycklig stråle, så de får möjlighet att lösa ett problem de kan sen tidigare. Det dialogiska mönstret är sonderande tal (Barnes & Todd, 1995, Mercer, 2000). D: Ja, just så, vi har en bestämd sträcka här...om vi testar den här, den är ju 70, vi ska ju se djupet. Det ska ju vara toppen då...det behöver ju... F: Vad hög är brasan då? E: Ja, precis, det vet vi ju inte. D: Och om man säger, en majbrasa kan ju vara ganska hög. E: Men vi får väl ta en stråle från majbrasan. D: Ja från den översta typ. E. Ja. Det blir ju enklare än att ta hela brasan, men det kommer ju att... F: Ska vi säga att θ 1 är 70, typ? En annan grupp upptäcker mer, och även här är det dialogiska mönstret sonderande: N: Vi ska ha den minsta och det största avståndet från vattenytan. J: Den kommer ju alltid att vara 20 m ifrån... N: men då kommer det ju helt klart att bero på hur höga flammorna är! M: va? N: Nu är det här det minsta, men det största djupet kommer ju att bero på hur högt brasan är.kommer ju att krympa ju längre ned fisken är...och...då... J: Just det. Men...kommer den här att ändras när man går längre och längre ned? N: Nej, den här sträckan är ju given, så det kommer inte att ändras. (läser högt texten igen) N: Det måste ju vara beroende av höjden på brasan. Den här sträckan...fisken kan ju kolla brantare på något sätt... J: Ja, den är 20m alltid. J: man skulle kunna göra så här också why not? Ritar strålbrytningen i ett annat läge på vattenytan. De två problemen som valdes för ljusbrytning respektive ljudbrytning är olika, på så sätt att i första uppgiften med ljusbrytning ges numeriska data och studenternas problemlösningsstrategi blir att pröva en beräkning med Snell s lag som de alla behärskar. En grupp upptäcker att deras antaganden är orimliga, och hinner påbörja en djupare kvalitativ analys som avslöjar att utan en orimlig approximation av majbrasan som en punktkälla, kommer alltid någon stråle att träffa fisken. De uttrycker sig i begreppsberättelser där de kan uttrycka sig sammanhängande med hjälp av fysikaliska resonemang. Andra blandar begrepp och storheter i en mindre koherent uttryckssätt, som vi uppfattar som med mindre discoursive fluency och mer discoursive imitation. Blandning av begreppsberättelse och variabelsymboler förekommer ofta, t ex: Men jag vet, det här är inga vågfronter, vågfronterna är såna här(beskriver med handen)...en våg som kommer in bryts, så här är det, så kan λ2 komma att vara större än λ1, eftersom vi vet att i mediet går det fortare. SLUTSATSER Ljusbrytning som är framställd med samma representation i alla läroböcker, och strålmodellen är studenternas första prioritet vid problemlösning när de själva ritar bilder. Ljudbrytning behandlads inte lika utförligt med bilder och studenternas erfarenheter från lektioner är begränsade. De utgår istället i stor utsträckning från sina vardagserfarenheter. Många av deras erfarenheter kan hänföras till embodied knowledge eller bodily experiences. Studenterna använder bilder för att kommunicera sina resonemang, och har lätt för att gå in i sonderande samtal. Om problemet inte innehåller kvantiserade storheter minskar tendensen att direkt använda typlösningar, och mer möda läggs ner på analys av problemet. När studenten kan resonera med begrepp, förefaller det som analysen av problemet går lättare, än när studenten blandar begrepp, variabler och numeriska uttryck i sina resonemang. IMPLIKATIONER FÖR UNDERVISNING Mer fokus i undervisningen på kvalitativa problem, för att undvika att studenten alltid prövar med typlösningar och insättning av numerisk värden i formler. Mer fokus på hur representationer av ljusbrytning används så att de inte slentrianmässigt avbildas på samma sätt i alla sammanhang, utan varieras. Prioritera att ge tid för studenter att träna på att uttrycka sig om hur de ser på problemlösning ge dem möjlighet att utveckla begreppsberättelser istället för att blanda begrepp, storheter och numeriska värden i sina resonemang. Datainsamling till denna studie har gjorts inom VRprojektet Representationer och kunskapstraditioner, som drivs av Uppsala universitet. Utförligare redovisningar av studien kommer att publiceras.
5 REFERENCES Airey, J., & Linder, C. (2009). A disciplinary discourse perspective on university science Learning: Achieving fluency in a critical constellation of modes. Journal of Research in Science Teaching, 46(1), Barnes, D., & Todd, F. (1995). Communication and learning revisited: Making meaning through talk. Portsmouth, NH: Boynton/Cook Publishers. Enghag, M., Gustafsson, P., & Jonsson, G. (2007). From everyday life experiences to physics understanding occurring in small group work with context rich problems during introductory physics work at university Research in Science Education, 37: Heller P., Keith R., & Anderson S. (1992). Teaching problem solving through cooperative grouping. Part I. group versus individual problem solving. Am.J.Phys (60): Heller, P., & Hollabaugh,M. (1992). Teaching problem solving through cooperative grouping. Part II. Designing problems and structuring groups. Am.J.Phys(60): Kress, G. (Ed.). (2010). Multimodality: a social semiotic approach to contemporary communication London: Routledge. Lakoff, G. & Johnson, M. (1999) Philosophy in the flesh: the embodied mind and its challenge to Western thought, New York: Basic Books Mercer, N. (2000). Words and Minds: how we use language to think together. London: Routledge. Wells, G. (1999). Dialogic Inquiry- Towards a Sociocultural practice and theory of education. Cambridge: Cambridge University press.
Disciplinära diskurser i naturvetenskap och matematik
 Disciplinära diskurser i naturvetenskap och matematik Jonas Forsman, Staffan Andersson, Jannika Andersson Chronholm, Cedric Linder Avdelningen för fysikens didaktik, Institutionen för fysik och materialvetenskap,
Disciplinära diskurser i naturvetenskap och matematik Jonas Forsman, Staffan Andersson, Jannika Andersson Chronholm, Cedric Linder Avdelningen för fysikens didaktik, Institutionen för fysik och materialvetenskap,
Deliberate Practice på en kurs i kvantmekanik. Emma Wikberg (& Stefano Bonetti) Fysikum, SU
 Deliberate Practice på en kurs i kvantmekanik Emma Wikberg (& Stefano Bonetti) Fysikum, SU Generella principer Aktiv träning + feedback = effektiv inlärning Utnyttja klassrumstiden till problemlösning,
Deliberate Practice på en kurs i kvantmekanik Emma Wikberg (& Stefano Bonetti) Fysikum, SU Generella principer Aktiv träning + feedback = effektiv inlärning Utnyttja klassrumstiden till problemlösning,
Kärt barn har många namn Modeller, representationer och visualiseringar
 Naturvetenskap och teknik Gymnasieskola Modul: Modeller och representationer Del 1: Vad är modeller och representationer? Kärt barn har många namn Modeller, representationer och Gustav Bohlin, Linköpings
Naturvetenskap och teknik Gymnasieskola Modul: Modeller och representationer Del 1: Vad är modeller och representationer? Kärt barn har många namn Modeller, representationer och Gustav Bohlin, Linköpings
På vilka sätt kan mönster vara en ingång till att utveckla förmågan att uttrycka och argumentera för generaliseringar algebraiskt?
 På vilka sätt kan mönster vara en ingång till att utveckla förmågan att uttrycka och argumentera för generaliseringar algebraiskt? Jenny Fred, lärare på Ekensbergsskolan och doktorand vid Forskarskolan
På vilka sätt kan mönster vara en ingång till att utveckla förmågan att uttrycka och argumentera för generaliseringar algebraiskt? Jenny Fred, lärare på Ekensbergsskolan och doktorand vid Forskarskolan
Anna Öhman. Lic-forskarskolan i yrkesämnenas didaktik. Karlstads Universitet
 Anna Öhman Lic-forskarskolan i yrkesämnenas didaktik Karlstads Universitet Bedömningssamtal i frisörutbildningen Bedömning av yrkeskunnande inom hantverksprogrammets frisörutbildning Ett multimodalt perspektiv
Anna Öhman Lic-forskarskolan i yrkesämnenas didaktik Karlstads Universitet Bedömningssamtal i frisörutbildningen Bedömning av yrkeskunnande inom hantverksprogrammets frisörutbildning Ett multimodalt perspektiv
Fysik. Arbetslag: Gamma Klass: 8 C, D Veckor: 43-51, ht-2015 Akustik och optik (ljud och ljus) och astronomi Utdrag ur kursplanen i fysik:
 Fysik Arbetslag: Gamma Klass: 8 C, D Veckor: 43-51, ht-2015 Akustik och optik (ljud och ljus) och astronomi Utdrag ur kursplanen i fysik: - Använda kunskaper i fysik för att granska information, kommunicera
Fysik Arbetslag: Gamma Klass: 8 C, D Veckor: 43-51, ht-2015 Akustik och optik (ljud och ljus) och astronomi Utdrag ur kursplanen i fysik: - Använda kunskaper i fysik för att granska information, kommunicera
ATT LÖSA FYSIKPROBLEM I GRUPPDISKUSSIONER - HUR, VAD OCH VARFÖR?
 :a Högskolepedagogiska utvecklingskonferensen i Karlstad maj 0 ATT LÖSA FYSIKPROBLEM I GRUPPDISKUSSIONER - HUR, VAD OCH VARFÖR? Margareta Enghag, Gunnar Jonsson Avdelningen för Fysik och elektroteknik,
:a Högskolepedagogiska utvecklingskonferensen i Karlstad maj 0 ATT LÖSA FYSIKPROBLEM I GRUPPDISKUSSIONER - HUR, VAD OCH VARFÖR? Margareta Enghag, Gunnar Jonsson Avdelningen för Fysik och elektroteknik,
Kommunicera teknikinnehåll med nyanlända elever
 Kommunicera teknikinnehåll med nyanlända elever Tekniken i skolan #teknikeniskolan Anna Wirstedt Bakgrund Eget intresse i teknikundervisning och nyanlända elevers skolgång Skolinspektionens granskning
Kommunicera teknikinnehåll med nyanlända elever Tekniken i skolan #teknikeniskolan Anna Wirstedt Bakgrund Eget intresse i teknikundervisning och nyanlända elevers skolgång Skolinspektionens granskning
Kursnamn: Multimodal analys (Multimodal analysis)
 Kursnamn: Multimodal analys (Multimodal analysis) Omfattning (högskolepoäng): 7,5 hp Start och slutdatum: 2016-04-05--2016-06-03 Utbildningsnivå: Forskarnivå Huvudområde: Inget Forskarutbildningsämne:
Kursnamn: Multimodal analys (Multimodal analysis) Omfattning (högskolepoäng): 7,5 hp Start och slutdatum: 2016-04-05--2016-06-03 Utbildningsnivå: Forskarnivå Huvudområde: Inget Forskarutbildningsämne:
Handledning Det didaktiska kontraktet. 19 september 2012
 Handledning Det didaktiska kontraktet 19 september 2012 Dagens teman Begreppsföreställning och begreppskunskap igen Handledning Det didaktiska kontraktet Begreppsföreställning och begreppsdefinition Begreppsföreställning
Handledning Det didaktiska kontraktet 19 september 2012 Dagens teman Begreppsföreställning och begreppskunskap igen Handledning Det didaktiska kontraktet Begreppsföreställning och begreppsdefinition Begreppsföreställning
SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE.
 SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE. Vad gjorde vi förra gången? Har du några frågor från föregående lektion? 3. titta i ditt läromedel (boken) Vad ska vi göra idag? Optik och
SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE. Vad gjorde vi förra gången? Har du några frågor från föregående lektion? 3. titta i ditt läromedel (boken) Vad ska vi göra idag? Optik och
Föreläsning 2 (kap , 2.6 i Optics)
 5 Föreläsning 2 (kap 1.6-1.12, 2.6 i Optics) Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen
5 Föreläsning 2 (kap 1.6-1.12, 2.6 i Optics) Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen
Studieanvisning i Optik, Fysik A enligt boken Quanta A
 Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
När vi läste Skolverkets rapport Svenska elevers matematikkunskaper
 Florenda Gallos Cronberg & Truls Cronberg Två perspektiv på att utveckla algebraiska uttryck Svenska elever påstås ha svårt med mönstertänkande. Eller är det så att de inte får lärarledd undervisning i
Florenda Gallos Cronberg & Truls Cronberg Två perspektiv på att utveckla algebraiska uttryck Svenska elever påstås ha svårt med mönstertänkande. Eller är det så att de inte får lärarledd undervisning i
Vågfysik. Geometrisk optik. Knight Kap 23. Ljus. Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion)
 Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
Ljus och strålning. Klass: 9H
 Ljus och strålning Namn: Klass: 9H Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och samhället genomföra systematiska
Ljus och strålning Namn: Klass: 9H Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och samhället genomföra systematiska
3. Mekaniska vågor i 2 (eller 3) dimensioner
 3. Mekaniska vågor i 2 (eller 3) dimensioner Brytning av vågor som passerar gränsen mellan två material Eftersom utbredningshastigheten för en mekanisk våg med största sannolikhet ändras då den passerar
3. Mekaniska vågor i 2 (eller 3) dimensioner Brytning av vågor som passerar gränsen mellan två material Eftersom utbredningshastigheten för en mekanisk våg med största sannolikhet ändras då den passerar
Kan mentometrar slå flera flugor i en smäll? Att öka interaktionen och studentinflytandet på föreläsningar och formativa kursvärderingar.
 Kan mentometrar slå flera flugor i en smäll? Att öka interaktionen och studentinflytandet på föreläsningar och formativa kursvärderingar. Lennart Karlsson Johanna Nygren Spanne Anders Peterson Mål och
Kan mentometrar slå flera flugor i en smäll? Att öka interaktionen och studentinflytandet på föreläsningar och formativa kursvärderingar. Lennart Karlsson Johanna Nygren Spanne Anders Peterson Mål och
Program, FOU-dagen 120529
 Program, FOU-dagen 120529 1 Innehåll Program FoU-dagen... 3 Seminarium 1... 5 Decoding Sciences... 5 Seminarium 2... 5 Infödd, sent eller tidigt invandrad - elevgruppers prestationer och val av lösningsstrategier
Program, FOU-dagen 120529 1 Innehåll Program FoU-dagen... 3 Seminarium 1... 5 Decoding Sciences... 5 Seminarium 2... 5 Infödd, sent eller tidigt invandrad - elevgruppers prestationer och val av lösningsstrategier
Kapitel 35, interferens
 Kapitel 35, interferens Interferens hos ljusvågor, koherensbegreppet Samband för max och min för ideal dubbelspalt Samband för intensitetsvariation för ideal dubbelspalt Interferens i tunna filmer Michelson
Kapitel 35, interferens Interferens hos ljusvågor, koherensbegreppet Samband för max och min för ideal dubbelspalt Samband för intensitetsvariation för ideal dubbelspalt Interferens i tunna filmer Michelson
Ljus snabbare finns inte
 Ljus snabbare finns inte En morgon satt jag och tittade på en daggdroppe i gräset. Den blänkte i solen. Plötsligt märkte jag att droppen ändrade färg när jag flyttade huvudet litet. Kan du förklara det?
Ljus snabbare finns inte En morgon satt jag och tittade på en daggdroppe i gräset. Den blänkte i solen. Plötsligt märkte jag att droppen ändrade färg när jag flyttade huvudet litet. Kan du förklara det?
1. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft.
 Problem. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft. (p) Det finns många förklaringar, till exempel Hewitt med insekten
Problem. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft. (p) Det finns många förklaringar, till exempel Hewitt med insekten
Barns skärmbaserade texthantering:
 Barns skärmbaserade texthantering: Sammansatta texter och nya perspektiv på progression och bedömning Charlotte Engblom Yngre barn: 7 och 8 år Specifikt datorskärmar Barns skärmbaserade Bestående av flera
Barns skärmbaserade texthantering: Sammansatta texter och nya perspektiv på progression och bedömning Charlotte Engblom Yngre barn: 7 och 8 år Specifikt datorskärmar Barns skärmbaserade Bestående av flera
Fysik. Arbetslag: Gamma Klass: 8 S Veckor: 43-51, ht-2015 Akustik och optik (ljud och ljus) och astronomi Utdrag ur kursplanen i fysik:
 Fysik Arbetslag: Gamma Klass: 8 S Veckor: 43-51, ht-2015 Akustik och optik (ljud och ljus) och astronomi Utdrag ur kursplanen i fysik: - Använda kunskaper i fysik för att granska information, kommunicera
Fysik Arbetslag: Gamma Klass: 8 S Veckor: 43-51, ht-2015 Akustik och optik (ljud och ljus) och astronomi Utdrag ur kursplanen i fysik: - Använda kunskaper i fysik för att granska information, kommunicera
Mönster och Algebra. NTA:s första matematiktema. Per Berggren & Maria Lindroth
 Mönster och Algebra NTA:s första matematiktema Per Berggren & Maria Lindroth 1 Lgr11- Matematiska förmågor Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att
Mönster och Algebra NTA:s första matematiktema Per Berggren & Maria Lindroth 1 Lgr11- Matematiska förmågor Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att
Pedagogiskt café. Problemlösning
 Pedagogiskt café Problemlösning Vad är ett matematiskt problem? Skillnad mellan uppgift och problem - Uppgift är något som eleven träffat på tidigare, kan lösa med vanliga standardmetoder - Matematiskt
Pedagogiskt café Problemlösning Vad är ett matematiskt problem? Skillnad mellan uppgift och problem - Uppgift är något som eleven träffat på tidigare, kan lösa med vanliga standardmetoder - Matematiskt
Vardagssituationer och algebraiska formler
 Modul: Algebra Del 7: Kommunikation i algebraklassrummet Vardagssituationer och algebraiska formler Cecilia Kilhamn, Göteborgs Universitet och Jörgen Fors, Linnéuniversitetet En viktig del av algebran
Modul: Algebra Del 7: Kommunikation i algebraklassrummet Vardagssituationer och algebraiska formler Cecilia Kilhamn, Göteborgs Universitet och Jörgen Fors, Linnéuniversitetet En viktig del av algebran
Ett forskningsprojekt om matematikens roll i gymnasiefysiken
 Ett forskningsprojekt om matematikens roll i gymnasiefysiken Lena Hansson, Örjan Hansson, Kristina Juter och Andreas Redfors Sammanfattning Matematik är ett viktigt verktyg för fysiken och matematiken
Ett forskningsprojekt om matematikens roll i gymnasiefysiken Lena Hansson, Örjan Hansson, Kristina Juter och Andreas Redfors Sammanfattning Matematik är ett viktigt verktyg för fysiken och matematiken
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 33 - Ljus 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Vågrörelselära och optik Kapitel 33 - Ljus 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Peer-reviewed articles
 Publication list Dr. Margareta Enghag Peer-reviewed articles 1. Andersson, J. & Enghag, M. (in review) The Relation Between Students Communicative Moves During Laboratory Work in Physics and Outcomes of
Publication list Dr. Margareta Enghag Peer-reviewed articles 1. Andersson, J. & Enghag, M. (in review) The Relation Between Students Communicative Moves During Laboratory Work in Physics and Outcomes of
λ = T 2 g/(2π) 250/6 40 m
 Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
KURSPLAN. Att studera pedagogiska miljöer med hjälp av sociokulturell teoribildning. Socio-cultural theory and the study of educational practices
 UMEÅ UNIVERSITET Pedagogiska institutionen 901 87 Umeå KURSPLAN Att studera pedagogiska miljöer med hjälp av sociokulturell teoribildning Socio-cultural theory and the study of educational practices Forskarutbildningen:
UMEÅ UNIVERSITET Pedagogiska institutionen 901 87 Umeå KURSPLAN Att studera pedagogiska miljöer med hjälp av sociokulturell teoribildning Socio-cultural theory and the study of educational practices Forskarutbildningen:
Deltagarbaserad forskning, 7.5 högskolepoäng
 Deltagarbaserad forskning, 7.5 högskolepoäng Participatory Research Doktorandkurs/praktikerkurs vid Mälardalens högskola, Eskilstuna Hur forska i samverkan och samproduktion mellan högskola och samhälle?
Deltagarbaserad forskning, 7.5 högskolepoäng Participatory Research Doktorandkurs/praktikerkurs vid Mälardalens högskola, Eskilstuna Hur forska i samverkan och samproduktion mellan högskola och samhälle?
Optik 2018 Laborationsinstruktioner Våglära och optik FAFF30+40
 Optik 2018 Laborationsinstruktioner Våglära och optik FAFF30+40 Åsa Bengtsson: asa.bengtsson@fysik.lth.se Emma Persson: tfy15epe@student.lu.se Lärandemål I den här laborationen får Du experimentera med
Optik 2018 Laborationsinstruktioner Våglära och optik FAFF30+40 Åsa Bengtsson: asa.bengtsson@fysik.lth.se Emma Persson: tfy15epe@student.lu.se Lärandemål I den här laborationen får Du experimentera med
Planering Matematik åk 8 Samband, vecka
 Planering Matematik åk 8 Samband, vecka 4 2016 Syfte Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med
Planering Matematik åk 8 Samband, vecka 4 2016 Syfte Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med
Extramaterial till Matematik Y
 LIBR PROGRAMMRING OCH DIGITAL KOMPTNS xtramaterial till Matematik Y NIVÅ TT Geometri LÄRAR Desmos Geometry är ett matematikverktyg som bland annat kan hjälpa dig att avbilda geometriska figurer och göra
LIBR PROGRAMMRING OCH DIGITAL KOMPTNS xtramaterial till Matematik Y NIVÅ TT Geometri LÄRAR Desmos Geometry är ett matematikverktyg som bland annat kan hjälpa dig att avbilda geometriska figurer och göra
Sy$e. Möjliga innebörder i förmågan a5 föra och följa algebraiska resonemang undersöka förmågan att kunna föra algebraiska resonemang
 Möjliga innebörder i förmågan a5 föra och följa algebraiska resonemang Carolina Blomström, Jenny Fred och Sanna We5ergren STLS, FoU-enheten, Stockholms stad Sy$e undersöka förmågan att kunna föra algebraiska
Möjliga innebörder i förmågan a5 föra och följa algebraiska resonemang Carolina Blomström, Jenny Fred och Sanna We5ergren STLS, FoU-enheten, Stockholms stad Sy$e undersöka förmågan att kunna föra algebraiska
SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE.
 SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE. Vad gjorde vi förra gången? Har du några frågor från föregående lektion? 3. titta i ditt läromedel (boken) Vad ska vi göra idag? Optik och
SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE. Vad gjorde vi förra gången? Har du några frågor från föregående lektion? 3. titta i ditt läromedel (boken) Vad ska vi göra idag? Optik och
Avdelningen för fackspråk och kommunikation på Chalmers
 Språk och kommunikation på Matematik 1 (MMG200) ht-17 Hans Malmström Avdelningen för fackspråk och kommunikation Chalmers tekniska högskola mahans@chalmers.se Avdelningen för fackspråk och kommunikation
Språk och kommunikation på Matematik 1 (MMG200) ht-17 Hans Malmström Avdelningen för fackspråk och kommunikation Chalmers tekniska högskola mahans@chalmers.se Avdelningen för fackspråk och kommunikation
I detta arbetsområde ska eleven utveckla sin förmåga att:
 PP för arbetsområde: Ljud & Ljus Ur kursplanen för ämnet fysik I detta arbetsområde ska eleven utveckla sin förmåga att: diskutera, granska och ta ställning i frågor som handlar om ljud och buller planera
PP för arbetsområde: Ljud & Ljus Ur kursplanen för ämnet fysik I detta arbetsområde ska eleven utveckla sin förmåga att: diskutera, granska och ta ställning i frågor som handlar om ljud och buller planera
Matematiska undersökningar med kalkylprogram
 Matematik Grundskola årskurs 7-9 Modul: Matematikundervisning med digitala verktyg Del 7: Matematiska undersökningar med kalkylprogram Matematiska undersökningar med kalkylprogram Håkan Sollervall, Malmö
Matematik Grundskola årskurs 7-9 Modul: Matematikundervisning med digitala verktyg Del 7: Matematiska undersökningar med kalkylprogram Matematiska undersökningar med kalkylprogram Håkan Sollervall, Malmö
Spridningen är vanligtvis stor i en klass när det gäller vad elever tycker om,
 Kerstin Johnsson & Jonas Bergman Ärlebäck Godissugen! En tankeavslöjade aktivitet för att introducera området funktioner I den här artikeln diskuteras en aktivitet som introducerar funktioner i åk 8 genom
Kerstin Johnsson & Jonas Bergman Ärlebäck Godissugen! En tankeavslöjade aktivitet för att introducera området funktioner I den här artikeln diskuteras en aktivitet som introducerar funktioner i åk 8 genom
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Lokal pedagogisk planering i matematik för årskurs 9
 Lokal pedagogisk planering i matematik för årskurs 9 Arbetsområde 3. Ekvationer och geometri. Syfte formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder. reflektera
Lokal pedagogisk planering i matematik för årskurs 9 Arbetsområde 3. Ekvationer och geometri. Syfte formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder. reflektera
Matematik - Åk 9 Funktioner och algebra Centralt innehåll
 Matematik - Åk 9 Funktioner och algebra Centralt innehåll Innebörden av variabelbegreppet och dess användning i algebraiska uttryck, formler och ekvationer. Algebraiska uttryck, formler och ekvationer
Matematik - Åk 9 Funktioner och algebra Centralt innehåll Innebörden av variabelbegreppet och dess användning i algebraiska uttryck, formler och ekvationer. Algebraiska uttryck, formler och ekvationer
Stockholms Tekniska Gymnasium Prov Fysik 2 Mekanik
 Prov Fysik 2 Mekanik För samtliga uppgifter krävs om inte annat står antingen en tydlig och klar motivering eller fullständig lösning och att det går att följa lösningsgången. Fråga 1: Keplers tredje lag
Prov Fysik 2 Mekanik För samtliga uppgifter krävs om inte annat står antingen en tydlig och klar motivering eller fullständig lösning och att det går att följa lösningsgången. Fråga 1: Keplers tredje lag
Ljud njutning eller plåga
 Ljud njutning eller plåga Ljudets väg till örat Lärarhandledningen, uppgift 4, sida 473 (elevblad på sida 488), elevboken sida 156. Genomföra systematiska undersökningar i fysik. Sambandet mellan fysikaliska
Ljud njutning eller plåga Ljudets väg till örat Lärarhandledningen, uppgift 4, sida 473 (elevblad på sida 488), elevboken sida 156. Genomföra systematiska undersökningar i fysik. Sambandet mellan fysikaliska
Planering NO 8B, Vecka Ögat/Örat/Ljus/Ljud
 Planering NO 8B, Vecka 6 2016 Ögat/Örat/Ljus/Ljud Centralt innehåll Fysik Aktuella samhällsfrågor som rör fysik. Systematiska undersökningar. Formulering av enkla frågeställningar, planering, utförande
Planering NO 8B, Vecka 6 2016 Ögat/Örat/Ljus/Ljud Centralt innehåll Fysik Aktuella samhällsfrågor som rör fysik. Systematiska undersökningar. Formulering av enkla frågeställningar, planering, utförande
Np MaB vt 2002 NATIONELLT KURSPROV I MATEMATIK KURS B VÅREN 2002
 Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap. 3 sekretesslagen. För detta material gäller sekretessen fram till utgången av juni 00. Anvisningar Provtid
Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap. 3 sekretesslagen. För detta material gäller sekretessen fram till utgången av juni 00. Anvisningar Provtid
Lokal pedagogisk plan
 Syfte med arbetsområdet: Undervisningen ska ge eleverna möjligheter att använda och utveckla kunskaper och redskap för att formulera egna och granska andras argument i sammanhang där kunskaper i fysik
Syfte med arbetsområdet: Undervisningen ska ge eleverna möjligheter att använda och utveckla kunskaper och redskap för att formulera egna och granska andras argument i sammanhang där kunskaper i fysik
FYSIK ÅK 9 AKUSTIK OCH OPTIK. Fysik - Måldokument Lena Folkebrant
 Fysik - Måldokument Lena Folkebrant FYSIK ÅK 9 AKUSTIK OCH OPTIK Ljud är egentligen tryckförändringar i något material. För att ett ljud ska uppstå måste något svänga eller vibrera. När en gitarrsträng
Fysik - Måldokument Lena Folkebrant FYSIK ÅK 9 AKUSTIK OCH OPTIK Ljud är egentligen tryckförändringar i något material. För att ett ljud ska uppstå måste något svänga eller vibrera. När en gitarrsträng
3: Muntlig redovisning Vid tveksamhet om betygsnivå, kommer du att få ett kompletterande muntligt förhör.
 Prövning i Fysik 2 Prövningen i Fy 2 omfattar 1: Skriftligt prov Ett skriftligt prov görs på hela kursen. 2: Laborationer I kursen ingår att laborera och att skriva rapporter. Laborationerna görs en torsdag
Prövning i Fysik 2 Prövningen i Fy 2 omfattar 1: Skriftligt prov Ett skriftligt prov görs på hela kursen. 2: Laborationer I kursen ingår att laborera och att skriva rapporter. Laborationerna görs en torsdag
Planering Matematik åk 8 Algebra, vecka Centralt innehåll
 Planering Matematik åk 8 Algebra, vecka 49 2015 Centralt innehåll Innebörden av variabelbegreppet och dess användning i algebraiska uttryck, formler och ekvationer. Algebraiska uttryck, formler och ekvationer
Planering Matematik åk 8 Algebra, vecka 49 2015 Centralt innehåll Innebörden av variabelbegreppet och dess användning i algebraiska uttryck, formler och ekvationer. Algebraiska uttryck, formler och ekvationer
Samverkan i högre utbildning
 Samverkan i högre utbildning Karin Danielsson Öberg Studenters samverkan med omgivande samhälle är ett förekommande inslag i högre utbildning. Att sammanföra teori och praktik, så att teori tillämpas i
Samverkan i högre utbildning Karin Danielsson Öberg Studenters samverkan med omgivande samhälle är ett förekommande inslag i högre utbildning. Att sammanföra teori och praktik, så att teori tillämpas i
Pedagogik AV, Nätbaserat lärande, 7,5 hp
 1 (5) Kursplan för: Pedagogik AV, Nätbaserat lärande, 7,5 hp Education MA, On-line learning Allmänna data om kursen Kurskod Ämne/huvudområde Nivå Inriktning (namn) Högskolepoäng PE021A Pedagogik Avancerad
1 (5) Kursplan för: Pedagogik AV, Nätbaserat lärande, 7,5 hp Education MA, On-line learning Allmänna data om kursen Kurskod Ämne/huvudområde Nivå Inriktning (namn) Högskolepoäng PE021A Pedagogik Avancerad
Mål med temat vad är ljud?
 Vad är ljud? När vi hör är det luftens molekyler som har satts i rörelse. När en mygga surrar och låter är det för att den med sina vingar puttar på luften. När en högtalare låter är det för att den knuffar
Vad är ljud? När vi hör är det luftens molekyler som har satts i rörelse. När en mygga surrar och låter är det för att den med sina vingar puttar på luften. När en högtalare låter är det för att den knuffar
Studiehandledning. 7,5 högskolepoäng KURSKOD: DIA47F. Vårterminen 2014
 Institutionen för didaktik och pedagogik Studiehandledning Montessoripedagogikens didaktiska teori 1 7,5 högskolepoäng KURSKOD: DIA47F Vårterminen 2014 Besöksadress: Postadress: Fakturaadress: Frescativägen
Institutionen för didaktik och pedagogik Studiehandledning Montessoripedagogikens didaktiska teori 1 7,5 högskolepoäng KURSKOD: DIA47F Vårterminen 2014 Besöksadress: Postadress: Fakturaadress: Frescativägen
Lokal pedagogisk planering i matematik för åk 8
 Lokal pedagogisk planering i matematik för åk 8 Arbetsområde Geometri kap. 3 PRIO Syfte http://www.skolverket.se/laroplaner-amnen-ochkurser/grundskoleutbildning/sameskola/matematik#anchor2 formulera och
Lokal pedagogisk planering i matematik för åk 8 Arbetsområde Geometri kap. 3 PRIO Syfte http://www.skolverket.se/laroplaner-amnen-ochkurser/grundskoleutbildning/sameskola/matematik#anchor2 formulera och
Interaktiv undervisning
 Interaktiv undervisning Effektivare inlärningsmiljö genom små förändringar Magnus Gustafsson Institutionen för kemi 16 december, 2008 Magnus Gustafsson (Kemi, GU) Interaktiv undervisning 1 / 17 Magnus
Interaktiv undervisning Effektivare inlärningsmiljö genom små förändringar Magnus Gustafsson Institutionen för kemi 16 december, 2008 Magnus Gustafsson (Kemi, GU) Interaktiv undervisning 1 / 17 Magnus
Studiestrategier för dig som är visuell
 Studiestrategier för dig som är visuell Om du har en visuell (V) lärstil är synen din starkaste kanal för att ta in ny kunskap. Prova att använda en del eller alla av följande metoder: Stryk under och
Studiestrategier för dig som är visuell Om du har en visuell (V) lärstil är synen din starkaste kanal för att ta in ny kunskap. Prova att använda en del eller alla av följande metoder: Stryk under och
Naturvetenskaplig litteracitet inte bara en fråga om språk
 Naturvetenskaplig litteracitet inte bara en fråga om språk Maria Andrée Institutionen för matematikämnets och naturvetenskapsämnenas didaktik www.mnd.su.se/maria Scientific literacy has become an internationally
Naturvetenskaplig litteracitet inte bara en fråga om språk Maria Andrée Institutionen för matematikämnets och naturvetenskapsämnenas didaktik www.mnd.su.se/maria Scientific literacy has become an internationally
Hur gör man för att urskilja god undervisning? PLATO som redskap för klassrumsobservationer
 Hur gör man för att urskilja god undervisning? PLATO som redskap för klassrumsobservationer Michael Tengberg Karlstads universitet Syftet med passet att bidra med ett teoretiskt grundat verktyg för observation,
Hur gör man för att urskilja god undervisning? PLATO som redskap för klassrumsobservationer Michael Tengberg Karlstads universitet Syftet med passet att bidra med ett teoretiskt grundat verktyg för observation,
Problem med stenplattor
 Rolf Hedrén, Eva Taflin & Kerstin Hagland Problem med stenplattor Författarna har under flera år bedrivit ett forskningsprojekt med syfte att ta reda på hur lärare och elever tänker om lektioner kring
Rolf Hedrén, Eva Taflin & Kerstin Hagland Problem med stenplattor Författarna har under flera år bedrivit ett forskningsprojekt med syfte att ta reda på hur lärare och elever tänker om lektioner kring
LLEN10, Engelska för lärare i åk 4-6, 30,0 högskolepoäng English for teachers in years 4-6, 30.0 higher education credits
 UTBILDNINGSVETENSKAPLIGA FAKULTETSNÄMNDEN LLEN10, Engelska för lärare i åk 4-6, 30,0 högskolepoäng English for teachers in years 4-6, 30.0 higher education credits Grundnivå/First Cycle 1. Fastställande
UTBILDNINGSVETENSKAPLIGA FAKULTETSNÄMNDEN LLEN10, Engelska för lärare i åk 4-6, 30,0 högskolepoäng English for teachers in years 4-6, 30.0 higher education credits Grundnivå/First Cycle 1. Fastställande
Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från vänster, sträcka i ljusets riktning = positiv
 Avbildningskvalitet Föreläsning 1 2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Avbildningskvalitet Föreläsning 1 2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Ljuslaboration 2 ljusbrytning och reflektion
 Ljuslaboration 2 ljusbrytning och reflektion Namn: Klass: Syfte: Du ska förstå varför ljus bryts och vad totalreflektion är samt några tillämpningsområden för totalreflektion. 1. Du har kanske stuckit
Ljuslaboration 2 ljusbrytning och reflektion Namn: Klass: Syfte: Du ska förstå varför ljus bryts och vad totalreflektion är samt några tillämpningsområden för totalreflektion. 1. Du har kanske stuckit
Fallstudier. ü Ett teoretiskt ramverk kan vägleda i datainsamligen och analysen
 Fallstudier Fallstudier Studieobjekt: Samtida fenomen/företeelser i deras verkliga miljö Djupgående undersökning Exempel på forskningsfrågor: Hur? Varför? Forskaren styr eller kontrollerar inte studieobjektet
Fallstudier Fallstudier Studieobjekt: Samtida fenomen/företeelser i deras verkliga miljö Djupgående undersökning Exempel på forskningsfrågor: Hur? Varför? Forskaren styr eller kontrollerar inte studieobjektet
BFL102/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik mars :00 12:00. Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
 Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL12/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik 2 22 mars 216 8: 12: Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL12/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik 2 22 mars 216 8: 12: Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
Lokal pedagogisk planering i matematik för årskurs 9
 Lokal pedagogisk planering i matematik för årskurs 9 Arbetsområde 4. Samband och förändring Syfte formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder. reflektera
Lokal pedagogisk planering i matematik för årskurs 9 Arbetsområde 4. Samband och förändring Syfte formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder. reflektera
OPTIK läran om ljuset
 OPTIK läran om ljuset Vad är ljus Ljuset är en form av energi Ljus är elektromagnetisk strålning som färdas med en hastighet av 300 000 km/s. Ljuset kan ta sig igenom vakuum som är ett utrymme som inte
OPTIK läran om ljuset Vad är ljus Ljuset är en form av energi Ljus är elektromagnetisk strålning som färdas med en hastighet av 300 000 km/s. Ljuset kan ta sig igenom vakuum som är ett utrymme som inte
De förmågor som bedömts inom arbetsområdet är markerade i matrisen. Övriga förmågor är sådana som inte har behandlats den här terminen.
 Akustik och Optik Grundskola 7 9 LGR11 Fy De förmågor som bedömts inom arbetsområdet är markerade i matrisen. Övriga förmågor är sådana som inte har behandlats den här terminen. Förmåga att använda kunskaper
Akustik och Optik Grundskola 7 9 LGR11 Fy De förmågor som bedömts inom arbetsområdet är markerade i matrisen. Övriga förmågor är sådana som inte har behandlats den här terminen. Förmåga att använda kunskaper
Laboration i Geometrisk Optik
 Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
Trösklar i matematiklärandet
 Matematik, Specialpedagogik Grundskola åk 7 9 Modul: Inkludering och delaktighet lärande i matematik Del 7: Trösklar i matematiklärandet Trösklar i matematiklärandet Ingemar Holgersson, Högskolan Kristianstad
Matematik, Specialpedagogik Grundskola åk 7 9 Modul: Inkludering och delaktighet lärande i matematik Del 7: Trösklar i matematiklärandet Trösklar i matematiklärandet Ingemar Holgersson, Högskolan Kristianstad
Under hösten 2008 deltog jag i en kurs som hette Matematikundervisning
 Astrid Karlsson Mönsterproblem i dubbel bemärkelse Med utgångspunkt i det rika problemet Stenplattor synliggörs skillnader i elevers lösningar och hur problem som behandlar mönster kan leda in eleverna
Astrid Karlsson Mönsterproblem i dubbel bemärkelse Med utgångspunkt i det rika problemet Stenplattor synliggörs skillnader i elevers lösningar och hur problem som behandlar mönster kan leda in eleverna
Metod och material. Etnografisk ansats. Fältarbete: 3 klasser, 2 skolor, 42 lektioner
 Metod och material Etnografisk ansats Fältarbete: 3 klasser, 2 skolor, 42 lektioner Videoinspelningar med två kameror (62 h x 2), deltagande observationer, fältanteckningar, semistrukturerade intervjuer
Metod och material Etnografisk ansats Fältarbete: 3 klasser, 2 skolor, 42 lektioner Videoinspelningar med två kameror (62 h x 2), deltagande observationer, fältanteckningar, semistrukturerade intervjuer
Undervisa i matematik genom problemlösning
 Modul: Problemlösning Del 1: Matematikundervisning genom problemlösning Undervisa i matematik genom problemlösning Maria Larsson, Mälardalens högskola Att hjälpa barn att bli bättre problemlösare är inte
Modul: Problemlösning Del 1: Matematikundervisning genom problemlösning Undervisa i matematik genom problemlösning Maria Larsson, Mälardalens högskola Att hjälpa barn att bli bättre problemlösare är inte
Avdelningen för fackspråk och kommunika7on på Chalmers
 Matematik 1 (MMG200) Kommunikationsinslaget ht-18 Hans Malmström Vetenskapens kommunikation och lärande Chalmers tekniska högskola mahans@chalmers.se Avdelningen för fackspråk och kommunika7on på Chalmers
Matematik 1 (MMG200) Kommunikationsinslaget ht-18 Hans Malmström Vetenskapens kommunikation och lärande Chalmers tekniska högskola mahans@chalmers.se Avdelningen för fackspråk och kommunika7on på Chalmers
Beräkning med ord. -hur en dator hanterar perception. Linköpings universitet Artificiell intelligens 2 2010-10-03 Erik Claesson 880816-1692
 Beräkning med ord -hur en dator hanterar perception 2010-10-03 Erik Claesson 880816-1692 Innehåll Inledning... 3 Syfte... 3 Kan datorer hantera perception?... 4 Naturligt språk... 4 Fuzzy Granulation...
Beräkning med ord -hur en dator hanterar perception 2010-10-03 Erik Claesson 880816-1692 Innehåll Inledning... 3 Syfte... 3 Kan datorer hantera perception?... 4 Naturligt språk... 4 Fuzzy Granulation...
År 2006 hittade jag av en slump boken Rika matematiska problem inspiration
 Ulrihca Malmberg Att göra rika problem rika Att använda rika problem och utnyttja deras potential är inte helt lätt. Här behandlas några svårigheter och problem som visat sig och som varit utgångspunkt
Ulrihca Malmberg Att göra rika problem rika Att använda rika problem och utnyttja deras potential är inte helt lätt. Här behandlas några svårigheter och problem som visat sig och som varit utgångspunkt
Vågrörelselära & Kvantfysik, FK2002 29 november 2011
 Räkneövning 5 Vågrörelselära & Kvantfysik, FK00 9 november 0 Problem 35.9 En dykare som befinner sig på djupet D 3 m under vatten riktar en ljusstråle (med infallsvinkel θ i 30 ) mot vattenytan. På vilket
Räkneövning 5 Vågrörelselära & Kvantfysik, FK00 9 november 0 Problem 35.9 En dykare som befinner sig på djupet D 3 m under vatten riktar en ljusstråle (med infallsvinkel θ i 30 ) mot vattenytan. På vilket
Lgr 11 matriser i Favorit matematik 4 6
 Lgr 11 matriser i Favorit matematik 4 6 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla förmågan att De matematiska förmågor
Lgr 11 matriser i Favorit matematik 4 6 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla förmågan att De matematiska förmågor
I arbetet hanterar eleven flera procedurer och löser uppgifter av standardkaraktär med säkerhet, både utan och med digitala verktyg.
 Kunskapskrav Ma 2a Namn: Gy Betyg E D Betyg C B Betyg A 1. Begrepp Eleven kan översiktligt beskriva innebörden av centrala begrepp med hjälp av några representationer samt översiktligt beskriva sambanden
Kunskapskrav Ma 2a Namn: Gy Betyg E D Betyg C B Betyg A 1. Begrepp Eleven kan översiktligt beskriva innebörden av centrala begrepp med hjälp av några representationer samt översiktligt beskriva sambanden
Ökat personligt engagemang En studie om coachande förhållningssätt
 Lärarutbildningen Fakulteten för lärande och samhälle Individ och samhälle Uppsats 7,5 högskolepoäng Ökat personligt engagemang En studie om coachande förhållningssätt Increased personal involvement A
Lärarutbildningen Fakulteten för lärande och samhälle Individ och samhälle Uppsats 7,5 högskolepoäng Ökat personligt engagemang En studie om coachande förhållningssätt Increased personal involvement A
Att utforska matematiken tillsammans strategier för inkluderande klassrumssamtal
 Att utforska matematiken tillsammans strategier för inkluderande klassrumssamtal - implementering av Talk Moves i en svensk kontext Lisa Dimming, Marita Lundström, Margareta Engvall & Karin Forslund Frykedal
Att utforska matematiken tillsammans strategier för inkluderande klassrumssamtal - implementering av Talk Moves i en svensk kontext Lisa Dimming, Marita Lundström, Margareta Engvall & Karin Forslund Frykedal
IBSE Ett självreflekterande(självkritiskt) verktyg för lärare. Riktlinjer för lärare
 Fibonacci / översättning från engelska IBSE Ett självreflekterande(självkritiskt) verktyg för lärare Riktlinjer för lärare Vad är det? Detta verktyg för självutvärdering sätter upp kriterier som gör det
Fibonacci / översättning från engelska IBSE Ett självreflekterande(självkritiskt) verktyg för lärare Riktlinjer för lärare Vad är det? Detta verktyg för självutvärdering sätter upp kriterier som gör det
Vad betyder detta för hur eleverna möter universitetets skriftliga ämnes(fag)kulturer?
 Vad betyder detta för hur eleverna möter universitetets skriftliga ämnes(fag)kulturer? Mona Blåsjö Stockholms universitet Universitets/forskningsperspektiv Studenternas skrivmiljöer på universitetet Skrivforskning
Vad betyder detta för hur eleverna möter universitetets skriftliga ämnes(fag)kulturer? Mona Blåsjö Stockholms universitet Universitets/forskningsperspektiv Studenternas skrivmiljöer på universitetet Skrivforskning
Kravgränser. Provet består av Del B, Del C, Del D samt en muntlig del och ger totalt 63 poäng varav 24 E-, 21 C- och 18 A-poäng.
 Kravgränser Provet består av Del B, Del C, Del D samt en muntlig del och ger totalt 63 poäng varav 24 E-, 21 C- och 18 A-poäng. Kravgräns för provbetyget E: 17 poäng D: 25 poäng varav 7 poäng på minst
Kravgränser Provet består av Del B, Del C, Del D samt en muntlig del och ger totalt 63 poäng varav 24 E-, 21 C- och 18 A-poäng. Kravgräns för provbetyget E: 17 poäng D: 25 poäng varav 7 poäng på minst
Denna våg är. A. Longitudinell. B. Transversell. C. Något annat
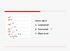 Denna våg är A. Longitudinell B. Transversell ⱱ v C. Något annat l Detta är situationen alldeles efter en puls på en fjäder passerat en skarv A. Den ursprungliga pulsen kom från höger och mötte en lättare
Denna våg är A. Longitudinell B. Transversell ⱱ v C. Något annat l Detta är situationen alldeles efter en puls på en fjäder passerat en skarv A. Den ursprungliga pulsen kom från höger och mötte en lättare
PDP som redskap för karriärutveckling i utbildning. Ola Tostrup
 PDP som redskap för karriärutveckling i utbildning Ola Tostrup - 16, 4, 47, 3 Dagens föreställning Vad innebär PDP och varför PDP Hur vi designat det inom utbildningen Kompetensbegreppet och vilka kompetenser
PDP som redskap för karriärutveckling i utbildning Ola Tostrup - 16, 4, 47, 3 Dagens föreställning Vad innebär PDP och varför PDP Hur vi designat det inom utbildningen Kompetensbegreppet och vilka kompetenser
RÖRELSE. - Mätningar och mätinstrument och hur de kan kombineras för att mäta storheter, till exempel fart, tryck och effekt.
 RÖRELSE Inledning När vi går, springer, cyklar etc. förflyttar vi oss en viss sträcka på en viss tid. Ibland, speciellt när vi har bråttom, tänker vi på hur fort det går. I det här experimentet undersöker
RÖRELSE Inledning När vi går, springer, cyklar etc. förflyttar vi oss en viss sträcka på en viss tid. Ibland, speciellt när vi har bråttom, tänker vi på hur fort det går. I det här experimentet undersöker
Att använda den didaktiska modellen organiserande syften för att planera och analysera naturvetenskaplig undervisning
 Att använda den didaktiska modellen organiserande syften för att planera och analysera naturvetenskaplig undervisning Malin Lavett Lagerström Licentiand NV-didaktik på Stockholms universitet NV/teknik-lärare
Att använda den didaktiska modellen organiserande syften för att planera och analysera naturvetenskaplig undervisning Malin Lavett Lagerström Licentiand NV-didaktik på Stockholms universitet NV/teknik-lärare
Peter Sohlberg Vetenskapsteori i forskningspraktiken
 Peter Sohlberg Vetenskapsteori i forskningspraktiken Allmänt om kursen Kursen syftar till: 1) att ge en bred översikt över det vetenskapsteoretiska fältet samt att ge kunskap om centrala vetenskapsteoretiska
Peter Sohlberg Vetenskapsteori i forskningspraktiken Allmänt om kursen Kursen syftar till: 1) att ge en bred översikt över det vetenskapsteoretiska fältet samt att ge kunskap om centrala vetenskapsteoretiska
Avdelningen för fackspråk och kommunikation på Chalmers. Språk och kommunikation på Matematik 1 (MMG200) ht- 16
 Språk och kommunikation på Matematik 1 (MMG200) ht- 16 Claes Ohlsson Avdelningen för fackspråk och kommunikation Chalmers tekniska högskola claeso@chalmers.se Avdelningen för fackspråk och kommunikation
Språk och kommunikation på Matematik 1 (MMG200) ht- 16 Claes Ohlsson Avdelningen för fackspråk och kommunikation Chalmers tekniska högskola claeso@chalmers.se Avdelningen för fackspråk och kommunikation
Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från vänster, sträcka i ljusets riktning = positiv
 Avbildningskvalitet Föreläsning 1-2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Avbildningskvalitet Föreläsning 1-2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Per Berggren och Maria Lindroth 2014-11-19
 Varierad matematikundervisning Per Berggren och Maria Lindroth 2014-11-19 Luffarschack Med en utmaning! Sfinxen En rik laborativ matematikuppgift som tar sin början i de första skolåren och fortsätter
Varierad matematikundervisning Per Berggren och Maria Lindroth 2014-11-19 Luffarschack Med en utmaning! Sfinxen En rik laborativ matematikuppgift som tar sin början i de första skolåren och fortsätter
Extramaterial till Matematik Y
 LIBR PROGRAMMRING OH DIGITAL KOMPTNS xtramaterial till Matematik Y NIVÅ TVÅ Geometri LÄRAR Desmos Geometry är ett matematikverktyg som bland annat kan hjälpa dig att avbilda geometriska figurer och göra
LIBR PROGRAMMRING OH DIGITAL KOMPTNS xtramaterial till Matematik Y NIVÅ TVÅ Geometri LÄRAR Desmos Geometry är ett matematikverktyg som bland annat kan hjälpa dig att avbilda geometriska figurer och göra
Fysik (TFYA14) Fö 5 1. Fö 5
 Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Att använda gester som en medierande resurs i mångspråkiga nv-klasser. Zeynep Ünsal
 Att använda gester som en medierande resurs i mångspråkiga nv-klasser Zeynep Ünsal zeynep.unsal@mnd.su.se Vilka är tvåspråkiga? Tvåspråkiga elever: De elever som använder två (eller fler) språk i sitt
Att använda gester som en medierande resurs i mångspråkiga nv-klasser Zeynep Ünsal zeynep.unsal@mnd.su.se Vilka är tvåspråkiga? Tvåspråkiga elever: De elever som använder två (eller fler) språk i sitt
TFYA58, Fysik, 8 hp, 3 delar
 1. Vågrörelselära (mekaniska vågor, optik, diffraktion ) 7x2 tim föreläsning 6x2tim lektion 2. Experimentell problemlösning TFYA58, Fysik, 8 hp, 3 delar Ht 1 Ht 2 2x1 tim föreläsning 2 st Richardslabbar
1. Vågrörelselära (mekaniska vågor, optik, diffraktion ) 7x2 tim föreläsning 6x2tim lektion 2. Experimentell problemlösning TFYA58, Fysik, 8 hp, 3 delar Ht 1 Ht 2 2x1 tim föreläsning 2 st Richardslabbar
