Handledning Det didaktiska kontraktet. 19 september 2012
|
|
|
- Erik Sundström
- för 8 år sedan
- Visningar:
Transkript
1 Handledning Det didaktiska kontraktet 19 september 2012
2 Dagens teman Begreppsföreställning och begreppskunskap igen Handledning Det didaktiska kontraktet
3 Begreppsföreställning och begreppsdefinition Begreppsföreställning och begreppsdefinition är inte färdig och mogen matematisk kunskap, utan provisorisk. Begreppsföreställningen skapas genom generalisering från exempel och användning av begreppet i olika sammanhang och behöver inte vara sammanhängande eller konsistent. Olika delar av begreppsföreställningen aktiveras i olika situationer. Delar som inte aktiveras tenderar att försvagas. Begreppsdefinitionen skapas antingen genom att ytinriktat, mekaniskt lärande av en formell eller informell definition eller genom en meningsskapande, personlig rekonstruktion av den formella eller informella definitionen. Begreppsföreställning och begreppskunskap kan ge motstridiga resultat vid en matematisk undersökning.
4 God begreppskunskap God kunskap betyder här användbar och livskraftig kunskap samt att kunskapen inte skapar hinder för fortsatt begreppsutveckling. Begreppsföreställningen innehåller flera olika representationer av begreppet. Begreppsföreställningen är rik på relationer till processer och till andra begrepp. Begreppsdefinitionen kan anpassas till olika representationer och tvärtom. Begreppsdefinitionen är generell. Begreppsdefinitionen kan förstås utifrån den (av andra) accepterade formella eller informella definitionen.
5 Något om Masons perspektiv Matematik lärs endast genom att den lärande aktivt engagerar sig i ämnet vilket innebär att aktivt skapa sin egen mening åt definitioner, satser och bevis tänka matematiskt, dvs generalisera och specialisera förmoda och övertyga föreställa sig och uttrycka organisera och klassificera formulera och lösa problem (Inledningen sid v till Masons bok)
6 Handledning Fyra sätt att interagera med studenten vid handledning (enligt Mason sig vii): Klargöra: Bege dig in i studentens begreppsvärld och arbeta i den. Låt studenten förklara. Utforska: Led studenterna i fruktbara riktningar när de försöker göra reda för detaljer och själva finna sammanhang. Öva: Led studenterna så att de förstärker metoder och teorier genom repetition och övning. Uttrycka: Led studenterna till att uttrycka sina insikter både muntligt och skriftligt. Undvik så kallad lotsning.
7 Interaktionen Studenten har alltid ansvar för sitt eget lärande. Exempel 1: Svara med en motfråga när en student ber dig förklara och visa hur man gör. Visa mig hur långt har du kommit.vad har du gjort? Vad skulle du kunna börja med? Kan du hitta något exempel i boken som du kan använda? Eller svara med någon strategi för problemlösning: Skriv ner vad du vet och vad du vill visa. Rita en figur.
8 Interaktionen Exempel 2: Svara alltid med en motfråga eller en uppmaning på frågan hur man förstår ett visst steg i en färdig lösning (t ex i boken). Förstår du hur de har kommit hit? Förklara för mig! Visa mig din lösning! Visa mig hur du skulle vilja (börja) lösa uppgiften! Träna dig som lärare att lämna över ansvaret till studenten.
9 Interaktionen Exempel 3: Svara alltid med en motfråga på uppmaningen att förklara igen. Vad står det i boken och anteckningarna? Läs högt! Kommer du ihåg vad jag/föreläsaren sa på föreläsningen? Vad tycker du att du förstår? Sätt fingret på just det som du inte förstår!
10 Aktivitet Kräv aktivitet av studenten. Exempel 1: Om du ställer upp och besvarar frågor på en mottagningstid: Begränsa tiden för varje student (ge mer tid om de är flera). Kräv att studenten har arbetat med problemet hemma och kan visa vad hon/han gjort och varför hon/han inte kommer vidare (konkret visa sitt arbete). Exempel 2: Genomför inte beräkningar och förenklingar åt studenten som du vet att hon/han kan klara själv. Här krävs det tålamod och ibland är det lämpligt att lämna studenten och komma tillbaka. Om nödvändigt, så ge endast ett första steg på vägen och återkom senare om det behövs. Exempel 3: Använd listor där studenterna prickar av vilka uppgifter de löst, vilka uppgifter de önskar få kommenterade och vilka de inte försökt lösa.
11 Kroppsspråk och kommunikation vid handledning Stå stadigt och rör dig lugnt - det ger en lugn och trygg atmosfär. Behåll en tydlig distans i rummet för att inte inkräkta på andras integritetsutrymme. Inta gärna en position på samma höjd som den du talar med. Sitt mittemot om det är möjligt. Det skapar en känsla av jämlikhet; om du står och den andra sitter blir den andra automatiskt underordnad. Se till att ha ögonkontakt. När du ställer en fråga så behåll koncentrationen på frågan och den som får frågan genom att rikta blicken. Undvik att fokusera på något annat, t ex dina anteckningar. Tveka inte att invänta ett svar, även om det tar tid. Om du kommunicerar med en liten grupp av studenter, så rikta budskapet omväxlande mot de olika personerna i gruppen. Om någon har ordet, så rikta uppmärksamheten mot henne/honom. Skriv inte i studenternas block. Matematikdidaktik Använd egna den 19papper september 2012 som du
12 Metoder Skapa en atmosfär av förmodanden. Acceptera förslag som du vet inte leder framåt. Peka på svårigheter eller orimliga konsekvenser. Be om en modifierad förmodan i stället för att avfärda en som felaktig. Ge aldrig negativ feedback på ett förslag eller en förmodan (dumt, onödigt, fel, borde du ha lärt dig i gymnasiet, gick vi igenom förra veckan,...). Uppmuntra studenten när hon/han har gjort en förmodan, gett ett förslag eller arbetar matematiskt.
13 Metoder Skapa debatt. Formulera ett problem med ja- och nejsvar (kan man hitta en funktion med den och den egenskapen? ska man använda den eller den fördelningen i ett visst fall?). Ha omröstning om svaret med efterföljande diskussion med argument, exempel och motexempel. Låt eventuellt studenterna diskutera i par först (kan vara tryggare). Diskutera lösningar som studenterna visar på tavlan. Hur tänkte du? Var det någon som löste uppgiften på något annat sätt? Eller låt flera studenter visa olika lösningar på samma uppgift. Diskutera för- och nackdelar med dem.
14 Metoder Arbeta med termer och begrepp. Ge studenterna ett antal nyckelord från satser, definitioner och metoder. Be dem göra fullständiga meningar i vilka orden ingår. Boken ska vara stängd! Låt dem arbeta i grupp och låt grupperna dela med sig till varandra. Ge studenterna ett antal viktiga egenskaper och be dem konstruera exempel på objekt som har egenskaperna. Be studenterna om exempel på ett objekt med vissa specifika egenskaper (eventuellt numeriska värden); ett vanligt och ett underligt.
15 Metoder Arbeta med metoder och algoritmer Låt studenterna skapa uppgifter som man löser med en viss metod. Be dem lösa varandras uppgifter. (Det här är ofta mycket lärorikt!) Be studenterna analysera övningsuppgifter som de löst. Vad illustrerar uppgifterna och vad kan man lära sig av dem? Har en viss uppgiften någon speciell knorr eller är det en standarduppgift på en viss metod? Fråga studenterna varför de tror att vi rekommenderar att de löser en viss uppgift. Be studenterna göra övningen ovan innan de löser uppgifterna. Be studenterna själva avgöra efter varje avsnitt hur pass säkra de känner sig på en viss metod, eventuellt på en skala från 1 till 5.
16 Det didaktiska kontraktet Enligt Brousseau är det didaktiska kontraktet en tyst överenskommelse som träder i kraft i varje didaktisk situation och som innebär att eleven/studenten inte handlar utifrån lärarens intentioner för lärandet, utan utifrån de specifika uppgifter som föreläggs och de specifika krav som ställs av läraren. Det kan vara mycket svårt att bryta det didaktiska kontraktet.
17 Det didaktiska kontraktet Några exempel på (oftast outtalade) överenskommelser som kan ingå i det didaktiska kontraktet mellan föreläsare och studenter: Föreläsaren går igenom allt som kommer att examineras; föreläsaren poängterar det som är särskilt viktigt genom att lägga mer tid eller större tryck på detta. Föreläsaren presenterar teorin så sammanhängande att anteckningarna kan ersätta kurslitteraturen. Ingen aktivitet (få frågor, tänka över något, ställa frågor) kan förväntas av studenterna under föreläsningen.
18 Det didaktiska kontraktet Frågor från studenterna ställs och besvaras utförligt ställs och besvaras kortfattat eller avfärdas ställs aldrig Deltagande alla studenter som deltar är närvarande i stort sett vid alla föreläsningar studenterna kommer och går (deltar i vissa föreläsningar, men uteblir från andra)
19 Att läsa Mason: Mathematics Teaching Practices Förordet v-viii Tutoring, s Mathematical powers, s Alsina, C. (2001). Why the professor must be a stimulating teacher. Towards a new paradigm of teaching mathematics at university level. In Holton, Derek (ed.) The teaching and learning of mathematics at university level: AN ICMI Study. Kluwer 3-12
Figur 1: Påverkan som processer. Vad tycker elever om matematik och matematikundervisning?
 Modul: Problemlösning Del 1: Matematiska problem Känsla för problem Lovisa Sumpter När vi arbetar med matematik är det många faktorer som påverkar det vi gör. Det är inte bara våra kunskaper i ämnet som
Modul: Problemlösning Del 1: Matematiska problem Känsla för problem Lovisa Sumpter När vi arbetar med matematik är det många faktorer som påverkar det vi gör. Det är inte bara våra kunskaper i ämnet som
Tekniska hjälpmedel. 19 september 2012
 Föreläsande Tekniska hjälpmedel 19 september 2012 Det didaktiska kontraktet Enligt Brousseau är det didaktiska kontraktet en tyst överenskommelse som träder i kraft i varje didaktisk situation och som
Föreläsande Tekniska hjälpmedel 19 september 2012 Det didaktiska kontraktet Enligt Brousseau är det didaktiska kontraktet en tyst överenskommelse som träder i kraft i varje didaktisk situation och som
Likhetstecknets innebörd
 Likhetstecknets innebörd Följande av Görel Sterner översatta och bearbetade text bygger på boken: arithmetic & algebra in elementary school. Portsmouth: Heinemann Elever i åk 1 6 fick följande uppgift:
Likhetstecknets innebörd Följande av Görel Sterner översatta och bearbetade text bygger på boken: arithmetic & algebra in elementary school. Portsmouth: Heinemann Elever i åk 1 6 fick följande uppgift:
Problemlösning, öppna frågor och formativ bedömning, hur? Margareta Bynke & Anna Gullberg Malmö Högskola, 2013
 Problemlösning, öppna frågor och formativ bedömning, hur? Margareta Bynke & Anna Gullberg Malmö Högskola, 2013 www.mentimeter.com 1.Skapa en fråga. 2.Låt klassen få rösta. Tag fram mobiltelefonen (det
Problemlösning, öppna frågor och formativ bedömning, hur? Margareta Bynke & Anna Gullberg Malmö Högskola, 2013 www.mentimeter.com 1.Skapa en fråga. 2.Låt klassen få rösta. Tag fram mobiltelefonen (det
Likhetstecknets innebörd
 Modul: Algebra Del 5: Algebra som språk Likhetstecknets innebörd Följande av Görel Sterner (2012) översatta och bearbetade text bygger på boken: Carpenter, T. P., Franke, M. L. & Levi, L. (2003). Thinking
Modul: Algebra Del 5: Algebra som språk Likhetstecknets innebörd Följande av Görel Sterner (2012) översatta och bearbetade text bygger på boken: Carpenter, T. P., Franke, M. L. & Levi, L. (2003). Thinking
Av kursplanen och betygskriterierna,
 KATARINA KJELLSTRÖM Muntlig kommunikation i ett nationellt prov PRIM-gruppen ansvarar för diagnosmaterial och de nationella proven i matematik för grundskolan. Här beskrivs de muntliga delproven i ämnesprovet
KATARINA KJELLSTRÖM Muntlig kommunikation i ett nationellt prov PRIM-gruppen ansvarar för diagnosmaterial och de nationella proven i matematik för grundskolan. Här beskrivs de muntliga delproven i ämnesprovet
En metod för aktiv redovisning av matematikuppgifter
 En metod för aktiv redovisning av matematikuppgifter Magnus Jacobsson och Inger Sigstam Matematiska institutionen 1. Introduktion Matematik på grundnivå är till stor del ett övningsämne, man lär sig matematik
En metod för aktiv redovisning av matematikuppgifter Magnus Jacobsson och Inger Sigstam Matematiska institutionen 1. Introduktion Matematik på grundnivå är till stor del ett övningsämne, man lär sig matematik
KORT FÖR ATT LEDA DISKUSSIONEN
 KORT FÖR ATT LEDA DISKUSSIONEN INNEHÅLL 1 Så här använder du diskussionskorten 2 Vad är dialog? 3 Förbättra din förmåga att lyssna 4 Förberedelser inför att föra en diskussion 5 Exempel ur manuset för
KORT FÖR ATT LEDA DISKUSSIONEN INNEHÅLL 1 Så här använder du diskussionskorten 2 Vad är dialog? 3 Förbättra din förmåga att lyssna 4 Förberedelser inför att föra en diskussion 5 Exempel ur manuset för
Kursplan. Matematik III med didaktisk inriktning. Lärarutbildningsnämnden Matematik
 Dnr: MAGL13/20172 Lärarutbildningsnämnden Matematik Kursplan Matematik III med didaktisk inriktning Kurskod: Kursens benämning: MAGL13 Matematik III med didaktisk inriktning Mathematics and Mathematics
Dnr: MAGL13/20172 Lärarutbildningsnämnden Matematik Kursplan Matematik III med didaktisk inriktning Kurskod: Kursens benämning: MAGL13 Matematik III med didaktisk inriktning Mathematics and Mathematics
Förstår studenter vad jag säger? Svar på minuten. Att använda mobiltelefoner för direkt studentåterkoppling
 Förstår studenter vad jag säger? Svar på minuten. Att använda mobiltelefoner för direkt studentåterkoppling Annika Andersson, Kalle Räisänen, Anders Avdic - Informatik, Handelshögskolan 2012-10-25 1 Agenda
Förstår studenter vad jag säger? Svar på minuten. Att använda mobiltelefoner för direkt studentåterkoppling Annika Andersson, Kalle Räisänen, Anders Avdic - Informatik, Handelshögskolan 2012-10-25 1 Agenda
KORT FÖR ATT LEDA DISKUSSIONEN
 KORT FÖR ATT LEDA DISKUSSIONEN INNEHÅLL 1 Så här använder du diskussionskorten 2 Vad är dialog? 3 Förbättra din förmåga att lyssna 4 Förberedelser inför att föra en diskussion 5 Exempel ur manuset för
KORT FÖR ATT LEDA DISKUSSIONEN INNEHÅLL 1 Så här använder du diskussionskorten 2 Vad är dialog? 3 Förbättra din förmåga att lyssna 4 Förberedelser inför att föra en diskussion 5 Exempel ur manuset för
Verktygsbanken. Grundskola åk 7 9, modul: Problemlösning. Maria Larsson, Mälardalens högskola och Andreas Bergwall, Örebro universitet
 Verktygsbanken Grundskola åk 7 9, modul: Problemlösning Maria Larsson, Mälardalens högskola och Andreas Bergwall, Örebro universitet Grundskola åk 7-9 Del: 1-8 Verktygsbanken Maria Larsson, Mälardalens
Verktygsbanken Grundskola åk 7 9, modul: Problemlösning Maria Larsson, Mälardalens högskola och Andreas Bergwall, Örebro universitet Grundskola åk 7-9 Del: 1-8 Verktygsbanken Maria Larsson, Mälardalens
Lärande i matematik - olika teoretiska perspektiv
 Lärande i matematik - olika teoretiska perspektiv Föreläsning i kursen Matematikdidaktik för högskolan Matematikcentrum, Lunds universitet Gerd Brandell Den didaktiska triangeln Tre parter är engagerade
Lärande i matematik - olika teoretiska perspektiv Föreläsning i kursen Matematikdidaktik för högskolan Matematikcentrum, Lunds universitet Gerd Brandell Den didaktiska triangeln Tre parter är engagerade
Avdelningen för fackspråk och kommunikation på Chalmers
 Språk och kommunikation på Matematik 1 (MMG200) ht-17 Hans Malmström Avdelningen för fackspråk och kommunikation Chalmers tekniska högskola mahans@chalmers.se Avdelningen för fackspråk och kommunikation
Språk och kommunikation på Matematik 1 (MMG200) ht-17 Hans Malmström Avdelningen för fackspråk och kommunikation Chalmers tekniska högskola mahans@chalmers.se Avdelningen för fackspråk och kommunikation
Resonemangsförmåga. Örjan Hansson, Högskolan Kristianstad
 Modul. Undervisa matematik utifrån förmågorna Del 5: Resonemangsförmåga Resonemangsförmåga Örjan Hansson, Högskolan Kristianstad Resonemangsförmåga handlar om att utveckla ett logiskt och systematiskt
Modul. Undervisa matematik utifrån förmågorna Del 5: Resonemangsförmåga Resonemangsförmåga Örjan Hansson, Högskolan Kristianstad Resonemangsförmåga handlar om att utveckla ett logiskt och systematiskt
I arbetet hanterar eleven flera procedurer och löser uppgifter av standardkaraktär med säkerhet, både utan och med digitala verktyg.
 Kunskapskrav Ma 2a Namn: Gy Betyg E D Betyg C B Betyg A 1. Begrepp Eleven kan översiktligt beskriva innebörden av centrala begrepp med hjälp av några representationer samt översiktligt beskriva sambanden
Kunskapskrav Ma 2a Namn: Gy Betyg E D Betyg C B Betyg A 1. Begrepp Eleven kan översiktligt beskriva innebörden av centrala begrepp med hjälp av några representationer samt översiktligt beskriva sambanden
Behövs ett nytt perspektiv på relationen undervisning-lärande? och kan Learning activity bidra med något?
 Behövs ett nytt perspektiv på relationen undervisning-lärande? och kan Learning activity bidra med något? INGER ERIKSSON Institutionen för de humanistiska och samhällsvetenskapliga ämnenas didaktik & Stockholm
Behövs ett nytt perspektiv på relationen undervisning-lärande? och kan Learning activity bidra med något? INGER ERIKSSON Institutionen för de humanistiska och samhällsvetenskapliga ämnenas didaktik & Stockholm
Extramaterial till Matematik X
 LIBR PROGRMMRING OH DIGITL KOMPTNS xtramaterial till Matematik X NIVÅ TT NIVÅ TVÅ NIVÅ TR Geometri LÄRR I den här uppgiften får du och dina elever bekanta er med det digitala verktyget Geoboard. leverna
LIBR PROGRMMRING OH DIGITL KOMPTNS xtramaterial till Matematik X NIVÅ TT NIVÅ TVÅ NIVÅ TR Geometri LÄRR I den här uppgiften får du och dina elever bekanta er med det digitala verktyget Geoboard. leverna
VFU i matematik ht 2015 MÅL
 VFU i matematik ht 2015 MÅL Syftet med kursen är att studenten ska förvärva kunskaper om och utveckla förmågan att leda och undervisa i matematik utifrån ett vetenskapligt förhållningssätt i relation till
VFU i matematik ht 2015 MÅL Syftet med kursen är att studenten ska förvärva kunskaper om och utveckla förmågan att leda och undervisa i matematik utifrån ett vetenskapligt förhållningssätt i relation till
Vårt projekt genomfördes under vårterminen Självreglering
 Carlsson, Dalsjö, Ingelshed & Larsson Bjud in eleverna att påverka sin matematikundervisning Fyra lärare beskriver hur deras elever blev inbjudna till att få insikt i och makt över sina egna lärandeprocesser
Carlsson, Dalsjö, Ingelshed & Larsson Bjud in eleverna att påverka sin matematikundervisning Fyra lärare beskriver hur deras elever blev inbjudna till att få insikt i och makt över sina egna lärandeprocesser
Avdelningen för fackspråk och kommunikation på Chalmers. Språk och kommunikation på Matematisk orientering (MVE235) ht- 16
 Språk och kommunikation på Matematisk orientering (MVE235) ht- 16 Hans Malmström Avdelningen för fackspråk och kommunikation Chalmers tekniska högskola mahans@chalmers.se Avdelningen för fackspråk och
Språk och kommunikation på Matematisk orientering (MVE235) ht- 16 Hans Malmström Avdelningen för fackspråk och kommunikation Chalmers tekniska högskola mahans@chalmers.se Avdelningen för fackspråk och
Vad innebär det att undervisa i algebra i årskurs 1 3? Vart ska dessa
 Åsa Brorsson Algebra för lågstadiet I denna artikel beskriver en lärare hur hon arbetar med algebra redan i de tidiga skolåren. Det är ett arbete som hjälper elever att förstå likhetstecknets betydelse,
Åsa Brorsson Algebra för lågstadiet I denna artikel beskriver en lärare hur hon arbetar med algebra redan i de tidiga skolåren. Det är ett arbete som hjälper elever att förstå likhetstecknets betydelse,
MATEMATISK KOMMUNIKATION Att tavelpresentera som en matematiker
 MATEMATISK KOMMUNIKATION Att tavelpresentera som en matematiker Presentationsteknik, särskilt tavelpresentation. Syfte: - Öva på att kommunicera matematik muntligt. - Stärka ämneskunskaperna. - Stärka
MATEMATISK KOMMUNIKATION Att tavelpresentera som en matematiker Presentationsteknik, särskilt tavelpresentation. Syfte: - Öva på att kommunicera matematik muntligt. - Stärka ämneskunskaperna. - Stärka
Problemlösning Fk- åk 3 19/ Pia Eriksson
 Problemlösning Fk- åk 3 19/12 2013 Pia Eriksson Fyra glaskulor och tre pappersstjärnor väger 63 gram. Tre glaskulor och två pappersstjärnor väger 46 gram. Alla glaskulor väger lika mycket och alla pappersstjärnor
Problemlösning Fk- åk 3 19/12 2013 Pia Eriksson Fyra glaskulor och tre pappersstjärnor väger 63 gram. Tre glaskulor och två pappersstjärnor väger 46 gram. Alla glaskulor väger lika mycket och alla pappersstjärnor
bedömning Per Berggren och Maria Lindroth
 Varierad undervisning och bedömning Per Berggren och Maria Lindroth 2013-01-22 Matematiska förmågor Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla
Varierad undervisning och bedömning Per Berggren och Maria Lindroth 2013-01-22 Matematiska förmågor Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla
Att kommunicera med personer med demenssjukdom
 Att kommunicera med personer med demenssjukdom Kommunikation är en viktig del i våra relationer och ett grundläggande behov. Vår identitet är nära sammankopplad med vårt språk. Vem vi är som person, skapas
Att kommunicera med personer med demenssjukdom Kommunikation är en viktig del i våra relationer och ett grundläggande behov. Vår identitet är nära sammankopplad med vårt språk. Vem vi är som person, skapas
Hands-On Math. Matematikverkstad. Förskolans nya läroplan 1 juli 2011. Matematik är en abstrakt och generell vetenskap
 Hands-On Math Matematikverkstad 09.00 10.30 & 10.45 12.00 Elisabeth.Rystedt@ncm.gu.se Lena.Trygg@ncm.gu.se eller ett laborativt arbetssätt i matematik Laborativ matematikundervisning vad vet vi? Matematik
Hands-On Math Matematikverkstad 09.00 10.30 & 10.45 12.00 Elisabeth.Rystedt@ncm.gu.se Lena.Trygg@ncm.gu.se eller ett laborativt arbetssätt i matematik Laborativ matematikundervisning vad vet vi? Matematik
Om mentorsverksamheten i matematik
 Om mentorsverksamheten i matematik Varje mentorstillfälle ska vara schemalagt en gång i veckan, med minst en föreläsning och en lektion innan varje tillfälle. Detta ger att studenterna kommer till mötet
Om mentorsverksamheten i matematik Varje mentorstillfälle ska vara schemalagt en gång i veckan, med minst en föreläsning och en lektion innan varje tillfälle. Detta ger att studenterna kommer till mötet
Visible teaching visible learning. Formativ bedömning en väg till bättre lärande
 Bedömning Summativ Formativ bedömning en väg till bättre lärande Gunilla Olofsson Formativ ------------------------------------------------- Bedömning som en integrerad del av lärandet Allsidig bedömning
Bedömning Summativ Formativ bedömning en väg till bättre lärande Gunilla Olofsson Formativ ------------------------------------------------- Bedömning som en integrerad del av lärandet Allsidig bedömning
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Provmoment: Tentamen Matematik och matematikdidaktik, 3 hp, tillfälle 1
 Matematik med didaktisk inriktning för grundlärare i förskoleklass och grundskolans a rskurs 1-3, III, VT18 7,5 högskolepoäng Provmoment: Tentamen Matematik och matematikdidaktik, 3 hp, tillfälle 1 Ladokkod:
Matematik med didaktisk inriktning för grundlärare i förskoleklass och grundskolans a rskurs 1-3, III, VT18 7,5 högskolepoäng Provmoment: Tentamen Matematik och matematikdidaktik, 3 hp, tillfälle 1 Ladokkod:
KOMMUNIKATION ATT SKAPA ETT BRA SAMTAL
 KOMMUNIKATION Detta dokument tar upp kommunikation, feeback och SMART:a mål, som ska verka som ett stöd under utvecklingssamtalet. Kommunikation är konsten att förmedla tankegångar, information och känslor
KOMMUNIKATION Detta dokument tar upp kommunikation, feeback och SMART:a mål, som ska verka som ett stöd under utvecklingssamtalet. Kommunikation är konsten att förmedla tankegångar, information och känslor
Bakgrundsinformation Kursens namn: Biomedicinsk laboratorievetenskap: Introduktion
 Kursrapport Bakgrundsinformation Kursens namn: Biomedicinsk laboratorievetenskap: Introduktion Termin: HT-2014 Termin1 Ladokkod: BA111C Kursansvarig: Ravi Danielsson Antal registrerade studenter: 65 Antal
Kursrapport Bakgrundsinformation Kursens namn: Biomedicinsk laboratorievetenskap: Introduktion Termin: HT-2014 Termin1 Ladokkod: BA111C Kursansvarig: Ravi Danielsson Antal registrerade studenter: 65 Antal
Formativ bedömning i matematikklassrummet
 Modul: Problemlösning Del 5: Bedömning i problemlösning Formativ bedömning i matematikklassrummet Peter Nyström (2012) Originalartikel från modul, Taluppfattning och tals användning, åk 1-3 Termen bedömning,
Modul: Problemlösning Del 5: Bedömning i problemlösning Formativ bedömning i matematikklassrummet Peter Nyström (2012) Originalartikel från modul, Taluppfattning och tals användning, åk 1-3 Termen bedömning,
Handledarutbildning inom Matematiklyftet. Catarina Wästerlid Utbildningstillfälle 1 17 oktober-2016
 Handledarutbildning inom Matematiklyftet Catarina Wästerlid Utbildningstillfälle 1 17 oktober-2016 1. Efter genomgången utbildning ska matematikhandledaren ha goda kunskaper om Matematiklyftets bakgrund
Handledarutbildning inom Matematiklyftet Catarina Wästerlid Utbildningstillfälle 1 17 oktober-2016 1. Efter genomgången utbildning ska matematikhandledaren ha goda kunskaper om Matematiklyftets bakgrund
IBSE Ett självreflekterande(självkritiskt) verktyg för lärare. Riktlinjer för lärare
 Fibonacci / översättning från engelska IBSE Ett självreflekterande(självkritiskt) verktyg för lärare Riktlinjer för lärare Vad är det? Detta verktyg för självutvärdering sätter upp kriterier som gör det
Fibonacci / översättning från engelska IBSE Ett självreflekterande(självkritiskt) verktyg för lärare Riktlinjer för lärare Vad är det? Detta verktyg för självutvärdering sätter upp kriterier som gör det
HF LEQ. Antal svar: 23
 HF - LEQ : GRUPPTILLHÖRIGHET Denna version av enkäten används om kursen har inkluderat olika grupper av kursdeltagare. Du bör då ha fått information om vilken grupp du ska välja nedan. Välj din grupp i
HF - LEQ : GRUPPTILLHÖRIGHET Denna version av enkäten används om kursen har inkluderat olika grupper av kursdeltagare. Du bör då ha fått information om vilken grupp du ska välja nedan. Välj din grupp i
Sandra Johansson The student seminar: a powerful tool for in-depth, critical discussion. Fritt översatt av Kajsa Eklund
 Sandra Johansson The student seminar: a powerful tool for in-depth, critical discussion Fritt översatt av Kajsa Eklund Seminarium En generell beskrivning Under utbildningen förekommer seminarier som en
Sandra Johansson The student seminar: a powerful tool for in-depth, critical discussion Fritt översatt av Kajsa Eklund Seminarium En generell beskrivning Under utbildningen förekommer seminarier som en
MATEMATIK- OCH FYSIKDIDAKTISKA ASPEKTER
 MATEMATIK- OCH FYSIKDIDAKTISKA ASPEKTER Xantcha 2013 2014 Examination. För godkänt betyg i kursen krävs: Samtliga skriftliga inlämningsuppgifter. Närvaro och aktivt deltagande under lektionerna. Frånvaro
MATEMATIK- OCH FYSIKDIDAKTISKA ASPEKTER Xantcha 2013 2014 Examination. För godkänt betyg i kursen krävs: Samtliga skriftliga inlämningsuppgifter. Närvaro och aktivt deltagande under lektionerna. Frånvaro
Reflektionsverktyg att utveckla modelleringsförmåga
 Modul: Undervisa matematik utifrån förmågorna Del 4: Modelleringsförmåga Reflektionsverktyg att utveckla modelleringsförmåga Örjan Hansson, Högskolan Kristianstad Experter i matematisk modellering framhäver
Modul: Undervisa matematik utifrån förmågorna Del 4: Modelleringsförmåga Reflektionsverktyg att utveckla modelleringsförmåga Örjan Hansson, Högskolan Kristianstad Experter i matematisk modellering framhäver
SKRIVA BREV OCH MUNTLIG PRESENTATION. Venus HT-18
 SKRIVA BREV OCH MUNTLIG PRESENTATION Venus HT-18 STRUKTUR I ETT BREV Datum Hälsningsfras: Hej! Inledning: Jag heter och ska berätta om Innehåll indelat i stycken med en sak per stycke. En tanke per mening,
SKRIVA BREV OCH MUNTLIG PRESENTATION Venus HT-18 STRUKTUR I ETT BREV Datum Hälsningsfras: Hej! Inledning: Jag heter och ska berätta om Innehåll indelat i stycken med en sak per stycke. En tanke per mening,
Det goda boksamtalet- en ömsesidig dialog Våra gemensamma tankar för att boksamtalet ska bli bra, Sa 1a och Språkintroduktionen.
 Våra gemensamma tankar för att boksamtalet ska bli bra, Sa 1a och Språkintroduktionen. I boksamtalet vill jag att de andra i gruppen ska- ha ett mordiskt intresse, brinnande blick, öronen på skaft och
Våra gemensamma tankar för att boksamtalet ska bli bra, Sa 1a och Språkintroduktionen. I boksamtalet vill jag att de andra i gruppen ska- ha ett mordiskt intresse, brinnande blick, öronen på skaft och
Jag ska göra en skiss. Jag gör ett diagram. Jag ska gissa!
 s. 2 PROBLEMLÖSNING Kapitel 4 PROBLEMLÖSNING ARBETSGÅNG Hmmm...vad är det egentligen som är mitt problem? Hur ska ni lösa problemet? Tänk fritt! Jag ska ställa upp en ekvation Jag ska göra en skiss Jag
s. 2 PROBLEMLÖSNING Kapitel 4 PROBLEMLÖSNING ARBETSGÅNG Hmmm...vad är det egentligen som är mitt problem? Hur ska ni lösa problemet? Tänk fritt! Jag ska ställa upp en ekvation Jag ska göra en skiss Jag
TIPS & TRIX. Praktiska tips för att träna dig själv och andra i ett motiverande ledarskap
 TIPS & TRIX Praktiska tips för att träna dig själv och andra i ett motiverande ledarskap 1 mod subst. ~et ORDLED: mod-et 1 förmåga att handla utan fruktan för följder vanl. för ett gott syfte och med insikt
TIPS & TRIX Praktiska tips för att träna dig själv och andra i ett motiverande ledarskap 1 mod subst. ~et ORDLED: mod-et 1 förmåga att handla utan fruktan för följder vanl. för ett gott syfte och med insikt
DD2458-224344 - 2014-12-19
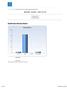 KTH / KURSWEBB / PROBLEMLÖSNING OCH PROGRAMMERING UNDER PRESS DD2458-224344 - 2014-12-19 Antal respondenter: 26 Antal svar: 18 Svarsfrekvens: 69,23 % RESPONDENTERNAS PROFIL (Jag är: Man) Det var typ en
KTH / KURSWEBB / PROBLEMLÖSNING OCH PROGRAMMERING UNDER PRESS DD2458-224344 - 2014-12-19 Antal respondenter: 26 Antal svar: 18 Svarsfrekvens: 69,23 % RESPONDENTERNAS PROFIL (Jag är: Man) Det var typ en
Ma7-Per: Algebra. Det andra arbetsområdet handlar om algebra och samband.
 Ma7-Per: Algebra Det andra arbetsområdet handlar om algebra och samband. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera
Ma7-Per: Algebra Det andra arbetsområdet handlar om algebra och samband. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera
Enkätresultat. Kursenkät, Flervariabelanalys. Datum: 2010-03-29 08:47:04. Aktiverade deltagare (MMGF20, V10, Flervariabelanalys) Grupp:
 Enkätresultat Enkät: Status: Kursenkät, Flervariabelanalys stängd Datum: 2010-03-29 08:47:04 Grupp: Besvarad av: 13(40) (32%) Aktiverade deltagare (MMGF20, V10, Flervariabelanalys) Helheten Mitt helhetsomdöme
Enkätresultat Enkät: Status: Kursenkät, Flervariabelanalys stängd Datum: 2010-03-29 08:47:04 Grupp: Besvarad av: 13(40) (32%) Aktiverade deltagare (MMGF20, V10, Flervariabelanalys) Helheten Mitt helhetsomdöme
Att leda en elevintervju
 Att leda en elevintervju En översiktsdiagnos, i form av ett skriftligt test till en klass, kan ge läraren användbar information. Det kan sätta ljuset på starka och svaga områden, i klassen som helhet identifiera
Att leda en elevintervju En översiktsdiagnos, i form av ett skriftligt test till en klass, kan ge läraren användbar information. Det kan sätta ljuset på starka och svaga områden, i klassen som helhet identifiera
8F Ma Planering v45-51: Algebra
 8F Ma Planering v45-51: Algebra Arbetsform under en vecka: Tisdagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa: Läsa på anteckningar
8F Ma Planering v45-51: Algebra Arbetsform under en vecka: Tisdagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa: Läsa på anteckningar
På vilka sätt kan mönster vara en ingång till att utveckla förmågan att uttrycka och argumentera för generaliseringar algebraiskt?
 På vilka sätt kan mönster vara en ingång till att utveckla förmågan att uttrycka och argumentera för generaliseringar algebraiskt? Jenny Fred, lärare på Ekensbergsskolan och doktorand vid Forskarskolan
På vilka sätt kan mönster vara en ingång till att utveckla förmågan att uttrycka och argumentera för generaliseringar algebraiskt? Jenny Fred, lärare på Ekensbergsskolan och doktorand vid Forskarskolan
Lgr 11 matriser i Favorit matematik 4 6
 Lgr 11 matriser i Favorit matematik 4 6 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla förmågan att De matematiska förmågor
Lgr 11 matriser i Favorit matematik 4 6 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla förmågan att De matematiska förmågor
9A Ma: Geometri. Det tredje arbetsområdet handlar om geometri.
 9A Ma: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda strategier
9A Ma: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda strategier
Bedömning av matematiska förmågor. Per Berggren och Maria Lindroth 2012-01-26
 Bedömning av matematiska förmågor Per Berggren och Maria Lindroth 2012-01-26 Matematiska förmågor Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla
Bedömning av matematiska förmågor Per Berggren och Maria Lindroth 2012-01-26 Matematiska förmågor Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla
Vid Göteborgs universitet pågår sedan hösten 2013 ett projekt under
 Christina Skodras Muffles truffles Undervisning i multiplikation med systematiskt varierade exempel I Nämnaren 2015:4 beskrivs ROMB-projektet övergripande i Unga matematiker i arbete. Här redovisas och
Christina Skodras Muffles truffles Undervisning i multiplikation med systematiskt varierade exempel I Nämnaren 2015:4 beskrivs ROMB-projektet övergripande i Unga matematiker i arbete. Här redovisas och
Matematiklyftet 2013/2014
 Matematiklyftet 2013/2014 Didaktiskt kontrakt Ruc 140522 AnnaLena Åberg 79 Matematiklärare 9 skolor? Elever 10 Rektorer 1 Förvaltningschef 2 Skolområdschefer 5 Matematikhandledare Hur ser ni på det didaktiska
Matematiklyftet 2013/2014 Didaktiskt kontrakt Ruc 140522 AnnaLena Åberg 79 Matematiklärare 9 skolor? Elever 10 Rektorer 1 Förvaltningschef 2 Skolområdschefer 5 Matematikhandledare Hur ser ni på det didaktiska
1. Inledning, som visar att man inte skall tro på allt man ser. Betrakta denna följd av tal, där varje tal är dubbelt så stort som närmast föregående
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Christian Gottlieb Gymnasieskolans matematik med akademiska ögon Induktion Dag 1 1. Inledning, som visar att man inte skall tro på allt man ser. Betrakta
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Christian Gottlieb Gymnasieskolans matematik med akademiska ögon Induktion Dag 1 1. Inledning, som visar att man inte skall tro på allt man ser. Betrakta
Dokumentera och följa upp
 Matematik Förskola Modul: Förskolans matematik Del 8: Dokumentera och följa upp Dokumentera och följa upp Ola Helenius, NCM, Maria L. Johansson, Luleå tekniska universitet, Troels Lange, Malmö universitet,
Matematik Förskola Modul: Förskolans matematik Del 8: Dokumentera och följa upp Dokumentera och följa upp Ola Helenius, NCM, Maria L. Johansson, Luleå tekniska universitet, Troels Lange, Malmö universitet,
7E Ma Planering v45-51: Algebra
 7E Ma Planering v45-51: Algebra Arbetsform under en vecka: Måndagar (40 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa: Läsa på anteckningar
7E Ma Planering v45-51: Algebra Arbetsform under en vecka: Måndagar (40 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa: Läsa på anteckningar
7G,H och D matematik planering Syftet med undervisningen är att du ska utveckla din förmåga att:
 Åsö grundskola VT2018 7G,H och D matematik planering Syftet undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem hjälp av matematik samt värdera valda strategier och metoder,
Åsö grundskola VT2018 7G,H och D matematik planering Syftet undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem hjälp av matematik samt värdera valda strategier och metoder,
Pedagogiskt café. Problemlösning
 Pedagogiskt café Problemlösning Vad är ett matematiskt problem? Skillnad mellan uppgift och problem - Uppgift är något som eleven träffat på tidigare, kan lösa med vanliga standardmetoder - Matematiskt
Pedagogiskt café Problemlösning Vad är ett matematiskt problem? Skillnad mellan uppgift och problem - Uppgift är något som eleven träffat på tidigare, kan lösa med vanliga standardmetoder - Matematiskt
Explorativ övning 5 MATEMATISK INDUKTION
 Explorativ övning 5 MATEMATISK INDUKTION Syftet med denna övning är att introducera en av de viktigaste bevismetoderna i matematiken matematisk induktion. Termen induktion är lite olycklig därför att matematisk
Explorativ övning 5 MATEMATISK INDUKTION Syftet med denna övning är att introducera en av de viktigaste bevismetoderna i matematiken matematisk induktion. Termen induktion är lite olycklig därför att matematisk
Lyssningsstrategier. En framgångsrik språkinlärare: Tror på sin förmåga att lära sig. Är motiverad. Är medveten om varför hon/han vill lära sig
 1 Lyssningsstrategier En framgångsrik språkinlärare: Tror på sin förmåga att lära sig Är motiverad Är medveten om varför hon/han vill lära sig Är inte rädd för att göra misstag Tar risker Är bra på att
1 Lyssningsstrategier En framgångsrik språkinlärare: Tror på sin förmåga att lära sig Är motiverad Är medveten om varför hon/han vill lära sig Är inte rädd för att göra misstag Tar risker Är bra på att
Introduktion och Praxisseminarium LG10MA och L910MA VFU1
 Introduktion och Praxisseminarium LG10MA och L910MA VFU1 Lärare åk 7-9 och Gy i matematik, 4,5 högskolepoäng Lärare: Bengt Andersson, Eva Taflin Introduktion: 19 November -13 VFU1 koppling till tidigare
Introduktion och Praxisseminarium LG10MA och L910MA VFU1 Lärare åk 7-9 och Gy i matematik, 4,5 högskolepoäng Lärare: Bengt Andersson, Eva Taflin Introduktion: 19 November -13 VFU1 koppling till tidigare
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Ma7-Per: Geometri. Det tredje arbetsområdet handlar om geometri.
 Ma7-Per: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda
Ma7-Per: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda
Svåra Samtal DISPOSITION. Bakgrund & Intervjuteknik. Workshop Svåra Samtal Pennskaftets Årliga Konferens Världskulturmuséet 5 mars 2008
 Pennskaftskonferens 2008 Världskulturmuseet 5 mars Svåra Samtal Anneli Larsson Lecturer, The Swedish National Police Academy Affiliated Researcher, University of Cambridge E-mail: 1 DISPOSITION 13.00 13.45
Pennskaftskonferens 2008 Världskulturmuseet 5 mars Svåra Samtal Anneli Larsson Lecturer, The Swedish National Police Academy Affiliated Researcher, University of Cambridge E-mail: 1 DISPOSITION 13.00 13.45
Avdelningen för fackspråk och kommunikation på Chalmers. Språk och kommunikation på Matematik 1 (MMG200) ht- 16
 Språk och kommunikation på Matematik 1 (MMG200) ht- 16 Claes Ohlsson Avdelningen för fackspråk och kommunikation Chalmers tekniska högskola claeso@chalmers.se Avdelningen för fackspråk och kommunikation
Språk och kommunikation på Matematik 1 (MMG200) ht- 16 Claes Ohlsson Avdelningen för fackspråk och kommunikation Chalmers tekniska högskola claeso@chalmers.se Avdelningen för fackspråk och kommunikation
BEDÖMNINGSSTÖD till TUMMEN UPP! svenska åk 3
 BEDÖMNINGSSTÖD till TUMMEN UPP! svenska åk 3 Det här är ett BEDÖMNINGSSTÖD till Tummen upp! svenska som hjälper dig att göra en säkrare bedömning av elevernas kunskaper i årskurs 3. Av tradition har man
BEDÖMNINGSSTÖD till TUMMEN UPP! svenska åk 3 Det här är ett BEDÖMNINGSSTÖD till Tummen upp! svenska som hjälper dig att göra en säkrare bedömning av elevernas kunskaper i årskurs 3. Av tradition har man
Rapport av genomförd lesson study av en lektion med temat bråk i gymnasiets A-kurs
 Rapport av genomförd lesson study av en lektion med temat bråk i gymnasiets A-kurs Klippa gräset Jenny klipper gräsmattan hos Bo på 2 timmar. Måns gör det på 4 timmar. Förberedelser Utifrån en diskussion
Rapport av genomförd lesson study av en lektion med temat bråk i gymnasiets A-kurs Klippa gräset Jenny klipper gräsmattan hos Bo på 2 timmar. Måns gör det på 4 timmar. Förberedelser Utifrån en diskussion
ACT- Att hantera stress och främja hälsa
 ACT- Att hantera stress och främja hälsa (ACT = Acceptance and Commitment Training) Kollegial handledning För att kontinuerligt bli bättre i rollen som gruppledare är det viktigt att öva. Det här är ett
ACT- Att hantera stress och främja hälsa (ACT = Acceptance and Commitment Training) Kollegial handledning För att kontinuerligt bli bättre i rollen som gruppledare är det viktigt att öva. Det här är ett
Bedömning av muntliga prestationer
 Modul: Bedömning för lärande och undervisning i matematik Del 6: Muntliga bedömningssituationer Bedömning av muntliga prestationer Karin Rösmer, Karin Landtblom, Gunilla Olofsson och Astrid Pettersson,
Modul: Bedömning för lärande och undervisning i matematik Del 6: Muntliga bedömningssituationer Bedömning av muntliga prestationer Karin Rösmer, Karin Landtblom, Gunilla Olofsson och Astrid Pettersson,
Lära matematik med datorn
 Lära matematik med datorn Ulrika Ryan Matematik för den digitala generationen Malmö högskola, Lunds Universitet, Göteborgs Universitet och NCM 3 gymnasieskolor och 2 grundskolor i Lunds kommun Matematik
Lära matematik med datorn Ulrika Ryan Matematik för den digitala generationen Malmö högskola, Lunds Universitet, Göteborgs Universitet och NCM 3 gymnasieskolor och 2 grundskolor i Lunds kommun Matematik
7F Ma Planering v2-7: Geometri
 7F Ma Planering v2-7: Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
7F Ma Planering v2-7: Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
Formativ bedömning i matematikklassrummet
 Modul: Taluppfattning och tals användning Del 4: Formativ bedömning Formativ bedömning i matematikklassrummet Peter Nyström, NCM Termen bedömning, eller pedagogisk bedömning kan uppfattas väldigt olika,
Modul: Taluppfattning och tals användning Del 4: Formativ bedömning Formativ bedömning i matematikklassrummet Peter Nyström, NCM Termen bedömning, eller pedagogisk bedömning kan uppfattas väldigt olika,
Rapport av genomförd "Lesson study" av en lektion med temat ekvationer i gymnasiets B-kurs. Bultar, muttrar och brickor
 Rapport av genomförd "Lesson study" av en lektion med temat ekvationer i gymnasiets B-kurs Bultar, muttrar och brickor Vågad problemlösning Förberedelser Ekvationssystem i matematik B ger progression från
Rapport av genomförd "Lesson study" av en lektion med temat ekvationer i gymnasiets B-kurs Bultar, muttrar och brickor Vågad problemlösning Förberedelser Ekvationssystem i matematik B ger progression från
MELLAN GYMNASIET OCH UNIVERSITETET
 STADIEÖVERGÅNGEN MELLAN GYMNASIET OCH UNIVERSITETET Erika Stadler Linnéuniversitetet Gymnasieelever om matematik och matematikundervisning i i En typisk mattelektion är att läraren går igenom på tavlan
STADIEÖVERGÅNGEN MELLAN GYMNASIET OCH UNIVERSITETET Erika Stadler Linnéuniversitetet Gymnasieelever om matematik och matematikundervisning i i En typisk mattelektion är att läraren går igenom på tavlan
Kursinformation. Statistik och geometri, 7 hp. inom kursen 973G10, 15 hp för Lärare i årskurs 4-6
 Kursinformation Statistik och geometri, 7 hp inom kursen 973G10, 15 hp för Lärare i årskurs 4-6 Kursen startar vecka 15 den 7 april 2014 Kursperiod Vecka 15-20 (7 april 17 maj) 2014 Lärare (kursansvarig
Kursinformation Statistik och geometri, 7 hp inom kursen 973G10, 15 hp för Lärare i årskurs 4-6 Kursen startar vecka 15 den 7 april 2014 Kursperiod Vecka 15-20 (7 april 17 maj) 2014 Lärare (kursansvarig
Guide Studieteknik. Tips för lättare studier!
 Guide Studieteknik Tips för lättare studier! 1 Läs- och anteckningsteknik Att läsa och att anteckna Det finns goda skäl till att göra anteckningar när du läser en text, lyssnar på en föreläsning, förbereder
Guide Studieteknik Tips för lättare studier! 1 Läs- och anteckningsteknik Att läsa och att anteckna Det finns goda skäl till att göra anteckningar när du läser en text, lyssnar på en föreläsning, förbereder
Studiehandledning M0038M Matematik I Differentialkalkyl Lp 1, 2016
 Studiehandledning M0038M Matematik I Differentialkalkyl Lp 1, 2016 Kursansvarig/Examinator: Staffan Lundberg, TVM Telefon: 0920-49 18 69 Rum: E882 E-post: Lärare i Skellefteå: Eva Lövf, tfn. 0910-58 53
Studiehandledning M0038M Matematik I Differentialkalkyl Lp 1, 2016 Kursansvarig/Examinator: Staffan Lundberg, TVM Telefon: 0920-49 18 69 Rum: E882 E-post: Lärare i Skellefteå: Eva Lövf, tfn. 0910-58 53
Utmanande uppgifter som utvecklar. Per Berggren och Maria Lindroth
 Utmanande uppgifter som utvecklar Per Berggren och Maria Lindroth 2014-11-12 Vilka förmågor ska utvecklas Problemlösning (Förstå frågan i en textuppgift, Använda olika strategier när jag löser ett problem,
Utmanande uppgifter som utvecklar Per Berggren och Maria Lindroth 2014-11-12 Vilka förmågor ska utvecklas Problemlösning (Förstå frågan i en textuppgift, Använda olika strategier när jag löser ett problem,
Välkomna till DIT012 IPGO
 Välkomna till DIT012 IPGO 1 Lärare och Handledare Kursansvariga, examinatorer, föreläsare och handledare Joachim von Hacht, hajo@chalmers.se, 772 1003 Handledare (se även kurssida) Alexander Sjösten, sjosten@chalmers.se
Välkomna till DIT012 IPGO 1 Lärare och Handledare Kursansvariga, examinatorer, föreläsare och handledare Joachim von Hacht, hajo@chalmers.se, 772 1003 Handledare (se även kurssida) Alexander Sjösten, sjosten@chalmers.se
Välkomna till DIT012 IPGO. Tyvärr en bug i Google Docs: Sidnummer stämmer inte alltid. Alla anteckningar börjar på sidan 1.
 Välkomna till DIT012 IPGO 1 Tyvärr en bug i Google Docs: Sidnummer stämmer inte alltid. Alla anteckningar börjar på sidan 1. Lärare och Handledare Kursansvariga, examinatorer, föreläsare och handledare
Välkomna till DIT012 IPGO 1 Tyvärr en bug i Google Docs: Sidnummer stämmer inte alltid. Alla anteckningar börjar på sidan 1. Lärare och Handledare Kursansvariga, examinatorer, föreläsare och handledare
Bedömning av matematiska förmågor. Per Berggren och Maria Lindroth
 Bedömning av matematiska förmågor Per Berggren och Maria Lindroth 2013-01-08 Matematiska förmågor Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla
Bedömning av matematiska förmågor Per Berggren och Maria Lindroth 2013-01-08 Matematiska förmågor Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla
Tal i bråkform. Kapitlet behandlar. Att förstå tal
 Tal i bråkform Kapitlet behandlar Test Användning av hälften och fjärdedel 2 Representation i bråkform av del av antal och av del av helhet 3, Bråkform i vardagssituationer Stambråk, bråkuttryck med 1
Tal i bråkform Kapitlet behandlar Test Användning av hälften och fjärdedel 2 Representation i bråkform av del av antal och av del av helhet 3, Bråkform i vardagssituationer Stambråk, bråkuttryck med 1
Om Lgr 11 och Favorit matematik 4 6
 Om Lgr 11 och Favorit matematik 4 6 TYDLIG OCH MEDVETEN MATEMATIKUNDERVISNING En stark koppling mellan läroplan/kunskaps mål, innehåll och bedömning finns för att medvetande göra eleverna om syftet med
Om Lgr 11 och Favorit matematik 4 6 TYDLIG OCH MEDVETEN MATEMATIKUNDERVISNING En stark koppling mellan läroplan/kunskaps mål, innehåll och bedömning finns för att medvetande göra eleverna om syftet med
8F Ma Planering v2-7 - Geometri
 8F Ma Planering v2-7 - Geometri Arbetsform under en vecka: Tisdagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
8F Ma Planering v2-7 - Geometri Arbetsform under en vecka: Tisdagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
Intervjuguide. Del 1. Att göra inför intervjun: Kort om intervjuguiden: a. Uppfattningar och intentioner. [8 min / 8 min]
![Intervjuguide. Del 1. Att göra inför intervjun: Kort om intervjuguiden: a. Uppfattningar och intentioner. [8 min / 8 min] Intervjuguide. Del 1. Att göra inför intervjun: Kort om intervjuguiden: a. Uppfattningar och intentioner. [8 min / 8 min]](/thumbs/52/30489320.jpg) Intervjuguide Att göra inför intervjun: Tänk igenom den besökta lektionen så att du kan beskriva den kort och neutralt. Titta på den använda läroboken så att du kan diskutera den med läraren. Ha ett anteckningspapper
Intervjuguide Att göra inför intervjun: Tänk igenom den besökta lektionen så att du kan beskriva den kort och neutralt. Titta på den använda läroboken så att du kan diskutera den med läraren. Ha ett anteckningspapper
Hur lär barn bäst? Mats Ekholm Karlstads universitet
 Hur lär barn bäst? Mats Ekholm Karlstads universitet Ståndpunkter som gäller de ungas motivation o För att lära bra behöver de unga belönas för vad de gör. Betyg är den främsta sporren för lärande. o För
Hur lär barn bäst? Mats Ekholm Karlstads universitet Ståndpunkter som gäller de ungas motivation o För att lära bra behöver de unga belönas för vad de gör. Betyg är den främsta sporren för lärande. o För
Funktioner, Algebra och Ekvationer År 9
 Undervisning Funktioner, Algebra och Ekvationer År 9 Mål att uppnå i år 9, ur Lpo 94 Utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och
Undervisning Funktioner, Algebra och Ekvationer År 9 Mål att uppnå i år 9, ur Lpo 94 Utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och
Realism och anti-realism och andra problem
 Realism och anti-realism och andra problem Vetenskap och verkligheten Vetenskapen bör beskriva verkligheten. Men vad är verkligheten? Är det vi tycker oss se av verkligheten verkligen vad verkligheten
Realism och anti-realism och andra problem Vetenskap och verkligheten Vetenskapen bör beskriva verkligheten. Men vad är verkligheten? Är det vi tycker oss se av verkligheten verkligen vad verkligheten
Kursplan för Matematik
 Sida 1 av 5 Kursplan för Matematik Inrättad 2000-07 SKOLFS: 2000:135 Ämnets syfte och roll i utbildningen Grundskolan har till uppgift att hos eleven utveckla sådana kunskaper i matematik som behövs för
Sida 1 av 5 Kursplan för Matematik Inrättad 2000-07 SKOLFS: 2000:135 Ämnets syfte och roll i utbildningen Grundskolan har till uppgift att hos eleven utveckla sådana kunskaper i matematik som behövs för
Matematiska undersökningar med kalkylprogram
 Matematik Grundskola årskurs 7-9 Modul: Matematikundervisning med digitala verktyg Del 7: Matematiska undersökningar med kalkylprogram Matematiska undersökningar med kalkylprogram Håkan Sollervall, Malmö
Matematik Grundskola årskurs 7-9 Modul: Matematikundervisning med digitala verktyg Del 7: Matematiska undersökningar med kalkylprogram Matematiska undersökningar med kalkylprogram Håkan Sollervall, Malmö
ÖVNINGAR KRING KOMMUNIKATION OCH PARRELATION
 ÖVNINGAR KRING KOMMUNIKATION OCH PARRELATION I detta dokument finns olika exempel på övningar ni kan göra i gruppen. Det krävs tid och man kan behöva pröva flera gånger för att bli bekväm i en övning.
ÖVNINGAR KRING KOMMUNIKATION OCH PARRELATION I detta dokument finns olika exempel på övningar ni kan göra i gruppen. Det krävs tid och man kan behöva pröva flera gånger för att bli bekväm i en övning.
DD1393 Mjukvarukonstruktion. Presentationsteknik. Linda Söderlindh, ECE/Språk Universitetsadjunkt i Retorik & teknikvetenskaplig kommunikation
 DD1393 Mjukvarukonstruktion Presentationsteknik Linda Söderlindh, ECE/Språk Universitetsadjunkt i Retorik & teknikvetenskaplig kommunikation Kommunikation på DD1393 1,5hp Föreläsning 1 Presentationsteknik
DD1393 Mjukvarukonstruktion Presentationsteknik Linda Söderlindh, ECE/Språk Universitetsadjunkt i Retorik & teknikvetenskaplig kommunikation Kommunikation på DD1393 1,5hp Föreläsning 1 Presentationsteknik
Ragnhild Löfgren, Astrid Berg & Martin Nelzén Institutionen för samhälls- och välfärdsstudier, ISV Linköpings universitet
 2017-02-02 Dnr LiU-2014-00147 1(7) Ragnhild Löfgren, Astrid Berg & Martin Nelzén Institutionen för samhälls- och välfärdsstudier, ISV Linköpings universitet LINKÖPINGS UNIVERSITET 2(7) När studenterna
2017-02-02 Dnr LiU-2014-00147 1(7) Ragnhild Löfgren, Astrid Berg & Martin Nelzén Institutionen för samhälls- och välfärdsstudier, ISV Linköpings universitet LINKÖPINGS UNIVERSITET 2(7) När studenterna
Addition och subtraktion generalisering
 Modul: Algebra Del 8: Avslutande reflektion och utvärdering Addition och subtraktion generalisering Håkan Lennerstad, Blekinge Tekniska Högskola & Cecilia Kilhamn, Göteborgs Universitet Detta lärandeobjekt
Modul: Algebra Del 8: Avslutande reflektion och utvärdering Addition och subtraktion generalisering Håkan Lennerstad, Blekinge Tekniska Högskola & Cecilia Kilhamn, Göteborgs Universitet Detta lärandeobjekt
Lösningsfokuserad terapi
 Lösningsfokuserad terapi Jeanette Niehof Leg. psykolog / logoped KBT terapeut steg 1 &2 EMDR terapeut Handledare 16 oktober 2013 Livet är som att cykla. För att hålla balansen måste du vara i rörelse.
Lösningsfokuserad terapi Jeanette Niehof Leg. psykolog / logoped KBT terapeut steg 1 &2 EMDR terapeut Handledare 16 oktober 2013 Livet är som att cykla. För att hålla balansen måste du vara i rörelse.
Kursmanual för SG1102 Mekanik, mindre kurs (6 hp)
 Version: 2016-12-19 Kursmanual för SG1102 Mekanik, mindre kurs (6 hp) Innehåll 1. Anmälningstider (tentor & KS:ar) 2. Lärandemål 3. Kurslitteratur 4. Föreläsningar 5. Övningar 6. Inlämningsuppgifter 7.
Version: 2016-12-19 Kursmanual för SG1102 Mekanik, mindre kurs (6 hp) Innehåll 1. Anmälningstider (tentor & KS:ar) 2. Lärandemål 3. Kurslitteratur 4. Föreläsningar 5. Övningar 6. Inlämningsuppgifter 7.
RAPPORT FÖR UTVÄRDERING AV AVSLUTAD KURS/DELKURS
 UPPSALA UNIVERSITET Institutionen för musikvetenskap RAPPORT FÖR UTVÄRDERING AV AVSLUTAD KURS/DELKURS Kurs: Musikteori 1/Musikvetenskap A Delkurs: Satslära/funktionsanalys Termin: VT 211 Totalt besvarade
UPPSALA UNIVERSITET Institutionen för musikvetenskap RAPPORT FÖR UTVÄRDERING AV AVSLUTAD KURS/DELKURS Kurs: Musikteori 1/Musikvetenskap A Delkurs: Satslära/funktionsanalys Termin: VT 211 Totalt besvarade
Problemlösning som metod
 Problemlösning som metod - för att lära matematik Fuengirola november 2014 eva.taflin@gu.se evat@du.se Problemlösningsmodulens övergripande syfte Att initiera utveckling av lärares egen undervisning utifrån
Problemlösning som metod - för att lära matematik Fuengirola november 2014 eva.taflin@gu.se evat@du.se Problemlösningsmodulens övergripande syfte Att initiera utveckling av lärares egen undervisning utifrån
