Laboration i Geometrisk Optik

Transkript

1 Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson)

2 Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen 2 4 Linser Att rita strålgångar Gauss Linsformel Speglar Att rita strålgångar Descartes spegelformel Strålgångsinställningar 8 7 Laborationsuppgifter Bestämning av brytningsindex för en glasplatta Bestämning av fokalavståndet för en konkav lins Bestämning av fokalavståndet för några konvexa linser Enkel grovuppskattning Bessels metod Grafisk metod Bestämning av fokalavståndet för en konkav spegel Linssystem i

3 1 Vad är geometrisk optik? I den geometriska optiken, eller stråloptiken, betraktar man ljuset som strålar. Strålarna refrakteras, eller bryts, vid ingång till ett medium med annat brytningsindex och reflekteras i speglande ytor. Hur ljuset bryts beskrivs av Snells lag och hur det reflekteras bestäms av reflektionslagen. Diffraktion, interferens och övriga fenomen som uppträder när ljuset betraktas som en våg förekommer inte. Geometrisk optik är alltså en approximation. För att approximationen skall vara giltig krävs att de linser och speglar vi använder är stora i förhållande till ljusvåglängden. Formlerna, t.ex. för avbildning, blir speciellt enkla om krökningsradierna är stora på de linser och speglar vi använder, samt att strålarna är centrala. Att kunna geometrisk optik tillhör en fysikers allmänbildning och man kan utifrån väldigt enkla formler snabbt förstå hur mikroskop, kikare och även mer komplexa optiska system fungerar. 2 Brytningsindex och dispersion Ljusets hastighet är konstant i vakuum men inte i ett medium. Hur snabbt ljus utbreder sig i ett medium bestäms av materialets brytningsindex n. Ljushastigheten i ett medium är v = c n (1) Brytningsindex n är alltså n = ljusets hastighet i vakuum ljusets hastighet i mediet (2) Brytningsindex är frekvensberoende. Rött ljus bryts annolunda än blått ljus. Detta fenomen kallas för dispersion. Ett exempel på dispersion är när solens strålar träffar ett prisma och ljuset delas upp i ett spektrum från blått till rött. 1

4 3 Snells lag och reflektionslagen I inledningen talas det om Snells lag och reflektionslagen. Snells lag talar om hur en inkommande stråle bryts i ett dielektrikum. Lagen lyder n i sin(θ i ) = n t sin(θ t ) (3) Beteckningarna i formeln finns beskrivna i figur 1 θi θr ni nt θt Figur 1: Figuren visar hur en inkommande stråle bryts respektive reflekteras i ett dielektrikum. Reflektionslagen lyder kort och gott infallsvinkeln θ i är lika med utfallsvinkeln θ r. Se figur 1 4 Linser 4.1 Att rita strålgångar När ett objekt skall avbildas genom ett linssystem är det viktigt att kunna rita en korrekt strålgång. Det finns ett antal strålar som man vet vart de hamnar efter att ha passerat en lins. Dessa strålar kallas för huvudstrålar. Bilden av ett objekt erhålls genom att dra dessa strålar från en punkt på objektet, genom linsen och sedan se var strålarna korsar varandra. Figur 2 visar huvudstrålar genom en konvex och en konkav lins. Symmetriaxeln i figur 2 kallas för den optiska axeln (o.a). 2

5 För en konvex lins gäller följande a) En stråle som är parallell med den optiska axeln bryts i linsen så att den passerar fokus (f). b) En stråle som går genom linsens mittpunkt passerar utan att brytas. c) En stråle som går genom fokus bryts av linsen så att den är parallell med den optiska axeln efter att ha passerat linsen. För en konkav lins gäller följande d) En stråle som är parallell med den optiska axeln bryts i linsen så att den ser ut att komma från fokus efter linsen e) En stråle som går genom linsens mittpunkt passerar utan att brytas. f) En stråle som passerar linsen på väg mot fokus bryts så att den är parallell med den optiska axeln efter att ha passerat linsen. Figur 2: Figuren visar huvdudstrålar från ett objekt genom en konvex och en konkav lins. 3

6 4.2 Gauss Linsformel Gauss linsformel återkommer ständigt i laborationen. Formeln kan användas för både konvexa och konkava linser. Senare kommer vi att se att den gäller även för speglar. Studera figur 3. Figuren visar ett reellt objekt (a > 0) som avbildas efter en konvex lins. Reellt objekt f f h Reell bild H a b Figur 3: Avbildning i en konvex lins. Gauss linsformel lyder 1 a + 1 b = 1 f (4) Avståndet a är mellan objekt och lins, avståndet b är mellan lins och bilden och f är linsens fokallängd. Man kan även visa att för den transversella förstoringen gäller M T = H h = b a (5) Gauss linsformel är väldigt användbar om man tänker på de teckenkonventioner som gäller. För en konvex lins är f positiv och för en konkav lins är f negativ. Tabellen nedan presenterar den teckenkonvention som används här och i kursboken (Pedrotti, Pedrotti, Pedrotti: Introduction to Optics). 4

7 Storhet + - a Reellt objekt Virtuellt objekt b Reell bild Virtuell bild f Konvex lins Konkav lins h Upprest objekt Inverterat objekt H Upprest bild Inverterad bild M T Upprest bild Inverterad bild Virtuell bild och virtuellt objekt är ofta lite svåra att förstå till en början och vi hänvisar till läroboken för utförlig förklaring. Kortfattat kan man säga att en virtuell bild aldrig kan visas på en skärm. En virtuell bild kan man se om man t.ex. tittar in i en spegel. Ett virtuellt objekt kommer vi att få exempel på i den sista laborationsuppgiften. 5

8 5 Speglar 5.1 Att rita strålgångar På samma sätt som för linser finns det regler för hur man ritar strålgångar för speglar. I fallet för speglar så finns det fyra strålar som man vet var de tar vägen efter reflektion. Dessa strålar finns utritade i figur 4 för både konvexa och konkava speglar. I figuren så är punkten R spegelns krökningsradie och f dess fokallängd. Figur 4: Det finns fyra strålar som man vet vart tar vägen efter reflektion i en spegel. 5.2 Descartes spegelformel Sambandet mellan avstånden objekt och spegel, a, bild och spegel, b, och en spegels krökningsradie, R, ges av Descartes spegel formel. 1 a + 1 b = 2 R (6) 6

9 Om man låter a så får man parallella strålar in mot spegeln. Parallella strålar faller igenom fokus, vilket betyder att b = f. Detta betyder att 1 b = 1 f = 2 R (7) Vi kan därför skriva om spegelformeln på samma form som Gauss linsformel 1 a + 1 b = 1 f (8) a h R H f V Figur 5: Avbildning i en konkav spegel. b Nu gäller följande teckenkonvention. Storheterna finns utmärkta i figur 5 Storhet + - a Vänster om V, Reellt objekt Höger om V, Virtuellt objekt b Vänster om V, Reell bild Höger om V, Virtuell bild f Konkav spegel Konvex spegel R Höger om V, Konvex spegel Vänster om V, Konkav spegel h Upprest objekt Inverterat objekt H Upprest bild Inverterad bild 7

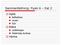
10 6 Strålgångsinställningar För att få ett väl fungerande optiskt system är det viktigt att speglar och linser placeras på ett korrekt sätt. Om inte så kan man få avbildningsfel eller dåligt med ljus genom systemet. Nedan följer några råd för att få en bra avbildning i ett optiskt system. - Ofta används en lampa för att belysa objekt som skall avbildas. Även om lampan ger ett väldigt divergent strålknippe kan den grovjusteras så att ljuskonen från lampan ligger horisontell och längs med den optiska axeln.(då glödtråden utgör en utbredd ljuskälla kan ej ett helt parallellt strålknippe fås.) - Optiska element som placeras i strålgången skall alla vara på samma höjd och vinkelräta mot den optiska axeln. Se även till att den skärm där bilden skall hamna på är vinkelrät mot det infallande ljuset. 7 Laborationsuppgifter 7.1 Bestämning av brytningsindex för en glasplatta I denna uppgift skall vi bestämma brytningsindex, n, för en glasplatta. Låt en laserstråle falla in mot en glasplatta så som visas i figur 6. Figur 6: Experimentuppställning 1 sedd uppifrån Laserljuset reflekteras i glasets första och andra yta, och ger upphov till multipelreflektion, se figur 7. (Använd området för bästa resultat.) Genom att använda reflektionslagen och Snells lag kan man visa att det vinkelräta avståndet, a, mellan två närliggande reflekterade strålar ges av a = 2d sin θ cos θ (n 2 sin 2 θ) 1/2 (9) 8

11 a θ d Figur 7: Multipelreflektion i en glasplatta I denna ekvation är d plattans tjocklek, n glasets brytningsindex och θ är infallsvinkeln. 1. Ställ upp experimentuppställningen enligt figur 6. Var noga med att glasytans normal ligger i samma plan som den inkommande laserstrålen. Kontrollera detta genom att se till att laserreflexen speglas tillbaka in i lasern vid Bestäm brytningsindex för glasplattan genom att mäta d och a för tre olika infallsvinklar θ. Var noga med att ni mäter a vinkelrät mot strålarnas utbredningsriktning. 3. Jämför ert uppmätta värde med ett tabellvärde. En härledning av ekvation 9 skall ingå i laborationsredogörelsen. 7.2 Bestämning av fokalavståndet för en konkav lins I denna uppgift skall vi bestämma fokallängden för en konkavlins. 1. Experimentuppställningen ses på figur Låt strålen från en He-Ne laser träffa en skärm vinkelrät. Avståndet mellan lins och skärm (D) bör vara ca 2m. 3. Markera ljuspunktens läge på ett papper som är fäst på skärmen. Placera den konkava linsen framför lasern vinkelrät mot strålen och justera linsen tills ljusfläcken ligger på samma ställe som förut, figur 8a. 4. Skjut nu den konkava linsen i sidled en sträcka x. Fläcken på skärmen kommer då att flytta sig y, figur 8b. 9

12 a) D He-Ne Laser b) D He-Ne Laser x y Figur 8: Experimentuppställning i uppgift 2. Bilden är sedd ovanifrån. Linsens fokallängd ges av ekvation 10. f = xd y (10) I denna formel är D avståndet mellan lins och skärm. 5. Gör tio olika mätningar på x och y. Beräkna f utifrån era mätningar. En härledning av ekvation 10 skall ingå i laborationsredogörelsen. 7.3 Bestämning av fokalavståndet för några konvexa linser Vi skall använda oss av tre olika metoder för att bestämma några konvexa linsers fokallängd Enkel grovuppskattning Innan man gör en nogrann mätning av en lins fokallängd kan man på ett enkelt sätt göra en uppskattning. 10

13 Avbilda taklampan i golvytan eller på ett vitt papper på golvet. Då taklampan är ganska långt borta från linsen så bör bilden hamna i närheten av linsens fokus. På så sätt kan man grovuppskatta linsens fokallängd. Gör detta med linserna märkta 10, 20 och Bessels metod Antag att vi vill avbilda ett objekt på en skärm. En konvex lins med fokalavståndet f kan placeras på två olika positioner så att en reell bild faller på skärmen. Om man känner avståndet mellan dessa båda positioner och avståndet mellan objekt och skärm kan man beräkna linsens fokallängd. Villkoret för att man skall kunna avbilda ett objekt på en skärm med en lins med fokallängd f är att avståndet objekt-skärm är större än 4f. Linsens fokallängd fås ur följande formel f = l2 d 2 4l (11) I denna formel är d avståndet mellan de positioner där man får en bild på skärmen och l är avståndet objekt-skärm. 1. Ställ upp uppställningen enligt figur 9. Välj avståndet l = 90cm. Figur 9: Experimentuppställning vid fokallängdsbestämmning med Bessels metod. 2. Bestäm fokalavståndet för tre linser märkta 10, 20 och 30, genom att mäta avståndet d mellan de positioner där man får en skarp avbildning på skärmen. 11

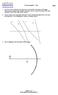
14 Härled ekvation 11 i redogörelsen. Visa också att det minsta avståndet mellan ett objekt och en skärm för skarp avbildning är 4f Grafisk metod I denna uppgift skall vi med en grafisk metod bestämma fokallängden på de tre linserna. I figur 10 avbildas ett objekt med en lins. Enligt figuren ser man att när objektet, med höjden h, är skarpt avbildat har det en bildhöjd H. h f f H b Figur 10: Avbildning av ett objekt genom en konvex lins. Med hjälp av likformiga trianglar och linsformeln så kan man visa att följande formel gäller för bildhöjden H = h f b h (12) I denna formel är b avståndet mellan lins och skärm. Vi ser att bildhöjden H är en linjär funktion av avståndet b. 1. Sätt upp experimentuppställning enligt figur 11 Figur 11: Experimentuppställning för den grafiska metoden. 12

15 2. Mät nu bildhöjden H för minst fem värde på b för alla tre linserna. I denna uppgift måste man alltså ändra avståndet mellan objekt och skärm, dvs flytta skärmen tills dess en ny skarp bild erhålls. 3. Plotta H som funktion av b i ett diagram och bestäm h och f ur skärningarna med axlarna. Härled ekvation 12 i redogörelsen. 7.4 Bestämning av fokalavståndet för en konkav spegel I denna uppgift skal vi bestämma fokalavståndet för en konkav spegel. Två olika metoder skall användas. Metod A 1.Ställ upp utrustningen enligt figuren 12 Figur 12: Experimentuppställning i uppgift 4A, metod A. (Strålarna i bilden följer inga strålgångsregler). Objektet vi skall avbilda är en belyst spaltöppning. Genom att ändra på avståndet mellan spegel och bländare och vrida något på spegeln kan vi avbilda bländaröppningen alldeles intill öppningen själv. 2. Mät avståndet mellan spegel och bländare och bestäm ur detta mätvärde spegelns fokallängd. Metod B I denna uppgift skall vi först kollimera ljuset från bländaröppningen för att sedan avbilda bländaröppningen intill linsen. För att skapa det kollimerade ljusknippet använder vi oss av en metod som kallas för autokollimering. Detta går ut på att man placerar en plan spegel 13

16 direkt efter linsen. Den plana spegeln reflekterar tillbaka ljuset genom linsen och avbildar bländaröppningen intill själva öppningen. Genom att flytta linsens läge så kan man få en perfekt avbildning av bländaröppningen. Då är ljuset efter linsen kollimerat. 1. Kollimera ljuset från bländaröppningen med en lins och en plan spegel. Figur 13: Experimentuppställning i uppgift 4B, metod B. (Strålarna i bilden följer inga strålgångsregler). 2. Låt det kollimerade ljuset istället träffa den konkava spegeln och avbilda nu bländaröppningen skarpt alldeles intill linsen (OBS ej bredvid spalten) se figur Bestäm avståndet mellan spegel och bild och bestäm ur det uppmätta värdet spegelns fokallängd. Jämför de båda metoderna. 7.5 Linssystem I denna serie av uppgifter skall vi studera avbildning genom två linser. Ett objekt som belyses av en glödlampa via en samlingslins användes. En skärm placeras l = 125cm från objektet. Avbilda objektet med lins med f = 30cm. Välj det läge som ger en förstorad bild. Lägg märke till avbildningsfelen. Prova om bilden blir bättre då man sätter in en bländare vid linsen. A. Vad är avståndet mellan objektet och L1? Vad är det teoretiska värdet enligt linsformeln. B. Placera en ny lins L2, (f=10cm) på ett avstånd 10cm från skärmen, se 14

17 Figur 14: Uppställningen som den ser ut i moment A. Figur 15: Uppställningen som den ser ut i moment B. figur 15. Justera L1 tills en bild uppstår på skärmen. C. Finns det nu flera möjliga lägen för L1 som ger en reell bild? D. Är bilden rättvänd eller upp och ner? E. Vad är avståndet objekt-l1? F. Vad är det teoretiska avståndet i fråga E? Låt L1 och L2 byta plats som i figur 16. Den slutliga bilden får nu ett annat läge, bilden hamnar alltså ej på skärmen. G. Blir den slutgiltiga bilden reell eller virtuell. (Testa genom att tillfälligt ändra skärmens position). Justera nu L2 så att en reell bild åter hamnar på skärmen. H. Finns det flera möjliga lägen för L2? I. Är bilden nu rättvänd eller upp och ned? J. Vad blir avståndet G-L2? 15

18 Figur 16: Uppställningen som den ser ut i moment F. K. Vad blir det teoretiska värdet i fråga J. Rita en strålgång över uppställningen i J. Skriv i skissen vad som är reella resp. virtuella objekt och bilder. 16