3) Sag formeln ger r=y 2 /(2s). y=a/2=15 mm, s=b c=4,5 mm ger r=25 mm. Då blir F=(n 1)/r=(1,5 1)/0,025=20 D
|
|
|
- Gustav Sandström
- för 6 år sedan
- Visningar:
Transkript
1
2 Facit: en avbildning Sfärisk gränsyta 1) l= 2,0 mm, n=4/3 och n =1. m=l/l =nl /(n l)=1,25 ger l = 1,875 mm. Avbildningsformeln för sfärisk gränsyta L =L+(n n)/r ger r= 2,5 mm. 2) Bilden måste hamna på näthinnan, så l =22,22 mm och l= 6,0 m ger L=1/ 6= 0,1667 D och L =(4/3)/0,02222=60 > m=l/l = 0, Det ger h=h /m=0,000004/0,00278=0,0014 m = 1,4 mm. 3) Sag formeln ger r=y 2 /(2s). y=a/2=15 mm, s=b c=4,5 mm ger r=25 mm. Då blir F=(n 1)/r=(1,5 1)/0,025=20 D 4) Styrka före operationen F=(1,336 1)/0,0078=43,1 D. Styrka efter operationen blir 38,1 D. Då blir krökningsradien r=(1,336 1)/38,1=0,00882 m. Sag formeln med y=3 mm ger att s före =y 2 /(2r före )=0,577 mm samt att s efter =0,510 mm. Differensen blir 67 μm. 5) F=(1,52 1)/0,2=2,6 D. L=1/ 0,15= 6,667 D. L =L+F > L = 6,667+2,6= 4,067 D. Notera att n är brytningsindex för bildrymden, trots att vi har negativ bildvergens, vilket ger l =n /L =1,52/ 4,067= 0,3738 m = 37,38 cm. Förstoring ges av m=l/l = 6,667/ 4,067=1,64, så bildstorleken blir 1,64 cm (rättvänd). 6) Sagformeln ger r= y 2 /2s= 1 m. Då blir F=(n n)/r=( 1 1)/ 1=2 D. Om l= 0,6 m blir L= 1,667 D och L =0,333 D. Det ger l = 1/0,333= 3 m. Förstoringen blir m=l/l = 1,667/0,333= 5 ggr. 7) L=1/ 0,3= 3,33 D. F=(n n)/r=( 1 1)/0,04= 50 D. L =L+F= 53,33 D Det ger bildavstånd l = 1/ 53,33=0,01875 m=18,75 mm. Bilden ligger alltså efter ytan (d.v.s. inuti glaskulan). Förstoringen blir m= 3,33/ 53,33=0,062, en förminskning. Då blir h =hm=4,2 mm. 8) F=(n n)/r=( 1 1)/0,1= 20 D. L= 10 D > L = 30 D > l =n /L = 1/ 30=0,0333 m. Förstoring blir m=l/l = 10/ 30=1/3. Bilden hamnar 3,33 cm efter spegeln och förminskas till en tredjedel och blir 1 cm stor (rättvänd). 9) F=(n n)/r=( 1 1)/ 0,15=13,33 D. L= 20 D > L = 6,67 D > l =n /L = 1/ 6,67=0,15 m. Förstoring blir m=l/l = 20/ 6,67=3. Bilden hamnar 15 cm efter spegeln och förstoras med en faktor tre till 9 cm (rättvänd). 10) F=(n n)/r= 2/0,008= 250 D. L=1/ 0,2= 5 D. L =L+F= 255 D. Det ger m= 5/ 255= 0,02, l =n /L =0,00392 l =3,92 mm. Bilden hamnar 3,92 mm inuti ögat och blir 60*0,02=1,2 mm stor.
3
4
5
6
7
8
9
10
11 19) När det inte är luft används främre fokallängd, h = tan(w )f =tan(w)f. Med F=60 D blir f= 1/60= 0,0167 m. Vinkeln 5 =5/60 =0,0833. Då blir h = 0,0167*tan(0,0833)= 0, m. 20) Förstoringen skall vara h /h=1,20/0,024=50. Det innebär att L/L = 50 (reellt objekt och reell bild innebär upp och nervänd avbildning) > L= 50L och l = 50l. Dessutom är l+l =4 (teckenkonventionen!). Det ger att 4+l= 50l > l= 0,0784 m, L= 12,75 D, L =0,255 D, med linsformeln blir F=13 D så f =0,077 m=77 mm. 21) Förstoringen är m=0,0042/ 0,21= 0,02. Halva höjden skall uppta vinkeln 15, vilket ger oss objektsavståndet. Då tan(15 )= (21/2)/l > l= 39,2 cm. Vi kan lösa ut L= 2,55 D, L =127,5 D, l =0,0078 m=7,8 mm. Linsformeln ger då f =7,6 mm. 22) Vi vet att l+l =500 mm > l =500+l. Linsformeln ger då 1/(0,5+l)=1/0,1+1/l. Detta blir en andragradsekvation som har två möjliga lösningar: l= 0,138 m och l= 0,362 m. Störst förstoring får man när objektet är nära linsen, så det första objektsavståndet ger en förstoring på 2,6. 23) Vi får att L= 10 D, L =10 D > F tot =20 D. Med F 2 =(1 1,5)/0,02= 25 D bör F 1 =45 D, och därmed r 1 =0,011 m, vilket innebär att det är en menisklins. 24) F=(n 1)(1/r 1 1/r 2 )=(1,53 1)(1/r 1 1/( 6r 1 ). Med F=5 D löses r 1 ut till 0,1237 m och därmed r 2 till 0,742 m. 25) F=(n 1)(R 1 R 2 ). Då R 2 är 0, F=5 D och n=1,62 kan vi lösa ut R 1 =8,06 D och därmed r 1 =1/ R 1 =0,124 m. 26) L= 3 D, L = 0,5 D > F=2,5 D. F=(n 1)(1/r 1 1/r 2 )= (1,52 1)(1/r 1 1/ r 1 )=2,5 gör att vi kan lösa ut r 1 =0,418 m. 27) L= 1,67 D, F= 4 D > L = 5,67 D > l = 0,176 m. Förstoring m=l/l = 1,67/ 5,67=0,295. Det ger storlek h =5*0,295=1,47 mm. 28) h'= f tan(w) > f =( )h /tan(5) > f =91 mm.
12
13
14 31) Två sfäriska gränsytor: r 1 =0,003 m, r 2 = 0,003 m, n 1 =4/3, n 1 =n 2 =1,6, n 2 =4/3. Styrkan i de båda ytorna blir (1,6 4/3)/0,003=88,89 D. Med l 1 = blir l 1 =1,6/88,89=0,018 m, l 2 =l 1 d=0,018 0,006=0,012 m, så L 2 =1,6/0,012=133,33 D, L 2 =222,22 D och l 2 =(4/3)/222,22=0,006 m. Således sitter näthinnan 6 mm efter linsen. 32) Objektet är i första linsens främre fokalplan, så mellanbilden hamnar i oändligheten. Då blir slutbilden i den andra linsens bakre fokalplan. Förstoringen blir L 1 /L 2 =4, vilket man också kan se med strålkonstruktion. 33) Strålkonstrukti on enligt figuren ger att bilden hamnar 150 mm efter den positiva linsen med förstoringen 1. Med L 1 = 20 D blir L 1 = 40 D, l 1 = 0,025 m, l 2 =l 1 d= 75 mm, L 2 = 13,33 D, L 2 =6,67 D > l 2 =150 mm. Förstoringen blir totalt (L 1 /L 1 )*(L 2 /L 2 )= 1. 34) 35) Givet l 3 = blir l 3 = 12 mm. Då l 2 =l 3 +d 2 = 12+32=20 mm > L 2 =50 D, L 2 =30 D, l 2 =0,03333 m (virtuellt objekt för andra avbildningen). Räknar vi vidare blir l 1 =l 2 +d 1 =133,33 mm och L 1 =7,5 D och L 1 =7,5 8,33= 0,83 D > l 1 = 1,2 m. 36) Givet l 3 =200 mm blir l 3 = mm. Då måste vi ha l 2 = och därmed l 2 = 10 mm. Då blir l 1 =l 2 +d 1 = 10+5= 5 mm, så lins ett ger en virtuell bild. Vi får L 1 = 200 D och därmed L 1 = 300 D så l 1 = 3,33 mm.
15
16
17
18 40) Strålkonstruktion enligt figuren ger att bilden hamnar 50 mm efter F med förstoring m= 2. Mätning ger att l= 37,5 mm och f E =25 mm. Avbildning ger L= 26,67 D, F E =40 D, L =13,33 D och därmed l =75 mm och m= 2. 41) Strålkonstruktion enligt bilden ger fokallängden 10 mm. 42) Strålkonstruktion ger f E =100 mm. 43) Först räknar vi ut ytornas brytkraft. F 1 =(n 1)/r 1 =(1,52 1)/0,0042=12,4 D och F 2 =(1 1,52)/0,15= 3,47 D. Sedan behöver vi systemets brytkraft: F E =F 1 +F 2 (d/n)f 1 F 2 =12,4 3,47 (10/1,52)*12,4*( 3,47)=9,2 D. Vi behöver även huvudplanens läge och räknar ut F v =F E /(1 (d/n)f 1 )=10,0 D och motsvarande F v =9,0 D. Det ger f v = 0,1111 m, f E = 0,1087 m (minustecken för att det är främre fokallängd), f v =0,1 m och f E =0,1087 m. Då får vi e=f v f E = 0,0024 m = 2,4 mm och e =f v f E = 0,0087 m = 8,7 mm. Då blir objektsavståndet 117,6 mm, vilket ger L= 8,5 D, L =L+F E =0,7 D och l =1,43 m. Förstoringen blir L/L = 8,5/0,7= 12 ggr.
19
20
21
22
23 förstoringsglaset och vi vill räkna ut hur den gick innan. Med l =0,4 m blir L =2,5 D och därmed L= 2,5 D så l= 0,4 m. Den synfältsbegränsande strålen skär optiska axeln 40 cm innan förstoringsglaset (och där hamnar IP). Vi får nu räkna med likformiga trianglar med den okända diametern d på förstoringsglaset, där vi vet att (40/25)*5=8 cm, vilket förstoringsglaset minst måste ha. 54) Följer vi strålarna ser vi att objektivet är AS och okularet FS. Att ögat placeras optimalt innebär att ögat placeras så att den synfältsbegränsande strålen går mitt genom ögat (därmed påverkar inte ögat synfältet). Där den synfältsbegränsande strålen går ut ur systemet kallas utträdespupill, UP. Synfältet begränsas alltså av strålen genom mitten av objektivet och kanten av okularet. Synfältsbegränsande strålen bryts ej mer innan det och vi kan direkt räkna med likformiga trianglar att synfältet blir (1000/0,135)*0,012=89 m. Vinkelförstoring och instrument 55) Vi avbildar lärarens ansikte: l= 0,3 m ger L= 3,33 D > L = 1,33 > l = 0,75 m. Bilden blir virtuell och hamnar 1,45 m från eleven. Bilden får den laterala förstoringen L/L =2,5. Synvinkel utan lins (i radianer) blir w=h/1 (där h är ansiktets storlek) och med lins w =h /1,45=2,5h/1,45=1,7h. Vinkelförstoringen blir alltså 1,7. 56) Vi antar en objektshöjd h. Avbildning ger objektsavstånd l= 0,1 m, L= 10 D. Med plan spegel är F=0 D och L = 10 D > l = 1/ 10=0,1 m, så bilden hamnar totalt 0,2 m från person och m= 10/ 10=1. Synvinkeln blir w=h/0,2=5h. Med krökt spegel blir istället F= 2/ 0,3=6,67 D och L = 3,33 D > l =0,3 m så bilden hamnar 0,4 m från personen. Förstoring blir m= 10/ 3,33=3. Således blir synvinkeln 3h/0,4. Vi kan räkna ut vinkelförstoringen som w krökt /w plan =(3h/0,4)/5h=1,5 ggr större med krökt. 57) Om betraktningsavståndet är rimligt (250 mm) blir synvinkel utan h/0,25 och synvinkel med 1,25h/0,25 (skillnaden i position är mindre än två tiondels millimeter, så avståndet är samma men bilden förstoras med den laterala förstoringen). M=w med /w utan =1,25. 58) Optisk tublängd g=d f obj f ok =160 mm. Vinkelförstoring är M=(gq)/( f obj f ok )=160*250/(4*50)=200. Synvinkel utan instrument med blodkropp på 250 mm avstånd blir i radianer h/q=32 mikroradianer. Genom mikroskopet får vi 200 ggr större = 6,4 milliradianer (0,37 grader). 59) Utan glasögon får vi anta synvinkel w. Mellanbilden hamnar i bakre fokalplanet till linsen, d.v.s. 10 cm bakom linsen och 30 cm från Gullan. Bildstorleken blir h = wf g om w är i radianer och liten. Vinkel med blir då h /0,3= wf g /0,3= w*0,1/0,3 och vinkel med/vinkel utan blir 1/3.
24 60) Med M=f objektiv /f okular =4 och f objektiv +f okular =120 mm kan vi direkt lösa ut att f objektiv =160mm och f okular = 40 mm. 61) Optimalt placerade innebär att ögat är vid UP, d.v.s. där bilden av AS i kikaren är. I kikare är objektivet AS. Kikaren har förstoringen 7 och objektivet har diametern 50 mm (det är vad märkningen står för). För teleskop och kikare gäller att D UP =D IP /M, så D UP =7,1 mm och därmed är ögat AS. Nu måste vi hitta IP, d.v.s. det objekt vars bild hamnar i ögat. Fast vi behöver inte läget, enbart diametern. För hela systemet kikare öga blev ögat AS, och därmed även UP. Fortfarande gäller att D IP =D UP *M=3*7=21 mm, vilket också är svaret. 62) Med objektshöjd h blir synvinkel med kontaktlins h/5 radianer. Avbildning i glasögat ger l= (5 0,013) och L= 0,2005 D > L = 10,2005 D och l = 0,098 m från glasögat. Avståndet till ögat blir (0,098+0,013)= 0,111 m. Mellanbilden får storlek h =(L/L )h=0,01966h. Synvinkel med blir 0,01966h/0,111=0,1771h. Kvoten mellan synvikel med och synvinkel utan blir 0,1771/0,2=0,89, vilket är vinkelförstoringen. 63) Slutbild i oändligheten betyder att mellanbilden ligger i okularets fokalplan, d.v.s. 162 mm efter lins 2. Sedan behöver vi förstoringen i objektivet. Så l 2 =0,162 > L 2 =6.17 D, F 2 =200 D > L 2 = 193,83 D > l 2 = 0,00516 m. Det är mellanbilden som skapas av lins 1, så l 1 =l 2 +d= 0, ,002= 0,00316 m och L 1 = 316,5 D > L 1 = 516,5 vilket ger oss objektsavståndet l 1 = 0,00194 eller 1,94 mm. Förstoringen i objektivet är den laterala förstoringen i avbildningen: m 1 m 2 =(L 1 /L 1 )(L 2 /L 2 )= 51. Okularet har förstoring som en lupp, d.v.s. M=F/4=40/4=10. Total förstoring i ett mikroskop är m objektiv M okular = 510 ggr. 64) Låt skålens radie vara r. Avbildning sker där l= 2r och L=n/( 2r). Skålen är en brytande sfärisk yta så F=(1 n)/( r). Då blir L = n/( 2r)+(1 n)/( r) och med n=4/3 blir l = 3r. Så totalt avstånd utan blir 3r, totalt avstånd med blir 4r. Vidare behöver vi laterala förstoringen. Den är L/L =2. Totalt blir vinkelförstoringen (2h/4r)/(h/3r)=1,5 ggr. 65) Med linsformeln beräknas L= 16,67 D > L =3,33 D > l =300 mm. Patientens korrektion skall alltså enligt korrektionsprincip lägga en bild 300 mm efter linsen i figuren. Om glasögat är placerat 14 mm innan ögat blir bildavståndet från glasögat 250 mm. Med objekt i oändligheten blir då F=1/0,25=4 D.
 Robert Rosén Recept för beräkning av huvudplan Frågeställning: Hur hittar man främre och bakre fokalpunkt, samt huvudplan (både för tjocka linser och system av tunna linser)? Varför skall huvudplan räknas?
Robert Rosén Recept för beräkning av huvudplan Frågeställning: Hur hittar man främre och bakre fokalpunkt, samt huvudplan (både för tjocka linser och system av tunna linser)? Varför skall huvudplan räknas?
Geometrisk optik. Syfte och mål. Innehåll. Utrustning. Institutionen för Fysik 2006-04-25
 Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från vänster, sträcka i ljusets riktning = positiv
 Avbildningskvalitet Föreläsning 1 2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Avbildningskvalitet Föreläsning 1 2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Föreläsning 9-10 (kap i Optics)
 38 Föreläsning 9-0 (kap 5.-5.6 i Optics) Huvudplan Önskan: Tänk om alla optiska system vore tunna linser så att L = L + F alltid gällde! Att räkna med mellanbilder genom ett system med många linser och
38 Föreläsning 9-0 (kap 5.-5.6 i Optics) Huvudplan Önskan: Tänk om alla optiska system vore tunna linser så att L = L + F alltid gällde! Att räkna med mellanbilder genom ett system med många linser och
Att räkna med mellanbilder genom ett system med många linser och gränsytor blir krångligt. Vi vill kunna avbilda genom alla ytor direkt.
 Föreläsning 9 0 Huvudplan Önskan: Tänk om alla optiska system vore tunna linser så att alltid gällde! Att räkna med mellanbilder genom ett system med många linser och gränsytor blir krångligt. Vi vill
Föreläsning 9 0 Huvudplan Önskan: Tänk om alla optiska system vore tunna linser så att alltid gällde! Att räkna med mellanbilder genom ett system med många linser och gränsytor blir krångligt. Vi vill
Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från vänster, sträcka i ljusets riktning = positiv
 Avbildningskvalitet Föreläsning 1-2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Avbildningskvalitet Föreläsning 1-2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Figur 6.1 ur Freeman & Hull, Optics
 1 Föreläsning 12 Kameran Figur 6.1 ur Freeman & Hull, Optics Kameran är ett instrument som till vissa delar fungerar mycket likt ett öga. Kamerans optik, det så kallade kameraobjektivet, motsvarar ögats
1 Föreläsning 12 Kameran Figur 6.1 ur Freeman & Hull, Optics Kameran är ett instrument som till vissa delar fungerar mycket likt ett öga. Kamerans optik, det så kallade kameraobjektivet, motsvarar ögats
LABORATION 2 MIKROSKOPET
 LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX (5) Att läsa före lab: LABORATION 2 MIKROSKOPET Synvinkel, vinkelförstoring, luppen och
LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX (5) Att läsa före lab: LABORATION 2 MIKROSKOPET Synvinkel, vinkelförstoring, luppen och
LABORATION 1 AVBILDNING OCH FÖRSTORING
 LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
Vågrörelselära & Kvantfysik, FK2002 1 december 2011
 Räkneövning 6 Vågrörelselära & Kvantfysik, FK2002 december 20 Problem 36.23 Avståndet mellan två konvexa linser i ett mikroskop, l = 7.5 cm. Fokallängden för objektivet f o = 0.8 cm och för okularet f
Räkneövning 6 Vågrörelselära & Kvantfysik, FK2002 december 20 Problem 36.23 Avståndet mellan två konvexa linser i ett mikroskop, l = 7.5 cm. Fokallängden för objektivet f o = 0.8 cm och för okularet f
LABORATION 2 MIKROSKOPET
 LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX 1 (6) LABORATION 2 MIKROSKOPET Att läsa i kursboken: sid. 189-194 Förberedelseuppgifter:
LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX 1 (6) LABORATION 2 MIKROSKOPET Att läsa i kursboken: sid. 189-194 Förberedelseuppgifter:
Föreläsning 11 (kap i Optics)
 45 Föreläsning 11 (kap 5.7-5.8 i Optics) Hittills har vi behandlat avbildningen i sig, dvs. var bilden av ett objekt hamnar och vilken förstoring det blir. Det finns också andra krav man kan ställa på
45 Föreläsning 11 (kap 5.7-5.8 i Optics) Hittills har vi behandlat avbildningen i sig, dvs. var bilden av ett objekt hamnar och vilken förstoring det blir. Det finns också andra krav man kan ställa på
Optik 1 Geometrisk och fysikalisk optik fo r optiker HT 2019
 Optik 1 Geometrisk och fysikalisk optik fo r optiker HT 2019 Optik 1 Innehållsförteckning Föreläsning 1 Vågfronter, strålar och bilder... 1 Föreläsning 2 Reflektion och brytning... 5 Föreläsning 3 Avbildning
Optik 1 Geometrisk och fysikalisk optik fo r optiker HT 2019 Optik 1 Innehållsförteckning Föreläsning 1 Vågfronter, strålar och bilder... 1 Föreläsning 2 Reflektion och brytning... 5 Föreläsning 3 Avbildning
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 34 - Optik 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Vågrörelselära och optik Kapitel 34 - Optik 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Övningstal i Avbildningskvalitet för optikerstuderande. Rita figurer och motivera ordentligt!
 Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Övningstal i Avbildningskvalitet för optikerstuderande. Rita figurer och motivera ordentligt!
 Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Teckenkonventionen: ljus in från vänster, ljusets riktning = positiv
 1 Avbildningskvalitet Föreläsning 1-2 Brytning i sfärisk yta Teckenkonventionen: ljus in från vänster, ljusets riktning = positiv Brytningslagen (Snells lag): n sin i = n sin i Paraxial approximation (vid
1 Avbildningskvalitet Föreläsning 1-2 Brytning i sfärisk yta Teckenkonventionen: ljus in från vänster, ljusets riktning = positiv Brytningslagen (Snells lag): n sin i = n sin i Paraxial approximation (vid
Vågrörelselära & Kvantfysik, FK2002 29 november 2011
 Räkneövning 5 Vågrörelselära & Kvantfysik, FK00 9 november 0 Problem 35.9 En dykare som befinner sig på djupet D 3 m under vatten riktar en ljusstråle (med infallsvinkel θ i 30 ) mot vattenytan. På vilket
Räkneövning 5 Vågrörelselära & Kvantfysik, FK00 9 november 0 Problem 35.9 En dykare som befinner sig på djupet D 3 m under vatten riktar en ljusstråle (med infallsvinkel θ i 30 ) mot vattenytan. På vilket
Laboration i Geometrisk Optik
 Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
Lösningarna inlämnas renskrivna vid laborationens början till handledaren
 Geometrisk optik Förberedelser Läs i vågläraboken om avbildning med linser (sid 227 241), ögat (sid 278 281), färg och färgseende (sid 281 285), glasögon (sid 287 290), kameran (sid 291 299), vinkelförstoring
Geometrisk optik Förberedelser Läs i vågläraboken om avbildning med linser (sid 227 241), ögat (sid 278 281), färg och färgseende (sid 281 285), glasögon (sid 287 290), kameran (sid 291 299), vinkelförstoring
Sammanfattning: Fysik A Del 2
 Sammanfattning: Fysik A Del 2 Optik Reflektion Linser Syn Ellära Laddningar Elektriska kretsar Värme Optik Reflektionslagen Ljus utbreder sig rätlinjigt. En blank yta ger upphov till spegling eller reflektion.
Sammanfattning: Fysik A Del 2 Optik Reflektion Linser Syn Ellära Laddningar Elektriska kretsar Värme Optik Reflektionslagen Ljus utbreder sig rätlinjigt. En blank yta ger upphov till spegling eller reflektion.
Tentamen i Fotonik , kl
 FAFF25-2013-08-26 Tentamen i Fotonik - 2013-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2013-08-26 Tentamen i Fotonik - 2013-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Geometrisk optik. Laboration
 ... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Geometrisk optik Linser och optiska instrument Avsikten med laborationen är att du ska få träning i att bygga upp avbildande optiska
... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Geometrisk optik Linser och optiska instrument Avsikten med laborationen är att du ska få träning i att bygga upp avbildande optiska
Övningstal i Avbildningskvalitet för optikerstuderande. Rita figurer och motivera ordentligt!
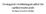 Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Studieanvisning i Optik, Fysik A enligt boken Quanta A
 Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Våglära och optik FAFF30 JOHAN MAURITSSON
 Våglära och optik FAFF30 JOHAN MAURITSSON Prismor A θ 1 n=1 n n=1 2 Prismor A δ 1 θ 1 θ 1 n=1 n n=1 3 Prismor A θ 2 θ 2 n=1 n n=1 4 Prismor A δ θ 1 θ 1 δ 1 δ 2 B θ 2 θ 2 n=1 n n=1 5 Prismor, dispersion
Våglära och optik FAFF30 JOHAN MAURITSSON Prismor A θ 1 n=1 n n=1 2 Prismor A δ 1 θ 1 θ 1 n=1 n n=1 3 Prismor A θ 2 θ 2 n=1 n n=1 4 Prismor A δ θ 1 θ 1 δ 1 δ 2 B θ 2 θ 2 n=1 n n=1 5 Prismor, dispersion
Övning 1 Dispersion och prismaeffekt
 Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du:
 Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du: A.Mer av dig själv. B.Mindre av dig själv. C.Lika mycket av dig själv. ⱱ Hur hög måste en spegel vara för att du ska
Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du: A.Mer av dig själv. B.Mindre av dig själv. C.Lika mycket av dig själv. ⱱ Hur hög måste en spegel vara för att du ska
Föreläsning 8: Linsdesign
 1 Föreläsning 8: Linsdesign Linsdesign Att välja linser med rätt krökningsradier på ytorna och av rätt material. Förutom paraxiala egenskaper såsom objekt- och bildavstånd och förstoring, så ställs andra
1 Föreläsning 8: Linsdesign Linsdesign Att välja linser med rätt krökningsradier på ytorna och av rätt material. Förutom paraxiala egenskaper såsom objekt- och bildavstånd och förstoring, så ställs andra
Exempelsamling i Ögats optik
 Exempelsamling i Ögats optik 1. Ett reducerat öga har n =1.336, F=62 och längden 26,2 mm. Vilken av följande linser fungerar bäst för a) avståndsseende och b) närarbete (0,5 m)? (i) +2 D (ii) -9 D (iii)
Exempelsamling i Ögats optik 1. Ett reducerat öga har n =1.336, F=62 och längden 26,2 mm. Vilken av följande linser fungerar bäst för a) avståndsseende och b) närarbete (0,5 m)? (i) +2 D (ii) -9 D (iii)
Mikroskopering. Matti Hotokka Fysikalisk kemi
 Mikroskopering Matti Hotokka Fysikalisk kemi Vad diskuteras Mikroskopens anatomi Sätt att belysa provet Praktiska aspekter Specialapplikationer Mikroskop Okular Objektiv Objektbord Kondensorlins Ljuskälla
Mikroskopering Matti Hotokka Fysikalisk kemi Vad diskuteras Mikroskopens anatomi Sätt att belysa provet Praktiska aspekter Specialapplikationer Mikroskop Okular Objektiv Objektbord Kondensorlins Ljuskälla
b) Calculate the dispersion in the vicinity of the Fraunhofer D line for each glass, using the Cauchy relation.
 3 Optiska instrument Uppgift 3. (Pedrotti 3 3 8) a) Approximate the Cauchy constants A and B for crown and flint glasses, using data for the C and F Fraunhofer lines from Table 3. Using these constants
3 Optiska instrument Uppgift 3. (Pedrotti 3 3 8) a) Approximate the Cauchy constants A and B for crown and flint glasses, using data for the C and F Fraunhofer lines from Table 3. Using these constants
Tentamen Optik, FYSA11, 2012-05-25
 Tentamen Otik, FYSA, 0-05-5 Hjälmedel: TEFYMA, ormelsamling, linjal, ickräknare och biogat ormelblad. Glöm inte att beskriva hur du kommer ram till dina svar. Även delvis lösta ugiter kan ge oäng.. Den
Tentamen Otik, FYSA, 0-05-5 Hjälmedel: TEFYMA, ormelsamling, linjal, ickräknare och biogat ormelblad. Glöm inte att beskriva hur du kommer ram till dina svar. Även delvis lösta ugiter kan ge oäng.. Den
Geometrisk optik. Innehåll. Inledning. Litteraturhänvisning. Förberedelseuppgifter. Geometrisk optik
 Geometrisk optik Innehåll Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande 1. Undersökning av tunna positiva linser... 3 2. Undersökning av tunna negativa linser... 3 3. Galileikikaren...
Geometrisk optik Innehåll Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande 1. Undersökning av tunna positiva linser... 3 2. Undersökning av tunna negativa linser... 3 3. Galileikikaren...
Geometrisk optik. Laboration FAFF25/FAFA60 Fotonik 2017
 Avsikten med denna laboration är att du ska få träning i att bygga upp avbildande optiska system, såsom enkla kikare och mikroskop, och på så vis få en god förståelse för dessas funktion. Redogörelsen
Avsikten med denna laboration är att du ska få träning i att bygga upp avbildande optiska system, såsom enkla kikare och mikroskop, och på så vis få en god förståelse för dessas funktion. Redogörelsen
Projektorobjektiv, MTF, aberrationer i projektorer, skärpedjup, Keystone, Scheimpflugvinkel
 Projektorobjektiv, MTF, aberrationer i projektorer, skärpedjup, Keystone, Scheimpflugvinkel Optiken till en projektor ska fylla fem funktioner i. Den ska hand om så stor del av ljuset från lampan (eller
Projektorobjektiv, MTF, aberrationer i projektorer, skärpedjup, Keystone, Scheimpflugvinkel Optiken till en projektor ska fylla fem funktioner i. Den ska hand om så stor del av ljuset från lampan (eller
λ = T 2 g/(2π) 250/6 40 m
 Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Hittills har vi bara använt sfäriska ytor, dvs delar av en sfär. Plana ytor är specialfall av sfär (oändlig krökningsradie, r= ).
 Föreläsning 5 Astigmatism Hittills har vi bara använt sfäriska ytor, dvs delar av en sfär. Plana ytor är specialfall av sfär (oändlig krökningsradie, r= ). Men det finns andra ytor än sfäriska, t.ex. Toriska
Föreläsning 5 Astigmatism Hittills har vi bara använt sfäriska ytor, dvs delar av en sfär. Plana ytor är specialfall av sfär (oändlig krökningsradie, r= ). Men det finns andra ytor än sfäriska, t.ex. Toriska
Mätning av fokallängd hos okänd lins
 Mätning av fokallängd hos okänd lins Syfte Labbens syfte är i första hand att lära sig hantera mätfel och uppnå god noggrannhet, även med systematiska fel. I andra hand är syftet att hantera linser och
Mätning av fokallängd hos okänd lins Syfte Labbens syfte är i första hand att lära sig hantera mätfel och uppnå god noggrannhet, även med systematiska fel. I andra hand är syftet att hantera linser och
Optik. Inledning. Fig. 1. Hålkameran
 Optik Inledning En stor del av den information som vi får från vår omgivning kommer till oss i form av ljus. I ögat omformas denna information till bilder som i hjärnan bearbetas och analyseras. Det sätt
Optik Inledning En stor del av den information som vi får från vår omgivning kommer till oss i form av ljus. I ögat omformas denna information till bilder som i hjärnan bearbetas och analyseras. Det sätt
v F - v c kallas dispersion
 Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Observera också att det inte går att både se kanten på fönstret och det där ute tydligt samtidigt.
 Om förstoringsglaset Du kan göra mycket med bara ett förstoringsglas! I många sammanhang i det dagliga livet förekommer linser. Den vanligast förekommande typen är den konvexa linsen, den kallas också
Om förstoringsglaset Du kan göra mycket med bara ett förstoringsglas! I många sammanhang i det dagliga livet förekommer linser. Den vanligast förekommande typen är den konvexa linsen, den kallas också
Övning 3 Fotometri. En källa som sprider ljus diffust kallas Lambertstrålare. Ex. bioduk, snö, papper.
 Övning 3 Fotometri Rymdvinkel: Ω [sr] Ω = π(1 cos(u)) πu Ω = r Ljusflöde: [lm] Ljusstyrka: I v = Ω [cd=lm/sr] u r Belysning: E v = A belyst [lx=lm/m ] Ljusemissionsförmåga: M v = A källa [lm/m ] Luminans:
Övning 3 Fotometri Rymdvinkel: Ω [sr] Ω = π(1 cos(u)) πu Ω = r Ljusflöde: [lm] Ljusstyrka: I v = Ω [cd=lm/sr] u r Belysning: E v = A belyst [lx=lm/m ] Ljusemissionsförmåga: M v = A källa [lm/m ] Luminans:
Eftersom brytningsindex n ändras med våglängden (färgen) kommer olika färger hos ljuset att brytas olika genom prismor och linser.
 Föreläsning 7 Kromatisk aberration Eftersom brytningsindex n ändras med våglängden (färgen) kommer olika färger hos ljuset att brytas olika genom prismor och linser. Dispersion: n ändras med våglängden
Föreläsning 7 Kromatisk aberration Eftersom brytningsindex n ändras med våglängden (färgen) kommer olika färger hos ljuset att brytas olika genom prismor och linser. Dispersion: n ändras med våglängden
Tentamen i Fotonik - 2014-08-26, kl. 08.00-13.00
 FAFF25-2014-08-26 Tentamen i Fotonik - 2014-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2014-08-26 Tentamen i Fotonik - 2014-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
LABORATION 6 Astigmatism och Distorsion
 LABORATION 6 Astigmatism och Distorsion Personnummer Namn Laborationen godkänd Datum Assistent 1 (5) LABORATION 6: Astigmatism och Distorsion Att läsa i kursboken: sid. 248 257, 261 266, 298 299 Förberedelseuppgifter
LABORATION 6 Astigmatism och Distorsion Personnummer Namn Laborationen godkänd Datum Assistent 1 (5) LABORATION 6: Astigmatism och Distorsion Att läsa i kursboken: sid. 248 257, 261 266, 298 299 Förberedelseuppgifter
Instuderingsfrågor extra allt
 Instuderingsfrågor extra allt För dig som vill lära dig mer, alla svaren finns inte i häftet. Sök på nätet, fråga en kompis eller läs i en grundbok som du får låna på lektion. Testa dig själv 9.1 1 Vilken
Instuderingsfrågor extra allt För dig som vill lära dig mer, alla svaren finns inte i häftet. Sök på nätet, fråga en kompis eller läs i en grundbok som du får låna på lektion. Testa dig själv 9.1 1 Vilken
Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid , ) Retinoskopet
 Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid 345-353, 358-362) Retinoskopet Utvecklat från oftalmoskopi under slutet av 1800-talet. Objektiv metod för att bestämma patientens
Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid 345-353, 358-362) Retinoskopet Utvecklat från oftalmoskopi under slutet av 1800-talet. Objektiv metod för att bestämma patientens
Tentamen i Fotonik - 2013-04-03, kl. 08.00-13.00
 FAFF25-2013-04-03 Tentamen i Fotonik - 2013-04-03, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2013-04-03 Tentamen i Fotonik - 2013-04-03, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
för M Skrivtid i hela (1,0 p) 3 cm man bryningsindex i glaset på ett 2. två spalter (3,0 p)
 Tentamen i tillämpad Våglära FAF260, 2016 06 01 för M Skrivtid 08.00 13.00 Hjälpmedel: Formelblad och miniräknare Uppgifterna är inte sorteradee i svårighetsgrad Börja varje ny uppgift på ett nytt blad
Tentamen i tillämpad Våglära FAF260, 2016 06 01 för M Skrivtid 08.00 13.00 Hjälpmedel: Formelblad och miniräknare Uppgifterna är inte sorteradee i svårighetsgrad Börja varje ny uppgift på ett nytt blad
1 AKUSTIK Håkan Wennlöf, I = P A m 2 P effekt, A arean effekten är spridd över (ofta en sfär, ljud utbreds sfärsiskt).
 AKUSTIK Håkan Wennlöf, hwennlof@kth.se Övning : Akustik. Intensitet är effekt per area I = P A [ ] W m 2 P effekt, A arean effekten är spridd över (ofta en sfär, ljud utbreds sfärsiskt). För ljudvåg gäller
AKUSTIK Håkan Wennlöf, hwennlof@kth.se Övning : Akustik. Intensitet är effekt per area I = P A [ ] W m 2 P effekt, A arean effekten är spridd över (ofta en sfär, ljud utbreds sfärsiskt). För ljudvåg gäller
Föreläsning 2 (kap , 2.6 i Optics)
 5 Föreläsning 2 (kap 1.6-1.12, 2.6 i Optics) Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen
5 Föreläsning 2 (kap 1.6-1.12, 2.6 i Optics) Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen
Optik. Läran om ljuset
 Optik Läran om ljuset Vad är ljus? Ljus är en form av energi. Ljus är elektromagnetisk strålning. Energi kan inte försvinna eller nyskapas. Ljuskälla Föremål som skickar ut ljus. I alla ljuskällor sker
Optik Läran om ljuset Vad är ljus? Ljus är en form av energi. Ljus är elektromagnetisk strålning. Energi kan inte försvinna eller nyskapas. Ljuskälla Föremål som skickar ut ljus. I alla ljuskällor sker
Laboration i Geometrisk Optik
 Laboration i Geometrisk Optik Stockholms Universitet 2014 Kontakt: olga. b ylund@ysik.su.se Instruktioner ör redogörelse ör laboration 1: Laboration 1 innehåller em experiment. Varje experiment bör presenteras
Laboration i Geometrisk Optik Stockholms Universitet 2014 Kontakt: olga. b ylund@ysik.su.se Instruktioner ör redogörelse ör laboration 1: Laboration 1 innehåller em experiment. Varje experiment bör presenteras
Intromatte för optikerstudenter 2018
 Intromatte för optikerstudenter 018 Rabia Akan rabiaa@kth.se Av Robert Rosén (01). Ändringar av Daniel Larsson, Jakob Larsson, Emelie Fogelqvist, Simon Winter och Rabia Akan (01-017). Kursmål Efter intromatten
Intromatte för optikerstudenter 018 Rabia Akan rabiaa@kth.se Av Robert Rosén (01). Ändringar av Daniel Larsson, Jakob Larsson, Emelie Fogelqvist, Simon Winter och Rabia Akan (01-017). Kursmål Efter intromatten
Intromatte för optikerstudenter
 Intromatte för optikerstudenter Av Robert Rosén (2012). Ändringar av Daniel Larsson (2013). Ändringar av Jakob Larsson och Emelie Fogelqvist (2014). Kursmål Efter intromatten vill vi att du inom matematik
Intromatte för optikerstudenter Av Robert Rosén (2012). Ändringar av Daniel Larsson (2013). Ändringar av Jakob Larsson och Emelie Fogelqvist (2014). Kursmål Efter intromatten vill vi att du inom matematik
Intromatte för optikerstudenter
 Intromatte för optikerstudenter Av Robert Rosén (2012). Ändringar av Daniel Larsson, Jakob Larsson, Emelie Fogelqvist och Simon Winter (2013 2016). Kursmål Efter intromatten vill vi att du inom matematik
Intromatte för optikerstudenter Av Robert Rosén (2012). Ändringar av Daniel Larsson, Jakob Larsson, Emelie Fogelqvist och Simon Winter (2013 2016). Kursmål Efter intromatten vill vi att du inom matematik
LABORATION 5 Aberrationer
 LABORATION 5 Aberrationer Personnuer Nan Laborationen godkänd Datu Assistent Kungliga Tekniska högskolan BIOX 1 (5) LABORATION 5: ABERRATIONER Att läsa i kursboken: sid. 233-248, 257-261, 470-472, 480-485,
LABORATION 5 Aberrationer Personnuer Nan Laborationen godkänd Datu Assistent Kungliga Tekniska högskolan BIOX 1 (5) LABORATION 5: ABERRATIONER Att läsa i kursboken: sid. 233-248, 257-261, 470-472, 480-485,
Optisk bänk En Virtuell Applet Laboration
 Optisk bänk En Virtuell Applet Laboration Bildkonstruktion med linser. Generell Applet Information: 1. Öppna en internet läsare och öppna Optisk Bänk -sidan (adress). 2. Använd FULL SCREEN. 3. När applet:en
Optisk bänk En Virtuell Applet Laboration Bildkonstruktion med linser. Generell Applet Information: 1. Öppna en internet läsare och öppna Optisk Bänk -sidan (adress). 2. Använd FULL SCREEN. 3. När applet:en
Kikaren. Synvinkel. Kepler och Galileikikare. Vinkelförstoring. Keplerkikaren. Keplerkikaren FAF260. Lars Rippe, Atomfysik/LTH 1
 Kikaren Synvinkel Ökar synvinkeln os avlägsna objekt 1 2 Vinkelörstoring Deinition: med optiskt instrument G utan optiskt instrument Kepler oc Galileikikare Avlägsna objekt (t. ex. med kikare): synvinkeln
Kikaren Synvinkel Ökar synvinkeln os avlägsna objekt 1 2 Vinkelörstoring Deinition: med optiskt instrument G utan optiskt instrument Kepler oc Galileikikare Avlägsna objekt (t. ex. med kikare): synvinkeln
Fysik A A B C D. Sidan 1 av 9 henrik.gyllensten@tabyenskilda.se. www.tabyenskilda.se/fy
 www.tabyenskilda.se/y ÖÖvvnni iinn ggssuuppppggi ii teer 1. Lars lyser med en icklampa mot ett prisma. Han kan då se ett spektrum på väggen bakom prismat. Spektrumet innehåller alla ärger. Vilken av dessa
www.tabyenskilda.se/y ÖÖvvnni iinn ggssuuppppggi ii teer 1. Lars lyser med en icklampa mot ett prisma. Han kan då se ett spektrum på väggen bakom prismat. Spektrumet innehåller alla ärger. Vilken av dessa
Vågfysik. Geometrisk optik. Knight Kap 23. Ljus. Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion)
 Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t 2π T x. s(x,t) = 2 cos [2π (0,4x/π t/π)+π/3]
![TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t 2π T x. s(x,t) = 2 cos [2π (0,4x/π t/π)+π/3] TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t 2π T x. s(x,t) = 2 cos [2π (0,4x/π t/π)+π/3]](/thumbs/94/118804794.jpg) TFEI0: Vågfysik Tentamen 14100: Svar och anvisningar Uppgift 1 a) Vågen kan skrivas på formen: vilket i vårt fall blir: s(x,t) =s 0 sin t π T x + α λ s(x,t) = cos [π (0,4x/π t/π)+π/3] Vi ser att periodtiden
TFEI0: Vågfysik Tentamen 14100: Svar och anvisningar Uppgift 1 a) Vågen kan skrivas på formen: vilket i vårt fall blir: s(x,t) =s 0 sin t π T x + α λ s(x,t) = cos [π (0,4x/π t/π)+π/3] Vi ser att periodtiden
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
LABORATION 5 Aberrationer
 LABORATION 5 Aberrationer Personnuer Nan Laborationen godkänd Datu Assistent Kungliga Tekniska högskolan BIOX 1 (5) LABORATION 5: ABERRATIONER Att läsa i kursboken: sid. 233-248, 257-261, 470-472, 480-485,
LABORATION 5 Aberrationer Personnuer Nan Laborationen godkänd Datu Assistent Kungliga Tekniska högskolan BIOX 1 (5) LABORATION 5: ABERRATIONER Att läsa i kursboken: sid. 233-248, 257-261, 470-472, 480-485,
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
Geometrisk optik F7 Reflektion och brytning F8 Avbildning med linser och speglar. Optiska system optiska instrument. Avbildning.
 Geometrisk optik F7 Relektion oc brytning F8 Avbildning med linser oc speglr F9 Optisk instrument 1 2 Avbildning i särisk ytor, tunn linser oc speglr Avbildning Linsormeln ger vbildning melln punkter på
Geometrisk optik F7 Relektion oc brytning F8 Avbildning med linser oc speglr F9 Optisk instrument 1 2 Avbildning i särisk ytor, tunn linser oc speglr Avbildning Linsormeln ger vbildning melln punkter på
Assistent: Markku Jääskeläinen Laborationen utfördes: 23 februari 2000
 Labrapport: Holografi Assistent: Markku Jääskeläinen Laborationen utfördes: 23 februari 2000 28 februari 2000 Sida 1 Inledning Labrapport: Holografi Teorin för holografi utvecklades redan 1948. Först när
Labrapport: Holografi Assistent: Markku Jääskeläinen Laborationen utfördes: 23 februari 2000 28 februari 2000 Sida 1 Inledning Labrapport: Holografi Teorin för holografi utvecklades redan 1948. Först när
Aquafloat 7x50 WP Compass
 Vattentät 7x50 kikare med kompass Artikel 102849 Aquafloat 7x50 WP Compass Instruktion för användning och underhåll Manual Artikel 102849 Uppdaterad Focus Nordic AB Box 55026 400 52 GÖTEBORG INNEHÅLL Allmän
Vattentät 7x50 kikare med kompass Artikel 102849 Aquafloat 7x50 WP Compass Instruktion för användning och underhåll Manual Artikel 102849 Uppdaterad Focus Nordic AB Box 55026 400 52 GÖTEBORG INNEHÅLL Allmän
AstroSwedens mikroskopskola - nybörjarmikroskopi. AstroSwedens mikroskopiskola att använda mikroskop
 AstroSwedens mikroskopiskola att använda mikroskop Fenomenet aberration. Varför mikroskop? En ensam lins kan förstora maximalt c:a 5-0 gånger. Ofta slipas dessa linser så enkelt som möjligt vilket gör
AstroSwedens mikroskopiskola att använda mikroskop Fenomenet aberration. Varför mikroskop? En ensam lins kan förstora maximalt c:a 5-0 gånger. Ofta slipas dessa linser så enkelt som möjligt vilket gör
Tillämpad vågrörelselära FAF260. Svängningar genererar vågor - Om en svängande partikel är kopplad till andra partiklar uppkommer vågor
 FF60 Tillämpad vågrörelselära FF60 Karaktäristiskt för periodiska svängningar är att det finns en återförande kraft riktad mot jämviktsläget y 0 F F F k y F m a 4 Svängningar genererar vågor - Om en svängande
FF60 Tillämpad vågrörelselära FF60 Karaktäristiskt för periodiska svängningar är att det finns en återförande kraft riktad mot jämviktsläget y 0 F F F k y F m a 4 Svängningar genererar vågor - Om en svängande
Tentamen i Fotonik , kl
 FAFF25-2015-03-20 Tentamen i Fotonik - 2015-03-20, kl. 14.00-19.15 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2015-03-20 Tentamen i Fotonik - 2015-03-20, kl. 14.00-19.15 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material?
 1 Föreläsning 2 Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen på samma sida är reflekterat
1 Föreläsning 2 Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen på samma sida är reflekterat
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 1 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus kan ses so elektroagnetiska vågor so rör sig fraåt. När vi ritar strålar
1 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus kan ses so elektroagnetiska vågor so rör sig fraåt. När vi ritar strålar
7:1 Skala. Arbetsblad. 4 cm. 2 cm. 12 cm. 3 cm. 9 cm Skala 1:3. 10 cm. Skala 1:5. Skala 1:9. ex. Skala 1:20
 :1 Skala Förminska 1 a) Hur lång är spiken i naturlig storlek? 4 cm b) Hur lång blir spiken i skala 1:2? 2 cm Skala 1:1 Skala 1:1 2 a) Hur lång är masken i naturlig storlek? b) Hur lång blir masken i skala
:1 Skala Förminska 1 a) Hur lång är spiken i naturlig storlek? 4 cm b) Hur lång blir spiken i skala 1:2? 2 cm Skala 1:1 Skala 1:1 2 a) Hur lång är masken i naturlig storlek? b) Hur lång blir masken i skala
fredag den 11 april 2014 M I N P O O L
 M I N P O O L http://en.wikipedia.org/wiki/file:backyardpool.jpg MIN FÖRSTA KLADD Min första kladd så kladda jag lite och då hade inte jag riktigt förstått uppgiften så jag bara kladda lite runt men det
M I N P O O L http://en.wikipedia.org/wiki/file:backyardpool.jpg MIN FÖRSTA KLADD Min första kladd så kladda jag lite och då hade inte jag riktigt förstått uppgiften så jag bara kladda lite runt men det
Förklara dessa begrepp: Ackommodera Avbildning, Brytning Brytningslagen Brytningsindex Brytningsvinkel Brännvidd Diffus och regelbunden reflektion
 Förklara dessa begrepp: Ackommodera, ögats närinställning, är förmågan att förändra brytkraften i ögats lins. Ljus från en enda punkt på ett avlägset objekt och ljus från en punkt på ett närliggande objekt
Förklara dessa begrepp: Ackommodera, ögats närinställning, är förmågan att förändra brytkraften i ögats lins. Ljus från en enda punkt på ett avlägset objekt och ljus från en punkt på ett närliggande objekt
Laboration i Geometrisk Optik
 Laboration i Geometrisk Optik Stockholms Universitet 2011 Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och relektionslagen 2 4 Linser 2 4.1 Att rita strålgångar........................
Laboration i Geometrisk Optik Stockholms Universitet 2011 Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och relektionslagen 2 4 Linser 2 4.1 Att rita strålgångar........................
Frågor av tentakaraktär för Vågor och Partiklar SK1131
 Frågor av tentakaraktär för Vågor och Partiklar SK1131 1. En halvledarlaser har 3 longitudinella moder (våglängder) separerade med 1 nm kring 1550 nm. Laserstrålen belyser ett diffraktionsgitter (reflexion,
Frågor av tentakaraktär för Vågor och Partiklar SK1131 1. En halvledarlaser har 3 longitudinella moder (våglängder) separerade med 1 nm kring 1550 nm. Laserstrålen belyser ett diffraktionsgitter (reflexion,
Tentamen i Optik FFY091
 Tentamen i Optik FFY091 Fredag 17 april 2015, kl. 14:00-18:00 (VV) Examinator och jourhavande lärare: Jörgen Bengtsson, tel. 0730-302737, finns på plats ca kl 15 och 17 för att svara på frågor. Tillåtna
Tentamen i Optik FFY091 Fredag 17 april 2015, kl. 14:00-18:00 (VV) Examinator och jourhavande lärare: Jörgen Bengtsson, tel. 0730-302737, finns på plats ca kl 15 och 17 för att svara på frågor. Tillåtna
E-strängen rör sig fyra gånger så långsamt vid samma transversella kraft, accelerationen. c) Hur stor är A-strängens våglängd?
 Problem. Betrakta en elgitarr. Strängarna är 660 mm långa. Stämningen är E-A-d-g-b-e, det vill säga att strängen som ger tonen e-prim (330 Hz) ligger två oktav högre i frekvens än E-strängen. Alla strängar
Problem. Betrakta en elgitarr. Strängarna är 660 mm långa. Stämningen är E-A-d-g-b-e, det vill säga att strängen som ger tonen e-prim (330 Hz) ligger två oktav högre i frekvens än E-strängen. Alla strängar
1. Betrakta en plan harmonisk elektromagnetisk våg i vakuum där det elektriska fältet E uttrycks på följande sätt (i SI-enheter):
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
Vi är beroende av ljuset för att kunna leva. Allt liv på jorden skulle ta slut och jordytan skulle bli öde och tyst om vi inte hade haft ljus.
 Källa: Fysik - Kunskapsträdet Vi är beroende av ljuset för att kunna leva. Allt liv på jorden skulle ta slut och jordytan skulle bli öde och tyst om vi inte hade haft ljus. Ljusets natur Ljusets inverkan
Källa: Fysik - Kunskapsträdet Vi är beroende av ljuset för att kunna leva. Allt liv på jorden skulle ta slut och jordytan skulle bli öde och tyst om vi inte hade haft ljus. Ljusets natur Ljusets inverkan
OPTIK läran om ljuset
 OPTIK läran om ljuset Vad är ljus Ljuset är en form av energi Ljus är elektromagnetisk strålning som färdas med en hastighet av 300 000 km/s. Ljuset kan ta sig igenom vakuum som är ett utrymme som inte
OPTIK läran om ljuset Vad är ljus Ljuset är en form av energi Ljus är elektromagnetisk strålning som färdas med en hastighet av 300 000 km/s. Ljuset kan ta sig igenom vakuum som är ett utrymme som inte
Geometrisk optik F7 Reflektion och brytning F8 Avbildning med linser och speglar. Optiska system optiska instrument. Avbildning. Parallella strålar
 Optisk system optisk instrument Geometrisk optik F7 elektion oc rytning F8 Avildning med linser oc speglr Optisk system F9 Optisk instrument 1 2 Optisk system optisk instrument epetition: Avildning i särisk
Optisk system optisk instrument Geometrisk optik F7 elektion oc rytning F8 Avildning med linser oc speglr Optisk system F9 Optisk instrument 1 2 Optisk system optisk instrument epetition: Avildning i särisk
WALLENBERGS FYSIKPRIS
 WALLENBERGS FYSIKPRIS KVALIFICERINGS- OCH LAGTÄVLING 7 januari 0 SVENSKA FYSIKERSAMFUNDET LÖSNINGSFÖRSLAG. (a) Falltiden fås ur (positiv riktning nedåt) s v 0 t + at t s 0 a s,43 s. 9,8 (b) Välj origo
WALLENBERGS FYSIKPRIS KVALIFICERINGS- OCH LAGTÄVLING 7 januari 0 SVENSKA FYSIKERSAMFUNDET LÖSNINGSFÖRSLAG. (a) Falltiden fås ur (positiv riktning nedåt) s v 0 t + at t s 0 a s,43 s. 9,8 (b) Välj origo
Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00
 FAFF25-2014-04-25 Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2014-04-25 Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Ovanstående figure beskriver ögonens konvergens vid två olika objektsavstånd (blått fall och grönt fall). Geometrin ger: 2 L
 3D-seende och 3D-visualisering Människans avståndsuppfattning bigger på flera olika stimuli från synsinnet. Det primära är emellertid konvergensen, dvs hur mycket ögonen behöver vinklas (skela), för att
3D-seende och 3D-visualisering Människans avståndsuppfattning bigger på flera olika stimuli från synsinnet. Det primära är emellertid konvergensen, dvs hur mycket ögonen behöver vinklas (skela), för att
Laboration i Geometrisk Optik
 Laboration i Geometrisk Optik Stockholms Universitet 2002 Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och relektionslagen 2 4 Linser 2 4.1 Att rita strålgångar........................
Laboration i Geometrisk Optik Stockholms Universitet 2002 Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och relektionslagen 2 4 Linser 2 4.1 Att rita strålgångar........................
Elevlaborationer Bordsoptik laser Art.nr: 54624
 Elevlaborationer Bordsoptik laser Art.nr: 54624 Laser En laserstråle är speciell på flera sätt den består av en enda färg, t.ex. röd eller grön. ljuset går nästan helt parallellt (utan att sprida ut sig).
Elevlaborationer Bordsoptik laser Art.nr: 54624 Laser En laserstråle är speciell på flera sätt den består av en enda färg, t.ex. röd eller grön. ljuset går nästan helt parallellt (utan att sprida ut sig).
Vågrörelselära, akustik och optik. Lösningsförslag till räkneuppgifter
 Vågrörelselära, akustik och optik. Lösningsförslag till räkneuppgifter Jonas Persson 5 juli 2007 Förord Som författare försöker man att anpassa sig till läsarna och presentera materialet på ett så lättläst
Vågrörelselära, akustik och optik. Lösningsförslag till räkneuppgifter Jonas Persson 5 juli 2007 Förord Som författare försöker man att anpassa sig till läsarna och presentera materialet på ett så lättläst
Övning 9 Tenta från Del A. Vägg på avståndet r = 2.0 m och med reflektansen R = 0.9. Lambertspridare.
 Övning 9 Tenta från 2016-08-24 Del A 1.) Du lyser med en ficklampa rakt mot en vit vägg. Vilken luminans får väggen i mitten av det belysta området? Ficklampan har en ljusstyrka på 70 cd och du står 2.0
Övning 9 Tenta från 2016-08-24 Del A 1.) Du lyser med en ficklampa rakt mot en vit vägg. Vilken luminans får väggen i mitten av det belysta området? Ficklampan har en ljusstyrka på 70 cd och du står 2.0
FAFF30 2013-03-21. Johan Mauritsson 1. Optiska system - optiska instrument Vetenskapsteori. Våglära och optik. Optiska system - optiska instrument
 Våglär oc optik Optisk system - optisk instrument Vetenskpsteori FAFF3 JOHAN MAURITSSON 2 Optisk system - optisk instrument Men örst Quiz Ögt Kmern Luppen Vinkelörstoring Mikroskopet Kikren Bländre oc
Våglär oc optik Optisk system - optisk instrument Vetenskpsteori FAFF3 JOHAN MAURITSSON 2 Optisk system - optisk instrument Men örst Quiz Ögt Kmern Luppen Vinkelörstoring Mikroskopet Kikren Bländre oc
Repetition Ljus - Fy2!!
 Repetition Ljus - Fy2 Egenskaper ör : Ljus är inte en mekanisk vågrörelse. Den tar sig ram utan problem även i vakuum och behöver alltså inget medium. Exakt vilken typ av vågrörelse är återkommer vi till
Repetition Ljus - Fy2 Egenskaper ör : Ljus är inte en mekanisk vågrörelse. Den tar sig ram utan problem även i vakuum och behöver alltså inget medium. Exakt vilken typ av vågrörelse är återkommer vi till
Föreläsning 9 10: Bildkvalitet (PSF och MTF)
 1 Föreläsning 9 10: Bildkvalitet (PSF och MTF) Att mäta bildkvalitet Bildkvaliteten påverkas av både aberrationer och diffraktion, men hur ska vi mäta den? Enklast är att avbilda ett objekt beskriva hur
1 Föreläsning 9 10: Bildkvalitet (PSF och MTF) Att mäta bildkvalitet Bildkvaliteten påverkas av både aberrationer och diffraktion, men hur ska vi mäta den? Enklast är att avbilda ett objekt beskriva hur
Optik, F2 FFY091 TENTAKIT
 Optik, F2 FFY091 TENTAKIT Datum Tenta Lösning Svar 2005-01-11 X X 2004-08-27 X X 2004-03-11 X X 2004-01-13 X 2003-08-29 X 2003-03-14 X 2003-01-14 X X 2002-08-30 X X 2002-03-15 X X 2002-01-15 X X 2001-08-31
Optik, F2 FFY091 TENTAKIT Datum Tenta Lösning Svar 2005-01-11 X X 2004-08-27 X X 2004-03-11 X X 2004-01-13 X 2003-08-29 X 2003-03-14 X 2003-01-14 X X 2002-08-30 X X 2002-03-15 X X 2002-01-15 X X 2001-08-31
MLBINO MLBINO BIFO. Binokulär läsning på kort avstånd. Bifocal ML Bino. Vår instegsmodell
 MLBINO Binokulär läsning på kort avstånd ADDItionsomfång: +4 till +20 dioptrier Synfält: 70º total Vikt: 26 34 gram läsavstånd: 25 8 cm Genom att titta på något på kortare avstånd kommer bilden på näthinnan
MLBINO Binokulär läsning på kort avstånd ADDItionsomfång: +4 till +20 dioptrier Synfält: 70º total Vikt: 26 34 gram läsavstånd: 25 8 cm Genom att titta på något på kortare avstånd kommer bilden på näthinnan
Tentamen i Fysik våglära, optik och atomfysik (FAF220),
 KURSLABORATORIET I FYSIK, LTH Tentamen i Fysik våglära, optik och atomfysik (FAF0), 0503 TID: 0503, KL. 3 HJÄLPMEDEL: UTDELAT FORMELBLAD, GODKÄND RÄKNARE. OBS. INGA LÖSBLAD! LÖSNINGAR: BÖRJA VARJE NY UPPGIFT
KURSLABORATORIET I FYSIK, LTH Tentamen i Fysik våglära, optik och atomfysik (FAF0), 0503 TID: 0503, KL. 3 HJÄLPMEDEL: UTDELAT FORMELBLAD, GODKÄND RÄKNARE. OBS. INGA LÖSBLAD! LÖSNINGAR: BÖRJA VARJE NY UPPGIFT
