Ljus, Lasrar och Optik - Skolpaket
|
|
|
- Johannes Abrahamsson
- för 8 år sedan
- Visningar:
Transkript
1 Ljus, Lasrar och Optik - Skolpaket
2 Skolpaketes innehåll: 1 rött laserblock, 635nm, <1mW 1 grönt laserblock, 532nm, <1mW 1 ljusblockset (röd, grön, blå) 1 vit LED 1 set med 3 frostade glaslinser 10 gradskivor 10 diffraktionsgitter 500 linjer/mm 3 speglar 3 spegelhållare 1 påse röda, gröna och genomskinnliga gummibjörnar 1 spruta 1 aktivitetsguide Lektionsförteckning : LEKTIONSTITEL ÅRSKURS/NIVÅ TID 1. Monokromatiskt ljus 7-9, gymnasiet 30 minuter 2. Kollimerat ljus 7-9, gymnasiet minuter 3. Koherent ljus 7-9, gymnasiet minuter 4. Absorption transmission, reflektion och gummibjörnar gymnasiet minuter 5. Lasermikroskop 4-9, gymnasiet minuter 6. Reflektion och brytning 4-9, gymnasiet minuter 7. Färgseparation och blandning minuter 8. Mätning av laserns våglängd gymnasiet minuter 9. Mätning av tjockleken på ett hårstrå med laser gymnasiet minuter
3 Lektion ett: Monokromatiskt ljus Sammanfattning Genom att jämföra spektrumet av vitt ljus med färgat LED-ljus samt laserljus, kommer eleverna att observera att laserljuset är monokromatiskt och består av en enda våglängd (färg). Tid: 30 minuter Nivå: 7-9, gymnasiet Material * ett ljusblockset (röd, grön, blå) med slitslock * ett rött och ett grönt laserblock * flera vita ljuskällor (LED, ficklampor, taklampor) * 10 stycken diffraktionsgitter Förberedelser 1. Ställ ljusblocken längst fram i klassrummet, riktade mot eleverna så att de kan se ljuset när du tänder dessa (senare) 2. Ställ lasrarna så att de emitterar sitt ljus BORT från eleverna och istället lyser på en vägg när du sätter på dem (senare) 3. Dela ut ett diffraktionsgitter till varje elev Diskussion och bakgrund Be eleverna att dela med sig av sina svar på frågan: Hur skiljer sig laserljus från annat ljus? Vad är det som gör en laser till just en laser? Utan att kommentera eller korrigera, skriv upp elevernas svar på tavlan synligt för alla. Om du kommer att fortsätta någon annan dag, skriv gärna upp dessa svar även på papper t.ex. Introducera lektionen genom att tala om för eleverna att de idag kommer att undersöka en egenskap hos laserljus. Tala inte om vilken egenskap som avses. Vi ska se om eleverna kan benämna denna egenskap genom att undersöka och observera.
4 Undersökning och observationer 1. Påminn eleverna att vitt ljus består av alla våglängder av ljus vitt ljus är vad vi ser när dessa olika våglängder av ljus detekteras samtidigt i våra ögon (i lagom proportion). 2. Introducera diffrationsgittret förklara att ett diffraktionsgitter separerar ljuset vi ser igenom det så att vi ser ett spektrum en unik signatur av våglängderna som ingår i ljuset vi ser på. 3. Demonstrera för eleverna om hur man använder diffrationsgittret; håll upp gittret vid ena ögat och titta emot en ljuskälla (OBS! titta ALDRIG rakt emot solen eller rakt in i en laser) titta nu åt sidan för att observera spektrumet. 4. Be eleverna att öva på att leta upp spektra från de olika tillgängliga vita ljuskällorna lysrör, glödlampor, en ficklampa t.ex. 5. Be eleverna att beskriva vad de ser en regnbåge. Be dem berätta vilka färger de ser, och i vilken ordning de syns. Be dem att berätta ifall färgerna är i samma ordning för alla ljuskällor eller om det varierar. Försäkra dig om att de kommer fram till att färgen lila alltid är närmast själva ljuskällan. 6. Berätta nu att eleverna ska observera ljusspektra från olika färgade LED källor. Sätt på ljusblocken och be eleverna att observera att det finns ett rött, ett grönt och ett blått ljusblock som innehåller en röd, en grön och en blå LED. 7. Be eleverna förutspå vad de kommer att se när de tittar på LED-ljusblocket. Kommer de att se ett spektrum? Eller bara en färg? Består LED-ljuset av flera våglängder, likt vitt ljus, eller är det bara en vånglängd? Be en elev som förutspår att de kommer att se ett spektrum att dela med sig av sitt resonemang. Likaså för en som förutspår inget spektrum. 8. Utan att kommentera eller korrigera be eleverna att själva se efter genom att använda diffraktionsgittret för att observera LED-ljuset från de röda, gröna och blåa ljusblocken. Eleverna kan behöva komma närmare för att kunna se ordentligt. 9. Be eleverna att dela med sig av sina observationer och förklara att även rött, grönt eller blått LED-ljus består av sina egna unika våglängder. 10. Till slut, be eleverna att förutspå av de kommer att se när de tittar på ljuset från den gröna och den röda lasern. Be eleverna att dela med sig av sina svar och resonemang. 11. Sätt på lasrarna riktade BORT från eleverna, och istället mot väggen. 12. Tala om för eleverna att de ALDRIG får titta direkt in i NÅGON laser NÅGONSIN! 13. Berätta för eleverna att de kommer att observera laserljusets spektrum genom att låta laserljuset passera genom diffraktionsgittret. 14. Placera diffrationsgittret framför varje laser och låt eleverna observera att det bara finns en enda färg även efter att diffrationsgittret har fått separera laserljuset. 15. Be eleverna att dela med sig och spekulera kring vad de ser. 16. Fråga Alltså vad är det för speciell egenskap hos laserljuset som vi har observerat idag? EN FÄRG, EN VÅGLÄNGD eller MONOKROMATISKT!!
5 Lektion två: Kollimerat ljus Sammanfattning By comparing LED light to LASER light, students will observe that LASER light is collimated (travels in parallel rays) Tid: minuter Nivå: 7-9, gymnasiet Material ett grönt laserblock ett rött laserblock ett grönt ljusblock med slitslocket borttaget ett rött ljusblock med slitslocket borttaget en linjal vitt papper Diskussion och bakgrund Berätta för eleverna att de kommer att observera en grundläggande egenskap hos laserljus idag en egenskap som gör lasrar mycket farligare och kraftfulla än andra ljuskällor de är vana vid även när lasers skickar ut väldigt lite effekt i stil med lasrarna som du har med dig (laserblocken). Laserljus är kollimerat strålarna är parallella med varandra. Jämför med vanligt ljus, som sprids ut eller divergerar när det utbreder sig. Den här lektionen demonstrerar resultatet av kollimering. Förberedelser 1. Dela upp eleverna i grupper om 5 2. Ge varje grupp en ljuskälla (antingen ett ljusblock eller ett laserblock), en linjal och ett ark vitt papper 3. Under tiden som eleverna samlar data, rita upp följande tabell på tavlan eller ett stort vitt papper längst fram i rummet.
6 Undersökning och observationer 1. Berätta för eleverna att de kommer att mäta ytan (arean) på ljuset som deras ljuskälla producerar på 3 olika avstånd från källan: 5, 10 och 15 cm. 2. Be eleverna att skriva ner formeln för ytan av: a. en rektangel: arean = b h (där b är bredden och h är höjden på rektangeln) b. en cirkel: arean = π r r = π r 2 (där r är radien på cirkeln) c. an ellips: arean = π A B (där A och B är stor- respektive lillaxelns längd på ellipsen, se figuren bredvid) 3. Be eleverna att lysa med sina ljuskällor på ett tomt vitt papper från olika avstånd (5, 10 och 15 cm) och beräkna ytan på fläcken med ljus vid varje avstånd. 4. Be en elev från varje grupp att komma fram och lägga in deras grupps data i tabellen. 5. Fråga klassen vad lägger ni märke till? Hur skiljer sig laserljuset från LED-ljuset? Det är kollimerat!
7 Datablad för elever Ljuskälla Avstånd Yta Röd LED 5 cm Grön LED 5 cm Blå LED 5 cm Grön LASER 5 cm Röd LASER 5 cm Röd LED 10 cm Grön LED 10 cm Blå LED 10 cm Grön LASER 10 cm Röd LASER 10 cm Röd LED 15 cm Grön LED 15 cm Blå LED 15 cm Röd LASER 15 cm Grön LED 15 cm
8 Lektion tre: Koherent ljus Sammanfattning: Genom att jämföra LED-ljus med laserljus kommer eleverna att observer att laserljus är koherent (utbreder sig i fas, eller i takt ). Tid: minuter Nivå: 7-9, gymnasiet Material ett grönt laserblock ett rött laserblock ett grönt ljusblock med slitslocket borttaget ett rött ljusblock med slitslocket borttaget vitt papper Förberedelser 1. Dela in eleverna i grupper om 4 2. Ge varje grupp en ljuskälla (antingen ett ljusblock eller ett laserblock), en linjal och ett ark vitt papper Diskussion och bakgrund Laserljus är koherent vilket betyder att det är i fas eller i takt. Detta betyder att alla ljusvågens toppar och dalar blir upplinjerade med varandra. Rita ett diagram på tavlan för att demonstrera:
9 Undersökning och observationer 1. Be varje grupp att hålla sin ljuskälla väldigt nära papperet, vid en liten vinkel, och observer vad de ser. Be dem diskutera med varandra och komma överens om en observation som de skriver ner. 2. Se till att grupperna byter ljuskälla med en annan grupp nu om gruppen hade en LED bör de nu få en laser om de hade en laser bör de nu få en LED. Be eleverna att upprepa steg ett med sina nya ljuskällor och jämföra. 3. Det som eleverna borde observera är ett speckelmönster med laserljuset och inget speckelmönster med LED-ljuset. De kan behöva en del vägledning och/eller skicka ljuskällan fram och tillbaka mellan grupperna några gånger för att lägga märke till den subtila skillnaden. 4. Förklara att ljus utbreder sig som vågor när vågorna är i fas (koherenta) kan de interferera med varandra på ett särskilt sätt. Koherenta vågor kan släcka ut varandra (destruktiv interferens) eller förstärka varandra (konstruktiv interferens). 5. Ett mönster av ljusa och mörka fläckar (väldigt, väldigt små) produceras av det koherenta laserljuset tack vare denna interferens men detta mönster produceras inte av LED-ljuset på grund av att LED-ljuset inte är koherent, eller i fas.
10 Lektion fyra: Absorption, transmission, reflektion och gummibjörnar Med inspiration från denna video som skissar processen - Sammanfattning: Gummibjörnar, visar det sig, är jättebra för att demonstrera de grundläggande men något abstrakta begreppen för interaktion mellan ljus och materia: absorption, transmission och reflektion. Tid: minuter Nivå: gymnasiet Material ett grönt laserblock ett rött laserblock en vit LED lampa 3 röda gummibjörnar 3 gröna gummibjörnar 3 genomskinnliga gummibjörnar 1 blad vanligt vitt papper 1 blad vaxat papper (smörgåspapper) 1 OH blad eller genomskinlig plastpåse Diskussion och bakgrund Ett vanligt missförstånd bland elever är att färg är en materialegenskap. Denna underliggande missuppfattning leder till alla möjliga missförstånd som idén att när vitt ljus passerar genom ett grönt objekt och därmed skapar ett grönt sken på papperet, att det skulle vara detta gröna objekt som lägger till färg till en annars klar, naturlig ljusstråle. Oavsett hur många gånger man säger det det är svårt för elever att greppa idén att när de ser ett rött objekt, det som verkligen händer är att de flesta av våglängderna som utgör det vita ljuset har absorberats av det röda objektet, och bara våglängder som vi kalla röda reflekteras. Det som eleverna ser är det röda ljuset som reflekteras till deras ögon.
11 När laserljus, som är monokromatiskt (består av en enda färg eller våglängd) träffar något, så absorberas det och ljusets energi omvandlas till värme, eller så reflekteras det, eller så transmitteras ljuset. Men det som de flesta elever är bekanta med är vitt ljus, som utgörs av många färger eller våglängder. Hur ljuset växelverkar med ett objekt beror på ljusets våglangd(er) och egenskaperna hos atomerna i objektet. Ett material absorberar ljusfrekvenser som matchar vibrationsfrekvensen hos elektronerna i atomerna som materialet består av. Eftersom olika material består av atomer vars elektroner vibrerar vid olika frekvenser, så absorberar olika material olika ljusfrekvenser. Detta bryter ner idén att anledningen till att ljus passerar genom ett material eller inte skulle bero enbart på dess tjocklek. Ljus som inte absorberas av ett material kommer att antingen reflekteras eller transmitteras. Hur vi uppfattar färg är starkt beroende av hur ljus växelverkar med materia. Så färgen fanns aldrig i objektet bara i ljuset som belyste det och slutligen reflekterades in i våra ögon. Följande hands-on demonstration kommer att ge eleverna en intuitiv känsla för detta fenomen och börja bryta igenom deras missuppfattningar rörande ljus och färg. Demonstration 1. Lys med den vita LED-lampan mot eleverna och påminn dem att vitt ljus består av många ( alla ) våglängder eller frekvenser av ljus. Förklara att en LED är en ljuskälla och att de kan se ljuset som emitteras direkt ifrån LED-lampan. 2. Fråga vad händer när det vita ljuset växelverkar med någonting? 3. Vänd dig mot eleverna och lys med LED-lampan emot det vita pappersarket och fråga vad händer med ljuset? 4. Upprepa med det vaxade papperet och med en genomskinlig plastpåse. 5. Diskutera i termer av transmission, reflektion och absorption.
12 Förberedelser Dela in eleverna i 3 grupper och ge varje grupp ett Elevdatablad. Gör i ordning 3 stationer vid varje station ska det finnas en ljuskälla (ett grönt laserblock, ett rött laserblock eller en vit LED-lampa), en ark med vitt papper och 3 gummibjörnar (ett grönt, ett rött och ett ofärgat). Undersökning och observationer 1. Påminn eleverna om lasersäkerhets reglerna. 2. Berätta för eleverna att de kommer att skriva ner sina observationer av hur olika ljuskällor växelverkar med olika material 3 olika färgers gummibjörnar. 3. Instruera eleverna om att de ska lysa med ljuset ifrån varje ljuskälla på varje färgs gummibjörn och skriva ner sina observationer. De ska leta särskilt efter hur och om ljuset transmitteras, reflekteras och absorberas av de olika gummibjörnarna. 4. När alla grupper hunnit samla in data från alla tre stationer, be dem att titta igenom sina observationer och sin data för att komma fram till en eller flera slutsatser om hur ljuset beter sig. Be dem skriva ner sina slutsatser på sina datablad. Slutsatser och diskussion Be eleverna att dela med sig av sina observationer: Uppförde sig alla ljuskällor på samma sätt? När observerade du absorption, transmission och reflektion? Varför kunde inte det gröna ljuset passera genom den röda gummibjörnen? Och varför kunde inte det röda laserljuset inte passera genom den gröna gummibjörnen? Varför blev det vita ljuset rött när det hade passerat genom den röda gummibjörnen, och blev istället grönt när det passerade genom den gröna gummibjörnen? Eleverna kanske föreslår att gummibjörnarna färgar det vita ljuset, som man färglägger ett vitt papper. Påminn eleverna att vitt ljus består av alla synliga våglängder på ljus. Hjälp dem att koppla tanken att den röda gummibjörnen egentligen bara tillåter de röda våglängderna på ljuset att transmitteras eller reflekteras alla andra våglängder (färger) absorberas (och vi kan inte se ljuset som har absorberats av gummibjörnen). Detta resulterar i att det enda ljuset som kan passera genom gummibjörnen är det röda ljuset. (Eleverna kanske inser att det också är anledningen till att gummibjörnen ser röd ut: när vitt ljus studsar mot den, så är det bara de röda våglängderna som når fram till våra ögon; de andra våglängderna absorberas.) Samma sak gäller för gröna gummibjörnen men med grönt istället för rött. Eleverna upptäcker att strålen från det röda laserblocket passerar igenom den röda gummibjörnen, men inte den gröna! Påminn dem om att gröna gummibjörnen endast släpper igenom grönt ljus och blockerar andra våglängder och därför kan det röda laserljuset inte passera igenom den gröna gummibjörnen.
13 Lektion fem: Lasermikroskop Adapterad från Gorzad Planinsic, Water-Drop Projector Sammanfattning: En enkel experimentuppställning omvandlar en droppe vatten ifrån t.ex. en damm till en sfärisk lins för att synliggöra den mikroskopiska världen däri. Effekten är dramatisk och blir en engagerande introduktion till linser och geometrisk optik. Tid: minuter Nivå: 4-9, gymnasiet (beroende på matematiken) Material ett grönt laserblock en spruta ett labbstativ tejp tom vägg vatten från en damm, bäck, sjö, flod eller hav en stadig hand och lite tålamod En liten droppe vatten från t.ex. en damm ihop med en laserstråle från ett laserblock blir till en sfärisk lins med en kraftig förstoring.
14 Förberedelser För att ställa i ordning denna enkla med starkt engagerande demonstration, fyll en spruta med vatten från t.ex. en damm eller bäck. Bor man nära kusten kan man gärna hämta lite havsvatten. Är man inte i närheten av en damm, flod eller annat vattendrag kan man samla in vatten ifrån en pöl eller annan stillastående vattenansamling som troligtvis innehåller några små (0,2 0,5 mm) levande organismer. Fyll en spruta med det insamlade vattenprovet. Sätt fast sprutan i ett labbstativ så att en droppe vatten hänger ifrån spetsen. Positionera vattendroppen så att den är upplinjerad med strålen från ett grönt laserblock så att strålen passerar genom mitten av droppen, vinkelrätt mot väggen. Din uppställning borde vara ungefär två meter ifrån en skärm eller tom vit vägg där en grön ljusfläck kommer att uppvisa en imponerande samling av encelliga djur, larver och loppor som flyter omkring och simmar. Detta är vanligtvis tillräckligt engagerande för att väcka elevernas intresse för den starka optiken som möjliggör denna imponerande syn. Diskussion och bakgrund För att en droppe vatten, hängande från en spruta, som vi har här, syns strålgången i figuren här till höger där man ser hur ljuset kommer in i och sedan ut ur linsen. Strålen som går genom mitten bryts inte alla andra strålar däremot bryts in mot normalen när de passerar från luft, med brytningsindex n 1 = 1 till vatten med brytningsindex n 2. För små vinklar, som vi har här, kan vi använda Snells lag: n 1 sin 1 = n 2 sin 2 som då blir n1 1 = n2 2. Alltså kan avvikelsen mot normalen vid ena ytan skrivas som: Detta är en generell ekvation som används för mycket små vinklar, och är användbar för att följa strålar ( ray tracing ) genom komplicerade system, som, trots vår enkla experimentuppställning, är just vad vi har här. För detta exempel, är avvikelsen när strålen passerar ifrån luften och in i vår droppe (första ytan):
15 Vid bortre ytan av droppen är strålen 2r gånger deviationen närmare optiska axeln alltså når den bortre ytan på en höjd h ifrån optiska axeln: Ändringen i strålens vinkel när den lämnar droppen är samma som vinkeländringen när den kommer in i droppen. Slutligen gäller att: När man tittar närmare på hur detta generella fenomen av ljus som passerar genom en sfärisk lins och därmed skapar en magnifik förstoring blir det snabbt rätt komplicerat och väl invecklat för gymnasieelever. Figuren nedan visar ett enkelt stråldiagram för situationen. Om ni vill undersöka matematiken bakom detta finns det en utmärkt artikel av Gorazd Planinsic som omnämndes i början av denna lektion. Adapterad från Gorzad Planinsic, Water-Drop Projector
16 Lektion sex: Reflektion och brytning Sammanfattning: Reflektion och brytning är två av de mest grundläggande begreppen om ljus som eleverna ska lära sig. Att lägga en del hands-on tid på att jobba med ljus och linser ger eleverna möjlighet att greppa dessa fundament innan de går vidare till mer komplicerade idéer. Tid: minuter Nivå: 4-9, gymnasiet Material ett set med ljusblock med slitslocken på ett rött och ett grönt laserblock (för äldre elever) gradskivor ett set med glaslinser 3 speglar med hållare 3 ark med aluminiumfolie Reflection Förberedelser Dela in eleverna i grupper om 3 och ge dem var sitt ljusblock, en gradskiva, en spegelremsa och ett ark med aluminiumfolie. Om du har en grupp äldre elever, använd även laserblocket. Påminn eleverna om att vara uppmärksamma på vart de reflekterade stålarna hamnar!!
17 Undersökning och observationer Be eleverna att lysa med ljusblocket mot spegeln och undersöka hur ljuset studsar. Be dem att justera vinkeln för ljuset som träffar spegeln och fråga: Vad la du märke till om hur ljuset studsar? - en förutspåbar, rak linje som rör sig när ljuskällan rör sig - se till att de lägger märke till att det är vinkeländringen, inte avståndet, som ändrar hur ljuset studsar. Mer avancerade elever kan kvantifiera sina observationer be eleverna placera spegeln i hållaren, i mitten på gradskivan så att spegeln är parallell med gradskivans 90-graders axel. Be eleverna att rikta in strålen i en 30-graders vinkel ( i förhållande till vertikala riktningen) rakt mot mitten av spegeln, och mät reflekterade strålens riktning i förhållande till vertikala riktningen. Be eleverna att anteckna sina resultat och upprepa med ytterligare två valfria vinklar. Håll en gruppdiskussion om det som eleverna kommit fram till. Eleverna borde lägga märke till att infallsvinkeln = reflektionsvinkeln. Därefter, be eleverna att vika aluminiumfolien snyggt för att göra en platt, blank yta. Upprepa ovanstående uppgift, precis som med spegeln. Eleverna kommer att observera att folien påverkar ljuset på liknande sätt som spegeln. Be eleverna att skrynkla ihop folien till en boll och upprepa undersökningen. Eleverna kommer snart att lägga märke till att ljuset sprids och studsar i alla riktningar. Förklara att, när en yta är rugglig, som den skrynkliga foliebiten, så studsar ljuset enligt samma regler som de just observerat: i en rak linje med infallsvinkel = reflektionsvinkel. Men, många strålar studsar mot många olika ytor, som därmed sprider stålarna när de träffar olika delar av den skrynkliga folien. Nu kan du förklara att ljus studsar ifrån allt vi ser. Allt ljus studsar som raka strålar. Allt vi någonsin ser är ljus som studsar mot olika ytor och skiner in i våra ögon.
18 Refraktion - Diskussion och bakgrund Förklara för eleverna att, trots att ljus vanligtvis bara åker rakt fram som raka linjer, så böjs det, det bryts (refrakteras) när det passerar ifrån ett medium (t.ex. luft) och in i ett annat (t.ex. vatten). Yngre elever kommer att få nytta av en del hands-on tid för att observera detta fenomen, medan mer avancerade elever kan lära sig att böjningen sker enligt Snells lag: n 1 Sinθ 1 = n 2 Sinθ 2 där n är brytningsindex för det medium som ljuset utbreds igenom och θ 1 är vinkeln mellan infallande strålen och normalen, och θ 2 är vinkeln mellan den brutna (refrakterade) strålen och normalen. (Normalen betyder riktningen vinkelrätt mot ytan.) Material Brytningsindex, n Luft Vatten 1.33 Glas 1.50 Bensin 1.31 Plast Diamant 2.5 Brytningsindex (n) varierar också med våglängden på ljuset. Brytningen uppstår på grund av att ljuset saktar in när det passerar ifrån luft och in i ett annat medium (t.ex. vatten eller glas). Ändringen i hastighet orsakar ändringen i riktningen för ljusets utbredning. Undersökning och observationer - Nybörjare 1. Sätt på slitslocken på var och en av de 3 ljusblocken så att de projicerar en linje. 2. Placera trapetslinsen ungefär 5 cm framför den av ljusblocken så att stålen går igenom linsen. 3. Observera att ljuset böjs när det når linsen, och sedan böjs igen när det lämnar linsen. Denna böjning kallas för brytning eller refraktion. 4. Förklara att ljus byter riktning för att den ändrar hastighet när den rör sig från ett medium (luft) till ett annat (glas).
19 5. Linjera sedan upp alla tre ljusblock så att de projicerar 3 parallella linjer. 6. För in konvergerande (konvexa) linsen genom att placera den cirka 5 cm framför de tre ljusblocken, och observera att linsen böjer ihop ljuset till en brännpunkt (fokalpunkt). 7. Upprepa med divergerande (konkava) linsen. Mera om Linser Linser ger oss möjlighet att använda det vi vet om hur ljuset bryts. Elever kan observera hur ljuset går igenom en konvex och en konkav lins för att fokusera ljuset till en fokalpunkt (brännpunkt). Fokalpunkten är där man vanligtvis tänker sig att bilden formas: vi använder alla möjliga sorters linser för att fokusera bilder. Exempel inkluderar: våra ögon, en kamera, ett mikroskop eller ett teleskop. Linser är en kraftful metod för att kontrollera och förstå ljus så att vi kan få användning för det. Det finns 4 faktorer som avgör fokallängden på en lins: 1. linsens brytningsindex n lins 2. brytningsindex för linsens omgivning n omg 3. krökningsradien på linsens främre yta r 1 4. krökningsradien på linsens bakre yta r 2 Matematiskt uttryckt, kan linsens fokallängd i luft beräknas med hjälp av: LINSMAKARENS EKVATION 1/f =((nlins/nomg) 1) (1/r1 1/r2) Notera att när linsen är konvex, blir fokallängden positiv och när linsen är konkav, blir fokallängden negativ.
20 Undersökning och observationer Mer avancerat 1. Skapa två parallella stråla med hjälp av två laserblock med linjeskapande linser insatta. 2. Placera konvergerande linsen i mitten på gradskivan som visas nedan, med 0 grader som normalen 3. Markera fokalpunkten, brännpunkten, där dessa två strålar konvergerar (korsar varandra). 4. Mät avståndet från linsens mittpunkt till fokalpunkten detta är fokallängden eller f i linsmakarens ekvation. 5. Använd detta värde och värden för n från tabellen ovan för glas och luft för att beräkna r. Notera att, eftersom båda ytor har samma krökningsradie, blir R 1 = R 2.
21 Tänk efter Om du skulle träffa en fisk med en laserstråle, borde du sikta strålen över, under eller rakt mot fisken för att få en direkt träff?
22 Lektion sju: Färgseparation och blandning Sammanfattning: Två enkla aktiviteter introducerar grunderna för ljus och färg till elever i grundskolan. Se hur vitt ljus består av många färger, och hur flera färger kan kombineras för att skapa vitt ljus. Tid: minuter Nivå: 4-7 Material en vit LED lampa 3 ljusblock med slitslocken på 10 diffraktionsgitter rumsbelysning solljus vitt papper vaxkritor eller märkpennor Förberedelser 1. Dela in eleverna i 5 grupper och ge varje grupp 2 diffraktionsgitter att dela på. 2. Längst fram i klassrummet, sätt på den vita LED lampan och rikta den mot eleverna. Undersökning och observationer 1. Be eleverna att turas om med att titta på LED ljuset genom diffraktionsgittret. Fråga: vad ser du? Hjälp eleverna att hitta regnbågarna mot sidorna av diffraktionsgittret. 2. Be eleverna att titta runt i rummet på andra ljuskällor. Tala om för eleverna att aldrig titta rakt mot solen under denna eller vilken annan aktivitet som helst. 3. Fråga eleverna hur färgerna är ordnade? Vilken färg är närmast ljuskällan? Vilken är längst ifrån? Är färgerna alltid i samma ordning, oavsätt vilken ljuskälla de tittar på, eller byter färgerna position?
23 4. Be eleverna att rita en bild av ljuset och regnbågen (regnbågarna) som de ser, med färgerna i rätt ordning. 5. Ställ sedan upp ljusblocket, med slitslocken på, längst fram i klassrummet. 6. Särr på det röda, gröna och blåa ljusblocket och be eleverna att upprepa övningen med varje färg titta på ljuskällorna genom diffraktionsgittret och rapportera vad de observerar. 7. Förklara att färgade LED lampor består bara av några av färgerna inte ett helt spektrum så de borde kunna se smala band med enskilda färger. Diskussion och övergång till nästa aktivitet Fråga Varifrån kommer färgerna i regnbågen? Förklara färgerna var redan där gömda i det vita ljuset och diffraktionsgittret separerade dem i sina individuella färger. Regndroppar kan också separera solljus i många färger så att vi kan se en regnbåde. Dessa färger är alltid där, inuti det vita ljuset som vi ser hela tiden, men vi kan inte se dem för att de vanligtvis är hopblandade för att ge oss det vita ljuset vi är vana vid. Skapa vitt ljus 1. Ta bort slitslocken från ljusblocken så att de projicerar breda stråk med färgat ljus. 2. Ställ ljusblocken uppe på en bänk eller ett bord med en skärm eller vit vägg framför så att eleverna kan se det projicerade ljuset. 3. Sätt på det röda och det blåa och be eleverna att förutspå vilken färg de kommer att se när du kombinerar dem. 4. Blanda ljuset från det röda och blåa ljusblocket för att visa rosa eller magenta. 5. Sätt på det blåa och det gröna och be eleverna att förutspå vilken färg de kommer att se när du kombinerar dem. 6. Blanda grönt och blått för att skapa ljusblått eller cyan. 7. Sätt på det gröna och det röda och be eleverna att förutspå vilken färg de kommer att se när du kombinerar dem. 8. Blanda det röda och det gröna för att bilda gult. 9. Sätt på alla tre ljusblock och be eleverna att förutspå vilken färg de kommer att se när du kombinerar dem. 10. Blanda alla tre för att avslöja hur man skapar vitt ljus.
24 Lektion åtta: Mätning av laserns våglängd Sammanfattning: Eleverna kommer att bestämma våglängden på laserblocket genom att samla in sex set med mätningar som kommer att ge dem möjlighet att lösa ut våglängden. Type to enter text Tid: minuter Nivå: gymnasiet Material rött laserblock grönt laserblock 10 diffraktionsgitter tom vägg eller skärm linjal/måttstock Diskussion och bakgrund Diffraktion är ett fenomen som beskriver hur ljus böjs när det passerar genom väldigt smala spalter eller förbi en väldigt liten barriär (som ett hårstrå). Se bilden till höger som visar diffraktion (böjning) av vågor runt ett hörn. Tänk på ljuset som en våg, och betänk att när ljus passerar mycket små hinder (som ett hårstrå), så formas två separata vågmönster. Dessa mönster interfererar med varandra för att antingen förstärka vågmönstret (konstruktiv interferens) eller dämpa vågmönstret (destruktiv interferens).
25 Undersökning och observationer 1. Dela ut diffraktionsgitter och låt eleverna observera spektrumet de ser när de tittar mot olika ljuskällor genom gittret. 2. Förklara att gittret har många, många (vi kommer att se hur många strax) små repor, som ljuset måste böja sig runt när det passerar. När det vita ljuset böjs, kommer dess ingående våglängder att böjas och interferera med varandra och separeras som ett spektrum. 3. Vad händer när monokromatiskt (en enda färg/våglängd) ljus passerar genom den mycket smala slitsen av ett diffraktionsgitter? Vad skulle du förvänta skulle hända när en enda våglängd interfererar? Du kommer inte att se ett spektrum av färger därför att monokromatiskt ljus inte består av många våglängder. 4. Sätt ett rött laserblock på en stabil yta och lys med den genom diffraktionsgittret mot en tom vägg. Tejpa fast diffraktionsgittret på framsidan av laserblocket för att fästa det. 5. Göt samma sak med gröna laserblocket på en annan vägg. 6. Förklara att mönstret de ser beror på interferensmönstret av ljusvågen när den passerar igenom slitsen. 7. Introducera matten som beskriver detta fenomen: λ = (X) (d)/ L ; där d = avståndet mellan slitsarna (cm/linje), L = avståndet från gittret till skärmen och X = avståndet från ett maximum till nästa maximum. 8. Dela in klassen i två grupper, en kommer att arbeta med röda laserblocket och den andra arbetar med det gröna laserblocket. 9. Ge varje grupp ett elevdatablad. 10. Be varje elevgrupp skriva ner antal linjer/mm och konvertera till cm för att bestämma slitsbredden. 11. Eleverna kommer därefter att skriva upp avståndet från gittret till skärmen (L). 12. Därefter kommer eleverna att mäta avståndet från ett maximum (ljusfläcken starkaste position) till ett angränsande maximum (X). 13. Instruera eleverna till att utföra och tabellera dessa mätningar vid tre olika avstånd från skärmen eller väggen. 14. Jämför elevernas experimentella resultat med verkliga våglängden på laserblocken 635nm för rött och 532nm för grönt.
26 Datablad för elever LASERFÄRG: Diffraktionsgitter Linjer/mm Slitsbredd (d) cm/linje Avstånd från gitter till skärm (L) i cm Avstånd från maximum till maximum (X) Välj 3 avstånd från skärmen för mätningarna. Bestäm våglängden på lasern Använd värden på X, d och L från datan ovan och dubbelslits formeln: λ = (X) (d)/ L för att bestämma våglängden på lasern. Medelvärdesbilda era tre beräknade värden och bestäm ett slutligt medelvärde för våglängden. λ = (X) (d)/ L λ = (X) (d)/ L λ = (X) (d)/ L Medlevärde på våglängd Visa all insättning av mätdata i formeln Slutligt värde (cm) Slutligt värde (mikrometer)
27 Lektion nio: Mätning av tjockleken på ett hårstrå med laser Sammanfattning: Eleverna får bestämma tjockleken på ett hårstrå genom att anväda diffraktion och ett laserblock med känd våglängd. Tid: minuter Nivå: gymnasiet Material rött laserblock grönt laserblock tejp tom vägg eller skärm linjal/måttstock hårstrå (från en människa) Diskussion och bakgrund Se föregående lektion för en introduction till diffraction. Laser diffraktion kan användas för att mäta mycket små saker som hårstrån! Trots att vi vanligtvis tänker på diffraktion i termer av ljus som passerar genom en mycket smal slits, så sker diffraktion också när ljus passerar ett mycket smalt hinder.
Laboration i Geometrisk Optik
 Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
Ljuskällor. För att vi ska kunna se något måste det finnas en ljuskälla
 Ljus/optik Ljuskällor För att vi ska kunna se något måste det finnas en ljuskälla En ljuskälla är ett föremål som själv sänder ut ljus t ex solen, ett stearinljus eller en glödlampa Föremål som inte själva
Ljus/optik Ljuskällor För att vi ska kunna se något måste det finnas en ljuskälla En ljuskälla är ett föremål som själv sänder ut ljus t ex solen, ett stearinljus eller en glödlampa Föremål som inte själva
Vågfysik. Geometrisk optik. Knight Kap 23. Ljus. Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion)
 Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
OPTIK läran om ljuset
 OPTIK läran om ljuset Vad är ljus Ljuset är en form av energi Ljus är elektromagnetisk strålning som färdas med en hastighet av 300 000 km/s. Ljuset kan ta sig igenom vakuum som är ett utrymme som inte
OPTIK läran om ljuset Vad är ljus Ljuset är en form av energi Ljus är elektromagnetisk strålning som färdas med en hastighet av 300 000 km/s. Ljuset kan ta sig igenom vakuum som är ett utrymme som inte
Geometrisk optik. Syfte och mål. Innehåll. Utrustning. Institutionen för Fysik 2006-04-25
 Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Optik. Läran om ljuset
 Optik Läran om ljuset Vad är ljus? Ljus är en form av energi. Ljus är elektromagnetisk strålning. Energi kan inte försvinna eller nyskapas. Ljuskälla Föremål som skickar ut ljus. I alla ljuskällor sker
Optik Läran om ljuset Vad är ljus? Ljus är en form av energi. Ljus är elektromagnetisk strålning. Energi kan inte försvinna eller nyskapas. Ljuskälla Föremål som skickar ut ljus. I alla ljuskällor sker
λ = T 2 g/(2π) 250/6 40 m
 Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Gauss Linsformel (härledning)
 α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
Instuderingsfrågor extra allt
 Instuderingsfrågor extra allt För dig som vill lära dig mer, alla svaren finns inte i häftet. Sök på nätet, fråga en kompis eller läs i en grundbok som du får låna på lektion. Testa dig själv 9.1 1 Vilken
Instuderingsfrågor extra allt För dig som vill lära dig mer, alla svaren finns inte i häftet. Sök på nätet, fråga en kompis eller läs i en grundbok som du får låna på lektion. Testa dig själv 9.1 1 Vilken
Studieanvisning i Optik, Fysik A enligt boken Quanta A
 Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material?
 1 Föreläsning 2 Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen på samma sida är reflekterat
1 Föreläsning 2 Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen på samma sida är reflekterat
Föreläsning 2 (kap , 2.6 i Optics)
 5 Föreläsning 2 (kap 1.6-1.12, 2.6 i Optics) Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen
5 Föreläsning 2 (kap 1.6-1.12, 2.6 i Optics) Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen
Vad skall vi gå igenom under denna period?
 Ljus/optik Vad skall vi gå igenom under denna period? Vad är ljus? Ljuskälla? Reflektionsvinklar/brytningsvinklar? Färger? Hur fungerar en kikare? Hur fungerar en kamera/ ögat? Var använder vi ljus i vardagen
Ljus/optik Vad skall vi gå igenom under denna period? Vad är ljus? Ljuskälla? Reflektionsvinklar/brytningsvinklar? Färger? Hur fungerar en kikare? Hur fungerar en kamera/ ögat? Var använder vi ljus i vardagen
Optik, F2 FFY091 TENTAKIT
 Optik, F2 FFY091 TENTAKIT Datum Tenta Lösning Svar 2005-01-11 X X 2004-08-27 X X 2004-03-11 X X 2004-01-13 X 2003-08-29 X 2003-03-14 X 2003-01-14 X X 2002-08-30 X X 2002-03-15 X X 2002-01-15 X X 2001-08-31
Optik, F2 FFY091 TENTAKIT Datum Tenta Lösning Svar 2005-01-11 X X 2004-08-27 X X 2004-03-11 X X 2004-01-13 X 2003-08-29 X 2003-03-14 X 2003-01-14 X X 2002-08-30 X X 2002-03-15 X X 2002-01-15 X X 2001-08-31
 Optik Samverkan mellan atomer/molekyler och ljus elektroner atomkärna Föreläsning 7/3 200 Elektronmolnet svänger i takt med ljuset och skickar ut nytt ljus Ljustransmission i material Absorption elektroner
Optik Samverkan mellan atomer/molekyler och ljus elektroner atomkärna Föreläsning 7/3 200 Elektronmolnet svänger i takt med ljuset och skickar ut nytt ljus Ljustransmission i material Absorption elektroner
Ljusets interferens. Sammanfattning
 HERMODS DISTANSGYMNASIUM Naturvetenskapsprogrammet Emilia Dunfelt Fysik 2 2017-05-06 Ljusets interferens Sammanfattning I försöket undersöks ljusets vågegenskaper med hjälp av gitterekvationen. Två olika
HERMODS DISTANSGYMNASIUM Naturvetenskapsprogrammet Emilia Dunfelt Fysik 2 2017-05-06 Ljusets interferens Sammanfattning I försöket undersöks ljusets vågegenskaper med hjälp av gitterekvationen. Två olika
Övning 9 Tenta
 Övning 9 Tenta 014-11-8 1. När ljus faller in från luft mot ett genomskinligt material, med olika infallsvinkel, blir reflektansen den som visas i grafen nedan. Ungefär vilket brytningsindex har materialet?
Övning 9 Tenta 014-11-8 1. När ljus faller in från luft mot ett genomskinligt material, med olika infallsvinkel, blir reflektansen den som visas i grafen nedan. Ungefär vilket brytningsindex har materialet?
Laboration 1 Fysik
 Laboration 1 Fysik 2 2015 : Fysik 2 för tekniskt/naturvetenskapligt basår Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen på
Laboration 1 Fysik 2 2015 : Fysik 2 för tekniskt/naturvetenskapligt basår Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen på
Fysik. Laboration 3. Ljusets vågnatur
 Fysik Laboration 3 Ljusets vågnatur Laborationens syfte: att hjälpa dig att förstå ljusfenomen diffraktion och interferens och att förstå hur olika typer av spektra uppstår Utförande: laborationen skall
Fysik Laboration 3 Ljusets vågnatur Laborationens syfte: att hjälpa dig att förstå ljusfenomen diffraktion och interferens och att förstå hur olika typer av spektra uppstår Utförande: laborationen skall
1. Betrakta en plan harmonisk elektromagnetisk våg i vakuum där det elektriska fältet E uttrycks på följande sätt (i SI-enheter):
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
Förklara dessa begrepp: Ackommodera Avbildning, Brytning Brytningslagen Brytningsindex Brytningsvinkel Brännvidd Diffus och regelbunden reflektion
 Förklara dessa begrepp: Ackommodera, ögats närinställning, är förmågan att förändra brytkraften i ögats lins. Ljus från en enda punkt på ett avlägset objekt och ljus från en punkt på ett närliggande objekt
Förklara dessa begrepp: Ackommodera, ögats närinställning, är förmågan att förändra brytkraften i ögats lins. Ljus från en enda punkt på ett avlägset objekt och ljus från en punkt på ett närliggande objekt
SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE.
 SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE. Vad gjorde vi förra gången? Har du några frågor från föregående lektion? 3. titta i ditt läromedel (boken) Vad ska vi göra idag? Optik och
SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE. Vad gjorde vi förra gången? Har du några frågor från föregående lektion? 3. titta i ditt läromedel (boken) Vad ska vi göra idag? Optik och
Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du:
 Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du: A.Mer av dig själv. B.Mindre av dig själv. C.Lika mycket av dig själv. ⱱ Hur hög måste en spegel vara för att du ska
Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du: A.Mer av dig själv. B.Mindre av dig själv. C.Lika mycket av dig själv. ⱱ Hur hög måste en spegel vara för att du ska
Tentamen i Fotonik , kl
 FAFF25-2015-05-04 Tentamen i Fotonik - 2015-05-04, kl. 14.00-19.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2015-05-04 Tentamen i Fotonik - 2015-05-04, kl. 14.00-19.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Diffraktion och interferens Kapitel 35-36
 Diffraktion och interferens Kapitel 35-36 1.3.2016 Natalie Segercrantz Centrala begrepp Huygens princip: Tidsskillnaden mellan korresponderande punkter på två olika vågfronter är lika för alla par av korresponderande
Diffraktion och interferens Kapitel 35-36 1.3.2016 Natalie Segercrantz Centrala begrepp Huygens princip: Tidsskillnaden mellan korresponderande punkter på två olika vågfronter är lika för alla par av korresponderande
Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00
 FAFF25-2014-04-25 Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2014-04-25 Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 33 - Ljus 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Vågrörelselära och optik Kapitel 33 - Ljus 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Ljus och strålning. Klass: 9H
 Ljus och strålning Namn: Klass: 9H Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och samhället genomföra systematiska
Ljus och strålning Namn: Klass: 9H Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och samhället genomföra systematiska
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Tisdagen den 17 juni 2008 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 1,5 högskolepoäng, FK49 Tisdagen den 17 juni 28 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 1,5 högskolepoäng, FK49 Tisdagen den 17 juni 28 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare
Mätning av fokallängd hos okänd lins
 Mätning av fokallängd hos okänd lins Syfte Labbens syfte är i första hand att lära sig hantera mätfel och uppnå god noggrannhet, även med systematiska fel. I andra hand är syftet att hantera linser och
Mätning av fokallängd hos okänd lins Syfte Labbens syfte är i första hand att lära sig hantera mätfel och uppnå god noggrannhet, även med systematiska fel. I andra hand är syftet att hantera linser och
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
Diffraktion och interferens
 Institutionen för Fysik 005-10-17 Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det
Institutionen för Fysik 005-10-17 Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
Tentamen i Fotonik - 2014-08-26, kl. 08.00-13.00
 FAFF25-2014-08-26 Tentamen i Fotonik - 2014-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2014-08-26 Tentamen i Fotonik - 2014-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Övning 9 Tenta från Del A. Vägg på avståndet r = 2.0 m och med reflektansen R = 0.9. Lambertspridare.
 Övning 9 Tenta från 2016-08-24 Del A 1.) Du lyser med en ficklampa rakt mot en vit vägg. Vilken luminans får väggen i mitten av det belysta området? Ficklampan har en ljusstyrka på 70 cd och du står 2.0
Övning 9 Tenta från 2016-08-24 Del A 1.) Du lyser med en ficklampa rakt mot en vit vägg. Vilken luminans får väggen i mitten av det belysta området? Ficklampan har en ljusstyrka på 70 cd och du står 2.0
Vågrörelselära & Kvantfysik, FK2002 1 december 2011
 Räkneövning 6 Vågrörelselära & Kvantfysik, FK2002 december 20 Problem 36.23 Avståndet mellan två konvexa linser i ett mikroskop, l = 7.5 cm. Fokallängden för objektivet f o = 0.8 cm och för okularet f
Räkneövning 6 Vågrörelselära & Kvantfysik, FK2002 december 20 Problem 36.23 Avståndet mellan två konvexa linser i ett mikroskop, l = 7.5 cm. Fokallängden för objektivet f o = 0.8 cm och för okularet f
Tentamen i Fotonik , kl
 FAFF25-2015-03-20 Tentamen i Fotonik - 2015-03-20, kl. 14.00-19.15 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2015-03-20 Tentamen i Fotonik - 2015-03-20, kl. 14.00-19.15 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Syfte: Att se hur ljuset reflekteras i konkava och konvexa speglar. Men även i andra plana speglar.
 Ljusets reflektion Syfte: Att se hur ljuset reflekteras i konkava och konvexa speglar. Men även i andra plana speglar. Material: Optisk bänk Spänningskub Lins +10 Optiklampa Spalt med 5 spalter Spalthållare
Ljusets reflektion Syfte: Att se hur ljuset reflekteras i konkava och konvexa speglar. Men även i andra plana speglar. Material: Optisk bänk Spänningskub Lins +10 Optiklampa Spalt med 5 spalter Spalthållare
Böjning. Tillämpad vågrörelselära. Föreläsningar. Vad är optik? Huygens princip. Böjning vs. interferens FAF260. Lars Rippe, Atomfysik/LTH 1
 Tillämpad vågrörelselära 2 Föreläsningar Vad är optik? F10 och upplösning (kap 16) F11 Interferens och böjning (kap 17) F12 Multipelinterferens (kap 18) F13 Polariserat ljus (kap 20) F14 Reserv / Repetition
Tillämpad vågrörelselära 2 Föreläsningar Vad är optik? F10 och upplösning (kap 16) F11 Interferens och böjning (kap 17) F12 Multipelinterferens (kap 18) F13 Polariserat ljus (kap 20) F14 Reserv / Repetition
Handledning laboration 1
 : Fysik 2 för tekniskt/naturvetenskapligt basår Handledning laboration 1 VT 2017 Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen
: Fysik 2 för tekniskt/naturvetenskapligt basår Handledning laboration 1 VT 2017 Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen
Vi är beroende av ljuset för att kunna leva. Allt liv på jorden skulle ta slut och jordytan skulle bli öde och tyst om vi inte hade haft ljus.
 Källa: Fysik - Kunskapsträdet Vi är beroende av ljuset för att kunna leva. Allt liv på jorden skulle ta slut och jordytan skulle bli öde och tyst om vi inte hade haft ljus. Ljusets natur Ljusets inverkan
Källa: Fysik - Kunskapsträdet Vi är beroende av ljuset för att kunna leva. Allt liv på jorden skulle ta slut och jordytan skulle bli öde och tyst om vi inte hade haft ljus. Ljusets natur Ljusets inverkan
Tentamen i Fotonik , kl
 FAFF25-2013-08-26 Tentamen i Fotonik - 2013-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2013-08-26 Tentamen i Fotonik - 2013-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Optik 2018 Laborationsinstruktioner Våglära och optik FAFF30+40
 Optik 2018 Laborationsinstruktioner Våglära och optik FAFF30+40 Åsa Bengtsson: asa.bengtsson@fysik.lth.se Emma Persson: tfy15epe@student.lu.se Lärandemål I den här laborationen får Du experimentera med
Optik 2018 Laborationsinstruktioner Våglära och optik FAFF30+40 Åsa Bengtsson: asa.bengtsson@fysik.lth.se Emma Persson: tfy15epe@student.lu.se Lärandemål I den här laborationen får Du experimentera med
5. Elektromagnetiska vågor - interferens
 Interferens i dubbelspalt A λ/2 λ/2 Dal för ena vågen möter topp för den andra och vice versa => mörkt (amplitud = 0). Dal möter dal och topp möter topp => ljust (stor amplitud). B λ/2 Fig. 5.1 För ljusvågor
Interferens i dubbelspalt A λ/2 λ/2 Dal för ena vågen möter topp för den andra och vice versa => mörkt (amplitud = 0). Dal möter dal och topp möter topp => ljust (stor amplitud). B λ/2 Fig. 5.1 För ljusvågor
LABORATION 1 AVBILDNING OCH FÖRSTORING
 LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
Övning 1 Dispersion och prismaeffekt
 Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Vinkelupplösning, exempel hålkameran. Vinkelupplösning När är två punkter upplösta? FAF260. Lars Rippe, Atomfysik/LTH 1. Böjning i en spalt
 Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Diffraktion och interferens
 Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det är just detta fenomen som gör att
Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det är just detta fenomen som gör att
för gymnasiet Polarisation
 Chalmers tekniska högskola och November 2006 Göteborgs universitet 9 sidor + bilaga Rikard Bergman 1992 Christian Karlsson, Jan Lagerwall 2002 Emma Eriksson 2006 O4 för gymnasiet Polarisation Foton taget
Chalmers tekniska högskola och November 2006 Göteborgs universitet 9 sidor + bilaga Rikard Bergman 1992 Christian Karlsson, Jan Lagerwall 2002 Emma Eriksson 2006 O4 för gymnasiet Polarisation Foton taget
Denna våg är. A. Longitudinell. B. Transversell. C. Något annat
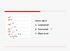 Denna våg är A. Longitudinell B. Transversell ⱱ v C. Något annat l Detta är situationen alldeles efter en puls på en fjäder passerat en skarv A. Den ursprungliga pulsen kom från höger och mötte en lättare
Denna våg är A. Longitudinell B. Transversell ⱱ v C. Något annat l Detta är situationen alldeles efter en puls på en fjäder passerat en skarv A. Den ursprungliga pulsen kom från höger och mötte en lättare
Fysik A A B C D. Sidan 1 av 9 henrik.gyllensten@tabyenskilda.se. www.tabyenskilda.se/fy
 www.tabyenskilda.se/y ÖÖvvnni iinn ggssuuppppggi ii teer 1. Lars lyser med en icklampa mot ett prisma. Han kan då se ett spektrum på väggen bakom prismat. Spektrumet innehåller alla ärger. Vilken av dessa
www.tabyenskilda.se/y ÖÖvvnni iinn ggssuuppppggi ii teer 1. Lars lyser med en icklampa mot ett prisma. Han kan då se ett spektrum på väggen bakom prismat. Spektrumet innehåller alla ärger. Vilken av dessa
Optisk bänk En Virtuell Applet Laboration
 Optisk bänk En Virtuell Applet Laboration Bildkonstruktion med linser. Generell Applet Information: 1. Öppna en internet läsare och öppna Optisk Bänk -sidan (adress). 2. Använd FULL SCREEN. 3. När applet:en
Optisk bänk En Virtuell Applet Laboration Bildkonstruktion med linser. Generell Applet Information: 1. Öppna en internet läsare och öppna Optisk Bänk -sidan (adress). 2. Använd FULL SCREEN. 3. När applet:en
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Repetition Ljus - Fy2!!
 Repetition Ljus - Fy2 Egenskaper ör : Ljus är inte en mekanisk vågrörelse. Den tar sig ram utan problem även i vakuum och behöver alltså inget medium. Exakt vilken typ av vågrörelse är återkommer vi till
Repetition Ljus - Fy2 Egenskaper ör : Ljus är inte en mekanisk vågrörelse. Den tar sig ram utan problem även i vakuum och behöver alltså inget medium. Exakt vilken typ av vågrörelse är återkommer vi till
Lösningarna inlämnas renskrivna vid laborationens början till handledaren
 Geometrisk optik Förberedelser Läs i vågläraboken om avbildning med linser (sid 227 241), ögat (sid 278 281), färg och färgseende (sid 281 285), glasögon (sid 287 290), kameran (sid 291 299), vinkelförstoring
Geometrisk optik Förberedelser Läs i vågläraboken om avbildning med linser (sid 227 241), ögat (sid 278 281), färg och färgseende (sid 281 285), glasögon (sid 287 290), kameran (sid 291 299), vinkelförstoring
Diffraktion och interferens
 Diffraktion och interferens Laboration i kursen Syfte Laborationen ska ge förståelse för begreppen interferens och diffraktion och hur de karaktäriseras genom experiment. Vidare visar laborationen exempel
Diffraktion och interferens Laboration i kursen Syfte Laborationen ska ge förståelse för begreppen interferens och diffraktion och hur de karaktäriseras genom experiment. Vidare visar laborationen exempel
Interferens och diffraktion
 Laborationsinstruktion Vågrörelselära Interferens och diffraktion VT11 Stockholms Universitet Innehåll Uppgift 1 Diffraktionsförsök med laserljus Uppgift Mäta våglängden med linjal Uppgift 3 Luftens brytningsindex
Laborationsinstruktion Vågrörelselära Interferens och diffraktion VT11 Stockholms Universitet Innehåll Uppgift 1 Diffraktionsförsök med laserljus Uppgift Mäta våglängden med linjal Uppgift 3 Luftens brytningsindex
Tentamen i Våglära och optik för F
 Tentamen i Våglära och optik för F FAFF30, 2013 06 03 Skrivtid 8.00 13.00 Hjälpmedel: Läroboken och miniräknare Uppgifterna är inte sorterade i svårighetsgrad Börja varje ny uppgift på ett nytt blad och
Tentamen i Våglära och optik för F FAFF30, 2013 06 03 Skrivtid 8.00 13.00 Hjälpmedel: Läroboken och miniräknare Uppgifterna är inte sorterade i svårighetsgrad Börja varje ny uppgift på ett nytt blad och
Kapitel 35, interferens
 Kapitel 35, interferens Interferens hos ljusvågor, koherensbegreppet Samband för max och min för ideal dubbelspalt Samband för intensitetsvariation för ideal dubbelspalt Interferens i tunna filmer Michelson
Kapitel 35, interferens Interferens hos ljusvågor, koherensbegreppet Samband för max och min för ideal dubbelspalt Samband för intensitetsvariation för ideal dubbelspalt Interferens i tunna filmer Michelson
Föreläsning 3: Radiometri och fotometri
 Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Tentamen i Optik för F2 (FFY091)
 CHALMERS TEKNISKA HÖGSKOLA 2008-08-26 Teknisk Fysik 08.30-12.30 Sal: V Tentamen i Optik för F2 (FFY091) Lärare: Bengt-Erik Mellander, tel. 772 3340 Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics
CHALMERS TEKNISKA HÖGSKOLA 2008-08-26 Teknisk Fysik 08.30-12.30 Sal: V Tentamen i Optik för F2 (FFY091) Lärare: Bengt-Erik Mellander, tel. 772 3340 Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics
Text, Sofia Ström. Foto, Ellen Kleiman. Ljusets reflektion. Syfte: Se hur ljusets reflekteras i konkava och konvexa speglar. Material: Optisk bänk
 Text, Sofia Ström. Foto, Ellen Kleiman. Ljusets reflektion Syfte: Se hur ljusets reflekteras i konkava och konvexa speglar. Optisk bänk Spänningskub Lins +10 Optiklampa Spalt med 5 spalter Spalthållare
Text, Sofia Ström. Foto, Ellen Kleiman. Ljusets reflektion Syfte: Se hur ljusets reflekteras i konkava och konvexa speglar. Optisk bänk Spänningskub Lins +10 Optiklampa Spalt med 5 spalter Spalthållare
Ljusets polarisation
 Ljusets polarisation Viktor Jonsson och Alexander Forsman 1 Sammanfattning Denna labb går ut på att lära sig om, och använda, ljusets polarisation. Efter utförd labb ska studenten kunna sätta upp en enkel
Ljusets polarisation Viktor Jonsson och Alexander Forsman 1 Sammanfattning Denna labb går ut på att lära sig om, och använda, ljusets polarisation. Efter utförd labb ska studenten kunna sätta upp en enkel
Fysik (TFYA14) Fö 5 1. Fö 5
 Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
OBS: Alla mätningar och beräknade värden ska anges i SI-enheter med korrekt antal värdesiffror. Felanalys behövs endast om det anges i texten.
 Speed of light OBS: Alla mätningar och beräknade värden ska anges i SI-enheter med korrekt antal värdesiffror. Felanalys behövs endast om det anges i texten. 1.0 Inledning Experiment med en laseravståndsmätare
Speed of light OBS: Alla mätningar och beräknade värden ska anges i SI-enheter med korrekt antal värdesiffror. Felanalys behövs endast om det anges i texten. 1.0 Inledning Experiment med en laseravståndsmätare
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER
 EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
Optik. Innehåll: I - Elektromagnetiska vågor radio och ljus. II - Reflexion och brytning. III - Ljusvågor. MNXA11 / Lund University
 Optik Innehåll: I - Elektromagnetiska vågor radio och ljus II - Reflexion och brytning III - Ljusvågor Kom ihåg Definition Amplitud, Våglängd, Frekvens, Våghastighet Mekaniska eller Elektromagnetiska vågor
Optik Innehåll: I - Elektromagnetiska vågor radio och ljus II - Reflexion och brytning III - Ljusvågor Kom ihåg Definition Amplitud, Våglängd, Frekvens, Våghastighet Mekaniska eller Elektromagnetiska vågor
Diffraktion och interferens
 Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det är just detta fenomen som gör att
Diffraktion och interferens Syfte och mål När ljus avviker från en rätlinjig rörelse kallas det för diffraktion och sker då en våg passerar en öppning eller en kant. Det är just detta fenomen som gör att
Observera också att det inte går att både se kanten på fönstret och det där ute tydligt samtidigt.
 Om förstoringsglaset Du kan göra mycket med bara ett förstoringsglas! I många sammanhang i det dagliga livet förekommer linser. Den vanligast förekommande typen är den konvexa linsen, den kallas också
Om förstoringsglaset Du kan göra mycket med bara ett förstoringsglas! I många sammanhang i det dagliga livet förekommer linser. Den vanligast förekommande typen är den konvexa linsen, den kallas också
Ljusets böjning och interferens
 Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen ska du studera två centrala vågfenomen: interferens och böjning. Du kommer bl.a. att studera hur ljusvågor böjs när de passerar
Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen ska du studera två centrala vågfenomen: interferens och böjning. Du kommer bl.a. att studera hur ljusvågor böjs när de passerar
FYSIK ÅK 9 AKUSTIK OCH OPTIK. Fysik - Måldokument Lena Folkebrant
 Fysik - Måldokument Lena Folkebrant FYSIK ÅK 9 AKUSTIK OCH OPTIK Ljud är egentligen tryckförändringar i något material. För att ett ljud ska uppstå måste något svänga eller vibrera. När en gitarrsträng
Fysik - Måldokument Lena Folkebrant FYSIK ÅK 9 AKUSTIK OCH OPTIK Ljud är egentligen tryckförändringar i något material. För att ett ljud ska uppstå måste något svänga eller vibrera. När en gitarrsträng
Vågrörelselära & Kvantfysik, FK2002 29 november 2011
 Räkneövning 5 Vågrörelselära & Kvantfysik, FK00 9 november 0 Problem 35.9 En dykare som befinner sig på djupet D 3 m under vatten riktar en ljusstråle (med infallsvinkel θ i 30 ) mot vattenytan. På vilket
Räkneövning 5 Vågrörelselära & Kvantfysik, FK00 9 november 0 Problem 35.9 En dykare som befinner sig på djupet D 3 m under vatten riktar en ljusstråle (med infallsvinkel θ i 30 ) mot vattenytan. På vilket
Ljusets böjning & interferens
 Ljusets böjning & interferens Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter 3 Appendix Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen
Ljusets böjning & interferens Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter 3 Appendix Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen
för M Skrivtid i hela (1,0 p) 3 cm man bryningsindex i glaset på ett 2. två spalter (3,0 p)
 Tentamen i tillämpad Våglära FAF260, 2016 06 01 för M Skrivtid 08.00 13.00 Hjälpmedel: Formelblad och miniräknare Uppgifterna är inte sorteradee i svårighetsgrad Börja varje ny uppgift på ett nytt blad
Tentamen i tillämpad Våglära FAF260, 2016 06 01 för M Skrivtid 08.00 13.00 Hjälpmedel: Formelblad och miniräknare Uppgifterna är inte sorteradee i svårighetsgrad Börja varje ny uppgift på ett nytt blad
3. Ljus. 3.1 Det elektromagnetiska spektret
 3. Ljus 3.1 Det elektromagnetiska spektret Synligt ljus är elektromagnetisk vågrörelse. Det följer samma regler som vi tidigare gått igenom för mekanisk vågrörelse; reflexion, brytning, totalreflexion
3. Ljus 3.1 Det elektromagnetiska spektret Synligt ljus är elektromagnetisk vågrörelse. Det följer samma regler som vi tidigare gått igenom för mekanisk vågrörelse; reflexion, brytning, totalreflexion
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 34 - Optik 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Vågrörelselära och optik Kapitel 34 - Optik 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Tentamen i Vågor och Optik 5hp F, Q, kandfys, gylärfys-programm, den 11. juni 2010
 Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 8-13 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 8-13 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Ljus, syn & strålning
 Ljus, syn & strålning Namn: Klass: 8G Ljus, syn och strålning Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och
Ljus, syn & strålning Namn: Klass: 8G Ljus, syn och strålning Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 36-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 36-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
(ii) Beräkna sidoförskjutningen d mellan in- och utgående strålar, uttryckt i vinklarna θ i och tjocklekar t i. (2p)
 Tentamen i Vågrörelselära(FK49) Datum: Onsdag, 4 Augusti,, Tid: 9: - 4: Tillåten Hjälp: Physics handbook eller dylikt och miniräknare Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen
Tentamen i Vågrörelselära(FK49) Datum: Onsdag, 4 Augusti,, Tid: 9: - 4: Tillåten Hjälp: Physics handbook eller dylikt och miniräknare Förklara resonemang och uträkningar klart och tydligt. Tentamensskrivningen
Elevlaborationer Bordsoptik laser Art.nr: 54624
 Elevlaborationer Bordsoptik laser Art.nr: 54624 Laser En laserstråle är speciell på flera sätt den består av en enda färg, t.ex. röd eller grön. ljuset går nästan helt parallellt (utan att sprida ut sig).
Elevlaborationer Bordsoptik laser Art.nr: 54624 Laser En laserstråle är speciell på flera sätt den består av en enda färg, t.ex. röd eller grön. ljuset går nästan helt parallellt (utan att sprida ut sig).
Ljusets böjning & interferens
 ... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Ljusets böjning & interferens Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen ska
... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Ljusets böjning & interferens Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen ska
Vinkelupplösning, exempel hålkameran. Vinkelupplösning När är två punkter upplösta? FAF260. Lars Rippe, Atomfysik/LTH 1. Böjning i en spalt
 Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Tentamen i Fotonik - 2015-08-21, kl. 08.00-13.00
 Tentamen i Fotonik - 2015-08-21, kl. 08.00-13.00 Tentamen i Fotonik 2011 08 25, kl. 08.00 13.00 FAFF25-2015-08-21 FAFF25 2011 08 25 FAFF25 2011 08 25 FAFF25 FAFF25 - Tentamen Fysik för Fysik C och i för
Tentamen i Fotonik - 2015-08-21, kl. 08.00-13.00 Tentamen i Fotonik 2011 08 25, kl. 08.00 13.00 FAFF25-2015-08-21 FAFF25 2011 08 25 FAFF25 2011 08 25 FAFF25 FAFF25 - Tentamen Fysik för Fysik C och i för
Institutionen för Fysik 2013-10-17. Polarisation
 Polarisation Syfte Syftet med denna laboration är att lära sig om ljusets polarisation. Du kommer att se exempel på opolariserat, linjär- och cirkulärpolariserat ljus. Exempel på komponenter som kan ändra
Polarisation Syfte Syftet med denna laboration är att lära sig om ljusets polarisation. Du kommer att se exempel på opolariserat, linjär- och cirkulärpolariserat ljus. Exempel på komponenter som kan ändra
Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics Handbook.
 CHALMERS TEKNISKA HÖGSKOLA 2009-01-13 Teknisk Fysik 14.00-18.00 Sal: V Tentamen i Optik för F2 (FFY091) Lärare: Bengt-Erik Mellander, tel. 772 3340 Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics
CHALMERS TEKNISKA HÖGSKOLA 2009-01-13 Teknisk Fysik 14.00-18.00 Sal: V Tentamen i Optik för F2 (FFY091) Lärare: Bengt-Erik Mellander, tel. 772 3340 Hjälpmedel: Typgodkänd räknare, Physics Handbook, Mathematics
Geometrisk optik reflektion och brytning. Optiska system F9 Optiska instrument. Elektromagnetiska vågor. Det elektromagnetiska spektrumet FAF260
 Geometrisk optik reflektion oh brytning Geometrisk optik F7 Reflektion oh brytning F8 Avbildning med linser Plana oh buktiga speglar Optiska system F9 Optiska instrument 1 2 Geometrisk optik reflektion
Geometrisk optik reflektion oh brytning Geometrisk optik F7 Reflektion oh brytning F8 Avbildning med linser Plana oh buktiga speglar Optiska system F9 Optiska instrument 1 2 Geometrisk optik reflektion
Kapitel 33 The nature and propagation of light. Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion)
 Kapitel 33 The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Kapitel 33 The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Färglära. Ljus är en blandning av färger som tillsammans upplevs som vitt. Färg är reflektion av ljus. I ett mörkt rum inga färger.
 Ljus är en blandning av färger som tillsammans upplevs som vitt. Färg är reflektion av ljus. I ett mörkt rum inga färger. Människans öga är känsligt för rött, grönt och blått ljus och det är kombinationer
Ljus är en blandning av färger som tillsammans upplevs som vitt. Färg är reflektion av ljus. I ett mörkt rum inga färger. Människans öga är känsligt för rött, grönt och blått ljus och det är kombinationer
Kursiverade ord är viktiga begrepp som skall förstås, kunna förklaras och dess relevans i detta sammanhang skall motiveras.
 Holografilab I denna lab kommer ett dubbelexponerat, transmissions hologram göras genom att bygga en holografiuppställning, dubbelexponera och framkalla en holografisk film. Dubbelexponerade hologram används
Holografilab I denna lab kommer ett dubbelexponerat, transmissions hologram göras genom att bygga en holografiuppställning, dubbelexponera och framkalla en holografisk film. Dubbelexponerade hologram används
Hur gör man. Kika försiktigt in genom hålen i luckorna. Vilken färg är det på insidan av lådan? Så fungerar det
 2. Svart låda Hur gör man Kika försiktigt in genom hålen i luckorna. Vilken färg är det på insidan av lådan? Så fungerar det Skåpet: Det enda vi kan se är ljus. Vi kan inte se hundar, bilar, bollar eller
2. Svart låda Hur gör man Kika försiktigt in genom hålen i luckorna. Vilken färg är det på insidan av lådan? Så fungerar det Skåpet: Det enda vi kan se är ljus. Vi kan inte se hundar, bilar, bollar eller
1. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft.
 Problem. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft. (p) Det finns många förklaringar, till exempel Hewitt med insekten
Problem. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft. (p) Det finns många förklaringar, till exempel Hewitt med insekten
1. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (1p)
 Problem Energi. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (p) b) Ge en tydlig förklaring av hur frekvens, period, våglängd och våghastighet hänger
Problem Energi. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (p) b) Ge en tydlig förklaring av hur frekvens, period, våglängd och våghastighet hänger
Geometrisk optik. Laboration
 ... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Geometrisk optik Linser och optiska instrument Avsikten med laborationen är att du ska få träning i att bygga upp avbildande optiska
... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Geometrisk optik Linser och optiska instrument Avsikten med laborationen är att du ska få träning i att bygga upp avbildande optiska
Tentamen i Fotonik - 2013-04-03, kl. 08.00-13.00
 FAFF25-2013-04-03 Tentamen i Fotonik - 2013-04-03, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2013-04-03 Tentamen i Fotonik - 2013-04-03, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Varför har månen faser? Lärarledd demonstration; lämplig för åk 4-5
 Varför har månen faser? Lärarledd demonstration; lämplig för åk 4-5 Syftet med övningen är att eleverna ska förstå vad som orsakar månens faser. Förslag på tillvägagångssätt och material: -- en jordglob
Varför har månen faser? Lärarledd demonstration; lämplig för åk 4-5 Syftet med övningen är att eleverna ska förstå vad som orsakar månens faser. Förslag på tillvägagångssätt och material: -- en jordglob
LABORATION 2 MIKROSKOPET
 LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX (5) Att läsa före lab: LABORATION 2 MIKROSKOPET Synvinkel, vinkelförstoring, luppen och
LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX (5) Att läsa före lab: LABORATION 2 MIKROSKOPET Synvinkel, vinkelförstoring, luppen och
Laboration i Geometrisk Optik
 Laboration i Geometrisk Optik Stockholms Universitet 2014 Kontakt: olga. b ylund@ysik.su.se Instruktioner ör redogörelse ör laboration 1: Laboration 1 innehåller em experiment. Varje experiment bör presenteras
Laboration i Geometrisk Optik Stockholms Universitet 2014 Kontakt: olga. b ylund@ysik.su.se Instruktioner ör redogörelse ör laboration 1: Laboration 1 innehåller em experiment. Varje experiment bör presenteras
EXPERIMENTELLT PROBLEM 1 BESTÄMNING AV LJUSVÅGLÄNGDEN HOS EN LASERDIOD
 EXPERIMENTELLT PROBLEM 1 BESTÄMNING AV LJUSVÅGLÄNGDEN HOS EN LASERDIOD UTRUSTNING Utöver utrustningen 1), 2) and 3), behöver du: 4) Lins monterad på en fyrkantig hållare. (MÄRKNING C). 5) Rakblad i en
EXPERIMENTELLT PROBLEM 1 BESTÄMNING AV LJUSVÅGLÄNGDEN HOS EN LASERDIOD UTRUSTNING Utöver utrustningen 1), 2) and 3), behöver du: 4) Lins monterad på en fyrkantig hållare. (MÄRKNING C). 5) Rakblad i en
