Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid , ) Retinoskopet
|
|
|
- Bengt Lundberg
- för 7 år sedan
- Visningar:
Transkript
1 Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid , ) Retinoskopet Utvecklat från oftalmoskopi under slutet av 1800-talet. Objektiv metod för att bestämma patientens (Px) brytningsfel (sfär, cylinder, axel), kräver alltså ingen aktivitet från Px. Ljus projiceras på Px:s näthinna och retinoskopet rörs fram och tillbaka. Optikern ser den del av ljuset som reflekteras tillbaka ut genom Px:s pupil. Genom att bedöma hur reflexen ser ut och rör sig när optikern vrider retinoskopet med olika provglas framför ögat kan optikern avgöra Px:s brytningsfel. Instrumentets uppbyggnad: Precis som för oftalmoskopet behöver vi ljus som kommer in i Px:s pupill längs med samma linje som optikern tittar. Därför används ofta en lösning med en spegel med ett litet hål i. Spegeln reflekterar ljuset från en ljuskälla (oftast en liten lampa nere i handtaget på retinoskopet) mot Px:s pupill och optikern tittar på reflexen från näthinnan genom hålet i spegeln (kallas för titthål). I denna kurs kommer vi att titta på retinoskopi där ljuset från lampan ger en ljusspalt på Px:s pupill. Spegeln gör alltså att man får en virtuell bild av lampan som ser ut att ligga bakom optikerns huvud. I de flesta retinoskop används även en flyttbar kondensorlins för att avbilda lampan och för att kunna förflytta bilden av lampan (så att man kan växla mellan plan- och konkavspegel effekt). Figuren nedan visar avbildningen av lampan (s) genom kondensorlins och spegel (se Fig i CVO): s = lampan s = mellanbild av lampan efter avbildning i kondensorlinsen s = bild av lampan efter avbildning i den plana spegeln 1
2 För enkelhets skull kommer vi i fortsättningen inte att rita ut avbildningen i lins och spegel utan endast sätta ut bilden av lampan (s ). I figuren nedan är optikerns öga inte utritat men antas sitta precis bakom titthålet. Följande avstånd är utsatta: w = arbetsavstånd mellan Px och titthål. Vanligt avstånd är 2/3 meter d.v.s. W =-1,5 D. x = avståndet mellan Px och bilden av lampan. Vanligt avstånd är 1 meter d.v.s. X =-1 D. Figuren ovan visar ett retinoskop med s.k. planspegel effekt, där ljuset efter spegeln divergerar. Man kan även skjuta kondensorlinsen så att ljuset ut från retinoskopet istället konvergerar och bilden av lampan hamnar mellan retinoskopet och Px:s öga, s.k. konkavspegel effekt. Den del av ljuset som träffar Px:s pupill kommer fortsätta in i ögat och belysa en del av näthinnan. Hur stor den belysta delen blir beror på ögats uppbyggnad och därmed dess brytningsfel. Optikern tittar på det reflekterade ljuset från denna belysta del. Effekt av att vrida retinoskopet: När retinoskopet vrids kommer den belysta fläcken på näthinnan att röra sig åt samma håll. Figuren nedan visar situationen sedd ifrån sidan när optikern vinklat retinoskopet uppåt med vinkel Ɵ, så att handtag förflyttats närmre Px och ljusspalten rör sig uppåt över Px:s öga med vinkel u. Belyst fläck rör sig också uppåt (vinkel u och punkterna U, Q, V). Notera att bilden av lampan (s ) i detta fall går nedåt. 2
3 Bilden av näthinnan ligger i Px:s fjärrpunkt (MR): Optikern tittar på ljuset som reflekteras tillbaka från Px:s näthinnan och avbildas ut genom Px:s öga. Med andra ord tittar optikern på bilden av den belysta fläcken som hamnar i Px:s M R (eftersom objekt placerade i M R avbildas till näthinnan och ses skarpt, så avbildas objekt på näthinnan till M R). I figurerna nedan betecknas bilden av näthinnan med U, Q, V och Px:s brytningsfel K= 1/k. Fall 1: Hyoperopi, där M R ligger bakom ögat (K > 0) Fig 17.9 i CVO Fall 2: Myopi, där M R ligger mellan bilden av lampan och ögat (K < X) Fig 17.7 i CVO Den stora fördelen med att använda sig av M R är att man slipper räkna på avbildning in i ögat, med andra ord behöver vi inte känna till ögats längd och brytkraft för att rita en korrekt bild över hur strålarna går. I kommande figurer kommer därför inte Px:s näthinna ritas ut och endast strålar utanför ögat kommer att ritas. Reflexens utseende: Den belysta fläcken agerar som en ljuskälla som reflekterar tillbaka en del av ljuset och lyser upp patientens pupill bakifrån. Vi kan därför betrakta varje punkt U, Q, V på näthinnan som en liten 3
4 punktkälla som avbildas till U, Q, V i planet för ögats fjärrpunkt. Det reflekterade ljuset kommer alltså ut från Px:s öga som om det kom ifrån (för Fall 1) eller är på väg mot (för Fall 2) U, Q, V. Det kommer alltså alltid att finnas en reflex ut ur Px:s pupill men optikern kan bara se den del av det reflekterade ljuset som passerar genom retinoskopets titthål. I figuren nedan visas ett retinoskop vinklat uppåt för en myop Px: Gröna strålar: ljus från retinoskopet på väg in i Px:s öga. Strålar är utritade från bilden av lampan till pupillens kanter. Bild av den belysta fläcken på näthinnan finns i M R. De gröna strålarna i kanten av pupillen anger kanten på den belysta fläcken både på näthinnan och i M R. Röda strålar: reflekterat ljus ut ut Px:s öga som kan passera titthålet. Strålarna är utritade från kanten av den belysta fläcken i M R till titthålets mitt. Vinkeln ø visar reflexens rörelse. Röd cirkel: markerar storleken på den möjliga reflexen ut ur Px:s öga (förutsätter att pupillen är mycket stor). Storleken bestäms av avståndet mellan de reflekterade (röda) strålarna i Px:s pupillplan. Rödskuggat område i Px:s pupill: verklig reflex som kommer ut ur Px:s pupill och passerar titthålet, så att optikern kan se den. Den verkliga reflexens läge och utbredning i pupillen är den del av den möjliga reflexen som finns inuti pupillen. Reflexens rörelse: I figuren ovan ser vi att den verkliga reflexen endast kommer att synas i nederdelen av Px:s pupill. Eftersom retinoskopet i figuren är vridet uppåt innebär detta att reflexen har gått åt andra hållet d.v.s. vi har fått en motrörelse. Ju mer vi vinklar retinoskopet desto mer neråt rör sig reflexen och till slut kommer den inte längre att synas i Px:s pupill. För en hyperop Px där M R ligger bakom ögat kommer reflexen istället att komma ut ur den övre delen av Px:s pupill, d.v.s. en medrörelse. Denna typ av ritning är tillräcklig för att bedöma reflexens riktning (och även dess hastighet och bredd som vi snart ska titta på) så länge som alla avstånd mellan s, titthål, M R och Px:s öga är skalenliga. Däremot kan man med fördel rita pupillen större för att den verkliga reflexen ska synas ordentligt. 4
5 För retinoskop med planspegel effekt gäller att (fall A och C möts i oändligheten): A: Svag myopi, M R bakom retinoskopets titthål ger medrörelse (ge mer plus) B: Myopi, M R framför retinoskopets titthål ger motrörelse (ge mer minus) C: Hyperopi, M R bakom Px:s öga ger medrörelse (ge mer plus) Detta är illustrerat i figuren nedan (se även fig i CVO). Punkterna A, B, C i figuren motsvarar mitten av bilden av den belysta fläcken i M R (Q ) och den gröna strålen går från bilden av lampan till mitten av Px:s pupill. De streckade linjerna motsvarar den röda mittstrålen för det reflekterade ljuset i de tre fallen och visar var i pupillen reflexen kommer att synas. Om man istället har ställt in retinoskopet på konkavspegel effekt kommer man få motrörelse för fall A och C, och medrörelse för fall B, eftersom bilden av lampan då ligger mellan titthålet och Px:s pupill. Om vi skulle behålla samma vinkel på retinoskopet i figuren ovan skulle s i så fall flytta ifrån att ha varit under och bakom titthålet till att hamna ovanför och framför titthålet. Provlinser, neutralpunkt och retinoskopi-lins: Målet med retinoskoperingen är att placera provglas framför Px:s öga till dess att optikern inte längre ser någon riktning på reflexens rörelse; det bara blinkar till när retinoskopet sveps över ögat. Detta är den s.k. neutralpunkten och innebär att Px:s M RM (fjärrpunkt med glas på) ligger i titthålet. Med andra ord kommer Px:s med detta provglas att vara lite myop, -1,5 D ifall ett arbetsavstånd på 2/3 m används. Detta korrigeras genom att lägga på -1,5 D (eller ta bort +1,5 D) efter att retinoskoperingen är klar. Alternativt kan en retinoskopilins på +1,50 D läggas i provbågen innan retinoskoperingen börjar. I figuren ovan användas K R för att beskriva detta fall. I så fall motsvarar neutralpunkten rätt avståndskorrektion (emmetropi), fall B är myopi med motrörelse och fall A och C är båda hyperopi med medrörelse. 5
6 Den möjliga reflexens hastighet: Vi uttrycker reflexens hastighet som hur mycket reflexen rör sig (ø) jämfört med hur mycket retinoskopet har vridits (Ɵ): = (W X) θ (W K) ekv i CVO OBS! Om det sitter provglas framför ögat betecknar K det kvarstående brytningsfelet. Nära neutralpunkten när K närmar sig W blir hastigheten på reflexen mycket stor Exempel: θ = +1 θ = 0,5 reflexen rör sig lika snabbt och åt samma håll som retinoskopet (medrörelse) reflexen rör sig hälften så snabbt och åt motsatt håll som retinoskopet (motrörelse) Härledning (med beteckningar enligt figuren nedan, se även fig i CVO): = h 2 (w k) vinkel i radianer (negativ i figuren) θ = h 1 (x w) u = h 1 x = h 2 k vinklar i radianer (positiva i figuren) Ametropi-faktor: Hastighetens beroende av ametropi (brytningsfel) = h 2 k = u (w k) h 2 k = (w k) k (k w) = W (W K) Retinoskopi-faktor: Hastighetens beroende av ljuskällans läge Hastighet: θ = u u θ = u θ = h 1 (x w) (x w) (W X) = = x h 1 x W Positiv för planspegel effekt, negativ för konkavspegel effekt W (W X) = (W X) (W K) W (W K) 6
7 Möjliga reflexens bredd: Vi uttrycker reflexens bredd som bredden på den möjliga reflexen () jämfört med pupilldiameter (g): = (K X) g (K W) ekv i CVO OBS! Om det sitter provglas framför ögat betecknar K det kvarstående brytningsfelet. Nära neutralpunkten när K närmar sig W blir reflexen mycket bred Exempel: g = 1 g = 2 möjlig reflex är lika stor som pupillen möjlig reflex är dubbelt så bred som pupillen, men den verkliga reflexen kan aldrig bli större än pupillen. Härledning (med beteckningar enligt figuren nedan, se även fig i CVO): = 2h w (w k) röda likformiga trianglar 2h g = (x k) x gröna likformiga trianglar g = 2h 2h g = w (x k) = (w k) x K (K X) = (K W) K (K X) (K W) 7
8 Reflexens rörelse vid astigmatism: När man sveper ljusspalten över ett astigmatiskt öga kommer reflexens hastighet (och även dess bredd) vara olika längs med ögats två huvudsnitt. Oftast försöker man att svepa längs med huvudsnitten ett i taget för att hitta brytningsfelet i varje huvudsnitt för sig. Exemplet nedan är taget ur CVO (fig 17.29) och visar hur reflexen ser ut om man inte sveper längs med ett huvudsnitt. Exempel: -1,75 / -0,25 x 50, retinoskopet sveps vertikalt nedåt, W=-1,50 D och X=-1,00 D. Titta på varje huvudsnitt för sig med brytningsfelen: K HS140=-2,00 D och K HS50=-1,75 D. Hastigheten på reflexen: θ = (W X) (W K) I HS140: θ = ( 1,50 D ( 1,00 D)) ( 1,50 D ( 2,00 D)) = 1 I HS50: θ = ( 1,50 D ( 1,00 D)) ( 1,50 D ( 1,75 D)) = 2 Figur i CVO är kopierad nedan och följande har gjorts för att rita ut reflexen: Punkten O i mitten betecknar pupillens centrum. Den infallande ljusspalt ritas som en grön horisontell linje (motsvarande mitten av ljusspalten) och eftersom den sveps nedåt ritas den en bit under pupillens centrum. Mät i figuren hur långt ljusspalten har rört sig från pupillens centrum längs med HS140 = 30 mm (O till C). Eftersom hastigheten här är -1 så har reflexen också rört sig 30 mm ifrån pupillens centrum, men åt andra hållet (motrörelse, O till C ). Mät i figuren hur långt ljusspalten har rört sig från pupillens centrum längs med HS50 = 26 mm (O till D). Eftersom hastigheten här är -2 så har reflexen rört sig dubbelt så långt 52 mm ifrån pupillens centrum, men åt andra hållet (motrörelse, O till D ). Reflexen ut ur pupillen kan nu ritas som ett rött streck (C till D, motsvarande mitten av den möjliga reflexen) som har rör sig snett uppåt. 8
3/19/13. Refraktionslära. Refraktionering. Kontrollera visus. Uppskatta felsynthet. Mätning av sfärisk felsynthet
 Refraktionslära Refraktionering Maja Östlund 2013-03-20 Donders metod - Sfär Stråltavla - Korscylinder - Franciscus Cornelis Donders 1818-1889 Kontrollera visus Monokulärt och binokulärt Uppskatta felsynthet
Refraktionslära Refraktionering Maja Östlund 2013-03-20 Donders metod - Sfär Stråltavla - Korscylinder - Franciscus Cornelis Donders 1818-1889 Kontrollera visus Monokulärt och binokulärt Uppskatta felsynthet
Figur 6.1 ur Freeman & Hull, Optics
 1 Föreläsning 12 Kameran Figur 6.1 ur Freeman & Hull, Optics Kameran är ett instrument som till vissa delar fungerar mycket likt ett öga. Kamerans optik, det så kallade kameraobjektivet, motsvarar ögats
1 Föreläsning 12 Kameran Figur 6.1 ur Freeman & Hull, Optics Kameran är ett instrument som till vissa delar fungerar mycket likt ett öga. Kamerans optik, det så kallade kameraobjektivet, motsvarar ögats
Hittills har vi bara använt sfäriska ytor, dvs delar av en sfär. Plana ytor är specialfall av sfär (oändlig krökningsradie, r= ).
 Föreläsning 5 Astigmatism Hittills har vi bara använt sfäriska ytor, dvs delar av en sfär. Plana ytor är specialfall av sfär (oändlig krökningsradie, r= ). Men det finns andra ytor än sfäriska, t.ex. Toriska
Föreläsning 5 Astigmatism Hittills har vi bara använt sfäriska ytor, dvs delar av en sfär. Plana ytor är specialfall av sfär (oändlig krökningsradie, r= ). Men det finns andra ytor än sfäriska, t.ex. Toriska
Föreläsning 3: Radiometri och fotometri
 Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Ögonlaboration 1(1) ÖGONLABORATION
 Ögonlaboration 1(1) Uppsala Universitet Institutionen för Neurovetenskap, Fysiologi VT 08 GS, LJ För Neural reglering och rörelse ÖGONLABORATION Avsikten med laborationen är att illustrera teoretisk bakgrund
Ögonlaboration 1(1) Uppsala Universitet Institutionen för Neurovetenskap, Fysiologi VT 08 GS, LJ För Neural reglering och rörelse ÖGONLABORATION Avsikten med laborationen är att illustrera teoretisk bakgrund
LABORATION 2 MIKROSKOPET
 LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX (5) Att läsa före lab: LABORATION 2 MIKROSKOPET Synvinkel, vinkelförstoring, luppen och
LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX (5) Att läsa före lab: LABORATION 2 MIKROSKOPET Synvinkel, vinkelförstoring, luppen och
Studieanvisning i Optik, Fysik A enligt boken Quanta A
 Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Exempelsamling i Ögats optik
 Exempelsamling i Ögats optik 1. Ett reducerat öga har n =1.336, F=62 och längden 26,2 mm. Vilken av följande linser fungerar bäst för a) avståndsseende och b) närarbete (0,5 m)? (i) +2 D (ii) -9 D (iii)
Exempelsamling i Ögats optik 1. Ett reducerat öga har n =1.336, F=62 och längden 26,2 mm. Vilken av följande linser fungerar bäst för a) avståndsseende och b) närarbete (0,5 m)? (i) +2 D (ii) -9 D (iii)
Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du:
 Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du: A.Mer av dig själv. B.Mindre av dig själv. C.Lika mycket av dig själv. ⱱ Hur hög måste en spegel vara för att du ska
Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du: A.Mer av dig själv. B.Mindre av dig själv. C.Lika mycket av dig själv. ⱱ Hur hög måste en spegel vara för att du ska
Laboration i Geometrisk Optik
 Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
λ = T 2 g/(2π) 250/6 40 m
 Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
OPTIK läran om ljuset
 OPTIK läran om ljuset Vad är ljus Ljuset är en form av energi Ljus är elektromagnetisk strålning som färdas med en hastighet av 300 000 km/s. Ljuset kan ta sig igenom vakuum som är ett utrymme som inte
OPTIK läran om ljuset Vad är ljus Ljuset är en form av energi Ljus är elektromagnetisk strålning som färdas med en hastighet av 300 000 km/s. Ljuset kan ta sig igenom vakuum som är ett utrymme som inte
Geometrisk optik. Syfte och mål. Innehåll. Utrustning. Institutionen för Fysik 2006-04-25
 Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
LABORATION 2 MIKROSKOPET
 LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX 1 (6) LABORATION 2 MIKROSKOPET Att läsa i kursboken: sid. 189-194 Förberedelseuppgifter:
LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX 1 (6) LABORATION 2 MIKROSKOPET Att läsa i kursboken: sid. 189-194 Förberedelseuppgifter:
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 34 - Optik 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Vågrörelselära och optik Kapitel 34 - Optik 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
3) Sag formeln ger r=y 2 /(2s). y=a/2=15 mm, s=b c=4,5 mm ger r=25 mm. Då blir F=(n 1)/r=(1,5 1)/0,025=20 D
 Facit: en avbildning Sfärisk gränsyta 1) l= 2,0 mm, n=4/3 och n =1. m=l/l =nl /(n l)=1,25 ger l = 1,875 mm. Avbildningsformeln för sfärisk gränsyta L =L+(n n)/r ger r= 2,5 mm. 2) Bilden måste hamna på
Facit: en avbildning Sfärisk gränsyta 1) l= 2,0 mm, n=4/3 och n =1. m=l/l =nl /(n l)=1,25 ger l = 1,875 mm. Avbildningsformeln för sfärisk gränsyta L =L+(n n)/r ger r= 2,5 mm. 2) Bilden måste hamna på
Förklara dessa begrepp: Ackommodera Avbildning, Brytning Brytningslagen Brytningsindex Brytningsvinkel Brännvidd Diffus och regelbunden reflektion
 Förklara dessa begrepp: Ackommodera, ögats närinställning, är förmågan att förändra brytkraften i ögats lins. Ljus från en enda punkt på ett avlägset objekt och ljus från en punkt på ett närliggande objekt
Förklara dessa begrepp: Ackommodera, ögats närinställning, är förmågan att förändra brytkraften i ögats lins. Ljus från en enda punkt på ett avlägset objekt och ljus från en punkt på ett närliggande objekt
LABORATION 6 Astigmatism och Distorsion
 LABORATION 6 Astigmatism och Distorsion Personnummer Namn Laborationen godkänd Datum Assistent 1 (5) LABORATION 6: Astigmatism och Distorsion Att läsa i kursboken: sid. 248 257, 261 266, 298 299 Förberedelseuppgifter
LABORATION 6 Astigmatism och Distorsion Personnummer Namn Laborationen godkänd Datum Assistent 1 (5) LABORATION 6: Astigmatism och Distorsion Att läsa i kursboken: sid. 248 257, 261 266, 298 299 Förberedelseuppgifter
LABORATION 1 AVBILDNING OCH FÖRSTORING
 LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
Vad skall vi gå igenom under denna period?
 Ljus/optik Vad skall vi gå igenom under denna period? Vad är ljus? Ljuskälla? Reflektionsvinklar/brytningsvinklar? Färger? Hur fungerar en kikare? Hur fungerar en kamera/ ögat? Var använder vi ljus i vardagen
Ljus/optik Vad skall vi gå igenom under denna period? Vad är ljus? Ljuskälla? Reflektionsvinklar/brytningsvinklar? Färger? Hur fungerar en kikare? Hur fungerar en kamera/ ögat? Var använder vi ljus i vardagen
1. Betrakta en plan harmonisk elektromagnetisk våg i vakuum där det elektriska fältet E uttrycks på följande sätt (i SI-enheter):
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
Föreläsning 11 (kap i Optics)
 45 Föreläsning 11 (kap 5.7-5.8 i Optics) Hittills har vi behandlat avbildningen i sig, dvs. var bilden av ett objekt hamnar och vilken förstoring det blir. Det finns också andra krav man kan ställa på
45 Föreläsning 11 (kap 5.7-5.8 i Optics) Hittills har vi behandlat avbildningen i sig, dvs. var bilden av ett objekt hamnar och vilken förstoring det blir. Det finns också andra krav man kan ställa på
Instuderingsfrågor extra allt
 Instuderingsfrågor extra allt För dig som vill lära dig mer, alla svaren finns inte i häftet. Sök på nätet, fråga en kompis eller läs i en grundbok som du får låna på lektion. Testa dig själv 9.1 1 Vilken
Instuderingsfrågor extra allt För dig som vill lära dig mer, alla svaren finns inte i häftet. Sök på nätet, fråga en kompis eller läs i en grundbok som du får låna på lektion. Testa dig själv 9.1 1 Vilken
Optik. Läran om ljuset
 Optik Läran om ljuset Vad är ljus? Ljus är en form av energi. Ljus är elektromagnetisk strålning. Energi kan inte försvinna eller nyskapas. Ljuskälla Föremål som skickar ut ljus. I alla ljuskällor sker
Optik Läran om ljuset Vad är ljus? Ljus är en form av energi. Ljus är elektromagnetisk strålning. Energi kan inte försvinna eller nyskapas. Ljuskälla Föremål som skickar ut ljus. I alla ljuskällor sker
Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från vänster, sträcka i ljusets riktning = positiv
 Avbildningskvalitet Föreläsning 1 2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Avbildningskvalitet Föreläsning 1 2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Vågfysik. Geometrisk optik. Knight Kap 23. Ljus. Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion)
 Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
Vågrörelselära & Kvantfysik, FK2002 29 november 2011
 Räkneövning 5 Vågrörelselära & Kvantfysik, FK00 9 november 0 Problem 35.9 En dykare som befinner sig på djupet D 3 m under vatten riktar en ljusstråle (med infallsvinkel θ i 30 ) mot vattenytan. På vilket
Räkneövning 5 Vågrörelselära & Kvantfysik, FK00 9 november 0 Problem 35.9 En dykare som befinner sig på djupet D 3 m under vatten riktar en ljusstråle (med infallsvinkel θ i 30 ) mot vattenytan. På vilket
Hur gör man. Stick in handen i den skålformade spegeln och hälsa på dig själv! Så fungerar det
 8. Spökhanden Hur gör man Stick in handen i den skålformade spegeln och hälsa på dig själv! Så fungerar det I en vanlig (plan) spegel ser spegelbilden ut att befinna sig en bit bakom spegelytan, men när
8. Spökhanden Hur gör man Stick in handen i den skålformade spegeln och hälsa på dig själv! Så fungerar det I en vanlig (plan) spegel ser spegelbilden ut att befinna sig en bit bakom spegelytan, men när
Extramaterial till Matematik Y
 LIBER PROGRAMMERING OCH DIGITAL KOMPETENS Extramaterial till Matematik Y NIVÅ TVÅ Geometri ELEV Desmos Geometry är ett matematikverktyg som bland annat kan hjälpa dig att avbilda geometriska figurer och
LIBER PROGRAMMERING OCH DIGITAL KOMPETENS Extramaterial till Matematik Y NIVÅ TVÅ Geometri ELEV Desmos Geometry är ett matematikverktyg som bland annat kan hjälpa dig att avbilda geometriska figurer och
Övning 9 Tenta från Del A. Vägg på avståndet r = 2.0 m och med reflektansen R = 0.9. Lambertspridare.
 Övning 9 Tenta från 2016-08-24 Del A 1.) Du lyser med en ficklampa rakt mot en vit vägg. Vilken luminans får väggen i mitten av det belysta området? Ficklampan har en ljusstyrka på 70 cd och du står 2.0
Övning 9 Tenta från 2016-08-24 Del A 1.) Du lyser med en ficklampa rakt mot en vit vägg. Vilken luminans får väggen i mitten av det belysta området? Ficklampan har en ljusstyrka på 70 cd och du står 2.0
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Övning 3 Fotometri. En källa som sprider ljus diffust kallas Lambertstrålare. Ex. bioduk, snö, papper.
 Övning 3 Fotometri Rymdvinkel: Ω [sr] Ω = π(1 cos(u)) πu Ω = r Ljusflöde: [lm] Ljusstyrka: I v = Ω [cd=lm/sr] u r Belysning: E v = A belyst [lx=lm/m ] Ljusemissionsförmåga: M v = A källa [lm/m ] Luminans:
Övning 3 Fotometri Rymdvinkel: Ω [sr] Ω = π(1 cos(u)) πu Ω = r Ljusflöde: [lm] Ljusstyrka: I v = Ω [cd=lm/sr] u r Belysning: E v = A belyst [lx=lm/m ] Ljusemissionsförmåga: M v = A källa [lm/m ] Luminans:
Övning 9 Tenta
 Övning 9 Tenta 014-11-8 1. När ljus faller in från luft mot ett genomskinligt material, med olika infallsvinkel, blir reflektansen den som visas i grafen nedan. Ungefär vilket brytningsindex har materialet?
Övning 9 Tenta 014-11-8 1. När ljus faller in från luft mot ett genomskinligt material, med olika infallsvinkel, blir reflektansen den som visas i grafen nedan. Ungefär vilket brytningsindex har materialet?
Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från vänster, sträcka i ljusets riktning = positiv
 Avbildningskvalitet Föreläsning 1-2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Avbildningskvalitet Föreläsning 1-2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Ljuskällor. För att vi ska kunna se något måste det finnas en ljuskälla
 Ljus/optik Ljuskällor För att vi ska kunna se något måste det finnas en ljuskälla En ljuskälla är ett föremål som själv sänder ut ljus t ex solen, ett stearinljus eller en glödlampa Föremål som inte själva
Ljus/optik Ljuskällor För att vi ska kunna se något måste det finnas en ljuskälla En ljuskälla är ett föremål som själv sänder ut ljus t ex solen, ett stearinljus eller en glödlampa Föremål som inte själva
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER
 EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
EXPERIMENTELLT PROBLEM 2 DUBBELBRYTNING HOS GLIMMER I detta experiment ska du mäta graden av dubbelbrytning hos glimmer (en kristall som ofta används i polariserande optiska komponenter). UTRUSTNING Förutom
Syfte: Att se hur ljuset reflekteras i konkava och konvexa speglar. Men även i andra plana speglar.
 Ljusets reflektion Syfte: Att se hur ljuset reflekteras i konkava och konvexa speglar. Men även i andra plana speglar. Material: Optisk bänk Spänningskub Lins +10 Optiklampa Spalt med 5 spalter Spalthållare
Ljusets reflektion Syfte: Att se hur ljuset reflekteras i konkava och konvexa speglar. Men även i andra plana speglar. Material: Optisk bänk Spänningskub Lins +10 Optiklampa Spalt med 5 spalter Spalthållare
Föreläsning 2 (kap , 2.6 i Optics)
 5 Föreläsning 2 (kap 1.6-1.12, 2.6 i Optics) Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen
5 Föreläsning 2 (kap 1.6-1.12, 2.6 i Optics) Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen
Vi är beroende av ljuset för att kunna leva. Allt liv på jorden skulle ta slut och jordytan skulle bli öde och tyst om vi inte hade haft ljus.
 Källa: Fysik - Kunskapsträdet Vi är beroende av ljuset för att kunna leva. Allt liv på jorden skulle ta slut och jordytan skulle bli öde och tyst om vi inte hade haft ljus. Ljusets natur Ljusets inverkan
Källa: Fysik - Kunskapsträdet Vi är beroende av ljuset för att kunna leva. Allt liv på jorden skulle ta slut och jordytan skulle bli öde och tyst om vi inte hade haft ljus. Ljusets natur Ljusets inverkan
Ljus, syn & strålning
 Ljus, syn & strålning Namn: Klass: 8G Ljus, syn och strålning Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och
Ljus, syn & strålning Namn: Klass: 8G Ljus, syn och strålning Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och
Lösningarna inlämnas renskrivna vid laborationens början till handledaren
 Geometrisk optik Förberedelser Läs i vågläraboken om avbildning med linser (sid 227 241), ögat (sid 278 281), färg och färgseende (sid 281 285), glasögon (sid 287 290), kameran (sid 291 299), vinkelförstoring
Geometrisk optik Förberedelser Läs i vågläraboken om avbildning med linser (sid 227 241), ögat (sid 278 281), färg och färgseende (sid 281 285), glasögon (sid 287 290), kameran (sid 291 299), vinkelförstoring
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 1 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus kan ses so elektroagnetiska vågor so rör sig fraåt. När vi ritar strålar
1 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus kan ses so elektroagnetiska vågor so rör sig fraåt. När vi ritar strålar
Att räkna med mellanbilder genom ett system med många linser och gränsytor blir krångligt. Vi vill kunna avbilda genom alla ytor direkt.
 Föreläsning 9 0 Huvudplan Önskan: Tänk om alla optiska system vore tunna linser så att alltid gällde! Att räkna med mellanbilder genom ett system med många linser och gränsytor blir krångligt. Vi vill
Föreläsning 9 0 Huvudplan Önskan: Tänk om alla optiska system vore tunna linser så att alltid gällde! Att räkna med mellanbilder genom ett system med många linser och gränsytor blir krångligt. Vi vill
Bästa optotyp för retinoskopi
 Institutionen för naturvetenskap Examensarbete Bästa optotyp för retinoskopi Lucien ElAwad Huvudområde: Optometri Nivå: Grundnivå Nr: 2011: O4 Bästa optotyp för retinoskopi Lucien ElAwad Examensarbete
Institutionen för naturvetenskap Examensarbete Bästa optotyp för retinoskopi Lucien ElAwad Huvudområde: Optometri Nivå: Grundnivå Nr: 2011: O4 Bästa optotyp för retinoskopi Lucien ElAwad Examensarbete
Geometrisk optik. Laboration
 ... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Geometrisk optik Linser och optiska instrument Avsikten med laborationen är att du ska få träning i att bygga upp avbildande optiska
... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Geometrisk optik Linser och optiska instrument Avsikten med laborationen är att du ska få träning i att bygga upp avbildande optiska
Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material?
 1 Föreläsning 2 Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen på samma sida är reflekterat
1 Föreläsning 2 Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen på samma sida är reflekterat
Fysik A A B C D. Sidan 1 av 9 henrik.gyllensten@tabyenskilda.se. www.tabyenskilda.se/fy
 www.tabyenskilda.se/y ÖÖvvnni iinn ggssuuppppggi ii teer 1. Lars lyser med en icklampa mot ett prisma. Han kan då se ett spektrum på väggen bakom prismat. Spektrumet innehåller alla ärger. Vilken av dessa
www.tabyenskilda.se/y ÖÖvvnni iinn ggssuuppppggi ii teer 1. Lars lyser med en icklampa mot ett prisma. Han kan då se ett spektrum på väggen bakom prismat. Spektrumet innehåller alla ärger. Vilken av dessa
Teckenkonventionen: ljus in från vänster, ljusets riktning = positiv
 1 Avbildningskvalitet Föreläsning 1-2 Brytning i sfärisk yta Teckenkonventionen: ljus in från vänster, ljusets riktning = positiv Brytningslagen (Snells lag): n sin i = n sin i Paraxial approximation (vid
1 Avbildningskvalitet Föreläsning 1-2 Brytning i sfärisk yta Teckenkonventionen: ljus in från vänster, ljusets riktning = positiv Brytningslagen (Snells lag): n sin i = n sin i Paraxial approximation (vid
Föreläsning 9-10 (kap i Optics)
 38 Föreläsning 9-0 (kap 5.-5.6 i Optics) Huvudplan Önskan: Tänk om alla optiska system vore tunna linser så att L = L + F alltid gällde! Att räkna med mellanbilder genom ett system med många linser och
38 Föreläsning 9-0 (kap 5.-5.6 i Optics) Huvudplan Önskan: Tänk om alla optiska system vore tunna linser så att L = L + F alltid gällde! Att räkna med mellanbilder genom ett system med många linser och
1. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft.
 Problem. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft. (p) Det finns många förklaringar, till exempel Hewitt med insekten
Problem. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft. (p) Det finns många förklaringar, till exempel Hewitt med insekten
ÖGONPÅVERKAN VID NÄRAKTIVITET Yvonne Löf, ortoptist Ögonmott. Växjö
 ÖGONPÅVERKAN VID NÄRAKTIVITET 170202 Yvonne Löf, ortoptist Ögonmott. Växjö 170202 Yvonne Löf, ortoptist ANATOMI ANATOMI ÖGONMUSKLER För att kunna se tydligt måste bilden hamna i gula fläcken. Riktningen
ÖGONPÅVERKAN VID NÄRAKTIVITET 170202 Yvonne Löf, ortoptist Ögonmott. Växjö 170202 Yvonne Löf, ortoptist ANATOMI ANATOMI ÖGONMUSKLER För att kunna se tydligt måste bilden hamna i gula fläcken. Riktningen
Hur gör man. Kika försiktigt in genom hålen i luckorna. Vilken färg är det på insidan av lådan? Så fungerar det
 2. Svart låda Hur gör man Kika försiktigt in genom hålen i luckorna. Vilken färg är det på insidan av lådan? Så fungerar det Skåpet: Det enda vi kan se är ljus. Vi kan inte se hundar, bilar, bollar eller
2. Svart låda Hur gör man Kika försiktigt in genom hålen i luckorna. Vilken färg är det på insidan av lådan? Så fungerar det Skåpet: Det enda vi kan se är ljus. Vi kan inte se hundar, bilar, bollar eller
Ovanstående figure beskriver ögonens konvergens vid två olika objektsavstånd (blått fall och grönt fall). Geometrin ger: 2 L
 3D-seende och 3D-visualisering Människans avståndsuppfattning bigger på flera olika stimuli från synsinnet. Det primära är emellertid konvergensen, dvs hur mycket ögonen behöver vinklas (skela), för att
3D-seende och 3D-visualisering Människans avståndsuppfattning bigger på flera olika stimuli från synsinnet. Det primära är emellertid konvergensen, dvs hur mycket ögonen behöver vinklas (skela), för att
Gauss Linsformel (härledning)
 α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
Text, Sofia Ström. Foto, Ellen Kleiman. Ljusets reflektion. Syfte: Se hur ljusets reflekteras i konkava och konvexa speglar. Material: Optisk bänk
 Text, Sofia Ström. Foto, Ellen Kleiman. Ljusets reflektion Syfte: Se hur ljusets reflekteras i konkava och konvexa speglar. Optisk bänk Spänningskub Lins +10 Optiklampa Spalt med 5 spalter Spalthållare
Text, Sofia Ström. Foto, Ellen Kleiman. Ljusets reflektion Syfte: Se hur ljusets reflekteras i konkava och konvexa speglar. Optisk bänk Spänningskub Lins +10 Optiklampa Spalt med 5 spalter Spalthållare
OBS: Alla mätningar och beräknade värden ska anges i SI-enheter med korrekt antal värdesiffror. Felanalys behövs endast om det anges i texten.
 Speed of light OBS: Alla mätningar och beräknade värden ska anges i SI-enheter med korrekt antal värdesiffror. Felanalys behövs endast om det anges i texten. 1.0 Inledning Experiment med en laseravståndsmätare
Speed of light OBS: Alla mätningar och beräknade värden ska anges i SI-enheter med korrekt antal värdesiffror. Felanalys behövs endast om det anges i texten. 1.0 Inledning Experiment med en laseravståndsmätare
About the optics of the eye
 About the optics of the eye Peter Unsbo Kungliga Tekniska Högskolan Biomedical and x-ray physics Visual Optics Innehåll Optiska begränsningar i ögat Hur mäter man ögats aberrationer? Hur skriver man vågfrontsrecept?
About the optics of the eye Peter Unsbo Kungliga Tekniska Högskolan Biomedical and x-ray physics Visual Optics Innehåll Optiska begränsningar i ögat Hur mäter man ögats aberrationer? Hur skriver man vågfrontsrecept?
Våglära och optik FAFF30 JOHAN MAURITSSON
 Våglära och optik FAFF30 JOHAN MAURITSSON Prismor A θ 1 n=1 n n=1 2 Prismor A δ 1 θ 1 θ 1 n=1 n n=1 3 Prismor A θ 2 θ 2 n=1 n n=1 4 Prismor A δ θ 1 θ 1 δ 1 δ 2 B θ 2 θ 2 n=1 n n=1 5 Prismor, dispersion
Våglära och optik FAFF30 JOHAN MAURITSSON Prismor A θ 1 n=1 n n=1 2 Prismor A δ 1 θ 1 θ 1 n=1 n n=1 3 Prismor A θ 2 θ 2 n=1 n n=1 4 Prismor A δ θ 1 θ 1 δ 1 δ 2 B θ 2 θ 2 n=1 n n=1 5 Prismor, dispersion
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
Ljus och strålning. Klass: 9H
 Ljus och strålning Namn: Klass: 9H Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och samhället genomföra systematiska
Ljus och strålning Namn: Klass: 9H Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och samhället genomföra systematiska
Version UB141104. Matematiska beräkningar av toppunktsavstånd, ack etc görs i kursen Ögats optik
 Grundläggande optometri 1 Ämneslista Vetenskapliga strimman Artikelläsning se separat dokument Ametropier sfäriska MR MP Ackommodationsvidd Ackommodationsområde Emmetropi Myopi Konsekvens av ackommodation
Grundläggande optometri 1 Ämneslista Vetenskapliga strimman Artikelläsning se separat dokument Ametropier sfäriska MR MP Ackommodationsvidd Ackommodationsområde Emmetropi Myopi Konsekvens av ackommodation
Tentamen i Fotonik - 2015-08-21, kl. 08.00-13.00
 Tentamen i Fotonik - 2015-08-21, kl. 08.00-13.00 Tentamen i Fotonik 2011 08 25, kl. 08.00 13.00 FAFF25-2015-08-21 FAFF25 2011 08 25 FAFF25 2011 08 25 FAFF25 FAFF25 - Tentamen Fysik för Fysik C och i för
Tentamen i Fotonik - 2015-08-21, kl. 08.00-13.00 Tentamen i Fotonik 2011 08 25, kl. 08.00 13.00 FAFF25-2015-08-21 FAFF25 2011 08 25 FAFF25 2011 08 25 FAFF25 FAFF25 - Tentamen Fysik för Fysik C och i för
Övning 4 Polarisation
 Övning 4 Polarisation Transmission genom ett polarisationsfilter Malus lag: I 1 = cos 2 (θ) θ I 1 Reflektion och transmission I R Polariserat! Opolariserat i B n n i B I T Brewstervinkeln (polarisation
Övning 4 Polarisation Transmission genom ett polarisationsfilter Malus lag: I 1 = cos 2 (θ) θ I 1 Reflektion och transmission I R Polariserat! Opolariserat i B n n i B I T Brewstervinkeln (polarisation
Geometrisk optik. Innehåll. Inledning. Litteraturhänvisning. Förberedelseuppgifter. Geometrisk optik
 Geometrisk optik Innehåll Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande 1. Undersökning av tunna positiva linser... 3 2. Undersökning av tunna negativa linser... 3 3. Galileikikaren...
Geometrisk optik Innehåll Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande 1. Undersökning av tunna positiva linser... 3 2. Undersökning av tunna negativa linser... 3 3. Galileikikaren...
Intromatte för optikerstudenter 2018
 Intromatte för optikerstudenter 018 Rabia Akan rabiaa@kth.se Av Robert Rosén (01). Ändringar av Daniel Larsson, Jakob Larsson, Emelie Fogelqvist, Simon Winter och Rabia Akan (01-017). Kursmål Efter intromatten
Intromatte för optikerstudenter 018 Rabia Akan rabiaa@kth.se Av Robert Rosén (01). Ändringar av Daniel Larsson, Jakob Larsson, Emelie Fogelqvist, Simon Winter och Rabia Akan (01-017). Kursmål Efter intromatten
för M Skrivtid i hela (1,0 p) 3 cm man bryningsindex i glaset på ett 2. två spalter (3,0 p)
 Tentamen i tillämpad Våglära FAF260, 2016 06 01 för M Skrivtid 08.00 13.00 Hjälpmedel: Formelblad och miniräknare Uppgifterna är inte sorteradee i svårighetsgrad Börja varje ny uppgift på ett nytt blad
Tentamen i tillämpad Våglära FAF260, 2016 06 01 för M Skrivtid 08.00 13.00 Hjälpmedel: Formelblad och miniräknare Uppgifterna är inte sorteradee i svårighetsgrad Börja varje ny uppgift på ett nytt blad
VIDVINKELOFTALMOSKOP BRUKSANVISNING
 VIDVINKELOFTALMOSKOP BRUKSANVISNING LÄS IGENOM ANVISNINGARNA OCH FÖLJ DEM NOGA Innehåll 1. Symboler 2. Varningar och försiktighetsåtgärder 3. Beskrivning av produkten 4. Komma igång 5. Apertur och filter
VIDVINKELOFTALMOSKOP BRUKSANVISNING LÄS IGENOM ANVISNINGARNA OCH FÖLJ DEM NOGA Innehåll 1. Symboler 2. Varningar och försiktighetsåtgärder 3. Beskrivning av produkten 4. Komma igång 5. Apertur och filter
Observera också att det inte går att både se kanten på fönstret och det där ute tydligt samtidigt.
 Om förstoringsglaset Du kan göra mycket med bara ett förstoringsglas! I många sammanhang i det dagliga livet förekommer linser. Den vanligast förekommande typen är den konvexa linsen, den kallas också
Om förstoringsglaset Du kan göra mycket med bara ett förstoringsglas! I många sammanhang i det dagliga livet förekommer linser. Den vanligast förekommande typen är den konvexa linsen, den kallas också
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 21 augusti 2008 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 1 augusti 008 kl 9-15 Hjälpmedel: handbok och räknare. Varje uppgift ger maximalt 4 poäng. Var
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 hp, FK4009 Torsdagen den 1 augusti 008 kl 9-15 Hjälpmedel: handbok och räknare. Varje uppgift ger maximalt 4 poäng. Var
Information om glasögon. Varför barn kan behöva glasögon.
 Information om glasögon. Varför barn kan behöva glasögon. Ögats lins skall liksom linsen i en kamera skapa en skarp bild av omvärlden. I kameran ligger bilden på filmen och i ögat ligger bilden på näthinnan
Information om glasögon. Varför barn kan behöva glasögon. Ögats lins skall liksom linsen i en kamera skapa en skarp bild av omvärlden. I kameran ligger bilden på filmen och i ögat ligger bilden på näthinnan
Geometrisk optik. Laboration FAFF25/FAFA60 Fotonik 2017
 Avsikten med denna laboration är att du ska få träning i att bygga upp avbildande optiska system, såsom enkla kikare och mikroskop, och på så vis få en god förståelse för dessas funktion. Redogörelsen
Avsikten med denna laboration är att du ska få träning i att bygga upp avbildande optiska system, såsom enkla kikare och mikroskop, och på så vis få en god förståelse för dessas funktion. Redogörelsen
Elektromagnetiska vågor (Ljus)
 Föreläsning 4-5 Elektromagnetiska vågor (Ljus) Ljus kan beskrivas som bestående av elektromagnetiska vågrörelser, d.v.s. ett tids- och rumsvarierande elektriskt och magnetiskt fält. Dessa ljusvågor följer
Föreläsning 4-5 Elektromagnetiska vågor (Ljus) Ljus kan beskrivas som bestående av elektromagnetiska vågrörelser, d.v.s. ett tids- och rumsvarierande elektriskt och magnetiskt fält. Dessa ljusvågor följer
3. Mekaniska vågor i 2 (eller 3) dimensioner
 3. Mekaniska vågor i 2 (eller 3) dimensioner Brytning av vågor som passerar gränsen mellan två material Eftersom utbredningshastigheten för en mekanisk våg med största sannolikhet ändras då den passerar
3. Mekaniska vågor i 2 (eller 3) dimensioner Brytning av vågor som passerar gränsen mellan två material Eftersom utbredningshastigheten för en mekanisk våg med största sannolikhet ändras då den passerar
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
5. Elektromagnetiska vågor - interferens
 Interferens i dubbelspalt A λ/2 λ/2 Dal för ena vågen möter topp för den andra och vice versa => mörkt (amplitud = 0). Dal möter dal och topp möter topp => ljust (stor amplitud). B λ/2 Fig. 5.1 För ljusvågor
Interferens i dubbelspalt A λ/2 λ/2 Dal för ena vågen möter topp för den andra och vice versa => mörkt (amplitud = 0). Dal möter dal och topp möter topp => ljust (stor amplitud). B λ/2 Fig. 5.1 För ljusvågor
Kapitel 35, interferens
 Kapitel 35, interferens Interferens hos ljusvågor, koherensbegreppet Samband för max och min för ideal dubbelspalt Samband för intensitetsvariation för ideal dubbelspalt Interferens i tunna filmer Michelson
Kapitel 35, interferens Interferens hos ljusvågor, koherensbegreppet Samband för max och min för ideal dubbelspalt Samband för intensitetsvariation för ideal dubbelspalt Interferens i tunna filmer Michelson
Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00
 FAFF25-2014-04-25 Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2014-04-25 Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Optik. Inledning. Fig. 1. Hålkameran
 Optik Inledning En stor del av den information som vi får från vår omgivning kommer till oss i form av ljus. I ögat omformas denna information till bilder som i hjärnan bearbetas och analyseras. Det sätt
Optik Inledning En stor del av den information som vi får från vår omgivning kommer till oss i form av ljus. I ögat omformas denna information till bilder som i hjärnan bearbetas och analyseras. Det sätt
Läs i vågläraboken om holografi (sid ) och sid 5 17 i detta kompendium.
 1 Förberedelser Läs i vågläraboken om holografi (sid 370-372) och sid 5 17 i detta kompendium. Gör följande uppgifter: Lösningarna inlämnas renskrivna vid laborationens början till handledaren för kontroll.
1 Förberedelser Läs i vågläraboken om holografi (sid 370-372) och sid 5 17 i detta kompendium. Gör följande uppgifter: Lösningarna inlämnas renskrivna vid laborationens början till handledaren för kontroll.
Uppgifter. Uppgifter. Uppgift 2. Uppgift 1
 Uppgift 1 Uppgift 2 Det första målet är att beräkna vinkeldiametern på ringen, det vill säga ringens apparenta diameter sedd från jorden i bågsekunder. Detta är vinkel a. De relativa positionerna för stjärnorna
Uppgift 1 Uppgift 2 Det första målet är att beräkna vinkeldiametern på ringen, det vill säga ringens apparenta diameter sedd från jorden i bågsekunder. Detta är vinkel a. De relativa positionerna för stjärnorna
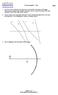
Parabeln och vad man kan ha den till
 Parabeln och vad man kan ha den till Anders Källén MatematikCentrum LTH anderskallen@gmail.com Sammanfattning I det här dokumentet diskuterar vi vad parabeln är för geometrisk konstruktion och varför den
Parabeln och vad man kan ha den till Anders Källén MatematikCentrum LTH anderskallen@gmail.com Sammanfattning I det här dokumentet diskuterar vi vad parabeln är för geometrisk konstruktion och varför den
Ljusets böjning och interferens
 Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen ska du studera två centrala vågfenomen: interferens och böjning. Du kommer bl.a. att studera hur ljusvågor böjs när de passerar
Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen ska du studera två centrala vågfenomen: interferens och böjning. Du kommer bl.a. att studera hur ljusvågor böjs när de passerar
PLISSEGARDIN PREMIUM. Monteringsoch bruksanvisning. Plisségardiner med handtag
 PLISSEGARDIN PREMIUM Monteringsoch bruksanvisning Plisségardiner med handtag A400 (BB 10) A410 (BB 20) A415 (BB 24) För att kunna säkerställa en problemfri funktion av plisségardinen krävs det att produkten
PLISSEGARDIN PREMIUM Monteringsoch bruksanvisning Plisségardiner med handtag A400 (BB 10) A410 (BB 20) A415 (BB 24) För att kunna säkerställa en problemfri funktion av plisségardinen krävs det att produkten
Holografi. Förberedelser. Referensvåg. Konstruktiv interferens. Läs i vågläraboken om holografi (sid ) och hela laborationsinstruktionen.
 Holografi Förberedelser Läs i vågläraboken om holografi (sid 370 372) och hela laborationsinstruktionen. Referensvåg 50 Objektvåg Gör följande uppgifter: Lösningarna inlämnas renskrivan vid laborationens
Holografi Förberedelser Läs i vågläraboken om holografi (sid 370 372) och hela laborationsinstruktionen. Referensvåg 50 Objektvåg Gör följande uppgifter: Lösningarna inlämnas renskrivan vid laborationens
Laboration i Geometrisk Optik
 Laboration i Geometrisk Optik Stockholms Universitet 2014 Kontakt: olga. b ylund@ysik.su.se Instruktioner ör redogörelse ör laboration 1: Laboration 1 innehåller em experiment. Varje experiment bör presenteras
Laboration i Geometrisk Optik Stockholms Universitet 2014 Kontakt: olga. b ylund@ysik.su.se Instruktioner ör redogörelse ör laboration 1: Laboration 1 innehåller em experiment. Varje experiment bör presenteras
Fysik. Ämnesprov, läsår 2012/2013. Delprov C. Årskurs. Elevens namn och klass/grupp
 Ämnesprov, läsår 2012/2013 Fysik Delprov C Årskurs 6 Elevens namn och klass/grupp Prov som återanvänds omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta prov återanvänds t.o.m.
Ämnesprov, läsår 2012/2013 Fysik Delprov C Årskurs 6 Elevens namn och klass/grupp Prov som återanvänds omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta prov återanvänds t.o.m.
Tentamen i Våglära och optik för F
 Tentamen i Våglära och optik för F FAFF30, 2013 06 03 Skrivtid 8.00 13.00 Hjälpmedel: Läroboken och miniräknare Uppgifterna är inte sorterade i svårighetsgrad Börja varje ny uppgift på ett nytt blad och
Tentamen i Våglära och optik för F FAFF30, 2013 06 03 Skrivtid 8.00 13.00 Hjälpmedel: Läroboken och miniräknare Uppgifterna är inte sorterade i svårighetsgrad Börja varje ny uppgift på ett nytt blad och
Laboration 1 Fysik
 Laboration 1 Fysik 2 2015 : Fysik 2 för tekniskt/naturvetenskapligt basår Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen på
Laboration 1 Fysik 2 2015 : Fysik 2 för tekniskt/naturvetenskapligt basår Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen på
Om ellipsen och hyperbelns optiska egenskaper
 Om ellipsen och hyperbelns optiska egenskaper Anders Källén MatematikCentrum LTH anderskallen@gmail.com Sammanfattning Ellipser och hyperbler är, liksom parabeln, s.k. kägelsnitt, dvs kurvor som uppkommer
Om ellipsen och hyperbelns optiska egenskaper Anders Källén MatematikCentrum LTH anderskallen@gmail.com Sammanfattning Ellipser och hyperbler är, liksom parabeln, s.k. kägelsnitt, dvs kurvor som uppkommer
Ljusets böjning & interferens
 Ljusets böjning & interferens Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter 3 Appendix Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen
Ljusets böjning & interferens Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter 3 Appendix Ljusets vågegenskaper Ljus kan liksom ljud beskrivas som vågrörelser och i den här laborationen
8. TRE- OCH FYRDUBBEL HUVUDBELYSNING
 8. TRE- OCH FYRDUBBEL HUVUDBELYSNING TREDUBBEL HUVUDBELYSNING Letar du efter ett mjukt ljus med en del sting i? Du har kommit till rätt kapitel. Den här tekniken liknar på sätt och vis den med två ljuskällor
8. TRE- OCH FYRDUBBEL HUVUDBELYSNING TREDUBBEL HUVUDBELYSNING Letar du efter ett mjukt ljus med en del sting i? Du har kommit till rätt kapitel. Den här tekniken liknar på sätt och vis den med två ljuskällor
Optik Synen och ögats behov. Hillevi Hemphälä Leg Optiker, licentiat, doktorand hillevi.hemphala@design.lth.se
 Optik Synen och ögats behov Hillevi Hemphälä Leg Optiker, licentiat, doktorand hillevi.hemphala@design.lth.se Ögats synfält -50 o 2 o 30 o Syngropen Gula fläcken, centrala seendet Synnerven -70 o Sidled-
Optik Synen och ögats behov Hillevi Hemphälä Leg Optiker, licentiat, doktorand hillevi.hemphala@design.lth.se Ögats synfält -50 o 2 o 30 o Syngropen Gula fläcken, centrala seendet Synnerven -70 o Sidled-
Böjning. Tillämpad vågrörelselära. Föreläsningar. Vad är optik? Huygens princip. Böjning vs. interferens FAF260. Lars Rippe, Atomfysik/LTH 1
 Tillämpad vågrörelselära 2 Föreläsningar Vad är optik? F10 och upplösning (kap 16) F11 Interferens och böjning (kap 17) F12 Multipelinterferens (kap 18) F13 Polariserat ljus (kap 20) F14 Reserv / Repetition
Tillämpad vågrörelselära 2 Föreläsningar Vad är optik? F10 och upplösning (kap 16) F11 Interferens och böjning (kap 17) F12 Multipelinterferens (kap 18) F13 Polariserat ljus (kap 20) F14 Reserv / Repetition
Tentamen i Fotonik , kl
 FAFF25-2015-03-20 Tentamen i Fotonik - 2015-03-20, kl. 14.00-19.15 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2015-03-20 Tentamen i Fotonik - 2015-03-20, kl. 14.00-19.15 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
TENTAMEN I TILLÄMPAD VÅGLÄRA FÖR M
 TENTAMEN I TILLÄMPAD VÅGLÄRA FÖR M 2012-01-13 Skrivtid: 8.00 13.00 Hjälpmedel: Formelblad och räknedosa. Uppgifterna är inte ordnade efter svårighetsgrad. Börja varje ny uppgift på ett nytt blad och skriv
TENTAMEN I TILLÄMPAD VÅGLÄRA FÖR M 2012-01-13 Skrivtid: 8.00 13.00 Hjälpmedel: Formelblad och räknedosa. Uppgifterna är inte ordnade efter svårighetsgrad. Börja varje ny uppgift på ett nytt blad och skriv
Tentamen i Vågor och Optik 5hp F, Q, kandfys, gylärfys-programm, den 15. mars 2010
 Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 14-19 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 14-19 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Laboration i Geometrisk Optik
 Laboration i Geometrisk Optik Stockholms Universitet 2002 Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och relektionslagen 2 4 Linser 2 4.1 Att rita strålgångar........................
Laboration i Geometrisk Optik Stockholms Universitet 2002 Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och relektionslagen 2 4 Linser 2 4.1 Att rita strålgångar........................
Tentamen i Optik FFY091
 Tentamen i Optik FFY091 Måndag 22 augusti 2016, kl. 14:00 18:00 För tentan gäller följande Jourhavande lärare: Ewa Simpanen, finns på plats ca kl 15:30 och 17, samt Jörgen Bengtsson, telefon 031 772 1591
Tentamen i Optik FFY091 Måndag 22 augusti 2016, kl. 14:00 18:00 För tentan gäller följande Jourhavande lärare: Ewa Simpanen, finns på plats ca kl 15:30 och 17, samt Jörgen Bengtsson, telefon 031 772 1591
