Optik. Inledning. Fig. 1. Hålkameran
|
|
|
- Sara Samuelsson
- för 8 år sedan
- Visningar:
Transkript
1 Optik Inledning En stor del av den information som vi får från vår omgivning kommer till oss i form av ljus. I ögat omformas denna information till bilder som i hjärnan bearbetas och analyseras. Det sätt vi tolkar och påverkas av de signaler av ljus som når oss är ganska komplicerat, medan steget från objekt till bild är ganska bra utrett fysikaliskt. Låt oss titta på ett enkelt avbildningssystem, hålkameran (Fig. 1.). Fig. 1. Hålkameran Varje punkt på objektet ger upphov till en ljusfläck i kamerans botten. Man borde vänta sig att om man minskar hålet i kameran mer och mer så skulle bilden bli skarpare och skarpare. Så är inte fallet utan man når en gräns då bilden inte längre blir bättre. (Fig. 2.) Den intuitiva uppfattningen att ljussignalerna går rakt fram stämmer inte längre. Denna modell för ljusets utbredning är inte tillräcklig om hålet blir för litet. Stråloptik s 1
2 Fig. 2. Avbildningen med hålkameran blir optimal för en viss hålstorlek, här 0,35 mm. Ljuset är ett flöde av partiklar (partikelmodellen) men också en vågrörelse (vågmodellen). Vi delar därför in optiken i två delar, stråloptik och vågoptik trots att partikel och vågaspekten blandas då vi betraktar fenomen i den lilla världen dvs. atomernas värld. Allt sedan slutet av 1800-talet har det ansetts uppenbart att ljuset är elektromagnetiskt till sin natur. Dessutom gäller det för ljuset att det sänds ut (och absorberas) i form av energikvanta, fotoner. Denna elektromagnetiska modell för ljuset som både tar hänsyn till ljusets våg och partikelegenskaper kallas fotonmodellen. Denna modell har som upphovsmän Planck och Einstein. Fotonernas hastighet i vakuum betecknas c. Enligt den senaste definitionen på längdenheten metern gäller att ljusets hastighet c kan skrivas exakt: c = m/s. För en vågrörelse gäller allmänt att: λ υ =! I denna ekvation betecknar! våglängden, " frekvensen och v vågutbrednings-hastigheten. Energin E för en foton ges av " = # υ där h är Plancks konstant med värdet 6,6262#10-34 Js. Stråloptik s 2
3 I stråloptiken ersätter vi vågfronter med strålar som går vinkelrätt mot vågfronterna. (Fig. 3.) Det är när ljuset träffar små strukturer som man inte längre kan dra raka strålar utan då bör ljusets vågnatur istället beaktas. Vågfronter Ljusstrålar Vågfronter Ljusstrålar Fig. 3. Ljusstrålarna går vinkelrätt mot vågfronterna. Strålknippe Stråloptik Tre typer av strålknippe finns. Divergent, parallellt och konvergent. (Fig. 4.) Ett strålknippe är divergent nära en ljuskälla, blir nästan parallellt på stora avstånd från ljuskällan och då knippet avbildas till en bildpunkt blir det konvergent. Fig. 4. Divergent, parallellt och konvergent strålknippe. Hur divergent ett knippe är beror på avståndet till ljuskällan och inte på hur stor del av allt som når t.ex. en yta. I figuren nedan (fig. 5.) är således knippet mera divergent i A i vänstra bilden än i B i högra. A B Fig. 5. Strålknippets divergens är bara beroende av avståndet till strålkällan. Man kan avgöra om objekt eller bild är reell eller virtuell genom att undersöka hur strålknippena ser ut. En reell bild kan uppfångas på en skärm vilket inte gäller om en virtuell sådan. I nedanstående figur framgår vilka olika typer av bilder och objekt som kan uppträda vid en optisk avbildning. Stråloptik s 3
4 Optiskt system Reelt objekt Reel bild Optiskt system Virtuellt objekt Virtuell bild Fig. 6. Strålknippets egenskaper före och efter ett optiskt system bestämmer vilken typ av objekt och bild det är. Det bör observeras att strålar som konvergerar mot en punkt blir divergenta efter punkten (fig. 7). Fig. 7. Omvandling från konvergent till divergent strålknippe. Reflexion Då ljus träffar en yta kommer vanligen en viss del att spridas tillbaka. Denna spridning sker ofta i många olika riktningar. Om ljuset speciellt träffar en yta som är plan dvs. jämn med ljusvåglängden som mått sker en reflexion mot ytan. I detta fall gäller reflexionslagen dvs. reflexionsvinkeln r, blir lika stor som infalls vinkeln i. (Fig. 8.) i r i r Spegel Spegel Fig. 8. Infallsvinkeln och reflexionsvinkeln är lika stora vid reflexion En yta som uppfyller ovannämnda krav på ytnoggrannhet kallas en spegel. En speglande yta reflekterar ofta bara en viss del av det infallande ljuset. Kvoten mellan reflekterad intensitet I r och infallande intensitet I i kallas reflektiviteten R dvs. $ = % %& ' Stråloptik s 4
5 För en glasyta eller en vattenyta är denna reflektivitet beroende av infallsvinkeln. För t.ex. glas är R = 4% vid vinkelrätt infall medan R närmar sig 100% vid strykande infall dvs. då i =90. Reflexionslagen kan sägas följa ur en allmän princip nämligen Fermat s princip som i sin enklaste version säger att ljusets väg representerar den snabbaste vägen mellan två punkter. Ljus via spegeln (Fig. 9.) från A till B måste således gå via punkten C. A A Fig. 9. Vägen från A till B via C är den kortaste och därmed den snabbaste. i r C Detta beror på att sträckan A CB blir den kortaste och därmed den snabbaste. Av detta följer att vinklarna i och r är lika. Lika väl som en stråle går från A till B via punkten C så kommer en stråle från B till A också att gå via punkten C. Detta är ett exempel på lagen om strålgångens omvändbarhet. Mera allmänt innebär denna lag att objekt och bild kan byta plats i ett optiskt system. Nedan (Fig. 10.) visas ett exempel på hur spegling i en planspegel kan se ut. B A B A B Fig. 10. Strålgången är omvändbar Det divergenta strålknippet från objektpunkten A är fortfarande divergent efter spegling i ytan och tycks komma från den virtuella bildpunkten B. Omvänt som i högra figuren kommer ett konvergent knippe mot den virtuella objektpunkten B att efter reflexionen konvergera mot den reella bildpunkten A. Stråloptik s 5
6 Brytning Ljusets hastighet är som nämnts oerhört stor, ungefär km/s eller 3#10 8 m/s. Detta motsvarar att ljuset från månen når oss på lite drygt en sekund. Då ljus går in i ett medium som är genomskinligt sänks hastigheten och i vatten är den i stället 2,3#10 8 m/s. Kvoten mellan ljushastigheten c i vakuum och dess hastighet v i ett medium benämns brytningsindex och betecknas med n, dvs. ) ( =! för vatten är värdet på n $ 1,33 och för glas gäller n $ 1,5. Brytningsindex varierar också något för olika färger. Detta är anledningen till den färguppdelning som sker i regnbågen. Då en ljusstråle träffar en yta under en sned vinkel erhålls en brytning av strålen. Brytningen beror på strålens infallsvinkel och brytningsindex. I detta sammanhang gäller brytningslagen: ( #$%' = ( #$% *! " Då n 2 är större än n 1 ser brytningen ut enligt figuren nedan. i n i n i 1 1 n 1 n2 n2 b b b n 2 Fig. 11. Brytning i en yta. Om en stråle kommer från andra hållet i förhållande till gränsytan kan s.k. totalreflexion uppträda. (Fig. 12.) n 1 n 1 i n 2 i ~ g n 2 Fig. 12. Totalreflexion och gränsvinkeln för totalreflexion. Då strålens infallsvinkel i minskas till en viss vinkel g = gränsvinkeln, kommer en stråle att erhållas som går ut parallellt med ytan. Totalreflexion används bl.a. i prismor för att man skall ha hög reflektivitet. Totalreflexion används också i optiska fibrer som kan leda ljus stora sträckor utan alltför stora förluster av ljus (se fig. 13 nästa sida). Stråloptik s 6
7 Mantel Mantel n n n c f c Fiberkärna n c < n f Fig. 13. Ljusets ledning i en optisk fiber. Reflexion mot buktig yta Då en ljusstråle träffar en speglande buktig yta reflekterar den i varje punkt som om ytan där vore plan. Genom att ytan lutar olika mycket i olika områden kan hela knippen ändra sin form. Parallella knippen kan omvandlas till konvergenta eller divergenta. Om den buktiga ytan är en sfär kommer ett divergent ljusknippe från sfärens centrum att återkastas tillbaka på sig själv (Fig. 14). M Sfärens centrum M Optisk axel Fig. 14. Reflexion i en sfär och optisk axel. En stråle som går från sfärens centrum till den buktiga ytans centrum definierar den optiska axeln. (Fig. 14.) Strålar som träffar den buktiga ytan och som är parallella med den optiska axeln kommer att konvergera mot eller divergera från den s.k. fokalpunkten F, belägen på halva radien (Fig. 15). M F F M Fig. 15. Fokalpunkt för konkav och konvex spegel. En förutsättning för att fokalpunkten skall vara väl definierad är att strålknippet ej är för brett. Strålar som kommer för långt ut från huvudaxeln kommer att skära denna axel något närmare spegeln. Denna effekt kallas sfärisk aberration (fig. 16 nästa sida). Stråloptik s 7
8 M f Fig. 16. Sfärisk aberration i en spegel. Det finns dock en yta som har väldefinierat fokus även för strålar som kommer långt ut från den optiska axeln. En sådan yta kallas paraboloid. Avbildning med speglar Ett föremål i ett optiskt system betraktas som en samling punktformiga ljuskällor vilka var och en sänder ut ett divergent strålknippe. Hur avbildas då ett objekt? Om objektet ligger långt borta från spegeln sker avbildningen nära spegelns fokus. En punkt i ett oändligt avlägset objekt som ligger på optiska axeln avbildas i fokus, medan en punkt utanför optiska axeln avbildas i fokalplanet. Detta plan har optiska axeln som normal och går genom fokus (Fig. 17). M F Optisk axel Fokalplan Fig. 17. Parallella strålar från en avlägsen objektpunkt konvergerar till en bildpunkt i spegelns fokalplan. Stråloptik s 8
9 Vid konstruktion av bilden då objektet ligger nära spegeln kan tre olika strålar dras från objektet. 1) Strålen som går parallellt med den optiska axeln. 2) En stråle som går genom spegelns medelpunkt. 3) En stråle som går genom fokus. Den första strålen reflekteras mot fokus, den andra återkastas i motsatt riktning och den sista går ut parallellt med optiska axeln efter reflexionen. M F Bildpunkt Fig. 18. Avbildning av pilspetsen. Andra punkter på objektpilen kommer att avbildas till punkter närmare den optiska axeln och vi får en hel bildpil. M F Fig. 19. Avbildning av andra punkter på pilen. Stråloptik s 9
10 Brytning av buktig yta Precis som med speglar leder brytning i en sfärisk yta till ett fokus. n 1 n 2 Fig. 20. Brytning i en sfärisk yta (n 1 = 1 och n 2 = 1,5) Avbildningen är liksom för speglar ej perfekt för randstrålar och den paraboliska spegeln motsvaras av en ellipsoid. I normala fall kombineras två ytor till en lins. Denna får två fokalpunkter som för en tunn lins ligger lika långt från linsens centrum. På samma sätt som för en spegel erhåller man också ett fokalplan vinkelrät ut från fokalpunkten. Hur ser då strålkonstruktionen ut med en lins? Liksom för en spegel är tre strålar viktiga: 1) Strålen genom första fokus. 2) Strålen genom linsens centrum. 3) Strålen parallellt med optiska axeln. Hur dessa strålar bryts framgår av nedanstående figur. f = +3 cm F 2 F 1 Fig. 21. Avbildning i en lins. Stråloptik s 10
11 Då ett föremål befinner sig på stort avstånd erhålls en bild alldeles vid fokus F 2 Fig. 22. Avbildning av ett avlägset objekt. De sneda strålarna representeras t.ex. toppen på ett berg, medan den optiska axeln pekar mot bergets fot. Den erhållna bilden är i detta fall kraftigt förminskad. Ur figurerna på nästa och efterföljande sida framgår hur avbildningen blir för olika objektavstånd för en positiv och en negativ lins. Då objektet befinner sig på avståndet 2f, fås symmetrisk avbildning där bilden blir lika stor som objektet. (Fig. 23c). Ett liknande fall erhålls för en negativ lins (Fig. 24g). I figuren är objektet virtuellt och är t.ex. en reell bild från ett tidigare optiskt system. Om objektet är placerat i linsens fokus (Fig. 23e och Fig. 24f.) hamnar bilden oändligt långt borta. Stråloptik s 11
12 a) Reell bild F 2 F 1 2f b) F 1 2f F 2 c) F 1 2f F 2 d) F 1 2f F 2 e) F 2 F 1 f) F 2 F 1 g) F 2 F 1 Fig. 23. Avbildningen i en positiv lins vid olika föremålsavstånd. Observera att det minsta avståndet mellan ett reellt föremål och dess reella bild är 4f. Detta erhålls då a = b = 2f. Stråloptik s 12
13 Virtuell bild a) F 1 F 2 b) F 2 F 1 c) d) e) f) g) 2f Fig. 24. Avbildning i en negativ lins vid olika föremålsavstånd. Här blir liksom på föregående sida ett symmetrifall då a = b = 2f, (Fig. f.) men f är negativt, dvs. både föremål och bild är virtuella. Stråloptik s 13
14 Linsformeln Låt oss titta på en speciell strålkonstruktion. f = + 3 cm x 2 y 1 F 2 F 1 y 2 x 1 f f 5 cm 7,5 cm Fig. 25. Likformiga trianglar vid avbildning. De två trianglarna vid F 1 innehåller samma vinklar (de är likformiga). Samma gäller de två vid F 2. Ur detta följer: +! ",! +! & - = = )*+) = = ) + " & - + " '(,,",! - " = )) )),,! " = - -, " Denna formel kallas Newtons formel och gäller allmänt i alla avbildningar. De teckenregler som gäller är att x 1 och x 2 är positiva om de ligger utanför sina respektive fokus. Om vi inför:. =,! + -).*+)* =," + -))#/)0/1)2$ " " " * )) ).* 4* ).* *-.- = -.*-.*-.*-!!! = + -. * Stråloptik s 14
15 Denna formel kallas linsformeln och ger oss möjlighet att räkna ut endera av bildens läge, brännvidden för linsen eller objektets läge, då de andra två är kända. Den ovan härledda Newtons formel kan ibland vara lättare att använda. I linsformeln räknas a positiv till vänster om linsen medan b räknas positiv till höger om linsen. Brännvidden f räknas positiv om parallella strålar konvergerar till ett fokus till höger om linsen. Förstoring Kvoten mellan bildens storlek och objektets storlek kallas förstoringen. För att vara strikt ger man denna ett negativt tecken då bilden blir upp och ner i förhållande till objektet. Förstoringen kan då skrivas. * / 0 %&. På samma sätt kan man definiera en djupförstoring som innebär hur bilden förskjutits längs optiska axeln då objektet flyttas längs denna. För denna förstoring gäller: a 2 ML = = MT b a betyder liten ändring av a osv Den sista likheten går att visa med hjälp av Newtons formel. Eftersom denna förstoring (den kallas longitudinell) alltid är negativ innebär detta att om ett objekt flyttas närmre linsen, ökar bildens avstånd till linsen. Ljusstyrka Hur ljus den bild blir som en lins ger av ett objekt beror på linsens storlek och hur stor bilden är. Om t.ex. solen avbildas av en lins, fördelas ljuset på en yta som är direkt proportionell mot brännvidden i kvadrat, och den mängd ljus som går igenom linsen är proportionell mot linsöppningens area (Fig. 26.). Strålar från solens kant f Solbild Fig. 26. Solbildens area är proportionell mot kvadraten på brännviddsavståndet. f Stråloptik s 15
16 Om linsöppningen har diametern D så blir bildens belysning proportionell mot (D/f) Talet D/f kallas den relativa aperturen eller linsens ljusstyrka och den antar för ett kameraobjektiv vissa speciella värden nämligen: 1:1,4, 1:2, 1:2,8, 1:4, 1:5,6 osv. Mellan talen finns en faktor! 8 " för att belysningen skall halveras då relativa aperturen ändras till nästa. Avbildningsfel Vid avbildning önskar man att varje punkt på objektet ger en väldefinierad punkt i bilden. Ofta blir det ingen bildpunkt utan ljuset sprids ut över en yta. Eftersom sfäriska ytor är så enkla och billiga att göra, använder man sådana i optiska sammanhang trots att t.ex. paraboloidytor eller andra asfäriska ytor ibland skulle ge mycket bättre punktavbildning. Nu är emellertid sådana ytor inte bra för snett infallande strålar då de ofta är sämre än sfäriska. De avbildningsfel som uppträder är beroende av hur stor del av linsytan som belyses, om ljusstrålarna kommer in asymmetriskt eller om vi har flera olika våglängder hos ljuset. Avbildningsfelen är ofta blandade men trots detta gör man en indelning i sfärisk aberration, koma, astigmatism, bildfältskrökning, distorsion och kromatisk aberration. I figurerna (fig. 27. a-f) på nästa sida är de olika avbildingsfelen schematiskt åskådliggjorda. Stråloptik s 16
17 a) Spherisk aberration d) Bildfältskrökning Krökt fokalyta F Gauss fokalplan Optisk axel b) Koma e) Distortion Odistorderad bild Kuddform Tunnform f) Kromatisk aberration grönt c) Astigmatism Minsta bildpunkt Lins blått rött : Primärt linjefokus 2: Sekundärt linjefokus Objektpunkt Fig 27 a-f. De olika avbildningsfelen hos en lins. Sfäriska aberration (Fig. 27a) ger upphov till olika fokus för strålar som träffar olika långt ut från huvudaxeln. Detta är den enda enfärgade (monokromatiska) aberration som uppträder för objektpunkter på huvudaxeln eller för strålar parallella med denna. Koma (Fig. 27b) uppträder då linsöppningen är stor och strålar kommer in snett mot linsen. En punkt avbildas till en yta som liknar en komet. Astigmatismen (Fig. 27c.) dominerar över koman om objektet ligger långt ifrån huvudaxeln Stråloptik s 17
18 och linsöppningen är liten. Denna ger upphov till två vinkelräta linjer på olika avstånd från linsen och mellan dessa lägen är bilden en ellips eller en cirkel. Bildfältskrökning (Fig. 27d.) kan erhållas även om linsen ger en punktavbildning och innebär att ett plant objekt avbildas på ett krökt bildplan. På samma sätt är fokalplanet krökt. Distorsion (Fig. 27e.) är en effekt som uppträder då ljuset kommer mycket snett in mot linsen och är t.ex. ett vanligt problem i vidvinkelobjektiv. Beroende på bländarens placering i det optiska systemet blir avbildningen kuddformad eller tunnformad. Kromatisk aberration (Fig. 27f.) är ett avbildningsfel som beror på att brytningsindex beror av våglängden, vilket gör att brännvidden för en positiv lins blir längre i rött än i blått. (kraftigt överdrivet i figuren) Optiska instrument Ögat För länge sedan trodde man att ljuset utgick från människans inre. När vi öppnade ögonen sändes vårt inre ljus ut och med detta avsökte vi vår omgivning. När vi sedan blundade blev allt omedelbart svart och därför ansåg man att ljusets hastighet var oändlig, ty även ljuset från den mest avlägsna stjärna dog ut omedelbart. Denna subjektiva uppfattning av ljuset och seendet lever kvar i vårt språkbruk. Man säger t.ex. hur långt ser Du i stället för hur långt ifrån ser du, kasta en blick på det här, betrakta, bestrålning osv. I ögat sker den huvudsakliga brytningen vid övergången från luften till hornhinnan (Fig. 28.), medan vi med ögonlinsen korrigerar brytningen så att både avlägsna och närbelägna objekt kan avbildas skarpt på näthinnan. Kring ögonlinsen finns en ringformad ciliarmuskel som ger denna variation av ögats brytningsförmåga. Detta kallas ackommodation och då muskeln är avslappnad är ett vanligt öga inställt på seende på långt avstånd. Hornhinna Främre ögonkammare Pupill Iris Ögonlins Näthinna Blinda fläcken Glaskroppen Gula fläcken Synnerv Visuell axel Optisk axel Fig. 28. Ögats uppbyggnad. Stråloptik s 18
19 Mängden ljus som kommer in i ögat regleras med iris eller regnbågshinnan. Ögats öppna del kallas pupillen, vilken kan variera från 2 mm i starkt ljus till 8 mm i mörker. Denna egenskap kallas adaption. På näthinnan finns ljuskänsliga celler, tappar och stavar. Tapparna fungerar som en finkornig lågkänslig färgfilm vilken fungerar i starkt ljus. Stavarna är däremot enbart svart-vitt-känsliga och fungerar bara i svagare ljus. Där synnerven går in i ögat finns en blind fläck medan det i näthinnans centrum finns en fläck fri från stavar, den gula fläcken. I denna är tapparna tätare packade och på denna fläck hamnar bilden när vi fixerar något. Från olika delar av näthinnan går ett nätverk av nervbanor som alla är förbundna med synnerven. Kameran Kameran liknar ögat i sin funktion. Filmen i nedanstående figur (Fig. 29.) motsvarar näthinnan, linssystemet som avbildar objektet i film- planet går att förskjuta (motsvarar ackommodationen) och i linssystemet finns en variabel bländare (motsvarar iris). I den spegelreflexkamera som är avbildad finns en spegel som före exponeringen speglar upp kamerabilden på en mattglasskiva, vilken betraktas med ett optiskt system bestående av fältlins, pentaprisma och okular. Pentaprisma Fältlins Mattglas Linssystem Okular Film Spegel Ridåslutare Fig. 29. Principbild av kamerans uppbyggnad. Då den ljuskänsliga filmen skall exponeras fälls spegeln upp och en ridåslutare bestämmer exponeringstiden (vanligen mellan 1 sekund och 1/1000:dels sekund). Denna exponeringstid väljs så att mängden ljus på filmen motsvarar filmens känslighet. Känsligheten anges i ASA eller DIN (numera ISO-enheter). En ökning med 3 enheter (DIN eller ISO) motsvarar en fördubbling av ASA-talet. Trots att linssystemet i en kamera kan innehålla många enskilda linser kan det ofta betraktas som en tunn lins. Detta betyder att trots att många brytningar sker i de olika linsytorna kan linssystemet ersättas med en tunn lins med en viss brännvidd och som är placerad på ett visst avstånd från filmplanet. På detta sätt kan man lättare behandla systemet matematiskt. Strålgången blir därmed också kraftigt förenklad (Fig. 30.). Stråloptik s 19
20 Fig. 30. Ett komplicerat linssytem kan ersättas med en enda tunn lins. Linssystemets brännnvidd och filmstorleken bestämmer kamerans bildvinkel (Fig. 31.). För ett vanligt 50 mm normalobjektiv till en 24x36-kamera är bildvinkeln ungefär 45. För vidvinkelobjektiv kan bildvinkeln bli så stor som 220 (fiskögonlins) medan ett teleobjektiv har en bildvinkel på några få grader. φ φ Fig. 31. Bildvinkeln hos ett kameraobjektiv. f Stråloptik s 20
21 Luppen En enda lins kan användas som hjälpmedel då man vill närmre betrakta något. I detta fall används linsen som förstoringsglas eller som lupp. Det är inte uppenbart vad som innebär förstoring i detta fall men man utgår från att föremålets normala storlek bestäms av hur stort det ser ut från avståndet 250 mm eller avståndet för tydligt seende (Fig. 32.). Näthinnebildens storlek är beroende av den synvinkel ett objekt upptar. Man definierar vinkelförstoringen G för ett optiskt instrument som kvoten mellan synvinkeln ß med instrument och synvinkeln α då objektet är på avståndet för tydligt seende: 1 % ' ( h α 250 mm Fig. 32. Objekt och bild på avståndet för tydligt seende. För en lupp med objektet placerat i fokus (Fig. 33.) hamnar bilden oändligt långt borta. Då är: # # "(- 9:% ( % $ ().*+) 9:% ' % $ ' ) 1 $ "(- - - h β β Fig. 33. Objektet i fokus till luppen med bilden i oändligheten. f Vinkelförstoringen ökar således om man minskar f. Man kan emellertid inte göra brännvidden för kort för enkla linser utan att få stora avbildningsfel. Med sammansatta och ofta korrigerade linser (ofta kombinationer som är akromatiska) kan man nå från 2 gångers till ungefär 20 gångers förstoring för en lupp. Stråloptik s 21
22 Mikroskopet Man anser att den holländske optikern Zacharias Janssen först uppfann mikroskopet omkring Galileo konstruerade sitt första Ett mikroskop består av ett objektiv med kort brännvidd och ett okular (en typ av lupp) med vilket man betraktar den förstorade bild som objektivet ger (Fig. 34 på nästa sida). Figuren är kraftigt förenklad i förhållande till ett modernt mikroskop ty både objektivet och luppen är normalt sammansatta linssystem som är korrigerade för avbildningsfel. Ur figuren framgår att objektivets (transversella) förstoring är: 2 / % -3* 0,, - # % 3* ' 3 3*, );<%) % " ) 3,' 4 ) / 0 % % )))))))) 3* -3* -3* (här bortser vi från tecken!) Avståndet L är standardiserat för mikroskop till 160 mm. Av denna anledning är mikroskopobjektiv märkta t.ex. 5x ( om f = 32 mm). Eftersom okularet är en lupp inställd på oändligheten blir dess vinkelförstoring 135 % "( Stråloptik s 22
23 Utträdespupill β f ok Okular Bild i oändligheten H f ok Fältbländare L = x i 250 mm α f ob f ob Objektiv x 0 h a) b) h Fig. 34. Förenklad bild av ett mikroskop Fig. 35. Synvinkeln utan mikroskop. Stråloptik s 23
24 Mikroskopets förstoring är som för luppen kvoten mellan synvinkeln med och utan instrument. Om objektet har storleken h så gäller ur fig. 35: ( $ # "(- )))3+)$);;5 Objektivet ger en bild med storleken 2 % / 0 3* ## Synvinkeln i okularet β blir då: ' % 2-35 Då kan vi skriva mikroskopets förstoring: 1 6'5& ' 2 "(- 2 "(- % % # % # % / # 1 3* ( - # # Mikroskopets förstoring är således produkten av objektivets transversella förstoring och okularets vinkelförstoring. I mikroskopet är det objektivets öppning som bestämmer mängden ljus in i systemet. Med ett kondensorsystem belyses objektet så att ljus fyller hela objektivet. Ljusflödet ut från mikroskopet koncentreras till systemets utträdespupill. Detta är ett ljust cirkulärt område som befinner sig strax ovanför okularet. Om man placerar ögat i utträdespupillen får man så ljus bild som möjligt medan bildfältet begränsas vinkelmässigt av ett utträdesfönster som är bilden av fältbländaren som är placerad i okularet (Fig. 34). Kikaren Det är ganska troligt att kikaren uppfanns långt tidigare än mikroskopet. Det fanns redan under 1300-talet slipade linser för glasögon och någon borde ha kombinerat två lämpliga linser till en kikare innan år 1608 då Lippershey sökte patent för sin uppfinning. Redan året efter konstruerade Galileo en egen kikare av linser och en orgelpipa. Det var med förbättrade versioner av denna hans första kikare som Galileo gjorde sina berömda astronomiska upptäckter. En kikare (Fig. 36.) består av ett objektiv med lång brännvidd kombinerad med ett okular. Om objektet är på oändligt avstånd hamnar den kraftigt förminskade bilden i objektivets fokus där den betraktas i fokus till ett okular. Stråloptik s 24
25 f ob d f ok Fig. 36. Förenklad bild av en kikare inställd för ett oändligt avlägset objekt. Kikarens förstoring definieras som synvinkeln till objektet med och utan instrument (avlägset objekt). I den enklare figuren nedan (Fig.37.) blir vinkelförstoringen: ' # -3* -3* 1 % $ # % ( - # Objektiv Okular α h β f ob f ok Fig. 37. Förenklad bild av en kikare. Liksom för mikroskopet har kikaren en utträdespupill. Denna är okularets bild av objektivet och kan konstrueras som om objektivet vore ett objekt (Fig. 38.). D ip Objektivet som objekt D up Utträdespupill f ob f ok Fig. 38. Konstruktion av utträdespupill i en kikare. I den ovan beskrivna kikaren blir den resulterande bilden upp och ner. I en prismakikare utnyttjas totalreflexion i två prismor för att vända på bilden (Fig. 39). Stråloptik s 25
26 Fig. 39. Prismakikare. På detta sätt får man dessutom en relativt kort kikare. En omvänd kikare används ofta för att expandera ett parallellt knippe från en laser (Fig. 40.). Då gäller: '( -3* % % 1-35 Fig. 40. Expansion av ett parallellt knippe av laserljus. Teleskopet Newton som felaktigt trodde att den kromatiska aberrationen orsakades av ljusets inneboende egenskap och inte på glassorten valde att använda speglade ytor i stället för linser för att avbilda avlägsna objekt. Han konstruerade sitt första teleskop 1668 strax efter att skotten James Greorgy uppfunnit det. Genom denna uppfinning kunde stora instrument byggas utan problem med genomskinlighet, upphängning och bubblor i glaset. Problemet med färgfel i linser löstes först 1733 då de första akromatiska linserna tillverkades. I dag har den största refraktorn en diameter på 1 m (Yerkes teleskop) medan den största reflektorn har diametern 10 m (Keke-teleskopet på Hawaii). Den senare består dock av 36 separata spegelsegment som är kopplade ihop. I figuren nedan (Fig. 41.) finns avbildat principen för Newtonreflektorn. I denna avbildar en konkav spegel via en snedställd liten spegel det avlägsna objektet så att bilden hamnar utanför teleskoptuben. Stråloptik s 26
27 Okular Konkav spegel Plan spegel Fig. 41. Newtonteleskopet. Teleskopets förstoring är liksom för kikaren: 1 - :; 7'; % % % ; 7 7 :; 8; Här är D sp spegelns diameter och f sp spegelns brännvidd. Arbetsprojektorn I en arbetsprojektor (Fig. 42.) placeras ett stordia på en asfärisk fresnellins. Fresnellinsen består av ett stort antal slipade trapetsformade ringar i acrylplast så att onödigt linsmaterial tagits bort (Fig. 43.). Spegel Avbildande lins Bild på skärmen Fresnellins Halogenlampa Fig. 42. Principen för arbetsprojektorn. Stråloptik s 27
28 Fig. 43. Asfärisk fresnellins med motsvarande asfäriska yta. Fresnellinsen koncentrerar ljuset från en intensiv halogenlampa på den avbildade linsen. Fresnellinsen är alltså bara till för att göra den resulterande bilden ljus. Genom att fresnellinser kan göras med stor ljusstyrka (stort D/f) är de bättre än vanliga kondensorlinser som används i projektorer. Spektroskopet Den färguppdelning som man får i ett prisma utnyttjas i ett spektroskop till att undersöka olika ljuskällors spektra. Spektroskopet (Fig. 44) består av tre huvuddelar: en kollimator, ett prisma eller ett gitter och en kikare. Ofta låter man en kondensorlins avbilda ljuskällan på spalten, men man kan också placera ljuskällan strax intill spalten. I kollimatorn skapas ett parallellt strålknippe som i prismat eller gittret delas upp i flera enfärgade strålknippe med olika utgångsriktning. Ljuskälla Spalt Lins Kollimator Prisma Objektiv r r v v Kikare r v Spektrum Okular Fig. 44. Spektroskopets uppbyggnad. Rött och violett ljus fokuseras på olika ställen i okularets fokalplan. Stråloptik s 28
29 I kikaren konvergerar knippena till ett antal enfärgade linjer (bilder av spalten) som betraktas med kikarens okular. Om man använder spektroskopet till att direkt mäta upp brytningsindex för prismaglaset eller till att bestämma våglängder, kallas instrumentet för en spektrometer. Ett sätt att mäta upp brytningsindex för prismat är att ställa in spektrometern på minimidevitation. Detta innebär att en linje i lampans spektrum har ett vändläge i kikaren då prismat roteras. Vid minimideviation går ljuset symmetriskt genom prismat enligt figuren nedan (Fig. 45.). δ min + α 2 n 1 n α α/2 2 δ min Fig. 45. Minimideviation i ett prisma. Då är vinkeln mellan ingående och utgående stråle minimal. Ur figuren fås: δmin + α δ sin min + α α 1sin = n sin n = α sin 2 Genom att mäta upp minimideviationsvinkeln δ min och prismats brytande vinkel α får man brytningsindex n för glassorten vid den aktuella våglängden. Då man tittar i ett spektroskop på olika ljuskällor finner man att dess spektrum varierar mycket i utseende. För upphettade gaser erhålls större eller mindre antal väldefinierade linjer medan för varma kroppar eller vätskor flyter linjerna ihop och vi får ett kontinuerligt spektrum. Spektrallampor är exempelvis av den första typen medan himmelsljuset eller ljuset från en vanlig glödlampa är av den senare typen. Ett spektrum kan sägas vara atomernas fingeravtryck och det ger värdefull information om elektron banorna i atomernas yttre delar. Stråloptik s 29
Geometrisk optik. Syfte och mål. Innehåll. Utrustning. Institutionen för Fysik 2006-04-25
 Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Geometrisk optik Syfte och mål Laborationens syfte är att du ska lära dig att: Förstå allmänna principen för geometrisk optik, (tunna linsformeln) Rita strålgångar Ställa upp enkla optiska komponenter
Optik. Läran om ljuset
 Optik Läran om ljuset Vad är ljus? Ljus är en form av energi. Ljus är elektromagnetisk strålning. Energi kan inte försvinna eller nyskapas. Ljuskälla Föremål som skickar ut ljus. I alla ljuskällor sker
Optik Läran om ljuset Vad är ljus? Ljus är en form av energi. Ljus är elektromagnetisk strålning. Energi kan inte försvinna eller nyskapas. Ljuskälla Föremål som skickar ut ljus. I alla ljuskällor sker
Instuderingsfrågor extra allt
 Instuderingsfrågor extra allt För dig som vill lära dig mer, alla svaren finns inte i häftet. Sök på nätet, fråga en kompis eller läs i en grundbok som du får låna på lektion. Testa dig själv 9.1 1 Vilken
Instuderingsfrågor extra allt För dig som vill lära dig mer, alla svaren finns inte i häftet. Sök på nätet, fråga en kompis eller läs i en grundbok som du får låna på lektion. Testa dig själv 9.1 1 Vilken
Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du:
 Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du: A.Mer av dig själv. B.Mindre av dig själv. C.Lika mycket av dig själv. ⱱ Hur hög måste en spegel vara för att du ska
Om du tittar på dig själv i en badrumsspegel som hänger på väggen och backar ser du: A.Mer av dig själv. B.Mindre av dig själv. C.Lika mycket av dig själv. ⱱ Hur hög måste en spegel vara för att du ska
OPTIK läran om ljuset
 OPTIK läran om ljuset Vad är ljus Ljuset är en form av energi Ljus är elektromagnetisk strålning som färdas med en hastighet av 300 000 km/s. Ljuset kan ta sig igenom vakuum som är ett utrymme som inte
OPTIK läran om ljuset Vad är ljus Ljuset är en form av energi Ljus är elektromagnetisk strålning som färdas med en hastighet av 300 000 km/s. Ljuset kan ta sig igenom vakuum som är ett utrymme som inte
Förklara dessa begrepp: Ackommodera Avbildning, Brytning Brytningslagen Brytningsindex Brytningsvinkel Brännvidd Diffus och regelbunden reflektion
 Förklara dessa begrepp: Ackommodera, ögats närinställning, är förmågan att förändra brytkraften i ögats lins. Ljus från en enda punkt på ett avlägset objekt och ljus från en punkt på ett närliggande objekt
Förklara dessa begrepp: Ackommodera, ögats närinställning, är förmågan att förändra brytkraften i ögats lins. Ljus från en enda punkt på ett avlägset objekt och ljus från en punkt på ett närliggande objekt
3. Ljus. 3.1 Det elektromagnetiska spektret
 3. Ljus 3.1 Det elektromagnetiska spektret Synligt ljus är elektromagnetisk vågrörelse. Det följer samma regler som vi tidigare gått igenom för mekanisk vågrörelse; reflexion, brytning, totalreflexion
3. Ljus 3.1 Det elektromagnetiska spektret Synligt ljus är elektromagnetisk vågrörelse. Det följer samma regler som vi tidigare gått igenom för mekanisk vågrörelse; reflexion, brytning, totalreflexion
Laboration i Geometrisk Optik
 Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
Laboration i Geometrisk Optik Stockholms Universitet 2002 Modifierad 2007 (Mathias Danielsson) Innehåll 1 Vad är geometrisk optik? 1 2 Brytningsindex och dispersion 1 3 Snells lag och reflektionslagen
Ljuskällor. För att vi ska kunna se något måste det finnas en ljuskälla
 Ljus/optik Ljuskällor För att vi ska kunna se något måste det finnas en ljuskälla En ljuskälla är ett föremål som själv sänder ut ljus t ex solen, ett stearinljus eller en glödlampa Föremål som inte själva
Ljus/optik Ljuskällor För att vi ska kunna se något måste det finnas en ljuskälla En ljuskälla är ett föremål som själv sänder ut ljus t ex solen, ett stearinljus eller en glödlampa Föremål som inte själva
Studieanvisning i Optik, Fysik A enligt boken Quanta A
 Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Sammanfattning: Fysik A Del 2
 Sammanfattning: Fysik A Del 2 Optik Reflektion Linser Syn Ellära Laddningar Elektriska kretsar Värme Optik Reflektionslagen Ljus utbreder sig rätlinjigt. En blank yta ger upphov till spegling eller reflektion.
Sammanfattning: Fysik A Del 2 Optik Reflektion Linser Syn Ellära Laddningar Elektriska kretsar Värme Optik Reflektionslagen Ljus utbreder sig rätlinjigt. En blank yta ger upphov till spegling eller reflektion.
λ = T 2 g/(2π) 250/6 40 m
 Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 34 - Optik 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Vågrörelselära och optik Kapitel 34 - Optik 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Vad skall vi gå igenom under denna period?
 Ljus/optik Vad skall vi gå igenom under denna period? Vad är ljus? Ljuskälla? Reflektionsvinklar/brytningsvinklar? Färger? Hur fungerar en kikare? Hur fungerar en kamera/ ögat? Var använder vi ljus i vardagen
Ljus/optik Vad skall vi gå igenom under denna period? Vad är ljus? Ljuskälla? Reflektionsvinklar/brytningsvinklar? Färger? Hur fungerar en kikare? Hur fungerar en kamera/ ögat? Var använder vi ljus i vardagen
LABORATION 2 MIKROSKOPET
 LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX (5) Att läsa före lab: LABORATION 2 MIKROSKOPET Synvinkel, vinkelförstoring, luppen och
LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX (5) Att läsa före lab: LABORATION 2 MIKROSKOPET Synvinkel, vinkelförstoring, luppen och
3) Sag formeln ger r=y 2 /(2s). y=a/2=15 mm, s=b c=4,5 mm ger r=25 mm. Då blir F=(n 1)/r=(1,5 1)/0,025=20 D
 Facit: en avbildning Sfärisk gränsyta 1) l= 2,0 mm, n=4/3 och n =1. m=l/l =nl /(n l)=1,25 ger l = 1,875 mm. Avbildningsformeln för sfärisk gränsyta L =L+(n n)/r ger r= 2,5 mm. 2) Bilden måste hamna på
Facit: en avbildning Sfärisk gränsyta 1) l= 2,0 mm, n=4/3 och n =1. m=l/l =nl /(n l)=1,25 ger l = 1,875 mm. Avbildningsformeln för sfärisk gränsyta L =L+(n n)/r ger r= 2,5 mm. 2) Bilden måste hamna på
Gauss Linsformel (härledning)
 α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
LABORATION 2 MIKROSKOPET
 LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX 1 (6) LABORATION 2 MIKROSKOPET Att läsa i kursboken: sid. 189-194 Förberedelseuppgifter:
LABORATION 2 MIKROSKOPET Personnummer Namn Laborationen godkänd Datum Assistent Kungliga Tekniska högskolan BIOX 1 (6) LABORATION 2 MIKROSKOPET Att läsa i kursboken: sid. 189-194 Förberedelseuppgifter:
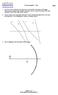
Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från vänster, sträcka i ljusets riktning = positiv
 Avbildningskvalitet Föreläsning 1 2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Avbildningskvalitet Föreläsning 1 2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Observera också att det inte går att både se kanten på fönstret och det där ute tydligt samtidigt.
 Om förstoringsglaset Du kan göra mycket med bara ett förstoringsglas! I många sammanhang i det dagliga livet förekommer linser. Den vanligast förekommande typen är den konvexa linsen, den kallas också
Om förstoringsglaset Du kan göra mycket med bara ett förstoringsglas! I många sammanhang i det dagliga livet förekommer linser. Den vanligast förekommande typen är den konvexa linsen, den kallas också
LABORATION 1 AVBILDNING OCH FÖRSTORING
 LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
LABORATION 1 AVBILDNING OCH FÖRSTORING Personnummer Namn Laborationen godkänd Datum Labhandledare 1 (6) LABORATION 1: AVBILDNING OCH FÖRSTORING Att läsa före lab: Vad är en bild och hur uppstår den? Se
Vi är beroende av ljuset för att kunna leva. Allt liv på jorden skulle ta slut och jordytan skulle bli öde och tyst om vi inte hade haft ljus.
 Källa: Fysik - Kunskapsträdet Vi är beroende av ljuset för att kunna leva. Allt liv på jorden skulle ta slut och jordytan skulle bli öde och tyst om vi inte hade haft ljus. Ljusets natur Ljusets inverkan
Källa: Fysik - Kunskapsträdet Vi är beroende av ljuset för att kunna leva. Allt liv på jorden skulle ta slut och jordytan skulle bli öde och tyst om vi inte hade haft ljus. Ljusets natur Ljusets inverkan
Föreläsning 2 (kap , 2.6 i Optics)
 5 Föreläsning 2 (kap 1.6-1.12, 2.6 i Optics) Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen
5 Föreläsning 2 (kap 1.6-1.12, 2.6 i Optics) Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen
Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från vänster, sträcka i ljusets riktning = positiv
 Avbildningskvalitet Föreläsning 1-2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
Avbildningskvalitet Föreläsning 1-2: Sfärisk aberration och koma Repetition: brytning och avbildning i sfärisk yta och tunn lins Figur 1: Figur 3.12 och 3.18 i Optics. Teckenkonventionen: ljus in från
4. Allmänt Elektromagnetiska vågor
 Det är ett välkänt faktum att det runt en ledare som det flyter en viss ström i bildas ett magnetiskt fält, där styrkan hos det magnetiska fältet beror på hur mycket ström som flyter i ledaren. Om strömmen
Det är ett välkänt faktum att det runt en ledare som det flyter en viss ström i bildas ett magnetiskt fält, där styrkan hos det magnetiska fältet beror på hur mycket ström som flyter i ledaren. Om strömmen
Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid , ) Retinoskopet
 Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid 345-353, 358-362) Retinoskopet Utvecklat från oftalmoskopi under slutet av 1800-talet. Objektiv metod för att bestämma patientens
Instrumentoptik, anteckningar för föreläsning 4 och 5 (CVO kap. 17 sid 345-353, 358-362) Retinoskopet Utvecklat från oftalmoskopi under slutet av 1800-talet. Objektiv metod för att bestämma patientens
Fysik. Laboration 3. Ljusets vågnatur
 Fysik Laboration 3 Ljusets vågnatur Laborationens syfte: att hjälpa dig att förstå ljusfenomen diffraktion och interferens och att förstå hur olika typer av spektra uppstår Utförande: laborationen skall
Fysik Laboration 3 Ljusets vågnatur Laborationens syfte: att hjälpa dig att förstå ljusfenomen diffraktion och interferens och att förstå hur olika typer av spektra uppstår Utförande: laborationen skall
Vågfysik. Geometrisk optik. Knight Kap 23. Ljus. Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion)
 Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
Vågfysik Geometrisk optik Knight Kap 23 Historiskt Ljus Newton (~1660): ljus är partiklar ( corpuscles ) ljus (skugga) vs. vattenvågor (diffraktion) Hooke, Huyghens (~1660): ljus är ett slags vågor Young
1. Betrakta en plan harmonisk elektromagnetisk våg i vakuum där det elektriska fältet E uttrycks på följande sätt (i SI-enheter):
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Måndagen den 5 maj 2008 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare.
Tentamen i Fotonik , kl
 FAFF25-2013-08-26 Tentamen i Fotonik - 2013-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2013-08-26 Tentamen i Fotonik - 2013-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
LABORATION 6 Astigmatism och Distorsion
 LABORATION 6 Astigmatism och Distorsion Personnummer Namn Laborationen godkänd Datum Assistent 1 (5) LABORATION 6: Astigmatism och Distorsion Att läsa i kursboken: sid. 248 257, 261 266, 298 299 Förberedelseuppgifter
LABORATION 6 Astigmatism och Distorsion Personnummer Namn Laborationen godkänd Datum Assistent 1 (5) LABORATION 6: Astigmatism och Distorsion Att läsa i kursboken: sid. 248 257, 261 266, 298 299 Förberedelseuppgifter
Denna våg är. A. Longitudinell. B. Transversell. C. Något annat
 Denna våg är A. Longitudinell B. Transversell ⱱ v C. Något annat l Detta är situationen alldeles efter en puls på en fjäder passerat en skarv A. Den ursprungliga pulsen kom från höger och mötte en lättare
Denna våg är A. Longitudinell B. Transversell ⱱ v C. Något annat l Detta är situationen alldeles efter en puls på en fjäder passerat en skarv A. Den ursprungliga pulsen kom från höger och mötte en lättare
SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE.
 SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE. Vad gjorde vi förra gången? Har du några frågor från föregående lektion? 3. titta i ditt läromedel (boken) Vad ska vi göra idag? Optik och
SÄTT DIG NER, 1. KOLLA PLANERINGEN 2. TITTA I DITT SKRIVHÄFTE. Vad gjorde vi förra gången? Har du några frågor från föregående lektion? 3. titta i ditt läromedel (boken) Vad ska vi göra idag? Optik och
Fysik A A B C D. Sidan 1 av 9 henrik.gyllensten@tabyenskilda.se. www.tabyenskilda.se/fy
 www.tabyenskilda.se/y ÖÖvvnni iinn ggssuuppppggi ii teer 1. Lars lyser med en icklampa mot ett prisma. Han kan då se ett spektrum på väggen bakom prismat. Spektrumet innehåller alla ärger. Vilken av dessa
www.tabyenskilda.se/y ÖÖvvnni iinn ggssuuppppggi ii teer 1. Lars lyser med en icklampa mot ett prisma. Han kan då se ett spektrum på väggen bakom prismat. Spektrumet innehåller alla ärger. Vilken av dessa
Tentamen i Fotonik , kl
 FAFF25-2015-03-20 Tentamen i Fotonik - 2015-03-20, kl. 14.00-19.15 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2015-03-20 Tentamen i Fotonik - 2015-03-20, kl. 14.00-19.15 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Föreläsning 8: Linsdesign
 1 Föreläsning 8: Linsdesign Linsdesign Att välja linser med rätt krökningsradier på ytorna och av rätt material. Förutom paraxiala egenskaper såsom objekt- och bildavstånd och förstoring, så ställs andra
1 Föreläsning 8: Linsdesign Linsdesign Att välja linser med rätt krökningsradier på ytorna och av rätt material. Förutom paraxiala egenskaper såsom objekt- och bildavstånd och förstoring, så ställs andra
Våglära och optik FAFF30 JOHAN MAURITSSON
 Våglära och optik FAFF30 JOHAN MAURITSSON Prismor A θ 1 n=1 n n=1 2 Prismor A δ 1 θ 1 θ 1 n=1 n n=1 3 Prismor A θ 2 θ 2 n=1 n n=1 4 Prismor A δ θ 1 θ 1 δ 1 δ 2 B θ 2 θ 2 n=1 n n=1 5 Prismor, dispersion
Våglära och optik FAFF30 JOHAN MAURITSSON Prismor A θ 1 n=1 n n=1 2 Prismor A δ 1 θ 1 θ 1 n=1 n n=1 3 Prismor A θ 2 θ 2 n=1 n n=1 4 Prismor A δ θ 1 θ 1 δ 1 δ 2 B θ 2 θ 2 n=1 n n=1 5 Prismor, dispersion
Lösningarna inlämnas renskrivna vid laborationens början till handledaren
 Geometrisk optik Förberedelser Läs i vågläraboken om avbildning med linser (sid 227 241), ögat (sid 278 281), färg och färgseende (sid 281 285), glasögon (sid 287 290), kameran (sid 291 299), vinkelförstoring
Geometrisk optik Förberedelser Läs i vågläraboken om avbildning med linser (sid 227 241), ögat (sid 278 281), färg och färgseende (sid 281 285), glasögon (sid 287 290), kameran (sid 291 299), vinkelförstoring
Geometrisk optik. Laboration
 ... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Geometrisk optik Linser och optiska instrument Avsikten med laborationen är att du ska få träning i att bygga upp avbildande optiska
... Laboration Innehåll 1 Förberedelseuppgifter 2 Laborationsuppgifter Geometrisk optik Linser och optiska instrument Avsikten med laborationen är att du ska få träning i att bygga upp avbildande optiska
Repetition Ljus - Fy2!!
 Repetition Ljus - Fy2 Egenskaper ör : Ljus är inte en mekanisk vågrörelse. Den tar sig ram utan problem även i vakuum och behöver alltså inget medium. Exakt vilken typ av vågrörelse är återkommer vi till
Repetition Ljus - Fy2 Egenskaper ör : Ljus är inte en mekanisk vågrörelse. Den tar sig ram utan problem även i vakuum och behöver alltså inget medium. Exakt vilken typ av vågrörelse är återkommer vi till
Eftersom brytningsindex n ändras med våglängden (färgen) kommer olika färger hos ljuset att brytas olika genom prismor och linser.
 Föreläsning 7 Kromatisk aberration Eftersom brytningsindex n ändras med våglängden (färgen) kommer olika färger hos ljuset att brytas olika genom prismor och linser. Dispersion: n ändras med våglängden
Föreläsning 7 Kromatisk aberration Eftersom brytningsindex n ändras med våglängden (färgen) kommer olika färger hos ljuset att brytas olika genom prismor och linser. Dispersion: n ändras med våglängden
Optik, F2 FFY091 TENTAKIT
 Optik, F2 FFY091 TENTAKIT Datum Tenta Lösning Svar 2005-01-11 X X 2004-08-27 X X 2004-03-11 X X 2004-01-13 X 2003-08-29 X 2003-03-14 X 2003-01-14 X X 2002-08-30 X X 2002-03-15 X X 2002-01-15 X X 2001-08-31
Optik, F2 FFY091 TENTAKIT Datum Tenta Lösning Svar 2005-01-11 X X 2004-08-27 X X 2004-03-11 X X 2004-01-13 X 2003-08-29 X 2003-03-14 X 2003-01-14 X X 2002-08-30 X X 2002-03-15 X X 2002-01-15 X X 2001-08-31
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi
 Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Föreläsning 14 och 15: Diffraktion och interferens i gitter, vanliga linser, diffraktiv optik och holografi Ljusets vågnatur Ljus är elektromagnetiska vågor som rör sig framåt. När vi ritar strålar så
Övningstal i Avbildningskvalitet för optikerstuderande. Rita figurer och motivera ordentligt!
 Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
 Optik Samverkan mellan atomer/molekyler och ljus elektroner atomkärna Föreläsning 7/3 200 Elektronmolnet svänger i takt med ljuset och skickar ut nytt ljus Ljustransmission i material Absorption elektroner
Optik Samverkan mellan atomer/molekyler och ljus elektroner atomkärna Föreläsning 7/3 200 Elektronmolnet svänger i takt med ljuset och skickar ut nytt ljus Ljustransmission i material Absorption elektroner
Vågrörelselära & Kvantfysik, FK2002 29 november 2011
 Räkneövning 5 Vågrörelselära & Kvantfysik, FK00 9 november 0 Problem 35.9 En dykare som befinner sig på djupet D 3 m under vatten riktar en ljusstråle (med infallsvinkel θ i 30 ) mot vattenytan. På vilket
Räkneövning 5 Vågrörelselära & Kvantfysik, FK00 9 november 0 Problem 35.9 En dykare som befinner sig på djupet D 3 m under vatten riktar en ljusstråle (med infallsvinkel θ i 30 ) mot vattenytan. På vilket
Övningstal i Avbildningskvalitet för optikerstuderande. Rita figurer och motivera ordentligt!
 Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Övningstal i Avbildningskvalitet för optikerstuderande Rita figurer och motivera ordentligt! Repetition av geometrisk optik 1. Ett objekt i luft ligger 400 mm innan en sfärisk gränsyta med krökningsradien
Fysik (TFYA14) Fö 5 1. Fö 5
 Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Tisdagen den 17 juni 2008 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 1,5 högskolepoäng, FK49 Tisdagen den 17 juni 28 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 1,5 högskolepoäng, FK49 Tisdagen den 17 juni 28 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare
Figur 6.1 ur Freeman & Hull, Optics
 1 Föreläsning 12 Kameran Figur 6.1 ur Freeman & Hull, Optics Kameran är ett instrument som till vissa delar fungerar mycket likt ett öga. Kamerans optik, det så kallade kameraobjektivet, motsvarar ögats
1 Föreläsning 12 Kameran Figur 6.1 ur Freeman & Hull, Optics Kameran är ett instrument som till vissa delar fungerar mycket likt ett öga. Kamerans optik, det så kallade kameraobjektivet, motsvarar ögats
Optik. Innehåll: I - Elektromagnetiska vågor radio och ljus. II - Reflexion och brytning. III - Ljusvågor. MNXA11 / Lund University
 Optik Innehåll: I - Elektromagnetiska vågor radio och ljus II - Reflexion och brytning III - Ljusvågor Kom ihåg Definition Amplitud, Våglängd, Frekvens, Våghastighet Mekaniska eller Elektromagnetiska vågor
Optik Innehåll: I - Elektromagnetiska vågor radio och ljus II - Reflexion och brytning III - Ljusvågor Kom ihåg Definition Amplitud, Våglängd, Frekvens, Våghastighet Mekaniska eller Elektromagnetiska vågor
Ljus och strålning. Klass: 9H
 Ljus och strålning Namn: Klass: 9H Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och samhället genomföra systematiska
Ljus och strålning Namn: Klass: 9H Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och samhället genomföra systematiska
Föreläsning 11 (kap i Optics)
 45 Föreläsning 11 (kap 5.7-5.8 i Optics) Hittills har vi behandlat avbildningen i sig, dvs. var bilden av ett objekt hamnar och vilken förstoring det blir. Det finns också andra krav man kan ställa på
45 Föreläsning 11 (kap 5.7-5.8 i Optics) Hittills har vi behandlat avbildningen i sig, dvs. var bilden av ett objekt hamnar och vilken förstoring det blir. Det finns också andra krav man kan ställa på
Tentamen Optik, FYSA11, 2012-05-25
 Tentamen Otik, FYSA, 0-05-5 Hjälmedel: TEFYMA, ormelsamling, linjal, ickräknare och biogat ormelblad. Glöm inte att beskriva hur du kommer ram till dina svar. Även delvis lösta ugiter kan ge oäng.. Den
Tentamen Otik, FYSA, 0-05-5 Hjälmedel: TEFYMA, ormelsamling, linjal, ickräknare och biogat ormelblad. Glöm inte att beskriva hur du kommer ram till dina svar. Även delvis lösta ugiter kan ge oäng.. Den
Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material?
 1 Föreläsning 2 Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen på samma sida är reflekterat
1 Föreläsning 2 Optiska ytor Vad händer med ljusstrålarna när de träffar en gränsyta mellan två olika material? Strålen in mot ytan kallas infallande ljus och den andra strålen på samma sida är reflekterat
Kapitel 33 The nature and propagation of light. Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion)
 Kapitel 33 The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Kapitel 33 The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Ljus, syn & strålning
 Ljus, syn & strålning Namn: Klass: 8G Ljus, syn och strålning Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och
Ljus, syn & strålning Namn: Klass: 8G Ljus, syn och strålning Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och
Tillämpad vågrörelselära FAF260. Svängningar genererar vågor - Om en svängande partikel är kopplad till andra partiklar uppkommer vågor
 FF60 Tillämpad vågrörelselära FF60 Karaktäristiskt för periodiska svängningar är att det finns en återförande kraft riktad mot jämviktsläget y 0 F F F k y F m a 4 Svängningar genererar vågor - Om en svängande
FF60 Tillämpad vågrörelselära FF60 Karaktäristiskt för periodiska svängningar är att det finns en återförande kraft riktad mot jämviktsläget y 0 F F F k y F m a 4 Svängningar genererar vågor - Om en svängande
för M Skrivtid i hela (1,0 p) 3 cm man bryningsindex i glaset på ett 2. två spalter (3,0 p)
 Tentamen i tillämpad Våglära FAF260, 2016 06 01 för M Skrivtid 08.00 13.00 Hjälpmedel: Formelblad och miniräknare Uppgifterna är inte sorteradee i svårighetsgrad Börja varje ny uppgift på ett nytt blad
Tentamen i tillämpad Våglära FAF260, 2016 06 01 för M Skrivtid 08.00 13.00 Hjälpmedel: Formelblad och miniräknare Uppgifterna är inte sorteradee i svårighetsgrad Börja varje ny uppgift på ett nytt blad
FYSIK ÅK 9 AKUSTIK OCH OPTIK. Fysik - Måldokument Lena Folkebrant
 Fysik - Måldokument Lena Folkebrant FYSIK ÅK 9 AKUSTIK OCH OPTIK Ljud är egentligen tryckförändringar i något material. För att ett ljud ska uppstå måste något svänga eller vibrera. När en gitarrsträng
Fysik - Måldokument Lena Folkebrant FYSIK ÅK 9 AKUSTIK OCH OPTIK Ljud är egentligen tryckförändringar i något material. För att ett ljud ska uppstå måste något svänga eller vibrera. När en gitarrsträng
Vågrörelselära & Kvantfysik, FK2002 1 december 2011
 Räkneövning 6 Vågrörelselära & Kvantfysik, FK2002 december 20 Problem 36.23 Avståndet mellan två konvexa linser i ett mikroskop, l = 7.5 cm. Fokallängden för objektivet f o = 0.8 cm och för okularet f
Räkneövning 6 Vågrörelselära & Kvantfysik, FK2002 december 20 Problem 36.23 Avståndet mellan två konvexa linser i ett mikroskop, l = 7.5 cm. Fokallängden för objektivet f o = 0.8 cm och för okularet f
Tentamen i Fotonik - 2013-04-03, kl. 08.00-13.00
 FAFF25-2013-04-03 Tentamen i Fotonik - 2013-04-03, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2013-04-03 Tentamen i Fotonik - 2013-04-03, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Elektromagnetiska vågor (Ljus)
 Föreläsning 4-5 Elektromagnetiska vågor (Ljus) Ljus kan beskrivas som bestående av elektromagnetiska vågrörelser, d.v.s. ett tids- och rumsvarierande elektriskt och magnetiskt fält. Dessa ljusvågor följer
Föreläsning 4-5 Elektromagnetiska vågor (Ljus) Ljus kan beskrivas som bestående av elektromagnetiska vågrörelser, d.v.s. ett tids- och rumsvarierande elektriskt och magnetiskt fält. Dessa ljusvågor följer
Tentamen i Fotonik - 2014-08-26, kl. 08.00-13.00
 FAFF25-2014-08-26 Tentamen i Fotonik - 2014-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2014-08-26 Tentamen i Fotonik - 2014-08-26, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Final i Wallenbergs Fysikpris
 Final i Wallenbergs Fysikpris 26-27 mars 2010. Teoriprov Lösningsförslag 1. a) Vattens värmekapacitivitet: Isens värmekapacitivitet: Smältvärmet: Kylmaskinen drivs med spänningen och strömmen. Kylmaskinens
Final i Wallenbergs Fysikpris 26-27 mars 2010. Teoriprov Lösningsförslag 1. a) Vattens värmekapacitivitet: Isens värmekapacitivitet: Smältvärmet: Kylmaskinen drivs med spänningen och strömmen. Kylmaskinens
AstroSwedens mikroskopskola - nybörjarmikroskopi. AstroSwedens mikroskopiskola att använda mikroskop
 AstroSwedens mikroskopiskola att använda mikroskop Fenomenet aberration. Varför mikroskop? En ensam lins kan förstora maximalt c:a 5-0 gånger. Ofta slipas dessa linser så enkelt som möjligt vilket gör
AstroSwedens mikroskopiskola att använda mikroskop Fenomenet aberration. Varför mikroskop? En ensam lins kan förstora maximalt c:a 5-0 gånger. Ofta slipas dessa linser så enkelt som möjligt vilket gör
Teckenkonventionen: ljus in från vänster, ljusets riktning = positiv
 1 Avbildningskvalitet Föreläsning 1-2 Brytning i sfärisk yta Teckenkonventionen: ljus in från vänster, ljusets riktning = positiv Brytningslagen (Snells lag): n sin i = n sin i Paraxial approximation (vid
1 Avbildningskvalitet Föreläsning 1-2 Brytning i sfärisk yta Teckenkonventionen: ljus in från vänster, ljusets riktning = positiv Brytningslagen (Snells lag): n sin i = n sin i Paraxial approximation (vid
Geometrisk optik reflektion och brytning. Optiska system F9 Optiska instrument. Elektromagnetiska vågor. Det elektromagnetiska spektrumet FAF260
 Geometrisk optik reflektion oh brytning Geometrisk optik F7 Reflektion oh brytning F8 Avbildning med linser Plana oh buktiga speglar Optiska system F9 Optiska instrument 1 2 Geometrisk optik reflektion
Geometrisk optik reflektion oh brytning Geometrisk optik F7 Reflektion oh brytning F8 Avbildning med linser Plana oh buktiga speglar Optiska system F9 Optiska instrument 1 2 Geometrisk optik reflektion
The nature and propagation of light
 Ljus Emma Björk The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Ljus Emma Björk The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
LABORATION 5 Aberrationer
 LABORATION 5 Aberrationer Personnuer Nan Laborationen godkänd Datu Assistent Kungliga Tekniska högskolan BIOX 1 (5) LABORATION 5: ABERRATIONER Att läsa i kursboken: sid. 233-248, 257-261, 470-472, 480-485,
LABORATION 5 Aberrationer Personnuer Nan Laborationen godkänd Datu Assistent Kungliga Tekniska högskolan BIOX 1 (5) LABORATION 5: ABERRATIONER Att läsa i kursboken: sid. 233-248, 257-261, 470-472, 480-485,
Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00
 FAFF25-2014-04-25 Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2014-04-25 Tentamen i Fotonik - 2014-04-25, kl. 08.00-13.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
Övning 9 Tenta
 Övning 9 Tenta 014-11-8 1. När ljus faller in från luft mot ett genomskinligt material, med olika infallsvinkel, blir reflektansen den som visas i grafen nedan. Ungefär vilket brytningsindex har materialet?
Övning 9 Tenta 014-11-8 1. När ljus faller in från luft mot ett genomskinligt material, med olika infallsvinkel, blir reflektansen den som visas i grafen nedan. Ungefär vilket brytningsindex har materialet?
Elevlaborationer Bordsoptik laser Art.nr: 54624
 Elevlaborationer Bordsoptik laser Art.nr: 54624 Laser En laserstråle är speciell på flera sätt den består av en enda färg, t.ex. röd eller grön. ljuset går nästan helt parallellt (utan att sprida ut sig).
Elevlaborationer Bordsoptik laser Art.nr: 54624 Laser En laserstråle är speciell på flera sätt den består av en enda färg, t.ex. röd eller grön. ljuset går nästan helt parallellt (utan att sprida ut sig).
Tentamen i Fotonik - 2015-08-21, kl. 08.00-13.00
 Tentamen i Fotonik - 2015-08-21, kl. 08.00-13.00 Tentamen i Fotonik 2011 08 25, kl. 08.00 13.00 FAFF25-2015-08-21 FAFF25 2011 08 25 FAFF25 2011 08 25 FAFF25 FAFF25 - Tentamen Fysik för Fysik C och i för
Tentamen i Fotonik - 2015-08-21, kl. 08.00-13.00 Tentamen i Fotonik 2011 08 25, kl. 08.00 13.00 FAFF25-2015-08-21 FAFF25 2011 08 25 FAFF25 2011 08 25 FAFF25 FAFF25 - Tentamen Fysik för Fysik C och i för
Hittills har vi bara använt sfäriska ytor, dvs delar av en sfär. Plana ytor är specialfall av sfär (oändlig krökningsradie, r= ).
 Föreläsning 5 Astigmatism Hittills har vi bara använt sfäriska ytor, dvs delar av en sfär. Plana ytor är specialfall av sfär (oändlig krökningsradie, r= ). Men det finns andra ytor än sfäriska, t.ex. Toriska
Föreläsning 5 Astigmatism Hittills har vi bara använt sfäriska ytor, dvs delar av en sfär. Plana ytor är specialfall av sfär (oändlig krökningsradie, r= ). Men det finns andra ytor än sfäriska, t.ex. Toriska
Kikaren. Synvinkel. Kepler och Galileikikare. Vinkelförstoring. Keplerkikaren. Keplerkikaren FAF260. Lars Rippe, Atomfysik/LTH 1
 Kikaren Synvinkel Ökar synvinkeln os avlägsna objekt 1 2 Vinkelörstoring Deinition: med optiskt instrument G utan optiskt instrument Kepler oc Galileikikare Avlägsna objekt (t. ex. med kikare): synvinkeln
Kikaren Synvinkel Ökar synvinkeln os avlägsna objekt 1 2 Vinkelörstoring Deinition: med optiskt instrument G utan optiskt instrument Kepler oc Galileikikare Avlägsna objekt (t. ex. med kikare): synvinkeln
Geometrisk optik. Laboration FAFF25/FAFA60 Fotonik 2017
 Avsikten med denna laboration är att du ska få träning i att bygga upp avbildande optiska system, såsom enkla kikare och mikroskop, och på så vis få en god förståelse för dessas funktion. Redogörelsen
Avsikten med denna laboration är att du ska få träning i att bygga upp avbildande optiska system, såsom enkla kikare och mikroskop, och på så vis få en god förståelse för dessas funktion. Redogörelsen
Övning 1 Dispersion och prismaeffekt
 Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
Övning 1 Dispersion och prismaeffekt Färg För att beteckna färger används dessa spektrallinjer: Blått (F): λ F = 486.1 nm Gult (d): λ d = 587.6 nm Rött (C): λ c = 656.3 nm (Väte) (Helium) (Väte) Brytningsindex
5. Elektromagnetiska vågor - interferens
 Interferens i dubbelspalt A λ/2 λ/2 Dal för ena vågen möter topp för den andra och vice versa => mörkt (amplitud = 0). Dal möter dal och topp möter topp => ljust (stor amplitud). B λ/2 Fig. 5.1 För ljusvågor
Interferens i dubbelspalt A λ/2 λ/2 Dal för ena vågen möter topp för den andra och vice versa => mörkt (amplitud = 0). Dal möter dal och topp möter topp => ljust (stor amplitud). B λ/2 Fig. 5.1 För ljusvågor
Föreläsning 3: Radiometri och fotometri
 Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Observera att uppgifterna inte är ordnade efter svårighetsgrad!
 TENTAMEN I FYSIK FÖR n, 13 APRIL 2010 Skrivtid: 8.00-13.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och försedda med svar. Kladdblad
TENTAMEN I FYSIK FÖR n, 13 APRIL 2010 Skrivtid: 8.00-13.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och försedda med svar. Kladdblad
E-strängen rör sig fyra gånger så långsamt vid samma transversella kraft, accelerationen. c) Hur stor är A-strängens våglängd?
 Problem. Betrakta en elgitarr. Strängarna är 660 mm långa. Stämningen är E-A-d-g-b-e, det vill säga att strängen som ger tonen e-prim (330 Hz) ligger två oktav högre i frekvens än E-strängen. Alla strängar
Problem. Betrakta en elgitarr. Strängarna är 660 mm långa. Stämningen är E-A-d-g-b-e, det vill säga att strängen som ger tonen e-prim (330 Hz) ligger två oktav högre i frekvens än E-strängen. Alla strängar
Geometrisk optik. Innehåll. Inledning. Litteraturhänvisning. Förberedelseuppgifter. Geometrisk optik
 Geometrisk optik Innehåll Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande 1. Undersökning av tunna positiva linser... 3 2. Undersökning av tunna negativa linser... 3 3. Galileikikaren...
Geometrisk optik Innehåll Inledning... 1 Litteraturhänvisning... 1 Förberedelseuppgifter... 1 Utförande 1. Undersökning av tunna positiva linser... 3 2. Undersökning av tunna negativa linser... 3 3. Galileikikaren...
TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t s(x,t) =s 0 sin 2π T x. v = fλ =3 5 m/s = 15 m/s
 140528: TFEI02 1 TFEI02: Vågfysik Tentamen 140528: Svar och anvisningar Uppgift 1 a) En fortskridande våg kan skrivas på formen: t s(x,t) =s 0 sin 2π T x λ Vi ser att periodtiden är T =1/3 s, vilket ger
140528: TFEI02 1 TFEI02: Vågfysik Tentamen 140528: Svar och anvisningar Uppgift 1 a) En fortskridande våg kan skrivas på formen: t s(x,t) =s 0 sin 2π T x λ Vi ser att periodtiden är T =1/3 s, vilket ger
Mätning av fokallängd hos okänd lins
 Mätning av fokallängd hos okänd lins Syfte Labbens syfte är i första hand att lära sig hantera mätfel och uppnå god noggrannhet, även med systematiska fel. I andra hand är syftet att hantera linser och
Mätning av fokallängd hos okänd lins Syfte Labbens syfte är i första hand att lära sig hantera mätfel och uppnå god noggrannhet, även med systematiska fel. I andra hand är syftet att hantera linser och
Lösningsförslag - tentamen. Fysik del B2 för tekniskt / naturvetenskapligt basår / bastermin BFL 122 / BFL 111
 Linköpings Universitet Institutionen för Fysik, Kemi, och Biologi Avdelningen för Tillämpad Fysik Mike Andersson Lösningsförslag - tentamen Torsdagen den 27:e maj 2010, kl 08:00 12:00 Fysik del B2 för
Linköpings Universitet Institutionen för Fysik, Kemi, och Biologi Avdelningen för Tillämpad Fysik Mike Andersson Lösningsförslag - tentamen Torsdagen den 27:e maj 2010, kl 08:00 12:00 Fysik del B2 för
Läs i vågläraboken om holografi (sid ) och sid 5 17 i detta kompendium.
 1 Förberedelser Läs i vågläraboken om holografi (sid 370-372) och sid 5 17 i detta kompendium. Gör följande uppgifter: Lösningarna inlämnas renskrivna vid laborationens början till handledaren för kontroll.
1 Förberedelser Läs i vågläraboken om holografi (sid 370-372) och sid 5 17 i detta kompendium. Gör följande uppgifter: Lösningarna inlämnas renskrivna vid laborationens början till handledaren för kontroll.
9 Ljus. Inledning. Fokus: Spektrum inte bara färger
 9 Ljus Inledning Kapitelinledningen på sidorna 158 159 i grundboken och sid 90 i lightboken handlar om solens strålar. Ljusstrålarna har färdats med den högsta hastighet som går, 300 000 km/s, från solens
9 Ljus Inledning Kapitelinledningen på sidorna 158 159 i grundboken och sid 90 i lightboken handlar om solens strålar. Ljusstrålarna har färdats med den högsta hastighet som går, 300 000 km/s, från solens
Tentamen i Fotonik , kl
 FAFF25-2015-05-04 Tentamen i Fotonik - 2015-05-04, kl. 14.00-19.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
FAFF25-2015-05-04 Tentamen i Fotonik - 2015-05-04, kl. 14.00-19.00 FAFF25 - Fysik för C och D, Delkurs i Fotonik Tillåtna hjälpmedel: Miniräknare, godkänd formelsamling (t ex TeFyMa), utdelat formelblad.
räknedosa. Lösningarna ska Kladdblad rättas. (1,0 p) vationen
 TENTAMEN I TILLÄMPAD VÅGLÄRA FÖR M Skrivtid: 8.00 13.00 Hjälpmedel: Formelblad och räknedosa. Uppgifterna är inte ordnade efter svårighetsgrad. Börja varje ny uppgift på ettt nytt blad och skriv bara på
TENTAMEN I TILLÄMPAD VÅGLÄRA FÖR M Skrivtid: 8.00 13.00 Hjälpmedel: Formelblad och räknedosa. Uppgifterna är inte ordnade efter svårighetsgrad. Börja varje ny uppgift på ettt nytt blad och skriv bara på
Böjning. Tillämpad vågrörelselära. Föreläsningar. Vad är optik? Huygens princip. Böjning vs. interferens FAF260. Lars Rippe, Atomfysik/LTH 1
 Tillämpad vågrörelselära 2 Föreläsningar Vad är optik? F10 och upplösning (kap 16) F11 Interferens och böjning (kap 17) F12 Multipelinterferens (kap 18) F13 Polariserat ljus (kap 20) F14 Reserv / Repetition
Tillämpad vågrörelselära 2 Föreläsningar Vad är optik? F10 och upplösning (kap 16) F11 Interferens och böjning (kap 17) F12 Multipelinterferens (kap 18) F13 Polariserat ljus (kap 20) F14 Reserv / Repetition
 Robert Rosén Recept för beräkning av huvudplan Frågeställning: Hur hittar man främre och bakre fokalpunkt, samt huvudplan (både för tjocka linser och system av tunna linser)? Varför skall huvudplan räknas?
Robert Rosén Recept för beräkning av huvudplan Frågeställning: Hur hittar man främre och bakre fokalpunkt, samt huvudplan (både för tjocka linser och system av tunna linser)? Varför skall huvudplan räknas?
Vad är ljus? Begrepp. Begrepp och svåra ord: Övningar. Foton, partikelrörelse, våglängd, prisma, spektrum, absorbera, reflektera.
 Vad är ljus? Ljus består av ljuspartiklar som kallas fotoner. Ljusenergi är fotoner. Om fotoner krockar med något kan de studsa (reflektera) eller omvandlas till värmeenergi (absorbera). Till exempel,
Vad är ljus? Ljus består av ljuspartiklar som kallas fotoner. Ljusenergi är fotoner. Om fotoner krockar med något kan de studsa (reflektera) eller omvandlas till värmeenergi (absorbera). Till exempel,
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 33 - Ljus 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Vågrörelselära och optik Kapitel 33 - Ljus 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Hur gör man. Kika försiktigt in genom hålen i luckorna. Vilken färg är det på insidan av lådan? Så fungerar det
 2. Svart låda Hur gör man Kika försiktigt in genom hålen i luckorna. Vilken färg är det på insidan av lådan? Så fungerar det Skåpet: Det enda vi kan se är ljus. Vi kan inte se hundar, bilar, bollar eller
2. Svart låda Hur gör man Kika försiktigt in genom hålen i luckorna. Vilken färg är det på insidan av lådan? Så fungerar det Skåpet: Det enda vi kan se är ljus. Vi kan inte se hundar, bilar, bollar eller
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
FACIT OCH KOMMENTARER
 ACIT OCH KOMMENTARER TESTA DIG SJÄLV, INALEN OCH PERSPEKTIV 361 5. L J US ACIT TILL TESTA DIG SJÄLV Testa dig själv 5.1 örklara begreppen ljuskälla Ett föremål som ger ifrån sig ljus, till exempel brinnande
ACIT OCH KOMMENTARER TESTA DIG SJÄLV, INALEN OCH PERSPEKTIV 361 5. L J US ACIT TILL TESTA DIG SJÄLV Testa dig själv 5.1 örklara begreppen ljuskälla Ett föremål som ger ifrån sig ljus, till exempel brinnande
OBS: Alla mätningar och beräknade värden ska anges i SI-enheter med korrekt antal värdesiffror. Felanalys behövs endast om det anges i texten.
 Speed of light OBS: Alla mätningar och beräknade värden ska anges i SI-enheter med korrekt antal värdesiffror. Felanalys behövs endast om det anges i texten. 1.0 Inledning Experiment med en laseravståndsmätare
Speed of light OBS: Alla mätningar och beräknade värden ska anges i SI-enheter med korrekt antal värdesiffror. Felanalys behövs endast om det anges i texten. 1.0 Inledning Experiment med en laseravståndsmätare
1. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (1p)
 Problem Energi. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (p) b) Ge en tydlig förklaring av hur frekvens, period, våglängd och våghastighet hänger
Problem Energi. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (p) b) Ge en tydlig förklaring av hur frekvens, period, våglängd och våghastighet hänger
