1 Minkostnadsflödesproblem i nätverk
|
|
|
- Jonas Samuelsson
- för 7 år sedan
- Visningar:
Transkript
1 Krister Svanberg, april Minkostnadsflödesproblem i nätverk Ett nätverk består av en given mängd noder numrerade från 1 till m (där m är antalet noder) samt en given mängd riktade bågar mellan vissa par av noderna. En båge som går från nod nr i till nod nr j betecknas (i, j) och ritas som en pil med spetsen vid nod j. Ibland kan det finns två bågar mellan två givna noder, dels en båge (i, j) från nod nr i till nod nr j, dels en båge (j, i) från nod nr j till nod nr i. Dessa måste man skilja på. Låt B beteckna mängden av bågar (i, j) i nätverket, och låt n beteckna antalet bågar i B. Det förutsätts genomgående att nätverket är sammanhängande, vilket betyder att det inte är fråga om ett antal separata nätverk som fullständigt saknar förbindelse med varann. Låt x ij beteckna flödet (av någon storhet) i bågen (i, j) B. Till varje båge (i, j) B hör en given kostnad per flödesenhet, betecknad c ij. Låt x IR n och c IR n vara vektorer med komponenterna x ij resp c ij, för (i, j) B, i någon väldefinierad ordning. Vissa noder är källnoder, i vilka nätverket fylls på med givna kvantiteter flöde ( utifrån ). Vissa noder är sänknoder, i vilka nätverket tappas av på givna kvantiteter flöde. De återstående noderna kallas mellannoder. I varje nod råder flödesbalans, dvs utflödet = inflödet, där utflödet från noden är summan av flödet i alla bågar ut från noden plus eventuell avtappning i noden (om det är en sänknod), medan inflödet till noden är summan av flödet i alla bågar in till noden plus eventuell påfyllning i noden (om det är en källnod). Låt b i beteckna hur mycket flöde som tillförs nätverket i nod nr i. För källnoder är b i > 0, m för sänknoder är b i < 0 och för mellannoder är b i = 0. Vi förutsätter att b i = 0. För att konkretisera den kommande framställningen ska vi utgå från ett nätverk bestående av fem stycken noder, dvs m = 5, numrerade från 1 till 5, samt följande bågmängd: B = {(1, 2), (1, 3), (2, 3), (2, 4), (3, 4), (3, 5), (4, 5)}, dvs n = 7. Läsaren rekommenderas att utan dröjsmål rita upp detta nätverk; den fortsatta läsningen kommer att underlättas väsentligt av en sådan figur. Vi antar att noderna nr 1 och 2 är källnoder med påfyllningen 40 resp 35 flödesenheter, medan noderna 3, 4 och 5 är sänknoder med avtappningen 30, 25 resp 20 flödesenheter. Vi antar vidare att kostnaderna per flödesenhet i de olika bågarna ges av c T = (c 12, c 13, c 23, c 24, c 34, c 35, c 45 ) = (2, 5, 2, 2, 1, 1, 2). (1.1) i=1 1
2 Minkostnadflödesproblemet svarande mot detta nätverk kan skrivas på följande form: MKF : minimera c T x då Ãx = b, x 0, (1.2) där x = (x 12, x 13, x 23, x 24, x 34, x 35, x 45 ) T, c = (c 12, c 13, c 23, c 24, c 34, c 35, c 45 ) T, b à = och b b 2 = b 3 b 4 = b 5 20 Denna matris à har linjärt beroende rader, ty med y T = ( ) T är y T à = ( ). Därmed är exempelvis den sista raden i à = summan av de övriga raderna i Ã. Likaså är den sista komponenten i vektorn b = summan av de övriga komponenterna i b. Det betyder att vi kan stryka (exempelvis) den sista av ekvationerna i systemet Ãx = b utan att påverka lösningsmängden till systemet, eftersom den sista ekvationen automatiskt blir uppfylld om de övriga ekvationerna är uppfyllda. Fortsättningsvis ska vi därför i stället skriva minkostnadsflödesproblemet på formen MKF : minimera c T x då Ax = b, x 0, (1.3) där (m 1) n matrisen A har erhållits genom att stryka sista raden i Ã, medan vektorn b IR m 1 har erhållits genom att stryka sista komponenten i b. Vi har alltså att A = och b = b 1 b 2 b 3 b 4 = Denna matris A har linjärt oberoende rader, ty den enda lösningen till y T A = 0 T, som på komponentform kan skrivas y 1 y 2 = 0, y 1 y 3 = 0, y 2 y 3 = 0, y 2 y 4 = 0, y 3 y 4 = 0, y 3 = 0 och y 4 = 0, är uppenbarligen y = 0. Vi ska nu visa hur simplexmetoden förenklas när den tillämpas på MKF-problemet (1.3). Eftersom A har linjärt oberoende rader så har varje baslösning m 1 st basvariabler och n m+1 st icke-basvariabler. Motsvarande basmatris A β är (m 1) (m 1), dvs 4 4. Det finns en trevlig tolkning av baslösningar till MKF problemet, baserat på begreppet uppspännande träd. En given delmängd av bågarna utgör ett uppspännande träd om dels varje nod i nätverket vidrörs av minst en båge ur delmängden, dels det delnätverk som bildas av bågarna ur delmängden är sammanhängande, dels det inte finns någon slinga bestående av bågar ur delmängden, utan hänsyn tagen till bågarnas riktning. 2
3 Sats: m 1 st kolonner ur (m 1) n matrisen A i ett MKF-problem är linjärt oberoende om och endast om motsvarande m 1 st bågar bildar ett uppspännande träd. Givet ett uppspännande träd, och därmed en motsvarande basmatris A β, så är det lätt att direkt i nätverket bestämma vilka värden de aktuella basvariablerna måste ha, dvs att lösa ekvationssystemet A β x β = b. Detta ska nu illustreras i vårt exempel. Välj exempelvis trädet bestående av bågarna B β = {(1, 2), (2, 3), (2, 4), (4, 5)}. (Rita figur!) Motsvarande basmatris A β respektive icke-basmatris A ν är då A β = och A ν = (1.4) De tre icke-basvariablerna x 13, x 34 och x 35 är samtliga = 0 i den aktuella baslösningen. Basvariablernas värden kan bestämmas i exempelvis följande ordning (se din figur): x 12 = 40, pga flödesbalansvillkoret i nod nr 1. x 23 = 30, pga flödesbalansvillkoret i nod nr 3. x 24 = 45, pga flödesbalansvillkoret i nod nr 2. x 45 = 20, pga flödesbalansvillkoret i nod nr 4. Här blev resultatet en tillåten baslösning, ty samtliga basvariablerna blev 0, men detta gäller inte för alla val av uppspännande träd. Vi ska senare antyda hur man på ett systematiskt sätt kan bestämma en tillåten baslösning att starta simplexmetoden från. Antag nu att vi, i likhet med ovan, har lyckats hitta en tillåten baslösning. Nästa steg är då att avgöra om denna lösning är optimal, genom att beräkna de reducerade kostnaderna r ij för icke-basvariablerna. Först ska då vektorn y IR m 1 beräknas ur ekvationssystemet y T A β = c T β, som i vårt fall, med y T = (y 1, y 2, y 3, y 4 ) och A β enligt (1.4), blir följande fyra ekvationer: y 1 y 2 = c 12, y 2 y 3 = c 23, y 2 y 4 = c 24 och y 4 = c 45. Om vi inför y 5 = 0 så kan dessa ekvationer kortfattat skrivas y i y j = c ij för alla (i, j) B β (dvs för alla basbågar). (1.5) Varje skalär y i svarar alltså mot en nod i nätverket. Värdet på dessa skalärer kan bestämmas direkt i nätverket i exempelvis följande ordning (se din figur): Först sätts y 5 = 0, vilket gäller per definition. Basbågen (4, 5) ger sedan att y 4 y 5 = c 45, dvs y 4 = c 45. Basbågen (2, 4) ger sedan att y 2 y 4 = c 24, dvs y 2 = y 4 + c 24. Basbågen (2, 3) ger sedan att y 2 y 3 = c 23, dvs y 3 = y 2 c 23. Basbågen (1, 2) ger slutligen att y 1 y 2 = c 12, dvs y 1 = y 2 + c 12. Enligt ovan är c T = (c 12, c 13, c 23, c 24, c 34, c 35, c 45 ) = (2, 5, 2, 2, 1, 1, 2). Då blir (i tur och ordning) y 5 = 0, y 4 = 2, y 2 = 4, y 3 = 2 och y 1 = 6. 3
4 Nästa steg är att beräkna reducerade kostnaderna ur formeln r T ν = c T ν y T A ν, som i vårt fall, med y T = (y 1, y 2, y 3, y 4 ) och A ν enligt (1.4), blir: r 13 = c 13 y 1 + y 3 = = 1, r 34 = c 34 y 3 + y 4 = = 1, r 35 = c 35 y 3 = 1 2 = 1. Om vi som tidigare inför y 5 = 0 så kan nyssnämnda uttryck kortfattat skrivas: r ij = c ij y i + y j för alla (i, j) B ν (dvs för alla icke-basbågar). (1.6) Om r ν 0 så är den aktuella tillåtna baslösningen optimal. Om minst en icke-basvariabel har r ij < 0 så ska vi byta bas genom att låta en av dessa icke-basvariabler bli en ny basvariabel. I exemplet ovan var r 35 = 1 (och övriga r ij 0), vilket medför att vi sätter x 35 = t och låter t öka från 0, medan övriga icke-basvariabler ligger kvar vid 0. Därvid ändras basvariablernas värden entydigt som funktion av t. Hur de ändras kan bestämmas i exempelvis följande ordning (se din figur): x 12 (t) = 40, pga flödesbalansvillkoret i nod nr 1. (Påverkas ej av t.) x 23 (t) = 30 + t, pga flödesbalansvillkoret i nod nr 3. x 24 (t) = 45 t, pga flödesbalansvillkoret i nod nr 2. x 45 (t) = 20 t, pga flödesbalansvillkoret i nod nr 4. Vi ser att den nya bågen (3, 5) tillsammans med några av trädbågarna (dvs några av bågarna svarande mot basvariabler) bildar en entydig slinga i nätverket. Varje basvariabel i denna slinga ändras med +t eller t. Basvariabler som inte ligger i slingan påverkas ej av t. Den basvariabel, bland de som ändras med t, som först blir = 0 då t växer ska ut ur basen. I vårt exempel kan t ökas till t = 20. Då blir x 45 = 0. Den nya tillåtna baslösningen ges av x 12 = 40, x 23 = 50, x 24 = 25, x 35 = 20 (basvariablerna) och x 13 = 0, x 34 = 0, x 45 = 0. Motsvarande uppspännande träd ges av B β = {(1, 2), (2, 3), (2, 4), (3, 5)}. (Rita figur.) Nu är en simplexiteration fullbordad och vi upprepar ovanstående steg. Skalärerna y i beräknas i exempelvis följande ordning: Först sätts y 5 = 0, vilket gäller per definition. Basbågen (3, 5) ger sedan att y 3 y 5 = c 35, dvs y 3 = c 35 = 1. Basbågen (2, 3) ger sedan att y 2 y 3 = c 23, dvs y 2 = y 3 + c 23 = 3. Basbågen (2, 4) ger sedan att y 2 y 4 = c 24, dvs y 4 = y 2 c 24 = 1. Basbågen (1, 2) ger slutligen att y 1 y 2 = c 12, dvs y 1 = y 2 + c 12 = 5. Nästa steg är att beräkna reducerade kostnaderna för icke-basvariablerna ur formeln r ij = c ij y i + y j, vilket ger r 13 = c 13 y 1 + y 3 = = 1, r 34 = c 34 y 3 + y 4 = = 1, r 45 = c 45 y 4 + y 5 = 2 1 = 1. Eftersom alla r ij 0 så är den aktuella tillåtna baslösningen ovan optimal. 4
5 Man kan notera att när simplexmetoden tillämpas på MKF enligt ovan så består kalkylerna enbart av additioner och subtraktioner. Därav följer att om alla b i och c ij är heltal så behöver man bara addera och subtrahera heltal, varvid exempelvis avrundningsfel aldrig uppkommer. Vidare följer att om alla b i är heltal så blir alla x ij hela tiden heltal. Speciellt kommer då den optimala lösning som metoden hittar att vara heltalig, trots att man inte explicit kräver det! Denna egenskap medför att man exempelvis kan lösa så kallade assignmentproblem (där variablerna är binära) som minkostnadsflödesproblem, utan att explicit kräva att varje variabel endast får anta något av värdena 0 och 1. Avslutningsvis ska antydas hur man kan bestämma en tillåten baslösning till MKF-problemet, utan att behöva pröva sig fram med gissade uppspännande träd. Utöka nätverket genom att först införa en extranod som vi kallar nummer m+1, dvs nummer 6 i vårt fall. Inför sedan m st extrabågar enligt följande: För varje källnod införs en båge från källnoden till extranoden. För varje sänknod införs en båge till sänknoden från extranoden. För varje mellannod införs antingen en båge från mellannoden till extranoden eller en båge till mellannoden från extranoden. I vårt exempel innebär detta att vi inför extrabågarna {(1, 6), (2, 6), (6, 3), (6, 4), (6, 5)}, utöver de ursprungliga bågarna. Betrakta sedan ett MKF-problem i detta utökade nätverk, där kostnadskoefficienterna c ij för extrabågarna väljs till ett stort tal M, så att flödet i dessa bågar blir väldigt dyrt, medan de ursprungliga bågarna i nätverket behåller sina från början givna c ij. En tillåten baslösning till detta utökade MKF-problem erhålls genom att till basvariabler välja de variabler som svarar mot extrabågarna (som utgör ett uppspännande träd till det utökade nätverket). Basvariablernas värden ges av x i,m+1 = b i 0 i bågar till extranoden, och x m+1,i = b i 0 i bågar från extranoden. I vårt exempel ges dessa basvariabelvärden av x 16 = 40, x 26 = 35, x 63 = 30, x 64 = 25 och x 65 = 20. Sedan appliceras simplexmetoden (som den har beskrivits ovan) på detta utökade MKFproblem. Eftersom extrabågarna är väldigt dyra i förhållande till de ursprungliga bågarna, så kommer simplexmetoden automatiskt att se till att flödet i alla extrabågar blir = 0 (om detta är möjligt), varvid flödet har förflyttats till det ursprungliga nätverkets bågar. Optimala lösningen till det utökade MKF-problemet kommer då att vara optimal lösning även till det ursprungliga nätverket. 5
Föreläsning 6: Nätverksoptimering
 Föreläsning 6: Nätverksoptimering. Minkostnadsflödesproblem i nätverk.. Modellering och grafteori.. Simplexmetoden. Föreläsning 6 - Ulf Jönsson & Per Enqvist Nätverksoptimering Minkostnadsflödesproblem
Föreläsning 6: Nätverksoptimering. Minkostnadsflödesproblem i nätverk.. Modellering och grafteori.. Simplexmetoden. Föreläsning 6 - Ulf Jönsson & Per Enqvist Nätverksoptimering Minkostnadsflödesproblem
1 LP-problem på standardform och Simplexmetoden
 Krister Svanberg, mars 202 LP-problem på standardform och Simplexmetoden I detta avsnitt utgår vi från LP-formuleringen (2.2) från föreläsning. Denna form är den bäst lämpade för en strömlinjeformad implementering
Krister Svanberg, mars 202 LP-problem på standardform och Simplexmetoden I detta avsnitt utgår vi från LP-formuleringen (2.2) från föreläsning. Denna form är den bäst lämpade för en strömlinjeformad implementering
Lösningar till SF1852 Optimeringslära för E, 16/1 08
 Lösningar till SF8 Optimeringslära för E, 6/ 8 Uppgift (a) Problemet är ett transportproblem, ett specialfall av minkostnadsflödesproblem Nätverket består av 7 st noder A,B,C,P,Q,R,S, alternativt kallade,,,7,
Lösningar till SF8 Optimeringslära för E, 6/ 8 Uppgift (a) Problemet är ett transportproblem, ett specialfall av minkostnadsflödesproblem Nätverket består av 7 st noder A,B,C,P,Q,R,S, alternativt kallade,,,7,
Flöde i nätverk. Flöde i nätverk. Specialfall av minkostnadsflödesproblemet
 Flöde i nätverk Graf: G = (N, B) Variabeldefinition: x ij = flöde i båge (i, j). Bågdata för båge (i, j): c ij : flödeskostnad per enhet. u ij : övre gräns för flödet. l ij : undre gräns för flödet. Bivillkor:
Flöde i nätverk Graf: G = (N, B) Variabeldefinition: x ij = flöde i båge (i, j). Bågdata för båge (i, j): c ij : flödeskostnad per enhet. u ij : övre gräns för flödet. l ij : undre gräns för flödet. Bivillkor:
Lösningar till SF1861/SF1851 Optimeringslära, 24/5 2013
 Lösningar till SF86/SF85 Optimeringslära, 4/5 03 Uppgift (a) Inför de 3 variablerna x ij = kvantitet (i sorten ton) som fabrik nr i åläggs att tillverka av produkt nr j, samt t = tiden (i sorten timmar)
Lösningar till SF86/SF85 Optimeringslära, 4/5 03 Uppgift (a) Inför de 3 variablerna x ij = kvantitet (i sorten ton) som fabrik nr i åläggs att tillverka av produkt nr j, samt t = tiden (i sorten timmar)
Lösningar till SF1861 Optimeringslära, 28 maj 2012
 Lösningar till SF86 Optimeringslära, 28 maj 202 Uppgift.(a) Då det primala problemet P är så är det motsvarande duala problemet D minimera 3x + x 2 då 3x + 2x 2 6 x + 2x 2 4 x j 0, j =, 2. maximera 6 +
Lösningar till SF86 Optimeringslära, 28 maj 202 Uppgift.(a) Då det primala problemet P är så är det motsvarande duala problemet D minimera 3x + x 2 då 3x + 2x 2 6 x + 2x 2 4 x j 0, j =, 2. maximera 6 +
1 Duala problem vid linjär optimering
 Krister Svanberg, april 2012 1 Duala problem vid linjär optimering Detta kapitel handlar om två centrala teoretiska resultat för LP, nämligen dualitetssatsen och komplementaritetssatsen. Först måste vi
Krister Svanberg, april 2012 1 Duala problem vid linjär optimering Detta kapitel handlar om två centrala teoretiska resultat för LP, nämligen dualitetssatsen och komplementaritetssatsen. Först måste vi
Lösningar till 5B1762 Optimeringslära för T, 24/5-07
 Lösningar till 5B76 Optimeringslära för T, 4/5-7 Uppgift (a) Först använder vi Gauss Jordans metod på den givna matrisen A = Addition av gånger första raden till andra raden ger till resultat matrisen
Lösningar till 5B76 Optimeringslära för T, 4/5-7 Uppgift (a) Först använder vi Gauss Jordans metod på den givna matrisen A = Addition av gånger första raden till andra raden ger till resultat matrisen
TNSL05 Optimering, Modellering och Planering. Föreläsning 10
 TNSL05 Optimering, Modellering och Planering Föreläsning 10 Agenda Kursens status Repetition Flödesnätverk Optimalitetsvillkor LP och Minkostandsflöde (MKF) Nätverkssimplex Känslighetsanalys Exempel: MKF
TNSL05 Optimering, Modellering och Planering Föreläsning 10 Agenda Kursens status Repetition Flödesnätverk Optimalitetsvillkor LP och Minkostandsflöde (MKF) Nätverkssimplex Känslighetsanalys Exempel: MKF
Föreläsning 10/11! Gruppuppgifter: Gruppuppgift 1: Alla har redovisat. Gruppuppgift 2: Alla har redovisat Gruppuppgift 3: På gång.
 Föreläsning 10 Agenda Kursens status Repetition Flödesnätverk Optimalitetsvillkor LP och Minkostandsflöde (MKF) Nätverkssimplex Känslighetsanalys Exempel: MKF och Nätverkssimplex Föreläsning 10/11! Gruppuppgifter:
Föreläsning 10 Agenda Kursens status Repetition Flödesnätverk Optimalitetsvillkor LP och Minkostandsflöde (MKF) Nätverkssimplex Känslighetsanalys Exempel: MKF och Nätverkssimplex Föreläsning 10/11! Gruppuppgifter:
Flöde i nätverk. Flöde i nätverk. Specialfall av minkostnadsflödesproblemet
 Flöde i nätverk Graf: G = (N, B) Variabeldefinition: x ij = flöde i båge (i, j). Bågdata för båge (i, j): c ij : flödeskostnad per enhet. u ij : övre gräns för flödet. l ij : undre gräns för flödet. Bivillkor:
Flöde i nätverk Graf: G = (N, B) Variabeldefinition: x ij = flöde i båge (i, j). Bågdata för båge (i, j): c ij : flödeskostnad per enhet. u ij : övre gräns för flödet. l ij : undre gräns för flödet. Bivillkor:
Hemuppgift 1, SF1861 Optimeringslära, VT 2017
 Hemuppgift 1, SF1861 Optimeringslära, VT 2017 Examinator: Krister Svanberg, tel: 790 7137, krille@math.kth.se. Labassistent: David Ek, daviek@kth.se, Lämnas i Matematiks svarta postlåda (SF) för inlämningsuppgifter,
Hemuppgift 1, SF1861 Optimeringslära, VT 2017 Examinator: Krister Svanberg, tel: 790 7137, krille@math.kth.se. Labassistent: David Ek, daviek@kth.se, Lämnas i Matematiks svarta postlåda (SF) för inlämningsuppgifter,
Flöde i nätverk. Flöde i nätverk. Specialfall av minkostnadsflödesproblemet. Specialfall av minkostnadsflödesproblemet. Slutsats.
 Flöde i nätverk Graf: G = (N, B) Variabeldefinition: x ij = flöde i båge (i, j). Bågdata för båge (i, j): c ij : flödeskostnad per enhet. u ij : övre gräns för flödet. l ij : undre gräns för flödet. Bivillkor:
Flöde i nätverk Graf: G = (N, B) Variabeldefinition: x ij = flöde i båge (i, j). Bågdata för båge (i, j): c ij : flödeskostnad per enhet. u ij : övre gräns för flödet. l ij : undre gräns för flödet. Bivillkor:
1 De fyra fundamentala underrummen till en matris
 Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem.
 Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Lösningar till tentan i SF1861 Optimeringslära, 1 juni 2017
 Lösningar till tentan i SF86 Optimeringslära, juni 7 Lösningarna är på svenska, utom lösningen av (a som är på engelska (a The considered network is illustrated in FIGURE below, where the supply at the
Lösningar till tentan i SF86 Optimeringslära, juni 7 Lösningarna är på svenska, utom lösningen av (a som är på engelska (a The considered network is illustrated in FIGURE below, where the supply at the
Lösningar till tentan i SF1861 Optimeringslära, 3 Juni, 2016
 Lösningar till tentan i SF86 Optimeringslära, 3 Juni, 6 Uppgift (a) We note that each column in the matrix A contains one + and one, while all the other elements in the column are zeros We also note that
Lösningar till tentan i SF86 Optimeringslära, 3 Juni, 6 Uppgift (a) We note that each column in the matrix A contains one + and one, while all the other elements in the column are zeros We also note that
1 Kvadratisk optimering under linjära likhetsbivillkor
 Krister Svanberg, april 0 Kvadratisk optimering under linjära likhetsbivillkor I detta kapitel behandlas följande kvadratiska optimeringsproblem under linjära likhetsbivillkor: xt Hx + c T x + c 0 då Ax
Krister Svanberg, april 0 Kvadratisk optimering under linjära likhetsbivillkor I detta kapitel behandlas följande kvadratiska optimeringsproblem under linjära likhetsbivillkor: xt Hx + c T x + c 0 då Ax
Föreläsning 6: Transportproblem (TP)
 Föreläsning 6: Transportproblem (TP) 1. Transportproblem 2. Assignmentproblem Föreläsning 6 Ulf Jönsson & Per Enqvist 1 Transportproblem Transportproblem Varor ska transporteras från fabriker till varuhus:
Föreläsning 6: Transportproblem (TP) 1. Transportproblem 2. Assignmentproblem Föreläsning 6 Ulf Jönsson & Per Enqvist 1 Transportproblem Transportproblem Varor ska transporteras från fabriker till varuhus:
Lösningsförslag till tentamen i SF1861 Optimeringslära för T. Torsdag 28 maj 2010 kl
 Lösningsförslag till tentamen i SF86 Optimeringslära för T. Torsdag 28 maj 2 kl. 4. 9. Examinator: Per Enqvist, tel. 79 62 98. (a) Inför variablerna x = (x sr, x sm, x sp, x sa, x sd, x gr, x gm, x gp,
Lösningsförslag till tentamen i SF86 Optimeringslära för T. Torsdag 28 maj 2 kl. 4. 9. Examinator: Per Enqvist, tel. 79 62 98. (a) Inför variablerna x = (x sr, x sm, x sp, x sa, x sd, x gr, x gm, x gp,
Optimeringslära Kaj Holmberg
 Tekniska Högskolan i Linköping Optimering för ingenjörer Matematiska Institutionen Lösning till tentamen Optimeringslära 26-6- Kaj Holmberg Lösningar Uppgift Hinkpackning (hink = tur med cykeln. Jag använder
Tekniska Högskolan i Linköping Optimering för ingenjörer Matematiska Institutionen Lösning till tentamen Optimeringslära 26-6- Kaj Holmberg Lösningar Uppgift Hinkpackning (hink = tur med cykeln. Jag använder
LP-problem. Vårt första exempel. Baslösningar representerar extrempunkter. Baslösningar representerar extrempunkter
 LP-problem Vårt första exempel Ett LP-problem: max z = c T x då Ax b, x 0. Den tillåtna mängden är en polyeder och konvex. Målfunktionen är linjär och konvex. Så problemet är konvext. Var ligger optimum?
LP-problem Vårt första exempel Ett LP-problem: max z = c T x då Ax b, x 0. Den tillåtna mängden är en polyeder och konvex. Målfunktionen är linjär och konvex. Så problemet är konvext. Var ligger optimum?
Föreläsning 2: Simplexmetoden. 1. Repetition av geometriska simplexmetoden. 2. Linjärprogrammeringsproblem på standardform.
 Föreläsning 2: Simplexmetoden. Repetition av geometriska simplexmetoden. 2. Linjärprogrammeringsproblem på standardform. 3. Simplexalgoritmen. 4. Hur bestämmer man tillåtna startbaslösningar? Föreläsning
Föreläsning 2: Simplexmetoden. Repetition av geometriska simplexmetoden. 2. Linjärprogrammeringsproblem på standardform. 3. Simplexalgoritmen. 4. Hur bestämmer man tillåtna startbaslösningar? Föreläsning
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp)
 Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Optimeringslära Kaj Holmberg
 Tekniska Högskolan i Linköping Optimering för ingenjörer Matematiska Institutionen Lösning till tentamen Optimeringslära 28-5-3 Kaj Holmberg Lösningar Uppgift a: P: Grafisk lösning ger x = 2/7 = 2 6/7,
Tekniska Högskolan i Linköping Optimering för ingenjörer Matematiska Institutionen Lösning till tentamen Optimeringslära 28-5-3 Kaj Holmberg Lösningar Uppgift a: P: Grafisk lösning ger x = 2/7 = 2 6/7,
Optimeringslära Kaj Holmberg
 Tekniska Högskolan i Linköping Optimering för ingenjörer Matematiska Institutionen Lösning till tentamen Optimeringslära 2018-08-31 Kaj Holmberg Lösningar Uppgift 1 1a: Inför slackvariabler x 5, x 6 och
Tekniska Högskolan i Linköping Optimering för ingenjörer Matematiska Institutionen Lösning till tentamen Optimeringslära 2018-08-31 Kaj Holmberg Lösningar Uppgift 1 1a: Inför slackvariabler x 5, x 6 och
1 Ickelinjär optimering under bivillkor
 Krister Svanberg, maj 2012 1 Ickelinjär optimering under bivillkor Hittills har vi behandlat optimeringsproblem där alla variabler x j kunnat röra sig fritt, oberoende av varann, och anta hur stora eller
Krister Svanberg, maj 2012 1 Ickelinjär optimering under bivillkor Hittills har vi behandlat optimeringsproblem där alla variabler x j kunnat röra sig fritt, oberoende av varann, och anta hur stora eller
2 = 3 = 1. ekvationssystem är beskriven som de vektorer X = 2 0 1 2. 1 1 0 2
 . Tisdagen 35 Igår visade vi att lösningsmängden W R 5 till ekvationssystemet 3x + x 2 + 3x 3 + 2x 4 x 5 = (..) 2x 2 + x 3 + 4x 4 + 2x 5 = 3x 3x 2 + x 3 6x 4 5x 5 = har bas u och u 2 och u 3 där 5 2 6
. Tisdagen 35 Igår visade vi att lösningsmängden W R 5 till ekvationssystemet 3x + x 2 + 3x 3 + 2x 4 x 5 = (..) 2x 2 + x 3 + 4x 4 + 2x 5 = 3x 3x 2 + x 3 6x 4 5x 5 = har bas u och u 2 och u 3 där 5 2 6
Optimeringslära Kaj Holmberg
 Tekniska Högskolan i Linköping TAOP88 Matematiska Institutionen Lösning till tentamen Optimeringslära 9--7 Kaj Holmberg Lösningar Uppgift a: Inför slackvariabler x 5, x 6 och x 7 Starta med slackvariablerna
Tekniska Högskolan i Linköping TAOP88 Matematiska Institutionen Lösning till tentamen Optimeringslära 9--7 Kaj Holmberg Lösningar Uppgift a: Inför slackvariabler x 5, x 6 och x 7 Starta med slackvariablerna
Hemuppgift 1, SF1861 Optimeringslära för T
 Hemuppgift 1, SF1861 Optimeringslära för T Examinator: Per Enqvist, tel: 790 6298, penqvist@math.kth.se. Assistenter: Amol Sasane, sasane@math.kth.se, Mikael Fallgren, werty@kth.se. Lämnas in till någon
Hemuppgift 1, SF1861 Optimeringslära för T Examinator: Per Enqvist, tel: 790 6298, penqvist@math.kth.se. Assistenter: Amol Sasane, sasane@math.kth.se, Mikael Fallgren, werty@kth.se. Lämnas in till någon
TNK049 Optimeringslära
 TNK49 Optimeringslära Clas Rydergren, ITN Föreläsning 7 Nätverksoptimering Billigaste uppspännande träd (MST) Billigaste väg (SP) Projektnätverk Minkostnadsflödesproblem Agenda Terminologi för grafer/nätverk
TNK49 Optimeringslära Clas Rydergren, ITN Föreläsning 7 Nätverksoptimering Billigaste uppspännande träd (MST) Billigaste väg (SP) Projektnätverk Minkostnadsflödesproblem Agenda Terminologi för grafer/nätverk
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF1624 Algebra och geometri
 SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Optimeringslära Kaj Holmberg
 Tekniska Högskolan i Linköping TAOP88 Matematiska Institutionen Lösning till tentamen Optimeringslära 28--24 Kaj Holmberg Uppgift Lösningar a: Målfunktionen är summan av konvexa funktioner (kvadrater och
Tekniska Högskolan i Linköping TAOP88 Matematiska Institutionen Lösning till tentamen Optimeringslära 28--24 Kaj Holmberg Uppgift Lösningar a: Målfunktionen är summan av konvexa funktioner (kvadrater och
Dagens ämnen. Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer
 Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
Dagens ämnen Linjära ekvationssystem: Successiv elimination Vektorer Definitionen Grundläggande räkneoperationer Bas och koordinater Ortsvektorer Linjära ekvationer Med en linjär ekvation i n variabler,
TAOP07/TEN1 OPTIMERINGSLÄRA GRUNDKURS för Y. Antal uppgifter: 7 Uppgifterna är inte ordnade efter svårighetsgrad.
 Matematiska institutionen Optimeringslära TENTAMEN TAOP07/TEN1 OPTIMERINGSLÄRA GRUNDKURS för Y Datum: 27 augusti 2013 Tid: 14-19 Hjälpmedel: Inga Antal uppgifter: 7 Uppgifterna är inte ordnade efter svårighetsgrad.
Matematiska institutionen Optimeringslära TENTAMEN TAOP07/TEN1 OPTIMERINGSLÄRA GRUNDKURS för Y Datum: 27 augusti 2013 Tid: 14-19 Hjälpmedel: Inga Antal uppgifter: 7 Uppgifterna är inte ordnade efter svårighetsgrad.
Linjär Algebra M/TD Läsvecka 1
 Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Tentamensinstruktioner. När Du löser uppgifterna
 Matematiska institutionen Optimeringslära TENTAMEN TAOP88/TEN 1 OPTIMERING FÖR INGENJÖRER för EMM Datum: 2 augusti 2011 Tid: 8.00-1.00 Hjälpmedel: Miniräknare Kurslitteratur: Kaj Holmberg: Optimering Anteckningar
Matematiska institutionen Optimeringslära TENTAMEN TAOP88/TEN 1 OPTIMERING FÖR INGENJÖRER för EMM Datum: 2 augusti 2011 Tid: 8.00-1.00 Hjälpmedel: Miniräknare Kurslitteratur: Kaj Holmberg: Optimering Anteckningar
De optimeringsproblem som kommer att behandlas i denna kurs kan alla (i princip) skrivas. 1 2 xt Hx + c T x. minimera
 Krister Svanberg, mars 2012 1 Introduktion De optimeringsproblem som kommer att behandlas i denna kurs kan alla (i princip) skrivas på följande allmänna form: f(x) (1.1) x F, där x = (x 1,..., x n ) T
Krister Svanberg, mars 2012 1 Introduktion De optimeringsproblem som kommer att behandlas i denna kurs kan alla (i princip) skrivas på följande allmänna form: f(x) (1.1) x F, där x = (x 1,..., x n ) T
Definition 1 Ett vektorrum M (över R) är en mängd element, vektorer, sådan att det finns en kommutativ operation + på mängden M som uppfyller
 April 27, 25 Vektorrum Definition Ett vektorrum M (över R) är en mängd element, vektorer, sådan att det finns en kommutativ operation + på mängden M som uppfyller. x M och y M = x + y M. 2. x + y = y +
April 27, 25 Vektorrum Definition Ett vektorrum M (över R) är en mängd element, vektorer, sådan att det finns en kommutativ operation + på mängden M som uppfyller. x M och y M = x + y M. 2. x + y = y +
Optimeringslära Kaj Holmberg
 Tekniska Högskolan i Linköping Optimering för ingenjörer Matematiska Institutionen Lösning till tentamen Optimeringslära 2018-01-02 Kaj Holmberg Lösningar Uppgift 1 1a: Den givna startlösningen är tillåten
Tekniska Högskolan i Linköping Optimering för ingenjörer Matematiska Institutionen Lösning till tentamen Optimeringslära 2018-01-02 Kaj Holmberg Lösningar Uppgift 1 1a: Den givna startlösningen är tillåten
Speciell användning av heltalsvariabler. Heltalsprogrammering. Antingen-eller-villkor: Exempel. Speciell användning av heltalsvariabler
 Heltalsprogrammering Speciell användning av heltalsvariabler max z = då c j x j j= a ij x j b i j= x j 0 x j heltal i =,..., m j =,..., n j =,..., n ofta x j u j j =,..., n Oftast c, A, b heltal. Ibland
Heltalsprogrammering Speciell användning av heltalsvariabler max z = då c j x j j= a ij x j b i j= x j 0 x j heltal i =,..., m j =,..., n j =,..., n ofta x j u j j =,..., n Oftast c, A, b heltal. Ibland
TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1. Omfattning. Innehåll 2012-01-20. Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra
 TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1 Omfattning Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll Olika aspekter av linjära ekvationssystem 1. skärning mellan geometriska
TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1 Omfattning Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll Olika aspekter av linjära ekvationssystem 1. skärning mellan geometriska
1 Positivt definita och positivt semidefinita matriser
 Krister Svanberg, april 1 1 Positivt definita och positivt semidefinita matriser Inom ickelinjär optimering, speciellt kvadratisk optimering, är det viktigt att på ett effektivt sätt kunna avgöra huruvida
Krister Svanberg, april 1 1 Positivt definita och positivt semidefinita matriser Inom ickelinjär optimering, speciellt kvadratisk optimering, är det viktigt att på ett effektivt sätt kunna avgöra huruvida
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Hemuppgift 2, SF1861 Optimeringslära för T, VT-10
 Hemuppgift 2, SF1861 Optimeringslära för T, VT-1 Kursansvarig: Per Enqvist, tel: 79 6298, penqvist@math.kth.se. Assistenter: Mikael Fallgren, werty@kth.se, Amol Sasane, sasane@math.kth.se. I denna uppgift
Hemuppgift 2, SF1861 Optimeringslära för T, VT-1 Kursansvarig: Per Enqvist, tel: 79 6298, penqvist@math.kth.se. Assistenter: Mikael Fallgren, werty@kth.se, Amol Sasane, sasane@math.kth.se. I denna uppgift
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Vektorer i planet och i rummet III Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Vektorer i planet och i rummet III Innehåll
Mer om analytisk geometri
 1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
Ett linjärprogrammeringsproblem på allmän form ser ut som
 Linjärprogrammering Ett linjärprogrammeringsproblem på allmän form ser ut som Minimera n j=1 c jx j x j 0 n j=1 a ijx j b i i =1, 2,...,m Variant: Vi kan vilja maximera istället. Vi kommer att studera
Linjärprogrammering Ett linjärprogrammeringsproblem på allmän form ser ut som Minimera n j=1 c jx j x j 0 n j=1 a ijx j b i i =1, 2,...,m Variant: Vi kan vilja maximera istället. Vi kommer att studera
1(8) x ijt = antal mobiltelefoner av typ i=1,,m, Som produceras på produktionslina 1,, n, Under vecka t=1,,t.
 1(8) (5p) Uppgift 1 Företaget KONIA tillverkar mobiltelefoner I en stor fabrik med flera parallella produktionslinor. För att planera produktionen de kommande T veckorna har KONIA definierat följande icke-negativa
1(8) (5p) Uppgift 1 Företaget KONIA tillverkar mobiltelefoner I en stor fabrik med flera parallella produktionslinor. För att planera produktionen de kommande T veckorna har KONIA definierat följande icke-negativa
TAOP33/TEN 2 KOMBINATORISK OPTIMERING GRUNDKURS för D och C
 Matematiska institutionen Optimeringslära TENTAMEN TAOP/TEN 2 KOMBINATORISK OPTIMERING GRUNDKURS för D och C Datum: 2 augusti 2011 Tid: 8.00-1.00 Hjälpmedel: Miniräknare Kurslitteratur: Kaj Holmberg: Optimering
Matematiska institutionen Optimeringslära TENTAMEN TAOP/TEN 2 KOMBINATORISK OPTIMERING GRUNDKURS för D och C Datum: 2 augusti 2011 Tid: 8.00-1.00 Hjälpmedel: Miniräknare Kurslitteratur: Kaj Holmberg: Optimering
Algebraiska egenskaper hos R n i)u + v = v + U
 Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 11
 M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 11 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 41 Linjär Algebra, Föreläsning
M0043M Integralkalkyl och Linjär Algebra, H14, Linjär Algebra, Föreläsning 11 Staffan Lundberg / Ove Edlund Luleå Tekniska Universitet Staffan Lundberg / Ove Edlund M0043M H14 1/ 41 Linjär Algebra, Föreläsning
3 1 = t 2 2 = ( 1) ( 2) 1 2 = A(t) = t 1 10 t
 SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF1624 Algebra och geometri Tentamen med lösningsförslag onsdag, 11 januari 2017
 SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
Lösningar till tentan i SF1861/51 Optimeringslära, 3 juni, 2015
 Lösningar till tentan i SF86/5 Optimeringslära, 3 juni, 25 Uppgift.(a) Första delen: The network is illustrated in the following figure, where all the links are directed from left to right. 3 5 O------O
Lösningar till tentan i SF86/5 Optimeringslära, 3 juni, 25 Uppgift.(a) Första delen: The network is illustrated in the following figure, where all the links are directed from left to right. 3 5 O------O
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
Minsta kvadratmetoden
 Minsta kvadratmetoden där Överbestämda ekvationssystem Det är lämpligt att uppfatta matrisen A som bestående av n kolonnvektorer: A a a a n a a a n a n a n a nn a j a j a nj a a a n j n Då kan vi skriva
Minsta kvadratmetoden där Överbestämda ekvationssystem Det är lämpligt att uppfatta matrisen A som bestående av n kolonnvektorer: A a a a n a a a n a n a n a nn a j a j a nj a a a n j n Då kan vi skriva
1 Konvexa optimeringsproblem grundläggande egenskaper
 Krister Svanberg, april 2012 1 Konvexa optimeringsproblem grundläggande egenskaper Ett optimeringsproblem är i viss mening godartat om det tillåtna området är en konvex mängd och den målfunktion som ska
Krister Svanberg, april 2012 1 Konvexa optimeringsproblem grundläggande egenskaper Ett optimeringsproblem är i viss mening godartat om det tillåtna området är en konvex mängd och den målfunktion som ska
x 1 x 2 T (X) = T ( x 3 x 4 x 5
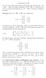 Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
TANA17 Matematiska beräkningar med Matlab
 TANA17 Matematiska beräkningar med Matlab Laboration 1. Linjär Algebra och Avbildningar Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion I denna övning skall
TANA17 Matematiska beräkningar med Matlab Laboration 1. Linjär Algebra och Avbildningar Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion I denna övning skall
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
18 juni 2007, 240 minuter Inga hjälpmedel, förutom skrivmateriel. Betygsgränser: 15p. för Godkänd, 24p. för Väl Godkänd (av maximalt 36p.
 HH / Georgi Tchilikov DISKRET MATEMATIK,5p. 8 juni 007, 40 minuter Inga hjälpmedel, förutom skrivmateriel. Betygsgränser: 5p. för Godkänd, 4p. för Väl Godkänd (av maximalt 36p.). Förenkla (så mycket som
HH / Georgi Tchilikov DISKRET MATEMATIK,5p. 8 juni 007, 40 minuter Inga hjälpmedel, förutom skrivmateriel. Betygsgränser: 5p. för Godkänd, 4p. för Väl Godkänd (av maximalt 36p.). Förenkla (så mycket som
Tentamensinstruktioner
 TNSL05 1(9) TENTAMEN Datum: 6 april 2018 Tid: 14-18 Provkod: TEN1 Kursnamn: TNSL05 Optimering, modellering och planering Institution: ITN Antal uppgifter: 5 Betygskrav: För godkänt krävs normalt 12 p,
TNSL05 1(9) TENTAMEN Datum: 6 april 2018 Tid: 14-18 Provkod: TEN1 Kursnamn: TNSL05 Optimering, modellering och planering Institution: ITN Antal uppgifter: 5 Betygskrav: För godkänt krävs normalt 12 p,
Tentamensinstruktioner
 TNSL05 1(8) TENTAMEN Datum: 1 april 2016 Tid: XXX Sal: XXX Provkod: TEN1 Kursnamn: TNSL05 Optimering, modellering och planering Institution: ITN Antal uppgifter: 5 Betygskrav: För godkänt krävs normalt
TNSL05 1(8) TENTAMEN Datum: 1 april 2016 Tid: XXX Sal: XXX Provkod: TEN1 Kursnamn: TNSL05 Optimering, modellering och planering Institution: ITN Antal uppgifter: 5 Betygskrav: För godkänt krävs normalt
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet 27 augusti 2013 Innehåll Linjära ekvationssystem
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet 27 augusti 2013 Innehåll Linjära ekvationssystem
reella tal x i, x + y = 2 2x + z = 3. Här har vi tre okända x, y och z, och vi ger dessa okända den naturliga
 . Lösningsmängden till homogena ekvationssystem I denna första föreläsning börjar vi med att repetera det grunnläggande begreppet inom linjär algebran. Linjär algebra är studiet av lösningsmängden till
. Lösningsmängden till homogena ekvationssystem I denna första föreläsning börjar vi med att repetera det grunnläggande begreppet inom linjär algebran. Linjär algebra är studiet av lösningsmängden till
Sats: Varje anslutningsmatris ar fullstandigt unimodular. Bevis: Lat m beteckna antalet rader i anslutningsmatrisen.
 Sats: Varje anslutningsmatris ar fullstandigt unimodular. Bevis: Lat m beteckna antalet rader i anslutningsmatrisen. Betrakta kvadratiska delmatriser av storlek n n, dar n m, och anvand induktion med avseende
Sats: Varje anslutningsmatris ar fullstandigt unimodular. Bevis: Lat m beteckna antalet rader i anslutningsmatrisen. Betrakta kvadratiska delmatriser av storlek n n, dar n m, och anvand induktion med avseende
Determinanter, egenvectorer, egenvärden.
 Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Lösningsförslag till tentamen i SF1861 Optimeringslära för T. Onsdag 25 augusti 2010 kl
 Lösningsförslag till tentamen i SF86 Optimeringslära för T. Onsdag 25 augusti 2 kl. 4. 9. Examinator: Per Enqvist, tel. 79 62 98. (a) Vi har ett nätverksflödesproblem med 5 noder. Låt x = (x 2, x 3, x
Lösningsförslag till tentamen i SF86 Optimeringslära för T. Onsdag 25 augusti 2 kl. 4. 9. Examinator: Per Enqvist, tel. 79 62 98. (a) Vi har ett nätverksflödesproblem med 5 noder. Låt x = (x 2, x 3, x
LINJÄRA AVBILDNINGAR
 LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET MED MATRISINVERSER = = =
 Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Vektorrum. EX. Plan och linjer i rummet genom origo. Allmänt; mängden av lösningar till AX = 0.
 Vektorrum Denna kurs handlar till stor del om s k linjära rum eller vektorrum. Dessa kan ses som generaliseringar av R n. Skillnaden består främst i att teorin nu blir mer abstrakt. Detta är själva poängen;
Vektorrum Denna kurs handlar till stor del om s k linjära rum eller vektorrum. Dessa kan ses som generaliseringar av R n. Skillnaden består främst i att teorin nu blir mer abstrakt. Detta är själva poängen;
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 016 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 016 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1.
5B1146 med Matlab. Laborationsr. Laborationsgrupp: Sebastian Johnson Erik Lundberg, Ann-Sofi Åhn ( endst tal1-3
 1 Revision 4 2006-12-16 2. SIDFÖRTECKNING 5B1146 med Matlab Laborationsr Laborationsgrupp: Sebastian Johnson, Ann-Sofi Åhn ( endst tal1-3 Titel Sida 1. Uppgift 1.8.1....3 2. Uppgift 1.8.2....6 3. Uppgift
1 Revision 4 2006-12-16 2. SIDFÖRTECKNING 5B1146 med Matlab Laborationsr Laborationsgrupp: Sebastian Johnson, Ann-Sofi Åhn ( endst tal1-3 Titel Sida 1. Uppgift 1.8.1....3 2. Uppgift 1.8.2....6 3. Uppgift
TENTAMEN. Tentamensinstruktioner. Datum: 30 augusti 2018 Tid: 8-12
 1( 9) TENTAMEN Datum: 30 augusti 2018 Tid: 8-12 Provkod: TEN1 Kursnamn: Optimering, modellering och planering Institution: ITN Antal uppgifter: 5 Betygskrav: För godkänt krävs normalt 12 p, betyg kräver
1( 9) TENTAMEN Datum: 30 augusti 2018 Tid: 8-12 Provkod: TEN1 Kursnamn: Optimering, modellering och planering Institution: ITN Antal uppgifter: 5 Betygskrav: För godkänt krävs normalt 12 p, betyg kräver
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Skalärprodukt Innehåll Skalärprodukt - Inledning
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Sidor i boken Figur 1: Sträckor
 Sidor i boken 37-39 Vektorer Det vi ska studera här är bara en liten del av den teori du kommer att stifta bekantskap med i dina fortsatta studier i kursen Linjär algebra. Många av de objekt man arbetar
Sidor i boken 37-39 Vektorer Det vi ska studera här är bara en liten del av den teori du kommer att stifta bekantskap med i dina fortsatta studier i kursen Linjär algebra. Många av de objekt man arbetar
TNK049 Optimeringslära
 TNK09 Optimeringslära Clas Rydergren ITN Föreläsning Simplemetoden på tablåform och algebraisk form Fas I (startlösning) Känslighetsanalys Tolkning av utdata Agenda Halvtidsutvärdering Simplemetoden (kap..8)
TNK09 Optimeringslära Clas Rydergren ITN Föreläsning Simplemetoden på tablåform och algebraisk form Fas I (startlösning) Känslighetsanalys Tolkning av utdata Agenda Halvtidsutvärdering Simplemetoden (kap..8)
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Lösningar till tentan i 5B1760 Linjär och kvadratisk optimering, 17 december 2003.
 Lösningar till tentan i 5B7 Linjär och kvadratisk optimering, 7 december 3 Uppgift (a) 3 Vi använder Gauss-Jordans metod för att överföra A 3 5 till trappstegsform 3 7 Addition av ( ) gånger första raden
Lösningar till tentan i 5B7 Linjär och kvadratisk optimering, 7 december 3 Uppgift (a) 3 Vi använder Gauss-Jordans metod för att överföra A 3 5 till trappstegsform 3 7 Addition av ( ) gånger första raden
Optimeringslära 2013-11-01 Kaj Holmberg
 Tekniska Högskolan i Linköping Optimering för ingenjörer Matematiska Institutionen Lösning till tentamen Optimeringslära 23-- Kaj Holmberg Uppgift a: Problemet skrivet i standardform är: Lösningar min
Tekniska Högskolan i Linköping Optimering för ingenjörer Matematiska Institutionen Lösning till tentamen Optimeringslära 23-- Kaj Holmberg Uppgift a: Problemet skrivet i standardform är: Lösningar min
min c 1 x 1 + c 2 x 2 då x 1 + x 2 = 1, x 1 {0, 1}, x 2 {0, 1} plus andra bivillkor. Vi måste göra k st av n alternativ:
 Heltalsprogrammering Speciell användning av heltalsvariabler max z = då n c j x j j= n a ij x j b i j= x j 0 x j heltal i =,..., m j =,..., n j =,..., n ofta x j u j j =,..., n Oftast c, A, b heltal. Ibland
Heltalsprogrammering Speciell användning av heltalsvariabler max z = då n c j x j j= n a ij x j b i j= x j 0 x j heltal i =,..., m j =,..., n j =,..., n ofta x j u j j =,..., n Oftast c, A, b heltal. Ibland
1. Ekvationer 1.1. Ekvationer och lösningar. En linjär ekvation i n variabler x 1,..., x n är en ekvation på formen. 2x y + z = 3 x + 2y = 0
 1. Ekvationer 1.1. Ekvationer och lösningar. En linjär ekvation i n variabler x 1,..., x n är en ekvation på formen a 1 x 1 + a 2 x 2 + a n x n = b, med givna tal a 1,..., a n och b. Ett linjärt ekvationssystem
1. Ekvationer 1.1. Ekvationer och lösningar. En linjär ekvation i n variabler x 1,..., x n är en ekvation på formen a 1 x 1 + a 2 x 2 + a n x n = b, med givna tal a 1,..., a n och b. Ett linjärt ekvationssystem
Föreläsning 8 i kursen Ma III, #IX1305, HT 07. (Fjärde föreläsningen av Bo Åhlander)
 Föreläsning 8 i kursen Ma III, #IX1305, HT 07. (Fjärde föreläsningen av Bo Åhlander) Böiers 5.3 Relationer. Vi har definierat en funktion f: A B som en regel som kopplar ihop ett element a A, med ett element
Föreläsning 8 i kursen Ma III, #IX1305, HT 07. (Fjärde föreläsningen av Bo Åhlander) Böiers 5.3 Relationer. Vi har definierat en funktion f: A B som en regel som kopplar ihop ett element a A, med ett element
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
min c 1 x 1 + c 2 x 2 då x 1 + x 2 = 1, x 1 {0, 1}, x 2 {0, 1} plus andra bivillkor. Vi måste göra k st av n alternativ:
 Heltalsprogrammering Speciell användning av heltalsvariabler max z = då c j x j a ij x j b i x j 0 x j heltal i =,..., m j =,..., n j =,..., n ofta x j u j j =,..., n Oftast c, A, b heltal. Ibland u j
Heltalsprogrammering Speciell användning av heltalsvariabler max z = då c j x j a ij x j b i x j 0 x j heltal i =,..., m j =,..., n j =,..., n ofta x j u j j =,..., n Oftast c, A, b heltal. Ibland u j
Analys o Linjär algebra. Lektion 7.. p.1/65
 Analys o Lektion 7 p1/65 Har redan (i matlab bla) stött på tal-listor eller vektorer av typen etc Vad kan sådana tänkas representera/modellera? Hur kan man räkna med sådana? Skall närmast fokusera på ordnade
Analys o Lektion 7 p1/65 Har redan (i matlab bla) stött på tal-listor eller vektorer av typen etc Vad kan sådana tänkas representera/modellera? Hur kan man räkna med sådana? Skall närmast fokusera på ordnade
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
Moment 4.2.1, 4.2.2, 4.2.3, Viktiga exempel 4.1, 4.3, 4.4, 4.5, 4.6, 4.13, 4.14 Övningsuppgifter 4.1 a-h, 4.2, 4.3, 4.4, 4.5, 4.
 Moment 4.2.1, 4.2.2, 4.2., 4.2.4 Viktiga exempel 4.1, 4., 4.4, 4.5, 4.6, 4.1, 4.14 Övningsuppgifter 4.1 a-h, 4.2, 4., 4.4, 4.5, 4.7 Många av de objekt man arbetar med i matematiken och naturvetenskapen
Moment 4.2.1, 4.2.2, 4.2., 4.2.4 Viktiga exempel 4.1, 4., 4.4, 4.5, 4.6, 4.1, 4.14 Övningsuppgifter 4.1 a-h, 4.2, 4., 4.4, 4.5, 4.7 Många av de objekt man arbetar med i matematiken och naturvetenskapen
8 Minsta kvadratmetoden
 Nr, april -, Amelia Minsta kvadratmetoden. Ekvationssystem med en lösning, -fallet Ett linjärt ekvationssystem, som ½ +7y = y = har en entydig lösning om koefficientdeterminanten, här 7, är skild från
Nr, april -, Amelia Minsta kvadratmetoden. Ekvationssystem med en lösning, -fallet Ett linjärt ekvationssystem, som ½ +7y = y = har en entydig lösning om koefficientdeterminanten, här 7, är skild från
