Linjär Algebra. Roy Skjelnes. Matematiska Institutionen, KTH.
|
|
|
- Oliver Joakim Persson
- för 8 år sedan
- Visningar:
Transkript
1 Linjär Algebra Tio förrätter och två efterrätter Roy Skjelnes Matematiska Institutionen, KTH.
2 Inledande ord Detta häftet är baserad på en föreläsningsserie jag gav Varje kapitel tillsvarar en föreläsning, och riktar sig till gymnasiseelever som läser kursen Linjär Algebra för gymnasister. I år består kursen av 12 föreläsningar, och inte 16 som var antalet De fyra föreläsningarna jag har skurit bort från den ursprungliga kursen finns med som Appendix. Föreläsningsnotaterna är inspirerad och modellerad efter kursheftet Matriser og Vektorrom av Dan Laksov. Under läsåret hittade eleveran flera fel i föreläsningsnotaterna, och specielt vill jag nämna Andrian Kimiaei (Norra Real), André Sahlsten (Farsta Gymnasium) och Omar Wazir (Huddinge Gymnasium). Det finns fortfarande månge fel där ute, och jag undrar på vem som upptäcker nästa fel. Roy Skjelnes Stockholm, 23 September, ii
3 Innehåll 1 Matrisaritmetik Matriser Skalärprodukt Matrismultiplikation Uppgifter Matrisaritmetik II Matriser Matrismultiplikation Uppgifter Avbildningar av planet Euklidiska planet Matrisavbildningar Linjäritet Uppgifter Geometri i planet Vektorer och ortogonalitet Linjer Normallinjer Ekvation för linjer Avstånd från en punkt till en linje Uppgifter Area och determinant Area av parallellogram Area och avbildningar Sammansätning Singuljära matriser Uppgifter iii
4 6 Lösningar till ekvationssystem Ekvationer Systematisk lösning av ekvationssystem Gauss-Jordan elimination Uppgifter Elementära matriser Elementära radoperationer och matriser Uppgifter Konstruktion av invers matris Reducerad trappstegsform Konstruktion av invers Uppgifter Determinanten Permutationer Uppgifter Egenskaper till determinanten Inversioner Uppgifter Markov kedjor Iterativ fördelning Slutfördelningen Oberoende av initialvärdet Google og informasjonssortering Nettet Rangering Iterering A Ortogonal dekomposition 69 A.1 Avståndsformeln A.2 Spegling A.3 Uppgifter B Linjära avbildningar 73 B.1 Avbildningar B.2 Bildrum B.3 Uppgifter iv
5 C Komplexa tal 78 C.1 Representation av tal C.2 Reella talen som matriser C.3 Komplexa talen som talplanet C.4 Geometrisk tolkning av produkt D PS3 och krypteringsmissar 85 D.1 Kryptering D.2 Elliptisk kurva D.3 Gruppen till en elliptisk kurva D.4 Primtalskroppar D.5 Krypteringsalgoritmen D.6 Felaktig implementering E LaTex 92 E.1 Att skriva matematisk text v
6 Föreläsning 1 Matrisaritmetik 1.1 Matriser Vi skall definiera något som kallas (2 2)-matriser, och sedan utveckla aritmetik på dessa. Matriserna är inte tal, men kan nästan behandlas som tal. [ ] a b Definition En (2 2)-matris A = är fyra reella tal a, b, c, d c d ordnade i ett rektangel När vi i detta kapitlet skriver matris menar vi alltid en (2 2)-matris. Exempel Exempler på matriser är [ ] [ ] π, [ ] [ ] a b α β Definition Två matriser A = och B = adderas och c d γ δ ger en ny matris [ ] a + α b + β A + B =. c + γ d + δ Exempel Vi ser att A + B = B + A. 1.2 Skalärprodukt Vi har att [ ] 2a 2b A + A =, 2c 2d och detta vill vi skriva som 2A. Vi gör följande definition. 1
7 Definition (Skalarmultiplikation). För varje tal k, och varje matris A, definierar vi matrisen [ ] ka kb k A =. kc kd Av definition av skalärprodukt får vi att Vi har också att A } + A + {{ + A } = n A. n kopior 0 A = [ ] Matrisen som bara [ består ] av nollor kallas noll-matrisen av uppenbara skäl. 0 0 Vi skriver 0 = för denna matris. Och vi har A = 0. Märk att 0 i vänstreledet ovan är talen 0, medan 0 i högerledet ovan är noll-matrisen. Vi har också den trevliga identiteten av matriser Mera notation. Vi har A + 0 = A. [ ] a b 1 A =. c d Vi vill i fortsätningen skriva A för matrisen 1 A. Detta betyder att vi istället för B + 1 A skriver B A. Märk också att vi nu har } A A {{ A } = n A. n kopior Exempel Vi kan nu lösa matrisekvationer på formen 4X + 2A = B, där A och B är givna matriser. Vi adderar matrisen 2A på båda sidor och får att vänsterledet blir 4X + 2A 2A = 4X + 0 = 4X, medan högerledet blir B 2A. Sedan multiplicerar vi ekvationen med skalären 1 4, vilket ger X = 1 4 B 1 2 A. 2
8 1.3 Matrismultiplikation Vi har definierad addition (och subtraktion) av matriser, samt skalärmultiplikation. Vi vill också ha multiplikation, två matriser skall multipliceras ihop och ger en matris. Innan vi definierar detta vill vi skriva matriserna lite annorlunda. En matris [ ] a1,1 a A = 1,2 a 2,1 a 2,1 består av två rader och två kolonner. Talen i matrisen kallas koefficienter och är indexerade efter vilken rad och kolonn dessa står placerad i. Koefficient a 1,2, t.ex. är i rad 1 och kolonn 2. [ ] [ ] a1,1 a Definition Låt A = 1,2 b1,1 b och B = 1,2 vara två matriser. Vi definerar produkten AB som matrisen a 2,1 a 2,2 b 2,1 b 2,2 [ ] c1,1 c AB = 1,2 c 2,1 c 2,2 där koefficienterna ges av följande formler c 1,1 = a 1,1 b 1,1 + a 1,2 b 2,1 c 1,2 = a 1,1 b 1,2 + a 1,2 b 2,2 c 2,1 = a 2,1 b 1,1 + a 2,2 b 2,1 c 2,2 = a 2,1 b 1,2 + a 2,2 b 2, Ser ni mönstret i galskapen, och specielt hur man kommer ihåg formlerna utan att lära dessa utantill? Om du inte ser mönstret be någon, mig t.ex. för att förklara hur man utför matrisprodukten. Exempel Vi har att [ ] [ ] = [ ] Märk att AB inte alltid är det samma som BA. T.ex, har vi att [ ] [ ] [ ] = vilket inte är lika med produkten ovan. Vidare har vi att nollmatrisen multiplicerad med en godtycklig matris ger nollmatrisen A 0 = 0 A = 0. [ ] 1 0 Definition Vi definierar identitetsmatrisen 1 =
9 Identitetsmatrisen fungerar som talet 1 med avseende på matrismultiplikation. Vi har nämligen att [ ] [ ] [ ] 1 0 a1,1 a 1,2 a1,1 a = 1, a 2,1 a 2,1 a 2,1 a 2,1 Det vill säga att 1 A = A för varje matris A. Vi har också att A 1 = A, vilket läsaren uppmuntras kolla. Sats Låt A, B och C vara godtyckliga matriser. Vi har att matrisprodukten är associativ, det vill säga Proof. See Uppgift (AB)C = A(BC). Definition En matris A är inverterbar om det finns någon matris B sådan att AB = 1 och BA = 1. En matris som inte är inverterbar kallas singuljär. Exempel Matrisen A = [ ] är inverterbar. Detta fördi matrisen [ ] 2 1 B = har egenskapen att AB = BA = 1 (Kolla!). Exempel Nollmatrisen är uppenbarligen singuljär. Ett annat exempel är matrisen [ ] 1 0 A =. 2 0 Att matrisen A är singuljär kan man visa [ på ] följande sätt. Antaga att A a b är invertebar. Då finns en matris B = sådan att AB = BA = 1. c d Produkten AB är [ ] [ ] [ ] 1 0 a b a c =. 2 0 c d 2a 2c Om denna produkt skulle vara lik med identitetsmatrisen måste a = 1 och 2a = 0, och c = 0 och 2c = 1. Detta är omöjligt. Detta betyder att matrisen A inte kan vara inverterbar, vilket betyder att matrisen är singuljär. 4
10 Sats Om matrisen A är inverterbar då finns det enbart en matris B sådan att AB = BA = 1. Proof. Låt B och C vara två matriser sådana att AB = BA = 1 och AC = CA = 1. Vi skall visa att B = C. Vi har vilket var vad vi skulle visa. B = B 1 = B (AC) = (BA) C = 1 C = C Om en matris A är invertebar då kallas matrisen B som är sådan att AB = BA = 1 för inversen till A. Inversen till A betecknar vi med A 1. Exempel Om vi nu har en matrisekvation AX = B, där A och B är givna matriser, och X är den sökta matrisen. Om vi har att matrisen A är inverterbar, då kan vi lösa denna uppgift på vanligt sätt, det vill säga som om det handlade om vanliga tal. Ekvationen AX = B multiplicerar vi med A 1, från vänster, och vi får att Det vill säga att X = A 1 B. A 1 AX = 1 X = A 1 B. 1.4 Uppgifter Uppgift Beräkna matriserna AB, BA och A 2 när A = [ ] [ d ad bc c ad bc och B = b ad bc a ad bc [ ] [ ] a b Uppgift Låt A = vara en matris där ad bc 0. Definiera c d matrisen ] B =. Använd matrisen B för att visa att matrisen A är inverterbar. Uppgift Använd Uppgift för att konstruera inversen till matriserna [ ] [ ] A =, B =
11 Uppgift Använd matriserna i Uppgift för att bestämma matrisen X i följande tre uttryck a) AX = B b) XA = B och c) AXB = 1. Uppgift Betrakta tre godtycklig matriser A, B och C. Beräkna först AB och BC, och sedan (AB)C och A(BC). Om du nu har räknat rätt har du att de två matriserna är lika, det vill säga (AB)C = A(BC), och du har visat Sats
12 Föreläsning 2 Matrisaritmetik II Vi definierada förra gången (2 2)-matriser och multiplikation av sådana. Idag skall vi definiera dessa begrepp mera allmänt. 2.1 Matriser Låt m och n vara två fixerade positiva heltal. En (m n)-matris A är ett ordnat rektangel med m n tal, a 1,1 a 1,2 a 1,n a 2,1 a 2,2 a 2,n A =... a m,1 a m,2 a m,n Märk att en (m n)-matris består av m-rader och n-kolonner. Talen i matrisen A kallas koefficienter och indexeringen av dessa ges vid rad och kolonn. Koefficient a i,j är placerad på rad i och kolonn j. En kompakt notation för matrisen är A = (a i,j ), var vi inte äns indikerar antalet rader och kolonner i matrisen. Antalet rader och kolonner refereras till storleken till matrisen. Exempel Exempler på matriser är [ ] 1 π 1 2 3, Den första matrisen är en (1 3)-matris, och den andra är (3 2). 7
13 Definition Två matriser A och B av samma storlek adderas koefficientvis, och ger en ny matris av samma storlek. Om k är ett tal, så definieras skalärmultiplikationenen k A som matrisen av samma storlek som A, men där varje koefficient är multiplicerad med k. Exempel Vi ser att A + B = B + A Innan vi definierar matrisprodukten vill vi innföra lite summationsnotation. Vi vill använda symbolen för sum, och specielt vill vi använda symbolen för att på ett kompakt sätt beskriva summering. Om vi har givet siffror a 1,..., a n, och vi vill summera dessa då skriver vi n a i = a 1 + a a n. i=1 Märk att nedre index indikerar var summationen börjar, och över index indikerar var summationen slutar. Exempel Till exempel vill vi skriva och 7 a i = a 3 + a 4 + a 5 + a 6 + a 7, i=3 5 (13 i) 2i = i=3 2.2 Matrismultiplikation Vi har definierad addition (och subtraktion) av matriser, samt skalärmultiplikation. Definition Låt A vara en (m p)-matris, och B en (p n)-matris. Vi definierar produkten AB som (m n)-matrisen med koefficienter där 1 i m, och 1 j n. c i,j = p a i,k b k,j, Exempel Betrakta matriserna [ ] A = och B = k=1 8
14 Matrisen A är (2 4) och B är (4 2). Detta betyder att vi kan utföra produkten [ ] [ ] AB = =, men också produkten BA = = Nollmatrisen som är matrisen med enbart noll som koefficienter, skriver vi fortfarande 0. Läsaren måste själv ha koll på vilke storlek nollmatrisen har. För varje positivt heltal n definierar vi identitetsmatrisen 1 som (n n)- matrisen { 1 om i = j 1 = (δ i,j ) där δ i,j = 0 om i j Symbolen δ i,j kallas Kronecker deltaet. Inversen till en (n n)-matris A definieras som (n n)-matrisen B som har egenskapen att AB = BA = 1, där 1 betyder identitetsmatrisen av storlek (n n). Inte alla matriser har invers, men om en matris A har en invers så är denna unik och vi skriver A 1 för denna matris. Exempel Betrakta matriserna A = och Om vi utför matrisprodukten AB korrekt får vi AB = = Och läsaren kollar själv att BA = 1. Detta betyder att B = A 1, men också att A = B 1. Exempel Betrakta ekvationssystemet x + 2y + 3z = 4 2x + 5y + 3z = 2 x + 8z = 1. 9
15 Detta system kan skrivas som matrisekvationen x 4 A y = 2, z 1 där matrisen A = Vi såg i Exempel (2.2.4) att matrisen B = är inversen till A, det vill säga B = A 1. Multiplicerar vi matrisekvationen med A 1 från vänster får vi x x 4 A 1 A y = y = A 1 2. z z 1 Vi har vidare att A = Detta betyder att ekvationssystement har den unika lösningen x = 119, y = 39 och z = Uppgifter Uppgift Beräkna matrisprodukten Uppgift Använd informationen i Exemplet för att lösa matrisekvationen x y = z 3 10
16 Uppgift Två personer är och dricker två sorters läsk (sic!). Den ena personen konsumerar 15 glas av sort A och 10 glas av sort B. Detta kostar 63 SEK. Den andra personen konsumerar 25 glas av sort A, och 17 glas av sort B, till en summa av 106 SEK. Hur mycket kostade sort A per glas? Lös denna uppgiften på följande sätt. Först skriver du ekvationerna som kommer från texten på matrisform. Sedan inverterar du den givna (2 2)-matrisen (använd formeln som gavs förra veckan), och multiplicerar med inversen från vänster. Uppgift Låt A vara en godtycklig (m n)-matris, och låt 1 vara identitetsmatrisen av rätt storlek. Visa att A 1 = A. 11
17 Föreläsning 3 Avbildningar av planet 3.1 Euklidiska planet Vi kommer att behandla linjära avbildningar av planet i detalj. Det mera allmänna fallet är behandlat i Appendix B. Definition Det Euklidiska planet är mängden av alla ordnade par av reella tal. Denna mängd skriver vi som R 2. Med andra ord R 2 = {(x, y) reella tal x och y}. Planet känner vi oss förtroliga med. Vi skall nu börja titta på en klass av avbildningar från planet till sig själv. 3.2 Matrisavbildningar [ ] a b Låt A = vara en fixerad (2 2)-matris. Vi använder denna för att c d definiera en avbildning T A : R 2 R 2 på följande sätt. Låt (x, y) vara ett godtycklig element i R 2. Vi definierar T A (x, y) = (ax + by, cx + dy). Detta anger vad elementet (x, y) skall skickas till, nämligen elementet (ax + by, cx+dy). Sättet vi använder matrisen A är som följer. Vi tar det godtyckliga elementet (x, y) och skriver denna som en (2 1)-matris, och multipliceras sedan med matrisen A från vänster (x, y) A [ x y ] [ ] [ ] a b x = = c d y 12 [ ] ax + by (ax + by, cx + dy). cx + dy
18 Efter matrismultiplikation med A har vi en (2 1)-matris som vi lägger ned och betraktar som en punkt (ax + by, cx + dy) i planet. [ ] 2 1 Exempel Låt A =. Denna matris ger avbildningen 4 3 T A : R 2 R 2 som skickar elementet (x, y) till (2x + y, 4x + 3y). Specielt ser vi att (1, 0) skickas till (2, 4) och att (0, 1) skickas till (1, 3). Vi har att (1, 1) skickas till (3, 7), och att (0, 0) skickas till (0, 0). Det kan vara instruktivt nu att rita upp kvadratet med hörn i punkterna (0, 0), (1, 0), (0, 1) och (1, 1) och sedan se vad detta kvadrat skickas till under avbildningen T A. 3.3 Linjäritet I Exemplet (3.2.1) ovan kan vi märka oss att första kolumnen i matrisen A är precis koordinaterna för T (1, 0) och att andra kolumnen är koordinaterna till T (0, 1). Dessa två element kommer att spela en viktig roll i fortsätningen, och vi ger dessa egna namn. Definition Elementet (1, 0) skriver vi som e 1 och elementet (0, 1) skriver vi som e 2. Dessa två element kallas standard basen för R Låt oss återgå till Exemplet (3.2.1). Elementet (1, 1) = e 1 + e 2, och vi har att T A (1, 1) ges som matrismultiplikation med matrisen A från vänster. Notera dock att vi har A [ ] 1 = A 1 [ ] 1 + A 0 [ ] 0. 1 Med andra ord har vi att T A (1, 1) = T A (e 1 ) + T A (e 2 ). Lemma Låt A vara en (2 2)-matris, och betrakta avbildningen T A : R 2 R 2. För varje element (x, y) i R 2 har vi att T A (x, y) = xt A (e 1 ) + yt A (e 2 ). Proof. Vi har att (x, y) = (x, 0) + (0, y) = x (1, 0) + y (0, 1). Matrismultiplikation ger nu [ ] x A = A (x [ ] [ ] [ ] [ ] 1 0 ) y = x A + y A. y Med andra ord att T A (x, y) = xt A (e 1 ) + yt A (e 2 ). 13
19 Definition En avbildning f : R 2 R 2 kallas linjär om för alla element (x, y) i R 2. f(x, y) = x f(e 1 ) + y f(e 2 ), Avbildningar i allmänhet kan var obeskrivligt komplicerade, men dessa skall vi inte fokusera på. Vi skall enbart betrakta linjära avbildningar. En linär avbildning är bestämd av sitt värde på två element, nämligen e 1 och e 2. Vi har sätt att en matrisavbildning T A, det vill säga en avbildning som kommer från multiplikation med en matris A, är linjär. Detta är nämligen kontentan av Lemma (B.1.6.1). Det omvända gäller också. Sats Låt f : R 2 R 2 vara en linjär avbildning. Då finns en (2 2)- matris A sådan att matrisavbildningen T A är den linjära avbildningen f. Mera precist har vi att om f(e 1 ) = (a, b) och f(e 2 ) = (c, d) då ges [ ] a c A =. b d Proof. Se uppgifterna Notera att koordinaterna till f(e 1 ) kommer som första kolumn, ej rad i matrisen A. Likadant är koordinaterna till f(e 2 ) andra kolumn i matrisen. Exempel Låt f : R 2 R 2 vara givet som spegling om y-axeln. Då har vi att f(x, y) = ( x, y). ( ) Detta är en linjär avbildning då f(x 1 + x 2, y 1 + y 2 ) = ( (x 1 + x 2 ), y 1 + y 2 ) = f(x 1, y 1 ) + f(x 2, y 2 ), och vi har att f(c(x, y)) = ( cx, cy) = cf(x, y). Vi har vidare att f(e[ 1 ) = e ] 1 = ( 1, 0) och att f(e 2 ) = e 2 = (0, 1). 1 0 Detta ger matrisen A =. Detta betyder att A [ x y 0 1 ] = [ ] Vilket sammanfaller med uttrycket ( ). [ ] x = y [ ] x. y Exempel Låt f : R 2 R 2 vara rotation med π radianer (eller 3 om du vill 60 grader) moturs, omkring elementet (0, 0). Detta är en linjär avbildning, vilket betyder att det finns en matris A sådan att T A = f. Om man ritar en tydlig figur ser man att f(e 1 ) = (cos( π 3 ), sin(π 3 )) = (1 2, 3 2 ). 14
20 Den triangel som förekommer i denna tänkta figur vill också förekomma i din figur när du vill beskriva f(e 2 ). Du får att Detta ger matrisen f(e 2 ) = ( sin( π 3 ), cos(π 3 )) = ( 3 2, 1 2 ). A = [ Specielt betyder detta att f(2, 5) har koordinater [ ] [ ] A = Definition Bildrummet till en avbildning f : R 2 R 2 är alla punkt (y 1, y 2 ) som är på formen (y 1, y 2 ) = f(x 1, x 2 ), för någon punkt (x 1, x 2 ). 3.4 Uppgifter Uppgift Låt f : R 2 R 2 vara rotation med π radianer omkring 4 origo (0, 0), men medurs. Avbildningen är linjär. Beskriv matrisen A som är sådan att f = T A. Uppgift Avbildningen T A : R 2 R 2 ges av matrisen [ ] 1 2 A =. 3 6 Visa att punkten P = ( 1, 2) är med i bildrummet till avbildningen T A. Bestäm också en punkt Q som inte är med i bildrummet till T A. Uppgift Visa Sats (3.3.6). Låt f vara en avbildning från planet till planet, och konstruera matrisen A som Sats (3.3.6) anger. Använd nu linjäritetet till f för att visa att f(x, y) = T A (x, y) för alla (x, y) i R 2, vilket betyder att f = T A. Uppgift Låt T A : R 2 R 2 vara den linjära avbildning vi får vid rotation med θ grader, moturs, omkring origo. Använd en bra figur för och visa att matrisen A som beskriver avbildningen T A är [ ] cos(θ) sin(θ) A = sin(θ) cos(θ) ]. 15
21 Föreläsning 4 Geometri i planet När du läser denna text är det bra om du ritar bilder för att exemplifiera innehållet. Det är lite komplicerad med i.tex, och därför avstår jag från att lägga vid illustrationer även om dessa är mycket hjälpsamma. 4.1 Vektorer och ortogonalitet Det Euklidiska plnaet betecknas med R 2 och är mängden av alla ordnade reella tal, R 2 = {(a, b) reella tal a och b}. Ett element (a, b) i R 2 kallas ibland för en punkt P = (a, b) och ibland för en vektor v = (a, b). Även om det används olika namn för element i planet, är det viktigt att komma ihåg att det alltid handlar om samma begrepp. Anledningarna till de olika namnen är mera av psykologisk art. Blant annat ritar vi en punkt P = (a, b) som en prick i planet, medan en vektor v = (a, b) ofta ritas som en pil som börjar i origo, och slutar i (a, b). Definition Längden till en vektor v = (a, b) är definierad som talet a2 + b 2, och vi skriver v för detta tal Det är klart att det är Pytagoras Sats som ligger till grunn för definitionen ovan. Ritar man upp vektor v = (a, b) som en pil ser vi att pilens längd blir hypotenus i en triangel där katerna har längd a och b Vi märker oss att längden till en vektor v = (a, b) alltid är ett ickenegativt tal, och att den enda vektor v = (a, b) med längd v = 0 är noll-vektorn v = (0, 0). 16
22 Definition Betrakta två vektorer u = (a, b) och v = (c, d). Deras skalärprodukt är talet definierad som < u, v >= ac + bd. Exempel Om n = (a, b) är en vektor har vi att < n, n >= a 2 + b 2 = n 2. Lemma För alla vektorer u, v och w, och alla tal t har vi att följande identiteter gäller 1) < u + v, w >=< u, w > + < v, w > 2) < tu, w >= t < u, w >. Proof. Se uppgifterna. Definition Två vektorer u och v är vinkelräta (och ibland säger vi ortogonala) om deras skalarprodukt < u, v >= 0. Exempel Betrakta vektorn u = (2, 5) och vektorn v = ( 10, 4). Dessa två vektorer är vinkelräta då 4.2 Linjer < u, v >= 2 ( 1) = 0. Låt P = (p 1, p 2 ) vare en punkt, och v = (c, d) en vektor skilld från nollvektorn (0, 0). Ritar du in vektorerna P + v, P + 2v, P + 3v, P v, P v så inser du att dessa ligger alla på linjen som går genom punkten P och har riktning v. Vi definierar linjen L genom punkten P och med riktningsvektor v, som mängden L = {P + tv tal t} Märk att mängden som en linje L utgör, kan skrivas med en massa olika riktningsvektorer och olika punkt. Om P är någon punkt på linjen L och vektorn v är nollskild, och sådan att v = s v, för något tal s, då har vi att L = {P + tv tal t} = {P + tv tal t}. 17
23 Med riktningsvektorn v till linjen L fixerad får vi parallella linjer L = {Q + tv tal t} till L = {P + tv tal t}, när vi varierar punkten som riktningsvektoren utgår i från. Exempel Linjen genom origo, och med riktningsvektor v = (3, 4) är mängden {(3t, 4t) tal t}. 4.3 Normallinjer Låt L vara en given linje i planet. Om v och v är två riktningsvektorer för linjen L då finns det tal s sådan att v = sv. Specielt har vi att om en vektor n = (a, b) är vinkelrät med v så följer det av Lemma (4.1) att n också är vinkelrät med v. En nollskild vektor n = (a, b) som är vinkelrät med riktningsvektorerna till linjen L kallas en normalvektor till linjen L. En normallinje N till linjen L, genom en punkt P är linjen N = {P + tn tal t} där n = (a, b) (0, 0) är någon normalvektor till linjen L. 4.4 Ekvation för linjer En linje i planet kan skrivas som lösningarna till en ekvation på formen ax + by + c = 0, för några tal a, b och c, där a och b inte båda kan vara noll. Detta betyder att för en given linje L så finns tal a, b och c sådan att L = {(x, y) ax + by + c = 0} Inte heller ekvationerna är unika. En linje L som ges av ekvatationen ax + by + c = 0, ges också av ekvationen atx = bty + ct = 0, där talet t 0. Lemma Låt en linje L vara given som L = {P + tv tal t}, där P = (p 1, p 2 ), och v = (v 1, v 2 ) (0, 0). Låt n = (a, b) vara en nollskild normalvektor för linjen L. En ekvation för linjen L är där c = ap 1 bp 2. ax + by + c = 0, 18
24 Proof. Betrakta linjen L = {P + tv talt}, där P = (p 1, p 2 ), coh med riktningsvektor v = (v 1, v 2 ). Låt n = (a, b) vara någon normalvektor till linjen L, och betrakta en godtycklig punkt (x, y) i planet. Differansen (x p 1, y p 2 ) är en vektor. Flyttar vi pilen som representerar vektorn (x p 1, y p 2 ) till att börja i punkten P, d aa vill pilen sluta i (x, y). Denna differansvektor (x p 1, y p 2 ) ligger på linjen L och och endast om vektorn är vinkelrät med normalvektorn n = (a, b). Rita en bra bild här. Vi har att (x p 1, y p 2 ) är vinkelrät med normalvektorn n om och endast om deras prickprodukt är noll. Vi använder Lemma (4.1) för att beräkna prickprodukten, och vi får att < (x p 1, y p 2 ), (a, b) >= ax ap 1 + by p 2 b = 0. Det vill säga att en ekvation för linjen L ges som ax + by + c = 0, med c = ap 1 bp 2. Lemma Låt L vara en linje som ges som nollsställemängden till ekvationen ax + by + c = 0. Låt P = (p 1, p 2 ) vara någon punkt sådan att ap 1 + bp 2 = c. Då ges linjen av Proof. Se uppgifterna. L = {P + t( b, a) tal t}. Exempel Linjen L = {(3t, 4t) lösningarna till ekvationen 4x + 3y = 0. tal t} kan också beskrivas som 4.5 Avstånd från en punkt till en linje Låt Q vara en given punkti planet, och L en given linje. För varje punkt P på linjen kan vi mäta avståndet från Q till punkten P. Avståndet ges som längden av vektorn Q P. Det finns en punkt R på linjen där avståndet till Q är den minsta, och detta avstånd kallar vi avståndet från Q till linjen L. Vi vill beräkna detta avstånd. En ny bild här. Steg 1 Låt linjen L vara given av ekvationen ax + by + c = 0. 19
25 Vi vill beräkna avståndet från linjen L till punkten Q = (q 1, q 2 ). Vi låter P = (p 1, p 2 ) vara någon punkt på linjen, det vill säga att ap 1 + bp 2 + c = 0. ( ) Låt v vara en riktningsvektor till linjen, och vi har att L = {P + tv tal t}. Låt vidare n = (a, b) vara en normalvektor till linjen L, det vill säga en vektor sådan att < n, v >= 0. Vi betraktar differansen Q P. Detta är en vektor som vi kan tänka på som en pil som börjar i origo och slutar i koordinaterna Q P. Denna vektor kan vi skriva som Q P = w + u, där w = tv och u = sn. Rita nu en förklarande bild. Vi har att Q P = tv + sn. Steg 2 Avståndet vi försöker bestämma är längden av vektorn s n. Om vi nu betraktar skalärprodukten < Q P, n > så har vi från Lemma (4.1) att < Q P, n >= t < v, n > +s < n, n >= 0 + s n 2. Detta är en ekvation bestående av tal. Vektorn n = (a, b) antar vi är nollskild, och specielt har vi att n 2 0. Därmed har vi ett uttryck för talet s = 1 < Q P, n >. ( ) n 2 Sats Låt L vara linjen som ges av ekvationen ax + by + c = 0, och låt Q = (q 1, q 2 ) vara en godtycklig punkt i planet. Avståndet från punkten Q till linjen L är aq 1 + bq 2 + c a2 + b 2. Proof. Vi har ovan ( ) sett att avståndet ges som längden av vekorn sn, där n = (a, b) och s = 1 < Q P, n >. Vi har att längden sn är n 2 (as)2 + (bs) 2 = s 2 (a 2 + b 2 ) = s a 2 + b 2 = s n. ( ) Vi vill nu bestämma ett uttryck för beloppet s till talet s. Vi använder Lemma (4.1) och får att < Q P, n >=< Q, n > < P, n >. 20
26 Vi har vidare att < Q, n >=< (q 1, q 2 ), (a, b) >= aq 1 + bq 2, och då också att < P, n >= ap 1 + bp 2. Punkten P var på linjen, och vi har från ( ) att < P, n >= c. Detta ger att s = 1 n 2 < Q P, n > = 1 n 2 aq 1 + bq 2 ( c). Använder vi nu slutligen ( ) ser vi att avståndet från punkten Q till linjen L ges som sn = aq 1 + bq 2 + c n n 2 = aq 1 + bq 2 + c a2 + b Uppgifter Uppgift Beräkna avståndet från punken Q = (1, 2) till linjen L som ges av ekvationen 3x + 4y = 5. Uppgift Använd definitionen av skalärprodukt för att visa båda påståenden in Lemma (4.1). Uppgift Visa Lemma (4.4.2), t.ex. på följande sätt. Låt L vara linjen som ges av ekvationen ax + by + c = 0 och låt L vara linjen L = {P + tv tal t}, där P och v är som i Lemmat. För att visa att L = L måste vi visa att varje punkt i L är med i L, och omvänd. Låt Q vara en punkt i L. Skriv ut vad detta betyder, och kolla att koordinaterna till Q satisfierar ekvatioenen som bestämmer L. Då har du visat att L L. För att visa det omvända kan du använda Lemma (4.4.2). 21
27 Föreläsning 5 Area och determinant Förra gången visade vi en formel för avstandet mellan en punkt P = (p, q) och en linje L. Om linjen L var given som nollställenmängden till ekvationen ax + by + c = 0, då var avståndet given av formeln ap + bq + c a2 + b Area av parallellogram Två punkt P och Q i planet vill tillsammans med origo och punkten P + Q bilda ett parallellogram. Och varje parallellogram bestäms av två hörnpunkter P och Q. Märk att vi tillåter degenererade parallellogram. Om P och Q ligger på samma linje genom origo, vill de fyra hörnen inte ge ett parallellogram i ordets vanliga mening, men enbart ett linjesegment. Vi tillater dock sådana fall. Proposition Låt P = (p 1, p 2 ) och Q = (q 1, q 2 ) vara två punkt i planet. Arean av det parallellogram som punkterna P, Q, P + Q och origo spänner upp är p 1 q 2 p 2 q 1 Proof. Arean ges som bekant av höjden multiplicerad med bredden. Bredden kan vi bestämma via Pytagoras Sats som Q = q q 2 2. Höjden är precis avståndet från P till linjen L som går genom origo och Q. En ekvation för linjen L genom Q och origo, är q 2 x q 1 y = 0. Av Sats (4.5.1) får vi nu att höjden i parallellogrammet är q 2 p 1 q 1 p 2. q q2 2 22
28 Multiplicerar vi nu uttryck för höjd med uttrycket för bredd erhålls det önskade svar. 5.2 Area och avbildningar Vi har att en linjär avbildning T : R 2 R 2 ges som matrismultiplikation med en given (2 2)-matris A. Vi kommer ihåg att matrisens två kolonner ges av koordinaterna till T (1, 0) och T (0, 1). Om vi låter (a, b) = T (1, 0), och (c, d) = T (0, 1) har vi att matrisen [ ] a c A = b d bestämmer avbildningen T. Determinanten till matrisen A är talet som vi bekantade oss med i Uppgift det(a) = ad bc, ( ) Proposition Låt T : R 2 R 2 vara en linjär avbildning, given som matrismultiplikation med matrisen A. Låt Ω vara enhetskvadratet i R 2 med hörn (0, 0), (1, 0), (0, 1) och (1, 1). Bilden av Ω under avbildningen T är ett parallellogram, och arean till parallellogrammet T (Ω) är det(a). Proof. Vi har att Ω avbildas på parallellogrammet med hörn T (1, 0) = (a, b) och T (0, 1) = (c, d). Arean av parallellogramet ges av Proposition (5.2.1) som beloppet av ad bc, vilket också är uttrycket för determinanten. 5.3 Sammansätning Om T : R 2 R 2 och U : R 2 R 2 är två funktioner från planet till planet, kan vi definiera deras komposition. Vi har kompositionsfunktionen U T : R 2 R 2 som är funktionen vi får vid att först använda T och sedan använda U. Med andra ord, en godtycklig punkt (x, y) i planet skickas till punkten (x, y) T (x, y) U(T (x, y)). Läsaren bör lägga notationen på minnet. Funktionssammansätning läses från höger mot vänster. Kompositionen U T betyder att T används först, och sedan U. Kompositionen T U betyder at U används först och sedan T. Om funktionerna U och T båda är linjära är dessa givna av matriser och matrismultiplikation. 23
29 Lemma Om matrisen A ger avbildningen T och matrisen B ger avbildningen U, då ges sammansätningen U T av matrisprodukten BA. Proof. Se uppgifterna. Exempel [ Låt] den linjära avbildningen T : R 2 R 2 vara given av a c matrisen A =. Vi har av Proposition (5.2.1) att arean av parallellogrammet som enhetskvadratet skickas till under T, har area ad bc. b d Antag nu att arean är nollskild. Då har vi från tidligare att matrisen A är inverterbar, och inversen ges av matrisen [ ] 1 d c B =. ad bc b a Betrakta nu den linjära avbildningen U : R 2 R 2 som ges vid matrisen B och matrismultiplikation med denna. Av Proposition (5.2.1) har vi att enhetskvadratet skickas med U till ett parallellogram med area det(b). Beräknar man determinanten till B får man att det(b) = 1 ad bc = 1 det(a). Vad händer med enhetskvadraten under sammansätningen U T? Först har vi en avbildning T som skickar enhetskvadratet till ett parallellogram med hörnpunkter P = (a, b) och Q = (c, d). Sedan har vi en avbildning U som skickar enhetskvadratet till ett parallellogram med hörnpunkt P = 1 1 (d, b) och Q = ( c, a). Men sammansättningen ges av ad cd ad bc Lemma (5.3.1) av matrisprodukten BA. Då B är inversen till A har vi att BA är identitetsmatrisen, och det följer att sammansätningen U T är identitetsavbildningen. Med andra ord skicka enhetskvadratet till enhetskvadratet. 5.4 Singuljära matriser En matris A vars determinant är noll, kallas singuljär. Hur ser dessa ut? Låt A vara given, och betrakta den tillhörande linjära avbildningen T A : R 2 R 2. Första kolonnen i A ges av koordinaterna till T A (1, 0) = (a, b). Om (a, b) = (0, 0) då är det klart att determinanten till A är noll. Antag därför att (a, b) (0, 0). Då finns det en unik linje L genom origo och punkten (a, b). Om punkten T (0, 1) inte hamnar på punkten L då vill enhetskvadratet hamna på ett ekta parallellogram med area olika noll. Därför, om A skall 24
30 bli singuljär så måste punkten T (0, 1) hamna på linjen L. Alla punkter på linjen L är på formen t(a, b), för någon skalär. Med andra ord har vi att andra kolonnen i matrisen A är (at, bt). Detta betyder att de singuljära matriserna är på form [ ] [ ] a ta 0 c A = eller A =. b tb 0 d 5.5 Uppgifter Uppgift Betrakta den linjära avbildningen T : R 2 R 2 som är bestämd av T (2, 0) = (2, 4) och T (0, 5) = (3, 7). Hitta matrisen A som beskriver avbildningen T. Uppgift Betrakta den linjära avbildningen T : R 2 R 2 som är bestämd av T (2, 1) = (2, 4) och T (2, 3) = (3, 7). Hitta matrisen A som beskriver avbildningen T (Skriv nu upp ett ekvationssystem som du löser vid invertering av en matris). Uppgift Visa Lemma (5.3.1). Visa först att sammansätningen U T är linjär. Och visa sedan att sammansätningen ges av matrisen BA. 25
31 Föreläsning 6 Lösningar till ekvationssystem 6.1 Ekvationer En linjär ekvation i n variabler x 1,..., x n är en ekvation på formen a 1 x 1 + a 2 x 2 + a n x n = b, med givna tal a 1,..., a n och b. Ett linjärt ekvationssystem i n variabler x 1,..., x n är ett ändligt antal linjära ekvationer i variablerna x 1,..., x n. Exempel Följande två linjära ekvationer { 2x y + z = 3 x + 2y = 0 är ett ekvationssystem i tre varible x, y och z. Systemet består av två ekvationer Ett allmänt linjärt ekvationssystem skriver vi vanligtvis som a 1,1 x 1 + a 1,2 x a 1,n x n = b 1 a 2,1 x 1 + d 2,2 x a 2,n x n = b 2 ( ) = ( ). a m,1 x 1 + a m,2 x a m,n x n = b m Med detta menas att vi har givna tal a i,j för varje 1 i m och varje 1 j n, samt talen b 1,..., b m. Variablerna är x 1,..., x n, och det är n styck av dessa. Antalet linjära ekvationer i systemet är m Lösningsmängden till ett givet ekvationssystem är alla ordnade n- tupler av reella tal (t 1,..., t n ) som satisfierar alla m ekvationer som förekommer 26
32 i ekvationssystemet. Detta betyder att för varje i = 1,..., m har vi att (t 1,..., t n ) är sådan att a i,1 t 1 + a i,2 t a i,n t n = b i Kom ihåg att mängden av alla ordnade n-tupler av reella tal bildar det Euklidiska n-rummet R n. Lösningsmängden till ett ekvationssystem i n variabler blir alltid en delmängd i R n. Exempel Betrakta igen ekvationssystemet i Exemplet (6.1.1). Den sista ekvationen ger at x = 2y, vilket insatt i den första ekvationen ger att 2 ( 2y) y + z = 3. Det vill säga att z = 3 + 5y. Lösningsmängden till ekvationssystemet är alla punkt i R 3 på formen för godtyckliga tal t. ( 2t, t, 3 + 5y) 6.2 Systematisk lösning av ekvationssystem När man skall lösa mera komplexa system än sådana enkla som i Exemplet (6.1.1) lönar det sig att vara mera systematisk. Vi börjar med att observera tre enkla operationer som inte ändrar lösningsmängden till ett system. Radbyte Givet ett ekvationssystem ( ). Detta system består av m ekvationer som vi vill referera till rader. Det är klart att om vi byter plats på rader i ett ekvationssystem så ändras inte lösningsmängden. Multiplikation med ett nollskild tal Givet ett ekvationssystem ( ). Om vi tar och multiplicerar en rad i ekvationssystemet med ett nollskild tal c 0, då får vi ett nytt ekvationssystem. Men, det är klart att lösningsmängden inte ändrar sig. Eller? Addera en rad med en annan Givet ett ekvationssystem ( ). Multiplicera en given rad i med ett tal c, och addera denna nya rad till raden j. I det nya ekvationssystemet ( ) har vi ändrat enbart rad j, men lösningsmängden är den samma. Denna operation på ekvationsystemet är inte lika uppenbar som de två föregående. Notera nu att raden j i det nya ekvationssystemet är (a j,1 + ca i,1 )x 1 + (a j,2 + ca i,2 )x (a j,n + ca i,n )x n = b j + cb i. Kolla nu (se Uppgifterna) att en lösning (t 1,..., t n ) till ekvationssystemet ( ) också är en lösning till det nya ekvationssystemet ( ), och vice versa. 27
33 Elementära radoperationer Vi kan manipulera ett ekvationssystem med de tre operationerna ovan, utan att ändra lösningsmängden. Dessa operationer kallas elementära radoperationer. Exempel Betrakta ekvationssystemet x + 3y + z = 2 2x + 7y = 2 x 4y + 3z = 1 ( ) Vi tar och adderar -2 gånger rad ett till rad två. Den enda rad som ändrar sig blir rad två. Ekvationssystemet blir nu x + 3y + z = 2 y 2z = 2 x 4y + 3z = 1 Sedan tar vi och adderar 1 gånger rad ett till rad tre. Ekvationssystemet blir nu x + 3y + z = 2 y 2z = 2 y + 4z = 3 Ekvationssystemet har nu variabeln x enbart i den första raden. Låt oss nu ta -3 gånger rad två och addera till rad ett, och sedan tar vi och adderar 1 gånger rad två till rad tre. Ekvationssystemet blir x + 7z = 8 y 2z = 2 2z = 1 Variabeln y förekommer nu enbart i rad två. Vi multiplicerar rad tre med 1, 2 och sedn an tar vi 2 gånger rad tre och adderar till rad två, och slutligen -7 gånger rad tre och adderar till rad 1. Detta ger ekvationssystemet x = 9 2 y = 1 ( ) z = 1 2 Notera att vi har enbart användt elementära radoperationer på ekvationssystemet ( ). Detta betyder att lösningsmängden till ( ) är precis den samma som lösningsmängden till ( ). Men lösningsmängden till ( ) är lätt att läsa ut, ( 9 2, 1, 1 2 ). 28
34 6.3 Gauss-Jordan elimination Tillvägasättet som gjordes i Exemplet (6.2.1) kan appliceras på alla ekvationssystem, och kallas Gauss-Jordan elimination. Den almänna algoritmen är som följer. Betrakta ett givet ekvationssystem ( ). Börja med första kolumn. Om alla a 1,1,..., a m,1 är lika med noll, fortsätt till kolumn två. Om inte, plocka ut en rad i där a i,1 0. Byt plats på raderna 1 och i. Mulitplicera nu den, nya, första raden med a 1 1,1. Detta betyder nu att den första raden är x 1 + a 1,2x 2 + a 1,nx n = b 1, där a 1,j = a i,j a i,1 och b 1 = b i a i,1. Sedan använder vi rad 1 för att eliminera all förekomster av x 1 i de andra raderna. Dvs, multiplicera rad ett med a 2,1 och addera tilll rad två, multiplicera rad ett med a 3,1 och addera till rad tre, osv. Ekvationssystemet blir då på formen x 1 +a 1,2x a 1,nx n = b 1 a 2,2x a 2,nx n = b 2. a m,2x a m,nx n = b m Nu är vi klara med variabeln x 1. Vi tittar nu på kolumn två, men inte på rad ett. Vi stryker bort rad ett för ett tag. Om alla siffror a 2,2,..., a m,2 är noll fortsätter vi till kolumn tre. Om det finns en siffra a j,2 som är nollskild, byt plats med rad 2 och j, multiplicera rad 2 med a 1 j,2. Rad två blir nu på formen x 2 + a 2,3x a 2,nx n = b 2, där vi hela tiden byter namn på koefficienterna. Men, vad koefficienterna är spelar inte någon roll. Nu använder vi rad två för att eliminera alla förekomster av variabeln x 2 i raderna 3,..., m och i rad 1. Detta beskriver Gauss-Jordan eliminationen, som vi sluta efter ett ändligt antal steg. Exempel Betrakta ekvationssystemet x 1 + 2x 2 + x 3 3x 4 + 5x 5 + x 6 = 1 3x 1 + 6x 2 + 6x 3 15x x 5 + x 6 = 2 2x 1 + 4x 2 + 3x 3 8x x 5 + x 6 = 3 5x x 2 + 7x 3 19x x 5 + 2x 6 = 11 Det är lite trist och jobbigt att ta med alla variabler när vi utför Gauss-Jordan eliminationen. Och därför skippar vi just detta. Systemet ovan skriver vi 29.
35 istället som matrisen Vi utför de elementära radoperationerna som följer. Vi har en ledande etta i första raden, första kolumen. Denna använder vi för att eleminera talen i första kolumn, i raderna 2, 3 och 4. Detta ger Vi är nu klara med kolumn ett. I kolumn två finns det enbart noll på raderna 2, 3 och 4. Vi fortsätter därför till kolumn tre. Vi byter plats på rad 2 och 3. Och sedan fixar vi till att det blir noll över och under den ledande ettan. Nu borde ni få fram matrisen Vi fortsätter till kolumn fyra, men i raderna tre och fyra finns bara nollor. Vi fortsätter till kolumn fem, och här finns det också enbart nollor i raderna tre och fyra. Vi fortsätter till kolumn sex, och här har vi en ledande etta. Vi fixar nollor över och under den ledande ettan i rad tre, och erhåller Här terminerar Gauss-Jordan algoritmen, och vi skall kunna läsa av lösningsmängden. Vi börjar med den sista ledanden ettan, den i rad tre. Rad tre betyder att x 6 = 4. Det finns ingen ledande etta i kolumn fem, vilket betyder att x 5 = s kan väljas godtyckligt. Likadant kan x 4 = t väljas godtyckligt. I rad två har vi en ledande etta för kolumn tre, detta betyder x 3 2x 4 + 2x 5 = 3. 30
36 Med andra ord att x 3 = 3+2t 2s. Det finns inga ledande ettor för kolumn två, och detta betyder att x 2 = u också kan väljas godtyckligt. Slutligen har vi att x 1 + 2x 2 x 4 + 3x 5 = 8. Detta betyder att lösningsmängden till ekvationssystemet är alla punkt i R 6 på formen ( 8 2u + t 3s, u, 3 + 2t 2s, t, s, 4), med godtyckliga tal s, t och u. 6.4 Uppgifter Gauss-Jordan eliminationen är inte svår att varken lära sig eller att förstå. Om Gauss-Jordan eliminationen är oklar, prata med någon för att genast få klarhet omkring detta. Uppgift Lös ekvationssystemet 2x + 3y + 4z = 2 2x + 5y + z = 5. 4x + 10y z = 1 Uppgift Visa att radoperationen som beskrivs som addera en rad till en annan i Sektion 6.2 inte ändrar lösningsmängden. Uppgift Visa att de tre radoperationerna i Sektion 6.2 faktisk enbart består av två operationer. 31
37 Föreläsning 7 Elementära matriser 7.1 Elementära radoperationer och matriser Vi påminner om att ett ekvationssystem är ett ändligt antal linjära ekvationer i ett ändligt antal okända. Vi skriver ett ekvationssystem som a 1,1 x 1 + a 1,2 x a 1,n x n = b 1 a 2,1 x 1 + d 2,2 x a 2,n x n = b 2 ( ). a m,1 x 1 + a m,2 x a m,n x n = b m Lösningsmängden till ekvationssystemet ( ) är en delmängd av R n. Vi har att det Euklidiska n-rummet R n är mängden av alla ordnade n-tupler av reella tal. Lösningsmängden till ( ) är alla ordnade n-tupler (t 1,..., t n ) som satisfierar ekvationerna i ekvationssystemet Ekvationssystemen kan lösas på ett systematisk sätt. Den algoritm vi använder kallas Gauss-Jordan elimination, och använder sig av tre elementära radoperationer. De elementära radoperationerna var a) multiplicera en rad med ett noll-skild tal b) byta plats på två rader och c) addera till en given rad en multipel av en annan rad. De elementära radoperationerna ändrar inte lösningsmängden till ekvationssystemet, men själva ekvationssystemet. Vi använder elementära radoperationer för att få fram ett ekvationssystem varifrån vi lätt kan läsa av lösningsmängden. Exempel Betrakta ekvationssystemet, i tre okända x, y och z. x + y = 3 y + 2z = 1. ( ) 2x + y + z = 2 32
38 Som brukligt skriver vi upp totalmatrisen till systemet för att inte behöva skriva upp de okända varje gång. Totalmatrisen är ( ) I första kolonnen har vi en ledande 1, och vi vill åstadkomma 0 under denna ledande 1. Detta ordnar vi om vi adderar till den tredje raden -2 gånger den första raden. Denna operation ger matrisen ( ) Nu är vi klara med första kolumnen, och fortsätter med andra kolumn. Vi andvänder 1 på plats (2, 2) som ledande etta. Vi skaffar oss noll ovan och under denna ledande 1 i två steg. Till den tredje raden adderar vi 1 gånger av rad 2, och sedan tar vi och adderar till den första raden -1 gånger rad 2. Detta ger matrisen ( ) Slutligen arbetar vi med den tredje kolumnen. Vi multiplicerar rad 3 med 1 3 och skaffar oss en ledande etta. Till den andra raden adderar vi -2 gånger tredje raden, och till den första raden adderar vi 2 gånger tredje raden. Detta ger matrisen ( ) Nu kan vi läsa av lösningsmängden till ekvationssystemet ( ) som Lösningsmängden är en punkt i R 3. (0, 3, 1) En viktig ingredient i linjär algebran är matrismultiplikation. Låt a 1 a 2 a n A = b 1 b 2 b n c 1 c 2 c n d 1 d 2 d n 33
39 vara en given (4 n) matris. Och betrakta följande tre matriser k k 0 E 1 (k) = , E 2,3 = , E 1,3(k) = Märk att dessa tre matriser är små modifikationer av identitetsmatrisen. Vi har vidare att alla tre matriser kan från vänster multipliceras med matrisen A. Vi erhåller att E 1 (k)a = ka 1 ka 2 ka n b 1 b 2 b n c 1 c 2 c n d 1 d 2 d n det vill säga att multiplikation med matrisen E 1 (k) blir det samma som att multiplicera rad 1 i matrisen A med talet k. Vi har att a 1 a 2 a n E 2,3 A = c 1 c 2 c n b 1 b 2 b n, d 1 d 2 d n det vill säga att multiplikation med matrisen E 2,3 byter plats på raderna två och tre i matrisen A. Och slutligen har vi att E 1,3 (k)a =, a 1 + kc 1 a 2 + kc 2 a n + kc n b 1 b 2 b n c 1 c 2 c n d 1 d 2 d n det vill säga att multiplikation med matrisen E 1,3 (k) tar och adderar till den första raden k gånger rad 3. Definition Vi definierar elementära matriser att vara följande (n n)- matriser. a) Givet 1 i n, och ett nollskild tal k. Låt E i (k) vara matrisen vi får vid att byta ut koefficient (i, i) i identitetsmatrisen med k. b) Givet 1 i < j n. Låt E i,j vara matrisen vi får vid att byta plats på raderna i och j i identitetsmatrisen. 34,
40 c) Givet 1 i, j n, i j, och k ett tal. Låt E i,j (k) vara matrisen vi får vid att byta ut koefficient (i, j) i identitetsmatrisen med k. Sats Låt A vara en (n m)-matris. Att utföra en elementär radoperation på matrisen A är det samma som att multiplicera A från vänster med en (n n) elementär matris. Mera precist har vi a) Att utföra multiplikationen E i (k)a är att multiplicera rad i av matrisen A med talet k. b) Att utföra multiplikationen E i,j A är att byta plats på raderna i och j i matrisen A. c) Att utföra multliplikationen E i,j (k)a är att till raden i av A addera k gånger raden j av A. Proof. Detta är en lämplig uppgift. Exempel Låt oss återgå till exemplet ovan, och ekvationssystemet ( ). Totalmatrisen till systemet är A = Den första elementära radoperationen vi gjorde var att till rad 3 addera -2 gånger rad 1. I tärmer av elementära matriser betyder det att multiplicera totalmatrisen A med E 3,1 ( 2) = Vi har att E 3,1 ( 2)A = vilket är precis matrisen ( ). För att komma till matrisen ( ) gjorde vi två elementära radoperationer. Det första vi gjorde var att till den tredje raden addera 1 gång rad 2, och detta tillsvarar matrisen E 3,2 (1). Sedan tok vi till den första raden -1 gånger rad 2, det vill säga matrisen E 1,2 ( 1). Matrisen ( ) får vi som produkten E 1,2 ( 1)E 3,2 (1)E 3,2 ( 2)A =
41 Slutligen, det vi gjorde sedan var att multiplicera med E 3 ( 1 ), sedan multiplicera med E 2,3 ( 2), och helt till sist multiplicerade vi med E 1,3 (2). Hela 3 exemplet ges av matrisproukten E 1,3 (2)E 2,3 ( 2)E 3 ( 1 3 )E 1,2( 1)E 3,2 (1)E 3,2 ( 2)A. ( ) Notera att det är viktigt att hålla reda på ordningen i matrisprodukten. Utför man produkten ( ) så får man matrisen ( ) En (n n) matris B är inversen till matrisen A om AB och BA båda blir identitetsmatrisen. Sats Varje elementär matris är inverterbar, och inversen till en elementär matris är själv en elementär matris. Mera precist har vi att 1. Elementärmatrisen E i (k) har invers E i ( 1 k ). 2. Elementärmatrisen E i,j har invers E i,j. 3. Elementär matrisen E i,j (k) har invers E i,j ( k). Proof. Vi visar först påståendet i (1). Låt B vara en elementär matris på formen E i (k). Då är k 0, och vi kan bilda elementärmatrisen E i ( 1 ). Av k Sats (7.1.5) följer det att E i ( 1 )B är det samma som att multiplicera rad i k av matrisen B med 1. Rad i i matrisen B = E k i(k) har k i plats i, och noll annars. Det är nu klart att E i ( 1)B = 1. Vi har då visat att E k i( 1)E k i(k) = 1 för alla nollskilda k, och speciellt också att E i (k)e i ( 1 ) = 1. Då har vi visat k påstående (1). Se uppgifterna för (2) och (3). Exempel Betrakta matrisen B = Denna matris är den vänstra delen av totalmatrisen i första exemplet. Det följer av beräkningarna vi gjorde att produkten ( ) att E 1,3 (2)E 2,3 ( 2)E 3 ( )E 1,2( 1)E 3,2 (1)E 3,2 ( 2)B = Låt X = E 1,3 (2)E 2,3 ( 2)E 3 ( 1 3 )E 1,2( 1)E 3,2 (1)E 3,2 ( 2). Vi har att XB = 1, det vill säga att när vi mulplicerar matrisen B med matrisen X från vänster 36
Linjär algebra Tio förrätter och två efterrätter Roy Skjelnes
 Linjär algebra Tio förrätter och två efterrätter Roy Skjelnes Matematiska Institutionen, KTH Typsatt med L A TEX 2ε och TikZ Kompilerad 8 september 2014 Inledande ord Detta häfte är baserat på en föreläsningsserie
Linjär algebra Tio förrätter och två efterrätter Roy Skjelnes Matematiska Institutionen, KTH Typsatt med L A TEX 2ε och TikZ Kompilerad 8 september 2014 Inledande ord Detta häfte är baserat på en föreläsningsserie
Proof. Se uppgifterna. Definition 1.6. Två vektorer u och v är vinkelräta (ortogonala) om < u, v >= 0.
 1. Punkt och Linjer När du läser denna text är det bra om du ritar bilder för att exemplifiera innehållet. Det är lite komplicerad med i.tex, och därför avstår jag från att lägga vid illustrationer även
1. Punkt och Linjer När du läser denna text är det bra om du ritar bilder för att exemplifiera innehållet. Det är lite komplicerad med i.tex, och därför avstår jag från att lägga vid illustrationer även
1. Ekvationer 1.1. Ekvationer och lösningar. En linjär ekvation i n variabler x 1,..., x n är en ekvation på formen. 2x y + z = 3 x + 2y = 0
 1. Ekvationer 1.1. Ekvationer och lösningar. En linjär ekvation i n variabler x 1,..., x n är en ekvation på formen a 1 x 1 + a 2 x 2 + a n x n = b, med givna tal a 1,..., a n och b. Ett linjärt ekvationssystem
1. Ekvationer 1.1. Ekvationer och lösningar. En linjär ekvation i n variabler x 1,..., x n är en ekvation på formen a 1 x 1 + a 2 x 2 + a n x n = b, med givna tal a 1,..., a n och b. Ett linjärt ekvationssystem
Linjär algebra Tio förrätter och två efterrätter Roy Skjelnes
 Linjär algebra Tio förrätter och två efterrätter Roy Skjelnes Matematiska Institutionen, KTH Typsatt med L A TEX 2ε och TikZ Kompilerad 7 september 2015 Inledande ord Detta häfte är baserat på en föreläsningsserie
Linjär algebra Tio förrätter och två efterrätter Roy Skjelnes Matematiska Institutionen, KTH Typsatt med L A TEX 2ε och TikZ Kompilerad 7 september 2015 Inledande ord Detta häfte är baserat på en föreläsningsserie
c d Z = och W = b a d c för några reella tal a, b, c och d. Vi har att a + c (b + d) b + d a + c ac bd ( ad bc)
 1 Komplexa tal 11 De reella talen De reella talen skriver betecknas ofta med symbolen R Vi vill inte definiera de reella talen här, men vi noterar att för varje tal a och b har vi att a + b och att ab
1 Komplexa tal 11 De reella talen De reella talen skriver betecknas ofta med symbolen R Vi vill inte definiera de reella talen här, men vi noterar att för varje tal a och b har vi att a + b och att ab
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
x 1 x 2 x 3 x 4 mera allmänt, om A är en (m n)-matris, då ger matrismultiplikationen en avbildning T A : R n R m.
 Fredagen 006 Avbildningar Låt A vara matrisen () = 0 0 Till varje vektor X i R får vi vid matrismultiplikationen AX en vektor i R Mera explicit, om X = x x x x är en given punkt i R, då får vi punkten
Fredagen 006 Avbildningar Låt A vara matrisen () = 0 0 Till varje vektor X i R får vi vid matrismultiplikationen AX en vektor i R Mera explicit, om X = x x x x är en given punkt i R, då får vi punkten
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
ax + y + 2z = 3 ay = b 3 (b 3) z = 0 har (a) entydig lösning, (b) oändligt många lösningar och (c) ingen lösning.
 UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
Veckoblad 1, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Veckoblad, Linjär algebra IT, VT Under den första veckan ska vi gå igenom (i alla fall stora delar av) kapitel som handlar om geometriska vektorer. De viktigaste teoretiska begreppen och resultaten i kapitlet
Uppsala Universitet Matematiska Institutionen Bo Styf. Svar till tentan. Del A. Prov i matematik Linj. alg. o geom
 Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
14 september, Föreläsning 5. Tillämpad linjär algebra
 14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
15 september, Föreläsning 5. Tillämpad linjär algebra
 5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
Matriser. En m n-matris A har följande form. Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. 0 1, 0 0. Exempel 1
 Matriser En m n-matris A har följande form a 11... a 1n A =.., a ij R. a m1... a mn Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. Exempel 1 1 0 0 1, 0 0 ( 1 3 ) 2, ( 7 1 2 3 2, 1 3, 2 1
Matriser En m n-matris A har följande form a 11... a 1n A =.., a ij R. a m1... a mn Vi skriver också A = (a ij ) m n. m n kallas för A:s storlek. Exempel 1 1 0 0 1, 0 0 ( 1 3 ) 2, ( 7 1 2 3 2, 1 3, 2 1
Enhetsvektorer. Basvektorer i två dimensioner: 1 1 Basvektorer i tre dimensioner: Enhetsvektor i riktningen v: v v
 Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
Vektoraddition u + v = u + v = [ ] u1 u 2 u 1 u 2 + u 3 + [ v1 v 2 ] = v 1 v 2 = v 3 [ u1 + v 1 u 2 + v 2 u 1 + v 1 u 2 + v 2 u 3 + v 3 ] Multiplikation med skalär α u = α [ u1 u 2 α u = α ] = u 1 u 2
(a) Bestäm för vilka värden på den reella konstanten c som ekvationssystemet är lösbart. (b) Lös ekvationssystemet för dessa värden på c.
 UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Veckoblad 4, Linjär algebra IT, VT2010
 Veckoblad, Linjär algebra IT, VT Under den fjärde veckan ska vi under måndagens föreläsning se hur man generaliserar vektorer i planet och rummet till vektorer med godtycklig dimension. Vi kommer också
Veckoblad, Linjär algebra IT, VT Under den fjärde veckan ska vi under måndagens föreläsning se hur man generaliserar vektorer i planet och rummet till vektorer med godtycklig dimension. Vi kommer också
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Linjär Algebra M/TD Läsvecka 2
 Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser. 2.2-2.3 Matrisinvers, karakterisering
Linjär Algebra M/TD Läsvecka 2 Omfattning och Innehåll 2.1 Matrisoperationer: addition av matriser, multiplikation av matris med skalär, multiplikation av matriser. 2.2-2.3 Matrisinvers, karakterisering
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
6. Matriser Definition av matriser 62 6 MATRISER. En matris är ett rektangulärt schema av tal: a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A =
 62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
62 6 MATRISER 6 Matriser 6 Definition av matriser En matris är ett rektangulärt schema av tal: A a a 2 a 3 a n a 2 a 22 a 23 a 2n a m a m2 a m3 a mn Matrisen A säges vara av typ m n, där m är antalet rader
Lösningar till utvalda uppgifter i kapitel 1
 Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
Lösningar till utvalda uppgifter i kapitel. Vi utnyttjar definitionen av skalärprodukt som ger att u v u v, där α är (minsta) vinkeln mellan u v. I vårt fall så får vi 7 =. Alltså är den sökta vinkeln
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
SF1624 Algebra och geometri Lösningsförsag till modelltentamen
 SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
5 Linjär algebra. 5.1 Addition av matriser 5 LINJÄR ALGEBRA
 5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
Vektorgeometri. En vektor v kan representeras genom pilar från en fotpunkt A till en spets B.
 Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
reella tal x i, x + y = 2 2x + z = 3. Här har vi tre okända x, y och z, och vi ger dessa okända den naturliga
 . Lösningsmängden till homogena ekvationssystem I denna första föreläsning börjar vi med att repetera det grunnläggande begreppet inom linjär algebran. Linjär algebra är studiet av lösningsmängden till
. Lösningsmängden till homogena ekvationssystem I denna första föreläsning börjar vi med att repetera det grunnläggande begreppet inom linjär algebran. Linjär algebra är studiet av lösningsmängden till
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
= ( 1) ( 1) = 4 0.
 MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
Moment 6.1, 6.2 Viktiga exempel Övningsuppgifter T6.1-T6.6
 Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
Moment 6., 6. Viktiga exempel 6.-6. Övningsuppgifter T6.-T6.6 Matriser Definition. En matris är ett schema med m rader och n kolonner eller kolumner, som vi kallar dem i datalogin innehållande m n element.
Dagens program. Linjära ekvationssystem och matriser
 Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
Dagens program Matriser Räkneoperationer och räknelagar Linjära ekvationssystem och matriser Matrisform av ekvationssystem Elementära radoperationer Trappstegsmatriser, rang och lösningsstruktur Matrisinvers,
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. t 2
 SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
SF1624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 2010 DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
Moment Viktiga exempel Övningsuppgifter
 Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång.
Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång.
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
P Q = ( 2, 1, 1), P R = (0, 1, 0) och QR = (2, 2, 1). arean = 1 2 P Q P R
 1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp)
 Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna 1-4.
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna -. Föreläsningarna, 6/9 /9 : I sammanfattningen kommer en del av det vi tagit
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna -. Föreläsningarna, 6/9 /9 : I sammanfattningen kommer en del av det vi tagit
Veckoblad 3, Linjär algebra IT, VT2010
 Veckoblad 3, Linjär algebra IT, VT Vi inleder den tredje veckan med att gå igenom begreppen determinant och invers matris som vi inte hann med i vecka, se veckoblad för övningar etc på dessa avsnitt. Därefter
Veckoblad 3, Linjär algebra IT, VT Vi inleder den tredje veckan med att gå igenom begreppen determinant och invers matris som vi inte hann med i vecka, se veckoblad för övningar etc på dessa avsnitt. Därefter
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem.
 Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
KOKBOKEN 1. Håkan Strömberg KTH STH
 KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
KOKBOKEN 1 Håkan Strömberg KTH STH Hösten 2006 Håkan Strömberg 2 KTH Syd Innehåll Olikheter.................................... 6................................. 6 Uppgift 2.................................
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Vektorgeometri för gymnasister Per-Anders Svensson http://w3.msi.vxu.se/users/pa/vektorgeometri/gymnasiet.html Institutionen för datavetenskap, fysik och matematik Linnéuniversitetet Vektorer i planet
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Explorativ övning Vektorer
 Eplorativ övning Vektorer Syftet med denna övning är att ge grundläggande kunskaper om vektorräkning och dess användning i geometrin Liksom många matematiska begrepp kommer vektorbegreppet från fysiken
Eplorativ övning Vektorer Syftet med denna övning är att ge grundläggande kunskaper om vektorräkning och dess användning i geometrin Liksom många matematiska begrepp kommer vektorbegreppet från fysiken
M = c c M = 1 3 1
 N-institutionen Mikael Forsberg Prov i matematik Matematik med datalogi, mfl. Linjär algebra ma4a Deadline :: 8 9 4 Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på ny
N-institutionen Mikael Forsberg Prov i matematik Matematik med datalogi, mfl. Linjär algebra ma4a Deadline :: 8 9 4 Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på ny
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Föreläsning 13 Linjär Algebra och Geometri I
 Föreläsning 13 Linjär Algebra och Geometri I Se slide 1: det är i rymden oftast lättast att jobba med parametrar för linjer och ekvationer för plan. Exempel: Låt l : (x, y, z) = (1 t, 3 + t, 4t), t R och
Föreläsning 13 Linjär Algebra och Geometri I Se slide 1: det är i rymden oftast lättast att jobba med parametrar för linjer och ekvationer för plan. Exempel: Låt l : (x, y, z) = (1 t, 3 + t, 4t), t R och
Linjära avbildningar. Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. x 1 x 2. x = R n = x n
 Linjära avbildningar Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. R n = { x = x x. x n } x, x,..., x n R. Vi räknar med vektorer x, y likandant som i planet och i rymden. vektorsumma:
Linjära avbildningar Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. R n = { x = x x. x n } x, x,..., x n R. Vi räknar med vektorer x, y likandant som i planet och i rymden. vektorsumma:
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
Moment 5.5 Övningsuppgifter I 5.60a. 5.60b, 5.60.c, 61
 Moment 5.5 Övningsuppgifter I 5.0a. 5.0b, 5.0.c, 1 Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång. Kvadratiska
Moment 5.5 Övningsuppgifter I 5.0a. 5.0b, 5.0.c, 1 Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång. Kvadratiska
Subtraktion. Räkneregler
 Matriser En matris är en rektangulär tabell av tal, 1 3 17 4 3 2 14 4 0 6 100 2 Om matrisen har m rader och n kolumner så säger vi att matrisen har storlek m n Index Vi indexerar elementen i matrisen genom
Matriser En matris är en rektangulär tabell av tal, 1 3 17 4 3 2 14 4 0 6 100 2 Om matrisen har m rader och n kolumner så säger vi att matrisen har storlek m n Index Vi indexerar elementen i matrisen genom
TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1. Omfattning. Innehåll 2012-01-20. Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra
 TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1 Omfattning Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll Olika aspekter av linjära ekvationssystem 1. skärning mellan geometriska
TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1 Omfattning Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll Olika aspekter av linjära ekvationssystem 1. skärning mellan geometriska
SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 2 Fredagen den 28 januari, 2011
 SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 2 Fredagen den 28 januari, 2011 UPPGIFT (1) Låt V vara mängden av vektorer (x 1, x 2, x 3 ) i R 3 som uppfyller
SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 2 Fredagen den 28 januari, 2011 UPPGIFT (1) Låt V vara mängden av vektorer (x 1, x 2, x 3 ) i R 3 som uppfyller
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
x 1 x 2 T (X) = T ( x 3 x 4 x 5
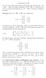 Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
Lördagen 6 Nu vill vi fokusera på linjära avbildningar från vektorrum W Om T : R n R n är en linjär avbildning, och W R n ett vektorrum, då har vi en inducerad avbildning T W : W R m Och denna avbildning
LINJÄRA AVBILDNINGAR
 LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MVE520 Linjär algebra LMA515 Matematik, del C
 MATEMATIK Chalmers tekniska högskola Tentamen MVE52 Linjär algebra LMA55 Matematik, del C Hjälpmedel: inga Datum: 28-8-29 kl 8 2 Telefonvakt: Sebastian Jobjörnsson ankn 6457 Examinator: Håkon Hoel Tentan
MATEMATIK Chalmers tekniska högskola Tentamen MVE52 Linjär algebra LMA55 Matematik, del C Hjälpmedel: inga Datum: 28-8-29 kl 8 2 Telefonvakt: Sebastian Jobjörnsson ankn 6457 Examinator: Håkon Hoel Tentan
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer I Innehåll
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
8(x 1) 7(y 1) + 2(z + 1) = 0
 Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
Mer om analytisk geometri
 1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING 1
 STOCKHOLMS UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra II LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING Lös ekvationssystemet x + y + z 9 x + 4y 3z 3x + 6z 5z med hjälp av Gausselimination Lösning:
STOCKHOLMS UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra II LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING Lös ekvationssystemet x + y + z 9 x + 4y 3z 3x + 6z 5z med hjälp av Gausselimination Lösning:
MATEMATIK GU. LLMA60 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 2014. Block 5, översikt
 MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
MATRISTEORI. Pelle Pettersson MATRISER. En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens
 MATRISTEORI Pelle Pettersson ALLMÄN MATRISKUNSKAP MATRISER En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens element Exempel Matrisen 2 3 4 5 6 har två rader och
MATRISTEORI Pelle Pettersson ALLMÄN MATRISKUNSKAP MATRISER En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens element Exempel Matrisen 2 3 4 5 6 har två rader och
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET MED MATRISINVERSER = = =
 Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer II Innehåll
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Linjär Algebra M/TD Läsvecka 1
 Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.
![Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4. Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.](/thumbs/93/112939298.jpg) LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer III Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Räta linjens och planets ekvationer III Innehåll
Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34. Planet Ett plan i rummet är bestämt då
 Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34 Planet Ett plan i rummet är bestämt då två icke parallella riktningar, v 1 och v 2, och en punkt P 1 i planet är givna.
Moment 4.11 Viktiga exempel 4.32, 4.33 Övningsuppgifter Ö4.18-Ö4.22, Ö4.30-Ö4.34 Planet Ett plan i rummet är bestämt då två icke parallella riktningar, v 1 och v 2, och en punkt P 1 i planet är givna.
Linjär Algebra, Föreläsning 2
 Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
Linjär Algebra, Föreläsning 2 Tomas Sjödin Linköpings Universitet Geometriska vektorer, rummen R n och M n 1 En (geometrisk) vektor är ett objekt som har storlek och riktning, men inte någon naturlig startpunkt.
LINJÄR ALGEBRA II LEKTION 3
 LINJÄR ALGEBRA II LEKTION 3 JOHAN ASPLUND INNEHÅLL Basbyten Kolonnrum, radrum och nollrum 3 Linjära avbildningar från R n till R m 4 Uppgifter 3 46:3 3 47:a 3 48:3a 4 48:a 4 49:9 4 40:7a,b BASBYTEN Om
LINJÄR ALGEBRA II LEKTION 3 JOHAN ASPLUND INNEHÅLL Basbyten Kolonnrum, radrum och nollrum 3 Linjära avbildningar från R n till R m 4 Uppgifter 3 46:3 3 47:a 3 48:3a 4 48:a 4 49:9 4 40:7a,b BASBYTEN Om
En vektor är mängden av alla sträckor med samma längd och riktning.
 En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
En vektor är mängden av alla sträckor med samma längd och riktning. Slappdefinition En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition. Räkning med vektorer. Bas och koordinater. En vektor är mängden av alla sträckor med samma längd och riktning.
 Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
Slappdefinition En vektor är mängden av alla sträckor med samma längd och riktning. En vektor är en riktad sträcka som får parallellförflyttas. Tänk på vektorn som en pil. Betecknar vektorer med små bokstäver
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
x+2y 3z = 7 x+ay+11z = 17 2x y+z = 2
 Problem 1. Avgör för vilka värden på a som ekvationssystemet nedan har oändligt antal lösningar. Ange lösningarna i dessa fall! Lösning: Genom x+2y 3z = 7 x+ay+11z = 17 2x y+z = 2 1 2 3 1 a 11 2 1 1 =
Problem 1. Avgör för vilka värden på a som ekvationssystemet nedan har oändligt antal lösningar. Ange lösningarna i dessa fall! Lösning: Genom x+2y 3z = 7 x+ay+11z = 17 2x y+z = 2 1 2 3 1 a 11 2 1 1 =
