4. Optimal styrning. 4. Optimal styrning. Vad är optimal styrning?
|
|
|
- Henrik Vikström
- för 9 år sedan
- Visningar:
Transkript
1 reglerteni Reglerteni II / KEH. Optimal styrning. Optimal styrning Vad är optimal styrning? I allmänna termer an reglertenisa problem formleras på följande sätt: Välj styrsignaler så att systemet beter sig så bra som möjligt Svårigheten ligger vanligtvis i att formlera vad som är så bra som möjligt. Om man an formlera detta matematist samt har en representativ processmodell an man lösa reglerproblemet systematist: man löser helt enelt det matematisa optimeringsproblemet. Eempel på pratisa problemställningar är att bestämma optimal väg genom ett nätver från en pnt A till en pnt B beräna optimal styrstrategi för en satsvis celllosa- eller soceroare minimera tiden det tar att byta pappersvalitet på en pappersmasin bestämma optimal styrstrategi vid tillverning av halvledare an bestå av delsteg designa en process bestående av flera delprocesser så att anläggnings- och driftsostnaderna minimeras Reglerteni II Tillståndsmetoder 9
2 reglerteni Reglerteni II / KEH. Optimal styrning Öppen styrning Öppen styrning är en speciell typ av styrproblem där man inte tnyttjar återoppling; den optimala strategin beränas helt tgående från processmodellen och ett matematist godhetsriterim även ostnadsfntion, förlstfntion. Typisa problem av denna typ är att bestämma billigaste vägen minimera tiden för en versamhet alloera resrser Ofta ombineras öppen styrning med återopplad reglering på en lägre nivå. T.e. problemet att bestämma optimal temperatrprofil som fntion av tiden för en satsreator är ett öppet styrproblem, men temperatren realiseras genom återopplad reglering. I detta fall är problemet att generera optimala börvärden Reglerteni II Tillståndsmetoder 9
3 reglerteni Reglerteni II / KEH. Optimal styrning Övning.. Ett eempel på billigaste färdväg Vi sall resa från pnt A till pnt B i nedanstående schema, där vi sall välja en av flera möjliga resrtter så att resans totalostnad minimeras. Kostnaderna för de möjliga delrtterna finns tmärta i figren. Vilen väg sall vi välja från pnt A till pnt B? A B Reglerteni II Tillståndsmetoder 9
4 reglerteni Reglerteni II / KEH. Optimal styrning. Dynamis programmering Dynamis programmering, tveclad av Richard Bellman i sltet av 95-talet, är en optimeringsmetod som är speciellt lämplig för problem som an ppdelas i en serie delproblem, som an behandlas seventiellt så att varje delproblem medför ett beslt dvs en styråtgärd. Typisa problemställningar är att bestämma billigaste vägen alloera resrser Dynamis programmering bygger på optimalitetsprincipen: De optimala beslten styråtgärderna från och med ett godtycligt steg i besltsprocessen dvs de efterföljande beslten får inte bero på hr tillståndet i detta steg ppnåtts. Vad betyder detta? Vi an ocså formlera optimalitetsprincipen på följande sätt: Oberoende av vad vi gjort fram till steg n i besltsprocessen, sall vi i fortsättningen göra det som är optimalt för de efterföljande stegen i besltsprocessen. Denna princip har som följd att det ofta är fördelatigt att beräna den optimala strategin startande från sltändan av den seventiella besltsprocessen. Reglerteni II Tillståndsmetoder 9
5 reglerteni Reglerteni II / KEH. Dynamis Programmering.. Eempel på öppen styrning tan begränsningar Ett dynamist system besrivs av den tidsdisreta evationen, Beräna styråtgärderna, och som minimerar förlstfntionen t dt då tillståndet t antas förändras linjärt med tiden mellan samplingspnterna. Samplingsintervallet är h tidsenhet och inga begränsningar eisterar för. Eftersom t förändras linjärt mellan samplingspnterna gäller t t, t,,, vilet gör att förlstfntionen an srivas d t t. Optimal styrning 5
6 reglerteni Reglerteni II / KEH.. Öppen styrning tan begränsningar Lösning genom ordinär optimering Eftersom styrsignalernas storle i detta fall inte bidrar till förlstfntionen an man lia väl optimera diret med avseende på, och och därefter beräna de optimala styrsignalerna när de optimala tillstånden, och är ända. Vi sall alltså bestämma,, min där Eftersom variablerna sanar begränsningar gäller vid minimm,,. Dynamis programmering 6
7 .. Öppen styrning tan begränsningar. Dynamis programmering Laboratoriet för reglerteni Reglerteni II / KEH Vi får,, dvs ränat från sltet samt ,85 min 5 5 5
8 .. Öppen styrning tan begränsningar. Dynamis programmering 8 Laboratoriet för reglerteni Reglerteni II / KEH Lösning genom dynamis programmering Vi sriver förlstfntionen som, och börjar med att minimera det sista steget = samma som tidigare Därefter minimerar vi stegen = +. Vi har med samma Alla steg med och ger 6 6 samma
9 .. Öppen styrning tan begränsningar. Dynamis programmering 9 Laboratoriet för reglerteni Reglerteni II / KEH Sboptimala lösningar På grnd av förlstfntionens form, ligger det nära till hand att minimera varje steg var för sig, dvs att minimera loalt: som är fel lösning tom för sista steget. Denna sboptimala lösning optimal i varje steg ger, sb En dead-beat strategi, ger och, dead.
10 reglerteni Reglerteni II / KEH.. Öppen styrning tan begränsningar Kommentarer I detta mycet enla fall var metoden med dynamis programmering nappast enlare än ordinär optimering. Vi an doc onstatera följande: Om antalet steg varit större hade det doc varit besvärligt att optimera globalt med avseende på alla optimeringsvariabler samtidigt. Vid användning av dynamis programmering blir de ensilda stegen inte besvärligare. Om förlstfntionen är mer omplicerad, inlderande t.e. styrsignaler, blir det ocså besvärligare att optimera globalt i ett steg. Vid användning av dynamis programmering blir varje ensilt steg normalt inte nämnvärt svårare. Ifall man har begränsningar på tillståndvariablerna tsignalerna och/eller styrsignalerna, blir traditionell optimering mycet besvärlig, anse omöjlig. Begränsningar an relativ enelt beatas vid dynamis programmering då problemet löses stegvis. En nacdel med dynamis programmering är det stora antal olia alternativ som måste sparas ifall man inte an ttryca sambanden analytist the crse of dimensionality.. Dynamis programmering
11 reglerteni Reglerteni II / KEH. Dynamis programmering.. Eempel på öppen styrning med begränsningar Antag att styrsignalerna, och i det ovan behandlade eemplet endast an anta jämna heltalsvärden. Då an problemet i princip inte lösas analytist genom nollställning av partialderivator, varen genom ordinär optimering eller dynamis programmering. En möjlighet är att avrnda den analytisa lösningens styrsignaler till närmaste jämna heltal, men det finns inget som garanterar att detta ger den optimala heltalslösningen. Det finns avancerade matematisa metoder för lösning av heltalsproblem som vi doc inte sall behandla här. En fördel med heltalsproblem är doc att det vanligtvis endast finns ett ändligt antal möjliga lösningar, vilet betyder att man i princip an analysera alla tänbara lösningar. Genom användning av dynamis programmering, ev. ombinerad med någon fndamental analys av problemets natr och nödvändiga egensaper för den optimala lösningen, an man ofta lösa denna typ av problem förhållandevis enelt.. Optimal styrning
12 reglerteni Reglerteni II / KEH.. Öppen styrning med begränsningar Eempel med begränsningar Uppgiften är att minimera nder bivilloren modellen,, samt,,,. Det är enelt att övertyga sig om att för den optimala lösningen måste gälla, ifall, att samt att och inte har samma tecen eftersom minimerar varje jämfört med. Man inser då, med hjälp av modellen, att de optimala styrsignalerna och tillstånden måste satisfiera,, 6, 8,,,,, 6, 8,,,, 6,,, 6, 8,,,, 6,,, Det vore möjligt att begränsa styrsignalerna ytterligare med en mer ingående inledande analys, vilet vi doc inte gör.. Dynamis programmering
13 reglerteni Reglerteni II / KEH.. Öppen styrning med begränsningar I stället tnyttjar vi dynamis programmering för att hitta den sltliga lösningen. Med hjälp av modellen Steget = an ttrycet för srivas Eftersom gäller för lösningen av det obegränsade fallet, är det ocså en möjlig lösning i detta fall, ifall det finns en tillåten lösning som satisfierar sambandet.,, fås a Om blir. b Om, 6, som är ett jämnt heltal. Bidraget till förlstfntionen är inte ett jämnt heltal. Närmast till hands ligger lösningarna samma bidrag, som är jämna heltal. Kontroll visar att både + och ger. Inget annat tillåtet ger här ett mindre.. Dynamis programmering
14 reglerteni Reglerteni II / KEH.. Öppen styrning med begränsningar Stegen = + a Vi har,. Modellsambandet Möjligheterna är i i ger, och 5 6. Dynamis programmering och ii som ger och ii 8.,,, 6, ii bättre om 8. Här är i bättre mindre om b Vi har, 6 och således, 6 och ii 6 Möjligheterna är i i 8 samt 5 6 som ger och ii 6 6. Här är i bättre om, dvs alltid. 6 är således inte en möjlig optimal lösning.
15 reglerteni Reglerteni II / KEH.. Öppen styrning med begränsningar Alla steg a i Vi har,,, 6 då,, 6, 8, Minimm. Sambandet samt 88 fås för 8. ger,,, 6 och a ii Här är 8. Sambandet samt ger och Detta fall är alltså sämre än a i Dynamis programmering 5
16 reglerteni Reglerteni II / KEH.. Öppen styrning med begränsningar b i Här är,,, 6, 8,, 6, 8,. Sambandet och samt 8 8 ger Minimm fås för 6 och 8. Även detta är sämre än a i. Den optimala lösningen Den optimala lösningen är fall a i som för 8,, ger 88 9,,, med Obs att denna lösning med denna förlstfntion är bättre än dead-beat strategin, som,,,. även satisfierar begränsningarna. Dynamis programmering 6
17 reglerteni Reglerteni II / KEH. Dynamis programmering.. Allmän formlering av lösning med dynamis programmering Sambandet mellan tillstånden och samt en styråtgärd an allmänt srivas f,,,, där f är en godtyclig fntion, som inte behöver vara linjär och inte behöver vara densamma för alla. Antag att man önsar styra systemet från tillståndet till N så att förlstfntionen N g minimeras. Här är g en godtyclig fntion som anger ostnaden att gå från tillståndet till med styrsignalen. Om man inledningsvis har en ostnad g som är beroende av tillståndet, an detta elimineras med hjälp av modellsambandet. Därmed an slttillståndet N alltid elimineras från förlstfntionen. Optimal styrning,
18 reglerteni Reglerteni II / KEH.. Allmän formlering av lösning Låt betecna ostnaden för den optimala vägen dvs den minimala ostnaden från tillståndet till slttillståndet N. Då gäller ppenbarligen N N samt för sccessivt minsande, N,, : g, ming, f, min Minimering i varje steg enligt valfri metod, med beatande av ev. begränsningar ger en optimal styrsignal som fntion av, betecnad *, matematist ttryct: arg ming, f, Till slt erhålles för min och är änt. Tillståndet, varefter. Dynamis programmering 8, som an bestämmas då begynnelsetillståndet an därefter beränas enligt modellsambandet med an bestämmas, osv * och för alla. Mär att betecningarna här avvier från betecningarna i de tidigare eemplen.
19 reglerteni Reglerteni II / KEH. Optimal styrning. Maimmprincipen Optimalitetsprincipen ger en strategi för att finna den optimala lösningen när ett problem an delas pp i ett antal delsteg, som an lösas seventiellt. Detta förtsätter att ocså förlstfntion an ppdelas så, att en viss förlst är förnippad varje ensilt delsteg. Maimmprincipen ger villor som den optimala lösningen bör ppfylla för mera allmänna optimeringsproblem, som inte nödvändigtvis an ppdelas i ett antal delproblem som löses seventiellt. Dessa villor ger inte diret den optimala lösningen, men de gör det vanligtvis möjligt att finna den. Benämningen maimmprincipen följer av att problemen tidigare formlerades som maimeringsproblem; nförtiden minimerar vi hellre. Principen benämnes ofta Pontryagins maimmprincip eller minimmprincip efter en av pphovsmännen. Maimmprincipen ger optimalitetsvillor för generella styrproblem; ett antal vitiga specialfall inlderar var för sig stora lasser optimala styrproblem. Reglerteni II Tillståndsmetoder 9 9
20 reglerteni Reglerteni II / KEH. Maimmprincipen.. Det optimala styrproblemet Det optimala styrproblemet an i ontinerlig tid formleras på följande sätt: Minimera förlstfntionen nder bivilloren f t f t L t, tdt..a t f, t t..b t U, t tf..c, ψ t..d f Här är..b modellen för det dynamisa systemet,..c definierar ev. begränsningar på de tillgängliga styrsignalerna,..d ger begynnelsetillstånd och ett ev. bivillor relaterat till slttillståndet. Vitiga specialfall som förenlar lösningen fås när slttiden t f är given inga bivillor ψ tf begränsar slttillståndet tf förlstfntionen har speciellt enel form. Optimal styrning
21 reglerteni Reglerteni II / KEH. Maimmprincipen.. Given slttid, obegränsat slttillstånd I det fall, att slttiden t f är given och slttillståndet lösningen t, t ppfylla följande villor: t är obegränsat, bör den optimala f där min H, t, p t H, t, t p, t t t f..a U T H p,, L, p f,..b är den s.. Hamiltonfntionen och där p ppfyller den adjngerade evationen H, t, p t p t, T t p t f T t f..c. Optimal styrning
22 reglerteni Reglerteni II / KEH.. Given slttid, obegränsat slttillstånd Eempel.. Styrning i strömmande vatten. En båt med lägesoordinaten, rör sig i ett område med varierande ström. Styrvariabeln är lia med båtens hastighet relativt vattnet i -ritning, styrvariabeln dess hastighet i -ritningen. Vattnets hastighet är v i -ritningen och i - ritningen. Båten startar i origo och man vill förflytta sig så långt som möjligt i -led på T tidsenheter. Vila är de optimala styråtgärderna då de är begränsade så att båtens fart relativt vattnet är onstant =? Detta ger optimeringsproblemet nder bivilloren min T, v,,. Maimmprincipen
23 reglerteni Reglerteni II / KEH.. Given slttid, obegränsat slttillstånd Här är förlstfntionens L, vilet ger T T v,,, H p p f p p v p De adjngerade evationerna blir H, t, p t p v p p t t t p t p v H, t, p t p v p t t T p T p T T T T T T. Maimmprincipen
24 reglerteni Reglerteni II / KEH.. Given slttid, obegränsat slttillstånd Enligt..a sall styrsignalerna väljas som lösningen till pv p min H, t, p t min p v p min p U Man an enelt visa att p p p, p p p satisfierar den optimala lösningen. Av ttrycen för de adjngerade evationerna följer t t t p t och p t p d p v d v d Om vattnets hastighet v t.e. varierar linjärt med, så att v, fås med beatande av p t t T p T, att. Maimmprincipen
25 reglerteni Reglerteni II / KEH. Maimmprincipen.. Minimaltidsproblem I ett minimaltidsproblem vill man genom styråtgärder minimera den tid det tar att från ett givet tgångstillstånd ppnå ett visst slttillstånd. I detta fall blir förlstfntionen så enel som t f d t t vilet i de tidigare ttrycen motsvaras av tf L t t. I detta fall eisterar alltid ett villor ψ t, som slttillståndet bör satisfiera. f f och, För ett linjärt system begränsat av t A t B t ma i t, i,,dim i ψ, tf. Optimal styrning 5
26 reglerteni Reglerteni II / KEH.. Minimaltidsproblem an man visa att den optimala styrstrategin i allmänhet har formen ma T i, p t bi ma T i ma T i p bi i, p t bi t sign t där b i är i :te olonnen av B och p t är en lösning till den adjngerade evationen. T Fntionen sign p t b i byter tecen vi något visst värde på t, som beror av systemet och de gällande begränsningarna. Denna typ av styrning allas bang-bang-styrning. Allmänt an man säga att en styrsignal, som alltid antar sitt största eller minsta värde med ändligt många välingar däremellan, är av bang-bang typ. Dead-beat-reglering, som egentligen är lösningen till ett minimaltidsproblem, leder vanligtvis till bang-bang-reglering.. Maimmprincipen 6
4. Optimal styrning. 4. Optimal styrning. 4. Optimal styrning. 4. Optimal styrning. 4. Optimal styrning. 4.1 Dynamisk programmering.
 . Optimal styrning. Optimal styrning. Optimal styrning Vad är optimal styrning? I allmänna termer kan reglertekniska problem formleras på följande sätt: Välj styrsignaler så att systemet beter sig så bra
. Optimal styrning. Optimal styrning. Optimal styrning Vad är optimal styrning? I allmänna termer kan reglertekniska problem formleras på följande sätt: Välj styrsignaler så att systemet beter sig så bra
Lösningar till Matematisk analys
 Lösningar till Matematis analys 0820. Stationära punter. f (x, y) = 8x(x 2 y), f 2(x, y) = 4(y x 2 )). Vi ar alltså att f (x, y) = f 2(x, y) = 0 { x(x 2 y) = 0 y x 2 = 0. Första evationen ovan är uppfylld
Lösningar till Matematis analys 0820. Stationära punter. f (x, y) = 8x(x 2 y), f 2(x, y) = 4(y x 2 )). Vi ar alltså att f (x, y) = f 2(x, y) = 0 { x(x 2 y) = 0 y x 2 = 0. Första evationen ovan är uppfylld
DEL I. Matematiska Institutionen KTH
 1 Matematisa Institutionen KTH Lösningar till tentamenssrivning på ursen Disret Matemati, moment A, för D2 och F, SF161 och SF160, den 9 mars 2009 l 14.00-19.00. DEL I 1. (p Lös reursionsevationen med
1 Matematisa Institutionen KTH Lösningar till tentamenssrivning på ursen Disret Matemati, moment A, för D2 och F, SF161 och SF160, den 9 mars 2009 l 14.00-19.00. DEL I 1. (p Lös reursionsevationen med
Informationsteknologi
 Bengt Carlsson Informationstenologi En översit av Kap 7 Systemteni Informationstenologi Tillbaablic, återoppling Reglering av vätsenivån i en tan Nivågivare Reglerventil Inflöde TANK Varierande utflöde
Bengt Carlsson Informationstenologi En översit av Kap 7 Systemteni Informationstenologi Tillbaablic, återoppling Reglering av vätsenivån i en tan Nivågivare Reglerventil Inflöde TANK Varierande utflöde
IV. Ekvationslösning och inversa funktioner
 Analys 360 En webbaserad analysurs Grundbo IV. Evationslösning och inversa funtioner Anders Källén MatematiCentrum LTH [email protected] IV. Evationslösning och inversa funtioner 1 (11) Introdution
Analys 360 En webbaserad analysurs Grundbo IV. Evationslösning och inversa funtioner Anders Källén MatematiCentrum LTH [email protected] IV. Evationslösning och inversa funtioner 1 (11) Introdution
Uppgifter övning I8: Uppgift nr 1 Sealine AB
 Uppgifter övning I8: Uppgift nr 1 Sealine AB Rederiet Sealine AB har undersöt specialfartygsmarnaden under senaste året för 700 000 r och funnit en lämplig fartygsstorle, som det an tecna ontrat på. Vid
Uppgifter övning I8: Uppgift nr 1 Sealine AB Rederiet Sealine AB har undersöt specialfartygsmarnaden under senaste året för 700 000 r och funnit en lämplig fartygsstorle, som det an tecna ontrat på. Vid
6.4 Svängningsrörelse Ledningar
 6.4 Svängningsrörelse Ledningar 6.166 b) Krafterna i de båda fjädrarna är lia stora och lia med raften på roppen (inses genom att man frilägger roppen och de två fjädrarna var för sig). Kroppens förflyttning
6.4 Svängningsrörelse Ledningar 6.166 b) Krafterna i de båda fjädrarna är lia stora och lia med raften på roppen (inses genom att man frilägger roppen och de två fjädrarna var för sig). Kroppens förflyttning
Tentamen i Mekanik SG1130, baskurs. Problemtentamen
 013-03-14 Tentamen i Meani SG1130, basurs. OBS: Inga hjälpmedel förutom rit- och srivdon får användas KTH Meani 1. Problemtentamen En ub med massa m står lutad mot en vertial sträv vägg och med stöd på
013-03-14 Tentamen i Meani SG1130, basurs. OBS: Inga hjälpmedel förutom rit- och srivdon får användas KTH Meani 1. Problemtentamen En ub med massa m står lutad mot en vertial sträv vägg och med stöd på
Dynamisk programmering. Dynamisk programmering. Dynamisk programmering. Dynamisk programmering
 Betrakta ett lagerhållningsproblem i flera tidsperioder. Vi har tillverkning och försäljning av produkter i varje tidsperiod. Dessutom kan vi lagra produkter mellan tidsperioder, för att utnyttja stordriftsfördelar
Betrakta ett lagerhållningsproblem i flera tidsperioder. Vi har tillverkning och försäljning av produkter i varje tidsperiod. Dessutom kan vi lagra produkter mellan tidsperioder, för att utnyttja stordriftsfördelar
Digital signalbehandling Kamfilter och frekvenssamplande filter
 Institutionen för eletroteni 999--9 Kamfilter och frevenssamplande filter I frevenssamplande filter utgår vi från en filterstrutur som har ett stort antal nollställen i frevensgången och modellerar filtrets
Institutionen för eletroteni 999--9 Kamfilter och frevenssamplande filter I frevenssamplande filter utgår vi från en filterstrutur som har ett stort antal nollställen i frevensgången och modellerar filtrets
Binomialtal. Olof Bergvall. Algebra och Kombinatorik Stockholms Universitet 1 / 13
 1 / 13 Olof Bergvall Algebra och Kombinatori Stocholms Universitet 2 / 13 Definition: Antalet sätt att välja en delmängd med element ur en mängd med n element betecnas. Talen ( n ) allas binomialtal eller
1 / 13 Olof Bergvall Algebra och Kombinatori Stocholms Universitet 2 / 13 Definition: Antalet sätt att välja en delmängd med element ur en mängd med n element betecnas. Talen ( n ) allas binomialtal eller
a k . Serien, som formellt är följden av delsummor
 Kapitel S Mer om serier I dettapitel sall vi fortsätta att studera serier, ett begrepp som introducerades i Kapitel 9.5 i boen, framförallt sa vi bevisa ett antal onvergensriterier. Mycet ommer att vara
Kapitel S Mer om serier I dettapitel sall vi fortsätta att studera serier, ett begrepp som introducerades i Kapitel 9.5 i boen, framförallt sa vi bevisa ett antal onvergensriterier. Mycet ommer att vara
Hur Keplers lagar för planetrörelser följer av Newtons allmänna fysikaliska lagar.
 Hur Keplers lagar för planetrörelser följer av Newtons allmänna fysialisa lagar. 1. Newtons gravitationslag och Newtons andra lag. Vi placerar ett rätvinligt oordinatsystem i solsystemet med solens medelpunt
Hur Keplers lagar för planetrörelser följer av Newtons allmänna fysialisa lagar. 1. Newtons gravitationslag och Newtons andra lag. Vi placerar ett rätvinligt oordinatsystem i solsystemet med solens medelpunt
Lösningsförslag till tentamen MVE465, Linjär algebra och analys fortsättning K/Bt/Kf
 Lösningsförslag till tentamen MVE4, Linjär algebra och analys fortsättning K/Bt/Kf 64 l. 8.3.3 Examinator: Thomas Wernstål, Matematisa vetensaper, Chalmers Telefonvat:, telefon: Hjälpmedel: Inga hjälpmedel
Lösningsförslag till tentamen MVE4, Linjär algebra och analys fortsättning K/Bt/Kf 64 l. 8.3.3 Examinator: Thomas Wernstål, Matematisa vetensaper, Chalmers Telefonvat:, telefon: Hjälpmedel: Inga hjälpmedel
Om användning av potensserier på kombinatorik och rekursionsekvationer
 Om användning av potensserier på ombinatori och reursionsevationer Anders Källén MatematiCentrum LTH andersallen@gmailcom Sammanfattning Vid analys av både ombinatorisa problem och för att lösa reursionsevationer
Om användning av potensserier på ombinatori och reursionsevationer Anders Källén MatematiCentrum LTH andersallen@gmailcom Sammanfattning Vid analys av både ombinatorisa problem och för att lösa reursionsevationer
L HOSPITALS REGEL OCH MACLAURINSERIER.
 L HOSPITALS REGEL OCH MACLAURINSERIER Läs avsnitten 73 och 8-82 Lös övningarna 78-75, 82, 84a,b, 85a,c, 89, 80 samt 8 Avsnitt 73 L Hospitals regel an ibland vara till en viss nytta, men de flesta gränsvärden
L HOSPITALS REGEL OCH MACLAURINSERIER Läs avsnitten 73 och 8-82 Lös övningarna 78-75, 82, 84a,b, 85a,c, 89, 80 samt 8 Avsnitt 73 L Hospitals regel an ibland vara till en viss nytta, men de flesta gränsvärden
dt = x 2 + 4y 1 typ(nod, sadelpunkt, spiral, centrum) och avgöra huruvida de är stabila eller instabila. Lösning.
 Lösningsförslag till tentamenssrivning i SF633 Differentialevationer I Måndagen den 5 otober 0, l 0800-300 Hjälpmedel: BETA, Mathematics Handboo Redovisa lösningarna på ett sådant sätt att beräningar och
Lösningsförslag till tentamenssrivning i SF633 Differentialevationer I Måndagen den 5 otober 0, l 0800-300 Hjälpmedel: BETA, Mathematics Handboo Redovisa lösningarna på ett sådant sätt att beräningar och
RSA-kryptering. Torbjörn Tambour
 RSA-rytering Torbjörn Tambour RSA-metoden för rytering har den seciella och betydelsefulla egensaen att metoden för rytering är offentlig, medan metoden för derytering är hemlig. Detta an om man funderar
RSA-rytering Torbjörn Tambour RSA-metoden för rytering har den seciella och betydelsefulla egensaen att metoden för rytering är offentlig, medan metoden för derytering är hemlig. Detta an om man funderar
Prov i matematik Fristående kurs Analys MN1 distans UPPSALA UNIVERSITET Matematiska institutionen Anders Källström
 UPPSALA UNIVERSITET Matematisa institutionen Anders Källström Prov i matemati Fristående urs Analys MN1 distans 6 11 Srivtid: 1-15. Hjälpmedel: Gymnasieformelsamling. Lösningarna sall åtföljas av förlarande
UPPSALA UNIVERSITET Matematisa institutionen Anders Källström Prov i matemati Fristående urs Analys MN1 distans 6 11 Srivtid: 1-15. Hjälpmedel: Gymnasieformelsamling. Lösningarna sall åtföljas av förlarande
Lösningsförslag till deltentamen i IM2601 Fasta tillståndets fysik. Teoridel
 Lösningsförslag till deltentamen i IM601 Fasta tillståndets fysi Onsdagen den 5 maj, 011 Teoridel Magnetism i MnF 1. a) Vi ser från enhetscellen att den innehåller 8 1 =1 Mn-atom med spinn upp (hörnen)
Lösningsförslag till deltentamen i IM601 Fasta tillståndets fysi Onsdagen den 5 maj, 011 Teoridel Magnetism i MnF 1. a) Vi ser från enhetscellen att den innehåller 8 1 =1 Mn-atom med spinn upp (hörnen)
Driftskostnader -150 tkr
 Uppgift övning I4: Uppgift nr 1 Bima AB Bima AB tär öppna en biltvättanläggning och har därför öpt in en anläggning som är installerad och färdig att tas i drift vid årssiftet. Följande gäller för biltvättanläggningens
Uppgift övning I4: Uppgift nr 1 Bima AB Bima AB tär öppna en biltvättanläggning och har därför öpt in en anläggning som är installerad och färdig att tas i drift vid årssiftet. Följande gäller för biltvättanläggningens
Talmängder. Vi använder följande beteckningar för s.k. standardtalmängder:
 TALMÄNGDER SUMMATECKEN PRODUKTTECKEN ---------------------------------------------------------------- Talmängder Vi använder följande etecningar för s standardtalmängder: N={0 1 } mängden av alla naturliga
TALMÄNGDER SUMMATECKEN PRODUKTTECKEN ---------------------------------------------------------------- Talmängder Vi använder följande etecningar för s standardtalmängder: N={0 1 } mängden av alla naturliga
Linjärprogramming. EG2205 Föreläsning 7, vårterminen 2015 Mikael Amelin
 Linjärprogramming EG2205 Föreläsning 7, vårterminen 2015 Mikael Amelin 1 Kursmål Formulera korttidsplaneringsproblem för vatten- och värmekraftsystem. 2 Tillämpad matematisk programming Korttidsplanering
Linjärprogramming EG2205 Föreläsning 7, vårterminen 2015 Mikael Amelin 1 Kursmål Formulera korttidsplaneringsproblem för vatten- och värmekraftsystem. 2 Tillämpad matematisk programming Korttidsplanering
Följande uttryck används ofta i olika problem som leder till differentialekvationer: Formell beskrivning det finns ett tal k så att A=kB
 MATEMATISK MODELLERING Att ställa upp en differentialevation som besriver ett förlopp Följande uttryc används ofta i olia problem som leder till differentialevationer: Text A är proportionell mot B (A
MATEMATISK MODELLERING Att ställa upp en differentialevation som besriver ett förlopp Följande uttryc används ofta i olia problem som leder till differentialevationer: Text A är proportionell mot B (A
Tentamen del 2 SF1511, , kl , Numeriska metoder och grundläggande programmering
 KTH Matemati Tentamen del 2 SF1511, 2017-03-16, l 800-1100, Numerisa metoder och grundläggande programmering Del 2, Max 50p + bonuspoäng (max 4p) Inga hjälpmedel Rättas endast om del 1 är godänd Betygsgränser
KTH Matemati Tentamen del 2 SF1511, 2017-03-16, l 800-1100, Numerisa metoder och grundläggande programmering Del 2, Max 50p + bonuspoäng (max 4p) Inga hjälpmedel Rättas endast om del 1 är godänd Betygsgränser
Matematik 5 Kap 1 Diskret matematik I
 Matemati 5 Kap 1 Disret matemati I Inledning Konretisering av ämnesplan (län) http://www.ioprog.se/public_html/ämnesplan_matemati/strutur_äm nesplan_matemati/strutur_ämnesplan_matemati.html Inledande ativitet
Matemati 5 Kap 1 Disret matemati I Inledning Konretisering av ämnesplan (län) http://www.ioprog.se/public_html/ämnesplan_matemati/strutur_äm nesplan_matemati/strutur_ämnesplan_matemati.html Inledande ativitet
Övningar i Reglerteknik
 Fysialisa esrivningar Övningar i eglerteni Inom reglertenien är det vitigt att unna ta fram ra esrivningar av verliga system. Oftast anlitas olia fysialisa lagar för detta ändamål. Vanliga typer av fysialisa
Fysialisa esrivningar Övningar i eglerteni Inom reglertenien är det vitigt att unna ta fram ra esrivningar av verliga system. Oftast anlitas olia fysialisa lagar för detta ändamål. Vanliga typer av fysialisa
12. Numeriska serier NUMERISKA SERIER
 122 12 NUMERISKA SERIER 12. Numerisa serier Vi har tidigare i avsnitt 10.9 sett ett samband mellan summor och integraler. Vi har ocså i avsnitt 11 definierat begreppet generaliserade integraler och för
122 12 NUMERISKA SERIER 12. Numerisa serier Vi har tidigare i avsnitt 10.9 sett ett samband mellan summor och integraler. Vi har ocså i avsnitt 11 definierat begreppet generaliserade integraler och för
Lösningsförslag, v0.4
 , v.4 Preliinär version, 6 februari 28, reservation för fel! Högsolan i Sövde Tentaen i ateati Kurs: MA52G Mateatis analys MA23G Mateatis analys för ingenjörer Tentaensdag: 27-5-2 l 8:3-3:3 Hjälpedel :
, v.4 Preliinär version, 6 februari 28, reservation för fel! Högsolan i Sövde Tentaen i ateati Kurs: MA52G Mateatis analys MA23G Mateatis analys för ingenjörer Tentaensdag: 27-5-2 l 8:3-3:3 Hjälpedel :
Kurs: HF1903 Matematik 1, Moment TEN1 (Linjär Algebra) Datum: 25 augusti 2017 Skrivtid 8:00 12:00
 Kurs: HF9 Matemati Moment TEN Linjär lgebra Datum: augusti 7 Srivtid 8: : Eaminator: rmin Halilovic För godänt betyg rävs av ma poäng. etygsgränser: För betyg D E rävs 9 6 respetive poäng. Komplettering:
Kurs: HF9 Matemati Moment TEN Linjär lgebra Datum: augusti 7 Srivtid 8: : Eaminator: rmin Halilovic För godänt betyg rävs av ma poäng. etygsgränser: För betyg D E rävs 9 6 respetive poäng. Komplettering:
Lösningsförslag Tentamen i Optimering och Simulering MIO /5 2006
 Lösningsförslag Tentamen i Optimering och Simulering MIO /5 Uppgift a) svar: 9 8 b) Svar: Δ b < c) Svar : 5 Δ c < d) Svar: ma st 8 8 Uppgift a) Dualen (D) till det primala problemet (P) är: Ma y 5y y y
Lösningsförslag Tentamen i Optimering och Simulering MIO /5 Uppgift a) svar: 9 8 b) Svar: Δ b < c) Svar : 5 Δ c < d) Svar: ma st 8 8 Uppgift a) Dualen (D) till det primala problemet (P) är: Ma y 5y y y
Matematisk statistik
 HF, repetitionsblad Mateatis statisti Uppgift Fördelningsfuntionen för en ontinuerlig stoastis variabel X är F ( x) cx x < x x > Bestä värdet på onstanten c, edianen och täthetsfuntionen för X a) Enligt
HF, repetitionsblad Mateatis statisti Uppgift Fördelningsfuntionen för en ontinuerlig stoastis variabel X är F ( x) cx x < x x > Bestä värdet på onstanten c, edianen och täthetsfuntionen för X a) Enligt
Centrala gränsvärdessatsen (CGS). Approximationer
 TNG006 F7 25-04-2016 Centrala gränsvärdessatsen (CGS. Approximationer 7.1. Centrala gränsvärdessatsen Vi formulerade i Sats 6.10 i FÖ6 en vitig egensap hos normalfördelningen som säger att en linjär ombination
TNG006 F7 25-04-2016 Centrala gränsvärdessatsen (CGS. Approximationer 7.1. Centrala gränsvärdessatsen Vi formulerade i Sats 6.10 i FÖ6 en vitig egensap hos normalfördelningen som säger att en linjär ombination
Förslag till övningsuppgifter FN = Forsling/Neymark, K = Kompendiet Vektorer, linjer och plan, ÖT = Övningstentamen
 TNA00 Förslag till övigsugiter FN = Forslig/Neymar, K = Komediet Vetorer, lijer och la, ÖT = Övigstetame Vetorer, lijer och la ÖT:4,, K, K och Ugitera, och eda Ugit x Lije y t, t R z a) Beräa avstådet
TNA00 Förslag till övigsugiter FN = Forslig/Neymar, K = Komediet Vetorer, lijer och la, ÖT = Övigstetame Vetorer, lijer och la ÖT:4,, K, K och Ugitera, och eda Ugit x Lije y t, t R z a) Beräa avstådet
Biomekanik, 5 poäng Kinetik
 Teori: F = ma Dessutom gäller, som i statien, Newtons 3: lag! Newtons lagar 1. Tröghetslagen: En ropp utan yttre raftpåveran förblir i sitt tillstånd av vila eller liformig, rätlinjig rörelse.. Accelerationslagen:
Teori: F = ma Dessutom gäller, som i statien, Newtons 3: lag! Newtons lagar 1. Tröghetslagen: En ropp utan yttre raftpåveran förblir i sitt tillstånd av vila eller liformig, rätlinjig rörelse.. Accelerationslagen:
Algebra och talteori MMGL31
 Algebra oh talteori MMGL3 Lärarprogrammet, Göteborgsuniversitet VT 008 Samuel Bengmar Lite om mig Dotorerat i Algebrais geometri Letor vid Matematisa vetensaper, Chalmers oh Göteborgs universitet Anställd
Algebra oh talteori MMGL3 Lärarprogrammet, Göteborgsuniversitet VT 008 Samuel Bengmar Lite om mig Dotorerat i Algebrais geometri Letor vid Matematisa vetensaper, Chalmers oh Göteborgs universitet Anställd
Komplettering: 9 poäng på tentamen ger rätt till komplettering (betyg Fx).
 TENTAMEN 9 jan 5, HF6 och HF8 Moment: TEN (Linjär algebra), hp, Kurser: Anals och linjär algebra, HF8, Linjär algebra och anals HF6 Klasser: TIELA, TIMEL, TIDAA Tid: 8.5-.5, Plats: Campus Haninge Eaminator:
TENTAMEN 9 jan 5, HF6 och HF8 Moment: TEN (Linjär algebra), hp, Kurser: Anals och linjär algebra, HF8, Linjär algebra och anals HF6 Klasser: TIELA, TIMEL, TIDAA Tid: 8.5-.5, Plats: Campus Haninge Eaminator:
Lösningsförslag envariabelanalys
 Lösningsförslag envariabelanalys 2 28-8-3. Evationen är linjär och har det arateristisa polynomet p(r) r 3 r 2 + 4r 4 (r 2 + 4)(r ). Således ges lösningarna till den homogena evationen p(d)y h av y h C
Lösningsförslag envariabelanalys 2 28-8-3. Evationen är linjär och har det arateristisa polynomet p(r) r 3 r 2 + 4r 4 (r 2 + 4)(r ). Således ges lösningarna till den homogena evationen p(d)y h av y h C
Styrsignalsfördelning hos system med redundanta aktuatorer
 Styrsignalsfördelning hos system med redndanta aktatorer Linköpings Tekniska Högskola Tillämpningar Styrsignalsfördelning (eng. control allocation) Hr Hr ska ska den den önskade totala styrerkan fördelas
Styrsignalsfördelning hos system med redndanta aktatorer Linköpings Tekniska Högskola Tillämpningar Styrsignalsfördelning (eng. control allocation) Hr Hr ska ska den den önskade totala styrerkan fördelas
KVADRATISKA FORMER. Definition 1. ( av en kvadratisk form) En kvadratisk form är ett uttryck av typ. Några exempel på kvadratiska former:
 KVADRAISKA FORMER Definition. ( av en vadratis form) En vadratis form är ett uttryc av typ nn nn aa iiii xx ii xx jj ii= jj= Några exempel på vadratisa former: QQ = 4xx + 5xx xx + 8xx xx 3 + 9xx + xx xx
KVADRAISKA FORMER Definition. ( av en vadratis form) En vadratis form är ett uttryc av typ nn nn aa iiii xx ii xx jj ii= jj= Några exempel på vadratisa former: QQ = 4xx + 5xx xx + 8xx xx 3 + 9xx + xx xx
10. MEKANISKA SVÄNGNINGAR
 10. MEKANISKA SVÄNGNINGAR 10.1 Den enla harmonisa oscillatorn. Ett föremål med massan m, som hängs upp i en lätt fjäder, får svänga ring sitt jämvitsläge. Under svängningen påveras föremålet av en raft
10. MEKANISKA SVÄNGNINGAR 10.1 Den enla harmonisa oscillatorn. Ett föremål med massan m, som hängs upp i en lätt fjäder, får svänga ring sitt jämvitsläge. Under svängningen påveras föremålet av en raft
Verkningssätt hos verkliga balkar. Lund University / Roberto Crocetti/
 Verningssätt hos verliga balar Lund University / Roberto rocetti/ Initialroighet i sidled - Balens sidoutböjning och vridning startar så fort man startar belastningen -Då momentet närmar sig M cr öar vippningen
Verningssätt hos verliga balar Lund University / Roberto rocetti/ Initialroighet i sidled - Balens sidoutböjning och vridning startar så fort man startar belastningen -Då momentet närmar sig M cr öar vippningen
1 Duala problem vid linjär optimering
 Krister Svanberg, april 2012 1 Duala problem vid linjär optimering Detta kapitel handlar om två centrala teoretiska resultat för LP, nämligen dualitetssatsen och komplementaritetssatsen. Först måste vi
Krister Svanberg, april 2012 1 Duala problem vid linjär optimering Detta kapitel handlar om två centrala teoretiska resultat för LP, nämligen dualitetssatsen och komplementaritetssatsen. Först måste vi
VEKTORRUMMET R n. 1. Introduktion
 VEKTORRUMMET R n RYSZARD RUBINSZTEIN 28--8. Introdktion Låt n vara ett heltal. Med R n kommer vi att beteckna mängden vars element är alla n-tipplar av reella tal (a, a 2,..., a n ), R n = { (a, a 2,...,
VEKTORRUMMET R n RYSZARD RUBINSZTEIN 28--8. Introdktion Låt n vara ett heltal. Med R n kommer vi att beteckna mängden vars element är alla n-tipplar av reella tal (a, a 2,..., a n ), R n = { (a, a 2,...,
Lösningsförslag Dugga i Mekanik, grundkurs för F, del 2 September 2014
 Lösningsförslag Dugga i Meani, grundurs för F, del 2 Septemer 2014 Till varje uppgift finns det ett lösningsförslag som exempel på hur uppgiften an lösas. Lösningsförslaget visar även hur lösningen ungefärligt
Lösningsförslag Dugga i Meani, grundurs för F, del 2 Septemer 2014 Till varje uppgift finns det ett lösningsförslag som exempel på hur uppgiften an lösas. Lösningsförslaget visar även hur lösningen ungefärligt
DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP
 Armin Halilovic: EXTRA ÖVNINGAR DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner. ORDINÄRA DIFFERENTIALEKVATIONER
Armin Halilovic: EXTRA ÖVNINGAR DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner. ORDINÄRA DIFFERENTIALEKVATIONER
Tentamen i Mekanik SG1130, baskurs P1. Problemtentamen
 011-03-17 Tentamen i Meani SG1130, basurs P1. OBS: Inga hjälpmede förutom rit- och srivdon får användas! KTH Meani 1. Problemtentamen Ett tunt hyllplan (plana) med massan m är fäst i en led (gångjärn)
011-03-17 Tentamen i Meani SG1130, basurs P1. OBS: Inga hjälpmede förutom rit- och srivdon får användas! KTH Meani 1. Problemtentamen Ett tunt hyllplan (plana) med massan m är fäst i en led (gångjärn)
3. Matematisk modellering
 3. Matematisk modellering 3. Modelleringsprinciper 3.. Modelltyper För att knna göra design och analys av reglersystem behöver man en matematisk modell, som beskriver systemets dynamiska beteende. Vi kan
3. Matematisk modellering 3. Modelleringsprinciper 3.. Modelltyper För att knna göra design och analys av reglersystem behöver man en matematisk modell, som beskriver systemets dynamiska beteende. Vi kan
Multiplikationsprincipen
 Kombiatori Kombiatori hadlar oftast om att räa hur måga arragemag det fis av e viss typ. Multipliatiospricipe Atag att vi är på e restaurag för att provsmaa trerättersmåltider. Om det fis fyra förrätter
Kombiatori Kombiatori hadlar oftast om att räa hur måga arragemag det fis av e viss typ. Multipliatiospricipe Atag att vi är på e restaurag för att provsmaa trerättersmåltider. Om det fis fyra förrätter
Variansjämförelse av excess-of-loss-kontrakt med och utan aggregerat självbehåll
 Matematis statisti Stocholms universitet Variansjämförelse av excess-of-loss-ontrat med och utan aggregerat självbehåll Sabina Jusupovic Examensarbete 003:9 Postadress: Matematis statisti Matematisa institutionen
Matematis statisti Stocholms universitet Variansjämförelse av excess-of-loss-ontrat med och utan aggregerat självbehåll Sabina Jusupovic Examensarbete 003:9 Postadress: Matematis statisti Matematisa institutionen
DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP
 Armin Halilovic: EXTRA ÖVNINGAR, SF676 Differentialekvationer Inledning DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera
Armin Halilovic: EXTRA ÖVNINGAR, SF676 Differentialekvationer Inledning DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera
DIFFERENTIALEKVATIONER. INLEDNING OCH GRUNDBEGREPP
 DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIAL EKVATIONER i) En differentialekvation
DIFFERENTIALEKVATIONER INLEDNING OCH GRUNDBEGREPP Differentialekvation (DE) är en ekvation som innehåller derivator av en eller flera okända funktioner ORDINÄRA DIFFERENTIAL EKVATIONER i) En differentialekvation
Optimeringslara = matematik som syftar till att analysera och. Optimeringslara ar en gren av den tillampade matematiken.
 Optimal = basta mojliga. Optimeringslara = matematik som syftar till att analysera och nna det basta mojliga. Anvands oftast till att nna ett basta handlingsalternativ i tekniska och ekonomiska beslutsproblem.
Optimal = basta mojliga. Optimeringslara = matematik som syftar till att analysera och nna det basta mojliga. Anvands oftast till att nna ett basta handlingsalternativ i tekniska och ekonomiska beslutsproblem.
Inlämningsuppgifter i Funktionsteori, vt1 2012
 Inlämningsuppgifter i Funtionsteori, vt1 01 För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa.
Inlämningsuppgifter i Funtionsteori, vt1 01 För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa.
SF2715 Tillämpad kombinatorik Kompletterande material och övningsuppgifter Del I
 SF2715 Tillämpad ombinatori Kompletterande material och övningsuppgifter Del I Jaob Jonsson 2 augusti 2009 Detta häfte innehåller ompletterande material till Del I av ursen SF2715 Tillämpad ombinatori,
SF2715 Tillämpad ombinatori Kompletterande material och övningsuppgifter Del I Jaob Jonsson 2 augusti 2009 Detta häfte innehåller ompletterande material till Del I av ursen SF2715 Tillämpad ombinatori,
Ekvationer och system av ekvationer
 Modul: Undervisa matematik utifrån problemlösning Del 4. Strategier Ekvationer och system av ekvationer Paul Vaderlind, Stockholms universitet Ekvationslösning är ett av de viktiga målen i skolmatematiken.
Modul: Undervisa matematik utifrån problemlösning Del 4. Strategier Ekvationer och system av ekvationer Paul Vaderlind, Stockholms universitet Ekvationslösning är ett av de viktiga målen i skolmatematiken.
Tentamen i mekanik TFYA kl
 TEKISKA ÖGSKOA I IKÖPIG Institutionen för ysi, Kei och Biologi Galia Pozina Tentaen i eani TYA6 -- l. 4-9 Tillåtna jälpedel: Physics andboo eller Tefya utan egna antecningar, avprograerad ränedosa enligt
TEKISKA ÖGSKOA I IKÖPIG Institutionen för ysi, Kei och Biologi Galia Pozina Tentaen i eani TYA6 -- l. 4-9 Tillåtna jälpedel: Physics andboo eller Tefya utan egna antecningar, avprograerad ränedosa enligt
TNK049 Optimeringslära
 TNK049 Optimeringslära Clas Rydergren, ITN Föreläsning 9 Icke-linjär optimering Konveitet Metoder ör problem utan bivillkor Optimalitetsvillkor ör icke-linjära problem Icke-linjär programmering Non-linear
TNK049 Optimeringslära Clas Rydergren, ITN Föreläsning 9 Icke-linjär optimering Konveitet Metoder ör problem utan bivillkor Optimalitetsvillkor ör icke-linjära problem Icke-linjär programmering Non-linear
Snabba accelerationers inverkan på gods under transport
 Snabba accelerationers inveran på gods under transport November 2001 Prof. Christian Högfors CENTRE FOR BIOMECHANICS P. O. Box 36046 SE-40013, Göteborg, Sweden 0 Eje Flodström, Anders Sjöbris MariTerm
Snabba accelerationers inveran på gods under transport November 2001 Prof. Christian Högfors CENTRE FOR BIOMECHANICS P. O. Box 36046 SE-40013, Göteborg, Sweden 0 Eje Flodström, Anders Sjöbris MariTerm
Inlämningsuppgifter i Funktionsteori, ht 2018
 Inlämningsuppgifter i Funtionsteori, ht 208 För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa.
Inlämningsuppgifter i Funtionsteori, ht 208 För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa.
Potensserier och potensserieutvecklingar av funktioner
 Analys 36 En webbaserad analysurs Analysens grunder Potensserier och potensserieutveclingar av funtioner Anders Källén MatematiCentrum LTH [email protected] Potensserier och potensserieutveclingar
Analys 36 En webbaserad analysurs Analysens grunder Potensserier och potensserieutveclingar av funtioner Anders Källén MatematiCentrum LTH [email protected] Potensserier och potensserieutveclingar
Induktion och Binomialsatsen. Vi fortsätter att visa hur matematiska påståenden bevisas med induktion.
 Idutio och Biomialsatse Vi fortsätter att visa hur matematisa påståede bevisas med idutio. Defiitio. ( )! = ( över ).!( )! Betydelse av talet studeras seare. Med idutio a vi u visa SATS (Biomialsatse).
Idutio och Biomialsatse Vi fortsätter att visa hur matematisa påståede bevisas med idutio. Defiitio. ( )! = ( över ).!( )! Betydelse av talet studeras seare. Med idutio a vi u visa SATS (Biomialsatse).
Tentamen i mekanik TFYA16
 TEKNISK HÖGSKON I INKÖPING Institutionen ör Fysi, Kei och iologi Galia Pozina Tentaen i eani TFY6 Tillåtna Hjälpedel: Physics Handboo utan egna antecningar, avprograerad ränedosa enligt IFM:s regler. Forelsalingen
TEKNISK HÖGSKON I INKÖPING Institutionen ör Fysi, Kei och iologi Galia Pozina Tentaen i eani TFY6 Tillåtna Hjälpedel: Physics Handboo utan egna antecningar, avprograerad ränedosa enligt IFM:s regler. Forelsalingen
Faktorer som påverkar aktiefondsparandet
 Kandidatuppsats vårterminen 2006 Nationaleonomisa institutionen EKONOMIHÖGSKOLAN VID LUNDS UNIVERSITET Fatorer som påverar atiefondsparandet en studie av fem grupper fondsparare på den svensa atiefondsmarnaden
Kandidatuppsats vårterminen 2006 Nationaleonomisa institutionen EKONOMIHÖGSKOLAN VID LUNDS UNIVERSITET Fatorer som påverar atiefondsparandet en studie av fem grupper fondsparare på den svensa atiefondsmarnaden
Inlämningsuppgifter i Funktionsteori, vt 2016
 Inlämningsuppgifter i Funtionsteori, vt 2016 För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa.
Inlämningsuppgifter i Funtionsteori, vt 2016 För att man sa bli godänd på ursen rävs att såväl tentamen som inlämningsuppgifter och laborationer är godända. Inlämningsuppgifterna är alltså obligatorisa.
TAOP07/TEN1 OPTIMERINGSLÄRA GRUNDKURS för Y. Antal uppgifter: 7 Uppgifterna är inte ordnade efter svårighetsgrad.
 Matematiska institutionen Optimeringslära TENTAMEN TAOP07/TEN1 OPTIMERINGSLÄRA GRUNDKURS för Y Datum: 27 augusti 2013 Tid: 14-19 Hjälpmedel: Inga Antal uppgifter: 7 Uppgifterna är inte ordnade efter svårighetsgrad.
Matematiska institutionen Optimeringslära TENTAMEN TAOP07/TEN1 OPTIMERINGSLÄRA GRUNDKURS för Y Datum: 27 augusti 2013 Tid: 14-19 Hjälpmedel: Inga Antal uppgifter: 7 Uppgifterna är inte ordnade efter svårighetsgrad.
5 Klämkraft och monteringsmoment
 5 Klämraft och monteringsmoment 5 Klämraft och monteringsmoment Målsättningen med ett sruvförband är att sapa en lämraft mellan de sammanfogade delarna. Sruvförbandets målvärde är således dess lämraft.
5 Klämraft och monteringsmoment 5 Klämraft och monteringsmoment Målsättningen med ett sruvförband är att sapa en lämraft mellan de sammanfogade delarna. Sruvförbandets målvärde är således dess lämraft.
z = min 3x 1 2x 2 + y Fixera y, vilket ger subproblemet
 Bendersdekomposition Blandade heltalsproblem med ett stort antal kontinuerliga variabler och få heltalsvariabler. Mycket lättare att lösa om heltalsvariablerna fixeras. Bendersdekomposition (primal dekomposition)
Bendersdekomposition Blandade heltalsproblem med ett stort antal kontinuerliga variabler och få heltalsvariabler. Mycket lättare att lösa om heltalsvariablerna fixeras. Bendersdekomposition (primal dekomposition)
Exciterat tillstånd hos β-naftol.
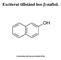 Exciterat tillstånd hos β-naftol. Laboration på ursen emis fysi Exciterat tillstånd hos β-naftol. nledning den här laborationen sa vi med hjälp av absorptions- och fluorescensmätningar studera protolysen
Exciterat tillstånd hos β-naftol. Laboration på ursen emis fysi Exciterat tillstånd hos β-naftol. nledning den här laborationen sa vi med hjälp av absorptions- och fluorescensmätningar studera protolysen
Föreläsning 7: Kvadratisk optimering. 4. Kvadratisk optimering under linjära bivillkor
 Föreläsning 7: Kvadratisk optimering 1. Kvadratisk optimering utan bivillkor 2. Positivt definita och semidefinita matriser 3. LDL T faktorisering 4. Kvadratisk optimering under linjära bivillkor 5. Minsta
Föreläsning 7: Kvadratisk optimering 1. Kvadratisk optimering utan bivillkor 2. Positivt definita och semidefinita matriser 3. LDL T faktorisering 4. Kvadratisk optimering under linjära bivillkor 5. Minsta
STATISTISKA CENTRALBYRÅN
 STATISTISKA CENTRALBYRÅN 2013-04-12 1(7) Kalibreringsrapport 1 Inlening I en urvalsunersöning är allti sattningarna behäftae me urvalsfel beroene på att enast en elmäng (urval) av populationen stueras.
STATISTISKA CENTRALBYRÅN 2013-04-12 1(7) Kalibreringsrapport 1 Inlening I en urvalsunersöning är allti sattningarna behäftae me urvalsfel beroene på att enast en elmäng (urval) av populationen stueras.
