Andra föreläsningen kapitel 7. Patrik Lundström
|
|
|
- Joakim Engström
- för 8 år sedan
- Visningar:
Transkript
1 Andra föreläsningen kapitel 7 Patrik Lundström
2 Kvantisering i klassisk fysik: Uppkomst av heltalskvanttal För att en stående våg i en ring inte ska släcka ut sig själv krävs att den är tillbaka som den började efter ett helt varv. Ett annat sätt att beskriva detta är att säga att det krävs ett helt antal våglängder får plats på ringens omkrets. Vågfunktionen måste därför innehålla kvanttal som är heltal.
3 Kvantisering i klassisk fysik: Uppkomst av halvtalskvanttal För att en linjär stående våg (t.ex. en svängande gitarrsträng) inte ska släcka ut sig själv krävs att den har värdet noll i början och slutet på strängen. Ett annat sätt att beskriva detta är att säga att det krävs en multipel av halva antal våglängder får plats på strängen. Vågfunktionen måste därför innehålla kvanttal som är hel- eller halvtal.
4 Två namn ni bör känna till Erwin Schrödinger: Mest känd för Schrödingerekvationen som bland annat kan användas för att beräkna elektroners energier i godtyckliga atomer. Werner Heisenberg: Mest känd för sin osäkerhetsrelation.
5 Schrödingerekvationen En ekvation som utgående de Broglies hypotes beskriver materievågor, till exempel för elektroner som är bundna till atomkärnor. Schrödingerekvationen kan skrivas: H ψ n = E n ψ n Hamiltonoperatorn Elektronens energi I ord säger ekvationen: Om vi verkar på vågfunktionen med Hamiltonoperatorn får vi tillbaka samma vågfunktion multiplicerad med elektronens energi Vågfunktionen
6 Mer om Schrödingerekvationen Hamiltonoperatorn är exempel på en operator, ett annat ord för matematisk instruktion. Hamiltonoperatorn är den operator som beskriver energi och dess utseende är ungefär: derivera två gånger (för att få den kinetiska energin) och addera den potentiella energin. Det exakta utseendet är beroende av vilket system som studeras. Schrödingerekvationen är ett exempel på ett egenvärdesproblem.
7 Schrödingerekvationens lösningar När Schrödingerekvationen löses erhålls 1) Elektronens energi (E n ) 2) Vågfunktionen (ψ n ) Normalt finns flera lösningar, det vill säga elektronen tillåts ha olika energier där varje energi är associerad med en viss vågfunktion.
8 Styrkor och svagheter med Schrödingerekvationen + Duplicerar Bohrs resultat för väteatomen ooch förser dem med ytterligare detaljer + Fungerar bra för atomer med godtyckligt antal elektroner - Kan vara mycket svår att lösa och ofta omöjlig att lösa exakt
9 Vad betyder vågfunktionen??? Schrödingers första tolkning var att den beskrev att elektronen inte var en partikel utan var utsmetad som vågen. Den tolkningen var inte användbar. En bättre tolkning kom något år senare av Max Born och som är den som gäller än idag är att kvadraten på vågfunktionen beskriver sannolikheten att hitta elektronen på ett visst ställe. (Anledningen att det är kvadraten på vågfunktionen och inte vågfunktionen själv som ska användas är att en vågfunktion kan vara negativ, vilket inte sannolikheter kan vara.)
10 Borns tolkning av vågfunktion Det betyder att den relativa sannolikheten att hitta elektronen på platserna x 1, y 1, z 1 och x 2, y 2, z 2 ges av ψ x 1, y 1, z 1 2 ψ x 2, y 2, z 2 2 = N 1 N 2 Det går också att beräkna sannolikheten att elektronen ska befinna sig i området mellan x 1, y 1, z 1 och x 2, y 2, z 2 som ψ x 1, y 1, z 1 2 dd x 2,y 2,z 2 x 1,y 1,z 1
11 Exempel: Antag att en vågfunktion kan skrivas ψ x = A x 1 x, 0 x 1. Beräkna relativa sannolikheten att finna elektronen i punkterna x=0.2 och x=0.5! Lösning: ψ = A = A 2 ψ = A = A 2 Relativa sannolikheten blir därför / =
12 Varför pratar vi om sannolikheter??? Heisenbergs osäkerhetsrelation Det går aldrig att samtidigt säga exakt var en partikel befinner sig och hur snabbt den färdas. Relationen mellan hur mycket osäkerhet det är i de två storheterna ges av Heisenbergs osäkerhetsrelation Δx Δ mm = h 4π där Δx är osäkerheten i position och Δ mm är osäkerheten i produkten av dess massa och hastighet (rörelsemängd). Detta är ett mycket viktigt resultat och är essensen av skillnaden mellan klassisk mekanik och kvantmekanik.
13 Begreppet orbital En orbital är en beteckning för det område där det är 90% sannolikhet att hitta en elektron som beskrivs av en viss vågfunktion. Olika orbitaler har olika utbredning och olika form (mer om det senare).
14 Egenskaper hos lösningarna till Schrödingerekvationen När Schrödingerekvationen löses får inte bara ett utan tre kvanttal. De är Huvudkvanttalet (energikvanttalet) som beskriver energin. Bikvanttalet (rörelsemängdsmomentskvanttalet). Magnetiska kvanttalet
15 Huvudkvanttalet Huvudkvanttalet (energikvanttalet) som beskriver energin. För väteatomen är det endast huvudkvanttalet som avgör energin. Detta kvanttal betecknas n och kan anta heltalsvärdena n = 1,2,3,4 När kvanttalet ökar, ökar elektronens energi. Elektroner som har ett visst huvudkvanttal sägs ibland tillhöra ett visst atomskal. Ibland ges atomskalen beteckningarna K, L, M, N
16 Bikvanttalet Bikvanttalet (rörelsemängdsmomentskvanttalet). Detta kvanttal har också heltalsvärden men de kan inte variera fritt utan de tillåtna värdena beror på kvanttalet n. De tillåtna värdena är l = 0,1,2, (n 1). Bikvanttalet avgör formen på orbitalerna.
17 Bikvanttalet Det är vanligt att ge bikvanttalet bokstavsbeteckningar i stället för siffror enligt l Beteckning 0 s 1 p 2 d 3 f 4 g
18 Det magnetiska kvanttalet Magnetiska kvanttalet som kan anta heltalsvärden. Kvanttalet betecknas m l och de tillåtna värdena beror på kvanttalet l och beroendet är m l = l, l + 1,, l 1, l. Kvanttalet avgör hur orbitalerna är orienterade. Det avgör också hur energin påverkas vid interaktion med magnetfält.
19 Exempel: Vilka bikvanttal är tillåtna för en elektron som har huvudkvanttalet a) n=1? b) n=3? Vilka magnetiska kvanttal är tillåtna för en elektron med huvudkvanttalet a) n=1? b) n=3?
20 Vågfunktionens egenskaper De flesta typer av orbitaler har områden där det är exakt noll sannolikhet att finna elektronen. Sådana områden kallas noder. Notera dock att elektronen kan röra sig mellan områden som separeras av noder. Nod
21 Vågfunktionens egenskaper: s-orbitaler En orbitals form och riktning beror av kvanttalen n, l och m l. Orbitaler med l = 0 (och därför med nödvändighet m l = 0), s-orbitaler, är lättast att beskriva eftersom de ser likadana ut i alla riktningar. Endast radien från origo som avgör elektrontätheten Eftersom l = 0 för finns bara en 1s, en 2s etc. orbital. s-orbitaler i olika skal skiljer sig genom att de har olika många noder.
22 Vågfunktionens egenskaper: p-orbitaler För n=2 finns en s-orbital och 3 p-orbitaler (l = 1 m l = -1, 0, 1) För väteatomen har alla orbitaler med ett givet värde på n samma energi. Vi säger att de är degenererade. Däremot har de inte samma form. Det finns en 2s orbital och tre 2p orbitaler, nämligen 2p x, 2p y och 2p z.
23 s- och p-orbitaler p z orbital där elektrontätheten är färgkodad p-orbitaler där endast gränsytan för 90% sannolikhet är indikerad
24 d-orbitaler
25 Vågfunktioner vs. orbitaler Väteatomens fem vågfunktioner med lägst energi: Röda områden har positiva värden på vågfunktionen och blå områden har negativa värden. Varför kan inte vågfunktionen själv användas som ett mått på sannolikheten att finna elektronen i ett visst område?
26 Kvantmekanisk beskrivning av väteatomen 1. Elektronen beskrivs som en stående våg. Dess beteende ges av lösningarna till Schrödingerekvationen som avgör tillåtna energier och orbitaler. 2. Modellen gör inte anspråk på att kunna säga exakt var elektronen befinner sig, och Heisenbergs osäkerhetsprincip visar faktiskt att det är fundamentalt omöjligt. I stället utgör kvadraten på vågfunktionen ett relativt mått på sannolikheten att finna elektronen på en viss plats. 3. Storleken på en orbital definieras som den yta inom vilket det är 90% chans att finna elektronen. 4. Väteatomen har många tillåtna orbitaler. I sitt grundtillstånd ockuperas orbitalen 1s. Elektronen kan exciteras till orbitaler med högre energi om energi tillförs.
27 Ett fjärde kvanttal: spinn Klassisk beskrivning av spinn: En elektron roterar inte bara runt atomkärnan utan även runt sin egen axel. Rotationen runt egna axeln beskrivs av kvanttalet m s som kan vara +½ (elektronen spinner åt ena hållet) eller -½ (elektronen spinner åt andra hållet). Obs!! Denna beskrivning stämmer illa med verkligheten på många punkter men kan trots det användas för att hjälpa till att tänka sig hur spinn fungerar.
28 Ett fjärde kvanttal: spinn Den klassiska förklaringen till att en elektron som spinner får magnetiska egenskaper som beror på vilket håll den spinner åt och orsaken till uppkomsten till begreppet spinn. Det kan inte nog understrykas att den här bilden är stämmer illa med verkligheten. Begreppet spinn har dock levt kvar.
29 Pauliprincipen Två elektroner i en given atom kan inte ha samtliga fyra kvanttal, n, l, m l och m s likadana. Alternativ formulering: Det bara kan finnas två elektroner i samma orbital.
30 Atomer med fler än en elektron Interaktioner som behöver beskrivas i Schrödingerekvationen för en atom med två elektroner: 1. Interaktionen mellan elektron 1och kärnan 2. Interaktionen mellan elektron 2 och kärnan 3. Interaktionen mellan elektron 1 och elektron 2 4. och förstås elektronernas rörelseenergi
31 Svårigheten med att flerelektronatomer Hur ska vi kunna beskriva interaktionen mellan två elektroner om vi inte vet exakt var de befinner sig på Heisenbergs osäkerhetsprincip? Problemet kallas elektronkorrelationsproblemet och innebär att vi inte lösa Schrödingerekvationen exakt utan måste göra approximationer. En sådan approximation är att en elektron rör sig i ett laddningsfält som är summan av kärnans attraktion och medelvärdet av de andra elektronernas repulsion.
32 Skärmning Totala attraktionen till kärnan minskas genom närvaro av andra elektroner. Det får till följd att en given elektron binds svagare till kärnan än om elektronen varit ensam. Fenomenet kallas skärmning.
33 Schrödingerekvationens lösningar för flerelektronatomer Eftersom approximationer gjorts lösningarna också approximationer Dock: Lösningarna är mycket lika de för väteatomen Således: 1s, 2s, 2p, 3s, 3p, 3d orbitaler även i detta fall
34 Viktig skillnad mot väteatomen För flerelektronatomer har INTE elektroner i s, p, d orbitaler i samma atomskal (samma huvudkvanttal) samma energi. (mer om detta i morgon)
35 En förklaring till olika energier för s-, p-, och d- orbitaler i atomer med flera elektroner Det är större att sannolikhet att hitta en 2s elektron nära kärnan än en 2p elektron. Samma resonemang gäller för andra orbitaler.
Väteatomen. Matti Hotokka
 Väteatomen Matti Hotokka Väteatomen Atom nummer 1 i det periodiska systemet Därför har den En proton En elektron Isotoper är möjliga Protium har en proton i atomkärnan Deuterium har en proton och en neutron
Väteatomen Matti Hotokka Väteatomen Atom nummer 1 i det periodiska systemet Därför har den En proton En elektron Isotoper är möjliga Protium har en proton i atomkärnan Deuterium har en proton och en neutron
KEMA00. Magnus Ullner. Föreläsningsanteckningar och säkerhetskompendium kan laddas ner från
 KEMA00 Magnus Ullner Föreläsningsanteckningar och säkerhetskompendium kan laddas ner från http://www.kemi.lu.se/utbildning/grund/kema00/dold Användarnamn: Kema00 Lösenord: DeltaH0 F2 Periodiska systemet
KEMA00 Magnus Ullner Föreläsningsanteckningar och säkerhetskompendium kan laddas ner från http://www.kemi.lu.se/utbildning/grund/kema00/dold Användarnamn: Kema00 Lösenord: DeltaH0 F2 Periodiska systemet
Kapitel 7. Atomstruktur och periodicitet. Kvantmekanik Aufbau Periodiska systemet
 Avsnitt 7.1 Elektromagnetisk strålning Kapitel 7 Fyrverkeri i olika färger Atomstruktur och periodicitet Copyright Cengage Learning. All rights reserved 2 Illuminerad saltgurka Kapitel 7 Innehåll Kvantmekanik
Avsnitt 7.1 Elektromagnetisk strålning Kapitel 7 Fyrverkeri i olika färger Atomstruktur och periodicitet Copyright Cengage Learning. All rights reserved 2 Illuminerad saltgurka Kapitel 7 Innehåll Kvantmekanik
Kapitel 7. Atomstruktur och periodicitet
 Kapitel 7 Atomstruktur och periodicitet Avsnitt 7.1 Elektromagnetisk strålning Fyrverkeri i olika färger Copyright Cengage Learning. All rights reserved 2 Avsnitt 7.2 Materians karaktär Illuminerad saltgurka
Kapitel 7 Atomstruktur och periodicitet Avsnitt 7.1 Elektromagnetisk strålning Fyrverkeri i olika färger Copyright Cengage Learning. All rights reserved 2 Avsnitt 7.2 Materians karaktär Illuminerad saltgurka
Utveckling mot vågbeskrivning av elektroner. En orientering
 Utveckling mot vågbeskrivning av elektroner En orientering Nikodemus Karlsson Februari 00 . Bohrs Postulat Niels Bohr (885-96) ställde utifrån iakttagelser upp fyra postulat gällande väteatomen ¹:. Elektronen
Utveckling mot vågbeskrivning av elektroner En orientering Nikodemus Karlsson Februari 00 . Bohrs Postulat Niels Bohr (885-96) ställde utifrån iakttagelser upp fyra postulat gällande väteatomen ¹:. Elektronen
Kapitel 7. Atomstruktur och periodicitet. Kvantmekanik Aufbau Periodiska systemet
 Kapitel 7 Innehåll Kapitel 7 Atomstruktur och periodicitet Kvantmekanik Aufbau Periodiska systemet Copyright Cengage Learning. All rights reserved 2 Kapitel 7 Innehåll 7.1 Elektromagnetisk strålning 7.2
Kapitel 7 Innehåll Kapitel 7 Atomstruktur och periodicitet Kvantmekanik Aufbau Periodiska systemet Copyright Cengage Learning. All rights reserved 2 Kapitel 7 Innehåll 7.1 Elektromagnetisk strålning 7.2
4-1 Hur lyder Schrödingerekvationen för en partikel som rör sig i det tredimensionella
 KVANTMEKANIKFRÅGOR Griffiths, Kapitel 4-6 Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths.
KVANTMEKANIKFRÅGOR Griffiths, Kapitel 4-6 Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths.
1.5 Våg partikeldualism
 1.5 Våg partikeldualism 1.5.1 Elektromagnetisk strålning Ljus uppvisar vågegenskaper. Det är bland annat möjligt att åstadkomma interferensmönster med ljus det visades av Young redan 1803. Interferens
1.5 Våg partikeldualism 1.5.1 Elektromagnetisk strålning Ljus uppvisar vågegenskaper. Det är bland annat möjligt att åstadkomma interferensmönster med ljus det visades av Young redan 1803. Interferens
c = λ ν Vågrörelse Kap. 1. Kvantmekanik och den mikroskopiska världen Kvantmekanik 1.1 Elektromagnetisk strålning
 Kap. 1. Kvantmekanik och den mikroskopiska världen Modern teori för atomer/molekyler kan förklara atomers/molekylers egenskaper: Kvantmekanik I detta och nästa kapitel: atomers egenskaper och periodiska
Kap. 1. Kvantmekanik och den mikroskopiska världen Modern teori för atomer/molekyler kan förklara atomers/molekylers egenskaper: Kvantmekanik I detta och nästa kapitel: atomers egenskaper och periodiska
Instuderingsfrågor, Griffiths kapitel 4 7
 Joakim Edsjö 15 oktober 2007 Fysikum, Stockholms Universitet Tel.: 08-55 37 87 26 E-post: edsjo@physto.se Instuderingsfrågor, Griffiths kapitel 4 7 Teoretisk Kvantmekanik II HT 2007 Tanken med dessa frågor
Joakim Edsjö 15 oktober 2007 Fysikum, Stockholms Universitet Tel.: 08-55 37 87 26 E-post: edsjo@physto.se Instuderingsfrågor, Griffiths kapitel 4 7 Teoretisk Kvantmekanik II HT 2007 Tanken med dessa frågor
F3: Schrödingers ekvationer
 F3: Schrödingers ekvationer Backgrund Vi behöver en ny matematik för att beskriva elektroner, atomer och molekyler! Den nya fysiken skall klara av att beskriva: Experiment visar att för bundna system så
F3: Schrödingers ekvationer Backgrund Vi behöver en ny matematik för att beskriva elektroner, atomer och molekyler! Den nya fysiken skall klara av att beskriva: Experiment visar att för bundna system så
Kvantmekanik. Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen (och i den makroskopiska!) Kvantmekanik.
 Kap. 7. Kvantmekanik: introduktion 7A.1- I begynnelsen Kvantmekanik Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen och i den makroskopiska! Kvantmekanik Klassisk fysik Specialfall!
Kap. 7. Kvantmekanik: introduktion 7A.1- I begynnelsen Kvantmekanik Kvantmekaniken: De naturlagar som styr förlopp i den mikroskopiska världen och i den makroskopiska! Kvantmekanik Klassisk fysik Specialfall!
Kvantmekanik. Kapitel Natalie Segercrantz
 Kvantmekanik Kapitel 38-39 Natalie Segercrantz Centrala begrepp Schrödinger ekvationen i en dimension Fotoelektriska effekten De Broglie: partikel-våg dualismen W 0 beror av materialet i katoden minimifrekvens!
Kvantmekanik Kapitel 38-39 Natalie Segercrantz Centrala begrepp Schrödinger ekvationen i en dimension Fotoelektriska effekten De Broglie: partikel-våg dualismen W 0 beror av materialet i katoden minimifrekvens!
Milstolpar i tidig kvantmekanik
 Den klassiska mekanikens begränsningar Speciell relativitetsteori Höga hastigheter Klassisk mekanik Kvantmekanik Små massor Små energier Stark gravitation Allmän relativitetsteori Milstolpar i tidig kvantmekanik
Den klassiska mekanikens begränsningar Speciell relativitetsteori Höga hastigheter Klassisk mekanik Kvantmekanik Små massor Små energier Stark gravitation Allmän relativitetsteori Milstolpar i tidig kvantmekanik
Dugga i FUF040 Kvantfysik för F3/Kf3
 Dugga i FUF040 Kvantfysik för F3/Kf3 fredagen den 23 oktober 2015 kl 14.00-16.00 i V Examinator: Måns Henningson, ankn 3245. Inga hjälpmedel. Ringa in bokstaven svarande mot det unika rätta svaret på svarsblanketten!
Dugga i FUF040 Kvantfysik för F3/Kf3 fredagen den 23 oktober 2015 kl 14.00-16.00 i V Examinator: Måns Henningson, ankn 3245. Inga hjälpmedel. Ringa in bokstaven svarande mot det unika rätta svaret på svarsblanketten!
Fysik TFYA86. Föreläsning 11/11
 Fysik TFYA86 Föreläsning 11/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 40-42* (*) 40.1-4 (översikt) 41.6 (uteslutningsprincipen) 42.1, 3, 4, 6, 7 koncept enklare uppgifter Översikt
Fysik TFYA86 Föreläsning 11/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 40-42* (*) 40.1-4 (översikt) 41.6 (uteslutningsprincipen) 42.1, 3, 4, 6, 7 koncept enklare uppgifter Översikt
Atom- och kärnfysik med tillämpningar -
 Atom- och kärnfysik med tillämpningar - Föreläsning 8 Gillis Carlsson gillis.carlsson@matfys.lth.se 19 Oktober, 2012 Föreläsningarna i kvantmekanik LP1 V1: Repetition av kvant-nano kursen. Sid 5-84 V2:
Atom- och kärnfysik med tillämpningar - Föreläsning 8 Gillis Carlsson gillis.carlsson@matfys.lth.se 19 Oktober, 2012 Föreläsningarna i kvantmekanik LP1 V1: Repetition av kvant-nano kursen. Sid 5-84 V2:
BFL122/BFL111 Fysik för Tekniskt/ Naturvetenskapligt Basår/ Bastermin Föreläsning 7 Kvantfysik, Atom-, Molekyl- och Fasta Tillståndets Fysik
 Föreläsning 7 Kvantfysik 2 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det
Föreläsning 7 Kvantfysik 2 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det
Fysik TFYA86. Föreläsning 10/11
 Fysik TFYA86 Föreläsning 10/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 38-41* (*) 38.1, 38.4, 39.1-3, 6 40.1-4 (översikt) koncept enklare uppgifter Översikt och breddningskurs!
Fysik TFYA86 Föreläsning 10/11 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 38-41* (*) 38.1, 38.4, 39.1-3, 6 40.1-4 (översikt) koncept enklare uppgifter Översikt och breddningskurs!
Kvantmekanik - Gillis Carlsson
 Kvantmekanik - Föreläsning 1 Gillis Carlsson gillis.carlsson@matfys.lth.se LP2 Föreläsningarna i kvantmekanik LP1 V1): Repetition av kvant-nano kursen. Sid 5-84 V2 : V3 : Formalism (I). Sid 109-124, 128-131,
Kvantmekanik - Föreläsning 1 Gillis Carlsson gillis.carlsson@matfys.lth.se LP2 Föreläsningarna i kvantmekanik LP1 V1): Repetition av kvant-nano kursen. Sid 5-84 V2 : V3 : Formalism (I). Sid 109-124, 128-131,
Atom- och kärnfysik med tillämpningar -
 Atom- och kärnfysik med tillämpningar - Föreläsning 6 Gillis Carlsson gillis.carlsson@matfys.lth.se 10 Oktober, 2013 Föreläsningarna i kvantmekanik LP1 V1 : Repetition av kvant-nano kursen. Sid 5-84 V2
Atom- och kärnfysik med tillämpningar - Föreläsning 6 Gillis Carlsson gillis.carlsson@matfys.lth.se 10 Oktober, 2013 Föreläsningarna i kvantmekanik LP1 V1 : Repetition av kvant-nano kursen. Sid 5-84 V2
1-1 Hur lyder den tidsberoende Schrödingerekvationen för en partikel som rör sig längs x-axeln? Definiera ingående storheter!
 KVANTMEKANIKFRÅGOR, GRIFFITHS Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths. 1 Kapitel
KVANTMEKANIKFRÅGOR, GRIFFITHS Tanken med dessa frågor är att de ska belysa de centrala delarna av kursen och tjäna som kunskapskontroll och repetition. Kapitelreferenserna är till Griffiths. 1 Kapitel
Fysik TFYA68. Föreläsning 11/14
 Fysik TFYA68 Föreläsning 11/14 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 38-39* (*) 38.1, 38.4, 39.1-3, 6 koncept enklare uppgifter Översikt och breddningskurs! 2 Introduktion Kvantmekanik
Fysik TFYA68 Föreläsning 11/14 1 Kvantmekanik och Materialuppbyggnad University Physics: Kapitel 38-39* (*) 38.1, 38.4, 39.1-3, 6 koncept enklare uppgifter Översikt och breddningskurs! 2 Introduktion Kvantmekanik
Kapitel 4. Materievågor
 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Kapitel 4. Materievågor 1 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Överblick Överblick Kring 1925 började många viktiga kvantkoncept ha sett
Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Kapitel 4. Materievågor 1 Kvantfysikens grunder, 2017 Kapitel 4. Materievågor Överblick Överblick Kring 1925 började många viktiga kvantkoncept ha sett
2.4. Bohrs modell för väteatomen
 2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
Kommer sig osäkerheten av att vår beskrivning av naturen är ofullständig, eller av att den fysiska verkligheten är genuint obestämd?
 Inte mycket verkar säkert här...? Våg-partikeldualitet Ett system kan ha både vågoch partikelegenskaper i samma experiment. Vågfunktionen har en sannolikhetstolkning. Heisenbergs osäkerhetsrelation begränsar
Inte mycket verkar säkert här...? Våg-partikeldualitet Ett system kan ha både vågoch partikelegenskaper i samma experiment. Vågfunktionen har en sannolikhetstolkning. Heisenbergs osäkerhetsrelation begränsar
Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. 0 x < 0
 LÖSNINGAR TILL Deltentamen i kvantformalism, atom och kärnfysik med tillämpningar för F3 9-1-15 Tid: kl 8.-1. (MA9A. Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. Poäng: Vid varje uppgift
LÖSNINGAR TILL Deltentamen i kvantformalism, atom och kärnfysik med tillämpningar för F3 9-1-15 Tid: kl 8.-1. (MA9A. Hjälpmedel: Det för kursen ociella formelbladet samt TeFyMa. Poäng: Vid varje uppgift
Mendelevs periodiska system
 Mendelevs periodiska system Notera luckorna som betecknar element som var okända vid den tiden. Med hjälp av systement lyckades Mendelev förutsäga dessa grundämnens egenskaper. Vårt nuvarande periodiska
Mendelevs periodiska system Notera luckorna som betecknar element som var okända vid den tiden. Med hjälp av systement lyckades Mendelev förutsäga dessa grundämnens egenskaper. Vårt nuvarande periodiska
Tentamen. TFYA35 Molekylfysik, TEN1 24 oktober 2016 kl Skrivsal: G34, G36, G37
 Thomas Ederth IFM / Molekylär Fysik ted@ifm.liu.se Tentamen TFYA35 Molekylfysik, TEN1 24 oktober 216 kl. 8.-13. Skrivsal: G34, G36, G37 Tentamen omfattar 6 problem som vardera kan ge 4 poäng. För godkänt
Thomas Ederth IFM / Molekylär Fysik ted@ifm.liu.se Tentamen TFYA35 Molekylfysik, TEN1 24 oktober 216 kl. 8.-13. Skrivsal: G34, G36, G37 Tentamen omfattar 6 problem som vardera kan ge 4 poäng. För godkänt
1.7. Tolkning av våg partikeldualiteten
 1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.11] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.11] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
Kemi Grundläggande begrepp. Kap. 1. (Se även repetitionskompendiet på hemsidan.)
 Föreläsning 1. Kemins indelning Enheter Atomer, isotoper och joner Grundämnen och periodiska systemet Atomernas elektronstruktur och atomorbitaler Periodiska egenskaper Kemi Grundläggande begrepp. Kap.
Föreläsning 1. Kemins indelning Enheter Atomer, isotoper och joner Grundämnen och periodiska systemet Atomernas elektronstruktur och atomorbitaler Periodiska egenskaper Kemi Grundläggande begrepp. Kap.
2.4. Bohrs modell för väteatomen
 2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
2.4. Bohrs modell för väteatomen [Understanding Physics: 19.4-19.7] Som vi sett, är den totala energin för elektronen i väteatomen E = 1 2 mv2 = e2 8πɛ 0 r. Eftersom L = mvr för cirkulära banor, så kan
1. INLEDNING 2. TEORI. Arbete A4 Ab initio
 Arbete A4 Ab initio 1. INLEDNING Med Ab inition-metoder kan man, utgående från kvantmekanikens grundlagar, beräkna egenskaper som t.ex. elektronisk energi, jämviktskonformation eller dipolmoment för atomära
Arbete A4 Ab initio 1. INLEDNING Med Ab inition-metoder kan man, utgående från kvantmekanikens grundlagar, beräkna egenskaper som t.ex. elektronisk energi, jämviktskonformation eller dipolmoment för atomära
Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25.
 GÖTEBORGS UNIVERSITET Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25 Delkurs 4 KVANTMEKANIK: GRUNDER, TILLÄMPNINGAR
GÖTEBORGS UNIVERSITET Fysiska institutionen april 1983 Hans Linusson, Carl-Axel Sjöblom, Örjan Skeppstedt januari 1993 FY 2400 april 1998 Distanskurs LEKTION 25 Delkurs 4 KVANTMEKANIK: GRUNDER, TILLÄMPNINGAR
Fysikaliska modeller
 Fysikaliska modeller Olika syften med fysiken Grundforskarens syn Finna förklaringar på skeenden i naturen Ställa upp lagar för fysikaliska skeenden Kritiskt granska uppställda lagar Kontrollera uppställda
Fysikaliska modeller Olika syften med fysiken Grundforskarens syn Finna förklaringar på skeenden i naturen Ställa upp lagar för fysikaliska skeenden Kritiskt granska uppställda lagar Kontrollera uppställda
Kvantmekaniska atommodellens grunder för kemilärare
 Kvantmekaniska atommodellens grunder för kemilärare Experiments are the only means of knowledge at our disposal. The rest is poetry, imagination. - Max Planck Katariina Tammi Kandidatarbete Lärarubildningsenheten
Kvantmekaniska atommodellens grunder för kemilärare Experiments are the only means of knowledge at our disposal. The rest is poetry, imagination. - Max Planck Katariina Tammi Kandidatarbete Lärarubildningsenheten
Rydbergs formel. Bohrs teori för väteliknande system
 Chalmers Tekniska Högskola och Göteborgs Universitet Sektionen för Fysik och Teknisk Fysik Arne Rosén, Halina Roth Uppdaterad av Erik Reimhult, januari A4 Enelektronspektrum Namn... Utförd den... Godkänd
Chalmers Tekniska Högskola och Göteborgs Universitet Sektionen för Fysik och Teknisk Fysik Arne Rosén, Halina Roth Uppdaterad av Erik Reimhult, januari A4 Enelektronspektrum Namn... Utförd den... Godkänd
Vågrörelselära & Kvantfysik, FK januari 2012
 Räkneövning 9 Vågrörelselära & Kvantfysik, FK00 9 januari 0 Problem 4.3 En elektron i vila accelereras av en potentialskillnad U = 0 V. Vad blir dess de Broglie-våglängd? Elektronen tillförs den kinetiska
Räkneövning 9 Vågrörelselära & Kvantfysik, FK00 9 januari 0 Problem 4.3 En elektron i vila accelereras av en potentialskillnad U = 0 V. Vad blir dess de Broglie-våglängd? Elektronen tillförs den kinetiska
7. Atomfysik väteatomen
 Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det nödvändigt att betrakta
Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus som vågrörelser och ibland är det nödvändigt att betrakta
Preliminärt lösningsförslag till Tentamen i Modern Fysik,
 Preliminärt lösningsförslag till Tentamen i Modern Fysik, SH1009, 008 05 19, kl 14:00 19:00 Tentamen har 8 problem som vardera ger 5 poäng. Poäng från inlämningsuppgifter tillkommer. För godkänt krävs
Preliminärt lösningsförslag till Tentamen i Modern Fysik, SH1009, 008 05 19, kl 14:00 19:00 Tentamen har 8 problem som vardera ger 5 poäng. Poäng från inlämningsuppgifter tillkommer. För godkänt krävs
Kvantmekanik II (FK5012), 7,5 hp
 Joakim Edsjö Fysikum, Stockholms Universitet Tel.: 8-5537876 E-post: edsjo@physto.se Lösningar till Kvantmekanik II (FK51, 7,5 hp 3 januari 9 Lösningar finns även tillgängliga på http://www.physto.se/~edsjo/teaching/kvant/index.html.
Joakim Edsjö Fysikum, Stockholms Universitet Tel.: 8-5537876 E-post: edsjo@physto.se Lösningar till Kvantmekanik II (FK51, 7,5 hp 3 januari 9 Lösningar finns även tillgängliga på http://www.physto.se/~edsjo/teaching/kvant/index.html.
TENTAMEN I FYSIKALISK KEMI KURS: KEM040 Institutionen för kemi Göteborgs Universitet Datum: LÄS DETTA FÖRST!
 TENTAMEN I FYSIKALISK KEMI KURS: KEM040 Institutionen för kemi Del: QSM Göteborgs Universitet Datum: 111206 Tid: 8.30 14.30 Ansvariga: Gunnar Nyman tel: 786 9035 Jens Poulsen tel: 786 9089 Magnus Gustafsson
TENTAMEN I FYSIKALISK KEMI KURS: KEM040 Institutionen för kemi Del: QSM Göteborgs Universitet Datum: 111206 Tid: 8.30 14.30 Ansvariga: Gunnar Nyman tel: 786 9035 Jens Poulsen tel: 786 9089 Magnus Gustafsson
FK Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 16 december 2015, kl 17:00-22:00
 FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 16 december 015, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 16 december 015, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
2.14. Spinn-bankopplingen
 2.14. Spinn-bankopplingen [Understanding Physics: 19.12-19.16] I avsnitt 2.12 konstaterade vi, att elektronen, som enligt Bohrs modell rör sig i en cirkelbana, kommer att ge upphov till en strömslinga,
2.14. Spinn-bankopplingen [Understanding Physics: 19.12-19.16] I avsnitt 2.12 konstaterade vi, att elektronen, som enligt Bohrs modell rör sig i en cirkelbana, kommer att ge upphov till en strömslinga,
Kvantmekanik och kemisk bindning I 1KB501
 Kvantmekanik och kemisk bindning I 1KB501 TENTAMEN, 013-06-05, 8.00-13.00 Tillåtna hjälpmedel: Miniräknare, bifogade formelsamlingar. Börja på nytt blad för varje nytt problem, och skriv din kod på varje
Kvantmekanik och kemisk bindning I 1KB501 TENTAMEN, 013-06-05, 8.00-13.00 Tillåtna hjälpmedel: Miniräknare, bifogade formelsamlingar. Börja på nytt blad för varje nytt problem, och skriv din kod på varje
KE02: Kemins mikrovärld
 KE02: Kemins mikrovärld Annika Nyberg annika.nyberg@mattliden.fi samt wilma! Kursbok: Kaila et al KEMI 2 Kemins mikrovärld Bedömning Prov: 80% Inlämningsuppgifter: 20% Period 1: KE02 Period 3: KE04 (KE05
KE02: Kemins mikrovärld Annika Nyberg annika.nyberg@mattliden.fi samt wilma! Kursbok: Kaila et al KEMI 2 Kemins mikrovärld Bedömning Prov: 80% Inlämningsuppgifter: 20% Period 1: KE02 Period 3: KE04 (KE05
3.5. Schrödingerekvationen för atomer med en elektron
 3.5. Schrödingerekvationen för atomer med en elektron [Understanding Physics: 19.5-19.8] Bohrs teori lyckas väl förklara energinivåerna för en atom med en elektron, och således också spektrallinjerna,
3.5. Schrödingerekvationen för atomer med en elektron [Understanding Physics: 19.5-19.8] Bohrs teori lyckas väl förklara energinivåerna för en atom med en elektron, och således också spektrallinjerna,
8. Atomfysik - flerelektronatomer
 Flerelektronatomer På motsvarande sätt som för väteatomen kommer elektronerna i atomerna hos grundämnen som har två eller fler elektroner också att vara instängda inom ett litet område runt kärnan. Det
Flerelektronatomer På motsvarande sätt som för väteatomen kommer elektronerna i atomerna hos grundämnen som har två eller fler elektroner också att vara instängda inom ett litet område runt kärnan. Det
2.7. Egenfunktionernas tolkning - fortsättning
 2.7. Egenfunktionernas tolkning - fortsättning [Understanding Physics: 19.7-19.10] Förra gången såg vi, att sannolikhetstätheten består av tre delar, en radiell del och två vinkelberoende delar. Vi skall
2.7. Egenfunktionernas tolkning - fortsättning [Understanding Physics: 19.7-19.10] Förra gången såg vi, att sannolikhetstätheten består av tre delar, en radiell del och två vinkelberoende delar. Vi skall
8-10 Sal F Generellt om kursen/utbildningen. Exempel på nanofenomen runt oss
 Upplägg och planering för NanoIntro 15; Lars Samuelson (lars.samuelson@ftf.lth.se): Måndag 31/8: Presentationer av deltagarna 8-10 Sal F Generellt om kursen/utbildningen. Exempel på nanofenomen runt oss
Upplägg och planering för NanoIntro 15; Lars Samuelson (lars.samuelson@ftf.lth.se): Måndag 31/8: Presentationer av deltagarna 8-10 Sal F Generellt om kursen/utbildningen. Exempel på nanofenomen runt oss
Kurs PM, Modern Fysik, SH1011
 Kurs PM, Modern Fysik, SH1011 Allmänt Kurshemsida finns på http://www.mi.physics.kth.se/web/teaching_modern_physics_sh1011.htm dock hänvisas till BILDA för fortlöpande information och uppdateringar. Föreläsningar
Kurs PM, Modern Fysik, SH1011 Allmänt Kurshemsida finns på http://www.mi.physics.kth.se/web/teaching_modern_physics_sh1011.htm dock hänvisas till BILDA för fortlöpande information och uppdateringar. Föreläsningar
TENTAMEN I KVANTFYSIK del 1 (5A1324 och 5A1450) samt KVANTMEKANIK (5A1320) med SVAR och LÖSNINGSANVISNINGAR Tisdagen den 5 juni 2007
 TENTAMEN I KVANTFYSIK del (5A4 och 5A45) samt KVANTMEKANIK (5A) med SVAR och LÖSNINGSANVISNINGAR Tisdagen den 5 juni 7 HJÄLPMEDEL: Formelsamling i Fysik (teoretisk fysik KTH), matematiska tabeller, dock
TENTAMEN I KVANTFYSIK del (5A4 och 5A45) samt KVANTMEKANIK (5A) med SVAR och LÖSNINGSANVISNINGAR Tisdagen den 5 juni 7 HJÄLPMEDEL: Formelsamling i Fysik (teoretisk fysik KTH), matematiska tabeller, dock
1.7. Tolkning av våg partikeldualiteten
 1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.12] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
1.7. Tolkning av våg partikeldualiteten [Understanding Physics: 13.7-13.12] En egenskap som är gemensam för både vågor och partiklar är förmågan att överföra energi. I vartdera fallet kan man representera
2.8. Sannolikhetstäthetens vinkelberoende
 2.8. Sannolikhetstäthetens vinkelberoende [Understanding Physics: 19.7 (s. 590)-19.11] Härnäst skall vi studera vinkelberoendet av egenfunktionerna för n = 1 och n = 2. Den allmänna lösningen till den
2.8. Sannolikhetstäthetens vinkelberoende [Understanding Physics: 19.7 (s. 590)-19.11] Härnäst skall vi studera vinkelberoendet av egenfunktionerna för n = 1 och n = 2. Den allmänna lösningen till den
Innehåll. Fysik Relativitetsteori. fy8_modernfysik.notebook. December 19, Relativitetsteorin Ljusets dualism Materiens struktur Kärnfysik
 Fysik 8 Modern fysik Innehåll Relativitetsteorin Ljusets dualism Materiens struktur Kärnfysik 1. Relativitetsteori Speciella relativitetsteorin Allmänna relativitetsteorin Two Postulates Special Relativity
Fysik 8 Modern fysik Innehåll Relativitetsteorin Ljusets dualism Materiens struktur Kärnfysik 1. Relativitetsteori Speciella relativitetsteorin Allmänna relativitetsteorin Two Postulates Special Relativity
Kvantkemi. - M. W. Hanna, Quantum Mechanics in Chemistry, Benjamin, Menlo Park, CA, 1969.
 III. Kvantkemi Kvantkemi III-1 Källor: - M. W. Hanna, Quantum Mechanics in Chemistry, Benjamin, Menlo Park, CA, 1969. - M. Karplus och R. N. Porter, Atoms & Molecules. An Introduction for Students in Physical
III. Kvantkemi Kvantkemi III-1 Källor: - M. W. Hanna, Quantum Mechanics in Chemistry, Benjamin, Menlo Park, CA, 1969. - M. Karplus och R. N. Porter, Atoms & Molecules. An Introduction for Students in Physical
Litiumatomens spektrum
 Litiumatomens spektrum Datorlaboration i Atom- och kärnfysik FAFF10 version 2010b av Sara Bargi och Jonas Cremon, omarbetning av tidigare version Före laborationens utförande ska du ha läst igenom avsnitt
Litiumatomens spektrum Datorlaboration i Atom- och kärnfysik FAFF10 version 2010b av Sara Bargi och Jonas Cremon, omarbetning av tidigare version Före laborationens utförande ska du ha läst igenom avsnitt
1.13. Den rektangulära potentialbrunnen
 1.13. Den rektangulära potentialbrunnen [Understanding Physics: 13.13-13.15(b)] Vi betraktar en partikel med massan m som är innesluten i en rektangulär potentialbrunn med oändligt höga sidor, dvs U =
1.13. Den rektangulära potentialbrunnen [Understanding Physics: 13.13-13.15(b)] Vi betraktar en partikel med massan m som är innesluten i en rektangulär potentialbrunn med oändligt höga sidor, dvs U =
Vågfysik. Ljus: våg- och partikelbeteende
 Vågfysik Modern fysik & Materievågor Kap 25 (24 1:st ed.) Ljus: våg- och partikelbeteende Partiklar Lokaliserade Bestämd position & hastighet Kollision Vågor Icke-lokaliserade Korsar varandra Interferens
Vågfysik Modern fysik & Materievågor Kap 25 (24 1:st ed.) Ljus: våg- och partikelbeteende Partiklar Lokaliserade Bestämd position & hastighet Kollision Vågor Icke-lokaliserade Korsar varandra Interferens
Tentamen i Modern fysik, TFYA11/TENA
 IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Torsdagen den 28/8 2014 kl. 14.00-18.00 i T1 och S25 Tentamen består av 2 A4-blad (inklusive
IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Torsdagen den 28/8 2014 kl. 14.00-18.00 i T1 och S25 Tentamen består av 2 A4-blad (inklusive
s 1 och s 2 är icke kvantmekaniska partiklar? e. (1p) Vad blir sannolikheterna i uppgifterna b, c och d om vinkeln = /2?
 FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 7e mars 018, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
FK003 - Kvantfysikens principer, Fysikum, Stockholms universitet Tentamensskrivning, onsdag 7e mars 018, kl 17:00 - :00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror du klarar
Tentamen i Modern fysik, TFYA11/TENA
 IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Onsdagen den 27/3 2013 kl. 08.00-12.00 i T1 och T2 Tentamen består av 2 A4-blad (inklusive detta)
IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Onsdagen den 27/3 2013 kl. 08.00-12.00 i T1 och T2 Tentamen består av 2 A4-blad (inklusive detta)
Parbildning. Om fotonens energi är mer än dubbelt så stor som elektronens vileoenergi (m e. c 2 ):
 Parbildning Vi ar studerat två sätt med vilket elektromagnetisk strålning kan växelverka med materia. För ögre energier ar vi även en tredje: Parbildning E mc Innebär att omvandling mellan energi oc massa
Parbildning Vi ar studerat två sätt med vilket elektromagnetisk strålning kan växelverka med materia. För ögre energier ar vi även en tredje: Parbildning E mc Innebär att omvandling mellan energi oc massa
BFL122/BFL111 Fysik för Tekniskt/ Naturvetenskapligt Basår/ Bastermin Föreläsning 10 Relativitetsteori den 26 april 2012.
 Föreläsning 10 Relativa mätningar Allting är relativt är ett välbekant begrepp. I synnerhet gäller detta när vi gör mätningar av olika slag. Många mätningar består ju i att man jämför med någonting. Temperatur
Föreläsning 10 Relativa mätningar Allting är relativt är ett välbekant begrepp. I synnerhet gäller detta när vi gör mätningar av olika slag. Många mätningar består ju i att man jämför med någonting. Temperatur
Molekylorbitaler. Matti Hotokka
 Molekylorbitaler Matti Hotokka Betrakta två väteatomer + ( ) ( ) 1s A 1 s B 1 s ( A) 1 s( B) + s 1 ( A) s 1 ( B) ' 1 s ( A) 1 s( B) Vätemolekylens molekylorbitaler När atomerna bildar en molekyl smälter
Molekylorbitaler Matti Hotokka Betrakta två väteatomer + ( ) ( ) 1s A 1 s B 1 s ( A) 1 s( B) + s 1 ( A) s 1 ( B) ' 1 s ( A) 1 s( B) Vätemolekylens molekylorbitaler När atomerna bildar en molekyl smälter
Rep. Kap. 27 som behandlade kraften på en laddningar från ett B-fält.
 Rep. Kap. 7 som behandlade kraften på en laddningar från ett -fält. Kraft på laddning i rörelse Kraft på ström i ledare Gauss sats för -fältet Inte så användbar som den för E-fältet, eftersom flödet här
Rep. Kap. 7 som behandlade kraften på en laddningar från ett -fält. Kraft på laddning i rörelse Kraft på ström i ledare Gauss sats för -fältet Inte så användbar som den för E-fältet, eftersom flödet här
1 Hur förklarar du att det blev ett interferensmönster i interferensexperimentet med elektroner?
 Session: okt28 Class Points Avg: 65.38 out of 100.00 (65.38%) 1 Hur förklarar du att det blev ett interferensmönster i interferensexperimentet med elektroner? A 0% Vi måste ha haft "koincidens", dvs. flera
Session: okt28 Class Points Avg: 65.38 out of 100.00 (65.38%) 1 Hur förklarar du att det blev ett interferensmönster i interferensexperimentet med elektroner? A 0% Vi måste ha haft "koincidens", dvs. flera
1.13. Den tidsoberoende Schrödinger ekvationen
 1.13. Den tidsoberoende Schrödinger ekvationen [Understanding Physics: 13.12-13.14] Den tidsberoende Schrödinger ekvationen för en fri partikel som rör sig i en dimension är en partiell differentialekvation
1.13. Den tidsoberoende Schrödinger ekvationen [Understanding Physics: 13.12-13.14] Den tidsberoende Schrödinger ekvationen för en fri partikel som rör sig i en dimension är en partiell differentialekvation
Atomer, ledare och halvledare. Kapitel 40-41
 Atomer, ledare och halvledare Kapitel 40-41 Centrala begrepp Kvantiserade energinivåer i atomer Elektronspinn och finstruktur Elektronen i en atom både banimpulsmoment, som karakteriseras av kvanttalet
Atomer, ledare och halvledare Kapitel 40-41 Centrala begrepp Kvantiserade energinivåer i atomer Elektronspinn och finstruktur Elektronen i en atom både banimpulsmoment, som karakteriseras av kvanttalet
Fysikaliska krumsprång i spexet eller Kemister och matematik!
 Fysikaliska krumsprång i spexet eller Kemister och matematik! Mats Linder 10 maj 2009 Ingen sammanfattning. Sammanfattning För den hugade har vi knåpat ihop en liten snabbguide till den fysik och kvantmekanik
Fysikaliska krumsprång i spexet eller Kemister och matematik! Mats Linder 10 maj 2009 Ingen sammanfattning. Sammanfattning För den hugade har vi knåpat ihop en liten snabbguide till den fysik och kvantmekanik
3.3. Den kvantmekaniska fria elektronmodellen
 3.3. Den kvantmekaniska fria elektronmodellen [Understanding Physics: 20.3-20.7] I kvantmekaniken behandlas ledningselektronerna som ett enda fermionsystem, på ett liknande sätt som elektronerna i flerelektronatomer.
3.3. Den kvantmekaniska fria elektronmodellen [Understanding Physics: 20.3-20.7] I kvantmekaniken behandlas ledningselektronerna som ett enda fermionsystem, på ett liknande sätt som elektronerna i flerelektronatomer.
Tentamen, Kvantfysikens principer FK2003, 7,5 hp
 Tentamen, Kvantfysikens principer FK2003, 7,5 hp Tid: 17:00-22:00, tisdag 3/3 2015 Hjälpmedel: utdelad formelsamling, utdelad miniräknare Var noga med att förklara införda beteckningar och att motivera
Tentamen, Kvantfysikens principer FK2003, 7,5 hp Tid: 17:00-22:00, tisdag 3/3 2015 Hjälpmedel: utdelad formelsamling, utdelad miniräknare Var noga med att förklara införda beteckningar och att motivera
9. Materiens magnetiska egenskaper. 9.0 Grunder: upprepning av elektromagnetism
 530117 Materialfysik vt 2010 9. Materiens magnetiska egenskaper [Callister, Ashcroft-Mermin, Kittel, etc. Se också anteckningarna för Fasta Tillståndets fysik kapitel 14-15] 9.0 Grunder: upprepning av
530117 Materialfysik vt 2010 9. Materiens magnetiska egenskaper [Callister, Ashcroft-Mermin, Kittel, etc. Se också anteckningarna för Fasta Tillståndets fysik kapitel 14-15] 9.0 Grunder: upprepning av
9. Materiens magnetiska egenskaper
 530117 Materialfysik vt 2010 9. Materiens magnetiska egenskaper [Callister, Ashcroft-Mermin, Kittel, etc. Se också anteckningarna för Fasta Tillståndets fysik kapitel 14-15] 9.0 Grunder: upprepning av
530117 Materialfysik vt 2010 9. Materiens magnetiska egenskaper [Callister, Ashcroft-Mermin, Kittel, etc. Se också anteckningarna för Fasta Tillståndets fysik kapitel 14-15] 9.0 Grunder: upprepning av
1 Speciell relativitetsteori
 TFFY17 Modern fysik Y: Lektion 1 1 1 Speciell relativitetsteori 1.1 Einsteins postulat 1. Fysikens lagar är desamma i alla inertialramar. 2. Ljusets hastighet är densamma (c 3 10 8 m/s) i alla inertialramar.
TFFY17 Modern fysik Y: Lektion 1 1 1 Speciell relativitetsteori 1.1 Einsteins postulat 1. Fysikens lagar är desamma i alla inertialramar. 2. Ljusets hastighet är densamma (c 3 10 8 m/s) i alla inertialramar.
Materialfysik2010 Kai Nordlund
 9.0 Grunder: upprepning av elektromagnetism 530117 Materialfysik vt 2010 Magnetism har alltid dipolkaraktär Monopoler existerar ej! 9. Materiens magnetiska egenskaper Grundekvationer: (Yttre) magnetfält:
9.0 Grunder: upprepning av elektromagnetism 530117 Materialfysik vt 2010 Magnetism har alltid dipolkaraktär Monopoler existerar ej! 9. Materiens magnetiska egenskaper Grundekvationer: (Yttre) magnetfält:
Lösningar Heureka 2 Kapitel 14 Atomen
 Lösningar Heureka Kapitel 14 Atomen Andreas Josefsson Tullängsskolan Örebro Lo sningar Fysik Heureka Kapitel 14 14.1) a) Kulorna från A kan ramla på B, C, D, eller G (4 möjligheter). Från B kan de ramla
Lösningar Heureka Kapitel 14 Atomen Andreas Josefsson Tullängsskolan Örebro Lo sningar Fysik Heureka Kapitel 14 14.1) a) Kulorna från A kan ramla på B, C, D, eller G (4 möjligheter). Från B kan de ramla
Kvantbrunnar -Kvantiserade energier och tillstånd
 Kvantbrunnar -Kvantiserade energier och tillstånd Inledning Syftet med denna laboration är att undersöka kvantiseringen av energitillstånd i kvantbrunnar. Till detta används en java-applet som hittas på
Kvantbrunnar -Kvantiserade energier och tillstånd Inledning Syftet med denna laboration är att undersöka kvantiseringen av energitillstånd i kvantbrunnar. Till detta används en java-applet som hittas på
Atom-, Molekyl- och Fasta Tillståndets Fysik
 Föreläsning 8/9 Atom-, Molekyl- och Fasta Tillståndets Fysik Flerelektronatomer På motsvarande sätt som för väteatomen kommer elektronerna i atomerna hos grundämnen som har två eller fler elektroner också
Föreläsning 8/9 Atom-, Molekyl- och Fasta Tillståndets Fysik Flerelektronatomer På motsvarande sätt som för väteatomen kommer elektronerna i atomerna hos grundämnen som har två eller fler elektroner också
Lösningar - Rätt val anges med fet stil i förekommande fall (obs att svaren på essäfrågorna inte är uttömmande).
 STOCKHOLMS UNIVERSITET FYSIKUM Tentamensskrivning i Materiens Minsta Byggstenar, 5p. Lördag den 15 juli, kl. 9.00 14.00 Lösningar - Rätt val anges med fet stil i förekommande fall (obs att svaren på essäfrågorna
STOCKHOLMS UNIVERSITET FYSIKUM Tentamensskrivning i Materiens Minsta Byggstenar, 5p. Lördag den 15 juli, kl. 9.00 14.00 Lösningar - Rätt val anges med fet stil i förekommande fall (obs att svaren på essäfrågorna
Vågrörelselära & Kvantfysik, FK januari 2012
 Räkneövning 10 Vågrörelselära & Kvantfysik, FK2002 9 januari 20 Problem 42.1 Vad är det orbitala rörelsemängdsmomentet, L, för en elektron i a) 3p-tillståndet b) 4f-tillståndet? Det orbitala rörelsemängdsmomentet
Räkneövning 10 Vågrörelselära & Kvantfysik, FK2002 9 januari 20 Problem 42.1 Vad är det orbitala rörelsemängdsmomentet, L, för en elektron i a) 3p-tillståndet b) 4f-tillståndet? Det orbitala rörelsemängdsmomentet
Svar och anvisningar
 170317 BFL10 1 Tenta 170317 Fysik : BFL10 Svar och anvisningar Uppgift 1 a) Den enda kraft som verkar på stenen är tyngdkraften, och den är riktad nedåt. Alltså är accelerationen riktad nedåt. b) Vid kaströrelse
170317 BFL10 1 Tenta 170317 Fysik : BFL10 Svar och anvisningar Uppgift 1 a) Den enda kraft som verkar på stenen är tyngdkraften, och den är riktad nedåt. Alltså är accelerationen riktad nedåt. b) Vid kaströrelse
Välkomna till Kvantfysikens principer!
 Välkomna till Kvantfysikens principer! If you think you understand quantum theory, you don t understand quantum theory. Richard Feynman Quantum mechanics makes absolutely no sense. Roger Penrose If quantum
Välkomna till Kvantfysikens principer! If you think you understand quantum theory, you don t understand quantum theory. Richard Feynman Quantum mechanics makes absolutely no sense. Roger Penrose If quantum
Svar och anvisningar
 160322 BFL102 1 Tenta 160322 Fysik 2: BFL102 Svar och anvisningar Uppgift 1 a) Centripetalkraften ligger i horisontalplanet, riktad in mot cirkelbanans mitt vid B. A B b) En centripetalkraft kan tecknas:
160322 BFL102 1 Tenta 160322 Fysik 2: BFL102 Svar och anvisningar Uppgift 1 a) Centripetalkraften ligger i horisontalplanet, riktad in mot cirkelbanans mitt vid B. A B b) En centripetalkraft kan tecknas:
GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin 2
 GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin Tid: Plats: Ansvarig: Hjälpmedel: Tisdag juni 009, kl 8 30 13 30 V-huset Lennart Sjögren,
GÖTEBORGS UNIVERSITET Institutionen för fysik LÖSNINGAR TILL TENTAMEN I MEKANIK B För FYP100, Fysikprogrammet termin Tid: Plats: Ansvarig: Hjälpmedel: Tisdag juni 009, kl 8 30 13 30 V-huset Lennart Sjögren,
Tentamen i Modern fysik, TFYA11/TENA
 IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Torsdagen den 29/8 2013 kl. 14.00-18.00 i TER2 Tentamen består av 2 A4-blad (inklusive detta)
IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Torsdagen den 29/8 2013 kl. 14.00-18.00 i TER2 Tentamen består av 2 A4-blad (inklusive detta)
Frielektron fermigas i en kristall. L z. L y L x. h 2 2m FRIELEKTRONMODELLEN
 FRIELEKTRONMODELLEN I frielektronmodellen (FEM) behandlas valenselektronerna som en gas. Elektronerna rör sig obehindrat i kristallen och växelverkar varken med jonerna eller med varandra. Figuren nedan
FRIELEKTRONMODELLEN I frielektronmodellen (FEM) behandlas valenselektronerna som en gas. Elektronerna rör sig obehindrat i kristallen och växelverkar varken med jonerna eller med varandra. Figuren nedan
Kinetisk Gasteori. Daniel Johansson January 17, 2016
 Kinetisk Gasteori Daniel Johansson January 17, 2016 I kursen har vi under två lektioner diskuterat kinetisk gasteori. I princip allt som sades på dessa lektioner sammanfattas i texten nedan. 1 Lektion
Kinetisk Gasteori Daniel Johansson January 17, 2016 I kursen har vi under två lektioner diskuterat kinetisk gasteori. I princip allt som sades på dessa lektioner sammanfattas i texten nedan. 1 Lektion
Tentamen i Modern fysik, TFYA11/TENA
 IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Lördagen den 25/8 2012 kl. 14.00-18.00 i TER4 och TERD Tentamen består av 2 A4-blad (inklusive
IFM - Institutionen för Fysik, Kemi och Biologi Linköpings universitet Tentamen i Modern fysik, TFYA11/TENA Lördagen den 25/8 2012 kl. 14.00-18.00 i TER4 och TERD Tentamen består av 2 A4-blad (inklusive
Molekylmekanik. Matti Hotokka
 Molekylmekanik Matti Hotokka Makroskopiskt material Består av enskilda molekyler Makroskopiskt material För att förstå det makroskopiska materialets egenskaper måste enskilda molekyler undersökas Modeller
Molekylmekanik Matti Hotokka Makroskopiskt material Består av enskilda molekyler Makroskopiskt material För att förstå det makroskopiska materialets egenskaper måste enskilda molekyler undersökas Modeller
Information om kursen
 Information om kursen Föreläsningar: Magnus Axelsson och Emma Wikberg Räkneövningar: Thomas Kvorning Kurshemsida: www.fysik.su.se/~emma/kvantprinciperna Kontaktinformation Schema Skannade föreläsningsanteckningar
Information om kursen Föreläsningar: Magnus Axelsson och Emma Wikberg Räkneövningar: Thomas Kvorning Kurshemsida: www.fysik.su.se/~emma/kvantprinciperna Kontaktinformation Schema Skannade föreläsningsanteckningar
1 Den Speciella Relativitetsteorin
 1 Den Speciella Relativitetsteorin Den speciella relativitetsteorin är en fysikalisk teori om lades fram av Albert Einstein år 1905. Denna teori beskriver framför allt hur utfallen (dvs resultaten) från
1 Den Speciella Relativitetsteorin Den speciella relativitetsteorin är en fysikalisk teori om lades fram av Albert Einstein år 1905. Denna teori beskriver framför allt hur utfallen (dvs resultaten) från
Andra EP-laborationen
 Andra EP-laborationen Christian von Schultz Magnus Goffeng 005 11 0 Sammanfattning I denna rapport undersöker vi perioden för en roterande skiva. Vi kommer fram till, både genom en kraftanalys och med
Andra EP-laborationen Christian von Schultz Magnus Goffeng 005 11 0 Sammanfattning I denna rapport undersöker vi perioden för en roterande skiva. Vi kommer fram till, både genom en kraftanalys och med
Kosmologi - läran om det allra största:
 Kosmologi - läran om det allra största: Dikter om kosmos kunna endast vara viskningar. Det är icke nödvändigt att bedja, man blickar på stjärnorna och har känslan av att vilja sjunka till marken i ordlös
Kosmologi - läran om det allra största: Dikter om kosmos kunna endast vara viskningar. Det är icke nödvändigt att bedja, man blickar på stjärnorna och har känslan av att vilja sjunka till marken i ordlös
Number 14, 15, 16, and 17 also in English. Sammanställning av tentamensuppgifter Kvant EEIGM (MTF057).
 LULEÅ TEKNISKA UNIVERSITET Hans Weber, Avdelningen för Fysik, 2004 Number 14, 15, 16, and 17 also in English. Sammanställning av tentamensuppgifter Kvant EEIGM (MTF057). 1. Partikel i en en dimensionell
LULEÅ TEKNISKA UNIVERSITET Hans Weber, Avdelningen för Fysik, 2004 Number 14, 15, 16, and 17 also in English. Sammanställning av tentamensuppgifter Kvant EEIGM (MTF057). 1. Partikel i en en dimensionell
FAFA Föreläsning 7, läsvecka 3 13 november 2017
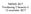 FAFA55 2017 Föreläsning 7, läsvecka 3 13 november 2017 Schrödingers ekvation kan tolkas som en ekvation som har sin utgångspunkt i A) konservering av rörelsemängd B) energikonservering C) Newtons andra
FAFA55 2017 Föreläsning 7, läsvecka 3 13 november 2017 Schrödingers ekvation kan tolkas som en ekvation som har sin utgångspunkt i A) konservering av rörelsemängd B) energikonservering C) Newtons andra
Kvantmekanik II - Föreläsning 10
 Kvantmekanik II - Föreläsning 10 Degenererad störningsteori (tidsoberoende) Joakim Edsjö edsjo@fysik.su.se Kvantmekanik II Föreläsning 10 Joakim Edsjö 1/26 Degenererad störningsteori Innehåll 1 Allmänt
Kvantmekanik II - Föreläsning 10 Degenererad störningsteori (tidsoberoende) Joakim Edsjö edsjo@fysik.su.se Kvantmekanik II Föreläsning 10 Joakim Edsjö 1/26 Degenererad störningsteori Innehåll 1 Allmänt
= v! p + r! p = r! p, ty v och p är dt parallella. Definiera som en ny storhet: Rörelsemängdsmoment: H O
 1 KOMIHÅG 15: --------------------------------- Definitioner: Den potentiella energin, mekaniska energin Formulera: Energiprincipen ---------------------------------- Föreläsning 16: FLER LAGAR-härledning
1 KOMIHÅG 15: --------------------------------- Definitioner: Den potentiella energin, mekaniska energin Formulera: Energiprincipen ---------------------------------- Föreläsning 16: FLER LAGAR-härledning
Atom-, Molekyl- och Fasta Tillståndets Fysik
 Föreläsning 7/8 Atom-, Molekyl- och Fasta Tillståndets Fysik Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus
Föreläsning 7/8 Atom-, Molekyl- och Fasta Tillståndets Fysik Partiklars vågegenskaper Som kunnat konstateras uppträder elektromagnetisk strålning ljus som en dubbelnatur, ibland behöver man beskriva ljus
Den Speciella Relativitetsteorin DEL I
 Den Speciella Relativitetsteorin DEL I Elektronens Tvilling Den unge patentverksarbetaren År 1905 publicerar en ung patentverksarbetare tre artiklar som revolutionerar fysiken. En av dessa artiklar är
Den Speciella Relativitetsteorin DEL I Elektronens Tvilling Den unge patentverksarbetaren År 1905 publicerar en ung patentverksarbetare tre artiklar som revolutionerar fysiken. En av dessa artiklar är
