Tentamen i IE1304 Reglerteknik Måndag 16/
|
|
|
- Carina Sandström
- för 6 år sedan
- Visningar:
Transkript
1 Ttm IE34 Rglrt Måg 6/ Allmä ormto Emtor: Wllm Sqvt. Avrg lärr: Wllm Sqvt, tl Cmpu t, Ttmuppgtr hövr t åtrläm är u lämr rvg. Hjälpml: Rär/Grrär. ur ormll hr ogt ttm. Ttm omttg Iormto om rättg oh tyg Motvr ll vr. Tllr oh rägr om vät m lögr lär orm. Om vrt på råg är "4" å måt u oå tl om vrör. Oulltägt motvr vr gr t ull poäg! Ttm g mmlt 5 p gåg 56p, goägrä går v 5 p. V tt orr ttmtlläll upp tll 6 tr poäg lägg tll rå uromgåg tr mrr. Totlt 56p F E D C B A Rulttt ml t måg 6 prl.
2 . p Vl övrörguto X Y hr rtlvto? y " 3y y 3 Vl övrörguto X Y hr ID-rgultor? y 5 t. p Vlt tgvr hr ölj övrörguto? Avä Lpltrorm tll. t >. yt? Y G X 4 3. p rtlråutvl ölj polyom 9 3 G p F. E pro hr övrörguto. D åtroppl lgt gur. V lr övrörguto ör R Y? Blohmruto. Rur lohmt tll övrörguto ör R Y å lågt t går.
3 5. p Bogrm. Ag övrörguto om övrtämmr m ölj Bo-grm. Där urv lutr är lutg /. 6. p Är tt tl övrörguto? Motvr vrt! 3 4 Rooth Hurwt mto. Avä mto ör tt vgör om ämrpolyomt är tlt p Rtm oh ttlgtm. Mrr gur på vrlt, läm tt hur m mätr rtm t r oh hur m mätr ttlgtm t ±%. 3
4 8. 6p E ol hr lutrutg m t om yll m pump. S gur. E tryor m tt RC-ltr mätr väthöj t. T hr tvärttr A m. Mll höj t oh utlöt rår mt u h. Sor ltrt tår v R Ω oh C µf oh hr tt örtärg. ump hr örtärg. Tg rm övrörguto R Y rå rrtorht tll uttorht. 9. 8p E pro hr övrörguto G. Rt övrörguto Bogrm på vrlt, läm tt. Grr -l. Rt lopputo. Brä uto ϕ ör,, 4, 8. S grmmt. Brä Φ m? A??? t?? m π C r 4
5 . p Btäm -trorm ör trt gl. Ag på å gtv oh potv orm. Btäm trt motvrght tll 5 G G. p Avgör om tå ytm är tlt. 555 H p E pro rglr m -tgrr polplrg rgultor. ro rv m ölj rvto y [ ],5y[ ] 5u[ ] 5u[ ] Btäm övrörguto p Dmor rgultor oh t tt ll polr lgg,5. 3p Rt lohm ör hl ytmt. p Vl ärgr höv ör tt trormr ovtå polplrg rgultor tll -t rgultor? Srv r övrörguto ör -t rgultor. p Jämör vlttvt -t rgultor m urpruglg rgultor. p 5
6 3. 6p E pro rv m tå lohm. ro rv på tlltåorm m två tlltå oh. Sgl u är tyrgl, v är rglr torht oh y är mätgl. täll upp ytmt på tlltåorm. Välj tyrr o orm. 4p rä ttoärvär v tlltåytmt rå. Avä httg ör u oh v. p 4. p E pol vä ör tt rörgrtt mät poto ho järär. är ör ört pol rå hållt oh ortättr ut gom r ä. S hur pol rt R, rt X oh mp Z vrrr m järär poto. Rt tr urvor på vrlt, läm tt. Ly tll! 6
7 Formll v ttm Rglrt IE34 Rgultortypr Rgultor Futo Övrörguto G -rgultor u t u t G I-rgultor D-lä ID-rgultor u t T I t t t t u t TD t t t u t t t t TD TI t h u T TI D h h mplgpro örtärg T I tgrrgt T D rvrgt G T G T D G T D TI Drt ID, örutättr hög mplgrv Lpltrormtll Lpltrorm F Tuto t t > Lpltrorm F Tuto t t > δ t mpuluto σ t tguto t t rmputo 3 t t t t t t t t t o t [ o t] ot t t α Dämpt: t t F α Förröjgt: t T t T F Bgylvärt: lm t lm F t t lm Slutvärt: lm F t I 7
8 Drvrgt: L[ t ] F t Itgrtot: L t t F L t t Suprpotorgl: [ ] F F Sm mll tgvr oh övrörguto -vr Itgrto G G E tott Itgrtotott G G T T Två tottr G T T E tottöt L G T Itgrtoöt L G Ar org pro m övrväg G Ar org ytm m ompl röttr Ljärt oämp ytmt gvägg ζ rltv ämpg M mml övrväg t t ör mml övrväg G M Bo-grm ζ ζ π ζ t π ζ 8
9 Blohm ruto rglr Fyl mollr M ytm M F M Nwto r lg t Fjär F järott Dämpr F ämpott t Trm pro E Ergl t Värmrg ut E T V ρ T tmprtur [] V volym [m 3 ] värmptt [J/g] ρ tt [g/m 3 ] Eltr ytm U Rtor R I R rt U otor I U Spol I Nvårglrg Mtrll V volym [m 3 ] u lö [m 3 /] u ut utlö [m 3 /] C C pt L L ut V t u u ut Frvly G G ϕ G ϕ HASOR ϕ A G ϕ ϕ rg A 9
10 Bogrm ör grutorr Förtärg G G j rg G j Drvrg G G j rg G j 9 Tott ämr G T G j T rg G j rtt Itgrrg G G j rg G G j 9 G j rg G j Döt L 8 L π Tott täljr T G G j rg T G j rtt ζt G G j rg G j rt ζt T T ζt T I oh D-rgultorr Bogrm I-rgultor Bogrm D-rgultor Bogrm I-rgultor. Dmor m mrgl φ m. Rgultor Bogrm plr m tt 5 v φ m. Totlt uppå å ö mrgl φ m. Stltt Nyqut örl tltt rtrum ör öpp ytmt. Stlt om: G j G j < v rg 8 Agrt. Stlt om: Slut ytmt polr lggr vätr hlvplt.
11 Stlttmrglr π jälvväggrv är rg G j 8 roovr rv är G j A m mpltu mrgl A m G π φ m mrgl φ rg G j m 8 Routh Hurwt mto rtrt vto: B B B > Tlhm: > B B Om ll tl ört olum är potv hr rtrt vto ll röttr vätr hlvpl.
12 vrtå rglrl, tt oggrht tgorm örvärärg tghöj rmporm örvärärg h rmp lutg v tgtörg tghöj Sht tgt t r,4 Zglr-Nhol mto ör ID-tällg är örtärg å jälvvägg uppommr v rglrg. π T G π π : I : ID :,5,6,45 T I,85T,5 T T D,5T Lmmto ör I-tällg V lmmto mät tgvrt rå t öpp ytmt oh jämör m tgvrt rå pro m tott T oh öt L. L G T L upptt m hjälp v tgt ärg m tl. T upptt ur trgl gur, llr om t tr öt L, rm tll 63% v lutvärt. T λ L S T I T M m{l, T} l p M < p < 3 p p tlty
13 3 -trormtll Trt uto -trorm F po rpr. -trorm F g rpr. htpul S httg htrmp htprl 3 3 potluto L örröj pul L L L S örröjt tg L L o o o o o o o Suprpotorgl: [ ] F F Z Förjutgt: [ ] L F L Z Bgyl oh lutvärtr: lm F lm lm F Drtrg Drtrg m orml h t G L Z H h är mplgpro. Stgvrt trorm.
14 Drtrg m tll Lär lgr ågr ormlr Mt vrtmto Övrtämt vtoytm y A r T T T T Flutjämt A y A A r r A A A y Mtl r A\y y utglvtor A mätt mtr r prmtrvtor Drt rvly jh H H jh H A H j rg LF S S h Smplgrv måt vr mt ult å hög om högt glrv ör tt uv vgtoro. 4
15 5 Drt tltt För tltt övrörguto H h ll polr om htrl. Shur-Coo tlttrtrum motvrr Rooth Hurwt. rtrt vto: > A > Tlhm: 3 Stlt om,,, ll är potv vrtå rglrl, tt oggrht tgorm örvärärg R H H lm tghöj rmporm örvärärg lm R H H h h rmp lutg v tgtörg tghöj R v H H H lm olplrgrgultor p p p D B C A v tgrrg C, ur räg lt A. p D C B r
16 6 Tlltåmollr ör oturlg ytm Sytmrvg: ABu yc A ytmmtr B glmtr C utglmtr D rtmtr Grll orm ör lvrl ytm [ ] [ ] u y u Grll orm ör lrvrl ytm. tlltåvrlr, p glr, q utglr. q q q q p p p p y y y u u u Dgolorm G λ λ λ : [ ] y u β β β λ λ λ Styrr o orm [ ] y u Trormr tlltåmoll tll övrörguto ABu yc {L:} XAXBU YCX GCI-A - B
17 Fgurl tll uppgtr 7, 9, 4 Etrm: Förm: roummr: Uppg. 7. t r t ±% Uppg. 4. R X Z Uppg 9. 7
Tentamen med lösningar i IE1304 Reglerteknik Måndag 16/
 Tetme me löigr i IE4 Reglertei Måg 6/ 9.-. Allmä iformtio Emitor: Willim Sqvit. Avrig lärre: Willim Sqvit, tel 8-79 4487 Cmpu Kit, Tetmeuppgifter behöver ite återläm är u lämr i i rivig. Hjälpmeel: Räre/rfräre.
Tetme me löigr i IE4 Reglertei Måg 6/ 9.-. Allmä iformtio Emitor: Willim Sqvit. Avrig lärre: Willim Sqvit, tel 8-79 4487 Cmpu Kit, Tetmeuppgifter behöver ite återläm är u lämr i i rivig. Hjälpmeel: Räre/rfräre.
Tentamen i ETEF05 Elenergiteknik för kl 8:00-13:00 i C525
 t EEF5 Elgtkk 7-8-4 ö kl 8:-: C55 llåt älpl: äko, ll, bog ollg t btå v totlt 5 ppgt på lgt 6 poäg. Fö gokät ltt på tt käv p, ö btgt käv 4p oc ö btgt käv 5p. Obv tt tlg bäkg åt ov ö tt åll poäg på pktv
t EEF5 Elgtkk 7-8-4 ö kl 8:-: C55 llåt älpl: äko, ll, bog ollg t btå v totlt 5 ppgt på lgt 6 poäg. Fö gokät ltt på tt käv p, ö btgt käv 4p oc ö btgt käv 5p. Obv tt tlg bäkg åt ov ö tt åll poäg på pktv
Blåsen nu alla (epistel nr 25)
 lås al (epstel nr 25) ext musk: Carl Mchael ellman oprano 4 3 rr: Eva oller 2004 lto or 4 3 4 3 lå - s Fåg - r - al - tt - ta, hör öl - jor - fs - kar - sval - ås - kan sprt - ta ur stt går rum; e - gas
lås al (epstel nr 25) ext musk: Carl Mchael ellman oprano 4 3 rr: Eva oller 2004 lto or 4 3 4 3 lå - s Fåg - r - al - tt - ta, hör öl - jor - fs - kar - sval - ås - kan sprt - ta ur stt går rum; e - gas
Affärsnätverka framgångsrikt
 Grt Thorto 2011 ffärätvr frmgågrit Cri Kivit CochHut i Siv B CochHut i Sivi B 08-333 131 - Lutmrgt 52, 113 58 Stocholm Migltilr t CochHut i Sivi B 08-333 131 - Lutmrgt 52, 113 58 Stocholm Migltilr t 1
Grt Thorto 2011 ffärätvr frmgågrit Cri Kivit CochHut i Siv B CochHut i Sivi B 08-333 131 - Lutmrgt 52, 113 58 Stocholm Migltilr t CochHut i Sivi B 08-333 131 - Lutmrgt 52, 113 58 Stocholm Migltilr t 1
Statistisk mekanik (forts) Kanonisk ensemble. E men. p 1. Inledande statistisk mekanik:
 Förläsg 4 Förra gåg: Dt totala rörlsmägdsmomtt J = L+S är ocså vatsrat. J j( j där j s, s,..., s, s J z m j där m j j, j,..., j, j Foto som utsäds(absorbras vd övrgågar har sp= gör att j att ädras. Ildad
Förläsg 4 Förra gåg: Dt totala rörlsmägdsmomtt J = L+S är ocså vatsrat. J j( j där j s, s,..., s, s J z m j där m j j, j,..., j, j Foto som utsäds(absorbras vd övrgågar har sp= gör att j att ädras. Ildad
Louise. Hayde. Nadja. kommer Förbandet är ju nästan klara showen börjar snart och vi har inte ens kommit in än
 l v M Tl på v ll omp T OP Mo D m k u f. lo k o oc gg f å y l T J, m h mobl vg! D lk h komm å ho kk? V gå! Jg h US 7 gåg föu på fvl, m å o jg mglåg få c, u vll jg å lg fm, jj! Och h jg u kk jg få uogf Hy
l v M Tl på v ll omp T OP Mo D m k u f. lo k o oc gg f å y l T J, m h mobl vg! D lk h komm å ho kk? V gå! Jg h US 7 gåg föu på fvl, m å o jg mglåg få c, u vll jg å lg fm, jj! Och h jg u kk jg få uogf Hy
Matte C. Översikt. Funktioner. Derivatan. Användning av derivatan. Exponentialfunktionen. Logaritmiska funktioner. Geometriska summor
 Mtte C Översikt Fuktioer Poteslgr Potesuktioer Polomuktioer o Väde/vtgde uktio o M/mi pukter tersspukt o Tget Lösigsmetoder ör : grdre Rtioell uktioer Derivt Deiitio v derivt o Vis ör C Deriverigsregler:
Mtte C Översikt Fuktioer Poteslgr Potesuktioer Polomuktioer o Väde/vtgde uktio o M/mi pukter tersspukt o Tget Lösigsmetoder ör : grdre Rtioell uktioer Derivt Deiitio v derivt o Vis ör C Deriverigsregler:
1. M öt et s öp pn an d e S ve n fö r k la r a r mö t et ö p p nat k lo c k a n 13. 5 0 i me d le ms k o nt o r et.
 Styrels e möte 7mars 2010 Bila gor: 1. D ago r d ning 2. N är va r o lis t a 1. M öt et s öp pn an d e S ve n fö r k la r a r mö t et ö p p nat k lo c k a n 13. 5 0 i me d le ms k o nt o r et. 2. F o rma
Styrels e möte 7mars 2010 Bila gor: 1. D ago r d ning 2. N är va r o lis t a 1. M öt et s öp pn an d e S ve n fö r k la r a r mö t et ö p p nat k lo c k a n 13. 5 0 i me d le ms k o nt o r et. 2. F o rma
Beteckningar för områdesreserveringar: T/kem Landskapsplanering
 kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
TENTAMEN Datum: 18 aug 11 TEN2: TRANSFORMMETODER
 TENTAMEN Daum: aug TEN: TRANSFORMMETODER Program:. Daa/ lkro och. Gamla udr Mdicikkik Kur: MATEMATIK Kurkod HF, H Skrivid::5-:5 Hjälpmdl: Formlblad dla u låmpl och miiräkar av vilk p om hl. Lärar: Armi
TENTAMEN Daum: aug TEN: TRANSFORMMETODER Program:. Daa/ lkro och. Gamla udr Mdicikkik Kur: MATEMATIK Kurkod HF, H Skrivid::5-:5 Hjälpmdl: Formlblad dla u låmpl och miiräkar av vilk p om hl. Lärar: Armi
p Följ Kraft Där, Strå
 Sånger söndg e domsöndg 0 Söndgsmorgon J.Hydn/J.O.Wlln Söndgsmorgon Musk v J.Hy. Svsk text v J.O.Wlln. Öpp r! Hel An skl bn skl nä kors ms d r m, ljud! bön, ljud? känn m vs, n rym m Se L Hur An m tds t
Sånger söndg e domsöndg 0 Söndgsmorgon J.Hydn/J.O.Wlln Söndgsmorgon Musk v J.Hy. Svsk text v J.O.Wlln. Öpp r! Hel An skl bn skl nä kors ms d r m, ljud! bön, ljud? känn m vs, n rym m Se L Hur An m tds t
På en landsväg. % Œ. œ œ. j œ # # œ œ j œ. œ J. œ œ œ œ œ. œ œ œ. œ œ# œ œ # œ œ œ œ. œ œ œ œ. œ œ j. œ œ œ j œ Œ ? # # œ œ. œ J. œ œ. œ œ. œ œ.
 Sälvklrt g sunger från herlgt köpt noter S ul På lndsväg % 1 På lnds väg n mot kväl l n ly ser ö ver Hpply sngng 1 På lnds väg n mot st n 2 St kväl l 3 Stnn ly ser n kommer ö ver stl t Trd: Puerto Rco
Sälvklrt g sunger från herlgt köpt noter S ul På lndsväg % 1 På lnds väg n mot kväl l n ly ser ö ver Hpply sngng 1 På lnds väg n mot st n 2 St kväl l 3 Stnn ly ser n kommer ö ver stl t Trd: Puerto Rco
Omtentamen med lösningar i IE1304 Reglerteknik Fredag 12/
 Omeme me löigr i IE Reglerekik Freg /6 5.-. Allmä iformio Emior: Willim Sqvi. Avrig lärre: Willim Sqvi, el -79 7 mpu i, Temeuppgifer ehöver ie åerläm är u lämr i i krivig. Hjälpmeel: Räkre/rfräkre. ure
Omeme me löigr i IE Reglerekik Freg /6 5.-. Allmä iformio Emior: Willim Sqvi. Avrig lärre: Willim Sqvi, el -79 7 mpu i, Temeuppgifer ehöver ie åerläm är u lämr i i krivig. Hjälpmeel: Räkre/rfräkre. ure
Fysiktävlingen Lösningsförslag. Uppgift 1. Vi får anta att kinetisk energi övergår i lägesenergi, och att tyngdpunkten lyftes 6,5 m.
 SVESK FYSIKESMFUDET Fysiktälingen 006. Lösningsörslg. Uppgit. Vi år nt tt kinetisk energi öergår i lägesenergi, och tt tyngdpunkten lytes 6,5 m. m mgh gh t s gh 00 9,8 6,5 8,85 8,9 s Stöten stången mot
SVESK FYSIKESMFUDET Fysiktälingen 006. Lösningsörslg. Uppgit. Vi år nt tt kinetisk energi öergår i lägesenergi, och tt tyngdpunkten lytes 6,5 m. m mgh gh t s gh 00 9,8 6,5 8,85 8,9 s Stöten stången mot
äkta Bredband, ett krav för framtidens multiservice nät?
 äkta Bredband, ett krav för framtidens multiservice nät? U lf V in n e ra s D e s ig n c o n s u lta n t, C is c o S y s te m s 2 0 0 2, C is c o S y s te m s, In c. A ll rig h ts re s e rv e d. U lf V
äkta Bredband, ett krav för framtidens multiservice nät? U lf V in n e ra s D e s ig n c o n s u lta n t, C is c o S y s te m s 2 0 0 2, C is c o S y s te m s, In c. A ll rig h ts re s e rv e d. U lf V
Snickerier. Räcken & Stolpar, Snickarglädje, Ett företag inom Södra
 Trätr o Proutr so år st på tt us Srr Rä & Stopr, Srä, Träår, Stopsyst, Iprrt Ett ört o Sör Tstyps yr o ystr Ao & Srä 1840-1900 Ao & Srä Hus rå är pro är v på r ott v utsöt ystr o srr. Vor uppör trä tt
Trätr o Proutr so år st på tt us Srr Rä & Stopr, Srä, Träår, Stopsyst, Iprrt Ett ört o Sör Tstyps yr o ystr Ao & Srä 1840-1900 Ao & Srä Hus rå är pro är v på r ott v utsöt ystr o srr. Vor uppör trä tt
ffi8cf Till föijd crv devqlveringen av den svensko kronon uppstod kursföriuster på 75 miljoner kronor på moderbologets utländsko lån.
 ffi8cf Pressmeddelonde Aktiebologet SKF:s styrelse sommonträdde föjonde uppgifter lömnodes om resultotet noderno 1977. p& onsdogerl, vorvid för de försto åtto må- SKF-koncernen Under perioden jonuori ti
ffi8cf Pressmeddelonde Aktiebologet SKF:s styrelse sommonträdde föjonde uppgifter lömnodes om resultotet noderno 1977. p& onsdogerl, vorvid för de försto åtto må- SKF-koncernen Under perioden jonuori ti
Gävleborgs Bridgeförbund Bridgerally
 bg gföb gy 2010-2011 RÖDA ff m INTE m ttpg. g. Otb It 2- Ap 2 x pg Et fm bt tg mt fm bt p- ch tb ttpg. D gö m p tgt. ö h m p ö h m D M - P p ö h m D M - g Pc Nm Kbb At tg Tt pg 25/7 4/10 5/10 12/10 14/10
bg gföb gy 2010-2011 RÖDA ff m INTE m ttpg. g. Otb It 2- Ap 2 x pg Et fm bt tg mt fm bt p- ch tb ttpg. D gö m p tgt. ö h m p ö h m D M - P p ö h m D M - g Pc Nm Kbb At tg Tt pg 25/7 4/10 5/10 12/10 14/10
TENTAMEN Datum: 4 feb 12
 TENTAMEN Daum: b Tid: 8:5-:5 TEN: TRANSFORMMETODER Program: Daa/ lkro och Gamla udr Mdicikkik Kur: MATEMATIK Kurkod HF, 6H Skrivid:8:5-:5 Hjälpmdl: Formlblad dla u låmpl och miiräkar av vilk p om hl Lärar:
TENTAMEN Daum: b Tid: 8:5-:5 TEN: TRANSFORMMETODER Program: Daa/ lkro och Gamla udr Mdicikkik Kur: MATEMATIK Kurkod HF, 6H Skrivid:8:5-:5 Hjälpmdl: Formlblad dla u låmpl och miiräkar av vilk p om hl Lärar:
Gävleborgs Bridgeförbund Bridgerally
 bg gföb gy 2010-2011 RÖDA ff m INTE m ttpg. g. Otb It 2- Ap 2 x pg Et fm bt tg mt fm bt p- ch tb ttpg. ö h m p ö h m D M - P p ö h m D M - g Pc Nm Kbb At tg Tt pg 25/7 4/10 5/10 12/10 14/10 18/10 19/10
bg gföb gy 2010-2011 RÖDA ff m INTE m ttpg. g. Otb It 2- Ap 2 x pg Et fm bt tg mt fm bt p- ch tb ttpg. ö h m p ö h m D M - P p ö h m D M - g Pc Nm Kbb At tg Tt pg 25/7 4/10 5/10 12/10 14/10 18/10 19/10
26,4 21,8 21,8 21,8 1:27 22,7 22,4 19,4 21,7 18,3 18,6 23,1 19,8 26,2 17,7 15,9 1:45 15,5 24,4 16,3 15,5 1: ,2 10,3 18,6 1:28.
 .,,,,,,,,, :,, r. ÅKSVÄG SPLLKR RÄ OR R L TUK il l n t T O LB.. T ti ÖS LTUK OTO R-R STO,,, :,,,,,,,,,,,,,,, RG lu j ÄG LSV TUULHUKKUJ,,,,, risnäs,,, :,,,,,,,,,,,, risnäs,,,,,,, :, :,,,,,,,,,,,,,,,,,,,,,,,,,,
.,,,,,,,,, :,, r. ÅKSVÄG SPLLKR RÄ OR R L TUK il l n t T O LB.. T ti ÖS LTUK OTO R-R STO,,, :,,,,,,,,,,,,,,, RG lu j ÄG LSV TUULHUKKUJ,,,,, risnäs,,, :,,,,,,,,,,,, risnäs,,,,,,, :, :,,,,,,,,,,,,,,,,,,,,,,,,,,
är ett tal som betecknas det(a) eller Motivering: Determinanter utvecklades i samband med lösningsmetoder för kvadratiska linjära system.
 Armi Hlilovi: EXTRA ÖVNINGAR Determiter DETERMINANTER A Determiter v r orige Determite v e mtris A följe är ett tl som etes eta eller Eempel: 6. oh efiiers eligt Motiverig: Determiter utveles i sm me lösigsmetoer
Armi Hlilovi: EXTRA ÖVNINGAR Determiter DETERMINANTER A Determiter v r orige Determite v e mtris A följe är ett tl som etes eta eller Eempel: 6. oh efiiers eligt Motiverig: Determiter utveles i sm me lösigsmetoer
Snickerier. Räcken & Stolpar, Snickarglädje, Ett företag inom Södra
 Trätjr o Proutr so år st på tt us Srr Rä & Stopr, Sräj, Träår, Stopsyst, Iprrt Ett ört o Sör Tstyps yr o ystjr Ao & Sräj 1840-1900 Hus rå är pro är v på r ott v utsöt ystjr o srr. Vor uppör trä tt vär
Trätjr o Proutr so år st på tt us Srr Rä & Stopr, Sräj, Träår, Stopsyst, Iprrt Ett ört o Sör Tstyps yr o ystjr Ao & Sräj 1840-1900 Hus rå är pro är v på r ott v utsöt ystjr o srr. Vor uppör trä tt vär
.1fl.=::5, =E; E=E*r;!;E 5. d5eige?2a U. i i o = .2 B=lJ3S. - :'x.=f= o.. () ie.:.: (J'O tr:1= l,r'\ E cj-o -, ^i.i.= -i -., l-n.
 L... 't. ' l, 'l, r{ r. 'r U 6l q/ 'l >' 'p tr. 3 b+ 91 r9 '.Q 1 > Y_r )t,)24., _ ' g * A/;Al ccgc' uj6 5 cgx 9 (J r l,?
L... 't. ' l, 'l, r{ r. 'r U 6l q/ 'l >' 'p tr. 3 b+ 91 r9 '.Q 1 > Y_r )t,)24., _ ' g * A/;Al ccgc' uj6 5 cgx 9 (J r l,?
F6 PP kap 4.1, linjära ekvationssystem
 F3 E3 & 3 Pge of 5 F6 PP k 4. lär ekvtotem Om vektorer och mtrer ormer etc. e PP 5-8. V väder eteckge för Eukldk orme v e -vektor. Oft väd m-orme m ll e vektor-orm ocer e orm för lär vldgr Det gäller u
F3 E3 & 3 Pge of 5 F6 PP k 4. lär ekvtotem Om vektorer och mtrer ormer etc. e PP 5-8. V väder eteckge för Eukldk orme v e -vektor. Oft väd m-orme m ll e vektor-orm ocer e orm för lär vldgr Det gäller u
Hvor tilfreds er du med din togrejse?
 Hvor tlrs r u m n tors? V r ov or n ælp tl t svr tt spørskm. Dn svr skl ælp os tl t skr n o kvltt totrkkn på Kystnn o ovr Ørsun. Spørskmrn nsmls mrr tot. På orån tk o ortst o rs! Inormtonsrkn k l m n o
Hvor tlrs r u m n tors? V r ov or n ælp tl t svr tt spørskm. Dn svr skl ælp os tl t skr n o kvltt totrkkn på Kystnn o ovr Ørsun. Spørskmrn nsmls mrr tot. På orån tk o ortst o rs! Inormtonsrkn k l m n o
FORMELSAMLING ELTEKNIK
 FOELALG ELTEKK Liström s + + + + +...... Om s lg erieoliges ersättigsresists rllelloliges ersättigsresists rllelloliges ersättigsresists. Fler v smm värde. rllelloliges ersättigsresists. Edst resistser
FOELALG ELTEKK Liström s + + + + +...... Om s lg erieoliges ersättigsresists rllelloliges ersättigsresists rllelloliges ersättigsresists. Fler v smm värde. rllelloliges ersättigsresists. Edst resistser
f(x)dx definieras som arean av ytan som begränsas av y = f(t), y = 0, t = a och t = b, se figur.
 Föreläsning. Integrl En förenkl efinition Antg tt f(x) å x b och tt f(x) är kontinuerlig är. Den bestäm integrlen b f(x)x efiniers som ren v ytn som begränss v y = f(t), y =, t = och t = b, se figur. Insättningsformeln
Föreläsning. Integrl En förenkl efinition Antg tt f(x) å x b och tt f(x) är kontinuerlig är. Den bestäm integrlen b f(x)x efiniers som ren v ytn som begränss v y = f(t), y =, t = och t = b, se figur. Insättningsformeln
Ekvationen (ekv1) kan bl. annat beskriva värmeledningen i en tunn stav där u( x, temperaturen i punkten x vid tiden t.
 Armi Halilovi: EXRA ÖVNINGAR Värmldigsvaio VÄRMEEDNINGSEKVAIONEN Vi braar öljad PDE u u v där > är osa Evaio v a bl aa bsriva värmldig i u sav där u bar mpraur i pu vid id därör am värmldigsvaio Radvärdsproblm
Armi Halilovi: EXRA ÖVNINGAR Värmldigsvaio VÄRMEEDNINGSEKVAIONEN Vi braar öljad PDE u u v där > är osa Evaio v a bl aa bsriva värmldig i u sav där u bar mpraur i pu vid id därör am värmldigsvaio Radvärdsproblm
TSDT18/84 SigSys Kap 7 Fouriertransformanalys av tidskontinuerliga signaler 1 1 Kap 7 Fouriertransformanalys av tidskontinuerliga signaler 2
 Kap 7 Fourirrasormaalys av idskoiurliga sigalr Kap 7 Fourirrasormaalys av idskoiurliga sigalr Fourirrasorm Fourirrasorm ill x(: F F { x( } X( x( j d Ivrsa ourirrasorm ill X(: { X( } x( π X( j d Jr. ourirsri:
Kap 7 Fourirrasormaalys av idskoiurliga sigalr Kap 7 Fourirrasormaalys av idskoiurliga sigalr Fourirrasorm Fourirrasorm ill x(: F F { x( } X( x( j d Ivrsa ourirrasorm ill X(: { X( } x( π X( j d Jr. ourirsri:
Tillståndsmaskiner. Moore-automat. Mealy-automat. William Sandqvist
 Tllstånsmsknr Moor-utomt Mly-utomt Wllm Snvst wllm@kth.s ÖH. Bstäm tllstånsrm oh tllstånstll ör skvnskrtsn. Vlkn v mollrn Mly llr Moor pssr n på krtsn? Wllm Snvst wllm@kth.s . Ur krtsshmt kn öljn smn ställs
Tllstånsmsknr Moor-utomt Mly-utomt Wllm Snvst wllm@kth.s ÖH. Bstäm tllstånsrm oh tllstånstll ör skvnskrtsn. Vlkn v mollrn Mly llr Moor pssr n på krtsn? Wllm Snvst wllm@kth.s . Ur krtsshmt kn öljn smn ställs
Medborgarnas synpunkter på skattesystemet, skattefusket och Skatteverkets kontroll Resultat från en riksomfattande undersökning hösten 2006
 M y å y, S R å ö ö 2006 R 2007:3 3 Fö S ö 1996 å ö å å ö. Uö ä å ä: Mä ( ä) ä. Mä ä å y y,, ä ä å y S ä. I å 2006 å ö ä y, (ä). D (ä) 2007:4, M y å S ä. Uö y : ö ö ä y S, ö ö ö å S,, ä ä å ä å y ö. Fä
M y å y, S R å ö ö 2006 R 2007:3 3 Fö S ö 1996 å ö å å ö. Uö ä å ä: Mä ( ä) ä. Mä ä å y y,, ä ä å y S ä. I å 2006 å ö ä y, (ä). D (ä) 2007:4, M y å S ä. Uö y : ö ö ä y S, ö ö ö å S,, ä ä å ä å y ö. Fä
F & 34 ø øl ø øl ø V. ø øl ø. &øl ø# øl ø øl ø ? F. &speg - lar Hår - ga - ber - get. ? ú ø ú ø ú ø. Hårga-Låten. som - mar - nat - ten, i
 L L L L V Hm l är blek VSpel man n är HårgaLåt L L L mar nat t, n g matt, L Text: Carl Peter Wckström Sats: Robert Sund (.2) L L # Ljus L nans vat t sg be satt L # Hm l är blek Spel man L n L är V mar
L L L L V Hm l är blek VSpel man n är HårgaLåt L L L mar nat t, n g matt, L Text: Carl Peter Wckström Sats: Robert Sund (.2) L L # Ljus L nans vat t sg be satt L # Hm l är blek Spel man L n L är V mar
sona HUfVUDREDAKTOR: RED.-SEKR ETER ARE: YMNASTIKDIREKTORENS är också det numera ett gouteradt
 R (48 8 Å R G Ö G JU 9 G UG URR UURR RR R R R Ö G R W G R YRR G C " " x x G C G zé G G J J G R U R ; 4 W R R wz R U R G z U! Ö! 8 7 87 9 4 9 W! G x x x ^ é J!!??! J G? G 4 R R 4 98 x R 4 47 4 9 R ; R 8
R (48 8 Å R G Ö G JU 9 G UG URR UURR RR R R R Ö G R W G R YRR G C " " x x G C G zé G G J J G R U R ; 4 W R R wz R U R G z U! Ö! 8 7 87 9 4 9 W! G x x x ^ é J!!??! J G? G 4 R R 4 98 x R 4 47 4 9 R ; R 8
Fiskars avdelning pä Finlands Mässas 50-àrs jubileumsmässa.
 Fiskars avdelning pä Finlands Mässas 50-àrs jubileumsmässa. O Y F IS K A R S A B Verksamhetsberättelse för 1969, bolagets 86 verksamhetsär. E x t e m f ö r s ä l j n i n g o c h e x p o r t ( 1 0 0 0 m
Fiskars avdelning pä Finlands Mässas 50-àrs jubileumsmässa. O Y F IS K A R S A B Verksamhetsberättelse för 1969, bolagets 86 verksamhetsär. E x t e m f ö r s ä l j n i n g o c h e x p o r t ( 1 0 0 0 m
Arborelius, Olof Per Ulrik. Olof Arborelius. : Minnesutställning anordnad af Svenska konstnärernas förening Stockholm 1916.
 Arborelus, Olof Per Ulrk Olof Arborelus. : Mnnesutställnng anordnad af Svenska konstnärernas förenng 1916. Stockholm 1916. EOD Mljoner böcker bara en knapptrycknng bort. I mer än 10 europeska länder! Tack
Arborelus, Olof Per Ulrk Olof Arborelus. : Mnnesutställnng anordnad af Svenska konstnärernas förenng 1916. Stockholm 1916. EOD Mljoner böcker bara en knapptrycknng bort. I mer än 10 europeska länder! Tack
13 eecm= 4rr^ 4 r2cm= 4lL ^ 24 lm6cm= 4Oe ^ = l7: 2s 4m2crrr =? az ^ 2815dm. zo rcm= 4Ot. e edm= 0.? 1032cm= 431 114cm= 4o?
 Lfi,ngd i deeimalform 1 12dm= 4Z ---------------- 21 8m7 = 0 12 ro= --------a 4?o 13 ee= 4rr = 2 of 322m58= lre za 33 73 dm= Zr J_m 1032= 431 30 2m4dm.-..7-114= 4o? * 31 25dm= 4tf 14 2 m65 = 21 6f 346m5dm=
Lfi,ngd i deeimalform 1 12dm= 4Z ---------------- 21 8m7 = 0 12 ro= --------a 4?o 13 ee= 4rr = 2 of 322m58= lre za 33 73 dm= Zr J_m 1032= 431 30 2m4dm.-..7-114= 4o? * 31 25dm= 4tf 14 2 m65 = 21 6f 346m5dm=
TENTAMEN. Digital signalbehandling. Sven Knutsson. Typgodkänd räknare
 Istitutioe för dt- och eletrotei 5-5-4 TETAME KURSAM PROGRAM: m Eletro- och dtigejörslije å / läsperiod årsurs /läsperiod 3 KURSBETECKIG LET39 96 EAMIATOR Sve Kutsso TID FÖR TETAME Fredg 7 ugusti 4 l 3.3
Istitutioe för dt- och eletrotei 5-5-4 TETAME KURSAM PROGRAM: m Eletro- och dtigejörslije å / läsperiod årsurs /läsperiod 3 KURSBETECKIG LET39 96 EAMIATOR Sve Kutsso TID FÖR TETAME Fredg 7 ugusti 4 l 3.3
Sju advent- och julsånger i satser för blandad kör SAB av Karl-Fredrik Jehrlander
 ju advent- julsånger satser bnd kör av Karl-Fredrk Jehrnr dvent... 2 Den sg g... 6 Dng dong!... 8 Ej upplysta gårr... 9 Hersång...10 tl tt...12 Jord hmmel...14 (8) =92 dvent uns. 1.Vn n su sar Text: rtt
ju advent- julsånger satser bnd kör av Karl-Fredrk Jehrnr dvent... 2 Den sg g... 6 Dng dong!... 8 Ej upplysta gårr... 9 Hersång...10 tl tt...12 Jord hmmel...14 (8) =92 dvent uns. 1.Vn n su sar Text: rtt
Gävleborgs Bridgeförbund Bridgerally
 bg gföbu gy 2010-2011 RÖDA ff m INTE m ttpg. g. Otb 2- u Ap 2 x pg Et fm bt tg mt fm bt p- ch tb ttpg. ö h m H u p ö h m H u D M - P p H u ö h m D M - g Pc Nm Kubb At tg Tt pg 25/7 4/10 5/10 12/10 14/10
bg gföbu gy 2010-2011 RÖDA ff m INTE m ttpg. g. Otb 2- u Ap 2 x pg Et fm bt tg mt fm bt p- ch tb ttpg. ö h m H u p ö h m H u D M - P p H u ö h m D M - g Pc Nm Kubb At tg Tt pg 25/7 4/10 5/10 12/10 14/10
SÖDRA FLERBOSTADSH USEN
 Bjöovä, 181130- Göyfko SÖDR LERBOSTDSH USEN Nl vl k ä Dv fälkk hä Bv k Ej y öy k p l ä fj lo Bk Växä på jälkl, 200-600 v y k ä l c p o p Ö fö Håjo y Hlvöpp håjo y: Tääck//jöl/k 363,7 2 k p l ä fj lo Håjo
Bjöovä, 181130- Göyfko SÖDR LERBOSTDSH USEN Nl vl k ä Dv fälkk hä Bv k Ej y öy k p l ä fj lo Bk Växä på jälkl, 200-600 v y k ä l c p o p Ö fö Håjo y Hlvöpp håjo y: Tääck//jöl/k 363,7 2 k p l ä fj lo Håjo
Vårnatt. l l l l l l 2 4. f f f f 6 l 8 l l l l l 2 4 kz k s k k. l l l l l l 2 l l 4. k k k f k k k j kz kk k
 Soro 1 Soro 2 Ato 1 Ato 2 Teor 1 Teor 2 Bss 1 Bss 2 Pio 1 Pio 2 G =6 Vårtt Keyed by Gör Westig Gor@WestigHisso.et No dymic or temo exressios! Icomete io otes! Wihem Stehmmr yr. Oscr Lewerti f f f f 6 8
Soro 1 Soro 2 Ato 1 Ato 2 Teor 1 Teor 2 Bss 1 Bss 2 Pio 1 Pio 2 G =6 Vårtt Keyed by Gör Westig Gor@WestigHisso.et No dymic or temo exressios! Icomete io otes! Wihem Stehmmr yr. Oscr Lewerti f f f f 6 8
st tt r s s ss r t r r r t rs r st ä r st r
 st tt r s r 3 3 t t 1t r r s ss r t r r r t rs r st ä r st r st ts r3 s s r3 s s t t t t st tt r s r 3 st tt Ö t ts r t r 3 3 t t 1t r r t r r r t t r 1 rt s r ss s t r 1 rt s r Pr 1 s r r t str r r Präs
st tt r s r 3 3 t t 1t r r s ss r t r r r t rs r st ä r st r st ts r3 s s r3 s s t t t t st tt r s r 3 st tt Ö t ts r t r 3 3 t t 1t r r t r r r t t r 1 rt s r ss s t r 1 rt s r Pr 1 s r r t str r r Präs
Gävleborgs Bridgeförbund Bridgerally
 bg gföbu gy 2011-2012 RÖDA ff m INTE m ttpg. g. Otb 2- u Ap 2 x pg Et fm bt tg mt fm bt p- ch tb ttpg. A göm h mx 50MP 1/7-11 H u ö h m p ö h m H u D M - P H u p ö h m D M - g Pc Nm Kubb At tg Tt pg 24/7
bg gföbu gy 2011-2012 RÖDA ff m INTE m ttpg. g. Otb 2- u Ap 2 x pg Et fm bt tg mt fm bt p- ch tb ttpg. A göm h mx 50MP 1/7-11 H u ö h m p ö h m H u D M - P H u p ö h m D M - g Pc Nm Kubb At tg Tt pg 24/7
R app o r t T A n a l y s a v f as t p r o v. Ut f ä r dad P e r S a mu el s s on
 S i da 1 (14 ) A n k o m s tdatum 2018-07 - 09 M R M K on s u l t AB Ut f ä r dad 2018-07 - 16 P e r S a mu el s s on T a v as tg a t a n 34 118 24 S to ck ho lm S w e d en P r o j e kt B e s tnr S p å
S i da 1 (14 ) A n k o m s tdatum 2018-07 - 09 M R M K on s u l t AB Ut f ä r dad 2018-07 - 16 P e r S a mu el s s on T a v as tg a t a n 34 118 24 S to ck ho lm S w e d en P r o j e kt B e s tnr S p å
Sångerna är lämpliga att framföra vid bröllop, speciella fester och romantiska tillfällen för Kärlekens skull... GE 11176
 FÖROR So en sträng å gtrren och so tonern dn vs..., så börjr texten Ulrk Neuns underbr Kärleksvls. Vd kn vr ljuvlgre än gtrrens sröd och nnerlg ton so tllsns ed sången kn sk sådn stänng och rontsk tosfär.
FÖROR So en sträng å gtrren och so tonern dn vs..., så börjr texten Ulrk Neuns underbr Kärleksvls. Vd kn vr ljuvlgre än gtrrens sröd och nnerlg ton so tllsns ed sången kn sk sådn stänng och rontsk tosfär.
Diskreta stokastiska variabler
 Definitioner: Diskret stokstisk vribler Utfllet i ett slumpmässigt försök i form v ett reellt tl, betrktt innn försöket utförts, klls för stokstisk vribel eller slumpvribel (oft betecknd ξ, η ) Ett resultt
Definitioner: Diskret stokstisk vribler Utfllet i ett slumpmässigt försök i form v ett reellt tl, betrktt innn försöket utförts, klls för stokstisk vribel eller slumpvribel (oft betecknd ξ, η ) Ett resultt
HOMOGENA DIFFERENTIALEKVATIONSSYSTEM MED KONSTANTA KOEFFICIENTER
 HOMOGENA DIFFERENTIALEKVATIONSSYSTEM MED KONSTANTA KOEFFICIENTER Vi brr sysm v lijär omog DE (v förs ordig) md os offiir dx x x d dx x x d dx x x d där x ), x ( ),, x ( ) är ob fuior v vribl ( Ovsåd sysm
HOMOGENA DIFFERENTIALEKVATIONSSYSTEM MED KONSTANTA KOEFFICIENTER Vi brr sysm v lijär omog DE (v förs ordig) md os offiir dx x x d dx x x d dx x x d där x ), x ( ),, x ( ) är ob fuior v vribl ( Ovsåd sysm
1--861". o '" CI CI .: ;: .:.. 0 ~ M ~ ~ D022 :: '" OJ .. ;. C :: i- 0- Kungl Järnvägsstyrelsen str 422 Mbr regnr 114 Ut
 Kungl Järnvägsstyrlsn str 422 Mbr rgnr 114 Ut 1 1 59 9.. POSTVAGAR 22 1--861". n ;-1'1-- J : Q..: ;: : 2 x OJ 2 OJ : C Q. C OJ Q. - ;..:..: ë3 V' - "' c n - a. OJ l: l: OJ l: l: OJ ;: C C Q. Q) : - C Q.
Kungl Järnvägsstyrlsn str 422 Mbr rgnr 114 Ut 1 1 59 9.. POSTVAGAR 22 1--861". n ;-1'1-- J : Q..: ;: : 2 x OJ 2 OJ : C Q. C OJ Q. - ;..:..: ë3 V' - "' c n - a. OJ l: l: OJ l: l: OJ ;: C C Q. Q) : - C Q.
FOURIERSERIER. Definition 1. (Trigonometrisk serie) Ett utryck av följande form. är en trigonometrisk serie.
 Armi Hlilovic: EXRA ÖVNINGAR FOURIERSERIER Deiiio. rigoomerisk serie E uryck v öljde orm [ cos x b si x ] är e rigoomerisk serie. Amärkig: Förs erme skriver vi som v prkisk skäl som vi örklrr ed. Deiiio.
Armi Hlilovic: EXRA ÖVNINGAR FOURIERSERIER Deiiio. rigoomerisk serie E uryck v öljde orm [ cos x b si x ] är e rigoomerisk serie. Amärkig: Förs erme skriver vi som v prkisk skäl som vi örklrr ed. Deiiio.
VECKANS LILLA POSTKODVINST á 1.000 kronor Inom nedanstående postkoder vinner följande 245 lottnummer 1.000 kronor vardera:
 Dragningsresultat vecka 42-2015 Här nedan kan du se om du är en av de lyckliga vinnarna i veckans utlottning i Svenska PostkodLotteriet. När du har vunnit betalar vi automatiskt ut dina vinstpengar till
Dragningsresultat vecka 42-2015 Här nedan kan du se om du är en av de lyckliga vinnarna i veckans utlottning i Svenska PostkodLotteriet. När du har vunnit betalar vi automatiskt ut dina vinstpengar till
Digital Signalbehandling i multimedia
 LH, Lud Uivrsi örläsig Digil Siglhdlig i mulimdi EI65 Digil Siglhdlig Smplig AD Digil sig. hdl. Digil krs DA Lågpssilr Lågpssilr Rkosrukio Digil Sigl Procssig: Pricipls, Algorihms, d Applicios. Joh G.
LH, Lud Uivrsi örläsig Digil Siglhdlig i mulimdi EI65 Digil Siglhdlig Smplig AD Digil sig. hdl. Digil krs DA Lågpssilr Lågpssilr Rkosrukio Digil Sigl Procssig: Pricipls, Algorihms, d Applicios. Joh G.
Tävlingskalender, trav och galopp 2016 ( ) datum
 Tävlingskalender, trav och galopp 2016 (2015-11-09) datum Januari 2016 01-jan Fr Mp 02-jan Lö Ro (V75) 03-jan Sö Bs Tä gal 04-jan Må F Ös 05-jan Ti Ö J 06-jan On S (V86) 07-jan To G Å 08-jan Fr Bo S (V65)
Tävlingskalender, trav och galopp 2016 (2015-11-09) datum Januari 2016 01-jan Fr Mp 02-jan Lö Ro (V75) 03-jan Sö Bs Tä gal 04-jan Må F Ös 05-jan Ti Ö J 06-jan On S (V86) 07-jan To G Å 08-jan Fr Bo S (V65)
SKOLRESA. På Gotland!
 2016 * SKOLRESA På Gotld! Skolpkt I pktt igå följd: Båt t/, luch/middg v på övft. Butf Viby Hm-KippbyViby Hm. Logi i um/tugo md hlpio. Fi té hl vitl till Kippby Somm- & Vttld. Eklt pivät fö hl kl! Miigolf
2016 * SKOLRESA På Gotld! Skolpkt I pktt igå följd: Båt t/, luch/middg v på övft. Butf Viby Hm-KippbyViby Hm. Logi i um/tugo md hlpio. Fi té hl vitl till Kippby Somm- & Vttld. Eklt pivät fö hl kl! Miigolf
Karlstads Universitet Maskinteknik /HJo
 Karlstads Unverstet asnten 9-4-7/Ho orsonssvängnngar I roterande masner nns rs ör torsonnvängnngar, dvs vrdsvängnngar som överlagras på rotatonen. Perodsa störnngar som excterar dessa svängnngar an t.ex.
Karlstads Unverstet asnten 9-4-7/Ho orsonssvängnngar I roterande masner nns rs ör torsonnvängnngar, dvs vrdsvängnngar som överlagras på rotatonen. Perodsa störnngar som excterar dessa svängnngar an t.ex.
I FÖRFRÅGNINGSUNDERLAG LIU HUS A Kv INTELLEKTET 1 LINKÖPING FÖRKLARINGAR 4-6: 520 A B PLAN 1, DEL 1 INREDNINGSPLAN INREDNING
 9944-306:1703 9951-306:1703 9968-306:1704 306:1702 9987-306:1702 113: 51 TÅLLUC 13:193:C 10x6 uk 1100 ÖG ÖPPT TLL 2 P 13.193 13:193 51 4-6: 1 TÅLLUC 10x6 uk ÖG LYTT. H 13:193 PR LYTT. +40.100 +40.100 520
9944-306:1703 9951-306:1703 9968-306:1704 306:1702 9987-306:1702 113: 51 TÅLLUC 13:193:C 10x6 uk 1100 ÖG ÖPPT TLL 2 P 13.193 13:193 51 4-6: 1 TÅLLUC 10x6 uk ÖG LYTT. H 13:193 PR LYTT. +40.100 +40.100 520
Opp, Amaryllis (Fredmans sång nr 31)
 Opp, marylls (Fredmans sång nr 1) Text musk: Carl Mchael Bellman rr: Eva Toller 05 Tenor 1 1Opp, Tag - ma - ryl - ls, vak - na mn ll -! äd - ret stl -, d re - var dra-gen; bör - jar -gen, Tenor 2 Basso
Opp, marylls (Fredmans sång nr 1) Text musk: Carl Mchael Bellman rr: Eva Toller 05 Tenor 1 1Opp, Tag - ma - ryl - ls, vak - na mn ll -! äd - ret stl -, d re - var dra-gen; bör - jar -gen, Tenor 2 Basso
Volym och dubbelintegraler över en rektangel
 Volym oh dubbelintegrler över en rektngel All funktioner nedn nts vr kontinuerlig. Om f (x i intervllet [, b], så är ren v mängden {(x, y : y f (x, x b} lik med integrlen b f (x dx. Låt = [, b] [, d] =
Volym oh dubbelintegrler över en rektngel All funktioner nedn nts vr kontinuerlig. Om f (x i intervllet [, b], så är ren v mängden {(x, y : y f (x, x b} lik med integrlen b f (x dx. Låt = [, b] [, d] =
Bröderna fara väl vilse ibland (epistel nr 35)
 Brödera fara väl vilse ilad (epistel r 35) Text musik: Carl Michael Bellma Teor 1 8 6 Arr: Eva Toller 2008 Teor 2 6 8 Basso 1 8 6.. Basso 2 8 6 1.Brö- der - a fa - ra väl vil - se i-lad om gla - se me
Brödera fara väl vilse ilad (epistel r 35) Text musik: Carl Michael Bellma Teor 1 8 6 Arr: Eva Toller 2008 Teor 2 6 8 Basso 1 8 6.. Basso 2 8 6 1.Brö- der - a fa - ra väl vil - se i-lad om gla - se me
Skyarna tjockna (epistel nr 21)
 Skyarna tockna (epistel nr 21) Text musik: Carl Michael Bellman Arr: Eva Toller 2009 Tenor 1 3 8 Tenor 2 3 8... Basso 1 8 3 1.Sky - ar - na. tock - na, stär - nor- na. slock - na, stor - mar- na. Basso
Skyarna tockna (epistel nr 21) Text musik: Carl Michael Bellman Arr: Eva Toller 2009 Tenor 1 3 8 Tenor 2 3 8... Basso 1 8 3 1.Sky - ar - na. tock - na, stär - nor- na. slock - na, stor - mar- na. Basso
OV F IS K A R S A B. Verksamhetsberättelse för 1973 bolagets 90 verksamhetsàr
 F= OV F IS K A R S A B Verksamhetsberättelse för 1973 bolagets 90 verksamhetsàr Verksamhetsberättelse för 1973 A L L M Ä N E K O N O M I S K Ö V E R S I K T D en e k o n o m is k a u tv e c k lin g e n
F= OV F IS K A R S A B Verksamhetsberättelse för 1973 bolagets 90 verksamhetsàr Verksamhetsberättelse för 1973 A L L M Ä N E K O N O M I S K Ö V E R S I K T D en e k o n o m is k a u tv e c k lin g e n
Kapitel 8. Kap.8, Potentialströmning
 Kpitel 8 Kp.8, Voticitet (epetition) Hstighetspotentil Stömfunktionen Supeposition Cikultion -dimensionell kopp Kutt-Joukovskis lftkftsteoem Komple potentil Rottionssmmetisk potentilstömning Rottion v
Kpitel 8 Kp.8, Voticitet (epetition) Hstighetspotentil Stömfunktionen Supeposition Cikultion -dimensionell kopp Kutt-Joukovskis lftkftsteoem Komple potentil Rottionssmmetisk potentilstömning Rottion v
Linköpings Universitet IFM Kemi Formelsamling för Fysikalisk kemi Termodynamik, Spektroskopi & Kinetik. 2 van der Waals gasekvation
 Lnköngs Unvrstt IFM Km 8-1-17 Formlsamlng ör Fyskalsk km rmodynamk, Sktrosko & Kntk Gasr. a n + ( nb) n R van dr Waals gaskvaton Z n R Komrssblttsaktor r nd r rducrad, c krtsk varabl Rducrad varablr c
Lnköngs Unvrstt IFM Km 8-1-17 Formlsamlng ör Fyskalsk km rmodynamk, Sktrosko & Kntk Gasr. a n + ( nb) n R van dr Waals gaskvaton Z n R Komrssblttsaktor r nd r rducrad, c krtsk varabl Rducrad varablr c
VECKANS LILLA POSTKODVINST á 1.000 kronor Inom nedanstående postkoder vinner följande 219 lottnummer 1.000 kronor vardera:
 Dragningsresultat vecka 27-2015 Här nedan kan du se om du är en av de lyckliga vinnarna i veckans utlottning i Svenska PostkodLotteriet. När du har vunnit betalar vi automatiskt ut dina vinstpengar till
Dragningsresultat vecka 27-2015 Här nedan kan du se om du är en av de lyckliga vinnarna i veckans utlottning i Svenska PostkodLotteriet. När du har vunnit betalar vi automatiskt ut dina vinstpengar till
f(x i ) Vi söker arean av det gråfärgade området ovan. Området begränsas i x-led av de två x-värdena där kurvan y = x 2 2x skär y = 0, d.v.s.
 Dg. Remsummor och tegrler Rekommederde uppgfter 5.. Del upp tervllet [, 3] lk stor deltervll och väd rektglr med dess deltervll som bs för tt beräk re v området uder = +, över =, smt mell = och = 3. V
Dg. Remsummor och tegrler Rekommederde uppgfter 5.. Del upp tervllet [, 3] lk stor deltervll och väd rektglr med dess deltervll som bs för tt beräk re v området uder = +, över =, smt mell = och = 3. V
Lösningar till repetitionstentamen i EF för π3 och F3
 Lösningr till repetitionstentmen i EF för π3 oh F3 Lösning problem Från Poyntingvektorn (r, t = E(r, t H(r, t = A ẑ η 0 konstterr vi tt vågens utbredningsriktning ê är vilket leder till tt dess vågvektor
Lösningr till repetitionstentmen i EF för π3 oh F3 Lösning problem Från Poyntingvektorn (r, t = E(r, t H(r, t = A ẑ η 0 konstterr vi tt vågens utbredningsriktning ê är vilket leder till tt dess vågvektor
Nr 3 år 2005 Med programmet för augusti - oktober
 För Landskrona FBU-förening och 54:e HV komp. Nr 3 år 2005 Med programmet för augusti - oktober !"# $ $% #$ &'$ $ &($$) *!)$ ) +, -.$ $ / 01 1. )#*!.01.1 2. 123 4,1 4.!" # $%& '( ) * # +* +'(, +'( -./%
För Landskrona FBU-förening och 54:e HV komp. Nr 3 år 2005 Med programmet för augusti - oktober !"# $ $% #$ &'$ $ &($$) *!)$ ) +, -.$ $ / 01 1. )#*!.01.1 2. 123 4,1 4.!" # $%& '( ) * # +* +'(, +'( -./%
FÄRGLAGD A STENSUNDSVÄGEN BOSTÄDER BILPLATSER GARAGE 86 ST
 STNSUNSVÄN Ø Ø : Ø OSTÄR S TRO RK ST 3 RK 3 ST RK ST SUMM 7 ST 663 ILPLTSR +. +.3 R 6 ST -3 /. +.7 MRK Lr 5 ST SUMM ST.5 + IV. > VI SO P 3 677 b 3 3 UN SL TRO +.5 + 3.5 + 6. VÄ PL NN g V S +7 +3. +.6.5
STNSUNSVÄN Ø Ø : Ø OSTÄR S TRO RK ST 3 RK 3 ST RK ST SUMM 7 ST 663 ILPLTSR +. +.3 R 6 ST -3 /. +.7 MRK Lr 5 ST SUMM ST.5 + IV. > VI SO P 3 677 b 3 3 UN SL TRO +.5 + 3.5 + 6. VÄ PL NN g V S +7 +3. +.6.5
VECKANS LILLA POSTKODVINST á 1.000 kronor Inom nedanstående postkoder vinner följande 172 lottnummer 1.000 kronor vardera:
 Dragningsresultat vecka 12-2015 Här nedan kan du se om du är en av de lyckliga vinnarna i veckans utlottning i Svenska PostkodLotteriet. När du har vunnit betalar vi automatiskt ut dina vinstpengar till
Dragningsresultat vecka 12-2015 Här nedan kan du se om du är en av de lyckliga vinnarna i veckans utlottning i Svenska PostkodLotteriet. När du har vunnit betalar vi automatiskt ut dina vinstpengar till
R S T. k a fp n a f s a f a f LAPLACETRANSFORMEN. (Enkelsidig) laplacetransform, forts. z. Antag. xt dt. Följaktligen existerar.
 Atg Fö 6, 7 & 8 - Lplcetrsormlys 1 LAPLACETRANSFORMEN Låt ~x t xt e t, där R, såd tt z ~x t dt< ågot 0 > 0 R S T xt z < 0 0 xt dt Fölktlge exsterr F F l l ~ q xt q xt (el. grudde.) Fö 6, 7 & 8 - Lplcetrsormlys
Atg Fö 6, 7 & 8 - Lplcetrsormlys 1 LAPLACETRANSFORMEN Låt ~x t xt e t, där R, såd tt z ~x t dt< ågot 0 > 0 R S T xt z < 0 0 xt dt Fölktlge exsterr F F l l ~ q xt q xt (el. grudde.) Fö 6, 7 & 8 - Lplcetrsormlys
Folkets Parkskullen. Holmtebo. Gusum Vargbrogärdet. Ringarums Prästgård. Borg. Gryt Konvaljekullen. Öppet landskap med cykelavstånd till centrum.
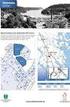 Holmtebo Öppet ladskap med cykelavståd till cetrum. Rigarums Prästgård Naturära boede, cetralt i kyrkby. Folkets Parkskulle Bo ära service, atur och det glittrade havet. Kovaljekulle Attraktiva i skärgårdsära
Holmtebo Öppet ladskap med cykelavståd till cetrum. Rigarums Prästgård Naturära boede, cetralt i kyrkby. Folkets Parkskulle Bo ära service, atur och det glittrade havet. Kovaljekulle Attraktiva i skärgårdsära
Änglahyss succé i repris
 4 Dc 2014 - J 2015 Äly ccé i pi P Ny b S i Si Ec l i! Li Bb P 2 S i l Di! D c c j i c l ii. Ny c l bl.. ij i é, l p p pp i, blyc 10, lc py, b c i l, ji i USA. Mi i ll j p c x i l i. V ib c i l i? V l J
4 Dc 2014 - J 2015 Äly ccé i pi P Ny b S i Si Ec l i! Li Bb P 2 S i l Di! D c c j i c l ii. Ny c l bl.. ij i é, l p p pp i, blyc 10, lc py, b c i l, ji i USA. Mi i ll j p c x i l i. V ib c i l i? V l J
som gör formeln (*) om vi flyttar första integralen till vänsterledet.
 Armi Hlilovic: EXTRA ÖVNNGAR Prtill itgrtio PARTELL NTEGRATON uu(vv ( dddd uu(vv( uu (vv(dddd ( ), (pppppppppppppppp iiiiiiiiiiiiiiiiiiiiii) KKKKKKKKKKKKKK: uuuu dddd uuuu uu vv dddd Förklrig: Eligt produktrgl
Armi Hlilovic: EXTRA ÖVNNGAR Prtill itgrtio PARTELL NTEGRATON uu(vv ( dddd uu(vv( uu (vv(dddd ( ), (pppppppppppppppp iiiiiiiiiiiiiiiiiiiiii) KKKKKKKKKKKKKK: uuuu dddd uuuu uu vv dddd Förklrig: Eligt produktrgl
Transformkodning. Transformkodning. Transformkodning. Transformkodning Grundläggande idé. Linjära transformer. Linjära transformer ( ) ( ) ( )
 6 8 6 Grudläggad idé Atag att vi parar ihop lmt i bild i bloc om två Om vi väljr att aat oordiatsystm, t.x rotrar gradr 8 6 6 och plottar dssa par som xy oordiatr i graf 6 ( rad frå Labild) 8 6 8 6 8 så
6 8 6 Grudläggad idé Atag att vi parar ihop lmt i bild i bloc om två Om vi väljr att aat oordiatsystm, t.x rotrar gradr 8 6 6 och plottar dssa par som xy oordiatr i graf 6 ( rad frå Labild) 8 6 8 6 8 så
Differentialrelationer. Repetition Energiekvationen Vorticitet Strömfunktionen Hastighetspotential Potentialströmning
 Differentialrelationer Reetition Energiekationen orticitet Strömfnktionen Hastighetsotential Potentialströmning Reetition Kaitel 3 Reetition, Kaitel 3 Energiekationen ( ) ( )da n g h d g dt d W W Q CS
Differentialrelationer Reetition Energiekationen orticitet Strömfnktionen Hastighetsotential Potentialströmning Reetition Kaitel 3 Reetition, Kaitel 3 Energiekationen ( ) ( )da n g h d g dt d W W Q CS
Digital signalbehandling Föreläsningsanteckningar
 Iiuio ör d- och lroi Digil iglhdlig Förläigcigr --7 Kur gr grudupr om ldr i mmi uryc, vi hir i i på pri implimrigr m ämr ädå dl å i örigåd. Vrör digil iglhdlig? Poiiv grrd oggrh (gräd v l ir) rproducrrh
Iiuio ör d- och lroi Digil iglhdlig Förläigcigr --7 Kur gr grudupr om ldr i mmi uryc, vi hir i i på pri implimrigr m ämr ädå dl å i örigåd. Vrör digil iglhdlig? Poiiv grrd oggrh (gräd v l ir) rproducrrh
FÖ 5: Kap 1.6 (fr.o.m. sid. 43) Induktionsbevis
 FÖ 5: K.6 fr.o.m. sid. Idutiosevis Fultet och iomiloefficieter Defiitio v! "-fultet" och iomiloefficieter " över " Disussio och evis v egeser.7 och.8. och.7 för ll =,,,...,.8 Av.8 följer t.e. tt, och Disussio
FÖ 5: K.6 fr.o.m. sid. Idutiosevis Fultet och iomiloefficieter Defiitio v! "-fultet" och iomiloefficieter " över " Disussio och evis v egeser.7 och.8. och.7 för ll =,,,...,.8 Av.8 följer t.e. tt, och Disussio
Patie nts äke rhe ts be rätte ls e för Slotts s tade ns Läkarhus Re hab o Häls a år 2015
 Patie nts äke rhe ts be rätte ls e för Slotts s tade ns Läkarhus Re hab o Häls a år 2015 Ko s tn ad s s tälle n u m m e r 1 6 3 9 8 0, 1 6 3 9 9 8 I enlighet med 3 kap 10 patientsäkerhetslagen (2010:659)
Patie nts äke rhe ts be rätte ls e för Slotts s tade ns Läkarhus Re hab o Häls a år 2015 Ko s tn ad s s tälle n u m m e r 1 6 3 9 8 0, 1 6 3 9 9 8 I enlighet med 3 kap 10 patientsäkerhetslagen (2010:659)
Reglerteknik Ö6. Köp övningshäfte på kårbokhandeln. William Sandqvist
 eglerteknik Ö6 öp övninghäfte på kårbokhndeln Willim Sndqvit willim@kth.e . Stbilitet Vilk proceer är tbil? y y 6y x x b y 6y 8y x c y y y x 4x d y y y y u 5u e y 7 y y 4y u u f y y y 6y u 7u g h 6 4 Willim
eglerteknik Ö6 öp övninghäfte på kårbokhndeln Willim Sndqvit willim@kth.e . Stbilitet Vilk proceer är tbil? y y 6y x x b y 6y 8y x c y y y x 4x d y y y y u 5u e y 7 y y 4y u u f y y y 6y u 7u g h 6 4 Willim
vara en T- periodisk funktion som är integrerbar på intervallet ges av formlerna
 Armi Hlilovic: EXRA ÖVNINGAR FOURIERSERIER Deiitio (rigoometrisk serie Ett utryck v öljde orm [ cos( Ωx b si( Ω x är e trigoometrisk serie ] Amärkig: Först terme skriver vi som v prktisk skäl som vi örklrr
Armi Hlilovic: EXRA ÖVNINGAR FOURIERSERIER Deiitio (rigoometrisk serie Ett utryck v öljde orm [ cos( Ωx b si( Ω x är e trigoometrisk serie ] Amärkig: Först terme skriver vi som v prktisk skäl som vi örklrr
Formelblad Atom- och Kärnfysik
 melbla Atm- ch Känfysik Rybe: ν = 1 λ = R ( 1 n 2 1 m 2 ) Z 2 E n = hcr Z2 n 2 hcr = m e(e 2 /4πɛ ) 2 2 2 = 1, 66 ev M R = R m e + M (massk.) Alkalilika system, me n = n δ l : E = hcr (Z eff ) 2 E S =
melbla Atm- ch Känfysik Rybe: ν = 1 λ = R ( 1 n 2 1 m 2 ) Z 2 E n = hcr Z2 n 2 hcr = m e(e 2 /4πɛ ) 2 2 2 = 1, 66 ev M R = R m e + M (massk.) Alkalilika system, me n = n δ l : E = hcr (Z eff ) 2 E S =
A LT B A R Y TO N. enkelt
 A LT SOPRAN sahlt nklt B A R Y TO N Innhåll: Amn - låt rns lja råda 2 Du ljuvast n Gud har männs kär Gud ll oss väl 6 Halluja 7 Hlg 8 följr dg Gud 9 Julat Do 10 Kom, öppna dn dörr 11 r 12 Må dn väg gå
A LT SOPRAN sahlt nklt B A R Y TO N Innhåll: Amn - låt rns lja råda 2 Du ljuvast n Gud har männs kär Gud ll oss väl 6 Halluja 7 Hlg 8 följr dg Gud 9 Julat Do 10 Kom, öppna dn dörr 11 r 12 Må dn väg gå
;l )i. ~~ i I nrt-- t ILi' - i ii' i I i. o! illl I!, i I I, I! I
 -;; '=, f"rrjj. j (. 11 bo/.1 _..,; BODO " 1 '--.------215,.1 '---1 f-2!- 2265.------------ -865 -----------------+-.----2265 1---.----.-.--.-----,--------1318 285 -.--;r--------- 778 nrt-- t L' - '! lll!,,!
-;; '=, f"rrjj. j (. 11 bo/.1 _..,; BODO " 1 '--.------215,.1 '---1 f-2!- 2265.------------ -865 -----------------+-.----2265 1---.----.-.--.-----,--------1318 285 -.--;r--------- 778 nrt-- t L' - '! lll!,,!
Interpolation. Interpolation. Teknisk-vetenskapliga beräkningar 1. Några tillämpningar. Interpolation. Basfunktioner. Definitioner. Kvadratiskt system
 Ierpolao Några llämpgar Ierpolao odelluoer som saserar gva puer Amerg rörelser,.e. ead lm Blder ärger salg Gra Dsre represeao -> ouerlg Peder Joasso Ierpolao V äer puer,.., V söer e uo P så a P P erpolerar
Ierpolao Några llämpgar Ierpolao odelluoer som saserar gva puer Amerg rörelser,.e. ead lm Blder ärger salg Gra Dsre represeao -> ouerlg Peder Joasso Ierpolao V äer puer,.., V söer e uo P så a P P erpolerar
Föreläsning 6: Kapitel 10 Beräkning av egenskaper hos reglersystem. Sådana egenskaper är Stabilitet Statisk noggrannhet Snabbhet mm
 Förläning 6: Kapitl 0 Bräkning av gnkapr ho rglrytm Sådana gnkapr är Stabilitt Statik noggrannht Snabbht mm Stabilitt Kan avgöra md Nyqvitkritrit Polbtämning Routh mtod 2 Nyqvitkritrit tt grafikt tabilittkritrium
Förläning 6: Kapitl 0 Bräkning av gnkapr ho rglrytm Sådana gnkapr är Stabilitt Statik noggrannht Snabbht mm Stabilitt Kan avgöra md Nyqvitkritrit Polbtämning Routh mtod 2 Nyqvitkritrit tt grafikt tabilittkritrium
fgr S-v"r,Jsö Södl]a pgq.tsbg,qeå?rqni.ng- år Iq60 { avs*r tirlsn L?.5,1959-22.5.1960 ).
![fgr S-vr,Jsö Södl]a pgq.tsbg,qeå?rqni.ng- år Iq60 { avs*r tirlsn L?.5,1959-22.5.1960 ). fgr S-vr,Jsö Södl]a pgq.tsbg,qeå?rqni.ng- år Iq60 { avs*r tirlsn L?.5,1959-22.5.1960 ).](/thumbs/29/13687394.jpg) & Verksamhet sberät te 1 * fgr S-v"r,Jsö Södl]a pgq.tsbg,qeå?rqni.ng- år Iq60 { avs*r tirlsn L?.5,1959-22.5.1960 ). tq 7 * {tao Sorn styrelse har fungo3s;: ordf. B. Lundblarl toilt Si-irsetrrr.P;'r Unze1l
& Verksamhet sberät te 1 * fgr S-v"r,Jsö Södl]a pgq.tsbg,qeå?rqni.ng- år Iq60 { avs*r tirlsn L?.5,1959-22.5.1960 ). tq 7 * {tao Sorn styrelse har fungo3s;: ordf. B. Lundblarl toilt Si-irsetrrr.P;'r Unze1l
FORMLER TILL NATIONELLT PROV I MATEMATIK KURS C OCH D
 (7 FORMLER TILL NTIONELLT PROV I MTEMTIK KURS OH D LGER Rgl dgdsktio ( + = + + ( = + (kdigsgl ( + ( = (kojugtgl ( + = + + + ( = + + = ( + ( + = ( ( + + Ektio + p+ q = ött p p p = + q o = dä + = p o = q
(7 FORMLER TILL NTIONELLT PROV I MTEMTIK KURS OH D LGER Rgl dgdsktio ( + = + + ( = + (kdigsgl ( + ( = (kojugtgl ( + = + + + ( = + + = ( + ( + = ( ( + + Ektio + p+ q = ött p p p = + q o = dä + = p o = q
undanträngda luften vilket motsvarar Flyft kraft skall först användas för att lyfta samma volym helium samt ballongens tyngd.
 FYSIKTÄVLINGEN Finalen - teori 1 maj 001 LÖSNINGSFÖRSLAG SVENSKA FYSIKERSAMFUNDET 1 Vi beräknar först lyftkraften för en ballong Antag att ballongen är sfärisk med diametern 4πr 4π 0,15 0 cm Den har då
FYSIKTÄVLINGEN Finalen - teori 1 maj 001 LÖSNINGSFÖRSLAG SVENSKA FYSIKERSAMFUNDET 1 Vi beräknar först lyftkraften för en ballong Antag att ballongen är sfärisk med diametern 4πr 4π 0,15 0 cm Den har då
1 Dimensionsanalys och π-satsen.
 Dimensionsanalys och π-satsen. Då man örsöker ställa upp en matematisk modell ör något ysikaliskt enomen skall man alltid göra dimensionsanalys. Dimensionsanalys handlar om att undersöka hur givna ysikaliska
Dimensionsanalys och π-satsen. Då man örsöker ställa upp en matematisk modell ör något ysikaliskt enomen skall man alltid göra dimensionsanalys. Dimensionsanalys handlar om att undersöka hur givna ysikaliska
SOS HT10. Punktskattning. Inferens för medelvärde ( ) och varians (σ 2 ) för ett stickprov. Punktskattningen räcker inte!
 aa O HT0 ervallkag uwe@mah.uu.e h://www.mah.uu.e/uwe/o_ht0 ervallkag rouko ere ör meelväre () och vara (σ ) ör e ckrov kag av är är kä kag av är är okä me or kag av är är okä och e heller or *A kaa e aaravvkele
aa O HT0 ervallkag uwe@mah.uu.e h://www.mah.uu.e/uwe/o_ht0 ervallkag rouko ere ör meelväre () och vara (σ ) ör e ckrov kag av är är kä kag av är är okä me or kag av är är okä och e heller or *A kaa e aaravvkele
7 Inställning av PID-regulatorer
 7 Intällnng av PID-regulatorer 7. PID-regulatorer 7. Spekatoner oh pretanakrterer. Pretana (elmnerng av törnngar, börväreöljnng). Stabltet (tabltetmargnal, robuthet) Stabltet har kuterat, pretana kan enera
7 Intällnng av PID-regulatorer 7. PID-regulatorer 7. Spekatoner oh pretanakrterer. Pretana (elmnerng av törnngar, börväreöljnng). Stabltet (tabltetmargnal, robuthet) Stabltet har kuterat, pretana kan enera
Höstlov i Motala 2010
 Höstlv i Mtl 2010 1-5 vbr S prgrt ch läs tt s sr udr årt på: tl.s/ug Bwlig Mtl Bwlighll Öppttidr Mådg 1/11 13.00-16.00 Tisdg 2/11 12.00-16.00 Osdg 3/11 13.00-16.00 Trsdg 4/11 12.00-16.00 Frdg 5/11 12.00-16.00
Höstlv i Mtl 2010 1-5 vbr S prgrt ch läs tt s sr udr årt på: tl.s/ug Bwlig Mtl Bwlighll Öppttidr Mådg 1/11 13.00-16.00 Tisdg 2/11 12.00-16.00 Osdg 3/11 13.00-16.00 Trsdg 4/11 12.00-16.00 Frdg 5/11 12.00-16.00
GOSPEL PÅ SVENSKA 2. Innehåll
 GOSPEL PÅ SVENSKA 2 Innehåll Kom oh se 7 Lovsung vår Gud 8 Barmhärtige Gud 10 Igen 11 är min Herde 1 Ditt Ord estår 16 redo 18 När delar 21 Herre hör vår ön 2 Vår ader 2 ör mig 26 O Herre längtar 28 Hallelua,
GOSPEL PÅ SVENSKA 2 Innehåll Kom oh se 7 Lovsung vår Gud 8 Barmhärtige Gud 10 Igen 11 är min Herde 1 Ditt Ord estår 16 redo 18 När delar 21 Herre hör vår ön 2 Vår ader 2 ör mig 26 O Herre längtar 28 Hallelua,
Inlämningsuppgift 2 i Digital signalbehandling ESS040, HT 2010 Måndagen den 22 november 2010 i E:B.
 Ilämigsuppgift i Digital sigalbhadlig ESS040, T 00 Mådag d ovmbr 00 i EB. I kurs gs två obligatoriska ilämigsuppgiftr som kombiras md frivilliga duggor. Ilämigsuppgiftra är obligatoriska och rsättr 6 timmars
Ilämigsuppgift i Digital sigalbhadlig ESS040, T 00 Mådag d ovmbr 00 i EB. I kurs gs två obligatoriska ilämigsuppgiftr som kombiras md frivilliga duggor. Ilämigsuppgiftra är obligatoriska och rsättr 6 timmars
Västerviks Museum & Naturum Västervik -där Natur och Kultur möts SKOLPROGRAM 2014-2015
 Värv Muu & Nuru Värv -där Nur och Kulur ö SKOLPROGRAM 2014-2015 Värv Muu 0490 211 77 www.vrvuu. Värv Muu Solprogr Värv Muu hr hl ou o rboråd och rbjudr ägd vr o rör Tjubygd ulurrv och ulurljör. Nu hr v
Värv Muu & Nuru Värv -där Nur och Kulur ö SKOLPROGRAM 2014-2015 Värv Muu 0490 211 77 www.vrvuu. Värv Muu Solprogr Värv Muu hr hl ou o rboråd och rbjudr ägd vr o rör Tjubygd ulurrv och ulurljör. Nu hr v
bruksanvisning/ user manual
 bruksanvisning/ user manual IBU 50 - IBU 50 RF L ä s d e n n a b r u k s a n v i s n i n g f ö r s t! B ä s t a k u n d, T a c k f ö r a t t d u h a r v a l t a t t k -p ö pra o deun k t C. y lvii n dhao
bruksanvisning/ user manual IBU 50 - IBU 50 RF L ä s d e n n a b r u k s a n v i s n i n g f ö r s t! B ä s t a k u n d, T a c k f ö r a t t d u h a r v a l t a t t k -p ö pra o deun k t C. y lvii n dhao
Sammanfattning, Dag 9
 Smmnfttning, Dg 9 Idg studerde vi begrepp sklärprudokt (eller innerprodukt), norm och ortogonlitet på ett llmänt vektorrum. Vi börjde med en kort repetition på smm begrep för vektorrummet R 3. I rummet
Smmnfttning, Dg 9 Idg studerde vi begrepp sklärprudokt (eller innerprodukt), norm och ortogonlitet på ett llmänt vektorrum. Vi börjde med en kort repetition på smm begrep för vektorrummet R 3. I rummet
Schrödingerekvationen i 3 dim: Väteatomen.
 Föläsig : Schödigkvtio i di: Vätto. Lösts v Schödig 96. Fökl spktllij få vätt och vis däd tt S. fg!!! Schödig kv i D: Ψ(, t) U( )Ψ(, t) i Ψ(, t) t Solikhtstolkig: Ψ(, t) d Noig: Ψ(, t ) d Sttioä tillståd:
Föläsig : Schödigkvtio i di: Vätto. Lösts v Schödig 96. Fökl spktllij få vätt och vis däd tt S. fg!!! Schödig kv i D: Ψ(, t) U( )Ψ(, t) i Ψ(, t) t Solikhtstolkig: Ψ(, t) d Noig: Ψ(, t ) d Sttioä tillståd:
Att större akuta reparationer. Ansvarsfrihet fiir styrelsen
 Åmöte Smtillighete Bkbdet 24 ktbe 2012 Plt :Håktpkl mtl 1 Vl v dtide ch eketee ii tämm Till dde vlde Mget Eic ch till eketee vlde Mgu Tte 2 Vl v juteigmä Till juteigmä vlde Åke Glud ch Cut Gutv 3 Mötet
Åmöte Smtillighete Bkbdet 24 ktbe 2012 Plt :Håktpkl mtl 1 Vl v dtide ch eketee ii tämm Till dde vlde Mget Eic ch till eketee vlde Mgu Tte 2 Vl v juteigmä Till juteigmä vlde Åke Glud ch Cut Gutv 3 Mötet
Föreläsning 10. java.lang.string. java.lang.string. Stränghantering
 Föläig Stäghtig j.lg.stig E täg btå tt tl tc Stäg i ht om objt l Stig E täg it modifi ft tt d h pt! Stig - l : ch[] - cot : it + lgth(): it + chat(it): ch + idxof(ch): it E täg h: Ett äd och lägd Ett tl
Föläig Stäghtig j.lg.stig E täg btå tt tl tc Stäg i ht om objt l Stig E täg it modifi ft tt d h pt! Stig - l : ch[] - cot : it + lgth(): it + chat(it): ch + idxof(ch): it E täg h: Ett äd och lägd Ett tl
