Kap Dubbelintegraler.
|
|
|
- Erik Månsson
- för 7 år sedan
- Visningar:
Transkript
1 Kap ubbelintegraler. A. Beräkna följande dubbelintegraler a. d. (x + y) dxdy, över kvadraten x 3, y. (sin y + y cos x) dxdy, då ges av x π, y π. x cos xy dxdy, då ges av x π, y. xy cos (x + y ) dxdy, över x π, y π. C. Låt vara kvadraten x, y. Ange en Riemannsumma för xy dxdy, svarande mot en indelning av i kvadrater med sidan n och valet av (x k, y k ) punkter i kvadratens hörn. Beräkna integralen genom att låta n gå mot. A 3. Man beräknar en dubbelintegral f(x,y) dxdy och integrerar först med avseende på y. etta leder till beräkning av två enkelintegraler. Bestäm integrationsgränserna i dessa om a. ges av y x y och x begränsas av kurvorna y = x och y = x 4 är triangeln med hörnen i punkterna (,), (,) och (,) d. definieras genom x + y 5 och y x.
2 A 4. Följande upprepade enkelintegraler kan uppfattas som dubbelintegraler över ett område. Ange. x a. dx x / f(x,y) dy 4 x dx f(x,y) dy. x dx x f(x,y) dy A 5. Samma uppgift som i 3, men nu sker integrationen först i x-led. 6. Kasta om integrationsordningen x A a. dx f(x,y) dy x 3 e ln x A dx f (x,y) dy B 6 x dx B d. dy x 4 f(x,y) dy y f(x,y) dx + y dy y f(x,y) dx. y A 7. Beräkna följande dubbelintegraler: a. (xy + y ) dxdy, ges av x, y x + x + y dxdy, är den del av första kvadranten som begränsas av parabeln y = x samt linjerna y = och x = e x y dxdy, över triangeln med hörnen i punkterna (, ), (,) och (,)
3 A 7 d. dxdy, definieras genom x + y 6, x y och x e. xy dxdy, över fyrhörningen med hörnen i punkterna (,), (,), (,) och (,4) f. dxdy, då är triangeln med hörnen i punkterna + y 4 (,), (,) och (,) g. ( + x + y) dxdy, då begränsas av linjerna y = x, y = x och x = ± h. x y ey dxdy, då är fyrhörningen med hörnen i punkterna (,), (,), (,) och (,) i. y x dxdy, då begränsas av linjerna y + x =, x = och y = 4 j. dy y cos x 5 dx y k. (y x 8) dxdy, begränsas av y = x, y = (x ) och y = (x 4) l. ( x + y ) dxdy, definieras genom x + y m. (x + y) e y dxdy, över triangeln med hörnen i punkterna (,), (,) och (,) n. o. x dxdy, begränsas av hyperbeln xy = och linjerna y x =, y = x x y x 3 y 3 dxdy, begränsas av kurvan x 3 + y 3 = och koordinataxlarna 3
4 A 7 p. dx y sin y cos x y dy x q. r. y x dxdy, ges av x, y x och y x ( + x + y) dxdy, är triangeln med hörnen i punkterna (,), (,) och (,) s. e y dxdy, ges av x y t. x e xy dxdy, över området x, xy u. x 3 y dxdy, är cirkelskivan x + y r. B 8. Beräkna följande dubbelintegraler: a. d. x + y dxdy, definieras genom x y + y x + x 4 dxdy, ges av x och xy y x + xy dxdy, ges av y x x 3 ( + y) dxdy, över området x + y, x och y e. cos (x + y) dxdy, över kvadraten x π och y π f. x dxdy, då begränsas av parablerna y = x x och x = y y y g. dy y y y x + x 3 dx + y dxdy, då ges av x, + x3 4
5 B 8 h. cos yx dxdy, begränsas av kurvan yx 3 = π samt linjerna x =, x = och y = i. j. k. 3 y x dxdy, begränsas av y = x + x och y = x 3 + x (x y y 5 ) dxdy, över området y x y, y x + x dxdy, över triangeln med hörnen i punkterna 3 + x y (,), (,) och (, ) l. cos x y dxdy, ges av y x πy, y π m. dxdy, ges av y 3x 3y 9 (x + y) x n. x dxdy, då begränsas av y-axeln samt linjerna y =, x + y3 y = och y = x. B 9. Låt f(x,y) vara det största av talen 9y 4x och 8y 3x. Beräkna dubbelintegralen f(x,y) dxdy, då är rektangeln x, y. B. B. Beräkna x dxdy, över det område som begränsas av hyperbeln xy =, där x >, och dess normaler i punkterna (,) och (,). Bestäm, så att (x x y ) dxdy antar största möjliga värdet och bestäm detta värde. B. Låt f(a,b) = x 3 b + y3 a dxdy, där är rektangeln < x < a, < y < Bestäm eventuella lokala extrempunkter (och deras karaktär) till f. 5
6 B 3. Beräkna följande dubbelintegraler: a. ( heltalsdelen av (x + y) ) dxdy, då ges av x och y ( tecken av (x y + ) ) dxdy, då ges av x + y 4. B 4. Visa att lim r πr f(x,y) dxdy = f(,), där r är cirkelskivan r x + y r och f är en kontinuerlig funktion. 5. Bestäm projektionen på xy-planet av den kropp som begränsas av A a. paraboloiden z = x + y och planet z = x + y A paraboliska cylindrarna z = x och z = y A paraboloiden z = x + y och paraboliska cylindern z = y A d. paraboliska cylindern y = x samt planen x + y + z = 4 och z = A e. cylindrarna x + y = x och x + y = y samt planen z = och z = x + y A f. hyperboliska paraboloiden z = xy, planen x = och y = samt ytan xyz =. A g. paraboliska cylindern x = y samt planen x + y + z = och 3x + z = A h. ytan z = ( + y ) x samt planen x = y, x =, y =, z = A i. ytan z = (y x)(x y ) A j. ytan z = (y x) (y x + ) A k. planet z = och den del av klotet x + y + z = där z B l. ellipsoiden x + y + z xz =. 6
7 Ledningar till uppgifterna 5. a. (x + y) dxdy = dx 3 = x + dx =. 3 3 (x + y) dy = xy + y = y y = dx = (sin y + y cos x) dxdy = dy (sin y + y cos x) dx = = π/[(x sin y + y sin x)] x = π/ π/ x = dy = π sin y + y dy =. π x cos xy dxdy = dx x cos xy dy = [sin xy] y = y = dx = π = sin x dx =. π/ π/ π π d. xy cos(x + y ) dxdy = π dx xy cos(x + y ) dy = π = x sin(x + y ) y π = π dx = x y = sin(x + π) x sin x dx. e valda punkterna är på formen (m,l) och man behöver beräkna summan av termer ml, där m och l varierar mellan n n4 och n. 3 a-d. Skissera. 4 a- Integrationsgränserna i den inre integralen beskriver begränsningskurvorna y = y(x). 7
8 5 Jämför med 3. 6 a. x 3 y x, x y x 3 y, y. y ln x, x e e y x e, y. x 4 y x, 6 x + y x + y, y eller + y x y, y 8. d. y x y, y eller y x y, x x y x, y. 7 a. (xy + y ) dxdy = dx = x x3 dx =. x (xy + y ) dy = xy + y = x 3 y3 y = dx = + x + y dxdy = dy + x + y dx = [(ln( + x + y))] dy x = y y = (ln ln( + y)) dy =. x = e x y = e x e y. d. ela upp i två delmängder med linjen x =. Integrera över var och en av dessa delmängder. e. Integrera först i y-led. f. Integrera först i x-led. g. Skissera. ela upp i två delmängder. h. Skissera. Integrera först i x-led. i. ela upp i två delmängder A och B, på vilka y x är respektive : A = den del av som ligger under linjen y x. y x dxdy = A (y x) dxdy + B (x y) dxdy. j. Kasta om integrationsordningen. k. ela upp i två delmängder med linjen x =. Integrera först i y- led. l. På grund av symmetrin räcker det att integrera över första kvadranten. Resultatet multipliceras med 4. 8
9 7 m. Integrera först i x-led. Partialintegrera. n. Skissera. Integrera först i y-led. o. Om man börjar integrera i y-led kan y 3 = t substitueras. p. Kasta om integrationsordningen. q. Skissera. Integrera först i y-led. r. Integrera först i x-led. s. Integrera först i x-led. t. Integrera först i y-led. u. Grafen är symmetrisk med avseende på origo. 8 a. Integrera först i x-led. Substituera y = t. Integrera först i y-led. Substituera x y = t. Integrera först i y-led. Substituera y x = t. d. Integrera först i x-led. Observera att täljaren får faktorn ( + y). e. ela upp i delområden på vilka cos (x + y) har konstant tecken. f. Hur ligger kurvorna i förhållande till linjen y = x? ela upp i två delområden. g. Skissera det totala integrationsområdet. Uttryck summan som en integral. h. Integrera först i y-led. Substituera π x = t. i. Sök kurvornas skärningspunkter och undersök hur kurvorna ligger i förhållande till varandra. j. Grafen är symmetrisk med avseende på x-axeln. k. Grafen är symmetrisk med avseende på xz-planet. Integrera först i x-led. Substituera y = sin t. Observera att cos t = + cos t. l. Integrera först i x-led. Partiell integration i y-led. m. Integrera först i x-led. Substituera x = t. n. Integrera först i x-led. Partiell integration i y-led. 9 ela upp i två delar A och B på vilka 9y 4x 8y 3x respektive 9y 4x 8y 3x. A = den del av där y x. Skissera området. ela upp i två dubbelintegraler. Största värdet fås då integranden är i alla punkter på. 9
10 Beräkna integralen. Man får en stationär punkt (a,b) = (,). 3 a. Undersök på vilka delar av integranden är =, =, osv. Undersök på vilka delar av integranden är =, =. 4. Använd medelvärdessatsen. 5 a-h. Eliminera z. en erhållna ekvationen samt de kvarvarande sambanden (i defgh) beskriver randkurvorna till den sökta mängden. i-l. Andragradsekvationen definierar två kontinuerliga funktioner z = z(x,y) av typen z = ±. eras grafer utgör kroppens begränsning i z led (i 95 k är planet z = en del av begränsning). Identifiering av dessa funktioner ( = ) ger ekvationen för projektionens rand.
11 Svar till uppgifterna 5. a. 3. π + π 8.. d.. 3 a. d. 4. dx dx dx 5 x x / f(x,y) dy. x f(x,y) dy. x 5 x f(x,y) dy + 5 x dx x dx 5 x f(x,y) dy. x f(x,y) dy. x 4 4 a. x, x y x. x y, x. x y 4 x, x. 5 a. d. y dy f(x,y) dx + y y dy f(x,y) dx + 4 y dy dy y y f(x,y) dx + y 5 y dy f(x,y) dx. y 4 y dy f(x,y) dx. y dy y 5 f(x,y) dx + dy f(x,y) dx. 5 y f(x,y) dx. 5 y
12 6 a. d. 3 y dy y dy dx f(x,y) dx. + y + y x f(x,y) dx + x f(x,y) dy. 8 dy y + y e dye y f(x,y) dx. f(x,y) dx. 7 a. e. 5. ln. 4 (e + e ). d. 4 9 ( 8 ). f. g.. h ln ( + ). e. i j. sin 3. k. 8 ( ln ). l m.. n o. 4. p. ( cos ) sin. 35 q. 6. r. ln 3 3. s. (e ). t. e e. u.. 8 a. 3 ( ln ). arctan π 4 ln 5. π ln. d.. e. π. f g. 4 ln 3. h. π.
13 8 i.. j.. k. π 3 3. l. π. m. π 3 ( 3 ). n. ln x x y ; π 3. Lokalt minimum i punkten (,). 3 a. 6. 4π ln ( + 3) 4 ln. 5 a. (x ) + (y ). x + y. x + 4y. d. y x, x + y 4. e. x + y x, x + y y. f. xy, x, y. g. y x, x + y. h. y x. i. y x y. j. y x (y + ). k. x + y. l. 3x + 4y 4. 3
Kap Generaliserade multipelintegraler.
 Kap 4.3. Generaliserade multipelintegraler. 50. Beräkna följande generaliserade multipelintegraler: A a. dxdy, ges av x, 0 xy x A b. A c. A d. A e. K x ( + x 2 )( + x 2 y 2 ) dxdy, ges av x > 0, xy x dxdy,
Kap 4.3. Generaliserade multipelintegraler. 50. Beräkna följande generaliserade multipelintegraler: A a. dxdy, ges av x, 0 xy x A b. A c. A d. A e. K x ( + x 2 )( + x 2 y 2 ) dxdy, ges av x > 0, xy x dxdy,
1. Bestäm definitionsmängden och värdemängden till funktionen f(x,y) = 1 2x 2 3y 2. Skissera definitionsmängden, nivålinjerna och grafen till f.
 1. Bestäm definitionsmängden och värdemängden till funktionen f(x,y) = 1 2x 2 3y 2. Skissera definitionsmängden, nivålinjerna och grafen till f. 2. Beräkna gränsvärdet (eller visa att det inte finns):
1. Bestäm definitionsmängden och värdemängden till funktionen f(x,y) = 1 2x 2 3y 2. Skissera definitionsmängden, nivålinjerna och grafen till f. 2. Beräkna gränsvärdet (eller visa att det inte finns):
) 2 = 1, där a 1. x + b 2. y + c 2
 ap 7 Användningar av multipelintegraler Arean av ett plant område 0 Beräkna arean av det område som begränsas av följande kurvor: A a (x y) 2 + x 2 = a 2 A b xy =, xy = 8, y = x och y = 2x (x > ) A c y
ap 7 Användningar av multipelintegraler Arean av ett plant område 0 Beräkna arean av det område som begränsas av följande kurvor: A a (x y) 2 + x 2 = a 2 A b xy =, xy = 8, y = x och y = 2x (x > ) A c y
Visa att vektorfältet F har en potential och bestäm denna. a. F = (3x 2 y 2 + y, 2x 3 y + x) b. F = (2x + y, x + 2z, 2y 2z)
 Kap. 15.1 15.2, 15.4, 16.3. Vektorfält, integralkurva, konservativa fält, potential, linjeintegraler av vektorfält, enkelt sammanhängande område, oberoendet av vägen, Greens formel. A 1701. Undersök om
Kap. 15.1 15.2, 15.4, 16.3. Vektorfält, integralkurva, konservativa fält, potential, linjeintegraler av vektorfält, enkelt sammanhängande område, oberoendet av vägen, Greens formel. A 1701. Undersök om
Kontrollskrivning 1A
 Kontrollskrivning 1A i 5B1147 Flervariabelanalys för E, vt 2007. 1. Låt g(t) vara en deriverbar envariabelsfunktion. Visa att tvåvariabelsfunktionen f(x, y) = g(2x y 2 ) satisfierar den partiella differentialekvationen
Kontrollskrivning 1A i 5B1147 Flervariabelanalys för E, vt 2007. 1. Låt g(t) vara en deriverbar envariabelsfunktion. Visa att tvåvariabelsfunktionen f(x, y) = g(2x y 2 ) satisfierar den partiella differentialekvationen
1. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t).
 Repetition, analys.. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t). 2. Beräkna längden av kurvan r(t) =
Repetition, analys.. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t). 2. Beräkna längden av kurvan r(t) =
Kap Globala extremvärden, extremproblem med bivillkor.
 Kap 13.2 13.3. Globala extremvärden, extremproblem med bivillkor. A 1001. Sök det största och minsta värdet av funktionen f(x,y) = x 2 + 2y 2 x på cirkeln x 2 + y 2 = 1. A 1002. Vilka värden kan funktionen
Kap 13.2 13.3. Globala extremvärden, extremproblem med bivillkor. A 1001. Sök det största och minsta värdet av funktionen f(x,y) = x 2 + 2y 2 x på cirkeln x 2 + y 2 = 1. A 1002. Vilka värden kan funktionen
Kap 5.7, Beräkning av plana areor, rotationsvolymer, rotationsareor, båglängder.
 Kap 5.7, 7. 7.. Beräkning av plana areor, rotationsvolymer, rotationsareor, båglängder. 8. (A) Beräkna arean av det ändliga område som begränsas av kurvorna x a. y = + x och y = b. y = x e x och y = x
Kap 5.7, 7. 7.. Beräkning av plana areor, rotationsvolymer, rotationsareor, båglängder. 8. (A) Beräkna arean av det ändliga område som begränsas av kurvorna x a. y = + x och y = b. y = x e x och y = x
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
x ( f u 2y + f v 2x) xy = 24 och C = f
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
Låt vara en reell funktion av en reell variabel med definitionsmängden som är symmetrisk i origo.
 UDDA FUNKTIONER OCH DUBBELINTEGRALER. Från en variabelanalys vet vi att integral över ett symetrisk intervall, av en udda funktion är lika med 0. 0 om är udda. T ex 0 Här upprepar vi def. av udda ( och
UDDA FUNKTIONER OCH DUBBELINTEGRALER. Från en variabelanalys vet vi att integral över ett symetrisk intervall, av en udda funktion är lika med 0. 0 om är udda. T ex 0 Här upprepar vi def. av udda ( och
Lösning till kontrollskrivning 1A
 KTH Matematik Olle Stormark Lösning till kontrollskrivning 1A i SF1626 Flervariabelanalys för E, vt 28. Varje uppgift ger maximalt 3 poäng. För godkänt krävs minst 5 poäng sammanlagt. 1. Funktionen f(x,
KTH Matematik Olle Stormark Lösning till kontrollskrivning 1A i SF1626 Flervariabelanalys för E, vt 28. Varje uppgift ger maximalt 3 poäng. För godkänt krävs minst 5 poäng sammanlagt. 1. Funktionen f(x,
SF1626 Flervariabelanalys
 1 / 19 SF1626 Flervariabelanalys Föreläsning 1 Henrik Shahgholian Vid Institutionen för matematik, KTH VT 218, Period 3 2 / 19 SF1626 Flervariabelanalys agens Lektion ubbelintegraler: Avsnitt 14.1-14.2
1 / 19 SF1626 Flervariabelanalys Föreläsning 1 Henrik Shahgholian Vid Institutionen för matematik, KTH VT 218, Period 3 2 / 19 SF1626 Flervariabelanalys agens Lektion ubbelintegraler: Avsnitt 14.1-14.2
Inlämningsuppgift nr 2, lösningar
 UPPALA UNIVRITT MATMATIKA INTITUTIONN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 8 Inlämningsuppgift nr, lösningar. Visa att ekvationen x + x(y ) + (y ) + z + sin(yz) definierar z som en funktion
UPPALA UNIVRITT MATMATIKA INTITUTIONN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 8 Inlämningsuppgift nr, lösningar. Visa att ekvationen x + x(y ) + (y ) + z + sin(yz) definierar z som en funktion
har ekvation (2, 3, 4) (x 1, y 1, z 1) = 0, eller 2x + 3y + 4z = 9. b) Vi söker P 1 = F (1, 1, 1) + F (1, 1, 1) (x 1, y 1, z 1) = 2x + 3y + 4z.
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
SF1625 Envariabelanalys Lösningsförslag till tentamen
 SF1625 Envariabelanalys Lösningsförslag till tentamen 216-6-1 1. Derivera nedanstående funktioner med avseende på x och ange för vilka x derivatan existerar. Endast svar krävs. A. f(x) = arctan 1 x B.
SF1625 Envariabelanalys Lösningsförslag till tentamen 216-6-1 1. Derivera nedanstående funktioner med avseende på x och ange för vilka x derivatan existerar. Endast svar krävs. A. f(x) = arctan 1 x B.
Tentamen SF1626, Analys i flera variabler, Svar och lösningsförslag. 2. en punkt på randkurvan förutom hörnen, eller
 Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
DUBBELINTEGRALER. Rektangulära (xy) koordinater
 ubbelintegraler. -koordinater UBBELINTEGRALER. Rektangulära ( koordinater efinition. Låt zf(, vara en reell funktion av två variabler och. Vi delar integrationsområde (definitionsområde) i ändligt antal
ubbelintegraler. -koordinater UBBELINTEGRALER. Rektangulära ( koordinater efinition. Låt zf(, vara en reell funktion av två variabler och. Vi delar integrationsområde (definitionsområde) i ändligt antal
Dubbelintegraler och volymberäkning
 ubbelintegraler och volymberäkning Volym och dubbelintegraler över en rektangel Alla funktioner nedan antas vara kontinuerliga. Om f (x) i intervallet [a, b], så är arean av mängden {(x, y) : y f (x),
ubbelintegraler och volymberäkning Volym och dubbelintegraler över en rektangel Alla funktioner nedan antas vara kontinuerliga. Om f (x) i intervallet [a, b], så är arean av mängden {(x, y) : y f (x),
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 16-8-18 DEL A 1 Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x oc y = x Beräkna x-koordinaten
SF166 Flervariabelanalys Lösningsförslag till tentamen 16-8-18 DEL A 1 Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x oc y = x Beräkna x-koordinaten
SF1626 Flervariabelanalys Tentamen 18 augusti 2011, Svar och lösningsförslag
 SF166 Flervariabelanalys entamen 18 augusti 11, 14. - 19. Svar och lösningsförslag 1) Låt fx, y) = xy lnx + y ). I vilken riktning är riktningsderivatan till f i punkten 1, ) som störst, och hur stor är
SF166 Flervariabelanalys entamen 18 augusti 11, 14. - 19. Svar och lösningsförslag 1) Låt fx, y) = xy lnx + y ). I vilken riktning är riktningsderivatan till f i punkten 1, ) som störst, och hur stor är
SF1626 Flervariabelanalys
 Föreläsning 11 Institutionen för matematik KTH VT 2018 1 agens program Variabelsubstitution i dubbelintegraler Något om generaliserade integraler och medelvärden Bokens kapitel 14.4 och i någon mån också
Föreläsning 11 Institutionen för matematik KTH VT 2018 1 agens program Variabelsubstitution i dubbelintegraler Något om generaliserade integraler och medelvärden Bokens kapitel 14.4 och i någon mån också
Övningar till Matematisk analys III Erik Svensson
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik -8-8 Övningar till Matematisk analys III Erik Svensson. För varje gränsvärde nedan bestäm gränsvärdet eller visa att gränsvärdet inte existerar.
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik -8-8 Övningar till Matematisk analys III Erik Svensson. För varje gränsvärde nedan bestäm gränsvärdet eller visa att gränsvärdet inte existerar.
Repetition, Matematik 2 för lärare. Ï x + 2y - 3z = 1 Ô Ì 3x - y + 2z = a Ô Á. . Beräkna ABT. Beräkna (AB) T
 Repetition, Matematik 2 för lärare Ï -2x + y + 2z = 3 1. Ange för alla reella a lösningsmängden till ekvationssystemet Ì ax + 2y + z = 1. Ó x + 3y - z = 4 2. Vad är villkoret på talet a för att ekvationssystemet
Repetition, Matematik 2 för lärare Ï -2x + y + 2z = 3 1. Ange för alla reella a lösningsmängden till ekvationssystemet Ì ax + 2y + z = 1. Ó x + 3y - z = 4 2. Vad är villkoret på talet a för att ekvationssystemet
SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
(x + 1) dxdy där D är det ändliga område som begränsas av kurvorna
 UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik ES, W Flervariabelanalys 8 1 1 Skrivtid: 9-1. Inga hjälpmedel. Lösningarna skall åtföljas av förklarande text/figurer. Varje
UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik ES, W Flervariabelanalys 8 1 1 Skrivtid: 9-1. Inga hjälpmedel. Lösningarna skall åtföljas av förklarande text/figurer. Varje
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Lösningsförslag till tentamen Torsdag augusti 16, 2018 DEL A
 Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
SF1626 Flervariabelanalys Tentamen Torsdagen den 18 augusti 2016
 Institutionen för matematik SF166 Flervariabelanalys Tentamen Torsdagen den 18 augusti 16 Skrivtid: 8:-1: Tillåtna jälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF166 Flervariabelanalys Tentamen Torsdagen den 18 augusti 16 Skrivtid: 8:-1: Tillåtna jälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A. 1. En svängningsrörelse beskrivs av
 SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen 4-9-6 DEL A. Betrakta följande tre områden i planet: D = {(x, y): x y < 4}, D = {(x, y): x + y }, D 3 = {(x, y): 4x + 3y
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen 4-9-6 DEL A. Betrakta följande tre områden i planet: D = {(x, y): x y < 4}, D = {(x, y): x + y }, D 3 = {(x, y): 4x + 3y
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
Bestäm ekvationen för det plan som går genom punkten (1,1, 2 ) på kurvan och som spänns
 UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik Q Flervariabelanalys 8--1 Skrivtid: 8-1. Inga hjälpmedel. Lösningarna skall åtföljas av förklarande text/figurer. Tentand
UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik Q Flervariabelanalys 8--1 Skrivtid: 8-1. Inga hjälpmedel. Lösningarna skall åtföljas av förklarande text/figurer. Tentand
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud B 7, ifferential- och integralkalkyl II, del, flervariabel, för F. Tentamen tisdag 8 augusti 7, 4.-9. Förslag till lösningar.. Om F (x, y, z) x y + y z
Institutionen för Matematik, KTH Torbjörn Kolsrud B 7, ifferential- och integralkalkyl II, del, flervariabel, för F. Tentamen tisdag 8 augusti 7, 4.-9. Förslag till lösningar.. Om F (x, y, z) x y + y z
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Tentamen i Matematisk analys, HF1905 exempel 1 Datum: xxxxxx Skrivtid: 4 timmar Examinator: Armin Halilovic
 Tentamen i Matematisk analys, HF95 exempel atum: xxxxxx Skrivtid: timmar Examinator: Armin Halilovic För godkänt betyg krävs av max poäng Betygsgränser: För betyg A, B, C,, E krävs, 9, 6, respektive poäng
Tentamen i Matematisk analys, HF95 exempel atum: xxxxxx Skrivtid: timmar Examinator: Armin Halilovic För godkänt betyg krävs av max poäng Betygsgränser: För betyg A, B, C,, E krävs, 9, 6, respektive poäng
SF1646 Analys i flera variabler Tentamen 18 augusti 2011, Svar och lösningsförslag
 SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
Högskolan i Skövde (SK, JS) Svensk version Tentamen i matematik Lösningsförslag till del I
 Högskolan i Skövde (SK, JS) Svensk version Tentamen i matematik Lösningsförslag till del I Kurs: MA15G Matematisk Analys MA13G Matematisk analys för ingenjörer MA71A Matematik för lärare C, delkurs Matematisk
Högskolan i Skövde (SK, JS) Svensk version Tentamen i matematik Lösningsförslag till del I Kurs: MA15G Matematisk Analys MA13G Matematisk analys för ingenjörer MA71A Matematik för lärare C, delkurs Matematisk
Tentan , lösningar
 UPPALA UNIVERITET MATEMATIKA INTITUTIONEN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 2008 Tentan 2008-12-16, lösningar 1. Avgör om det finns någon punkt på ytan (x 1) 2 + 2(y 1) 2 + 2z 8 som är
UPPALA UNIVERITET MATEMATIKA INTITUTIONEN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 2008 Tentan 2008-12-16, lösningar 1. Avgör om det finns någon punkt på ytan (x 1) 2 + 2(y 1) 2 + 2z 8 som är
4x 2 dx = [polynomdivision] 2x x + 1 dx. (sin 2 (x) ) 2. = cos 2 (x) ) 2. t = cos(x),
![4x 2 dx = [polynomdivision] 2x x + 1 dx. (sin 2 (x) ) 2. = cos 2 (x) ) 2. t = cos(x), 4x 2 dx = [polynomdivision] 2x x + 1 dx. (sin 2 (x) ) 2. = cos 2 (x) ) 2. t = cos(x),](/thumbs/104/163513760.jpg) Lunds Tekniska Högskola Matematik Helsingborg Lösningar Analys, FMAA5 9-8-9. a) e sinx) cosx) dx e sinx) + C. b) 4x dx polynomdivision] x + x + x + dx x x + ] ln x + + ) ln) + ) ln) ln). c) Trigonometriska
Lunds Tekniska Högskola Matematik Helsingborg Lösningar Analys, FMAA5 9-8-9. a) e sinx) cosx) dx e sinx) + C. b) 4x dx polynomdivision] x + x + x + dx x x + ] ln x + + ) ln) + ) ln) ln). c) Trigonometriska
MVE465. Innehållsförteckning
 Lösningar på övningsuppgifter Detta dokument innehåller mina renskrivna lösningar på övningsuppgifter i kursen Linjär algebra och analys fortsättning (). Jag kan inte lova att samtliga lösningar är välformulerade
Lösningar på övningsuppgifter Detta dokument innehåller mina renskrivna lösningar på övningsuppgifter i kursen Linjär algebra och analys fortsättning (). Jag kan inte lova att samtliga lösningar är välformulerade
Tentamen: Lösningsförslag
 Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF1625 Envariabelanalys Lösningsförslag till tentamen 2015-01-12 DEL A 1. Betrakta funktionen f som ges av f(x) = xe 1/x. A. Bestäm definitionsmängden till f. B. Beräkna de fyra gränsvärdena lim x ± f(x)
SF1625 Envariabelanalys Lösningsförslag till tentamen 2015-01-12 DEL A 1. Betrakta funktionen f som ges av f(x) = xe 1/x. A. Bestäm definitionsmängden till f. B. Beräkna de fyra gränsvärdena lim x ± f(x)
= 0 genom att införa de nya
 UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik ES, IT, W Flervariabelanals 9 1 19 Skrivtid: 8 13. Inga hjälpmedel. Lösningarna skall åtföljas av förklarande text/figurer.
UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik ES, IT, W Flervariabelanals 9 1 19 Skrivtid: 8 13. Inga hjälpmedel. Lösningarna skall åtföljas av förklarande text/figurer.
Institutionen för matematik KTH. Tentamensskrivning, , kl B1119, Vektoranalys, för Open.
 Institutionen för matematik KTH Tentamensskrivning, 25 6 3, kl 8 3 5B9, Vektoranalys, för Open Uppgifterna 4 5 svarar mot varsitt moment i den kontinuerliga examinationen Av dessa uppgifter skall man bara
Institutionen för matematik KTH Tentamensskrivning, 25 6 3, kl 8 3 5B9, Vektoranalys, för Open Uppgifterna 4 5 svarar mot varsitt moment i den kontinuerliga examinationen Av dessa uppgifter skall man bara
5B1134 Matematik och modeller Lösningsförslag till tentamen den 11 oktober 2004
 KTH Matematik 5B4 Matematik och modeller Lösningsförslag till tentamen den oktober 4. Två av sidlängderna i en triangel är 8 m och m. En av vinklarna är 6. a) Bestäm alla möjliga värden för den tredje
KTH Matematik 5B4 Matematik och modeller Lösningsförslag till tentamen den oktober 4. Två av sidlängderna i en triangel är 8 m och m. En av vinklarna är 6. a) Bestäm alla möjliga värden för den tredje
Tentamen i Analys B för KB/TB (TATA09/TEN1) kl 08 13
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Joakim Arnlind Tentamen i Analys B för KB/TB (TATA9/TEN1) 212-5-22 kl 8 13 Inga hjälpmedel är tillåtna. Varje uppgift kan ge maximalt 3 poäng. Betygsgränser:
LINKÖPINGS UNIVERSITET Matematiska Institutionen Joakim Arnlind Tentamen i Analys B för KB/TB (TATA9/TEN1) 212-5-22 kl 8 13 Inga hjälpmedel är tillåtna. Varje uppgift kan ge maximalt 3 poäng. Betygsgränser:
Flervariabelanalys och Matlab Kapitel 3
 Flervariabelanalys och Matlab Kapitel 3 Thomas Wernstål Matematiska Vetenskaper 28 september 2012 3 Multipelintegraler 3.1 ubbelintegraler I detta kapitel skall vi studera olika sätt på vilket man kan
Flervariabelanalys och Matlab Kapitel 3 Thomas Wernstål Matematiska Vetenskaper 28 september 2012 3 Multipelintegraler 3.1 ubbelintegraler I detta kapitel skall vi studera olika sätt på vilket man kan
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF1625 Envariabelanalys Lösningsförslag till tentamen 215-1-27 DEL A 4 1. Betrakta funktionen f som ges av f(x) = 1 + x + (x 2). 2 A. Bestäm definitionsmängden till f. B. Bestäm alla intervall där f är
SF1625 Envariabelanalys Lösningsförslag till tentamen 215-1-27 DEL A 4 1. Betrakta funktionen f som ges av f(x) = 1 + x + (x 2). 2 A. Bestäm definitionsmängden till f. B. Bestäm alla intervall där f är
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 24-8-2 DEL A. Bestäm och skissera definitionsmängden till funktionen fx, y) = x 2 + y 2 + 2x 4y + + x. Är definitionsmängden kompakt? 4 p) Lösning.
SF626 Flervariabelanalys Lösningsförslag till tentamen 24-8-2 DEL A. Bestäm och skissera definitionsmängden till funktionen fx, y) = x 2 + y 2 + 2x 4y + + x. Är definitionsmängden kompakt? 4 p) Lösning.
Tentamen i matematik. f(x) = ln(ln(x)),
 Lösningsförslag Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA52G Matematisk Analys MA23G Matematisk analys för ingenjörer Tentamensdag: 203-05- kl 4.30-9.30 Hjälpmedel : Inga hjälpmedel utöver
Lösningsförslag Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA52G Matematisk Analys MA23G Matematisk analys för ingenjörer Tentamensdag: 203-05- kl 4.30-9.30 Hjälpmedel : Inga hjälpmedel utöver
x 2 = lim x 2 x 2 x 2 x 2 x x+2 (x + 3)(x + x + 2) = lim x 2 (x + 1)
 Matematik Hjälpmedel: Inga Chalmers Tekniska Högskola Tentamen 5--7 kl. 4: 8: Telefonvakt: Samuel Bengmark ankn.: 7-87644 Betygsgränser :a poäng, 4:a poäng, 5:a 4 poäng, max: 5 poäng Tentamensgranskning
Matematik Hjälpmedel: Inga Chalmers Tekniska Högskola Tentamen 5--7 kl. 4: 8: Telefonvakt: Samuel Bengmark ankn.: 7-87644 Betygsgränser :a poäng, 4:a poäng, 5:a 4 poäng, max: 5 poäng Tentamensgranskning
( ) = 2x + y + 2 cos( x + 2y) omkring punkten ( 0, 0), och använd sedan detta ( ).
 KTH matematik Tentamen i SF66 Flervariabelanalys den 7 juni kl 8.3. Tillåtet hjälpmedel: Endast Beta Mathematics Handbook. Tydliga lösningar med fullständiga meningar och utförliga motiveringar krävs för
KTH matematik Tentamen i SF66 Flervariabelanalys den 7 juni kl 8.3. Tillåtet hjälpmedel: Endast Beta Mathematics Handbook. Tydliga lösningar med fullständiga meningar och utförliga motiveringar krävs för
10 Beräkning av dubbelintegraler
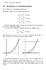 Nr,7april-,Amelia Beräkning av dubbelintegraler. Bte av integrationsordning Eempel (96) Kasta om integrationsordningen i a) b) c) Z Z e Z 6 Z d d d Z ln Z f(, )d f(, )d f(, )d. Lösning: Med hjälp av figurer
Nr,7april-,Amelia Beräkning av dubbelintegraler. Bte av integrationsordning Eempel (96) Kasta om integrationsordningen i a) b) c) Z Z e Z 6 Z d d d Z ln Z f(, )d f(, )d f(, )d. Lösning: Med hjälp av figurer
1 x. SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 26-3-2 DEL A. Låt D vara fyrhörningen med hörn i punkterna, ), 6, ),, 5) och 4, 5). a) Skissera fyrhörningen D och beräkna dess area. p) b) Bestäm
SF626 Flervariabelanalys Lösningsförslag till tentamen 26-3-2 DEL A. Låt D vara fyrhörningen med hörn i punkterna, ), 6, ),, 5) och 4, 5). a) Skissera fyrhörningen D och beräkna dess area. p) b) Bestäm
SF1625 Envariabelanalys Tentamen Måndagen den 12 januari 2015
 SF1625 Envariabelanalys Tentamen Måndagen den 12 januari 2015 Skrivtid: 08:00-13:00 Tillåtna hjälpmedel: inga Examinator: Lars Filipsson Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
SF1625 Envariabelanalys Tentamen Måndagen den 12 januari 2015 Skrivtid: 08:00-13:00 Tillåtna hjälpmedel: inga Examinator: Lars Filipsson Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
Tentamen i Envariabelanalys 2
 Linköpings universitet Matematiska institutionen Kurskod: TATA42 Provkod: TEN Tentamen i Envariabelanalys 2 206 0 8, 4 9 Inga hjälpmedel. Lösningarna ska vara fullständiga, välmotiverade, ordentligt skrivna
Linköpings universitet Matematiska institutionen Kurskod: TATA42 Provkod: TEN Tentamen i Envariabelanalys 2 206 0 8, 4 9 Inga hjälpmedel. Lösningarna ska vara fullständiga, välmotiverade, ordentligt skrivna
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
IV, SF1636(5B1210,5B1230).
 Lösningar till tentamensskrivning i Matematik I, F636(5B,5B3) Tisdagen den 9 augusti 8, kl 4-9 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar och resonemang
Lösningar till tentamensskrivning i Matematik I, F636(5B,5B3) Tisdagen den 9 augusti 8, kl 4-9 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar och resonemang
Studiehandledning till MMA128. Differential- och integralkalkyl III. Version
 Studiehandledning till MMA128 ifferential- och integralkalkyl III läsåret 2012/13 Version 2013-06-07 ursinformation för MMA128 Mål Avsikten med kursen MMA128 ifferential- och integralkalkyl III är att
Studiehandledning till MMA128 ifferential- och integralkalkyl III läsåret 2012/13 Version 2013-06-07 ursinformation för MMA128 Mål Avsikten med kursen MMA128 ifferential- och integralkalkyl III är att
UPPSALA UNIVERSITET Matematiska institutionen Michael Melgaard. Prov i matematik Prog: Datakand., Frist. kurser Derivator o integraler 1MA014
 UPPSALA UNIVERSITET Matematiska institutionen Michael Melgaard Jörgen Östensson Prov i matematik Prog: Datakand., Frist. kurser Derivator o integraler 1MA1 8 3 31 Skrivtid: 8: 13:. Tillåtna hjälpmedel:
UPPSALA UNIVERSITET Matematiska institutionen Michael Melgaard Jörgen Östensson Prov i matematik Prog: Datakand., Frist. kurser Derivator o integraler 1MA1 8 3 31 Skrivtid: 8: 13:. Tillåtna hjälpmedel:
SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015
 SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt
SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt
Typexempel med utförliga lösningar TMV130. Matem. Analys i En Var.. V, AT.
 Typexempel med utförliga lösningar TMV3. Matem. Analys i En Var.. V, AT. Försök alltid att lösa exemplen själv först. Integration. ([AE, Adams&Essex] Ex. 5.6. ) Beräkna integralen x + 6x + 3 dx LSN (Lösning).
Typexempel med utförliga lösningar TMV3. Matem. Analys i En Var.. V, AT. Försök alltid att lösa exemplen själv först. Integration. ([AE, Adams&Essex] Ex. 5.6. ) Beräkna integralen x + 6x + 3 dx LSN (Lösning).
Kap Funktioner av flera variabler, definitionsmängd, värdemängd, graf, nivåkurva. Gränsvärden, kontinuitet.
 Kap. 2. 2.2. Funktioner av flera variabler, definitionsmängd, värdemängd, graf, nivåkurva. Gränsvärden, kontinuitet. 20. Skissera definitionsmängden till följande funktioner: A a. f(,) = ln ( 2 2 ) A b.
Kap. 2. 2.2. Funktioner av flera variabler, definitionsmängd, värdemängd, graf, nivåkurva. Gränsvärden, kontinuitet. 20. Skissera definitionsmängden till följande funktioner: A a. f(,) = ln ( 2 2 ) A b.
= ( 1) xy 1. x 2y. y e
 Lösningsförslag, Matematik, B, E, I, IT, M, Media och T, -8- Den sista raden är nästan lika med den första raden med omvänt tecken Om vi därför adderar den första raden till den sista raden får vi en rad
Lösningsförslag, Matematik, B, E, I, IT, M, Media och T, -8- Den sista raden är nästan lika med den första raden med omvänt tecken Om vi därför adderar den första raden till den sista raden får vi en rad
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF165 Envariabelanalys Lösningsförslag till tentamen 01-1-10 DEL A 1. Låt funktionen f ha definitionsmängden D f =]0, [ och ges av f(x) = e x 1 x. (a) Finn f:s invers f 1. ( p) (b) Finn inversens värdemängd
SF165 Envariabelanalys Lösningsförslag till tentamen 01-1-10 DEL A 1. Låt funktionen f ha definitionsmängden D f =]0, [ och ges av f(x) = e x 1 x. (a) Finn f:s invers f 1. ( p) (b) Finn inversens värdemängd
SF1626 Flervariabelanalys Tentamen Tisdagen den 12 januari 2016
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den 2 januari 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den 2 januari 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
5B1134 Matematik och modeller Lösningsförslag till tentamen den 29 augusti 2005
 KTH Matematik 5B114 Matematik och modeller Lösningsförslag till tentamen den 29 augusti 2005 1. a) Om två av sidorna i en triangel är 5 meter respektive 6 meter. Vilka längder på den tredje sidans längd
KTH Matematik 5B114 Matematik och modeller Lösningsförslag till tentamen den 29 augusti 2005 1. a) Om två av sidorna i en triangel är 5 meter respektive 6 meter. Vilka längder på den tredje sidans längd
av envariabelfunktionen g(t) och flervariabelfunktionen t = h(x, y) = x 2 + e y.)
 Lösningsskisser till TATA69 Flervariabelanalys 16-1- 1 Stationära punkter ges av f (4x 3 + 4x, 3y + 6z, z + 6y (,,, dvs (x, y, z (,, eller (x, y, z (, 6, 18 Ur andraderivatorna fås de kvadratiska formerna
Lösningsskisser till TATA69 Flervariabelanalys 16-1- 1 Stationära punkter ges av f (4x 3 + 4x, 3y + 6z, z + 6y (,,, dvs (x, y, z (,, eller (x, y, z (, 6, 18 Ur andraderivatorna fås de kvadratiska formerna
4. Bestäm eventuella extrempunkter, inflexionspunkter samt horisontella och vertikala asymptoter till y = 1 x 1 + x, och rita funktionens graf.
 TM-Matematik Mikael Forsberg 73 1 3 31 Pär Hemström 7 3 57 För ingenjörs och distansstudenter Envariabelanalys ma3a 1 8 Skrivtid: 9:-1:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att
TM-Matematik Mikael Forsberg 73 1 3 31 Pär Hemström 7 3 57 För ingenjörs och distansstudenter Envariabelanalys ma3a 1 8 Skrivtid: 9:-1:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att
SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 2015 Skrivtid: 08:00-13:00 Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 2015 Skrivtid: 08:00-13:00 Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF165 Envariabelanalys Lösningsförslag till tentamen 15-4-7 DEL A 1. Låt f(x) = arcsin x + 1 x. A. Bestäm definitionsmängden till funktionen f. B. Bestäm funktionens största och minsta värde. (Om du har
SF165 Envariabelanalys Lösningsförslag till tentamen 15-4-7 DEL A 1. Låt f(x) = arcsin x + 1 x. A. Bestäm definitionsmängden till funktionen f. B. Bestäm funktionens största och minsta värde. (Om du har
Blandade A-uppgifter Matematisk analys
 TEKNISKA HÖGSKOLAN Matematik Blandade A-uppgifter Matematisk analys 1 Låt u = i och v = 1 + i Skriv det komplexa talet z = u/v på den polära formen re iϕ Svar: e i π Bestäm de reella tal x för vilka x
TEKNISKA HÖGSKOLAN Matematik Blandade A-uppgifter Matematisk analys 1 Låt u = i och v = 1 + i Skriv det komplexa talet z = u/v på den polära formen re iϕ Svar: e i π Bestäm de reella tal x för vilka x
TMV036 Analys och Linjär Algebra K Kf Bt, del C
 MATEMATIK Hjälpmedel: Inga Chalmers tekniska högskola Datum: -- kl 4 8 Tentamen Telefonvakt: Richard Lärkäng tel 3-8834 TMV36 Analys och Linjär Algebra K Kf Bt, del C Tentan rättas och bedöms anonymt Skriv
MATEMATIK Hjälpmedel: Inga Chalmers tekniska högskola Datum: -- kl 4 8 Tentamen Telefonvakt: Richard Lärkäng tel 3-8834 TMV36 Analys och Linjär Algebra K Kf Bt, del C Tentan rättas och bedöms anonymt Skriv
Tentamen i tmv036c och tmv035c, Analys och linjär algebra C för K, Kf och Bt A =, = det(a λi) = e 2t + c 2. x(t) = c 1. = c 1.
 Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
x (t) = 2 1 u = Beräkna riktnings derivatan av f i punkten a i riktningen u, dvs.
 MATEMATIK Chalmers tekniska högskola Tentamen -8-8, kl. 4.-8. TMV6 Analys och linjär algebra K Kf Bt, del C Telefonvakt: Adam Andersson, telefon: 7-884 Hjälpmedel: Inga, bara papper och penna. För full
MATEMATIK Chalmers tekniska högskola Tentamen -8-8, kl. 4.-8. TMV6 Analys och linjär algebra K Kf Bt, del C Telefonvakt: Adam Andersson, telefon: 7-884 Hjälpmedel: Inga, bara papper och penna. För full
SF1626 Flervariabelanalys Tentamen Måndagen den 21 mars 2016
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Måndagen den 2 mars 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF626 Flervariabelanalys Tentamen Måndagen den 2 mars 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
SF1626 Flervariabelanalys Bedömningskriterier till tentamen Måndagen den 16 mars 2015
 SF1626 Flervariabelanalys Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt att följa. Det
SF1626 Flervariabelanalys Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt att följa. Det
Tentamen i Analys B för KB/TB (TATA09/TEN1) kl 14 19
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Joakim Arnlind Tentamen i Analys B för KB/TB (TATA9/TEN) 23-8-22 kl 4 9 Inga hjälpmedel är tillåtna. Varje uppgift kan ge maximalt 3 poäng. Betygsgränser:
LINKÖPINGS UNIVERSITET Matematiska Institutionen Joakim Arnlind Tentamen i Analys B för KB/TB (TATA9/TEN) 23-8-22 kl 4 9 Inga hjälpmedel är tillåtna. Varje uppgift kan ge maximalt 3 poäng. Betygsgränser:
Institutionen för Matematik, KTH Lösningar till tentamen i Analys i en variabel för I och K (SF1644) 1/ e x h. (sin x) 2 1 cos x.
 Institutionen för Matematik, KTH Lösningar till tentamen i Analys i en variabel för I och K (SF644) /6 29. Bestäm med derivatans definition d dx ex. Derivatans definition är f (x) = lim h h ( f(x + h)
Institutionen för Matematik, KTH Lösningar till tentamen i Analys i en variabel för I och K (SF644) /6 29. Bestäm med derivatans definition d dx ex. Derivatans definition är f (x) = lim h h ( f(x + h)
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen DEL A
 SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 16-8-18 DEL A 1. Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x och y =
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 16-8-18 DEL A 1. Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x och y =
Lösningar till Matematisk analys
 Lösningar till Matematisk analys 685. Sätt fx x. Rotationskroppens volym är π fx dx π ] x 6 dx π 7 x7 π 7. Rotationskroppens area är summan av arean av kroppens mantelyta och arean av kroppens cirkulära
Lösningar till Matematisk analys 685. Sätt fx x. Rotationskroppens volym är π fx dx π ] x 6 dx π 7 x7 π 7. Rotationskroppens area är summan av arean av kroppens mantelyta och arean av kroppens cirkulära
Repetitionsuppgifter
 MVE5 H5 MATEMATIK Chalmers Repetitionsuppgifter Integraler och tillämpningar av integraler. (a) Beräkna (b) Avgör om den generaliserade integralen arctan(x) ( + x) dx. dx x x är konvergent eller divergent.
MVE5 H5 MATEMATIK Chalmers Repetitionsuppgifter Integraler och tillämpningar av integraler. (a) Beräkna (b) Avgör om den generaliserade integralen arctan(x) ( + x) dx. dx x x är konvergent eller divergent.
Problem inför KS 2. Problem i matematik CDEPR & CDMAT Flervariabelanalys. KTH -matematik
 KTH -matematik Problem i matematik EPR & MAT Flervariabelanalys Problem inför KS.. Låt F(, y, z) + y 3z + och G(, y, z) 3 + y 3 4z +. Visa att i en omgivning av punkten (,, ) definieras genom ekvationerna
KTH -matematik Problem i matematik EPR & MAT Flervariabelanalys Problem inför KS.. Låt F(, y, z) + y 3z + och G(, y, z) 3 + y 3 4z +. Visa att i en omgivning av punkten (,, ) definieras genom ekvationerna
1. För vilka värden på konstanterna a och b är de tre vektorerna (a,b,b), (b,a,b) och (b,b,a) linjärt beroende.
 Institutionen för matematik KTH MOELLTENTAMEN Tentamensskrivning, år månad dag, kl. x. (x + 5).. 5B33, Analytiska metoder och linjär algebra. Uppgifterna 5 svarar mot varsitt moment i den kontinuerliga
Institutionen för matematik KTH MOELLTENTAMEN Tentamensskrivning, år månad dag, kl. x. (x + 5).. 5B33, Analytiska metoder och linjär algebra. Uppgifterna 5 svarar mot varsitt moment i den kontinuerliga
Lösningar till MVE017 Matematisk analys i en variabel för I x 3x y = x. 3x2 + 4.
 Lösningar till MVE07 Matematisk analys i en variabel för I 8-0-0. (a Division ger y + 5x x 2 + 4 y x x2 + 4. 5x x 2 + 4 dx 5 2 ln(x2 + 4, vilket ger den integrerande faktorn (x 2 + 4 5/2. Ekvationen multipliceras
Lösningar till MVE07 Matematisk analys i en variabel för I 8-0-0. (a Division ger y + 5x x 2 + 4 y x x2 + 4. 5x x 2 + 4 dx 5 2 ln(x2 + 4, vilket ger den integrerande faktorn (x 2 + 4 5/2. Ekvationen multipliceras
Lösningsförslag till tentamen Tisdagen den 10 januari 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Tisdagen den januari 7 DEL A. En partikel rör sig så att positionen efter starten ges av (x, y, z (t cos t, t sin t, t
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Tisdagen den januari 7 DEL A. En partikel rör sig så att positionen efter starten ges av (x, y, z (t cos t, t sin t, t
Studietips inför kommande tentamen TEN1 inom kursen TNIU23
 Studietips inför kommande tentamen TEN1 inom kursen TNIU23 Lämplig ordning på sammanfattande studier inom denna kurs: Inled med att grundligt studera föreläsningsanteckningarna Därefter läs tillhörande
Studietips inför kommande tentamen TEN1 inom kursen TNIU23 Lämplig ordning på sammanfattande studier inom denna kurs: Inled med att grundligt studera föreläsningsanteckningarna Därefter läs tillhörande
Lösningsförslag till tentamen TMA043 Flervariabelanalys E2
 Lösningsförslag till tentamen TMA43 Flervariabelanalys E 4-8-3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Åse Fahlander, telefon: 73 88 34 Hjälpmedel: bifogat formelblad,
Lösningsförslag till tentamen TMA43 Flervariabelanalys E 4-8-3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Åse Fahlander, telefon: 73 88 34 Hjälpmedel: bifogat formelblad,
Lösningsförslag, preliminär version 0.1, 23 januari 2018
 Lösningsförslag, preinär version 0., 3 januari 08 Högskolan i Skövde Tentamen i matematik Kurs: MA5G Matematisk analys MA3G Matematisk analys för ingenjörer Tentamensdag: 08-0-03 kl 4:30-9:30 Hjälpmedel
Lösningsförslag, preinär version 0., 3 januari 08 Högskolan i Skövde Tentamen i matematik Kurs: MA5G Matematisk analys MA3G Matematisk analys för ingenjörer Tentamensdag: 08-0-03 kl 4:30-9:30 Hjälpmedel
1. Beräkna volymen av det område som begränsas av paraboloiden z = 4 x 2 y 2 och xy-planet. Lösning: Volymen erhålles som V = dxdydz.
 Lösningsförslag till tentamensskrivning i Matematik IV, F636(5B0,5B30). Tisdagen den januari 0, kl 400-900. Hjälpmedel: BETA, Mathematics Handbook. Redovisa lösningarna på ett sådant sätt att beräkningar
Lösningsförslag till tentamensskrivning i Matematik IV, F636(5B0,5B30). Tisdagen den januari 0, kl 400-900. Hjälpmedel: BETA, Mathematics Handbook. Redovisa lösningarna på ett sådant sätt att beräkningar
TENTAMEN. Ten2, Matematik 1 Kurskod HF1903 Skrivtid 13:15-17:15 Fredagen 25 oktober 2013 Tentamen består av 4 sidor
 TENTAMEN Ten, Matematik Kurskod HF93 Skrivtid 3:5-7:5 Fredagen 5 oktober 3 Tentamen består av sidor Hjälpmedel: Utdelat formelblad. Räknedosa ej tillåten. Tentamen består av uppgifter som totalt kan ge
TENTAMEN Ten, Matematik Kurskod HF93 Skrivtid 3:5-7:5 Fredagen 5 oktober 3 Tentamen består av sidor Hjälpmedel: Utdelat formelblad. Räknedosa ej tillåten. Tentamen består av uppgifter som totalt kan ge
SF1669 Matematisk och numerisk analys II Lösningsförslag till modelltentamen DEL A
 Institutionen för matematik SF1669 Matematisk och numerisk analys II Lösningsförslag till modelltentamen DEL A 1. Betrakta funktionen fx, y = x + y och området D som ges av olikheterna x, y och x + y 1.
Institutionen för matematik SF1669 Matematisk och numerisk analys II Lösningsförslag till modelltentamen DEL A 1. Betrakta funktionen fx, y = x + y och området D som ges av olikheterna x, y och x + y 1.
Lektion 3. Partiella derivator, differentierbarhet och tangentplan till en yta, normalen i en punkt till en yta, kedjeregeln
 Lektion 3 Partiella derivator, differentierbarhet och tangentplan till en yta, normalen i en punkt till en yta, kedjeregeln Innehål 1. Partiella derivator (12.3) 2. Differentierbarhet och tangentplan till
Lektion 3 Partiella derivator, differentierbarhet och tangentplan till en yta, normalen i en punkt till en yta, kedjeregeln Innehål 1. Partiella derivator (12.3) 2. Differentierbarhet och tangentplan till
LUNDS TEKNISKA HÖGSKOLA MATEMATIK. LÖSNINGAR FLERDIMENSIONELL ANALYS, FMA kl 8 13
 LUNS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR FLERIMENSIONELL ANALYS, FMA40 04-0- kl 8. Vi börjar med att rita triangelskivan. Linjen genom, och, har ekvationen y x+, linjen genom, och, har ekvationen y 4
LUNS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR FLERIMENSIONELL ANALYS, FMA40 04-0- kl 8. Vi börjar med att rita triangelskivan. Linjen genom, och, har ekvationen y x+, linjen genom, och, har ekvationen y 4
v0.2, Högskolan i Skövde Tentamen i matematik
 v0., 08-03-3 Högskolan i Skövde Tentamen i matematik Kurs: MA5G Matematisk analys MA3G Matematisk analys för ingenjörer Tentamensdag: 08-0-03 kl 4:30-9:30 Hjälpmedel : Inga hjälpmedel utöver bifogat formelblad.
v0., 08-03-3 Högskolan i Skövde Tentamen i matematik Kurs: MA5G Matematisk analys MA3G Matematisk analys för ingenjörer Tentamensdag: 08-0-03 kl 4:30-9:30 Hjälpmedel : Inga hjälpmedel utöver bifogat formelblad.
Chalmers tekniska högskola Datum: kl Telefonvakt: Jonny Lindström MVE475 Inledande Matematisk Analys
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 1715 kl. 14. - 18. Tentamen Telefonvakt: Jonny Lindström 733 674 MVE475 Inledande Matematisk Analys Tentan rättas och bedöms anonymt. Skriv
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 1715 kl. 14. - 18. Tentamen Telefonvakt: Jonny Lindström 733 674 MVE475 Inledande Matematisk Analys Tentan rättas och bedöms anonymt. Skriv
Kap Implicit givna funktioner
 Kap 12.8. Implicit givna funktioner A 701. Betrakta ekvationen x 2 y 2 = 0 och funktioner y = y(x). a. Hur många funktioner satisfierar ekvationen? b. Hur många kontinuerliga funktioner satisfierar ekvationen?
Kap 12.8. Implicit givna funktioner A 701. Betrakta ekvationen x 2 y 2 = 0 och funktioner y = y(x). a. Hur många funktioner satisfierar ekvationen? b. Hur många kontinuerliga funktioner satisfierar ekvationen?
Institutionen för matematik SF1626 Flervariabelanalys. Lösningsförslag till tentamen Måndagen den 5 juni 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
