Optimering av depåpositioner för den minimala bensinförbrukningen i öknen

Transkript

1 Optimering av depåpositioner för den minimala bensinförbrukningen i öknen

2 Frågeställning: En jeep kan sammanlagt ha 200 liter bensin i tanken samt i lösa dunkar. Jeepen kommer 2,5 km på 1 liter bensin. Vi ska färdas 1000 km in i öknen och bränslet finns endast vid startpunkten och vid målet. För att klara färden måste vi först placera ut bensin i depåer längs vägen. Hur mycket bränsle går det åt och var ska dunkarna placeras ut? Vilken lösning ger den bästa resan? Svar: Den minsta möjliga bensinvolymen som går åt för att åka 1000 km är 1 534,6 liter. Depåstoppunkterna är då 22.4, 60.9, 106.3, 161.9, 233.3, och km från start. Bensinvolymerna är 200, 400, 600, 800, 1000, 1200, 1400 och 1534,6. Den optimala lösningen hittades när det var olika avstånd mellan depåerna (metod 2) istället för konstanta. Lösning: Vi använder oss av programmen Excel och GeoGebra, vi räknar också algebraiskt. I Excel gör vi en anpassad beräkningsmodell där vi bara behöver ange avståndet (km) mellan depåerna. Sedan räknar programmet ut hur många liter det ska vara vid varje depå. Vi kommer också räkna algebraiskt för att försöka hitta den mest optimala resan. Svaren på den mest effektiva resan presenteras i GeoGebra (bild 1) Metod 1 Först gör vi en beräkningsmodell i Excel där tanken är att lätt kunna undersöka den totala volymen (l) bensin vid första depån. Vi behöver bara justera avståndet (km) mellan depåerna (när depåerna är konstanta och har samma antal km mellan sig hela vägen). Den här metoden är väldigt bra eftersom vi inte behöver räkna ut alla olika steg för hand, dock är den begränsad eftersom vi bara kan se konstanta depåstop. Vi kan alltså inte se hur mycket bensin det går åt om depåerna ligger på olika avstånd från start. Utförande av metod 1 Vi skapar ett Excel dokument med fem kolumner med rubrikerna: sträcka, bensinvolym vid depån (L), antal resor, avstånd (km) och bensinförbrukning (avstånd/2,5) =E$2/2,5 Först bestämmer vi vilket avstånd vi vill ha mellan depåerna, exempelvis 50 km. Då kan vi räkna ut vart depåerna ligger. Eftersom bilen kan rymma max 200 liter kan vi åka 500 km utan depåer. Det är därför sista depån ligger vid 500 km och där ska det finnas 200 liter. För då kan vi efter att vi har tankat vid 500 km depån åka hela vägen till mål utan att stanna och tanka. Sedan räknar vi baklänges från den sista depån till den första, vi räknar ut var de 2

3 andra stoppen ska ligga genom att använda formeln (=A2-E$2) Alltså subtraherar vi avståndet mellan depåerna, som alltid är E2. Därför skriver vi E$2 så programmet vet att i alltid menar E2. Talet vi subtraherar ifrån är alltid förgående depå. Nu när vi vet var depåerna ska ligga fortsätter vi att räkna ut vilken bensinvolym som ska finnas vid respektive stopp. Då måste vi samtidigt räkna ut antalet resor eftersom de är beroende av varandra. Det gör vi med följande formel =2*AVRUNDA.NEDÅT(B2/(B$2-2*F$2);0)+1 För att allt ska stämma måste vi avrunda nedåt för att få ett jämt antal resor och sedan delar vi förgående sträcka med bensinen vi dumpar. Vi adderar 1 för svaret ska alltid bli ett ojämnt tal eftersom när vi har dumpat bensin så måste vi åka en sista gång framåt för att komma till nästa depå med den sista bensinen. Allt multipliceras med 2 för det går två resor på en vända. Nu kan vi fortsätta med formeln för bensinvolymen =B2+(C2*F$2) där B2 är förgående volym, C2 är antalet resor och f$2 är hur mycket bensin det går åt/resa. Nu när alla formler är inskrivna är det bara att kopiera den till resten av kolumnen. Om vi nu ändrar avståndet anpassas allt annat också till det nya avståndet. På så sätt kan vi se den totala bensinförbrukningen för olika konstanta avstånd. Resultatet vi fick var att ju kortare avstånd mellan depåerna det var desto minde total bensin gick åt, men det är extremt opraktiskt att åka fram och tillbaka väldigt många gånger. Om vi tar 5 km som exempel så åker vi totalt 703 gånger mellan depåer och det är orimligt och tar väldigt lång tid eftersom det tar lång tid att lasta ur all bensin och så vidare. Metod 2: Nu ska vi lösa den här uppgiften algebrasikt och med hjälp av den här metoden kommer vi fram till det exakta svaret på uppgiften. För att lösningen ska bli så effektiv som möjligt behöver vi frakta mycket bensin en kortare sträcka. Den här metoden var svår att förstå till en början, men vi fick lite hjälp av internet och då blev det lättare. Grundtanken till den här metoden är att det är olika avstånd mellan alla depåer och att vi räknar ut var och en av depåerna för sig. Utförande av metod 2: Första depån kommer att placeras vid 500 meter och får kallas A. För att kunna fortsätta resten av resan behöver det vara 200 liter bensin vid depå A. Vi räknar baklänges och nästa depå döper vi till B. Hur mycket bensin ska då finnas vid B? Vi kallar sträckan för x. Det blir lättare om vi räknar med längdenheter som är 2,5 km eftersom vi kommer 2,5 kilometer på en liter bensin. Bensinen vi dumpar är i samtliga fall 200 2x eftersom vi inte vill köra tillbaka med bensin i dunkar. Vid A behöver det vara 200 2x = x och det är det mest effektiva sättet är att placera B så långt bort från A så att så lite bensin som möjligt går åt. Alltså 200/3 = x. Då kan vi fortsätta räkna ut placeringen av B med hjälp av formeln 500 (200/3) * 2,5 km räknat från A =

4 Vi åker från B till A tur och retur och dumpar bensin två gånger och varje vända är 200 km, alltså ska det finnas 400 liter vid B. B ligger på det mest effektiva avståndet från A och B är 2/3 av sträckan mellan startpunkten och A. Då är det rimligt att C ligger 2/3 från startsträckan till B. Dock är det inte alltid exakt 2/3 eftersom det krävs ett jämt antal liter vid varje depå och då måste vi kompensera. Vi ser också att samtidigt som mängden bensin som behövs fraktas ökar så minskar sträckan mellan depåerna. Beräkning av depå C: Vi ska frakta 400 liter bensin till B och vi börjar med att kolla hur många vändor vi ska åka. 333,333 km räknat i längdenheter = 333,333/2,5 = 133,333 och 2/3 av 133,333.. = 88,888 Då är avståndet mellan B och C 133,333 88,888 = 44,444 Hur mycket bensin dumpas då vid B varje vända? 200 2*44,444 = 111,111 Vi ska lämna av 400 liter bensin och då måste vi åka 400/111,111 = 3,6 gånger. Det är inte effektivt eftersom man inte kan åka 0,6 vända, alltså måste vi korrigera avståndet lite. Vi testar att avrunda till närliggande hela antal vändningar. Om vi åker 4 vändor blir det 4(200 2*44,444) + 44,444 = 488,9 liter och om vi åker 3 vändor blir det 3(200 2*44,444) + 44,444 = 377,777 liter. Vi ser då att vi kommer närmast 400 liter om vi åker 3 vändor. Då fortsätter vi att beräkna avståndet, vi vill veta x mellan B och C: 3(200 2x) + x = x = 400 5x = 200 x = 40 C befinner sig då vid positionen 133, = 93,33 längdenheter (233,333 km) från start. Resan krävde precis 3 vändor och varje vända är 200 liter, då måste det finnas 600 liter bensin i depå C. Nu när vi har en lösningsmetod så använder vi den på de kvarvarande depåerna. Uträkning av D: 2/3 av 93,333 = 62,222 Avståndet mellan C och D = 93,333 62,222 = 31,111 En dumpning blir då 200 2*31,111 = 137,777 och vi ska frakta 600 liter och då behöver vi åka (600 31,111)/137,777 = 4,13 gånger 4. Vi ska alltså frakta 600 liter bensin på 4 vändor. 4(200 2x) + x = x = 600 x = 200/7 Depå D ligger vid 93, /7 = 64,7619 längdenheter (161,9 km) från startpunkten. Vi åker 4 vändor med 200 liter bensin, alltså måste det finnas 800 liter vid D. Nu gör vi på samma sätt med E, F och G 4

5 E: x = 200/9 64, /9 = 42,5397 längdenheter (106,3 km.) Vi åker 5 vändor och det krävs 1000 liter bensin F: x = 200/11 42, /11 = 24,3579 längdenheter (60,9 km) 6 vändor, 1200 liter bensin G: x = 200/13 24, /13 = 8,9733 längdenheter ( 22,4 km) 7 vändor, 1400 liter bensin Nu ska vi räkna ut H, som är startpositionen. 2/3 av 8,9733 = 5,9822 8,9733 5,9822 = 2,9911 längdenheter. Då blir varje bensinlämning 200 2*2,9911 = 194,04 = 7,2 vändor. Det bästa vore att avrunda till 7 men eftersom detta är den sista vändan måste vi åka 8 vändor mellan H och G. Eftersom H inte ligger ett jämt antal vändor från G måste vi räkna ut hur mycket bensin vi måste ha med oss sista vändan. Vi kollar först hur mycket bensin vi har dumpat efter 7 vändor: 7*(200 2*8,9733) = 1274,374 liter. På åttonde vändan måste vi alltså ha med , ,9733 = 134, ,6 liter Nu ser vi att den totala bensinförbrukningen blir ,6 = liter 5

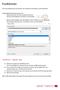
6 Metod 3 Nu ska vi anpassa våra svar från metod 2 till en kurva i GeoGebra. Det gör vi genom att skriva in depåns position som X-värde och antal liter bensin som Y-värde: A = (1000,0.01) B = (500,200) C = (333.3,400) D = (233.3,600) E = (161.9,800) F = (106.3,1000) G = (60.9,1200) H = (22.4,1400) I = (0,1534.6) (bild 1) Sedan anpassar vi en linje till punkterna och det gör vi genom att skiva in RegressionExp[{B, C, D, E, F, G, H, I}] i inmatningsfältet. Vi vet att det blir en exponentiell kurva och väljer därför RegressionExp. Anledningen till varför vi inte har med punkt A i regressionen är att kurvan blir helt fel då eftersom en exponentiell kurva som skär Y-axeln går mot 0 på X-axeln men skär aldrig. Vi har endast med A som en markering så vi ser hur placeringen av depåer ser ut. I bild 2 ser vi hur allt är uppbyggt, B är halva sträckan och de resterande depåerna är alltid 2/3 av avståndet mellan förgående depå och start. (bild 2) 6

7 Diskussion: Hela uppgiften går ut på att hitta en så optimal lösning som möjligt och vi har valt att angripa uppgiften på olika sätt och kan därför se olika slags resultat. Vilket är då bäst? Jo resultatet från den algebraiska metoden (metod 2), men kan vi vara 100% säkra på att det är den absolut bästa metoden? Nej men dock är en mer effektiv lösning inte särskilt trolig. Vi ser också att vi når högst effektivitet med depåstopp som inte är konstanta. För om vi ska få ett hyfsat liknande svar med hjälp av Excel metoden skulle vi behöva ha extremt många depåer och behöva åka över 100 vändor och man förstår direkt att det är oerhört ineffektivt. Dock kan den här uppgiften tolkas på olika sätt när den säger att vi ska hitta den bästa resan. Vad menas egentligen med den bästa resan? Är det den som går snabbast eller den som drar minst bensin? De två faktorerna går oftast hand i hand, men tiden blir ju längre om man stannar många gånger. Den minst effektiva resan skulle vara att köra 0,000 1 km och lämna 199,999.liter. Också att köra slut på 199,999 liter och lämna 0,000.1 liter bensin. Båda dessa lösningar är nästan praktiskt omöjliga och är de mest ineffektiva resorna. Så nästan alla lösningar mellan dessa extremer är ett möjligt svar. Fast det måste också finnas en optimal lösning som vi med stor sannolikhet har hittat. Källförteckning: Kjell Elfström, med Jeep-problemet (metod 2) 7