Fartbestämning med Dopplerradar

Transkript

1 Vågrörelselära, 5 poäng Uppsala Universitet Projektarbete Fartbestämning med Dopplerradar Per Mattsson, FA Olov Rosén, FA 1

2 1. Innehållsförteckning. Sammanfattning Inledning Teori Beteckningar Bestämning av objekts fart med hjälp av Dopplereffekten Osäkerhetsanalys Osäkerhet i f Osäkerhet i T Osäkerhet i v Experiment Experimentell uppställning Material Beskrivning av Dopplerradar Utförande Analys Uppskattning av τ Analys av T Analys av f Resultat Diskussion Bilagor Bilaga A Figurer från mätning

3 . Sammanfattning Vi har undersökt ett modelltågs fart med hjälp av en Dopplerradar. Vi gjorde två försök då tåget körs framåt, och två försök då tåget körs bakåt. När tåget kördes bakåt blev farten cirka 0.6 m/s. När tåget kördes framåt blev farten cirka 0.59 m/s. Resultatet tyder på att detta inte beror på slumpen, utan att farten faktiskt beror av åt vilket håll tåget körs. De uppmätta frekvenserna, som farten beräknades utifrån, skattades med hjälp av grafer som ritades upp av en dator. En förbättring inför framtida försök kan vara att använda ett datorprogram som beräknar frekvensen direkt, istället för att göra avläsningen från uppritad graf. 3. Inledning Målsättning med denna rapport är att bestämma farten hos ett modelltåg med hjälp av en Dopplerradar. Dopplerradarn vi använder sänder ut mikrovågor, vars frekvens förskjuts när de studsar mot ett föremål i rörelse. Detta kallas Dopplereffekten och är en viktig del av vågrörelseläran. Genom att studera de förskjutna vågorna kan vi sedan bestämma tågets fart. 4. Teori 4.1 Beteckningar v Föremålets (tågets) hastighet f Frekvens som sänds ut av sändaren f' Frekvens som upplevs av föremål (tåg) i rörelse mot/från sändare fd Svävningsfrekvens som mäts upp vid sändaren Tiden för N svävningsperioder T Svävningsperioden Ljusets hastighet u(x) Standardosäkerhet för x 4. Bestämning av objekts fart med hjälp av Dopplereffekten Om en stationär sändare utsänder en elektromagnetisk våg med vinkelfrekvensen så upplevs denna, enligt Physics Handbook (sid 63), som vinkelfrekvensen 1 ' = v cos 1 v / c 0 (4.1) av en observatör som rör sig med farten v relativt sändaren (se figur 4.1). 3

4 Figur 4.1 S är sändaren, och v observatörens hastighetsvektor Vi i kommer i detta experiment endast ha nytta av fallen då observatören rör sig rakt mot eller rakt från sändaren, dvs fallen då =0 och =. Och eftersom = f kan vi istället uttrycka sambandet mellan den sända och upplevda frekvensen som 1± f '= f v 1 v /c (4.) 0 Dessutom kommer det gälla att v c 0, så 1 v / c 0 1 / 1, och (4.) kan skrivas som f ' = f 1± v (4.3) Om observatören nu reflekterar vågen kommer observatören själv att fungera som en sändare, som sänder ut en våg med frekvensen f'. Den stationära sändaren blir nu en observatör som uppfattar v v v v v f ' ' = f ' 1± = f 1± = f 1± f 1± (4.4) Den sista approximationen utnyttjar att v c 0. Om vi nu läser av vågens frekvens vid sändaren måste vi också ta hänsyn till att vi där får en blandning av sändarens utgående våg och den reflekterade vågen. Eftersom dessa kommer ha olika frekvenser (f och f'') är det svävningsfrekvensen som kommer uppfattas, dvs f d = f f ' ' = f f 1± v v f = (4.5) Alltså, om en sändare sänder ut en mikrovåg som reflekterats av ett föremål i rörelse, rakt mot eller rakt från sändaren, och man sedan läser av svävningsfrekvensen vid sändaren så kan man få ut föremålets hastighet relativt sändaren med v= f d f (4.6) 4

5 Vid avläsning från dator är det lättast att få ut svävningsperioden T=1/fd, då får vi v= ft (4.7) 4.3 Osäkerhetsanalys Vi vill också veta hur stor osäkerheten för v i (4.7) blir. För att bestämma detta används följande osäkerhetsanalys Osäkerhet i f Om f mäts analogt så beskriver en triangulär täthetsfunktion f's sannolikhetsfördelning (se figur 4.) Figur 4. f's sannolikhetsfördelning f* är skattningen av f och d är halva längden på ett intervall man säkert kan anse innehåller f. För en sådan fördelning ges standardosäkerheten av. u f = f d f d 6 (4.8) 4.3. Osäkerhet i T För att bestämma perioden för svävningsfrekvensen kan man i en erhållen graf avläsa ett tidintervall som innehåller N perioder. Utifrån avläsningen skattas sedan så bra som möjligt med * och ett intervall ( * d, * + d) som med stor säkert kan anses innehålla bestäms (se figur 4.3). 5

6 Figur 4.3 Exempel på skattning av Skattningen för svävningsperioden T ges sedan av T* = */N, och tillhörande intervall blir (( * d)/n, ( * + d)/n ). Eftersom det handlar om en analog avläsning så använde vi även här en triangulär täthetsfunktion (se figur 4.4). Figur 4.4 T's sannolikhetsfördelning Standardosäkerheten för T blir då u T = d / N d / N d = 6 N 6 (4.9) 6

7 4.3.3 Osäkerhet i v Hastigheten v ges av (4.7), vilket är en funktion av f och T. Standardosäkerheten för v uttryck i u( f ) och u ( T ) fås av u v = v u f f v u T T c ft = u f c u f / f u T /T f T u T c f T = (4.10) 7

8 5. Experiment 5.1 Experimentell uppställning Material Dopplerradar (Gunn oscialltor med spänningsaggregat, cirkulator, frekvensmätare, detektor) Multimeter Tågbana Dator Tågbana med modelltåg Figur 5.1 Dopplerradar. Sänder ut mikrovågor och läser av svävningsfrekvensen 5.1. Beskrivning av Dopplerradar Dopplerradarn (se figur 5.1) kan sända ut mikrovågor av olika frekvens. Den vridbara ratten på Gunn oscillatorn används för att bestämma vilken frekvens som ska sändas ut. Skalan på Gunn oscillatorn är dock svåravläst och för att få ett mer exakt värde på den utsända frekvensen används frekvensmätaren kopplad till en voltmeter. Då frekvensmätaren är inställd på samma frekvens som den utgående vågen så kommer voltmätaren ge ett kraftigt utslag (beroende på att resonans uppstår), frekvensen kan då lätt läsas av på sidan av frekvensmätaren. Eftersom cirkulatorn inte är helt ideal läcker en liten effekt över från oscillatorporten till detektorporten. Därigenom erhålles alltså i detektorn en blandning av utgående och reflekterad våg, och det blir svävningsfrekvensen som registreras och sedan ritas upp av datorn Utförande Bestämning av utgående frekvens Först ställde vi in Gunn oscillatorn på att ge en utgående våg med en frekvens runt 10 GHz. För att få ett mer exakt värde på den utgående vågens frekvens användes frekvensmätaren (se 5.1.). När vi hade ställt frekvensmätaren där vi ansåg att kraftigast resonans uppstod noterade vi detta värde på f. 8

9 Figur 5. Experimentuppställning Mätning med Dopplerradar Dopplerradarn ställdes så att den sände ut mikrovågor parallellt med ena långsidan av rälsen (se figur 5.). Tåget förseddes med en metallplatta, som var avsedd att reflektera tillbaka mikrovågorna till detektorn. När tåget befann sig på mitten av långsidan startade vi mätningen. Mikrovågorna sändes då ut, reflekterades på metallplattan och registrerades av detektorn. Svävningsfrekvensen vid Dopplerradarns detektor uppmättes, och svängningarna ritades upp i graf på datorn. Mätningar genomfördes två gånger då tåget åkte framåt, och två gånger då det åkte bakåt. 6. Analys Beteckningarnas betydelse finns i avsnitt Uppskattning av τ Värdena på τ har har skattats från figurerna i Bilaga A, resultatet finns i tabell 6.1. Tabell 6.1 Skattning av τ där d är bredden för den triangulära täthetsfunktionen och N antalet perioder τ skattas över Försök Skattning av (s) d (s) N Analys av T Värdet på T = / N beräknas från tabell 6.1. Mätosäkerheten u(t) ges av (4.9), resultatet finns i tabell 6. Tabell 6. Analys av T Försök Skattning av T (s) d/n (s) 3.08E E 4.86E E 4 u(t) (s) 1.17E 4 1.6E 4 1.6E E 4 9

10 6.3 Analys av f Skattning av Dopplerradars utgående frekvens (se avsnitt 5.1.3): f* = 9809 MHz Om frekvensmätaren sedan sidställdes ± 1 MHz från f* så minskade multimeterns utslag så mycket att vi kunde med stor säkerhet anse att frekvensen låg inom f* ± 1 MHz. Mätosäkerheten i f blir enligt (4.8) u f = f 1 MHz f 1 MHz 1 = MHz Resultat Tågets hastighet v beräknas med (4.7), och mätosäkerheten i v med (4.10). Resultaten från de fyra försöken som gjordes finns i tabell 6.3 Tabell 6.3 Hastigheten v samt mätosäkerheten. Försök v (m / s) u( v ) (m / s).91e E 03.87E E 03 I mätning 1 och kör tåget bakåt, i mätning 3 och 4 kör det framåt I tabell 6.4 och figur 6.1 visas 95% konfidensintervall för v i de olika försöken Tabell % konfidensintervall för v Försök Undre gräns (m/s) Övre gräns (m/s) ,30E 01 6,5E 01 6,0E 01 v (m/s) 6,15E 01 6,10E 01 6,05E 01 6,00E 01 5,95E 01 5,90E 01 5,85E Försök nr Figur % konfidensintervall för v 10

11 7. Diskussion I experimentet gjordes fyra mätningar av tågets fart, två mätningar då tåget körde framåt, och två mätningar då tåget körde bakåt. Resultatet blev att de två mätningarna då tåget körde framåt gav något lägre fart än då tåget körde bakåt. Vi kan inte se någon anledning till varför mätmetoden skulle ge någon systematisk skillnad beroende på tågets färdriktning. Om man tittar på konfidensintervallen för de olika försöken så överlappar inte heller intervallen för de två försök då tåget körde bakåt med intervallen då tåget körde framåt, så skillnaden mellan farten framåt och farten bakåt är förmodligen inte heller ett resultat av slumpen. Den mest troliga förklaringen till skillnaden är nog att tåget faktisk åker olika fort åt de olika hållen. Metoden att bestämma fart med Dopplerradar har fördelen att man inte behöver ha någon utrustning på det föremål man vill mäta farten på. Vilket kan vara bra i sammanhang som t.ex. fartkontroll av bilister. Mätmetoden har även en liten standardavvikelse, vilket skulle vara önskvärt i sådana situationer. En komplikation vid uppställningen av utrustningen var att få Dopplerradarns vågor att gå helt parallellt med rälsen på långsidan vi skulle mäta på. Det gjorde vi med ögonmåttet vilket förstås inte blir helt perfekt, men uppskattningsvis så ställde vi den inte mer än ± 5 fel. Om man tittar på formel (4.1) ser man att maximala procentuella felet skulle bli (cos(0) cos(5))/cos(0) = 0.38 %, vilket borde vara försumbart. En annan felkälla man skulle kunna minska i framtida försök är det faktum att avläsningen av graferna har gjorts för hand. Ett datorprogram borde kunna göra den avläsningen, och ge en säkrare skattning av frekvensen. I vårt fall fungerade dessutom inte skrivaren, så vi fick ta kort på bildskärmen. Detta kan ha ökat felet vid avläsning. 11

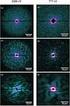
12 Bilagor Bilaga A Figurer från mätning Figur B.1 Mätning 1. Tåget kör bakåt Figur B. Mätning. Tåget kör bakåt 1

13 Figur B.3 Mätning 3. Tåget kör framåt Figur B.4 Mätning 4. Tåget kör framåt 13