Introduktion till strukturerade härledningar
|
|
|
- Karl-Erik Persson
- för 8 år sedan
- Visningar:
Transkript
1 Introduktion till strukturerade härledningar Strukturerade härledningar är en metod för att underlätta konstruktion, presentation och förståelsen av matematiska argument. Metoden är lämplig för matematiska bevis och algebraiska och aritmetiska beräkningar såväl som för geometriska konstruktioner och allmän problemlösning. Metoden kan användas då en lösning till ett problem kräver flera steg efter varandra. Den har använts på olika nivåer av matematikundervisning, från högstadienivå till universitetsnivå och tillämpad forskning. Metoden baserar sig på ett fast format för att presentera matematiska argument och användning av enkel logik. Det fasta formatet gör det enklare att förstå bevis och beräkningar och att kontrollera att de är korrekta. Målet med den här guiden är att visa hur strukturerade härledningar kan användas vid undervisning av matematik i gymnasiet. Metoden beskrivs med exempel, som steg för steg utvidgar metoden med nya funktioner och koncept. Introduktion till strukturerade härledningar Ralph-Johan Back ISBN Four Ferries Publishing
2
3 Introduktion till strukturerade härledningar Ralph-Johan Back Four Ferries Publishing i
4 Kontaktinformation Ralph-Johan Back, Professor i datavetenskap Åbo Akademi Joukahainengatan 3 5, Åbo, Finland mail: backrj@abo.fi, web: Ralph-Johan Back, All rights reserved. Four Ferries Publishing ISBN Cover picture: Tuncay. License: CC0. Source:: ii
5 Förord Strukturerade härledningar är en metod underlätta konstruktion, presentation och förståelsen av matematiska argument. Metoden är lämplig för matematiska bevis och algebraiska och aritmetiska beräkningar såväl som för geometriska konstruktioner och allmän problemlösning. Metoden kan alltid användas då en lösning till ett problem kräver flera steg efter varandra. Den har använts på olika nivåer av matematikundervisning, från högstadienivå till universitetsnivå och tillämpad forskning. Metoden baserar sig på ett fast format för att presentera matematiska argument och användning av enkel logik. Det fasta formatet gör det enklare att förstå bevis och beräkningar och att kontrollera att de är korrekta. Målet med den här guiden är att visa hur strukturerade härledningar kan användas vid undervisning av matematik i gymnasiet. Metoden beskrivs med exempel, som steg för steg utvidgar metoden med nya funktioner och koncept. Den här guiden är en utvidgad version av föregående manual som publicerades som Matematiikkaa logiikan avulla: Johdatus rakenteisiin päättelyketjuihin (Ralph-Johan Back, TUCS Lecture Notes 10, 2008). iii
6 Tackord Strukturerade härledningar utvecklades och metodens lämplighet för undervisning studerades i nära samarbete med medlemmarna av TUCS Learning and Reasoning laboratriet. Forskningslaboratoriet är ett samarbete mellan IT-institutionerna inom Åbo Akademi och Åbo Universitet. Jag vill tacka följande personer för intressanta och fruktbara diskussioner om metoden och för deras bidrag till dess utveckling (list är i alfabetisk ordning): Stefan Asikainen, Johannes Erikson, Matti Hutri, Tanja Kavander, Antti Lempinen, Linda Mannila, Mia Peltomäki, Viorel Preoteasa, Teemu Rajala, Tapio Salakoski, Petri Sallasmaa, Fredrik Sandström, Patrick Sibelius, Solveig Wallin and Joakim von Wright. Finlands Akademi och Teknologiindustrins 100 års jubileumsfond har finansierat forskningen som den här publikationen baserar sig på. iv
7 Innehåll Innehåll v 1 Inledning 1 2 Strukturerade uppgifter Strukturerade beräkningar Strukturerade uppgifter Deluppgifter Fokusera på deluttryck Textuppgifter Frågor och svar Att lösa ett problem steg för steg Framåtgående bevis Bakåtgående bevis Strukturerade härledningar Definitioner Modellering Härledningar och logik Logiska påståenden Kvantorer i gymnasiematematiken Exakta bevis Det allmänna formatet för en strukturerad härledning 41 7 Mera information 45 v
8
9 Kapitel 1 Inledning Den här boken är en introduktion till strukturerade härledningar. Strukturerade härledningar skrivs i ett fast format, som visar den övergripande strukturen i ett matematiskt argument och hur de olika delarna hör ihop. Formatet som används för att presentera strukturerade härledningar kräver att varje steg i en härledning motiveras genom att man explicit förklarar varför det är korrekt. Stegen i en härledning använder logiska symboler och logikens regler används även explicit, på samma sätt som algebraiska beteckningar och regler används explicit i algebra. Detta snabbar upp argumentet och gör det mer tillförlitligt. Strukturerade härledningar erbjuder ett enhetligt format för olika typer av matematiska resonemang som bevis, aritmetiska och algebraiska beräkningar, geometriska bevis, textuppgifter med mera. Metoden lämpar sig för alla nivåer i matematik, från högstadiet till universitetsnivå och forskning. Syftet med den här guiden är att ge en översikt av strukturerade härledningar med exempel tagna från gymasiematematiken. För att läsa texten krävs inte någon annan bakgrundsinformation än traditionell gymnasiematematik. 1
10
11 Kapitel 2 Strukturerade uppgifter En strukturerad uppgift kombinerar en matematisk uppgift och dess lösning i en enda presentation, med ett fast format. En strukturerad uppgift kan vara en matematisk sats och dess bevis, en algebraisk uppgift och dess lösning, en textuppgift och dess lösning och så vidare. I det här kapitlet visar vi med några exempel hur man presenterar olika matematiska problem och deras lösningar som strukturerade uppgifter. 2.1 Strukturerade beräkningar Vi beskriver först ett enkelt specialfall av en strukturerad uppgift, en strukturerad beräkning. Detvanligasättetattpresenteraenalgebraiskberäkningärattbildaen kedja av likheter, Den här kedjan motsvarar påståendena t 0 = t 1 =... = t n. t 0 = t 1 och t 1 = t 2 och...t n Ur den här kedjan kan vi dra slutsaten att t 0 = t n, 1 = t n eftersom likhet är transitiv. Följande exempel visar hur vi skriver en sådan beräkning som en strukturerad beräkning. Exempel 1. gäller. Visa att konjugatregeln, (a + b)(a b) =a 2 b 2 I en strukturerad beräkning skrivs varje uttryck på egen rad. Likhetstecknet mellan uttrycken skrivs också på egen rad, följd av motiveringen för att likheten gäller. Beviset ser då t på följande sätt: 3
12 2. Strukturerade uppgifter (a b)(a + b) = {regeln för multiplikation av polynom} a 2 + ab ba b 2 = {uttrycken ab och ba tar ut varandra} a 2 b 2 Beviset är en följd av tre algebraiska uttryck, med likhet emellan: (a b)(a + b) = a 2 + ab ab b 2 = a 2 b 2 Det här bevisar påståendet, eftersom likhet är en transitiv relation. Vi motiverar likheterna med egenskaperna hos polynom. Traditionellt skulle vi skriva beräkningen på följande sätt: (a b)(a + b) = a 2 + ab ba b 2 (enligt reglerna för multiplikation av polynom) = a 2 b 2 (uttrycken ab och ba tar ut varandra) I det här formatet måste både formeln och motiveringen få plats på samma rad. Det här innebär i praktiken att motiveringen måste vara kort. Den blir då ofta svår att förstå och det är lockande att lämna bort den från beräkningen. Men då går den grundläggande idén med matematiska bevis förlorad, att övertyga läsaren om att varje steg är matematiskt riktig, och att stegen i kombination med varandra leder till det önskade resultatet. Om motiveringarna lämnas bort måste läsare komma på dem själv. Det här gör det onödigt svårt att läsa och förstå ett bevis. Samtidigt ökar sannolikheten för missförstånd och fel, vilket i sin tur försvårar förståelsen av den efterföljande argumenteringen. Ur pedagogisk synvinkel är det särskilt viktigt att alla motiveringar skrivs ut tydligt. Det är då enklare för läraren att kontrollera att eleven verkligen förstår teorin bakom en uppgift och tillämpar den på rätt sätt. Eleverna kommer också att enklare kunna kontrollera att deras egna beräkningar är korrekta, genom att gå igenom varje steg var för sig, kontrollera att motiveringen gäller och att steget har utförts korrekt. En strukturerad beräkning reserverar en hel rad (eller mer än en rad om det behövs) för motiveringar, vilket innebär att det finns tillräckligt med utrymme för ordentliga motiveringar. Formatet tvingar en att motivera varje steg, eftersom en utelämnad motivering sticker ut i form av en tom parentes. I allmänhet skriver vi beräkningar i form av strukturerade beräkningar på följande sätt: 4
13 2.2. Strukturerade uppgifter t 0 1 {förklaring till att påstående t 0 1 t 1 gäller} t 1 2 {förklaring till att påståendet t 1 2 t 2 gäller} t 2. t n 1 n {förklaring till att påståendet t n 1 n t n gäller} t n I exemplet ovan är alla relationer i likheter. Varje påstående i beräkningen motiveras med ett argument som skrivs mellan hakparenteser, efter symbolen för relationen. En beräkning skrivs i två kolumner: den första innehåller symbolerna för relationerna (i exemplet = ) och specialtecknen (här sominleder härledningen och somavslutarden),denandrakolumneninnehålleruttrycken och motiveringarna. Mellan uttrycken kan förekomma vilken binär relation som helst. De vanligaste är eller, (ekvivalens), ) (implikation) och ( (omvänd implikation) för logiska påståenden och ordningsrelationer som =,<,>,apple, för aritmetiska och algebraiska påståenden. Vilka som helst binära relationer kan användas. Vi väljer ofta transitiva relationer (alla ovannämnda relationer är transitiva). Det är också möjligt att använda olika binära relationer i samma härledning. T.ex. likhet kan kombineras med vilken relation som helst: om a b och b = c, sågällerpåståendeta c också. Ett exempel på en icke-transitiv relation är olikhet: a 6= b och b 6= c betyder inte nödvändigtvis att a 6= c. Ettenkeltexempelpåmotsatsenär0 6= 1och 1 6= 0,som båda är sanna, men 0 6= 0 är inte sant. Därför leder flera olikheter efter varandra i en beräkning oftast inte till det önskade resultatet. 2.2 Strukturerade uppgifter Vi vill ofta vara noggranna med vilken uppgift vi löser och vilka antaganden som gäller. Då använder vi en allmän strukturerad uppgift. Följande exempel illustrerar det här formatet. 5
14 2. Strukturerade uppgifter Exempel 2. Visa att om a,b och c är icke-negativa tal, så gäller det att (1 + a)(1+b)(1+c) 1+a + b + c Vi formulerar uppgiften, antagandena och lösningen som en strukturerad uppgift. Visa att (1 + a)(1+b)(1+c) 1+a + b + c, då a,b,c 0 (1 + a)(1+b)(1+c) = {multiplicera uttrycken (1 + b) och (1 + c) med varandra} (1 + a)(1+b + c + bc) = {multiplicera uttrycken (1 + a) och (1 + b + c + bc) med varandra} 1+b + c + bc + a + ab + ac + abc {subtrahera det icke-negativa uttrycket ab + ac + bc + abc från uttrycket} 1+a + b + c Uppgiften vi vill lösa, Visa att (1 + a)(1+b)(1+c) 1+a + b + c skrivs direkt efter uppgiftstecknet idenandrakolumnen.påföljanderaderräknar vi upp antagandena. I det här exemplet finns endast ett antagande, a,b,c 0 Själva beviset är en strukturerad beräkning, som börjar efter vid -tecknet, precis som tidigare. -tecknet och slutar En strukturerad beräkning är ett specialfall av en strukturerad uppgift där man lämnat bort uppgiften och antagandena. Den är en kortare form av presentation, som är lämplig då det framgår ur sammanhanget vad vi vill bevisa och vilka antaganden som gäller. Vi använder strukturerade uppgifter då vi vill skriva ut exakt vilken uppgiften är och vilka antaganden vi får göra. I praktiken används båda formaten sida vid sida. En strukturerad uppgift har följande grundläggande format: 6
15 2.3. Deluppgifter Uppgift - antagande 1. - antagande m {en motivering för varför beräkningen löser uppgiften under de givna antagandena} t 0 1 {motivering av påstående t 0 1 t 1 } t 1 2 {motivering av påstående t 1 2 t 2 } t 2. t n 1 n {motivering av påstående t n 1 n t n } t n Vi skriver uppgiften som skall lösas efter -symbolen. Därefter räknar vi upp antagandena på skilda rader. Ett antagande markeras med ett. Om vi behöver hänvisa till enskilda antaganden så kan vi markera dem med bokstäver i parenteser (som (a), (b),... ). Beräkningen som följer efter antagandena börjar med en -symbol (läses bevisa att ). Beräkningen slutar med symbolen (läses vilket skulle bevisas ). Efter bevissymbolen kan vi skriva en motivering av varför beräkningen bevisar påståendet under givna antaganden. Vi använder två kolumner. Vi skriver specialsymboler som,, ochrelationssymbolsidenförstakolumnen och uppgiften, antaganden, uttryck och motiveringar i den andra kolumnen. Vi kommer att utvidga det här grundläggande formatet med flera nya funktione senare, som t.ex. deluppgifter, fakta och definitioner. Det här grundläggande formatet fungerar dock bra för at lösa enklare problem. 2.3 Deluppgifter Formatet ovan för en uppgift är tillräckligt när motiveringen för varje steg är relativt enkelt och kan skrivas på några få rader. När en motivering är mer komplicerad måste 7
16 2. Strukturerade uppgifter vi använda deluppgifter i motiveringarna. Exempel 3. Visa att m 2 n 2 3,dåm och n är positiva heltal och m>n.i den här härledningen använder vi två grundläggande aritmetiska regler: a + b apple a + b 0, då b apple b 0 (addition är monoton) ab apple ab 0, då a 0 och b apple b 0 (multiplikation är monoton) Vi bevisar påståendet på följande sätt. Visa att m 2 n 2 3,då m och n är positiva heltal och m>n m 2 n 2 = {konjugatregeln} (m n)(m + n) {multiplikation är monoton, enligt antagandena är m n 0 och m + n 3} (m n) 3 {multiplikation är monoton, enligt antagandena är m n 1 och 3 0} 1 3 = {räkna} 3 Det andra steget av härledningen är relativt komplicerat. Det hänvisar till regeln om multiplikations monotonitet, men vi kan bara använda regeln i det här fallet om villkoren m n 0 och m + n 3 uppfylls. Vi noterar att enligt antagandena uppfyller m och n följande villkor: m>nenligt antagandet, så m n>0 (då är också m n 0), n>0 enligt antagandet, så n 1, och m>n 1 enligt antagandet, så m 2, ochalltså.m + n 3. Vi kan skriva de här motiveringarna som oberoende (logiska) beräkningar på följande sätt: 8
17 2.3. Deluppgifter m>n m>noch n>0 {aritmetik} {aritmetik} m n>0 m n+1 and n 1 ) {aritmetik} m n 0 ) {aritmetik} m 2 and n 1 ) {aritmetik} m + n 3 Vi använder här ekvivalensrelationen mellan logiska påståenden. Relationen p p 0,därp och p 0 är logiska påståenden, säger att p och p 0 är lika sanna. En annan vanlig beteckning för ekvivalens är,, men beteckningen illustrerar bättre att det handlar om likhet mellan sanningsvärden. Ekvivalensrelationen är transitiv. Istället för att skriva de här extra motiveringarna var för sig i beviset kan vi inkludera dem direkt i form av deluppgifter, somvikanskrivaindragnaefterenmotivering. Antaganden som man gör i härledningar gäller då också i efterföljande deluppgifter. Längre fram kommer vi att visa att deluppgifter också kan innehålla egna antaganden. 9
18 2. Strukturerade uppgifter Exempel 4. Skriv om föregående bevis med hjälp av deluppgifter. Visa att m 2 n 2 3,då m och n är positiva heltal, och m>n m 2 n 2 = {konjugatregeln} (m n)(m + n) {multiplikation är monoton, enligt antagandena är m n 0 och m + n 3} m>n {aritmetik} m n>0 ) {aritmetik} m n 0 m>noch n>0 {aritmetik} m n +1och n 1 ) {aritmetik} m 2 och n 1 ) {aritmetik} m + n 3... (m n) 3 {multiplikation är monoton, enligt antagandena är m n 1 och 3 0} 1 3 = {räkna} 3 10
19 2.4. Fokusera på deluttryck Nedan till vänster har vi en enkel motivering för bevissteget t t 0,ochtillhöger en motivering med deluppgifter: t {motivering} t 0 t {motivering} uppgift 1. uppgift n... t 0 En motivering kan stödas av n olika deluppgifter, uppgift 1,..., uppgift n,därn 0. Deluppgifterna dras in ett steg till höger, så att de börjar vid följande kolumn. Det här gör det enklare att skilja mellan deluppgifterna och huvuduppgiften. Motiveringarna förklarar varför trt 0 är sant, om vi antar att varje deluppgift är sann. Eftersom deluppgifterna ibland kan vara rätt långa, så placerar vi tecknet... där det andra uttrycket (i det här fallet t 0 )somskallbevisasär.dethärgördetenklare att se var deluppgiften slutar och huvuduppgiften fortsätter. 2.4 Fokusera på deluttryck I många fall är det nödvändigt att räkna med långa och komplicerade uttryck. Då kan vi använda delberäkningar som fokuserar på en del av ett uttryck och modifiera det utan att skriva om hela uttrycket i varje steg. 11
20 2. Strukturerade uppgifter Exempel 5. Förenkla uttrycket p 7+2 p 11 + p 7 2 p 11. Lösningen ges som en strukturerad härledning med två delberäkningar, den ena innanför den andra. Förenkla uttrycket p 7+2 p 11 + p 7 2 p 11 p 7+2 p 11 + p 7 2 p 11 = {kvadrera uttrycket, förenkla det och ta kvadratroten av det förenklade uttrycket} ( p 7+2 p 11 + p 7 2 p 11) 2 = {kvadreringsregeln} 7+2 p p7+2 p 11 p7 2 p p 11 = {fokusera på deluttycket 2 p7+2 p 11 p7 2 p 11} 2 p7+2 p 11 p7 2 p 11 = {skriv under samma rottecken} q 2 (7 + 2 p 11) (7 2 p 11) = {konjugatregeln} 2 p = {förenkla} 2 p p p p 11 = {förenkla} p 5... p p 5 Det ursprungliga problemet var att förenkla ett rotuttryck. Vi förenklar kvadraten av uttrycket i en delberäkning. Kvadratroten av det förenklade uttrycket är sedan lösningen till det ursprungliga problemet. Vi förenklar det komplicerade rotuttrycket idelberäkningeninnanfördenhärberäkningen.närvifokuserarpåendastendel av uttrycket i delberäkningen blir det lättare att se vad vi modifierar. Dessutom gör vi färre misstag när vi inte behöver kopiera komplicerade uttryck från rad till rad. Att skriva och läsa den här typen av bevis blir lättare om vi använder en dator och en editor med stöd för indentering, och som kan visa och dölja indragna rader (en så kallad outlining editor). Det här gör det möjligt att välja hur detaljerat man vill studera beviset. Om man gömmer deluppgifterna så får man en bättre överblick över beviset, och genom att visa dem får man en mer detaljerad bild av beviset. När en delberäkning är gömd indikerar symbolen "..." att argumentet har gömda beräkningar. 12
21 2.5. Textuppgifter 2.5 Textuppgifter I en textuppgift beskriver man först en situation, och ger sedan i uppgift att bevisa eller beräkna något i den här situationen. I en strukturerad uppgift beskrivs situationen av antagandena. I följande exempel har vi angett antagandena med bokstäver, så att vi enklare kan hänvisa till dem i härledningen. Den första uppgiften kommer från mekaniken. Exempel 10. Sedan året 1960 har restiden för den snabbaste tågförbindelsen mellan Helsingfors och Villmanstrand förkortats med 37%. Beräkna hur många procent den genomsnittliga hastigheten då har ökat. Antag att tågbanans längd är oförändrad. Först skriver vi om uppgiften genom att lägga till beteckningarna som vi använder ibeviset.den omskrivna uppgiften är följande: Efter år 1960 har restiden t 0 för det snabbaste tåget mellan Helsingfors och Villmanstrand förkortats med 37 procent jämfört med den ursprungliga restiden t. Beräknamedhurmångaprocentp medelfarten v 0 har ökat jämfört med den ursprungliga medelfarten v. Viantaratt tågbanans längd s är oförändrad. Beräkna med hur många procent p farten har förändrats, då t 0 =0, 63 t {transitivitet, beräkna närmevärde} p = {definitionen av förändringsprocent} v 0 v v = {fysik: definitionen av medelfart v = s t,därs är sträckan man har rört sig och t är restiden} s t 0 s t s t = {förenkla} s t 0 s t 1 = {förenkla bråken} s t s t 0 1 = {förenkla, antaganden} 13
22 2. Strukturerade uppgifter 1 0, 63 1 {beräkna närmevärde} 0, 59 = {konvertera till procent: x% = x 100 } 59% Svar: medelfarten har ökat med 59%. 2.6 Frågor och svar I en matematisk uppgift måste man ofta hitta ett värde x som uppfyller vissa givna villkor, eller så måste man hitta varje värde x som uppfyller de givna villkoren. Ekvationslösning är ett exempel på denna vanliga typen av uppgift. Ofta sägs det inte explicit med avseende på vilken variabel man skall lösa en ekvation, eftersom det är uppenbart (variabeln x), men om en ekvation har många variabler och konstanter så kan en uppgift i den här formen vara tvetydig. I strukturerade härledningar kan vi beskriva en uppgift mer exakt när vi efter -symbolenangervilkenvariabelviletarefterochvilkavillkordenböruppfylla. Svaret ges efter -symbolen. Exempel 14 En planka har bredden 95 mm och längden 1,6 m. Den sågas i bitar med samma längd, som placeras bredvid varandra så att de bildar en kvadrat. Vilken är kvadratens maximala sidlängd? Låt n vara antalet bitar, n 2 Z +,ochlåtx vara bitarnas längd. Då gäller det att nx apple 1600, därlängdenhetenärmillimeter.vivetocksåattx = 95n, eftersom bitarna bildar en kvadrat. Vi beskriver situationen i figur 2.1 (notera att en bit kan bli över). x 95 mm n Figur 2.1: Kvadraten och den överblivna biten. Nu vill vi maximera värdet på x. 14
23 2.6. Frågor och svar Beräkna n 2 Z + som maximerar värdet x = 95n och uppfyller villkoret nx apple 1600 n maximerar värdet x = 95n, ochnx apple 1600 och n 2 Z + {förenkla villkoret} Förenkla nx apple 1600, då - x = 95n nx apple 1600 {använd antagandet x = 95n} n 95n apple 1600 {förenkla} n 2 apple 1600/95 {lös genom att anta att n 2 Z + ; 16 apple < 25} n apple 4... n maximerar värdet x = 95n, ochn apple 4 och n 2 Z + {x är en strängt växande funktion av n} n =4 n =4 Med andra ord, den största möjliga kvadraten är 4 95 = 380 (mm). 15
24
25 Kapitel 3 Att lösa ett problem steg för steg I föregående kapitel visade vi hur strukturerade uppgifter används för att lösa enkla matematiska uppgifter. När en lösning blir längre och mer komplicerad behöver vi emellertid metoder som tillåter oss att dela upp lösningen i mindre delar. Dessutom behöver vi en tydlig strategi för hur man ska lösa en uppgift. Inom matematik finns tre grundläggande strategier för att lösa mer komplicerade problem steg för steg: algebraiska beräkningar, framåtgående bevis och bakåtgående bevis. Vi har visat i föregående kapitel hur man löser problem med beräkningar. I ett framåtgående bevis räknar vi upp en följd av fakta som följer från antagandena och tidigare fakta och som hjälper med förståelsen och lösningen av problemet. Vi fortsätter tills vi har samlat så många fakta att vi kan lösa problemet direkt, med en beräkning eller genom ett slutligt faktum. Bakåtgående bevis börjar från det ursprungliga problemet och försöker reducera detta till enklare problem och lösa dessa, antingen direkt, eller genom att reducera dem till ännu enklare problem, osv. Strukturerade uppgifter gör det möjligt att använda alla de här bevisstrategierna samtidigt, i olika delar av en lösning. I det här kapitlet visar vi hur man använder framåtgående och bakåtgående bevis i strukturerade uppgifter. 3.1 Framåtgående bevis Då vi löser en uppgift har vi ofta en situation där vi inte direkt ser hur vi skall beräkna det önskade resultatet. Vi behöver förbereda beräkningen först genom att räkna upp några fakta som följer från antagandena och som vi behöver för att utföra beräkningarna. Vi skriver ett faktum på följande sätt: + {motivering} påstående 17
26 3. Att lösa ett problem steg för steg Vi markerar ett faktum med ett + -tecken, till skillnad från antaganden som vi markerar med ett -tecken. Ett faktum bör alltid komma med en motivering som förklarar hur faktumet följer från antagandena och tidigare fakta. Motiveringen skrivs före faktumet. Motiveringen kan vara enkel eller så kan den bygga på deluppgifter. Fakta kan numreras, och då skrivs siffrorna i hakparenteser (t.ex. [1], [2] osv.). Först visar vi med ett exempel hur man kan använda fakta för att lösa en uppgift. Exempel 11 Höjden mot hypotenusan i en rätvinklig triangel delar hypotenusan iförhållandet3:7.beräknaförhållandetmellankateternaslängder. Vi börjar med att rita en figur, som beskriver problemet: 3x 7x I nästa figur har vi namngett kateterna (a och b), hypotenusan (c) och höjden(h). 3x c a h 7x b Vi använder de här beteckningarna i beviset. Vi skriver själva beviset enligt följande modell. Först skriver vi ner några enkla fakta, som följer direkt från figuren. Baserat på dessa kan vi bevisa några andra fakta. Slutligen beräknar vi förhållandet mellan kateternas längder utgående från dessa fakta. Beräkna förhållandet a b [1] {från figuren} c = 10x [2] {figuren och Pythagoras sats} h 2 +9x 2 = a 2 [3] {figuren och Pythagoras sats} 18
27 3.1. Framåtgående bevis h x 2 = b 2 [4] {figuren och Pythagoras sats} a 2 + b 2 = 100x 2 [5] {eliminera h} [2] ^ [3] {observation [2] och [3]} h 2 +9x 2 = a 2^h x 2 = b 2 ) {subtrahera den första ekvationen från den andra ekvationen och förenkla} b 2 a 2 = 40x 2... b 2 a 2 = 40x 2 [6] {Beräkna b 2 } [4] ^ [5] {observation [4] och [5]} a 2 + b 2 = 100x 2^b 2 a 2 = 40x 2 ) {slå ihop ekvationerna} 2b 2 = 140x 2 {dividera båda leden med 2}... b 2 = 70x 2 b 2 = 70x 2 [7] {Beräkna a 2 } [4] ^ [6] {observation [4] och [6]} a 2 + b 2 = 100x 2^b 2 = 70x 2 ) {sätt in den andra ekvationen i den första ekvationen} a x 2 = 100x 2 {lös a 2 }... a 2 = 30x 2 a 2 = 30x 2 19
28 3. Att lösa ett problem steg för steg a b = {kvadratrotens definition, a och b är positiva tal} q a 2 b 2 = {observation [6] och [7]} q 30x 2 70x 2 = {reducera och förenkla} p 3 p 7 Följande exempel från den analytiska geometrin visar också hur man använder fakta iuppgifter.idethärexempletmarkerarviantagandenmedbokstäverochfaktamed siffror. Exempel 12. Beräkna den punkt på parabeln y = x 2 2x 3, därdenriktade vinkeln hos tangenten är 45. Vi kan omformulera problemet på följande sätt: Beräkna punkten (x 0,y 0 ) på parabeln y = x 2 2x 3 där den riktade vinkeln hos tangenten är 45. Beräkna punkten (x 0,y 0 ),då (a) y = f (x) =x 2 2x 3 för varje x 2 R, och (b) den riktade vinkeln hos tangenten i punkten (x 0,y 0 ) är = 45 [1] {beräkna derivatan i punkten x 0 } tangenten till parabeln i punkten (x 0,y 0 ) har den riktade vinkeln 45 {riktningskoefficienten k ges av den riktade vinkeln med formeln k = tan } tangentens riktningskoefficient i punkten (x 0,y 0 ) är tan 45 {tan 45 = 1}... f 0 (x 0 )=1 tangenten har riktningskoefficienten 1 i punkten (x 0,y 0 ) {derivatan av funktionen ger riktningskoefficienten} f 0 (x 0 )=1 [2] {beräkna värdet på variabeln x 0,observation[1]} 20
29 3.1. Framåtgående bevis f 0 (x 0 )=1 {antagande (a), beräknaderivatan} 2x 0 2=1 {lös x} x 0 = x 0 = 3 2 (x 0,y 0 ) = {observation [2]} ,y 0 = {beräkna värdet på y 0 med hjälp av antagande (a)} 3 2, = {räkna} 3 2, 15 4 Punkten vi söker är alltså (x 0,y 0 )=( 3 2, 15 4 ). Den allmänna formen för en strukturerad uppgift med fakta ser ut på följande sätt. 21
30 3. Att lösa ett problem steg för steg Uppgift - antagande 1. - antagande m + {motivering av faktumet} faktum 1. + {motivering av faktumet} faktum m {motivering för varför härledningen är en lösning till uppgiften med de givna antagandena och fakta} t 0 1 {motivering av påståendet t 0 1 t 1 } t 1 2 {motivering av påståendet t 1 2 t 2 } t 2. t n 1 n {motivering av påståendet t n 1 n t n} t n 3.2 Bakåtgående bevis Bakåtgående bevis kräver inte nya mekanismer, vi kan utföra dem med deluppgifter. Vi visar två exempel, där vi löser den givna uppgiften genom att reducera den ursprungliga uppgiften direkt till deluppgifter. Då behöver vi inte göra beräkningar på huvuduppgiftens nivå, och vi kan utelämna dem. Den första exemplet är ett fallbevis. I den här typen av bevis identifierar vi först varje möjligt fall, sedan visar vi att vårt påstående är sant i varje enskilt fall. Det är viktigt att de fall som vi behandlar omfattar varje möjlighet. Exempel 16. Bevisa att olikheten x +1 > 1 är sann utanför intervallet [ 2,0]. Visa att x +1 > 1, då 22
31 3.2. Bakåtgående bevis (a) x>0 _ x< 2 {fallbevis, enligt antagandet (a) är det tillräckligt att kontrollera fallen x>0 och x< 2 var för sig} Visa att x +1 > 1, då x>0 x +1 = {definition av absolutvärde, antagandet x>0} x +1 > {antagande} 0+1 = {räkna} 1 Visa att x +1 > 1, då x< 2 x +1 = {absolutvärdets definition, antagandet x< 2} (x + 1) = {förenkla} x 1 > {antagandet x< 2 dvs. x>2} 2 1 = {räkna} 1 Induktionsbevis är ett annat exempel där det lönar sig att reducera ett problem. I ett induktionsbevis behandlar vi två fall: basfallet och induktionssteget. Om vi kan bevisa båda stegen så är påståendet sant. 23
32 3. Att lösa ett problem steg för steg Exempel 14. Bevisa att för n 2 N med hjälp av induktion. Vi bevisar det här på följande sätt: n = Visa att n = n(n+1) 2 för n 2 N {induktionsbevis} n (n + 1) 2 Basfall: visa att n = n(n+1) 2,då n = n = n(n+1) 2 {sätt in antagandet n =0} 0= 0(0+1) 2 {multiplicera med noll} T Induktionssteg: visa att n 0 = n0 (n 0 +1) 2,då n 0 = n +1och n = n(n+1) n 0 = {antagande} n +(n + 1) = {induktionsantagande} n(n+1) 2 +(n + 1) = {beräkna en gemensam nämnare} n(n+1)+2(n+1) 2 = {distributiva lagen, kommutativa lagen} (n+1)(n+2) 2 = {antagandet n 0 = n +1} n 0 (n 0 +1) 2 24
33 Kapitel 4 Strukturerade härledningar En strukturerad härledning är en följd av härledningssteg, där varje steg är antingen ett antagande, en deklaration, ett faktum, en definition eller en uppgift. En strukturerad härledning är det traditionella sättet på vilket en matematiker arbetar med ett problem. Först försöker vi formulera problemet i matematisk form. När vi gör detta inser vi behovet av mer exakta antaganden, och kanske även några ytterligare antaganden. På samma sätt kanske vi behöver införa några nya begrepp, som vi definierar för att förenkla problemet. Nu kan vi fokusera på att lösa problemet. När vi har löst det ursprungliga problemet, ser vi kanske att det leder till andra intressanta resultat, som vi också kan studera i samma sammanhang. Dessa kräver ytterligare antaganden och nya definitioner och leder till nya problem, osv. Matematiska resonemang byggs upp lite på samma sätt som en roman, med en tydlig berättelse och en eller flera höjdpunkter. Skillnaden är att varje steg måste bevisas vara korrekt, eftersom ett enda fel kan förstöra hela strukturen. En strukturerad härledning ger mera frihet än strukturerade uppgifter när vi löser matematiska problem: Vi kan definiera nya begrepp före vi formulerar uppgifter och fakta som använder de här begreppen. Vi kan lösa flera uppgifter under samma antaganden, fakta och definitioner. Vi behöver inte presentera varje antagande genast, vi kan lägga till nya antaganden när de behövs. 25
34 4. Strukturerade härledningar Strukturerade härledningar generaliserar alla de konstruktioner som vi har beskrivit tidigare. En strukturerad uppgift är ett specialfall av en strukturerad härledning, en som bara har en uppgift. Ett enskilt antagande, beteckning, faktum eller definition är också ett specialfall av en strukturerad härledning. 4.1 Definitioner Den allmänna formen för en definition är: + Definiera c 1 2 A 1,...,c m 2 A {motivering} definitionsvillkor Det här definierar nya konstanter c 1 2 A 1,...,c m 2 A m,somvisedankananvända i den fortsatta härledningen. Motiveringen bör visa att vi (under de givna antagandena och tidigare fakta) kan ge värden för konstanterna som uppfyller definitionsvilkoret. En definierad konstant kan vara enkel, som ett reellt tal eller ett heltal, men den kan också vara en funktion. Vi kan använda definitioner också i strukturerade uppgifter, på samma sätt som fakta. De kan vara användbara när vi behöver t.ex. en kortare beteckning för något komplicerat koncept. Vanligtvis har en definition emellertid ett mera allmänt syfte. Vi använda den inta bara för att lösa ett problem, utan mera allmänt då vi analyserar någon teori eller modell. Då är definitionen en naturlig del av den allmänna utvecklingen av teorin och beskrivs bäst som ett steg i en strukturerad härledning. Exempel 15. Vi definierar följden a 0,a 1,a 2,... på följande sätt: a n = n 2n +1 då n =0, 1, 2, 3,....Visaatt(A)0 <a n < 1 2 då n 1, att(b)a n+1 >a n då n 0 och (C) beräkna lim n!1 a n. Vi löser den här uppgiften med en strukturerad härledning. Vi identifierar uppgifterna med stora bokstäver, A, B och C. + Definiera a : N! R {Funktionen a beskriver en följd, då vi betecknar a i = a(i), i=0, 1, 2,... Den här följden är väldefinierad, eftersom 2n +1> 0 då n =0, 1, 2,... } a n = n 2n +1 då n =0, 1, 2, 3,... 26
35 4.1. Definitioner A. Visa att 0 <a n < 1 2,då - n 2 N, n 1 0 <a n < 1 2 {definition a n } 0 < n 2n +1 < 1 2 {multiplicera båda leden med 2n +1,skriv dubbelolikheten som en konjunktion} 0 <n^ n< {enkelt} 2n <n^ 2n <2n +1 {enligt antagandet är n 1, sådetförstapåståendetärsant;detandrapå- ståendet är alltid sant} T B. Visa att a n+1 >a n,då - n 2 N a n+1 >a n {definition a n } n +1 2(n + 1) + 1 > n 2n +1 {enkelt} n +1 2n +3 > n 2n +1 {multiplicera med (2n + 3)(2n + 1), vilketärpositivtenligtantagandet} (2n + 1)(n + 1) > (2n + 3)n {enkelt} 2n 2 +3n +1> 2n 2 +3n {subtrahera 2n 2 +3n från båda leden} 1 > 0 27
36 4. Strukturerade härledningar {aritmetik} T C. Definiera lim n!1 a n lim n!1 a n = {enligt definitionen} lim n!1 n 2n +1 = {dividera både täljaren och nämnaren med n } lim n!1 = {enkelt} n n 2n n + 1 n lim n! n = { 1! 0 då n!1} n 1 2 lim n!1 a n = Modellering Strukturerade härledningar är användbara då vi vill modellera någon situation och sedan ställa frågor om modellen. Vi återkommer till uppgiften som vi presenterade tidigare,m tågförbindelsen mellan Helsingfors och Villmanstrand igen, men nu använder vi en strukturerad härledning. Det här betyder att vi först konstruerar en modell som beskriver uppgiften och sedan börjar vi lösa frågor relaterade till modellen. Då man modellerar är det ofta bra att ange hur vi betecknar olika storheter. Vi introducerar beteckningar i en deklaration, av formen + c 1 2 A 1,...,c m 2 A 28
37 4.2. Modellering Det här säger att vi inför nya konstanter kallade c 1,...,c m ihärledningen,där konstanten c 1 har ett värde som tillhör mängden A 1,konstantenc 2 tillhör mängden A 2 osv. Vi kan tolka en deklaration som ett specialfall av en definition, där vi endast anger den definierade konstantens namn och värdemängd. Vi kan begränsa konstantens värde senare med ytterligare antaganden, om det behövs. Exempel 16. Sedan året 1960 har restiden för den snabbaste tågförbindelsen mellan Helsingfors och Villmanstrand förkortats med 37%. Beräkna hur många procent den genomsnittliga hastigheten då har ökat. Antag att tågbanans längd är oförändrad. Vi börjar med att namnge konstanterna som vi använder för att beskriva uppgiften. + s 2 R avståndet mellan Helsingfors och Villmanstrand + t 2 R den ursprungliga restiden + t 0 2 R den nuvarande restiden Vi kan skriva kommentarer i en härledning efter " " tecknet. Här hjälper kommentarerna oss komma ihåg vad storheterna beskriver i det ursprungliga problemet. Vi behöver inte skriva en strukturerad härledning som ett enda stycke, utan vi kan lägga till text mellan stegen som här, för att göra det lättare att förstå hur lösningen framskrider. Sedan skriver vi antagandena: (a) t 0 =0.63 t (b) s>0,t>0,t 0 > 0 Notera antagandena som vi lade till, som säger att s, t, t 0 alla är större än noll. Det här följer från uppgiftens definition. Eftersom s>0 så kan restiden inte vara noll. Vi definierar hastigheten på normalt sätt: [1] Definiera v 2 R den ursprungliga medelhastigheten {v är väldefinierad, eftersom t > 0} v = s t [2] Definiera v 0 2 R den nuvarande medelhastigheten {v 0 är väldefinierad, eftersom t 0 > 0} v 0 = s t 0 29
38 4. Strukturerade härledningar Vi definierar förändringsprocenten på följande sätt: [3] Definiera p 2 R hastighetens förändringsprocent {p är väldefinierad: eftersom s, t > 0 så är v > 0} p = v0 v v Nu kan vi lösa uppgiften: p = {definition [3]} v 0 v v = {definition [1] och [2]} s t 0 s t s t = {förenkla} s t 0 s t 1 = {förenkla bråken} s t s t 0 1 = {förenkla, antagande} 1 0, 63 1 {beräkna närmevärde} 0, 59 = {konvertera till procent: x% = x 100 } 59% Svar: medelfarten har ökat med 59%. En strukturerad härledning är ett bättre sätt att presentera ett matematiskt resonemang än en strukturerad uppgift då resonemanget är långt och det finns ett behov av att förklara vad de olika stegen i härledningen används till. 30
39 Kapitel 5 Härledningar och logik Ett centralt inslag i en strukturerad härledning är användningen av logiska uttryck och regler i matematiska bevis och härledningar. Logik är naturligtvis en viktig del av varje bevis, men den används ofta på ett informellt sätt. I strukturerade härledningar används logiska beteckningar systematiskt och de logiska regler som utnyttjas anges explicit. Vi kan då göra beräkningar med logiska uttryck på samma sätt som vi idag gör med aritmetiska och algebraiska uttryck. 5.1 Logiska påståenden Vi har samlat de logiska beteckningar som vi använder i strukturerade härledningar ientabell5.1.beteckningarnaärrättvanliga,ävenomvihargjortnågraförändringar. Implikation kan också betecknas! och för ekvivalens finns även beteckningarna, och $. Konjunktion betecknas ibland med & ochdisjunktionmed. Universalkvantorn betecknas ibland med Ax ochexistenskvantornmed Ex. Vi har redan använt logiska beteckningar i tidigare exempel. I själva verket kräver gymnasiematematik en hel del logik både för att presentera och för att manipulera Tabell 5.1: Loogiska symboler och operationer T : sant, ettsantpåstende(true) F : falskt, ettfalsktpåstående(false) p : negation, påståendet p är falskt om p är sant, och sant om p är falskt p ^ q : konjunktion, påståendet är sant om p och q är båda sanna p _ q : disjuktion, påståendet är sant om p eller q (eller båda) är sanna p ) q : implikation, om p är sant, så är också q sant p q : ekvivalens, p är lika sant som q (8x : p (x)) : universalkvanttor n, p(x) är sant för varje värde för variabeln x (9x : p (x)) : existenskvanttorn, p(x) är sant för något värde för variabeln x 31
40 5. Härledningar och logik matematiska påståenden. Vi visar först hur vi behöver logik i gymnasiematematiken redan då löser en andragradsekvation. Exempel 6. Lös ekvationen 7x 2 6x =0. Följande strukturerade härledning löser ekvationen: Lös ekvationen 7x 2 6x =0 7x 2 6x =0 {distributiva lagen: a (b + c) =ab + ac} x (7x 6) = 0 {nollregeln: ab =0 (a =0_ b = 0)} x =0_ 7x 6=0 {lös den andra ekvationen} x =0_ x = 6 7 I härledningen skriver vi om det logiska påståendet 7x 2 6x =0med hjälp av steg som bevarar ekvivalensen mot till x =0_ x = 6 7,. Det senare uttrycket visar direkt vilka två värden för variabeln x som uppfyller ekvationen (variabeln x uppfyller ekvationen då dess värde är 0 eller 6 7 ). Varje steg motiveras med en regel. I första steget använder vi t.ex. den distributiva lagen för multiplikation, a (b + c) =ab + ac. Vi använder den här regeln i steget 7x 2 6x =0 x (7x 6) = 0, dvs. den omskrivna ekvationen är ekvivalent med den ursprungliga ekvationen. Det är värt att notera att vi ger lösningen till ekvationen som en disjunktion. Vi har visat att ekvationen 7x 2 6x =0är lika sann som ekvationen x =0_ x = 6 7. En ekvation ett logiskt påstående som kan vara sant för vissa värden på variabeln x och falskt för andra värden på x. Vi kan också använda strukturerade härledningar när vi uttrycker påståenden med naturligt språk. Följande exempel beskriver det här. 32
41 5.1. Logiska påståenden Exempel 7. Visa att k 2 + k är ett jämnt tal, för varje heltal k. Här är ett enkelt bevis av påståendet: Visa att k 2 + k är ett jämnt tal, då - k är ett heltal talet k 2 + k är jämnt {distributiva lagen} talet k (k + 1) är jämnt {en produkt är jämn om en av faktorerna är jämn} talet k är jämnt _ talet k +1är jämnt {ett av två på varandra följande tal är alltid jämnt} T I exemplet använder vi naturligt språk i logiska påståenden som k 2 +k är ett jämnt tal. Uppgiften var att bevisa att påståendet k + k är ett jämt tal är sant. Vi uttrycker det här på följande sätt (k 2 + k är ett jämnt tal) T, med andra ord, påståendet k 2 + k är ett jämnt tal är ekvivalent med sanningsvärdet T.Omvivillbevisapåståendetmedhjälpavenberäkningsåbör vi skriva påståendet som en ekvivalens. Eftersom p ) T alltid är sant räcker det med att visa att påståendet T ) p är sant. Följande exempel beskriver hur vi kan använda logiska regler när vi löser problem på gymnasienivå. Exempel 9. I en rätvinklig triangel är hypotenusans längd 15 cm, och omkretsen är 36 cm. Beräkna kateterna längder. I härledningen använder vi Pythagoras sats a 2 + b 2 = c 2, där a och b är kateterna och c är hypotenusan. Vi kan beräkna omkretsen på det vanliga sättet som summan av sidornas längder, dvs. a + b + c. Beräkna sidornas längder i triangeln, då (a) triangeln är rätvinklig och har kateterna a och b och hypotenusan c 33
42 5. Härledningar och logik (b) (c) c = 15 (cm) triangelns omkrets är 36 (cm) T {Pythagoras sats, antagande (a)} a 2 + b 2 = c 2 {antagande (b) och (c)} a 2 + b 2 = 15 2 ^ a + b + 15 = 36 {lös den andra ekvationen med avseende på b} a 2 + b 2 = 15 2 ^ b = 21 a {sätt in b från den andra ekvationen i den första ekvationen, 15 2 = 225} a 2 + (21 a) 2 = 225 ^ b = 21 a {beräkna (21 a) 2 } a a + a 2 = 225 ^ b = 21 a {förenkla den första ekvationen} 2a 2 42a = 0 ^ b = 21 a {lös andragradsekvationen} 2a 2 42a = 0 {rotformeln} a = ( 42)±p {förenkla} a = 42±p {förenkla} a = 42±6 4 {förenkla} a =9_ a = (a =9_ a = 12) ^ b = 21 a {distributiva lagen: (p _ q) ^ r =(p ^ r) _ (q ^ r)} (a =9^ b = 21 a) _ (a = 12 ^ b = 21 a) {sätt in värdet på variabeln a iekvationenförb} 34
43 5.2. Kvantorer i gymnasiematematiken Figur 5.1: A parabel som öppnar sig uppåt och neråt (a =9^ b = 21 9) _ (a = 12 ^ b = 21 12) {förenkla} (a =9^ b = 12) _ (a = 12 ^ b = 9) Svaret visar att kateternas längder är 9 cm och 12 cm. Vi började beviset med påståendet T.EftersomvivetattPythagorassatsärsann så kan vi använda antagande (a) för att visa att T a 2 + b 2 = c 2 Sedan visar vi att a 2 + b 2 = c 2 är ekvivalent med påståendet (a =9^ b = 12) _ (a = 12 ^ b = 9). EftersomT är sant så måste påståendet som vi får som resultat vara sant, och vi har löst uppgiften. 5.2 Kvantorer i gymnasiematematiken Nästa uppgift är ett exempel på en mera utmanande härledning, där vi utnyttjar universalkvanttorn för att formulera problemet. Exempel 8. För vilka värden på konstanten a är funktionen f : R! R alltid negativ, då f (x) = x 2 + ax + a 3 för varje x? I det här fallet kräver lösandet av huvuduppgiften att vi löser två deluppgifter (beräkna diskriminanten D f och beräkna dess nollställen). I resonemanget använder vi kurvorna i figur 5.1, som är parabler som öppnar sig uppåt och neråt. Vi löser uppgiften med hjälp av en strukturerad härledning på följande sätt. Beräkna för vilka värden på a funktionen f alltid är negativ, då 35
44 5. Härledningar och logik - f (x) = x 2 + ax + a 3 för varje x 2 R 8x : x 2 + ax + a 3 < 0 {grafen till funktion f är en parabel som öppnar sig neråt då andragradstermens koefficient är negativ; en sådan graf är alltid negativ om den saknar nollställen (figuren till vänster)} 8x : x 2 + ax + a 3 6= 0 {en andreagradsekvation saknar nollställen om diskriminanten D f är mindre än noll} D f < 0 {sätt in diskriminantens värde D f } Beräkna diskriminanten värde D f D f = {diskriminantenavax 2 + Bx + C =0ges av formeln B 2 4AC} a 2 4( 1) (a 3) = {förenkla} a 2 +4a a 2 +4a 12 < 0 {grafen till funktionen definierad av uttrycket a 2 +4a 12 är en parabel som öppnar sig uppåt då andragradstermens koefficient är positiv, därmed är grafen negativ mellan nollställena (figuren till höger)} Beräkna nollställena till polynomet a 2 +4a <a<2 a 2 +4a 12 = 0 {rotformeln} a = 4±p ( 12) 2 1 {lös} a =2_ a = 6 Därmed har vi bevisat att 8x : x 2 + ax + a 3 < 0 6 <a<2. 36
45 5.3. Exakta bevis Med andra ord är funktionen f negativ om och endast om 6 <a<2. I strukturerade härledningar kan vi fritt använda logiska påståenden och logiska inferensregler när vi motiverar likheten mellan påståenden. I detta fall behövde vi allkvantorn för att formulera problemet. Vi kan också använda extra material, såsom figurer, tabeller eller andra typer av stöd i strukturerade härledningar. I det föregående exemplet hänvisade vi till två figurer i beviset. Tilläggsmaterial presenteras utanför beviset, men det kan hänvisas till i härledningen. Vi utnyttjar även parablers allmänna egenskaper i beviset. I exemplet har vi bevisat ekvivalens mellan påståendena. Om vi endast bevisar implikationen åt höger (8x : x 2 + ax + a 3 < 0) ) 6 <a<2, så kan villkoren för konstanten a vara för svaga, vi kunde få extra värden som inte uppfyller de ursprungliga villkoren. Om vi å andra sidan endast visar att 8x : x 2 + ax + a 3 < 0 ( 6 <a<2, så är det möjligt att vi inte hittar varje värde på konstanten a som uppfyller de ursprungliga villkoren. Vi använder ekvivalens för att visa att villkoren uppfylls för de beräknade värdena på konstanten a och endast för dessa värden. 5.3 Exakta bevis I tidigare bevis har motiveringarna för stegen har varit ganska fria. Om vi vill göra bevis logiskt exakta är det viktigt att nämna vilken regel som vi har använt i varje steg. Vi bör även nämna hur vi har använt regeln och motivera varför vi kan använda regeln i detta sammanhang. Låt oss studera den distributiva lagen, som är en typisk regel från algebran: x(y + z) =xy + xz. Det här gäller för varje aritmetiskt uttryck x,y och z. Härärx,y och z så kallade metavariabler (eller syntaktiska variabler), som vi ersätter med konkreta uttryck då vi använder regeln. Vi kan skriva den exakta motiveringen av ett steg i ett bevis i formen {namn : regel, därsubstitution, villkorantagande gäller} I motiveringen nämns regelns namn (namn), 37
46 5. Härledningar och logik skrivs själva regeln ut vid behov (regel ), beskriver vi hur vi använder regeln (dvs. vilka värden som sätts in istället för den syntaktiska variabeln) (substitutioner) och vi konstaterar att antagandena för regelns användning är uppfyllda. Vi kan skriva en mera exakt motivering av ett steg där vi använder den distributiva lagen i formen: (a b)(a + b) = {distributiva lagen för addition: x (y + z) =xy + xz, därx := a b, y := a, z := b, villkoretatta b, a och b är aritmetiska uttryck gäller} (a b) a +(a b) b Här är x := a b, y := a och z := b substitutioner som vi använder i regeln. Därmed tillämpar vi den distributiva lagen så att vi väljer a b som variabel x, a som variabel y och b som variabel z. Vikonstaterarocksåattvikananvändaregeln eftersom varje uttryck är aritmetiskt. Efter att vi substituerat får vi ett specialfall av den distributiva lagen: (a b)(a + b) =(a b)a +(a b)b Vi kan skriva regeln direkt i motiveringen, som vi har gjort tidigare, eller så kan vi endast skriva namnet på regeln. Vi utelämnar ofta substitutionen om det framgår från bevissteget vilken substitution vi har använt. På samma sätt kan vi utelämnar villkoren om de är uppenbara från sammanhanget. Då kan vi skriva mycket korta motiveringar för bevisstegen, (a b)(a + b) = {distributiva lagen för addition} (a b)a +(a b)b Läsaren arbete blir då att lägga till nödvändiga detaljer, dvs. vad regeln faktiskt säger och vilken substitution vi har använt. Dessutom måste läsaren kontrollera att antagandena för att använda regeln gäller. 38
47 5.3. Exakta bevis Exempel 17. Vi bevisar konjugatregeln på nytt, men den här gången använder vi bara axiom för reella tal. Vi använder delhärledningar i beviset för att ge det samma struktur som det tidigare beviset, dvs. bevisen de har samma huvudsteg. Visa att (a b)(a + b) =a 2 b 2,medhjälpavaxiomenförreellatal {transitivitet} (a b)(a + b) = {bevisa med hjälp av axiom}... a 2 +( ba)+ba + b 2 = {bevisa med hjälp av axiom}... a 2 b 2 I det här beviset är delhärledningarna gömda, så att vi ser bevisets övergripande struktur. Delhärledningen i det första steget är följande: Bevisa att (a b)(a + b) =a 2 b 2 med hjälp av axiom (a b)(a + b) = {distributiva lagen för addition: x (y + z) =xy + xz, därx := a b, y := a, z := b} (a b)a +(a b)b = {kommutativa lagen: xy = yx, därx := a b, y := a} a(a b)+(a b)b = {kommutativa lagen: xy = yx, därx := a b, y := b} a(a b)+b(a b) = {definition av subtraktion: x y = x +( y), därx := a, y := b} a(a +( b)) + b(a +( b)) = {distributiva lagen för addition: x (y + z) = xy + xz, där x := a, y := a, z := b} aa + a ( b)+b(a +( b)) = {distributiva lagen för addition: x (y + z) = xy + xz, där x := b, y := a, z := b} aa + a ( b)+ba + b ( b) 39
48 5. Härledningar och logik = {kommutativa lagen: xy = yx, därx := a, y := b} aa +( b) a + ba + b ( b) = {multiplikation by additiva inversen: ( x) y = (xy), därx := b, y := a and y := b} aa +( ba)+ba +( bb) = {definition av potensen x 2 : x 2 = xx, därx := a och x := b} a 2 +( ba)+ba + b 2 Delhärledningen i det andra steget är följande: Bevisa att a 2 +( ba)+ba + b 2 = a 2 b 2 med hjälp av axiom a 2 +( ba)+ba + b 2 = {summan av motsatta tal: x + x =0,därx := ba} a b 2 = {addera noll: x +0=x, därx := a 2 } a 2 + b 2 = {definitionen av subtraktion: x y = x +( y), därx := a 2, y := b 2 } a 2 b 2 Det här mer exakta beviset är mycket längre eftersom varje steg endast utnyttjar axiom för reella tal. 40
49 Kapitel 6 Det allmänna formatet för en strukturerad härledning En strukturerad härledning har följande allmänna format härledning: härledningssteg 1 härledningssteg 2. härledningssteg n Med andra ord, en härledning är en följd av härledningssteg. Ett enskilt steg i härledningen är antingen ett antagande, en deklaration, ett faktum, en definition eller en (strukturerad) uppgift: härledningssteg: antagande deklaration faktum definition uppgift En (strukturerad) uppgift beskriver en matematikuppgift och dess lösning. En uppgift har följande allmänna form: 41
50 6. Det allmänna formatet för en strukturerad härledning uppgift: fråga - antagande. - antagande + deklaration motivering: {förklaring} uppgift. uppgift motivering påstående. + deklaration motivering påstående motivering uttryck rel motivering uttryck. rel motivering uttryck svar I en definitionen ingår varje del: deklaration, motivering och påstående. I ett faktum lämnar vi bort deklarationen. I en deklaration lämnar vi igen bort motiveringen och påståendet. En strukturerad beräkning är ett specialfall av en strukturerad uppgift som varken har frågor, antaganden, deklarationer, fakta eller definitioner och inget svar. Vi lämnar också bort -tecknet och den efterföljande motivering från beräkningen. Notera att i en strukturerad uppgift, så definieras uppgiften med hjälp av motiveringar och en motivering definieras med hjälp av uppgifter. Formatetförhärledningarna 42
TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor
 TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor Johan Thim 22 augusti 2018 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför Q
TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor Johan Thim 22 augusti 2018 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför Q
TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter
 TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter Johan Thim 15 augusti 2015 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför
TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter Johan Thim 15 augusti 2015 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför
LMA033/LMA515. Fredrik Lindgren. 4 september 2013
 LMA033/LMA515 Fredrik Lindgren Matematiska vetenskaper Chalmers tekniska högskola och Göteborgs universitet 4 september 2013 F. Lindgren (Chalmers&GU) Matematik 4 september 2013 1 / 25 Outline 1 Föreläsning
LMA033/LMA515 Fredrik Lindgren Matematiska vetenskaper Chalmers tekniska högskola och Göteborgs universitet 4 september 2013 F. Lindgren (Chalmers&GU) Matematik 4 september 2013 1 / 25 Outline 1 Föreläsning
Repetitionsuppgifter inför Matematik 1. Matematiska institutionen Linköpings universitet 2013
 Repetitionsuppgifter inför Matematik Matematiska institutionen Linköpings universitet 0 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Facit 4 Repetitionsuppgifter inför Matematik Repetitionsuppgifter
Repetitionsuppgifter inför Matematik Matematiska institutionen Linköpings universitet 0 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Facit 4 Repetitionsuppgifter inför Matematik Repetitionsuppgifter
Sanningsvärdet av ett sammansatt påstående (sats, utsaga) beror av bindeord och sanningsvärden för ingående påståenden.
 MATEMATISK LOGIK Matematisk logik formaliserar korrekta resonemang och definierar formellt bindeord (konnektiv) mellan påståenden (utsagor, satser) I matematisk logik betraktar vi påståenden som antingen
MATEMATISK LOGIK Matematisk logik formaliserar korrekta resonemang och definierar formellt bindeord (konnektiv) mellan påståenden (utsagor, satser) I matematisk logik betraktar vi påståenden som antingen
MATEMATIKENS SPRÅK. Avsnitt 1
 Avsnitt 1 MATEMATIKENS SPRÅK Varje vetenskap, liksom varje yrke, har sitt eget språk som ofta är en blandning av vardagliga ord och speciella termer. En instruktionshandbok för ett kylskåp eller för en
Avsnitt 1 MATEMATIKENS SPRÅK Varje vetenskap, liksom varje yrke, har sitt eget språk som ofta är en blandning av vardagliga ord och speciella termer. En instruktionshandbok för ett kylskåp eller för en
Repetitionsuppgifter inför Matematik 1-973G10. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter inför Matematik - 7G0 Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 4 Facit Repetitionsuppgifter inför
Repetitionsuppgifter inför Matematik - 7G0 Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 4 Facit Repetitionsuppgifter inför
Lösningar till utvalda uppgifter i kapitel 5
 Lösningar till utvalda uppgifter i kapitel 5 5.3. Vi använder Euklides algoritm och får 4485 = 1 3042 + 1443 3042 = 2 1443 + 156 1443 = 9 156 + 39 156 = 4 39. Alltså är sgd(3042, 4485) = 39. Om vi startar
Lösningar till utvalda uppgifter i kapitel 5 5.3. Vi använder Euklides algoritm och får 4485 = 1 3042 + 1443 3042 = 2 1443 + 156 1443 = 9 156 + 39 156 = 4 39. Alltså är sgd(3042, 4485) = 39. Om vi startar
Repetitionsuppgifter i Matematik inför Basår. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Övningshäfte 2: Induktion och rekursion
 GÖTEBORGS UNIVERSITET MATEMATIK 1, MMG200, HT2017 INLEDANDE ALGEBRA Övningshäfte 2: Induktion och rekursion Övning D Syftet är att öva förmågan att utgående från enkla samband, aritmetiska och geometriska,
GÖTEBORGS UNIVERSITET MATEMATIK 1, MMG200, HT2017 INLEDANDE ALGEBRA Övningshäfte 2: Induktion och rekursion Övning D Syftet är att öva förmågan att utgående från enkla samband, aritmetiska och geometriska,
sanningsvärde, kallas utsagor. Exempel på utsagor från pass 1 är
 PASS 7. EKVATIONSLÖSNING 7. Grundbegrepp om ekvationer En ekvation säger att två matematiska uttryck är lika stora. Ekvationen har alltså ett likhetstecken och två deluttryck på var sin sida om likhetstecknet.
PASS 7. EKVATIONSLÖSNING 7. Grundbegrepp om ekvationer En ekvation säger att två matematiska uttryck är lika stora. Ekvationen har alltså ett likhetstecken och två deluttryck på var sin sida om likhetstecknet.
2 Matematisk grammatik
 MATEMATISK GRAMMATIK Matematisk grammatik.1 Skriva matematik Matematisk grammatik, minst lika kul som det låter, och hur man skriver matematik är nästan lika viktigt som vad man skriver. En grammatisk
MATEMATISK GRAMMATIK Matematisk grammatik.1 Skriva matematik Matematisk grammatik, minst lika kul som det låter, och hur man skriver matematik är nästan lika viktigt som vad man skriver. En grammatisk
NpMa3c vt Kravgränser
 Kravgränser Provet består av ett muntligt delprov (Del A) och tre skriftliga delprov (Del B, Del C och Del D). Tillsammans kan de ge 66 poäng varav 25 E-, 24 C- och 17 A-poäng. Observera att kravgränserna
Kravgränser Provet består av ett muntligt delprov (Del A) och tre skriftliga delprov (Del B, Del C och Del D). Tillsammans kan de ge 66 poäng varav 25 E-, 24 C- och 17 A-poäng. Observera att kravgränserna
Övningshäfte 1: Logik och matematikens språk
 GÖTEBORGS UNIVERSITET MATEMATIK 1, MMG200, HT2014 INLEDANDE ALGEBRA Övningshäfte 1: Logik och matematikens språk Övning A Målet är att genom att lösa och diskutera några inledande uppgifter få erfarenheter
GÖTEBORGS UNIVERSITET MATEMATIK 1, MMG200, HT2014 INLEDANDE ALGEBRA Övningshäfte 1: Logik och matematikens språk Övning A Målet är att genom att lösa och diskutera några inledande uppgifter få erfarenheter
Medan bevis och exakta definitioner är vardagsmat för en universitetsstuderande,
 Linda Mannila Strukturerade härledningar ökar förståelsen Strukturerade härledningar är ett specifikt format för att presentera beräkningar och bevis på ett klart och tydligt sätt som dessutom lämpar sig
Linda Mannila Strukturerade härledningar ökar förståelsen Strukturerade härledningar är ett specifikt format för att presentera beräkningar och bevis på ett klart och tydligt sätt som dessutom lämpar sig
Utvidgad aritmetik. AU
 Utvidgad aritmetik. AU Delområdet omfattar följande tio diagnoser som är grupperade i tre delar, negativa tal, potenser och närmevärden: AUn1 Negativa tal, taluppfattning AUn Negativa tal, addition och
Utvidgad aritmetik. AU Delområdet omfattar följande tio diagnoser som är grupperade i tre delar, negativa tal, potenser och närmevärden: AUn1 Negativa tal, taluppfattning AUn Negativa tal, addition och
Kontinuitet och gränsvärden
 Kapitel Kontinuitet och gränsvärden.1 Introduktion till kontinuerliga funktioner Kapitlet börjar med allmänna definitioner. Därefter utvidgar vi successivt familjen av kontinuerliga funktioner, genom specifika
Kapitel Kontinuitet och gränsvärden.1 Introduktion till kontinuerliga funktioner Kapitlet börjar med allmänna definitioner. Därefter utvidgar vi successivt familjen av kontinuerliga funktioner, genom specifika
Sats. Om t är en rätvinklig triangel så är summan av kvadraterna på kateterna i t lika med kvadraten på hypotenusan.
 Lunds tekniska högskola Datavetenskap Lennart Andersson Föreläsningsanteckningar EDAF10 3 Predikatlogik 3.1 Motivering I satslogiken är de minsta beståndsdelarna satslogiska variabler som kan anta värdena
Lunds tekniska högskola Datavetenskap Lennart Andersson Föreläsningsanteckningar EDAF10 3 Predikatlogik 3.1 Motivering I satslogiken är de minsta beståndsdelarna satslogiska variabler som kan anta värdena
Induktion, mängder och bevis för Introduktionskursen på I
 Induktion, mängder och bevis för Introduktionskursen på I J A S, ht 04 1 Induktion Detta avsnitt handlar om en speciell teknik för att försöka bevisa riktigheten av påståenden eller formler, för alla heltalsvärden
Induktion, mängder och bevis för Introduktionskursen på I J A S, ht 04 1 Induktion Detta avsnitt handlar om en speciell teknik för att försöka bevisa riktigheten av påståenden eller formler, för alla heltalsvärden
Ekvationer och system av ekvationer
 Modul: Undervisa matematik utifrån problemlösning Del 4. Strategier Ekvationer och system av ekvationer Paul Vaderlind, Stockholms universitet Ekvationslösning är ett av de viktiga målen i skolmatematiken.
Modul: Undervisa matematik utifrån problemlösning Del 4. Strategier Ekvationer och system av ekvationer Paul Vaderlind, Stockholms universitet Ekvationslösning är ett av de viktiga målen i skolmatematiken.
Matematik med lite logik
 Ralph-Johan Back Matematik med lite logik Logik för strukturerade härledningar Turku Centre for Computer Science IMPEd Resource Centre TUCS Lecture Notes No 8, Oct 2008 Matematik med lite logik Logik
Ralph-Johan Back Matematik med lite logik Logik för strukturerade härledningar Turku Centre for Computer Science IMPEd Resource Centre TUCS Lecture Notes No 8, Oct 2008 Matematik med lite logik Logik
1. Inledning, som visar att man inte skall tro på allt man ser. Betrakta denna följd av tal, där varje tal är dubbelt så stort som närmast föregående
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Christian Gottlieb Gymnasieskolans matematik med akademiska ögon Induktion Dag 1 1. Inledning, som visar att man inte skall tro på allt man ser. Betrakta
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Christian Gottlieb Gymnasieskolans matematik med akademiska ögon Induktion Dag 1 1. Inledning, som visar att man inte skall tro på allt man ser. Betrakta
1 Addition, subtraktion och multiplikation av (reella) tal
 Omstuvat utdrag ur R Pettersson: Förberedande kurs i matematik Addition, subtraktion och multiplikation av (reella) tal För reella tal gäller som bekant bl.a. följande räkneregler: (a + b) + c = a + (b
Omstuvat utdrag ur R Pettersson: Förberedande kurs i matematik Addition, subtraktion och multiplikation av (reella) tal För reella tal gäller som bekant bl.a. följande räkneregler: (a + b) + c = a + (b
INDUKTION OCH DEDUKTION
 Explorativ övning 3 INDUKTION OCH DEDUKTION Syftet med övningen är att öka Din problemlösningsförmåga och bekanta Dig med olika bevismetoder. Vårt syfte är också att öva skriftlig framställning av matematisk
Explorativ övning 3 INDUKTION OCH DEDUKTION Syftet med övningen är att öka Din problemlösningsförmåga och bekanta Dig med olika bevismetoder. Vårt syfte är också att öva skriftlig framställning av matematisk
Likhetstecknets innebörd
 Likhetstecknets innebörd Följande av Görel Sterner översatta och bearbetade text bygger på boken: arithmetic & algebra in elementary school. Portsmouth: Heinemann Elever i åk 1 6 fick följande uppgift:
Likhetstecknets innebörd Följande av Görel Sterner översatta och bearbetade text bygger på boken: arithmetic & algebra in elementary school. Portsmouth: Heinemann Elever i åk 1 6 fick följande uppgift:
Ekvationer och olikheter
 Kapitel Ekvationer och olikheter I kapitlet bekantar vi oss med första och andra grads linjära ekvationer och olikheter. Vi ser också på ekvationer och olikheter med absolutbelopp och kvadratrötter. När
Kapitel Ekvationer och olikheter I kapitlet bekantar vi oss med första och andra grads linjära ekvationer och olikheter. Vi ser också på ekvationer och olikheter med absolutbelopp och kvadratrötter. När
Matematik med lite logik
 Ralph-Johan Back Matematik med lite logik Strukturerade härledningar som allmänt bevisformat Turku Centre for Computer Science IMPEd Resource Centre TUCS Lecture Notes No 9, Oct 2008 Matematik med lite
Ralph-Johan Back Matematik med lite logik Strukturerade härledningar som allmänt bevisformat Turku Centre for Computer Science IMPEd Resource Centre TUCS Lecture Notes No 9, Oct 2008 Matematik med lite
Talmängder. Målet med första föreläsningen:
 Moment 1..1, 1.., 1..4, 1..5, 1.. 1..5, 1..6 Viktiga exempel 1.7, 1.8, 1.8,1.19,1. Handräkning 1.7, 1.9, 1.19, 1.4, 1.9 b,e 1.0 a,b Datorräkning 1.6-1.1 Målet med första föreläsningen: 1 En första kontakt
Moment 1..1, 1.., 1..4, 1..5, 1.. 1..5, 1..6 Viktiga exempel 1.7, 1.8, 1.8,1.19,1. Handräkning 1.7, 1.9, 1.19, 1.4, 1.9 b,e 1.0 a,b Datorräkning 1.6-1.1 Målet med första föreläsningen: 1 En första kontakt
Sidor i boken V.L = 8 H.L. 2+6 = 8 V.L. = H.L.
 Sidor i boken 119-11 Andragradsekvationer Dagens tema är ekvationer, speciellt andragradsekvationer. Men först några ord om ekvationer i allmänhet. En ekvation är en likhet som innehåller ett (möjligen
Sidor i boken 119-11 Andragradsekvationer Dagens tema är ekvationer, speciellt andragradsekvationer. Men först några ord om ekvationer i allmänhet. En ekvation är en likhet som innehåller ett (möjligen
Prov 1 2. Ellips 12 Numeriska och algebraiska metoder lösningar till övningsproven uppdaterad 20.5.2010. a) i) Nollställen för polynomet 2x 2 3x 1:
 Ellips Numeriska och algebraiska metoder lösningar till övningsproven uppdaterad.. Prov a) i) ii) iii) =,, = st 9,876 =,9876,99 = 9,9,66,66 =,7 =,7 Anmärkning. Nollor i början av decimaltal har ingen betydelse
Ellips Numeriska och algebraiska metoder lösningar till övningsproven uppdaterad.. Prov a) i) ii) iii) =,, = st 9,876 =,9876,99 = 9,9,66,66 =,7 =,7 Anmärkning. Nollor i början av decimaltal har ingen betydelse
Röd kurs. Multiplicera in i parenteser. Mål: Matteord. Exempel. 1 a) 4(x- 5) b) 5(3 + x) 3 Om 3(a + 4) = 36, vad är då 62 2 FUNKTIONER OCH ALGEBRA
 Röd kurs Mål: I den här kursen får du lära dig att: ~ multiplicera parenteser ~ använda kvadreringsregler ~ använda konjugatregeln ~ uttrycka formler på olika sätt Matteord första kvadreringsregeln andra
Röd kurs Mål: I den här kursen får du lära dig att: ~ multiplicera parenteser ~ använda kvadreringsregler ~ använda konjugatregeln ~ uttrycka formler på olika sätt Matteord första kvadreringsregeln andra
Lokal pedagogisk planering i matematik för årskurs 9
 Lokal pedagogisk planering i matematik för årskurs 9 Arbetsområde 3. Ekvationer och geometri. Syfte formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder. reflektera
Lokal pedagogisk planering i matematik för årskurs 9 Arbetsområde 3. Ekvationer och geometri. Syfte formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder. reflektera
Tal och polynom. Johan Wild
 Tal och polynom Johan Wild 14 augusti 2008 Innehåll 1 Inledning 3 2 Att gå mellan olika typer av tal 3 3 De hela talen och polynom 4 3.1 Polynom........................... 4 3.2 Räkning med polynom...................
Tal och polynom Johan Wild 14 augusti 2008 Innehåll 1 Inledning 3 2 Att gå mellan olika typer av tal 3 3 De hela talen och polynom 4 3.1 Polynom........................... 4 3.2 Räkning med polynom...................
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson LÄSANVISNINGAR VECKA 36 VERSION 1. ARITMETIK FÖR RATIONELLA OCH REELLA TAL, OLIKHETER, ABSOLUTBELOPP ADAMS P.1 Real Numbers and the Real
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson LÄSANVISNINGAR VECKA 36 VERSION 1. ARITMETIK FÖR RATIONELLA OCH REELLA TAL, OLIKHETER, ABSOLUTBELOPP ADAMS P.1 Real Numbers and the Real
MATEMATIKPROV, LÅNG LÄROKURS BESKRIVNING AV GODA SVAR
 MATEMATIKPROV, LÅNG LÄROKURS 8906 BESKRIVNING AV GODA SVAR Examensämnets censorsmöte har godkänt följande beskrivningar av goda svar Av en god prestation framgår det hur examinanden har kommit fram till
MATEMATIKPROV, LÅNG LÄROKURS 8906 BESKRIVNING AV GODA SVAR Examensämnets censorsmöte har godkänt följande beskrivningar av goda svar Av en god prestation framgår det hur examinanden har kommit fram till
Matematik med litet logik
 Matematik med litet logik Ralph-Johan Back (gemensamt arbete med Joakim von Wright) Åbo Akademi, Institutionen för Informationsbehandling TUCS - Turku Centre for Computer Science 14 oktober 2005 TUCS/Åbo
Matematik med litet logik Ralph-Johan Back (gemensamt arbete med Joakim von Wright) Åbo Akademi, Institutionen för Informationsbehandling TUCS - Turku Centre for Computer Science 14 oktober 2005 TUCS/Åbo
TATM79: Föreläsning 3 Komplexa tal
 TATM79: Föreläsning 3 Komplexa tal Johan Thim 22 augusti 2018 1 Komplexa tal Definition. Det imaginära talet i uppfyller att i 2 = 1. Detta är alltså ett tal vars kvadrat är negativ. Det kan således aldrig
TATM79: Föreläsning 3 Komplexa tal Johan Thim 22 augusti 2018 1 Komplexa tal Definition. Det imaginära talet i uppfyller att i 2 = 1. Detta är alltså ett tal vars kvadrat är negativ. Det kan således aldrig
Lösningar till Algebra och kombinatorik
 Lösningar till Algebra och kombinatorik 091214 1. Av a 0 = 1 och rekursionsformeln får vi successivt att a 1 = 1 + a 0 1 a 0 = 1 + 1 1 1 = 2, a 2 = 1 + a 1 1 a 0 + 1 a 1 = 1 + 2 1 + 1 = 4, 2 a 3 = 1 +
Lösningar till Algebra och kombinatorik 091214 1. Av a 0 = 1 och rekursionsformeln får vi successivt att a 1 = 1 + a 0 1 a 0 = 1 + 1 1 1 = 2, a 2 = 1 + a 1 1 a 0 + 1 a 1 = 1 + 2 1 + 1 = 4, 2 a 3 = 1 +
Likhetstecknets innebörd
 Modul: Algebra Del 5: Algebra som språk Likhetstecknets innebörd Följande av Görel Sterner (2012) översatta och bearbetade text bygger på boken: Carpenter, T. P., Franke, M. L. & Levi, L. (2003). Thinking
Modul: Algebra Del 5: Algebra som språk Likhetstecknets innebörd Följande av Görel Sterner (2012) översatta och bearbetade text bygger på boken: Carpenter, T. P., Franke, M. L. & Levi, L. (2003). Thinking
Sidor i boken 110-113, 68-69 2, 3, 5, 7, 11,13,17 19, 23. Ett andragradspolynom Ett tiogradspolynom Ett tredjegradspolynom
 Sidor i boken 110-113, 68-69 Räkning med polynom Faktorisering av heltal. Att primtalsfaktorisera ett heltal innebär att uppdela heltalet i faktorer, där varje faktor är ett primtal. Ett primtal är ett
Sidor i boken 110-113, 68-69 Räkning med polynom Faktorisering av heltal. Att primtalsfaktorisera ett heltal innebär att uppdela heltalet i faktorer, där varje faktor är ett primtal. Ett primtal är ett
Instuderingsfrågor för Endimensionell analys kurs B1
 Instuderingsfrågor för Endimensionell analys kurs B1 Anvisningar Avsikten med följande frågor är att hjälpa dig med självkontroll av dina kunskaper. Om du känner dig osäker på svaren bör du slå upp motsvarande
Instuderingsfrågor för Endimensionell analys kurs B1 Anvisningar Avsikten med följande frågor är att hjälpa dig med självkontroll av dina kunskaper. Om du känner dig osäker på svaren bör du slå upp motsvarande
Tema: Pythagoras sats. Linnéa Utterström & Malin Öberg
 Tema: Pythagoras sats Linnéa Utterström & Malin Öberg Innehåll: Introduktion till Pythagoras sats! 3 Pythagoras sats! 4 Variabler! 5 Potenser! 5 Att komma tillbaka till ursprunget! 7 Vi bevisar Pythagoras
Tema: Pythagoras sats Linnéa Utterström & Malin Öberg Innehåll: Introduktion till Pythagoras sats! 3 Pythagoras sats! 4 Variabler! 5 Potenser! 5 Att komma tillbaka till ursprunget! 7 Vi bevisar Pythagoras
Bedömningsanvisningar
 Bedömningsanvisningar Exempel på ett godtagbart svar anges inom parentes. Till en del uppgifter är bedömda elevlösningar bifogade för att ange nivån på bedömningen. Om bedömda elevlösningar finns i materialet
Bedömningsanvisningar Exempel på ett godtagbart svar anges inom parentes. Till en del uppgifter är bedömda elevlösningar bifogade för att ange nivån på bedömningen. Om bedömda elevlösningar finns i materialet
Sidor i boken f(x) = a x 2 +b x+c
 Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
inte följa någon enkel eller fiffig princip, vad man nu skulle mena med det. All right, men
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Christian Gottlieb Gymnasieskolans matematik med akademiska ögon Induktion Dag 2. Explicita formler och rekursionsformler. Dag mötte vi flera talföljder,
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Christian Gottlieb Gymnasieskolans matematik med akademiska ögon Induktion Dag 2. Explicita formler och rekursionsformler. Dag mötte vi flera talföljder,
Föreläsning 1. Kursinformation All viktig information om kursen ska kunna läsas på kursens hemsida
 Föreläsning 1 Kursinformation All viktig information om kursen ska kunna läsas på kursens hemsida http://www2.math.uu.se/ rikardo/ baskursen/index.html Mängdlära * En "samling" av tal kallas för en mängd.
Föreläsning 1 Kursinformation All viktig information om kursen ska kunna läsas på kursens hemsida http://www2.math.uu.se/ rikardo/ baskursen/index.html Mängdlära * En "samling" av tal kallas för en mängd.
Gamla tentemensuppgifter
 Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
Inte heller idag någon ny teori! Gamla tentemensuppgifter 1 Bestäm det andragradspolynom vars kurva skär x-axeln i x = 3 och x = 1 och y-axeln i y = 3 f(x) = (x 3)(x + 1) = x x 3 är en bra start, men vi
Utveckling av undervisningen i matematik och datateknik i gymnasiet
 Utveckling av undervisningen i matematik och datateknik i gymnasiet Ralph-Johan Back Åbo Akademi, Avdelningen för Informationsteknologi CREST Learning and Reasoning laboratoriet 22 mars 2007 Gymnasieundervisning
Utveckling av undervisningen i matematik och datateknik i gymnasiet Ralph-Johan Back Åbo Akademi, Avdelningen för Informationsteknologi CREST Learning and Reasoning laboratoriet 22 mars 2007 Gymnasieundervisning
Läsanvisningar till kapitel 6 i Naturlig matematik. Avsnitt 6.6 ingår inte.
 Läsanvisningar till kapitel 6 i Naturlig matematik Avsnitt 6.6 ingår inte. Avsnitt 6.1 Detta avsnitt illustrerar hur sekanten övergår i en tangent genom att den ena skärningspunkten rör sig mot den andra.
Läsanvisningar till kapitel 6 i Naturlig matematik Avsnitt 6.6 ingår inte. Avsnitt 6.1 Detta avsnitt illustrerar hur sekanten övergår i en tangent genom att den ena skärningspunkten rör sig mot den andra.
Lokala mål i matematik
 Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
MATEMATIKPROV, LÅNG LÄROKURS BESKRIVNING AV GODA SVAR
 MATEMATIKPROV, LÅNG LÄROKURS 6..019 BESKRIVNING AV GODA SVAR Examensämnets censorsmöte har godkänt följande beskrivningar av goda svar. Av en god prestation framgår det hur examinanden har kommit fram
MATEMATIKPROV, LÅNG LÄROKURS 6..019 BESKRIVNING AV GODA SVAR Examensämnets censorsmöte har godkänt följande beskrivningar av goda svar. Av en god prestation framgår det hur examinanden har kommit fram
Lösa ekvationer på olika sätt
 Lösa ekvationer på olika sätt I denna aktivitet ska titta närmare på hur man kan lösa ekvationer på olika sätt. I kurserna lär du dig att lösa första- och andragradsekvationer exakt med algebraiska metoder.
Lösa ekvationer på olika sätt I denna aktivitet ska titta närmare på hur man kan lösa ekvationer på olika sätt. I kurserna lär du dig att lösa första- och andragradsekvationer exakt med algebraiska metoder.
Övning log, algebra, potenser med mera
 Övning log, algebra, potenser med mera Uppgift nr 1 Förenkla uttrycket x 3 + x 3 + x 3 + x 3 + x 3 Uppgift nr 2 Förenkla x x x+x x x Uppgift nr 3 Skriv på enklaste sätt x 2 x x x 8 x x x Uppgift nr 4 Förenkla
Övning log, algebra, potenser med mera Uppgift nr 1 Förenkla uttrycket x 3 + x 3 + x 3 + x 3 + x 3 Uppgift nr 2 Förenkla x x x+x x x Uppgift nr 3 Skriv på enklaste sätt x 2 x x x 8 x x x Uppgift nr 4 Förenkla
A1:an Repetition. Philip Larsson. 6 april Kapitel 1. Grundläggande begrepp och terminologi
 A1:an Repetition Philip Larsson 6 april 013 1 Kapitel 1. Grundläggande begrepp och terminologi 1.1 Delmängd Om ändpunkterna ska räknas med används symbolerna [ ] och raka sträck. Om ändpunkterna inte skall
A1:an Repetition Philip Larsson 6 april 013 1 Kapitel 1. Grundläggande begrepp och terminologi 1.1 Delmängd Om ändpunkterna ska räknas med används symbolerna [ ] och raka sträck. Om ändpunkterna inte skall
D. x 2 + y 2 ; E. Stockholm ligger i Sverige; F. Månen är en gul ost; G. 3 2 = 6; H. x 2 + y 2 = r 2.
 Logik Vid alla matematiskt resonemang måste man vara säker på att man verkligen menar det man skriver ner på sitt papper. Därför måste man besinna hur man egentligen tänker. Den vetenskap, som sysslar
Logik Vid alla matematiskt resonemang måste man vara säker på att man verkligen menar det man skriver ner på sitt papper. Därför måste man besinna hur man egentligen tänker. Den vetenskap, som sysslar
Andragradsekvationer. + px + q = 0. = 3x 7 7 3x + 7 = 0. q = 7
 Andragradsekvationer Tid: 70 minuter Hjälpmedel: Formelblad. Alla andragradsekvationer kan skrivas på formen Vilket värde har q i ekvationen x = 3x 7? + E Korrekt svar. B (q = 7) x + px + q = 0 (/0/0)
Andragradsekvationer Tid: 70 minuter Hjälpmedel: Formelblad. Alla andragradsekvationer kan skrivas på formen Vilket värde har q i ekvationen x = 3x 7? + E Korrekt svar. B (q = 7) x + px + q = 0 (/0/0)
Ekvationslösning genom substitution, rotekvationer
 Sidor i boken -3, 70-73 Ekvationslösning genom substitution, rotekvationer Rotekvationer Med en rotekvation menas en ekvation, i vilken den obekanta förekommer under ett rotmärke. Observera att betecknar
Sidor i boken -3, 70-73 Ekvationslösning genom substitution, rotekvationer Rotekvationer Med en rotekvation menas en ekvation, i vilken den obekanta förekommer under ett rotmärke. Observera att betecknar
Kvalificeringstävling den 30 september 2008
 SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
Bedömningsanvisningar
 Bedömningsanvisningar Exempel på ett godtagbart svar anges inom parentes. Till en del uppgifter är bedömda elevlösningar bifogade för att ange nivån på bedömningen. Om bedömda elevlösningar finns i materialet
Bedömningsanvisningar Exempel på ett godtagbart svar anges inom parentes. Till en del uppgifter är bedömda elevlösningar bifogade för att ange nivån på bedömningen. Om bedömda elevlösningar finns i materialet
Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen.
 Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Upphämtningskurs i matematik
 Upphämtningskurs i matematik C.J. 2013 Föreläsningsunderlaget är uppbyggt utgående från kurserna i den långa gymnasiematematiken, ellips-kursböckerna (Schilds förlag) har använts som förebild. Böckerna
Upphämtningskurs i matematik C.J. 2013 Föreläsningsunderlaget är uppbyggt utgående från kurserna i den långa gymnasiematematiken, ellips-kursböckerna (Schilds förlag) har använts som förebild. Böckerna
Övningshäfte 2: Komplexa tal (och negativa tal)
 LMA110 VT008 ARITMETIK OCH ALGEBRA DEL Övningshäfte : Komplexa tal (och negativa tal) Övningens syfte är att bekanta sig med komplexa tal och att fundera på några begreppsliga svårigheter som negativa
LMA110 VT008 ARITMETIK OCH ALGEBRA DEL Övningshäfte : Komplexa tal (och negativa tal) Övningens syfte är att bekanta sig med komplexa tal och att fundera på några begreppsliga svårigheter som negativa
PASS 4. POLYNOM, MINNESREGLERNA. 4.1 Kvadreringsreglerna. Kvadraten på en summa
 PASS 4. POLYNOM, MINNESREGLERNA 4.1 Kvadreringsreglerna Kvadraten på en summa Den finländska modellfamiljen med mamma, pappa och två barn äger ett kvadratformat hus. Här nedan i figur 4 har vi en planritning
PASS 4. POLYNOM, MINNESREGLERNA 4.1 Kvadreringsreglerna Kvadraten på en summa Den finländska modellfamiljen med mamma, pappa och två barn äger ett kvadratformat hus. Här nedan i figur 4 har vi en planritning
Abstrakt algebra för gymnasister
 Abstrakt algebra för gymnasister Veronica Crispin Quinonez Sammanfattning. Denna text är föreläsningsanteckningar från föredraget Abstrakt algebra som hölls under Kleindagarna på Institutet Mittag-Leffler
Abstrakt algebra för gymnasister Veronica Crispin Quinonez Sammanfattning. Denna text är föreläsningsanteckningar från föredraget Abstrakt algebra som hölls under Kleindagarna på Institutet Mittag-Leffler
Matematik EXTRAUPPGIFTER FÖR SKOLÅR 7-9
 Matematik EXTRAUPPGIFTER FÖR SKOLÅR 7-9 Matematik Extrauppgifter för skolår 7-9 Pärm med kopieringsunderlag. Fri kopieringsrätt inom utbildningsenheten! Författare: Mikael Sandell Copyright 00 Sandell
Matematik EXTRAUPPGIFTER FÖR SKOLÅR 7-9 Matematik Extrauppgifter för skolår 7-9 Pärm med kopieringsunderlag. Fri kopieringsrätt inom utbildningsenheten! Författare: Mikael Sandell Copyright 00 Sandell
Lösningar till udda övningsuppgifter
 Lösningar till udda övningsuppgifter Övning 1.1. (i) {, } (ii) {0, 1,, 3, 4} (iii) {0,, 4, 6, 8} Övning 1.3. Påståendena är (i), (iii) och (v), varav (iii) och (v) är sanna. Övning 1.5. andra. (i) Nej.
Lösningar till udda övningsuppgifter Övning 1.1. (i) {, } (ii) {0, 1,, 3, 4} (iii) {0,, 4, 6, 8} Övning 1.3. Påståendena är (i), (iii) och (v), varav (iii) och (v) är sanna. Övning 1.5. andra. (i) Nej.
Högskoleprovet Kvantitativ del
 Högskoleprovet Kvantitativ del Här följer anvisningar till de kvantitativa delproven XYZ, KVA, NOG och DTK. Provhäftet innehåller 40 uppgifter och den totala provtiden är 55 minuter. XYZ Matematisk problemlösning
Högskoleprovet Kvantitativ del Här följer anvisningar till de kvantitativa delproven XYZ, KVA, NOG och DTK. Provhäftet innehåller 40 uppgifter och den totala provtiden är 55 minuter. XYZ Matematisk problemlösning
Svar och arbeta vidare med Student 2008
 Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Algebra och rationella uttryck
 Algebra och rationella uttryck - 20 Uppgift nr Förenkla x0 y 6 z 5 25 y 2 Uppgift nr 2 Uppgift nr 3 ab b 5a - a² 9a där a 0. där b 0. Uppgift nr 4 Multiplicera in i parentesen 2x(4 + 2x 3 ) Uppgift nr
Algebra och rationella uttryck - 20 Uppgift nr Förenkla x0 y 6 z 5 25 y 2 Uppgift nr 2 Uppgift nr 3 ab b 5a - a² 9a där a 0. där b 0. Uppgift nr 4 Multiplicera in i parentesen 2x(4 + 2x 3 ) Uppgift nr
Här är två korta exempel på situationer då vi tillämpar den distributiva lagen:
 Modul: Algebra Del 8: Avslutande reflektion och utvärdering Distributiva lagen Cecilia Kilhamn, Göteborgs Universitet Distributiva lagen a (b + c) = a b + a c Den distributiva lagen kallas den räknelag
Modul: Algebra Del 8: Avslutande reflektion och utvärdering Distributiva lagen Cecilia Kilhamn, Göteborgs Universitet Distributiva lagen a (b + c) = a b + a c Den distributiva lagen kallas den räknelag
Diagnostiskt test för Lp03
 Diagnostiskt test för Lp --6, kl. 9.5 Inga miniräknare/formelsamlingar. Redovisa dina resonemang/räkningar.. Skriv namn, vilket år du senast läste matematik, vilken kurs det var, vilket betyg du fick..
Diagnostiskt test för Lp --6, kl. 9.5 Inga miniräknare/formelsamlingar. Redovisa dina resonemang/räkningar.. Skriv namn, vilket år du senast läste matematik, vilken kurs det var, vilket betyg du fick..
Övningshäfte 2: Komplexa tal
 LMA100 VT007 ARITMETIK OCH ALGEBRA DEL Övningshäfte : Komplexa tal Övningens syfte är att bekanta sig med komplexa tal. De komplexa talen, som är en utvidgning av de reella talen, kom till på 1400 talet
LMA100 VT007 ARITMETIK OCH ALGEBRA DEL Övningshäfte : Komplexa tal Övningens syfte är att bekanta sig med komplexa tal. De komplexa talen, som är en utvidgning av de reella talen, kom till på 1400 talet
MA 11. Hur starkt de binder. 2 Reella tal 3 Slutledning 4 Logik 5 Mängdlära 6-7 Talteori 8 Diofantiska ekvationer 9 Fördjupning och kryptografi
 MA 11 Talteori och logik 2 Reella tal 3 Slutledning 4 Logik 5 Mängdlära 6-7 Talteori 8 Diofantiska ekvationer 9 Fördjupning och kryptografi propositionssymboler: bokstäver konnektiv Paranteser konnektiv
MA 11 Talteori och logik 2 Reella tal 3 Slutledning 4 Logik 5 Mängdlära 6-7 Talteori 8 Diofantiska ekvationer 9 Fördjupning och kryptografi propositionssymboler: bokstäver konnektiv Paranteser konnektiv
MAA7 Derivatan. 2. Funktionens egenskaper. 2.1 Repetition av grundbegerepp
 MAA7 Derivatan 2. Funktionens egenskaper 2.1 Repetition av grundbegerepp - Det finns vissa begrepp som återkommer i nästan alla kurser i matematik. Några av dessa är definitionsmängd, värdemängd, största
MAA7 Derivatan 2. Funktionens egenskaper 2.1 Repetition av grundbegerepp - Det finns vissa begrepp som återkommer i nästan alla kurser i matematik. Några av dessa är definitionsmängd, värdemängd, största
5B1134 Matematik och modeller Lösningsförslag till tentamen den 11 oktober 2004
 KTH Matematik 5B4 Matematik och modeller Lösningsförslag till tentamen den oktober 4. Två av sidlängderna i en triangel är 8 m och m. En av vinklarna är 6. a) Bestäm alla möjliga värden för den tredje
KTH Matematik 5B4 Matematik och modeller Lösningsförslag till tentamen den oktober 4. Två av sidlängderna i en triangel är 8 m och m. En av vinklarna är 6. a) Bestäm alla möjliga värden för den tredje
Algebra, kvadreringsregler och konjugatregeln
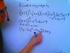 Algebra, kvadreringsregler och Uppgift nr 1 Multiplicera in i parentesen x(9 + 2y) Uppgift nr 2 Multiplicera in i parentesen 3x(7 + 5y) Uppgift nr 3 x² + 3x Uppgift nr 4 xy + yz Uppgift nr 5 5yz + 2xy
Algebra, kvadreringsregler och Uppgift nr 1 Multiplicera in i parentesen x(9 + 2y) Uppgift nr 2 Multiplicera in i parentesen 3x(7 + 5y) Uppgift nr 3 x² + 3x Uppgift nr 4 xy + yz Uppgift nr 5 5yz + 2xy
Föreläsning 3: Ekvationer och olikheter
 Föreläsning 3: Ekvationer och olikheter En ekvation är en likhet som innehåller en flera obekanta storheter. Exempel: x = 9, x är okänd. t + t + 1 = 7, t är okänd. Vi säger att ett värde på den obekanta
Föreläsning 3: Ekvationer och olikheter En ekvation är en likhet som innehåller en flera obekanta storheter. Exempel: x = 9, x är okänd. t + t + 1 = 7, t är okänd. Vi säger att ett värde på den obekanta
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 4. b) = 3 1 = 2
 Kapitel.1 101, 102 Exempel som löses i boken 10 a) x= 1 11+ x= 11+ 1 = 2 c) x= 11 7 x= 7 11 = 77 b) x= 5 x 29 = 5 29 = 6 d) x= 2 26 x= 26 2= 1 10 a) x= 6 5+ 9 x= 5+ 9 6= 5+ 5= 59 b) a = 8a 6= 8 6= 2 6=
Kapitel.1 101, 102 Exempel som löses i boken 10 a) x= 1 11+ x= 11+ 1 = 2 c) x= 11 7 x= 7 11 = 77 b) x= 5 x 29 = 5 29 = 6 d) x= 2 26 x= 26 2= 1 10 a) x= 6 5+ 9 x= 5+ 9 6= 5+ 5= 59 b) a = 8a 6= 8 6= 2 6=
Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet.
 Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet. 1. a) Bestäm ekvationen för den räta linjen i figuren. (1/0/0) b) Rita i koordinatsystemet en rät linje
Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet. 1. a) Bestäm ekvationen för den räta linjen i figuren. (1/0/0) b) Rita i koordinatsystemet en rät linje
7E Ma Planering v45-51: Algebra
 7E Ma Planering v45-51: Algebra Arbetsform under en vecka: Måndagar (40 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa: Läsa på anteckningar
7E Ma Planering v45-51: Algebra Arbetsform under en vecka: Måndagar (40 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa: Läsa på anteckningar
PASS 2. POTENSRÄKNING. 2.1 Definition av en potens
 PASS. POTENSRÄKNING.1 Definition av en potens Typiskt för matematik är ett kort, lätt och vackert framställningssätt. Den upprepade additionen går att skriva kortare i formen där anger antalet upprepade
PASS. POTENSRÄKNING.1 Definition av en potens Typiskt för matematik är ett kort, lätt och vackert framställningssätt. Den upprepade additionen går att skriva kortare i formen där anger antalet upprepade
Instuderingsfrågor för Endimensionell analys kurs B1 2011
 Instuderingsfrågor för Endimensionell analys kurs B1 2011 Anvisningar Avsikten med följande frågor är att hjälpa dig med självkontroll av dina kunskaper. Om du känner dig osäker på svaren bör du slå upp
Instuderingsfrågor för Endimensionell analys kurs B1 2011 Anvisningar Avsikten med följande frågor är att hjälpa dig med självkontroll av dina kunskaper. Om du känner dig osäker på svaren bör du slå upp
Högpresterande. Särskilt begåvade
 Talangfulla elever Högpresterande Särskilt begåvade (från NP Ma C 2011) Nedan ges derivatans värde hos en funktion ff i en given punkt PP. lim h 0 2 + h 5 + 3 (2 5 + 3) h = 80. a) Ange funktionen ff. b)
Talangfulla elever Högpresterande Särskilt begåvade (från NP Ma C 2011) Nedan ges derivatans värde hos en funktion ff i en given punkt PP. lim h 0 2 + h 5 + 3 (2 5 + 3) h = 80. a) Ange funktionen ff. b)
Kapitel 4. Funktioner. 4.1 Definitioner
 Kapitel 4 Funktioner I det här kapitlet kommer vi att undersöka funktionsbegreppet. I de första sektionerna genomgås definitionen av begreppet funktion och vissa egenskaper som funktioner har. I slutet
Kapitel 4 Funktioner I det här kapitlet kommer vi att undersöka funktionsbegreppet. I de första sektionerna genomgås definitionen av begreppet funktion och vissa egenskaper som funktioner har. I slutet
Avd. Matematik VT z = 2 (1 + 3i) = 2 + 6i, z + w = (1 + 3i) + (1 + i) = i + i = 2 + 4i.
 STOCKHOLMS UNIVERSITET iagnostiskt prov Lösningar MTEMTISK INSTITUTIONEN Vektorgeometri och funktionslära vd. Matematik VT 20 Lösning till uppgift (Komplexa tal) Vi börjar med första och andra uträkningen.
STOCKHOLMS UNIVERSITET iagnostiskt prov Lösningar MTEMTISK INSTITUTIONEN Vektorgeometri och funktionslära vd. Matematik VT 20 Lösning till uppgift (Komplexa tal) Vi börjar med första och andra uträkningen.
14 min 60 s min 42 s 49m 2 =18 s m 2, alltså samma tid. Vi kan säga att den tid som mamman behövde åt dammsugning var beroende av husets storlek.
 PASS 10. FUNKTIONER 10.1 Grundbegrepp om funktioner Mamman i den finländska modellfamiljen från pass fyra brukade dammsuga det 100 m 2 stora huset varje lördag. Det tog 30 minuter. Efter att pappan hade
PASS 10. FUNKTIONER 10.1 Grundbegrepp om funktioner Mamman i den finländska modellfamiljen från pass fyra brukade dammsuga det 100 m 2 stora huset varje lördag. Det tog 30 minuter. Efter att pappan hade
8F Ma Planering v45-51: Algebra
 8F Ma Planering v45-51: Algebra Arbetsform under en vecka: Tisdagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa: Läsa på anteckningar
8F Ma Planering v45-51: Algebra Arbetsform under en vecka: Tisdagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa: Läsa på anteckningar
Algebra, exponentialekvationer och logaritmer
 Höstlov Uppgift nr 1 Ge en lösning till ekvationen 0 434,2-13x 3 Ange både exakt svar och avrundat till två decimalers noggrannhet. Uppgift nr 2 Huvudräkna lg20 + lg50 Uppgift nr 3 Ge en lösning till ekvationen
Höstlov Uppgift nr 1 Ge en lösning till ekvationen 0 434,2-13x 3 Ange både exakt svar och avrundat till två decimalers noggrannhet. Uppgift nr 2 Huvudräkna lg20 + lg50 Uppgift nr 3 Ge en lösning till ekvationen
Övningshäfte 6: 2. Alla formler är inte oberoende av varandra. Försök att härleda ett par av de formler du fann ur några av de övriga.
 GÖTEBORGS UNIVERSITET MATEMATIK 1, MAM100, HT2005 MATEMATISK BASKURS Övningshäfte 6: Syftet med övningen är att utforska strukturen hos talsystemen under addition respektive multiplikation samt sambandet
GÖTEBORGS UNIVERSITET MATEMATIK 1, MAM100, HT2005 MATEMATISK BASKURS Övningshäfte 6: Syftet med övningen är att utforska strukturen hos talsystemen under addition respektive multiplikation samt sambandet
Lösningar och kommentarer till uppgifter i 1.1
 Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
Polynomekvationer (Algebraiska ekvationer)
 Polynomekvationer (Algebraiska ekvationer) Faktorsatsen 1. Pettersson: teori och exempel på sid. 21-22 Det intressanta är följande idé: Om man på något sätt (Vilket det är en annan fråga, se nedan!) har
Polynomekvationer (Algebraiska ekvationer) Faktorsatsen 1. Pettersson: teori och exempel på sid. 21-22 Det intressanta är följande idé: Om man på något sätt (Vilket det är en annan fråga, se nedan!) har
Kravgränser. Provet består av Del B, Del C, Del D samt en muntlig del och ger totalt 63 poäng varav 24 E-, 21 C- och 18 A-poäng.
 Kravgränser Provet består av Del B, Del C, Del D samt en muntlig del och ger totalt 63 poäng varav 24 E-, 21 C- och 18 A-poäng. Kravgräns för provbetyget E: 17 poäng D: 25 poäng varav 7 poäng på minst
Kravgränser Provet består av Del B, Del C, Del D samt en muntlig del och ger totalt 63 poäng varav 24 E-, 21 C- och 18 A-poäng. Kravgräns för provbetyget E: 17 poäng D: 25 poäng varav 7 poäng på minst
MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET MED MATRISINVERSER = = =
 Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Matematiska institutionen Stockholms universitet CG Matematik med didaktisk inriktning 2 Problem i Algebra, geometri och kombinatorik Snedsteg 5 MULTIPLIKATION AV MATRISER, BASER I RUMMET SAMT FÖRSTA MÖTET
Explorativ övning 5 MATEMATISK INDUKTION
 Explorativ övning 5 MATEMATISK INDUKTION Syftet med denna övning är att introducera en av de viktigaste bevismetoderna i matematiken matematisk induktion. Termen induktion är lite olycklig därför att matematisk
Explorativ övning 5 MATEMATISK INDUKTION Syftet med denna övning är att introducera en av de viktigaste bevismetoderna i matematiken matematisk induktion. Termen induktion är lite olycklig därför att matematisk
2. 1 L ä n g d, o m k r e t s o c h a r e a
 2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
8-3 Kvadreringsreglerna och konjugatregeln. Namn:
 8-3 Kvadreringsreglerna och konjugatregeln. Namn: Inledning I kapitlet med matematiska uttryck lärde du dig hur man förenklade ett uttryck med en faktor framför en parentes genom att multiplicera varje
8-3 Kvadreringsreglerna och konjugatregeln. Namn: Inledning I kapitlet med matematiska uttryck lärde du dig hur man förenklade ett uttryck med en faktor framför en parentes genom att multiplicera varje
Explorativ övning 5 MATEMATISK INDUKTION
 Explorativ övning 5 MATEMATISK INDUKTION Syftet med denna övning är att introducera en av de viktigaste bevismetoderna i matematiken matematisk induktion. Termen induktion är lite olycklig därför att matematisk
Explorativ övning 5 MATEMATISK INDUKTION Syftet med denna övning är att introducera en av de viktigaste bevismetoderna i matematiken matematisk induktion. Termen induktion är lite olycklig därför att matematisk
Talmängder N = {0,1,2,3,...} C = {a+bi : a,b R}
 Moment 1..1, 1.., 1..4, 1..5 Viktiga exempel 1., 1.4, 1.8 Övningsuppgifter I 1.7, 1.8, 1.9 Extrauppgifter 1,,, 4 Den teori och de exempel, som kommer att presenteras här, är normalt vad jag kommer att
Moment 1..1, 1.., 1..4, 1..5 Viktiga exempel 1., 1.4, 1.8 Övningsuppgifter I 1.7, 1.8, 1.9 Extrauppgifter 1,,, 4 Den teori och de exempel, som kommer att presenteras här, är normalt vad jag kommer att
Dockvetviattimånga situationer räcker inte de naturliga talen. För att kunna hantera negativa tal har de hela talen definierats:
 Kapitel Introduktion I detta kapitel kommer vi främst att behandla grundbegrepp. Vi undersöker några speciella samlingar av tal (kallas mängder), matematiska symboler och ser på vissa räkneregler. Dessa
Kapitel Introduktion I detta kapitel kommer vi främst att behandla grundbegrepp. Vi undersöker några speciella samlingar av tal (kallas mängder), matematiska symboler och ser på vissa räkneregler. Dessa
