PASS 4. POLYNOM, MINNESREGLERNA. 4.1 Kvadreringsreglerna. Kvadraten på en summa
|
|
|
- Filip Persson
- för 9 år sedan
- Visningar:
Transkript
1 PASS 4. POLYNOM, MINNESREGLERNA 4.1 Kvadreringsreglerna Kvadraten på en summa Den finländska modellfamiljen med mamma, pappa och två barn äger ett kvadratformat hus. Här nedan i figur 4 har vi en planritning av huset. Figur 4. I vänstra delen av figur 4 ser vi att föräldrarnas rum är en kvadrat med sidan 5 m och tamburen en kvadrat med sidan 3 m. I högra delen av figur 5 har vi ersatt 5 m och 3 m med a respektive b. Vi bestämmer arean av hela huset genom att först bestämma areorna av de enskilda rummen i vänstra delen av figuren: Rum Arean av rummet i kvadratmeter Tambur 3 3=9 Kök 3 5=15 Barnkammare 5 3=15 Föräldrarnas rum 5 5=25 AREAN AV HELA HUSET =64 På ett annat sätt är arean av hela huset i kvadratmeter = =64=8 8.
2 Sedan bestämmer arean av hela huset genom att bestämma areorna av de enskilda rummen i högra delen av figuren. Nu änvänder vi bokstäver i stället för siffror. Rum Arean av rummet Tambur b b=b 2 Kök b a=ab Barnkammare a b=ab Föräldrarnas rum a a=a 2 AREAN AV HELA HUSET b 2 ab ab a 2 =a 2 2ab b 2 På ett annat sätt är arean av hela huset a b a b = a b 2. Härav följer nu att a b 2 =a 2 2ab b 2 något som vi kan bevisa algebraiskt på följande sätt: a b 2 = a b a b =a 2 ab ab b 2 =a 2 2ab b 2. Vi har härlett minnesregeln för kvadraten på en summa. a b 2 =a 2 2ab b 2 Kvadraten på en differens Föräldrarna i en annan finländsk modellfamilj i grannskapet konstaterade att deras kvadratiska hus med sidan 10 m hade blivit för stort för att barnen hade flyttat ut till en annan ort. Pappan i familjen tänkte göra huset mindre men ändå behålla det kvadratiskt för att sänka värmekostnaderna. Här nedan i figur 5 har vi en planritning av huset. De streckade linjerna föreställer husets ursprungliga storlek. Pappan lämnade endast föräldrarummet kvar.
3 Figur 5. I vänstra delen av figur 5 ser vi att föräldrarnas rum är en kvadrat med sidan 7 m och tamburen är en kvadrat med sidan 3m. Hela huset hade ursprungligen sidan 10 m. I högra delen av figur 5 har vi ersatt 10 m med a, 3 m med b och 7 m med a-b. Vi bestämmer arean av huset i vänstra delen av figuren efter att pappan gjorde det mindre genom att först bestämma arean av föräldrarnas rum i kvadratmeter: A=7 7=49. På ett annat sätt är arean av föräldrarnas rum i kvadratmeter = =49. Sedan bestämmer vi arean av föräldrarnas rum genom att använda högra delen av figur 5 och bokstäver i stället för siffror. Föräldrarnas rum har arean a b a b = a b 2 kvadrat med sidan a b. för att det är en Arean av föräldrarummet får vi också genom att först bestämma husets ursprungliga area. Den är a 2. Av den här arean subtraherar vi areorna av tamburen b 2, köket a b b=ab b 2 och barnkammaren a b b=ab b 2. Så är arean av föräldrarummet a 2 b 2 ab b 2 ab b 2 =a 2 b 2 ab b 2 ab b 2 =a 2 2ab b 2. Härav följer nu att a b 2 =a 2 2ab b 2 något som vi kan bevisa algebraiskt på följande sätt: a b 2 = a b a b =a 2 ab ba b 2 =a 2 2ab b 2. Vi har härlett minnesregeln för kvadraten på en differens. a b 2 =a 2 2ab b Konjugatregeln Med hjälp av konjugatregeln kan vi beräkna produkten av en summa och en differens. Den utflyttade sonen i den finländska modellfamiljen bor i en studielägenhet. Planritningen av studielägenheten har vi i figur 6. Med hjälp av figuren bestämmer vi den sammanlagda arean av köket och vardagsrummet.
4 Figur 6. Vi får den sammanlagda arean av köket och vardagsrummet genom att bestämma arean av den kvadrat som innehåller vardagsrummet, köket och badrummet. Sedan subtraherar vi av den här arean ytan av badrummet. Alltså A VARDAGSRUM OCH KÖK =a 2 b 2. Ett annat sätt att beräkna den sammanlagda arean av köket och vardagsrummet är att vi först märker att areorna av köket och balkongen är lika stora. Båda två har arean a b b=ab b 2 Så får vi den sammanlagda arean av köket och vardagsrummet genom att addera areorna av vardagsrummet och balkongen. Vardagsrummet och balkongen bildar tillsammans en rektangel med sidorna a b och a b. Alltså A VARDAGSRUM OCH KÖK =A VARDAGSRUM A BALKONG = a b a b. Härav följer nu att a b a b =a 2 b 2 något som vi kan bevisa algebraiskt på följande sätt: a b a b =a 2 ab ba b 2 =a 2 b 2. Vi har härlett konjugatregeln. a b a b =a 2 b Tilläpningar på minnesregler Minnesreglerna, alltså kvadreringsreglerna och konjugatregeln, bör vi kunna utantill. Av det kommer vi att ha en stor nytta i fortsättningen. Dessutom gäller det att kunna tillämpa smidigt minnesreglerna åt båda riktningarna. Vi utvecklar uttrycket x 2 2 då vi skriver det som ett
5 polynom utan parentes. Exempel 1. Skriv x 2 2 som polynom med hjälp av minnesregeln för kvadraten på en summa. Vi använder formeln a b 2 =a 2 2ab b 2. Nu är a= x och b=2. Så får vi x 2 2 =x 2 2 x =x 2 4x 4. Har du förstått? I x 1 2 är lika med a) x b) x 2 2x 1 c) 2x 2 1 Har du förstått? II 3x 2a 2 är lika med a) 3x 2 12xa 2a 2 b) 9x 2 12xa 4a 2 c) 3x 2 2a 2 Har du förstått? III x 5 2 är lika med a) x 2 10x 25 b) x 2 25 c) x 2 10 x 25 Exempel 2. Skriv x 2y 2 som polynom med hjälp av minnesregeln för kvadraten på en differens. Vi använder formeln a b 2 =a 2 2ab b 2. Nu är a= x och b=2y. Så får vi x 2y 2 =x 2 2 x 2y 2y 2 = x 2 4xy 4y 2 Har du förstått? IV a är lika med a) 1 a2 4 b) a =1 a c) a 2 a 1 4 Exempel 3. Skriv som polynom med hjälp av konjugatregeln. a) a 2 a 2 b) 2x 3 2x 3 c) Vi använder formeln a b a b =a 2 b 2 i alla punkter. I a)-punkten är a=a och b=2. Så är a 2 a 2 =a =a 2 4. I b)-punkten är a=2x och b=3. Vi får 2x 3 2x 3 = 2x =4x 2 9. I c)-punkten är a= och b=. Nu får vi = 2 2 =
6 Har du förstått? V c d c d är lika med a) d 2 c 2 b) c 2 2cd d 2 c) c 2 d 2 Exempel 4. Skriv 1 3 a a 1 som polynom. 2 Enligt konjugatregeln får vi 1 3 a a 1 2 = a 1 2= 2 a Har du förstått? VI x 1 12 x är lika med a) 1 12 x 2 b) x c) x2 Exempel 5. Skriv x y y x som polynom. x y y x kan vi skriva på formen x y [ x y ]= x y [ 1 x y ]= 1 x y 2 Nu kan vi använda kvadreringsregeln. Vi får x y y x = x y 2 = x 2 2xy y 2 = x 2 2xy y 2 Har du förstått? VII 2 är lika med a) 2 b) c) 2 2 Har du förstått? VIII 2 är lika med a) 2 b) 2 2 c) Har du förstått? IX är lika med a) 2 2 b) c) 2 2 Har du förstått? X är lika med a) b) c) Begreppsfrågor IV
7 1. Vad avses med minnesreglerna? Räkna upp dem vid namn. 2. Hur kan man geometriskt bevisa kvadreringsreglerna? 3. Med vilken regel kan man beräkna produkten av en summa och en differens? 4. Ett polynom består av kvadraten på en variabel, kvadraten på en konstant och dubbla produkten av variabeln och konstanten. Ge ett exempel på ett sådant här polynom. Kan man kvadrera polynomet? 5. Vilken regel skall man använda då man vill skriva en differens som en produkt? 6. Hur har man använt minnesreglerna i räkneoperationen 16=25 9= =4 2 = = = = =16? 4.5 Uppgifter Skriv uttrycken i uppgifterna 1-4 som polynom. Förenkla uttrycken i uppgifterna a) e f 2 b) 5 x 2 c) d) a y 2 e) x 7 2 f) a) a 1 a 1 b) 2 z 2 z c) 2a 2 2a 2 d) hy ab hy ab 3. a) x 1,5 x 1,5 b) 1 2 a a 1 4 c) a b b a 4. a) 2a 3 3b 2 2a 3 3b 2 b) 1,5 x 0,5 y 2 c) a) a a b ab b) mn m n 5 c) x y x y 2x 2 y 2 6. a) 2x x x 2 x 2 b) 3m n m 3n 3 m n m n 7. a) m 2n 2 m 2 4n 2 b) 2m n 2 n 4m n c) 3a b 3a b 3a b 2 8. a) ab 2x 2 ab 2x 2 4abx b) 5ab xy xy 5ab xy 5ab 2 10 abxy 9. a) 3m 2 n 3 2 m 4 9n 6 10 m 4 n 6 b) ab 2 ab a 2 b ab a 2 b 2 ab 1 a 3 b 2 10.* Låt P a,b = a 2 b 2 a 2 b 2 a b a b 2ab b a a 2 b 2 a b 2 2. Bestäm värdet av P a,b då a) a=1,b= 1 b) a=b.
Har du förstått? I De här talen är primtal a) 29,49 och 61 b) 97, 83 och 89 c) 0, 2 och 3.
 PASS 5. FAKTORISERING AV POLYNOM 5. Nyttan av faktorisering och faktorisering av heltal Har vi nytta av att kunna faktorisera polynom? Ja det har vi. Bra kunskaper i faktorisering av polynom möjliggör
PASS 5. FAKTORISERING AV POLYNOM 5. Nyttan av faktorisering och faktorisering av heltal Har vi nytta av att kunna faktorisera polynom? Ja det har vi. Bra kunskaper i faktorisering av polynom möjliggör
a), c), e) och g) är olikheter. Av dem har c) och g) sanningsvärdet 1.
 PASS 9. OLIKHETER 9. Grundbegrepp om olikheter Vi får olikheter av ekvationer om vi byter ut likhetstecknet mot något av tecknen > (större än), (större än eller lika med), < (mindre än) eller (mindre än
PASS 9. OLIKHETER 9. Grundbegrepp om olikheter Vi får olikheter av ekvationer om vi byter ut likhetstecknet mot något av tecknen > (större än), (större än eller lika med), < (mindre än) eller (mindre än
Sidor i boken 110-113, 68-69 2, 3, 5, 7, 11,13,17 19, 23. Ett andragradspolynom Ett tiogradspolynom Ett tredjegradspolynom
 Sidor i boken 110-113, 68-69 Räkning med polynom Faktorisering av heltal. Att primtalsfaktorisera ett heltal innebär att uppdela heltalet i faktorer, där varje faktor är ett primtal. Ett primtal är ett
Sidor i boken 110-113, 68-69 Räkning med polynom Faktorisering av heltal. Att primtalsfaktorisera ett heltal innebär att uppdela heltalet i faktorer, där varje faktor är ett primtal. Ett primtal är ett
varandra. Vi börjar med att behandla en linjes ekvation med hjälp av figur 7 och dess bildtext.
 PASS 8 EKVATIONSSYSTEM OCH EN LINJES EKVATION 8 En linjes ekvation En linjes ekvation kan framställas i koordinatsystemet Koordinatsystemet består av x-axeln och yaxeln X-axeln är vågrät och y-axeln lodrät
PASS 8 EKVATIONSSYSTEM OCH EN LINJES EKVATION 8 En linjes ekvation En linjes ekvation kan framställas i koordinatsystemet Koordinatsystemet består av x-axeln och yaxeln X-axeln är vågrät och y-axeln lodrät
Repetitionsuppgifter i Matematik inför Basår. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Röd kurs. Multiplicera in i parenteser. Mål: Matteord. Exempel. 1 a) 4(x- 5) b) 5(3 + x) 3 Om 3(a + 4) = 36, vad är då 62 2 FUNKTIONER OCH ALGEBRA
 Röd kurs Mål: I den här kursen får du lära dig att: ~ multiplicera parenteser ~ använda kvadreringsregler ~ använda konjugatregeln ~ uttrycka formler på olika sätt Matteord första kvadreringsregeln andra
Röd kurs Mål: I den här kursen får du lära dig att: ~ multiplicera parenteser ~ använda kvadreringsregler ~ använda konjugatregeln ~ uttrycka formler på olika sätt Matteord första kvadreringsregeln andra
Algebra, kvadreringsregler och konjugatregeln
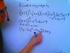 Algebra, kvadreringsregler och Uppgift nr 1 Multiplicera in i parentesen x(9 + 2y) Uppgift nr 2 Multiplicera in i parentesen 3x(7 + 5y) Uppgift nr 3 x² + 3x Uppgift nr 4 xy + yz Uppgift nr 5 5yz + 2xy
Algebra, kvadreringsregler och Uppgift nr 1 Multiplicera in i parentesen x(9 + 2y) Uppgift nr 2 Multiplicera in i parentesen 3x(7 + 5y) Uppgift nr 3 x² + 3x Uppgift nr 4 xy + yz Uppgift nr 5 5yz + 2xy
8-1 Formler och uttryck. Namn:.
 8-1 Formler och uttryck. Namn:. Inledning Ibland vill du lösa lite mer komplexa problem. Till exempel: Kalle är dubbelt så gammal som Stina, och tillsammans är de 33 år. Hur gammal är Kalle och Stina?
8-1 Formler och uttryck. Namn:. Inledning Ibland vill du lösa lite mer komplexa problem. Till exempel: Kalle är dubbelt så gammal som Stina, och tillsammans är de 33 år. Hur gammal är Kalle och Stina?
Manipulationer av algebraiska uttryck
 Manipulationer av algebraiska uttryck Valentina Chapovalova SMaL-kursen i Mullsjö 19 juni 2018 Kluring 1 Bestäm produkten (x a) (x b) (x c)... (x z) Lösning kluring 1 Bestäm produkten (x a) (x b) (x c)..
Manipulationer av algebraiska uttryck Valentina Chapovalova SMaL-kursen i Mullsjö 19 juni 2018 Kluring 1 Bestäm produkten (x a) (x b) (x c)... (x z) Lösning kluring 1 Bestäm produkten (x a) (x b) (x c)..
Algebra, exponentialekvationer och logaritmer
 Höstlov Uppgift nr 1 Ge en lösning till ekvationen 0 434,2-13x 3 Ange både exakt svar och avrundat till två decimalers noggrannhet. Uppgift nr 2 Huvudräkna lg20 + lg50 Uppgift nr 3 Ge en lösning till ekvationen
Höstlov Uppgift nr 1 Ge en lösning till ekvationen 0 434,2-13x 3 Ange både exakt svar och avrundat till två decimalers noggrannhet. Uppgift nr 2 Huvudräkna lg20 + lg50 Uppgift nr 3 Ge en lösning till ekvationen
Sammanfattningar Matematikboken Z
 Sammanfattningar Matematikboken Z KAPitel procent och statistik Procent Ordet procent betyder hundradel och anger hur stor del av det hela som något är. Procentform och 45 % = 0,45 6,5 % = 0,065 decimalform
Sammanfattningar Matematikboken Z KAPitel procent och statistik Procent Ordet procent betyder hundradel och anger hur stor del av det hela som något är. Procentform och 45 % = 0,45 6,5 % = 0,065 decimalform
Javisst! Uttrycken kan bli komplicerade, och för att få lite överblick över det hela så gör vi det så enkelt som möjligt för oss.
 8-2 Förenkling av uttryck. Namn: eller Konsten att räkna algebra och göra livet lite enklare för sig. Inledning I föregående kapitel lärde du dig vad ett matematiskt uttryck är för någonting och hur man
8-2 Förenkling av uttryck. Namn: eller Konsten att räkna algebra och göra livet lite enklare för sig. Inledning I föregående kapitel lärde du dig vad ett matematiskt uttryck är för någonting och hur man
Repetitionsuppgifter inför Matematik 1. Matematiska institutionen Linköpings universitet 2013
 Repetitionsuppgifter inför Matematik Matematiska institutionen Linköpings universitet 0 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Facit 4 Repetitionsuppgifter inför Matematik Repetitionsuppgifter
Repetitionsuppgifter inför Matematik Matematiska institutionen Linköpings universitet 0 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Facit 4 Repetitionsuppgifter inför Matematik Repetitionsuppgifter
4-7 Pythagoras sats. Inledning. Namn:..
 Namn:.. 4-7 Pythagoras sats Inledning Nu har du lärt dig en hel del om trianglar. Du vet vad en spetsig och en trubbig triangel är liksom vad en liksidig och en likbent triangel är. Vidare vet du att vinkelsumman
Namn:.. 4-7 Pythagoras sats Inledning Nu har du lärt dig en hel del om trianglar. Du vet vad en spetsig och en trubbig triangel är liksom vad en liksidig och en likbent triangel är. Vidare vet du att vinkelsumman
Sidor i boken V.L = 8 H.L. 2+6 = 8 V.L. = H.L.
 Sidor i boken 119-11 Andragradsekvationer Dagens tema är ekvationer, speciellt andragradsekvationer. Men först några ord om ekvationer i allmänhet. En ekvation är en likhet som innehåller ett (möjligen
Sidor i boken 119-11 Andragradsekvationer Dagens tema är ekvationer, speciellt andragradsekvationer. Men först några ord om ekvationer i allmänhet. En ekvation är en likhet som innehåller ett (möjligen
Bonusmaterial till Lära och undervisa matematik från förskoleklass till åk 6. Ledning för att lösa problemen i Övningar för kapitel 5, sid 138-144
 Bonusmaterial till Lära och undervisa matematik från förskoleklass till åk 6 Ledning för att lösa problemen i Övningar för kapitel 5, sid 138-144 Avsikten med de ledtrådar som ges nedan är att peka på
Bonusmaterial till Lära och undervisa matematik från förskoleklass till åk 6 Ledning för att lösa problemen i Övningar för kapitel 5, sid 138-144 Avsikten med de ledtrådar som ges nedan är att peka på
NMCC Sigma 8. Täby Friskola 8 Spets
 NMCC Sigma 8 Täby Friskola 8 Spets Sverige 2016 1 Innehållsförteckning Innehållsförteckning... 1 Inledning... 2 Sambandet mellan figurens nummer och antalet små kuber... 3 Metod 1... 3 Metod 2... 4 Metod
NMCC Sigma 8 Täby Friskola 8 Spets Sverige 2016 1 Innehållsförteckning Innehållsförteckning... 1 Inledning... 2 Sambandet mellan figurens nummer och antalet små kuber... 3 Metod 1... 3 Metod 2... 4 Metod
A B C D E. 2 Det står KANGAROO på mitt paraply. Du kan se det på bilden. A B C D E
 N G A RA Kängurutävlingen 2015 Benjamin Trepoängsuppgifter 1 Vilken figur är skuggad till hälften? Slovakien 2 Det står KANGAROO på mitt paraply. Du kan se det på bilden. Vilken av följande bilder är inte
N G A RA Kängurutävlingen 2015 Benjamin Trepoängsuppgifter 1 Vilken figur är skuggad till hälften? Slovakien 2 Det står KANGAROO på mitt paraply. Du kan se det på bilden. Vilken av följande bilder är inte
Matematik 92MA41 (15hp) Vladimir Tkatjev
 Matematik 92MA41 (15hp) Vladimir Tkatjev Lite inspiration Går det att konstruera 6 kvadrater av 12 tändstickor? Hur gör man då? (Nämnaren, Nr 2, 2005) Litet klurigt kanske, bygg en kub av stickorna: Uppgift
Matematik 92MA41 (15hp) Vladimir Tkatjev Lite inspiration Går det att konstruera 6 kvadrater av 12 tändstickor? Hur gör man då? (Nämnaren, Nr 2, 2005) Litet klurigt kanske, bygg en kub av stickorna: Uppgift
Repetitionsuppgifter inför Matematik 1-973G10. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter inför Matematik - 7G0 Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 4 Facit Repetitionsuppgifter inför
Repetitionsuppgifter inför Matematik - 7G0 Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 4 Facit Repetitionsuppgifter inför
Matematik och modeller Övningsuppgifter
 Matematik och modeller Övningsuppgifter Beräkna a) d) + 6 b) 7 (+) + ( 9 + ) + 9 e) 8 c) ( + (5 6)) f) + Förenkla följande uttryck så långt som möjligt a) ( ) 5 b) 5 y 6 5y c) y 5 y + y y d) +y y e) (
Matematik och modeller Övningsuppgifter Beräkna a) d) + 6 b) 7 (+) + ( 9 + ) + 9 e) 8 c) ( + (5 6)) f) + Förenkla följande uttryck så långt som möjligt a) ( ) 5 b) 5 y 6 5y c) y 5 y + y y d) +y y e) (
1 RUM & KÖK 1 RUM & KÖK RÄTTVIS HYRA SÅ BERÄKNAR BOTKYRKABYGGEN DIN LÄGENHETS HYRA
 RÄTTVIS HYRA SÅ BERÄKNAR BOTKYRKABYGGEN DIN LÄGENHETS HYRA såhär BestäMs hyran Tre faktorer inverkar när Rättvis hyra beräknas. Rättvis hyra finns det någon sån? Rättvis hyra - som infördes av Botkyrkabyggen
RÄTTVIS HYRA SÅ BERÄKNAR BOTKYRKABYGGEN DIN LÄGENHETS HYRA såhär BestäMs hyran Tre faktorer inverkar när Rättvis hyra beräknas. Rättvis hyra finns det någon sån? Rättvis hyra - som infördes av Botkyrkabyggen
Trepoängsproblem. Kängurutävlingen 2011 Cadet. 1 Vilket av följande uttryck har störst värde? 1 A: B: C: D: E: 2011
 Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
DE FYRA RÄKNESÄTTEN (SID. 11) MA1C: AVRUNDNING
 DE FYRA RÄKNESÄTTEN (SID. 11) 1. Benämn med korrekt terminologi talen som: adderas. subtraheras. multipliceras. divideras.. Addera 10 och. Dividera sedan med. Subtrahera 10 och. Multiplicera sedan med..
DE FYRA RÄKNESÄTTEN (SID. 11) 1. Benämn med korrekt terminologi talen som: adderas. subtraheras. multipliceras. divideras.. Addera 10 och. Dividera sedan med. Subtrahera 10 och. Multiplicera sedan med..
Svar och arbeta vidare med Student 2008
 Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Problem 1 2 3 4 5 6 7 Svar
 Känguru Cadet, svarsblankett Namn Klass/Grupp Poängsumman Känguruskuttet Ta lös svarsblanketten. Skriv ditt svarsalternativ under numret. Lämna rutan tom om du inte vet svaret. Gissa inte, felaktigt svar
Känguru Cadet, svarsblankett Namn Klass/Grupp Poängsumman Känguruskuttet Ta lös svarsblanketten. Skriv ditt svarsalternativ under numret. Lämna rutan tom om du inte vet svaret. Gissa inte, felaktigt svar
8-3 Kvadreringsreglerna och konjugatregeln. Namn:
 8-3 Kvadreringsreglerna och konjugatregeln. Namn: Inledning I kapitlet med matematiska uttryck lärde du dig hur man förenklade ett uttryck med en faktor framför en parentes genom att multiplicera varje
8-3 Kvadreringsreglerna och konjugatregeln. Namn: Inledning I kapitlet med matematiska uttryck lärde du dig hur man förenklade ett uttryck med en faktor framför en parentes genom att multiplicera varje
Algebra och rationella uttryck
 Algebra och rationella uttryck - 20 Uppgift nr Förenkla x0 y 6 z 5 25 y 2 Uppgift nr 2 Uppgift nr 3 ab b 5a - a² 9a där a 0. där b 0. Uppgift nr 4 Multiplicera in i parentesen 2x(4 + 2x 3 ) Uppgift nr
Algebra och rationella uttryck - 20 Uppgift nr Förenkla x0 y 6 z 5 25 y 2 Uppgift nr 2 Uppgift nr 3 ab b 5a - a² 9a där a 0. där b 0. Uppgift nr 4 Multiplicera in i parentesen 2x(4 + 2x 3 ) Uppgift nr
14 min 60 s min 42 s 49m 2 =18 s m 2, alltså samma tid. Vi kan säga att den tid som mamman behövde åt dammsugning var beroende av husets storlek.
 PASS 10. FUNKTIONER 10.1 Grundbegrepp om funktioner Mamman i den finländska modellfamiljen från pass fyra brukade dammsuga det 100 m 2 stora huset varje lördag. Det tog 30 minuter. Efter att pappan hade
PASS 10. FUNKTIONER 10.1 Grundbegrepp om funktioner Mamman i den finländska modellfamiljen från pass fyra brukade dammsuga det 100 m 2 stora huset varje lördag. Det tog 30 minuter. Efter att pappan hade
Avd. Matematik VT z = 2 (1 + 3i) = 2 + 6i, z + w = (1 + 3i) + (1 + i) = i + i = 2 + 4i.
 STOCKHOLMS UNIVERSITET iagnostiskt prov Lösningar MTEMTISK INSTITUTIONEN Vektorgeometri och funktionslära vd. Matematik VT 20 Lösning till uppgift (Komplexa tal) Vi börjar med första och andra uträkningen.
STOCKHOLMS UNIVERSITET iagnostiskt prov Lösningar MTEMTISK INSTITUTIONEN Vektorgeometri och funktionslära vd. Matematik VT 20 Lösning till uppgift (Komplexa tal) Vi börjar med första och andra uträkningen.
26:e Städernas turnering, Våren 2005
 6:e Städernas turnering, Våren 005 Problem med facit till A-omgången Y1. Två punkter M och N ligger på en graf y=px +qx+r, där koefficienterna p,q,r är heltal. Visa att om avståndet MN är ett heltal så
6:e Städernas turnering, Våren 005 Problem med facit till A-omgången Y1. Två punkter M och N ligger på en graf y=px +qx+r, där koefficienterna p,q,r är heltal. Visa att om avståndet MN är ett heltal så
ANDRA BASER ÄN TIO EXTRAMATERIAL TILL. Matematikens grunder. för lärare. Anders Månsson
 ANDRA BASER ÄN TIO EXTRAMATERIAL TILL Matematikens grunder för lärare Anders Månsson Extramaterial till boken Matematikens grunder för lärare (art.nr. 38994), Anders Månsson. Till Tallära-kapitlet: Andra
ANDRA BASER ÄN TIO EXTRAMATERIAL TILL Matematikens grunder för lärare Anders Månsson Extramaterial till boken Matematikens grunder för lärare (art.nr. 38994), Anders Månsson. Till Tallära-kapitlet: Andra
Exempelsamling :: Vektorintro V0.95
 Exempelsamling :: Vektorintro V0.95 Mikael Forsberg :: 2 noember 2012 1. eräkna summan a ektorerna (1, 2) och (3, 1) mha geometrisk addition 2. Tå ektorer u = ( 2, 3) och adderas och blir ektorn w = (1,
Exempelsamling :: Vektorintro V0.95 Mikael Forsberg :: 2 noember 2012 1. eräkna summan a ektorerna (1, 2) och (3, 1) mha geometrisk addition 2. Tå ektorer u = ( 2, 3) och adderas och blir ektorn w = (1,
INDUKTION OCH DEDUKTION
 Explorativ övning 3 INDUKTION OCH DEDUKTION Syftet med övningen är att öka Din problemlösningsförmåga och bekanta Dig med olika bevismetoder. Vårt syfte är också att öva skriftlig framställning av matematisk
Explorativ övning 3 INDUKTION OCH DEDUKTION Syftet med övningen är att öka Din problemlösningsförmåga och bekanta Dig med olika bevismetoder. Vårt syfte är också att öva skriftlig framställning av matematisk
TATA42: Föreläsning 10 Serier ( generaliserade summor )
 TATA42: Föreläsning 0 Serier ( generaliserade summor ) Johan Thim 5 maj 205 En funktion s: N R brukar kallas talföljd, och vi skriver ofta s n i stället för s(n). Detta innebär alltså att för varje heltal
TATA42: Föreläsning 0 Serier ( generaliserade summor ) Johan Thim 5 maj 205 En funktion s: N R brukar kallas talföljd, och vi skriver ofta s n i stället för s(n). Detta innebär alltså att för varje heltal
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Vektorer i planet och i rummet III Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Vektorer i planet och i rummet III Innehåll
Läxa 1 efter sidan 11
 Läxa 1 efter sidan 11 1 Skriv det tal som har a) 5 tiotusental 3 tusental 8 hundratal 7 tiotal 4 ental b) 9 hundratusental 2 tiotusental 5 tusental 4 hundratal 3 ental c) 2 hundratusental 4 tusental 9
Läxa 1 efter sidan 11 1 Skriv det tal som har a) 5 tiotusental 3 tusental 8 hundratal 7 tiotal 4 ental b) 9 hundratusental 2 tiotusental 5 tusental 4 hundratal 3 ental c) 2 hundratusental 4 tusental 9
Konsten att bestämma arean
 Konsten att bestämma arean Lektion Ett (Matematiskt område - Talmängder) Vad är viktigast? Introducera tanken om att felet skulle kunna vara viktigare än svaret. Vad väger äpplet? Gissa. Jämför med mätvärdet
Konsten att bestämma arean Lektion Ett (Matematiskt område - Talmängder) Vad är viktigast? Introducera tanken om att felet skulle kunna vara viktigare än svaret. Vad väger äpplet? Gissa. Jämför med mätvärdet
Explorativ övning 11 GEOMETRI
 Explorativ övning 11 GEOMETRI Syftet med denna övning är att ge kunskaper om grundläggande geometriska begrepp och resultat om geometriska figurer. Vi vill också ge en uppfattning om geometri som en matematisk
Explorativ övning 11 GEOMETRI Syftet med denna övning är att ge kunskaper om grundläggande geometriska begrepp och resultat om geometriska figurer. Vi vill också ge en uppfattning om geometri som en matematisk
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 2014
 SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
Enklare uppgifter, avsedda för skolstadiet.
 Årgång 11, 1927 Första häftet 265. Lös ekvationssystemet { x 3 5x + 2y = 0 y 3 + 2x 5y = 0 266. Visa att uttrycket na n+1 (n + 1)a n + 1 där a och n äro positiva hela tal och a > 2, alltid innehåller en
Årgång 11, 1927 Första häftet 265. Lös ekvationssystemet { x 3 5x + 2y = 0 y 3 + 2x 5y = 0 266. Visa att uttrycket na n+1 (n + 1)a n + 1 där a och n äro positiva hela tal och a > 2, alltid innehåller en
Lennart Carleson. KTH och Uppsala universitet
 46 Om +x Lennart Carleson KTH och Uppsala universitet Vi börjar med att försöka uppskatta ovanstående integral, som vi kallar I, numeriskt. Vi delar in intervallet (, ) i n lika delar med delningspunkterna
46 Om +x Lennart Carleson KTH och Uppsala universitet Vi börjar med att försöka uppskatta ovanstående integral, som vi kallar I, numeriskt. Vi delar in intervallet (, ) i n lika delar med delningspunkterna
RödGrön-spelet Av: Jonas Hall. Högstadiet. Tid: 40-120 minuter beroende på variant Material: TI-82/83/84 samt tärningar
 Aktivitetsbeskrivning Denna aktivitet är utformat som ett spel som spelas av en grupp elever. En elev i taget agerar Gömmare och de andra är Gissare. Den som är gömmare lagrar (gömmer) tal i några av räknarens
Aktivitetsbeskrivning Denna aktivitet är utformat som ett spel som spelas av en grupp elever. En elev i taget agerar Gömmare och de andra är Gissare. Den som är gömmare lagrar (gömmer) tal i några av räknarens
Gemensam presentation av matematiskt område: Geometri Åldersgrupp: år 5
 Gemensam presentation av matematiskt område: Geometri Åldersgrupp: år 5 Mål för lektionen: Eleverna skall kunna skilja på begreppen area och omkrets. Koppling till strävansmål: - Att eleven utvecklar intresse
Gemensam presentation av matematiskt område: Geometri Åldersgrupp: år 5 Mål för lektionen: Eleverna skall kunna skilja på begreppen area och omkrets. Koppling till strävansmål: - Att eleven utvecklar intresse
Snabbslumpade uppgifter från flera moment.
 Snabbslumpade uppgifter från flera moment. Uppgift nr Ställ upp och dividera utan hjälp av miniräknare talet 48 med 2 Uppgift nr 2 Skriv talet 3 8 00 med hjälp av decimalkomma. Uppgift nr 3 Uppgift nr
Snabbslumpade uppgifter från flera moment. Uppgift nr Ställ upp och dividera utan hjälp av miniräknare talet 48 med 2 Uppgift nr 2 Skriv talet 3 8 00 med hjälp av decimalkomma. Uppgift nr 3 Uppgift nr
R AKNE OVNING VECKA 1 David Heintz, 31 oktober 2002
 RÄKNEÖVNING VECKA David Heintz, 3 oktober 22 Innehåll Uppgift 27. 2 Uppgift 27.8 4 3 Uppgift 27.9 6 4 Uppgift 27. 9 5 Uppgift 28. 5 6 Uppgift 28.2 8 7 Uppgift 28.4 2 Uppgift 27. Determine primitive functions
RÄKNEÖVNING VECKA David Heintz, 3 oktober 22 Innehåll Uppgift 27. 2 Uppgift 27.8 4 3 Uppgift 27.9 6 4 Uppgift 27. 9 5 Uppgift 28. 5 6 Uppgift 28.2 8 7 Uppgift 28.4 2 Uppgift 27. Determine primitive functions
1Mer om tal. Mål. Grundkursen K 1
 Mer om tal Mål När eleverna har studerat det här kapitlet ska de: förstå vad som menas med kvadratrot och kunna räkna ut kvadratro ten av ett tal kunna skriva, använda och räkna med tal i tiopotensform
Mer om tal Mål När eleverna har studerat det här kapitlet ska de: förstå vad som menas med kvadratrot och kunna räkna ut kvadratro ten av ett tal kunna skriva, använda och räkna med tal i tiopotensform
UPPGIFT 2 KVADRATVANDRING
 UPPGIFT 1 LYCKOTAL Lyckotal är en serie heltal, som hittas på följande sätt. Starta med de naturliga talen: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13... Sök upp det första talet i serien, som är större
UPPGIFT 1 LYCKOTAL Lyckotal är en serie heltal, som hittas på följande sätt. Starta med de naturliga talen: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13... Sök upp det första talet i serien, som är större
1 Addition, subtraktion och multiplikation av (reella) tal
 Omstuvat utdrag ur R Pettersson: Förberedande kurs i matematik Addition, subtraktion och multiplikation av (reella) tal För reella tal gäller som bekant bl.a. följande räkneregler: (a + b) + c = a + (b
Omstuvat utdrag ur R Pettersson: Förberedande kurs i matematik Addition, subtraktion och multiplikation av (reella) tal För reella tal gäller som bekant bl.a. följande räkneregler: (a + b) + c = a + (b
Algebra, polynom & andragradsekvationer en pampig rubrik på ett annars relativt obetydligt dokument
 Algebra, polynom & andragradsekvationer en pampig rubrik på ett annars relativt obetydligt dokument Distributiva lagen a(b + c) = ab + ac 3(x + 4) = 3 x + 3 4 = 3x + 12 3(2x + 4) = 3 2x + 3 4 = 6x + 12
Algebra, polynom & andragradsekvationer en pampig rubrik på ett annars relativt obetydligt dokument Distributiva lagen a(b + c) = ab + ac 3(x + 4) = 3 x + 3 4 = 3x + 12 3(2x + 4) = 3 2x + 3 4 = 6x + 12
Ekvationssystem - Övningar
 Ekvationssystem - Övningar Uppgift nr 1 y = 5x x + y = 54 Uppgift nr 2 y = 2x x + y = 12 Uppgift nr 3 y = 3x + 7 4x + y = 35 Uppgift nr 4 y = 4x - 18 3x + y = 38 Uppgift nr 5 2x - 2y = -4 x - 3y = 4 Uppgift
Ekvationssystem - Övningar Uppgift nr 1 y = 5x x + y = 54 Uppgift nr 2 y = 2x x + y = 12 Uppgift nr 3 y = 3x + 7 4x + y = 35 Uppgift nr 4 y = 4x - 18 3x + y = 38 Uppgift nr 5 2x - 2y = -4 x - 3y = 4 Uppgift
Repetition av matematik inför kurs i statistik 1-10 p.
 Karlstads universitet Leif Ruckman Summasymbolen. Repetition av matematik inför kurs i statistik 1-10 p. I stället för att skriva en lång instruktion att vissa värden skall summeras brukar man använda
Karlstads universitet Leif Ruckman Summasymbolen. Repetition av matematik inför kurs i statistik 1-10 p. I stället för att skriva en lång instruktion att vissa värden skall summeras brukar man använda
Laboration: Att inhägna ett rektangulärt område
 Laboration: Att inhägna ett rektangulärt område Du har tillgång till ett hoprullat staket som är 30 m långt. Med detta vill du inhägna ett område och använda allt staket. Du vill göra inhägnaden rektangelformad.
Laboration: Att inhägna ett rektangulärt område Du har tillgång till ett hoprullat staket som är 30 m långt. Med detta vill du inhägna ett område och använda allt staket. Du vill göra inhägnaden rektangelformad.
FÖRBEREDANDE KURS I MATEMATIK 1
 FÖRBEREDANDE KURS I MATEMATIK 1 Till detta kursmaterial finns prov och lärare på Internet Ger studiepoäng Kostnadsfritt Fortlöpande anmälan på wwwmathse Eftertryck förbjudet utan tillåtelse 2007 MATHSE
FÖRBEREDANDE KURS I MATEMATIK 1 Till detta kursmaterial finns prov och lärare på Internet Ger studiepoäng Kostnadsfritt Fortlöpande anmälan på wwwmathse Eftertryck förbjudet utan tillåtelse 2007 MATHSE
Arbetsblad 3:1. Tolka uttryck. 1 Kajsa är a år gammal. Para ihop varje påstående med rätt uttryck.
 Arbetsblad :1 sid 78, 92 Tolka uttryck 1 Kajsa är a år gammal. Para ihop varje påstående med rätt uttryck. a) Karin är tre gånger så gammal: b) Katta är år yngre: a + a c) Kristina är en tredjedel så gammal:
Arbetsblad :1 sid 78, 92 Tolka uttryck 1 Kajsa är a år gammal. Para ihop varje påstående med rätt uttryck. a) Karin är tre gånger så gammal: b) Katta är år yngre: a + a c) Kristina är en tredjedel så gammal:
 Kursombud sökes! Kursens syfte är att ge en introduktion till metoder för att förutsäga realtidsegenskaper hos betjäningssystem, i synnerhet för data- och telekommunikationssystem. Såväl enkla betjäningssystem,
Kursombud sökes! Kursens syfte är att ge en introduktion till metoder för att förutsäga realtidsegenskaper hos betjäningssystem, i synnerhet för data- och telekommunikationssystem. Såväl enkla betjäningssystem,
Version 0.82. Linjär algebra kapiltet från ett ODE-kompendium. Mikael Forsberg
 Version.8 Linjär algebra kapiltet från ett ODE-kompendium Mikael Forsberg 8 Den här boken är typsatt av författaren med hjälp av L A TEX. Alla illustrationer är utförda av Mikael Forsberg med hjälp av
Version.8 Linjär algebra kapiltet från ett ODE-kompendium Mikael Forsberg 8 Den här boken är typsatt av författaren med hjälp av L A TEX. Alla illustrationer är utförda av Mikael Forsberg med hjälp av
Tillbyggnad av enbostadshus
 EXEMPELRITNINGAR FÖR Tillbyggnad av enbostadshus Kundtjänst Plan och bygg 090-16 13 61 Vad är en tillbyggnad? En tillbyggnad är en åtgärd som ökar en byggnads volym. Exempel på tillbyggnader är källarutgrävning,
EXEMPELRITNINGAR FÖR Tillbyggnad av enbostadshus Kundtjänst Plan och bygg 090-16 13 61 Vad är en tillbyggnad? En tillbyggnad är en åtgärd som ökar en byggnads volym. Exempel på tillbyggnader är källarutgrävning,
Riksfinal. Del 1: 6 uppgifter Tid: 60 min Maxpoäng: 18 (3p/uppgift) OBS! Skriv varje uppgift på separat papper och lagets namn på samtliga papper.
 Riksfinal Del 1: 6 uppgifter Tid: 60 min Maxpoäng: 18 (3p/uppgift) Hjälpmedel: Endast skrivmateriel, ingen miniräknare OBS Skriv varje uppgift på separat papper och lagets namn på samtliga papper. Fullständiga
Riksfinal Del 1: 6 uppgifter Tid: 60 min Maxpoäng: 18 (3p/uppgift) Hjälpmedel: Endast skrivmateriel, ingen miniräknare OBS Skriv varje uppgift på separat papper och lagets namn på samtliga papper. Fullständiga
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Studiehandledning till. MMA121 Matematisk grundkurs. Version 2012-09-03
 Studiehandledning till MMA Matematisk grundkurs läsåret 0/ Version 0-09-0 Kursinformation för MMA Mål Avsikten med kursen MMA Matematisk grundkurs är att ge grundläggande kunskaper i matematik, av betydelse
Studiehandledning till MMA Matematisk grundkurs läsåret 0/ Version 0-09-0 Kursinformation för MMA Mål Avsikten med kursen MMA Matematisk grundkurs är att ge grundläggande kunskaper i matematik, av betydelse
PASS 2. POTENSRÄKNING. 2.1 Definition av en potens
 PASS. POTENSRÄKNING.1 Definition av en potens Typiskt för matematik är ett kort, lätt och vackert framställningssätt. Den upprepade additionen går att skriva kortare i formen där anger antalet upprepade
PASS. POTENSRÄKNING.1 Definition av en potens Typiskt för matematik är ett kort, lätt och vackert framställningssätt. Den upprepade additionen går att skriva kortare i formen där anger antalet upprepade
Tentamen i Flervariabelanalys F/TM, MVE035
 Tetame i Flervariabelaalys F/TM, MV35 8 3 kl. 8.3.3. Hjälpmedel: Iga, ej räkedosa. Telefo: Oskar Hamlet tel 73-8834 För godkät krävs mist 4 poäg. Betyg 3: 4-35 poäg, betyg 4: 36-47 poäg, betyg 5: 48 poäg
Tetame i Flervariabelaalys F/TM, MV35 8 3 kl. 8.3.3. Hjälpmedel: Iga, ej räkedosa. Telefo: Oskar Hamlet tel 73-8834 För godkät krävs mist 4 poäg. Betyg 3: 4-35 poäg, betyg 4: 36-47 poäg, betyg 5: 48 poäg
205. Begrepp och metoder. Jacob Sjöström jacobsjostrom@gmail.com
 205. Begrepp och metoder Bo Sjöström bo.sjostrom@mah.se Jacob Sjöström jacobsjostrom@gmail.com Hur hög är en stapel med en miljon A4-papper? 100 st 80 grams har höjden 1 cm 1000 1 dm 1 000 000 1000 dm
205. Begrepp och metoder Bo Sjöström bo.sjostrom@mah.se Jacob Sjöström jacobsjostrom@gmail.com Hur hög är en stapel med en miljon A4-papper? 100 st 80 grams har höjden 1 cm 1000 1 dm 1 000 000 1000 dm
A1:an Repetition. Philip Larsson. 6 april Kapitel 1. Grundläggande begrepp och terminologi
 A1:an Repetition Philip Larsson 6 april 013 1 Kapitel 1. Grundläggande begrepp och terminologi 1.1 Delmängd Om ändpunkterna ska räknas med används symbolerna [ ] och raka sträck. Om ändpunkterna inte skall
A1:an Repetition Philip Larsson 6 april 013 1 Kapitel 1. Grundläggande begrepp och terminologi 1.1 Delmängd Om ändpunkterna ska räknas med används symbolerna [ ] och raka sträck. Om ändpunkterna inte skall
Föreläsning 3: Ekvationer och olikheter
 Föreläsning 3: Ekvationer och olikheter En ekvation är en likhet som innehåller en flera obekanta storheter. Exempel: x = 9, x är okänd. t + t + 1 = 7, t är okänd. Vi säger att ett värde på den obekanta
Föreläsning 3: Ekvationer och olikheter En ekvation är en likhet som innehåller en flera obekanta storheter. Exempel: x = 9, x är okänd. t + t + 1 = 7, t är okänd. Vi säger att ett värde på den obekanta
Ordlista 1A:1. siffra. tal. antal. räkneord. Dessa tio ord ska du träna. Öva orden
 Ordlista 1A:1 Öva orden Dessa tio ord ska du träna siffra En siffra är ett tecken. Dessa är siffrorna: 0, 1, 2, 3, 4, 5, 6, 7, 8 och 9 tal antal räkneord Ett tal skrivs med en eller flera siffror. Talet
Ordlista 1A:1 Öva orden Dessa tio ord ska du träna siffra En siffra är ett tecken. Dessa är siffrorna: 0, 1, 2, 3, 4, 5, 6, 7, 8 och 9 tal antal räkneord Ett tal skrivs med en eller flera siffror. Talet
Lathund algebra och funktioner åk 9
 Lathund algebra och funktioner åk 9 För att bli en rackare på att lösa ekvationer är det viktigt att man kan sina förutsättningar, dvs vilka matematiska regler som gäller. Prioriteringsreglerna (vilken
Lathund algebra och funktioner åk 9 För att bli en rackare på att lösa ekvationer är det viktigt att man kan sina förutsättningar, dvs vilka matematiska regler som gäller. Prioriteringsreglerna (vilken
NATIONELLT PROV I MATEMATIK KURS A VÅREN 1996. Tidsbunden del
 NATIONELLT PROV I MATEMATIK KURS A VÅREN 1996 Tidsbunden del Anvisningar Provperiod 10 maj - 1 juni 1996. Provtid Hjälpmedel Provmaterialet 120 minuter utan rast. Miniräknare och formelsamling. Formelblad
NATIONELLT PROV I MATEMATIK KURS A VÅREN 1996 Tidsbunden del Anvisningar Provperiod 10 maj - 1 juni 1996. Provtid Hjälpmedel Provmaterialet 120 minuter utan rast. Miniräknare och formelsamling. Formelblad
Prov Antal uppgifter Uppgiftsnummer Rekommenderad provtid
 2011-10-29 Provpass 2 Svarshäfte nr. Högskoleprovet Kvantitativ del l Provet innehåller 40 uppgifter Instruktion etta provhäfte består av fyra olika delprov. essa är XYZ (matematik), KV (kvantitativa jämförelser),
2011-10-29 Provpass 2 Svarshäfte nr. Högskoleprovet Kvantitativ del l Provet innehåller 40 uppgifter Instruktion etta provhäfte består av fyra olika delprov. essa är XYZ (matematik), KV (kvantitativa jämförelser),
Begrepp :: Determinanten
 c Mikael Forsberg 2008 1 Begrepp :: Determinanten Rekursiv definition :: Kofaktorutveckling Låt oss börja definiera determinanten för en 1 1 matris A = (a). En sådan matris är naturligtvis bara ett vanligt
c Mikael Forsberg 2008 1 Begrepp :: Determinanten Rekursiv definition :: Kofaktorutveckling Låt oss börja definiera determinanten för en 1 1 matris A = (a). En sådan matris är naturligtvis bara ett vanligt
Facit till Några extra uppgifter inför tentan Matematik Baskurs. x 2 x 3 1 2.
 KTH Matematik Lars Filipsson Facit till Några extra uppgifter inför tentan Matematik Baskurs 1. Låt f(x) = ln 2x + 4x 2 + 9 + ln 2x 4x 2 + 9. Bestäm definitionsmängd och värdemängd till f och rita kurvan
KTH Matematik Lars Filipsson Facit till Några extra uppgifter inför tentan Matematik Baskurs 1. Låt f(x) = ln 2x + 4x 2 + 9 + ln 2x 4x 2 + 9. Bestäm definitionsmängd och värdemängd till f och rita kurvan
Pernilla Falck Margareta Picetti Siw Elofsdotter Meijer. Matte. Safari. Direkt. Lärarhandledning. Andra upplagan, reviderade sidor
 Matte Direkt Pernilla Falck Margareta Picetti Siw Elofsdotter Meijer Safari 1A Lärarhandledning MS Enhetsdel Sist i varje kapitel finns ett avsnitt som i första hand tar upp enheter. Här i årskurs 1 handlar
Matte Direkt Pernilla Falck Margareta Picetti Siw Elofsdotter Meijer Safari 1A Lärarhandledning MS Enhetsdel Sist i varje kapitel finns ett avsnitt som i första hand tar upp enheter. Här i årskurs 1 handlar
OBSERVERA ATT DETTA EXEMPELMATERIAL INTE MOTSVARAR ETT HELT KURSPROV I OMFATTNING OCH INNEHÅLL.
 Matematik kurs b och c - Exempeluppgifter OBSERVERA ATT DETTA EXEMPELMATERIAL INTE MOTSVARAR ETT HELT KURSPROV I OMFATTNING OCH INNEHÅLL. Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv
Matematik kurs b och c - Exempeluppgifter OBSERVERA ATT DETTA EXEMPELMATERIAL INTE MOTSVARAR ETT HELT KURSPROV I OMFATTNING OCH INNEHÅLL. Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv
lena Alfredsson kajsa bråting patrik erixon hans heikne Matematik kurs 3c blå lärobok natur & kultur
 lena Alfredsson kajsa bråting patrik erion hans heikne Matematik 5000 kurs c blå lärobok natur & kultur NATUR & KULTUR Bo 7, 0 5 Stockholm Kundtjänst: Tel 08-5 85 00, order@nok.se Redaktion: Tel 08-5 86
lena Alfredsson kajsa bråting patrik erion hans heikne Matematik 5000 kurs c blå lärobok natur & kultur NATUR & KULTUR Bo 7, 0 5 Stockholm Kundtjänst: Tel 08-5 85 00, order@nok.se Redaktion: Tel 08-5 86
DN1230 Tillämpad linjär algebra Tentamen Onsdagen den 29 maj 2013
 TILLÄMPAD LINJÄR ALGEBRA, DN123 1 DN123 Tillämpad linjär algebra Tentamen Onsdagen den 29 maj 213 Skrivtid: 8-13 Tillåtna hjälpmedel: inga Examinator: Anna-Karin Tornberg Betygsgränser: Betyg A B C D E
TILLÄMPAD LINJÄR ALGEBRA, DN123 1 DN123 Tillämpad linjär algebra Tentamen Onsdagen den 29 maj 213 Skrivtid: 8-13 Tillåtna hjälpmedel: inga Examinator: Anna-Karin Tornberg Betygsgränser: Betyg A B C D E
Inglasat uterum/inglasad balkong
 Exempelritningar Inglasat uterum/inglasad balkong eskilstuna.se/bygga Vilka handlingar behövs när jag söker bygglov? Bygglov För att komma igång med ditt byggprojekt så snabbt som möjligt är det viktigt
Exempelritningar Inglasat uterum/inglasad balkong eskilstuna.se/bygga Vilka handlingar behövs när jag söker bygglov? Bygglov För att komma igång med ditt byggprojekt så snabbt som möjligt är det viktigt
Kängurutävlingen Matematikens Hopp 2001
 Kängurutävlingen Matematikens Hopp Del A 1.. Teckningarna föreställer talen, och med sina spegelbilder. Hur ska nästa teckning se ut? A B C D E Maria har sju pinnar. Hon bryter en mitt itu. Hur många pinnar
Kängurutävlingen Matematikens Hopp Del A 1.. Teckningarna föreställer talen, och med sina spegelbilder. Hur ska nästa teckning se ut? A B C D E Maria har sju pinnar. Hon bryter en mitt itu. Hur många pinnar
och symmetri Ur det centrala innehållet Förmågor Problemlösning Metod
 Längd, Kapitlets innehåll Kapitlet börjar med att eleverna får träna på längd i decimalform. De olika längdenheterna tränas och eleverna får själva mäta längd. Nästa avsnitt handlar om olika trianglar
Längd, Kapitlets innehåll Kapitlet börjar med att eleverna får träna på längd i decimalform. De olika längdenheterna tränas och eleverna får själva mäta längd. Nästa avsnitt handlar om olika trianglar
Upphämtningskurs i matematik
 Upphämtningskurs i matematik C.J. 2013 Föreläsningsunderlaget är uppbyggt utgående från kurserna i den långa gymnasiematematiken, ellips-kursböckerna (Schilds förlag) har använts som förebild. Böckerna
Upphämtningskurs i matematik C.J. 2013 Föreläsningsunderlaget är uppbyggt utgående från kurserna i den långa gymnasiematematiken, ellips-kursböckerna (Schilds förlag) har använts som förebild. Böckerna
Lektionsanteckningar 2: Matematikrepetition, tabeller och diagram
 Lektionsanteckningar 2: Matematikrepetition, tabeller och diagram 2.1 Grundläggande matematik 2.1.1 Potensfunktioner xmxn xm n x x x x 3 4 34 7 x x m n x mn x x 4 3 x4 3 x1 x x n 1 x n x 3 1 x 3 x0 1 1
Lektionsanteckningar 2: Matematikrepetition, tabeller och diagram 2.1 Grundläggande matematik 2.1.1 Potensfunktioner xmxn xm n x x x x 3 4 34 7 x x m n x mn x x 4 3 x4 3 x1 x x n 1 x n x 3 1 x 3 x0 1 1
Lösningsförslag Cadet 2014
 Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
En skärgårdsdröm Ett gammalt sommarställe har efter en totalrenovering fått ett helt nytt uttryck och blivit ett sommarnöje för flera generationer.
 En skärgårdsdröm Ett gammalt sommarställe har efter en totalrenovering fått ett helt nytt uttryck och blivit ett sommarnöje för flera generationer. Text Kajsa Ihre foto devis bionaz 086 [xxxxx xxxxxx xxxxx]
En skärgårdsdröm Ett gammalt sommarställe har efter en totalrenovering fått ett helt nytt uttryck och blivit ett sommarnöje för flera generationer. Text Kajsa Ihre foto devis bionaz 086 [xxxxx xxxxxx xxxxx]
Matematik CD för TB. tanv = motstående närliggande. tan34 = x 35. x = 35tan 34. x 23.6. cosv = närliggande hypotenusan. cos40 = x 61.
 Föreläning 8 Problem hämtade från boken idan 15 A 510 a) Rätvinklig triangel med vinkel och katet given. Mottående katet efterfråga. tan4 = x 5 x = 5tan 4 Svar:.6 cm x.6 A 510 b) Vinkel och hypotenuan
Föreläning 8 Problem hämtade från boken idan 15 A 510 a) Rätvinklig triangel med vinkel och katet given. Mottående katet efterfråga. tan4 = x 5 x = 5tan 4 Svar:.6 cm x.6 A 510 b) Vinkel och hypotenuan
Matematik 3000 kurs B
 Studieanvisning till läroboken Matematik 3000 kurs B Innehåll Kursöversikt...4 Så här jobbar du med boken...5 Studieenhet Sannolikhetslära...6 Studieenhet Linjära modeller...8 Studieenhet Icke-linjära
Studieanvisning till läroboken Matematik 3000 kurs B Innehåll Kursöversikt...4 Så här jobbar du med boken...5 Studieenhet Sannolikhetslära...6 Studieenhet Linjära modeller...8 Studieenhet Icke-linjära
ALGEBRA OCH FUNKTIONER
 ALGEBRA OCH FUNKTIONER Centralt innehåll Hantering av algebraiska uttrck och ekvationer. Generalisering av aritmetikens lagar. Begreppen polnom och rationellt uttrck. Kontinuerlig och diskret funktion.
ALGEBRA OCH FUNKTIONER Centralt innehåll Hantering av algebraiska uttrck och ekvationer. Generalisering av aritmetikens lagar. Begreppen polnom och rationellt uttrck. Kontinuerlig och diskret funktion.
Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning
 Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning Eleven skall år 1 Begrepp Jämförelse- och storleksord, t.ex. stor, större, störst. Positionssystemet
Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning Eleven skall år 1 Begrepp Jämförelse- och storleksord, t.ex. stor, större, störst. Positionssystemet
Känguru 2011 Student (gymnasiet åk 2 och 3)
 Känguru 011 Student sida 1 / 8 NAMN KLASS / GRUPP Pängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tm m du inte vill besvara den frågan. Gissa
Känguru 011 Student sida 1 / 8 NAMN KLASS / GRUPP Pängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tm m du inte vill besvara den frågan. Gissa
Hanne Solem Görel Hydén Sätt in stöten! MATEMATIK
 Hanne Solem Görel Hydén Sätt in stöten! MATEMATIK Multiplika tion Multiplikation, 5-tabellen Att multiplicera är detsamma som att addera samma tal flera gånger. Det kallar vi upprepad addition. 3 5 kan
Hanne Solem Görel Hydén Sätt in stöten! MATEMATIK Multiplika tion Multiplikation, 5-tabellen Att multiplicera är detsamma som att addera samma tal flera gånger. Det kallar vi upprepad addition. 3 5 kan
BEDÖMNINGSSTÖD. till TUMMEN UPP! matte inför betygssättningen i årskurs 6
 BEDÖMNINGSSTÖD till TUMMEN UPP! matte inför betygssättningen i årskurs 6 Det här är ett BEDÖMNINGSSTÖD som hjälper dig att göra en säkrare bedömning av elevernas kunskaper inför betygssättningen i årskurs
BEDÖMNINGSSTÖD till TUMMEN UPP! matte inför betygssättningen i årskurs 6 Det här är ett BEDÖMNINGSSTÖD som hjälper dig att göra en säkrare bedömning av elevernas kunskaper inför betygssättningen i årskurs
Avdelning 1, trepoängsproblem
 Avdelning 1, trepoängsproblem 1. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Var är kängurun? A: I cirkeln och i triangeln, men inte i kvadraten. B: I cirkeln
Avdelning 1, trepoängsproblem 1. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Var är kängurun? A: I cirkeln och i triangeln, men inte i kvadraten. B: I cirkeln
Jämställd tandreglering för barn och ungdomar mellan 3-19 år i Landstinget Kronoberg
 Jämställd tandreglering för barn och ungdomar mellan 3-19 år i Landstinget Kronoberg Bakgrund och introduktion: Det är fler flickor än pojkar som får tandregleringsbehandling i Kronoberg. Det finns dock
Jämställd tandreglering för barn och ungdomar mellan 3-19 år i Landstinget Kronoberg Bakgrund och introduktion: Det är fler flickor än pojkar som får tandregleringsbehandling i Kronoberg. Det finns dock
Inledning...3. Kravgränser...21. Provsammanställning...22
 Innehåll Inledning...3 Bedömningsanvisningar...3 Allmänna bedömningsanvisningar...3 Bedömningsanvisningar Del I...4 Bedömningsanvisningar Del II...5 Bedömningsanvisningar uppgift 11 (Max 5/6)...12 Kravgränser...21
Innehåll Inledning...3 Bedömningsanvisningar...3 Allmänna bedömningsanvisningar...3 Bedömningsanvisningar Del I...4 Bedömningsanvisningar Del II...5 Bedömningsanvisningar uppgift 11 (Max 5/6)...12 Kravgränser...21
Frågorna 1 till 6 ska svaras med sant eller falskt och ger vardera 1
 ATM-Matematik Mikael Forsberg 6-64 89 6 Matematik med datalogi, mfl. Skrivtid:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på ny sida. Använd ej baksidor.
ATM-Matematik Mikael Forsberg 6-64 89 6 Matematik med datalogi, mfl. Skrivtid:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på ny sida. Använd ej baksidor.
14. Potentialer och fält
 4. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
4. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
För att räkna upp, numrera, räkna antal och jämföra används ofta naturliga tal. Med vår vanliga decimalnotation (basen 10) skrivs dessa
 Avsnitt Olika typer av tal För att räkna upp, numrera, räkna antal och jämföra används ofta naturliga tal. Med vår vanliga decimalnotation (basen 0) skrivs dessa 0,,2,3,...,9,0,,... Samma naturliga tal
Avsnitt Olika typer av tal För att räkna upp, numrera, räkna antal och jämföra används ofta naturliga tal. Med vår vanliga decimalnotation (basen 0) skrivs dessa 0,,2,3,...,9,0,,... Samma naturliga tal
För att använda sifferkrypto använder man en rektangel om 5 gånger 6 bokstäver.
 Nämnarens kryptoskola 8. Sifferkrypto lärarsida För att använda sifferkrypto använder man en rektangel om 5 gånger 6 bokstäver. Siffror från 0 till 5 ovanför och 5 till 9 till vänster om rektangeln anger
Nämnarens kryptoskola 8. Sifferkrypto lärarsida För att använda sifferkrypto använder man en rektangel om 5 gånger 6 bokstäver. Siffror från 0 till 5 ovanför och 5 till 9 till vänster om rektangeln anger
Moment Viktiga exempel Övningsuppgifter
 Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång.
Moment Viktiga exempel Övningsuppgifter Inga Inga Inga Linjära ekvationssystem Vi har redan tidigare i kursen stött på linjära ekvationssystem. Nu är stunden kommen till en mera systematisk genomgång.
28 ALLT OM VILLOR & HUS
 Drömhuset på HEMMA hos Svantes och Ewas vackra hus är ritat och uppfört av Sävsjö Trähus, med Tony Sundberg som arkitekt och med Andreas Sjöholm som projektledare. Framsidan är inbjudande, med en rejäl
Drömhuset på HEMMA hos Svantes och Ewas vackra hus är ritat och uppfört av Sävsjö Trähus, med Tony Sundberg som arkitekt och med Andreas Sjöholm som projektledare. Framsidan är inbjudande, med en rejäl

