DN1230 Tillämpad linjär algebra Tentamen Onsdagen den 29 maj 2013
|
|
|
- Christoffer Lindström
- för 9 år sedan
- Visningar:
Transkript
1 TILLÄMPAD LINJÄR ALGEBRA, DN123 1 DN123 Tillämpad linjär algebra Tentamen Onsdagen den 29 maj 213 Skrivtid: 8-13 Tillåtna hjälpmedel: inga Examinator: Anna-Karin Tornberg Betygsgränser: Betyg A B C D E Fx Poäng För full poäng på en uppgift krävs att lösningarna är väl presenterade och lätta att följa. Det innebär speciellt att införda beteckningar ska definieras, att den logiska strukturen tydligt beskrivs i ord eller symboler och att resonemangen är väl motiverade och tydligt förklarade. Lösningar som allvarligt brister i dessa avseenden bedöms med högst två poäng. Lycka till! Uppgift 1 (6 poäng) a) Följande linje i lr 2 är given, x 4y + 8 =. i) Skriv upp linjens vektorekvation, x = x + tv. ii) Visa att vektorn n = (1, 4) är ortgonal mot den givna linjen. b) Om rangen av en 9 1 matris, A, är 5 (rank(a) = 5) viken dimension har då matrisen A s nollrum? c) Följande linjära system är givet där k är en godtycklig konstant. (5 k)x + y = 1 6x + (6 k)y = k i) För vilket värde/vilka värden på k har systemet en unik lösning? ii) För vilket värde/vilka värden på k är systemet inkonsistent? d) Låt y = (7, 6) och x = (4, 2). Skriv vektorn y som en summa av två ortogonala vektorer, en vektor i Span{x} och en vektor som är ortogonal mot x.
2 TILLÄMPAD LINJÄR ALGEBRA, DN123 2 a,i) Låt P 1(, 2) och P 2( 4, 1) vara två punkter på linjen. P 1P 2 = ( + 4, 2 1) är då en vektor parallell med linjen som kan skrivas x = (, 2) + t(4, 1) a,ii) För att n ska vara ortgonal mot linjen krävs att n v = vilket stämmer eftersom (1, 4) (4, 1) = b) rank(a) + nullity(a) = n dvs dimensionen av A s nollrum är 5. [ ] 5 k 1 c,i) Unik lösning om koefficientmatrisen, A =, är inverterbar, dvs om 6 6 k det(a). det(a) = (5 k)(6 k) 6 = (k 3)(k 8). Dvs systemet har en unik lösning om k 3 eller k 8. c,ii) När k = 8 är systemet inkonsistent. (När k = 3har systemet oändligt många lösningar.) d) Vi kan skriva y som y = αx + z. För att bestämma α kan vi använda oss av ortogonaliteten mellan z och x och skalärmultiplicera med x på båda sidor, y x = αx x + z x = αx x α = y x x x = 2. När vi har α kan vi beräka z som (7, 6) = 2(4, 2) + z z = ( 1, 2) och vi får att y = (8, 4) + ( 1, 2) Uppgift 2 (4 poäng) Följande datapunkter är givna (, ), (1, 1) samt (2, 3). a) Hitta den räta linje y = a + a 1 x som är bäst anpassad till punkterna i minsta kvadratmetodens mening. b) Hitta det andragradpolynom y = c + c 1 x + c 2 x 2 som går genom alla tre punkterna. a) Sätt in datapunkterna i den givna ansatsen a + a 1 = a + a 1 1 = 1 a + a 1 2 = 3 Detta kan vi skriva på formen Aa = b där 1 A = 1 1, b =
3 TILLÄMPAD LINJÄR ALGEBRA, DN123 3 För att lösa systemet, ställ upp normalekvationerna A T Aa = A T b och lös dessa för a. [ ] [ ] a = Detta ger att a=(-1/6,3/2) och y = 1/6 + 3/2x b) a) Sätt in datapunkterna i den givna ansatsen c + c 1 + c 2 2 = c + c c = 1 c + c c = 3 Detta kan vi skriva på formen Ac = b där 1 A = 1 1 1, b = Systemet löses för c = (, 1/2, 1/2) vilket ger att y = 1/2x + 1/2x 2. Uppgift 3 (5 poäng) a) Lös följande linjära ekvationssystem x y + z + w = 5 y z + 2w = 8 2x y 3z + 4w = 18. b) Systemet i a) kan skrivas på formen Ax = b där x = (x, y, z, w) och b = (5, 8, 18). Bestäm en bas för A s nollrum. a) Matrisen på reducerad rad-echelon form Vi har en fri parameter, w, som vi sätter till w = s (godtyckligt reellt tal). Lösningen blir: x = 13 3s y = 8 2s z = w = s
4 TILLÄMPAD LINJÄR ALGEBRA, DN123 4 som också kan skrivas på formen x 13 3 { y z = 8 + s 2 w 1 b) Matrisens nollrum ges av lösningsrummet till Ax =. På samma sätt som tidigare reducerar vi matrisen till rad-echelon form men nu har vi nollor i högerledet istället Lösningen kan skrivas som x 3 y z = s 2 w 1 dvs null(a) = Span{( 3, 2, 1)} och vektorn v = (( 3, 2, 1)) är en bas för null(a). Uppgift 4 (5 poäng) Låt U = Span{( 1,, 2, 1), ( 2, 1, 1, 2), (1,, 1, 1)}, ett underrum av lr 4. a) Bestäm en ortogonal bas för U. b) Definiera och ange det ortogonala komplementet (U ) of U. Lösning a): Låt v 1 = ( 1,, 2, 1), v 2 = ( 2, 1, 1, 2) och tag u 1 = v 1. Beräkna u 2 = v 2 v 2 u 1 u 1 u 2 1 = ( 2, 1, 1, 2) ( 1,, 2, 1) = ( 1, 1, 1, 1). 6 Låt v 3 = (1,, 1, 1). Beräkna ũ 3 = v 3 v 3 u 1 u 1 u 2 1 v 3 u 2 u 2 u 2 2 = (1,, 1, 1) 3 4 ( 1, 1, 1, 1) = 1 (1, 3, 1, 1). 4 Definiera u 3 = (1, 3, 1, 1).
5 TILLÄMPAD LINJÄR ALGEBRA, DN123 5 En ortogonal bas för U är {( 1,, 2, 1), ( 1, 1, 1, 1), (1, 3, 1, 1)}. Lösning b): U = {v lr 4 v u =, u U} = {v lr 4 v u i =, i = 1, 2, 3}, där u 1, u 2 och u 3 är basvektorerna för U definierade ovan. Sagt i ord, så är det ortogonala komplementet till U det underrum av lr 4 innehållande alla vektorer i lr 4 som är ortogonala mot alla vektorer i U, vilket de är om de är ortogonala mot basvektorerna för U. Utnyttja det faktum att nollrummet till en matris är det ortogonala komplementet till radrummet av matrisen. Låt u 1, u 2 och u 3 utgöra rader i en matris A, och lös Ax =. Gauss elimination ger x 1 = x 4, x 2 = x 3 =, x 4 fri. Dvs lösningen är på formen (x 4,,, x 4 ) = x 4 (1,,, 1), och nollrummet är Span{(1,,, 1)}. Dvs, U = Span{(1,,, 1)}. Uppgift 5 (5 poäng) Låt A = 1 4 k 2 1. a) Beräkna egenvärdena för A. b) För vilket värde/vilka värden på k är A diagonaliserbar? c) För vilket värde/vilka värden på k är A inverterbar? Lösning a): Bestäm egenvärdena till A: 1 λ 4 det(a λi) = k λ 2 1 λ = (k λ)(λ2 1 8) Dvs, vi har egenvärden λ = 3, 3, k. = (λ k)(λ + 3)(λ 3). Lösning b): Om k 3 och k 3, så har vi tre enkla egenvärden. Dessa tre egenvärden kommer att ha egenrum av dimension 1, och vi vet att matrisen är diagonaliserbar. Om k = 3 eller k = 3 så har vi ett dubbelt egenvärde, och måste kontrollera dimensionen på tillhörande egenrum. Låt k = 3, vilket ger det dubbla egenvärdet λ = (A 3I)v =
6 TILLÄMPAD LINJÄR ALGEBRA, DN123 6 Vi har endast en nollskild ekvation, och alltså två fria variabler. Dimensionen på egenrummet kommer att vara 2. Dvs matrisen är diagonaliserbar. Samma beräkning görs för k = 3, vilket ger det dubbla egenvärdet λ = 3. Slutsatsen blir det samma, även i detta fallet så är dimensionen av egenrummet 2 och matrisen är diagonaliserbar. Dvs, matrisen är diagonaliserbar för alla k. Lösning c): Determinanten av A kan räknas ut som produkten av egenvärdena. Vi får det A = 9k, vilket blir endast för k =. Dvs matrisen är inverterbar om k. Uppgift 6 (5 poäng) Låt e 1 = (1,, ), e 2 = (, 1, ) samt v = (2, 1, 1). a) Visa att vektorerna e 1, e 2 och v är linjärt oberoende samt skriv vektorn e 3 = (,, 1) som en linjärkombination av e 1, e 2 och v. b) Följande linjära transformation T : lr 3 lr 3, är sådan att 2 3 T (e 1 ) = 4, T (e 2 ) = 1, T (v) = Hitta transformationens standardmatris. a) Skriv e 3 som en linjärkombination av vektorerna (1,, ), (, 1, ) och (2, 1, 1), e 3 = a(1,, ) + b(, 1, ) + c(2, 1, 1). Vi behöver räkna ut a, b och c dvs lös systemet 1 2 a 1 2 a b = 1 1 b = 1 1 c 1 1 c 1 Detta ger oss att e 3 kan skrivas som e 3 = 2(1,, ) (, 1, ) + (2, 1, 1). b) Transformationen standardmatris, A, är given av att T (x) = Ax, där A ges av A = [T (e 1 ) T (e 2 ) T (e 3 )]. I uppgiften har vi redan T (e 1 ) och T (e 2 ) givna. Vi behöver bestämma T (e 3 ). Här använder vi oss av att e 3 kan skrivas som en linjärkombination av de vektorer för vilka vi känner till transformationen. Dvs T (e 3 ) = 2T (1,, ) T (, 1, ) + T (2, 1, 1) = 2(2, 4, 1) (3, 1, 2) + (, 2, 1) = ( 7, 11, 5) och slutligen kan vi skriva upp A som
7 TILLÄMPAD LINJÄR ALGEBRA, DN123 7 Uppgift 7 (5 poäng) Låt U = {p(x) P 2 3 p(x)dx = 3p(1)} (dvs låt U vara mängden av alla polynom p(x) i P 2 som uppfyller integralvillkoret 3 p(x)dx = 3p(1) ). a) Visa att U är ett underrum av P 2, vektorrummet av alla polynom av grad mindre eller lika med 2. b) Bestäm dimensionen av U. Bestäm en bas för U. a) Sluten under addition: 3 f(x)dx + 3 g(x)dx = 3f(1) + 3g(1) 3 h(x)dx = 3h(1) U, h(x) = f(x) + g(x) Sluten under skalärmultiplikation: k 3 f(x)dx = k3f(1) 3 h(x)dx = 3h(1) U, h(x) = kf(x). b) Bas för U: 3 a+bx+cx2 dx = 3(a+b+c) 3a+ 9b + 27c = 3(a+b+c) b = 4c. Det 2 3 generella polynomet i U kan då skrivas som p(x) = a + c(x 2 4x) och basen blir 1, x 2 4x och har dimension 2. Uppgift 8 (5 poäng) a) Antag att de två n n-matriserna A och B är similära. Visa att även A k och B k är similära. Två matriser är similära om det finns en inverterbar matris P sådan att B = P 1 AP. b) Antag att u är en vektor i lr n sådan att u u = 1. Låt P = uu T och Q = I n 2P. Visa att Q 2 = I n där I n är identitetsmatrisen av storlek n n. a) För similära matriser gäller att det finns en inverterbar matris P sådan att B = P 1 AP. Detta ger att B k = (P 1 AP ) k = (P 1 AP )(P 1 AP )(P 1 AP ) (P 1 AP ) = P 1 A k P. Dvs A k och B k är similära matriser. b) Q 2 = (I n 2P ) 2 = I n 2P I n 2I n P + 4P 2 = I n 4P + 4P 2. P 2 = (uu T ) 2 = uu T uu T = uu uu T = uu T = P. I n 4P + 4P 2 = I n 4P + 4P = I n
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 2014
 SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
Version 0.82. Linjär algebra kapiltet från ett ODE-kompendium. Mikael Forsberg
 Version.8 Linjär algebra kapiltet från ett ODE-kompendium Mikael Forsberg 8 Den här boken är typsatt av författaren med hjälp av L A TEX. Alla illustrationer är utförda av Mikael Forsberg med hjälp av
Version.8 Linjär algebra kapiltet från ett ODE-kompendium Mikael Forsberg 8 Den här boken är typsatt av författaren med hjälp av L A TEX. Alla illustrationer är utförda av Mikael Forsberg med hjälp av
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
3 1 = t 2 2 = ( 1) ( 2) 1 2 = A(t) = t 1 10 t
 SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng. Använd bifogat formulär för dessa 6 frågor.
 TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
SF1624 Algebra och geometri Tentamen Torsdag, 17 mars 2016
 SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
EXEMPEL OCH LÖSNINGAR I LINJÄR ALGEBRA II
 EXEMPEL OCH LÖSNINGAR I LINJÄR ALGEBRA II PER ALEXANDERSSON Sammanfattning. Detta är en samling kompletterande uppgifter till Linjär Algebra II för lärare. Exemplen är av varierande svårighetsgrad och
EXEMPEL OCH LÖSNINGAR I LINJÄR ALGEBRA II PER ALEXANDERSSON Sammanfattning. Detta är en samling kompletterande uppgifter till Linjär Algebra II för lärare. Exemplen är av varierande svårighetsgrad och
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
29 november, 2016, Föreläsning 21. Ortonormala baser (ON-baser) Gram-Schmidt s ortogonaliseringsprocess
 29 november, 2016, Föreläsning 21 Tillämpad linjär algebra Innehåll: Ortonormala baser (ON-baser) Gram-Schmidt s ortogonaliseringsprocess Minsta-kvadratmetoden - exempel 1. Uppgift. Tentamen 19/1-15, uppgift
29 november, 2016, Föreläsning 21 Tillämpad linjär algebra Innehåll: Ortonormala baser (ON-baser) Gram-Schmidt s ortogonaliseringsprocess Minsta-kvadratmetoden - exempel 1. Uppgift. Tentamen 19/1-15, uppgift
Tentamen TMV140 Linjär algebra Z
 Tentamen TMV40 Linjär algebra Z 307 kl. 08.30 2.30 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, 0703 088 304 Hjälpmedel: Inga, ej heller räknedosa För godkänt
Tentamen TMV40 Linjär algebra Z 307 kl. 08.30 2.30 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers Telefonvakt: Dawan Mustafa, 0703 088 304 Hjälpmedel: Inga, ej heller räknedosa För godkänt
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Vektorer i planet och i rummet III Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Vektorer i planet och i rummet III Innehåll
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng.
 ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
3x + y z = 0 4x + y 2z = 0 2x + y = Lös det överbestämda systemet nedan på bästa sätt i minsta kvadratmening. x = 1 x + y = 1 x + 2y = 2
 TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 734-433 kurser:: Linjär Algebra ma4a Matematik för ingenjörer ma3a 3 7 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och
TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 734-433 kurser:: Linjär Algebra ma4a Matematik för ingenjörer ma3a 3 7 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
1 basen B = {f 1, f 2 } där f 1 och f 2 skall uttryckas i koordinater i standardbasen.
 Akademin för teknik och miljö Rolf Källström telefonkontakt med examinator via tentamensvakten Matematiktentamen Ingenjörer, lärare, m fl Linjär algebra maa. 5 6 Skrivtid: 9... Inga hjälpmedel. Lösningarna
Akademin för teknik och miljö Rolf Källström telefonkontakt med examinator via tentamensvakten Matematiktentamen Ingenjörer, lärare, m fl Linjär algebra maa. 5 6 Skrivtid: 9... Inga hjälpmedel. Lösningarna
SF1624 Algebra och geometri Tentamen Torsdag, 9 juni 2016
 SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
TMV166 Linjär Algebra för M. Tentamen
 MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 3 6 kl. 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Tony Stillfjord,
MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 3 6 kl. 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Tony Stillfjord,
Del 1: Godkäntdelen. TMV141 Linjär algebra E
 Var god vänd! MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 26083 kl 0830 230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV4 Linjär algebra
Var god vänd! MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 26083 kl 0830 230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV4 Linjär algebra
1. (a) Bestäm alla värden på c som gör att matrisen A(c) saknar invers: 1 0 1. 1 c 1
 ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
SF1624 Algebra och geometri
 SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
SF64 Algebra och geometri Sjätte föreläsningen Mats Boij Institutionen för matematik KTH 5 januari, 07 Repetition Ett delrum i R n är slutet under addition x + y V om x, y V multiplikation med skalär a
x 2y + z = 1 (1) 2x + y 2z = 3 (2) x + 3y z = 4 (3)
 TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 74-4 kurser:: Linjär Algebra ma4a Matematik för ingenjörer maa 8 5 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta
TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 74-4 kurser:: Linjär Algebra ma4a Matematik för ingenjörer maa 8 5 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
UPPSALA UNIVERSITET Matematiska institutionen Styf. Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 2004
 UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. t 2
 SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
LINJÄR ALGEBRA II LEKTION 3
 LINJÄR ALGEBRA II LEKTION 3 JOHAN ASPLUND INNEHÅLL Basbyten Kolonnrum, radrum och nollrum 3 Linjära avbildningar från R n till R m 4 Uppgifter 3 46:3 3 47:a 3 48:3a 4 48:a 4 49:9 4 40:7a,b BASBYTEN Om
LINJÄR ALGEBRA II LEKTION 3 JOHAN ASPLUND INNEHÅLL Basbyten Kolonnrum, radrum och nollrum 3 Linjära avbildningar från R n till R m 4 Uppgifter 3 46:3 3 47:a 3 48:3a 4 48:a 4 49:9 4 40:7a,b BASBYTEN Om
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
3. Lös det överbestämda systemet nedan på bästa sätt i minsta kvadratmening. x + y = 1 x + 2y = 3 x + 3y = 4 x + 4y = 6
 TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 734-433 kurser:: Linjär Algebra ma4a Matematik för ingenjörer ma3a 5 4 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och
TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 734-433 kurser:: Linjär Algebra ma4a Matematik för ingenjörer ma3a 5 4 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och
SF1624 Algebra och geometri Tentamen Onsdag, 13 januari 2016
 SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA
 UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
Lösningar till MVE021 Linjär algebra för I
 Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
1 Ortogonalitet. 1.1 Skalär produkt. Man kan tala om vinkel mellan vektorer.
 Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
där β R. Bestäm de värden på β för vilka operatorn är diagonaliserbar. Ange även för respektive av dessa värden en bas av egenvektorer till F.
 MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MMA9 Linjär algebra Datum: 7 januari 04 Skrivtid:
MÄLARDALENS HÖGSKOLA Akademin för utbildning, kultur och kommunikation Avdelningen för tillämpad matematik Examinator: Lars-Göran Larsson TENTAMEN I MATEMATIK MMA9 Linjär algebra Datum: 7 januari 04 Skrivtid:
För ingenjörs- och distansstudenter Linjär Algebra ma014a 2015 02 26. ATM-Matematik Mikael Forsberg 0734-41 23 31
 ATM-Matematik Mikael Forsberg 074-4 För ingenjörs- och distansstudenter Linjär Algebra ma04a 0 0 Skrivtid: 09:00-4:00. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 074-4 För ingenjörs- och distansstudenter Linjär Algebra ma04a 0 0 Skrivtid: 09:00-4:00. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
Självkoll: Ser du att de två uttrycken är ekvivalenta?
 ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
y z 3 = 0 z 5 16 1 i )
 ATM-Matematik Mikael Forsberg 734-433 Sören Hector 7-46686 Rolf Källström 7-6939 Ingenjörer, Lantmätare och Distansstuderande, mfl. Linjär Algebra ma4a 4 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna
ATM-Matematik Mikael Forsberg 734-433 Sören Hector 7-46686 Rolf Källström 7-6939 Ingenjörer, Lantmätare och Distansstuderande, mfl. Linjär Algebra ma4a 4 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
2 = 3 = 1. ekvationssystem är beskriven som de vektorer X = 2 0 1 2. 1 1 0 2
 . Tisdagen 35 Igår visade vi att lösningsmängden W R 5 till ekvationssystemet 3x + x 2 + 3x 3 + 2x 4 x 5 = (..) 2x 2 + x 3 + 4x 4 + 2x 5 = 3x 3x 2 + x 3 6x 4 5x 5 = har bas u och u 2 och u 3 där 5 2 6
. Tisdagen 35 Igår visade vi att lösningsmängden W R 5 till ekvationssystemet 3x + x 2 + 3x 3 + 2x 4 x 5 = (..) 2x 2 + x 3 + 4x 4 + 2x 5 = 3x 3x 2 + x 3 6x 4 5x 5 = har bas u och u 2 och u 3 där 5 2 6
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
Del 1: Godkäntdelen. TMV142 Linjär algebra Z
 MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 26083 kl 0830 230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV42 Linjär algebra Z Tentan
MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 26083 kl 0830 230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV42 Linjär algebra Z Tentan
Inför tentamen i Linjär algebra TNA002.
 Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)
![A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p) A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)](/thumbs/93/112249032.jpg) SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 2 Fredagen den 28 januari, 2011
 SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 2 Fredagen den 28 januari, 2011 UPPGIFT (1) Låt V vara mängden av vektorer (x 1, x 2, x 3 ) i R 3 som uppfyller
SF1624 Algebra och geometri Lösningsförslag med bedömningskriterier till kontrollskrivning 2 Fredagen den 28 januari, 2011 UPPGIFT (1) Låt V vara mängden av vektorer (x 1, x 2, x 3 ) i R 3 som uppfyller
Institutionen för Matematik TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F1, TMA671 2005-08-26. DAG: Fredag 26 augusti 2005 TID: 8.30-12.
 Institutionen för Matematik Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67 5-8-6 DAG: Fredag 6 augusti 5 TID: 8.3-.3 SAL: V Ansvarig: Ivar Gustafsson, tel: 77 94 Förfrågningar: Ivar Gustafsson
Institutionen för Matematik Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F, TMA67 5-8-6 DAG: Fredag 6 augusti 5 TID: 8.3-.3 SAL: V Ansvarig: Ivar Gustafsson, tel: 77 94 Förfrågningar: Ivar Gustafsson
SF1624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 2010 DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
8(x 1) 7(y 1) + 2(z + 1) = 0
 Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
1. (a) (1p) Undersök om de tre vektorerna nedan är linjärt oberoende i vektorrummet
 1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
2s + 3t + 5u = 1 5s + 3t + 2u = 1 3s 3u = 1
 ATM-Matematik Mikael Forsberg 074-4 För studenter på distans och campus Linjär algebra ma04a 04 0 5 Skrivtid: 09:00-4:00. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja
ATM-Matematik Mikael Forsberg 074-4 För studenter på distans och campus Linjär algebra ma04a 04 0 5 Skrivtid: 09:00-4:00. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
SF1624 Algebra och geometri Bedömningskriterier till tentamen Fredagen den 22 oktober, 2010
 SF1624 Algebra och geometri Bedömningskriterier till tentamen Fredagen den 22 oktober, 2010 Allmänt gäller följande: Om lösningen helt saknar förklarande text till beräkningar och formler ges högst två
SF1624 Algebra och geometri Bedömningskriterier till tentamen Fredagen den 22 oktober, 2010 Allmänt gäller följande: Om lösningen helt saknar förklarande text till beräkningar och formler ges högst två
Definition 1 Ett vektorrum M (över R) är en mängd element, vektorer, sådan att det finns en kommutativ operation + på mängden M som uppfyller
 April 27, 25 Vektorrum Definition Ett vektorrum M (över R) är en mängd element, vektorer, sådan att det finns en kommutativ operation + på mängden M som uppfyller. x M och y M = x + y M. 2. x + y = y +
April 27, 25 Vektorrum Definition Ett vektorrum M (över R) är en mängd element, vektorer, sådan att det finns en kommutativ operation + på mängden M som uppfyller. x M och y M = x + y M. 2. x + y = y +
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
14 september, Föreläsning 5. Tillämpad linjär algebra
 14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
14 september, 2016 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition av inversen av en matris Förra gången: Linjära ekvationer och dess lösningar
Algebraiska egenskaper hos R n i)u + v = v + U
 Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Matematik med datalogi, mfl. Linjär algebra ma014a ATM-Matematik Mikael Forsberg
 ATM-Matematik Mikael Forsberg 6-64 89 6 Matematik med datalogi, mfl. Linjär algebra ma4a Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje n uppgift
ATM-Matematik Mikael Forsberg 6-64 89 6 Matematik med datalogi, mfl. Linjär algebra ma4a Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje n uppgift
Övningstenta 001. Alla Linjär Algebra. TM-Matematik Sören Hector Mikael Forsberg. 1. x 2y z + v = 0 z + u + v = 3 x + 2y + 2u + 2v = 4 z + 2u + 5v = 0
 TM-Matematik Sören Hector Mikael Forsberg Alla Linjär Algebra Övningstenta. x z + v z + u + v 3 x + + u + v 4 z + u + 5v. (a) Bestäm storleken (absolutbeloppet) och argumentet till z i. (b) Uttrck på formen
TM-Matematik Sören Hector Mikael Forsberg Alla Linjär Algebra Övningstenta. x z + v z + u + v 3 x + + u + v 4 z + u + 5v. (a) Bestäm storleken (absolutbeloppet) och argumentet till z i. (b) Uttrck på formen
A = v 2 B = = (λ 1) 2 16 = λ 2 2λ 15 = (λ 5)(λ+3). E 5 = Span C =
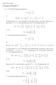 KTH Matematik Lösningar till Kapitel 7 A a Karakteristiska polynomet av detλi A det A λ λ λ b Egenvdena av A nollställen till karakteristiska polynomet alltså har A egenvdet λ c Motsvarande egenrum E lösningsrummet
KTH Matematik Lösningar till Kapitel 7 A a Karakteristiska polynomet av detλi A det A λ λ λ b Egenvdena av A nollställen till karakteristiska polynomet alltså har A egenvdet λ c Motsvarande egenrum E lösningsrummet
För studenter på distans och campus Linjär algebra ma014a 2014 02 10. ATM-Matematik Mikael Forsberg 0734-41 23 31
 ATM-Matematik Mikael Forsberg 734-4 3 3 För studenter på distans och campus Linjär algebra maa Skrivtid: 9:-:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
ATM-Matematik Mikael Forsberg 734-4 3 3 För studenter på distans och campus Linjär algebra maa Skrivtid: 9:-:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp)
 Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Stora bilden av Linjära algebran. Vektorrum, linjära transformationer, matriser (sammanfattning av begrepp) Linjär algebra består av tre grenar eller koncept: geometriska begreppet av vektorrum, analysbegreppet
Uppgifter, 2015 Tillämpad linjär algebra
 Geometri. Uppgifter, 25 Tillämpad linjär algebra. Uppgift. Låt (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av linjära
Geometri. Uppgifter, 25 Tillämpad linjär algebra. Uppgift. Låt (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av linjära
Uppgifter, 2014 Tillämpad linjär algebra
 Geometri. Uppgifter, 24 Tillämpad linjär algebra. Uppgift. Låt A = (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av
Geometri. Uppgifter, 24 Tillämpad linjär algebra. Uppgift. Låt A = (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av
Linjär algebra. Lars-Åke Lindahl
 Linjär algebra Lars-Åke Lindahl 2009 Fjärde upplagan c 2009 Lars-Åke Lindahl, Matematiska institutionen, Uppsala universitet Innehåll Förord................................. v 1 Linjära ekvationssystem
Linjär algebra Lars-Åke Lindahl 2009 Fjärde upplagan c 2009 Lars-Åke Lindahl, Matematiska institutionen, Uppsala universitet Innehåll Förord................................. v 1 Linjära ekvationssystem
Extraövningar, linjär algebra
 Extraövningar, linjär algebra Uppgifter markerade med * kan innehålla något moment som är kursivt, medan uppgifter markerade med ** kan vara av det svårare slaget och innehålla något moment som inte ingår
Extraövningar, linjär algebra Uppgifter markerade med * kan innehålla något moment som är kursivt, medan uppgifter markerade med ** kan vara av det svårare slaget och innehålla något moment som inte ingår
Tentamen i Linjär algebra (TATA31/TEN1) 2013 08 24, 14 19.
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
Crash Course Algebra och geometri. Ambjörn Karlsson c januari 2016
 Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Hjälpmedel: inga Chalmers tekniska högskola Datum: kl Telefonvakt: Peter Hegarty (a) Låt (3p)
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 5 kl 4 8 Tentamen Telefonvakt: Peter Hegarty 766-7787 TMV4/86: Linjär algebra Z/TD Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 5 kl 4 8 Tentamen Telefonvakt: Peter Hegarty 766-7787 TMV4/86: Linjär algebra Z/TD Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
15 september, Föreläsning 5. Tillämpad linjär algebra
 5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
5 september, 5 Föreläsning 5 Tillämpad linjär algebra Innehåll Matriser Algebraiska operationer med matriser Definition och beräkning av inversen av en matris Förra gången: Linjära ekvationer och dess
x + y + z + 2w = 0 (a) Finn alla lösningar till ekvationssystemet y + z+ 2w = 0 (2p)
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1. Omfattning. Innehåll 2012-01-20. Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra
 TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1 Omfattning Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll Olika aspekter av linjära ekvationssystem 1. skärning mellan geometriska
TMV166/186 Linjär Algebra M/TD 2011/2012 Läsvecka 1 Omfattning Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll Olika aspekter av linjära ekvationssystem 1. skärning mellan geometriska
Lösningar till linjära problem med MATLAB
 5B1146 - Geometri och algebra Mikrolelektronik, TH ista ösningar till linjära problem med MATAB Av: oel Nilsson, alikzus@home.se atrik osonen, pkosonen@kth.se 26-12-4 roblem 1 Man ska bestämma ett tredjegradspolynom:
5B1146 - Geometri och algebra Mikrolelektronik, TH ista ösningar till linjära problem med MATAB Av: oel Nilsson, alikzus@home.se atrik osonen, pkosonen@kth.se 26-12-4 roblem 1 Man ska bestämma ett tredjegradspolynom:
Omtentamen i DV & TDV
 Umeå Universitet Institutionen för Datavetenskap Gunilla Wikström (e-post wikstrom) Omtentamen i Teknisk-Vetenskapliga Beräkningar för DV & TDV Tentamensdatum: 2005-06-07 Skrivtid: 9-15 Hjälpmedel: inga
Umeå Universitet Institutionen för Datavetenskap Gunilla Wikström (e-post wikstrom) Omtentamen i Teknisk-Vetenskapliga Beräkningar för DV & TDV Tentamensdatum: 2005-06-07 Skrivtid: 9-15 Hjälpmedel: inga
kvivalenta. Ange rangen för A samt en bas för kolonnrummet för A. och U =
 MATEMATIK Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola Datum: 9-- kl 8 Tentamen Telefonvakt: Aron Lagerberg tel 76-786 Linjär Algebra Z (tmv4) Skriv tentamenskod tydligt på samtliga
MATEMATIK Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola Datum: 9-- kl 8 Tentamen Telefonvakt: Aron Lagerberg tel 76-786 Linjär Algebra Z (tmv4) Skriv tentamenskod tydligt på samtliga
Linjär Algebra M/TD Läsvecka 1
 Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
Linjär Algebra M/TD Läsvecka 1 Omfattning: Lay, kapitel 1.1-1.9, Linjära ekvationer i linjär algebra Innehåll: Olika aspekter av linjära ekvationssystem: skärning mellan geometriska objekt, linjärkombination
1 x 1 x 2 1 x x 2 x 2 2 x 3 2 A = 1 x 3 x 2 3 x x 4 x 2 4 x 3 4
 KARLSTADS UNIVERSITET Avdelningen för matematik Tentamen i Linjär Algebra, 7,5p för MAGA4 Mån -6-7, 8.5-3.5 på Kau Ansvarig lärare: Ilie Barza, tel.54-7 5 95 Hjälpmedel: Skrivdon. Maximalt antal poäng:
KARLSTADS UNIVERSITET Avdelningen för matematik Tentamen i Linjär Algebra, 7,5p för MAGA4 Mån -6-7, 8.5-3.5 på Kau Ansvarig lärare: Ilie Barza, tel.54-7 5 95 Hjälpmedel: Skrivdon. Maximalt antal poäng:
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
A = x
 Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
denna del en poäng. 1. (Dugga 1.1) (a) Beräkna u (v 2u) om v = u och u har längd 3. Motivera ert svar.
 Kursen edöms med etyg 3, 4, 5 eller underkänd, där 5 är högsta etyg För godkänt etyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt 3 poäng För var och en av
Kursen edöms med etyg 3, 4, 5 eller underkänd, där 5 är högsta etyg För godkänt etyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt 3 poäng För var och en av
2 1 1 s s. M(s) = (b) Beräkna inversen för det minsta positiva heltalsvärdet på s som gör matrisen inverterbar.
 TM-Matematik Mikael Forsberg 7 Linjär algebra/matematik för ingenjörer maa, maa 5 6 Skrivtid: 9:-:. Inga hjälpmedel förutom pennor, sudd, linjal, gradskiva. Lösningarna skall vara fullständiga och lätta
TM-Matematik Mikael Forsberg 7 Linjär algebra/matematik för ingenjörer maa, maa 5 6 Skrivtid: 9:-:. Inga hjälpmedel förutom pennor, sudd, linjal, gradskiva. Lösningarna skall vara fullständiga och lätta
LINJÄR ALGEBRA II LEKTION 1
 LINJÄR ALGEBRA II LEKTION JOHAN ASPLUND INNEHÅLL. VEKTORRUM OCH DELRUM Hel kursen Linjär Algebr II hndlr om vektorrum och hur vektorrum (eller linjär rum, som de iblnd klls) beter sig. Tidigre hr mn ntgligen
LINJÄR ALGEBRA II LEKTION JOHAN ASPLUND INNEHÅLL. VEKTORRUM OCH DELRUM Hel kursen Linjär Algebr II hndlr om vektorrum och hur vektorrum (eller linjär rum, som de iblnd klls) beter sig. Tidigre hr mn ntgligen
TMV142/186 Linjär algebra Z/TD
 MATEMATIK Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Chalmers tekniska högskola Datum: 2018-08-27 kl 1400 1800 Tentamen Telefonvakt: Anders Hildeman ank 5325 TMV142/186 Linjär algebra Z/TD Skriv
MATEMATIK Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Chalmers tekniska högskola Datum: 2018-08-27 kl 1400 1800 Tentamen Telefonvakt: Anders Hildeman ank 5325 TMV142/186 Linjär algebra Z/TD Skriv
Chalmers tekniska högskola Datum: kl Telefonvakt: Linnea Hietala MVE480 Linjär algebra S
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
1 De fyra fundamentala underrummen till en matris
 Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
2x + y + 3z = 4 x + y = 1 x 2y z = 3
 ATM-Matematik Pär Hemström 7 6572 Sören Hector 7 4686 Mikael Forsberg 74 42 För studerande i linjär algebra Linjär algebra ma4a 225 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga
ATM-Matematik Pär Hemström 7 6572 Sören Hector 7 4686 Mikael Forsberg 74 42 För studerande i linjär algebra Linjär algebra ma4a 225 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga
6.1 Skalärprodukt, norm och ortogonalitet. TMV141 Linjär algebra E VT 2011 Vecka 6. Lärmål 6.1. Skalärprodukt. Viktiga begrepp
 6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
Kursplanering för Linjär algebra, HT 2003
 Kursplanering för Linjär algebra, HT 2003 Mikael Forsberg 12 augusti 2003 Innehåll 1 Kursbok 2 2 Kursinnehåll 2 2.1 Kursens uppläggning......................... 2 2.2 Målsättning..............................
Kursplanering för Linjär algebra, HT 2003 Mikael Forsberg 12 augusti 2003 Innehåll 1 Kursbok 2 2 Kursinnehåll 2 2.1 Kursens uppläggning......................... 2 2.2 Målsättning..............................
Lösningar till utvalda uppgifter i kapitel 8
 Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
(a) Bestäm för vilka värden på den reella konstanten c som ekvationssystemet är lösbart. (b) Lös ekvationssystemet för dessa värden på c.
 UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
