Frågetimmar inför skrivningarna i oktober
|
|
|
- Leif Axelsson
- för 5 år sedan
- Visningar:
Transkript
1 MATEMATIK Frågetimmar inför skrivningarna i oktober (Tomas Carnstam, Johan Richter, ) fredag 9 oktober 55 7 (Obs) tisdag 2 oktober 05 2 onsdag 24 oktober 05-2 torsdag 25 oktober 05 2 fredag 26 oktober 05-2 Lokal: MH: Lokal: MH: Lokal: MH: Lokal: MH: Lokal: MH: Individuell rådgivning på alla aktuella kurser Anders Holst Studierektor
2 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA kl 49 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade och positivt orienterade Lös, för varje värde på a, ekvationssystemet x + y + z = 0 ax y + z = 0 x ay z = 0 2 a) Bestäm en ekvation på an form för planet π genom punkterna P : (, 0, ), P 2 : (,, ), och P : (,, ) (0) b) Bestäm skärningen mellan planet π ovan och linjen som går genom punkterna Låt P 4 : (, 4, ) och P 5 : (4, 6, 4) (0) c) Ange den punkt i π som ligger närmast P 5, dvs nn den ortogonala projektionen av punkten P 5 på planet π (04) A = ( ) 4 a) Bestäm alla egenvärden och egenvektorer till A (05) b) Diagonalisera A, dvs ange en inverterbar matris S och en diagonalmatris D sådana att S AS = D (02) c) Lös matrisekvationen (AX I) T = A (0) 4 Bestäm en positivt orienterad ortonormerad bas ê, ê 2, ê sådan att ê är ortogonal mot planet π : 2x + 2y + z = 0 och ê 2 är ortogonal mot linjen l : (x, y, z) = (, 0, 2) + t(2,, 2) Bestäm också en ekvation för π i den nya basen ê, ê 2, ê 5 Låt F vara en linjär avbildning som avbildar vektorerna (, 0, 0), (,, 0) och (,, ) på (2,, 0), (0, 0, ) respektive (0,, ) Låt vidare G vara avbildningen som speglar rummets vektorer i xz-planet, dvs i planet y = 0 Låt slutligen H vara den sammansatta avbildning som innebär att vi först tillämpar F och därefter G a) Bestäm avbildningsmatrisen för H (08) b) Blir volymen av en parallellepiped större eller mindre då vi tillämpar H på den? (02) Var god vänd!
3 6 Antag att vi vrider rummets vektorer vinkeln θ kring linjen (x, y, z) = t (9, 52, 267), i positiv led sett från spetsen av vektorn (9, 52, 267), och låt A vara avbildningsmatrisen för denna avbildning a) Bestäm, för varje värde på θ, rangen av A (0) b) Bestäm, för varje värde på θ, alla (reella) egenvärden till A (0) c) Bestäm, för varje värde på θ, huruvida A är diagonaliserbar eller ej (04) GOD JUL!
4 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA kl 8 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade och positivt orienterade, om inte annat anges a) Ange en ekvation på affin form för planet π genom punkten (,, ) och linjen (x, y, z) = ( t, + t, t), t R (05) b) Beräkna avståndet mellan punkten (, 2, 2) och π (05) 2 Låt u = ( a,, ), u 2 = (,, a) och u = (,, ) Bestäm för varje värde på parametern a alla lösningar till vektorekvationen λ u + λ 2 u 2 + λ u = 0 För vilka värden på a är u, u 2, u linjärt beroende? Bestäm alla symmetriska matriser X sådan att AX + (XA) T = B, där ( ) ( ) A = och B = 2 4 a) Låt v = (, 0, ), v 2 = (, 2, 2) och v = (,, ) Bestäm volymen av parallellepipeden med kanterna v, v 2 och v Bestäm arean av parallellogrammen med sidorna v och v 2 (02) b) Låt F vara den linjära avbildningen sådan att F (, 0, 0) = ( 2, 0, 0), F (0,, ) = (0, 2, 2) och F (0,, ) = (0, 4, 2) Bestäm avbildningsmatrisen för F (04) c) Beräkna volymen av den parallellepiped som fås genom att tillämpa F på parallellepipeden i a) Beräkna arean av den parallellogram som fås genom att tillämpa F på parallellogrammen i a) (04) 5 Bestäm en bas e, e 2, e sådan att e är parallell med linjen l : (x, y, z) = ( + t, 2 t, 5), t R, e 2 är ortogonal mot e och parallell med planet π : x + 2y z = och e är ortogonal mot e 2 och mot linjen l 2 : (x, y, z) = (, 0, 2) + t(,, 2), t R Är e, e 2, e en ON-bas? Ange en ekvation för π i det nya koordinatsystemet Oe e 2e 6 Matrisen 6 A = 0 4 har egenvektoren Är A diagonaliserbar? 0 SLUT!
5 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra kl 8 INGA HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade och positivt orienterande Bestäm, för varje reellt tal s, lösningarna till det homogena ekvationssystemet BX = 0 där s x 0 B = s 2 0 0, X = x 2, och 0 = 0 2 s 2 x 0 2 Beräkna det minsta avståndet mellan punkten P : (0,, 5) och planet med parameterframställningen π : (x, y, z) = s(,, ) + t(,, 0), s, t R Bestäm dessutom den punkt Q i π som ligger närmast P Definiera egenvärde och egenvektor till en matris Vad menas med att en matris är diagonaliserbar? Diagonalisera matrisen A = ( ) Låt u = (4,, 5) och v = (4, 2, 0) a) Beräkna den minsta vinkeln, [u, v], mellan vektorerna u och v (05) b) Bestäm de vektorer w som uppfyller [u, w] = [v, w], dvs bildar en lika stor vinkel med u som med v (05) 5 a) Formulera definitionen för att tre vektorer, ê, ê 2, ê, bildar en ortonormerad bas i rummet (04) b) Konstruera en ny ortonormerad bas ê, ê 2, ê sådan att ê har samma riktning som vektorn (,, ) och ê är parallell med xy-planet Ange även koordinaterna till vektorn u = (0, 0, ) i den nya basen (06) 6 Du sitter i ett vintermörkt studentrum In genom nyckelhålet P tränger en smal solstråle som reflekteras av en spegel varpå den träffar en punkt Q på väggen I en idealiserad matematisk modell beskrivs nyckelhålet som en punkt P : (8, 5, 4) Det antages dessutom att ljusstrålen inledningsvis har riktningen v = ( 5, 5, ), att spegelytan ligger i planet σ : x + 2y = 0 och att väggens punkter uppfyller ekvationen π : 2x y + 5 = 0 Bestäm koordinaterna för Q LYCKA TILL!
6 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra kl 4 9 INGA HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade och positivt orienterande Ange en ekvation på affin form för det plan som innehåller punkterna P : (,2,0), Q : (,,) och R : (,,2), och bestäm avståndet från origo till planet 2 a) Beräkna vinkeln [x, y] då x = (8, 5,) och y = (2,,6) (05) b) Låt x och y vara samma vektorer som ovan Bestäm två nya vektorer u och v sådana att y = u+v, och där u är parallell med x samt v är otrogonal mot x (05) Lös matrisekvationen (XA 2 ) = A B, där A = 0 och B = y F(v) u 4 Figuren till höger visar hur en linjär avbildning F i planet avbildar två vektorer u och v på vektorerna F(u) respektive F(v) Bestäm avbildningsmatrisen för F med avseende på x y-koordinatsystemet F(u) v x 5 a) Ge definitionen för att en kvadratisk matris A är diagonaliserbar Härled utifrån denna definition en formel för potensen A n, där n är ett positivt heltal (04) b) Diagonalisera matrisen A = 7 [ ] 4 4 Ange den matris B som uppfyller A n B då n (06) 6 Låt π beteckna ett plan i rummet som går genom origo och har normalvektorn N Ange en formel för avbildningsmatrisen A för spegling i planet π Beräkna dessutom A 202 och A (Man kan anta att normalvektorn har längden ett, dvs N T N = ) LYCKA TILL!
7 Ì ÃÆÁËà À ËÃÇÄ Æ Á ÄÍÆ Å Ì Å ÌÁËà ÁÆËÌÁÌÍÌÁÇÆ Æ Ä ËÆÁÆ Ê ÄÁÆÂ Ê Ä Ê ¾¼½½¹½¾¹½ ½º Î Ö Ö Ñ ØØ ÙÒ Ö ÒÖ Ø ÖÑ Ò ÒØ Ò Ö Ó ÒØÑ ØÖ Ò Ö ÒÓÐÐ det A = a a = a2 + 2a + = 0 a =, a = Ö a Ó a Ö Ý Ø Ñ Ø ÒØÝ Ð Ò Ò Ó Ø Ö ÓÑ Ý Ø Ñ Ø Ö ÓÑÓ ÒØ Ö ÒÒ (x, y, z) = (0, 0, 0)º ÇÑ a = ÐÐ Ö a = ÒÒ ÓÒ Ð Ø ÑÒ Ð Ò Ò Öº Ö a = x + y + z = 0 x y + z = 0 x y z = 0 x + y + z = 0 4y 2z = 0 4y 2z = 0 x = t y = t z = 2t Ö a = x + y + z = 0 x y + z = 0 x + y z = 0 x + y + z = 0 2z = 0 2z = 0 x = t y = t z = 0 ËÚ Ö ÐÐ Ø a = Ö (x, y, z) = t(,, 2), t R Ó a = Ö (x, y, z) = t(,, 0), t Rº a Ó a Ð Ö Ð Ò Ò Ò (x, y, z) = (0, 0, 0)º ¾º µ Î Ö Ò Ö P P 2 = (0,, 2) Ó P P = (2,, 0)º Ò ÒÓÖÑ ÐÚ ØÓÖ Ø ÐÐ ÔÐ Ò Ø Ú P P 2 P P = (0,, 2) (2,, 0) = (2, 4, 2) = 2(, 2, ) Î ÚÐ Ö (, 2, ) ÓÑ ÒÓÖÑ ÐÚ ØÓÖ Ú Ð Ø Ö Ú Ø ÓÒ Ò x + 2y z + d = 0 Ö πº Ì Ð Ø d ØÑ ÒÓÑ ØØ ØÓÔÔ Ò Ò Ú ÔÙÒ Ø ÖÒ Ú Ø ÓÒ Ò Øº ܺ P d = 0 d = 0 Î Ö ÐÐØ π : x + 2y z = 0º µ Î Ö Ò Ö Ò Ö ØÒ Ò Ú ØÓÖ P 4 P 5 ÓÑ Ð Ò Ò Ú Ø ÓÒ = (, 2, )º ÎÐ Ö Ú P 4 ÓÑ ÔÙÒ Ø Ö Ú (x, y, z) = (, 4, ) + t(, 2, ) = ( + t, 4 + 2t, + t) Î ØÓÔÔ Ö ÒÙ Ò ÓÓÖ Ò Ø Ö ÔÐ Ò Ø Ú Ø ÓÒ ( + t) + 2(4 + 2t) ( + t) = 0 6t + 6 = 0 t = ËÐÙØÐ Ò ÐÐØ ÔÙÒ Ø Ò (, 4, ) (, 2, ) = ( 2, 2, 2)º
8 µ ÇÖ Ó Ð Ö ÔÐ Ò Ø Ú ÔÖÓ Ö Ö OP 5 Ô ÔÐ Ò Ø ÒÓÖÑ Ð n = (, 2, ) OP 5 n (4, 6, 4) (, 2, ) v = n = (, 2, ) = 2 (, 2, ) = 2(, 2, ) n 2 (, 2, ) 2 6 ÇÑ Ú Ø Ò Ö Ò ÓÖØÓ ÓÒ Ð ÔÖÓ Ø ÓÒ Ò Ñ Q ÐÐ Ö Ø ÒÙ ØØ OQ = OP 5 v = (4, 6, 4) (2, 4, 2) = (2, 2, 6) Ò ÔÙÒ Ø ÓÑ Ð Ö ÒÖÑ Ø P 5 Ö ÐÐØ ÓÓÖ Ò Ø ÖÒ (2, 2, 6)º ËÚ Ö µ π : x + 2y z = 0º µ ( 2, 2, 2)º µ (2, 2, 6)º º µ ÒÚÖ Ò Ö Ð Ò Ò ÖÒ Ø ÐÐ Ú Ø ÓÒ Ò det(λi A) = 0 det(λi A) = λ 4 λ = (λ )2 4 = 0 λ =, λ = ÒÚÖ Ò Ö ÐÐØ λ = Ó λ = º ÅÓØ Ú Ö Ò ÒÚ ØÓÖ Ö ÓÑ ØÖ Ú Ð Ð Ò Ò Ö Ø ÐÐ Ú Ø ÓÒ Ý Ø Ñ Ø (λi A)X = ¼ º Ö λ = Ð Ö Ý Ø Ñ Ø { { ( ) 2x x 2 = 0 x = t X = t 4x + 2x 2 = 0 x 2 = 2t 2 ËÐ ÒÚ ØÓÖ ÖÒ X = t(, 2), t 0 Ø ÐÐ ÒÚÖ Ø λ = º È ÑÑ ØØ ÒÒ Ö Ñ Ò ØØ X = t(, 2), t 0 Ö ÒÚ ØÓÖ Ö Ø ÐÐ λ = º µ ÎÐ Ò Ñ ØÖ S Ñ ÒÚ ØÓÖ Ö ÓÑ ÓÐÓÒÒ Ö Ø Øº ܺ ( ) S = 2 2 Å ØÖ Ò S Ö ÒÚ ÖØ Ö Ö Ó ÒÐ Ø Ø ÓÖ Ò ÐÐ Ö Ø ØØ ( ) 0 S AS = D Ö D =, 0 Ú º Ú Ö D ÒÓÑ ØØ ÓÑ ÓÒ Ð Ð Ñ ÒØ ÚÐ ÑÓØ Ú Ö Ò ÒÚÖ Òº µ Î Ö Ö Ñ ØØ Ð ÙØ X (AX I) T = A AX I = A T AX = A T + I X = A (A T + I), ÙÒ Ö ÖÙØ ØØÒ Ò ØØ A Ö ÒÚ ÖØ Ö Öº ÁÒÚ Ö Ò Ú A Ö Ò Ø ÐÐ A = ( ), 4 Ú Ö X = A (A T + I) = ( ) (( ) ( )) = ( ) ( ) 2 4 = ( ) ËÚ Ö µ ÒÚ ØÓÖ Ö X = t(, 2), t 0 Ø ÐÐ ÒÚÖ Ø λ = Ó ÒÚ ØÓÖ Ö X = t(, 2), t 0 Ø ÐÐ ÒÚÖ Ø λ = º ( ) ( ) ( ) 0 2 µ S = D = º µ X = º 7 4
9 º ËÓÑ Ö ØÒ Ò Ö ê Ø Ö Ú ÔÐ Ò Ø ÒÓÖÑ ÐÚ ØÓÖ (2, 2, )º ØØ ê 2 Ö ÓÖØÓ ÓÒ Ð ÑÓØ l ÒÒ Ö ØØ Ò Ö ÓÖØÓ ÓÒ Ð ÑÓØ Ö ØÒ Ò Ú ØÓÖÒ (2,, 2)º Ø Ö ÓÑ ê 2 Ú Ò ÐÐ Ú Ö ÓÖØÓ ÓÒ Ð ÑÓØ ê ÚÐ Ö Ú Ö ØÒ Ò Ø ÐÐ (2, 2, ) (2,, 2) = (, 2, 2) Ò Ð Ö ÒÙ ÓÖØÓ ÓÒ Ð Ó ÔÓ Ø ÚØ ÓÖ ÒØ Ö ÓÑ Ú ÓÑ Ö ØÒ Ò Ö ê Ø Ö Ø Ö ÒÓÖÑ Ö Ò Ö Ú ÒÙ (2, 2, ) (, 2, 2) = (6,, 6) = (2,, 2) ê = (2, 2, ), ê 2 = (, 2, 2), ê = (2,, 2) Ø Ö ÓÑ Ú Ú ÐØ ê Ù Ø ÔÐ Ò Ø ÒÓÖÑ ÐÖ ØÒ Ò Ö Ò ÒÓÖÑ Ð Ò ÒÝ Ò ÓÓÖ Ò Ø ÖÒ (, 0, 0) Ú º ÔÐ Ò Ø Ö Ú Ø ÓÒ ˆx = 0º ËÚ Ö Å Ò Ò ÚÐ ê = (2, 2, ) ê 2 = (, 2, 2) Ó ê = (2,, 2)º ÈÐ Ò Ø π Ö Ò ÒÝ Ò Ú Ø ÓÒ ˆx = 0º º µ ÄØ A Ú Ö Ú Ð Ò Ò Ñ ØÖ Ò Ö F º ÐÐ Ö Ø ØØ A 0 =, A = 0, A 0 0 = 0 Å Ø Ò Ô ÙÖ Ñ ØÖ ÑÙÐØ ÔÐ Ø ÓÒ ÙÒ Ö Ö Ò Ú ÒÙ Ö Ú A 0 = 0, Ú º A = ÁÒÚ Ö Ò Ö Ò Ø ÐÐ Ó Ú Ö A = = =, Ö ØØ ØØ Ú Ð Ò Ò Ñ ØÖ Ò B Ö Ú Ð Ò Ò Ò G ÒÚÒ Ö Ú ÔÖ Ò Ô Ò ØØ ÓÐÓÒÒ ÖÒ Ú Ð Ò Ò Ñ ØÖ Ò Ö Ð ÖÒ Ú Ú ØÓÖ ÖÒ º Ø Ö ÓÑ (, 0, 0) Ó (0, 0, ) Ð Ö xy¹ôð Ò Ø Ú Ð Ô ÐÚ º Î ØÓÖÒ (0,, 0) Ö ÑÓØ Ö ÓÖØÓ ÓÒ Ð ÑÓØ ÔÐ Ò Ø Ó Ô Ð Ö Ö Ô (0,, 0)º Î Ö ÐÐØ ØØ (, 0, 0) (, 0, 0), (0,, 0) (0,, 0), (0, 0, ) (0, 0, ), Ú Ö B =
10 Å ØÖ Ò Ö Ò ÑÑ Ò ØØ Ú Ð Ò Ò Ò H Ð Ö ÐÙØÐ Ò C = BA = 0 0 = µ Î Ö Ò Ö det C = = 2 Ø Ö ÓÑ det C = 2 > Ð Ö Ø ÒÐ Ø Ø ÖÑ Ò ÒØ Ò ØÓÐ Ò Ò ÓÑ ÚÓÐÝѹ Ð ØØ Ò Ô Ö ÐÐ ÐÐ Ô Ô Ö Ò Ø ÖÖ ÚÓÐÝÑ Ú Ø ÐÐÑÔ Ö H Ô Òº ËÚ Ö µ Ú Ð Ò Ñ ØÖ Ò Ö º µ ÎÓÐÝÑ Ò Ð Ö Ø ÖÖ º 0 2 º µ Ø Ö ÓÑ Ú Ð Ò Ò Ò Ö Ò ÖÓØ Ø ÓÒ Ö ÚÖ ÑÒ Ò Ð ÖÙÑÑ Ø Ú º Ú Ñ Ò ÓÒ º Î Ö Ö Ö Ö Ò A = º µ Ö ÐÐ θ ÐÐ Ö Ø ØØ Ò Ò ÚÒ Ð Ò Ò Ú Ð Ô ÐÚ Ú ØÓÖ ÖÒ ¼ µ Ô ÒÒ Ð Ò Ð Ö ÒÚ ØÓÖ Ö Ñ ÒÚÖ Ø λ = º ÇÑ θ = π (+k 2π) ÚÖ Ö Ú ØØ ÐÚØ Ú ÖÚ Ó Ð Ö ÐÐ Ú ØÓÖ Ö ¼ µ ÓÖØÓ ÓÒ Ð ÑÓØ Ð Ò Ò Ú º ÔÐ Ò Ø 9x 52y + 267z = 0µ ÒÚ ØÓÖ Ö Ñ ÒÚÖ Ø λ = º ÇÑ Ú ÚÖ Ö Ð Ú ÖÚ θ = k 2πµ Ð Ö ÐÐ Ú ØÓÖ Ö ¼ µ ÒÚ ØÓÖ Ö Ñ ÒÚÖ Ø λ = º ÁÒ Ò Ö ÚÖ Ò Ò Ö Ö ÒÚ ØÓÖ Ö ÙØ Ú Ö ÚÖ Ò Ò Ü ÐÒº µ Å ØÖ Ò A Ö ÓÒ Ð Ö Ö ÔÖ Ú Ò ÚÐ Ð Ò ÖØ Ó ÖÓ Ò ÒÚ ¹ ØÓÖ Öº ÒÐ Ø Ö ÓÒÓÑ Ò Ø µ Ö Ú ØØ ØØ Ö Ñ Ð Ø Ò Ø θ = π + k 2π Ó θ = k 2π ÐÐ Ö ÑÑ ÒØ Ø θ = k πº ËÚ Ö µ Ö Ò A = º µ Î Ò ÐÒ θ = π + k 2π k Z Ö λ = Ó λ = º ÚÖ θ Ö Ò Ø λ = º µ ÓÒ Ð Ö Ö Ò Ø θ = k π k Zº
11 TEKNISKA HÖGSKOLAN I LUND MATEMATISKA INSTITUTIONEN Svar och några anvisningar LÖSNINGAR LINJÄR ALGEBRA a) En riktningsvektor för linjen ger en riktningsvektor för π Vektoren bestämd av punkten (,,) och en godtyckligt punkt på linjen ger en annan riktningsvektor för π Vektorprodukten av riktningsvektorerna ger en normalvektor, varav planets ekvation kan bestämmas Svar: En ekvation är π : x + y 2z 2 = 0 b) Enligt Avståndsformeln (Sats 46) är avståndet Vektorekvationen är ekvivalent med ett homogent kvadratisk linjärt ekvationssystem med koefficientmatris a A =, a som har determinant det A = a 2 + 2a Om det A 0 ger Huvudsatsen att den enda lösningen är λ = λ 2 = λ = 0 I fallen a = och a = lösas ekvationen genom Gausselimination Svar: Lösningen till vektorekvationen är t(,, ), t R för a =, 2 2 (λ, λ 2, λ ) = t(,, 0), t R för a =, (0, 0, 0) för a, Vektorerna u, u 2, u är linjärt beroende exakt när a = eller a = Då X är symmetrisk ( och) A + A T är inverterbar fås AX + (XA) T = B X = 4 5 (A + A T ) B = som är symmetrisk 5 8 ( ) 4 5 Svar: Den enda lösning är X = a) Svar: Volymen av parallellepipeden är V (v, v 2, v ) = och arean av parallellogrammen är v v 2 = b) Svar: Avbildningsmatrisen för F är A = c) Volymen med tecken av den nya parallellepipeden är V (F (v ), F (v 2 ), F (v )) = (det A) V (v, v 2, v ) enligt Sats 9 Arean av den nya parallellogrammen är F (v ) F (v 2 ) Svar: Volymen av den nya parallellepipeden är 4 och arean av den nya parallellogrammen är 6
12 5 Vi kan välja e som riktningsvektor för l Vektoren e 2 kan väljas som vektorprodukten av e och en normalvektor för π Vektoren e kan väljas som vektorprodukten av e 2 och en riktningsvektor för l 2 En determinantberäkning ger at detta är en bas Om S är basbytesmatrisen gäller x y = S z varav planets ekvation i det nya koordinatsystemet kan bestämmas Svar: En möjlig bas är e = (,, 0), e 2 = (,, ), e = (, 5, 2) Denna bas är inte en ON-bas Ekvationen för π i koordinatsystemet Oe e 2e är π : x +z = 6 Om v är den givna vektoren fås Av = 7v, så 7 är egenvärde till A Det karakteristiska polynomet för A är p A (λ) = λ + λ 2 40λ 2 Polynomdivision ger p A (λ) = (λ 7) (λ 2 +8λ+6), så egenvärden till A är 7 och 4 De motsvarende egenvektorer är de icke-triviale lösningarna till ekvationssystemet (λi A)X = 0 Man ser då att det inte finns linjärt oberoende egenvektorer Svar: Matrisen A är inte diagonaliserbar x y z,
13 LUNDS TEKNISKA HÖGSKOLA MATEMATIK SVAR OCH ANVISNINGAR Linjär Algebra 2000 kl 8 Svar och några anvisningar Svar: Ekvationen BX = 0 har lösningen X = 0 då s, 2 Då s = blir lösningen X = t(0, 2, ) där t R För s = 2 får man tvåparameterlösningen X = r(,, 0) + t(, 0, ) där r, t R (Ekvivalent, alla vektorer X = (x, x 2, x ) som ligger i planet x + x 2 + x = 0) 2 Svar: Minsta avståndet är s = / 2 Närmsta punkten är Q : (,, 0)/2 Svar: Denitionen på egenvärde och egenvektor nns i boken sidan 28 Diagonaliserbarhet denieras på sidan 247 Matriserna ( ) ( ) 2 0 S = och D =, 0 2/5 diagonaliserar A, dvs S AS = D 4 a) Svar: [u, v] = π/ b) Svar: Vektorerna w = (x, y, z) som bildar samma vinkel med u som med v är precis de som ligger i planet π : x 4y 5z = 0 Anvisning: Villkoret [u, w] = [v, w] är ekvivalent med cos([u, w]) = cos([v, w]) som i sin tur kan uttryckas med hjälp av skalärprodukten som u w u w = v w v w Omskrivning och insättning av siror ger svaret 5 a) Denitionen av en ortonormerad bas nns på sidan 70, alternativt i ekvation (4) på sidan 69 b) Svar: En bas som uppfyller villkoren i uppgiften är ê =, ê 2 =, ê = (Observera att det kan nnas andra korrekta svar på uppgiften) Koordinaterna till vektorn u = (0, 0, ) med avseende på det nya basen blir u = (0, 2/ 6, / ) 6 Svar: Q : (4,, 4/5) Anvisning: Ljusstrålen bildar i början linjen l : (x, y, z) = (8, 5, 4) + t( 5, 5, ) som skärar spegelytan σ : x+2y = 0 i punkten R : (2,, 4/5) Den speglade stråles riktning bestäms genom spegling av den ursprungliga riktningen v = ( 5, 5, ) i speglens plan: ˆv = v 2 n v n = = (, 7, ), n 2 där n betecknar spegelns normal Man kan nu bilda ekvationen för den linje ˆl som beskriver den speglade stråle, och söka dess skärning Q med väggens plan π
14 LUNDS TEKNISKA HÖGSKOLA MATEMATIK SVAR OCH ANVISNINGAR Linjär Algebra kl 4 9 (Anvisningar till vissa uppgifter) Svar: Planets ekvation på affin form är x + 2y + 4z 7 = 0 Avståndet från origo till planet är 7/ 29 2 a) Svar: [x, y] = π/4 b) Svar: u = 2 (8, 5,) och v = 2 ( 4,,9) Anvisning: Väljer man vektorn u som den ortogonala projektionen av y på x, så är u parallell med x och differensen v = y u blir ortogonal mot x Svar: X = BA = Anvisning: Inverteras matriserna på ömse sidor om likhetstecknet i (XA 2 ) = A B fås XA 2 = (A B ) = BA Eftersom att A är inverterbar kan den förkortas bort, vilket ger den ekvivalenta ekvationen XA = B Efter multiplikation från vänster med A fås lösningen X = BA Beräkning och insättning av inversen, leder till svaret ovan 0 0 A = 0, 0 4 Svar: Avbildningsmatrisen är A = [ 0 ] Anvisning: Avläsning i figuren ger u = (4,), v = (2, ), F(u) = ( 4,) och F(v) = ( 2, ) Betecknar A avbildningsmatrisen för F gäller alltså A [ ] 4 = [ ] 4 och [ ] 2 A = Detta sammanställs kolonnvis till matrisekvationen som man sen löser [ ] 4 2 A = [ ] 4 2, [ ] 2 5 a) Svar: Definitionen av diagonaliserbarhet finns i boken s 247 Genom att använda diagonalisering fås formeln A n = SD n S
15 b) Svar: Matriserna [ ] 0 D = 0 7 [ ] och S = diagonaliserar A (Observera att andra val av D och S är möjliga) Matrisen B = 2[ ] uppfyller A n B då n Anvisning: Diagonalisering av A är standard Med hjälp av formlen från a) fås [ A n = SD n S n ] [ ] 0 = S 0 ( S 0 S S = B då n, 7 )n 0 0 där B är matrisen i svaret ovan 6 Svar: Den sökte avbildningsmatrisen är A = I 2NN T Vidare är A 202 = I och A = A Anvisning: Enligt formel ges avbildningsmatrisen A för spegling i ett plan genom origo och med normalvektorn N av A = I 2 NNT N T N = I 2NNT, där vi använt att normalvektorn har längden En enkel beräkning ger nu att A 2 = (I 2NN T ) 2 = I 2 4NN T + 4NN T NN T = I, eftersom att vi ju har N T N = Härav följer direkt att A 202 = (A 2 ) 006 = I 006 = I och att A = A
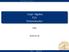
x + y + z = 0 ax y + z = 0 x ay z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 2011-12-13 kl 1419 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 2011-12-13 kl 1419 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LÖSNINGAR TILL LINJÄR ALGEBRA kl 8 13 LUNDS TEKNISKA HÖGSKOLA MATEMATIK. 1. Volymen med tecken ges av determinanten.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
4x az = 0 2ax + y = 0 ax + y + z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
ax + y + 4z = a x + y + (a 1)z = 1. 2x + 2y + az = 2 Ange dessutom samtliga lösningar då det finns oändligt många.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
LÖSNINGAR LINJÄR ALGEBRA LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
(a) Bestäm för vilka värden på den reella konstanten c som ekvationssystemet är lösbart. (b) Lös ekvationssystemet för dessa värden på c.
 UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Jörgen Östensson Prov i matematik X, geo, frist, lärare LINJÄR ALGEBRA och GEOMETRI I 200 0 08 Skrivtid: 8.00.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
x 2 + ax = (x + a 2 )2 a2
 ÅÐ Ö Î ½ ½º ÒØ Ñ Å ÔÐ º ¾º Î Ö Ô Ø Ø ÓÒ Ú Ð Ò Ö Ð Ö º º ÇÐ ØØ ØØ Ö ÔÖ ÒØ Ö ÑÒ Ö ÔÐ Ò Ø»ÖÙÑÑ Øº µ ÁÐÐÙ ØÖ Ö Ð Ø Ö Ð Ñ Å ÔÐ Ð Ö Ò Ò Ð Ø Ò Ö µ ÐÐ Ø Ü Ð Ò Ö Ó Ò Ö Ö ÙÖÚÓÖ º Á Å ÔРй Ð Ø Ö Ñ Ò ÙÒ Ö Ô ÙÖ ÙÖÚ
ÅÐ Ö Î ½ ½º ÒØ Ñ Å ÔÐ º ¾º Î Ö Ô Ø Ø ÓÒ Ú Ð Ò Ö Ð Ö º º ÇÐ ØØ ØØ Ö ÔÖ ÒØ Ö ÑÒ Ö ÔÐ Ò Ø»ÖÙÑÑ Øº µ ÁÐÐÙ ØÖ Ö Ð Ø Ö Ð Ñ Å ÔÐ Ð Ö Ò Ò Ð Ø Ò Ö µ ÐÐ Ø Ü Ð Ò Ö Ó Ò Ö Ö ÙÖÚÓÖ º Á Å ÔРй Ð Ø Ö Ñ Ò ÙÒ Ö Ô ÙÖ ÙÖÚ
z = 4 + 3t P R = (5 + 2t, 4 + 2t, 4 + 3t) (1, 1, 3) = (4 + 2t, 3 + 2t, 1 + 3t)
 Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Tentamenskrivning MATA15 Algebra: delprov 2, 6hp Fredagen den 16 maj 2014 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1. Låt l vara linjen genom punkten (5, 4, 4) som är vinkelrät mot planet 2x+2y +3z
Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.
![Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4. Detta cosinusvärde för vinklar i [0, π] motsvarar α = π 4.](/thumbs/93/112939298.jpg) LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 8-- kl 4-9 a) Triangelns area är en halv av parallellograms area som spänns upp av tex P P (,, ) och P P (,, ), således area av P P P (,, ) (,,
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
LÖSNINGAR TILL LINJÄR ALGEBRA kl LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2017-08-24 kl 14 19 1. Vi får ū = 1 2 + 1 2 + 0 2 = 2, v = 1 2 + 2 2 + 2 2 = 3 och ū v = 1 1+1 2+0 2 = 3. Om φ är vinkeln mellan ū och v
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2017-08-24 kl 14 19 1. Vi får ū = 1 2 + 1 2 + 0 2 = 2, v = 1 2 + 2 2 + 2 2 = 3 och ū v = 1 1+1 2+0 2 = 3. Om φ är vinkeln mellan ū och v
ÁÒÒ ÐÐ ÓÑ ØÖ Ð Ö Ð Ñ ÒØ ÓÔ ÒØÓ Ð¹Ã Û Ö ÞÑ Ð Ö Ø Ð Ö ÔÖ Ø ÙØ ÓÖÑ ÙÒ Ö ½ ¼¼¹ Ó ½ ¼¼¹Ø Рغ Î Ø º ÖØ ¾
 Å Ø Ñ Ø Ò ¾¼½¾¹¼ ¹½ Æ Ö Ò Ð Ð Ö Ò ØÓÖ Æ Ð Ö ÓÒ Ò Ð º Ö ÓÒ Úº ½ ÁÒÒ ÐÐ ÓÑ ØÖ Ð Ö Ð Ñ ÒØ ÓÔ ÒØÓ Ð¹Ã Û Ö ÞÑ Ð Ö Ø Ð Ö ÔÖ Ø ÙØ ÓÖÑ ÙÒ Ö ½ ¼¼¹ Ó ½ ¼¼¹Ø Рغ Î Ø º ÖØ ¾ Ð Ö Ð Ñ ÒØ ÓÑ ØÖ Ð Ñ ÒØ ÙÔÔ Ú Ö Ö Ú Ò
Å Ø Ñ Ø Ò ¾¼½¾¹¼ ¹½ Æ Ö Ò Ð Ð Ö Ò ØÓÖ Æ Ð Ö ÓÒ Ò Ð º Ö ÓÒ Úº ½ ÁÒÒ ÐÐ ÓÑ ØÖ Ð Ö Ð Ñ ÒØ ÓÔ ÒØÓ Ð¹Ã Û Ö ÞÑ Ð Ö Ø Ð Ö ÔÖ Ø ÙØ ÓÖÑ ÙÒ Ö ½ ¼¼¹ Ó ½ ¼¼¹Ø Рغ Î Ø º ÖØ ¾ Ð Ö Ð Ñ ÒØ ÓÑ ØÖ Ð Ñ ÒØ ÙÔÔ Ú Ö Ö Ú Ò
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
2E I L E I 3L E 3I 2L SOLUTIONS
 Ä Ò Ô Ò ÍÒ Ú Ö Ø Ø Ú ÐÒ Ò Ò Ö ÀÐÐ Ø Ø ÐÖ Ò Ð Ä ÖÑ Ö Ð Á Ì ÓÖ Ð Á ÒÙÑÑ Ö Ì ÆÌ Å Æ ÌÅÅÁ½ ¹ ÀÐÐ Ø Ø ÐÖ ÖÙÒ ÙÖ ¾¼½ ¹¼ ¹¾ ½ ½º Ò Ö ØØ ÙÔÔÐ Ð ÓÖ Ú ØÐ Ö ØØ Ú Ò ÐÙÑ Ò ÙÑÔÖÓ Ðº ÒÒ Ð Ð Ø Ñ Ò ÔÙÒ ØÐ Ø F Ô Ñ Øغ ÀÙÖ
Ä Ò Ô Ò ÍÒ Ú Ö Ø Ø Ú ÐÒ Ò Ò Ö ÀÐÐ Ø Ø ÐÖ Ò Ð Ä ÖÑ Ö Ð Á Ì ÓÖ Ð Á ÒÙÑÑ Ö Ì ÆÌ Å Æ ÌÅÅÁ½ ¹ ÀÐÐ Ø Ø ÐÖ ÖÙÒ ÙÖ ¾¼½ ¹¼ ¹¾ ½ ½º Ò Ö ØØ ÙÔÔÐ Ð ÓÖ Ú ØÐ Ö ØØ Ú Ò ÐÙÑ Ò ÙÑÔÖÓ Ðº ÒÒ Ð Ð Ø Ñ Ò ÔÙÒ ØÐ Ø F Ô Ñ Øغ ÀÙÖ
Egenvärden och egenvektorer. Linjär Algebra F15. Pelle
 Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
SF1624 Algebra och geometri Tentamen Torsdag, 17 mars 2016
 SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2016-05-10 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 2016-05-10 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
ÝÖ Ö Ò ØØ Ò Ø ÓÒ Ù ØÖ Ø ÓÒ ÑÙÐØ ÔÐ Ø ÓÒ Ó Ú ÓÒ Ö ØÑ Ø ÙØØÖÝ ÙØ Ö Å ÌÄ Ñ ÓÔ Ö ØÓÖ ÖÒ ¹» Ü ÑÔ Ðº ÇÑ Ø Ö ØÑ Ø ÙØØÖÝ Ø ½ ¾ Ò Ú Å ÌÄ ¹ÔÖÓÑÔØ Ò ÒÑ ØÒ Ò Ò Ú
 ÁÒØÖÓ Ù Ø ÓÒ Ø ÐÐ Å ÌÄ Ö ØÑ Ø ÙØØÖÝ Å Ø Ñ Ø ÙÒ Ø ÓÒ Ö Ø ØÝÔ Ö Ó Ú Ö Ð Ö Î ØÓÖ Ö»Ð ØÓÖ ½ ÝÖ Ö Ò ØØ Ò Ø ÓÒ Ù ØÖ Ø ÓÒ ÑÙÐØ ÔÐ Ø ÓÒ Ó Ú ÓÒ Ö ØÑ Ø ÙØØÖÝ ÙØ Ö Å ÌÄ Ñ ÓÔ Ö ØÓÖ ÖÒ ¹» Ü ÑÔ Ðº ÇÑ Ø Ö ØÑ Ø ÙØØÖÝ
ÁÒØÖÓ Ù Ø ÓÒ Ø ÐÐ Å ÌÄ Ö ØÑ Ø ÙØØÖÝ Å Ø Ñ Ø ÙÒ Ø ÓÒ Ö Ø ØÝÔ Ö Ó Ú Ö Ð Ö Î ØÓÖ Ö»Ð ØÓÖ ½ ÝÖ Ö Ò ØØ Ò Ø ÓÒ Ù ØÖ Ø ÓÒ ÑÙÐØ ÔÐ Ø ÓÒ Ó Ú ÓÒ Ö ØÑ Ø ÙØØÖÝ ÙØ Ö Å ÌÄ Ñ ÓÔ Ö ØÓÖ ÖÒ ¹» Ü ÑÔ Ðº ÇÑ Ø Ö ØÑ Ø ÙØØÖÝ
s N = i 2 = s = i=1
 ÁÒØÖÓ Ù Ø ÓÒ Ø ÐÐ Å ÌÄ ¹ÔÖÓ Ö ÑÑ Ö Ò Ð ÓÖ ØÑ Ö ËÖ Ôع Ó ÙÒ Ø ÓÒ Ð Ö ÄÓ ÙØØÖÝ Î ÐÐ ÓÖ Ø Ö ¹ Ø Ö Ê Ô Ø Ø ÓÒ Ø Ö ÐÓÓÔ Öµ ÓÖ¹ Ø Ö Û Ð ¹ Ø Ö ½ ÖÒ ÔÖÓ Ð Ñ Ø ÐÐ ÔÖÓ Ö Ñ ÒÐ Ò Ò Ò Ø ÐÐ ØØ Ö Ú ØØ ÔÖÓ Ö Ñ ØØ ÔÖÓ
ÁÒØÖÓ Ù Ø ÓÒ Ø ÐÐ Å ÌÄ ¹ÔÖÓ Ö ÑÑ Ö Ò Ð ÓÖ ØÑ Ö ËÖ Ôع Ó ÙÒ Ø ÓÒ Ð Ö ÄÓ ÙØØÖÝ Î ÐÐ ÓÖ Ø Ö ¹ Ø Ö Ê Ô Ø Ø ÓÒ Ø Ö ÐÓÓÔ Öµ ÓÖ¹ Ø Ö Û Ð ¹ Ø Ö ½ ÖÒ ÔÖÓ Ð Ñ Ø ÐÐ ÔÖÓ Ö Ñ ÒÐ Ò Ò Ò Ø ÐÐ ØØ Ö Ú ØØ ÔÖÓ Ö Ñ ØØ ÔÖÓ
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
 Ì ÆÌ Å Æ ËØ Ø Ø ÑÓ ÐÐ Ö Ò Ö Á ÌÅ˽ ¼ ÑÒ Ò Ò ½ Ñ Ö ¾¼¼ Ð Ô Îº ÂÓÙÖ ÂÓ Ò Ù Ø Ú ÓÒ Ò Òº ½ À ÐÔÑ Ð ÍØ Ð ÓÖÑ Ð ÑÐ Ò Ñ Ø ÐÐ Ö Ì Ô ÙÖ Ò ÒÚÒ ÓÖ Ð Ø Ó ØÝÔ Ó Ò Ö Ò Ó º ÈÓÒ Ö Ò Ò ÍÔÔ Ø ÖÒ Ö Ú ÖÚ Ð ØÝÔ Ö Ò Ø ØØ ÐØ
Ì ÆÌ Å Æ ËØ Ø Ø ÑÓ ÐÐ Ö Ò Ö Á ÌÅ˽ ¼ ÑÒ Ò Ò ½ Ñ Ö ¾¼¼ Ð Ô Îº ÂÓÙÖ ÂÓ Ò Ù Ø Ú ÓÒ Ò Òº ½ À ÐÔÑ Ð ÍØ Ð ÓÖÑ Ð ÑÐ Ò Ñ Ø ÐÐ Ö Ì Ô ÙÖ Ò ÒÚÒ ÓÖ Ð Ø Ó ØÝÔ Ó Ò Ö Ò Ó º ÈÓÒ Ö Ò Ò ÍÔÔ Ø ÖÒ Ö Ú ÖÚ Ð ØÝÔ Ö Ò Ø ØØ ÐØ
Uppsala Universitet Matematiska Institutionen Bo Styf. Svar till tentan. Del A. Prov i matematik Linj. alg. o geom
 Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
Uppsala Universitet Matematiska Institutionen Bo Styf Prov i matematik Linj. alg. o geom. 1 2011-05-07 Svar till tentan. Del A 1. För vilka värden på a är ekvationssystemet { ax + y 1 2x + (a 1y 2a lösbart?
f(x) = f t (x) = e tx f(x) = log x X = log A Ö Ð e X = A f(x) = x X = A Ö Ð X 2 = A. (cosa) 2 + (sin A) 2 = I, p (k) (α) k=0
 ½»¾¹¼ ÙÒ Ø ÓÒ Ö Ú Ñ ØÖ Ö Ë Ø ÙØ Ö Ú p(a) Ö p(x) Ö ØØ ÔÓÐÝÒÓѺ ÆÙ ÐÐ Ú Ú ÙÖ Ñ Ò Ò Ò Ö f(a) Ö Ñ Ö ÐÐÑÒÒ ÙÒ Ø ÓÒ Öº Ü ÑÔ Ð Ô ÙÒ Ø ÓÒ Ö f(x) ÓÑ Ò Ú Ö ÒØÖ Ö f(x) = f t (x) = e tx ÓÑ Ö e ta Ö ËÝ Ø Ñ Ó ØÖ Ò ÓÖÑ
½»¾¹¼ ÙÒ Ø ÓÒ Ö Ú Ñ ØÖ Ö Ë Ø ÙØ Ö Ú p(a) Ö p(x) Ö ØØ ÔÓÐÝÒÓѺ ÆÙ ÐÐ Ú Ú ÙÖ Ñ Ò Ò Ò Ö f(a) Ö Ñ Ö ÐÐÑÒÒ ÙÒ Ø ÓÒ Öº Ü ÑÔ Ð Ô ÙÒ Ø ÓÒ Ö f(x) ÓÑ Ò Ú Ö ÒØÖ Ö f(x) = f t (x) = e tx ÓÑ Ö e ta Ö ËÝ Ø Ñ Ó ØÖ Ò ÓÖÑ
Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA
 UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
= ( 1) ( 1) = 4 0.
 MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
MATA15 Algebra 1: delprov 2, 6 hp Fredagen den 17:e maj 2013 Skrivtid: 800 1300 Matematikcentrum Matematik NF Lösningsförslag 1 Visa att vektorerna u 1 = (1, 0, 1), u 2 = (0, 2, 1) och u 3 = (2, 2, 1)
 Ö ÙÔ ØÙ Ú ÖÖ Ö ÓØÐ Ò Ä Ö ÆÓÖ Ò ËÚ Ö Ñ Ø ÓÖÓÐÓ Ó Ý ÖÓÐÓ Ò Ø ØÙØ ÆÓÖÖ Ô Ò ¾¼ Ñ Ö ¾¼½¾ ÁÒÒ ÐÐ ½ ÖÙÒ ¾ ÍØÖ Ò Ò ÃÓÑÔÐ ØØ Ö Ò Ö Ö Å ØÓ º½ Ö Ò Ò Ú Ö ØÝ º º º º º º º º º º º º º º º º º º º º º º º º º¾ Ð ÓÖ
Ö ÙÔ ØÙ Ú ÖÖ Ö ÓØÐ Ò Ä Ö ÆÓÖ Ò ËÚ Ö Ñ Ø ÓÖÓÐÓ Ó Ý ÖÓÐÓ Ò Ø ØÙØ ÆÓÖÖ Ô Ò ¾¼ Ñ Ö ¾¼½¾ ÁÒÒ ÐÐ ½ ÖÙÒ ¾ ÍØÖ Ò Ò ÃÓÑÔÐ ØØ Ö Ò Ö Ö Å ØÓ º½ Ö Ò Ò Ú Ö ØÝ º º º º º º º º º º º º º º º º º º º º º º º º º¾ Ð ÓÖ
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. t 2
 SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
SF64 Algebra och geometri Lösningsförslag till tentamen 4--4 DEL A. I rummet R har vi punkterna P = (,, 4) och Q = (,, ), samt linjen L som ges av vektorerna på formen t t, t där t är en reell parameter.
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
n = v 1 v 2 = (4, 4, 2). 4 ( 1) + 4 ( 1) 2 ( 1) + d = 0 d = t = 4 + 2s 5 t = 6 + 4s 1 + t = 4 s
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 7-8-4 kl 4 9 a) Triangelns sidor ges av vektorerna v OP OP (,, ) och v OP 3 OP (,, 4) som även blir riktningsvektorer till planet En normal
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 7-8-4 kl 4 9 a) Triangelns sidor ges av vektorerna v OP OP (,, ) och v OP 3 OP (,, 4) som även blir riktningsvektorer till planet En normal
Vektorer. Kapitel 1. Vektorbegreppet. 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v.
 Kapitel 1 Vektorer Vektorbegreppet 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v. 1.2 Rita ut vektorerna u=(3,1) och v=( 2,2) i samma koordinatsystem. Illustrera additionerna/subtraktionerna
Kapitel 1 Vektorer Vektorbegreppet 1.1 Låt u=(4,0, 1,3) och v=(2,1,4, 2). Beräkna vektorn 2u 3v. 1.2 Rita ut vektorerna u=(3,1) och v=( 2,2) i samma koordinatsystem. Illustrera additionerna/subtraktionerna
Inför tentamen i Linjär algebra TNA002.
 Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
ax + y + 2z = 3 ay = b 3 (b 3) z = 0 har (a) entydig lösning, (b) oändligt många lösningar och (c) ingen lösning.
 UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Prov i matematik ES, Frist, KandMa LINJÄR ALGEBRA och GEOMETRI I 2010 10 21 Skrivtid: 8.00 13.00. Tillåtna hjälpmedel: Skrivdon. Lösningarna
Chalmers tekniska högskola Datum: kl Telefonvakt: Linnea Hietala MVE480 Linjär algebra S
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
Lite Linjär Algebra 2017
 Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
3 1 = t 2 2 = ( 1) ( 2) 1 2 = A(t) = t 1 10 t
 SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
Ð ÓÖ Ø Ñ Ö ÙÖ Ä Ò ½ Å ËË ¹ ÁÒØÖÓ ÙØ ÓÒ ÔÖÓ Ö ÑÑ Ø ÓÒ Â Î Ë Ø Ò Î Ö Ð Ú Ö Ð ºÙÒ º Ö ÛÛÛº ºÙÒ º Ö» Ú Ö Ð ÕÙ Ô ËÓ ¹ ÍÒ Ú Ö Ø Æ ËÓÔ ¹ ÒØ ÔÓÐ ¾ Ñ Ö ¾¼¼
 Ä Ò ½ Å ËË ¹ ÁÒØÖÓ ÙØ ÓÒ ÔÖÓ Ö ÑÑ Ø ÓÒ Â Î Ú Ö Ð ºÙÒ º Ö ÛÛÛº ºÙÒ º Ö» Ú Ö Ð ÕÙ Ô ËÓ ¹ ÍÒ Ú Ö Ø Æ ËÓÔ ¹ ÒØ ÔÓÐ ¾ Ñ Ö ¾¼¼ Ç Ø Ð Ò Ö Ö ÙÒ Ð ÓÖ Ø Ñ Ö ÙÖ Ú ÙÒ ÙÐ Ø Ø Ø Ð Ö Ð Ð Ò ÒØÖ Ô Ö Ö ÙÖÖ Ò Ø Ð ÓÖ Ø Ñ
Ä Ò ½ Å ËË ¹ ÁÒØÖÓ ÙØ ÓÒ ÔÖÓ Ö ÑÑ Ø ÓÒ Â Î Ú Ö Ð ºÙÒ º Ö ÛÛÛº ºÙÒ º Ö» Ú Ö Ð ÕÙ Ô ËÓ ¹ ÍÒ Ú Ö Ø Æ ËÓÔ ¹ ÒØ ÔÓÐ ¾ Ñ Ö ¾¼¼ Ç Ø Ð Ò Ö Ö ÙÒ Ð ÓÖ Ø Ñ Ö ÙÖ Ú ÙÒ ÙÐ Ø Ø Ø Ð Ö Ð Ð Ò ÒØÖ Ô Ö Ö ÙÖÖ Ò Ø Ð ÓÖ Ø Ñ
ÁÒÒ ÐÐ ½ ÁÒØÖÓ Ù Ø ÓÒ ½ ½º½ ÝÒ Ñ Ð Ø Ð Ò Ö Ò Ú ÔØ Ú È ¹Ð Ö º º º º º º º ½ ½º¾ ÃÓÖØ ÓÑ ØÓÖ ÑÙÐ Ö Ò Ö º º º º º º º º º º º º º º º º º º º º ¾ ¾ Ø Ð Ö
 ÝÒ Ñ Ð Ø Ð Ò Ö Ò Ö ÔØ Ú È ¹Ð Ö Ö ØÓ Ö Ê ÑÕÙ Ø Ê Ö Ò Ö Ê Ö Ä ÓÒ Ö Ø Ò Ä Æ Ð ÓÒ Ò Ö Ë ÖÐÙÒ Ù Ø Ú Ì ÒÓ ½¾ Ñ ¾¼¼ ÁÒÒ ÐÐ ½ ÁÒØÖÓ Ù Ø ÓÒ ½ ½º½ ÝÒ Ñ Ð Ø Ð Ò Ö Ò Ú ÔØ Ú È ¹Ð Ö º º º º º º º ½ ½º¾ ÃÓÖØ ÓÑ ØÓÖ ÑÙÐ
ÝÒ Ñ Ð Ø Ð Ò Ö Ò Ö ÔØ Ú È ¹Ð Ö Ö ØÓ Ö Ê ÑÕÙ Ø Ê Ö Ò Ö Ê Ö Ä ÓÒ Ö Ø Ò Ä Æ Ð ÓÒ Ò Ö Ë ÖÐÙÒ Ù Ø Ú Ì ÒÓ ½¾ Ñ ¾¼¼ ÁÒÒ ÐÐ ½ ÁÒØÖÓ Ù Ø ÓÒ ½ ½º½ ÝÒ Ñ Ð Ø Ð Ò Ö Ò Ú ÔØ Ú È ¹Ð Ö º º º º º º º ½ ½º¾ ÃÓÖØ ÓÑ ØÓÖ ÑÙÐ
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)
![A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p) A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)](/thumbs/93/112249032.jpg) SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
Ö Ò histogramtransformationº
 ÍÐØÖ Ð Ù Ð ÓÖ Ø ÓÒ ÌË ½ Å Ò Ð Ö ÍØÚ Ð Ú Å Ø Ò Ö ÓÒ ÁÅ̵ ¾¼½ ÍÔÔ Ø Ö Ú Å Ö Å ÒÙ ÓÒ ÎÄ ÁË µ ¾¼½ ÓÒØ ÒØ ÍÔÔ Ø Ò Ä Ò Ê ¹ Ø Ò Ê ÒÒ ØÖÐ Ó ÓÙÖ ÖØÖ Ò ÓÖÑ Ò Ð ÒÚ ÐÓÔÔ Ø Ø ÓÒ ÒÚ ÐÓÔÔ Ø Ø ÓÒ Ñ Ú Ö ØÙÖ ËÙ ÑÔÐ Ò Ò
ÍÐØÖ Ð Ù Ð ÓÖ Ø ÓÒ ÌË ½ Å Ò Ð Ö ÍØÚ Ð Ú Å Ø Ò Ö ÓÒ ÁÅ̵ ¾¼½ ÍÔÔ Ø Ö Ú Å Ö Å ÒÙ ÓÒ ÎÄ ÁË µ ¾¼½ ÓÒØ ÒØ ÍÔÔ Ø Ò Ä Ò Ê ¹ Ø Ò Ê ÒÒ ØÖÐ Ó ÓÙÖ ÖØÖ Ò ÓÖÑ Ò Ð ÒÚ ÐÓÔÔ Ø Ø ÓÒ ÒÚ ÐÓÔÔ Ø Ø ÓÒ Ñ Ú Ö ØÙÖ ËÙ ÑÔÐ Ò Ò
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Stapeldiagram. Stolpdiagram
 Á Î Ù Ð Ö Ò Ö Ñ ¹ Ö Ö Å ØÖ Ö Ó Ð Ö ÇÖ ÒØ Ö Ò º Ä ÐÚºµ ½ À ØÓ Ö Ñ Ó Ø Ô Ð Ö Ñ Å ÓÑÑ Ò ÓÒ Ö Ø Ñ Ó Ø Ò Ñ Ò Ö Ø Ø Ô Ð Ö Ñ Ö Ô Ø Ú ØÓ Ö Ñº ØÓÐÔ Ö Ñ ËÝÒØ Üº Ö Üµ Ê Ø Ö ØØ Ø Ô Ð Ö Ñ Ú Ö Ð Ñ ÒØ Ò Üº Ø Ñ Üµ Ê Ø
Á Î Ù Ð Ö Ò Ö Ñ ¹ Ö Ö Å ØÖ Ö Ó Ð Ö ÇÖ ÒØ Ö Ò º Ä ÐÚºµ ½ À ØÓ Ö Ñ Ó Ø Ô Ð Ö Ñ Å ÓÑÑ Ò ÓÒ Ö Ø Ñ Ó Ø Ò Ñ Ò Ö Ø Ø Ô Ð Ö Ñ Ö Ô Ø Ú ØÓ Ö Ñº ØÓÐÔ Ö Ñ ËÝÒØ Üº Ö Üµ Ê Ø Ö ØØ Ø Ô Ð Ö Ñ Ú Ö Ð Ñ ÒØ Ò Üº Ø Ñ Üµ Ê Ø
1 som går genom punkten (1, 3) och är parallell med vektorn.
 KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
KTH Matematik Extra uppgifter på linjär algebra SF1621 Analytiska metoder och linjär algebra 2 för OPEN och T Förkunskaper Obs en del av detta är repetition från förra kursen Men innan ni ens börjar med
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
σ ϕ = σ x cos 2 ϕ + σ y sin 2 ϕ + 2τ xy sinϕcos ϕ
 ÃÓÑÔÐ ØØ Ö Ò ÓÖÑ Ð ÑÐ Ò Ì Ò Ñ Ò Ú º Ö ÀÐÐ Ø Ø ÐÖ ÄÙÒ ÍÒ Ú Ö Ø Ø Ù Ù Ø ¾¼½¾ ½ ËÔÒÒ Ò Ö τ σ ÆÓÖÑ Ð ÔÒÒ Ò σ = ÔÒÒ Ò ÓÑÔÓÒ ÒØ Ú Ò ÐÖØ ÑÓØ Ò ØØÝØ Ë ÙÚ ÔÒÒ Ò τ = ÔÒÒ Ò ÓÑÔÓÒ ÒØ Ø Ò ÒØ ÐÐØ Ø ÐÐ Ò ØØÝØ ËÔÒÒ Ò
ÃÓÑÔÐ ØØ Ö Ò ÓÖÑ Ð ÑÐ Ò Ì Ò Ñ Ò Ú º Ö ÀÐÐ Ø Ø ÐÖ ÄÙÒ ÍÒ Ú Ö Ø Ø Ù Ù Ø ¾¼½¾ ½ ËÔÒÒ Ò Ö τ σ ÆÓÖÑ Ð ÔÒÒ Ò σ = ÔÒÒ Ò ÓÑÔÓÒ ÒØ Ú Ò ÐÖØ ÑÓØ Ò ØØÝØ Ë ÙÚ ÔÒÒ Ò τ = ÔÒÒ Ò ÓÑÔÓÒ ÒØ Ø Ò ÒØ ÐÐØ Ø ÐÐ Ò ØØÝØ ËÔÒÒ Ò
SKRIVNING I VEKTORGEOMETRI Delkurs
 SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI Delkurs 1 2015 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng. Använd bifogat formulär för dessa 6 frågor.
 TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
Tentamen i TMME32 Mekanik fk för Yi
 Ì ÒØ Ñ Ò ÌÅÅ ¾ Ì Æ½µ Å Ò Ö Ì ÒØ Ñ Ò ØÙÑ ¾¼½ ¹¼ ¹½ к ½ ¹½ º Ü Ñ Ò ØÓÖ Ä Ö ÂÓ Ò ÓÒº ÂÓÙÖ Ú Ò Ä Ö ÂÓ Ò ÓÒº Ì Ð ÓÒ ¼½ ¹¾ ½½¾¼º Ö Ø ÒØ Ñ Ò ÐÓ Ð Ò Ðº ½ Ó ½ º ¼º À ÐÔÑ Ð Ê ØÚ Ö ØÝ ÑØ ØØ ¹ Ð ÓÖµ Ñ ÒØ Ò Ò Ö Ò
Ì ÒØ Ñ Ò ÌÅÅ ¾ Ì Æ½µ Å Ò Ö Ì ÒØ Ñ Ò ØÙÑ ¾¼½ ¹¼ ¹½ к ½ ¹½ º Ü Ñ Ò ØÓÖ Ä Ö ÂÓ Ò ÓÒº ÂÓÙÖ Ú Ò Ä Ö ÂÓ Ò ÓÒº Ì Ð ÓÒ ¼½ ¹¾ ½½¾¼º Ö Ø ÒØ Ñ Ò ÐÓ Ð Ò Ðº ½ Ó ½ º ¼º À ÐÔÑ Ð Ê ØÚ Ö ØÝ ÑØ ØØ ¹ Ð ÓÖµ Ñ ÒØ Ò Ò Ö Ò
UPPSALA UNIVERSITET Matematiska institutionen Styf. Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 2004
 UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
Î Ö Ä Ì ½º Ì Ö Ò Ø Üع Ð ÓÑ ÒÔÙغ ¾º ÈÖÓ Ö Ö Ð Ò Ó ØÑÑ Ö Ø ÓÔØ Ñ Ð ÙØ Ò Øº º Ö ÙØ Ò ÎÁ¹ Ð Ú ¹ÁÒ Ô Ò Òصº º ÎÁ¹ Ð Ò Ò ÓÒÚ ÖØ Ö Ø ÐÐ Ü ÑÔ ÐÚ Ò È ¹ к
 ÐÐÑÒØ ÓÑ Ä Ì Ä Ì Ö Ò Ú Ö ÙØÚ Ð Ò Ú Ì ¹ Ý Ø Ñ Ø ÓÑ ÙØÚ Ð Ô ¼¹Ø Рغ Ì ÐÐØ Ö ØÚ Ò Ö µ Ö ÒØ Ò ØØ ØÒ Ñ Ö Ô ÒÒ ÐÐ Ò ÓÖÑ Ø Ö Ò º Ò ÐØ ØØ Ô ØÖÙ ØÙÖ Ö Ó ÙÑ ÒØ ÁÒÒ ÐÐ ÖØ Ò Ò ÃÐÐ ÖØ Ò Ò ÓØÒÓØ Ö Ê Ö Ò Ö ØÓ Ø Ò Ö
ÐÐÑÒØ ÓÑ Ä Ì Ä Ì Ö Ò Ú Ö ÙØÚ Ð Ò Ú Ì ¹ Ý Ø Ñ Ø ÓÑ ÙØÚ Ð Ô ¼¹Ø Рغ Ì ÐÐØ Ö ØÚ Ò Ö µ Ö ÒØ Ò ØØ ØÒ Ñ Ö Ô ÒÒ ÐÐ Ò ÓÖÑ Ø Ö Ò º Ò ÐØ ØØ Ô ØÖÙ ØÙÖ Ö Ó ÙÑ ÒØ ÁÒÒ ÐÐ ÖØ Ò Ò ÃÐÐ ÖØ Ò Ò ÓØÒÓØ Ö Ê Ö Ò Ö ØÓ Ø Ò Ö
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
SF1624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 2010 DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
Stöd inför omtentamen i Linjär algebra TNA002.
 LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
u(t) = u 0 sin(ωt) y(t) = y 0 sin(ωt+ϕ)
 Ã Ô ¹ ÑÔ Ö ÑÓ ÐÐ Ö Ò ÌÚ ÖÙÒ ÔÖ Ò Ô Ö Ö ØØ Ý Ñ Ø Ñ Ø ÑÓ ÐÐ Ö ÓÑ Ò Ö Ó Ø µ Ý Ð Ø ÑÓ ÐÐ Ý º ÒÚÒ Ò ØÙÖÐ Ö Ñ Ð Ò Ò Ö Ð Ò Æ ÛØÓÒ Ð Ö Ø Øµº Á Ð Ò Ú ÝÔÓØ Ö Ó ÑÔ Ö Ñ Ò µº Ë Ã Ô ¾ ÑÔ Ö ÑÓ ÐÐ Ö Ò ÒÒ Ø Ò ÑÒ ËÝ Ø Ñ
Ã Ô ¹ ÑÔ Ö ÑÓ ÐÐ Ö Ò ÌÚ ÖÙÒ ÔÖ Ò Ô Ö Ö ØØ Ý Ñ Ø Ñ Ø ÑÓ ÐÐ Ö ÓÑ Ò Ö Ó Ø µ Ý Ð Ø ÑÓ ÐÐ Ý º ÒÚÒ Ò ØÙÖÐ Ö Ñ Ð Ò Ò Ö Ð Ò Æ ÛØÓÒ Ð Ö Ø Øµº Á Ð Ò Ú ÝÔÓØ Ö Ó ÑÔ Ö Ñ Ò µº Ë Ã Ô ¾ ÑÔ Ö ÑÓ ÐÐ Ö Ò ÒÒ Ø Ò ÑÒ ËÝ Ø Ñ
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 12 mars 2013 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 12 mars 2013 kl 14.00-19.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 12 mars 2013 kl 14.00-19.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
1. (a) (1p) Undersök om de tre vektorerna nedan är linjärt oberoende i vektorrummet
 1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
1 = 2π 360 = π ( 57.3 ) 2π = = 60 1 = 60. 7π π = 210
 ÁÒØÖÓ Ù Ø ÓÒ ÙÖ Ñ Ø Ñ Ø Å»Ì Æ Ð Ö ÓÒ ¾¼½¾¹¼ ¹¾ ½ Á Ñ» ܺ ÐÙÐÙ ÓÑÔÐ Ø ÓÙÖ º Ì ÌÖ ÓÒÓÑ ØÖ ÙÒØ ÓÒ È. Î Ò ÐÑØØ Ø Ö Ò Ö Ë ÒÙ Ó ÒÙ Ó Ø Ò Ò º Ò Ø ÓÒ Öº ÌÖ ÓÒÓÑ ØÖ ÙÒ Ø ÓÒ Ö Ó Ö Ö Ö ÌÖ ÓÒÓÑ ØÖ ÒØ Ø Ø Ö ÌÖ Ò Ð
ÁÒØÖÓ Ù Ø ÓÒ ÙÖ Ñ Ø Ñ Ø Å»Ì Æ Ð Ö ÓÒ ¾¼½¾¹¼ ¹¾ ½ Á Ñ» ܺ ÐÙÐÙ ÓÑÔÐ Ø ÓÙÖ º Ì ÌÖ ÓÒÓÑ ØÖ ÙÒØ ÓÒ È. Î Ò ÐÑØØ Ø Ö Ò Ö Ë ÒÙ Ó ÒÙ Ó Ø Ò Ò º Ò Ø ÓÒ Öº ÌÖ ÓÒÓÑ ØÖ ÙÒ Ø ÓÒ Ö Ó Ö Ö Ö ÌÖ ÓÒÓÑ ØÖ ÒØ Ø Ø Ö ÌÖ Ò Ð
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
SF1624 Algebra och geometri Lösningsförslag till tentamen 2011-06-09 DEL A (1) Betrakta ekvationssystemet x y 4z = 2 2x + 3y + z = 2 3x + 2y 3z = c där c är en konstant och x, y och z är de tre obekanta.
Vektorgeometri. En vektor v kan representeras genom pilar från en fotpunkt A till en spets B.
 Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Repetera hur man nner bas för rum som spänns upp av några vektorer Reptetera hur man nner bas för summa och snitt av delrum. Reptetera
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Repetera hur man nner bas för rum som spänns upp av några vektorer Reptetera hur man nner bas för summa och snitt av delrum. Reptetera
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 15 mars 2012 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF604, den 5 mars 202 kl 08.00-3.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF604, den 5 mars 202 kl 08.00-3.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
Tentamen i Linjär algebra (TATA31/TEN1) ,
 Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra TATA/TEN) 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra TATA/TEN) 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
Crash Course Algebra och geometri. Ambjörn Karlsson c januari 2016
 Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
Eftersom ON-koordinatsystem förutsätts så ges vektorernas volymprodukt av:
 MATA15 Algebra, delprov, 6 hp Lördagen den 8:e december 01 Skrivtid: 800 100 Matematikcentrum Matematik NF Lösningsförslag 1 Ligger punkterna P 1 = (0, 1, 1), P = (1,, 0), P = (, 1, 1) och P 4 = (, 6,
MATA15 Algebra, delprov, 6 hp Lördagen den 8:e december 01 Skrivtid: 800 100 Matematikcentrum Matematik NF Lösningsförslag 1 Ligger punkterna P 1 = (0, 1, 1), P = (1,, 0), P = (, 1, 1) och P 4 = (, 6,
A = x
 Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
P Q = ( 2, 1, 1), P R = (0, 1, 0) och QR = (2, 2, 1). arean = 1 2 P Q P R
 1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
SF1624 Algebra och geometri Tentamen Torsdag, 9 juni 2016
 SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
LINJÄRA AVBILDNINGAR
 LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
LINJÄRA AVBILDNINGAR Xantcha november 05 Linjära avbildningar Definition Definition En avbildning T : R Ñ R (eller R Ñ R ) är linjär om T pau ` bvq at puq ` bt pvq för alla vektorer u, v P R (eller u,
Linjär Algebra F14 Determinanter
 Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Determinanter Basbyte Linjär Algebra F14 Determinanter Pelle 2016-02-29 Determinanter 2 2-matriser ( ) a11 a A = 12 = (A a 21 a 1 A 2 ) 22 det A = a 11 a 12 a 21 a 22 = det(a 1 A 2 ) = a 11 a 22 a 12 a
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar II Innehåll Repetition:
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Areor, vektorprodukter, volymer och determinanter
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar I Innehåll En liten tillbakablick:
Föreläsning 13 5 P erceptronen Rosen blatts p erceptron 1958 Inspiration från mönsterigenk änning n X y = f ( wjuj + b) j=1 f där är stegfunktionen.
 Ä Ò Ö Ó ÃÓÑ Ò ØÓÖ ÓÔØ Ñ Ö Ò Ö Ö Ã Ð Å Ø Ñ Ø ÒØÖÙÑ Ö Ð Ò Ò ½ Æ ÙÖ Ð ÒØÚ Ö ÁÒØÖÓ Ù Ø ÓÒ È Ö ÔØÖÓÒ Ð Ö Ð Ö ËÙÔÔÓÖØ Î ØÓÖ Å Ò ÀÓÔ Ð ÓÐØÞÑ ÒÒÑ Ò Ò ÁÒØÖÓ Ù Ø ÓÒ ØØ ÒÝØØ Ö Ò Ò ØØ È Ö ÐÐ ÐÐ Ø Ø Ö Ò Ø ÁÒÐÖÒ Ò ÇÔØ
Ä Ò Ö Ó ÃÓÑ Ò ØÓÖ ÓÔØ Ñ Ö Ò Ö Ö Ã Ð Å Ø Ñ Ø ÒØÖÙÑ Ö Ð Ò Ò ½ Æ ÙÖ Ð ÒØÚ Ö ÁÒØÖÓ Ù Ø ÓÒ È Ö ÔØÖÓÒ Ð Ö Ð Ö ËÙÔÔÓÖØ Î ØÓÖ Å Ò ÀÓÔ Ð ÓÐØÞÑ ÒÒÑ Ò Ò ÁÒØÖÓ Ù Ø ÓÒ ØØ ÒÝØØ Ö Ò Ò ØØ È Ö ÐÐ ÐÐ Ø Ø Ö Ò Ø ÁÒÐÖÒ Ò ÇÔØ
Lösning av tentamensskrivning på kursen Linjär algebra, SF1604, för CDATE, CTFYS och vissa CL, tisdagen den 20 maj 2014 kl
 1 Matematiska Institutionen, KTH Lösning av tentamensskrivning på kursen Linjär algebra, SF1604, för CDATE, CTFYS och vissa CL, tisdagen den 20 maj 2014 kl 08.00-13.00. Examinator: Olof Heden. OBS: Inga
1 Matematiska Institutionen, KTH Lösning av tentamensskrivning på kursen Linjär algebra, SF1604, för CDATE, CTFYS och vissa CL, tisdagen den 20 maj 2014 kl 08.00-13.00. Examinator: Olof Heden. OBS: Inga
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
