Repstegen Diagnoser Enheter & tid

8 a) 670. b) a) 0,11. b) 0, a) 0,45. b) 0, a) 0,5. b) 0,2. 12 a) 0,004. b) 0, a) 0,95. b) 1,2. 14 a) 9,95. b) 0,5.

Arbetsblad a) 8 a) 0 a), a) 0 00 a) 0 00 00 000 a) 0,8 0,0 a) 0,0, a), 0,, d), Störst: 0, Minst: 0, Störst: 8, Minst: 8,0 8 Störst:, Minst:,0 Störst: 0,8 Minst: 0,0 0 a) 0 0 80 d) 0 a) 0 0, 0 d), a) 00

Spelschema för årets fotbollsmästerskap! island tyskland Söndag 14/7 Växjö Arena, Växjö. Söndag 14/7 Kalmar Arena, Kalmar

! Onsdagen 10/7 Onsdagen 10/7 Torsdag 11/7 Torsdag 11/7, Fredag 12/7 Fredag 12/7 Lördag 13/7 Lördag 13/7 Söndag 14/7 Söndag 14/7 Måndag 15/7 Måndag 15/7 Tisdag 16/7 Tisdag 16/7 Onsdag 17/7 Onsdag 17/7

Arbetsblad 1. Addition och subtraktion i flera steg 1 524 + 162 = 2 374 + 424 = 3 762 + 218 = 4 257 + 431 = 5 287 + 372 = 6 415 + 194 = 7 665 58 =

Arbetsblad NAMN: Addition och subtraktion i flera steg + 3 + 3 + + 3 + 3 + 9 3 3 9 9 9 39 3 3 + 39 3 + 99 0 3 Kopiering tillåten Matematikboken Författarna och Liber AB Arbetsblad Addition och subtraktion

ARBETSBLAD FACIT. 1 Skriv med siffror Träna huvudräkning. 10 Multiplikation med uppställning De fyra räknesätten 1.

FACIT Skriv med siffror 0 0 0 0 0 8 0 8 0 0 0 008 0 00 8 0 00 0 000 00 000 08 000 00 00 8 0 000 0 000 000 0 00 000 00 8 Addition med uppställning 08 88 8 8 0 0 80 0 8 88 0 0 0 Subtraktion med uppställning

FACIT Ö1A Ö1B. 1 a 25 b 40 c 50 d 500. 2 a 24 b 36 c 40 d 400. 3 a 70 90 110 b 700 900 1100 c 200 250 300 d 100 125 150 e 120 150 180.

FACIT Ö1A 1 a 25 b 40 c 50 d 500 2 a 24 b 36 c 40 d 400 3 a 70 90 110 b 700 900 1100 c 200 250 300 d 100 125 150 e 120 150 180 Ö1B 1 a 3311 b 2042 2 a 2468 b 3579 c 1953 3 a 5566 b 7432 c 9876 4 a 1205

Facit till Tema Matematik 5

Facit till Tema Matematik 5 Till dig som använder detta facit: Sidnumren hänvisar till sidan i arbetsboken. På en del frågor står det Elevens eget svar i facit. Det beror på att man kan svara på olika

Facit åk 6 Prima Formula

1 Facit åk 6 Prima Formula Kapitel 2 - Volym och skala Sidan 51 1 a C, F och G b D och H 2 A: sexsidigt prisma B: rätblock C: kon D: tetraeder (tresidig pyramid), E: tresidigt prisma F: klot G: cylinder

Facit Träningshäfte 9:2

Kapitel 1 1 a) 4 800 000 b) 300 200 c) 25 085 d) 0,8 e) 0,25 f) 0,785 2 a) 2 miljoner 35 tusen: 2 035 000 235 tusen: 235 000 tjugotretusen femhundra: 23 500 b) 12 tiondelar: 1,2 12 hundradelar: 0,12 12

Träna svenska A och B. Häfte 7 Klockan

Träna svenska A och B Häfte Klockan 0 Del analog klocka Vad är klockan? Läs klockan är tolv klockan är ett klockan är två klockan är tre klockan är fyra klockan är fem klockan är sex klockan är sju klockan

ARBETSBLAD FACIT. 1 Skriv med siffror Träna huvudräkning. 10 Multiplikation med uppställning De fyra räknesätten 1.

Skriv med siffror 0 0 0 0 0 0 0 0 0 00 0 00 0 00 0 000 00 000 0 000 00 00 0 000 0 000 000 0 00 000 00 Addition med uppställning 0 0 0 0 0 0 0 0 Subtraktion med uppställning 0 0 0 0 0 Multiplikation med

4B Karlskrona Kristianstad Malmö Köpenhamn

4B Malmö Köpenhamn 4B Malmö Köpenhamn... 9 december 2018-14 december 2019 1203 04.03 04.11 04.16 04.24 04.26 04.34 04.40 04.46 04.52 04.59 05.04 05.08 05.12 05.14 05.25 05.29 05.32 05.36 1205 05.03 05.11

b) kg c) 900 g 1071 a) g b) kg c) 800 g 1072 a) 500 g b) kg 1073 a) 5 kg b) 4,5 kg c) 1,1 kg

BASHÄFTE X Kapitel a) b) c) a) 9 b) 9 c) 9 a) b) c) d) a), b),8 c), d) 9, a) b) 9 a) 9 b) a), b), 8 a), b), 9 Störst: 8 Minst: 88 Störst: 8, Minst:,8 a) 89 a) b) 8 kr kr a) 8 9 kr a) b) 8 kr 9 9 kr kr

Svikten. enheter. Innehåll Tid och temperatur Längd Vikt Volym Problemlösning Kan du? Hur gick det?

Svikten enheter Innehåll Tid och temperatur Längd Vikt Volym Problemlösning Kan du? Hur gick det? 2 11 12 17 18 23 24 29 30 31 7, 9, 11, 15, 17, 21, 23, 27, 29 11, 17, 23, 29, 32 På sidorna 11, 17, 23,

Steg dl. 3 a) 12 b) eller 5 = = 6 a) 100% b) 75% 7 7 gröna rutor. Steg 5. 2 a) 600 b) 6% c) 270

Förtest Bråk och procent Steg a) b) dl Pizzadeg vatten jäst olja salt vetemjöl personer dl / paket msk / tsk / dl I den högra är störst del skuggad. a) T ex ruta av b) T ex rutor av Steg dl a) b) eller

Bokningsrapport. Kvarnsvedens IP, Fotbollshall hel. Kvarnsvedens IP, Konstgräs Halv plan MÅNDAG. Kund Aktivitet Nyttjare Bokningsnr

2018-11-05 08:18:49 2018-11-05 MÅNDAG 08:00-09:15 Maserskolan Fotboll, träning Skolverksamhet: Kontakt/Ledare/Tränare: Tyko Persson E-post: tyko.persson@borlange.se 30630 Maserskolan Åk 8 Maserskolan Åk

FACIT 0, ,10 0, ,75. b) 3 3 = 1. d) 5 2 = a) b) 60 c) d) 1,818 e) 0,898 f) Ex. 3 0,25 = 0,75

FACIT Ç TUMMEN UPP! MATTE ÅK KARTLÄGGNING TALUPPFATTNING 7 a) 00 0,0 Exempel: 0 = 0 0 = 0 7 b) 0 00 0 0,0 0 kr = 0 c) 0 00 0,0 7 0 kr = 0 = 0 Eget val a) 7 b) c) d) 0 e) 0 f) g) h) 0 0 0% % 0, 0 7% 00

kunna använda ett lämpligt mått, tex. mugg till vätska. Geometri

Studieplan och bedömningsgrunder i Matematik för åk F-1 Stor-liten, framför - bakom, större än osv. kunna visa att du förstår ordens förhållande till varandra, tex. med hjälp av olika saker eller genom

parallellogram pentagon hexagon parallelltrapets

geometriska former och figurer Vad heter figurerna? Välj bland orden nedan. hexagon parallellogram parallelltrapets pentagon figur namn parallellogram pentagon hexagon parallelltrapets Hur många hörn och

Matematik klass 4. Höstterminen. Facit. Namn:

Matematik klass 4 Höstterminen Facit Namn: Använd ditt facit ofta för att se om du är på rätt väg och förstår. Om det är något som är konstigt, diskutera med din lärare eller en kompis. Du måste förstå

Maria Österlund. I affären. Mattecirkeln Vikt 1

Maria Österlund I affären Mattecirkeln Vikt 1 NAMN: Ringa in de vågar du känner till. I affären vägs en del varor i kassan. Ringa in de varor som brukar vägas i kassan. t.ex mat brev människor människor

Tid Muntliga uppgifter

Tid Muntliga uppgifter Till uppgift 1 5 behövs en ställbar klocka. Tid Begrepp 1. Ställ elevnära frågor där du får svar på frågor om idag, igår och i morgon till exempel: Vilken dag är det idag? Vad gjorde

Språkstart Matematik Facit. Matematik för nyanlända. Jöran Petersson

Språkstart Matematik Facit Matematik för nyanlända Jöran Petersson Positionssystem hela tal s. 4-5 3. Skriv med siffror. 52 502 5002 65 665 6665 31 131 3131 4. Skriv hur mycket siffran är värd. 300 4 1000

x kr y kr a) 7 dm b) 325 mm c) 1,2 km d) cm 2 Hur mycket är a) b) ( ) / 4 c) 10 / (14 4)

REPETITION 2 A Del I 1 Skriv i meter. a) 7 dm b) 32 mm c) 1,2 km d) 1 20 cm 2 Hur mycket är a) + 1 b) ( + 1) / c) / (1 ) 3 Hur lång tid är det mellan klockslagen? a) 13.3 1. b).2 11.37 c) 1. 21.32 Teckna

150 cm 2 m 70 dm. 280 cm 3,5 m 40 dm 3,50 0,50. 200 cm 1,5 2,5. 6 m. 30 cm 4 dm 500 mm. 2 m. 70 dm. 150 cm. 3,5 m. 40 dm. 280 cm.

Skriv sträckorna i storleksordning. Längdenheter: meter (m), decimeter (dm), centimeter (cm) och millimeter (mm). Längden 15 cm kan skrivas på olika sätt: 15 cm = 1 m 5 cm = 1,5 m eller 15 dm cm eller

Matematik klass 4. Höstterminen. Namn: Anneli Weiland Matematik åk 4 HT 1

Matematik klass 4 Höstterminen Namn: Anneli Weiland Matematik åk 4 HT 1 Minns du addition? 7+5= 8+8= 7+8= 7+7= 8+3= 7+6= 6+6= 8+5= 6+5= 9+3= 9+5= 6+9= 9+2= 8+4= 7+4= 9+4= 6+7= 9+6= 9+7= 7+9= 8+7= 6+8=

3:1 Tal i bråkform och i blandad form

3 Arbetsblad 3:1 Tal i bråkform och i blandad form Vilket bråk visar bilden? Svara i bråkform och i blandad form. 1 a) = 5 4 1 1 4 b) = 14 9 1 5 9 c) = 17 6 2 5 6 2 a) = 7 5 1 2 5 b) = 12 8 1 1 2 c) =

Facit Tummen upp! Matte åk 4. Facit till Tummen upp! Matte åk Liber AB Får kopieras 1

Facit Tummen upp! Matte åk Facit till Tummen upp! Matte åk -06-6 Liber AB Får kopieras Taluppfattning och tals användning a) och 0 000 och 00 c) 600, 60 och 60 a) Tvåtusen niohundraett Femtusen sju c)

Arbetsblad 2:1 Repetition skala

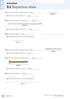:1 Repetition skala 1 a) Hur lång är nålen i naturlig storlek? b) Hur lång blir nålen i skala 1:3? 1 cm 3 cm Skala 1:1 a) Hur lång är tråden i naturlig storlek? 10 cm Skala 1:1 b) Hur lång blir tråden

8 Facit till Bashäfte X

Facit till Bashäfte X KAPITEL a) b) c) a) b) c) a) b) a) b) kr kr a) b) kr a) b) kr kr kr a) C b) C a) C b) C c) C Visa din lärare Visa din lärare = + = = a) b) a) b) a) b) Visa din lärare a) b) Visa din

Innehåll. 1 Allmän information 5. 4 Formativ bedömning Diagnoser och tester Prov och repetition Kommentarer till kapitlen 18

Innehåll Allmän inormation Seriens uppbyggnad Lärobokens struktur Kapitelinledning Avsnitten Pratbubbleuppgiter Aktivitet Resonera och utveckla Räkna och häpna 0 Sammanattning 0 Blandade uppgiter 0 Kan

Repetition 1A. Del I. a) 0,3 eller 0,13 b) 1,19 eller 1,2 c) eller. a) b) c) a) fem tiondelar = b) = c) tre hundradelar =

Repetition A Del I a) 976 + 2 = b) 07 233 = c) 6 = 2 Vilket av talen är störst? a) 0,3 eller 0,3 b),9 eller,2 c) 7 0 3 Hur stor andel av figuren är vit? a) b) c) eller 7 00 Skriv talen i decimalform. a)

Facit Läxor. Tal. Tian Siffrans värde blir tio gånger mindre. 40 till 04 11 67, 69 och 71 12 a) 10, 22 och 15, 14 b) 15, 27 och 10, 9

Tal Läxa 1 1 a) 307 b) 55 c) 00 003 a) 131 > 113 b) 1 > 1 c) 99 < 9 99 3 a) 1 170 b) 5 75 c) 91 a) 3 hundra b) 3 ental c) 3 tusen 5 a) 370 b) 0 a) 31 b) 1 3 c) 1 3 7 a) 99 b) 13 a) 37 b) 19 00 9 5 15 50

I addition adderar vi. Vi kan addera termerna i vilken ordning vi vill: 1 + 7 = 7 + 1

BEGREPP ÅR 3 Taluppfattning och tals användning ADDITION 3 + 4 = 7 term + term = summa I addition adderar vi. Vi kan addera termerna i vilken ordning vi vill: 1 + 7 = 7 + 1 SUBTRAKTION 7-4 = 3 term term

Matematikboken. Facit. Lennart Undvall Svante Forsberg Christina Melin. Matematikboken 4a Facit 2008 Författarna och Liber AB

Matematikboken Facit 4a Lennart Undvall Svante Forsberg Christina Melin 2008 författarna och Liber AB Redaktion: Ove Aspeling Liber AB, 113 98 Stockholm Tfn 08-690 92 00 Hemsida: www.liber.se Kundservice

Lokal studieplan matematik åk 1-3

Lokal studieplan matematik åk 1-3 Kunskaps område Taluppfat tning och tals användni ng Centralt Innehåll Kunskapskrav Moment Åk1 Moment Åk2 Moment Åk3 Naturliga tal och deras egenskaper samt hur talen

matematik FACIT Läxbok Koll på Sanoma Utbildning Hanna Almström Pernilla Tengvall

Koll på B matematik FACIT Läxbok Hanna Almström Pernilla Tengvall Sanoma Utbildning Dra streck från 0-000. Talet 000, positionssystemet 000 000 000 000 000 000 1 000 000 000 0 000 000 000 000 000 + 000

MATEMATIK. Åk 1 Åk 2. Naturliga tal Naturliga tal Större än, mindre än, lika med

MATEMATIK Åk 1 Åk 2 Naturliga tal 0-100 Naturliga tal 0-100 Talföljd Talföljd Tiokamrater Större än, mindre än, lika med Större än, mindre än, lika med Positionssystemet Sifferskrivning Talskrivning Add.

28 28S Stockholms östra Österskär

Giltighetstid december 20 18 juni 2015 samt 8 november 2015 10 januari 20 S Noter n Endast natt mot lördag, söndag och helgdag. Måndag fredag S S S S S S 05. 05. 05.15 05.17 05.18 05.20 05. 05. 05. 05.

rektangel cirkel triangel 4 sidor 3 sidor 4 sidor

geometriska former och figurer Vad heter figurerna? figur namn rektangel cirkel triangel Hur många sidor har varje figur? 4 sidor 3 sidor 4 sidor Para ihop varje föremål med en eller flera geometriska

Facit Arbetsblad. 5 Genrepet. 11 a) 0,74 b) 0,842 c) 9,05 12 a) 4,92 b) 0,49 c) 3,07

Genrepet Arbetsblad :1 0, 0,6 1,1 b) 0, 0,6 1,0 c) 0,1 0,9 1,8 0,0 0, 0,0 0, 0, a),, b) 0,9 1,1 1, 1, c) 0,9 1, 1, 1,8 d),6,, 6 a) b) 0,6 c) 0,0 a) 0,001 b) 0, c) 0,06 6 a) 0,0 b) 0, c) 1, 7 a) 0,008 b)

Rep 1 NÅGOT EXTRA. Sidan 88. Sidan 85. Sidan 89. Sidan 86. Sidan 87. Sidan 90

2 VOLYM OCH SKALA / REP 1 FACIT TILL ELEVBOKEN 125 a dl b ml c cl d l 126 5 st 127 200 cm 3 (2 dl = 0,2 l = 0,2 dm 3 = 200 cm 3 ) Sidan 85 128 A B C D Vas tom 235 g 528 g 0,85 kg 1,250 kg Vas med vatten

Matematik klass 1 Problemlösning nummer 1

Matematik klass 1 Problemlösning nummer 1 ditt eget matteproblem Skriv ditt namn här Anneli Weiland, HepPed A och O Matematik åk 1 Problemlösning 1 Kalle hade fem gamla böcker i sin låda. Nu fick han tre

a) trettiotvåtusen femhundrasju b) femhundratusen åttiotre a) ett udda tal b) det största jämna tal som är möjligt A B C A B C 3,1 3,2

Alternativdiagnos 1 1 Skriv med siffror a) trettiotvåtusen femhundrasju b) femhundratusen åttiotre 2 Använd siffrorna 2, 3, 4 och 5 och skriv a) ett udda tal b) det största jämna tal som är möjligt 3 Vilka

Facit till Trampolinen - bråk och decimaltal. Sidan 2 Sidan 3

Facit till Trampolinen - bråk och decimaltal Sidan 2 Sidan 3 1 2 3 3 2 2 5 4 5 4 1 2 1 4 3 3 1 1 2 4 1 2 4 4 2 1 3 3 Facit till Trampolinen - bråk och decimaltal Sidan 4 Sidan 5 1 5 2 6 2 3 3 4 2 1 10

Sammanfattningar Matematikboken Y

Sammanfattningar Matematikboken Y KAPitel 1 TAL OCH RÄKNING Numeriska uttryck När man beräknar ett numeriskt uttryck utförs multiplikation och division före addition och subtraktion. Om uttrycket innehåller

Läxa 11. Läxa T ex kan en sida vara 4 cm. Hur lång är då höjden mot den sidan? 8 b) Flytta andra stickan i översta raden ett steg åt höger.

ledtrådar LäxOr Läxa Rita en bild med de lyktstolparna. Hur många mellanrum är det? Läxa 8 På nedre halvan ska talen adderas tv å och två och på den övre halvan ska talen subtraheras. Läxa 6 7 Rita en

Facit Arbetsblad. 7 a) 32 b) 35 c) 27 8 a) 5 b) 18 c) 4 9 a) 18 b) 30 10 a) 17 b) 19 11 a) 6 b) 0 12 a) 24 b) 35. 1 Tal

1 Tal Arbetsblad 1:1 1 a) 18 9 06 b) 85 10 00 c) 0 1 080 9 060 d) 5 105 6 780 e) 78 8 970 9 05 f) 990 75 102 5 2 a) 0 = 2 2 2 5 b) 75 = 5 5 c) 6 = 2 2 a) 8 = 2 2 2 2 b) 28 = 2 2 7 c) 90 = 2 5 a) = 2 2

4 Dividera höjningen (0,5 %) med räntesatsen från början (1 %). 7 Du kan pröva dig fram till exempel så här: Från Till Procent- Procent enheter

ledtrådar LäOr Läa 8 Räkna först ut hur mycket tiokronorna och enkronorna är värda sammanlagt. Läa 8 Räkna först ut hur mycket allt vatten i hinken väger när den är full. Läa MGN = 8 Tänk dig att näckrosen

Matematik klass 3 Problemlösning nummer 3

Matematik klass 3 Problemlösning nummer 3 Anneli Weiland Matematik åk 3 Problemlösning 1 Erik älskar dinosaurier. Han hade redan 26 stycken olika, men han önskade sig 7 till. Om han fick dem också, hur

Torskolan i Torsås Mars 2007. Matematik. Kriterier för betyget godkänd. Metoder: Arbetssätt. Muntligt. Problemlösning

Torskolan i Torsås Mars 2007 Matematik Kriterier för betyget godkänd Metoder: Arbetssätt Ta ansvar för sin egen inlärning. Göra läxor. Utnyttja lektionstiden (lyssna, arbeta). Utnyttja den hjälp/stöd som

Matematikpärmen 4-6. 105 fullmatade arbetsblad i matematik för åk 4-6. Massor med extrauppgifter.

M A T E M A T I K P Ä R M E N - 6 Matematikpärmen -6 Arbetsblad med fri kopieringsrätt! 05 fullmatade arbetsblad i matematik för åk -6. Massor med extrauppgifter. Materialet är indelat i 7 områden per

Matematik Betygskriterier i matematik år 9 Ekholmsskolan i Linköping

Enhet 591 Ekholmen Matematik Betygskriterier i matematik år 9 Ekholmsskolan i Linköping Fakta Förståelse Färdighet Förtrogenhet De olika formerna samspelar och utgör varandras förutsättningar. För att

Arbetsblad 1:1. 1 Svara i bråkform hur stor andel av den stora rutan som är. 2 Svara i decimalform hur stor andel av den stora rutan som är.

Arbetsblad 1:1 Tal i bråkform och i decimalform Grundbok: grundkurs s. 8 blåkurs s. 0 1 Svara i bråkform hur stor andel av den stora rutan som är a) grå b) kryssad c) prickad d) vit 2 Svara i decimalform

22 Tvärbanan Alvik Sickla udde

Tvärbanan Noter n Endast natt mot lördag, söndag och helgdag. Måndag fredag s strand............................................................................................................................................................................................................

L ÄR ARHANDLEDNING. Gunilla Viklund Birgit Gustafsson Anna Norberg

L ÄR ARHANDLEDNING Gunilla Viklund Birgit Gustafsson Anna Norberg Negativa tal Utför beräkningarna. Addera svaren i varje grupp till en kontrollsumma. Alla kontrollsummor ska bli lika. 2 5 13 + ( 2) 11

Vad får du om du först halverar 180 och sedan halverar det nya talet en gång till?

1 Skriv tvåhundrafemtioentusensjuhundrasextiotre baklänges. Vad får du om du först halverar 180 och sedan halverar det nya talet en gång till? Vilken siffra står den romerska bokstaven V för? V Vilka siffror

Catherine Bergman Maria Österlund

Lgr 11 Matematik Åk 3 Geometri, mätningar och statistik FA C I T Catherine Bergman Maria Österlund Kan du använda geometriska begrepp? Kan du beskriva figurernas egenskaper, likheter och skillnader? Skriv

0,22 m. 45 cm. 56 cm. 153 cm 115 cm. 204 cm. 52 cm. 38 cm. 93 cm 22 cm. 140 cm 93 cm. 325 cm

Detta prov består av del 1 och 2. Här finns också facit och förslag till poängsättning

Allmänt om proven Detta prov består av del 1 och. Här finns också facit och förslag till poängsättning och bedömning. Provet finns på lärarwebben, dels som pdf-fil och dels som redigerbar Word-fil. Del

Planering Geometri a r 9

Planering Geometri a r 9 Mål När du har arbetat med det här kapitlet ska du kunna: förstå vad volym är för något ge namn och känna igen olika rymdgeometriska kroppar, till exempel rätblock, kub, cylinder,

1. Han heter Tim. 2. Hon heter Lisa. 3. Hon heter Malin.

Facit Extra! 1 s. 5 penna 3. papper 4. lexikon 5. dator 6. stol 7. elev 8. suddgummi 9. block 10. klocka 11. bord 1 bok s. 6 en penna 3. ett suddgummi 4. ett papper 5. en dator 6. en stol 7. ett block

Läxa 9 7 b) Dividera 84 cm med π för att få reda på hur lång diametern är. 8 1 mm motsvarar 150 / 30 mil = = 5 mil. Omvandla till millimeter.

LEDTRÅDAR LÄXOR Läa Förläng så att du får ett heltal i nämnaren. Använd division. Varje sekund klipper Karin, m =, m. Läa 0 ml = 0,0 liter Använd sambandet s = v t. Räkna ut hur mycket vattnet väger när

1 a) 8,3 b) 5,4. 2 a) 16,38 b) 20, m. 4 a) 6 cm 2 b) 5 cm 2. 5 a) m 2 b) m c) dm 2. 6 a) 12 m 2 b) 27 cm 2

epetition Facit epetition a) 9, 7, 2 a),, a),,7 A,2 B,9 C,7 a),,0 c) 0,2 2,0 m 2, m 2,2 m, m 7 a) 0, m 0,0 m c) 0, m a) 9 a) 0 2 a) 7 a) st st 2 a) 7 0 a),0 kr,0 kr,7 m,7 km T.ex. 7 valpar dl 9 0, m 20

Eva Björklund Heléne Dalsmyr. matematik. Koll på. Skriva Facit

Eva Björklund Heléne Dalsmyr 5B matematik Koll på Skriva Facit 6Ekvationer, uttryck och mönster 1 a) b) = c) d) 2 a) = b) c) = d) 3 a) < b) < c) < d) > 4 a) < b) < c) > d) < 5 a) < b) > c) < d) > Talet

Innehåll. 1 Allmän information 5. 4 Formativ bedömning 74. 5 Diagnoser och tester 90. 6 Prov och repetition 107. 2 Kommentarer till kapitlen 18

Innehåll 1 Allmän information Seriens uppbyggnad Lärobokens struktur 6 Kapitelinledning 7 Avsnitten 7 Pratbubbleuppgifter Aktivitet Taluppfattning och huvudräkning 9 Resonera och utveckla 9 Räkna och häpna

Min matematikordlista

1 Min matematikordlista Namn 2 ADJEKTIV STORLEK Skriv en mening om varje ord. Stor Större Störst 3 Liten Mindre Minst Rita något litet! Rita något som är ännu mindre! Rita något som är minst! 4 ANTAL Skriv

Övningsblad 1, sida 1. Övningsblad 1, sida 2. 1 a 1 h = min b 3 h = min c 6 h = min d 9 h = min

Övningsblad, sida Övningsblad, sida a h = min b h = min c h = min d h = min a 0 min = h b 0 min = h c 00 min = h d 0 min = h 0 Vilka tider är samma som 0 min? A h B, h C h 0 min D,0 h E, h 0 Detta är de

Eva Björklund Heléne Dalsmyr. matematik. Koll på. Skriva Facit

Eva Björklund Heléne Dalsmyr 5A matematik Koll på Skriva Facit 1 Tal i decimalform,3 1 a) 0,5 b) 0,7 c) 0, a) 4, b),1 c) 9,4 3 a) 35,8 b) 41, c) 0,9 4 a) 1,1 b) 4, c) 7,3 5 a) 13,4 b) 3,5 c) 91,7 a) 40,8

Vardagsord. Förstår ord som fler än, färre än osv. Har kunskap om hälften/dubbelt. Ex. Uppfattning om antal

TALUPPFATTNING Mål som eleven ska ha uppnått i slutet av det femte skolåret: Eleven skall ha förvärvat sådana grundläggande kunskaper i matematik som behövs för att kunna beskriva och hantera situationer

PRIMA MATEMATIK EXTRABOK 3 FACIT

PRIMA MATEMATIK EXTRABOK FACIT t.ex. Dela upp talet. = + + = + + = + + Dela upp talet i lika stora delar. = +, +++ = ++ = +, ++ = ++++ = + = + + Skriv alla uppdelningar du kan av talet, lika stora delar.,

Matematik. Ämnesprov, läsår 2014/2015. Delprov B. Årskurs. Elevens namn och klass/grupp

Ämnesprov, läsår 2014/2015 Matematik Delprov B Årskurs 6 Elevens namn och klass/grupp Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta

Vecka:1 Måndag Tisdag Onsdag Torsdag Fredag Lördag Söndag. Info: Färgade block - Bokade aktiviteter Fria block - Lediga tider för självträning

Vecka:1 Måndag Tisdag Onsdag Torsdag Fredag Lördag Söndag Datum: 02-jan 03-jan 04-jan 05-jan 06-jan 07-jan 08-jan 09:00 10:00 Fria block - Lediga tider för självträning och lägg i den vita brevlådan! 12:00

7F Ma Planering v2-7: Geometri

7F Ma Planering v2-7: Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar

Förmågor och Kunskapskrav

Fysik Årskurs 7 Förmågor och Kunskapskrav Använda kunskaper i fysik för att granska information, kommunicera och ta ställning i frågor som rör energi, teknik, miljö och samhälle F Y S I K Använda fysikens

1 Skriv med siffror a) tolvtusen femton b) fem hela och fyra hundradelar. b) 1000 0,04. 3 Skriv i kilogram a) 0,2 ton b) 4 hg c) 6400 g

1 Skriv med siffror a) tolvtusen femton b) fem hela och fyra hundradelar 2 Beräkna a) 0,7 50 d) 45110 b) 1000 0,04 e) 78,2/100 c) 0,08 0,5 f) 555511000 3 Skriv i kilogram a) 0,2 ton b) 4 hg c) 6400 g 4

PRIMA MATEMATIK EXTRABOK 2 FACIT

PRIMA MATEMATIK EXTRABOK FACIT Skriv rätt tecken. Välj mellan = < < 11 1 = > 1 0 = > 1 1 > > < = < < Skriv så att det stämmer. ; 11= ; 11 0 ; ; ; ; ; 1= ; 1 = ; ; ; 1 ; 0 1 ; 0 ; = ; ; Skriv rätt tecken.

8F Ma Planering v2-7 - Geometri

8F Ma Planering v2-7 - Geometri Arbetsform under en vecka: Tisdagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar

Arbetsblad 1:1. 1 Svara i bråkform hur stor andel av den stora rutan som är. 2 Svara i decimalform hur stor andel av den stora rutan som är.

Arbetsblad 1:1 Tal i bråkform och i decimalform Grundbok: grundkurs s. 8 blåkurs s. 0 1 Svara i bråkform hur stor andel av den stora rutan som är a) grå b) kryssad c) prickad d) vit 2 Svara i decimalform

Matematikbokens Prio kapitel Kap 3,.,Digilär, NOMP

Geometri Syftet undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem hjälp av matematik samt värdera valda strategier och metoder, - använda och analysera begrepp och samband

Matematik. Ämnesprov, läsår 2014/2015. Delprov C. Årskurs. Elevens namn och klass/grupp

Ämnesprov, läsår 2014/2015 Matematik Delprov C Årskurs 6 Elevens namn och klass/grupp Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta

Vardagsmatematik 1. SUSANNE SPARAR 10 KR I VECKAN. HUR MYCKET BLIR DET PÅ ETT ÅR?

Vardagsmatematik 1. SUSANNE SPARAR 10 KR I VECKAN. HUR MYCKET BLIR DET PÅ ETT ÅR? 2. VID EN HASTIGHETSKONTROLL STOPPADE POLISEN EN BILIST SOM KÖRDE 69 KM/H. HÖGSTA TILLÅTNA HASTIGHET VAR 50KM/H. HUR MYCKET

Lektion 2, måndagen den 1 februari, Svenska för internationella studenter, kurs 1

Lektion 2, måndagen den 1 februari, 2016 Svenska för internationella studenter, kurs 1 Hur man hälsar Hej! Hejsan! Tjenare! Tjena! Tja! God dag! God morgon! God middag! God afton! God natt! Hur man hälsar

Addition och subtraktion. Vilka uträkningar visas på tallinjerna nedan? Beräkna med huvudräkning 1 3 5 = 2 2 2 + 5 = 3 3 7 + 3 = 4 4 1 4 = 5 7 2 + 7 5

OH 1 Addition och subtraktion Vilka uträkningar visas på tallinjerna nedan? 1 = 7 6 1 0 1 + = 7 6 1 0 1 7 + = 7 6 1 0 1 1 = 7 6 1 0 1 Beräkna med huvudräkning 8 6 6 8 7 + 7 8 9 7 9 1 8 10 1 + 0 Kopiering

Matematik F- 6 Checklista för matematik K L A R A T Begreppsbildning år år år år år år år Kunna ord om: F 1 2 3 4 5 6 storlek ex störst, minst antal ex flera, färre volym ex mest, minst vikt ex tyngst,

Positionssystemet och enheter

strävorna 5A 5C Positionssystemet och enheter uttrycksformer tal geometri Avsikt och matematikinnehåll Aktiviteten utgår från en gammal och väl beprövad mall för att skapa struktur och ge förståelse för

Steg 10. 6 a) 0,129 b) 1,72 c) 2,05 7 a) 960 kr b) 1600 kr c) 14 kr 8 30% 9 a) 32% b) 60% c) 12% 10 20% 11 a) b) c) 2. 12 a) 135 b) c) 6 ( )

Bråk och procent Steg elever a) st b) st 0,, %,,,, 0 liter T ex och a) b) 0 a) 0, b) 0, c) 0, a) ( ) b) c) 00 0 a) b) c) a) ( 00) b) 0 ( 000) c) ( ) 000 a) 0, b) 0, c) 0, a) b) c) 0 a) b) a) > b) < c)

Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 2

Kapitel 2.1 2101, 2102, 2103, 2104 Exempel som löses i boken. 2105 Hela cirkeln är 100 %. Den ofärgade delen är 100 % - 45 % = 55 % 2106 a) Antalet färgade rutor 3 = b) 3 = 0, 6 c) 0,6 = 60 % Totala antalet

Repetitionsuppgifter 1

Repetitionsuppgifter 1 1 Vilka tal pekar pilarna på? a) b) Skriv talen med siffror 2 a) trehundra sju b) femtontusen fyrtiofem c) tvåhundrafemtusen tre 3 a) fyra tiondelar b) 65 hundradelar c) 15 tiondelar

Synnöve Carlsson. Gunilla Liljegren Margareta Picetti. Borgen. Facit

Synnöve Carlsson Borgen Gunilla Liljegren Margareta Picetti Facit 6B Sanoma Utbildning Postadress: Box 0091, 10 25 Stockholm Besöksadress: Alströmergatan 12, Stockholm Hemsida: www.sanomautbildning.se

Storvretaskolans Kursplan för Matematik F-klass- år 5

2010-11-01 Storvretaskolans Kursplan för Matematik F-klass- år 5 Skolan skall i sin undervisning sträva efter att eleven : utvecklar intresse för matematik samt tilltro till det egna tänkandet och den

Start Matematik facit

FACIT Start Matematik facit Årskurs 4-9 Facit till Start Matematik 47-60-0 Liber AB Får kopieras 2 Kapitel Siffror och tal a) 9-42 a) 9-42 c) 84 d) 555 e) -6 f) 7 400 c) 84 d) 555 e) -6 f) 7 400 g) 985

8 miljarder B. 8 miljoner B. 80 tusen B. 8 tusen B 8 MB 8 GB. 8 kb. 80 kb B B B B 32 MB 32 GB.

Tal Sida av 9 a) 000 9 000 c) 000 000 d) 9 000 000 e) 000 000 000 f) 9 000 000 000 a) 00 000 c) 00 000 d) 00 000 000 99 78 79 9 000 000 000 00 000 000 000 00 000 00 000 7 a) 8 kb 80 tusen B 80 kb 8 miljoner

Övningsuppgifter i matematik. Del 1 Grunderna i matematik Del 2 Uppgifter i läkemedelsberäkning

Övningsuppgifter i matematik. Del Grunderna i matematik Del Uppgifter i läkemedelsberäkning Del Grunderna i matematik. Hur många centimeter är en meter?. Vilken enhet saknas? a) Bilen är bred. b) Kastrullen

A: 111 B: 900 C: 909 D: 990 E: 999

3-poängsproblem 1. 1000 100 + 10 1 =? A: 111 B: 900 C: 909 D: 990 E: 999 2. Miriam har 16 kort, fyra av varje färg: 4 spader, 4 klöver, 4 ruter och 4 hjärter. Hon vill lägga dem på rutnätet här bredvid

4 Sätt in punkternas koordinater i linjens ekvation och se om V.L. = H.L. 5 Räkna först ut nya längden och bredden.

Läxor Läxa 7 En sådan timme skulle ha 00 00 s = 0 000 s. 8 a) O = π d och A = π r r. 0 Beräkna differensen mellan hela triangelns area och arean av den vita triangeln i toppen. Läxa 9 Hur stor andel målar

sträckan = tiden. hastigheten hastigheten = sträckan tiden 210 hastigheten = 3 = 70 Bilisten kör 70 km/h. tiden =

Enheter och skala I det här kapitlet kan du lära dig mer om hastighet att skriva minuter som del av timme att räkna om km/h till m/s något om hastigheter till sjöss om volymenheterna cm 3, dm 3 och m 3

Matematikbokens Prio kapitel Kap 3,.,Digilär, NOMP

Geometri Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, - använda och analysera begrepp

Matematik Steg: Bas. Mål att sträva mot Mål Målkriterier Omdöme Åtgärder/Kommentarer

Matematik Steg: Bas ha en grundläggande taluppfattning som omfattar naturliga tal och enkla tal i talområdet 0-10 bråk- och decimalform ordningstal upp till 5 ha en grundläggande rumsuppfattning och kunna

Välkommen till Mariagården/ Hantverkstorget aktiviteter för februari

1 [8] Välkommen till Mariagården/ Hantverkstorget aktiviteter för februari Onsdag 1 februari 10.15 10.45 Bokstunden på CD-nedre Vi börjar läsa Emil i Lönneberga 14.00-16.00 Öppen verksamhet i Brasrummet

Bok: X (fjärde upplagan) Kapitel : 3 Längd, tid och samband Kapitel : 4 Algebra och mönster

PLANERING MATEMATIK - ÅK 7 Bok: X (fjärde upplagan) Kapitel : 3 Längd, tid och samband Kapitel : 4 Algebra och mönster Elevens namn: markera med kryss vilka uppgifter du gjort Avsnitt: sidor ETT ETT TVÅ