Låt vara en reell funktion av en reell variabel med definitionsmängden som är symmetrisk i origo.
|
|
|
- Gunilla Johanna Fredriksson
- för 10 år sedan
- Visningar:
Transkript
1 UDDA FUNKTIONER OCH DUBBELINTEGRALER. Från en variabelanalys vet vi att integral över ett symetrisk intervall, av en udda funktion är lika med 0. 0 om är udda. T ex 0 Här upprepar vi def. av udda ( och jämna ) funktioner Låt vara en reell funktion av en reell variabel med definitionsmängden som är symmetrisk i origo. DEFINITION : Vi säger att funktionen är jämn om ö DEFINITION 2: Vi säger att funktionen är udda om ö av 0
2 Exempel. Följande funktioner är jämna: a) b) c) d) e) 4 f) 3 3 g) 5 Exempel 2. Några udda funktioner: a) b) c) d) e) Exempel 3. Följande funktioner är varken jämna eller udda: a) b) 5 c) d) e) Anmärkning: Följande regler kommer direkt från definitionen UDDA + UDDA= UDDA ( funktion) ( Ex: är en udda funktion) TAL*UDDA=UDDA ( Ex: 23 är en udda funktion) UDDA*JÄMN= UDDA ( Ex: är en udda funktion) UDDA* UDDA = JÄMN ( Ex: är en jämnfunktion) JÄMN * JÄMN = JÄMN ( Ex: är en jämnfunktion) När vi beräknar integral över ett symetriskt intervall, förenklar vi beräkning om det finns udda termer i integranden, som i nedanstående exempel: Uppgift. Beräkna integralen / a) / b) c) 3 5 d) Lösning a) 2 av 0
3 Vi har ett symmetriskt intervall [ /2, /2 ] och därför blir integralen av varje udda term lika med 0 ( vi har kvar endast integralen av icke udda termen 5: / / / = / =5 b) c) 0 d) 0 = UDDA FUNKTIONER OCH DUBBELINTEGRAL Ovanstående förenkling vid beräkning av en enkelintegral av udda funktioner över ett symmetrisk interval, kan vi också använda vid beräkning av en dubbelintegral om integrationsområde är symmetriskt i en av axlarna. FALL. Om i) integrationsområde D i xy planet definieras av, ( alltså området är symetrisk i x axeln ) och ii), är en udda funktion med avseende på y ( dvs,, för alla, ) då gäller,. Bevis: Enligt regler för enkelintegraler med udda integranden över symmetriskt intervall gäller Därför, för varje ( fixt ) x., =, av 0
4 Exempel. Beräkna där,, 2 5, }. Lösning 0 eftersom D är symmetrisk i x axeln och är en udda funktion på D med avseende på y ( uppenbart,, ) Uppgift 2. Låt,, 3, }. Beräkna a) 8 8 b) 5 c) Lösning b) Första tre termer i integranden, och är är udda med avseende på y ( för, tillfälligt, fixt x). T ex för tredje term gäller,, Kontrollera själv för första två termer. Om vi integrerar termviss får vi av 0
5 Svar: a) 0, b) 5 c) 0 ============================================================== FALL 2. Om i) integrationsområde D i xy planet definieras av, ( alltså området är symetrisk i y axeln ) och ii), är en udda funktion med avseende på x d y ( dvs,, för alla, ) då gäller,. ( Detta bevisas på samma sätt som i FALL ) -v(y) 0 c v(y) x Exempel. Beräkna 5 där,, 2 4, }. Lösning 5 0 eftersom D är symmetrisk i y axeln och 5 är en udda funktion på D med avseende på x. 5 av 0
6 Uppgift 3. Låt,, 3, 2}. Beräkna a) 4 b) 0 c) Svar: { Området,, 3, 2 2} är symmetriskt i y axeln. } a) 0 b) 0 = =0 arean(d)=80 c) =0+ = ========================================================= I nedanstående uppgift är integrationsområdet symmetriskt i både x och y axeln som vi utnyttjar för att förenkla beräkningen. Uppgift 4. Beräkna 5 4 där,, 9}. D 3 ( D är cirkeln som har radien=3 och centrum i origo) Lösning 5 4 = (*) = arean(d) = 4 9 =36 Anmärkning :. Den första integralen i (*) är 0 eftersom integranden 5 är en udda funktion på y och D är symmetrisk i x axeln. 2. Den andra integralen i (*) är 0 eftersom integranden är en udda funktion på x och D är symmetrisk även i y axeln. 6 av 0
7 JÄMNA INTEGRANDER Vi kan ( lite) förenkla beräkning av dubbelintegralen för funktioner som är jämna i en variabel ( t ex y) om området är symmetrisk kring en axel ( t ex x-axeln): FALL 3. Om i) integrationsområde D i xy-planet definieras av, ( alltså området är symetrisk i x-axeln ) och ii), är en jämn funktion med avseende på y ( dvs,, för alla, ) y u(x) då gäller,, a D D2 b x och därför -u(x),,, 2,. FALL 4. Om i) integrationsområde D i xy planet definieras av, ( alltså området är symetrisk i y axeln ) och ii), är en jämn funktion med avseende på x d y ( dvs,, för alla, ) då gäller -v(y) D2 D v(y), 2,. c 0 x 7 av 0
8 FALL 5. Alla fall F F4 kan generaliseras och användes på allmänna symmetriska område: Låt D vara ett integrationsområde i xy planet symmetriskt kring linjen L som är delad i två symmetriska områden. Låt, beteckna den punkt i D2 som är symmetrisk till,. A) Om y,, ( för alla, ) (x,y ) då är,, och därför D2 D (x,y),,. o x B) Om,, ( för alla, ) då är,, och därför,. Anmärkning: A, B kan enkel bevisas med hjälp av dubbelintegralens definition ( Riemannsummor ). Uppgift 5. Låt,. Beräkna, om a) D är triangeln med hörn i (0,0), (,0) och (0,). b) D är triangeln med hörn i (,0), (0,) och (,0) Tipps: Använd a). c) D är rektangeln med hörn i (,0), (0,), (,0) och (0, ) Tipps: Använd a) eller b). d) D definieras av Lösning a), = x+y= 8 av 0 0
9 ... 2 b) Punkten,, ä,. Eftersom,,, (för alla, ) har vi,, och därför, 2, enligt a 2 6 c) På grund av symmetri, eftersom,,,, gäller att, d) Lägg märke till att randlinjen består av fyra delar, ö,,, ä Därför är definitionsområde,, samma som i frågan c. Integranden i d är också samma som i c frågan, och därmed har integralen i d samma värde som den i frågan c dvs. Svar: a) /6, b) /3, c) 2/3, d 2/3 9 av 0
10 Uppgift6. Låt, 2. a) Beräkna, om D är triangeln med hörn i (0,0), (,0) och (,). b) Använd resultat i a) för att beräkna, om D är rektangeln med hörn i (0.0), (,0), (,) och (0,). Lösning:, 2 Först beräknar vi integralen 2 y=x (,) med hjälp av substitutionen ; 2 ( Vi tillfälligt betraktar x som en konstant ) 2 / / Från (*) har vi 2 / / 0 = / / / 5 0 b) Området är symmetrisk kring linjen. Om, är symmetrisk punkt till (x,y) kring linjen då är,, [alltså y och x byter plats]. Därför (x,y ) (x,y) (,),, 2 2,. Därför,, 2,, och därmed enligt a Svar: a) b) 0 av 0
DUBBELINTEGRALER. Rektangulära (xy) koordinater
 ubbelintegraler. -koordinater UBBELINTEGRALER. Rektangulära ( koordinater efinition. Låt zf(, vara en reell funktion av två variabler och. Vi delar integrationsområde (definitionsområde) i ändligt antal
ubbelintegraler. -koordinater UBBELINTEGRALER. Rektangulära ( koordinater efinition. Låt zf(, vara en reell funktion av två variabler och. Vi delar integrationsområde (definitionsområde) i ändligt antal
Vi antar att f och g ar begränsade och integrerbara funktioner på givna mätbara ( kvadrerbara) områden och att a, b ar konstanter.
 GNSKAPR HOS UBBLINTGRALR. Vi antar att f och g ar begränsade och integrerbara funktioner på givna mätbara ( kvadrerbara) områden och att a, b ar konstanter. å gäller:., 0 om arean() =0 ( dvs. om är en
GNSKAPR HOS UBBLINTGRALR. Vi antar att f och g ar begränsade och integrerbara funktioner på givna mätbara ( kvadrerbara) områden och att a, b ar konstanter. å gäller:., 0 om arean() =0 ( dvs. om är en
Kap Dubbelintegraler.
 Kap 4. 4.. ubbelintegraler. A. Beräkna följande dubbelintegraler a. d. (x + y) dxdy, över kvadraten x 3, y. (sin y + y cos x) dxdy, då ges av x π, y π. x cos xy dxdy, då ges av x π, y. xy cos (x + y )
Kap 4. 4.. ubbelintegraler. A. Beräkna följande dubbelintegraler a. d. (x + y) dxdy, över kvadraten x 3, y. (sin y + y cos x) dxdy, då ges av x π, y π. x cos xy dxdy, då ges av x π, y. xy cos (x + y )
Kap Generaliserade multipelintegraler.
 Kap 4.3. Generaliserade multipelintegraler. 50. Beräkna följande generaliserade multipelintegraler: A a. dxdy, ges av x, 0 xy x A b. A c. A d. A e. K x ( + x 2 )( + x 2 y 2 ) dxdy, ges av x > 0, xy x dxdy,
Kap 4.3. Generaliserade multipelintegraler. 50. Beräkna följande generaliserade multipelintegraler: A a. dxdy, ges av x, 0 xy x A b. A c. A d. A e. K x ( + x 2 )( + x 2 y 2 ) dxdy, ges av x > 0, xy x dxdy,
Modul 5: Integraler. Det är viktigt att du blir bra på att integrera, så träna mycket.
 Institutionen för Matematik SF625 Envariabelanalys Läsåret 27-28 Lars Filipsson Modul 5: Integraler Denna modul handlar om integraler. Det slås fast i en precis definition vad som menas med att en funktion
Institutionen för Matematik SF625 Envariabelanalys Läsåret 27-28 Lars Filipsson Modul 5: Integraler Denna modul handlar om integraler. Det slås fast i en precis definition vad som menas med att en funktion
SF1625 Envariabelanalys Lösningsförslag till tentamen
 SF1625 Envariabelanalys Lösningsförslag till tentamen 216-6-1 1. Derivera nedanstående funktioner med avseende på x och ange för vilka x derivatan existerar. Endast svar krävs. A. f(x) = arctan 1 x B.
SF1625 Envariabelanalys Lösningsförslag till tentamen 216-6-1 1. Derivera nedanstående funktioner med avseende på x och ange för vilka x derivatan existerar. Endast svar krävs. A. f(x) = arctan 1 x B.
har ekvation (2, 3, 4) (x 1, y 1, z 1) = 0, eller 2x + 3y + 4z = 9. b) Vi söker P 1 = F (1, 1, 1) + F (1, 1, 1) (x 1, y 1, z 1) = 2x + 3y + 4z.
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del, flervariabel, för F1. Tentamen onsdag 7 maj 9, 1.-19. 1. Låt F (x, y, z) sin(x + y z) + x + y + 6z. a)
SF1626 Flervariabelanalys
 1 / 19 SF1626 Flervariabelanalys Föreläsning 1 Henrik Shahgholian Vid Institutionen för matematik, KTH VT 218, Period 3 2 / 19 SF1626 Flervariabelanalys agens Lektion ubbelintegraler: Avsnitt 14.1-14.2
1 / 19 SF1626 Flervariabelanalys Föreläsning 1 Henrik Shahgholian Vid Institutionen för matematik, KTH VT 218, Period 3 2 / 19 SF1626 Flervariabelanalys agens Lektion ubbelintegraler: Avsnitt 14.1-14.2
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen 4-9-6 DEL A. Betrakta följande tre områden i planet: D = {(x, y): x y < 4}, D = {(x, y): x + y }, D 3 = {(x, y): 4x + 3y
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen 4-9-6 DEL A. Betrakta följande tre områden i planet: D = {(x, y): x y < 4}, D = {(x, y): x + y }, D 3 = {(x, y): 4x + 3y
SF1626 Flervariabelanalys
 Föreläsning 11 Institutionen för matematik KTH VT 2018 1 agens program Variabelsubstitution i dubbelintegraler Något om generaliserade integraler och medelvärden Bokens kapitel 14.4 och i någon mån också
Föreläsning 11 Institutionen för matematik KTH VT 2018 1 agens program Variabelsubstitution i dubbelintegraler Något om generaliserade integraler och medelvärden Bokens kapitel 14.4 och i någon mån också
Institutionen för Matematik. SF1625 Envariabelanalys. Modul 5 Integraler
 Institutionen för Matematik SF65 Envariabelanalys Läsåret 5/6 Modul 5 Integraler Denna modul omfattar kapitel 5 och avsnitt 6.-6. i kursboken Calculus av Adams och Esse och undervisas på tre föreläsningar,
Institutionen för Matematik SF65 Envariabelanalys Läsåret 5/6 Modul 5 Integraler Denna modul omfattar kapitel 5 och avsnitt 6.-6. i kursboken Calculus av Adams och Esse och undervisas på tre föreläsningar,
Kap 5.7, Beräkning av plana areor, rotationsvolymer, rotationsareor, båglängder.
 Kap 5.7, 7. 7.. Beräkning av plana areor, rotationsvolymer, rotationsareor, båglängder. 8. (A) Beräkna arean av det ändliga område som begränsas av kurvorna x a. y = + x och y = b. y = x e x och y = x
Kap 5.7, 7. 7.. Beräkning av plana areor, rotationsvolymer, rotationsareor, båglängder. 8. (A) Beräkna arean av det ändliga område som begränsas av kurvorna x a. y = + x och y = b. y = x e x och y = x
x ( f u 2y + f v 2x) xy = 24 och C = f
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Lösningsförslag till tentamen Torsdag augusti 16, 2018 DEL A
 Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
10 Beräkning av dubbelintegraler
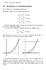 Nr,7april-,Amelia Beräkning av dubbelintegraler. Bte av integrationsordning Eempel (96) Kasta om integrationsordningen i a) b) c) Z Z e Z 6 Z d d d Z ln Z f(, )d f(, )d f(, )d. Lösning: Med hjälp av figurer
Nr,7april-,Amelia Beräkning av dubbelintegraler. Bte av integrationsordning Eempel (96) Kasta om integrationsordningen i a) b) c) Z Z e Z 6 Z d d d Z ln Z f(, )d f(, )d f(, )d. Lösning: Med hjälp av figurer
och kallas ytintegral AREAN AV EN BUKTIG YTA
 YTINTEGRALER Definition. Vi betraktar en funktion (xx, yy, zz) som är definierad på ytan Y. Vi delar ytan i ej- överlappande delar S i, väljer en punkt T i i varje S i och beräknar summan ii= ff(tt ii
YTINTEGRALER Definition. Vi betraktar en funktion (xx, yy, zz) som är definierad på ytan Y. Vi delar ytan i ej- överlappande delar S i, väljer en punkt T i i varje S i och beräknar summan ii= ff(tt ii
SAMMANFATTNING TATA41 ENVARIABELANALYS 1
 SAMMANFATTNING TATA4 ENVARIABELANALYS LÄST SOM EN DEL AV CIVILINGENJÖRSPROGRAMMET I INDUSTRIELL EKONOMI VID LITH, HT 04 Senast reviderad: 05-06-0 Författare: Viktor Cheng INNEHÅLLSFÖRTECKNING Diverse knep...3
SAMMANFATTNING TATA4 ENVARIABELANALYS LÄST SOM EN DEL AV CIVILINGENJÖRSPROGRAMMET I INDUSTRIELL EKONOMI VID LITH, HT 04 Senast reviderad: 05-06-0 Författare: Viktor Cheng INNEHÅLLSFÖRTECKNING Diverse knep...3
EXISTENS AV EN UNIK LÖSNING TILL FÖRSTAORDNINGENS BEGYNNELSEVÄRDESPROBLEM
 EXISTENS AV EN UNIK LÖSNING TILL FÖRSTAORDNINGENS BEGYNNELSEVÄRDESPROBLEM Vi betraktar ett begnnelsevärdesproblem IVP, initial-value problem) av första ordningen som är skrivet på normal form IVP1) Man
EXISTENS AV EN UNIK LÖSNING TILL FÖRSTAORDNINGENS BEGYNNELSEVÄRDESPROBLEM Vi betraktar ett begnnelsevärdesproblem IVP, initial-value problem) av första ordningen som är skrivet på normal form IVP1) Man
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF165 Envariabelanalys Lösningsförslag till tentamen 15-4-7 DEL A 1. Låt f(x) = arcsin x + 1 x. A. Bestäm definitionsmängden till funktionen f. B. Bestäm funktionens största och minsta värde. (Om du har
SF165 Envariabelanalys Lösningsförslag till tentamen 15-4-7 DEL A 1. Låt f(x) = arcsin x + 1 x. A. Bestäm definitionsmängden till funktionen f. B. Bestäm funktionens största och minsta värde. (Om du har
1. Bestäm definitionsmängden och värdemängden till funktionen f(x,y) = 1 2x 2 3y 2. Skissera definitionsmängden, nivålinjerna och grafen till f.
 1. Bestäm definitionsmängden och värdemängden till funktionen f(x,y) = 1 2x 2 3y 2. Skissera definitionsmängden, nivålinjerna och grafen till f. 2. Beräkna gränsvärdet (eller visa att det inte finns):
1. Bestäm definitionsmängden och värdemängden till funktionen f(x,y) = 1 2x 2 3y 2. Skissera definitionsmängden, nivålinjerna och grafen till f. 2. Beräkna gränsvärdet (eller visa att det inte finns):
Existensen av största och minsta värde är inte garanterad i det här fallet.
 OPTIMERING PÅ ICKE-KOMPAKTA OMRÅDEN. Låt f,..., ) vara en reell funktion med en icke-kompakt definitionsmängd D. ( n Eistensen av största och minsta värde är inte garanterad i det här fallet. För att bestämma
OPTIMERING PÅ ICKE-KOMPAKTA OMRÅDEN. Låt f,..., ) vara en reell funktion med en icke-kompakt definitionsmängd D. ( n Eistensen av största och minsta värde är inte garanterad i det här fallet. För att bestämma
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF1625 Envariabelanalys Lösningsförslag till tentamen 215-1-27 DEL A 4 1. Betrakta funktionen f som ges av f(x) = 1 + x + (x 2). 2 A. Bestäm definitionsmängden till f. B. Bestäm alla intervall där f är
SF1625 Envariabelanalys Lösningsförslag till tentamen 215-1-27 DEL A 4 1. Betrakta funktionen f som ges av f(x) = 1 + x + (x 2). 2 A. Bestäm definitionsmängden till f. B. Bestäm alla intervall där f är
Tentamen i matematik. f(x) = ln(ln(x)),
 Lösningsförslag Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA52G Matematisk Analys MA23G Matematisk analys för ingenjörer Tentamensdag: 203-05- kl 4.30-9.30 Hjälpmedel : Inga hjälpmedel utöver
Lösningsförslag Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA52G Matematisk Analys MA23G Matematisk analys för ingenjörer Tentamensdag: 203-05- kl 4.30-9.30 Hjälpmedel : Inga hjälpmedel utöver
11 Dubbelintegraler: itererad integration och variabelsubstitution
 Nr, april -5, Amelia ubbelintegraler: itererad integration och variabelsubstitution. Itererad integration tterligare eempel Eempel (97k) Beräkna ( ) och ( ). ( 8) dd om begränsas av, 5 3.75.5.5.5.5 3.75
Nr, april -5, Amelia ubbelintegraler: itererad integration och variabelsubstitution. Itererad integration tterligare eempel Eempel (97k) Beräkna ( ) och ( ). ( 8) dd om begränsas av, 5 3.75.5.5.5.5 3.75
MVE465. Innehållsförteckning
 Lösningar på övningsuppgifter Detta dokument innehåller mina renskrivna lösningar på övningsuppgifter i kursen Linjär algebra och analys fortsättning (). Jag kan inte lova att samtliga lösningar är välformulerade
Lösningar på övningsuppgifter Detta dokument innehåller mina renskrivna lösningar på övningsuppgifter i kursen Linjär algebra och analys fortsättning (). Jag kan inte lova att samtliga lösningar är välformulerade
x 2 + x 2 b.) lim x 15 8x + x 2 c.) lim x 2 5x + 6 x 3 + y 3 xy = 7
 TM-Matematik Mikael Forsberg 0734-41331 Pär Hemström 06-64896 För ingenjörs och distansstudenter Envariabelanalys ma034a 01 10 01 Skrivtid: 09:00-14:00. Inga hjälpmedel. Lösningarna skall vara fullständiga
TM-Matematik Mikael Forsberg 0734-41331 Pär Hemström 06-64896 För ingenjörs och distansstudenter Envariabelanalys ma034a 01 10 01 Skrivtid: 09:00-14:00. Inga hjälpmedel. Lösningarna skall vara fullständiga
Tisdag v. 2. Speglingar, translationer och skalningar
 1 Tisdag v 2 Speglingar, translationer och skalningar Ofta i matematik och i matematiska kurser är det så att man måste kunna några grundläggande exempel utantill och man måste kunna några regler som säger
1 Tisdag v 2 Speglingar, translationer och skalningar Ofta i matematik och i matematiska kurser är det så att man måste kunna några grundläggande exempel utantill och man måste kunna några regler som säger
Sådana avbildningar kallar vi bijektioner mellan A och B (eller från A till B).
 BIJEKTION, INJEKTION, SURJEKTION Allmän terminologi. I samband med variabelbyte vid beräkning av integraler har vi en avbildning mellan två mängder A och B, dvs en funktion f : A B. Vi har oftast krav
BIJEKTION, INJEKTION, SURJEKTION Allmän terminologi. I samband med variabelbyte vid beräkning av integraler har vi en avbildning mellan två mängder A och B, dvs en funktion f : A B. Vi har oftast krav
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF1625 Envariabelanalys Lösningsförslag till tentamen 211-1-18 DEL A 1. Låt x och y vara två tal vars summa är 6. Ange det minimala värdet som uttrycket 2x 2 + y 2 kan anta. Lösningsförslag. Eftersom vi
SF1625 Envariabelanalys Lösningsförslag till tentamen 211-1-18 DEL A 1. Låt x och y vara två tal vars summa är 6. Ange det minimala värdet som uttrycket 2x 2 + y 2 kan anta. Lösningsförslag. Eftersom vi
Dubbelintegraler och volymberäkning
 ubbelintegraler och volymberäkning Volym och dubbelintegraler över en rektangel Alla funktioner nedan antas vara kontinuerliga. Om f (x) i intervallet [a, b], så är arean av mängden {(x, y) : y f (x),
ubbelintegraler och volymberäkning Volym och dubbelintegraler över en rektangel Alla funktioner nedan antas vara kontinuerliga. Om f (x) i intervallet [a, b], så är arean av mängden {(x, y) : y f (x),
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 24-8-2 DEL A. Bestäm och skissera definitionsmängden till funktionen fx, y) = x 2 + y 2 + 2x 4y + + x. Är definitionsmängden kompakt? 4 p) Lösning.
SF626 Flervariabelanalys Lösningsförslag till tentamen 24-8-2 DEL A. Bestäm och skissera definitionsmängden till funktionen fx, y) = x 2 + y 2 + 2x 4y + + x. Är definitionsmängden kompakt? 4 p) Lösning.
MATEMATIK 5 veckotimmar
 EUROPEISK STUDENTEXAMEN 2010 MATEMATIK 5 veckotimmar DATUM : 4 Juni 2010 SKRIVNINGSTID : 4 timmar (240 minuter) TILLÅTNA HJÄLPMEDEL : Skolans formelsamling Icke-programmerbar, icke-grafritande räknedosa
EUROPEISK STUDENTEXAMEN 2010 MATEMATIK 5 veckotimmar DATUM : 4 Juni 2010 SKRIVNINGSTID : 4 timmar (240 minuter) TILLÅTNA HJÄLPMEDEL : Skolans formelsamling Icke-programmerbar, icke-grafritande räknedosa
Institutionen för matematik KTH. Tentamensskrivning, , kl B1210 och 5B1230 Matematik IV, för B, M, och I.
 Institutionen för matematik KTH Tentamensskrivning, 23--9, kl 4 9 5B2 och 5B23 Matematik IV, för B, M, och I Hjälpmedel: BETA, Mathematics Handbook För godkänt betyg 3 krävs 7 poäng, medan för betyg 4
Institutionen för matematik KTH Tentamensskrivning, 23--9, kl 4 9 5B2 och 5B23 Matematik IV, för B, M, och I Hjälpmedel: BETA, Mathematics Handbook För godkänt betyg 3 krävs 7 poäng, medan för betyg 4
Tentamen i Matematisk analys, HF1905 exempel 1 Datum: xxxxxx Skrivtid: 4 timmar Examinator: Armin Halilovic
 Tentamen i Matematisk analys, HF95 exempel atum: xxxxxx Skrivtid: timmar Examinator: Armin Halilovic För godkänt betyg krävs av max poäng Betygsgränser: För betyg A, B, C,, E krävs, 9, 6, respektive poäng
Tentamen i Matematisk analys, HF95 exempel atum: xxxxxx Skrivtid: timmar Examinator: Armin Halilovic För godkänt betyg krävs av max poäng Betygsgränser: För betyg A, B, C,, E krävs, 9, 6, respektive poäng
Tentamen SF1626, Analys i flera variabler, Svar och lösningsförslag. 2. en punkt på randkurvan förutom hörnen, eller
 Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
Läsanvisningar till Analys B, HT 15 Del 1
 Läsanvisningar till Analys B, HT 15 Del 1 Dag 1 Avsnitt 6.1 Definition av trappfunktion och integral av en trappfunktion. Räkneregler (de är mer eller mindre uppenbara). Definition av Riemannintegralen
Läsanvisningar till Analys B, HT 15 Del 1 Dag 1 Avsnitt 6.1 Definition av trappfunktion och integral av en trappfunktion. Räkneregler (de är mer eller mindre uppenbara). Definition av Riemannintegralen
Bestäm ekvationen för det plan som går genom punkten (1,1, 2 ) på kurvan och som spänns
 UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik Q Flervariabelanalys 8--1 Skrivtid: 8-1. Inga hjälpmedel. Lösningarna skall åtföljas av förklarande text/figurer. Tentand
UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik Q Flervariabelanalys 8--1 Skrivtid: 8-1. Inga hjälpmedel. Lösningarna skall åtföljas av förklarande text/figurer. Tentand
Tentamen i Envariabelanalys 2
 Linköpings universitet Matematiska institutionen Kurskod: TATA42 Provkod: TEN Tentamen i Envariabelanalys 2 206 0 8, 4 9 Inga hjälpmedel. Lösningarna ska vara fullständiga, välmotiverade, ordentligt skrivna
Linköpings universitet Matematiska institutionen Kurskod: TATA42 Provkod: TEN Tentamen i Envariabelanalys 2 206 0 8, 4 9 Inga hjälpmedel. Lösningarna ska vara fullständiga, välmotiverade, ordentligt skrivna
(x 3 + y)dxdy. D. x y = x + y. + y2. x 2 z z
 UPPAA UNIVERITET Matematiska institutionen Abrahamsson, 4715, 7-57 (tyf, 47119, 77-517) Prov i matematik IT, K, X, W, EI, MI, NVP samt fristående kurs. Flerdimensionell analys och Analys MN 5-1-9 krivtid:
UPPAA UNIVERITET Matematiska institutionen Abrahamsson, 4715, 7-57 (tyf, 47119, 77-517) Prov i matematik IT, K, X, W, EI, MI, NVP samt fristående kurs. Flerdimensionell analys och Analys MN 5-1-9 krivtid:
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
u av funktionen u = u(x, y, z) = xyz i punkten M o = (x o, y o, z o ) = (1, 1, 1) i riktningen mot punkten M 1 = (x 1, y 1, z 1 ) = (2, 3, 1)
 ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
Lösningar till Matematisk analys
 Lösningar till Matematisk analys 685. Sätt fx x. Rotationskroppens volym är π fx dx π ] x 6 dx π 7 x7 π 7. Rotationskroppens area är summan av arean av kroppens mantelyta och arean av kroppens cirkulära
Lösningar till Matematisk analys 685. Sätt fx x. Rotationskroppens volym är π fx dx π ] x 6 dx π 7 x7 π 7. Rotationskroppens area är summan av arean av kroppens mantelyta och arean av kroppens cirkulära
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
x 2 = lim x 2 x 2 x 2 x 2 x x+2 (x + 3)(x + x + 2) = lim x 2 (x + 1)
 Matematik Hjälpmedel: Inga Chalmers Tekniska Högskola Tentamen 5--7 kl. 4: 8: Telefonvakt: Samuel Bengmark ankn.: 7-87644 Betygsgränser :a poäng, 4:a poäng, 5:a 4 poäng, max: 5 poäng Tentamensgranskning
Matematik Hjälpmedel: Inga Chalmers Tekniska Högskola Tentamen 5--7 kl. 4: 8: Telefonvakt: Samuel Bengmark ankn.: 7-87644 Betygsgränser :a poäng, 4:a poäng, 5:a 4 poäng, max: 5 poäng Tentamensgranskning
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A. e 50k = k = ln 1 2. k = ln = ln 2
 SF625 Envariabelanalys Lösningsförslag till tentamen 23--24 DEL A. Den :a januari 26 låstes kg av ett visst radioaktivt ämne in i en källare. Ämnet sönderfaller i en takt som är direkt proportionell mot
SF625 Envariabelanalys Lösningsförslag till tentamen 23--24 DEL A. Den :a januari 26 låstes kg av ett visst radioaktivt ämne in i en källare. Ämnet sönderfaller i en takt som är direkt proportionell mot
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A. 1. En svängningsrörelse beskrivs av
 SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
Flervariabelanalys och Matlab Kapitel 3
 Flervariabelanalys och Matlab Kapitel 3 Thomas Wernstål Matematiska Vetenskaper 28 september 2012 3 Multipelintegraler 3.1 ubbelintegraler I detta kapitel skall vi studera olika sätt på vilket man kan
Flervariabelanalys och Matlab Kapitel 3 Thomas Wernstål Matematiska Vetenskaper 28 september 2012 3 Multipelintegraler 3.1 ubbelintegraler I detta kapitel skall vi studera olika sätt på vilket man kan
av envariabelfunktionen g(t) och flervariabelfunktionen t = h(x, y) = x 2 + e y.)
 Lösningsskisser till TATA69 Flervariabelanalys 16-1- 1 Stationära punkter ges av f (4x 3 + 4x, 3y + 6z, z + 6y (,,, dvs (x, y, z (,, eller (x, y, z (, 6, 18 Ur andraderivatorna fås de kvadratiska formerna
Lösningsskisser till TATA69 Flervariabelanalys 16-1- 1 Stationära punkter ges av f (4x 3 + 4x, 3y + 6z, z + 6y (,,, dvs (x, y, z (,, eller (x, y, z (, 6, 18 Ur andraderivatorna fås de kvadratiska formerna
SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015
 SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt
SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF165 Envariabelanalys Lösningsförslag till tentamen 01-1-10 DEL A 1. Låt funktionen f ha definitionsmängden D f =]0, [ och ges av f(x) = e x 1 x. (a) Finn f:s invers f 1. ( p) (b) Finn inversens värdemängd
SF165 Envariabelanalys Lösningsförslag till tentamen 01-1-10 DEL A 1. Låt funktionen f ha definitionsmängden D f =]0, [ och ges av f(x) = e x 1 x. (a) Finn f:s invers f 1. ( p) (b) Finn inversens värdemängd
Inlämningsuppgift nr 2, lösningar
 UPPALA UNIVRITT MATMATIKA INTITUTIONN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 8 Inlämningsuppgift nr, lösningar. Visa att ekvationen x + x(y ) + (y ) + z + sin(yz) definierar z som en funktion
UPPALA UNIVRITT MATMATIKA INTITUTIONN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 8 Inlämningsuppgift nr, lösningar. Visa att ekvationen x + x(y ) + (y ) + z + sin(yz) definierar z som en funktion
a (och liknande ekvationer). a har lösningar endast om 1 a 1 (eftersom 1 sin( x ) 1). 3 saknar lösningar.
 TRIGONOMETRISKA EKVATIONER A) Ekvationen sin( x) a (och liknande ekvationer) Ekvationen sin( x) a har lösningar endast om a (eftersom sin( x ) ) Exempelvis, ekvationen sin( x) saknar lösningar Uppgift
TRIGONOMETRISKA EKVATIONER A) Ekvationen sin( x) a (och liknande ekvationer) Ekvationen sin( x) a har lösningar endast om a (eftersom sin( x ) ) Exempelvis, ekvationen sin( x) saknar lösningar Uppgift
Modul 1 Mål och Sammanfattning
 Institutionen för Matematik SF1625 Envariabelanalys Läsåret 2016-2017 Lars Filipsson Modul 1 Mål och Sammanfattning 1. Reella tal. 1. MÅL FÖR MODUL 1 Känna till talsystememet och kunna använda notation
Institutionen för Matematik SF1625 Envariabelanalys Läsåret 2016-2017 Lars Filipsson Modul 1 Mål och Sammanfattning 1. Reella tal. 1. MÅL FÖR MODUL 1 Känna till talsystememet och kunna använda notation
SF1626 Flervariabelanalys Tentamen 18 augusti 2011, Svar och lösningsförslag
 SF166 Flervariabelanalys entamen 18 augusti 11, 14. - 19. Svar och lösningsförslag 1) Låt fx, y) = xy lnx + y ). I vilken riktning är riktningsderivatan till f i punkten 1, ) som störst, och hur stor är
SF166 Flervariabelanalys entamen 18 augusti 11, 14. - 19. Svar och lösningsförslag 1) Låt fx, y) = xy lnx + y ). I vilken riktning är riktningsderivatan till f i punkten 1, ) som störst, och hur stor är
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF1625 Envariabelanalys Lösningsförslag till tentamen 2012-10-17 DEL A 1. Visa att ekvationen x 3 12x + 1 = 0 har tre lösningar i intervallet 4 x 4. Motivera ordentligt! (4 p) Lösningsförslag. Vi skall
SF1625 Envariabelanalys Lösningsförslag till tentamen 2012-10-17 DEL A 1. Visa att ekvationen x 3 12x + 1 = 0 har tre lösningar i intervallet 4 x 4. Motivera ordentligt! (4 p) Lösningsförslag. Vi skall
Institutionen för Matematik. SF1625 Envariabelanalys. Lars Filipsson. Modul 1
 Institutionen för Matematik SF1625 Envariabelanalys Läsåret 2017-2018 Lars Filipsson Modul 1 1. MÅL FÖR MODUL 1 1. Reella tal. Känna till talsystememet och kunna använda notation för mängder och intervall
Institutionen för Matematik SF1625 Envariabelanalys Läsåret 2017-2018 Lars Filipsson Modul 1 1. MÅL FÖR MODUL 1 1. Reella tal. Känna till talsystememet och kunna använda notation för mängder och intervall
Här finns en definition av gränsvärde (enligt Adams Calculus) av en funktion då x går mot ett tal a ( s.k. epsilon delta definition).
 GRÄNSVÄRDEN OCH KONTINUITET Här finns en definition av gränsvärde (enligt Adams Calculus av en funktion då går mot ett tal a ( s.k. epsilon delta definition. Definition. ( Cauchy Vi säger att funktionen
GRÄNSVÄRDEN OCH KONTINUITET Här finns en definition av gränsvärde (enligt Adams Calculus av en funktion då går mot ett tal a ( s.k. epsilon delta definition. Definition. ( Cauchy Vi säger att funktionen
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF1625 Envariabelanalys Lösningsförslag till tentamen 2015-01-12 DEL A 1. Betrakta funktionen f som ges av f(x) = xe 1/x. A. Bestäm definitionsmängden till f. B. Beräkna de fyra gränsvärdena lim x ± f(x)
SF1625 Envariabelanalys Lösningsförslag till tentamen 2015-01-12 DEL A 1. Betrakta funktionen f som ges av f(x) = xe 1/x. A. Bestäm definitionsmängden till f. B. Beräkna de fyra gränsvärdena lim x ± f(x)
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Flervariabelanlys och Matlab Kapitel 3
 Flervariabelanlys och Matlab Kapitel 3 Thomas Wernstål Carl-Henrik Fant Matematiska Vetenskaper 17 september 2009 1 3 Multipelntegraler 3.1 ubbelintegraler Exempel. Vi skall beräkna dubbelintegralen (y
Flervariabelanlys och Matlab Kapitel 3 Thomas Wernstål Carl-Henrik Fant Matematiska Vetenskaper 17 september 2009 1 3 Multipelntegraler 3.1 ubbelintegraler Exempel. Vi skall beräkna dubbelintegralen (y
IV, SF1636(5B1210,5B1230).
 Lösningar till tentamensskrivning i Matematik I, F636(5B,5B3) Tisdagen den 9 augusti 8, kl 4-9 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar och resonemang
Lösningar till tentamensskrivning i Matematik I, F636(5B,5B3) Tisdagen den 9 augusti 8, kl 4-9 Hjälpmedel: BETA, Mathematics Handbook Redovisa lösningarna på ett sådant sätt att beräkningar och resonemang
Räta linjer i 3D-rummet: Låt L vara den räta linjen genom som är parallell med
 RÄTA LINJER OCH PLAN Räta linjer i 3D-rummet: Låt L vara den räta linjen genom punkten P = ( x, y, som är parallell med vektorn v = v, v, v ) 0. ( 3 P Räta linjens ekvation på parameterform kan man ange
RÄTA LINJER OCH PLAN Räta linjer i 3D-rummet: Låt L vara den räta linjen genom punkten P = ( x, y, som är parallell med vektorn v = v, v, v ) 0. ( 3 P Räta linjens ekvation på parameterform kan man ange
Enklare matematiska uppgifter
 Årgång 47, 1964 Första häftet 2457. ABC är en fix liksidig triangel. Linjerna AD och BE är parallella och skär linjerna BC och AC i D resp. E. Vidare är A 1, D 1, B 1 och E 1 mittpunkterna på sträckorna
Årgång 47, 1964 Första häftet 2457. ABC är en fix liksidig triangel. Linjerna AD och BE är parallella och skär linjerna BC och AC i D resp. E. Vidare är A 1, D 1, B 1 och E 1 mittpunkterna på sträckorna
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF625 Envariabelanalys Lösningsförslag till tentamen 206-0- DEL A. Betrakta funktionen f som ges av f(x) = x 2 arctan x. A. Bestäm definitionsmängden till f. B. Bestäm de intervall där f är växande respektive
SF625 Envariabelanalys Lösningsförslag till tentamen 206-0- DEL A. Betrakta funktionen f som ges av f(x) = x 2 arctan x. A. Bestäm definitionsmängden till f. B. Bestäm de intervall där f är växande respektive
SF1626 Flervariabelanalys Tentamen Tisdagen den 12 januari 2016
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den 2 januari 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den 2 januari 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen.
 Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Sidor i boken 40-4 Komposanter, koordinater och vektorlängd Ja, den här teorin gick vi igenom igår. Istället koncentrerar vi oss på träning inför KS3 och tentamen. Läxa 1. En rät linje, L 1, skär y-axeln
Om för en reellvärd funktion f som är definierad på mängden D gäller följande
 OPTIMERING PÅ KOMPAKTA OMRÅDEN. Om för en reellvärd funktion f som är definierad på mängden D gäller följande 1. D är en KOMPAKT mängd. funktionen f är KONTINUERLIG på D då antar f sitt största och sitt
OPTIMERING PÅ KOMPAKTA OMRÅDEN. Om för en reellvärd funktion f som är definierad på mängden D gäller följande 1. D är en KOMPAKT mängd. funktionen f är KONTINUERLIG på D då antar f sitt största och sitt
Tentan , lösningar
 UPPALA UNIVERITET MATEMATIKA INTITUTIONEN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 2008 Tentan 2008-12-16, lösningar 1. Avgör om det finns någon punkt på ytan (x 1) 2 + 2(y 1) 2 + 2z 8 som är
UPPALA UNIVERITET MATEMATIKA INTITUTIONEN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 2008 Tentan 2008-12-16, lösningar 1. Avgör om det finns någon punkt på ytan (x 1) 2 + 2(y 1) 2 + 2z 8 som är
SF1626 Flervariabelanalys Bedömningskriterier till tentamen Måndagen den 16 mars 2015
 SF1626 Flervariabelanalys Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt att följa. Det
SF1626 Flervariabelanalys Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt att följa. Det
Mer om generaliserad integral
 Föreläsning XI Mer om generaliserad integral Ex 64: Givet h(x) = ( x 2 5x + 2 ) e x/2. (a) Bestäm en p.f. till h(x). (b) Beräkna h(x)dx. (a) Vi har här en integrand som är en produkt av ett polynom av
Föreläsning XI Mer om generaliserad integral Ex 64: Givet h(x) = ( x 2 5x + 2 ) e x/2. (a) Bestäm en p.f. till h(x). (b) Beräkna h(x)dx. (a) Vi har här en integrand som är en produkt av ett polynom av
RIEMANNSUMMOR. Den bestämda integralen definieras med hjälp av Riemannsummor. Låt vara en begränsad funktion,, reella tal och. lim.
 RIEMANNSUMMOR Låt vara en begränsad funktion,, reella tal och. Den bestämda integralen definieras med hjälp av ä ä, ; lim. Om funktionen har en elementär primitivfunktion då är insättningsformeln (Newton-
RIEMANNSUMMOR Låt vara en begränsad funktion,, reella tal och. Den bestämda integralen definieras med hjälp av ä ä, ; lim. Om funktionen har en elementär primitivfunktion då är insättningsformeln (Newton-
Ekvationer och system av ekvationer
 Modul: Undervisa matematik utifrån problemlösning Del 4. Strategier Ekvationer och system av ekvationer Paul Vaderlind, Stockholms universitet Ekvationslösning är ett av de viktiga målen i skolmatematiken.
Modul: Undervisa matematik utifrån problemlösning Del 4. Strategier Ekvationer och system av ekvationer Paul Vaderlind, Stockholms universitet Ekvationslösning är ett av de viktiga målen i skolmatematiken.
LOGARITMEKVATIONER. Typ 1. och. Typ2. Vi ska visa först hur man löser två ofta förekommande grundekvationer
 LOGARITMEKVATIONER Vi ska visa först hur man löser två ofta förekommande grundekvationer Typ 1. log aa ff(xx) = nn och Typ2. log aa ff(xx) = log aa gg(xx) När vi löser logaritmekvationer måste vi tänka
LOGARITMEKVATIONER Vi ska visa först hur man löser två ofta förekommande grundekvationer Typ 1. log aa ff(xx) = nn och Typ2. log aa ff(xx) = log aa gg(xx) När vi löser logaritmekvationer måste vi tänka
SF1625 Envariabelanalys Tentamen Måndagen den 12 januari 2015
 SF1625 Envariabelanalys Tentamen Måndagen den 12 januari 2015 Skrivtid: 08:00-13:00 Tillåtna hjälpmedel: inga Examinator: Lars Filipsson Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
SF1625 Envariabelanalys Tentamen Måndagen den 12 januari 2015 Skrivtid: 08:00-13:00 Tillåtna hjälpmedel: inga Examinator: Lars Filipsson Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
Tentamen i tmv036c och tmv035c, Analys och linjär algebra C för K, Kf och Bt A =, = det(a λi) = e 2t + c 2. x(t) = c 1. = c 1.
 Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Kvalificeringstävling den 30 september 2008
 SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
 INVERSA FUNKTIONER DEFINITION. (invers funktion) Låt ff vara en funktion av en reell variabel med definitionsmängden DD ff och värdemängden VV ff. Vi säger att funktionen ff är inverterbar om ekvationen
INVERSA FUNKTIONER DEFINITION. (invers funktion) Låt ff vara en funktion av en reell variabel med definitionsmängden DD ff och värdemängden VV ff. Vi säger att funktionen ff är inverterbar om ekvationen
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
2. Avgör om x och z är implicit definierade som funktion av y via följande ekvationssystem. x 3 + xy + y 2 + z 2 = 0 x + x 3 y + xy 3 + xz 3 = 0
 ATM-Matematik Mikael Forsberg 734-41 3 31 För distans och campus Flervariabelanalys ma1b 14 1 Skrivtid: 9:-14:. Inga hjälpmedel, förutom den bifogade formelsamlingen. Lösningarna skall vara fullständiga
ATM-Matematik Mikael Forsberg 734-41 3 31 För distans och campus Flervariabelanalys ma1b 14 1 Skrivtid: 9:-14:. Inga hjälpmedel, förutom den bifogade formelsamlingen. Lösningarna skall vara fullständiga
Lektion 2. Funktioner av två eller flera variabler variabler
 Lektion 2 Funktioner av två eller flera variabler variabler Innehål 1. Grundlägande topologi (10.1) 2. Funktioner av två variabler (12.1) Innehål 1. Grundlägande topologi (10.1) 2. Funktioner av två variabler
Lektion 2 Funktioner av två eller flera variabler variabler Innehål 1. Grundlägande topologi (10.1) 2. Funktioner av två variabler (12.1) Innehål 1. Grundlägande topologi (10.1) 2. Funktioner av två variabler
SF1661 Perspektiv på matematik Tentamen 24 oktober 2013 kl Svar och lösningsförslag. z 11. w 3. Lösning. De Moivres formel ger att
 SF11 Perspektiv på matematik Tentamen 4 oktober 013 kl 14.00 19.00 Svar och lösningsförslag (1) Låt z = (cos π + i sin π ) och låt w = 1(cos π 3 + i sin π 3 ). Beräkna och markera talet z11 w 3 z 11 w
SF11 Perspektiv på matematik Tentamen 4 oktober 013 kl 14.00 19.00 Svar och lösningsförslag (1) Låt z = (cos π + i sin π ) och låt w = 1(cos π 3 + i sin π 3 ). Beräkna och markera talet z11 w 3 z 11 w
Quiz name: FV4 Date: 10/03/2015 Question with Most Correct Answers: #2 Total Questions: 11 Question with Fewest Correct Answers: #3
 Quiz name: FV4 Date: 10/03/2015 Question with Most Correct Answers: #2 Total Questions: 11 Question with Fewest Correct Answers: #3 1. Vilka av följande påståenden är sanna för en dubbelintegral av en
Quiz name: FV4 Date: 10/03/2015 Question with Most Correct Answers: #2 Total Questions: 11 Question with Fewest Correct Answers: #3 1. Vilka av följande påståenden är sanna för en dubbelintegral av en
Vi har. x (xy2 ) + y ( yz2 ) + z (zx2 ) = y 2 z 2 + x 2 = x 2 + y 2 z 2, xy 2 yz 2 zx 2
 Lektion 6, Flervariabelanals den februari 6.. Beräkna div F och rot F av F e + e. Divergensen och rotationen ges av div F F,,,, + + + +, rot F F,,,, e e e z, +,,,. rot F F,, e e e z z, z, z z z, + z, z
Lektion 6, Flervariabelanals den februari 6.. Beräkna div F och rot F av F e + e. Divergensen och rotationen ges av div F F,,,, + + + +, rot F F,,,, e e e z, +,,,. rot F F,, e e e z z, z, z z z, + z, z
Tentamen: Lösningsförslag
 Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
varandra. Vi börjar med att behandla en linjes ekvation med hjälp av figur 7 och dess bildtext.
 PASS 8 EKVATIONSSYSTEM OCH EN LINJES EKVATION 8 En linjes ekvation En linjes ekvation kan framställas i koordinatsystemet Koordinatsystemet består av x-axeln och yaxeln X-axeln är vågrät och y-axeln lodrät
PASS 8 EKVATIONSSYSTEM OCH EN LINJES EKVATION 8 En linjes ekvation En linjes ekvation kan framställas i koordinatsystemet Koordinatsystemet består av x-axeln och yaxeln X-axeln är vågrät och y-axeln lodrät
För att uttrycka den primitiva funktionen i den ursprungliga variabeln sätter vi in θ = arcsin 2x. Lektion 14, Envariabelanalys den 23 november 1999
 Lektion 4, Envariabelanalys den november 999 6.. Beräkna d 4. Det första vi observerar i integralen är uttrycket i nämnaren, 4. När ett uttryck av den här typen förekommer i en rationell integrand kan
Lektion 4, Envariabelanalys den november 999 6.. Beräkna d 4. Det första vi observerar i integralen är uttrycket i nämnaren, 4. När ett uttryck av den här typen förekommer i en rationell integrand kan
LUNDS TEKNISKA HÖGSKOLA MATEMATIK. LÖSNINGAR FLERDIMENSIONELL ANALYS, FMA kl 8 13
 LUNS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR FLERIMENSIONELL ANALYS, FMA40 04-0- kl 8. Vi börjar med att rita triangelskivan. Linjen genom, och, har ekvationen y x+, linjen genom, och, har ekvationen y 4
LUNS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR FLERIMENSIONELL ANALYS, FMA40 04-0- kl 8. Vi börjar med att rita triangelskivan. Linjen genom, och, har ekvationen y x+, linjen genom, och, har ekvationen y 4
SF1625 Envariabelanalys Tentamen Måndagen den 11 januari 2016
 SF625 Envariabelanalys Tentamen Måndagen den januari 206 Skrivtid: 08:00-3:00 Tillåtna hjälpmedel: inga Examinator: Lars Filipsson Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
SF625 Envariabelanalys Tentamen Måndagen den januari 206 Skrivtid: 08:00-3:00 Tillåtna hjälpmedel: inga Examinator: Lars Filipsson Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
också en lösning: Alla lösningar, i detta fall, ges av
 H009, Introduktionskurs i matematik Armin Halilovic TRIGONOMETRISKA EKVATIONER A) Ekvationen sin( x ) = a (och liknande ekvationer) Ekvationen sin( x ) = a har lösningar endast om a (eftersom sin( x )
H009, Introduktionskurs i matematik Armin Halilovic TRIGONOMETRISKA EKVATIONER A) Ekvationen sin( x ) = a (och liknande ekvationer) Ekvationen sin( x ) = a har lösningar endast om a (eftersom sin( x )
Lösningsförslag, preliminär version 0.1, 23 januari 2018
 Lösningsförslag, preinär version 0., 3 januari 08 Högskolan i Skövde Tentamen i matematik Kurs: MA5G Matematisk analys MA3G Matematisk analys för ingenjörer Tentamensdag: 08-0-03 kl 4:30-9:30 Hjälpmedel
Lösningsförslag, preinär version 0., 3 januari 08 Högskolan i Skövde Tentamen i matematik Kurs: MA5G Matematisk analys MA3G Matematisk analys för ingenjörer Tentamensdag: 08-0-03 kl 4:30-9:30 Hjälpmedel
v0.2, Högskolan i Skövde Tentamen i matematik
 v0., 08-03-3 Högskolan i Skövde Tentamen i matematik Kurs: MA5G Matematisk analys MA3G Matematisk analys för ingenjörer Tentamensdag: 08-0-03 kl 4:30-9:30 Hjälpmedel : Inga hjälpmedel utöver bifogat formelblad.
v0., 08-03-3 Högskolan i Skövde Tentamen i matematik Kurs: MA5G Matematisk analys MA3G Matematisk analys för ingenjörer Tentamensdag: 08-0-03 kl 4:30-9:30 Hjälpmedel : Inga hjälpmedel utöver bifogat formelblad.
1. Beräkna volymen av det område som begränsas av paraboloiden z = 4 x 2 y 2 och xy-planet. Lösning: Volymen erhålles som V = dxdydz.
 Lösningsförslag till tentamensskrivning i Matematik IV, F636(5B0,5B30). Tisdagen den januari 0, kl 400-900. Hjälpmedel: BETA, Mathematics Handbook. Redovisa lösningarna på ett sådant sätt att beräkningar
Lösningsförslag till tentamensskrivning i Matematik IV, F636(5B0,5B30). Tisdagen den januari 0, kl 400-900. Hjälpmedel: BETA, Mathematics Handbook. Redovisa lösningarna på ett sådant sätt att beräkningar
Generaliserade integraler. Definitionen. J amf orelsesatser. Vad skall vi j amf ora med? Absolutkonvergens Dagens amnen 1 / 10
 Dagens ämnen 1 / 10 Dagens ämnen Generaliserade integraler. 1 / 10 Dagens ämnen Generaliserade integraler. Definitionen. 1 / 10 Dagens ämnen Generaliserade integraler. Definitionen. Jämförelsesatser. 1
Dagens ämnen 1 / 10 Dagens ämnen Generaliserade integraler. 1 / 10 Dagens ämnen Generaliserade integraler. Definitionen. 1 / 10 Dagens ämnen Generaliserade integraler. Definitionen. Jämförelsesatser. 1
TENTAMEN HF1006 och HF1008
 TENTAMEN HF006 och HF008 Datum TEN 6 mars 06 Tid 8:-: Analys och linjär algebra, HF008 (Medicinsk teknik), lärare: Inge Jovik Analys och linjär algebra, HF008 (Elektroteknik), lärare: Marina Arakelyan
TENTAMEN HF006 och HF008 Datum TEN 6 mars 06 Tid 8:-: Analys och linjär algebra, HF008 (Medicinsk teknik), lärare: Inge Jovik Analys och linjär algebra, HF008 (Elektroteknik), lärare: Marina Arakelyan
Studietips inför kommande tentamen TEN1 inom kursen TNIU23
 Studietips inför kommande tentamen TEN1 inom kursen TNIU23 Lämplig ordning på sammanfattande studier inom denna kurs: Inled med att grundligt studera föreläsningsanteckningarna Därefter läs tillhörande
Studietips inför kommande tentamen TEN1 inom kursen TNIU23 Lämplig ordning på sammanfattande studier inom denna kurs: Inled med att grundligt studera föreläsningsanteckningarna Därefter läs tillhörande
z = z 2. z = z 2 z /z 2 = 1 1 z = x + c z(x) = x + c = ln x + c + c 2 y(x) = ln y = 0 y(x) = c 2
 Differentialekvationer II Modellsvar: Räkneövning 1 1. Lös differentialekvationen y = (y ) 2 med hjälp av substitutionen z(x) = y (x). Kommentar: detta är standard substitutionen för differentialekvationer
Differentialekvationer II Modellsvar: Räkneövning 1 1. Lös differentialekvationen y = (y ) 2 med hjälp av substitutionen z(x) = y (x). Kommentar: detta är standard substitutionen för differentialekvationer
Tentamen i Analys B för KB/TB (TATA09/TEN1) kl 08 13
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Joakim Arnlind Tentamen i Analys B för KB/TB (TATA9/TEN1) 212-5-22 kl 8 13 Inga hjälpmedel är tillåtna. Varje uppgift kan ge maximalt 3 poäng. Betygsgränser:
LINKÖPINGS UNIVERSITET Matematiska Institutionen Joakim Arnlind Tentamen i Analys B för KB/TB (TATA9/TEN1) 212-5-22 kl 8 13 Inga hjälpmedel är tillåtna. Varje uppgift kan ge maximalt 3 poäng. Betygsgränser:
Lösningar till Matematisk analys
 Lösningar till Matematis analys 0820. Stationära punter. f (x, y) = 8x(x 2 y), f 2(x, y) = 4(y x 2 )). Vi ar alltså att f (x, y) = f 2(x, y) = 0 { x(x 2 y) = 0 y x 2 = 0. Första evationen ovan är uppfylld
Lösningar till Matematis analys 0820. Stationära punter. f (x, y) = 8x(x 2 y), f 2(x, y) = 4(y x 2 )). Vi ar alltså att f (x, y) = f 2(x, y) = 0 { x(x 2 y) = 0 y x 2 = 0. Första evationen ovan är uppfylld
