Kapitel 3. Approximation av funktioner
|
|
|
- Frida Fredriksson
- för 8 år sedan
- Visningar:
Transkript
1 Kapitel 3. Approximation av funktioner Vi skall nu övergå till att beskriva, hur man i praktiken numeriskt beräknar funktioner. I allmänhet kan inte ens elementära funktioner såsom sinus- och cosinusfunktionerna beräknas exakt utom i speciella fall. Några av dem definieras också med hjälp av integraler som inte kan beräknas exakt algebraiskt eller analytiskt. Sålunda brukar man ofta definiera den naturliga logaritmfunktionen som ln x = Z x 1 1 t dt Metoder att beräkna dylika integraler skall vi studera senare. Andra funktioner (som t.ex. arcus tangenten) definieras som inversa funktioner. De blir då implicit definierade som lösningar till olinjära ekvationer som inte kan lösas algebraiskt. Detta är också något som vi skall studera senare. Vetenskapliga beräkningar III, Tom Sundius
2 Ofta är det mycket enklare att använda serieutvecklingar eller s.k. CORDIC algoritmer för att beräkna funktioner. Vid serieutvecklingen av funktioner är det viktigt att känna till konvergensradien, och att bestämma antalet termer som behövs för att reducera felet under en given toleransgräns. Därefter är det enkelt att summera det erforderliga antalet termer. Både om man använder serieutvecklingar och CORDIC algoritmer uppstår svårigheter då argumentet hamnar utanför konvergensintervallet. I sådana fall använder man oftast någon intervallreduktionsmetod. Ett exempel på detta är de vanliga trigonometriska funktionerna sinus och cosinus, som är periodiska med perioden 2π. Om man har bra algoritmer för att beräkna funktionerna inom intervallet [0, 2π], så kan man reducera större argument till detta intervall genom att subtrahera en multipel av 2π. Vetenskapliga beräkningar III, Tom Sundius
3 3.1. Serieutveckling av funktioner Det finns två fundamentala potensserier från vilka många andra kan härledas, nämligen den geometriska serien 1 1 x = x k = 1 + x + x ( x < 1) och exponentialserien Med hjälp av identiteten exp(x) = e x = x k k! = 1 + x + x2 2! + x3 3! +... ( x). e ix = cos x + i sin x Vetenskapliga beräkningar III, Tom Sundius
4 får vi serieutvecklingarna för de trigonometriska funktionerna: cos x = sin x = ( 1) k x 2k (2k)! ( 1) k x 2k+1 (2k + 1)! samt serieutvecklingarna för de hyperboliska funktionerna: cosh x = 1 2 (ex + e x ) = sinh x = 1 2 (ex e x ) = Genom att termvis integrera den geometriska serien får vi ln(1 x) = x k+1 k + 1 = 1 x2 2! + x4 4!... ( x) = x x3 3! + x5 5!... ( x) x 2k (2k)! = 1 + x2 2! + x4 3! +... ( x) x 2k+1 (2k + 1)! = x + x3 3! + x5 5! +... ( x) x2 = x 2 x ( x < 1), Vetenskapliga beräkningar III, Tom Sundius
5 och om vi ersätter x med x ln(1 + x) = ( 1) k+1 x k+1 k + 1 = x x2 2 + x3 3 x ( x 1). Denna metod att beräkna den naturliga logaritmen är dock inte särskilt effektiv. Eftersom serien konvergerar för x = 1, så har vi ln 2 = Om vi beräknar summan av de åtta första termerna i denna serie, får vi ln Eftersom det exakta värdet är , så är felet ca 0.06, eller närmare 9%. Serien konvergerar ytterst långsamt. En snabbare konvergent serie erhålls genom att subtrahera de båda logaritmiska serierna från varandra:! ln 1 + x x3 = ln(1 + x) ln(1 x) = 2 x + 1 x 3 + x Genom att lösa ekvationen 1+x 1 x ln 2 = 2 "1 + (1/3)2 3 3 = 2 får vi x = 1/3, så att + (1/3) # = (2k + 1)3 2k Vetenskapliga beräkningar III, Tom Sundius
6 Om vi vill beräkna logaritmen med ett fel som understiger 10 6 så får vi antalet termer N som behövs genom att kräva att olikheten N < N 10 6 skall gälla. Detta ger N 6, varför 6 termer är tillräckligt. Vi får då resultatet ln X som stämmer mycket väl överens med det exakta värdet. 1 = , (2k + 1)32k Som ett annat exempel skall vi studera hur man kan beräkna ett värde av π utgående från identiteten arctan 1 = π/4. Vi börjar med att konstruera en serieutveckling av denna funktion. Genom substitution av x = t 2 i den geometriska serien finner en serieutveckling av arcus tangentens derivata d dt arctan t = 1 1+t 2 : d dt arctan t = 1 t2 + t 4 t 6... som konvergerar för t < 1. Genom termvis integration av denna potensserie får vi arctan x = Z x 0 (1 t 2 + t 4 t 6...)dt = x x3 3 + x5 5 x7 7..., Vetenskapliga beräkningar III, Tom Sundius
7 som konvergerar för x 1. Vi finner således, att De åtta första termerna ger approximationen π 4 = arctan 1 = π 4 7X ( 1) k 2k + 1 = Om vi tillägger nästa term får vi , vilket fortfarande skiljer sig mycket från det korrekta värdet av π ( ). För dubbel precision enligt IEEE standarden, borde 2 53 termer beräknas! En betydligt snabbare konvergent serie får vi med hjälp av identiteten arctan 1 3 = π/6. Om vi substituerar detta argument i arcustangentens serieutveckling, så får vi π = 6 "3 1/2 3 3/ / = # = 2 3 ( 1) k (2k + 1)3 k Vetenskapliga beräkningar III, Tom Sundius
8 Felet i denna serieutveckling får man genom att beräkna storleken av den första bortlämnade termen. Om vi kräver enkel precisions nogrannhet, så måste felet bli mindre än 2 23, och antalet termer N bör vara så stort, att villkoret 2 3 (2N + 1)3 N < 2 23 är uppfyllt. Vi finner alltså N 13. Samma noggrannhet kräver minst 17 millioner termer, om man använder den förstnämnda metoden att beräkna π. Med hjälp av den nya serien får vi π 2 3 X13 ( 1) k (2k + 1)3 k = , vilket är ett verkligt bra resultat. Som ett sista exempel på användningen av serieutvecklingar, skall vi undersöka hur många termer som man behöver beräkna i exponentialserien för att uppnå en viss noggrannhet. Låt oss anta, att x 2 och att felet < Eftersom felet växer med x och serien är alternerande för x < 0, så kan vi nöja oss med att behandla x = 2. Vetenskapliga beräkningar III, Tom Sundius
9 P N 1 Om serien avbryts efter N termer, får vi approximationen exp x xk k! och det absoluta felet kan då uttryckas e N (x) = k=n = xn N! xn N! x k k! = xn N! + xn+1 (N + 1)! + xn+2 (N + 2)! +... # 1 + x N x 2 (N + 1)(N + 2) +... " " 1 + x N x 2 (N + 1) # = xn 1 N! 1 x, N+1 under förutsättning att 0 < x < N + 1. För x = 2 förenklas denna olikhet till e N (2) 2N N! N + 1 N 1, som alltså skall vara mindre än 10 5 enligt vårt antagande. Vetenskapliga beräkningar III, Tom Sundius
10 Efter prövning finner vi att ! , medan ! = För N = 12 blir faktorn N+1 N , så att övre gränsen blir , som är något för stort. Med 13 termer blir gränsen säkert mindre än 10 5 : ! Om x < 1 2, behöver vi endast medta 7 termer för att uppnå samma noggrannhet. Antalet termer som behövs växer alltså snabbt med x. För att beräkna exponentialfunktionen för stora värden av x kan man använda intervallreduktion. För att beräkna e 2 kan man alltså först använda 7 termer för att beräkna e 1 2, och sedan beräkna e 2 genom två kvadreringar : e 2 = [(e 1 2) 2 ] 2 (visserligen kommer felet då att växa, vilket man måste ta i beaktande). Vetenskapliga beräkningar III, Tom Sundius
11 3.2. CORDIC algoritmer Vi skall nu studera en metod som kan uppfattas som ett modernt sätt att interpolera i funktionstabeller. CORDIC metoden används för att approximativt beräkna funktionsvärden på alla moderna grafiska räknare, som t.ex. TI-85. Algoritmen är inte baserad på serieutveckling eller polynomapproximation, utan istället på ett elementärt system av iterativa ekvationer. CORDIC algoritmen COordinate Rotation DIgital Computer) infördes av Jack Volder år 1959 för att beräkna trigonometriska funktionsvärden, och utvidgades till andra elementära funktioner av John Walther år I CORDIC metoden används endast additioner, subtraktioner, skiftoperationer, jämförelser och uppladdning av lagrade konstanter, vilket gör den speciellt lämpad just för räknare och PC-processorer. Med CORDIC metoden kan man t.o.m. utföra multiplikation och division. CORDIC algoritmen kodas i decimalsystemet, eftersom det tar tid att konvertera från basen 10 till basen 2. Men det är lättare att förstå metoden, om den uttrycks i binärsystemet. Vetenskapliga beräkningar III, Tom Sundius
12 Den trigonometriska CORDIC algoritmen kan härledas ur en allmän rotation i planet: x = x cos φ y sin φ y = y cos φ + x sin φ som roterar en vektor vinkeln φ. Dessa ekvationer kan också skrivas i formen x = cos φ[x y tan φ] y = cos φ[y + x tan φ] Om rotationsvinklarna begränsas på sådant sätt att tan φ = ±2 k, så kan multiplikationen med tangenten uttryckas som en skiftoperation, och man får godtyckliga rotationsvinklar genom att upprepa ett antal elementära rotationer av detta slag. Emedan cos(arctan x) = (1 + x 2 ) 1/2, så kan vi sätta K k = cos(arctan 2 k ) = ( k ) 1/2 och uttrycka de successiva rotationerna i formen där konstanten d k = ±1. x k+1 = K k [x k d k y k 2 k ] y k+1 = K k [y k + d k x k 2 k ], Vetenskapliga beräkningar III, Tom Sundius
13 Skalningsfaktorerna K k behöver inte sättas ut, och kan beaktas senare. Deras produkt kommer att småningom närma sig gränsvärdet Genom ackumulering av vinkelrotationerna tillkommer ytterligare en differensekvation: z k+1 = z k d k arctan 2 k. I allmänhet kan algoritmen uttryckas med hjälp av tre iterativa ekvationer av formen: x k+1 = x k mδ k y k 2 k y k+1 = y k + δ k x k 2 k z k+1 = z k δ k σ k, där värdet av konstanterna m, δ k och σ k beror på vilken typ av beräkning som skall utföras. m är antingen 0, 1 eller 1. Värdet m = 1 används för trigonometriska och inversa trigonometriska funktioner, medan m = 1 används för hyperboliska, inversa hyperboliska och logaritmiska funktioner, liksom även för kvadratrötter. Värdet m = 0 används slutligen för multiplikation och division. Värdet av δ k bestäms av två signum-funktioner: δ k = sgn(z k ) = ( 1, om zk 0 1, om z k < 0 eller δ k = sgn(y k ) = ( 1, om yk < 0 1, om y k 0. Vetenskapliga beräkningar III, Tom Sundius
14 Den förstnämnda funktionen kallas för rotationsmoden, där z värdena reduceras mot 0, och den andra kallas vektoriseringsmoden, där y värdena reduceras mot 0. Observera, att beräkningen av δ k endast kräver en jämförelse. Talen σ k är lagrade konstanter, vilkas värden beror av värdet på m. Om m = 1, så är σ k = arctan 2 k, om m = 0, så är σ k = 2 k, och om m = 1, så är σ k = tanh 1 2 k. För att kunna använda dessa ekvationer, måste man ange utgångsvärdena x 0,y 0 och z 0. Ett av dessa tal (t.ex. z 0 ) kan vara den vinkel vars sinus vi önskar beräkna. Eller också kan två av talen (t.ex. x 0 och y 0 ) vara täljare och nämnare i den kvot vi vill approximera. I varje fall måste utgångsvärdena var begränsade till ett visst intervall kring origo, så att man kan försäkra sig om konvergens. Som vi ser av exemplen, kommer en av variablerna att gå mot noll, medan någon av de andra närmar sig den önskade approximationen. Vi skall nu tillämpa CORDIC algoritmen på division. Antag att m = 0, δ k = sgn(y k ) och σ k = 2 k. Nedanstående iterativa ekvationer kommer då att ge successiva approximationer för kvoten y 0 /x 0 då y 0 /x 0 2: x k+1 = x 0 y k+1 = y k + δ k x 0 2 k z k+1 = z k δ k 2 k (σ k = 2 k ) Som vi ser, innehåller ekvationerna endast additioner, subtraktioner, jämförelser och binära skiftoperationer. Vetenskapliga beräkningar III, Tom Sundius
15 Om z 0 = 0, så finner vi att z n+1 y 0 /x 0 < 2 n, förutsatt att y 0 /x 0 2. Detta inses på följande sätt. Efter ett stort P P n antal iterationer n, så är y k+1 0, och vi får y 0 δ kx 0 2 k, n eller alltså y 0 /x 0 δp k2 k med ett fel som understiger 2 n. Å andra sidan följer av den tredje n ekvationen ovan att z n+1 = δ k2 k (eftersom z 0 = 0), varav påståendet följer. Som ett exempel på användningen, kan vi beräkna 1.2/ Vi får då x 0 = 2.3 samt k y k z k δ k Som vi ser, är felet i z < 2 8 = Vetenskapliga beräkningar III, Tom Sundius
16 För att approximera sinus och cosinus av en vinkel z 0 = θ, π/2 θ π/2 använder vi CORDIC algoritmen med m = 1, δ k = sgn(z k ) och σ k = arctan 2 k : x k+1 = x k δ k y k 2 k y k+1 = y k + δ k x k 2 k z k+1 = z k δ k arctan 2 k (σ k = arctan 2 k ) Begynnelsevärdena är x 0 = K = Q n j=0 cos(σ j), y 0 = 0 och z 0 = θ, som är den givna vinkeln (i radianer). På grund av det sätt varpå z konstrueras, kommer z k att närma sig 0. Därvid närmar sig x cos θ och y sin θ, som vi ser av exemplet nedan. Nedanstående MATLAB program gör 47 iterationer av algoritmen för att approximera sinus och cosinus av en vinkel θ inom intervallet [ π/2, π/2]. Vi ger också en utskrift från programmet, som visar hur z värdena avtar, samtidigt som x värdena närmar sig cos 1 och y värdena sin 1. function cordtrig(t) n=48; x=zeros(n,1); y=x; z=x; s=2.^(0:-1:-46); sig=atan(s); K=prod(cos(sig)); x(1)=k; y(1)=0; z(1)=t; Vetenskapliga beräkningar III, Tom Sundius
17 for j=1:n-1, del=sign(z(j)); if del == 0 del =1; end; x(j+1) = x(j) - del*y(j)*s(j); y(j+1) = y(j) + del*x(j)*s(j); z(j+1) = z(j) - del*sig(j); end answer = [x y z] Resultatet av en beräkning med t = 1 (endast början och slutet): Vetenskapliga beräkningar III, Tom Sundius
18 Varför fungerar algoritmen? Låt oss först analysera geometrin genom att omskriva ekvationerna för x och y i matrisform: 1 xk xk+1 y k+1 = δk 2 k δ k 2 k 1 y k Eftersom σ k = arctan 2 k så är tan σ k = 2 k och sin σ k = cos σ k 2 k. Vetenskapliga beräkningar III, Tom Sundius
19 Härav följer, att den tvåradiga matrisen ovan kan skrivas 1 cos σ k δ k cos σ k 2 k cos σ k δ k cos σ k 2 k = 1 cos σk δ k sin σ k cos σ k cos σ k δ k sin σ k cos σ k Detta är en skalad rotation i planet, eftersom matrisen cos(δk σ k ) sin(δ k σ k ) sin(δ k σ k ) cos(δ k σ k ) = 1 cos(δk σ k ) sin(δ k σ k ) cos σ k sin(δ k σ k ) cos(δ k σ k ). ger upphov till en motsols rotation med rotationsvinkeln δ k σ k = ±σ k = ± arctan 2 k, medan faktorn 1/ cos σ k skalar resultatet. Geometriskt kommer vektorn (x k, y k ) att roteras vinkeln ±σ k = ± arctan 2 k, varpå den töjs ut med en faktor 1/ cos σ k. Härefter är det lätt att se att algoritmen fungerar. Av ekvationen z k+1 = z k δ k arctan 2 k och z 0 = θ följer att z n+1 P P n = θ δ kσ k. Man kan visa, att för stora värden av n gäller z n+1 0, n och således är θ δ kσ k. Vetenskapliga beräkningar III, Tom Sundius
20 Genom att kombinera n + 1 rotationer, finner vi att x värdena närmar sig cos θ och y värdena närmar sig sin θ: x1 = 1 cos(δ0 σ 0 ) sin(δ 0 σ 0 ) K y 1 cos σ 0 sin(δ 0 σ 0 ) cos(δ 0 σ 0 ) 0 x2 y 2 =. xn+1 y n+1 = 1 K 1 cos(δ0 σ 0 + δ 1 σ 1 ) sin(δ 0 σ 0 + δ 1 σ 1 ) cos σ 0 cos σ 1 sin(δ 0 σ 0 + δ 1 σ 1 ) cos(δ 0 σ 0 + δ 1 σ 1 ) 1 cos( P n δ kσ k ) n cos σ 0 cos σ 1... cos σ n sin( cos θ sin θ sin θ cos θ K 0 = K n sin( P δ kσ k ) δ n kσ k ) cos( δ kσ k ) cos θ sin θ 0 K 0 Av programkoden ovan verkar det som om man borde känna värden både av arctan och cosinus för att kunna använda den. Observera dock, att endast speciella värden av σ k och cos σ k behövs då algoritmen kodas i hårdvaran. Dessa värden kan beräknas på förhand och lagras i flyttalsprocessorn. Vetenskapliga beräkningar III, Tom Sundius
Approximation av funktioner
 Vetenskapliga beräkningar III 8 Kapitel Approximation av funktioner Vi skall nu övergå till att beskriva, hur man i praktiken numeriskt beräknar funktioner I allmänhet kan inte ens elementära funktioner
Vetenskapliga beräkningar III 8 Kapitel Approximation av funktioner Vi skall nu övergå till att beskriva, hur man i praktiken numeriskt beräknar funktioner I allmänhet kan inte ens elementära funktioner
SF1625 Envariabelanalys Lösningsförslag till tentamen
 SF1625 Envariabelanalys Lösningsförslag till tentamen 216-6-1 1. Derivera nedanstående funktioner med avseende på x och ange för vilka x derivatan existerar. Endast svar krävs. A. f(x) = arctan 1 x B.
SF1625 Envariabelanalys Lösningsförslag till tentamen 216-6-1 1. Derivera nedanstående funktioner med avseende på x och ange för vilka x derivatan existerar. Endast svar krävs. A. f(x) = arctan 1 x B.
SF1625 Envariabelanalys
 Föreläsning 7 Institutionen för matematik KTH 12 september 2016 Injektiva funktioner En funktion är en regel som till varje tal i definitionsmängden ordnar ett bestämt tal i värdemängden. Injektiva funktioner
Föreläsning 7 Institutionen för matematik KTH 12 september 2016 Injektiva funktioner En funktion är en regel som till varje tal i definitionsmängden ordnar ett bestämt tal i värdemängden. Injektiva funktioner
TATA42: Föreläsning 6 Potensserier
 TATA4: Föreläsning 6 Potensserier Johan Thim januari 7 Vi ska nu betrakta serier där termerna inte längre är konstanter. Speciellt ska vi studera så kallade potensserier. Dessa definieras som a k x k a
TATA4: Föreläsning 6 Potensserier Johan Thim januari 7 Vi ska nu betrakta serier där termerna inte längre är konstanter. Speciellt ska vi studera så kallade potensserier. Dessa definieras som a k x k a
Kontinuitet och gränsvärden
 Kapitel Kontinuitet och gränsvärden.1 Introduktion till kontinuerliga funktioner Kapitlet börjar med allmänna definitioner. Därefter utvidgar vi successivt familjen av kontinuerliga funktioner, genom specifika
Kapitel Kontinuitet och gränsvärden.1 Introduktion till kontinuerliga funktioner Kapitlet börjar med allmänna definitioner. Därefter utvidgar vi successivt familjen av kontinuerliga funktioner, genom specifika
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson, Sebastian Pöder
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson, Sebastian Pöder Tentamen ENVARIABELANALYS M 204-2-08 SVAR OCH ANVISNINGAR UPPGIFTER. e 3x2 lim = e x2 ( 3x 2 +...) = lim ( x 2 +...) = lim
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson, Sebastian Pöder Tentamen ENVARIABELANALYS M 204-2-08 SVAR OCH ANVISNINGAR UPPGIFTER. e 3x2 lim = e x2 ( 3x 2 +...) = lim ( x 2 +...) = lim
Lösningsförslag till tentan i 5B1115 Matematik 1 för B, BIO, E, IT, K, M, ME, Media och T,
 Institutionen för Matematik, KTH. Lösningsförslag till tentan i 5B5 Matematik för B, BIO, E, IT, K, M, ME, Media och T, 8.. Visa att påståendet P n : n + n < 4 n är sant för n =,, 4.... (a) P : + = 4 +
Institutionen för Matematik, KTH. Lösningsförslag till tentan i 5B5 Matematik för B, BIO, E, IT, K, M, ME, Media och T, 8.. Visa att påståendet P n : n + n < 4 n är sant för n =,, 4.... (a) P : + = 4 +
Instuderingsfrågor i Funktionsteori
 Instuderingsfrågor i Funktionsteori Anvisningar. Avsikten med dessa instuderingsfrågor är att ge Dig möjlighet att fortlöpande kontrollera att Du någorlunda behärskar kursens teori. Om Du märker att Du
Instuderingsfrågor i Funktionsteori Anvisningar. Avsikten med dessa instuderingsfrågor är att ge Dig möjlighet att fortlöpande kontrollera att Du någorlunda behärskar kursens teori. Om Du märker att Du
LÖSNINGSFÖRSLAG TILL TENTAMEN 2 SF1664
 LÖSNINGSFÖRSLAG TILL TENTAMEN 2 SF1664 Tillämpad envariabelanalys med numeriska metoder för CFATE1 den 1 mars 214 kl 8.-1. 1. Bestäm värdemängden till funktionen f(x) = 2 arctan x + ln (1 + x 2 ), där
LÖSNINGSFÖRSLAG TILL TENTAMEN 2 SF1664 Tillämpad envariabelanalys med numeriska metoder för CFATE1 den 1 mars 214 kl 8.-1. 1. Bestäm värdemängden till funktionen f(x) = 2 arctan x + ln (1 + x 2 ), där
Konvergens för iterativa metoder
 Konvergens för iterativa metoder 1 Terminologi Iterativa metoder används för att lösa olinjära (och ibland linjära) ekvationssystem numeriskt. De utgår från en startgissning x 0 och ger sedan en följd
Konvergens för iterativa metoder 1 Terminologi Iterativa metoder används för att lösa olinjära (och ibland linjära) ekvationssystem numeriskt. De utgår från en startgissning x 0 och ger sedan en följd
5B1134 Matematik och modeller Lösningsförslag till tentamen den 29 augusti 2005
 KTH Matematik 5B114 Matematik och modeller Lösningsförslag till tentamen den 29 augusti 2005 1. a) Om två av sidorna i en triangel är 5 meter respektive 6 meter. Vilka längder på den tredje sidans längd
KTH Matematik 5B114 Matematik och modeller Lösningsförslag till tentamen den 29 augusti 2005 1. a) Om två av sidorna i en triangel är 5 meter respektive 6 meter. Vilka längder på den tredje sidans längd
Läsanvisningar till kapitel 4 i Naturlig matematik
 Läsanvisningar till kapitel 4 i Naturlig matematik Avsnitt 4.1 I kapitel 4 kommer du att möta de elementära funktionerna. Dessa är helt enkelt de vanligaste funktionerna som vi normalt arbetar med. Här
Läsanvisningar till kapitel 4 i Naturlig matematik Avsnitt 4.1 I kapitel 4 kommer du att möta de elementära funktionerna. Dessa är helt enkelt de vanligaste funktionerna som vi normalt arbetar med. Här
Uppsala Universitet Matematiska Institutionen Bo Styf. Genomgånget på föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf Envariabelanalys, 10 hp STS, X 010-10-7 Genomgånget på föreläsningarna 11-15. Föreläsning 11, 4/11 010: Här kommer vi in i kapitel 4, som handlar om
Uppsala Universitet Matematiska Institutionen Bo Styf Envariabelanalys, 10 hp STS, X 010-10-7 Genomgånget på föreläsningarna 11-15. Föreläsning 11, 4/11 010: Här kommer vi in i kapitel 4, som handlar om
SF1661 Perspektiv på matematik Tentamen 24 oktober 2013 kl Svar och lösningsförslag. z 11. w 3. Lösning. De Moivres formel ger att
 SF11 Perspektiv på matematik Tentamen 4 oktober 013 kl 14.00 19.00 Svar och lösningsförslag (1) Låt z = (cos π + i sin π ) och låt w = 1(cos π 3 + i sin π 3 ). Beräkna och markera talet z11 w 3 z 11 w
SF11 Perspektiv på matematik Tentamen 4 oktober 013 kl 14.00 19.00 Svar och lösningsförslag (1) Låt z = (cos π + i sin π ) och låt w = 1(cos π 3 + i sin π 3 ). Beräkna och markera talet z11 w 3 z 11 w
Prov 1 2. Ellips 12 Numeriska och algebraiska metoder lösningar till övningsproven uppdaterad 20.5.2010. a) i) Nollställen för polynomet 2x 2 3x 1:
 Ellips Numeriska och algebraiska metoder lösningar till övningsproven uppdaterad.. Prov a) i) ii) iii) =,, = st 9,876 =,9876,99 = 9,9,66,66 =,7 =,7 Anmärkning. Nollor i början av decimaltal har ingen betydelse
Ellips Numeriska och algebraiska metoder lösningar till övningsproven uppdaterad.. Prov a) i) ii) iii) =,, = st 9,876 =,9876,99 = 9,9,66,66 =,7 =,7 Anmärkning. Nollor i början av decimaltal har ingen betydelse
2301 OBS! x används som beteckning för både vinkeln x och som x-koordinat
 2301 OBS! x används som beteckning för både vinkeln x och som x-koordinat A Punkten P har koordinaterna x och y P = (x, y) i enhetscirkeln gäller att { x = cos x y = sin x P = (cos x, sin x) För vinkeln
2301 OBS! x används som beteckning för både vinkeln x och som x-koordinat A Punkten P har koordinaterna x och y P = (x, y) i enhetscirkeln gäller att { x = cos x y = sin x P = (cos x, sin x) För vinkeln
Lösningar till MVE017 Matematisk analys i en variabel för I x 3x y = x. 3x2 + 4.
 Lösningar till MVE07 Matematisk analys i en variabel för I 8-0-0. (a Division ger y + 5x x 2 + 4 y x x2 + 4. 5x x 2 + 4 dx 5 2 ln(x2 + 4, vilket ger den integrerande faktorn (x 2 + 4 5/2. Ekvationen multipliceras
Lösningar till MVE07 Matematisk analys i en variabel för I 8-0-0. (a Division ger y + 5x x 2 + 4 y x x2 + 4. 5x x 2 + 4 dx 5 2 ln(x2 + 4, vilket ger den integrerande faktorn (x 2 + 4 5/2. Ekvationen multipliceras
Funktionsserier och potensserier. som gränsvärdet av partialsummorna s n (x) =
 Funktionsserier och potensserier Viktiga exempel på funktionsföljder är funktionsserier. Summan s(x) av f k (x) definieras som gränsvärdet av partialsummorna s n (x) = n f k (x) för varje fixt x I. Serien
Funktionsserier och potensserier Viktiga exempel på funktionsföljder är funktionsserier. Summan s(x) av f k (x) definieras som gränsvärdet av partialsummorna s n (x) = n f k (x) för varje fixt x I. Serien
Kap Generaliserade multipelintegraler.
 Kap 4.3. Generaliserade multipelintegraler. 50. Beräkna följande generaliserade multipelintegraler: A a. dxdy, ges av x, 0 xy x A b. A c. A d. A e. K x ( + x 2 )( + x 2 y 2 ) dxdy, ges av x > 0, xy x dxdy,
Kap 4.3. Generaliserade multipelintegraler. 50. Beräkna följande generaliserade multipelintegraler: A a. dxdy, ges av x, 0 xy x A b. A c. A d. A e. K x ( + x 2 )( + x 2 y 2 ) dxdy, ges av x > 0, xy x dxdy,
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF1625 Envariabelanalys Lösningsförslag till tentamen 215-1-27 DEL A 4 1. Betrakta funktionen f som ges av f(x) = 1 + x + (x 2). 2 A. Bestäm definitionsmängden till f. B. Bestäm alla intervall där f är
SF1625 Envariabelanalys Lösningsförslag till tentamen 215-1-27 DEL A 4 1. Betrakta funktionen f som ges av f(x) = 1 + x + (x 2). 2 A. Bestäm definitionsmängden till f. B. Bestäm alla intervall där f är
Dugga 2 i Matematisk grundkurs
 Linköpings tekniska högskola Matematiska institutionen Tillämpad matematik Kurskod: TATA68 Provkod: TEN Inga hjälpmedel är tillåtna. Dugga i Matematisk grundkurs 013 16 kl 8.00 1.00 Lösningarna skall vara
Linköpings tekniska högskola Matematiska institutionen Tillämpad matematik Kurskod: TATA68 Provkod: TEN Inga hjälpmedel är tillåtna. Dugga i Matematisk grundkurs 013 16 kl 8.00 1.00 Lösningarna skall vara
1.1 Den komplexa exponentialfunktionen
 TATM79: Föreläsning 8 Komplexa exponentialfunktionen och binomiska ekvationer Johan Thim augusti 07 Komplexa tal på polär form Ett komplex tal z = a+bi kan som bekant betraktas som en punkt i komplexa
TATM79: Föreläsning 8 Komplexa exponentialfunktionen och binomiska ekvationer Johan Thim augusti 07 Komplexa tal på polär form Ett komplex tal z = a+bi kan som bekant betraktas som en punkt i komplexa
TMV225+TMV176 Inledande matematik M, TD Sammanfattning. Läsanvisningar inför tentamen.
 TMV225+TMV176 Inledande matematik M, TD Sammanfattning. Läsanvisningar inför tentamen. 2008 10 14 A. Talsystemen. (Adams P.1. Anteckningar från introkursen.) N de naturliga talen Z de hela talen Q de rationella
TMV225+TMV176 Inledande matematik M, TD Sammanfattning. Läsanvisningar inför tentamen. 2008 10 14 A. Talsystemen. (Adams P.1. Anteckningar från introkursen.) N de naturliga talen Z de hela talen Q de rationella
Lösningsförslag envariabelanalys
 Lösningsförslag envariabelanalys 09-06-05. Ekvationen är linjär och har det karakteristiska polynomet pr) = r 4 + r 3 + 5r = r r + r + 5) = r r + i)r + + i). Således ges lösningarna till den homogena ekvationen
Lösningsförslag envariabelanalys 09-06-05. Ekvationen är linjär och har det karakteristiska polynomet pr) = r 4 + r 3 + 5r = r r + r + 5) = r r + i)r + + i). Således ges lösningarna till den homogena ekvationen
Kap Inversfunktion, arcusfunktioner.
 Kap 3. 3.5. Inversfunktion, arcusfunktioner. 30. (A) Förenkla uttrycken så långt som möjligt a. ln 8 ln + ln 8 ln + ln b. ln 3 log 0 3 log 0 e + 3 ln 3 log 3 e 30. (A) Lös ekvationerna a. e x = e x b.
Kap 3. 3.5. Inversfunktion, arcusfunktioner. 30. (A) Förenkla uttrycken så långt som möjligt a. ln 8 ln + ln 8 ln + ln b. ln 3 log 0 3 log 0 e + 3 ln 3 log 3 e 30. (A) Lös ekvationerna a. e x = e x b.
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF1625 Envariabelanalys Lösningsförslag till tentamen 214-1-24 DEL A 1. Låt f(x) = e x sin x. A. Bestäm alla kritiska (stationära) punkter till funktionen f. B. Avgör vilka av de kritiska punkterna som
SF1625 Envariabelanalys Lösningsförslag till tentamen 214-1-24 DEL A 1. Låt f(x) = e x sin x. A. Bestäm alla kritiska (stationära) punkter till funktionen f. B. Avgör vilka av de kritiska punkterna som
5B1134 Matematik och modeller Lösningsförslag till tentamen den 13 januari T = 1 ab sin γ. b sin β = , 956 0, 695 0, 891
 KTH Matematik 5B1134 Matematik modeller Lösningsförslag till tentamen den 13 januari 6 1. a) Bestäm sidlängderna i en triangel med vinklarna 44, 63 73 om arean av triangeln är 64 cm. Ange svaren som närmevärden
KTH Matematik 5B1134 Matematik modeller Lösningsförslag till tentamen den 13 januari 6 1. a) Bestäm sidlängderna i en triangel med vinklarna 44, 63 73 om arean av triangeln är 64 cm. Ange svaren som närmevärden
Modul 5: Integraler. Det är viktigt att du blir bra på att integrera, så träna mycket.
 Institutionen för Matematik SF625 Envariabelanalys Läsåret 27-28 Lars Filipsson Modul 5: Integraler Denna modul handlar om integraler. Det slås fast i en precis definition vad som menas med att en funktion
Institutionen för Matematik SF625 Envariabelanalys Läsåret 27-28 Lars Filipsson Modul 5: Integraler Denna modul handlar om integraler. Det slås fast i en precis definition vad som menas med att en funktion
2320 a. Svar: C = 25. Svar: C = 90
 2320 a Utgå ifrån y = sin x Om vi subtraherar 25 från vinkeln x, så kommer den att "senareläggas" med 25 och således förskjuts grafen åt höger y = sin(x 25 ) Svar: C = 25 b Utgå ifrån y = sin x Om vi adderar
2320 a Utgå ifrån y = sin x Om vi subtraherar 25 från vinkeln x, så kommer den att "senareläggas" med 25 och således förskjuts grafen åt höger y = sin(x 25 ) Svar: C = 25 b Utgå ifrån y = sin x Om vi adderar
Institutionen för Matematik, KTH Lösningar till tentamen i Analys i en variabel för I och K (SF1644) 1/ e x h. (sin x) 2 1 cos x.
 Institutionen för Matematik, KTH Lösningar till tentamen i Analys i en variabel för I och K (SF644) /6 29. Bestäm med derivatans definition d dx ex. Derivatans definition är f (x) = lim h h ( f(x + h)
Institutionen för Matematik, KTH Lösningar till tentamen i Analys i en variabel för I och K (SF644) /6 29. Bestäm med derivatans definition d dx ex. Derivatans definition är f (x) = lim h h ( f(x + h)
SF1661 Perspektiv på matematik Tentamen 20 oktober 2011 kl Svar och lösningsförslag
 Hans Thunberg KTH Matematik SF66 Perspektiv på matematik Tentamen 0 oktober 0 kl 08.00.00 Svar och lösningsförslag () Bestäm ekvationen för den cirkel som passerar genom punkten (, 4) och har sin medelpunkt
Hans Thunberg KTH Matematik SF66 Perspektiv på matematik Tentamen 0 oktober 0 kl 08.00.00 Svar och lösningsförslag () Bestäm ekvationen för den cirkel som passerar genom punkten (, 4) och har sin medelpunkt
f (a) sin
 Hur kan datorn eller räknedosan känna till värdet hos till exempel sin0.23 eller e 2.4? Denna fråga är berättigad samtidigt som ingen tror att apparaterna innehåller en gigantisk tabell. Svaret på frågan
Hur kan datorn eller räknedosan känna till värdet hos till exempel sin0.23 eller e 2.4? Denna fråga är berättigad samtidigt som ingen tror att apparaterna innehåller en gigantisk tabell. Svaret på frågan
Fall 1 2x = sin 1 (1) + n 2π 2x = π 2 + n 2π. x = π 4 + n π. Fall 2 2x = π sin 1 (1) + n 2π. 2x = π π 2 + n 2π
 48 a sin x + cos x = cos x Trigonometriska ettan sin v + cos v = 1 1 = cos x cos x = 1 x = ±cos 1 (1) + n π x = 0 + n π x = n π b sin x cos x = 1 Multiplicera båda led med sin x cos x = 1 sin x cos x =
48 a sin x + cos x = cos x Trigonometriska ettan sin v + cos v = 1 1 = cos x cos x = 1 x = ±cos 1 (1) + n π x = 0 + n π x = n π b sin x cos x = 1 Multiplicera båda led med sin x cos x = 1 sin x cos x =
Euler-Mac Laurins summationsformel och Bernoulliska polynom
 46 Euler-Mac Laurins summationsformel och Bernoulliska polynom Lars Hörmander Lunds Universitet Datorer gör det möjligt att genomföra räkningar som tidigare varit otänkbara, exempelvis att beräkna summan
46 Euler-Mac Laurins summationsformel och Bernoulliska polynom Lars Hörmander Lunds Universitet Datorer gör det möjligt att genomföra räkningar som tidigare varit otänkbara, exempelvis att beräkna summan
v0.2, Högskolan i Skövde Tentamen i matematik
 v0., 08-03-3 Högskolan i Skövde Tentamen i matematik Kurs: MA5G Matematisk analys MA3G Matematisk analys för ingenjörer Tentamensdag: 08-0-03 kl 4:30-9:30 Hjälpmedel : Inga hjälpmedel utöver bifogat formelblad.
v0., 08-03-3 Högskolan i Skövde Tentamen i matematik Kurs: MA5G Matematisk analys MA3G Matematisk analys för ingenjörer Tentamensdag: 08-0-03 kl 4:30-9:30 Hjälpmedel : Inga hjälpmedel utöver bifogat formelblad.
Lösningsförslag TATM
 Lösningsförslag TATM9 0-0-0. a) Summan är geometrisk med kvoten q = / och termer. Alltså, 50 k = 50 k+ = k ) ) ) ) =. k= k= b) Från definitionen av binomialkoefficienter ser vi att ) ) n n nn ) 6 = = =
Lösningsförslag TATM9 0-0-0. a) Summan är geometrisk med kvoten q = / och termer. Alltså, 50 k = 50 k+ = k ) ) ) ) =. k= k= b) Från definitionen av binomialkoefficienter ser vi att ) ) n n nn ) 6 = = =
Lektion 1. Kurvor i planet och i rummet
 Lektion 1 Kurvor i planet och i rummet Innehål Plankurvor Rymdkurvor Innehål Plankurvor Rymdkurvor Tangentvektorn och tangentens ekvation Innehål Plankurvor Rymdkurvor Tangentvektorn och tangentens ekvation
Lektion 1 Kurvor i planet och i rummet Innehål Plankurvor Rymdkurvor Innehål Plankurvor Rymdkurvor Tangentvektorn och tangentens ekvation Innehål Plankurvor Rymdkurvor Tangentvektorn och tangentens ekvation
M0038M Differentialkalkyl, Lekt 10, H15
 M0038M Differentialkalkyl, Lekt 10, H15 Staffan Lundberg Luleå Tekniska Universitet Staffan Lundberg M0038M H15 1/ 31 Repetition Lekt 9 Bestäm största värdet av 5 sin v + 12 cos v. Staffan Lundberg M0038M
M0038M Differentialkalkyl, Lekt 10, H15 Staffan Lundberg Luleå Tekniska Universitet Staffan Lundberg M0038M H15 1/ 31 Repetition Lekt 9 Bestäm största värdet av 5 sin v + 12 cos v. Staffan Lundberg M0038M
10x 3 4x 2 + x. 4. Bestäm eventuella extrempunkter, inflexionspunkter samt horizontella och vertikala asymptoter. y = x 1 x + 1
 TM-Matematik Mikael Forsberg Pär Hemström Övningstenta Envariabelanalys ma034a ovnt--vt0 Skrivtid: 5 timmar. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
TM-Matematik Mikael Forsberg Pär Hemström Övningstenta Envariabelanalys ma034a ovnt--vt0 Skrivtid: 5 timmar. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
Betygskriterier Matematik D MA p. Respektive programmål gäller över kurskriterierna
 Betygskriterier Matematik D MA04 00p Respektive programmål gäller över kurskriterierna MA04 är en nationell kurs och skolverkets kurs- och betygskriterier finns på http://www3.skolverket.se/ Detta är vår
Betygskriterier Matematik D MA04 00p Respektive programmål gäller över kurskriterierna MA04 är en nationell kurs och skolverkets kurs- och betygskriterier finns på http://www3.skolverket.se/ Detta är vår
5. Förklara varför sannolikheten att en slumpvis vald lottorad har 7 rätt är x + x 2 innehåller termen 14x. Bestäm
 VECKANS UPPGIFTER MENY FÖR HELA MOMENT 3 5B3 Amelia fr P och T ht 004 Uppgifter till Vecka 4. Förklara hur ett induktionsbevis fungerar.. Bevisa att 4 n är jämnt delbart med 3 för n =,, 3,... 3. Bevisa
VECKANS UPPGIFTER MENY FÖR HELA MOMENT 3 5B3 Amelia fr P och T ht 004 Uppgifter till Vecka 4. Förklara hur ett induktionsbevis fungerar.. Bevisa att 4 n är jämnt delbart med 3 för n =,, 3,... 3. Bevisa
5B1134 Matematik och modeller Lösningsförslag till tentamen den 11 oktober 2004
 KTH Matematik 5B4 Matematik och modeller Lösningsförslag till tentamen den oktober 4. Två av sidlängderna i en triangel är 8 m och m. En av vinklarna är 6. a) Bestäm alla möjliga värden för den tredje
KTH Matematik 5B4 Matematik och modeller Lösningsförslag till tentamen den oktober 4. Två av sidlängderna i en triangel är 8 m och m. En av vinklarna är 6. a) Bestäm alla möjliga värden för den tredje
Institutionen för Matematik. SF1625 Envariabelanalys. Modul 5 Integraler
 Institutionen för Matematik SF65 Envariabelanalys Läsåret 5/6 Modul 5 Integraler Denna modul omfattar kapitel 5 och avsnitt 6.-6. i kursboken Calculus av Adams och Esse och undervisas på tre föreläsningar,
Institutionen för Matematik SF65 Envariabelanalys Läsåret 5/6 Modul 5 Integraler Denna modul omfattar kapitel 5 och avsnitt 6.-6. i kursboken Calculus av Adams och Esse och undervisas på tre föreläsningar,
Lösningsförslag TATM
 Lösningsförslag TATM79 08-0-04 a Binomialsatsen medför att b Eftersom 5 = 3 + 4i 3 i 5 5 k 5 k k = 3 5 80 4 + 80 3 40 + 0 4i 3 = 3 + 4i3 + i 0 gäller att realdelen blir 9 4 + 3 = + i3 5 = 9 + i3, c Summan
Lösningsförslag TATM79 08-0-04 a Binomialsatsen medför att b Eftersom 5 = 3 + 4i 3 i 5 5 k 5 k k = 3 5 80 4 + 80 3 40 + 0 4i 3 = 3 + 4i3 + i 0 gäller att realdelen blir 9 4 + 3 = + i3 5 = 9 + i3, c Summan
DIFFERENTIALEKVATIONER AV FÖRSTA ORDNINGEN
 SUBSTITUTIONER I DIFFERENTIALEKVATIONER AV FÖRSTA ORDNINGEN Innehåll: I) Allmänt om substitutioner i förstaordningens DE II) Ekvationer av tpen ( ) F( ) ------------------------------------------------------------------------------------
SUBSTITUTIONER I DIFFERENTIALEKVATIONER AV FÖRSTA ORDNINGEN Innehåll: I) Allmänt om substitutioner i förstaordningens DE II) Ekvationer av tpen ( ) F( ) ------------------------------------------------------------------------------------
Fixpunktsiteration. Kapitel Fixpunktsekvation. 1. f(x) = x = g(x).
 Kapitel 5 Fixpunktsiteration 5.1 Fixpunktsekvation En algebraisk ekvation kan skrivas på följande två ekvivalenta sätt (vilket innebär att lösningarna är desamma). 1. f(x) = 0. En lösning x kallas en rot
Kapitel 5 Fixpunktsiteration 5.1 Fixpunktsekvation En algebraisk ekvation kan skrivas på följande två ekvivalenta sätt (vilket innebär att lösningarna är desamma). 1. f(x) = 0. En lösning x kallas en rot
x 2 5x + 4 2x 3 + 3x 2 + 4x + 5. d. lim 2. Kan funktionen f definieras i punkten x = 1 så att f blir kontinuerlig i denna punkt? a.
 . Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
. Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Något om Taylors formel och Mathematica
 HH/ITE/BN Taylors formel och Mathematica Något om Taylors formel och Mathematica Bertil Nilsson 207-0-0 I am the best Ett av Brooks många ödmjuka inlägg i den infekterade striden som under början av 700
HH/ITE/BN Taylors formel och Mathematica Något om Taylors formel och Mathematica Bertil Nilsson 207-0-0 I am the best Ett av Brooks många ödmjuka inlägg i den infekterade striden som under början av 700
NpMa3c vt Kravgränser
 Kravgränser Provet består av ett muntligt delprov (Del A) och tre skriftliga delprov (Del B, Del C och Del D). Tillsammans kan de ge 66 poäng varav 25 E-, 24 C- och 17 A-poäng. Observera att kravgränserna
Kravgränser Provet består av ett muntligt delprov (Del A) och tre skriftliga delprov (Del B, Del C och Del D). Tillsammans kan de ge 66 poäng varav 25 E-, 24 C- och 17 A-poäng. Observera att kravgränserna
601. (A) Bestäm MacLaurinutvecklingarna av ordning 2 till följande uttryck. Resttermen ges på ordoform.
 Kap 4.8 4.9. Taylors formel, Lagranges restterm, stort ordo, entydigheten, approimationer, uppskattning av felet, Maclaurins formel, l'hospitals regel. 60. (A) Bestäm MacLaurinutvecklingarna av ordning
Kap 4.8 4.9. Taylors formel, Lagranges restterm, stort ordo, entydigheten, approimationer, uppskattning av felet, Maclaurins formel, l'hospitals regel. 60. (A) Bestäm MacLaurinutvecklingarna av ordning
6.2 Implicit derivering
 6. Implicit derivering 6 ANALYS 6. Implicit derivering Gränsvärden, som vi just tittat på, är ju en fundamental del av begreppet derivata, och i mattekurserna i gymnasiet har vi roat oss med att hitta
6. Implicit derivering 6 ANALYS 6. Implicit derivering Gränsvärden, som vi just tittat på, är ju en fundamental del av begreppet derivata, och i mattekurserna i gymnasiet har vi roat oss med att hitta
LABORATION 2. Trapetsregeln, MATLAB-funktioner, ekvationer, numerisk derivering
 SF1518,SF1519,numpbd15 LABORATION 2 Trapetsregeln, MATLAB-funktioner, ekvationer, numerisk derivering - Genomför laborationen genom att göra de handräkningar och MATLAB-program som begärs. Var noga med
SF1518,SF1519,numpbd15 LABORATION 2 Trapetsregeln, MATLAB-funktioner, ekvationer, numerisk derivering - Genomför laborationen genom att göra de handräkningar och MATLAB-program som begärs. Var noga med
Signaler några grundbegrepp
 Kapitel 2 Signaler några grundbegrepp I detta avsnitt skall vi behandla några grundbegrepp vid analysen av signaler. För att illustrera de problemställningar som kan uppstå skall vi först betrakta ett
Kapitel 2 Signaler några grundbegrepp I detta avsnitt skall vi behandla några grundbegrepp vid analysen av signaler. För att illustrera de problemställningar som kan uppstå skall vi först betrakta ett
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF165 Envariabelanalys Lösningsförslag till tentamen 01-1-10 DEL A 1. Låt funktionen f ha definitionsmängden D f =]0, [ och ges av f(x) = e x 1 x. (a) Finn f:s invers f 1. ( p) (b) Finn inversens värdemängd
SF165 Envariabelanalys Lösningsförslag till tentamen 01-1-10 DEL A 1. Låt funktionen f ha definitionsmängden D f =]0, [ och ges av f(x) = e x 1 x. (a) Finn f:s invers f 1. ( p) (b) Finn inversens värdemängd
Kap 5.7, Beräkning av plana areor, rotationsvolymer, rotationsareor, båglängder.
 Kap 5.7, 7. 7.. Beräkning av plana areor, rotationsvolymer, rotationsareor, båglängder. 8. (A) Beräkna arean av det ändliga område som begränsas av kurvorna x a. y = + x och y = b. y = x e x och y = x
Kap 5.7, 7. 7.. Beräkning av plana areor, rotationsvolymer, rotationsareor, båglängder. 8. (A) Beräkna arean av det ändliga område som begränsas av kurvorna x a. y = + x och y = b. y = x e x och y = x
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen DEL A
 SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 16-8-18 DEL A 1. Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x och y =
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 16-8-18 DEL A 1. Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x och y =
Matematik D (MA1204)
 Matematik D (MA104) 100 p Betygskriterier med eempeluppgifter Värmdö Gymnasium Betygskriterier enligt Skolverket Kriterier för betyget Godkänd Eleven använder lämpliga matematiska begrepp, metoder och
Matematik D (MA104) 100 p Betygskriterier med eempeluppgifter Värmdö Gymnasium Betygskriterier enligt Skolverket Kriterier för betyget Godkänd Eleven använder lämpliga matematiska begrepp, metoder och
BASPROBLEM I ENDIMENSIONELL ANALYS 1 Jan Gustavsson
 Matematikcentrum Matematik BASPROBLEM I ENDIMENSIONELL ANALYS Jan Gustavsson. Algebraiska förenklingar.. Reella andragradsekvationer.. Enkla rotekvationer - eventuellt med falsk rot.. Enkla absolutbeloppsproblem.
Matematikcentrum Matematik BASPROBLEM I ENDIMENSIONELL ANALYS Jan Gustavsson. Algebraiska förenklingar.. Reella andragradsekvationer.. Enkla rotekvationer - eventuellt med falsk rot.. Enkla absolutbeloppsproblem.
Mer om funktioner och grafik i Matlab
 CTH/GU 2017/2018 Matematiska vetenskaper Mer om funktioner och grafik i Matlab 1 Inledning Först skall vi se lite på funktioner som redan finns i Matlab, (elementära) matematiska funktioner som sinus och
CTH/GU 2017/2018 Matematiska vetenskaper Mer om funktioner och grafik i Matlab 1 Inledning Först skall vi se lite på funktioner som redan finns i Matlab, (elementära) matematiska funktioner som sinus och
Kap. P. Detta kapitel utgör Inledande kurs i matematik. I kapitlet beskrivs vilka bakgrundskunskaper som förutsätts.
 5B1103, Differential och integralkalkyl II, del 1. LÄSANVISNINGAR TILL R.A. ADAMS, CALCULUS, A COMPLETE COURSE, 4TH ED. OMFATTNING: kapitel 1.1 1.5, Appendix III, 2, 3.1 3.4, 3.5 till def. 13, 17.7 t.o.m.
5B1103, Differential och integralkalkyl II, del 1. LÄSANVISNINGAR TILL R.A. ADAMS, CALCULUS, A COMPLETE COURSE, 4TH ED. OMFATTNING: kapitel 1.1 1.5, Appendix III, 2, 3.1 3.4, 3.5 till def. 13, 17.7 t.o.m.
Föreläsning 1. X kallas för funktionens definitionsmängd, mängden av funktionens alla värden kallas funktionens värdemängd.
 Föreläsning 1 Kursinformation All viktig information om kursen ska kunna läsas på kursens hemsida http://www.math.uu.se/ rikardo/ envariabelanalys/huvudsidor/index.html Funktioner En funktion f, från mängden
Föreläsning 1 Kursinformation All viktig information om kursen ska kunna läsas på kursens hemsida http://www.math.uu.se/ rikardo/ envariabelanalys/huvudsidor/index.html Funktioner En funktion f, från mängden
DERIVATA. = lim. x n 2 h h n. 2
 DERIVATA Läs avsnitten 6.-6.5. Lös övningarna 6.cd, 6.2, 6.3bdf, 6.4abc, 6.5bcd, 6.6bcd, 6.7, 6.9 oc 6.. Läsanvisningar Allmänt gäller som vanligt att bevisen inte ingår i kursen, men det är mycket nyttigt
DERIVATA Läs avsnitten 6.-6.5. Lös övningarna 6.cd, 6.2, 6.3bdf, 6.4abc, 6.5bcd, 6.6bcd, 6.7, 6.9 oc 6.. Läsanvisningar Allmänt gäller som vanligt att bevisen inte ingår i kursen, men det är mycket nyttigt
Lösningsmetodik för FMAF01: Funktionsteori
 Lösningsmetodik för FMAF0: Funktionsteori Johannes Larsson, I2 0 mars 204 Allmänt Detta är lösningsmetoder för de vanligaste tentauppgifterna, grupperade efter hur ofta de kommer på tentan och därmed också
Lösningsmetodik för FMAF0: Funktionsteori Johannes Larsson, I2 0 mars 204 Allmänt Detta är lösningsmetoder för de vanligaste tentauppgifterna, grupperade efter hur ofta de kommer på tentan och därmed också
Lösningsförslag, preliminär version 0.1, 23 januari 2018
 Lösningsförslag, preinär version 0., 3 januari 08 Högskolan i Skövde Tentamen i matematik Kurs: MA5G Matematisk analys MA3G Matematisk analys för ingenjörer Tentamensdag: 08-0-03 kl 4:30-9:30 Hjälpmedel
Lösningsförslag, preinär version 0., 3 januari 08 Högskolan i Skövde Tentamen i matematik Kurs: MA5G Matematisk analys MA3G Matematisk analys för ingenjörer Tentamensdag: 08-0-03 kl 4:30-9:30 Hjälpmedel
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 6, Differential- och integralkalkyl II, del, envariabel, för F. Tentamen torsdag 3 maj 7, 8.-3. Förslag till lösningar.. Ange definitions- och värdemängderna
Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 6, Differential- och integralkalkyl II, del, envariabel, för F. Tentamen torsdag 3 maj 7, 8.-3. Förslag till lösningar.. Ange definitions- och värdemängderna
5B1134 Matematik och modeller
 KTH Matematik 1 5B1134 Matematik och modeller 2006-09-11 2 Andra veckan Trigonometri Veckans begrepp enhetscirkeln, trigonometriska ettan trigonometrisk funktion, sinuskurva period, fasförskjutning, vinkelhastighet
KTH Matematik 1 5B1134 Matematik och modeller 2006-09-11 2 Andra veckan Trigonometri Veckans begrepp enhetscirkeln, trigonometriska ettan trigonometrisk funktion, sinuskurva period, fasförskjutning, vinkelhastighet
LABORATION cos (3x 2 ) dx I =
 SF1518,SF1519,numpbd14 LABORATION 2 Trapetsregeln, ekvationer, ekvationssystem, MATLAB-funktioner Studera kapitel 6 och avsnitt 5.2.1, 1.3 och 3.8 i NAM parallellt med arbetet på denna laboration. Genomför
SF1518,SF1519,numpbd14 LABORATION 2 Trapetsregeln, ekvationer, ekvationssystem, MATLAB-funktioner Studera kapitel 6 och avsnitt 5.2.1, 1.3 och 3.8 i NAM parallellt med arbetet på denna laboration. Genomför
Repetitionsuppgifter
 MVE5 H5 MATEMATIK Chalmers Repetitionsuppgifter Integraler och tillämpningar av integraler. (a) Beräkna (b) Avgör om den generaliserade integralen arctan(x) ( + x) dx. dx x x är konvergent eller divergent.
MVE5 H5 MATEMATIK Chalmers Repetitionsuppgifter Integraler och tillämpningar av integraler. (a) Beräkna (b) Avgör om den generaliserade integralen arctan(x) ( + x) dx. dx x x är konvergent eller divergent.
Uppgift 1. Bestäm definitionsmängder för följande funktioner 2. lim
 Tentamen (TEN) i MATEMATIK, HF 7 dec 7 Tid :-7: KLASS: BP 7 Lärare: Armin Halilovic Hjälpmedel: Miniräknare av vilken typ som helst, en formelsamling och ett bifogat formelblad. Denna lapp lämnar du in
Tentamen (TEN) i MATEMATIK, HF 7 dec 7 Tid :-7: KLASS: BP 7 Lärare: Armin Halilovic Hjälpmedel: Miniräknare av vilken typ som helst, en formelsamling och ett bifogat formelblad. Denna lapp lämnar du in
A1:an Repetition. Philip Larsson. 6 april Kapitel 1. Grundläggande begrepp och terminologi
 A1:an Repetition Philip Larsson 6 april 013 1 Kapitel 1. Grundläggande begrepp och terminologi 1.1 Delmängd Om ändpunkterna ska räknas med används symbolerna [ ] och raka sträck. Om ändpunkterna inte skall
A1:an Repetition Philip Larsson 6 april 013 1 Kapitel 1. Grundläggande begrepp och terminologi 1.1 Delmängd Om ändpunkterna ska räknas med används symbolerna [ ] och raka sträck. Om ändpunkterna inte skall
SF1625 Envariabelanalys Lösningsförslag till tentamen DEL A
 SF1625 Envariabelanalys Lösningsförslag till tentamen 2015-01-12 DEL A 1. Betrakta funktionen f som ges av f(x) = xe 1/x. A. Bestäm definitionsmängden till f. B. Beräkna de fyra gränsvärdena lim x ± f(x)
SF1625 Envariabelanalys Lösningsförslag till tentamen 2015-01-12 DEL A 1. Betrakta funktionen f som ges av f(x) = xe 1/x. A. Bestäm definitionsmängden till f. B. Beräkna de fyra gränsvärdena lim x ± f(x)
Explorativ övning 7 KOMPLEXA TAL
 Explorativ övning 7 KOMPLEXA TAL Övningens syfte är att bekanta sig med komplexa tal. De komplexa talen, som är en utvidgning av de reella talen, kom till på 1400 talet då man försökte lösa kvadratiska
Explorativ övning 7 KOMPLEXA TAL Övningens syfte är att bekanta sig med komplexa tal. De komplexa talen, som är en utvidgning av de reella talen, kom till på 1400 talet då man försökte lösa kvadratiska
D 1 u(x, y) = e x (1 + x + y 2 ), D 2 u(x, y) = 2ye x + 1, (x, y) R 2.
 Differentialekvationer I Modellsvar till räkneövning 4 De frivilliga uppgifterna U1 och U2 påminner om nyttiga kunskaper, och räknas inte för extrapoäng (fråga vid behov). U1. Sök en potentialfunktion
Differentialekvationer I Modellsvar till räkneövning 4 De frivilliga uppgifterna U1 och U2 påminner om nyttiga kunskaper, och räknas inte för extrapoäng (fråga vid behov). U1. Sök en potentialfunktion
Lösningsförslag TATM
 Lösningsförslag TATM79 016-09-6 1 a) Vi isolerar x + och kvadrerar ekvationen observera att det då bara blir en implikation!): + x + = x x + = x ) x + = x ) = x 1x + 1 x 1 x + 10 = 0 x = 1 6 ± 7 6 Eftersom
Lösningsförslag TATM79 016-09-6 1 a) Vi isolerar x + och kvadrerar ekvationen observera att det då bara blir en implikation!): + x + = x x + = x ) x + = x ) = x 1x + 1 x 1 x + 10 = 0 x = 1 6 ± 7 6 Eftersom
6.3. Direkta sökmetoder
 6.3. Direkta sökmetoder Förutom de nyss nämnda metoderna för att uppsöka ett minimum av en funktion av en variabel finns det en enkel metod som baserar sig på polynomapproximation av funktionen. Om vi
6.3. Direkta sökmetoder Förutom de nyss nämnda metoderna för att uppsöka ett minimum av en funktion av en variabel finns det en enkel metod som baserar sig på polynomapproximation av funktionen. Om vi
Kapitel 4. Iterativ lösning av ekvationer
 Kapitel 4. Iterativ lösning av ekvationer Vi skall nu undersöka, har man löser numeriskt ekvationer av formen f(x) = 0. Dylika ekvationer kallas också olinjära, eftersom funktionen oftast har ett olinjärt
Kapitel 4. Iterativ lösning av ekvationer Vi skall nu undersöka, har man löser numeriskt ekvationer av formen f(x) = 0. Dylika ekvationer kallas också olinjära, eftersom funktionen oftast har ett olinjärt
Tentamen i Envariabelanalys 1
 Linköpings universitet Matematiska institutionen Matematik och tillämpad matematik Kurskod: TATA4 Provkod: TEN Tentamen i Envariabelanalys 4--8 kl. 8.. Inga hjälpmedel. Lösningarna ska vara fullständiga,
Linköpings universitet Matematiska institutionen Matematik och tillämpad matematik Kurskod: TATA4 Provkod: TEN Tentamen i Envariabelanalys 4--8 kl. 8.. Inga hjälpmedel. Lösningarna ska vara fullständiga,
Lösningsförslag till tentamen Torsdag augusti 16, 2018 DEL A
 Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
Prov i matematik Distans, Matematik A Analys UPPSALA UNIVERSITET Matematiska institutionen
 UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik Distans, Matematik A Analys 23 2 5 Skrivtid: -5. Hjälpmedel: Gymnasieformelsamling. Lösningarna skall åtföljas av förklarande
UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik Distans, Matematik A Analys 23 2 5 Skrivtid: -5. Hjälpmedel: Gymnasieformelsamling. Lösningarna skall åtföljas av förklarande
a n β n + a n 1 β n a 0 + a 1 β 1 + a 2 β , x = r β e ; 0.1 r < 1; e = heltal.
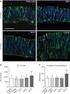 De iakttagna fenomenen beror på avrundningsfel, och vi skall därför studera talframställningen i datorer. Vid beräkningar för hand är det vanligt att man uttrycker tal i tiopotensframställningen, men i
De iakttagna fenomenen beror på avrundningsfel, och vi skall därför studera talframställningen i datorer. Vid beräkningar för hand är det vanligt att man uttrycker tal i tiopotensframställningen, men i
TATA42: Föreläsning 5 Serier ( generaliserade summor )
 TATA42: Föreläsning 5 Serier ( generaliserade summor ) Johan Thim 0 januari 207 En funktion s: N R brukar kallas talföljd, och vi skriver ofta s n i stället för s(n). Detta innebär alltså att för varje
TATA42: Föreläsning 5 Serier ( generaliserade summor ) Johan Thim 0 januari 207 En funktion s: N R brukar kallas talföljd, och vi skriver ofta s n i stället för s(n). Detta innebär alltså att för varje
Lektion 6, Envariabelanalys den 14 oktober Låt oss krympa f:s definitionsmängd till en liten omgivning av x = x 2.
 Lektion 6, Envariabelanals den 4 oktober 999 Låt f vara en kontinuerligt deriverbar funktion vars graf är återgiven i figuren till höger. Besvara följande frågor. Låt oss krmpa f:s definitionsmängd till
Lektion 6, Envariabelanals den 4 oktober 999 Låt f vara en kontinuerligt deriverbar funktion vars graf är återgiven i figuren till höger. Besvara följande frågor. Låt oss krmpa f:s definitionsmängd till
Bose-Einsteinkondensation. Lars Gislén, Malin Sjödahl, Patrik Sahlin
 Bose-Einsteinkondensation Lars Gislén, Malin Sjödahl, Patrik Sahlin 3 mars, 009 Inledning Denna laboration går ut på att studera Bose-Einsteinkondensation för bosoner i en tredimensionell harmonisk-oscillatorpotential.
Bose-Einsteinkondensation Lars Gislén, Malin Sjödahl, Patrik Sahlin 3 mars, 009 Inledning Denna laboration går ut på att studera Bose-Einsteinkondensation för bosoner i en tredimensionell harmonisk-oscillatorpotential.
5B1147. Envariabelanalys. MATLAB Laboration. Laboration 1. Gränsvärden och Summor
 5B47 MATLAB Laboration Laboration Gränsvärden och Summor joycew@kth.se uvehag@kth.se Innehåll Uppgift a... Problem... Lösning... Grafisk bestämning av gränsvärden... Beräkning av gränsvärden...2 Uppgift
5B47 MATLAB Laboration Laboration Gränsvärden och Summor joycew@kth.se uvehag@kth.se Innehåll Uppgift a... Problem... Lösning... Grafisk bestämning av gränsvärden... Beräkning av gränsvärden...2 Uppgift
Några saker att tänka på inför dugga 2
 LINKÖPINGS UNIVERSITET 17 oktober 017 Matematiska institutionen TATA68 Matematik och tillämpad matematik Några saker att tänka på inför dugga Dugga omfattar HELA kursen, så titta även på de tips som lämnades
LINKÖPINGS UNIVERSITET 17 oktober 017 Matematiska institutionen TATA68 Matematik och tillämpad matematik Några saker att tänka på inför dugga Dugga omfattar HELA kursen, så titta även på de tips som lämnades
x 2 5x + 4 2x 3 + 3x 2 + 4x + 5. d. lim 2. Kan funktionen f definieras i punkten x = 1 så att f blir kontinuerlig i denna punkt? a.
 . Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim 0. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
. Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim 0. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
7 november 2014 Sida 1 / 21
 TANA09 Föreläsning 2 Talrepresentation i datorer. Flyttalssystem. Datoraritmetik och Beräkningsfel. Beräkningsfelsanalys och Kancellation. Serier och Resttermsuppskattningar. Tillämpning - Beräkning av
TANA09 Föreläsning 2 Talrepresentation i datorer. Flyttalssystem. Datoraritmetik och Beräkningsfel. Beräkningsfelsanalys och Kancellation. Serier och Resttermsuppskattningar. Tillämpning - Beräkning av
Lösningsförslag till TATA42-tentan
 Lösningsförslag till TATA-tentan 8-6-.. Då ekvationen är linjär av första ordningen löses den enklast med hjälp av integrerande faktor (I.F.). Skriv först ekvationen på standardform. (+ )y y + y + + y
Lösningsförslag till TATA-tentan 8-6-.. Då ekvationen är linjär av första ordningen löses den enklast med hjälp av integrerande faktor (I.F.). Skriv först ekvationen på standardform. (+ )y y + y + + y
TANA17 Matematiska beräkningar med Matlab
 TANA17 Matematiska beräkningar med Matlab Laboration 1. Linjär Algebra och Avbildningar Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion I denna övning skall
TANA17 Matematiska beräkningar med Matlab Laboration 1. Linjär Algebra och Avbildningar Namn: Personnummer: Epost: Namn: Personnummer: Epost: Godkänd den: Sign: Retur: 1 Introduktion I denna övning skall
+ 5a 16b b 5 då a = 1 2 och b = 1 3. n = 0 där n = 1, 2, 3,. 2 + ( 1)n n
 Repetition, Matematik I.. Bestäm koefficienten vid 2 i utvecklingen av ( + 2 2 ) 5. 2. Bestäm koefficienten vid 2 i utvecklingen av ( + ) n för n =, 2,,.. Beräkna a 5 5a 2b + 5a 2b 2 5a 2 b + 5a 6b 2b
Repetition, Matematik I.. Bestäm koefficienten vid 2 i utvecklingen av ( + 2 2 ) 5. 2. Bestäm koefficienten vid 2 i utvecklingen av ( + ) n för n =, 2,,.. Beräkna a 5 5a 2b + 5a 2b 2 5a 2 b + 5a 6b 2b
Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int,
![Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int, Rita även upp grafen till Fourierseriens summa på intervallet [ 2π, 3π], samt ange summans värde i punkterna π, 0, π, 2π. (5) S(t) = c n e int,](/thumbs/87/95082344.jpg) Institutionen för matematik KTH Tentamensskrivning, 003-08-5, kl. 14.00 19.00. 5B10/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3) krävs 18 poäng, medan
Institutionen för matematik KTH Tentamensskrivning, 003-08-5, kl. 14.00 19.00. 5B10/ Diff och Trans del, för F och T. Hjälpmedel: BETA, Mathematics Handbook. För godkänt betyg 3) krävs 18 poäng, medan
Fyra fyror. Mikael Knutsson. Tredje utgåvan, Mikael Knutsson
 Fyra fyror Mikael Knutsson Tredje utgåvan, 2003-11-23 2001-2003 Mikael Knutsson 1 Inledning Man får använda fyra fyror, varken mer eller mindre. Med dem skall man skriva talet n. Man får sätta in dem efter
Fyra fyror Mikael Knutsson Tredje utgåvan, 2003-11-23 2001-2003 Mikael Knutsson 1 Inledning Man får använda fyra fyror, varken mer eller mindre. Med dem skall man skriva talet n. Man får sätta in dem efter
5B1134 Matematik och modeller Lösningsförslag till tentamen den 12 januari 2005
 KTH Matematik B Matematik modeller Lösningsförslag till tentamen den januari. a) I en triangel är två av sidlängderna 7 respektive 8 längdeneter vinkeln mellan dessa sidor är. Bestäm den tredje sidans
KTH Matematik B Matematik modeller Lösningsförslag till tentamen den januari. a) I en triangel är två av sidlängderna 7 respektive 8 längdeneter vinkeln mellan dessa sidor är. Bestäm den tredje sidans
MA2047 Algebra och diskret matematik
 MA047 Algebra och diskret matematik Något om trigonometriska funktioner Mikael Hindgren 7 oktober 08 Enhetscirkeln Definition (Vinkelmåttet radianer) l.e. Den vinkel som motsvarar en båge med längden l.e.
MA047 Algebra och diskret matematik Något om trigonometriska funktioner Mikael Hindgren 7 oktober 08 Enhetscirkeln Definition (Vinkelmåttet radianer) l.e. Den vinkel som motsvarar en båge med längden l.e.
x 2 5x + 4 2x 3 + 3x 2 + 4x + 5. d. lim 2. Kan funktionen f definieras i punkten x = 1 så att f blir kontinuerlig i denna punkt? a.
 . Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
. Beräkna följande gränsvärden: a. lim 2 5 + 6 2 2. b. lim 2 5 + 4 3 + 2 4 2. c. lim. d. lim 2 3 + 3 2 + 4 + 5 2 + + 3 + 2 2 + 3 + 4. 2. Kan funktionen f definieras i punkten = så att f blir kontinuerlig
Lösningsförslag obs. preliminärt, reservation för fel
 Lösningsförslag obs. preliminärt, reservation för fel v0.6, 4 april 04 Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA5G Matematisk Analys MA3G Matematisk analys för ingenjörer Tentamensdag:
Lösningsförslag obs. preliminärt, reservation för fel v0.6, 4 april 04 Högskolan i Skövde (SK, JS) Tentamen i matematik Kurs: MA5G Matematisk Analys MA3G Matematisk analys för ingenjörer Tentamensdag:
sin (x + π 2 ) = sin x cos π 2 + cos x sin π 2 = cos π 2 = 0 sin π 2 = 1 Svar: cos x
 33 a Använd additionsformel för sinus sin(x + 55 ) = sin x cos 55 + cos x sin 55 cos 55 och sin 55 beräknas med tekniskt hjälpmedel TI-räknare c Använd additionsformel för sinus sin (x + π ) = sin x cos
33 a Använd additionsformel för sinus sin(x + 55 ) = sin x cos 55 + cos x sin 55 cos 55 och sin 55 beräknas med tekniskt hjälpmedel TI-räknare c Använd additionsformel för sinus sin (x + π ) = sin x cos
MAA151 Envariabelkalkyl läsåret 2016/17
 Lektionsuppgifter A Omgång 1 (5) Funktioner 1. Bestäm inversen till funktionen f efiniera enligt f() = 1/ 1. Specificera speciellt inversens efinitionsmäng och väremäng. Skissa även i ett och samma koorinatsystem
Lektionsuppgifter A Omgång 1 (5) Funktioner 1. Bestäm inversen till funktionen f efiniera enligt f() = 1/ 1. Specificera speciellt inversens efinitionsmäng och väremäng. Skissa även i ett och samma koorinatsystem
