FACIT TILL OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B kl. 08:15 13:15
|
|
|
- Kjell Lundberg
- för 9 år sedan
- Visningar:
Transkript
1 FACIT TILL OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B kl. 08:15 1:15 Ansvrig Lärr: Donl F. Ross Hjälpml: Ing. Algoritmrn finns i rspktiv uppgiftrn. Btygsgräns: *** OBS *** Kurs: Tntmn: Lrn: Mx 60p, M röm gokän 50p, Ik utn röm gokän 40p, Gokän 0p (vrv minimum 15p från tntmn, 15p från lrn) Mx 0p, tyg 5: 26p-0p, tyg 4: 21p-25p, tyg : 15p-20p Mx 0p, tyg 5: 26p-0p, tyg 4: 21p-25p, tyg : 15p-20p SKRIV TYDLIGT LÄS UPPGIFTERNA NOGGRANT Ang ll ntgnn. (1) G tt kortfttt svr till följn uppgiftr (()-(j)). () En finition v n mäng Dfinition: An unorr olltion of uniqu ntitis hving ommon proprty (ttriut). Exmpl: St of olours: {r, grn, lu, yllow,..., lk () En finition v n skvns Dfinition: An orr olltion of ntitis (not nssrily uniqu) hving ommon proprty (ttriut) with sussor rltionship fin twn ntitis. Exmpl: Dys of th wk: (Mony, Tusy,..., Suny) () En finition v tt trä Dfinition: An unorr/orr olltion of ntitis (not nssrily uniqu) hving ommon proprty (ttriut) with snnt rltionship fin twn ntitis. Exmpl: Fil irtoris in omputing systms () En finition v n grf Dfinition: An unorr olltion of ntitis (not nssrily uniqu) hving ommon proprty (ttriut) with (gnrl) rltionship fin twn ntitis. Exmpl: A Tlphon / Computr ntwork (in ft ny ntwork) () En finition v n smling Dfinition: An unorr/orr numr of ntitis (not nssrily uniqu) hving ommon proprty (ttriut) possily with rltionship fin twn ntitis. Exmpl: st, squn, tr, grph DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 1 v 17
2 Förklr Din xmpl ((f)-(j)) m någr mningr FULL: PERFECT: BT hight h with xtly 2 h -1 lmnts COMPLETE: prft on th nxt lowst lvl AND th lowst lvl is fill from th lft vry no hs xtly 2 or 0 hilrn (f) Ett xmpl v tt fullt trä som int är kompltt (g) Ett xmpl v tt kompltt trä som int är fullt (h) Ett xmpl v tt trä som är vrkn fullt llr kompltt llr prfkt (i) Ett xmpl v implmnttionsstrktion Gt n st funtions on th ttriuts of n ADT (j) Ett xmpl v svnsrkursion (til rursion) int: siz (List) { if is_mpty (List) rturn 0; rturn 1 + siz(til(list)); Totlt 5p DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 2 v 17
3 (2) G tt kortfttt svr till följn uppgiftr. () En finition v rkursion Dfinition 1: An ntity prtilly fin in trms of itslf is rursivly fin Dfinition 2: A funtion whih lls itslf unr rtin onitions is rursivly fin. () En förklring v strktion Dfinition 1: MODELLING ABSTRACTION Th pross of slting rtin proprtis (ttriuts) of n ntity to rprsnt tht ntity in givn sitution. Exmpl 1: In rlity informtion out stunt ( rl worl ntity) my inlu proprtis (ttriuts) suh s STUDENT (nm, t of irth, gnr, rss, pnumr, tlphon numr, moil numr, hir olour, y olour, fthr's nm, mothr's nm, t....) Som of this informtion n "strt" s STUDENT (nm, t of irth, gnr, rss, pnumr) in ts for xmpl to "rprsnt" (or mol) stunt Dfinition 2: COLLECTION ABSTRACTION Th pross of gnrlising ommon proprtis n oprtions of th st, squn, tr n grph. Eh is olltion with th squn, tr n grph lso hving rltionships fin - squn (sussor/prssor), tr (lft hil, right hil), grph ( gnrl rltionship rprsnting istn, ost, onntion). Exmpl 2: A olltion n fin s omprising ntitis n rltionships, oth with possil ttriuts n oprtions suh s is_mpty(), rinlity(), (), rmov(), fin(), isply(). Dfinition : IMPLEMENTATION ABSTRACTION Th pross of slting rtin proprtis of Dt Typ inpnnt of th implmnttion of tht Dt Typ - hn th xprssion Astrt Dt Typ Exmpl : A squn my implmnt using n rry of vlus n n inx to tht rry rrys (vlu, nxt) n n inx rors/struturs n pointrs ( link list) In ll ss, t mor strt lvl, rtin proprtis n oprtions pply in oth implmnttions.g. first, nxt, numr of lmnts In ll ss w hv strutur (rry(s)/list) whih rprsnts olltion of lmnts n rfrn (inx/pointr) to n iniviul lmnt in th olltion. DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin v 17
4 () Priniprn kom hshning Dfinition: Th mpping of vlu (oftn ky vlu) to position in linr sp (hsh sp) y mns of hsh funtion h. h: ky => position ( mpping from ky sp to hsh sp) Issus: min vntg: srh tim is O(1) (i.. onstnt) ollision hnling (i.. if h(x) mps to th sm position s h(y)) th istriution of vlus in th ky sp if this is known, som form of optimistion my ppli th lo ftor in th hsh sp (s th nimtion low) th numr of pros rquir (inrss s th lo ftor inrss) () Priniprn kom Kruskls lgoritm Divi th grph into omponnts (G ) with on no in h omponnt initilly n priority quu (PQ) for h g (lowst ost first). Work through th PQ ing n g to th grph (G ) of nos iff 2 istint omponnts r onnt until th grph ontins on omponnt th Miniml Spnning Tr (MST). () Om mn skull lägg till skvnsn (1, 4, 22, 14, 4, 8, 44, 7) i tt hshutrymm (hsh sp) m 10 pltsr, vilkn kollisionshntringsmto v linjär proning (linr proing) oh kvrtisk proning (qurti proing) är säkrr? Förklr vrför. Choos linr proing sin qurti proing nnot gurnt suss if th lo ftor is ov 50%. Hr thr r 8 lmnts n 10 pls giving lo of 80%. Totlt 5p DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 4 v 17
5 () Rkursion Skriv (psuo)ko till n rkursiv funktion (llr två rkursiv funktionr) för tt räkn frm ntlt kntr (gs) i n grf. Ang ll ntgn. 5p Assumptions: Strutur: typf strut nolm * norf; typf strut nolm { hr nnm; int ninfo; norf gs; norf nos; nolm; + orrsponing gt/st funtions pr ttriut n h/til oprtions for oth th no list (nos) n th g list (gs). G is rfrn to th grph, th is_mpty(r) funtion is fin. stti int _ngs(norf E) { rturn is_mpty(e)? 0 : 1 + _ngs(til(e)); stti int _siz(norf G) { rturn is_mpty(g)? 0 : _ngs(gt_gs(nh(g))) + _siz(ntil(g)); DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 5 v 17
6 (4) Grfoprtionr En grf kn skrivs som n virtull (llr strkt) mskin. I grflortionn, filn grph.h är fktiskt n skrivning v nn virtull mskin. Innhållt v grph.h gs nn. /**************************************************************************/ /* funtion prototyps - oprtions on th Grph ( virtul mhin) */ /**************************************************************************/ /* Grph = (V, E) whr V is st of vrtis/nos n E st of gs */ /* Thr r limit numr of oprtions (9) whih n ppli to G */ /**************************************************************************/ voi _isply_jlist(); /* isply G s n jny list */ voi _isply_jmtrix(); /* isply G s n jny mtrix*/ voi _no(hr ); /* vrtx (no) to G */ voi _rmno(hr ); /* rmov vrtx (no) from G */ voi _g(hr s, hr, int v);/* n g (with wight) to G*/ voi _rmg(hr s, hr ); /* rmov n g from G */ int _is_nmmr(hr ); /* is no mmr of G? */ int _is_mmr(hr s, hr ); /* is n g mmr of G? */ int _siz(); /* th numr of nos in G */ /**************************************************************************/ I front-n:n kn mn spifir förvillkor (pronitions) till vrj oprtion ovn m hjälp v n llr flr v ss 9 funktionr. Ang förvillkort/förvillkorn till vrj v först ått oprtionrn ovn. Dvs i (i) f_isply_jlist(), (ii) f_isply_jmtrix(), (iii) f_no(), (iv) f_rmno(), (v) f_g(), (vi) f_rmg(), (vii) f_is_nmmr(), (viii) f_is_mmr(). Kom ihåg tt ifrån front-n:n kn mn utför tt smtl m nvänrn för tt gär olik värn smt skriv flmln. (5p) (i) f_isply_jlist() voi f_isply_jlist() { if (_siz()==0) ui_putgrphempty(); ls { ui_puttitllist(); _isply_jlist(); (ii) f_isply_jmtrix() voi f_isply_jmtrix() { if (_siz()==0) ui_putgrphempty(); ls { ui_puttitlmtrix(); _isply_jmtrix(); DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 6 v 17
7 (iii) f_no() voi f_no() { hr ; = ui_gtno(); if (_is_nmmr()) ui_putnoerror(); ls _no(); (iv) f_rmno() voi f_rmno() { hr ; if (_siz()==0) ui_putgrphempty(); ls { = ui_gtno(); if(!_is_nmmr()) ui_putnonoerror(); ls _rmno(); (v) f_g() voi f_g() { hr s, ; int w; if (_siz()==0) ui_putgrphempty(); ls { s = ui_gtno(); if (!_is_nmmr(s)) ui_putnoerror(s); ls { = ui_gtno(); if (!_is_nmmr()) ui_putnoerror(); ls if (_is_mmr(s, )) ui_putegerror(s, ); ls { w = ui_gtwight(); _g(s,, w); if (ui_ismou() && (!= s)) _g(, s, w); DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 7 v 17
8 (vi) f_rmg() voi f_rmg() { hr s, ; if (_siz()==0) ui_putgrphempty(); ls { s = ui_gtno(); if (!_is_nmmr(s)) ui_putnonoerror(s); ls { = ui_gtno(); if (!_is_nmmr()) ui_putnonoerror(); ls if (!_is_mmr(s, )) ui_putnoegerror(s, ); ls { _rmg(s, ); if (ui_ismou()) { if (!_is_mmr(, s)) ui_putnoegerror(s, ); ls _rmg(, s); (vii) f_is_nmmr() voi f_is_nmmr() { hr ; if (_siz()==0) ui_putgrphempty(); ls { = ui_gtno(); if (_is_nmmr()) ui_putnofoun(); ls ui_putnonotfoun(); DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 8 v 17
9 (viii) f_is_mmr() voi f_is_mmr() { hr s, ; if (_siz()==0) ui_putgrphempty(); ls { s = ui_gtno(); if (!_is_nmmr(s)) ui_putnonoerror(s); ls { = ui_gtno(); if (!_is_nmmr()) ui_putnonoerror(); ls if (_is_mmr(s, )) ui_putegfoun(s, ); ls ui_putegnotfoun(s, ); DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 9 v 17
10 (5) Prims lgoritm ) Tillämp Prims lgoritm (nn) på n orikt grfn: (--, --, --, --, --, --, --, --f, --f, --f). Börj m no. Ang ll ntgnn oh vis ll räkningr oh mllnrsultt. V rprsntrr rsulttt? Ang vrj stg i in räkning. Ant tt norn lgrs i närlistn (jny list) i lftisk orning smt tt mn sökr ftr t miniml värt i lftisk orning. Rit lrsulttt ftr vrj itrtion. ) Förklr priniprn kom Prims lgoritm. (p) (2p) Totlt 5p Ang *ll* ntgnn oh vis *ll* räkningr oh mllnrsultt Prim ( no v) -- v is th strt no { U = {v; for i in (V-U) { low-ost[i] = C[v,i]; losst[i] = v; whil (!is_mpty (V-U) ) { i = first(v-u); min = low-ost[i]; k = i; for j in (V-U-k) if (low-ost[j] < min) { min = low-ost[j]; k = j; isply(k, losst[k]); U = U + k; for j in (V-U) if ( C[k,j] < low-ost[j] ) ) { low-ost[j] = C[k,j]; losst[j] = k; DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 10 v 17
11 Th prinipl is tht th MST grows from th on omponnt (hr ) y onnting this omponnt to ny othr omponnt ( no) y th hpst g SO FAR foun this lst proviso rvls tht Prim s is GREEDY lgorithm i.. us lol st solution. S low for th lultions. Drw th grph (n possily skth th nswr us Krusklls for quik hk!): Cost 15 f f DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 11 v 17
12 Drw th ost mtrix C n rry D f f f lowost losst Min g: lowost: --- losst: --- U = {, V-U = {,,,f min = ; k = Rjust osts: if C[k,j] < lowost[j] thn { lowost[j] = C[k,j]; losst[j] = k j = ; if C[,] < lowost[] thn { lowost[] = C[,]; losst[] = < no hng j = ; if C[,] < lowost[] thn { lowost[] = C[,]; losst[] = < no hng j = ; if C[,] < lowost[] thn { lowost[] = C[,]; losst[] = < -- j = f; if C[,f] < lowost[f] thn { lowost[f] = C[,f]; losst[f] = < no hng f f f lowost losst DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 12 v 17
13 Min g: lowost: losst: --- U = {,, V-U = {,,f min = ; k = Rjust osts: if C[k,j] < lowost[j] thn { lowost[j] = C[k,j]; losst[j] = k j = ; if C[,] < lowost[] thn { lowost[] = C[,]; losst[] = < no hng j = ; if C[,] < lowost[] thn { lowost[] = C[,]; losst[] = < no hng j = f; if C[,f] < lowost[f] thn { lowost[f] = C[,f]; losst[] = < --f f f f lowost losst Min g: lowost: --- losst: --- U = {,,, V-U = {,f min = ; k = Rjust osts: if C[k,j] < lowost[j] thn { lowost[j] = C[k,j]; losst[j] = k j = ; if C[,] < lowost[] thn { lowost[] = C[,]; losst[] = < no hng j = f; if C[,f] < lowost[f] thn { lowost[f] = C[,f]; losst[f] = < no hng Min g: lowost: --- losst: --- U = {,,,, V-U = {f min = ; k = Rjust osts: if C[k,j] < lowost[j] thn { lowost[j] = C[k,j]; losst[j] = k j = f; if C[,f] < lowost[f] thn { lowost[f] = C[,f]; losst[f] = < no hng Finlly th rmining no no (thr r no furthr lultions) Min g: lowost: --- losst: --- U = {,,,,f V-U = { QED MST gs --, --, --, --, --f Totl ost = 15 (Confirm using Kruskl s) DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 1 v 17
14 Prinipl: to uil th MST from singl omponnt y hoosing th hpst g to nonomponnt nos from th lst no. Aov strt with, g istns (infinit if no g), hoos th hpst (--) n this to th omponnt. Now rhk if thr r hpr gs from to th non-omponnt nos. Rpt until ll th nos r onnt. So th omponnt vlops s (), (--), (--, --1, -4-, -5-, --f) (s ov). Strt Grph Solution f f f lowost losst DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 14 v 17
15 (6) Dijkstr + SPT (Shortst Pth Tr) Tillämp n givn Dijkstr_SPT lgoritmn (nn) på n rikt grfn, (,, 1), (,, 12), (,, 20), (,, 60), (,, 50), (,, 0), (,, 40) SPT = Shortst Pth Tr - vs kortst väg trät (KVT) från n no till ll nr. Börj m no. Vis vrj stg i in räkningr. Ang *ll* ntgnn oh vis *ll* räkningr oh mllnrsultt Rit vrj stg i konstruktionn v SPT:t vs vis till oh m nor oh kntr som läggs till mn sn ts ort. (p) Förklr priniprn kom Dijkstrs_SPT lgoritm. (2p) Totlt 5p Dijkstrs lgoritm m n utökning för SPT Dijkstr_SPT ( ) { S = { for (i in V-S) { D[i] = C[, i] --- initilis D - (g ost) E[i] = --- initilis E - SPT (g) L[i] = C[, i] --- initilis L - SPT (ost) for (i in 1..( V -1)) { hoos w in V-S suh tht D[w] is minimum S = S + {w forh ( v in V-S ) if (D[w] + C[w,v] < D[v]) { D[v] = D[w] + C[w,v] E[v] = w L[v] = C[w,v] DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 15 v 17
16 Initilis D, E, L D: E: L: w is (min vlu in D) S = {, V-S = {,, v = min (D[], D[]+C (,)) min(1, 12+ ) no hng v = min (D[], D[]+C (,)) min(, 12+0) v = min (D[], D[]+C (,)) min(20, 12+40) no hng D: E: L: D: E: L: v = min (D[], D[]+C (,)) v = min (D[], D[]+C (,)) w is (min vlu in D) S = {,, V-S = {, min(42, 1+60) no hng min(20, 1+ ) no hng D: E: L: DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 16 v 17
17 D: E: L: v = min (D[], D[]+C (,)) w is (min vlu in D) S = {,,, V-S = { min(42, 20+ ) no hng D: E: L: This is th finl rsult. Costs: (1), (42), (12), (20) SPT gs: (1), (12), (0), (20) Prinipl similr to Prims i. uil omponnt stp y stp SPT DFR Dtstrukturr oh lgoritmr, DAV B0, omtntmn Fit Sin 17 v 17
FACIT TILL OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B kl. 08:15 13:15
 Krlsts univrsitt Fit till DSA omtntmn 08 Dtvtnskp FACIT TILL OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B0 08 kl. 08: : Ansvrig Lärr: Donl F. Ross Hjälpml: Ing. Algoritmrn inns i rspktiv uppgitrn llr
Krlsts univrsitt Fit till DSA omtntmn 08 Dtvtnskp FACIT TILL OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B0 08 kl. 08: : Ansvrig Lärr: Donl F. Ross Hjälpml: Ing. Algoritmrn inns i rspktiv uppgitrn llr
FACIT TILL ORDINARIE TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03. 150112 kl. 08:15 13:15
 FACIT TILL ORDINARIE TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 1501 kl. 08:15 13:15 Ansvrig Lärr: Donl F. Ross Hjälpml: Ing. Algoritmrn finns i rspktiv uppgiftrn llr i ilogrn. *** OBS *** Btygsgräns:
FACIT TILL ORDINARIE TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 1501 kl. 08:15 13:15 Ansvrig Lärr: Donl F. Ross Hjälpml: Ing. Algoritmrn finns i rspktiv uppgiftrn llr i ilogrn. *** OBS *** Btygsgräns:
FACIT TILL OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B kl. 08:15 13:15
 Krlsts univrsitt DSA tntmn 150817 - Fcit Dtvtnskp FACIT TILL OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 150817 kl. 08:15 13:15 Ansvrig Lärr: Donl F. Ross Hjälpml: Ing. Algoritmrn inns i rspktiv
Krlsts univrsitt DSA tntmn 150817 - Fcit Dtvtnskp FACIT TILL OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 150817 kl. 08:15 13:15 Ansvrig Lärr: Donl F. Ross Hjälpml: Ing. Algoritmrn inns i rspktiv
FACIT TILL OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B kl. 08:15 13:15
 FACIT TILL OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 140818 kl. 08:15 13:15 Ansvarig Lärar: Donald F. Ross Hjälpmdl: Inga. Algoritmrna finns i d rspktiv uppgiftrna. Btygsgräns: *** OBS *** Kurs:
FACIT TILL OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 140818 kl. 08:15 13:15 Ansvarig Lärar: Donald F. Ross Hjälpmdl: Inga. Algoritmrna finns i d rspktiv uppgiftrna. Btygsgräns: *** OBS *** Kurs:
General comment the exam was not well done at all. The usual faults were to blame
 Commnts on th xm n qustions. Gnrl commnt th xm ws not wll on t ll. Th usul fults wr to blm 1. NOT READING THE QUESTION CAREFULLY TO START WITH - xmpls. 1() - rcursiv finition not function!!! b. 1() tr
Commnts on th xm n qustions. Gnrl commnt th xm ws not wll on t ll. Th usul fults wr to blm 1. NOT READING THE QUESTION CAREFULLY TO START WITH - xmpls. 1() - rcursiv finition not function!!! b. 1() tr
OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B kl. 14:15 19:15
 OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 150609 kl. 14:15 19:15 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna eller i bilogarna. *** OBS ***
OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 150609 kl. 14:15 19:15 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna eller i bilogarna. *** OBS ***
TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B kl. 14:00-19:00
 TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 170117 kl. 14:00-19:00 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna eller i bilagarna. *** OBS *** Betygsgräns:
TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 170117 kl. 14:00-19:00 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna eller i bilagarna. *** OBS *** Betygsgräns:
TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03. 120612 kl. 08:15 13:15
 TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 120612 kl. 08:15 13:15 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Bilaga A algoritmer Ni som har läst från och med HT 2006 Betygsgräns: *** OBS *** Kurs:
TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 120612 kl. 08:15 13:15 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Bilaga A algoritmer Ni som har läst från och med HT 2006 Betygsgräns: *** OBS *** Kurs:
Föreläsning 11: Grafer, isomorfi, konnektivitet
 Förläsning 11: Grfr, isomorfi, konnktivitt En orikt nkl grf (V, E) står v hörn, V, oh kntr, E, vilk förinr istinkt nor: ing pilr, ing öglor, int multipl kntr mlln hörn. Två hörn u,v V är grnnr om t finns
Förläsning 11: Grfr, isomorfi, konnktivitt En orikt nkl grf (V, E) står v hörn, V, oh kntr, E, vilk förinr istinkt nor: ing pilr, ing öglor, int multipl kntr mlln hörn. Två hörn u,v V är grnnr om t finns
ORDINARIE TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B kl. 08:15 13:15
 ORDINARIE TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 150112 kl. 08:15 13:15 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna eller i bilogarna. ***
ORDINARIE TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 150112 kl. 08:15 13:15 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna eller i bilogarna. ***
OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B kl. 08:15 13:15
 OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 140818 kl. 08:15 13:15 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna. Betygsgräns: *** OBS *** Kurs:
OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 140818 kl. 08:15 13:15 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna. Betygsgräns: *** OBS *** Kurs:
Algoritmer och datastrukturer, föreläsning 11
 Aloritmr oh tstrukturr, förläsnin Dnn förläsnin hnlr rfr. En rf hr n män nor (vrtx) oh n män år (). Ett xmpl är: A E F B D G H C Z Dnn rf hr följn män v nor: {A, B, C, D, E, F, G, H, Z Dn hr följn män
Aloritmr oh tstrukturr, förläsnin Dnn förläsnin hnlr rfr. En rf hr n män nor (vrtx) oh n män år (). Ett xmpl är: A E F B D G H C Z Dnn rf hr följn män v nor: {A, B, C, D, E, F, G, H, Z Dn hr följn män
ORDINARIE TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B kl. 08:15 13:15
 ORDINARIE TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 160119 kl. 08:15 13:15 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna eller i bilogarna. ***
ORDINARIE TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 160119 kl. 08:15 13:15 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna eller i bilogarna. ***
OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B kl. 08:15-13:15
 OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 170331 kl. 08:15-13:15 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna eller i bilagarna. *** OBS ***
OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 170331 kl. 08:15-13:15 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna eller i bilagarna. *** OBS ***
4 Example exam questions
 4 Exmple exm questions Omvnl uttryket ( ) e / (f g / h ) från infix till postfix me hjälp v en stk oh vis vrje steg i proessen. (5p) Vis sen me hjälp v en stk hur mn skulle eräkn et postfix uttrykets väre
4 Exmple exm questions Omvnl uttryket ( ) e / (f g / h ) från infix till postfix me hjälp v en stk oh vis vrje steg i proessen. (5p) Vis sen me hjälp v en stk hur mn skulle eräkn et postfix uttrykets väre
OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B kl. 09:00 14:00
 OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 160402 kl. 09:00 14:00 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna eller i bilogarna. *** OBS ***
OMTENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 160402 kl. 09:00 14:00 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna eller i bilogarna. *** OBS ***
v v v v 5 v v v 4 (V,E ) (V,E)
 . Grftori Btylsn v ilr som stö oh inspirtion för mtmtisk rsonmng kn knppst övrsktts. Stuirn v nkl ilr hr gtt oss grftorin. Tyvärr, llr lykligtvis, visr t sig snt tt nkl oh nturlig frågställningr om nkl
. Grftori Btylsn v ilr som stö oh inspirtion för mtmtisk rsonmng kn knppst övrsktts. Stuirn v nkl ilr hr gtt oss grftorin. Tyvärr, llr lykligtvis, visr t sig snt tt nkl oh nturlig frågställningr om nkl
Tillståndsmaskiner. Moore-automat. Mealy-automat. William Sandqvist
 Tllstånsmsknr Moor-utomt Mly-utomt Wllm Snvst wllm@kth.s ÖH. Bstäm tllstånsrm oh tllstånstll ör skvnskrtsn. Vlkn v mollrn Mly llr Moor pssr n på krtsn? Wllm Snvst wllm@kth.s . Ur krtsshmt kn öljn smn ställs
Tllstånsmsknr Moor-utomt Mly-utomt Wllm Snvst wllm@kth.s ÖH. Bstäm tllstånsrm oh tllstånstll ör skvnskrtsn. Vlkn v mollrn Mly llr Moor pssr n på krtsn? Wllm Snvst wllm@kth.s . Ur krtsshmt kn öljn smn ställs
VECKANS LILLA POSTKODVINST á 1.000 kronor Inom nedanstående postkoder vinner följande 249 lottnummer 1.000 kronor vardera:
 Dragningsresultat vecka 10-2015 Här nedan kan du se om du är en av de lyckliga vinnarna i veckans utlottning i Svenska PostkodLotteriet. När du har vunnit betalar vi automatiskt ut dina vinstpengar till
Dragningsresultat vecka 10-2015 Här nedan kan du se om du är en av de lyckliga vinnarna i veckans utlottning i Svenska PostkodLotteriet. När du har vunnit betalar vi automatiskt ut dina vinstpengar till
a n = A2 n + B4 n. { 2 = A + B 6 = 2A + 4B, S(5, 2) = S(4, 1) + 2S(4, 2) = 1 + 2(S(3, 1) + 2S(3, 2)) = 3 + 4(S(2, 1) + 2S(2, 2)) = 7 + 8 = 15.
 1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D och F, SF161 och SF160, den juni 008 kl 08.00-1.00. DEL I 1. (p) Lös rekursionsekvationen
1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D och F, SF161 och SF160, den juni 008 kl 08.00-1.00. DEL I 1. (p) Lös rekursionsekvationen
VATEK Multifix kopplingar för alla rörtyper
 Vtk_logo_cmyk-2012.pf 1 2011-11-25 13.09 VATEK Multifix kopplingr för ll rörtypr VATEK MULTIFIX ÄR EN SERIE rgfst rörkopplingr för ll typr v rör till å vttn och gslningr. Kopplingrn introucrs i Svrig v
Vtk_logo_cmyk-2012.pf 1 2011-11-25 13.09 VATEK Multifix kopplingr för ll rörtypr VATEK MULTIFIX ÄR EN SERIE rgfst rörkopplingr för ll typr v rör till å vttn och gslningr. Kopplingrn introucrs i Svrig v
Laboration 1a: En Trie-modul
 Lbortion 1: En Tri-modul 1 Syft Progrmmring md rfrnsr, vlusning, tstning, kt m.m. Vi hr trolign int hunnit gå ignom llt, viss skr får ni br cctr så läng. S ävn kodxml å kurssidn. 2 Bkgrund Vi skll undr
Lbortion 1: En Tri-modul 1 Syft Progrmmring md rfrnsr, vlusning, tstning, kt m.m. Vi hr trolign int hunnit gå ignom llt, viss skr får ni br cctr så läng. S ävn kodxml å kurssidn. 2 Bkgrund Vi skll undr
100318/Thomas Munther IDE-sektionen/Högskolan i Halmstad. Formelsamling Reglerteknik
 38/Thoms Munther IDE-sektionen/Högskoln i Hlmstd Formelsmling Reglerteknik Smbnd melln stegsvr och överföringsfunktion ( insignlen u är nedn ett steg med mplitud = som pplicers vid t=, där är llmänt y/
38/Thoms Munther IDE-sektionen/Högskoln i Hlmstd Formelsmling Reglerteknik Smbnd melln stegsvr och överföringsfunktion ( insignlen u är nedn ett steg med mplitud = som pplicers vid t=, där är llmänt y/
Robin Ekman och Axel Torshage. Hjälpmedel: Miniräknare
 Umå univritt Intitutionn för matmatik oh matmatik tatitik Roin Ekman oh Axl Torhag Tntamn i matmatik Introduktion till dikrt matmatik Löningförlag Hjälpmdl: Miniräknar Löningarna kall prntra på tt ådant
Umå univritt Intitutionn för matmatik oh matmatik tatitik Roin Ekman oh Axl Torhag Tntamn i matmatik Introduktion till dikrt matmatik Löningförlag Hjälpmdl: Miniräknar Löningarna kall prntra på tt ådant
F8: Logiska komponenter. Introduktion. Koder. Avkodare. Logiska komponenter
 Innhåll: - Avkor - Diitl kor - 2-4 vkor - 7-smnts isply - Kor - Multiplxr - Dmultiplxr F8: Loisk komponntr Loisk komponntr Introuktion Dt är növänit tt skp mr komplx ylok än runlän rinrn (n, or, not) som
Innhåll: - Avkor - Diitl kor - 2-4 vkor - 7-smnts isply - Kor - Multiplxr - Dmultiplxr F8: Loisk komponntr Loisk komponntr Introuktion Dt är növänit tt skp mr komplx ylok än runlän rinrn (n, or, not) som
Magnus Nielsen, IDA, Linköpings universitet
 Föreläsning 6 Sply-trä. rioritetsköer oh hepr. TDDC91,TDDE22,725G97: DALG Utskriftsversion v föreläsning i Dtstrukturer oh lgoritmer 19 septemer 2017 Mgnus Nielsen, IDA, Linköpings universitet 6.1 Innehåll
Föreläsning 6 Sply-trä. rioritetsköer oh hepr. TDDC91,TDDE22,725G97: DALG Utskriftsversion v föreläsning i Dtstrukturer oh lgoritmer 19 septemer 2017 Mgnus Nielsen, IDA, Linköpings universitet 6.1 Innehåll
Föreläsning 7 Datastrukturer (DAT037)
 Föreläsning 7 Datastrukturer (DAT037) Fredrik Lindblad 1 2016-11-21 1 Slides skapade av Nils Anders Danielsson har använts som utgångspunkt. Se http://www.cse.chalmers.se/edu/year/2015/course/dat037 Förra
Föreläsning 7 Datastrukturer (DAT037) Fredrik Lindblad 1 2016-11-21 1 Slides skapade av Nils Anders Danielsson har använts som utgångspunkt. Se http://www.cse.chalmers.se/edu/year/2015/course/dat037 Förra
FACIT TILL TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03. 140114 kl. 08:15 13:15
 FACIT TILL TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 140114 kl. 08:15 13:15 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna. Betygsgräns: *** OBS
FACIT TILL TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 140114 kl. 08:15 13:15 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna. Betygsgräns: *** OBS
En krona dagen om dag ona om r e k n n E E n n k e g o r a d m o a n
 g E o E E o g o Ambssörr/profilr Jököpigs Sör IF Rlf Eström Björ Norqvist Mukl IFK Uvll IK Ovol HK Coutry Flkbrgs FF Örgryt IS Värmo IK Brg Skoftbys IF GK Kroppskultur Dgrfors IF Gfl IF Äglholms FF Ljugskil
g E o E E o g o Ambssörr/profilr Jököpigs Sör IF Rlf Eström Björ Norqvist Mukl IFK Uvll IK Ovol HK Coutry Flkbrgs FF Örgryt IS Värmo IK Brg Skoftbys IF GK Kroppskultur Dgrfors IF Gfl IF Äglholms FF Ljugskil
StyleView Scanner Shelf
 StyleView Scnner Shelf User's Guide Mximl vikt: 2 ls ( kg) SV-vgn & Huvud-enhet Alterntiv - LCD-vgnr Alterntiv 2 - Lptop-vgnr Alterntiv 3 - Väggspår Alterntiv 4 - Bksid v SV-vgn 3 6 7 Reduce Reuse Recycle
StyleView Scnner Shelf User's Guide Mximl vikt: 2 ls ( kg) SV-vgn & Huvud-enhet Alterntiv - LCD-vgnr Alterntiv 2 - Lptop-vgnr Alterntiv 3 - Väggspår Alterntiv 4 - Bksid v SV-vgn 3 6 7 Reduce Reuse Recycle
Innehåll. Träd. Träd. Traversering av träd. Binära träd. Datastrukturer och algoritmer Datastrukturer. Algoritmer.
 Innhåll Dtstrukturr och lgoritmr Progrmmringsmtodik - för kognitionsvtr, 5DV059 - md inriktning mot kognition, 5DV06 2008-01-1 Dtstrukturr Träd, grfr, mängdr Algoritmr komplxittsnlys Läsnvisning: Dss bildr
Innhåll Dtstrukturr och lgoritmr Progrmmringsmtodik - för kognitionsvtr, 5DV059 - md inriktning mot kognition, 5DV06 2008-01-1 Dtstrukturr Träd, grfr, mängdr Algoritmr komplxittsnlys Läsnvisning: Dss bildr
Collections och annat nyttigt
 Va innbär programmring? Collctions och annat nyttigt En stor l av tin så sättr man ihop olika algoritmr och atastrktrr så att fnkar för st t aktlla problmt. Förhoppningsvis så ägnar man också n hl l ti
Va innbär programmring? Collctions och annat nyttigt En stor l av tin så sättr man ihop olika algoritmr och atastrktrr så att fnkar för st t aktlla problmt. Förhoppningsvis så ägnar man också n hl l ti
093-H5. 093-H5X Komplett kit passar efter katalysator Complete kit fi ts to catalyst 093-H5R
 Corsa B Coupé 1.2i/1.4i/1.6i/1.6GSi 93-093-H5 093-25 093-35 093-45 093-M5 Ändrör/tailpipe: 90 mm Corsa B Coupé 1.2i/1.4i/1.6i/1.6GSi 93-093-H5X 093-25 093-35 093-45X 093-M5 Ändrör/tailpipe: DTM-design
Corsa B Coupé 1.2i/1.4i/1.6i/1.6GSi 93-093-H5 093-25 093-35 093-45 093-M5 Ändrör/tailpipe: 90 mm Corsa B Coupé 1.2i/1.4i/1.6i/1.6GSi 93-093-H5X 093-25 093-35 093-45X 093-M5 Ändrör/tailpipe: DTM-design
Elementær diskret matematikk, MA0301, våren 2011
 Lösningsförslag Elmntær iskrt matmatikk, MA00, vårn 0 Oppgav Varj or motsvarar n prmutation av storlk från 9 bokstävrna i TRONDHEIM Alltså är antalt sökta or P(9,) = 9 8 7 6 På liknan sätt får vi att t
Lösningsförslag Elmntær iskrt matmatikk, MA00, vårn 0 Oppgav Varj or motsvarar n prmutation av storlk från 9 bokstävrna i TRONDHEIM Alltså är antalt sökta or P(9,) = 9 8 7 6 På liknan sätt får vi att t
Beteckningar för områdesreserveringar: T/kem Landskapsplanering
 kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
Uppskatta ordersärkostnader för tillverkningsartiklar
 Handbk i matrialstyrning - Dl B Paramtrar ch ariablr B 12 Uppskatta rdrsärkstnadr för tillrkningsartiklar Md rdrsärkstnadr för tillrkningsartiklar ass alla d kstnadr sm tör dn dirkta ärdförädlingn är förknippad
Handbk i matrialstyrning - Dl B Paramtrar ch ariablr B 12 Uppskatta rdrsärkstnadr för tillrkningsartiklar Md rdrsärkstnadr för tillrkningsartiklar ass alla d kstnadr sm tör dn dirkta ärdförädlingn är förknippad
äkta Bredband, ett krav för framtidens multiservice nät?
 äkta Bredband, ett krav för framtidens multiservice nät? U lf V in n e ra s D e s ig n c o n s u lta n t, C is c o S y s te m s 2 0 0 2, C is c o S y s te m s, In c. A ll rig h ts re s e rv e d. U lf V
äkta Bredband, ett krav för framtidens multiservice nät? U lf V in n e ra s D e s ig n c o n s u lta n t, C is c o S y s te m s 2 0 0 2, C is c o S y s te m s, In c. A ll rig h ts re s e rv e d. U lf V
1. lösa differentialekvationer (DE) och system av DE med konstanta koefficienter
 Armin Hlilovic: EXTRA ÖVNINGAR plcrnormr APACETRANSFORMER plcrnormr nvän bl nn ör lö irnilkvionr DE och ym v DE m konn koicinr lö någr ypr v ingrlkvionr bämm bili ho linjär ym Diniion å vr inir ör plcrnormn
Armin Hlilovic: EXTRA ÖVNINGAR plcrnormr APACETRANSFORMER plcrnormr nvän bl nn ör lö irnilkvionr DE och ym v DE m konn koicinr lö någr ypr v ingrlkvionr bämm bili ho linjär ym Diniion å vr inir ör plcrnormn
Making room for tomorrow
 Byggnsgui Byggnsgui 2013 Byggnsgui 2013 Innrvägg Allmänt 4-5 Sknor oh rglr 6-7 Montg 8-9 WllClik 10-11 Typr oh gruppr 12-15 Väggnyklr 16-21 Typövrsikt 22-25 Väggruppr C 26-65 Väggruppr C+ 66-93 Väggruppr
Byggnsgui Byggnsgui 2013 Byggnsgui 2013 Innrvägg Allmänt 4-5 Sknor oh rglr 6-7 Montg 8-9 WllClik 10-11 Typr oh gruppr 12-15 Väggnyklr 16-21 Typövrsikt 22-25 Väggruppr C 26-65 Väggruppr C+ 66-93 Väggruppr
Tentamen MMG610 Diskret Matematik, GU
 Tentamen MMG610 Diskret Matematik, GU 2017-01-04 kl. 08.30 12.30 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers/GU Telefonvakt: Peter Hegarty, telefon: 0766 377 873 Hjälpmedel: Inga hjälpmedel,
Tentamen MMG610 Diskret Matematik, GU 2017-01-04 kl. 08.30 12.30 Examinator: Peter Hegarty, Matematiska vetenskaper, Chalmers/GU Telefonvakt: Peter Hegarty, telefon: 0766 377 873 Hjälpmedel: Inga hjälpmedel,
abbcba a) A regular expression over
 1 CD5560 FABER Forml Lnguges, Automt nd Models of Computtion Exerise Mälrdlen University 007 NEXT WEEK! Midterm Exm 1 Regulr Lnguges Ple: U-114 Time: Tuesdy 007-04-4, 10:15-1:00 t is OPEN BOOK. This mens
1 CD5560 FABER Forml Lnguges, Automt nd Models of Computtion Exerise Mälrdlen University 007 NEXT WEEK! Midterm Exm 1 Regulr Lnguges Ple: U-114 Time: Tuesdy 007-04-4, 10:15-1:00 t is OPEN BOOK. This mens
FÄRGLAGD A STENSUNDSVÄGEN BOSTÄDER BILPLATSER GARAGE 86 ST
 STNSUNSVÄN Ø Ø : Ø OSTÄR S TRO RK ST 3 RK 3 ST RK ST SUMM 7 ST 663 ILPLTSR +. +.3 R 6 ST -3 /. +.7 MRK Lr 5 ST SUMM ST.5 + IV. > VI SO P 3 677 b 3 3 UN SL TRO +.5 + 3.5 + 6. VÄ PL NN g V S +7 +3. +.6.5
STNSUNSVÄN Ø Ø : Ø OSTÄR S TRO RK ST 3 RK 3 ST RK ST SUMM 7 ST 663 ILPLTSR +. +.3 R 6 ST -3 /. +.7 MRK Lr 5 ST SUMM ST.5 + IV. > VI SO P 3 677 b 3 3 UN SL TRO +.5 + 3.5 + 6. VÄ PL NN g V S +7 +3. +.6.5
LINJÄR ALGEBRA II LEKTION 1
 LINJÄR ALGEBRA II LEKTION JOHAN ASPLUND INNEHÅLL. VEKTORRUM OCH DELRUM Hel kursen Linjär Algebr II hndlr om vektorrum och hur vektorrum (eller linjär rum, som de iblnd klls) beter sig. Tidigre hr mn ntgligen
LINJÄR ALGEBRA II LEKTION JOHAN ASPLUND INNEHÅLL. VEKTORRUM OCH DELRUM Hel kursen Linjär Algebr II hndlr om vektorrum och hur vektorrum (eller linjär rum, som de iblnd klls) beter sig. Tidigre hr mn ntgligen
Exempel 9.3. Present. Output. w w Next state
 9.3 Vi skriver en tillståndstabell och börjar med att dela in i grupper med olika utsignal, dvs nolla respektive etta. I tabellen markerar asterisker (*) stabila tillstånd. Vi kompletterar alltså Figur
9.3 Vi skriver en tillståndstabell och börjar med att dela in i grupper med olika utsignal, dvs nolla respektive etta. I tabellen markerar asterisker (*) stabila tillstånd. Vi kompletterar alltså Figur
Snickerier. Räcken & Stolpar, Snickarglädje, Hyllplan, Trädgård, Stolpsystem. Trädetaljer och Produkter som håller stilen på ditt hus
 Srr Trätr Prutr s år st på tt us Rä & Stpr, Srä, Hyp, Träår, Stpsyst Ett ört Sör-r Tstyps yr ystr A & Srä 1840-1900 Hus rå är pr är v på r tt v utsöt ystr srr. Vr uppör trä tt vär räss uppsr räsr. Isprt
Srr Trätr Prutr s år st på tt us Rä & Stpr, Srä, Hyp, Träår, Stpsyst Ett ört Sör-r Tstyps yr ystr A & Srä 1840-1900 Hus rå är pr är v på r tt v utsöt ystr srr. Vr uppör trä tt vär räss uppsr räsr. Isprt
Snickerier. Räcken & Stolpar, Snickarglädje, Ett företag inom Södra
 Trätjr o Proutr so år st på tt us Srr Rä & Stopr, Sräj, Träår, Stopsyst, Iprrt Ett ört o Sör Tstyps yr o ystjr Ao & Sräj 1840-1900 Hus rå är pro är v på r ott v utsöt ystjr o srr. Vor uppör trä tt vär
Trätjr o Proutr so år st på tt us Srr Rä & Stopr, Sräj, Träår, Stopsyst, Iprrt Ett ört o Sör Tstyps yr o ystjr Ao & Sräj 1840-1900 Hus rå är pro är v på r ott v utsöt ystjr o srr. Vor uppör trä tt vär
Ulefos Multifi x Rörkopplingar för alla rörtyper
 Ulfos Multifi x Rörkopplingr för ll rörtypr ULEFOS MULTIFIX är n sri rgfst rörkopplingr för ll typr v rör. För gs välj pckning v NBR. Kopplingrn introucrs i Svrig v Ulfos i slutt v 90-tlt och hr sn ss
Ulfos Multifi x Rörkopplingr för ll rörtypr ULEFOS MULTIFIX är n sri rgfst rörkopplingr för ll typr v rör. För gs välj pckning v NBR. Kopplingrn introucrs i Svrig v Ulfos i slutt v 90-tlt och hr sn ss
Föreläsning 7. Splay-träd. Prioritetsköer och heapar. Union/Find TDDC70/91: DALG. Innehåll. Innehåll. 1 Splay-träd
 Föreläsning 7 Sply-träd. rioritetsköer oh hepr. Union/Find TDDC70/1: DALG Utskriftsversion v föreläsning i Dtstrukturer oh lgoritmer 7 septemer 01 Tommy Färnqvist, IDA, Linköpings universitet 7.1 Innehåll
Föreläsning 7 Sply-träd. rioritetsköer oh hepr. Union/Find TDDC70/1: DALG Utskriftsversion v föreläsning i Dtstrukturer oh lgoritmer 7 septemer 01 Tommy Färnqvist, IDA, Linköpings universitet 7.1 Innehåll
FACIT TILL TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03
 FACIT TILL TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 170117 kl. 14:00-19:00 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna eller i bilagarna. ***
FACIT TILL TENTAMEN I DATASTRUKTURER OCH ALGORITMER DVG B03 170117 kl. 14:00-19:00 Ansvarig Lärare: Donald F. Ross Hjälpmedel: Inga. Algoritmerna finns i de respektive uppgifterna eller i bilagarna. ***
Insamlingsforumbilden. Den nya givaren
 Insamlingsforumbilden #IF2013 "The greatest danger in times of turbulence is not the turbulence it is to act with yesterday's logic. Peter Drucker ANTECKNINGSBOKEN PRESENTATIONER: www.frii.se DEN NYA GIVAREN
Insamlingsforumbilden #IF2013 "The greatest danger in times of turbulence is not the turbulence it is to act with yesterday's logic. Peter Drucker ANTECKNINGSBOKEN PRESENTATIONER: www.frii.se DEN NYA GIVAREN
Referensexemplar. Vi önskar er Lycka till! 1. Välkommen till Frö-Retaget
 t g a t R Frö ar pl m x ns r f R 1 1. Välkommn till Frö-Rtagt Hj, nu ska du och dina klasskompisar starta rt alldls gna förtag. Vi på FramtidsFrön har valt att kalla dt Frö-Rtag. Md Frö mnar vi att du
t g a t R Frö ar pl m x ns r f R 1 1. Välkommn till Frö-Rtagt Hj, nu ska du och dina klasskompisar starta rt alldls gna förtag. Vi på FramtidsFrön har valt att kalla dt Frö-Rtag. Md Frö mnar vi att du
2014-2015. Programinformation Teknikcollege Allhamra. Kinda Lärcentrum Kontakt. Teknisk utbildning, för framtida anställning
 Kid Lärctrum Ktkt www.kidlrctrum.s lrctrum@kid.s Bsök ss på Klmrväg 18 i Kis tl: 0494-191 73/190 00 Prgrmifrmti Tkikcllg Allhmr 2014-2015 Tkisk utbildig, för frmtid ställig Skl Tkikcllg Allhmr är lit skl
Kid Lärctrum Ktkt www.kidlrctrum.s lrctrum@kid.s Bsök ss på Klmrväg 18 i Kis tl: 0494-191 73/190 00 Prgrmifrmti Tkikcllg Allhmr 2014-2015 Tkisk utbildig, för frmtid ställig Skl Tkikcllg Allhmr är lit skl
Information Coding / Computer Graphics, ISY, LiTH. Integrationsmetoder
 Integrationsmetoder Datorspel är tidsdiskreta Explicita analytiska funktioner för hastighet och acceleration saknas Position är integral av hastighet Hastighet är integral av acceleration Eulerintegrering
Integrationsmetoder Datorspel är tidsdiskreta Explicita analytiska funktioner för hastighet och acceleration saknas Position är integral av hastighet Hastighet är integral av acceleration Eulerintegrering
Ett förspel till Z -transformen Fibonaccitalen
 Ett förspel till Z -trnsformen Fibonccitlen Leonrdo Pisno vnligen klld Leonrdo Fiboncci, den knske störste mtemtiker som Europ frmburit före renässnsen skrev år 10 en bok (Liber bci) i räknelär. J, fktiskt.
Ett förspel till Z -trnsformen Fibonccitlen Leonrdo Pisno vnligen klld Leonrdo Fiboncci, den knske störste mtemtiker som Europ frmburit före renässnsen skrev år 10 en bok (Liber bci) i räknelär. J, fktiskt.
Tentamen i Databasteknik
 Tentmen i Dtsteknik lördgen den 22 oktoer 2005 Tillåtn hjälpmedel: Allt upptänkligt mteril Använd r frmsidn på vrje ld. Skriv mx en uppgift per ld. Motiver llt, dokumenter egn ntgnden. Oläslig/oegriplig
Tentmen i Dtsteknik lördgen den 22 oktoer 2005 Tillåtn hjälpmedel: Allt upptänkligt mteril Använd r frmsidn på vrje ld. Skriv mx en uppgift per ld. Motiver llt, dokumenter egn ntgnden. Oläslig/oegriplig
729G04 - Hemuppgift, Diskret matematik
 79G04 - Hemuppgift, Diskret matematik 5 oktober 015 Dessa uppgifter är en del av examinationen i kursen 79G04 Programmering och diskret matematik. Uppgifterna ska utföras individuellt och självständigt.
79G04 - Hemuppgift, Diskret matematik 5 oktober 015 Dessa uppgifter är en del av examinationen i kursen 79G04 Programmering och diskret matematik. Uppgifterna ska utföras individuellt och självständigt.
FÖRELÄSNING 1 ANALYS MN1 DISTANS HT06
 FÖRELÄSNING ANALYS MN DISTANS HT06 JONAS ELIASSON Detta är föreläsningsanteckningar för distanskursen Matematik A - analysdelen vid Uppsala universitet höstterminen 2006. Förberedande material Här har
FÖRELÄSNING ANALYS MN DISTANS HT06 JONAS ELIASSON Detta är föreläsningsanteckningar för distanskursen Matematik A - analysdelen vid Uppsala universitet höstterminen 2006. Förberedande material Här har
Uppsala universitet Institutionen för lingvistik och filologi. Grundbegrepp: Noder (hörn) och bågar (kanter)
 Grfer Jokim Nivre Uppsl universitet Institutionen för lingvistik oh filologi Översikt Grunegrepp: Noer (hörn) oh ågr (knter) Grfteoretisk egrepp: Stigr oh ykler Delgrfer oh smmnhängne grfer Rikte oh orikte
Grfer Jokim Nivre Uppsl universitet Institutionen för lingvistik oh filologi Översikt Grunegrepp: Noer (hörn) oh ågr (knter) Grfteoretisk egrepp: Stigr oh ykler Delgrfer oh smmnhängne grfer Rikte oh orikte
Mitt barn skulle aldrig klottra!...eller?
 Mitt brn skull ldrig klottr!...llr? trtgi! ls n n tu n g n r h y Täb g och in sn ly b, g in n k c y m ts Gnom u i lyckts v r h l ri t m t g li å rt klott unn. m m o k i t r tt lo k sk in m Hjälp oss tt
Mitt brn skull ldrig klottr!...llr? trtgi! ls n n tu n g n r h y Täb g och in sn ly b, g in n k c y m ts Gnom u i lyckts v r h l ri t m t g li å rt klott unn. m m o k i t r tt lo k sk in m Hjälp oss tt
1. M öt et s öp pn an d e S ve n fö r k la r a r mö t et ö p p nat k lo c k a n 13. 5 0 i me d le ms k o nt o r et.
 Styrels e möte 7mars 2010 Bila gor: 1. D ago r d ning 2. N är va r o lis t a 1. M öt et s öp pn an d e S ve n fö r k la r a r mö t et ö p p nat k lo c k a n 13. 5 0 i me d le ms k o nt o r et. 2. F o rma
Styrels e möte 7mars 2010 Bila gor: 1. D ago r d ning 2. N är va r o lis t a 1. M öt et s öp pn an d e S ve n fö r k la r a r mö t et ö p p nat k lo c k a n 13. 5 0 i me d le ms k o nt o r et. 2. F o rma
Frami transportbult 2,5kN
 07/2012 Orginlbruksnvisning 999281910 sv Sprs för frmtid behov Frmi trnsportbult 2,5kN rt.nr 588494000 fr.o.m. tillverkningsår 2009 Orginlbruksnvisning Frmi trnsportbult 2,5kN Produktbeskrivning d Underhåll
07/2012 Orginlbruksnvisning 999281910 sv Sprs för frmtid behov Frmi trnsportbult 2,5kN rt.nr 588494000 fr.o.m. tillverkningsår 2009 Orginlbruksnvisning Frmi trnsportbult 2,5kN Produktbeskrivning d Underhåll
Jag vill inte vara ensam
 Jg ill ine r ensm Krl-Gunnr Sensson G =132 f l m n o u s s s z f l l u z mp n s s n s s n s s n s s s s n s s n s s mps s n s s n s s n s s n s s n s s n ff s s s s s s s s s s s s mp s s s s s s s s s
Jg ill ine r ensm Krl-Gunnr Sensson G =132 f l m n o u s s s z f l l u z mp n s s n s s n s s n s s s s n s s n s s mps s n s s n s s n s s n s s n s s n ff s s s s s s s s s s s s mp s s s s s s s s s
Föreläsning Datastrukturer (DAT036)
 Föreläsning Datastrukturer (DAT036) Nils Anders Danielsson 2012-11-13 Idag Mer om grafer: Topologisk sortering. Kortaste vägen. Bredden först-sökning. Dijkstras algoritm. Floyd-Warshall. Topologisk sortering
Föreläsning Datastrukturer (DAT036) Nils Anders Danielsson 2012-11-13 Idag Mer om grafer: Topologisk sortering. Kortaste vägen. Bredden först-sökning. Dijkstras algoritm. Floyd-Warshall. Topologisk sortering
0 a. a -Â n 2 p n. beskriver på sedvanligt sätt en a-periodisk utvidgning av f. Nedanför ritas en partialsumma av Fourierserien.
 Sinus- och cosinusserier I slutet v kursen där vi skll lös differentilekvtioner på ändlig intervll v typen H, L, behöver vi konstruer Fourierserier med en viss typ v uppförnde i intervllens ändpunkter.
Sinus- och cosinusserier I slutet v kursen där vi skll lös differentilekvtioner på ändlig intervll v typen H, L, behöver vi konstruer Fourierserier med en viss typ v uppförnde i intervllens ändpunkter.
!"# $%&'! "#$ '!"# $%&'! ()*+,-%&./%&01 $%& 2! :$+(; "#!$%&!$%& ) $+%& <=$>% <A0$%&!$%&BC DE 8FGBH IJKL MN0OF 4 PQRS T 056U) $%&VW<A$%&U"
 !"# $%&'! "#$ '!"# $%&'! ()*+,-%&./%&01 $%& 2!0345678 9 :$+(; "#!$%&!$%& ) $+%& % &?@
!"# $%&'! "#$ '!"# $%&'! ()*+,-%&./%&01 $%& 2!0345678 9 :$+(; "#!$%&!$%& ) $+%& % &?@
GRAFISK PROFILMANUAL SUNDSVALL NORRLANDS HUVUDSTAD
 GRAFISK PROFILMANUAL SUNDSVALL NORRLANDS HUVUDSTAD INLEDNING Sundsvall Norrlands huvudstad Sundsvall Norrlands huvudstad, är båd tt nuläg och n önskan om n framtida position. Norrlands huvudstad är int
GRAFISK PROFILMANUAL SUNDSVALL NORRLANDS HUVUDSTAD INLEDNING Sundsvall Norrlands huvudstad Sundsvall Norrlands huvudstad, är båd tt nuläg och n önskan om n framtida position. Norrlands huvudstad är int
Addition och subtraktion
 Sidor i boken 35-39 Addition och subtrktion Vi börjr med lite ritmetik. Heltlsddition innebär ing som helst problem. Här tr vi lämpligen räknedosn till hjälp. Eempel. 3+00+5 = 7 Så länge ll nämnre är lik
Sidor i boken 35-39 Addition och subtrktion Vi börjr med lite ritmetik. Heltlsddition innebär ing som helst problem. Här tr vi lämpligen räknedosn till hjälp. Eempel. 3+00+5 = 7 Så länge ll nämnre är lik
POSTKODVINSTER á 1.000 kronor Inom nedanstående postkoder vinner följande 244 lottnummer 1.000 kronor vardera:
 Dragningsresultat vecka 52-2014 Här nedan kan du se om du är en av de lyckliga vinnarna i veckans utlottning i Svenska PostkodLotteriet. När du har vunnit betalar vi automatiskt ut dina vinstpengar till
Dragningsresultat vecka 52-2014 Här nedan kan du se om du är en av de lyckliga vinnarna i veckans utlottning i Svenska PostkodLotteriet. När du har vunnit betalar vi automatiskt ut dina vinstpengar till
Listor = generaliserade strängar. Introduktion till programmering SMD180. Föreläsning 8: Listor. Fler listor. Listindexering.
 1 Introduktion till progrmmering SMD180 Föreläsning 8: Listor 2 Listor = generliserde strängr Strängr = sekvenser v tecken Listor = sekvenser v vd som helst [10, 20, 30, 40] # en list v heltl ["spm", "ungee",
1 Introduktion till progrmmering SMD180 Föreläsning 8: Listor 2 Listor = generliserde strängr Strängr = sekvenser v tecken Listor = sekvenser v vd som helst [10, 20, 30, 40] # en list v heltl ["spm", "ungee",
Föreläsning 8 Datastrukturer (DAT037)
 Föreläsning 8 Datastrukturer (DAT037) Fredrik Lindblad 1 2016-11-23 1 Slides skapade av Nils Anders Danielsson har använts som utgångspunkt. Se http://www.cse.chalmers.se/edu/year/2015/course/dat037 Förra
Föreläsning 8 Datastrukturer (DAT037) Fredrik Lindblad 1 2016-11-23 1 Slides skapade av Nils Anders Danielsson har använts som utgångspunkt. Se http://www.cse.chalmers.se/edu/year/2015/course/dat037 Förra
Rev No. Magnetic gripper 3
 Magnetic gripper 1 Magnetic gripper 2 Magnetic gripper 3 Magnetic gripper 4 Pneumatic switchable permanent magnet. A customized gripper designed to handle large objects in/out of press break/laser cutting
Magnetic gripper 1 Magnetic gripper 2 Magnetic gripper 3 Magnetic gripper 4 Pneumatic switchable permanent magnet. A customized gripper designed to handle large objects in/out of press break/laser cutting
Tentamen i Eleffektsystem 2C1240 4 poäng
 Tentmen i Eleffektytem C40 4 poäng Ondgen 5 december 004 kl 4.00-9.00 (Frågetund: 5.00, 6.00 och 7.30) Hjälpmedel: En hndkriven A4-id, Bet eller Joefon, fickräknre. Endt en uppgift per bld! Teern lämn
Tentmen i Eleffektytem C40 4 poäng Ondgen 5 december 004 kl 4.00-9.00 (Frågetund: 5.00, 6.00 och 7.30) Hjälpmedel: En hndkriven A4-id, Bet eller Joefon, fickräknre. Endt en uppgift per bld! Teern lämn
Dugga Datastrukturer (DAT036)
 Dugga Datastrukturer (DAT036) Duggans datum: 2012-11-21. Författare: Nils Anders Danielsson. För att en uppgift ska räknas som löst så måste en i princip helt korrekt lösning lämnas in. Enstaka mindre
Dugga Datastrukturer (DAT036) Duggans datum: 2012-11-21. Författare: Nils Anders Danielsson. För att en uppgift ska räknas som löst så måste en i princip helt korrekt lösning lämnas in. Enstaka mindre
INLÄMNINGSUPPGIFT 2 (Del 2, MATEMATISK STATISTIK) Kurs: MATEMATIK OCH MATEMATISK STATISTIK 6H3000
 INLÄMNINGSUPPGIFT 2 (Del 2, MATEMATISK STATISTIK) Kurs: MATEMATIK OCH MATEMATISK STATISTIK 6H3000 Lärare: Armin Halilovic armin@syd.kth.se www.syd.kth.se/armin tel 08 790 4810 Inlämningsuppgift 2 består
INLÄMNINGSUPPGIFT 2 (Del 2, MATEMATISK STATISTIK) Kurs: MATEMATIK OCH MATEMATISK STATISTIK 6H3000 Lärare: Armin Halilovic armin@syd.kth.se www.syd.kth.se/armin tel 08 790 4810 Inlämningsuppgift 2 består
M edlem sblad för H allsbergsn aturskyddsförening N r2 1999
 M edlem sblad för H allsbergsn aturskyddsförening N r2 1999 Majviva En ca decimeterhög vacker viva med violetta blommor Majvivan är ganska sällsynt på öppen, fuktig, kalkrik mark. Kalkkärr mm. Minskande.
M edlem sblad för H allsbergsn aturskyddsförening N r2 1999 Majviva En ca decimeterhög vacker viva med violetta blommor Majvivan är ganska sällsynt på öppen, fuktig, kalkrik mark. Kalkkärr mm. Minskande.
Föreläsning 7b. 3329 Längdskalan är L = 2 3
 Föreläsning 7b 3329 Längdskln är L = 2 3 eller 2 : 3 som det oft skrivs i smbnd med krtor. Från teorin får vi tt A, reskln är längdskln i kvdrt det vill säg A = L 2. I denn uppgift ger det A = ( ) 2 2
Föreläsning 7b 3329 Längdskln är L = 2 3 eller 2 : 3 som det oft skrivs i smbnd med krtor. Från teorin får vi tt A, reskln är längdskln i kvdrt det vill säg A = L 2. I denn uppgift ger det A = ( ) 2 2
Föreläsning Datastrukturer (DAT037)
 Föreläsning Datastrukturer (DAT037) Nils Anders Danielsson 2015-11-20 Idag Grafer: Terminologi. Datastrukturer. Topologisk sortering. Kortaste vägen. Bredden först-sökning. Dijkstras algoritm. (Vi får
Föreläsning Datastrukturer (DAT037) Nils Anders Danielsson 2015-11-20 Idag Grafer: Terminologi. Datastrukturer. Topologisk sortering. Kortaste vägen. Bredden först-sökning. Dijkstras algoritm. (Vi får
MER MASSAGE - MINDRE LJUD
 MR MSSG - MINR LJU Nytt unikt bottensystem med vttenmssge Nytt unikt system - dkr med ljusterpi System sic, ett något enklre mssgesystem Nytt system i xclusive serien Revolutionernde tyst mssge ger en
MR MSSG - MINR LJU Nytt unikt bottensystem med vttenmssge Nytt unikt system - dkr med ljusterpi System sic, ett något enklre mssgesystem Nytt system i xclusive serien Revolutionernde tyst mssge ger en
Omtentamen i DV & TDV
 Umeå Universitet Institutionen för Datavetenskap Gunilla Wikström (e-post wikstrom) Omtentamen i Teknisk-Vetenskapliga Beräkningar för DV & TDV Tentamensdatum: 2005-06-07 Skrivtid: 9-15 Hjälpmedel: inga
Umeå Universitet Institutionen för Datavetenskap Gunilla Wikström (e-post wikstrom) Omtentamen i Teknisk-Vetenskapliga Beräkningar för DV & TDV Tentamensdatum: 2005-06-07 Skrivtid: 9-15 Hjälpmedel: inga
VECKANS LILLA POSTKODVINST á 1.000 kronor Inom nedanstående postkoder vinner följande 219 lottnummer 1.000 kronor vardera:
 Dragningsresultat vecka 27-2015 Här nedan kan du se om du är en av de lyckliga vinnarna i veckans utlottning i Svenska PostkodLotteriet. När du har vunnit betalar vi automatiskt ut dina vinstpengar till
Dragningsresultat vecka 27-2015 Här nedan kan du se om du är en av de lyckliga vinnarna i veckans utlottning i Svenska PostkodLotteriet. När du har vunnit betalar vi automatiskt ut dina vinstpengar till
Datastrukturer och algoritmer. Modell/tillämpningar för träd. Innehåll. Organisation och terminologi (2) Organisation och terminologi (1)
 Dtstrukturr och lgoritmr Förläsning 9 Träd Innhåll Modllr/tillämpningr för träd Orgnistion och trminologi Signturdigrm för ordnt träd Olik typr v träd Trädlgoritmr Implmnttion v träd Modll/tillämpningr
Dtstrukturr och lgoritmr Förläsning 9 Träd Innhåll Modllr/tillämpningr för träd Orgnistion och trminologi Signturdigrm för ordnt träd Olik typr v träd Trädlgoritmr Implmnttion v träd Modll/tillämpningr
5B1816 Tillämpad mat. prog. ickelinjära problem. Optimalitetsvillkor för problem med ickelinjära bivillkor
 5B1816 Tillämpad mat. prog. ickelinjära problem Föreläsning 3 Optimalitetsvillkor för problem med ickelinjära bivillkor A. Forsgren, KTH 1 Föreläsning 3 5B1816 2005/2006 Optimalitetsvillkor för ickelinjära
5B1816 Tillämpad mat. prog. ickelinjära problem Föreläsning 3 Optimalitetsvillkor för problem med ickelinjära bivillkor A. Forsgren, KTH 1 Föreläsning 3 5B1816 2005/2006 Optimalitetsvillkor för ickelinjära
Tentamen 2008_03_10. Tentamen Del 1
 Tntamn 28_3_ Tntamn Dl KS motsvarar (Dluppgift -2) Dluppgift Dt dcimala hltalt 95 är givt. a) Ang talt i dt hadcimala talsstmt. b) Ang talt i dt binära talsstmt. c) Ang talt md BCD-kod Dluppgift 2 z z
Tntamn 28_3_ Tntamn Dl KS motsvarar (Dluppgift -2) Dluppgift Dt dcimala hltalt 95 är givt. a) Ang talt i dt hadcimala talsstmt. b) Ang talt i dt binära talsstmt. c) Ang talt md BCD-kod Dluppgift 2 z z
Max. partikelstorlek 5 µm. Tillslagstid enligt DIN VDE 0580 100 %
 Gripdon oh vkuumkomponenter Ejektorer Med Losslåsningsventil Med ljuddämpre Med kventil, Med filter Vkuumrytre: Elektronisk st PNP oh st nlog Med luftsprutomtik Omgivningstempertur min./mx. +0 C / +0 C
Gripdon oh vkuumkomponenter Ejektorer Med Losslåsningsventil Med ljuddämpre Med kventil, Med filter Vkuumrytre: Elektronisk st PNP oh st nlog Med luftsprutomtik Omgivningstempertur min./mx. +0 C / +0 C
The Next Generation platform Snabbguide
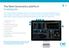 Sngui Vi hr skpt nn sngui för tt u på tt nklt sätt kn knt ig m mång v vår vrktyg oh funktionr i vår plttform. Lär ig vr u hittr prouktr tt hnl, nyhtr, grfr, plr olik Orrtypr, övrvk in positionr, liv-hjälp
Sngui Vi hr skpt nn sngui för tt u på tt nklt sätt kn knt ig m mång v vår vrktyg oh funktionr i vår plttform. Lär ig vr u hittr prouktr tt hnl, nyhtr, grfr, plr olik Orrtypr, övrvk in positionr, liv-hjälp
säkerhetsutrustning / SAFETY EQUIPMENT
 säkerhetsutrustning / SAFETY EQUIPMENT Hastighetsvakt / Speed monitor Kellves hastighetsvakter används för att stoppa bandtransportören när dess hastighet sjunker under beräknade minimihastigheten. Kellve
säkerhetsutrustning / SAFETY EQUIPMENT Hastighetsvakt / Speed monitor Kellves hastighetsvakter används för att stoppa bandtransportören när dess hastighet sjunker under beräknade minimihastigheten. Kellve
Webbregistrering pa kurs och termin
 Webbregistrering pa kurs och termin 1. Du loggar in på www.kth.se via den personliga menyn Under fliken Kurser och under fliken Program finns på höger sida en länk till Studieöversiktssidan. På den sidan
Webbregistrering pa kurs och termin 1. Du loggar in på www.kth.se via den personliga menyn Under fliken Kurser och under fliken Program finns på höger sida en länk till Studieöversiktssidan. På den sidan
Sångerna är lämpliga att framföra vid bröllop, speciella fester och romantiska tillfällen för Kärlekens skull... GE 11176
 FÖROR So en sträng å gtrren och so tonern dn vs..., så börjr texten Ulrk Neuns underbr Kärleksvls. Vd kn vr ljuvlgre än gtrrens sröd och nnerlg ton so tllsns ed sången kn sk sådn stänng och rontsk tosfär.
FÖROR So en sträng å gtrren och so tonern dn vs..., så börjr texten Ulrk Neuns underbr Kärleksvls. Vd kn vr ljuvlgre än gtrrens sröd och nnerlg ton so tllsns ed sången kn sk sådn stänng och rontsk tosfär.
 Kmerobjektiv oc elokusering Zoomobjektiv Ett kmerobjektiv sk normlt vbil ett objekt som beinner sig på någr meters vstån på en ilm i en krtig örminskning. Det innebär tt okllängen på et objektiv mn sk
Kmerobjektiv oc elokusering Zoomobjektiv Ett kmerobjektiv sk normlt vbil ett objekt som beinner sig på någr meters vstån på en ilm i en krtig örminskning. Det innebär tt okllängen på et objektiv mn sk
Om oss DET PERFEKTA KOMPLEMENTET THE PERFECT COMPLETION 04 EN BINZ ÄR PRECIS SÅ BRA SOM DU FÖRVÄNTAR DIG A BINZ IS JUST AS GOOD AS YOU THINK 05
 Om oss Vi på Binz är glada att du är intresserad av vårt support-system för begravningsbilar. Sedan mer än 75 år tillverkar vi specialfordon i Lorch för de flesta olika användningsändamål, och detta enligt
Om oss Vi på Binz är glada att du är intresserad av vårt support-system för begravningsbilar. Sedan mer än 75 år tillverkar vi specialfordon i Lorch för de flesta olika användningsändamål, och detta enligt
C100-LED Duschhörn med LED-Belysning
 SVENSKA C100-LE uschhörn med LE-elysning COPYRIGHT CAINEX A ARUMSPROUKTER, LJUNGY, SWEEN MONTERINGSANVISNING Totl höjd: 1900 mm 6 mm härdt gls A 900 800 700 884 784 684 C 900 800 800 884 784 784 39 8 Prod.#
SVENSKA C100-LE uschhörn med LE-elysning COPYRIGHT CAINEX A ARUMSPROUKTER, LJUNGY, SWEEN MONTERINGSANVISNING Totl höjd: 1900 mm 6 mm härdt gls A 900 800 700 884 784 684 C 900 800 800 884 784 784 39 8 Prod.#
Flera kvantifierare Bevis Direkt bevis Motsägelse bevis Kontrapositivt bevis Fall bevis Induktionsprincipen. x y (x > 0) (y > 0) xy > 0 Domän D = R
 Föreläsning Flera kvantifierare Bevis Direkt bevis Motsägelse bevis Kontrapositivt bevis Fall bevis Induktionsprincipen För att göra ett påstående av en öppen utsaga med flera variabler behövs flera kvantifierare.
Föreläsning Flera kvantifierare Bevis Direkt bevis Motsägelse bevis Kontrapositivt bevis Fall bevis Induktionsprincipen För att göra ett påstående av en öppen utsaga med flera variabler behövs flera kvantifierare.
Göm ninjorna. Det här projektet kommer att bygga på din kunskap om CCS-kung fu.
 Nivå 2 Göm ninjorna All Code Clubs must be registered. By registering your club we can measure our impact, and we can continue to provide free resources that help children learn to code. You can register
Nivå 2 Göm ninjorna All Code Clubs must be registered. By registering your club we can measure our impact, and we can continue to provide free resources that help children learn to code. You can register
Sektion I LÅGFRIKTIONSPLAST. Kedjeglidlister Glidlister Styrlister Band, Plattor, Rundstång Specialdetaljer. Sektion I - Sid
 Sktion LÅGFRKTONSPLST Kdjglidlitr Glidlitr Styrlitr and, Plattor, Rundtång Spcialdtaljr Sktion - Sid Kvalittr och användningområdn Kvalitt PED 1000REG En privärd högmolkylär polytn md god nötningbtändight
Sktion LÅGFRKTONSPLST Kdjglidlitr Glidlitr Styrlitr and, Plattor, Rundtång Spcialdtaljr Sktion - Sid Kvalittr och användningområdn Kvalitt PED 1000REG En privärd högmolkylär polytn md god nötningbtändight
6 Rekursion. 6.1 Rekursionens fyra principer. 6.2 Några vanliga användningsområden för rekursion. Problem löses genom:
 6 Rekursion 6.1 Rekursionens fyra principer Problem löses genom: 1. förenkling med hjälp av "sig själv". 2. att varje rekursionssteg löser ett identiskt men mindre problem. 3. att det finns ett speciellt
6 Rekursion 6.1 Rekursionens fyra principer Problem löses genom: 1. förenkling med hjälp av "sig själv". 2. att varje rekursionssteg löser ett identiskt men mindre problem. 3. att det finns ett speciellt
Föreläsning 6: Introduktion av listor
 Föreläsning 6: Introduktion av listor Med hjälp av pekare kan man bygga upp datastrukturer på olika sätt. Bland annat kan man bygga upp listor bestående av någon typ av data. Begreppet lista bör förklaras.
Föreläsning 6: Introduktion av listor Med hjälp av pekare kan man bygga upp datastrukturer på olika sätt. Bland annat kan man bygga upp listor bestående av någon typ av data. Begreppet lista bör förklaras.
TENTAMEN. Linjär algebra och analys Kurskod HF1006. Skrivtid 8:15-13:00. Onsdagen 17 november 2010. Tentamen består av 3 sidor
 TENTAMEN Linjär algebra och analys Kurskod HF1006 Skrivtid 8:15-13:00 Onsdagen 17 november 2010 Tentamen består av 3 sidor Hjälpmedel: Mathematica samt allt tryckt material Tentamen består av 12 uppgifter,
TENTAMEN Linjär algebra och analys Kurskod HF1006 Skrivtid 8:15-13:00 Onsdagen 17 november 2010 Tentamen består av 3 sidor Hjälpmedel: Mathematica samt allt tryckt material Tentamen består av 12 uppgifter,
Oleopass Bypass-oljeavskiljare av betong för markförläggning
 Instlltionsnvisning Oleopss Bypss-oljevskiljre v etong för mrkförläggning Figur 1 P C H G F E D B I J L M Q 0 O N O Innehåll: Uppyggnd och ingående komponenter... 1 Hlssystem... 2 Lossning... 2 Schkt,
Instlltionsnvisning Oleopss Bypss-oljevskiljre v etong för mrkförläggning Figur 1 P C H G F E D B I J L M Q 0 O N O Innehåll: Uppyggnd och ingående komponenter... 1 Hlssystem... 2 Lossning... 2 Schkt,
Arvika 2019_243 Stömne Bertil Persson Betongteknik AB DECIBEL - Huvudresultat Beräkning: VKV SWE99TM VKV typ Ljuddata
 SVENSKA BESTÄMMELSER FÖR EXTERNT BULLER FRÅN LANDBASERADE VINDKRAFTVERK 2019-03-02 07:25 / 1 Beräkningen är baserad på den av Statens Naturvårdsverk rekommenderad metod "Ljud från landbaserade vindkraftverk",
SVENSKA BESTÄMMELSER FÖR EXTERNT BULLER FRÅN LANDBASERADE VINDKRAFTVERK 2019-03-02 07:25 / 1 Beräkningen är baserad på den av Statens Naturvårdsverk rekommenderad metod "Ljud från landbaserade vindkraftverk",

