Analytiska trafikmodeller
|
|
|
- Mikael Olofsson
- för 10 år sedan
- Visningar:
Transkript
1 Analytiska trafikmodeller För cirkulationsplatser med obevakade övergångsställen Sammanfattning Cirkulationsplatser har de senaste 30 åren blivit en allt vanligare korsningstyp i Sverige. För att uppskatta kapaciteten för en cirkulationsplats används både analytiska trafikmodeller och simulering som verktyg. Analytiska trafikmodeller såsom CapCal har dock svårigheter i att beräkna framkomlighetsmått då gång- och cykeltrafik finns på övergångsställen vid cirkulationsplatsen. Det är klarlagt att ett övergångsställe efter en cirkulationsplats kan ge blockerande effekter bakåt, men vilka flödesnivåer av fordons-, gång- och cykeltrafik som är kritiska är ännu inte fastlagda. I detta examensarbete har en amerikansk analytisk beräkningsmodell som beräknar dessa kapacitetsförluster undersökts och jämförts med simuleringar i VISSIM. Detta för att utvärdera om beräkningsmodellen kan vara lämplig att lägga in i CapCal för att förbättra programmet. Resultaten visar att beräkningsmodellen kan uppskatta om en kapacitetsreduktion kommer att inträffa men hur korrekt storleken på reduktionen blir är svårt att avgöra. Slutsatsen och rekommendationen är att CapCal bör utökas med beräkningsmodellen. Detta för att varna när framkomlighetsmåtten blir för osäkra för att kunna användas till analyser av en cirkulationsplats prestanda. Analytical traffic models For roundabouts with unsignalized crossings Abstract Roundabouts have become a more common type of intersection in Sweden over the last 30 years. In order to evaluate the roundabout performance both analytical models and simulation models are being used. Analytical traffic models such as CapCal have difficulties estimating the performance of the roundabout if there are pedestrians and bicyclists at crossings located close to the roundabout. It is well known that a crossing located after a roundabout exit can cause an up-stream blocking effect that affects the performance of the roundabout. But the different flows of vehicles, pedestrians and bicyclists causing this effect are not known. In this thesis an American analytical model estimating a percentage loss of capacity due to the crossing has been investigated and compared to simulations in VISSIM. The purpose of this investigation is to examine if the analytical model is suitable to implement into CapCal. The results show that the analytical model can estimate if a capacity loss will occur, but the magnitude of this loss is harder to evaluate. The conclusion and recommendation is that the analytical model should be implemented into CapCal. The model is to be used as a warning system if the results in CapCal are too uncertain to use for analysis of the roundabout performance. i
2 Förord Att skriva det här examensarbetet har varit roligt och enormt lärorikt. Det har gett mig chansen att fördjupa mina kunskaper om trafikmodeller i allmänhet och hur simuleringar i VISSIM kan användas. Ett stort och varmt tack till Trivector och för att jag har fått sitta på kontoret i Stockholm och skriva min rapport. Tack även till mina två handledare Andreas Allström och Johan Olstam som ställt upp och svarat på frågor och bollat idéer med mig när det behövts. Tack till Albania Nissan (Bibbi) och Harilaos Koutsopoulos på Trafik och Logistik, KTH för bra synpunkter. Astrid Stockholm, februari 2010 ii
3 Innehållsförteckning 1 INLEDNING Bakgrund Problemformulering och syfte Avgränsningar Metod Hypotes Rapportens struktur LITTERATURSTUDIE Cirkulationsplatsen Historia och funktion Typer av cirkulationsplatser Utformning av cirkulationsplatser med gång- och cykeltrafik Trafikmodeller Trafikmodellen CapCal CapCals beräkningsmodell för cirkulationsplatser Analytiska trafikmodeller J Griffiths; A mathematical model of a nonsignalized pedestrian crossing M Marlow och G Maycock; The effect of zebra crossings on junction entry capacities Rodegerdts & Blackwelder; Analytical analysis of pedestrian effects on roundabout exit capacity Val av modell för vidare undersökning DATAINSAMLING Val av plats och data Solna Rissne Malmö Lund RESULTAT Den analytiska modellen Solna Rissne iii
4 4.1.3 Malmö Lund Västra Lund Södra Lund Östra ANALYS OCH MODELLUTVECKLING Beteenden och effekter som syns på filmen men ej kan fångas upp genom simulationen Resultat från simuleringen samt analys Solna Rissne Jämförelse i resultat mellan den analytiska modellen och simuleringen Uppskattning av antal blockerande händelser Resultat från regressionsanalysen DISKUSSION OCH SLUTSATS Brister i datainsamlingen och analysen Regressionsanalysen Användbarhet av den analytiska modellen Rekommendationer för CapCal REFERENSER Litteratur Figurer BILAGOR... I Bilaga I Beräkningar för den analytiska modellen... II Solna... II Rissne... IV Malmö, Annetorpsvägen... V Lund, Västra... VI Lund, Södra... VII Lund, Östra... VIII Bilaga II Parameterinställningar i simuleringen... X Bilaga III Resultat simuleringen... XI Cirkulationsplatsen i Rissne... XI Beskrivande statistik... XII Cirkulationsplatsen i Solna... XXIV iv
5 Bilaga IV Regressionsanalysen... XXXIV Regression 1... XXXV Regression 2... XXXVIII Regression 3... XLII Regression 4... XLV Regression 5... XLVIII Figurförteckning FIGUR 1.1 ILLUSTRATION AV DE KÖER SOM BILDAS I CIRKULATIONSPLATSEN DÅ ÖVERGÅNGSSTÄLLET BLOCKERAS AV FOTGÄNGARE... 2 FIGUR 2.1 HUVUDELEMENTEN I CIRKULATIONSPLATSEN... 5 FIGUR 2.2 VÄJNINGSLINJE FÖRE RESPEKTIVE EFTER ÖVERGÅNGSTÄLLE OCH CYKELÖVERFART... 6 FIGUR 2.3 MODELLSTRUKTUR FÖR CAPCAL... 9 FIGUR 2.4 LÄNGDEN (L) OCH BREDDEN (W) PÅ VÄXLINGSSTRÄCKAN FIGUR 2.5 DE OLIKA FLÖDENA IN I CIRKULATIONSPLATSEN FIGUR 2.6 ILLUSTRATION AV EFFEKTERNA AV KORTA KÖRFÄLTSBLOCKERINGAR FIGUR 2.7 DEN EXTRA BLOCKERINGSTID SOM ORSAKAS AV ATT FORDON FORTSÄTTER ATT ANLÄNDA TILL SLUTET AV KÖN DÅ DEN BÖRJAT AVVECKLAS FIGUR 2.8 Q E, DEN KÖLÄNGD I ANTAL FORDON SOM FÅR PLATS MELLAN ÖVERGÅNGSSTÄLLET OCH UTFARTEN UTAN ATT BLOCKERA DET CIRKULERANDE FLÖDET FIGUR 2.9 ILLUSTRATION AV DEN KÖ SOM BLOCKERAR DEN CIRKULERANDE STRÖMMEN, ANKOMSTER OCH AVVECKLING AV KÖN ANTAS JÄMT FÖRDELANDE FIGUR 5.1 KONFIDENSINTERVALL FÖR TOTAL RESTID FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I SOLNA 36 FIGUR 5.2 KONFIDENSINTERVALL FÖR TOTAL FÖRDRÖJNING FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I SOLNA 39 FIGUR 5.3 KONFIDENSINTERVALL FÖR GENOMSNITTLIG FÖRDRÖJNING PER FORDON (SEKUNDER) FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I SOLNA FIGUR 5.4 KONFIDENSINTERVALL FÖR TOTALT ANTAL STOPP FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I SOLNA 40 FIGUR 5.5 KONFIDENSINTERVALL FÖR GENOMSNITTLIGT ANTAL STOPP PER FORDON FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I SOLNA FIGUR 5.6 KONFIDENSINTERVALL FÖR ANTAL BLOCKERANDE HÄNDELSER I SOLNA FIGUR 5.7 KONFIDENSINTERVALL FÖR TOTAL RESTID FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I RISSNE 43 FIGUR 5.8 KONFIDENSINTERVALL FÖR TOTAL FÖRDRÖJNING FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN RISSNE 47 FIGUR 5.9 KONFIDENSINTERVALL FÖR GENOMSNITTLIG FÖRDRÖJNING PER FORDON FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN RISSNE FIGUR 5.10 KONFIDENSINTERVALL FÖR TOTALT ANTAL STOPP FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN RISSNE FIGUR 5.11 KONFIDENSINTERVALL FÖR GENOMSNITTLIGT ANTAL STOPP PER FORDON FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN RISSNE FIGUR 5.12 KONFIDENSINTERVALL FÖR ANTAL BLOCKANDE HÄNDELSER I RISSNE FIGUR 5.13 ILLUSTRATION AV RESULTAT FRÅN DE OLIKA SCENARIO FÖR DEN ANALYTISKA MODELLEN OCH SIMULERINGEN FIGUR D-PLOT FÖR DEN TOTALA FÖRDRÖJNINGEN I TIMMAR FIGUR D-PLOT FÖR DEN PROCENTUELLA KAPACITETSFÖRLUSTEN v
6 FIGUR 5.16 BRANT LUTNING PÅ GC-AXELN DÅ FORDONSFLÖDET ÄR HÖGT FIGUR 5.17 SVAG LUTNING PÅ GC-AXELN DÅ FORDONSFLÖDET ÄR LÅGT FIGUR D-PLOT FÖR ANTAL BLOCKERANDE HÄNDELSER BEROENDE AV FORDONSFLÖDET OCH GC- FLÖDET 56 Bildförteckning BILD 3.1 STILLBILD FRÅN FILMEN FRÅN SOLNA BILD 3.2 STILLBILD FRÅN FILMEN FRÅN RISSNE BILD 3.3 STILLBILD FRÅN FILMEN FRÅN MALMÖ BILD 3.4 STILLBILD FRÅN FILMEN FRÅN LUND BILD 5.1 BILD FRÅN VISSIM SIMULERINGEN AV CIRKULATIONSPLATSEN I SOLNA BILD 5.2 BILD FRÅN VISSIM SIMULERINGEN AV CIRKULATIONSPLATSEN I RISSNE BILD 5.3 VÄNSTERSVÄNGANDE FORDONSSTRÖM FRÅN GUSTAV III:S BOULEVARD Tabeller TABELL 2.1 SAMMANSÄTTNINGEN AV ÖVERORDNAT FLÖDE TABELL 3.1 UPPMÄTTA VÄRDEN FRÅN SOLNA TABELL 3.2 UPPMÄTTA VÄRDEN FRÅN RISSNE TABELL 3.3 UPPMÄTTA VÄRDEN FRÅN MALMÖ TABELL 3.4 UPPMÄTTA VÄRDEN FRÅN LUND - VÄSTRA TABELL 3.5 UPPMÄTTA VÄRDEN FRÅN LUND - SÖDRA TABELL 3.6 UPPMÄTTA VÄRDEN FRÅN LUND - ÖSTRA TABELL 5.1 MEDELVÄRDET FÖR TOTAL RESTID (TIMMAR) FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I SOLNA 36 TABELL 5.2 MEDELRESTIDEN PER FORDON FÖR OLIKA RUTTER GENOM CIRKULATIONSPLATSEN I SOLNA TABELL 5.3 MEDELVÄRDET FÖR TOTAL FÖRDRÖJNING (TIMMAR) FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I SOLNA TABELL 5.4 MEDELVÄRDET FÖR GENOMSNITTLIG FÖRDRÖJNING (SEKUNDER) FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I SOLNA TABELL 5.5 MEDELVÄRDET FÖR TOTALT ANTAL STOPP FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I SOLNA 40 TABELL 5.6 MEDELVÄRDET FÖR GENOMSNITTLIGT ANTAL STOPP PER FORDON FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I SOLNA TABELL 5.7 MEDELVÄRDET FÖR TOTAL RESTID (TIMMAR) FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I RISSNE 42 TABELL 5.8 MEDELRESTIDEN PER FORDON FÖR OLIKA RUTTER GENOM CIRKULATIONSPLATSEN I RISSNE TABELL 5.9 MEDELVÄRDET FÖR TOTAL FÖRDRÖJNING (TIMMAR) FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I RISSNE TABELL 5.10 MEDELVÄRDET FÖR GENOMSNITTLIG FÖRDRÖJNING PER FORDON (SEKUNDER) FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I RISSNE TABELL 5.11 MEDELVÄRDET FÖR TOTALT ANTAL STOPP FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I RISSNE 48 TABELL 5.12 MEDELVÄRDET FÖR GENOMSNITTLIGT ANTAL STOPP FÖR SIMULERINGEN AV CIRKULATIONSPLATSEN I RISSNE TABELL 5.13 JÄMFÖRELSE AV RESULTAT MELLAN DEN ANALYTISKA MODELLEN OCH SIMULERING I VISSIM TABELL 5.14 DE OLIKA TESTADE MULTIPLA REGRESSIONSANALYSERNA vi
7 TABELL 5.15 RESULTATEN FÖR DE TESTADE MULTIPLA REGRESSIONSANALYSERNA TABELL 5.16 MATRIS ÖVER ANTALET BLOCKERANDE HÄNDELSER PER STUDIETIMMA FÖR REGRESSION vii
8 1 Inledning 1.1 Bakgrund Detta examensarbete handlar om analytiska trafikmodeller för cirkulationsplatser med övergångställen. Examensarbetet är en del av FUD-projektet (Forsknings- och Utvecklingsprojekt finansierat av Vägverket) Kapacitetsmodeller i Korsningar (KAKOR). Projektet KAKOR syftar till att bedöma beräkningsmodellen CapCals användningsområden och framtida användning samt vilka övriga kapacitetsmodeller likvärdiga CapCal det finns på marknaden idag (Vägverket 2008). Anledningen till examensarbetet är den kunskapsbrist som finns för hur fotgängare och cyklister på övergångsställen påverkar framkomligheten i cirkulationsplatser. CapCal kan idag inte beräkna effekterna på kapaciteten när det finns fotgängare och cyklister på övergångsställen i nära anslutning till cirkulationsplatsen. Detta är en av de större bristerna i programmet och en undersökning om möjligheterna att förbättra detta är därför efterfrågad. 1.2 Problemformulering och syfte Som en del av FUD-projekten KAKOR fanns en undersökning riktad till CapCal-användarna rörande programmets användningsområden och dess brister. I undersökningen rörande cirkulationsplatsmodellen framkom det att det fanns brister i; beräkningsmodellen för tvåfältiga cirkulationsplatser att små cirkulationsplatser ej kunde beräknas effekterna av gång- och cykeltrafikens påverkan i cirkulationsplatsen kunde ej hanteras på ett korrekt sätt. Bristerna i beräkningsmodellen för gång- och cykeltrafiks påverkan på kapaciteten är känt sedan tidigare. Forskningen inom detta område är begränsad och få analytiska beräkningsmodeller liknande CapCal finns tillgängliga (Allström A och Olstam O 2010). Att närvaron av gång- och cykeltrafik i cirkulationsplatser reducerar framkomligheten och kapaciteten är känt men vilka flöden som är kritiska är fortfarande ej klarlagt (SKL 2008, s.32). I en cirkulationsplats finns problemet att effekterna av ett övergångställe vid en utfart inte bara påverkar den enskilda utfartens funktion utan även hela cirkulationens, se Figur
9 Figur 1.1 Illustration av de köer som bildas i cirkulationsplatsen då övergångsstället blockeras av fotgängare Möjligheten att förbättra beräkningsmodellen för cirkulationsplatser i CapCal är efterfrågad. Syftet med detta examensarbete är därför att studera och utvärdera tillgängliga analytiska beräkningsmodeller för att se om någon av dessa modeller kan vara lämpliga för att förbättra CapCal. Målet blir således att kunna ge rekommendationer om lämpliga analytiska modellers för- och nackdelar samt hur korrekta dessa är för att uppskatta gång- och cykeltrafikens effekter på kapaciteten i cirkulationsplatsen. 1.3 Avgränsningar De avgränsningar som gjorts i examensarbetet är Endast enfältiga cirkulationsplatser med övergångsställen har undersökts. Orsakerna till detta är dels att övergångställen i plan vid cirkulationsplatser ej bör byggas om det finns mer än ett körfält i vardera riktning samt dels att de analytiska modeller som undersökts inte omfattar cirkulationsplatser med fler än ett körfält. Endast effekterna av övergångsställen efter en cirkulationsplats har studerats. Effekterna av ett övergångsställe före en cirkulationsplats omnämns i litteraturstudien och hanteras delvis av CapCal idag. Valet att endast studera övergångsställen efter en cirkulationsplats är dels på grund av dess mer markanta effekter på övriga infarter i cirkulationsplatsen samt CapCals brist inom detta område. Framkomlighets- och säkerhetsaspekten för fotgängare och cyklister med cirkulationsplats som korsningstyp har inte studerats. 1.4 Metod Metoden för detta examensarbete har varit att göra en djupare litteraturstudie för tre befintliga analytiska beräkningsmodeller för cirkulationsplatser med övergångsställen. Litteraturstudien gav bakgrund till den modell som har valts ut som lämplig att om möjligt utveckla CapCal med. För att 2
10 kunna utvärdera modellens egenskaper och brister har en datainsamling från film samt simulering i VISSIM gjorts. De analytiska beräkningsmodeller som ingår i litteraturstudien har valts ut i samråd med handledarna Andreas Allström och Johan Olstam. Efter genomförd litteraturstudie och modellbeskrivning valdes en modell ut för att vidare undersökning. Valideringen av beräkningsmodellen genomfördes genom att studera filmer från cirkulationsplatser med gång- och cykeltrafik. Filmerna är tagna under 2009 av Trivector och KTH för SNE-projektet Kapacitet i små cirkulationsplatser. Från filmerna gjordes en manuell databearbetning av det data som behövdes för den utvalda beräkningsmodellen. Beräkningsmodellens möjlighet att uppskatta kapacitetsnedsättningen jämfördes sedan mot VISSIMsimuleringar för att på så sätt värdera modellens korrekthet. Varje utformningstyp av cirkulationsplats och/eller flödesnivå simulerades tio gånger med olika slumpfrö för att få fram ett medelvärde. För att jämföra olika alternativ från simuleringen testades värdena dels med 95 % konfidensinterval samt med ensidiga t-test där två sampel antar olika varianser. 1.5 Hypotes Hypotesen är att det finns en eller fler analytiska beräkningsmodeller tillgängliga som är möjliga att utveckla CapCal med. Detta för att förbättra programmets egenskaper vad gällande gång- och cykeltrafikanters effekter på framkomligheten i cirkulationsplatsen. 1.6 Rapportens struktur Inledningsvis i kapitel 2, Litteraturstudien, presenteras cirkulationsplatsens historia, funktion samt vilka speciella krav gång- och cykeltrafik i cirkulationsplatser ställer. Därefter presenteras vad en trafikmodell är samt hur trafikmodellen CapCal är uppbyggd. Detta ger bakgrund och förståelse för hur de tre analytiska modellerna som undersökts fungerar samt vilken modell som slutligen valts ut för undersökning. I kapital 3 och 4 finns datainsamlingen samt resultat för den analytiska trafikmodellen. I kapitel 5 ges analyser och jämförelser mellan den analytiska modellen och simuleringarna i VISSIM. Rapporten avslutas i kapitel 6 med en slutsats och diskussion samt förslag till vidare studier och modellutveckling. 3
11 2 Litteraturstudie I litteraturstudien presenteras cirkulationsplatsen funktion, historia och utformning för att ge bakgrund till de speciella förutsättningar som finns för att göra trafikmodeller som beskriver cirkulationsplatser. Slutligen presenteras de tre olika analytiska trafikmodellerna som undersökts närmre i detta examensarbete samt den diskussion som föranlett valet av modell. 2.1 Cirkulationsplatsen Historia och funktion En cirkulationsplats är en korsningstyp där de ingående vägarna möts och separeras av en rondell. Rondellen skapar en enkelriktad motsols körning i cirkulation där alla inkommande fordon har väjningsplikt mot det cirkulerande flödet. En cirkulationsplats definieras som Plats som enligt lokal trafikföreskrift ska vara cirkulationsplats och som är utmärkt med vägmärke för cirkulationsplats. (Näringsdepartementet 2001, 2) Den moderna cirkulationsplatsen utvecklades i Storbritannien under 1960-talet. Dess för innan förekom en snarlik lösning, trafikcirkeln. Trafikcirkeln var en korsningstyp med flera negativa effekter. Utformning medgav nämligen att hög hastighet kunde hållas. Olycksrisken var stor då de inkörande fordonen hade företräde och trafikcirkeln blev dessutom blockerad vid höga flöden. På grund av dessa problem införde man 1966 i Storbritannien väjningsplikt för inkörande fordon i cirkulationsplatsen. Detta tillsammans med ändrad utformning som sänkte hastigheterna i den cirkulerande strömmen gjorde att olyckorna minskade både i omfattning och i svårighetsgrad (FHWA 2000, s.23) fanns det 150 cirkulationsplatser i Sverige. År 2008 hade antalet ökat till 1500 och det bara på det kommunala väg- och gatunätet (SKL 2008). Idag utformas cirkulationsplatser så att låg hastighet måste hållas i cirkulationen samt att vinkeln mellan det inkommande flödet och det cirkulerande flödet är spetsig. Dessa två egenskaper gör cirkulationsplatsen trafiksäker och följderna av olyckor mindre svåra än vid andra korsningstyper (VGU 2004, Korsningar s. 116). Däremot är andelen olyckor med fotgängare och cyklister inblandade högre än för andra jämförbara korsningstyper. Hastigheten för det cirkulerande flödet bör därför vara låg (FHWA 2000, s.23). Cirkulationsplatsen som korsningstyp lämpar sig bäst när trafikflödena i de anslutande vägarna är relativt jämt fördelade med mycket svängande trafik (VGU 2004, Korsningar s. 117) Typer av cirkulationsplatser Cirkulationsplatser kan vara två-, tre-, fyr- eller flerbenta och ha ett eller flera cirkulerande körfält. Huvudelementen i cirkulationsplatsen är cirkulation (körbanan runt rondellen), rondell, tillfarter och frånfarter, se Figur 2.1 (VGU 2004, Korsningar s. 117). 4
12 Figur 2.1 Huvudelementen i cirkulationsplatsen Vägverkets handbok Vägar och gators utformning (VGU) definierar tre olika typer av cirkulationsplatser beroende på rondellens egenskaper: Normal cirkulationsplats. Rondellens radie är minst 11 m och ej överkörbar. Liten cirkulationsplats. Rondellen består av två delar. En inre rondell med radie minst 2 m och en yttre rondell med radie minst 7 m. Den yttre rondellen är helt eller delvis överkörbar. Minicirkulationsplats. Rondellen är helt överkörbar och radien är oftast mindre än 7 m. Vilken typ av cirkulationsplats som väljs beror dels på vilket tillgängligt utrymme som finns på platsen samt dels på vilken trafiksituation som cirkulationsplatsen dimensioneras för (VGU 2004, Korsningar s. 118) Utformning av cirkulationsplatser med gång- och cykeltrafik Cirkulationsplatser med gång- och cykeltrafik utformas beroende av mängden gående och cyklister som förväntas passera samt hur motortrafiken och gång- och cykeltrafiken har separerats på inkommande vägar och gator. Där gång- och cykeltrafik passerar cirkulationen i plan ska den dimensionerande hastigheten vara högst 30 km/h och antalen körfält bör begränsas till en tillfart och en frånfart. Om fler körfält krävs för att kunna hantera det förväntade fordonsflödet förordas att antingen gång- och cykelöverfarten förskjuts (ca 50 m ut från cirkulationsplatsen på den inkommande vägen) samt signalregleras, eller att en helt signalreglerad korsning väljs istället (VGU 2004, Korsningar s. 128). En enfältig cirkulationsplats kan hantera inkommande fordon/dygn om fordonen fördelas ungefär lika på de inkommande vägarna (SKL 2008, s.30). Det finns tre olika principiella lösningar för att skilja gående och cyklister från bilister vid korsning i plan. Gång- och cykelbana Cyklister i cykelfält/ vägren/blandtrafik och gående på gångbana Cyklister och gående i blandtrafik Cyklister i blandtrafik i cirkulationen är ifrågasatt på grund av cyklisternas sårbarhet i den komplexa trafiksituationen (FHWA 2000, s. 34). Men det kan accepteras enligt VGU förutsatt att 5
13 Inkommande Årsdygnstrafik (ÅDT) < ca fordon Inkommande cykeltrafik < ca 1000 cyklar/dygn Cykeltrafiken är enkelriktad i anslutande ben Cirkulationen är enfältig (VGU 2004, Korsningar s. 130) En gång- och cykelpassage vid en cirkulationsplats kan placeras på två olika sätt; antingen med väjningslinjen före övergångsstället och cykelöverfarten eller efter densamma, se Figur 2.2 (VGU 2004, Korsningar s. 136). Figur 2.2 Väjningslinje före respektive efter övergångställe och cykelöverfart Båda alternativen har sina för- respektive nackdelar. Att placera väjningslinjen efter övergångsstället med en lucka emellan dessa som i alternativ 1 har fördelen att bilisten vid infart kommer att möta situationen i två steg. Först måste bilisten väja för eventuella gående och cyklister och därefter finna en lämplig lucka i den cirkulerande strömmen för att köra in i cirkulationen. Vid utfart från cirkulationsplatsen finns även fördelar med alternativ 1 då en bilist kan stanna och släppa fram gående och cyklister på övergångsstället utan att stoppa det cirkulerande flödet. Det finns dessutom fördelar för synskadade och för barn med att placera övergångsstället en bit från själva cirkulationen. För synskadade som är beroende av sin hörsel då de ska passera övergångsstället kan en placering allt för nära det cirkulerande flödet göra ljudbilden svårtolkad (VGU 2004, Korsningar s. 132). För barn som har svårare att ta in komplexa trafikmiljöer kan ett övergångställe en bit från cirkulationen vara att föredra (SKL 2008, s.30). Nackdelen med alternativ 1 är att sträckan för fotgängarna och cyklisten att gå/cykla kan bli längre om avståndet mellan väjningslinjen och övergångsstället ökas, dessutom kan hastigheterna vid övergångsstället vara högre. Det kan även för alternativ 1 finnas behov av att bredda och förlänga mittrefugen och en ytkrävande och svårplacerad trafiklösning kan därför bli resultatet (VGU 2004, Korsningar s. 132). 6
14 2.2 Trafikmodeller En trafikmodell är en förenklad representation av ett verkligt trafiksystem. Beroende på vilka delar av trafiksystemet som ska beskrivas skiljer sig modellerna åt vad gäller detaljeringsgrad och utformning. Trafikmodeller är abstrakta, analytiska och bygger på en teori om hur verkligheten ser ut (Ortúzar D 1990, s.2). De två huvudsakliga sätten att utveckla en sådan teori om verkligheten är att antingen ha ett deduktivt angreppssätt, dvs. att först bygga en modell utifrån teorier och sedan testa denna modell mot observationer. Det andra sättet är induktivt, dvs. att börja med insamlade data och utifrån dessa försöka bygga en modell som passar (Ortúzar D 1990, s.16). Utvecklandet av mer komplexa trafikmodeller tog fart på 1970-talet då datorerna gjorde det möjligt att hantera och analysera större mängder data (Ortúzar D 1990, s.20). Trafikmodeller kan delas in i olika grupper beroende på egenskaper och/eller användningsområde. De tre huvudsakliga indelningarna är efter beräkningsmetod o analytisk/simulering efter de ingående parametrarnas egenskaper o deterministisk (förutbestämd) / stokastisk (slumpvis) efter detaljeringsgrad o mikronivå/mesonivå/makronivå (Allström A m.fl. 2008, s.9) De förutbestämda (deterministiska) modellerna har ofta en analytisk beräkningsmetod. Simulering som beräkningsmetod är däremot vanligare för de slumpvisa (stokastiska) modellerna (Allström A m.fl. 2008, s.9). De vanligaste analytiska modellerna för enskilda korsningar är mikromodeller som beskriver t ex en korsning eller annat mindre område. En mikromodell utgår från enskilda fordons eller förares beteende. En mesomodell har ett mer generellt förarbeteende, däremot beskrivs trafiken detaljerat. En mesomodell kan på grund av sin lägre detaljeringsgrad beskriva ett större område, t ex flera korsningar efter varandra. Makromodellen är den minst detaljerade modellen då den har en generell beskrivning av fordonen som flöden och densitet. Makromodeller kan användas för att beskriva resemönster i ett större område, t ex inom en stad eller stadsdel (FHWA 2001, s.8). En simuleringsmodell kan även den vara både på mikro-, meso- eller makronivå. De vanligaste mikrosimuleringsmodellerna styrs av förarnas beteende och interaktion med andra trafikanter under en viss bestämd tidperiod (Allström A m.fl. 2008, s.10). Interaktionerna kan vara sådana som omkörning, körfältsbyte etc. De flesta trafiksimuleringsmodellerna är utvecklade för att studera tätortsmiljöer där mycket interaktioner emellan förarna sker. Fördelarna för simuleringsmodeller kontra de analytiska modellerna i korsningar och då köområden studeras är att ett större område kan undersökas, effekter av t ex närliggande korsningar kan enkelt studeras specialvarianter av korsningsutformningar och/eller regleringssituationer kan undersökas de beskriver trafiksystemets stokastiska och dynamiska natur på ett bättre sätt de beskriver trafikstyrda signaler på ett mer korrekt sätt de ger möjlighet att visualisera resultaten, t ex. med filmsekvenser av fordonsrörelserna olika typer av trafikantbeteenden kan testas mot varandra Nackdelarna med simuleringsmodeller jämfört med de analytiska modellerna är att 7
15 de flesta simuleringsmodeller ger inte några automatiska beräkningar av framkomlighetsmått. Exempelvis kapacitet, belastningsgrad och geometrisk fördröjning måste räknas fram manuellt de tar tid att bygga upp modellen och kalibrera den körningar av modellen och analyser tar längre tid att jämföra olika alternativ tar längre tid de kräver större mängd data både för indata med även för kalibrering och validering insamling av de data som krävs är ofta kostsam och tidskrävande utveckling av simuleringsmodeller pågår fortfarande då det är ett relativt nytt forsknings- och utvecklingsområde de ställer högre krav på användaren då deras uppbyggnad är komplex. För att korrekt kunna tolka resultaten krävs kunskaper om modellens uppbyggnad och funktion. de är relativt kostsamma att köpa in och lära sig (FHWA 2001, s.9-10, Allström A m.fl. 2008, s.10) Vilken av modellerna (analytisk eller simulering) man ska använda beror på situationen samt vad som ska studeras. De analytiska modellerna är bäst lämpade för analyser av standardlösningar eller då enklare och/eller snabba överslagsberäkningar ska göras. Simuleringsmodellerna passar istället bättre då speciella utformnings- eller regleringssituationer ska undersökas (Allström A m.fl. 2008, s.10) Trafikmodellen CapCal CapCal är ett program framtaget av Trivector i samarbete med Vägverket för beräkning av kapacitet och framkomlighet i korsningar. CapCal bygger ursprungligen på en datoriserad version av handboken Beräkning av kapacitet, kölängd, fördröjning i vägtrafikanläggningar (VV TV ) (Statens vägverk, 1977) (Allström A m.fl., 2008, s.11). Fyra olika korsningstyper kan hanteras i programmet; korsningar med stopplikt, korsningar med väjningsplikt, signalreglerade korsningar och cirkulationsplatser. Indata i CapCal är korsningens geometriska utformning samt trafikflödena. Utdata är kapaciteten som redovisas som belastningsgrader, kölängd och fördröjning (Allström A m.fl., 2008, s.12). Programmet kan även göra beräkningar av fordons- och emissionseffekter samt fördröjningsoch olyckskostnader (Aronsson A, Bellinger A 2005, s. 15). CapCal är en mikromodell, den är deterministisk och är uppbyggd kring teorierna om kritiskt tidsavstånd och mättnadsflöden (Allström A m.fl., 2008, s. 12). 8
16 2.2.2 CapCals beräkningsmodell för cirkulationsplatser CapCal kan hantera cirkulationsplatser med upp till fyra till-/ frånfarter och två körfält genom cirkulationen. Beräkningsmodellen i programmet har sex grundläggande steg, se Figur 2.3. Beräkning av överordnat flöde Körfältsfördelning Beräkning av kritiska tidsavstånd och följdtider Korrigering för korta körfält Beräkning av betjäningstider och kapacitet Beräkning av framkomlighetsmått Figur 2.3 Modellstruktur för CapCal Beräkning av kritiska tidsavstånd och följdtider Beräkningsmodellen för cirkulationsplatser är baserad på teorierna kring kritiskt tidsavstånd (tidsluckor). Det kritiska tidsavståndet kan definieras genom att två olika fordonsströmmar identifieras; en överordnad ström och en underordnad ström. I en cirkulationsplats är den överordnade strömmen de runt rondellen cirkulerande fordonen och de underordnade fordonen är de som väntar på att kunna ansluta till den cirkulerande strömmen. För att ett underordnat fordon på ett säkert sätt ska kunna ansluta till den överordnade strömmen krävs det en tidslucka mellan två fordon i den överordnade strömmen som är större eller lika med det kritiska tidsavståndet. Det kritiska tidsavståndets storlek beror således av hur föraren i det underordnade fordonet kompromissar mellan väntan på en tillräckligt stor tidslucka för att säkert kunna köra ut och den extra fördröjning den väntan medför (Hagring O 2001, s.9). Då olika förare har olika säkerhets- och tiduppfattningar varierar således det kritiska tidsavståndet. CapCal är en statisk mikromodell och därför antas alla fordon behöva samma kritiska tidslucka för att kunna ansluta till den överordnade trafikströmmen (Allström A m.fl s. 2). Tiden mellan två fordon som kör in i den överordnade strömmen definieras som följdtid. Det betyder att N fordon kan köra in den överordnade strömmen vid en tidslucka h om T + N 1 T 0 T + NT 0 9
17 Där T kritisk tidslucka T 0 följdtiden h en tidslucka N antal fordon Den teoretiska modellen CapCal för tidsluckorna utnyttjar två olika parametrar; längden och bredden av växlingssträckan (w L ) samt andelen tung trafik (p HV ), se Figur 2.5. T T 0 (Allström m.fl s. 8). T = 5,659 0,062w L + 1,1 p HV 0,056 T 0 = 2,40 + 1,1(p HV 0,061) en kritisk tidslucka i den överordnade strömmen. T antas vara samma för alla fordon samt oberoende av väntetiden följdtid, dvs den tidslucka som behövs mellan ett fordon som lämnar kön och ett fordon i den överordnade strömmen för att det fordon som står som nummer två i kön också ska kunna lämna kön Figur 2.4 Längden (L) och bredden (W) på växlingssträckan Beräkning av överordnat flöde De olika flödena illustreras i Figur 2.5. Det överordnade flödet (q Al + q At + q Bl ) beräknas som summan av flödet i raktframkörande (q At ) vänstersvängande trafikström från tillfarten till vänster (q Al ) flödet i vänstersvängande trafikström från motsatt tillfart (q Bl ) Det överordnade flödet består således av det cirkulerandeflödet men även av de fotgängare och cyklister som passerar infarten. För fotgängare och cyklister som passerar utfarten tas ingen hänsyn till 10
18 i CapCal. Storleken och fördelningen av det överordnade flödet beror på huruvida cirkulationsplatsen har ett eller två cirkulerande körfält. Figur 2.5 Tabell 2.1 De olika flödena in i cirkulationsplatsen Sammansättningen av överordnat flöde Underordnat flöde Överordnat flöde q Dl q Al + q At + q Bl q Dt q Al + q At + q Bl q Dr q Al + q At + q Bl Fotgängare och cyklister i cirkulationsplatsen Cyklister inne i cirkulationsplatser adderas till det överordnade flödet med en personbilsekvivalent om 0,5. Det innebär att en cyklist i cirkulationsplatsen är lika med en halv extra personbil. Om cyklisterna däremot endast passerar på övergångsställena och cykelöverfarterna ska dessa hanteras och adderas som fotgängarflöde. Fotgängarflödet ska adderas till det överordnade flödet om ett övergångsställe finns mellan väjningslinjen och den cirkulerande strömmen med en personbilsekvivalent om 0,5 (Allström A m.fl s. 5-7). För effekterna av ett övergångsställe efter en cirkulationsplats finns ingen beräkningsdel i programmet. 11
19 Beräkning av betjäningstider och kapacitet Alla cirkulerande fordon antas vara överordnade i CapCal och beskrivs av en M3- tidsavståndsfördelning (Allström A m.fl s. 9). Kapaciteten per körfält (för cirkulationsplatser med ett körfält) uttrycks som där där q Δ p HV flödet minsta tidsavstånd mellan fordonen andel tung trafik C = αq e (λt Δ) 1 e (λt 0) α = 0,910 1,545q Δ = 1 + p HV 1,8 αq λ = 1 qδ Den genomsnittliga betjäningstiden för ett fordon i kö uttrycks som den inverterade kapaciteten C -1 = D q. Betjäningstiden för ett fordon som ej köar uttrycks som D n. För beräkning av belastningsgrad används en iterativ beräkningsgång. Körfältsfördelning CapCal har en algoritm för när två underordnade strömmar delar på två eller flera körfält. Flödet fördelas då mellan körfälten så att belastningsgraden dem emellan blir ungefär lika stora. Korrigering för korta körfält och andra faktorer som påverkar kapaciteten I CapCal finns även ett beräkningssteg för att ta hänsyn till korta körfält och den problematik som finns om dessa blir blockerade och ej kan nyttjas fullt ut, se Figur 2.6. I bilden till vänster har ett svart fordon som vill in i det korta högra körfältet blockerat för fordon som vill köra rakt fram i det långa körfältet medans i mittenbilden har de vita fordonen blockerat det korta högra körfältet. I båda fallen kan inte körfältens kapacitet nyttjas fullt ut. 12
20 Figur 2.6 Illustration av effekterna av korta körfältsblockeringar Andra faktorer som påverkar kapaciteten är kopplade till körfälten i sig snarare än rörelserna i dem. För att ta hänsyn till dessa övriga faktorer antas de sinsemellan vara oberoende av varandra och därför multiplicerbara. Två olika korrektionsfaktorer förekommer i CapCal. Korrektionsfaktor för cyklar i cirkulationen o Cyklar antas påverka kapaciteten i cirkulationsplatsen om körfältsbredden är mindre än 4,0 m. Korrektionsfaktor beroende av körfältsbredden o En körfältsbredd eller en infart smalare än 5,0 m antas påverka kapaciteten (Allström A m.fl s. 15) Beräkning av framkomlighetsmått Följande framkomlighetsmått beräknas i CapCal (Linderholm L 2010 s ). Flöde per körfält Kapacitet per körfält, dvs det största fordonsflöde som kan avvecklas Belastningsgraden, kvoten mellan flöde och kapacitet, dvs den utnyttjade kapaciteten Medelkölängden under beräknad timme Kölängd 90-percentil, d.v.s. under 90 % av tiden är kölängden kortare än redovisad kölängd CapCal beräknar dessutom ett antal fördröjningsmått. Interaktionsfördröjning (konfliktfördröjning), d.v.s. den fördröjning som uppstår på grund av konflikter med andra fordon Geometrisk fördröjning, d.v.s. fördröjning på grund av retardation och acceleration jämfört med om korsningen ej existerade (körning samma sträcka på rak väg) Den totala fördröjningen. Det antas att retardationsfördröjningen "tas upp" under interaktionsfördröjningen om tiden för retardation underskrider interaktionsfördröjningen. I 13
21 den totala fördröjningen ingår accelerationsfördröjningen samt det största värdet av interaktionsfördröjning och retardationsfördröjning Andel fördröjda på grund av interaktionsfördröjning Andel fördröjda på grund av korsningens geometriska utformning (exkl. de som fördröjs på grund av interaktion) Andel totalt fördröjda, summan av fördröjda p.g.a. interaktion (konflikt) respektive korsningens geometri ndel fordon som måste stanna CapCal kan även beräkna kostnader som bränsleförbrukning och emissionseffekter. 14
22 2.3 Analytiska trafikmodeller I litteraturstudien har tre analytiska beräkningsmodeller för cirkulationsplatser med övergångställen studerats. Den första modellen är framtagen i början av 1980-talet av professor Jeff Griffiths vid University of Wales Institute of Science and Technology. Den andra modellen som delvis bygger på antaganden gjorda av Griffiths är framtagen av M Marlow och G Maycock vid TRL (UK s Transport and Research Laboratory) år Den sista modellen, som studerats och sedan även valts ut att testas ytterligare, är en modell framtagen i USA år 2005 av Lee A. Rodegerdts och Glenn E. Blackwelder vid Kittelson and Associates, Inc. I litteraturstudien kommer de två första modellernas uppbyggnad beskrivas mer översiktigt och den tredje modellen av Rodegertds och Blackwelder mer ingående J Griffiths; A mathematical model of a nonsignalized pedestrian crossing Griffiths modell är inte en modell specifikt framtagen för cirkulationsplatser utan en modell som beskriver vilka kölängder olika fotgängarflöden på övergångställen ger upphov till. Dock är modellen intressant att studera då dess beräkningsmetod är använd och utvecklad inom flertalet andra analytiska trafikmodeller (Hubberten m.fl , Kreisel 2007). Modellen är i huvudsak uppbyggd av tre delar. Den första delen behandlar fördelningen av de tidsperioder då fordon kan korsa respektive inte korsa övergångsstället. Den andra delen handlar om hur fordonsköns längd kan uppskattas och beräknas. Den sista delen beräknar väntetid och kölängd för fotgängarna Fördelningen av effektiva grön- och rödtider Den första delen av modellen beskriver fördelningen av de tidsperioder då fordon kan korsa respektive inte korsa övergångsstället dessa benämns som effektiva grön- respektive rödtider. Ett antagande som görs är att fotgängarna har strikt företräde vid övergångstället. Det är dock enligt modellen orealistiskt att anta att ett fordon som redan börjat passera övergångsstället genast stannar för en fotgängare som anländer till övergångsstället då passagen redan påbörjats. Därför antas det att om en fotgängare anländer till övergångsstället och att det just då passerar ett fordon stannar fotgängaren och väntar på att få passera tills att fordonet har passerat (Griffiths J 1981, s. 224). Den tid då övergångstället är belastat med fotgängare betecknas som effektiv rödtid. Om ytterligare en fotgängare anländer inom tiden α från det att en fotgängare börjat gå över övergångsstället korsar även den fotgängaren övergångsstället. Denna process fortsätter tills att en tidslucka större än α uppstår mellan fotgängarna, det vill säga att övergångstället är tomt på fotgängare (ibid). Den effektiva gröntiden definieras som den tid då övergångstället inte är belastat med fotgängare (ibid). Fördelningen av effektiv röd- och gröntid uttrycks med hjälp av täthetsfunktionerna för dessa. Täthetsfunktionen beskriver hur sannolika två resultat är i förhållande till varandra. Täthetsfunktionen för den effektiva rödtiden, r(t), består av en diskret (fast) komponent (t=α) motsvarande en effektiv rödtid alstrad av en fotgängare. Den kontinuerliga komponenten av r(t); (t > α) är väntetiden för ett fordon längst fram i kön (ibid). Då r(t) består av både en kontinuerlig och en diskret komponent kan en Laplace-transformation göra att differentialekvationen för täthetsfunktionen omvandlas till en algebraisk ekvation som blir lättare att lösa. Täthetsfunktionen för den effektiva gröntiden, g(t), uttrycks som en multipel av β under förutsättning att kön av fordon aldrig töms under tiden som den effektiva gröntiden pågår. β är tidavståndet mellan fordonen under mättnadsflödet. Problem uppstår att 15
23 uttrycka den effektiva gröntiden som en multipel av β då det inte finns några fordon i kö i början av en effektiv gröntid eller om kön hinner tömmas under den effektiva gröntiden. Vid en sådan händelse blir täthetsfunktionen för den effektiva gröntiden ingen multipel av β. Men för att undvika algebraiska komplikationer antas det i modellen att den effektiva gröntiden alltid är en multipel av β (ibid) Beräkning av fordonsköns längd Modellen bygger således på att fordon som anländer till ett övergångsställe möts av olika alternerande perioder då de kan korsa eller inte korsa övergångsstället (effektiva röda och gröna perioder). Den stora skillnaden mellan ett obevakat övergångsställe som i den här modellen och ett signalreglerat övergångsställe är hur de effektiva gröna och röda perioderna genereras. I ett oreglerat övergångsställe genereras de gröna och röda perioderna av hur fotgängarna anländer till övergångstället vilket gör beräkningen mer komplicerad än om man har ett signalstyrt övergångsställe med fasta grön- och rödtider (Griffiths J 1981, s. 225). Om man antar att den effektiva gröntiden är rβ kan upp till r fordon passera under förutsättning att dessa fordon anländer till korsningen innan nästa fotgängare gör så. Om det är i (<r) fordon som väntar vid övergångstället då nästa effektiva gröntid inleds, kan upp till (r-i) fordon passera innan den effektiva gröntidens slut (ibid). Författarnas invändning mot ovanstående är; att om de i fordonen som ursprungligen stod vid övergångsstället passerar med interval av β, och att det sedan går litet tid innan fler fordon anländer till övergångstället blir det omöjligt att avveckla r eller fler fordon, var och en separerade med tidsavståndet β (Griffiths J 1981, s.226). Enligt fördelningsfunktionen för den effektiva gröntiden finns det ingen maximal längd av den effektiva gröntiden, dock är sannolikheten för längre perioder liten. I modellen antas det, för att lättare kunna göra beräkningar, att den effektiva gröntiden har en viss maxlängd av Nβ (ibid.). För att kunna beräkna alla möjliga kombinationer av kölängder anammar Griffiths de köteorier med analys av inbyggd Markowkedja framtagna av Kendall (Kendall D.G 1953). En Markowkedja antar en regenereringspunkt där processens fortsatta förlopp bestäms utifrån det befintliga tillståndet utan kunskap om dess förflutna förlopp. Modellen uttrycker π(j i) som sannolikheten för att kön har j fordon i regenereringspunkten samt att det var i fordon i föregående regenereringspunkt. För att uttrycka alla möjliga värden av π(j i) tas en övergångsmatris fram där k G (j rβ) är sannolikheten att j fordon anländer till övergångsstället under den effektiva gröntiden rβ och k R (j) är sannolikheten att j fordon anländer till övergångsstället under den effektiva rödtiden. Alla element i övergångsmatrisen är reella tal mellan 0 och 1. Modellen studerar även vad som händer då antalet fordon som kan passera under en effektiv grönperiod går mot oändligheten. Slutligen ges den genomsnittliga kölängden vid början av en effektiv grönperiod samt det maximala möjliga fordonsflödet. Modellen beräknar även fram sannolikheten för att en kö är upplöst vid slutet av en effektiv grönperiod (Griffiths J 1981, s. 229) Väntetid och kölängd för fotgängarna En fotgängare som anländer till övergångsstället under en effektiv grönperiod tvingas vänta tills nästa multipel av β innan han/hon kan börja korsa gatan. Den genomsnittliga fördröjningen hos de fotgängare som blir fördröjda är då β/2. Modellen beräknar slutligen fram sannolikheten att en kö av fotgängare av längden N samt det genomsnittliga antalet av fotgängare (Griffiths J 1981, s. 231). 16
24 2.3.2 M Marlow och G Maycock; The effect of zebra crossings on junction entry capacities Modellen beskriver hur två olika kapacitetsnedsättande effekter kan beräknas. Effekten av ett övergångställe före en korsning Effekten av ett övergångställe efter en korsning Effekterna av ett övergångsställe före korsningen Effekterna av ett övergångsställe före en korsning beror enligt författarna av två faktorer (Marlow M m.fl , s.2). Den relativa kapaciteten för fordonen dels vid övergångsstället samt dels vid väjningslinjen före korsningen Avståndet mellan övergångsstället och väjningslinjen. Övergångstället och väjningslinjen benämns som var sin faktor som påverkar framkomligheten och kapaciteten. När dessa två faktorer ligger nära varandra är de seriekopplade och påverkar således varandras prestationsförmåga. Modellen beskriver bara sambandet då kapaciteten i övergångstället överstiger kapaciteten i korsningen. Anledningen till att endast studera det scenariot är att det omvända innebär att korsningens kapacitet blir högre än övergångställets. Flaskhalsen i systemet blir övergångsstället då korsningen som ligger efter denna teoretiskt sett klarar av att avveckla all trafik som kommer förbi övergångsstället. Kapaciteten för hela systemet uttrycks som en andel av kapaciteten för den senare faktorn (väjningslinjen) (Marlow M m.fl , s.3). M = R + R 2 + R N+1 R = förhållandet mellan kapaciteten hos den första och den andra faktorn R = Kapaciteten os första faktorn (övergångstället) Kapciteten os den andra faktorn (väjningslinjen vid korsningen) N = magasinets längd, dvs. antal fordon som ryms mellan de två faktorerna Om R 1 ges M av M = RN+2 R R N+2 1 Uttrycket ovan togs fram genom att simulera ett övergångsställe och en väjningslinje placerade efter varandra med slumpvisa ankomster och olika kapacitetsförhållanden. Detta testades med olika kapaciteter och avstånd mellan övergångsstället och väjningslinjen (ibid). 17
25 Om kapacitetskvoten mellan övergångsstället och väjningslinjen är given liksom antalet fordon som får plats emellan dem, får man fram den faktor som ska multipliceras med kapaciteten hos den sista faktorn (väjningslinjen) för att få fram den övergripande kapaciteten hos systemet. Författarna ger två olika förslag på beräkningsmodeller för att ta fram kapaciteten för övergångstället respektive kapaciteten för väjningslinjen vid cirkulationen. Kapacitet för väjningslinjen vid cirkulationen beräknas genom att studera relationen mellan kapaciteten hos ingående flöde samt det cirkulerande flödet och de geometriska egenskaperna på platsen. Kapaciteten för övergångstället tas fram med hjälp av Griffiths modell (se 2.3.1). Problem uppstår dock med att använda en kvot mellan väjningslinjens och övergångsställets kapacitet då flödet av fotgängare går mot noll. Då flödet av fotgängarna går mot noll beror kapaciteten i korsningen endast av väjningslinjens kapacitet. Men om flödet av fordon sätts till noll ger det en kapacitet för fordonen lika med mättnadsflödet hos inkommande flödet, och det i kombination med förutspådda väjningslinjeflödet sänker orealistiskt mycket kapaciteten. Anledningen till denna effekt beror på fördelningen av betjäningstid vid korsningen. I ekvationen för övergångsställets kapacitet består den genomsnittliga betjäningstiden av två huvudelement (Marlow M m.fl , s.4); En approximerad konstant faktor (β) som motsvarar tidsavstånden mellan fordonen under mättnadsflöde och En slumpvist tidsluckesökande faktor beroende av fotgängarflödet Ekvationen är endast korrekt när betjäningstiderna är slumpvisa. Vid högt flöde av fotgängare blir betjäningstiden för fordon tämligen bra approximerad mot den slumpvisa modellen. Men vid lågt flöde av fotgängare (och vid inget fotgängarflöde alls) blir mättnadsflödesfaktorn av betjäningstiden dominerande. Då detta flöde snarare är konstant än slumpvist går en kvot mellan väjningslinjens och övergångsställets kapacitet inte att använda. För att komma runt detta problem introducerar modellen begreppet faktisk kapacitet. Det är den kapacitet som skulle nås om effekterna av den konstanta betjäningstiden vid övergångsstället kunde elimineras från ekvationen. Men det vore felaktigt att ta bort denna faktor av betjäningstiden för alla flödesnivåer av fotgängare. Vid höga flöden av fotgängare, när trafiken endast kan avvecklas som enskilda fordon snarare än som strömmar eller kolonner av fordon, blir distributionen av betjäningstiderna approximativt slumpvisa och den faktiska kapaciteten för övergångsstället överensstämmer väl med den ursprungliga kapaciteten. Därför ska en andel av β subtraheras, motsvarande den andel av tiden som övergångstället är belastad med mättnadsflödet av fordon, när kolonner med mer än ett fordon (med approximativt konstant tidavstånd) passerar övergångsstället. Då flödet av fotgängare minskar ökar den faktiska kapaciteten och när flödet av fotgängare är noll går den mot oändligheten. Då den faktiska kapaciteten går mot oändligheten gör även kvoten mellan väjningslinjens och övergångställets kapacitet så vilket leder till att M ökar mot oändligheten. Då M är den faktor som kapaciteten vid väjningslinjen ska multipliceras med leder det till, då fotgängarflödet är noll, att kapaciteten för övergångsställets- /väjningslinjekombinationen blir samma som om endast väjningslinjen fanns att ta hänsyn till (Marlow M m.fl , s.5) Effekterna av övergångställe efter korsning Ett övergångsställe efter korsningen kan ge blockerande effekter bakåt då det bildas en kö av fordon som sträcker sig så pass långt bakåt att infarterna till cirkulationen påverkas. Antalet fordon som kan köa innan de når den tidigare infarten uttrycks i modellen som D. När antalet stillastående fordon i kö är större än D blir kapaciteten hos infarten i cirkulationsplatsen reducerad. Den proportionella 18
26 minskning denna blockerande effekt har på ingående kapacitet är lika med den andel tid för vilken kön genererad av övergångsstället överstiger D fordon (Marlow M m.fl , s.6). Beräkningen av den efterfrågade sannolika kölängden är inte lätt att göra på grund av de komplexa betjäningstiderna vid övergångsstället. Betjäningstiden består som ovan nämnt både av slumpvisa och konstanta faktorer. Samma ekvation framtagen av Griffiths för övergångställets kapacitet används för ett övergångställe efter cirkulationen. Som tidigare nämnt är ekvationen beroende av flertalet faktorer. Modellen föreslår därför möjligheten att kombinera några av dessa parametrar och producera en tillräckligt exakt (±5 % som sämst) tabell för praktisk användning utifrån Griffiths metod. Sannolikheten för en kö av längden q uttrycks därför som en kombination av kvoten mellan trafikflödet och den faktiska kapaciteten för övergångstället och kvoten mellan tiden det tar för en fotgängare att korsa övergångstället och det genomsnittliga tidsavståndet mellan fordonen. Förslaget är att de tabeller som tagits fram i rapporten skall användas som stöd vid planering av nya cirkulationsplatser med övergångsställen (Marlow M m.fl , s.11) Rodegerdts & Blackwelder; Analytical analysis of pedestrian effects on roundabout exit capacity Modellen studerar effekterna av nedsatt kapacitet i in- och utfarterna på grund av inverkan från övergångställena. Författarna anser att ett övergångställe vid en infart till en cirkulationsplats inte nämnvärt påverkar resten av cirkulationens kapacitet och därför ej kan anses vara ett stort problem. Av den anledningen ges ingen modell som beskriver effekterna av ett övergångsställe före en cirkulationsplats. Författarna konstaterar dock att ett övergångställe efter en cirkulationsplats ger en mer markant effekt på cirkulationsplatsens prestanda som helhet och presenterar därför en modell för effekterna av ett övergångsställe efter en cirkulationsplats. Modellen består av två delar. Den första delen behandlar hur tillgängliga tidsluckor i fordonsströmmen för fotgängarna kan uppskattas. Den andra delen är den analys av effekterna som uppkommer då fordon som lämnar cirkulationen stoppas av t ex en fotgängare på ett övergångsställe Analys av tillgängliga tidsluckor i fordonsströmmen för fotgängarna För att bestämma ett approximativt värde på blockeringstiden av övergångsstället då en fotgängare korsar har modellen en ekvation som består av en reaktions-/uppfattningstid för fotgängaren samt den tid det tar för fotgängaren att korsa övergångsstället. T B G R w s Blockeringstiden (s) Tillräcklig tidslucka (s) T B = G = R + w s fotgängarens uppfattnings/reaktionstid (s) sträcka att korsa (vägens/övergångställets bredd) (m) gånghastighet hos fotgängarna (m/s) (Rodegerdts L m.fl. 2005, s.3) För att bedöma i vilken mån tillräckliga tidsluckor G finns tillgängliga i fordonsströmmen tillämpas enklare tidsavståndsteorier från den amerikanska handboken Highway Capacity Manual. Genom att anta att tidsavstånden mellan fordonen är exponentiellt fördelade kan antalet tidsluckor G tillgängliga i 19
27 fordonsströmmen beräknas (Rodegerdts L m.fl. 2005, s.4). Författarna påpekar dock att antagandet om exponentiellt tidsavstånd mellan fordonen inte är helt korrekt på grund av den komplexa trafiksituations som råder i en cirkulationsplats, men att det är en tillräckligt korrekt approximation för den enkla modellen. När det förväntade antalet fotgängare överskrider det förväntade antalet tidsluckor per timme måste fordonen stanna och lämna företräde för fotgängarna för att ge dem tillräcklig tid för att korsa gatan. Ekvationen är konstruerad så att fordonstrafiken aldrig ger företräde för fotgängarna. Då detta inte är den verkliga situationen i de flesta länder bör formeln inte användas för att beskriva användbarheten hos ett övergångsställe utan istället för att visa i vilken utsträckning tillräckliga tidsluckor finns i fordonsströmmen för fotgängare att passera över gatan (Rodegerdts L m.fl. 2005, s.5) Effekterna av en blockerande händelse vid en cirkulationsplatsutfart I modellen beräknas sannolikheten för en kö av längden q genom att anta Poisson-fördelad ankomst för fordonen. Blockeringstiden då en fotgängare korsar övergångsstället, antas vara konstant och lika med längden av den faktiska blockerande händelsen (T B ) plus tiden det tar att lösa upp den genomsnittliga kön (3600*Q avg /S E ). Att använda en konstant blockeringstid för att beräkna sannolikheten för en kö av längden q är ett förenklat antagande då det i verkligheten fluktuerar då olika personer behöver olika lång tid på sig att passera övergångsstället (Rodegerdts L m.fl. 2005, s.5). Sannolikheten för att en kö av längden q kommer att inträffa under en blockerande händelse uttrycks som; P queue q = e V E T B Q avg S E V E T B Q avg Det verkar dock som ett tryckfel har smugit sig in här då rätt formel bör vara; P queue q = q! S E e V E 3600 T B Q avg S E V E 3600 T B Q avg Denna formel ger rätt resultat på modellens egna exempel och det är därför det uttrycket som tills vidare använts. q! S E q q P queue (q) sannolikheten att en kö av längden q kommer inträffa under en blockerande händelse. Dvs sannolikheten att en kö av längden q skapas då en fotgängare blockerar övergångsstället Q avg V E T B genomsnittlig förväntad kö beroende på trafikflödet V E utfarten flödet av fordon vid utfarten (fordon/timme) längden av en blockerande händelse (s) S E mättnadsflöde (avvecklingsflödet, då den blockerande händelsen försvinner) (fordon/timme) q kölängd i fordon (används för att beräkna sannolikheten för en viss kös längd) Termen 3600Q avg står för den extra blockeringstid orsakad av avvecklingen av kön efter slutet av den S E faktiska blockerande händelsen (Rodegerdts L m.fl. 2005, s.5). Figur 2.7 visar relationen. 20
28 Figur 2.7 Den extra blockeringstid som orsakas av att fordon fortsätter att anlända till slutet av kön då den börjat avvecklas Q avg, den genomsnittligt förväntade kön uttrycks som: Q avg V E T B genomsnittlig förväntad kö Q avg = V E T B V E S E flödet av fordon på den utfart som studeras (fordon/timme) längd av den blockerande händelsen (sekunder) S E mättnadsflödet (det flöde som uppkommer då den blockerande händelsen försvinner, dvs avvecklingsflödet) (fordon/timme) Genom att använda Q avg för att definiera längden av kön kommer sannolikheten för längre köer att underskattas något, men den underskattningen förväntas ha relativt liten effekt på slutresultatet (Rodegerdts m.fl. 2005, s.6). Längden av kön, t queue, är tiden för vilken kön är längre än den kritiska kölängden Q E. Q E motsvarar den kölängd, i antal fordon, som kan få plats mellan övergångsstället och avfarten från cirkulationen utan att störa det cirkulerande flödet i cirkulationen. Q E kan därför ses som en buffertzon för köer, se Figur 2.8 och Figur
29 Q E Buffertzonen där x antal fordon kan köa utan att påverka det cirkulerande flödet Figur 2.8 Q E, den kölängd i antal fordon som får plats mellan övergångsstället och utfarten utan att blockera det cirkulerande flödet t queue q = 1 Q E T q B q S E t queue q = 0 för q < Q E för q Q E t queue (q) Q E T B S E q L E L v Q E = L E L V rundat uppåt till närmsta antal ela fordon varaktigheten för vilken kön q är längre än den kritiska kölängden Q E, dvs varaktigheten för att kön sträcker sig in i den cirkulerande strömmen motsvarar den kölängd som kan få plats mellan övergångsstället och avfarten från cirkulationen utan att störa det cirkulerande flödet i cirkulationen (fordon) längden av den blockerande händelsen (sekunder) mättnadsflöde(det flöde som blir då den blockerande händelsen försvinner, avvecklingsflödet) (fordon/timme) kölängd (används för att beräkna sannolikheten för en viss kölängd) Avstånd mellan övergångsstället (den blockerande händelsen) och det cirkulerande flödet (m) fordonslängd, ca 7,5 m (Rodegerdts L m.fl. 2005, s.7) 22
30 Figur 2.9 Illustration av den kö som blockerar den cirkulerande strömmen, ankomster och avveckling av kön antas jämt fördelande Så snart sannolikheten och varaktigheten av varje kö av längden q är känd kan man beräkna den genomsnittliga varaktigheten av en blockerande kö för varje blockerande händelse genom att bestämma sannolikheten för en kö med längden q och multiplicera det med dess längd. Korta köer har hög sannolikhet men kort livslängd och långa köer har låg sannolikhet men lång livslängd (Rodegerdts L m.fl. 2005, s.8). t avg P queue (q) t queue (q) q t avg = q= q=0 P queue q t queue (q) genomsnittlig livslängd för en blockerande kö per blockeringshändelse sannolikheten att en kö av längden q inträffar under en blockerande händelse varaktigheten för en kö av längden q vilken är längre än en kö av längden Q E kölängd (används för att beräkna sannolikheten för en viss kölängd) Modellen beräknar den totala tid, t block, under studietiden då utfartsköer blockerar det cirkulerande flödet. Modellen antar som tidigare nämnts att fordonen i den cirkulerande strömmen blir helt blockerade så fort buffertzonen blir full. Värdet för t block beräknas genom att antalet blockerande händelser multipliceras med den genomsnittliga livslängden för en blockerande händelse. t block = n event t avg 23
31 t block cirkulationen n even t ave den totala tiden under vilken utfartsköer blockerar det cirkulerande flödet i antalet blockerande händelser under studietiden genomsnittlig livslängd för en blockerande kö (Rodegerdts L m.fl. 2005, s.9) Genom att använda den totala tiden under vilken en utfartskö blockerar det cirkulerande flödet i cirkulationen kan kapacitetsnedsättningen för den infarten närmast utfarten i cirkulationsplatsinfarten beräknas. C adj C bas t block s studerat (ibid) C adj = C base 1 justerad kapacitet av cirkulationens infart t block s studerat ursprungliga kapaciteten av cirkulationens infart tidslängden under vilken det cirkulerande flödet är blockerat under studietiden antal sekunder som studietiden är, vanligtvis en timme dvs 3600 sekunder Genom att använda ekvationen kan man bestämma om kapacitetsnedsättningen på grund av problem vid en utfart med övergångsställe kan accepteras utan att orsaka allt för kraftiga fördröjningar. 2.4 Val av modell för vidare undersökning Ingen av de tre modellerna i litteraturstudien har någon enskild beräkningsdel som tar hänsyn till cirkulationsplatser med mer än ett körfält vilket är en brist då CapCal kan hantera upp till två körfält genom cirkulationen. Rodegerdts och Blackwelders modell kan dock användas då det finns fler än ett körfält men ingen kapacitetsnedsättning per körfält kan räknas fram. Att inte kunna använda modellerna på övergångsställen som korsar fler än ett körfält får ändå ses som ett mindre problem, då övergångsställe i plan inte bör byggas när det finns fler än ett körfält i cirkulationsplatsen (VGU 2004, Korsningar s. 128). Griffiths modell har ett köteoretiskt angreppsätt för att beräkna kölängderna vilket ger hög detaljeringsgrad. Styrkan hos Griffiths modell är just dess grundläggande matematiska analys för hur köer vid övergångsställen bildas och avvecklas. Nackdelen är att modellen inte är specifikt framtagen eller anpassad för cirkulationsplatser och den komplexa trafikmiljö som där råder. Att den måste anpassas för cirkulationsplatsen som korsningsform gör att den kräver mer ingående beräknings- och programmeringsinsatser än de övriga två modellerna för att kunna passa CapCals beräkningsmodell. Marlow och Maycocks modell bygger delvis på Griffiths modell, men har den nackdelen att den inte presenterar en vidareutveckling av hur kapaciteten sätts ned på grund av sannolikheterna för de olika köerna på ett detaljerat sätt. Modellen beskriver endast sannolikheterna för de olika kölängderna vid olika kvoter mellan tidsavstånden hos fotgängarna respektive mättnadsflöden hos fordonen. Det är även en nackdel att Marlow och Maycocks modell inte undersöker scenariot då övergångsstället har lägre kapacitet än väjningslinjen och hur detta påverkar cirkulationsplatsens funktion. Den sista modellen i litteraturstudien, Rodegerdts och Blackwelders, beskriver vilken procentuell kapacitetsnedsättning ett övergångsställe i en utfart ger för den närmsta infarten. Nackdelarna med denna modell är den stora mängd antaganden och förenklingar som är gjorda, till exempel tar poissonfördelad ankomst av fordonen bort en stor del av den dynamiska natur trafiken uppvisar. Att 24
32 avståndet mellan utfarten och den tidigare infarten inte tas med som en parameter i modellen är negativt då det borde påverka fordonsköernas effekter. Konstant kötillväxt, köavveckling och fotgängarbeteende är ytterligare några förenklingar som är gjorda. Den största nackdelen med Rodegerdts och Blackwelder är dock att antalet blockerande händelser (N) under den tidsperiod som studeras kraftigt påverkar resultatet. Rodegerdts och Blackwelder presenterar inte hur antalet blockerande händelse per tidsperiod kan uppskattas, de beskriver således ingen relation mellan antalet blockerande händelser, fotgängarflödet och fordonsflödet. För att kunna utnyttja deras modell måste någon form av relation mellan dessa flöden och antal blockerande händelser tas fram. Trots problemen med att uppskatta antalet blockerande händelser per timme samt de förenklingar som är gjorda är ändå Rodegerdts och Blackwelders modell den mest lättillgängliga och lättanalyserade modellen. Rodegertds och Blackwelders modell beräknar som tidigare nämnts en kapacitetsförlust för den infarten som ligger närmast utfarten. CapCal ger kapacitet och fördröjningar per körfält vilket gör att Rodegertds och Blackwelders modell är applicerbar i beräkningsmodellen då det endast finns ett körfält/infart genom cirkulationsplatsen. Rodegerdts och Blackwelders modell kan därför anses bäst i det avseendet och den valdes därför ut för vidare undersökning och validering, se kapitel 3 och 4. För att slutligen kunna rekommendera Rodegerdts och Blackwelders modell som lämplig för CapCal måste den dock utvecklas. Den utveckling av modellen som krävs är att finna ett sätt att uppskatta antalet blockerande händelser (N) per studietimma utifrån fordonsflödet i utfarten samt fotgängar- och cykelflödet på övergångsstället, se kapitel 5. 25
33 3 Datainsamling I detta kapitel presenteras den datainsamling som gjort för att validera den utvalda beräkningsmodellen av Rodegerdts och Blackwelder. 3.1 Val av plats och data Data har samlats in från film. Sex olika övergångsställen vid fyra olika cirkulationsplatser har mätts. Två av cirkulationsplatserna ligger i Stockholmsområdet (Solna och Rissne) och de övriga två ligger i Skåne (Malmö och Lund). Från varje cirkulationsplats har data samlats in under en timmes tid. De data som har mätts från film är: Antal fotgängare o Antal av dessa fotgängare som anländer i grupp. Antal cyklister o Antalet av dessa cyklister som anländer i grupp. Antalet blockerande händelser (dvs. antal gånger som en fotgängare/cyklist på övergångsstället orsakar en fordonskö som sträcker sig in i cirkulationen) Genomsnittlig blockeringstid (dvs. den tid en fotgängare/cyklist tar på sig för att korsa övergångsstället) Antal fordon i utfarten 26
34 3.1.1 Solna Kolonnvägen Gustav III:s boulevard Bild 3.1 Stillbild från filmen från Solna. Cirkulationsplatsen är som Bild 3.1 visar trebent med ett övergångsställe i den södra utfarten på Kolonnvägen. Filmen är tagen den 8 juni 2009 och mätningar gjorda från filmen är från mellan klockan till klockan Följande värden uppmättes från filmen, se Tabell 3.1. Tabell 3.1 Solna Uppmätta värden från Solna Antal fotgängare, varav i grupp Antal cyklister varav i grupp Antal blockerande händelser, N Antal fordon i utfarten, VE Genomsnittlig längd av en blockerande händelse 79 st 16 st 54 st 8 st 54 st 1056 st 5 sek 27
35 3.1.2 Rissne Rissneleden Örsvägen Bild 3.2 Stillbild från filmen från Rissne. Cirkulationsplatsen är som Bild 3.2 visar fyrbent med övergångställen på det västra och södra benet. Filmen är tagen den 26 maj 2009 mätningar gjorda från filmen är från mellan klockan till klockan på det västra övergångsstället (närmast kameran). Mätningar gjordes inte på det södra övergångsstället (det till höger på bilden) då endast ett fåtal fotgängare korsade det under studietimmen. I Tabell 3.2 presenteras de uppmätta värdena från filmen. Tabell 3.2 Rissne Uppmätta värden från Rissne Antal fotgängare varav i grupp Antal cyklister varav i grupp Antal blockerande händelser, N Antal fordon i utfarten, VE Genomsnittlig längd av en blockerande händelse 154 st 51 st 15 st 0 st 8 st 311 st 4,5 sek 28
36 3.1.3 Malmö Annetorpsvägen - Elinelundsvägen Bild 3.3 Stillbild från filmen från Malmö Cirkulationsplatsen är som Bild 3.3 visar fyrbent med övergångsställen på tre av de fyra anslutande vägarna. Mätningar har gjorts på övergångstället närmast kameran. Filmen är inspelad den 9 juni 2009 och mätningar gjorda från filmen är från mellan klockan till Mätningar har inte gjorts på de övriga övergångsställena då filmens kvalité var för dålig pga av regn för att kunna se fotgängarna ordentligt. Det kan även finnas anledning att tro att dagen då filmen spelades in inte är representativ för cirkulationsplatsens funktion. Regnet gjorde antagligen att antalet gång- och cykeltrafikanter var färre än normalt, men detta kan inte bekräftas då det bara finns film från en dag. I Tabell 3.3 presenteras de uppmätta värdena. Tabell 3.3 Malmö Uppmätta värden från Malmö Antal fotgängare varav i grupp Antal cyklister varav i grupp Antal blockerande händelser, N Antal fordon i utfarten, VE Genomsnittlig längd av en blockerande händelse 28 st 14 st 11 st 4 st 10 st 748 st 6 sek 29
37 3.1.4 Lund Södravägen Arkivgatan Bild 3.4 Stillbild från filmen från Lund Cirkulationsplatsen är som Bild 3.4 visar fyrbent med korsande övergångsställen på alla av de fyra anslutande vägarna. Mätningar har gjorts på det västra(1), södra(2) och östra (3) övergångstället. Filmen är inspelad den 19 maj 2009 och mätningar gjorda från filmen är från mellan klockan till I Tabell 3.4, 3.5 och 3.6 finns de uppmätta värdena. Tabell 3.4 Uppmätta värden från Lund - Västra Lund, Södra vägen, Västra(1) övergångsstället Antal fotgängare varav i grupp Antal cyklister varav i grupp Antal blockerande händelser, N Antal fordon i utfarten, VE Genomsnittlig längd av en blockerande händelse 25 st 6 st 79 st 21 st 19 st 597 st 4,5 sek 30
38 Tabell 3.5 Uppmätta värden från Lund - Södra Lund, Arkivgatan, Södra(2) övergångsstället Antal fotgängare varav i grupp Antal cyklister varav i grupp Antal blockerande händelser, N Antal fordon i utfarten, VE Genomsnittlig längd av en blockerande händelse Tabell 3.6 Uppmätta värden från Lund - Östra 17 st 13 st 114 st 60 st 10 st 447 st 5 sek Lund, Södravägen, Östra (3) övergångsstället Antal fotgängare varav i grupp Antal cyklister varav i grupp Antal blockerande händelser, N Antal fordon i utfarten, VE Genomsnittlig längd av en blockerande händelse 36 st 17 st 90 st 27 st 13 st 429 st 5 sek 31
39 4 Resultat I kapitel 4 presenteras de resultat som den analytiska modellen gav för de sex olika övergångsställena. 4.1 Den analytiska modellen Kapacitetsnedsättningen (för infarten som ligger närmast utfarten där övergångsstället ligger) för de olika cirkulationsplatserna med Rodegerdts och Blackwelders modell kan ses nedan. För beräkningar se bilaga I. Det är bara en cirkulationsplats (Solna) där modellen visar att övergångsstället verkligen har en tydlig kapacitetsnedsättande effekt något som även kunde ses från filmerna då köer inte var något större problem vid de övriga cirkulationsplatserna. Detta då både fordons- och GC-flödet var relativt lågt i de övriga cirkulationsplatserna Solna Kapacitetsförlust i infarten pga. övergångsstället 17,93 % Max 15 min ( ) 22,41 % Rissne Kapacitetsförlust i infarten pga. övergångsstället 0,12 % Max 15 min ( ) 0,18 % Malmö Kapacitetsförlust i infarten pga. övergångsstället 2,65 % Max 15 min ( ) 3,29 % Lund Västra Kapacitetsförlust i infarten pga. övergångsstället 0,30 % Max 15 min ( ) 0,67 % Lund Södra Kapacitetsförlust i infarten pga. övergångsstället 2,70 % Max 15 min ( ) 6,00 % Lund Östra Kapacitetsförlust i infarten pga. övergångsstället 1,62 % Max 15 min ( ) 4,02 % 32
40 5 Analys och modellutveckling I analys och modellutvecklingskapitlet jämförs resultaten från den analytiska modellen med simuleringar i VISSIM. Dessutom presenteras en metod för att kunna uppskatta parametern Antal blockerande händelser i den analytiska modellen av Rodegerdts och Blackwelder. För att jämföra resultaten för den analytiska modellen av Rodegerdts och Blackwelder (se kapitel 4) väljs cirkulationsplatserna i Solna och Rissne ut för att simuleras i VISSIM. Anledningen till att cirkulationsplatsen i Solna väljs är dels för att den är den enda cirkulationsplats där övergångsstället visade sig ge någon tydlig kapacitetsnedsättande effekt. Cirkulationsplatsen är även trebent vilket ger färre olika flöden att mäta från filmen. Det finns dessutom bara ett övergångsställe som kan påverka resultaten. Cirkulationsplatsen i Rissne väljs ut att simuleras då den till skillnad från den i Solna visade sig i den analytiska modellen inte ha någon större kapacitetsnedsättande effekt på grund av övergångsstället. Båda cirkulationsplatserna som simulerats ligger i Stockholmsområdet vilket även påverkade valet av dessa då platsbesök var möjligt. Resultaten från simuleringen har tagits fram genom att göra tio körningar med olika slumpfrö vardera för cirkulationsplatsen med och utan övergångsstället. De tio simuleringarna ger sedan ett sammanlagt medelvärde som jämförts. För ytterligare detaljer om simuleringen och parameterinställningar se Bilaga II. Resultaten från Rodegerdts och Blackwelders modell är en procentuell kapacitetsförlust för cirkulationsplatsen som helhet. Resultaten från simuleringen presenteras som skillnader mellan cirkulationsplatsen med och utan övergångsställe samt den statistiska säkerheten i dessa skillnader. Följande parametrar har mätts i simuleringen: Total restid (timmar) Total restid per fordon (sekunder) för de olika rutterna (färdvägarna) genom cirkulationsplatsen Total fördröjning (timmar) Genomsnittlig fördröjning per fordon (sekunder) Totalt antal stopp samt Genomsnittligt antal stopp per fordon Dessutom har kölängderna mätts vid två punkter. Mätpunkt 1 placerad vid övergångsstället och mätpunkt 2 vid utfarten från cirkulationsplatsen, se Bild 5.1 och
41 Bild 5.1 Bild från VISSIM simuleringen av cirkulationsplatsen i Solna Bild 5.2 Bild från VISSIM simuleringen av cirkulationsplatsen i Rissne Varje kölängd som registrerades vid båda kömätarna noterades som en blockerande händelse. Detta är en förenkling men då det skulle ta allt för lång tid att studera de 20 filmerna från simuleringen och manuellt notera antalet blockerande händelser har denna metod valts. Då VISSIM inte kan beräkna kapaciteten för cirkulationen är ett mått på antal blockerande händelser något som kan jämföras mot filmen för att uppskatta simuleringens korrekthet. Att exakt samma typ av resultat ej kan erhållas för simuleringen som den analytiska beräkningsmodellen är negativt, men resultaten såsom total restid och total fördröjning från simuleringen kan ändå ge en fingervisning huruvida den analytiska modellen är korrekt. 5.1 Beteenden och effekter som syns på filmen men ej kan fångas upp genom simulationen Då filmen från cirkulationsplatsen i Solna studeras och jämförs mot visualiseringen av simuleringen kan två beteenden hos trafikanterna i cirkulationsplatsen noteras som är svåra att ta hänsyn till i simuleringen. Vänstersvängande fordon på Gustav III:s Boulevard 34
42 Bild 5.3 Vänstersvängande fordonsström från Gustav III:s Boulevard De fordon som svänger vänster från Gustav III:s Boulevard in på Kolonnvägen utgör den största fordonsströmmen, se Bild 5.3. De fordonen uppvisar en större tendens att köra i kolonn och hänga på fordonet framför då de kör in i cirkulationen. Det leder i vissa fall till att de fordon som kör rakt igenom cirkulationen på Kolonnvägen tvingas stanna/bromsa inne i cirkulationen för att inte krocka med de vänstersvängande fordonen som borde lämnat företräde. Detta fenomen kan inte simulationen ta hänsyn till. Bilisterna stannar längre ifrån övergångsstället än nödvändigt Om en bilist inne i cirkulationen upptäcker en fotgängare som är på väg att passera övergångsstället sänker den bilisten hastigheten för att hela tiden kunna vara rullande och slippa stanna. Ibland måste ändå bilisten stanna helt men då stannar fordonet ofta så pass långt från övergångsstället att bakdelen på fordonet sticker ut i cirkulationen och blockerar för de bakomvarande fordonen att passera. Inbromsningsbeteendet som kan ses på filmen har inte kunnat fångas i simuleringen. 35
43 5.2 Resultat från simuleringen samt analys Resultat och tabeller från simuleringen som inte finns i detta kapitel finns i Bilaga III. Nedan följer en sammanfattning av de viktigaste uppmätta värdena som är intressanta för jämförelse med den analytiska beräkningsmodellen Solna Följande resultat presenteras från simuleringen av cirkulationsplatsen i Solna; Total restid för fordonen Restid för fordon för olika rutter Fördröjning för fordonen Stopp för fordonen Antal blockerande händelser, dvs då fordonskön orsakad av fotgängarna och cyklisterna på övergångsstället växer sig in i cirkulationen Total restid (timmar) Den totala restiden i cirkulationsplatsen med övergångsstället är drygt 5 timmar längre än för cirkulationsplatsen utan övergångsstället (t-test: p<0,05). Den totala restiden är varje fordons restid adderad. Tabell 5.1 Medelvärdet för total restid (timmar) för simuleringen av cirkulationsplatsen i Solna Medelvärde Med övergångsställe Utan övergångsställe 20,66 h 15,43 h 95 % konfidensinterval för total restid 14,78 16,09 19,46 21,86 0,00 5,00 10,00 15,00 20,00 25,00 30,00 35,00 40,00 Total restid i timmar Med övergångsställe Utan övergångsställe Figur 5.1 Konfidensintervall för total restid för simuleringen av cirkulationsplatsen i Solna 36
44 Att skillnaden i restid i cirkulationsplatsen med och utan övergångsstället är signifikant kan konfidensintervallen i Figur 5.1 illustrera. Då intervallen ej skär varandra visar det på att restiderna i cirkulationsplatsen skiljer sig åt beroende på om ett övergångsställe finns eller inte. Restid för olika rutter (sekunder) Medelrestid per fordon genom cirkulationsplatsen kan även studeras per rutt. Restidminskningen per rutt ligger mellan 0,6 och 4 sekunder för om övergångsstället inte är belastat med några fotgängare. Tabell 5.2 Medelrestiden per fordon för olika rutter genom cirkulationsplatsen i Solna Resvägar i cirkulationsplatsen Medelrestid i sekunder, Solna Skillnad Signifikant Med övergångsstället Utan övergångsstället skillnad Rutt 1 20,72 s 17,33 s -3,39 s Ja (t-test: p<0,05) Rutt 2 16,7 s 12,69 s -4,01 s Ja (t-test: p<0,05) Rutt 3 10,55 s 9,95 s -0,6 s Ja (t-test: p<0,05) 37
45 Rutt 4 20,55 s 16,69 s -3,86 s Ja (t-test: p<0,05) Rutt 5 14,3 s 13,45 s -0,68 s Nej (t-test p>0,05) Rutt 6 10,28 s 9,08 s -1,2 s Ja (t-test: p<0,05) Som Tabell 5.2 ovan visar påverkas restiden negativt för alla rutter utom en av övergångsstället. Att det är rutt 5 som inte påverkas av övergångsstället är inte förvånande då den rutten ligger längst från övergångsstället. Korrelationen mellan signifikant skillnad i restid och om övergångstället korsas av rutten är stark (63 %). Det är bara rutt 4 som inte korsar övergångsstället men ändå uppvisar påverkan på restiden då övergångsstället finns. Detta kan bero på att köer växer in i cirkulationen och blockerar för det vänstersvängande flödet på rutt 4. Fördröjning Fördröjning delas in i total fördröjning, dvs den adderade fördröjningen för alla fordon samt genomsnittlig fördröjning, dvs den genomsnittliga fördröjningen per fordon. 38
46 Total fördröjning (timmar) Den totala fördröjningen är cirka 4 timmar längre för cirkulationsplatsen med övergångsstället än utan, se Tabell 5.3. Skillnaden i total fördröjning för denna datamängd är signifikant (t-test: p<0,05), se Figur 5.2. Tabell 5.3 Medelvärdet för total fördröjning (timmar) för simuleringen av cirkulationsplatsen i Solna Medelvärde Med övergångsställe Utan övergångsställe 9,69 h 5,77 h 95 % konfidensinterval för total fördröjning 5,16 6,38 8,54 10,84 0,00 2,00 4,00 6,00 8,00 10,00 12,00 14,00 Total fördröjning (timmar) Med övergångsställe Utan övergångsställe Figur 5.2 Konfidensintervall för total fördröjning för simuleringen av cirkulationsplatsen i Solna Genomsnittlig fördröjning per fordon (sekunder) Den genomsnittliga fördröjningen per fordon i sekunder skiljer sig åt med ca 7 sekunder beroende på om det finns ett övergångsställe eller ej i cirkulationsplatsen, se Tabell 5.4. Skillnaden för den här datamängden är signifikant och illustreras med ett konfidensintervall i Figur 5.3 (t-test: p<0,05). Tabell 5.4 Medelvärdet för genomsnittlig fördröjning (sekunder) för simuleringen av cirkulationsplatsen i Solna Medelvärde Med övergångsställe Utan övergångsställe 18,39 s 11,74 s 39
47 95 % konfidensinterval för genomsnittlig fördröjning 10,52 12,97 16,25 20,54 0,00 5,00 10,00 15,00 20,00 25,00 30,00 35,00 40,00 Genomsnittlig fördröjning per fordon i sekunder Med övergångsställe Utan övergångsställe Figur 5.3 Konfidensintervall för genomsnittlig fördröjning per fordon (sekunder) för simuleringen av cirkulationsplatsen i Solna Antal stopp Antal stopp presenteras som dels som den adderade mängden stopp för alla fordon och dels som det genomsnittligt antal stopp som ett fordon gör. Totalt antal stopp Totalt antal stopp i simuleringen är knappt 500 fler för cirkulationsplatsen med övergångsstället jämfört med det utan, se Tabell 5.5. Skillnaden är signifikant, se Figur 5.4 (t-test: p<0,05). Tabell 5.5 Medelvärdet för totalt antal stopp för simuleringen av cirkulationsplatsen i Solna Med övergångsställe 1239 Utan övergångsställe 743 Medelvärde 95 % konfidensinterval för totalt antal stopp Totalt antal stopp Med övergångsställe Utan övergångsställe Figur 5.4 Konfidensintervall för totalt antal stopp för simuleringen av cirkulationsplatsen i Solna 40
48 Genomsnittligt antal stopp per fordon Genomsnittligt antal stopp per fordon ökar då det finns ett övergångsställe jämfört med om det inte finns, se Tabell 5.6. Skillnaden är signifikant, se Figur 5.5 (t-test: p<0,05). Tabell 5.6 Medelvärdet för genomsnittligt antal stopp per fordon för simuleringen av cirkulationsplatsen i Solna Med övergångsställe 0,654 Utan övergångsställe 0,420 Medelvärde 95 % konfidensinterval för genomsnittligt antal stopp per fordon 0,386 0,453 0,588 0,719 0,000 0,200 0,400 0,600 0,800 1,000 Genomsnittligt antal stopp per fordon Med övergångsställe Utan övergångsställe Figur 5.5 Konfidensintervall för genomsnittligt antal stopp per fordon för simuleringen av cirkulationsplatsen i Solna Antal blockerande händelser orsakade av övergångsstället i Solna Från filmen uppmättes 54 blockerande händelser under studietimman. Från simuleringarna uppmättes med hjälp av kömätarna i genomsnitt 49 blockerande händelser då det fanns ett övergångsställe. 41
49 95 % konfidensinterval för antal blockerande händelser 0,00 20,00 40,00 60,00 80,00 100,00 Antal blockerande händelser Konfidensinterval för simuleringen Sant värde från filmen Figur 5.6 Konfidensintervall för antal blockerande händelser i Solna Då det inte fanns ett övergångsställe uppmättes inga blockerande händelser. Konfidensintervallet för simuleringen innefattar det sanna värdet som uppmättes från filmen. Detta tyder på att simuleringen har fångat verkligheten på ett korrekt sätt Rissne Följande resultat presenteras från simuleringen av cirkulationsplatsen i Rissne; Total restid för fordonen Restid för fordon för olika rutter Fördröjning för fordonen Stopp för fordonen Antal blockerande händelser, dvs då fordonskön orsakad av fotgängarna och cyklisterna på Total restid (timmar) Medelvärdet för den totala restiden i cirkulationsplatsen ökar med ca 1 timme då det finns ett övergångsställe, se Tabell 5.7. Tabell 5.7 Med övergångsställe Utan övergångsställe Medelvärdet för total restid (timmar) för simuleringen av cirkulationsplatsen i Rissne Medelvärde 4,66 h 3,69 h Då konfidensintervallen ej skär varandra visar det på att det är en signifikant tidsminskning för fordonen i cirkulationsplatsen utan övergångsstället, se Figur 5.7 (t-test: p<0,05). 42
50 95 % konfidensinterval för total restid 3,55 3,83 4,48 4,85 0,00 2,00 4,00 6,00 8,00 10,00 Total restid i timmar Med övergångsställe Utan övergångsställe Figur 5.7 Konfidensintervall för total restid för simuleringen av cirkulationsplatsen i Rissne Restid för olika rutter (sekunder) Medelrestid per fordon genom cirkulationsplatsen i Rissne kan även studeras per rutt, se Tabell 5.8. Tabell 5.8 Medelrestiden per fordon för olika rutter genom cirkulationsplatsen i Rissne Medelrestid i sekunder i Rissne Resvägar i systemet Med övergångsstället Utan övergångsstället Skillnad Signifikant skillnad Rutt 1 8,4 s 7,7 s -0,7 s Ja (t-test p<0,05) Rutt 2 9,32 s 9,18 s -0,14 s Nej (t-test p>0,05) 43
51 Rutt s s -0,25 s Nej (t-test p>0,05) Rutt 4 10,02 s 9,51 s -0,51 s Ja (t-test p<0,05) Rutt 5 13,53 s 12,69 s -0,84 s Ja (t-test p<0,05) Rutt 6 13,77 s 13,03 s -0,74 s Ja (t-test p<0,05) 44
52 Rutt 7 9,91 s 9,73 s -0,18 s Nej (t-test p>0,05) Rutt 8 9,91 s 9,85 s -0,06 Nej (t-test p>0,05) Rutt 9 12,78 s 12,23 s -0,55 Ja (t-test p<0,05) Rutt 10 10,49 s 10,33 s -0,16 s Nej (t-test p<0,05) 45
53 Rutt 11 12,61 s 11,99 s -0,62 s Ja (t-test p<0,05) Rutt 12 13,86 s 13,69 s -0,17 s Nej (t-test p<0,05) Korrelationen mellan signifikant restidsminskning och om övergångsstället korsas av rutten (antingen i infart eller i utfarten) är 100 %. Det innebär att i denna simulering blir det en signifikant restidsökning endast för de rutter som korsar övergångsstället. Detta kan tyda på att köer som växer sig in i cirkulationen och blockerar för svängande fordon inte är ett större problem. Fördröjning Fördröjning presenteras som total fördröjning samt genomsnittlig fördröjning. Total fördröjning (timmar) Den totala fördröjningen är cirka 11 minuter längre för cirkulationsplatsen med övergångsstället, se Tabell 5.9. Då konfidensintervallen för cirkulationsplatsen ej skär varandra visar det att det är en signifikant tidsminskning för systemet som helhet utan övergångsstället, se Figur 5.8 (t-test: p<0,05). Tabell 5.9 Medelvärdet för total fördröjning (timmar) för simuleringen av cirkulationsplatsen i Rissne Med övergångsställe 1,06 Utan övergångsställe 0,88 Medelvärde 46
54 95 % konfidensinterval för total fördröjning 0,82 0,94 0,98 1,13 0,00 0,50 1,00 1,50 2,00 2,50 3,00 Total fördröjning i timmar Med övergångsställe Utan övergångsställe Figur 5.8 Konfidensintervall för total fördröjning för simuleringen av cirkulationsplatsen Rissne Genomsnittlig fördröjning per fordon (sekunder) Den genomsnittliga fördröjningen per fordon skiljer sig inte åt i Rissne vare sig det finns ett övergångsställe eller inte vid cirkulationsplatsen (t-test p>0,05), se Figur 5.9 där konfidensintervallen skär varandra. Resultatet är inte förvånande då även den analytiska modellen visade små effekter på kapaciteten på grund av övergångsstället. Tabell 5.10 Medelvärdet för genomsnittlig fördröjning per fordon (sekunder) för simuleringen av cirkulationsplatsen i Rissne Med övergångsställe 3,14 Utan övergångsställe 3,07 Medelvärde 95 % konfidensinterval för genomsnittlig fördröjning per fordon 2,95 3,18 2,99 3,29 0,00 1,00 2,00 3,00 4,00 5,00 Genomsnittlig fördröjning per fordon i sekunder Med övergångsställe Utan övergångsställe Figur 5.9 Konfidensintervall för genomsnittlig fördröjning per fordon för simuleringen av cirkulationsplatsen Rissne 47
55 Antal stopp Antal stopp presenteras som totalt antal stopp samt genomsnittligt antal stopp. Totalt antal stopp Medelvärdet för totalt antal stopp är högre för cirkulationsplatsen med övergångsstället än utan, se Tabell Konfidensintervallen skär dock varandra vilket gör att några slutsatser om skillnaden i antal stopp inte kan dras, se Figur Dock så är skillnaden signifikant, men svagt (t-test: p<0,05). Tabell 5.11 Med övergångsställe 125 Utan övergångsställe 97 Medelvärdet för totalt antal stopp för simuleringen av cirkulationsplatsen i Rissne Medelvärde 95 % konfidensinterval för totalt antal stopp Med övergångsställe Utan övergångsställe Totalt antal stopp Figur 5.10 Konfidensintervall för totalt antal stopp för simuleringen av cirkulationsplatsen Rissne Genomsnittligt antal stopp per fordon Genomsnittligt antal stopp per fordon skiljer sig inte heller åt nämnvärt vare sig det finns ett övergångsställe eller inte, se Tabell 5.12 och Figur 5.11, skillnaden är inte signifikant (t-test: p>0,05). Tabell 5.12 Medelvärdet för genomsnittligt antal stopp för simuleringen av cirkulationsplatsen i Rissne Med övergångsställe 0,103 Utan övergångsställe 0,094 Medelvärde 48
56 95 % konfidensinteraval för genomsnittligt antal stopp 0,084 0,103 0,090 0,115 0,000 0,200 0,400 0,600 0,800 1,000 Genomsnittligt antal stopp per fordon Med övergångsställe Utan övergångsställe Figur 5.11 Konfidensintervall för genomsnittligt antal stopp per fordon för simuleringen av cirkulationsplatsen Rissne Antal blockerande händelser orsakade av övergångsstället i Rissne Från filmen uppmättes totalt 8 blockerande händelser under studietimmen. Från simuleringen uppmättes även där i genomsnitt 8 blockerande händelser men variationen var relativt stor. Då det inte fanns ett övergångsställe i cirkulationsplatsen uppmättes inga blockerande händelser. Konfidensintervallet för de 10 simuleringar innefattar det sanna värdet mätt från filmen vilket tyder på att simuleringarna väl överensstämmer med verkligheten, se Figur % konfidensinterval för antal blockerande händelser Konfidensinterval för simuleringen Sant värdet från filmen Antal blockerande händelser Figur 5.12 Konfidensintervall för antal blockande händelser i Rissne 49
57 5.3 Jämförelse i resultat mellan den analytiska modellen och simuleringen Både resultaten från den analytiska modellen och simuleringarna av cirkulationsplatserna i Solna och Rissne visar att övergångsstället vid hög belastning ger en negativ effekt på cirkulationsplatsens prestationsförmåga. Den analytiska modellen visar att kapacitetsreduktionen på grund av övergångsstället i Solna är nästan 18 %. Det kan jämföras mot simuleringens resultat som visar att den totala restiden ökar med drygt 5 timmar om övergångsstället finns. Simuleringen av cirkulationsplatsen i Rissne visade inte på lika stora effekter av övergångsstället som vid simuleringen i Solna. Den analytiska modellens resultat för cirkulationsplatsen i Rissne gav inte heller några större kapacitetsförluster på grund av övergångsstället (0,12 %). Samstämmigheten mellan den analytiska modellens och simuleringens resultat kan därför anses vara hög för båda de undersökta cirkulationsplatserna. Att jämföra en procentuell kapacitetsreduktion mot restidsförkortningar, reduktion i antal stopp etc. är dock svårt. Simuleringen kan i detta fall visa om trenden i resultaten är korrekt. Resultaten från simuleringen av de två cirkulationsplatserna tyder på att den analytiska modellen kan uppskatta om en kapacitetsreduktion pga. ett övergångsställe kommer att ske. Det är svårt att bedöma hur korrekt uppskattningen av storleken på kapacitetsreduktionen är då kapaciteten inte kan på ett enkelt sätt beräknas i simuleringen. Det finns vissa metoder framtagna av andra författare för hur kapaciteten kan uppskattas från en simulering (Refsnes och Thorsson, 2006). Dock är den metoden tyvärr inte tillämplig i detta fall utan att ge väldigt mycket merarbete. För att illustrera hur olika flöden påverkar den analytiska modellen respektive den totala fördröjningen i en VISSIM simulering har scenarion i Tabell 5.13 för cirkulationsplatsen i Solna testats. 50
58 Tabell 5.13 Jämförelse av resultat mellan den analytiska modellen och simulering i VISSIM VISSIM Simulering Total fördröjning Analytiska trafikmodellen % kapacitetsförlust Kommentar Basscenario 9,69 timmar 17,93 % Ökning av flödena Scenario % fordon, oförändrat gång och cykelflöde (GC) Scenario 1b + 5 % fordon, oförändrat GC Scenario 2 Oförändrat fordon, + 15 % GC Scenario % fordon, + 15 % GC Scenario 3b + 5 % fordon, + 15 % GC 20,66 timmar 22,58 % All trafik gick inte igenom systemet. (9/10 simuleringar) 14,58 timmar 19,64 % All trafik gick inte igenom systemet (5/10 simuleringar) 10,89 timmar 18,10 % 24,02 timmar 27,32% All trafik gick inte igenom systemet. (9/10 simuleringar) 15,64 timmar 20,75 % All trafik gick inte igenom systemet (5/10 simuleringar) Minskning av flödena Scenario 4-10 % fordon, oförändrat GC Scenario 5 Oförändrat fordon, - 15 % GC Scenario 6-10 % fordon, - 15 % GC 4,81 timmar 13,17 % 8,86 timmar 15,54 % 4,47 timmar 11,52 % Fordonsflödena minskar, GC flödena ökar Scenario 7-10 % fordon, + 15 % GC Fordonsflödena ökar, GC flödena minskar 5,25 timmar 13,76 % All trafik gick inte igenom systemet (7/10 simuleringar) Scenario % fordon, - 15 % GC Scenario % fordon, - 15 % GC 12,89 timmar 17,19 % All trafik gick inte igenom systemet (4/10 simuleringar) 18,82 timmar 20,73 % All trafik gick inte igenom systemet (7/10 simuleringar) 51
59 GC-flöde Kapacitetsförlust % Plot av fördröjning och kapacitetsförlust 30,00% 25,00% R² = 0, ,00% 15,00% De olika scenario 10,00% 5,00% 0,00% Linjär (De olika scenario) Fördröjning i timmar Figur 5.13 Illustration av resultat från de olika scenario för den analytiska modellen och simuleringen Resultaten från Tabell 5.13 kan visualiseras med 3D-plottar där de tre olika axlarna motsvarar; fordonsflöde i utfarten, GC-flödet och den totala fördröjningen i timmar/kapacitetsförlusten i procent. 30 Total fördröjning i timmar, simuleringsresultat Fordonsflöde i utfarten Figur D-plot för den totala fördröjningen i timmar 52
60 Kapacitetsförlust i procent 40,00% 30,00% 20,00% 10,00% 0,00% ,00%-40,00% 20,00%-30,00% 10,00%-20,00% 0,00%-10,00% 1162 Fordonsflöde i utfarten Figur D-plot för den procentuella kapacitetsförlusten Figur 5.14 och 5.15 visar att både den totala fördröjningen och kapacitetsförlusten ökar då fordonsflödet och GC-flödet ökar. Det verkar även utifrån plottarna som att kapacitetsförlusten och den totala fördröjningen inte är linjärt beroende av fordonsflödet i utfarten och GC-flödet. Detta kan ses i 3D-plottarna då GC-axeln viker av brant uppåt då både fordonsflödet och GC-flödet blir högt, se Figur Figur 5.16 Brant lutning på GC-axeln då fordonsflödet är högt Då fordonsflödet är lågt verkar däremot GC-flödets storlek ha mindre betydelse då ökningen på GCaxeln lutar svagt uppåt, se Figur
61 Figur 5.17 Svag lutning på GC-axeln då fordonsflödet är lågt Några slutsatser om vilken typ av samband som finns mellan de olika flödena och kapacitetsförlusten/fördröjningen går tyvärr inte att dra med de få datapunkter som simulerats men tendenser som illustrerats i Figur 5.16 och 5.17 går att visa. 5.4 Uppskattning av antal blockerande händelser För att Rodegerdts och Blackwelders modell skall vara användbar i ett beräkningsprogram som CapCal måste som tidigare nämnts antal blockerande händelser per timme skattas. Hypotesen är att antalet blockerande händelser är kopplat till fordonsflödet respektive fotgängar- och cyklistflödet på övergångsstället. För att testa denna hypotes kan man försöka skatta antalet blockerande händelser med hjälp av multipel linjär regressionsanalys. I en regressionsanalys försöker man finna en linjär ekvation som beskriver antalet blockerande händelser utifrån en mängd oberoende variabler såsom fordonsflöde och fotgängarflöde. I regressionsanalysen skattas variablernas parametrar samt en eventuell konstant samt hur korrekta de är. Från filmen har 25 observationer gjorts. Varje observation motsvarar data mätta under en 15 minuters period som sedan multiplicerats med fyra för att få dem mätta i timmar. De uppmätta värdena från filmen är fordonsflöde, fotgängarflöde, andel fotgängare som anländer i grupp, cykelflöde, andel cyklister som anländer i grupp samt antal blockerande händelser. Anledningen till att mäta andelen fotgängare och cyklister som anländer i grupp är att få en uppfattning om det faktiska antalet möjliga tillfällen då ett stopp skulle kunna inträffa. För att illustrera vikten av att notera andelen som anländer i grupp, kan man jämföra två olika övergångsställen där båda korsas av 50 fotgängare under en timme. I det ena övergångsstället anländer de 50 fotgängarna relativt jämt utspridda under en timmes tid och de orsakar var och en ett möjligt tillfälle då fordon kan tvingas stanna. I det andra övergångsstället anländer alla fotgängarna tillsammans i en grupp (t ex en stor turistgrupp) och de orsakar därför bara ett möjligt stopp. Effekterna av fotgängarna på framkomligheten beror antagligen därför i hög grad på hur många av 54
62 dem som anländer i grupp och hur många som anländer enskilt. För att hantera effekterna av att fotgängare och cyklister som anländer i grupp har ett justerat fotgängar- och cyklistflöde tagits fram. Det justerade fotgängarflödet uttrycks som: Där V fot V fotg y fot totalt antal fotgängare V just.fot = V fot V fotg y fot antalet fotgängare som anländer i grupp 2,5, den genomsnittlig storlek på en fotgängargrupp (mätt från filmerna) Den minsta och vanligast förekommande gruppen bestod i filmen av två fotgängare och den största uppmätta gruppen i data bestod av sju fotgängare (ett tillfälle). Det justerade cyklistflödet uttrycks på samma sätt: V cyk V cykg y cyk totalt antal cyklister V just.cyk = V cyk V cykg y cyk antalet cyklister som anländer i grupp 2, den genomsnittlig storlek på en grupp cyklister (mätt från filmerna) Det justerade värdena för fotgängar- och cyklistflödet är sedan de värden som använts i dataundersökningen. För att undersöka lämpligheten att göra en regressionsanalys på datamaterialet plottas antal blockerande händelser per timma mot fordonsflödet och fotgängar- och cyklistflödet. Om sambanden mellan fordons-, fotgängar- och cyklistflöden och antalet blockerande händelser illustreras med en 3D-plot syns det att topparna för antalet blockerande händelser är då fordonsflödet är högt och GC-flödet är relativt högt, se Figur
63 3D-plot för antal blockerande händelser GC-flöde Fordonsflöde Figur D-plot för antal blockerande händelser beroende av fordonsflödet och GC-flödet För att finna en ekvation som beskriver antalet blockerande händelser utifrån GC-flödet och fordonsflödet har följande regressioner testats. Valet av olika regressioner att testa har dels valts ut med trial and error. Då få data finns har det varit svårt utifrån denna att se vilken typ av regressionslinje som skulle kunna vara den mest lämpliga. Som Figur 5.18 visade verkar inte en linjärt samband vara det mest lämpliga men det bör ändå testas för att utesluta den teorin. Regressionsanalysen är gjort i Excel från 25 observationer från filmerna. De olika testade regressionerna finns i Tabell Tabell 5.14 De olika testade multipla regressionsanalyserna Ekvation Kommentar Antagande Regression 1 n block = α + β 1 fordonsflö det + β 2 fotgängar oc cykelflödet GC-flödet har hanterats som ett gemensamt flöde. justerat Linjärt samband Regression 2 n block = α + β 1 fordonsflö det + β 2 fotgängarflödet justerat + β 3 cyklistflödet justerat GC-flödet har hanterats som två separata flöden, ett fotgängarflöde och ett cyklistflöde. Linjärt samband 56
64 Regression 3 Regression 4 Regression 5 GC-flödet har hanterats som ett n block = α + β 1 fordonsflödet gemensamt flöde. + β 2 GC flödet Flödet har inte justerats mot hur många som anländer i grupp. n block GC-flödet har tagits = α + β 1 i kvadrat för att testa fordonsflö det + β 2 om det ger ett annat 2 resultat än de linjära fotgängar oc cykelflödet justerat regressionerna. Antar inte linjärt samband mellan de oberende- och beroende n block parametrarna. = α + β 1 Den naturliga fordonsflö det + β 2 logaritmen för GCflödet ln har testats för fotgängar oc cykelflödet justerat att testa om det ger ett annat resultat än de linjära regressionerna Linjärt samband Icke linjärt samband Icke linjärt samband Resultat från regressionsanalysen Resultaten från de fem regressionsanalyserna visar att antalet blockerande händelser kan skattas relativt väl från data bestående av flödet av fordon, fotgängare och cyklister Regressionsstatistiken från de fem olika regressionerna presenteras i Tabell Resultaten visar att alla regressioners R- kvadrat hamnar runt 0,8. Ingen regression särskiljer sig från de andra. För alla resultat från regressionsanalys se Bilaga IV. Med den mängd indata som ingått i regressionsanalysen verkar det som att ett linjärt samband skulle kunna beskriva antalet blockerande händelser relativ väl. Från det enklaste sambandet (regression 1) kan en matris beskrivande antalet blockerande händelser tas fram, se Tabell Alla värden < 0 har sats till 0. Ekvationen som matrisen bygger på har dock vissa brister. Till exempel så kan ju inte ett GC-flöde på 10 fotgängare/cyklister /timme orsaka mer än 10 blockerande händelser per timme oavsett hur stor fordonsflödet är därför har matrisen manuellt justerats för dessa brister i ekvationen. 57
65 Tabell 5.15 Resultaten för de testade multipla regressionsanalyserna Regressionsstatistik Ekvation Regression 1 Regression 2 Regression 3 Regression 4 Regression 5 Multipel-R 0,904 R-kvadrat 0,818 Justerad R-kvadrat 0,801 Standardfel 8,304 Observationer 25,000 Multipel-R 0,909 R-kvadrat 0,827 Justerad R-kvadrat 0,802 Standardfel 8,285 Observationer 25,000 Multipel-R 0,907 R-kvadrat 0,822 Justerad R-kvadrat 0,806 Standardfel 8,193 Observationer 25,000 Multipel-R 0,885 R-kvadrat 0,784 Justerad R-kvadrat 0,764 Standardfel 9,044 Observationer 25,000 Multipel-R 0,903 R-kvadrat 0,816 Justerad R-kvadrat 0,799 Standardfel 8,341 Observationer 25,000 n block = 40,79 + 0,061 fordonsflöde + 0,229 GCflöde n block = ,064 fordonsflöde + 0,21 fotgängarflöde + 0,225 cyklistflöde n block = ,065 fordonsflöde + 0,21 GCflöde n block = 44,42 + 0,065 fordonsflöde + 0,001 GCflöde 2 n block = ,06 fordonsflöde + 18,67 ln(gcflöde) 58
66 Tabell 5.16 Matris över antalet blockerande händelser per studietimma för regression 1 Gång- och cykel- flöde/tim me Fordon s- flöde/ timme
67 6 Diskussion och slutsats 6.1 Brister i datainsamlingen och analysen Då filmerna i datainsamlingen inte är filmade för detta examensarbete utan för ett annat projekt (SNEprojekt Kapacitet i Små cirkulationsplatser) finns det vissa brister i dem. Ett problem är att kölängderna ej kan mätas från filmen då bilden inte täcker hela kön. Det är även en brist att inte fler cirkulationsplatser med kapacitetsproblem filmats, men det var inte heller syftet med SNE-projektet. Det var bara en plats (Solna) där det var tydligt både från filmerna och från analysen att det fanns kapacitetsproblem på grund av övergångsstället. Mer data från cirkulationsplatser med kapacitetsproblem skulle därför ha varit värdefulla för att kunna validera hur korrekt den analytiska beräkningsmodellen är. I de statistiska test som gjorts från simuleringarna har endast 10 observationer ingått i varje datamängd och testats mot varandra vilket kan anses vara för lågt för att kunna dra slutsatser ifrån. Tillvägagångssättet i examensarbete för att uppskatta antalet blockerande händelser i simuleringen har varit att placera två kömätare nära varandra och därefter manuellt notera alla tillfällen i utdatafilen då båda kömätarna noterar en kö och översätta det till en blockerande händelser. Om detta är ett lämpligt sätt att uppskatta antalet blockerande händelser i simuleringen kan ifrågasättas. Ett alternativt sätt hade varit att studera filmen från simuleringen och manuellt notera varje gång en blockerande händelse inträffar. Men då detta skulle ta väldigt lång tid att genomföra valdes metoden att studera utdatafilerna istället Regressionsanalysen Den vidareutveckling som gjorts av den analytiska modellen har varit att uppskatta antalet blockerande händelser per timma från ett givet fordons-, gång- och cykelflöde. Regressionsanalysen visade att antalet blockerande händelser går att uppskatta med de ingående parametrarna. Fem olika ekvationer togs fram i regressionsanalysen. Då resultaten blev likvärdiga för samtliga regressioner kan någon slutsats om vilken typ av samband som bäst beskriver antalet blockerande händelser vara svårt att dra. Ytterligare tester och mätningar behöver därför genomföras innan detta säkert går att konstatera. För den datamängd som ingått verkade inte antalet personer som anlände i grupp påverka resultatet märkbart, se regression 3 i Tabell Det kan i och för sig bero på att ingen extremsituation då ett väldigt stort antal personer samtidigt korsade övergångsstället fanns med i datamängden. För att ytterligare förbättra regressionsanalysen måste därför mer extrema förhållanden testas, till exempel då det finns många cyklister och få fotgängare och vice versa. Datamängden för regressionsanalysen innefattade inte heller scenariot då GC-flödet är 0. Intuitivt blir ju antalet blockerande händelser då 0 för alla nivåer av fordonsflöden. Men detta konstruerade scenariot har inte tagits med i regressionsanalysen. Ytterligare en intressant vidareutveckling av examensarbetet och regressionsanalysen är att undersöka om ekvationen för antalet blockerande händelser även är tillämplig på andra korsningstyper än cirkulationsplatser. För att samla ytterligare indata till regressionsmodellen kan simulering vara ett verktyg att använda sig av. Som ovan nämnts kan inte antalet blockerande händelser mätas direkt i utdata från VISSIM men det kan däremot noteras om simuleringen studeras eller två kömätare används. 60
68 6.2 Användbarhet av den analytiska modellen Resultaten från både den analytiska modellen och simuleringen visar att gång- och cykeltrafik på övergångsställen vid cirkulationsplatser påverkar framkomligheten och kapaciteten vilket är känt sedan tidigare. De tendenser som kan utläsas ur de data- och modelltester som gjorts är att ett högt fordonsflöde, såsom i Solna, verkar vara mer känsligt för störningar än ett lägre fordonsflöde, även om gång- och cykelflödet kan vara mycket högt i det senare fallet. Vilka nivåer för fordonsflödet/gångoch cykeltrafikflödet som är kritiska har dock inte helt kunnat klarläggas med de indata som ingått. En intressant vidareutveckling av examensarbetet skulle därför kunna vara att ytterligare identifiera hur olika nivåer av fordons-, gång- och cykelflöden påverkar framkomligheten. För att identifiera dessa nivåer kan simulering vara en lämplig metod då olika värden på flödena lätt kan varieras. Användningsområdet för analytiska trafikmodeller, såsom den undersökta modellen, ligger framförallt i dess förmåga att snabbt kunna utvärdera effekterna av en viss utformning och belastningsgrad. Modellens främsta styrka är att relativt få indataparametrar behövs för analysen; mättnadsflödet, fordonsflöde vid utfarten, gång- och cykelflödet samt den tid det tar för en genomsnittlig fotgängare att korsa gatan. Resultatet från den analytiska modellen kan därför användas som ett första steg för att undersöka om det finns behov för en mer noggrann analys eller simulering av cirkulationsplatsen. Resultaten visade att det var endast en cirkulationsplats där den analytiska modellen uppskattade att kapacitetsnedsättningen på grund av övergångsstället blev högre än 5 %. En analytisk trafikmodell kan spara tid och pengar genom att utvärdera vilka delar i ett trafiksystem som kan vara värda att simulera. Men mycket av den exakthet som ges av en simulering går dock förlorad. För att analytiska trafikmodeller för cirkulationsplatser med GC-trafik ska kunna konkurrera som analysmetod mot simuleringsmodellerna måste mer forskning och utveckling av modellerna göras. Som litteraturstudien visade finns det ytterst få analytiska modeller tillgängliga, antagligen på grund av att gång- och cykeltrafik i cirkulationsplatser hittills har varit relativt ovanligt, både i Sverige och utomlands. Men ju fler cirkulationsplatser som byggs, desto vanligare blir det att konflikter med oskyddade trafikanter uppstår och därmed ökar intresset att utveckla nya modeller. 6.4 Rekommendationer för CapCal CapCal har idag en inbyggd funktion som varnar för en blockering av korta körfält i en korsning. Den analytiska modellen som testats skulle kunna användas som ett liknande varningssystem för blockering av cirkulationsplatsinfarter. Om CapCal beräknar att kapacitetsförlusten i en infart på grund av övergångsstället överstiger en viss förbestämd procentsats, kommer en varningsruta upp som varnar för att den kapacitet som beräknas kan vara felaktig på grund av gång- och cykelflödet. Detta bör ses som en indikation på att en simulering är mer lämpligt som analysverktyg för att kunna uppskatta framkomlighetsmåtten i cirkulationen. Ett alternativ till en bestämd procentsats är att ange maximalt antal gånger under en studietimme som kölängderna får överstiga en viss längd, utan att programmet varnar för kapacitetsförluster. Den analytiska modellen föreslår att kapacitetsnedsättningen ska beräknas som: I CapCal ges kapaciteten av: C adj = C base 1 t block 3600 C = αq e (λt Δ) 1 e (λt 0) 61
69 Om dessa två modeller skulle slås ihop skulle det ge justerad kapacitet i CapCal som: C adj = αq e (λt Δ) 1 e (λt 0) 1 t block 3600 Rekommendationen i dagsläget är att inte presentera kapaciteten som den justerade kapaciteten i ekvationen ovan innan ytterligare tester gjorts av beräkningsmodellen. Däremot kan och bör förslaget att införa ett varningssystem läggas in i CapCal. För att uppskatta antalet blockerande händelser är rekommendationen att använda sig av resultaten från regression 1. Detta trots att ett linjärt samband inte verkar vara helt korrekt för att beskriva antalet blockerande händelser. Men det linjära sambandet kan vara tillräckligt bra för den enkla överslagsberäkning som den analytiska beräkningsmodellen ger. För att göra resultaten från regression 1 mer robusta måste vissa begränsningar gällande minsta/största fordons- och GC-flöde läggas till ekvationen. 62
70 7 Referenser 7.1 Litteratur ALLSTRÖM A, HAGRING O och LINDERHOLM L. (2005). CapCal 3.2 Model descpription of roundabouts, Report 2006:xx April xx 06, Trivector Traffic AB ALLSTRÖM A, JANSON OLSTAM J och THORSSON T, (2008), Analys av modeller för framkomlighet i korsningar, KAKOR_projektrapport ver 1.0, Stockholm/Lund ALLSTRÖM A och JANSON OLSTAM J, (2010), Kapacitetsmodeller i korsningar (KAKOR) slutrapport etapp 2, VTI, Trivector Traffic AB, RPD, Stockholm/Lund ARONSSON A, BELLINGER A (2005), Utvärdering av CapCals förmåga att beräkna framkomlighet, Linköpings tekniska universitet, Norrköping DE DIOS ORTÚZAR J, WILUMSEN LUIS G (1990). Modelling transport third issue, England: Wiley FHWA (US DEPARTMENT OF TRANSPORT, FEDERAL HIGHWAY ADMINISTRATION) (2004), Traffic Analysis Toolbox Volume 1: Traffic Analysis Tools Primer, Oakland Kalifornien GRIFFITHS J (1981), A mathematical model of a nonsignalized pedestrian crossing, Transport Science, Vol 15, No.3 HAGRING O (2001), Förslag till modell för beräkning av framkomlighet, Institutionen för Teknik och Samhälle, Trafikteknik, Lunds Tekniska Högskola, Lund HAGRING O (2000), Effects of OD flows on roundabout entry capacity, Institutionen för Teknik och Samhälle, Trafikteknik, Lunds Tekniska Högskola, Lund HUBBERTEN C, SCHLAICH J, FRIEDRICH M (2009), Einfluss von Fußgängern auf den Verkehrsablauf an kleinen eistreifigen Kreisverkehrsplätzen, Strassenverkehrstechnik 53 oktober 2009, sida KENDALL D.G (1953), Stochastic Process Occurring in the Theory of Queues and Their Analysis by the method of imbedded Markov Chain Ann. Math Stat 24 KREISEL-Handbuch, Anhang A (2007) LINDERHOLM L. (2010), Beräkningsmanual CapCal, MARLOW M, MAYCOCK G (1982), The effect of zebra crossings on junction entry capacities, Transport and Road Research Laboraty, Supplementary report 724. England. Department of transport NÄRINGSDEPARTEMENTET (2001), Förordning (2001:651) om vägtrafikdefinitioner RODEGERDTS L A, BLACKWELDER G E (2005) Analytical analysis of pedestrian effects on roundabout exit capacity, Kittelson and Associates Inc, USA REFSNES H och THORSSON T (2006), Hur förhåller sig resultat från VISSIM till resultat från CapCal, Teknikutvecklingsprojekt, WSP SVERIGES KOMMUNER OCH LANDSTING (2008), Att köra i cirklar, Kommentus TRAFIKKONTORET STOCKHOLM STAD (2005), Handledning för nöjda beställare och utförare av mikrosimuleringsuppdrag, Version 1.0 VÄGVERKET (2004), VGU VV Publikation 2004:80, Borlänge VÄGVERKET (2008), Utvecklingsprojekt Kapacitetsmodeller i korsningar, Borlänge 63
71 7.2 Figurer Om annat än egentillverkade bilder, figurer etc. FIGUR 1.1 TOLLAZZI T, LERHER T, SRAML M, The use of Micro-Simulation in Determining the Capacity Roundabout with a Multi-Channel Pedestrian Flow, 2007, Journal of Mechanical Engeneering, vol , s. 335 FIGUR 2.1 VÄGVERKET, VGU VV Publikation 2004:80, ; 1; Korsningar: sida 117, Figur 7-97 FIGUR 2.2 VÄGVERKET, VGU VV Publikation 2004:80, ; 1; Korsningar: sida 136 Figur FIGUR 2.3 ALLSTRÖM A, HAGRING O, LINDERHOLM L (2005), CapCal 3.2 Model descpription of roundabouts, Report 2006:xx April xx 06, Trivector Traffic AB FIGUR 2.4 HAGRING O (2000), The effect of OD flows on roundabout entry capacity, Institutionen för Teknik och Samhälle, Trafikteknik, Lunds Tekniska Högskola, Lund FIGUR 2.5 ALLSTRÖM A, HAGRING O, LINDERHOLM L (2005), CapCal 3.2 Model descpription of roundabouts, Report 2006:xx April xx 06, Trivector Traffic AB FIGUR 2.6 ALLSTRÖM A, CapCal Metodbeskrivning, Trivector Traffic AB FIGUR 2.7 RODEGERDTS LA, BLACKWELDER G E (2005) Analytical analysis of pedestrian effects on roundabout exit capacity, Kittelson and Associates Inc, USA, sida 6 FIGUR 2.9 RODEGERDTS LA, BLACKWELDER G E (2005) Analytical analysis of pedestrian effects on roundabout exit capacity, Kittelson and Associates Inc, USA, sida 8 64
72 Bilagor BILAGOR TABELL I.I... II TABELL I.II... IV TABELL I.III... V TABELL I.IV... VI TABELL I.V... VII TABELL I.VI... VIII TABELL III.I... XI TABELL III.II... XI TABELL III.III... XII TABELL III.IV... XIII TABELL III.V... XIV TABELL III.VI... XIV TABELL III.VII... XV TABELL III.VIII... XV TABELL III.IX... XVI TABELL III.X... XVI TABELL III.XI... XVII TABELL III.XII... XVII TABELL III.XIII... XVIII TABELL III.XIV... XVIII TABELL III.XV... XIX TABELL III.XVI... XIX TABELL III.XVII... XX TABELL III.XVIII... XXI TABELL III.XIX... XXII TABELL III.XX... XXIII TABELL III.XXI... XXIV TABELL III.XXII... XXIV TABELL III.XXIII... XXV TABELL III.XXIV... XXVI TABELL III.XXV... XXVII TABELL III.XXVI... XXVII TABELL III.XXVII... XXVIII TABELL III.XXVIII... XXVIII TABELL III.XXIX... XXIX TABELL III.XXX... XXIX TABELL III.XXXI... XXX TABELL III.XXXII... XXXI TABELL III.XXXIII... XXXI TABELL III.XXXIV... XXXIII TABELL IV.I... XXXIV TABELL IV.II... XXXV FIGUR IV.I... XXXVII FIGUR IV.II... XXXVII I
73 FIGUR IV.III... XXXVIII FIGUR IV.IV... XXXVIII TABELL IV.III... XXXVIII FIGUR IV.V... XL FIGUR IV.VI... XL FIGUR IV.VII... XLI FIGUR IV.VIII... XLI FIGUR IV.VIX... XLII FIGUR IV.IX... XLII TABELL IV.IV... XLII FIGUR IV.X... XLIII FIGUR IV.XI... XLIV FIGUR IV.XII... XLIV FIGUR IV.XIII... XLV TABELL IV.V... XLV FIGUR IV.XIV... XLVI FIGUR IV.XV... XLVII FIGUR IV.XVI... XLVII FIGUR IV.XVII... XLVIII TABELL IV.VI... XLVIII FIGUR IV.XVIII... XLIX FIGUR IV.XIX... L FIGUR IV.XX... L FIGUR IV.XXI... LI Bilaga I Beräkningar för den analytiska modellen Solna Tabell I.I Solna Tid: Antal fotgängare 79 Antal cyklister 54 Antal blockerande händelser 54 Antal fordon i utfarten, VE 1056 Per timme Längden av en blockerande händelse 5 Sek Mättnadsflöde 1800 Qe 0 Qavg 3, II
74 Sekunder på en timme 3600 Summan av q P(q) t(q) P(q) * t(q) P(q)*t(q) 1 0, , , , , , , , , , , , , , , , , , Konvergerar mot 7 0, , , , , , , sekunder 9 0, , , , , , , , , III
75 12 0, , , ,53247E , , ,6557E , , tblock 645, sekunder 17,93% Kapacitetsförlusten Kapacitetsförlust 17,93% 15 min topp ( ) 22,41% Rissne Tabell I.II Rissne Antal fotgängare 154 Antal cyklister 15 Antal blockerande händelser 8 Antal fordon i utfarten, VE 311 Per timme Längden av en blockerande händelse 4,5 sek mättnadsflöde 1800 Qe 1 Qavg 0, sekunder på en timme 3600 Summan q P(q) t(q) P(q) * t(q) P(q)*t(q) 1 0, , ,25 0, , , , , , ,375 0, , , ,6 0, , ,48328E-05 13,75 0, , av IV
76 7 1,99205E-06 15, ,15882E-05 0, Konvergerar mot 8 1,39824E-07 17,9375 2,50809E-06 0, , ,72388E ,74478E-07 0, sekunder 10 4,8987E-10 22,05 1,08016E ,50069E-11 24, ,02439E-10 tblock 4, sekunder 0,12% Kapacitetsförlusten Kapacitetsförlusten 0,12% 15 min topp ( ) 0,18% Malmö, Annetorpsvägen Tabell I.III Malmö Tid: Annetorpsv.- Elinelundsv 1 Antal fotgängare 28 Antal cyklister 11 Antal blockerande händelser 10 Antal fordon i utfarten, VE 748 Per timme Längden av en blockerande händelse 6 sek Mättnadsflöde 1800 Qe 0 Qavg 2, Sekunder på en timme 3600 Summan q P(q) t(q) P(q) * t(q) P(q)*t(q) 1 0, , , , , , , , , , , , , , , av 6 0, , , Konvergerar V
77 mot 7 0, , , , , , , sekunder 9 0, , , ,36683E , , ,23463E , , tblock 95, sekunder Kapacitetsförlusten 2,65% 2,65% Kapacitetsförlusten Topp 15 min( ) 3,29% Lund, Västra Tabell I.IV Lund Södrav - Arkivgatan Antal fotgängare 17 Antal cyklister 110 Antal blockerande händelser 10 Antal fordon i utfarten, VE 447 Per timme Längden av en blockerande händelse 5 sek mättnadsflöde 1800 Qe 1 Qavg 0, sekunder på en timme 3600 q P(q) t(q) P(q) * t(q) 1 0, VI Summan av P(q)*t(q) 2 0, ,5 0, , , , , , , ,75 0, , , , ,
78 6 0, , , , Konvergerar mot 7 2,2778E-05 16, , , , ,35166E-06 18,375 4,32118E-05 1, sekunder 9 2,15815E-07 20, ,41223E-06 1, ,78251E-08 22,5 4,01065E-07 1, ,33841E-09 24, ,28519E-08 1, tblock 10, sekunder Kapacitetsförlusten 0,30% 0,30% Kapacitetsförlusten Topp 15 min( ) 0,67% Lund, Södra Tabell I.V Lund Södrav - Arkivgatan Antal fotgängare 25 Antal cyklister 79 Antal blockerande händelser 19 Antal fordon i utfarten, VE 597 Per timme Längden av en blockerande händelse 4,5 sek mättnadsflöde 1800 Qe 0 Qavg 1, sekunder på en timme 3600 Summan q P(q) t(q) P(q) * t(q) P(q)*t(q) 1 0, ,5 2, , , ,5 1, , , ,5 0, , , ,5 0, , , ,5 0, , av VII
79 6 0, ,5 0, , Konvergerar mot 7 0, ,5 0, , , ,53825E-05 20,5 0, , sekunder 9 1,84234E-06 22,5 4,14527E-05 5, ,98589E-07 24,5 4,86543E-06 5, ,94602E-08 26,5 5,15696E-07 5, tblock 97, sekunder Kapacitetsförlusten 2,70% Topp 15 min( ) 6,00% 2,70% Kapacitetsförluste n Lund, Östra Tabell I.VI Lund Södrav Arkivgatan Antal fotgängare 36 Antal cyklister 90 Antal blockerande händelser 13 Antal fordon i utfarten, VE 429 Per timme Längden av en blockerande händelse 5 sek Mättnadsflöde 1800 Qe 0 Qavg 0, Sekunder på en timme 3600 Summan q P(q) t(q) P(q) * t(q) P(q)*t(q) 1 0, , , , , , , , , av VIII
80 4 0, , , , , , , , , Konvergerar mot 7 1,62686E , , , ,59082E ,34072E-05 4, sekunder 9 1,38273E ,18028E-06 4, ,08168E ,70419E-07 4, ,69245E ,07696E-08 4, tblock 55, sekunder Kapacitetsförlusten 1,54% 1,54% Kapacitetsförlusten Topp 15 min( ) 4,02% IX
81 Bilaga II Parameterinställningar i simuleringen Solna Rissne Hastighet o Bilar 40 km/h o Tunga fordon 40 km/h o Fotgängare 5 km/h o Cyklister 10 km/h o Reduced speed areas 30 km/h Andel tunga fordon 2 % Conflict areas o Front gap; 0 s o Rear gap; 0 s o Safety distance factor; 1 Queue counter 2 st, avstånd mellan: 5,5 m o Max headway 10 m o Time interval 30 sekunder Hastighet o Bilar 40 km/h o Tunga fordon 40 km/h o Fotgängare 5 km/h o Cyklister 10 km/h o Reduced speed areas 30 km/h Andel tunga fordon 5 % Conflict areas o Front gap; 0 s o Rear gap; 0 s o Safety distance factor; 1 Queue counter 2 st, avstånd mellan: 5 m o Max headway 10 m o Time interval 30 sekunder X
82 Bilaga III Resultat simuleringen Cirkulationsplatsen i Rissne Tabell III.I Med övergångsställe Simulering nr Genomsnittli g försening per fordon (sek) Genomsnittligt antal stopp/fordon Total försening (timmar) Totalt antal stopp 1 2,748 0,082 0, ,22 Total (timmar) 2 3,034 0,078 0, , ,38 0,116 1, , ,911 0,086 0, ,42 5 3,22 0,126 1, , ,462 0,12 1, , ,117 0,104 1, , ,217 0,118 1, , ,122 0,094 1, , ,176 0,102 1, ,905 restid Medel 3,1387 0,1026 1, ,7 4,6623 Tabell III.II Utan övergångsställe Simulering nr Genomsnittli g försening per fordon (sek) Genomsnittlig t antal stopp/fordon XI Total försening (timmar) Totalt antal stopp 1 2,768 0,077 0, , ,931 0,084 0, , ,234 0,119 0, , ,879 0,086 0, , ,108 0,103 0, , ,148 0,081 0, , ,016 0,096 0, , ,18 0,107 0, ,91 Total restid (timmar)
83 9 3,155 0,1 0, , ,232 0,086 0, ,979 Medel 3,0651 0,0939 0, ,1 3,6906 Beskrivande statistik Tabell III.III Total restid (timmar) Med övergångsställe Total restid (timmar) Utan övergångsställe Medelvärde 4,6623 Medelvärde 3,6906 Standardfel 0, Standardfel 0, Medianvärde 4,759 Medianvärde 3,7175 Typvärde #SAKNAS! Typvärde ######## Standardavvikelse 0, Standardavvikelse 0, Varians 0, Varians 0, Toppighet Snedhet - 1, Toppighet -0, , Snedhet -0,41141 Variationsvidd 0,688 Variationsvidd 0,663 Minimum 4,22 Minimum 3,316 Maximum 4,908 Maximum 3,979 Summa 46,623 Summa 36,906 Antal 10 Antal 10 Konfidensnivå(95,0%) 0, Konfidensnivå(95,0%) 0, t-test: Två sampel antar olika varianser Med övergångsstället Medelvärde 4,662 3,691 Varians 0,067 0,040 Observationer 10,000 10,000 Antagen medelvärdesskillnad 0,000 fg 17,000 t-kvot 9,407 XII Utan övergångsstället
84 P(T<=t) ensidig 0,000 t-kritisk ensidig 1,740 P(T<=t) tvåsidig 0,000 t-kritisk tvåsidig 2,110 Tabell III.IV Ruttider Time Trav Trav Trav Trav Trav Trav Trav Trav Trav Trav Trav Trav MED All All All All All All All All All All All All No,: Name 1H 2H 1R 1V 2R 2V 3R 3H 3V 4H 4R 4V 1 8,2 10 9,1 13,1 12,9 12,6 9, ,1 12,5 13,1 2 7,9 9,6 9,1 12,9 13,5 13,7 9,8 9,7 12,2 10,3 12,7 13,7 3 8,5 10,7 9, ,5 14,1 9,4 9,9 13,3 10,2 12,6 15,1 4 8,4 9,7 9,7 12,7 13,5 13,6 9,2 9,2 12,7 10,5 12,3 13,4 5 8,6 10, ,8 14,2 10, ,4 10,6 12,5 13,3 6 8,8 10,2 9 14,1 14,3 14,2 9,9 10,2 13,5 9,9 13,1 14,2 7 8,7 9,5 9,3 13,7 13,2 13,6 9,9 9,5 12,7 11, ,2 8 8,3 9,3 9,2 13,8 13,3 14,1 10, ,9 10,9 12,6 13,9 9 8,3 10,5 9,1 13,6 13,9 13,6 9,8 10,6 12,6 10,3 12,4 13,7 10 8,3 10 9,3 14,2 13, , ,5 10,9 12,4 14 MEDEL 8,4 10,02 9,32 13,51 13,53 13,77 9,91 9,91 12,78 10,49 12,61 13,86 UTAN 1 7,7 9,7 9,1 12,5 12,4 12,5 9,5 9,8 12,2 10,1 11,6 12,8 2 7,5 9,5 9 12,9 12,6 12,8 9,2 10,7 12 9,9 11,9 13,3 3 7,8 9,9 9,4 13,7 13,1 13,2 9,2 10,1 13,5 9,6 11,7 13,5 4 7,6 9,5 9,4 12,2 12,6 13 9,4 9 12,1 10,3 11,9 13,4 5 7,9 9,8 9,7 12,9 12,8 13, , ,2 6 7,7 9,5 9 14, ,2 9,7 9,6 11,9 10,2 12,1 14,1 7 7,4 9,1 9,4 13,1 12,4 13,1 9,6 9,4 11,7 11,2 12,3 14,3 8 7,5 9,1 9,1 13,3 12,5 13,1 10,6 10,1 12,6 10,2 12,3 14,3 9 7,7 9,8 8,7 13, ,9 9,9 10, ,5 11,9 13,9 XIII
85 10 8,2 9, ,5 13,3 10,2 9,6 12,1 11,3 12,2 14,1 MEDEL 7,7 9,51 9,18 13,26 12,69 13,03 9,73 9,85 12,23 10,33 11,99 13,69 SKILLNA D -0,7-0,51-0,14-0,25-0,84-0,74-0,18-0,06-0,55-0,16-0,62-0,17 Tabell III.V Rutt 1 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 8,4 7,7 Varians 0, , Observationer Antagen medelvärdesskillnad 0 fg 18 t-kvot 6, P(T<=t) ensidig 2,87709E-06 t-kritisk ensidig 1, P(T<=t) tvåsidig 5,75418E-06 t-kritisk tvåsidig 2, Tabell III.VI Rutt 2 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 9,32 9,18 Varians 0, ,084 Observationer Antagen medelvärdesskillnad 0 fg 18 XIV
86 t-kvot 1, P(T<=t) ensidig 0, t-kritisk ensidig 1, P(T<=t) tvåsidig 0, t-kritisk tvåsidig 2, Tabell III.VII Rutt 3 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 13,51 13,26 Varians 0, , Observationer Antagen medelvärdesskillnad 0 fg 17 t-kvot 0, P(T<=t) ensidig 0, t-kritisk ensidig 1, P(T<=t) tvåsidig 0, t-kritisk tvåsidig 2, Tabell III.VIII Rutt 4 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 10,02 9,51 Varians 0, , Observationer Antagen medelvärdesskillnad 0 XV
87 fg 15 t-kvot 2, P(T<=t) ensidig 0, t-kritisk ensidig 1, P(T<=t) tvåsidig 0, t-kritisk tvåsidig 2, Tabell III.IX Rutt 5 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 13,53 12,69 Varians 0, , Observationer Antagen medelvärdesskillnad 0 fg 16 t-kvot 5, P(T<=t) ensidig 1,91446E-05 t-kritisk ensidig 1, P(T<=t) tvåsidig 3,82892E-05 t-kritisk tvåsidig 2, Tabell III.X Rutt 6 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 13,77 13,03 Varians 0, , Observationer Antagen 0 XVI
88 medelvärdesskillnad fg 13 t-kvot 4, P(T<=t) ensidig 0, t-kritisk ensidig 1, P(T<=t) tvåsidig 0, t-kritisk tvåsidig 2, Tabell III.XI Rutt 7 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 9,91 9,85 Varians 0, , Observationer Antagen medelvärdesskillnad 0 fg 17 t-kvot 0, P(T<=t) ensidig 0, t-kritisk ensidig 1, P(T<=t) tvåsidig 0, t-kritisk tvåsidig 2, Tabell III.XII Rutt 8 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 9,91 9,73 Varians 0, , Observationer XVII
89 Antagen medelvärdesskillnad 0 fg 18 t-kvot 0, P(T<=t) ensidig 0, t-kritisk ensidig 1, P(T<=t) tvåsidig 0, t-kritisk tvåsidig 2, Tabell III.XIII Rutt 9 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 12,78 12,23 Varians 0, , Observationer Antagen medelvärdesskillnad 0 fg 17 t-kvot 2, P(T<=t) ensidig 0, t-kritisk ensidig 1, P(T<=t) tvåsidig 0, t-kritisk tvåsidig 2, Tabell III.XIV Rutt 10 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 10,49 10,33 Varians 0, , XVIII
90 Observationer Antagen medelvärdesskillnad 0 fg 17 t-kvot 0, P(T<=t) ensidig 0, t-kritisk ensidig 1, P(T<=t) tvåsidig 0, t-kritisk tvåsidig 2, Tabell III.XV Rutt 11 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 12,61 11,99 Varians 0, , Observationer Antagen medelvärdesskillnad 0 fg 18 t-kvot 5, P(T<=t) ensidig 1,39644E-05 t-kritisk ensidig 1, P(T<=t) tvåsidig 2,79289E-05 t-kritisk tvåsidig 2, Tabell III.XVI Rutt 12 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 13,86 13,69 XIX
91 Varians 0, , Observationer Antagen medelvärdesskillnad 0 fg 18 t-kvot 0, P(T<=t) ensidig 0, t-kritisk ensidig 1, P(T<=t) tvåsidig 0, t-kritisk tvåsidig 2, Tabell III.XVII Total försening (timmar) Med övergångsställe Total försening (timmar) Utan övergångsställe Medelvärde 1,0566 Medelvärde 0,8814 Standardfel 0, Standardfel 0, Medianvärde 1,082 Medianvärde 0,8885 Standardavvikelse 0, Standardavvikelse 0, Varians 0, Varians 0, Toppighet Snedhet - 0, Toppighet -0, , Snedhet -0,49785 Variationsvidd 0,32 Variationsvidd 0,257 Minimum 0,861 Minimum 0,733 Maximum 1,181 Maximum 0,99 Summa 10,566 Summa 8,814 Antal 10 Antal 10 Konfidensnivå(95,0%) 0, Konfidensnivå(95,0%) 0, t-test: Två sampel antar olika varianser Med Utan övergångsstället övergångsstället Medelvärde 1,057 0,881 XX
92 Varians 0,011 0,007 Observationer 10,000 10,000 Antagen medelvärdesskillnad 0,000 fg 17,000 t-kvot 4,126 P(T<=t) ensidig 0,000 t-kritisk ensidig 1,740 P(T<=t) tvåsidig 0,001 t-kritisk tvåsidig 2,110 Tabell III.XVIII Genomsnittlig försening per fordon (sek) Med övergångsställe Genomsnittlig försening per fordon (sek) Utan övergångsställe Medelvärde 3,1387 Medelvärde 3,0651 Standardfel 0, Standardfel 0, Medianvärde 3,149 Medianvärde 3,128 Standardavvikelse 0, Standardavvikelse 0, Varians 0, Varians 0, Toppighet 0, Toppighet -0,58579 Snedhet - 0, Snedhet -0,77814 Variationsvidd 0,714 Variationsvidd 0,466 Minimum 2,748 Minimum 2,768 Maximum 3,462 Maximum 3,234 Summa 31,387 Summa 30,651 Antal 10 Antal 10 Konfidensnivå(95,0%) 0, Konfidensnivå(95,0%) 0, t-test: Två sampel antar olika varianser Med Utan övergångsställe övergångsställe Medelvärde 3,1387 3,0651 Varians 0, , Observationer Antagen medelvärdesskillnad 0 fg 17 XXI
93 t-kvot 0, P(T<=t) ensidig 0, t-kritisk ensidig 1, P(T<=t) tvåsidig 0, t-kritisk tvåsidig 2, Tabell III.XIX Totalt antal stopp Med övergångsställe Totalt antal stopp Utan övergångsställe Medelvärde 124,7 Medelvärde 97,1 Standardfel 7, Standardfel 5, Medianvärde 130 Medianvärde 97,5 Standardavvikelse 24, Standardavvikelse 16,36018 Varians 605, Varians 267,6556 Toppighet Snedhet - 1, Toppighet -0, , Snedhet 0, Variationsvidd 64 Variationsvidd 53 Minimum 89 Minimum 73 Maximum 153 Maximum 126 Summa 1247 Summa 971 Antal 10 Antal 10 Konfidensnivå(95,0%) 17, Konfidensnivå(95,0%) 11,70337 t-test: Två sampel antar olika varianser Med Utan övergångsstället övergångsstället Medelvärde Varians Observationer Antagen medelvärdesskillnad 0 fg 16 t-kvot 2,954 P(T<=t) ensidig 0,005 t-kritisk ensidig 1,746 P(T<=t) tvåsidig 0,009 t-kritisk tvåsidig 2,120 XXII
94 Tabell III.XX Genomsnittligt antal stopp/fordon Med övergångsställe Genomsnittligt antal stopp/fordon Utan övergångsställe Medelvärde 0,1026 Medelvärde 0,0939 Standardfel 0, Standardfel 0, Medianvärde 0,103 Medianvärde 0,091 Typvärde #SAKNAS! Typvärde 0,086 Standardavvikelse 0, Standardavvikelse 0, Varians 0, Varians 0, Toppighet Snedhet - 1, Toppighet -0, , Snedhet 0, Variationsvidd 0,048 Variationsvidd 0,042 Minimum 0,078 Minimum 0,077 Maximum 0,126 Maximum 0,119 Summa 1,026 Summa 0,939 Antal 10 Antal 10 Konfidensnivå(95,0%) 0, Konfidensnivå(95,0%) 0, t-test: Två sampel antar olika varianser Med Utan övergångsstället övergångsstället Medelvärde 0,103 0,094 Varians 0,000 0,000 Observationer 10,000 10,000 Antagen medelvärdesskillnad 0,000 fg 17,000 t-kvot 1,266 P(T<=t) ensidig 0,111 t-kritisk ensidig 1,740 P(T<=t) tvåsidig 0,223 t-kritisk tvåsidig 2,110 XXIII
95 Cirkulationsplatsen i Solna Tabell III.XXI Med övergångsställe Simulering nr Total restid Genomsnittlig försening (sek) Genomsnittligt antal stopp/fordon Total försening (timmar) 1 21,478 20,419 0,784 10, ,476 18,312 0,654 9, ,081 18,623 0,696 9, ,033 13,499 0,529 7, ,416 20,066 0,633 10, ,178 17,309 0,606 9, ,248 23,118 0,749 12, ,637 21,519 0,76 11, ,387 14,993 0,535 7, ,636 16,084 0,59 8, Antal stopp Medel 20,657 18,3942 0,6536 9, ,2 Tabell III.XXII Utan övergångsställe Simulering nr Total restid Genomsnittlig försening (sek) Genomsnittligt antal stopp/fordon Total försening (timmar) 1 15,891 12,336 0,429 6, ,744 12,455 0,434 6, ,653 9,937 0,34 4, ,357 9,881 0,372 4, ,625 14,792 0,447 7, ,158 12,951 0,483 6, ,242 11,076 0,434 5, ,936 12,475 0,437 6, ,721 9,15 0,357 4, ,999 12,356 0,462 6, Medel 15, ,7409 0,4195 5, ,5 Antal stopp XXIV
96 Tabell III.XXIII Beskrivande statistik Total restid (timmar) Med övergångsställe Total restid (timmar) Utan övergångsställe Medelvärde 20,657 Medelvärde 15,4326 Standardfel 0, Standardfel 0, Medianvärde 20,7785 Medianvärde 15,8175 Typvärde #SAKNAS! Typvärde #SAKNAS! Standardavvikelse 1, Standardavvikelse 0, Varians 2, Varians 0, Toppighet -0, Toppighet -0, Snedhet - 0, Snedhet -0, Variationsvidd 5,215 Variationsvidd 2,904 Minimum 18,033 Minimum 13,721 Maximum 23,248 Maximum 16,625 Summa 206,57 Summa 154,326 Antal 10 Antal 10 Konfidensnivå(95,0%) 1, Konfidensnivå(95,0%) 0, t-test: Två sampel antar olika varianser Med Utan övergångsstället övergångsstället Medelvärde 20,657 15,433 Varians 2,823 0,840 Observationer 10,000 10,000 Antagen medelvärdesskillnad 0,000 fg 14,000 t-kvot 8,632 P(T<=t) ensidig 0,000 t-kritisk ensidig 1,761 P(T<=t) tvåsidig 0,000 t-kritisk tvåsidig 2,145 XXV
97 Ruttider Tabell III.XXIV Time Trav Trav Trav Trav Trav Trav MED All All All All All All No.: Name ,4 18,5 10,8 22,3 14,6 10,1 2 19,9 16,2 10,7 18,4 13,9 9,8 3 21,4 17,1 10,8 24,9 14,8 10,5 4 20,4 15,7 10,5 17,2 14,4 10,5 5 21,5 16,7 10,7 20,2 15,9 10,6 6 21, , ,3 10,2 7 21,5 15,6 10,5 18,2 13,4 10,3 8 20,9 18,2 10,3 22,9 13,7 10, ,3 10,2 19,8 13, ,7 10,7 19,6 14,4 10,1 MEDEL 20,72 16,7 10,55 20,55 14,13 10,28 Time Trav Trav Trav Trav Trav Trav UTAN All All All All All All No.: Name ,5 13, ,3 12, ,3 13, ,4 14,2 9,1 3 17,5 11,2 9,8 15,8 13,3 9,1 4 17,6 12,1 9,7 15,4 14 8,9 5 17,9 13,2 10,3 17,6 13,9 8,9 6 17,3 13,2 9,9 18,8 11,2 9,1 7 17,5 12,7 9,9 15,8 14,3 9,3 8 17, , ,8 9,2 9 17,1 11,7 9,9 16,1 13,6 9, ,3 13,5 9,9 16,7 13,8 9,1 Medel 17,33 12,69 9,95 16,69 13,45 9,08 XXVI
98 Tabell III.XXV Rutt 1 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 20,72 17,33 Varians 0, , Observationer Antagen medelvärdesskillnad 0 fg 13 t-kvot 12, P(T<=t) ensidig 4,54897E-09 t-kritisk ensidig 1, P(T<=t) tvåsidig 9,09793E-09 t-kritisk tvåsidig 2, Tabell III.XXVI Rutt 2 t-test: Två sampel antar olika varianser Variabel 1 XXVII Variabel 2 Medelvärde 16,7 12,69 Varians 1, , Observationer Antagen medelvärdesskillnad 0 fg 15 t-kvot 8, P(T<=t) ensidig 1,03E-07 t-kritisk ensidig 1,75305 P(T<=t) tvåsidig 2,06E-07 t-kritisk tvåsidig 2,13145
99 Tabell III.XXVII Rutt 3 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 10,55 9,95 Varians 0, , Observationer Antagen medelvärdesskillnad 0 fg 17 t-kvot 6, P(T<=t) ensidig 1,40359E-06 t-kritisk ensidig 1, P(T<=t) tvåsidig 2,80719E-06 t-kritisk tvåsidig 2, Tabell III.XXVIII Rutt 4 t-test: Två sampel antar olika varianser Variabel 1 XXVIII Variabel 2 Medelvärde 20,55 16,69 Varians 5, , Observationer Antagen medelvärdesskillnad 0 fg 12 t-kvot 4, P(T<=t) ensidig 0, t-kritisk ensidig 1, P(T<=t) tvåsidig 0,
100 t-kritisk tvåsidig 2, Tabell III.XXIX Rutt 5 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 14,13 13,45 Varians 0, , Observationer Antagen medelvärdesskillnad 0 fg 18 t-kvot 1, P(T<=t) ensidig 0, t-kritisk ensidig 1, P(T<=t) tvåsidig 0, t-kritisk tvåsidig 2, Tabell III.XXX Rutt 6 t-test: Två sampel antar olika varianser Variabel 1 Variabel 2 Medelvärde 10,28 9,08 Varians 0,084 0, Observationer Antagen medelvärdesskillnad 0 fg 12 t-kvot 12, P(T<=t) ensidig 2,30059E-08 t-kritisk ensidig 1, XXIX
101 P(T<=t) tvåsidig 4,60119E-08 t-kritisk tvåsidig 2, Tabell III.XXXI Genomsnittlig försening per fordon (sek) Med övergångsställe Genomsnittlig försening per fordon (sek) Utan övergångsställe Medelvärde 18,3942 Medelvärde 11,7409 Standardfel 0, Standardfel XXX 0, Medianvärde 18,4675 Medianvärde 12,346 Standardavvikelse 3, Standardavvikelse Varians 9, Varians Toppighet -0, Toppighet Snedhet -0, Snedhet 1, , , , Variationsvidd 9,619 Variationsvidd 5,642 Minimum 13,499 Minimum 9,15 Maximum 23,118 Maximum 14,792 Summa 183,942 Summa 117,409 Antal 10 Antal 10 Konfidensnivå(95,0%) 2, t-test: Två varianser sampel antar olika Med övergångsställe t Medelvärde 18,394 11,741 Varians 9,009 2,936 Observationer 10,000 10,000 Antagen medelvärdesskillnad 0,000 fg 14,000 t-kvot 6,088 Konfidensnivå(95,0% ) Utan övergångsstället 1,
102 P(T<=t) ensidig 0,000 t-kritisk ensidig 1,761 P(T<=t) tvåsidig 0,000 t-kritisk tvåsidig 2,145 Tabell III.XXXII Total försening (timmar) Med övergångsställe Total försening (timmar) Utan övergångsställe Medelvärde 9,6907 Medelvärde 5,7706 Standardfel 0, Standardfel 0, Medianvärde 9,737 Medianvärde 6,0865 Standardavvikelse 1, Standardavvikelse 0, Varians 2, Varians 0, Toppighet -0, Toppighet -0,63925 Snedhet -0, Snedhet -0,29336 Variationsvidd 5,152 Variationsvidd 2,741 Minimum 7,094 Minimum 4,38 Maximum 12,246 Maximum 7,121 Summa 96,907 Summa 57,706 Antal 10 Antal 10 Konfidensnivå(95,0 %) 1, Konfidensnivå(95,0%) 0, t-test: Två sampel antar olika varianser Utan Med övergångstället övergångsställe t Medelvärde 9,691 5,771 Varians 2,587 0,718 Observationer 10,000 10,000 Antagen medelvärdesskillnad 0,000 fg 14,000 t-kvot 6,819 P(T<=t) ensidig 0,000 t-kritisk ensidig 1,761 P(T<=t) tvåsidig 0,000 t-kritisk tvåsidig 2,145 Tabell III.XXXIII XXXI
103 Totalt antal stopp Med övergångsställe Totalt antal stopp Med övergångsställe Medelvärde 1239,2 Medelvärde 742,5 Standardfel 56, Standardfel 28,01795 Medianvärde 1208,5 Medianvärde 770,5 Standardavvikelse 177, Standardavvikelse 88,60054 Varians 31611,95556 Varians 7850,056 Toppighet Snedhet - 1, Toppighet -0, , Snedhet -0,56112 Variationsvidd 484 Variationsvidd 258 Minimum 990 Minimum 604 Maximum 1474 Maximum 862 Summa Summa 7425 Antal 10 Antal 10 Konfidensnivå(95,0%) 127, Konfidensnivå(95,0%) 63,38101 t-test: Två sampel antar olika varianser Med Utan övergångsstället övergångsstället Medelvärde Varians 31611, ,056 Observationer Antagen medelvärdesskillnad 0 fg 13 t-kvot 7,907 P(T<=t) ensidig 0,000 t-kritisk ensidig 1,771 P(T<=t) tvåsidig 0,000 t-kritisk tvåsidig 2,160 XXXII
104 Tabell III.XXXIV Genomsnittligt antal stopp/fordon Med övergångsställe Genomsnittligt antal stopp/fordon Med övergångsställe Medelvärde 0,6536 Medelvärde 0,4195 Standardfel 0, Standardfel 0, Medianvärde 0,6435 Medianvärde 0,434 Standardavvikelse 0, Standardavvikelse 0, Varians 0, Varians 0,00221 Toppighet - 1, Toppighet -0,74012 Snedhet 0, Snedhet -0,65195 Variationsvidd 0,255 Variationsvidd 0,143 Minimum 0,529 Minimum 0,34 Maximum 0,784 Maximum 0,483 Summa 6,536 Summa 4,195 Antal 10 Antal 10 Konfidensnivå(95,0%) 0, Konfidensnivå(95,0%) 0, t-test: Två sampel antar olika varianser Med övergångsstället Utan övergångsstället Medelvärde 0,654 0,420 Varians 0,008 0,002 Observationer 10,000 10,000 Antagen medelvärdesskillnad 0,000 fg 13,000 t-kvot 7,189 P(T<=t) ensidig 0,000 t-kritisk ensidig 1,771 P(T<=t) tvåsidig 0,000 t-kritisk tvåsidig 2,160 XXXIII
105 Bilaga IV Regressionsanalysen Tabell IV.I Indata Flöden / 15min Plats Solna Solna Solna Solna Lund, Dalbyv Malmö, Anne1 Malmö, Anne1 Malmö, Anne1 Malmö, Anne1 Rissne Rissne Rissne Rissne Lund, Arkivg Tid Fordon sflöde Fotgäng arflöde varav i grupp Cyklis tflöde varav i grupp Justerat Fot+cyklistflö de Antal blockerande händelser Lund, XXXIV
106 Arkivg 8.10 Lund, Arkivg Lund, Arkivg Lund, Södrav Lund, Södrav Lund, Södrav Lund, Södrav Lund, Södrav.3 Lund, Södrav.4 Lund, Södrav.5 Lund, Södrav Regression 1 Tabell IV.II Koefficienter Standardfel t-kvot p-värde Konstant -40,787 6,497-6,278 0,000 Fordonsflöde 0,061 0,007 9,184 0,000 Justerat GC-flöde 0,229 0,041 5,627 0,000 RESIDUALUTDATA Observation Uppskattat Antal blockerande händelser Residualer Standardiserade residual 1 49,342-13,342-1, ,445-4,445-0, ,326 22,674 2, ,930 2,070 0,260 XXXV
107 5 7,069 0,931 0, ,712 1,288 0, ,250-9,250-1, ,399-1,399-0, ,522-8,522-1, ,061 3,939 0, ,091-7,091-0, ,440-15,440-1, ,069 0,931 0, ,447-1,447-0, ,496 3,504 0, ,615-2,615-0, ,884 5,884 0, ,026 10,974 1, ,390-7,390-0, ,834 2,166 0, ,262 4,738 0, ,514 0,486 0, ,864 6,136 0, ,953 6,047 0, ,823-0,823-0,104 XXXVI
108 Antal blockerande händelser Antal blockernade händelser 80 Fordonsflöde Regressionskurva Number of blocking events Uppskattat Number of blocking events Fordons flöde Figur IV.I 80 Justerat GC-flöde Regressionskurva Number of blocking events Uppskattat Number of blocking events Justerat GC-flöde Figur IV.II XXXVII
109 Residualer Residualer 25,000 20,000 15,000 10,000 5,000 0,000-5,000-10,000-15,000-20,000 Residualdiagram GC-trafik justerat Figur IV.III 25,000 20,000 15,000 10,000 5,000 0,000-5,000-10,000-15,000-20,000 Residualdiagram Fordonsflöde Figur IV.IV Regression 2 Tabell IV.III Koefficienter Standardfel t-kvot p-värde Konstant -43,010 6,719-6,401 0,000 Fordonsflöde 0,064 0,007 9,434 0,000 Fotgängarflöde, justerat 0,211 0,045 4,651 0,000 Cyklistflöde, justerad 0,225 0,042 5,305 0,000 XXXVIII
110 RESIDUALUTDATA Observation 1 47, , Uppskattat Antal blockerande händelser Residualer Standardiserade residual - 11, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , XXXIX
111 antal blockerande händelser Residualer 23 27, , , , , , , , , Fordons flöde residualdiagram Fordons flöde Figur IV.V Fordonsflöde Regressionskurva Number of blocking events Uppskattat Number of blocking events Fordonsflöde Figur IV.VI XL
112 antal blockerande händelser Residualer Justerat fotgängarflöde residualdiagram Fotgängarflöde, justerat Figur IV.VII 80 Justerat fotgängarflöde Regressionskurva Number of blocking events Justerat fotgängarflöde Uppskattat Number of blocking events Figur IV.VIII XLI
113 antal blockerande händelser Residualer Justerat cyklistflöde residualdiagram Cyklistflöde. justerat Figur IV.VIX 80 Justerat cyklistflöde Regressionskurva Justerat cyklistflöde Number of blocking events Uppskattat Number of blocking events Figur IV.IX Regression 3 Tabell IV.IV Koefficienter Standardfel t-kvot p-värde Konstant -44,4226 6, , ,66E-06 Fordonsflöde 0, , , ,34E-09 GC-flöde 0, , , ,65E-06 RESIDUALUTDATA Observation Uppskattat Antal blockerande händelser Residualer Standardiserade residual XLII
114 Residualer 1 47, ,8399-1, , , , , , , , , , , , , , , , , , , ,2094-1,2094-0, , , , , , , , , , , ,9583-1, , , , , , , , , , , , , , , , , ,0207 1, , , , , , , , , , , , , , , , , , , , , , Fordonsflöde residualdiagram Fordonsflöde Figur IV.X XLIII
115 Residualer Antal blockerande händelser Fordonsflöde Regressionskurva Fordonsflöde Number of blocking events Uppskattat Number of blocking events Figur IV.XI 25 GC-flöde residualdiagram GC-flöde Figur IV.XII XLIV
116 Antal blockerande händelser GC-flöde Regressionskurva GC-flöde Number of blocking events Uppskattat Number of blocking events Figur IV.XIII Regression 4 Tabell IV.V Koefficienter Standardfel t-kvot p-värde Konstant -30, , , ,05E-05 Fordonsflöde 0, , , ,33E-08 GC-flöde^2 0, , , ,15E-05 RESIDUALUTDATA Observation Uppskattat Antal blockerande händelser Residualer Standardiserade residual 1 47, ,744-1, , , , , , , , , , , , , , , , , ,6975-1, , , , , ,6233-1, , , ,64392 XLV
117 Residualer 11 15, , , , ,0483-2, , , , , , , , , , , , , , , , , ,8079 1, , , , , , , , , , , , , , , , , , , , , , Fordonsflöde residualdiagram Fordonsflöde Figur IV.XIV XLVI
118 Residualer Antal blcokerande händelser Fordonsflöde Regressionskurva Number of blocking events Uppskattat Number of blocking events Fordonsflöde Figur IV.XV GC-flöde^2 residualdiagram GC-flöde^2 Figur IV.XVI XLVII
119 Antal blockerande händelser GC-flöde^2 Regressionskurva Number of blocking events Uppskattat Number of blocking events GC-flöde^2 Figur IV.XVII Regression 5 Tabell IV.VI Koefficienter Standardfel t-kvot p-värde Konstant -101, , , ,21E-06 Fordonsflöde 0, , , ,58E-09 Ln(GC-flöde) 18, , , ,29E-05 Observation Uppskattat Antal blockerande händelser Residualer Standardiserade residual 1 50, ,4663-1, , , , , , , , , , , , , , , , , ,0072-1, , , , , , , , , , , , , , ,2902-1,41383 XLVIII
120 Residualer 13 7, , , , , , , , , , , , , ,278 0, , , , , , , , , , , , , , , , , , , , , , , , ,44394 Fordonsflöde residualdiagram Fordonsflöde Figur IV.XVIII XLIX
121 Residualer Antal blockerande händelser Fordonsflöde Regressionskurva Fordonsflöde Number of blocking events Uppskattat Number of blocking events Figur IV.XIX 30 ln(gc-flöde) residualdiagram ,000 1,000 2,000 3,000 4,000 5,000 6, ln(gc-flöde) Figur IV.XX L
122 Antal blockerande händelser ln(gc-flöde) Regressionskurva ,000 2,000 4,000 6, ln(gc-flöde) Number of blocking events Uppskattat Number of blocking events Figur IV.XXI LI
Analytiska trafikmodeller för cirkulationsplatser med gångoch cykeltrafik
 Analytiska trafikmodeller för cirkulationsplatser med gångoch cykeltrafik Examensarbete 2010 KTH Astrid Bergman, Trivector Traffic Bakgrund & syfte Litteraturstudie och val av modell Datainsamling och
Analytiska trafikmodeller för cirkulationsplatser med gångoch cykeltrafik Examensarbete 2010 KTH Astrid Bergman, Trivector Traffic Bakgrund & syfte Litteraturstudie och val av modell Datainsamling och
PM Trafikanalys Spekeröds handelsområde och verksamheter
 Konsult: ÅF Infrastructure AB Uppdragsansvarig: Åsa Nyqvist Beställare: Stenungsunds kommun Kontaktperson: Marcus Broman Interngranskare: Johan Hallberg Handläggare: Robin Hjalmarsson Datum: 2017-02-15
Konsult: ÅF Infrastructure AB Uppdragsansvarig: Åsa Nyqvist Beställare: Stenungsunds kommun Kontaktperson: Marcus Broman Interngranskare: Johan Hallberg Handläggare: Robin Hjalmarsson Datum: 2017-02-15
Förslag till utformning av cykelöverfart
 INFORMATIONSMATERIAL 2015-06-16 1 (6) Tillväxt och samhällsbyggnad Erik Levander Förslag till utformning av cykelöverfart Cykelöverfart innebär en prioritering av cykeltrafikens framkomlighet. Cykelöverfarten
INFORMATIONSMATERIAL 2015-06-16 1 (6) Tillväxt och samhällsbyggnad Erik Levander Förslag till utformning av cykelöverfart Cykelöverfart innebär en prioritering av cykeltrafikens framkomlighet. Cykelöverfarten
ICA Grytan, Västerås - Trafikanalys med hjälp av trafiksimulering i Vissim. Uppdragsnr: (11)
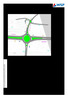 \\ser71sth1se.se.wspgroup.com\projects\7021\2013\10189249 - ICA Grytan, Västerås\5_Beräkningar\Vissim\Rapport\PM Trafikanalys ICA Grytan.docx Mall: Memo.dot ver 1.0 Uppdragsnr: 10189249 1 (11) PM ICA Grytan,
\\ser71sth1se.se.wspgroup.com\projects\7021\2013\10189249 - ICA Grytan, Västerås\5_Beräkningar\Vissim\Rapport\PM Trafikanalys ICA Grytan.docx Mall: Memo.dot ver 1.0 Uppdragsnr: 10189249 1 (11) PM ICA Grytan,
Granskning av trafikförslag utifrån kapacitet och utformning
 1 PM 2017:90 Matilda Segernäs 2017-11-06 Granskning av trafikförslag utifrån kapacitet och utformning Flaket 10, Ica Kvantum Åhus Innehåll 1. Inledning 2 2. Förutsättningar för beräkningar 4 2.1 Trafikmängd
1 PM 2017:90 Matilda Segernäs 2017-11-06 Granskning av trafikförslag utifrån kapacitet och utformning Flaket 10, Ica Kvantum Åhus Innehåll 1. Inledning 2 2. Förutsättningar för beräkningar 4 2.1 Trafikmängd
TÄBY SIMHALL. Kapacitetsanalys Stora Marknadsvägen. Rapport Upprättad av: Frida Aspnäs, Tobias Thorsson
 TÄBY SIMHALL Kapacitetsanalys Stora Marknadsvägen Rapport 2016-02-04 Upprättad av: Frida Aspnäs, Tobias Thorsson TÄBY SIMHALL Kapacitetsanalys Stora Marknadsvägen KUND Täby Kommun KONSULT WSP Analys &
TÄBY SIMHALL Kapacitetsanalys Stora Marknadsvägen Rapport 2016-02-04 Upprättad av: Frida Aspnäs, Tobias Thorsson TÄBY SIMHALL Kapacitetsanalys Stora Marknadsvägen KUND Täby Kommun KONSULT WSP Analys &
Korsningsutredning Färjestadsskolan Karlstads kommun
 Korsningsutredning Färjestadsskolan Karlstads kommun Korsningsutredning Färjestadsskolan Ramböll Malmö Beställare: Karlstads kommun (Emma Rönnbäck) Uppdragsnummer: 1320038706 Datum: 2018-11-01 Utgåva:
Korsningsutredning Färjestadsskolan Karlstads kommun Korsningsutredning Färjestadsskolan Ramböll Malmö Beställare: Karlstads kommun (Emma Rönnbäck) Uppdragsnummer: 1320038706 Datum: 2018-11-01 Utgåva:
PM TRAFIKUTREDNING TOMTEBOVÄGEN
 UPPDRAG Coop Tomtebo UPPDRAGSNUMMER 2433490000 UPPDRAGSLEDARE Krister Johansson, HIFAB UPPRÄTTAD AV Katarina Lindberg DATUM 10-05 Bakgrund och syfte Coop AB planerar att etablera en ny butik på en i dagsläget
UPPDRAG Coop Tomtebo UPPDRAGSNUMMER 2433490000 UPPDRAGSLEDARE Krister Johansson, HIFAB UPPRÄTTAD AV Katarina Lindberg DATUM 10-05 Bakgrund och syfte Coop AB planerar att etablera en ny butik på en i dagsläget
Uppsala kommun, plan- och byggnadsnämnden. Dnr PBN , VATTENFALLS FRAMTIDA ANGÖRING FRÅN STÅLGATAN. Trafikutredning
 VATTENFALLS FRAMTIDA ANGÖRING FRÅN STÅLGATAN Trafikutredning 2017-05-29 Uppsala kommun, plan- och byggnadsnämnden. Dnr PBN 2013-000404, 2017-05-29 VATTENFALLS FRAMTIDA ANGÖRING FRÅN STÅLGATAN Trafikutredning
VATTENFALLS FRAMTIDA ANGÖRING FRÅN STÅLGATAN Trafikutredning 2017-05-29 Uppsala kommun, plan- och byggnadsnämnden. Dnr PBN 2013-000404, 2017-05-29 VATTENFALLS FRAMTIDA ANGÖRING FRÅN STÅLGATAN Trafikutredning
ÅVS E4/E6/E20 Helsingborg
 Arbetsrapport ÅVS E4/E6/E20 Helsingborg Kapacitetsstudie trafikplats Vasatorp utblick 2030 Malmö 2015-09-25 ÅVS E4/E6/E20 Helsingborg Kapacitetsstudie trafikplats Vasatorp utblick 2030 Arbetsrapport Datum
Arbetsrapport ÅVS E4/E6/E20 Helsingborg Kapacitetsstudie trafikplats Vasatorp utblick 2030 Malmö 2015-09-25 ÅVS E4/E6/E20 Helsingborg Kapacitetsstudie trafikplats Vasatorp utblick 2030 Arbetsrapport Datum
Trafikanalys Vingpennan
 Datum: 2012-09-13 Beteckning: 1 (36) Trafikanalys Vingpennan Vectura/Transport och samhälle Niklas Alvaeus Box 1062, 551 10 Jönköping Utredare Besök: Järnvägsgatan 3 [email protected] Växel: 0771-159
Datum: 2012-09-13 Beteckning: 1 (36) Trafikanalys Vingpennan Vectura/Transport och samhälle Niklas Alvaeus Box 1062, 551 10 Jönköping Utredare Besök: Järnvägsgatan 3 [email protected] Växel: 0771-159
När du ska korsa en gata
 När du ska korsa en gata Information från Örebro kommun I den här broschyren finns exempel som beskriver hur du som går, cyklar eller kör ett fordon ska bete dig vid olika typer av korsningar enligt trafiklagstiftningen.
När du ska korsa en gata Information från Örebro kommun I den här broschyren finns exempel som beskriver hur du som går, cyklar eller kör ett fordon ska bete dig vid olika typer av korsningar enligt trafiklagstiftningen.
Trafikutredning Tosterö
 Svenska Hem Entreprenad Stockholm 2017-10-17 Datum 2017-10-17 Uppdragsnummer 1320022838 Utgåva/Status Version 1 Eva-Lena Nilsson Malin Lagervall Johan Wahlstedt Uppdragsledare Handläggare Granskare Ramböll
Svenska Hem Entreprenad Stockholm 2017-10-17 Datum 2017-10-17 Uppdragsnummer 1320022838 Utgåva/Status Version 1 Eva-Lena Nilsson Malin Lagervall Johan Wahlstedt Uppdragsledare Handläggare Granskare Ramböll
Området Vårvik med ny bro i Trollhättan Kompletterande simuleringar
 Området Vårvik med ny bro i Trollhättan Kompletterande simuleringar 2018-09-19 Under våren 2018 genomfördes en trafikanalys för Vårvik (fd Knorren) och Hjulkvarnelund i Trollhättan (Trafikanalyser Vårvik
Området Vårvik med ny bro i Trollhättan Kompletterande simuleringar 2018-09-19 Under våren 2018 genomfördes en trafikanalys för Vårvik (fd Knorren) och Hjulkvarnelund i Trollhättan (Trafikanalyser Vårvik
TRAFIK- OCH KAPACITETSANALYS AV STORGATAN I VÄXJÖ
 RAPPORT TRAFIK- OCH KAPACITETSANALYS AV STORGATAN I VÄXJÖ FÖRHANDSKOPIA 2017-08-18 UPPDRAG 278989, Korsningar Storgatan- Smedjegatan/Arabygatan Titel på rapport: Trafik- och kapacitetsanalys av Storgatan
RAPPORT TRAFIK- OCH KAPACITETSANALYS AV STORGATAN I VÄXJÖ FÖRHANDSKOPIA 2017-08-18 UPPDRAG 278989, Korsningar Storgatan- Smedjegatan/Arabygatan Titel på rapport: Trafik- och kapacitetsanalys av Storgatan
PM 2. Sickla Vägplan: Trafiksimuleringar Inledning
 Uppdragsnr: 10183321 1 (8) PM 2 Sickla Vägplan: Trafiksimuleringar 14-09-30 \\SER01COL1SE\Common Projects\5661\10183321\3_Dokument\36_PM_Rapport\Trafik\PM 2 - Sickla köpkvarter trafiksimuleringar_140921.docx
Uppdragsnr: 10183321 1 (8) PM 2 Sickla Vägplan: Trafiksimuleringar 14-09-30 \\SER01COL1SE\Common Projects\5661\10183321\3_Dokument\36_PM_Rapport\Trafik\PM 2 - Sickla köpkvarter trafiksimuleringar_140921.docx
Trafikutredning Tvetavägen
 Telge Inköp AB Version 1 Stockholm 2018-08-17 Datum 2018-08-17 Uppdragsnummer 1320035759 Utgåva/Status Version 1 Svante Nyberg Malin Lagervall Andreas Samuelsson Uppdragsledare Handläggare Granskare Ramböll
Telge Inköp AB Version 1 Stockholm 2018-08-17 Datum 2018-08-17 Uppdragsnummer 1320035759 Utgåva/Status Version 1 Svante Nyberg Malin Lagervall Andreas Samuelsson Uppdragsledare Handläggare Granskare Ramböll
SCENARIO VÄLSVIKEN. Karlstad trafikmodell
 SCENARIO VÄLSVIKEN Karlstad trafikmodell 2017-05-16 SCENARIO VÄLSVIKEN Karlstad trafikmodell KUND Karlstads Kommun KONSULT WSP Analys & Strategi 121 88 Stockholm-Globen Besök: Arenavägen 7 Tel: +46 10
SCENARIO VÄLSVIKEN Karlstad trafikmodell 2017-05-16 SCENARIO VÄLSVIKEN Karlstad trafikmodell KUND Karlstads Kommun KONSULT WSP Analys & Strategi 121 88 Stockholm-Globen Besök: Arenavägen 7 Tel: +46 10
VU 94S-2 7 Korsningar 109 (200) 7.7 Detaljutformning
 VU 94S-2 7 Korsningar 109 (200) 7.7.7 Korsningstyp D - cirkulationsplats I tidigare utredningar skall målsättningen för projektet vara fastlagt och val av korsningstyp ha gjorts enligt kapitel 7.5. Platsen
VU 94S-2 7 Korsningar 109 (200) 7.7.7 Korsningstyp D - cirkulationsplats I tidigare utredningar skall målsättningen för projektet vara fastlagt och val av korsningstyp ha gjorts enligt kapitel 7.5. Platsen
ATRIUM LJUNGBERG AB. Kapacitetsanalys Sickla industriväg-smedjegatan. Granskningsversion Stockholm
 ATRIUM LJUNGBERG AB Kapacitetsanalys Sickla industriväg-smedjegatan Granskningsversion 2016-10-11 Stockholm Kapacitetsanalys Sickla industriväg- Smedjegatan Datum 2016-10-11 Uppdragsnummer 1320023808 Utgåva/Status
ATRIUM LJUNGBERG AB Kapacitetsanalys Sickla industriväg-smedjegatan Granskningsversion 2016-10-11 Stockholm Kapacitetsanalys Sickla industriväg- Smedjegatan Datum 2016-10-11 Uppdragsnummer 1320023808 Utgåva/Status
TRAFIKUTREDNING SKUTBERGET
 KARLSTADS KOMMUN TRAFIKUTREDNING SKUTBERGET FÖRSTUDIE TRAFIKLÖSNING FÖR SKUTBERGETS ENTRÉ OCH TEMAPARK 2018-02-26 TRAFIKUTREDNING SKUTBERGET Förstudie trafiklösning för Skutbergets entré och temapark Karlstads
KARLSTADS KOMMUN TRAFIKUTREDNING SKUTBERGET FÖRSTUDIE TRAFIKLÖSNING FÖR SKUTBERGETS ENTRÉ OCH TEMAPARK 2018-02-26 TRAFIKUTREDNING SKUTBERGET Förstudie trafiklösning för Skutbergets entré och temapark Karlstads
Cykelöverfarter. Malmö stads arbete med cykelöverfarter och en policy för detta. Trafik och Gatudagarna 151019
 Cykelöverfarter Malmö stads arbete med cykelöverfarter och en policy för detta Trafik och Gatudagarna 151019 Bakgrund Nya trafikregler då cyklister korsar körbana - Gäller från 2014-09-01 då alla cykelöverfarter
Cykelöverfarter Malmö stads arbete med cykelöverfarter och en policy för detta Trafik och Gatudagarna 151019 Bakgrund Nya trafikregler då cyklister korsar körbana - Gäller från 2014-09-01 då alla cykelöverfarter
Kallebäck - Trafikanalys
 Uppdragsansvarig Johan Hallberg Handläggare Robin Hjalmarsson Mottagare Trafikkontoret, Göteborgs stad Joachim Karlgren Datum 2017-07-07 Projekt-ID 735243 Kallebäck - Trafikanalys 1 Bakgrund Kallebäcksmotet
Uppdragsansvarig Johan Hallberg Handläggare Robin Hjalmarsson Mottagare Trafikkontoret, Göteborgs stad Joachim Karlgren Datum 2017-07-07 Projekt-ID 735243 Kallebäck - Trafikanalys 1 Bakgrund Kallebäcksmotet
RAPPORT. Trafikutredning för handelsetablering på Algutsrum 20:10 MÖRBYLÅNGA KOMMUN STOCKHOLM TRAFIKPLANERING UPPDRAGSNUMMER 7000175000 1.
 repo001.docx 2012-03-2914 MÖRBYLÅNGA KOMMUN Trafikutredning för handelsetablering på Algutsrum 20:10 UPPDRAGSNUMMER 7000175000 STOCKHOLM TRAFIKPLANERING JOHANNA FICK UPPDRAGSLEDARE KARIN RENSTRÖM GRANSKARE
repo001.docx 2012-03-2914 MÖRBYLÅNGA KOMMUN Trafikutredning för handelsetablering på Algutsrum 20:10 UPPDRAGSNUMMER 7000175000 STOCKHOLM TRAFIKPLANERING JOHANNA FICK UPPDRAGSLEDARE KARIN RENSTRÖM GRANSKARE
PM Kapacitetsanalys Dergårdsområdet, Lerums kommun
 Handläggare Cecilia Norberg Tel +46 10 505 31 38 Mobil +46 73 066 92 80 E-post [email protected] Mottagare Lerums kommun Jakob Aldén Datum 2017-01-27 Projekt-ID 723019 PM Kapacitetsanalys Dergårdsområdet,
Handläggare Cecilia Norberg Tel +46 10 505 31 38 Mobil +46 73 066 92 80 E-post [email protected] Mottagare Lerums kommun Jakob Aldén Datum 2017-01-27 Projekt-ID 723019 PM Kapacitetsanalys Dergårdsområdet,
Analys av trafiken i Oskarshamn vid ankomst Gotlandsfärja
 1 (11) PM Analys av trafiken i Oskarshamn vid ankomst Gotlandsfärja Ansvarig mikrosimulering/trafikanalys: Handläggare mikrosimulering: Författare detta PM: Granskning detta PM: Sebastian Hasselblom Felicia
1 (11) PM Analys av trafiken i Oskarshamn vid ankomst Gotlandsfärja Ansvarig mikrosimulering/trafikanalys: Handläggare mikrosimulering: Författare detta PM: Granskning detta PM: Sebastian Hasselblom Felicia
18.13 KORSNINGAR. VU 94S-2 18 Mötesfri landsväg och motortrafikled 37 (59) 18.13 Korsningar
 VU 94S-2 18 Mötesfri landsväg och motortrafikled 37 (59) 18.13 KORSNINGAR Korsningar bör placeras i övergångssträckor. Plankorsningar bör normalt utformas som typ C eventuellt med förskjutning eller som
VU 94S-2 18 Mötesfri landsväg och motortrafikled 37 (59) 18.13 KORSNINGAR Korsningar bör placeras i övergångssträckor. Plankorsningar bör normalt utformas som typ C eventuellt med förskjutning eller som
Trafikering
 Huddinge kommun planerar för en utbyggnad av Gräsvretens industriområde och en ny in-och utfart till området. Kommunen behöver stöd med att bedöma trafikmängder till och från det planerade området, få
Huddinge kommun planerar för en utbyggnad av Gräsvretens industriområde och en ny in-och utfart till området. Kommunen behöver stöd med att bedöma trafikmängder till och från det planerade området, få
Stöd till planarbete och projektering - Brevikshalvön. 1 Bakgrund. Uppdragsnr: (9)
 Uppdragsnr: 10235378 1 (9) PM Stöd till planarbete och projektering - Brevikshalvön 1 Bakgrund Kommunen vill bygga en cykelbana utmed Nytorpsvägens södra sida. I dag är gång och cykeltrafiken hänvisad
Uppdragsnr: 10235378 1 (9) PM Stöd till planarbete och projektering - Brevikshalvön 1 Bakgrund Kommunen vill bygga en cykelbana utmed Nytorpsvägens södra sida. I dag är gång och cykeltrafiken hänvisad
13 Stigningsfält och omkörningsfält
 13 Stigningsfält och omkörningsfält Med stigningsfält avses extra körfält i backar, placerat till vänster om ordinarie körfält i stigningens riktning. Med omkörningsfält avses extra körfält på begränsad
13 Stigningsfält och omkörningsfält Med stigningsfält avses extra körfält i backar, placerat till vänster om ordinarie körfält i stigningens riktning. Med omkörningsfält avses extra körfält på begränsad
Väg 222, tpl Kvarnholmen
 PM Trafik Väg 222, tpl Kvarnholmen Nacka kommun, Stockholms län 2014-10-31 Projektnummer: 107350 Dokumenttitel: PM Trafik, Väg 222, tpl Kvarnholmen, Nacka kommun, Stockholms län Skapat av: M Young Dokumentdatum:
PM Trafik Väg 222, tpl Kvarnholmen Nacka kommun, Stockholms län 2014-10-31 Projektnummer: 107350 Dokumenttitel: PM Trafik, Väg 222, tpl Kvarnholmen, Nacka kommun, Stockholms län Skapat av: M Young Dokumentdatum:
FÖRDJUPADE TRAFIKSTUDIER FÖR NY ETABLERING INOM SOLBACKEN 1:3, YSTAD KOMMUN
 FÖRDJUPADE TRAFIKSTUDIER FÖR NY ETABLERING INOM SOLBACKEN 1:3, YSTAD KOMMUN Rapport Ramböll Trafik och Samhällsplanering Helsingborg 2 FÖRDJUPADE TRAFIKSTUDIER FÖR NY ETABLERING INOM SOLBACKEN 1:3, YSTAD
FÖRDJUPADE TRAFIKSTUDIER FÖR NY ETABLERING INOM SOLBACKEN 1:3, YSTAD KOMMUN Rapport Ramböll Trafik och Samhällsplanering Helsingborg 2 FÖRDJUPADE TRAFIKSTUDIER FÖR NY ETABLERING INOM SOLBACKEN 1:3, YSTAD
Utvärdering av Capcals förmåga att beräkna framkomlighet
 Examensarbete LITH-ITN-KTS-EX--05/035--SE Utvärdering av Capcals förmåga att beräkna framkomlighet Anna Aronsson Anneli Bellinger 2005-05-23 Department of Science and Technology Linköpings Universitet
Examensarbete LITH-ITN-KTS-EX--05/035--SE Utvärdering av Capcals förmåga att beräkna framkomlighet Anna Aronsson Anneli Bellinger 2005-05-23 Department of Science and Technology Linköpings Universitet
TRAFIKUTREDNING BJÖRKLUNDA I HÄSSLEHOLM
 RAPPORT TRAFIKUTREDNING BJÖRKLUNDA I HÄSSLEHOLM SLUTRAPPORT 2017-07-07 UPPDRAG 277661, Björklunda trafikutredning Titel på rapport: Trafikutredning Björklunda i Hässleholm Status: Datum: 2017-07-07 MEDVERKANDE
RAPPORT TRAFIKUTREDNING BJÖRKLUNDA I HÄSSLEHOLM SLUTRAPPORT 2017-07-07 UPPDRAG 277661, Björklunda trafikutredning Titel på rapport: Trafikutredning Björklunda i Hässleholm Status: Datum: 2017-07-07 MEDVERKANDE
Kapacitetsutredning korsningen Ångbåtsvägen/Bryggavägen Ekerö kommun
 Kapacitetsutredning korsningen Ångbåtsvägen/Bryggavägen Beställare: Box 205 178 23 Ekerö Beställarens representant: Emelie Greiff Konsult: Uppdragsledare Handläggare Norconsult AB Karl Grankvists väg 1A
Kapacitetsutredning korsningen Ångbåtsvägen/Bryggavägen Beställare: Box 205 178 23 Ekerö Beställarens representant: Emelie Greiff Konsult: Uppdragsledare Handläggare Norconsult AB Karl Grankvists väg 1A
Kapacitetsstudie kring Uppsala resecentrum - Mikrosimulering
 STADSBYGGNADSFÖRVALTNINGEN KSN-2014-132 Underlag till arbetet med Översiktsplan för Uppsala kommun 2014-09-11 UNDERLAGSRAPPORT: Kapacitetsstudie kring Uppsala resecentrum - Mikrosimulering RAPPORTFÖRFATTARE
STADSBYGGNADSFÖRVALTNINGEN KSN-2014-132 Underlag till arbetet med Översiktsplan för Uppsala kommun 2014-09-11 UNDERLAGSRAPPORT: Kapacitetsstudie kring Uppsala resecentrum - Mikrosimulering RAPPORTFÖRFATTARE
TRAFIKMODELL ÖSTERSUND
 UPPDRAGSNUMMER: 7001358 TRAFIKMODELL ÖSTERSUND KAPACITETSUTREDNING FÖR NYEXPLOATERING VID LILLÄNGE HANDELSOMRÅDE SWECO SOCIETY JOACIM THELIN SARA JOHANSSON repo002.docx 2013-06-14 Sweco 1 Inledning Bakgrund
UPPDRAGSNUMMER: 7001358 TRAFIKMODELL ÖSTERSUND KAPACITETSUTREDNING FÖR NYEXPLOATERING VID LILLÄNGE HANDELSOMRÅDE SWECO SOCIETY JOACIM THELIN SARA JOHANSSON repo002.docx 2013-06-14 Sweco 1 Inledning Bakgrund
Exempel på fysiska åtgärder. Bilaga 1
 Dnr Sida 1 (5) 2016-09-16 Handläggare Lotten Svedberg 08-508 262 15 Exempel på fysiska åtgärder. Bilaga 1 Kontoret föreslår att arbeta med ett antal typåtgärder längs sträckorna för att få bättre hastighetsefterlevnad
Dnr Sida 1 (5) 2016-09-16 Handläggare Lotten Svedberg 08-508 262 15 Exempel på fysiska åtgärder. Bilaga 1 Kontoret föreslår att arbeta med ett antal typåtgärder längs sträckorna för att få bättre hastighetsefterlevnad
PM: Trafikanalys Skra Bro
 2016-04-28 Lina Svensson PM: Trafikanalys Skra Bro Med anledning av framtida exploateringar i området vid Skra Bro har en trafikanalys gjorts internt på Trafikkontoret för att säkerställa kapaciteten på
2016-04-28 Lina Svensson PM: Trafikanalys Skra Bro Med anledning av framtida exploateringar i området vid Skra Bro har en trafikanalys gjorts internt på Trafikkontoret för att säkerställa kapaciteten på
Cirkulationsplatser Förslag till modell för beräkning av framkomlighet
 Bulletin 200 Cirkulationsplatser Förslag till modell för beräkning av framkomlighet Ola Hagring 2001 Lunds Tekniska Högskola Institutionen för Teknik och samhälle Avdelning Trafikteknik CODEN:LUTVDG/(TVTT-3169)1-37/2001
Bulletin 200 Cirkulationsplatser Förslag till modell för beräkning av framkomlighet Ola Hagring 2001 Lunds Tekniska Högskola Institutionen för Teknik och samhälle Avdelning Trafikteknik CODEN:LUTVDG/(TVTT-3169)1-37/2001
PM TRAFIKUTREDNING TOMTEBOVÄGEN
 UPPDRAG Coop Tomtebo UPPDRAGSNUMMER 2433490000 UPPDRAGSLEDARE Krister Johansson, HIFAB UPPRÄTTAD AV Katarina Lindberg, Eva Maaherra Lövheim DATUM 2016-05-09 Bakgrund och syfte Coop AB planerar att etablera
UPPDRAG Coop Tomtebo UPPDRAGSNUMMER 2433490000 UPPDRAGSLEDARE Krister Johansson, HIFAB UPPRÄTTAD AV Katarina Lindberg, Eva Maaherra Lövheim DATUM 2016-05-09 Bakgrund och syfte Coop AB planerar att etablera
Trafikanalys Nacka Strand
 UPPDRAG Nacka Strand UPPDRAGSNUMMER 435762 UPPDRAGSLEDARE Emma Wiklund UPPRÄTTAD AV Tan Na Cheng DATUM 23-8-9 Trafikanalys Nacka Strand Inledning Denna behandlar trafikanalysen gjord med Capcal för förmiddagens
UPPDRAG Nacka Strand UPPDRAGSNUMMER 435762 UPPDRAGSLEDARE Emma Wiklund UPPRÄTTAD AV Tan Na Cheng DATUM 23-8-9 Trafikanalys Nacka Strand Inledning Denna behandlar trafikanalysen gjord med Capcal för förmiddagens
Trafikanalys av Leråkersmotet
 Uppdragsledare Johan Hallberg Handläggare Robin Hjalmarsson Mottagare Göteborgs stad Trafikkontoret Anna Fant E-post [email protected] Datum 2017-12-19 Projekt ID 742436 Trafikanalys av Leråkersmotet
Uppdragsledare Johan Hallberg Handläggare Robin Hjalmarsson Mottagare Göteborgs stad Trafikkontoret Anna Fant E-post [email protected] Datum 2017-12-19 Projekt ID 742436 Trafikanalys av Leråkersmotet
Nya Öjersjövägen. Trafikutredning. Partille kommun
 Trafikutredning Nya Öjersjövägen Partille kommun ÅF-Infrastructure AB, Grafiska vägen 2, Box 1551, SE-40151 Göteborg Sverige Telefon +46 10 505 00 00, Säte i Stockholm, www.afconsult.com Org.nr 556185-2103,
Trafikutredning Nya Öjersjövägen Partille kommun ÅF-Infrastructure AB, Grafiska vägen 2, Box 1551, SE-40151 Göteborg Sverige Telefon +46 10 505 00 00, Säte i Stockholm, www.afconsult.com Org.nr 556185-2103,
Trafikutredning Kv. Cirkusängen - Sundbyberg
 1 (9) Trafikutredning Med anledning av uppförandet av ett nytt huvudkontor för Swedbank på kvarteret Cirkusängen i Sundbyberg syftar denna trafikutredning till att belysa befintlig och framtida trafiksituation.
1 (9) Trafikutredning Med anledning av uppförandet av ett nytt huvudkontor för Swedbank på kvarteret Cirkusängen i Sundbyberg syftar denna trafikutredning till att belysa befintlig och framtida trafiksituation.
TRAFIKMODELL ÖSTERSUND
 UPPDRAGSNUMMER: 7000177 TRAFIKMODELL ÖSTERSUND KAPACITETSUTREDNING FÖR NYEXPLOATERING VID LILLÄNGE HANDELSOMRÅDE SWECO TRANSPORTSYSTEM SARA JOHANSSON Sweco Ändringsförteckning Version Datum Förändring
UPPDRAGSNUMMER: 7000177 TRAFIKMODELL ÖSTERSUND KAPACITETSUTREDNING FÖR NYEXPLOATERING VID LILLÄNGE HANDELSOMRÅDE SWECO TRANSPORTSYSTEM SARA JOHANSSON Sweco Ändringsförteckning Version Datum Förändring
Trafikutredning TCR Oskarshamn
 2014-02-17, sid 1(12) Trafikutredning TCR Oskarshamn 2014-02-17, sid 2(12) Beställare Kristian Wendelboe Wendelboe West Properties Uppdragsledare/Trafikplanerare Trafikplanerare Patrik Lundqvist Karin
2014-02-17, sid 1(12) Trafikutredning TCR Oskarshamn 2014-02-17, sid 2(12) Beställare Kristian Wendelboe Wendelboe West Properties Uppdragsledare/Trafikplanerare Trafikplanerare Patrik Lundqvist Karin
Trafikanalys av Backavägen med mikrosimulering
 1 (10) PM Trafikanalys av Backavägen med mikrosimulering Ansvarig mikrosimulering: Författare detta PM: Granskning mikrosimulering: Granskning detta PM: Sebastian Hasselblom Sebastian Hasselblom Sandra
1 (10) PM Trafikanalys av Backavägen med mikrosimulering Ansvarig mikrosimulering: Författare detta PM: Granskning mikrosimulering: Granskning detta PM: Sebastian Hasselblom Sebastian Hasselblom Sandra
RAPPORT. Simulering av variabel hastighet i korsning
 RAPPORT Simulering av variabel hastighet i korsning Dokumenttitel: Simulering av variabel hastighet i korsning Skapat av: Johnny Alf Dokumentdatum: 2011-03-08 Dokumenttyp: Rapport DokumentID: Ärendenummer:
RAPPORT Simulering av variabel hastighet i korsning Dokumenttitel: Simulering av variabel hastighet i korsning Skapat av: Johnny Alf Dokumentdatum: 2011-03-08 Dokumenttyp: Rapport DokumentID: Ärendenummer:
TRAFIKUTREDNING HAMNEN, YSTAD
 PM TRAFIKUTREDNING HAMNEN, YSTAD SLUTVERSION 2017-09-22 Tyréns AB 205 19 Malmö Besök: Isbergs gata 15 Tel:010 452 20 00 www.tyrens.se Säte: Stockholm Org.nr: 556194-7986 2(19) INNEHÅLLSFÖRTECKNING INLEDNING...
PM TRAFIKUTREDNING HAMNEN, YSTAD SLUTVERSION 2017-09-22 Tyréns AB 205 19 Malmö Besök: Isbergs gata 15 Tel:010 452 20 00 www.tyrens.se Säte: Stockholm Org.nr: 556194-7986 2(19) INNEHÅLLSFÖRTECKNING INLEDNING...
Trafik-PM till detaljplaner i Dingelsundet
 Sid 1(13) TEKNIK- OCH FASTIGHETSFÖRVALTNINGEN Rapport, daterad 2017-06-16 Karl Borgstrand [email protected] Trafik-PM till detaljplaner i Dingelsundet Karlstads kommun Webbplats karlstad.se E-post
Sid 1(13) TEKNIK- OCH FASTIGHETSFÖRVALTNINGEN Rapport, daterad 2017-06-16 Karl Borgstrand [email protected] Trafik-PM till detaljplaner i Dingelsundet Karlstads kommun Webbplats karlstad.se E-post
TRAFIKALSTRING BRILLINGE ÅVC
 RAPPORT TRAFIKALSTRING BRILLINGE ÅVC RAPPORT 2016-12-16 Uppsala kommun, plan- och byggnadsnämnden. Dnr PBN 2015-000522, 2016-12-16 UPPDRAG 272040, Kretsloppsparken Brillinge ÅVC Titel på rapport: Trafikalstring
RAPPORT TRAFIKALSTRING BRILLINGE ÅVC RAPPORT 2016-12-16 Uppsala kommun, plan- och byggnadsnämnden. Dnr PBN 2015-000522, 2016-12-16 UPPDRAG 272040, Kretsloppsparken Brillinge ÅVC Titel på rapport: Trafikalstring
Sammanställning av trafikförutsättningar för detaljplan Ubbarp 8:20 och Vist 10:25 mfl, Ulricehamns kommun
 ULRICEHAMNS KOMMUN Sammanställning av trafikförutsättningar för detaljplan Ubbarp 8:20 och Vist 10:25 mfl, Ulricehamns kommun ADRESS COWI AB Skärgårdsgatan 1 Box 12076 402 41 Göteborg TEL 010 850 10 00
ULRICEHAMNS KOMMUN Sammanställning av trafikförutsättningar för detaljplan Ubbarp 8:20 och Vist 10:25 mfl, Ulricehamns kommun ADRESS COWI AB Skärgårdsgatan 1 Box 12076 402 41 Göteborg TEL 010 850 10 00
Beteenden, trafiksäkerhet och effektutvärdering 3D & AI för mätning och uppföljning
 Beteenden, trafiksäkerhet och effektutvärdering 3D & AI för mätning och uppföljning Smarter Traffic Solutions for a Safer Future Amritpal Singh, VD Viscando Traffic Systems AB www.viscando.com +46 31 7570
Beteenden, trafiksäkerhet och effektutvärdering 3D & AI för mätning och uppföljning Smarter Traffic Solutions for a Safer Future Amritpal Singh, VD Viscando Traffic Systems AB www.viscando.com +46 31 7570
Trafiklots förbi vägarbete. Verktyg för att ta fram förlängd restid och kötid för vägarbeten med olika längd och trafikmängd
 Trafiklots förbi vägarbete Verktyg för att ta fram förlängd restid och kötid för vägarbeten med olika längd och trafikmängd Titel: Trafiklots förbi vägarbete - Verktyg för att ta fram förlängd restid och
Trafiklots förbi vägarbete Verktyg för att ta fram förlängd restid och kötid för vägarbeten med olika längd och trafikmängd Titel: Trafiklots förbi vägarbete - Verktyg för att ta fram förlängd restid och
Trafikutredning Måby Hotell
 Peab Fastighetsutveckling Sverige AB Stockholm 2018-08-10 Datum 2018-08-10 Uppdragsnummer 1320035340 Utgåva/Status 1.0 Svante Nyberg Svante Nyberg Andreas Samuelsson Anna-Karin Ekman Uppdragsledare Handläggare
Peab Fastighetsutveckling Sverige AB Stockholm 2018-08-10 Datum 2018-08-10 Uppdragsnummer 1320035340 Utgåva/Status 1.0 Svante Nyberg Svante Nyberg Andreas Samuelsson Anna-Karin Ekman Uppdragsledare Handläggare
Bedömningen av trafiksäkerheten i korsningen är baserad på olycksstatistikanalysen och konfliktstudien.
 Bilaga 2. Analys från konflikt- och observationsstudierna Trafiksäkerhet Bedömningen av trafiksäkerheten i korsningen är baserad på olycksstatistikanalysen och konfliktstudien. Olycksstatistik Trafiksäkerhetshöjande
Bilaga 2. Analys från konflikt- och observationsstudierna Trafiksäkerhet Bedömningen av trafiksäkerheten i korsningen är baserad på olycksstatistikanalysen och konfliktstudien. Olycksstatistik Trafiksäkerhetshöjande
PM Trafikutredning Snurrom verksamheter
 PM Trafikutredning Snurrom verksamheter Bakgrund och syfte Planering pågår för nya verksamheter i anslutning till Norra vägen och E22 i norra delen av staden. Trafikutredningen ska undersöka hur området
PM Trafikutredning Snurrom verksamheter Bakgrund och syfte Planering pågår för nya verksamheter i anslutning till Norra vägen och E22 i norra delen av staden. Trafikutredningen ska undersöka hur området
Kapacitetsanalys Skeppsrondellen, Håbo
 Handläggare Amer Aslam Tel +46 (0)10 505 14 03 Mobil +46 (0)72 249 90 29 E-mail [email protected] Datum 2015-10-15 Uppdragsnr 708847 Förprojektering VA och gator inom planområde Väppeby 7:18 m.fl.
Handläggare Amer Aslam Tel +46 (0)10 505 14 03 Mobil +46 (0)72 249 90 29 E-mail [email protected] Datum 2015-10-15 Uppdragsnr 708847 Förprojektering VA och gator inom planområde Väppeby 7:18 m.fl.
Tillgänglighet för personer med synskada i cirkulationsplatser jämfört med andra korsningstyper sammanfattning av enkätstudie
 Bulletin 243 Tillgänglighet för personer med synskada i cirkulationsplatser jämfört med andra korsningstyper sammanfattning av enkätstudie Lisa Sakshaug Christer Hydén Åse Svensson 2009 1 Lunds Tekniska
Bulletin 243 Tillgänglighet för personer med synskada i cirkulationsplatser jämfört med andra korsningstyper sammanfattning av enkätstudie Lisa Sakshaug Christer Hydén Åse Svensson 2009 1 Lunds Tekniska
PM NORRA STÄKSÖN TRAFIK
 PM NORRA STÄKSÖN TRAFIK KONCEPT 2014-08-25 1 Bakgrund Planering för ny etablering på norra delen av Stäksön pågår. Som ett led i arbetet studeras förutsättningarna för trafiken i området. För att etableringen
PM NORRA STÄKSÖN TRAFIK KONCEPT 2014-08-25 1 Bakgrund Planering för ny etablering på norra delen av Stäksön pågår. Som ett led i arbetet studeras förutsättningarna för trafiken i området. För att etableringen
7 Anvisningsmärken. 7.1 Allmänt. 7.2 Kommentarer till vissa anvisningsmärken
 7 Anvisningsmärken 7.1 Allmänt Anvisningsmärken är, som namnet antyder, märken som ger anvisningar till trafikanterna. Anvisningar som ges med anvisningsmärken har oftast en direkt eller indirekt tvingande
7 Anvisningsmärken 7.1 Allmänt Anvisningsmärken är, som namnet antyder, märken som ger anvisningar till trafikanterna. Anvisningar som ges med anvisningsmärken har oftast en direkt eller indirekt tvingande
TRAFIKANALYS FANFAREN
 KARLSTADS KOMMUN TRAFIKANALYS FANFAREN KARLSTAD 2017-06-22 TRAFIKANALYS FANFAREN Karlstad Karlstads Kommun KONSULT WSP Analys & Strategi 121 88 Stockholm-Globen Besök: Arenavägen 7 Tel: +46 10 7225000
KARLSTADS KOMMUN TRAFIKANALYS FANFAREN KARLSTAD 2017-06-22 TRAFIKANALYS FANFAREN Karlstad Karlstads Kommun KONSULT WSP Analys & Strategi 121 88 Stockholm-Globen Besök: Arenavägen 7 Tel: +46 10 7225000
Notera att illustrationerna i denna broschyr är förenklade.
 Cykelöverfarter Informationen i denna broschyr baseras på Trafikförordningen (1998:1276) Vägmärkesförordningen (2007:90) Lag om vägtrafikdefinitioner (2001:559) Förordning om vägtrafikdefinitioner (2001:651).
Cykelöverfarter Informationen i denna broschyr baseras på Trafikförordningen (1998:1276) Vägmärkesförordningen (2007:90) Lag om vägtrafikdefinitioner (2001:559) Förordning om vägtrafikdefinitioner (2001:651).
Cykelpassager och cykelöverfarter
 Cykelpassager och cykelöverfarter 1 Vem är fordonsförare? Fordonsförare är den som för ett fordon, dvs. en anordning på hjul, band eller medar. Bestämmelser om fordonsförare gäller även för den som rider
Cykelpassager och cykelöverfarter 1 Vem är fordonsförare? Fordonsförare är den som för ett fordon, dvs. en anordning på hjul, band eller medar. Bestämmelser om fordonsförare gäller även för den som rider
Trafikanalys av Dragonvägen - Odensalavägen, Märsta
 SIGTUNA KOMMUN Trafikanalys av Dragonvägen - Odensalavägen, Märsta 2012-12-13 Uppsala Trafikanalys av Dragonvägen - Odensalavägen, Märsta Datum 2012-12-13 Uppdragsnummer 61381254612 Utgåva/Status Version
SIGTUNA KOMMUN Trafikanalys av Dragonvägen - Odensalavägen, Märsta 2012-12-13 Uppsala Trafikanalys av Dragonvägen - Odensalavägen, Märsta Datum 2012-12-13 Uppdragsnummer 61381254612 Utgåva/Status Version
PM Trafik Långflon 2 avseende detaljplan för del av Aspberget 1:127, 1:128 och 1:234
 Bilaga 3 PM Trafik Author Gustav Silverin Phone +46 10 505 54 71 E-mail [email protected] Date 2015-02-20 Project ID 704807 Client KLARA arkitektbyrå ab PM Trafik Långflon 2 avseende detaljplan
Bilaga 3 PM Trafik Author Gustav Silverin Phone +46 10 505 54 71 E-mail [email protected] Date 2015-02-20 Project ID 704807 Client KLARA arkitektbyrå ab PM Trafik Långflon 2 avseende detaljplan
Hastighetsdämpande åtgärder vid Bergsgatan/Almbacksgatan samt Bergsgatan/Monbijougatan TN
 Malmö stad Fastighets- och gatukontoret 1 (7) 2019-04-15 Tjänsteskrivelse Vår referens Marie Lindeberg Sekreterare [email protected] Hastighetsdämpande åtgärder vid Bergsgatan/Almbacksgatan samt
Malmö stad Fastighets- och gatukontoret 1 (7) 2019-04-15 Tjänsteskrivelse Vår referens Marie Lindeberg Sekreterare [email protected] Hastighetsdämpande åtgärder vid Bergsgatan/Almbacksgatan samt
Väg 44, förbifart Lidköping, delen Lidköping-Källby
 Väg 44, förbifart Lidköping, delen Lidköping-Källby Lidköping och Götene kommuner, Västra Götalands län Projektnummer: 101598 PM Trafikanalys 2013-03-15 Titel: Väg 44 förbifart Lidköping, delen Lidköping-Källby,
Väg 44, förbifart Lidköping, delen Lidköping-Källby Lidköping och Götene kommuner, Västra Götalands län Projektnummer: 101598 PM Trafikanalys 2013-03-15 Titel: Väg 44 förbifart Lidköping, delen Lidköping-Källby,
Cirkulationsplats i Bollebygd
 1 PM 2013:45 Joachim Karlgren Björn Sax Kaijser 2014-01-13 Cirkulationsplats i Bollebygd Förslag på utformning av ny tillfart Åldermansgatan 13 SE-227 64 Lund / Sweden Telefon +46 (0)10-456 56 Fax + 46
1 PM 2013:45 Joachim Karlgren Björn Sax Kaijser 2014-01-13 Cirkulationsplats i Bollebygd Förslag på utformning av ny tillfart Åldermansgatan 13 SE-227 64 Lund / Sweden Telefon +46 (0)10-456 56 Fax + 46
Trafikanalys TA-plan Fisksätra trafikplats
 UPPDRAG Analys TA-plan Fisksätra tpl UPPDRAGSNUMMER 7001219000 UPPDRAGSLEDARE Joacim Thelin UPPRÄTTAD AV Joacim Thelin DATUM Trafikanalys TA-plan Fisksätra trafikplats Sweco har fått i uppdrag av Nacka
UPPDRAG Analys TA-plan Fisksätra tpl UPPDRAGSNUMMER 7001219000 UPPDRAGSLEDARE Joacim Thelin UPPRÄTTAD AV Joacim Thelin DATUM Trafikanalys TA-plan Fisksätra trafikplats Sweco har fått i uppdrag av Nacka
Trafikutredning Gubbängsfältet
 Trafikutredning Gubbängsfältet 2013-12-05 Magnus Lind WSP Samhällsbyggnad Uppdragsnr: 10190219 2 (14) Innehållsförteckning 1 Bakgrund... 3 2 Problemformulering... 4 2.1 Alternativa matningar till området...
Trafikutredning Gubbängsfältet 2013-12-05 Magnus Lind WSP Samhällsbyggnad Uppdragsnr: 10190219 2 (14) Innehållsförteckning 1 Bakgrund... 3 2 Problemformulering... 4 2.1 Alternativa matningar till området...
RAPPORT. Trafikanalys Uddevallavägen/Kongahällagatan/Trollhättevägen KUNGÄLVS KOMMUN UPPDRAGSNUMMER SWECO SOCIETY AB
 KUNGÄLVS KOMMUN Trafikanalys Uddevallavägen/Kongahällagatan/Trollhättevägen UPPDRAGSNUMMER 12601187 SWECO SOCIETY AB ROYA ELYASI - POUR IBIS FELIU NIVA MARCUS TORSTENFELT Rapporten är framtagen av Sweco
KUNGÄLVS KOMMUN Trafikanalys Uddevallavägen/Kongahällagatan/Trollhättevägen UPPDRAGSNUMMER 12601187 SWECO SOCIETY AB ROYA ELYASI - POUR IBIS FELIU NIVA MARCUS TORSTENFELT Rapporten är framtagen av Sweco
Trafikutredning Storvreta
 Trafikutredning Storvreta 2008.05.22 Resultat från trafikanalyser Projektorganisation Uppsala kommun Projektledare Pernilla Hessling, Stadsbyggnadskontoret Uppdragsansvarig Handläggare Trafiksimulering
Trafikutredning Storvreta 2008.05.22 Resultat från trafikanalyser Projektorganisation Uppsala kommun Projektledare Pernilla Hessling, Stadsbyggnadskontoret Uppdragsansvarig Handläggare Trafiksimulering
Svensk författningssamling
 Svensk författningssamling Förordning om ändring i trafikförordningen (1998:1276); SFS 2014:1035 Utkom från trycket den 29 juli 2014 utfärdad den 17 juli 2014. Regeringen föreskriver i fråga om trafikförordningen
Svensk författningssamling Förordning om ändring i trafikförordningen (1998:1276); SFS 2014:1035 Utkom från trycket den 29 juli 2014 utfärdad den 17 juli 2014. Regeringen föreskriver i fråga om trafikförordningen
PM Trafik. 1. Förutsättningar. Trafikutredning detaljplan ETERN 3, Umeå
 Trafik Datum 2014-06-04 Uppdrag Planförfattare Från Till nummer Trafikutredning detaljplan ETERN 3, Umeå Planavdelningen Umeå kommun Mats Burström, Gustav Edvinsson, Ramböll Sv AB Anders Dieter Aubry,
Trafik Datum 2014-06-04 Uppdrag Planförfattare Från Till nummer Trafikutredning detaljplan ETERN 3, Umeå Planavdelningen Umeå kommun Mats Burström, Gustav Edvinsson, Ramböll Sv AB Anders Dieter Aubry,
MILJÖBILDER. Nr 3 oktober 2015, Årgång 16. Förvirring och rättsosäkerhet i trafiken råder när det gäller:
 1(10) MILJÖBILDER Nr 3 oktober 2015, Årgång 16 Förvirring och rättsosäkerhet i trafiken råder när det gäller: o Att köra i cirkulationsplatser o Cykelpassager och cykelöverfarter o Omkörning på väg o Utfart
1(10) MILJÖBILDER Nr 3 oktober 2015, Årgång 16 Förvirring och rättsosäkerhet i trafiken råder när det gäller: o Att köra i cirkulationsplatser o Cykelpassager och cykelöverfarter o Omkörning på väg o Utfart
Riktlinjer för passager i Västerås
 nternati i Västerås Beslutad av Tekniska nämnden 20 maj 2008 program policy handlingsplan riktlinje program policy handlingsplan riktlinje uttrycker värdegrunder och förhållningssätt för arbetet med utvecklingen
nternati i Västerås Beslutad av Tekniska nämnden 20 maj 2008 program policy handlingsplan riktlinje program policy handlingsplan riktlinje uttrycker värdegrunder och förhållningssätt för arbetet med utvecklingen
TRAFIKUTREDNING NYTT VERKSAMHETSOMRÅDE I ROSERSBERG
 TRAFIKUTREDNING NYTT VERKSAMHETSOMRÅDE I ROSERSBERG 2012-10- INNEHÅLL Bakgrund och Syfte 3 Förutsättningar 3 Effekter av planerat verksamhetsområde 3 Framkomlighet 3 Alternativ 1 - anslutning till Skansvägen
TRAFIKUTREDNING NYTT VERKSAMHETSOMRÅDE I ROSERSBERG 2012-10- INNEHÅLL Bakgrund och Syfte 3 Förutsättningar 3 Effekter av planerat verksamhetsområde 3 Framkomlighet 3 Alternativ 1 - anslutning till Skansvägen
PM TRAFIKUTREDNING E16 HANRÖLEDEN - VÄG 293 LEKSANDSVÄGEN STIGAREGATAN I FALUN
 COOP FASTIGHETER AB PM TRAFIKUTREDNING E16 HANRÖLEDEN - VÄG 293 LEKSANDSVÄGEN STIGAREGATAN I FALUN Falun 2015-04-23 PM TRAFIKUTREDNING E16 HANRÖLEDEN VÄG 293 LEKSANDSVÄGEN STIGAREGATAN I FALUN Datum 2015-04-23
COOP FASTIGHETER AB PM TRAFIKUTREDNING E16 HANRÖLEDEN - VÄG 293 LEKSANDSVÄGEN STIGAREGATAN I FALUN Falun 2015-04-23 PM TRAFIKUTREDNING E16 HANRÖLEDEN VÄG 293 LEKSANDSVÄGEN STIGAREGATAN I FALUN Datum 2015-04-23
Bilisters beteende vid övergångsställe
 Bilisters beteende vid övergångsställe Observationer av bilisters benägenhet att lämna gående företräde vid fem obevakade övergångsställen i Stockholm stad. Linda Hallenberg RAP. 1 mars 2005 Innehållsförteckning
Bilisters beteende vid övergångsställe Observationer av bilisters benägenhet att lämna gående företräde vid fem obevakade övergångsställen i Stockholm stad. Linda Hallenberg RAP. 1 mars 2005 Innehållsförteckning
Trafikanalys. Alingsås Östra Ängabo
 Trafikanalys Alingsås Östra Ängabo Sammanfattning Vectura har på uppdrag av Alingsås kommun fått i uppdrag att göra en översyn kring hur trafikflödet som genereras från planerad bebyggelse i Östra Ängabo
Trafikanalys Alingsås Östra Ängabo Sammanfattning Vectura har på uppdrag av Alingsås kommun fått i uppdrag att göra en översyn kring hur trafikflödet som genereras från planerad bebyggelse i Östra Ängabo
PM Trafik. Södra Årby. Tyréns - Arvid Gentele 1(13) Uppdragsnr: Rapportnr: Rev (): l tl t t\ut d i \T é T fik PM k t LGS d
 1(13) PM Trafik Södra Årby 20111031 Tyréns - Arvid Gentele 2(13) Inledning En ny stadsdel, Södra Årby, planeras i anslutning till Läggesta station. Området omfattar bostäder, verksamheter och samhällsservice.
1(13) PM Trafik Södra Årby 20111031 Tyréns - Arvid Gentele 2(13) Inledning En ny stadsdel, Södra Årby, planeras i anslutning till Läggesta station. Området omfattar bostäder, verksamheter och samhällsservice.
1 Bakgrund 1. 2 Nuläge Trafikflöde och hastighet Kollektivtrafik 2. 3 Nyetablering 2
 Innehållsförteckning 1 Bakgrund 1 2 Nuläge 1 2.1 Trafikflöde och hastighet 1 2.2 Kollektivtrafik 2 3 Nyetablering 2 3.1.1 Sikt 3 3.1.2 Avfartsramp E20 Väg 509 5 3.1.3 Tillgänglighet och trafiksäkerhet
Innehållsförteckning 1 Bakgrund 1 2 Nuläge 1 2.1 Trafikflöde och hastighet 1 2.2 Kollektivtrafik 2 3 Nyetablering 2 3.1.1 Sikt 3 3.1.2 Avfartsramp E20 Väg 509 5 3.1.3 Tillgänglighet och trafiksäkerhet
Cykelvett. Cykla lagligt och säkert Tips och råd
 Cykelvett Cykla lagligt och säkert Tips och råd Rätt utrustning Enligt lag måste en cykel ha: Ringklocka Broms I mörker måste cykeln också ha: Vit reflex och strålkastare med vitt eller gult ljus fram
Cykelvett Cykla lagligt och säkert Tips och råd Rätt utrustning Enligt lag måste en cykel ha: Ringklocka Broms I mörker måste cykeln också ha: Vit reflex och strålkastare med vitt eller gult ljus fram
PM ang trafik kring ett planerat parkeringsgarage på Davidshallstorg.
 1 2006-11-23 PM ang trafik kring ett planerat parkeringsgarage på Davidshallstorg. Trafiksituation idag På torget finns idag 88 parkeringsplatser och på de angränsande gatorna runt omkring torget finns
1 2006-11-23 PM ang trafik kring ett planerat parkeringsgarage på Davidshallstorg. Trafiksituation idag På torget finns idag 88 parkeringsplatser och på de angränsande gatorna runt omkring torget finns
