Biomekanik, 5 poäng Moment
|
|
|
- Erika Forsberg
- för 8 år sedan
- Visningar:
Transkript
1 (kraftmoment) En resulterande (obalanserad kraft) strävar efter att ändra en kropps rörelsetillstånd. Den kan också sträva efter att vrida en kropp. Måttet på kraftens förmåga att vrida kroppen runt en axel är dess moment runt den aktuella axeln. Enhet för moment: Nm. = Kraft * hävstångsarm = *d Viktigt: Hävstångsarm är vinkelräta avståndet från kraftens verkningslinje till vridaxeln (rotationspunkten) Om kraftens verkningslinje går igenom vridaxeln blir momentet noll Om flera krafter samtidigt verkar på en kropp bestäms krafternas sammantagna vridningsverkan av det resulterande momentet. Detta bestäms genom addition av samtliga verkande moment, M R = l Ett moment har alltid en viss vridningsriktning. När moment adderas måste man ta hänsyn till vridningsriktningen (med- och moturs etc.). Om M R = 0, dvs. om momenten tar ut varandra har vi momentjämvikt (rotationsjämvikt). P. Carlsson
2 Varignons teorem En krafts verkan på en kropp förändras inte om kraften ersätts med sina komposanter. Om detta gäller fullt ut måste det även gälla att: En krafts moment med avseende på en viss axel är lika med summan av komposanternas moment Grafisk illustration av Varignons teorem Ur figur b (positiv momentriktning medurs): M O = R d = P p + Q q P. Carlsson 2
3 Ytterligare illustration av Varignons teorem Ex. Bestäm momentverkan av 600 N- kraften runt punkt O. Svar: M o = 260 Nm P. Carlsson 3
4 Kraftsumma, momentsumma Vi antar att flera krafter, ett s.k. kraftsystem, verkar på en kropp. Deras gemensamma kraftverkan bestäms av kraftsumman Σ. Def: = n i I figuren har vi tre verkande krafter: 3 = i = Summeringen delas lämpligen upp i komposanter: x = n ix, = y n iy, R = ( Σ ) 2 ( ) 2 x + Σy På samma sätt definieras momentsumman med avseende på (den godtyckliga) axeln O. n M O = M Oi Positiv momentriktning måste definieras. I fig. får vi (moturs): M O = d + 2d 2 3d 3 P. Carlsson 4
5 Ex 2. Bestäm kraftsumma och momentsumma vid balkens infästning A. Svar: x =,65 kn, y =,6 kn, R = 2,0 kn, M A = 2,22 knm (moturs) P. Carlsson 5
6 Kraftpar, rent moment Ett kraftpar bildas av två lika stora, motriktade krafter. Tecknas kraftparets momentsumma runt en godtycklig axel O får vi (moturs pos.): Σ M O = ( a + d) a = d summan beror endast på krafternas belopp och avståndet mellan deras verkningslinjer! Mer om kraftsumma, momentsumma I det generella fallet finns det både krafter och (rena) moment som verkar på en kropp. ör krafter och system i figuren gäller: = 3 i M O = d + + 2d 2 3d 3 M M 2 (positiv riktning medurs) P. Carlsson 6
7 Reduktion av kraftsystem Handlar om att omvandla komplicerade kraftsystem till enkla system som är ekvivalenta (dvs. har samma verkan) som de ursprungliga. Steg I Vi behöver veta hur man flyttar angreppspunkten för en kraft. I figuren vill vi flytta kraften :s angreppspunkt från A till B. Lägg två motriktade krafter av :s storlek och riktning i B (ändrar ej kraft- och momentsumma) Ersätt det uppkomna kraftparet med ett rent moment med storleken M = d. Kvar i B finns (den flyttade) kraften samt momentet M = d (som ej är knutet till B). P. Carlsson 7
8 Steg II Vi ska nu visa att ett godtyckligt kraftsystem kan reduceras till ett kraftsystem som består av högst en kraft och ett rent moment. Vi antar att fig a) innehåller n st krafter och m st rena moment (i figuren är 3 krafter och 2 moment utritade). Enligt steg I kan varje kraft flyttas så att den angriper i en godtycklig punkt O om vi samtidigt adderar ett rent moment för vaje kraft. Mot kraften i svarar alltså momentet i d i osv. Resultatet av operationen visas i fig b) Därefter adderas krafterna till en enda kraft och momenten adderas till ett enda moment enligt (se fig. c): R = M O n = n i d i i + m M i Man kan också räkna fram en angreppspunkt för krafternas resultant (P i figur), där resultanten får ett moment lika med M O runt punkt O. Avståndet d till angreppspunkten fås ur det enkla sambandet M O = Pd, där d är avståndet från resultant till punkt O. Denna enda kraft ersätter då även momentet M O (benämt M i figuren). P. Carlsson 8
9 Ex. 3 Bestäm kraftsumma och angreppspunkt för krafternas resultant samt momentsumma för balken i figuren. Utgå från infästningspunkten vid momentberäkningen. Svar: y = -3 kn (riktad nedåt), M = 3 knm (medurs) Resultantens angreppspunkt: d = 4,33 m från infästningen. P. Carlsson 9
10 Sammanfattning Ett godtyckligt, tvådimensionellt kraftsystem kan alltid reduceras till en kraft och ett rent moment. Kraftens angreppspunkt, reduktionspunkten, kan väljas godtyckligt. Observera dock att momentsumman får olika värden beroende på vald reduktionspunkt. Om kraftsumman är skild från noll, kan systemet reduceras till enbart en kraft med given verkningslinje. Om kraftsumman är lika med noll, kan systemet reduceras till ett rent moment. P. Carlsson 0
11 Studium av krafter moment i armbåge 5g 5g Med hur stor kraft m måste bicepsmuskeln verka för att hålla emot en massa om 5 kg i de båda fallen ovan? Avstånd mellan armbågsled och kraftens angreppspunkt är 40 cm i både A och B. Svar: ma = 50g, mb = 00g Hur skiljer sig personerna A och B sig åt vad gäller styrka och snabbhet? Vi antar att biceps utvecklar samma kraft i båda fallen. P. Carlsson
12 Ex 4. En tyngd mg hålls uppe med armens muskelkraft. Vilken är tyngdens verkan i leden A resp. B? (Övriga massor försummas.) Ersätt alltså i tur och ordning i dessa punkter kraften mg men en kraft och ett rent moment! Svar: Punkt A vid armbågen: A = mg, M A = mgd Punkt B vid axel: B = mg, M B = mg(c+d) P. Carlsson 2
13 Ex 5. En man som tränar axelmuskulaturen börjar övningen med armen i vertikalt, avslappnat läge OA enl. figur (gummibandet är då nätt och jämt sträckt). Han lyfter sedan armen till det horisontella läget OB. Gummibandets fjäderkonstant är k = 60 N/m, dvs. det går åt kraften 60 N för att sträcka gummibandet sträckan m. Beräkna momentet runt axeln i punkt O, dvs. M o, med hjälp av den kraft som bandet drar i handen vid B. Svar: M o = 26,8 Nm (moturs) P. Carlsson 3
14 Inre och yttre krafters moment Rörelse i kroppen uppstår genom att musklerna producerar (inre) moment runt en ledaxel. Hävstångens längd är till stor del avgörande för muskelns förmåga att utveckla ett moment. Armbågsböjare Knäled Yttre moment kan t. ex. produceras av tyngdkrafter, normalkrafter etc. P. Carlsson 4
Krafter och moment. mm F G (1.1)
 1 Krafter och moment 1.1 Inledning örståelsen för hur olika typer av krafter påverkar strukturer i vår omgivning är grundläggande för ingenjörsvetenskapen inom byggnadskonsten. Gravitationskraften är en
1 Krafter och moment 1.1 Inledning örståelsen för hur olika typer av krafter påverkar strukturer i vår omgivning är grundläggande för ingenjörsvetenskapen inom byggnadskonsten. Gravitationskraften är en
mm F G (1.1) F mg (1.2) P (1.3)
 Sid 1-1 1 1.1 Krafter och moment Inledning örståelsen för hur olika tper av krafter påverkar strukturer i vår omgivning är grundläggande för ingenjörsvetenskapen inom bggnadskonsten. Gravitationskraften
Sid 1-1 1 1.1 Krafter och moment Inledning örståelsen för hur olika tper av krafter påverkar strukturer i vår omgivning är grundläggande för ingenjörsvetenskapen inom bggnadskonsten. Gravitationskraften
Introduktion till Biomekanik - Statik VT 2006
 http://apachepersonal.miun.se/~petcar/biomekanikintro.htm Innehåll Terminologi inom biomekanik. Skelettets, musklernas, senors och ligamentens funktion och uppbyggnad. Statik, kinematik och kinetik. Idrotts-
http://apachepersonal.miun.se/~petcar/biomekanikintro.htm Innehåll Terminologi inom biomekanik. Skelettets, musklernas, senors och ligamentens funktion och uppbyggnad. Statik, kinematik och kinetik. Idrotts-
KOMIHÅG 3: Kraft är en vektor med angreppspunkt och verkningslinje. Kraftmoment: M P. = r PA
 1 KOMIHÅG 3: --------------------------------- Kraft är en vektor med angreppspunkt och verkningslinje. Kraftmoment: M P = r PA " F, r P =momentpunkt, r A angreppspunkt, r PA = r A " r P. - Oberoende av
1 KOMIHÅG 3: --------------------------------- Kraft är en vektor med angreppspunkt och verkningslinje. Kraftmoment: M P = r PA " F, r P =momentpunkt, r A angreppspunkt, r PA = r A " r P. - Oberoende av
Biomekanik Belastningsanalys
 Biomekanik Belastningsanalys Skillnad? Biomekanik Belastningsanalys Yttre krafter och moment Hastigheter och accelerationer Inre spänningar, töjningar och deformationer (Dynamiska påkänningar) I de delar
Biomekanik Belastningsanalys Skillnad? Biomekanik Belastningsanalys Yttre krafter och moment Hastigheter och accelerationer Inre spänningar, töjningar och deformationer (Dynamiska påkänningar) I de delar
Målsättningar Proffesionell kunskap. Kunna hänvisa till lagar och definitioner. Tydlighet och enhetliga beteckningar.
 1 Föreläsning 1: INTRODUKTION Målsättningar Proffesionell kunskap. Kunna hänvisa till lagar och definitioner. Tydlighet och enhetliga beteckningar. Kursens olika delar Teorin Tentamen efter kursen och/eller
1 Föreläsning 1: INTRODUKTION Målsättningar Proffesionell kunskap. Kunna hänvisa till lagar och definitioner. Tydlighet och enhetliga beteckningar. Kursens olika delar Teorin Tentamen efter kursen och/eller
Biomekanik, 5 poäng Jämviktslära
 Jämvikt Vid jämvikt (ekvilibrium) är en kropp i vila eller i rätlinjig rörelse med konstant hastighet. Jämvikt kräver att: Alla verkande krafter tar ut varandra, Σ F = 0 (translationsjämvikt) Alla verkande
Jämvikt Vid jämvikt (ekvilibrium) är en kropp i vila eller i rätlinjig rörelse med konstant hastighet. Jämvikt kräver att: Alla verkande krafter tar ut varandra, Σ F = 0 (translationsjämvikt) Alla verkande
K-uppgifter Strukturmekanik/Materialmekanik
 K-uppgifter Strukturmekanik/Materialmekanik K 1 Bestäm resultanten till de båda krafterna. Ange storlek och vinkel i förhållande till x-axeln. y 4N 7N x K 2 Bestäm kraftens komposanter längs x- och y-axeln.
K-uppgifter Strukturmekanik/Materialmekanik K 1 Bestäm resultanten till de båda krafterna. Ange storlek och vinkel i förhållande till x-axeln. y 4N 7N x K 2 Bestäm kraftens komposanter längs x- och y-axeln.
Till Kursen MEKANIK MSGB21
 Välkommen! Till Kursen MEKANIK MSGB21 Kursansvar: Hans Johansson 21F226 Föreläsningar: Hans Johansson & Anders Gåård Övningar: Anders Gåård 21F229 Mikael Åsberg 21D209 Hans Johansson 21F226 Sekreterare:
Välkommen! Till Kursen MEKANIK MSGB21 Kursansvar: Hans Johansson 21F226 Föreläsningar: Hans Johansson & Anders Gåård Övningar: Anders Gåård 21F229 Mikael Åsberg 21D209 Hans Johansson 21F226 Sekreterare:
KOMIHÅG 2: Kraft är en vektor med angreppspunkt och verkningslinje. Kraftmoment: M P. = r PA
 1 KOMIHÅG 2: --------------------------------- Kraft är en vektor me angreppspunkt och verkningslinje. Kraftmoment: M P = r PA ", r P =momentpunkt, r A angreppspunkt, r PA = r A " r P. - Oberoene av om
1 KOMIHÅG 2: --------------------------------- Kraft är en vektor me angreppspunkt och verkningslinje. Kraftmoment: M P = r PA ", r P =momentpunkt, r A angreppspunkt, r PA = r A " r P. - Oberoene av om
Lösningar Heureka 2 Kapitel 2 Kraftmoment och jämvikt
 Lösningar Heureka Kapitel Kraftmoment och jämvikt Andreas Josefsson Tullängsskolan Örebro Lo sningar Fysik Heureka Kapitel.1) Vi väljer en vridningsaxel vid brädans kontaktpunkt med ställningen till vänster,
Lösningar Heureka Kapitel Kraftmoment och jämvikt Andreas Josefsson Tullängsskolan Örebro Lo sningar Fysik Heureka Kapitel.1) Vi väljer en vridningsaxel vid brädans kontaktpunkt med ställningen till vänster,
Rapport LUTFD2/TFHF-3089/1-16/(2013) Föreläsningsexempel i Teknisk mekanik
 Rapport LUTFD2/TFHF-3089/1-16/(2013) Föreläsningsexempel i Teknisk mekanik Håkan Hallberg vd. för Hållfasthetslära Lunds Universitet December 2013 Exempel 1 Två krafter,f 1 och F 2, verkar enligt figuren.
Rapport LUTFD2/TFHF-3089/1-16/(2013) Föreläsningsexempel i Teknisk mekanik Håkan Hallberg vd. för Hållfasthetslära Lunds Universitet December 2013 Exempel 1 Två krafter,f 1 och F 2, verkar enligt figuren.
Inlämningsuppgift 1. 1/ Figuren visar ett energischema för Ulla som går uppför en trappa. I detta fall sker en omvandling av energi i Ullas muskler.
 Inlämningsuppgift 1 1/ Figuren visar ett energischema för Ulla som går uppför en trappa. I detta fall sker en omvandling av energi i Ullas muskler. Oftast använder vi apparater och motorer till att omvandla
Inlämningsuppgift 1 1/ Figuren visar ett energischema för Ulla som går uppför en trappa. I detta fall sker en omvandling av energi i Ullas muskler. Oftast använder vi apparater och motorer till att omvandla
Biomekanik, 5 poäng Introduktion -Kraftbegreppet. Mekaniken är en grundläggande del av fysiken ingenjörsvetenskapen
 Biomekanik Mekanik Skillnad? Ambition: Att ge översiktliga kunskaper om mekaniska sammanhang och principer som hör samman med kroppsrörelser och rörelser hos olika idrottsredskap. Mekaniken är en grundläggande
Biomekanik Mekanik Skillnad? Ambition: Att ge översiktliga kunskaper om mekaniska sammanhang och principer som hör samman med kroppsrörelser och rörelser hos olika idrottsredskap. Mekaniken är en grundläggande
Målsättningar Proffesionell kunskap om mekanik. Kunna hänvisa till lagar och definitioner. Tydlighet och enhetliga beteckningar.
 1 Föreläsning 1: INTRODUKTION Målsättningar Proffesionell kunskap om mekanik. Kunna hänvisa till lagar och definitioner. Tydlighet och enhetliga beteckningar. Kursens olika delar Teorin Tentamen efter
1 Föreläsning 1: INTRODUKTION Målsättningar Proffesionell kunskap om mekanik. Kunna hänvisa till lagar och definitioner. Tydlighet och enhetliga beteckningar. Kursens olika delar Teorin Tentamen efter
Välkommen! Till Kursen MEKANIK MSGB21. Föreläsningar & kursansvar:
 Välkommen! Till Kursen MEKANIK MSGB21 Föreläsningar & kursansvar: Hans Johansson 21F226 Övningar: Lennart Berglund 21F227 Jens Ekengren 21D215 Anders Gåård 21F229 Sekreterare: Marika Johansson 21F218 Ur
Välkommen! Till Kursen MEKANIK MSGB21 Föreläsningar & kursansvar: Hans Johansson 21F226 Övningar: Lennart Berglund 21F227 Jens Ekengren 21D215 Anders Gåård 21F229 Sekreterare: Marika Johansson 21F218 Ur
M12 Mekanikens grunder Steg 2 Krafter och moment
 M12 Mekanikens grunder Steg 2 Krafter och moment Namn: Kurs: Datum: Lektion 1: 2 Mekanikens grunder Kraft Exempel 1 Ex. 1 Rymdfärjan Columbus har just placerat ut den sista satelliten för denna gång och
M12 Mekanikens grunder Steg 2 Krafter och moment Namn: Kurs: Datum: Lektion 1: 2 Mekanikens grunder Kraft Exempel 1 Ex. 1 Rymdfärjan Columbus har just placerat ut den sista satelliten för denna gång och
Grundläggande om krafter och kraftmoment
 Grundläggande om krafter och kraftmoment Text: Nikodemus Karlsson Original character art by Esa Holopainen, http://www.verikoirat.com/ Krafter - egenskaper och definition Vardaglig betydelse Har med påverkan
Grundläggande om krafter och kraftmoment Text: Nikodemus Karlsson Original character art by Esa Holopainen, http://www.verikoirat.com/ Krafter - egenskaper och definition Vardaglig betydelse Har med påverkan
WALLENBERGS FYSIKPRIS 2014
 WALLENBERGS FYSIKPRIS 2014 Tävlingsuppgifter (Finaltävlingen) Riv loss detta blad och lägg det överst tillsammans med de lösta tävlingsuppgifterna i plastmappen. Resten av detta uppgiftshäfte får du behålla.
WALLENBERGS FYSIKPRIS 2014 Tävlingsuppgifter (Finaltävlingen) Riv loss detta blad och lägg det överst tillsammans med de lösta tävlingsuppgifterna i plastmappen. Resten av detta uppgiftshäfte får du behålla.
KRAFTER. Peter Gustavsson Per-Erik Austrell
 KRATER Peter Gustavsson Per-Erik Austrell örord Denna skrift har tagits fram för att utgöra kurslitteratur i kursen Mekanik för Industri Design vid Lunds Tekniska Högskola. Skriften börjar med en introduktion
KRATER Peter Gustavsson Per-Erik Austrell örord Denna skrift har tagits fram för att utgöra kurslitteratur i kursen Mekanik för Industri Design vid Lunds Tekniska Högskola. Skriften börjar med en introduktion
Uppgifter till KRAFTER. Peter Gustavsson Per-Erik Austrell
 Uppgifter till KRAFTER Peter Gustavsson Per-Erik Austrell 1 Innehåll 1 Introduktion till statiken... 3 A-uppgifter... 3 2 Krafter... 5 A-uppgifter... 5 B-uppgifter... 5 3 Moment... 7 A-uppgifter... 7 B-uppgifter...
Uppgifter till KRAFTER Peter Gustavsson Per-Erik Austrell 1 Innehåll 1 Introduktion till statiken... 3 A-uppgifter... 3 2 Krafter... 5 A-uppgifter... 5 B-uppgifter... 5 3 Moment... 7 A-uppgifter... 7 B-uppgifter...
Tentamen i Mekanik 5C1107, baskurs S2. Problemtentamen
 005-05-7 Tentamen i Mekanik 5C1107, baskurs S. OBS: Inga hjälpmede förutom rit- och skrivdon får användas! KTH Mekanik 1. Problemtentamen En homogen stång med massan m är fäst i ena änden i en fritt vridbar
005-05-7 Tentamen i Mekanik 5C1107, baskurs S. OBS: Inga hjälpmede förutom rit- och skrivdon får användas! KTH Mekanik 1. Problemtentamen En homogen stång med massan m är fäst i ena änden i en fritt vridbar
VSMA01 - Mekanik ERIK SERRANO
 VSMA01 - Mekanik ERIK SERRANO Översikt Kursintroduktion Kursens syfte och mål Kursprogram Upprop Inledande föreläsning Föreläsning: Kapitel 1. Introduktion till statik Kapitel 2. Att räkna med krafter
VSMA01 - Mekanik ERIK SERRANO Översikt Kursintroduktion Kursens syfte och mål Kursprogram Upprop Inledande föreläsning Föreläsning: Kapitel 1. Introduktion till statik Kapitel 2. Att räkna med krafter
SG1108 Tillämpad fysik, mekanik för ME1 (7,5 hp)
 Läsåret 11/12 Utförliga lärandemål SG1108 Tillämpad fysik, mekanik för ME1 (7,5 hp) Richard Hsieh Huvudsakligt innehåll: Vektoralgebra och dimensionsbetraktelser. Kraft och kraftmoment. Kraftsystem; kraftpar,
Läsåret 11/12 Utförliga lärandemål SG1108 Tillämpad fysik, mekanik för ME1 (7,5 hp) Richard Hsieh Huvudsakligt innehåll: Vektoralgebra och dimensionsbetraktelser. Kraft och kraftmoment. Kraftsystem; kraftpar,
Tentamen i Mekanik SG1107, baskurs S2. Problemtentamen
 010-05-6 Tentamen i Mekanik SG1107, baskurs S OBS: Inga hjälpmede förutom rit- och skrivdon får användas! KTH Mekanik Problemtentamen 1 En cylinder med massan M vilar på en homogen horisontell planka med
010-05-6 Tentamen i Mekanik SG1107, baskurs S OBS: Inga hjälpmede förutom rit- och skrivdon får användas! KTH Mekanik Problemtentamen 1 En cylinder med massan M vilar på en homogen horisontell planka med
KRAFTER. Peter Gustavsson Per-Erik Austrell
 KRATER Peter Gustavsson Per-Erik Austrell örord Denna skrift har tagits fram för att utgöra kurslitteratur i kursen Mekanik för Industri Design vid Lunds Tekniska Högskola. Skriften börjar med en introduktion
KRATER Peter Gustavsson Per-Erik Austrell örord Denna skrift har tagits fram för att utgöra kurslitteratur i kursen Mekanik för Industri Design vid Lunds Tekniska Högskola. Skriften börjar med en introduktion
Härled utgående från hastighetssambandet för en stel kropp, d.v.s. v B = v A + ω AB
 . Härled utgående från hastighetssambandet för en stel kropp, d.v.s. v B v A + ω AB motsvarande samband för accelerationer: a B a A + ω ω AB + a AB. Tolka termerna i uttrycket för specialfallet plan rörelse
. Härled utgående från hastighetssambandet för en stel kropp, d.v.s. v B v A + ω AB motsvarande samband för accelerationer: a B a A + ω ω AB + a AB. Tolka termerna i uttrycket för specialfallet plan rörelse
Tentamen i SG1140 Mekanik II för M, I. Problemtentamen
 2010-10-23 Tentamen i SG1140 Mekanik II för M, I. OBS: Inga hjälpmedel förutom rit- och skrivdon får användas! KTH Mekanik 1. Problemtentamen Triangelskivan i den plana mekanismen i figuren har en vinkelhastighet
2010-10-23 Tentamen i SG1140 Mekanik II för M, I. OBS: Inga hjälpmedel förutom rit- och skrivdon får användas! KTH Mekanik 1. Problemtentamen Triangelskivan i den plana mekanismen i figuren har en vinkelhastighet
Belastningsanalys, 5 poäng Balkteori Moment och tvärkrafter. Balkböjning Teknisk balkteori Stresses in Beams
 Balkböjning Teknisk balkteori Stresses in Beams Som den sista belastningstypen på en kropps tvärsnitt kommer vi att undersöka det böjande momentet M:s inverkan. Medan man mest är intresserad av skjuvspänningarna
Balkböjning Teknisk balkteori Stresses in Beams Som den sista belastningstypen på en kropps tvärsnitt kommer vi att undersöka det böjande momentet M:s inverkan. Medan man mest är intresserad av skjuvspänningarna
Uppgifter till KRAFTER
 Uppgifter till KRAFTER Peter Gustavsson Per-Erik Austrell 1 Innehåll 1 Introduktion till statiken... 3 A-uppgifter...3 2 Krafter... 5 A-uppgifter...5 B-uppgifter...5 3 Moment... 7 A-uppgifter...7 B-uppgifter...9
Uppgifter till KRAFTER Peter Gustavsson Per-Erik Austrell 1 Innehåll 1 Introduktion till statiken... 3 A-uppgifter...3 2 Krafter... 5 A-uppgifter...5 B-uppgifter...5 3 Moment... 7 A-uppgifter...7 B-uppgifter...9
Introduktion till Biomekanik - Statik VT 2006
 Pass 4 Jämvikt, fortsättning Vid jämvikt (ekvilibrium) är en kropp i vila eller i rätlinjig rörelse med konstant hastighet. Statisk jämvikt (vila) Dynamisk jämvikt (rörelse i konstant hastighet) (ge ex)
Pass 4 Jämvikt, fortsättning Vid jämvikt (ekvilibrium) är en kropp i vila eller i rätlinjig rörelse med konstant hastighet. Statisk jämvikt (vila) Dynamisk jämvikt (rörelse i konstant hastighet) (ge ex)
En ideal op-förstärkare har oändlig inimedans, noll utimpedans och oändlig förstärkning.
 F5 LE1460 Analog elektronik 2005-11-23 kl 08.15 12.00 Alfa En ideal op-förstärkare har oändlig inimedans, noll utimpedans och oändlig förstärkning. ( Impedans är inte samma sak som resistans. Impedans
F5 LE1460 Analog elektronik 2005-11-23 kl 08.15 12.00 Alfa En ideal op-förstärkare har oändlig inimedans, noll utimpedans och oändlig förstärkning. ( Impedans är inte samma sak som resistans. Impedans
Musklernas uppbyggnad
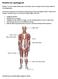 Musklernas uppbyggnad Muskler och senor bildar tillsammans med skelett, leder och fogar det som brukar kallas för rörelseapparaten. Genom att musklerna som är fästa vid skelettet kan dra ihop sig skapas
Musklernas uppbyggnad Muskler och senor bildar tillsammans med skelett, leder och fogar det som brukar kallas för rörelseapparaten. Genom att musklerna som är fästa vid skelettet kan dra ihop sig skapas
Sträck ut efter träningen
 Sträck ut efter träningen När du har tränat är det dags igen. Hoppar du över stretchingen får du lättare ömma, styva och korta muskler. Det är viktigt att uttänjningen sker i en lugn och behärskad takt.
Sträck ut efter träningen När du har tränat är det dags igen. Hoppar du över stretchingen får du lättare ömma, styva och korta muskler. Det är viktigt att uttänjningen sker i en lugn och behärskad takt.
Problemtentamen. = (3,4,5)P, r 1. = (0,2,1)a F 2. = (0,0,0)a F 3. = (2,"3,4)P, r 2
 2015-MM-DD Övningstentamen i Mekanik SG1130, grundkurs B1. OBS: Inga hjälpmede förutom rit- och skrivdon får användas! KTH Mekanik 1. Problemtentamen Ett kraftsystem består av tre krafter som angriper
2015-MM-DD Övningstentamen i Mekanik SG1130, grundkurs B1. OBS: Inga hjälpmede förutom rit- och skrivdon får användas! KTH Mekanik 1. Problemtentamen Ett kraftsystem består av tre krafter som angriper
Övningsbeskrivningar Åtgärdsprogram 1
 Övningsbeskrivningar Åtgärdsprogram 1 "Box Position Mät ut med hjälp av pinnen: lite mer än axelbrett mellan fötterna, pinnen ska gå i linje med fotens inre sida och axelns yttre sida. Aktiv Sidoböjning
Övningsbeskrivningar Åtgärdsprogram 1 "Box Position Mät ut med hjälp av pinnen: lite mer än axelbrett mellan fötterna, pinnen ska gå i linje med fotens inre sida och axelns yttre sida. Aktiv Sidoböjning
Tentamen i Mekanik SG1130, baskurs P1 m fl. Problemtentamen OBS: Inga hjälpmedel förutom rit- och skrivdon får användas!
 014-03-17 Tentamen i Mekanik SG1130, baskurs P1 m fl OBS: Inga hjälpmedel förutom rit- och skrivdon får användas! 1 KTH Mekanik Problemtentamen En tunn homogen stav i jämvikt med massan m har i ena ändpunkten
014-03-17 Tentamen i Mekanik SG1130, baskurs P1 m fl OBS: Inga hjälpmedel förutom rit- och skrivdon får användas! 1 KTH Mekanik Problemtentamen En tunn homogen stav i jämvikt med massan m har i ena ändpunkten
my baby carrier SVENSKA BRUKSANVISNING
 my baby carrier BRUKSANVISNING SVENSKA Integrerat huvudstöd VIKTIGT! SPARA BRUKS- ANVISNINGEN SÅ ATT DU HAR DEN TILL HANDS OM DU SKULLE BEHÖVA DEN IGEN! Integrerad ryggförlängning... > VARNINGAR VARNING:
my baby carrier BRUKSANVISNING SVENSKA Integrerat huvudstöd VIKTIGT! SPARA BRUKS- ANVISNINGEN SÅ ATT DU HAR DEN TILL HANDS OM DU SKULLE BEHÖVA DEN IGEN! Integrerad ryggförlängning... > VARNINGAR VARNING:
Tillåtna hjälpmedel: Physics Handbook, Beta, kalkylator i fickformat, samt en egenhändigt skriven A4-sida med valfritt innehåll.
 Tentamen i Mekanik förf, del B Måndagen 12 januari 2004, 8.45-12.45, V-huset Examinator och jour: Martin Cederwall, tel. 7723181, 0733-500886 Tillåtna hjälpmedel: Physics Handbook, Beta, kalkylator i fickformat,
Tentamen i Mekanik förf, del B Måndagen 12 januari 2004, 8.45-12.45, V-huset Examinator och jour: Martin Cederwall, tel. 7723181, 0733-500886 Tillåtna hjälpmedel: Physics Handbook, Beta, kalkylator i fickformat,
Tentamen i Mekanik SG1130, baskurs P1. Problemtentamen
 010-06-07 Tentamen i Mekanik SG1130, baskurs P1 OBS: Inga hjälpmede förutom rit- och skrivdon får användas! KTH Mekanik 1 Problemtentamen En homogen mast med massan M och längden 10a hålls stående i vertikalt
010-06-07 Tentamen i Mekanik SG1130, baskurs P1 OBS: Inga hjälpmede förutom rit- och skrivdon får användas! KTH Mekanik 1 Problemtentamen En homogen mast med massan M och längden 10a hålls stående i vertikalt
varandra. Vi börjar med att behandla en linjes ekvation med hjälp av figur 7 och dess bildtext.
 PASS 8 EKVATIONSSYSTEM OCH EN LINJES EKVATION 8 En linjes ekvation En linjes ekvation kan framställas i koordinatsystemet Koordinatsystemet består av x-axeln och yaxeln X-axeln är vågrät och y-axeln lodrät
PASS 8 EKVATIONSSYSTEM OCH EN LINJES EKVATION 8 En linjes ekvation En linjes ekvation kan framställas i koordinatsystemet Koordinatsystemet består av x-axeln och yaxeln X-axeln är vågrät och y-axeln lodrät
Splitsning av flätade linor gjorda av polyester eller nylon.
 Denna splits är inte lämplig för dubbelflätade linor vars styrka enbart beror på styrkan i kärnan. Öglesplitsen används för att placera en permanent ögla i änden av ett rep, i allmänhet för förtöjning
Denna splits är inte lämplig för dubbelflätade linor vars styrka enbart beror på styrkan i kärnan. Öglesplitsen används för att placera en permanent ögla i änden av ett rep, i allmänhet för förtöjning
= v! p + r! p = r! p, ty v och p är dt parallella. Definiera som en ny storhet: Rörelsemängdsmoment: H O
 1 KOMIHÅG 15: --------------------------------- Definitioner: Den potentiella energin, mekaniska energin Formulera: Energiprincipen ---------------------------------- Föreläsning 16: FLER LAGAR-härledning
1 KOMIHÅG 15: --------------------------------- Definitioner: Den potentiella energin, mekaniska energin Formulera: Energiprincipen ---------------------------------- Föreläsning 16: FLER LAGAR-härledning
Introduktion till Biomekanik - Statik VT 2006
 Kurskompendie, 150kr Kurshemsida (internt på miun) http://apachepersonal.miun.se/~petcar/biomekanikintro.htm (externt) www.miun.se/personal/peter.carlsson/biomekanikintro.htm Föreläsare Marie Lund, marie.lund@miun.se
Kurskompendie, 150kr Kurshemsida (internt på miun) http://apachepersonal.miun.se/~petcar/biomekanikintro.htm (externt) www.miun.se/personal/peter.carlsson/biomekanikintro.htm Föreläsare Marie Lund, marie.lund@miun.se
a), c), e) och g) är olikheter. Av dem har c) och g) sanningsvärdet 1.
 PASS 9. OLIKHETER 9. Grundbegrepp om olikheter Vi får olikheter av ekvationer om vi byter ut likhetstecknet mot något av tecknen > (större än), (större än eller lika med), < (mindre än) eller (mindre än
PASS 9. OLIKHETER 9. Grundbegrepp om olikheter Vi får olikheter av ekvationer om vi byter ut likhetstecknet mot något av tecknen > (större än), (större än eller lika med), < (mindre än) eller (mindre än
Instuderingsfrågor Skelettet, med svar
 Skelettet gör så att vi kan stå upp och röra på oss. Förutom emaljen så är ben det hårdaste material vi har i vår kropp. 1. Vad är det skelettet gör? Svar: Skelettet gör så att vi kan stå upp och röra
Skelettet gör så att vi kan stå upp och röra på oss. Förutom emaljen så är ben det hårdaste material vi har i vår kropp. 1. Vad är det skelettet gör? Svar: Skelettet gör så att vi kan stå upp och röra
Testa din förmåga att röra en kroppsdel och hålla andra helt stilla. Sätt score för varje del: 0=Klarar; 1=Klarar inte.
 Test Protokoll : GG Fysiska tester Kropp och hälsa 1. Kroppslängd Mät din kroppslängd när du står uppsträckt barfota. Kroppslängd 2. Kroppsvikt Mät helst kroppsvikten naken på morgonen efter toalettbesök
Test Protokoll : GG Fysiska tester Kropp och hälsa 1. Kroppslängd Mät din kroppslängd när du står uppsträckt barfota. Kroppslängd 2. Kroppsvikt Mät helst kroppsvikten naken på morgonen efter toalettbesök
Kurvlängd och geometri på en sfärisk yta
 325 Kurvlängd och geometri på en sfärisk yta Peter Sjögren Göteborgs Universitet 1. Inledning. Geometrin på en sfärisk yta liknar planets geometri, med flera intressanta skillnader. Som vi skall se nedan,
325 Kurvlängd och geometri på en sfärisk yta Peter Sjögren Göteborgs Universitet 1. Inledning. Geometrin på en sfärisk yta liknar planets geometri, med flera intressanta skillnader. Som vi skall se nedan,
TENTAMEN I HÅLLFASTHETSLÄRA FÖR I2 MHA 051. 6 april 2002 08.45 13.45 (5 timmar) Lärare: Anders Ekberg, tel 772 3480
 2002-04-04:anek TENTAMEN I HÅFASTHETSÄRA FÖR I2 MHA 051 6 april 2002 08.45 13.45 (5 timmar) ärare: Anders Ekberg, tel 772 3480 Maximal poäng är 15. För godkänt krävs 6 poäng. AMÄNT Hjälpmedel 1. äroböcker
2002-04-04:anek TENTAMEN I HÅFASTHETSÄRA FÖR I2 MHA 051 6 april 2002 08.45 13.45 (5 timmar) ärare: Anders Ekberg, tel 772 3480 Maximal poäng är 15. För godkänt krävs 6 poäng. AMÄNT Hjälpmedel 1. äroböcker
Välkommen! Mikael Widerdal
 Välkommen! Den här titeln du håller i din hand innehåller de bästa och mest kraftfulla mentala redskap från de 20 år som jag utbildat, coachat och föreläst för människor i hela Sverige. Den här är indelad
Välkommen! Den här titeln du håller i din hand innehåller de bästa och mest kraftfulla mentala redskap från de 20 år som jag utbildat, coachat och föreläst för människor i hela Sverige. Den här är indelad
Ovningsbankens Handbollspaket Styrketräning
 Ovningsbankens Handbollspaket Styrketräning Ovningsbankens handbollspaket riktar sig i första hand till tränare men även den ambitiösa spelaren. Handbollspaketet har framställts genom flera års tränarerfarenhet
Ovningsbankens Handbollspaket Styrketräning Ovningsbankens handbollspaket riktar sig i första hand till tränare men även den ambitiösa spelaren. Handbollspaketet har framställts genom flera års tränarerfarenhet
Tentamen i SG1140 Mekanik II. Problemtentamen
 010-01-14 Tentamen i SG1140 Mekanik II KTH Mekanik 1. OBS: Inga hjälpmedel förutom rit- och skrivdon får användas! Problemtentamen Triangelskivan i den plana mekanismen i figuren har en vinkelhastighet
010-01-14 Tentamen i SG1140 Mekanik II KTH Mekanik 1. OBS: Inga hjälpmedel förutom rit- och skrivdon får användas! Problemtentamen Triangelskivan i den plana mekanismen i figuren har en vinkelhastighet
TÄBYVAGGAN (4 m. och 3 m.) MONTAGEBESKRIVNING. Bild 1: Vagga 4x2,6 m. OBS! DENNA BESKRIVNING SKALL LÄSAS OCH FÖLJAS VID MONTAGE! Material (Bild 3):
 TÄBYVAGGAN (4 m. och 3 m.) MONTAGEBESKRIVNING Bild 1: Vagga 4x2,6 m. OBS! DENNA BESKRIVNING SKALL LÄSAS OCH FÖLJAS VID MONTAGE! Verktyg mm (Bild 2): Insexnyckel 5 mm av bra stålkvalitet med långt skaft,
TÄBYVAGGAN (4 m. och 3 m.) MONTAGEBESKRIVNING Bild 1: Vagga 4x2,6 m. OBS! DENNA BESKRIVNING SKALL LÄSAS OCH FÖLJAS VID MONTAGE! Verktyg mm (Bild 2): Insexnyckel 5 mm av bra stålkvalitet med långt skaft,
/ ^'u*/ Vridmoment. Extrauppgifter. version 0.11 [131110]
![/ ^'u*/ Vridmoment. Extrauppgifter. version 0.11 [131110] / ^'u*/ Vridmoment. Extrauppgifter. version 0.11 [131110]](/thumbs/51/27437942.jpg) Extrauppgifter Vridmoment version 0.11 [131110] Christian Karlsson Uppgiterna 4.29 4.32 tar upp några saker som boken inte tar upp och bör göras med extra mycket eftertanke. Uppgifterna 4.33 4.40 är blandade
Extrauppgifter Vridmoment version 0.11 [131110] Christian Karlsson Uppgiterna 4.29 4.32 tar upp några saker som boken inte tar upp och bör göras med extra mycket eftertanke. Uppgifterna 4.33 4.40 är blandade
Tillämpad biomekanik, 5 poäng Övningsuppgifter
 , plan kinematik och kinetik 1. Konstruktionen i figuren används för att överföra rotationsrörelse för stången till en rätlinjig rörelse för hjulet. a) Bestäm stångens vinkelhastighet ϕ& som funktion av
, plan kinematik och kinetik 1. Konstruktionen i figuren används för att överföra rotationsrörelse för stången till en rätlinjig rörelse för hjulet. a) Bestäm stångens vinkelhastighet ϕ& som funktion av
Högtalare, hatthylla
 Anvisningsnr Version Art. nr. 8633950 1.0 Högtalare, hatthylla D3902043 Sida 1 / 11 Utrustning A0000162 D3902044 Sida 2 / 11 INLEDNING Läs igenom hela instruktionen innan monteringen påbörjas. Noteringar
Anvisningsnr Version Art. nr. 8633950 1.0 Högtalare, hatthylla D3902043 Sida 1 / 11 Utrustning A0000162 D3902044 Sida 2 / 11 INLEDNING Läs igenom hela instruktionen innan monteringen påbörjas. Noteringar
6.2 Partikelns kinetik - Tillämpningar Ledningar
 6.2 Partikelns kinetik - Tillämpningar Ledningar 6.13 Det som känns som barnets tyngd är den uppåtriktade kraft F som mannen påverkar barnet med. Denna fås ur Newton 2 för barnet. Svar i kilogram måste
6.2 Partikelns kinetik - Tillämpningar Ledningar 6.13 Det som känns som barnets tyngd är den uppåtriktade kraft F som mannen påverkar barnet med. Denna fås ur Newton 2 för barnet. Svar i kilogram måste
Linnéuniversitetet. Naturvetenskapligt basår. Laborationsinstruktion 1 Kaströrelse och rörelsemängd
 Linnéuniversitetet VT2013 Institutionen för datavetenskap, fysik och matematik Program: Kurs: Naturvetenskapligt basår Fysik B Laborationsinstruktion 1 Kaströrelse och rörelsemängd Uppgift: Att bestämma
Linnéuniversitetet VT2013 Institutionen för datavetenskap, fysik och matematik Program: Kurs: Naturvetenskapligt basår Fysik B Laborationsinstruktion 1 Kaströrelse och rörelsemängd Uppgift: Att bestämma
Plannja Lättbalk Teknisk information
 BSAB 96 HSB Maj 2000 Plannja Lättbalk Teknisk information INNEHÅLLSFÖRTECKNING 1. TVÄRSNITTSDATA.. 2 2. ALLMÄNT.. 3 2.1. Z-balkars verkningssätt.. 3 2.2. C-balkars verkningssätt.. 4 3. DIMENSIONERING AV
BSAB 96 HSB Maj 2000 Plannja Lättbalk Teknisk information INNEHÅLLSFÖRTECKNING 1. TVÄRSNITTSDATA.. 2 2. ALLMÄNT.. 3 2.1. Z-balkars verkningssätt.. 3 2.2. C-balkars verkningssätt.. 4 3. DIMENSIONERING AV
ANVÄNDARMANUAL. Tack för att ni köpt Cross Line laser LEO 7 Innan du använder den läs denna användarmanual.
 ANVÄNDARMANUAL Tack för att ni köpt Cross Line laser LEO 7 Innan du använder den läs denna användarmanual. Innehåll 1. Funktion... 3 2. Säkerhet... 3 3. Egenskap... 4 4. Driftmanual... 5 5. Metod... 5
ANVÄNDARMANUAL Tack för att ni köpt Cross Line laser LEO 7 Innan du använder den läs denna användarmanual. Innehåll 1. Funktion... 3 2. Säkerhet... 3 3. Egenskap... 4 4. Driftmanual... 5 5. Metod... 5
Gäddan i Hammarsjön en inledande fiskeribiologisk undersökning
 Gäddan i Hammarsjön en inledande fiskeribiologisk undersökning MS Naturfakta Mikael Svensson Box 107 283 22 Osby 0479-10536, 0705-910536 Gäddan i Hammarsjön Enligt uppgifter från vissa håll är gäddorna
Gäddan i Hammarsjön en inledande fiskeribiologisk undersökning MS Naturfakta Mikael Svensson Box 107 283 22 Osby 0479-10536, 0705-910536 Gäddan i Hammarsjön Enligt uppgifter från vissa håll är gäddorna
ATF, kontroll resp. byte ATF-nivå, kontroll
 Sida 1 av 6 ATF, kontroll resp. byte ATF-nivå, kontroll Observera! Multitronic 01J växellådan behöver en annan ATF än stegautomaterna. Bara den ATF för CVTväxellåda som finns att få som reservdel får användas
Sida 1 av 6 ATF, kontroll resp. byte ATF-nivå, kontroll Observera! Multitronic 01J växellådan behöver en annan ATF än stegautomaterna. Bara den ATF för CVTväxellåda som finns att få som reservdel får användas
Automatic Systems. Mekanisk enhet vändkors Standardarm TR4XX FÄLTMANUAL. Intergate AB Kilegatan 1 452 97 Strömstad Tel: 0526-605 26 Fax: 0526-605 33
 A5-B5 Automatic Systems Mekanisk enhet vändkors Standardarm TR4XX FÄLTMANUAL Intergate AB Kilegatan 1 452 97 Strömstad Tel: 0526-605 26 Fax: 0526-605 33 Intergate AB reserverar sig för produktförändringar
A5-B5 Automatic Systems Mekanisk enhet vändkors Standardarm TR4XX FÄLTMANUAL Intergate AB Kilegatan 1 452 97 Strömstad Tel: 0526-605 26 Fax: 0526-605 33 Intergate AB reserverar sig för produktförändringar
FÖRBEREDELSER INFÖR DELTENTAMEN OCH TENTAMEN
 FÖRBEREDELSER INFÖR DELTENTAMEN OCH TENTAMEN Repetera de övningsuppgifter som kännts besvärliga. Om du behöver mera övning så kan du välja fritt bland de övningsuppgifter i Problemsamlingen som överhoppats.
FÖRBEREDELSER INFÖR DELTENTAMEN OCH TENTAMEN Repetera de övningsuppgifter som kännts besvärliga. Om du behöver mera övning så kan du välja fritt bland de övningsuppgifter i Problemsamlingen som överhoppats.
2.2 Tvådimensionella jämviktsproblem Ledningar
 2.2 Tvådimensionella jämviktsproblem Ledningar 2.2 Sfären påverkas av tre krafter. Enligt resonemanget om trekraftsystem i kapitel 2.2(a) måste krafternas verkningslinjer då skära varandra i en punkt,
2.2 Tvådimensionella jämviktsproblem Ledningar 2.2 Sfären påverkas av tre krafter. Enligt resonemanget om trekraftsystem i kapitel 2.2(a) måste krafternas verkningslinjer då skära varandra i en punkt,
8-4 Ekvationer. Namn:..
 8-4 Ekvationer. Namn:.. Inledning Kalle är 1,3 gånger så gammal som Pelle, och tillsammans är de 27,6 år. Hur gamla är Kalle och Pelle? Klarar du att lösa den uppgiften direkt? Inte så enkelt! Ofta resulterar
8-4 Ekvationer. Namn:.. Inledning Kalle är 1,3 gånger så gammal som Pelle, och tillsammans är de 27,6 år. Hur gamla är Kalle och Pelle? Klarar du att lösa den uppgiften direkt? Inte så enkelt! Ofta resulterar
Eurocode Software AB. CAEBBK04 Sprickbredd. Användarmanual
 Sprickbredd Användarmanual Eurocode Software AB 1 Innehåll 1 INLEDNING 3 1.1 ANVÄNDNINGSOMRÅDEN 3 2 INSTRUKTIONER 4 2.1 KOMMA IGÅNG MED 4 2.2 INDATA 5 2.2.1 BETONG & ARMERING 6 2.2.2 TVÄRSNITT 6 2.2.3
Sprickbredd Användarmanual Eurocode Software AB 1 Innehåll 1 INLEDNING 3 1.1 ANVÄNDNINGSOMRÅDEN 3 2 INSTRUKTIONER 4 2.1 KOMMA IGÅNG MED 4 2.2 INDATA 5 2.2.1 BETONG & ARMERING 6 2.2.2 TVÄRSNITT 6 2.2.3
Bruksanvisning - kort version
 Bruksanvisning - kort version MOTOmed viva2 Redskap för rörelseterapi med motorhjälp MOTOmed viva2 giltig från Software-version 2.0 norwegisch MOTOmed viva2 Rörelseterapi med motorhjälp Manöverenhet Handtag
Bruksanvisning - kort version MOTOmed viva2 Redskap för rörelseterapi med motorhjälp MOTOmed viva2 giltig från Software-version 2.0 norwegisch MOTOmed viva2 Rörelseterapi med motorhjälp Manöverenhet Handtag
Föreläsning 7 - Faktormarknader
 Föreläsning 7 - Faktormarknader 2012-11-22 Faktormarknader En faktormarknad är en marknad där produktionsfaktorer prissätts och omsätts. Arbetsmarknaden Individen Hela marknaden Efterfrågan på arbetskraft
Föreläsning 7 - Faktormarknader 2012-11-22 Faktormarknader En faktormarknad är en marknad där produktionsfaktorer prissätts och omsätts. Arbetsmarknaden Individen Hela marknaden Efterfrågan på arbetskraft
Manual för Anmälan till Sittgruppen, enligt Värmlandsmodellen
 1 (7) Manual för Anmälan till Sittgruppen, enligt Värmlandsmodellen Denna manual är framtagen för att ge vägledning att fylla i Anmälan till Sittgruppen. Strukturen/rubrikerna följer Anmälningsformulärets
1 (7) Manual för Anmälan till Sittgruppen, enligt Värmlandsmodellen Denna manual är framtagen för att ge vägledning att fylla i Anmälan till Sittgruppen. Strukturen/rubrikerna följer Anmälningsformulärets
Trycket beror på ytan
 Inledning Trycket beror på ytan Du har två föremål med samma massa och balanserar dem på varsin handflata. Det ena föremålet har en mycket smalare stödyta än det andra. Förmodligen känns föremålet med
Inledning Trycket beror på ytan Du har två föremål med samma massa och balanserar dem på varsin handflata. Det ena föremålet har en mycket smalare stödyta än det andra. Förmodligen känns föremålet med
Begrepp :: Determinanten
 c Mikael Forsberg 2008 1 Begrepp :: Determinanten Rekursiv definition :: Kofaktorutveckling Låt oss börja definiera determinanten för en 1 1 matris A = (a). En sådan matris är naturligtvis bara ett vanligt
c Mikael Forsberg 2008 1 Begrepp :: Determinanten Rekursiv definition :: Kofaktorutveckling Låt oss börja definiera determinanten för en 1 1 matris A = (a). En sådan matris är naturligtvis bara ett vanligt
KOMPLETTERINGAR TILL FYSIK A FÖR TEKNIK/NATURVETENSKAPLIGA BASÅRET N 2. Juni 2006 NILS ALMQVIST
 KOMPLETTERINGAR TILL YSIK A ÖR TEKNIK/NATURVETENSKAPLIGA BASÅRET Mg N N Juni 006 NILS ALMQVIST INSTITUTIONEN ÖR TILLÄMPAD YSIK, MASKIN- OCH MATERIALTEKNIK örord Detta kompendium och bifogade laborationshandledningar
KOMPLETTERINGAR TILL YSIK A ÖR TEKNIK/NATURVETENSKAPLIGA BASÅRET Mg N N Juni 006 NILS ALMQVIST INSTITUTIONEN ÖR TILLÄMPAD YSIK, MASKIN- OCH MATERIALTEKNIK örord Detta kompendium och bifogade laborationshandledningar
Kapitel 10: Sidvärtsrörelser
 Kapitel 10: Den här övningen (öppna) har så många förtjänster att jag räknar den som alpha och omega bland alla övningar för hästen som syftar till att utveckla fullständig lösgjordhet och perfekt rörlighet
Kapitel 10: Den här övningen (öppna) har så många förtjänster att jag räknar den som alpha och omega bland alla övningar för hästen som syftar till att utveckla fullständig lösgjordhet och perfekt rörlighet
ELEKTRISKT LÖPBAND PD111 BRUKSANVISNING
 ELEKTRISKT LÖPBAND PD111 BRUKSANVISNING Läs anvisningarna noggrant före användning och spara på lämpligt ställe. Kontrollpanel sökning hastighet tid avstånd kalorier På/av Bruksanvisning Nödstoppbrytare
ELEKTRISKT LÖPBAND PD111 BRUKSANVISNING Läs anvisningarna noggrant före användning och spara på lämpligt ställe. Kontrollpanel sökning hastighet tid avstånd kalorier På/av Bruksanvisning Nödstoppbrytare
Repetitionsuppgifter i Matematik inför Basår. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
STÄNG AV FÖNSTER. Regler FLAGGSPECTRUM I FLAGGSPECTRUM II FLAGGSPECTRUM III FLAGGSPECTRUM STJÄRNSPEL
 Sivu 1/5 STÄNG AV FÖNSTER Regler FLAGGSPECTRUM I FLAGGSPECTRUM II FLAGGSPECTRUM III FLAGGSPECTRUM STJÄRNSPEL Ett spännande sätt att lära sig känna igen länder och huvudstäder. Ett utomordentligt kännetecken
Sivu 1/5 STÄNG AV FÖNSTER Regler FLAGGSPECTRUM I FLAGGSPECTRUM II FLAGGSPECTRUM III FLAGGSPECTRUM STJÄRNSPEL Ett spännande sätt att lära sig känna igen länder och huvudstäder. Ett utomordentligt kännetecken
Åtkomlighet för Räddningstjänsten
 PM Åtkomlighet för Räddningstjänsten Upprättad: 2012-10-24/ EM Diarienr: 2012/107-MBR-191 Reviderad: Godkänd av: Stellan Jakobsson Avdelningschef, Mälardalens Brand- och Räddningsförbund Inledning Detta
PM Åtkomlighet för Räddningstjänsten Upprättad: 2012-10-24/ EM Diarienr: 2012/107-MBR-191 Reviderad: Godkänd av: Stellan Jakobsson Avdelningschef, Mälardalens Brand- och Räddningsförbund Inledning Detta
Matematik för sjöingenjörsprogrammet
 Matematik för sjöingenjörsprogrammet Matematiska Vetenskaper 9 augusti 01 Innehåll 5 komplexa tal 150 5.1 Inledning................................ 150 5. Geometrisk definition av de komplexa talen..............
Matematik för sjöingenjörsprogrammet Matematiska Vetenskaper 9 augusti 01 Innehåll 5 komplexa tal 150 5.1 Inledning................................ 150 5. Geometrisk definition av de komplexa talen..............
Vanliga avdrag i rallylydnad
 Vanliga avdrag i rallylydnad SAMMANSTÄLLNING AV VANLIGA AVDRAG FRÅN DOMARKONFERENSEN 2014 GENERELLA AVDRAG Sträckt koppel -1 SK Nosar kortvarigt på marken, banmaterial eller person -1 NOS Hunden som tillfälligt
Vanliga avdrag i rallylydnad SAMMANSTÄLLNING AV VANLIGA AVDRAG FRÅN DOMARKONFERENSEN 2014 GENERELLA AVDRAG Sträckt koppel -1 SK Nosar kortvarigt på marken, banmaterial eller person -1 NOS Hunden som tillfälligt
https://se-fotboll.s2s.net/sessionview.php?id=2347104&_format_for_print=1
 Sida 1 av 5 Vem, vad, var och när Titel Lag/grupp Mv - Tillbakaspel (Djupledsspel i anfall) PF9 Datum Torsdag, 31 December 2015 Tid 00:00-01:30 Plats Total tid Gjord av Mv - Tillbakaspel (Djupledsspel
Sida 1 av 5 Vem, vad, var och när Titel Lag/grupp Mv - Tillbakaspel (Djupledsspel i anfall) PF9 Datum Torsdag, 31 December 2015 Tid 00:00-01:30 Plats Total tid Gjord av Mv - Tillbakaspel (Djupledsspel
Reglerteknik M3. Inlämningsuppgift 3. Lp II, 2006. Namn:... Personnr:... Namn:... Personnr:...
 Reglerteknik M3 Inlämningsuppgift 3 Lp II, 006 Namn:... Personnr:... Namn:... Personnr:... Uppskattad tid, per person, för att lösa inlämningsuppgiften:... Godkänd Datum:... Signatur:... Påskriften av
Reglerteknik M3 Inlämningsuppgift 3 Lp II, 006 Namn:... Personnr:... Namn:... Personnr:... Uppskattad tid, per person, för att lösa inlämningsuppgiften:... Godkänd Datum:... Signatur:... Påskriften av
Var ligger tyngdkrafternas enkraftsresultant? Totala tyngdkraftmomentet (mätt i origo) för kropp bestående av partiklar: M O. # m j.
 1 KOMIHÅG 4: --------------------------------- Enkraftsresultantens existens. Vanliga resultanter vid analys av jämvikter. Jämviktsanalys: a) Kraftanalys - rita+symboler b) Jämviktslagar- Euler 1+2 c)
1 KOMIHÅG 4: --------------------------------- Enkraftsresultantens existens. Vanliga resultanter vid analys av jämvikter. Jämviktsanalys: a) Kraftanalys - rita+symboler b) Jämviktslagar- Euler 1+2 c)
Del 2 Monteringsanvisning motor. Boxline Modern Ribbline Futura (Basic)
 Del 2 Monteringsanvisning motor Boxline Modern Ribbline Futura (Basic) Montering motor Ta fram frikopplaren och studera dess funktion. Frikopplaren löper i kedjehusets spår och "klickas" i sitt läge. Dra
Del 2 Monteringsanvisning motor Boxline Modern Ribbline Futura (Basic) Montering motor Ta fram frikopplaren och studera dess funktion. Frikopplaren löper i kedjehusets spår och "klickas" i sitt läge. Dra
Lektionsanteckningar 2: Matematikrepetition, tabeller och diagram
 Lektionsanteckningar 2: Matematikrepetition, tabeller och diagram 2.1 Grundläggande matematik 2.1.1 Potensfunktioner xmxn xm n x x x x 3 4 34 7 x x m n x mn x x 4 3 x4 3 x1 x x n 1 x n x 3 1 x 3 x0 1 1
Lektionsanteckningar 2: Matematikrepetition, tabeller och diagram 2.1 Grundläggande matematik 2.1.1 Potensfunktioner xmxn xm n x x x x 3 4 34 7 x x m n x mn x x 4 3 x4 3 x1 x x n 1 x n x 3 1 x 3 x0 1 1
Fk 74.59(8)SE. NAF-Turnex pneumatiska manöverdon
 NAF-Turnex pneumatiska manöverdon för on/off och reglering, NAF 791290/92/94, NAF 791390/92/94 Fk 74.59(8)SE 11.02 Primära egenskaper NAFs pneumatiska manöverdon är konstruerat för 90 vridningsvinkel och
NAF-Turnex pneumatiska manöverdon för on/off och reglering, NAF 791290/92/94, NAF 791390/92/94 Fk 74.59(8)SE 11.02 Primära egenskaper NAFs pneumatiska manöverdon är konstruerat för 90 vridningsvinkel och
Manual Elstyrning EL130
 Manual Elstyrning EL130-3 drifter Läs noga igenom manualen innan arbetet påbörjas! Titel Reg. Nr Sist sparad Rev. Nr Sidor EL130_rev1 100-130 2008-06-10 1 20 1 Innehållsförteckning 1 Tillverkardeklaration
Manual Elstyrning EL130-3 drifter Läs noga igenom manualen innan arbetet påbörjas! Titel Reg. Nr Sist sparad Rev. Nr Sidor EL130_rev1 100-130 2008-06-10 1 20 1 Innehållsförteckning 1 Tillverkardeklaration
TRÄNINGSINSTRUKTIONER
 I. Träningsinstruktioner för 10-12 år Teknik (Koordination) Åldern 10 till 12 år brukar kallas för den motoriska guldåldern, eftersom barn i den här åldern är särskilt mottagliga för inlärning av koordination
I. Träningsinstruktioner för 10-12 år Teknik (Koordination) Åldern 10 till 12 år brukar kallas för den motoriska guldåldern, eftersom barn i den här åldern är särskilt mottagliga för inlärning av koordination
Abstrakt algebra för gymnasister
 Abstrakt algebra för gymnasister Veronica Crispin Quinonez Sammanfattning. Denna text är föreläsningsanteckningar från föredraget Abstrakt algebra som hölls under Kleindagarna på Institutet Mittag-Leffler
Abstrakt algebra för gymnasister Veronica Crispin Quinonez Sammanfattning. Denna text är föreläsningsanteckningar från föredraget Abstrakt algebra som hölls under Kleindagarna på Institutet Mittag-Leffler
5 genvägar till mer muskler
 5 genvägar till mer muskler Idag verkar det som att allt som är större, snabbare och starkare är bättre. Normen är att gå allt mer mot det extrema. Det gäller allt från extra starka huvudvärkstabletter,
5 genvägar till mer muskler Idag verkar det som att allt som är större, snabbare och starkare är bättre. Normen är att gå allt mer mot det extrema. Det gäller allt från extra starka huvudvärkstabletter,
2013-09-03. Välkomna till Högskoleingenjörsprogrammet i byggteknik. Annika Moström Universitetslektor i byggteknik. Ingenjör.
 Välkomna till Högskoleingenjörsprogrammet i byggteknik Annika Moström Universitetslektor i byggteknik 3 Ingenjör Latinets ingénieur - uppfinning, krigsmaskin även handhavare av kastmaskin Teoretiskt och
Välkomna till Högskoleingenjörsprogrammet i byggteknik Annika Moström Universitetslektor i byggteknik 3 Ingenjör Latinets ingénieur - uppfinning, krigsmaskin även handhavare av kastmaskin Teoretiskt och
Måttinstruktioner 11/11/2013. AnySuit.se och HappyTie.se. Kroppsmått. Att förstå vid mätning. Exakta plaggmått. Plaggets längd
 Måttinstruktioner 1 AnySuit.se och HappyTie.se 2 AnySuit.se grundades 2007 och är en av de första skrädderierna på Internet. Tack vare vår långa erfarenhet har vi lärt oss kundens behov och att sy rätt
Måttinstruktioner 1 AnySuit.se och HappyTie.se 2 AnySuit.se grundades 2007 och är en av de första skrädderierna på Internet. Tack vare vår långa erfarenhet har vi lärt oss kundens behov och att sy rätt
LABORATIONSHÄFTE NUMERISKA METODER GRUNDKURS 1, 2D1210 LÄSÅRET 03/04. Laboration 3 3. Torsionssvängningar i en drivaxel
 Lennart Edsberg Nada, KTH December 2003 LABORATIONSHÄFTE NUMERISKA METODER GRUNDKURS 1, 2D1210 M2 LÄSÅRET 03/04 Laboration 3 3. Torsionssvängningar i en drivaxel 1 Laboration 3. Differentialekvationer
Lennart Edsberg Nada, KTH December 2003 LABORATIONSHÄFTE NUMERISKA METODER GRUNDKURS 1, 2D1210 M2 LÄSÅRET 03/04 Laboration 3 3. Torsionssvängningar i en drivaxel 1 Laboration 3. Differentialekvationer
Lärarmanual för Simkampen
 Lärarmanual för Simkampen Lärarmanualen är tänkt att använda som ett hjälpmedel vid simundervisningen inför Sim- kampen. Materialet innehåller ett antal övningar med skiftande svårighetsgrad och förslag
Lärarmanual för Simkampen Lärarmanualen är tänkt att använda som ett hjälpmedel vid simundervisningen inför Sim- kampen. Materialet innehåller ett antal övningar med skiftande svårighetsgrad och förslag
BERGS BALANSSKALA MANUAL
 1 BERGS BALANSSKALA MANUAL Instruktion Visa och förklara för patienten före varje moment som han/hon ska utföra. Det är det första försöket som ska poängsättas.det är därför mycket viktigt att patienten
1 BERGS BALANSSKALA MANUAL Instruktion Visa och förklara för patienten före varje moment som han/hon ska utföra. Det är det första försöket som ska poängsättas.det är därför mycket viktigt att patienten
Hanne Solem Görel Hydén Sätt in stöten! MATEMATIK
 Hanne Solem Görel Hydén Sätt in stöten! MATEMATIK Multiplika tion Multiplikation, 5-tabellen Att multiplicera är detsamma som att addera samma tal flera gånger. Det kallar vi upprepad addition. 3 5 kan
Hanne Solem Görel Hydén Sätt in stöten! MATEMATIK Multiplika tion Multiplikation, 5-tabellen Att multiplicera är detsamma som att addera samma tal flera gånger. Det kallar vi upprepad addition. 3 5 kan
TENTAMEN: Design och konstruktion av grafiska gränssnitt DAT215
 TENTAMEN: Design och konstruktion av grafiska gränssnitt DAT215 DAG: 14 mars, 2011 TID: 8.30 12.30 SAL: Hörsalsvägen Ansvarig: Olof Torgersson, tel. 772 54 06. Institutionen för tillämpad informationsteknologi.
TENTAMEN: Design och konstruktion av grafiska gränssnitt DAT215 DAG: 14 mars, 2011 TID: 8.30 12.30 SAL: Hörsalsvägen Ansvarig: Olof Torgersson, tel. 772 54 06. Institutionen för tillämpad informationsteknologi.
Övningstenta Svar och anvisningar. Uppgift 1. a) Hastigheten v(t) får vi genom att integrera: v(t) = a(t)dt
 Övningstenta 015 Svar och anvisningar Uppgift 1 a) Hastigheten v(t) får vi genom att integrera: v(t) = a(t)dt tillsammans med begynnelsevillkoret v(0) = 0. Vi får: v(t) = 0,5t dt = 1 6 t3 + C och vi bestämmer
Övningstenta 015 Svar och anvisningar Uppgift 1 a) Hastigheten v(t) får vi genom att integrera: v(t) = a(t)dt tillsammans med begynnelsevillkoret v(0) = 0. Vi får: v(t) = 0,5t dt = 1 6 t3 + C och vi bestämmer
Matematik Åk 9 Provet omfattar stickprov av det centrala innehållet i Lgr-11. 1. b) c) d)
 1. b) c) d) a) Multiplikation med 100 kan förenklas med att flytta decimalerna lika många stg som antlet nollor. 00> svar 306 b) Använd kort division. Resultatet ger igen rest. Svar 108 c) Att multiplicera
1. b) c) d) a) Multiplikation med 100 kan förenklas med att flytta decimalerna lika många stg som antlet nollor. 00> svar 306 b) Använd kort division. Resultatet ger igen rest. Svar 108 c) Att multiplicera
Underhåll av mättavlan
 1. Tillsyn efter varje skjutning 2. Tillsyn varje vecka 3. Underhållsarbete efter ca 1 500-2 000 skott 1. Tillsyn efter varje skjutning Efter varje skjutning skall tavlans fram och baksida kontrolleras.
1. Tillsyn efter varje skjutning 2. Tillsyn varje vecka 3. Underhållsarbete efter ca 1 500-2 000 skott 1. Tillsyn efter varje skjutning Efter varje skjutning skall tavlans fram och baksida kontrolleras.
