Googles sidrankning - linjär algebra värt en förmögenhet
|
|
|
- Karl-Erik Ek
- för 5 år sedan
- Visningar:
Transkript
1 Googles sidrankning - linjär algebra värt en förmögenhet
2 Outline 1 Sökmotorer 2 Grafteori Linjär algebra 3
3 Målet Utifrån användarens sökord lista de mest relevanta webbsidorna. Dessutom i en ordning som motsvarar graden av relevans för användaren.
4 Förutsättningar En första förutsättning är att man har en (alltid) aktuell databas med nödvändig information om alla sidor på internet.
5 Förutsättningar En första förutsättning är att man har en (alltid) aktuell databas med nödvändig information om alla sidor på internet. Intressantare (ur matematiksynpunkt) är den efterföljande frågeställningen:
6 Förutsättningar En första förutsättning är att man har en (alltid) aktuell databas med nödvändig information om alla sidor på internet. Intressantare (ur matematiksynpunkt) är den efterföljande frågeställningen: Hur kan man vaska fram guldkornen ur denna sörja av miljarder webbsidor.
7 Nätet är stort Sökmotorer indexerar ungefär 50 miljarder sidor (2012).
8 Nätet är stort Sökmotorer indexerar ungefär 50 miljarder sidor (2012). I stort sett varje sökning ger tusentals eller miljontals träar.
9 Nätet är stort Sökmotorer indexerar ungefär 50 miljarder sidor (2012). I stort sett varje sökning ger tusentals eller miljontals träar. Hur ska man lyckas presentera de sidor som är mest intressanta?
10 Före 1998 Då byggde sökresultaten enbart på innehållet i varje sida. Sökte efter sökorden i titel, nyckelord, adress och i texten.
11 Före 1998 Då byggde sökresultaten enbart på innehållet i varje sida. Sökte efter sökorden i titel, nyckelord, adress och i texten. Rangordningen mellan sidor byggde bara på hur viktiga sökorden var för olika sidor. Inte hur viktiga sidorna själva var.
12 Före 1998 Då byggde sökresultaten enbart på innehållet i varje sida. Sökte efter sökorden i titel, nyckelord, adress och i texten. Rangordningen mellan sidor byggde bara på hur viktiga sökorden var för olika sidor. Inte hur viktiga sidorna själva var. Man ck vara klurig för att hitta en sökning som sållade ut de sidor man var intresserad av.
13 Före 1998 Då byggde sökresultaten enbart på innehållet i varje sida. Sökte efter sökorden i titel, nyckelord, adress och i texten. Rangordningen mellan sidor byggde bara på hur viktiga sökorden var för olika sidor. Inte hur viktiga sidorna själva var. Man ck vara klurig för att hitta en sökning som sållade ut de sidor man var intresserad av. Mot slutet började nätet bli så stort att sökmotorerna var i det närmaste värdelösa.
14 Revolutionen 1998 Sökmotorn Google kom i beta-version 1998 och året efter släpptes en ociell version.
15 Revolutionen 1998 Sökmotorn Google kom i beta-version 1998 och året efter släpptes en ociell version. Plötsligt fanns det en sökmotor där sidorna du var intresserad av låg högt upp på första sidan och inte (i bästa fall) någonstans på sidan 8.
16 Revolutionen 1998 Sökmotorn Google kom i beta-version 1998 och året efter släpptes en ociell version. Plötsligt fanns det en sökmotor där sidorna du var intresserad av låg högt upp på första sidan och inte (i bästa fall) någonstans på sidan 8. Kändes som ett mirakel!
17 Inget mirakel utan smart använding av ca 100 år gammal matematik.
18 Idén i korthet Utnyttja den struktur som länkarna mellan sidorna ger.
19 Idén i korthet Utnyttja den struktur som länkarna mellan sidorna ger. Modellera detta med en riktad graf.
20 Idén i korthet Utnyttja den struktur som länkarna mellan sidorna ger. Modellera detta med en riktad graf. Använda en matris M som svarar mot slumpvandring på denna graf.
21 Idén i korthet Utnyttja den struktur som länkarna mellan sidorna ger. Modellera detta med en riktad graf. Använda en matris M som svarar mot slumpvandring på denna graf. Perron-Frobenius sats: M t har egenvärdet 1 och dess egenvektor v har bara positiva element.
22 Idén i korthet Utnyttja den struktur som länkarna mellan sidorna ger. Modellera detta med en riktad graf. Använda en matris M som svarar mot slumpvandring på denna graf. Perron-Frobenius sats: M t har egenvärdet 1 och dess egenvektor v har bara positiva element. Vektorn v ger en rankning av alla sidor.
23 Grafteori Linjär algebra Outline 1 Sökmotorer 2 Grafteori Linjär algebra 3
24 Grafteori Linjär algebra Outline 1 Sökmotorer 2 Grafteori Linjär algebra 3
25 Grafteori Linjär algebra Graf En graf består av en mängd V med noder och en mängd E med kanter. Bildligt kan man tänka sig noderna som punkter och en kant som en kurva mellan två noder
26 Grafteori Linjär algebra Graf som modell Grafer kan användas som modell för många skiftande fenomen såsom
27 Grafteori Linjär algebra Graf som modell Grafer kan användas som modell för många skiftande fenomen såsom Nätverk
28 Grafteori Linjär algebra Graf som modell Grafer kan användas som modell för många skiftande fenomen såsom Nätverk Transportförbindelser
29 Grafteori Linjär algebra Graf som modell Grafer kan användas som modell för många skiftande fenomen såsom Nätverk Transportförbindelser Datastrukturer
30 Grafteori Linjär algebra Exempel på sociala nätverk Låt V vara mängden av alla personer som publicerat minst en artikel i en matematisk tidskrift. Det nns en kant mellan två personer i V om de publicerat en artikel ihop. Eller, låt V vara alla personer som har ett konto på LinkedIn och det nns en kant mellan två personer om de har anknyntning.
31 Grafteori Linjär algebra Riktad graf I en riktad graf är kanterna enkelriktade
32 Grafteori Linjär algebra Riktad graf som modell Riktade grafer kan användas som modell för
33 Grafteori Linjär algebra Riktad graf som modell Riktade grafer kan användas som modell för Vägnät. Noderna är korsningar och kanter är vägstumpar (som ju kan vara enkelriktade) mellan korsningar.
34 Grafteori Linjär algebra Riktad graf som modell Riktade grafer kan användas som modell för Vägnät. Noderna är korsningar och kanter är vägstumpar (som ju kan vara enkelriktade) mellan korsningar. Internet. Noderna består av sidor och kanterna är länkar mellan sidor.
35 Grafteori Linjär algebra Vägar och avstånd En väg i en graf är en följd av kanter (som ligger efter varandra) och avståndet mellan två noder är längden på den kortaste vägen.
36 Grafteori Linjär algebra Erdös-talet Paul Erdös är den mest produktive (räknat i antal publicerade artiklar) matematikern genom tiderna och han skrev minst en artikel tillsammans med totalt 511 andra matematiker. Det nns alltså 511 kanter från honom till andra noder i grafen där V är mängden av alla personer som publicerat minst en artikel i en matematisk tidskrift och en kant mellan två personer i V om de publicerat en artikel ihop.
37 Grafteori Linjär algebra Erdös-talet Paul Erdös är den mest produktive (räknat i antal publicerade artiklar) matematikern genom tiderna och han skrev minst en artikel tillsammans med totalt 511 andra matematiker. Det nns alltså 511 kanter från honom till andra noder i grafen där V är mängden av alla personer som publicerat minst en artikel i en matematisk tidskrift och en kant mellan två personer i V om de publicerat en artikel ihop. En persons Erdös-tal är avståndet från personen till Erdös i denna grafen.
38 Grafteori Linjär algebra Vägar på internet En väg från en sida A till en annan sida B i den riktade grafen som representerar internet är ett sätt att klicka sig från A till B. Avståndet mellan A och B är minsta antalet klick från A till B.
39 Grafteori Linjär algebra Sammanhängande Man säger att en graf är sammanhängande om det nns väg mellan varje par av noder.
40 Grafteori Linjär algebra Slumpvandring på graf En slumpvandring på en graf är, precis som det låter, att man tar sig från nod till nod via kanter som väljs slumpmässigt
41 Grafteori Linjär algebra Outline 1 Sökmotorer 2 Grafteori Linjär algebra 3
42 Grafteori Linjär algebra Egenvärden och egenvektorer Om M är en kvadratisk matris så säger man att v är en egenvektor till M med egenvärdet λ om Mv = λv.
43 Grafteori Linjär algebra Egenvärden och egenvektorer Om M är en kvadratisk matris så säger man att v är en egenvektor till M med egenvärdet λ om Mv = λv. Med andra ord så ändrar inte M riktningen på v (möjligen motsatt riktning om λ är negativt).
44 Grafteori Linjär algebra Egenvärden och egenvektorer Om M är en kvadratisk matris så säger man att v är en egenvektor till M med egenvärdet λ om Mv = λv. Med andra ord så ändrar inte M riktningen på v (möjligen motsatt riktning om λ är negativt). Exempelvis har en identitetsmatris I alla vektorer som egenvektor med egenvärdet 1 och en matris som svarar mot rotation kring origo i planet saknar (reell) egenvektor.
45 Grafteori Linjär algebra Grannmatris För en graf med n noder är grannmatrisen den n n-matris A vars element denieras genom { 1 om kant mellan nod i och nod j (från nod i till nod j), a ij = 0 annars.
46 Grafteori Linjär algebra Exempel på grannmatris har grannmatrisen
47 Grafteori Linjär algebra Exempel på grannmatris har grannmatrisen
48 Grafteori Linjär algebra Övergångsmatris För slumpvandringen på en graf med n noder är övergångsmatrisen den n n-matris A vars element denieras genom a ij = sannolikheten att man går till nod j om man är i nod i.
49 Grafteori Linjär algebra Exempel på övergångsmatris har övergångsmatrisen /2 1/2 0 1/2 0 1/2 1/3 1/3 1/3 0
50 Grafteori Linjär algebra Exempel på övergångsmatris har övergångsmatrisen /3 1/3 1/3 0
51 Grafteori Linjär algebra Perron-Frobenius sats Sats som bevisades i 2 steg av Oskar Perron (1907) och Ferdinand Georg Frobenius (1912). I detta sammanhanget säger satsen: Om A är övergångsmatrisen för en slumpvandring på en sammanhängande graf, så gäller för transponatet A t att denna matris har egenvärdet 1 med en unik egenvektor v. Dessutom gäller att alla andra egenvärden till A t har absolutbeloppet mindre än 1 och alla element i v är positiva.
52 Outline 1 Sökmotorer 2 Grafteori Linjär algebra 3
53 Ranka sidor efter viktighetsgrad Man brukar länka till sidor som är viktiga. Ju er som länkar till en sida, desto viktigare är den.
54 Ranka sidor efter viktighetsgrad Man brukar länka till sidor som är viktiga. Ju er som länkar till en sida, desto viktigare är den. Länkar från en sida som bara länkar till några få utvalda är viktigare än länkar från en sida som länkar till många sidor.
55 Ranka sidor efter viktighetsgrad Man brukar länka till sidor som är viktiga. Ju er som länkar till en sida, desto viktigare är den. Länkar från en sida som bara länkar till några få utvalda är viktigare än länkar från en sida som länkar till många sidor. Viktiga sidor länkar till viktiga sidor. (Det är bättre att ha länkar från viktiga sidor än från mindre viktiga sidor.)
56 En formel för vikten, version 1 Låt v(p i ) vara vikten för sidan P i. Vi vill lägga ihop antalet länkar till den sida P i vi ska räkna ut vikt(ighet)en för. Om B i är mängden av sidor som länkar till P i och #(P j P i ) antalet länkar från sidan P j till sidan P i får vi v(p i ) = P j B i #(P j P i ). På detta sätt blir det väldigt lätt att skapa sidor med hög vikt. Dessa vikter svarar mot att välja godtycklig länk på nätet och följa den.
57 En formel för vikten, version 2 Antag att samtliga sidor har vikt 1 att fördela till de sidor de länkar till. Då kommer varje länk från sidan P j med l j länkar bara ge vikten 1/l j till den sida länken går till. Vi får v(p i ) = #(P j P i ). l j P j B i Något svårare att skapa sidor med hög vikt, men med hjälp av många sidor går det. Svarar mot att välja godtycklig sida på nätet och följa slumpmässig kant från den sidan.
58 En formel för vikten, version 3 Vi låter nu varje sida få sin egen vikt att fördela till de andra sidorna. Om P j har l j länkar, så ger varje länk vikten v(p j )/l j till den sida den leder till. Om B i är mängden av sidor som länkar till P i får vi då v(p i ) = v(p j )#(P j P i ). l j P j B i Svarar mot att välja en godtycklig sida och sedan upprepade gånger följa en slumpmässig kant. En slumpvandring på internet! Nu går det inte längre att själv ge hög vikt åt egna sidor. Men vi får ett annat problem.
59 En formel för vikten, version 3 Vi låter nu varje sida få sin egen vikt att fördela till de andra sidorna. Om P j har l j länkar, så ger varje länk vikten v(p j )/l j till den sida den leder till. Om B i är mängden av sidor som länkar till P i får vi då v(p i ) = v(p j )#(P j P i ). l j P j B i Svarar mot att välja en godtycklig sida och sedan upprepade gånger följa en slumpmässig kant. En slumpvandring på internet! Nu går det inte längre att själv ge hög vikt åt egna sidor. Men vi får ett annat problem. Vi måste räkna ut alla vikter samtidigt!
60 Nätet som en graf
61 ... och som (transponatet av) en övergångsmatris
62 Viktformel som matrismultiplikation Viktformeln v(p i ) = P j B i v(p j ) l j v(p 2 ) = v(p 1) 2 anger, till exempel för P 2, att + v(p 3) 2 + v(p 4). 3
63 Viktformel som matrismultiplikation Viktformeln v(p i ) = P j B i v(p j ) l j v(p 2 ) = v(p 1) 2 anger, till exempel för P 2, att + v(p 3) 2 + v(p 4). 3 Det är precis så som matrismultiplikation fungerar. Om vektorn v består av vikterna (v(p 1 ), v(p 2 ),..., v(p 8 )), så får vi som resultat Hv =
64 Viktformel som matrismultiplikation Viktformeln v(p i ) = P j B i v(p j ) l j v(p 2 ) = v(p 1) 2 anger, till exempel för P 2, att + v(p 3) 2 + v(p 4). 3 Det är precis så som matrismultiplikation fungerar. Om vektorn v består av vikterna (v(p 1 ), v(p 2 ),..., v(p 8 )), så får vi som resultat Hv = v.
65 Att räkna ut alla vikterna samtidigt Det är vektorn v som innehåller vikterna. Vi vill hitta v så att Hv = v. Med andra ord ska v vara en egenvektor med egenvärdet 1.
66 Att räkna ut alla vikterna samtidigt Det är vektorn v som innehåller vikterna. Vi vill hitta v så att Hv = v. Med andra ord ska v vara en egenvektor med egenvärdet 1. Det är lätt att beräkna egenvektorer till mycket små matriser: Man denierar ett polynom av samma grad som matrisens storlek, med koecienter från matrisen, och hittar sedan nollställen till polynomet. För Google blir det ett polynom av grad 50 miljarder. Huga!
67 En speciell matris Matrisen H är speciell på era sätt.
68 En speciell matris Matrisen H är speciell på era sätt. Den har inga negativa värden.
69 En speciell matris Matrisen H är speciell på era sätt. Den har inga negativa värden. Kolumnerna summerar till 1.
70 Perron-Frobenius sats För en matris H med icke-negativa element vars kolumner summerar till 1 gäller att
71 Perron-Frobenius sats För en matris H med icke-negativa element vars kolumner summerar till 1 gäller att den har egenvärdet 1 med unik egenvektor;
72 Perron-Frobenius sats För en matris H med icke-negativa element vars kolumner summerar till 1 gäller att den har egenvärdet 1 med unik egenvektor; alla andra egenvärden λ uppfyller λ < 1;
73 Perron-Frobenius sats För en matris H med icke-negativa element vars kolumner summerar till 1 gäller att den har egenvärdet 1 med unik egenvektor; alla andra egenvärden λ uppfyller λ < 1; egenvektorn till egenvärdet 1 har bara positiva element.
74 Iterera fram viktvektorn Antag att varje vektor kan skrivas som en summa av egenvektorer: v = a 1 v 1 + a 2 v 2 + a 3 v a n v n. Räknereglerna H(v 1 + v 2 ) = Hv 1 + Hv 2 och H(av) = a(hv) ger då Hv = H(a 1 v 1 + a 2 v 2 + a 3 v a n v n )
75 Iterera fram viktvektorn Antag att varje vektor kan skrivas som en summa av egenvektorer: v = a 1 v 1 + a 2 v 2 + a 3 v a n v n. Räknereglerna H(v 1 + v 2 ) = Hv 1 + Hv 2 och H(av) = a(hv) ger då Hv = H(a 1 v 1 + a 2 v 2 + a 3 v a n v n ) = H(a 1 v 1 ) + H(a 2 v 2 ) + H(a 3 v 3 ) H(a n v n )
76 Iterera fram viktvektorn Antag att varje vektor kan skrivas som en summa av egenvektorer: v = a 1 v 1 + a 2 v 2 + a 3 v a n v n. Räknereglerna H(v 1 + v 2 ) = Hv 1 + Hv 2 och H(av) = a(hv) ger då Hv = H(a 1 v 1 + a 2 v 2 + a 3 v a n v n ) = H(a 1 v 1 ) + H(a 2 v 2 ) + H(a 3 v 3 ) H(a n v n ) = a 1 (Hv 1 ) + a 2 (Hv 2 ) + a 3 (Hv 3 ) a n (Hv n )
77 Iterera fram viktvektorn Antag att varje vektor kan skrivas som en summa av egenvektorer: v = a 1 v 1 + a 2 v 2 + a 3 v a n v n. Räknereglerna H(v 1 + v 2 ) = Hv 1 + Hv 2 och H(av) = a(hv) ger då Hv = H(a 1 v 1 + a 2 v 2 + a 3 v a n v n ) = H(a 1 v 1 ) + H(a 2 v 2 ) + H(a 3 v 3 ) H(a n v n ) = a 1 (Hv 1 ) + a 2 (Hv 2 ) + a 3 (Hv 3 ) a n (Hv n ) = a 1 λ 1 v 1 + a 2 λ 2 v 2 + a 3 λ 3 v a n λ n v n
78 Iterera fram viktvektorn Antag att varje vektor kan skrivas som en summa av egenvektorer: v = a 1 v 1 + a 2 v 2 + a 3 v a n v n. Räknereglerna H(v 1 + v 2 ) = Hv 1 + Hv 2 och H(av) = a(hv) ger då Hv = H(a 1 v 1 + a 2 v 2 + a 3 v a n v n ) = H(a 1 v 1 ) + H(a 2 v 2 ) + H(a 3 v 3 ) H(a n v n ) = a 1 (Hv 1 ) + a 2 (Hv 2 ) + a 3 (Hv 3 ) a n (Hv n ) = a 1 λ 1 v 1 + a 2 λ 2 v 2 + a 3 λ 3 v a n λ n v n H 2 v = a 1 λ 2 1 v 1 + a 2 λ 2 2 v 2 + a 3 λ 2 3 v a n λ 2 n v n
79 Iterera fram viktvektorn Antag att varje vektor kan skrivas som en summa av egenvektorer: v = a 1 v 1 + a 2 v 2 + a 3 v a n v n. Räknereglerna H(v 1 + v 2 ) = Hv 1 + Hv 2 och H(av) = a(hv) ger då Hv = H(a 1 v 1 + a 2 v 2 + a 3 v a n v n ) = H(a 1 v 1 ) + H(a 2 v 2 ) + H(a 3 v 3 ) H(a n v n ) = a 1 (Hv 1 ) + a 2 (Hv 2 ) + a 3 (Hv 3 ) a n (Hv n ) = a 1 λ 1 v 1 + a 2 λ 2 v 2 + a 3 λ 3 v a n λ n v n H 2 v = a 1 λ 2 1 v 1 + a 2 λ 2 2 v 2 + a 3 λ 2 3 v a n λ 2 n v n H 3 v = a 1 λ 3 1 v 1 + a 2 λ 3 2 v 2 + a 3 λ 3 3 v a n λ 3 n v n
80 Iterera fram viktvektorn Antag att varje vektor kan skrivas som en summa av egenvektorer: v = a 1 v 1 + a 2 v 2 + a 3 v a n v n. Räknereglerna H(v 1 + v 2 ) = Hv 1 + Hv 2 och H(av) = a(hv) ger då Hv = H(a 1 v 1 + a 2 v 2 + a 3 v a n v n ) = H(a 1 v 1 ) + H(a 2 v 2 ) + H(a 3 v 3 ) H(a n v n ) = a 1 (Hv 1 ) + a 2 (Hv 2 ) + a 3 (Hv 3 ) a n (Hv n ) = a 1 λ 1 v 1 + a 2 λ 2 v 2 + a 3 λ 3 v a n λ n v n H 2 v = a 1 λ 2 1 v 1 + a 2 λ 2 2 v 2 + a 3 λ 2 3 v a n λ 2 n v n H 3 v = a 1 λ 3 1 v 1 + a 2 λ 3 2 v 2 + a 3 λ 3 3 v a n λ 3 n v n H 4 v = a 1 λ 4 1 v 1 + a 2 λ 4 2 v 2 + a 3 λ 4 3 v a n λ 4 n v n.
81 Iterera fram viktvektorn Antag att varje vektor kan skrivas som en summa av egenvektorer: v = a 1 v 1 + a 2 v 2 + a 3 v a n v n. Räknereglerna H(v 1 + v 2 ) = Hv 1 + Hv 2 och H(av) = a(hv) ger då Hv = H(a 1 v 1 + a 2 v 2 + a 3 v a n v n ) = H(a 1 v 1 ) + H(a 2 v 2 ) + H(a 3 v 3 ) H(a n v n ) = a 1 (Hv 1 ) + a 2 (Hv 2 ) + a 3 (Hv 3 ) a n (Hv n ) = a 1 λ 1 v 1 + a 2 λ 2 v 2 + a 3 λ 3 v a n λ n v n H 2 v = a 1 λ 2 1 v 1 + a 2 λ 2 2 v 2 + a 3 λ 2 3 v a n λ 2 n v n H 3 v = a 1 λ 3 1 v 1 + a 2 λ 3 2 v 2 + a 3 λ 3 3 v a n λ 3 n v n H 4 v = a 1 λ 4 1 v 1 + a 2 λ 4 2 v 2 + a 3 λ 4 3 v a n λ 4 n v n. Om λ 1 = 1 och λ i < 1 för i 2 så går H j v mot a 1 v 1.
82 Ger egenvektorn en ranking Eftersom egenvektorn bara innehåller positiva element blir det en ranking.
83 En slutgiltig formel för vikten I själva verket så inför man en dämpningsfaktor för att ta hand om det faktum att nätet inte är sammanhängande och att vissa sidor saknar utgående länkar. Dämpningsfaktorn kan man tänka på som sannolikheten att en person väljer en länk på sidan och inte väljer en sida på måfå. Om vi betecknar dämpningsfaktorn med d och totala antalet sidor men N så blir den slutgiltiga formeln v(p i ) = 1 d N + d v(p j )#(P j P i ). l j P j B i Beräkningen med hjälp av denna formel blir i stort sett samma som utan dämpningsfaktor.
Rangordning av internetsidor - ett egenvärdesproblem för positiva matriser
 Rangordning av internetsidor - ett egenvärdesproblem för positiva matriser Ett litet nätverk med 8 noder och ett antal länkar mellan noderna: 8 1 2 7 3 6 5 4 Hur kan vi rangordna noder? Vilken är viktigast?
Rangordning av internetsidor - ett egenvärdesproblem för positiva matriser Ett litet nätverk med 8 noder och ett antal länkar mellan noderna: 8 1 2 7 3 6 5 4 Hur kan vi rangordna noder? Vilken är viktigast?
Grafer och grannmatriser
 Föreläsning 2, Linjär algebra IT VT2008 Som avslutning på kursen ska vi knyta samman linjär algebra med grafteori och sannolikhetsteori från första kursen. Resultatet blir så kallade slumpvandringar på
Föreläsning 2, Linjär algebra IT VT2008 Som avslutning på kursen ska vi knyta samman linjär algebra med grafteori och sannolikhetsteori från första kursen. Resultatet blir så kallade slumpvandringar på
Föreläsn. anteckn. TMV206-VT13. Vecka 6-7. Egenvärden och Egenvektorer. Kap. 8-9
 Föreläsn. Anteckn., Linjär algebra IT VT2013/Genkai Zhang 1 Föreläsn. anteckn. TMV206-VT13. Vecka 6-7. Egenvärden och Egenvektorer. Kap. 8-9 Det tredje huvuda momentet av kursen är egenvektorer/egenvärden
Föreläsn. Anteckn., Linjär algebra IT VT2013/Genkai Zhang 1 Föreläsn. anteckn. TMV206-VT13. Vecka 6-7. Egenvärden och Egenvektorer. Kap. 8-9 Det tredje huvuda momentet av kursen är egenvektorer/egenvärden
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Repetera hur man nner bas för rum som spänns upp av några vektorer Reptetera hur man nner bas för summa och snitt av delrum. Reptetera
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Repetera hur man nner bas för rum som spänns upp av några vektorer Reptetera hur man nner bas för summa och snitt av delrum. Reptetera
Föreläsn. anteckn. HT13. Vecka 6-7. Egenvärden och Egenvektorer. Slumpvandringar på Grafer. Kap. 8-9
 Föreläsn. Anteckn., Linjär algebra D HT01/Genkai Zhang 1 Föreläsn. anteckn. HT1. Vecka 6-7. Egenvärden och Egenvektorer. Slumpvandringar på Grafer. Kap. 8-9 Det 4:de huvuda momentet av kursen är egenvektorer/egenvärden
Föreläsn. Anteckn., Linjär algebra D HT01/Genkai Zhang 1 Föreläsn. anteckn. HT1. Vecka 6-7. Egenvärden och Egenvektorer. Slumpvandringar på Grafer. Kap. 8-9 Det 4:de huvuda momentet av kursen är egenvektorer/egenvärden
Egenvärden och egenvektorer
 Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Lösningar till utvalda uppgifter i kapitel 8
 Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Tentamen i Linjär algebra (TATA31/TEN1) ,
 Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra TATA/TEN) 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra TATA/TEN) 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
SF1624 Algebra och geometri Tentamen Torsdag, 17 mars 2016
 SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Självkoll: Ser du att de två uttrycken är ekvivalenta?
 ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Crash Course Algebra och geometri. Ambjörn Karlsson c januari 2016
 Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
UPPSALA UNIVERSITET Matematiska institutionen Styf. Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 2004
 UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
Linjär Algebra, Föreläsning 20
 Linjär Algebra, Föreläsning 20 Tomas Sjödin Linköpings Universitet Symmetriska avbildningar, repetition F : E E sägs vara symmetrisk om (F (u) v) = (u F (v)) gäller för all u, v i det Euklidiksa rummet
Linjär Algebra, Föreläsning 20 Tomas Sjödin Linköpings Universitet Symmetriska avbildningar, repetition F : E E sägs vara symmetrisk om (F (u) v) = (u F (v)) gäller för all u, v i det Euklidiksa rummet
Geometriska vektorer
 Föreläsning 1, Linjär algebra IT VT2008 1 Geometriska vektorer De begrepp som linjär algebra kretsar kring är vektorer och matriser Dessa svarar mot datorernas fält (`arra') av dimension ett respektive
Föreläsning 1, Linjär algebra IT VT2008 1 Geometriska vektorer De begrepp som linjär algebra kretsar kring är vektorer och matriser Dessa svarar mot datorernas fält (`arra') av dimension ett respektive
Diagonalisering och linjära system ODE med konstanta koe cienter.
 Diagonalisering och linjära system ODE med konstanta koe cienter. Variabelbyte i linjära system di erentialekvationer. Målet med det kapitlet i kursen är att lösa linjära system di erentialekvationer på
Diagonalisering och linjära system ODE med konstanta koe cienter. Variabelbyte i linjära system di erentialekvationer. Målet med det kapitlet i kursen är att lösa linjära system di erentialekvationer på
SF1624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 2010 DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Tentamen i Linjär algebra , 8 13.
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: ETE5 Provkod: TEN Tentamen i Linjär algebra 5 8, 8. Inga hjälpmedel. Ej räknedosa. Resultatet meddelas vi e-post. För godkänt räcker
LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: ETE5 Provkod: TEN Tentamen i Linjär algebra 5 8, 8. Inga hjälpmedel. Ej räknedosa. Resultatet meddelas vi e-post. För godkänt räcker
Tentamen i ETE305 Linjär algebra , 8 13.
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk ( p) ( p) ( p) ( p) ( p) ( p) Tentamen i ETE Linjär algebra, 8. Inga hjälpmedel. Ej räknedosa. Resultatet meddelas vi e-post. För godkänt räcker
LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk ( p) ( p) ( p) ( p) ( p) ( p) Tentamen i ETE Linjär algebra, 8. Inga hjälpmedel. Ej räknedosa. Resultatet meddelas vi e-post. För godkänt räcker
1. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x 1 = (2, 3, 5), x 2 = (3, 1, 1) och x 3 = (1, 3, 0).
 N-institutionen Mikael Forsberg 06-64 89 6 Prov i matematik Matematik med datalogi, mfl. Linjär algebra mk06a Testtenta. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x = (,, 5),
N-institutionen Mikael Forsberg 06-64 89 6 Prov i matematik Matematik med datalogi, mfl. Linjär algebra mk06a Testtenta. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x = (,, 5),
Laboration 0: Del 2. Benjamin Kjellson Introduktion till matriser, vektorer, och ekvationssystem
 Laboration 0: Del 2 Benjamin Kjellson 2016 03 21 Introduktion till matriser, vektorer, och ekvationssystem I den här filen får ni en kort introduktion till hur man hanterar och räknar med matriser i R,
Laboration 0: Del 2 Benjamin Kjellson 2016 03 21 Introduktion till matriser, vektorer, och ekvationssystem I den här filen får ni en kort introduktion till hur man hanterar och räknar med matriser i R,
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
Lösningar till MVE021 Linjär algebra för I
 Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
x + y + z + 2w = 0 (a) Finn alla lösningar till ekvationssystemet y + z+ 2w = 0 (2p)
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
SF1624 Algebra och geometri Tentamen Onsdag, 13 januari 2016
 SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
19. Spektralsatsen Spektralsatsen SPEKTRALSATSEN
 9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
Linjär algebra Föreläsning 10
 Linjär algebra Föreläsning 10 IT-programmet, Chalmers 2006 Samuel Bengmark Repetition Handlade om kvadratiska matriser. Kvadratiska ekvationssystem har: Unik lösning omm Det(A) 0. Har oändligt antal lösningar
Linjär algebra Föreläsning 10 IT-programmet, Chalmers 2006 Samuel Bengmark Repetition Handlade om kvadratiska matriser. Kvadratiska ekvationssystem har: Unik lösning omm Det(A) 0. Har oändligt antal lösningar
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 15 mars 2012 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF604, den 5 mars 202 kl 08.00-3.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF604, den 5 mars 202 kl 08.00-3.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Linjär algebra kurs TNA002
 Linjär algebra kurs TNA002 Lektionsanteckningar klass ED1 I detta dokument finns ett utdrag av de tavelanteckningar som uppkommit under lektionstid under kursen TNA002. Alltså kan detta dokument långt
Linjär algebra kurs TNA002 Lektionsanteckningar klass ED1 I detta dokument finns ett utdrag av de tavelanteckningar som uppkommit under lektionstid under kursen TNA002. Alltså kan detta dokument långt
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Determinanter, egenvectorer, egenvärden.
 Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
4x az = 0 2ax + y = 0 ax + y + z = 0
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING LINJÄR ALGEBRA 206-03-4 kl 8 3 INGA HJÄLPMEDEL Lösningarna skall vara försedda med ordentliga motiveringar Alla koordinatsystem får antas vara ortonormerade
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
Prov i matematik F2, X2, ES3, KandFys2, Lärare, Frist, W2, KandMat1, Q2 LINJÄR ALGEBRA II
 UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Bo Styf Prov i matematik F, X, ES, KandFys, Lärare, Frist, W, KandMat1, Q LINJÄR ALGEBRA II 010 08 4 Skrivtid: 1400 1900 Tillåtna hjälpmedel:
UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Bo Styf Prov i matematik F, X, ES, KandFys, Lärare, Frist, W, KandMat1, Q LINJÄR ALGEBRA II 010 08 4 Skrivtid: 1400 1900 Tillåtna hjälpmedel:
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
6.1 Skalärprodukt, norm och ortogonalitet. TMV141 Linjär algebra E VT 2011 Vecka 6. Lärmål 6.1. Skalärprodukt. Viktiga begrepp
 6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
SF1624 Algebra och geometri Tentamen med lösningsförslag onsdag, 11 januari 2017
 SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
SF64 Algebra och geometri Tentamen med lösningsförslag onsdag, januari 7. (a) För vilka värden på k har ekvationssystemet (med avseende på x, y och z) kx + ky + z 3 x + ky + z 4x + 3y + 3z 8 en entydig
LÖSNINGAR TILL LINJÄR ALGEBRA kl 8 13 LUNDS TEKNISKA HÖGSKOLA MATEMATIK. 1. Volymen med tecken ges av determinanten.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR TILL LINJÄR ALGEBRA 2018-08-29 kl 8 1 1 Volymen med tecken ges av determinanten a 2 2 2 4 2 1 2a 1 = a 2 2 2 0 4 2 = 4(a 2)(1 a) 0 2a 1 Parallellepipedens volym
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
Linjär Algebra 764G01: Kommentarer och läsanvisningar till kursboken
 Linjär Algebra 764G01: Kommentarer och läsanvisningar till kursboken Här följer kommentarer om sånt i boken som kan behövas förtydligas samt anvisningar om vad som ska läsas, eller snarare vilka delar
Linjär Algebra 764G01: Kommentarer och läsanvisningar till kursboken Här följer kommentarer om sånt i boken som kan behövas förtydligas samt anvisningar om vad som ska läsas, eller snarare vilka delar
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
November 24, Egenvärde och egenvektor. (en likformig expansion med faktor 2) (en rotation 30 grader moturs)
 Fö : November 4, 7 Egenvärde och egenvektor Definition s 9: Låt A resp T : R n R n vara en n n-matris resp en linjär avbildning En icke-trivial vektor v R n kallas en egenvektor till A resp till T med
Fö : November 4, 7 Egenvärde och egenvektor Definition s 9: Låt A resp T : R n R n vara en n n-matris resp en linjär avbildning En icke-trivial vektor v R n kallas en egenvektor till A resp till T med
Egenvärden och egenvektorer. Linjär Algebra F15. Pelle
 Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)
![A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p) A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)](/thumbs/93/112249032.jpg) SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
Chalmers tekniska högskola Datum: kl Telefonvakt: Linnea Hietala MVE480 Linjär algebra S
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
8(x 1) 7(y 1) + 2(z + 1) = 0
 Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösningsförsök till tentamensskrivningen på kursen Linjär algebra, SF60, den juni 0 kl 08.00-.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
tal. Mängden av alla trippel av reella tal betecknas med R 3 och x 1 x 2 En sekvens av n reella tal betecknas med (x 1, x 2,, x n ) eller
 Augusti, 5 Föreläsning Tillämpad linjär algebra Innehållet: linjen R, planet R, rummet R, oh vektor rummet R n Matriser punkter oh vektorer i planet, rummet, oh R n Linjen, planet, rummet, oh vektor rummet
Augusti, 5 Föreläsning Tillämpad linjär algebra Innehållet: linjen R, planet R, rummet R, oh vektor rummet R n Matriser punkter oh vektorer i planet, rummet, oh R n Linjen, planet, rummet, oh vektor rummet
Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA
 UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
Tentamen i Linjär algebra (TATA31/TEN1) ,
 Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN) 9 6, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst
Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN) 9 6, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst
LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING 1
 STOCKHOLMS UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra II LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING Lös ekvationssystemet x + y + z 9 x + 4y 3z 3x + 6z 5z med hjälp av Gausselimination Lösning:
STOCKHOLMS UNIVERSITET MATEMATISKA INSTITUTIONEN Linjär algebra II LÖSNINGAR TILL UPPGIFTER TILL RÄKNEÖVNING Lös ekvationssystemet x + y + z 9 x + 4y 3z 3x + 6z 5z med hjälp av Gausselimination Lösning:
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
Uppgifter, 2015 Tillämpad linjär algebra
 Geometri. Uppgifter, 25 Tillämpad linjär algebra. Uppgift. Låt (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av linjära
Geometri. Uppgifter, 25 Tillämpad linjär algebra. Uppgift. Låt (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av linjära
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2016-05-10 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 2016-05-10 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Tentamen i Linjär algebra (TATA31/TEN1) ,
 Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN) 7 8 9, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst
Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN) 7 8 9, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst
Del 1: Godkäntdelen. TMV142 Linjär algebra Z
 MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 130313 kl 0830 1230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV142 Linjär algebra Z Tentan
MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 130313 kl 0830 1230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV142 Linjär algebra Z Tentan
ax + y + 4z = a x + y + (a 1)z = 1. 2x + 2y + az = 2 Ange dessutom samtliga lösningar då det finns oändligt många.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
Institutionen för Matematiska Vetenskaper TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F1/TM1, TMA671 2014-05-26
 Institutionen för Matematiska Vetenskaper Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F/TM, TMA67 4-5-6 DAG: Måndag 6 maj 4 TID: 4. - 8. SAL: V Ansvarig: Ivar Gustafsson, tel: 75-33545 Förfrågningar:
Institutionen för Matematiska Vetenskaper Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F/TM, TMA67 4-5-6 DAG: Måndag 6 maj 4 TID: 4. - 8. SAL: V Ansvarig: Ivar Gustafsson, tel: 75-33545 Förfrågningar:
ANDRAGRADSKURVOR Vi betraktar ekvationen
 ANDRAGRADSKURVOR Vi betraktar ekvationen Ax + Bxy + Cy + Dx + Fy + G 0 (ekv) där minst en av A,B, eller C är skild från 0 En andragradskurva är mängden av alla punkter vilkas koordinater satisfierar en
ANDRAGRADSKURVOR Vi betraktar ekvationen Ax + Bxy + Cy + Dx + Fy + G 0 (ekv) där minst en av A,B, eller C är skild från 0 En andragradskurva är mängden av alla punkter vilkas koordinater satisfierar en
TMV206: Linjär algebra
 Matematiska vetenskaper Lösningsförslag till tentamen Chalmers tekniska högskola 2018-06-07, 14:00 18:00 TMV206: Linjär algera Uppgift 1 Linjerna skär varandra om det finns någon punkt (x,y, z) som uppfyller
Matematiska vetenskaper Lösningsförslag till tentamen Chalmers tekniska högskola 2018-06-07, 14:00 18:00 TMV206: Linjär algera Uppgift 1 Linjerna skär varandra om det finns någon punkt (x,y, z) som uppfyller
TAMS79: Föreläsning 10 Markovkedjor
 TAMS79: Föreläsning 0 Markovkedjor Johan Thim december 08 0. Markovkedjor Vi ska nu betrakta en speciell tidsdiskret diskret stokastisk process, nämligen Markovkedjan. Vi börjar med en definition Definition.
TAMS79: Föreläsning 0 Markovkedjor Johan Thim december 08 0. Markovkedjor Vi ska nu betrakta en speciell tidsdiskret diskret stokastisk process, nämligen Markovkedjan. Vi börjar med en definition Definition.
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 april 5 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 8- Hjälpmedel : Inga hjälpmedel
12. SINGULÄRA VÄRDEN. (u Av) u v
 . SINGULÄRA VÄRDEN Vårt huvudresultat sen tidigare är Sats.. Varje n n matris A kan jordaniseras, dvs det finns en inverterbar matris S sån att S AS J där J är en jordanmatris. Om u och v är två kolonnvektorer
. SINGULÄRA VÄRDEN Vårt huvudresultat sen tidigare är Sats.. Varje n n matris A kan jordaniseras, dvs det finns en inverterbar matris S sån att S AS J där J är en jordanmatris. Om u och v är två kolonnvektorer
5 Linjär algebra. 5.1 Addition av matriser 5 LINJÄR ALGEBRA
 5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
5 LINJÄR ALGEBRA 5 Linjär algebra En kul gren av matematiken som inte fått speciellt mycket utrymme i gymnasiet men som har många tillämpningsområden inom t.ex. fysik, logistik, ekonomi, samhällsplanering
SF1624 Algebra och geometri Lösningsförsag till modelltentamen
 SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
Instuderingsuppgifter & Läsanvisningar till Linjär Algebra II för lärare
 Instuderingsuppgifter & Läsanvisningar till Linjär Algebra II för lärare Per Alexandersson February 27, 2013 Abstract Här är läsanvisningar samt några kompletterande uppgifter till materialet i kursboken
Instuderingsuppgifter & Läsanvisningar till Linjär Algebra II för lärare Per Alexandersson February 27, 2013 Abstract Här är läsanvisningar samt några kompletterande uppgifter till materialet i kursboken
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
Lösningar kommer att läggas ut på kurshemsidan första arbetsdagen efter tentamenstillfället. Resultat meddelas via epost från LADOK.
 Matematik Chalmers tekniska högskola 8-8-7 Tentamen Linjär algebra D (TMV6), Linjär algebra GU (MMGD) Telefonvakt: Carl Lundholm, ankn 679 Plats och tid: Johanneberg, 4:-8: Inga hjälpmedel. Kalkylator
Matematik Chalmers tekniska högskola 8-8-7 Tentamen Linjär algebra D (TMV6), Linjär algebra GU (MMGD) Telefonvakt: Carl Lundholm, ankn 679 Plats och tid: Johanneberg, 4:-8: Inga hjälpmedel. Kalkylator
Lösning av tentamensskrivning på kursen Linjär algebra, SF1604, för CDATE, CTFYS och vissa CL, tisdagen den 20 maj 2014 kl
 1 Matematiska Institutionen, KTH Lösning av tentamensskrivning på kursen Linjär algebra, SF1604, för CDATE, CTFYS och vissa CL, tisdagen den 20 maj 2014 kl 08.00-13.00. Examinator: Olof Heden. OBS: Inga
1 Matematiska Institutionen, KTH Lösning av tentamensskrivning på kursen Linjär algebra, SF1604, för CDATE, CTFYS och vissa CL, tisdagen den 20 maj 2014 kl 08.00-13.00. Examinator: Olof Heden. OBS: Inga
A = v 2 B = = (λ 1) 2 16 = λ 2 2λ 15 = (λ 5)(λ+3). E 5 = Span C =
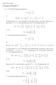 KTH Matematik Lösningar till Kapitel 7 A a Karakteristiska polynomet av detλi A det A λ λ λ b Egenvdena av A nollställen till karakteristiska polynomet alltså har A egenvdet λ c Motsvarande egenrum E lösningsrummet
KTH Matematik Lösningar till Kapitel 7 A a Karakteristiska polynomet av detλi A det A λ λ λ b Egenvdena av A nollställen till karakteristiska polynomet alltså har A egenvdet λ c Motsvarande egenrum E lösningsrummet
Inför tentamen i Linjär algebra TNA002.
 Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
A = x
 Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Egenvärden, egenvektorer
 Egenvärden, egenvektorer Om en matris är kvadratisk (dvs n n) kan vi beräkna egenvärden och egenvektorer till matrisen. Polynomet p(λ) = det(a λi) kallas det karakterisktiska polynomet för A. Ett nollställe
Egenvärden, egenvektorer Om en matris är kvadratisk (dvs n n) kan vi beräkna egenvärden och egenvektorer till matrisen. Polynomet p(λ) = det(a λi) kallas det karakterisktiska polynomet för A. Ett nollställe
LYCKA TILL! kl 8 13
 LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
LUNDS TEKNISK HÖGSKOL MTEMTIK TENTMENSSKRIVNING Linjär algebra 0 0 kl 8 3 ING HJÄLPMEDEL Förklara dina beteckningar och motivera lösningarna väl Om inget annat anges är koordinatsystemen ortonormerade
3 1 = t 2 2 = ( 1) ( 2) 1 2 = A(t) = t 1 10 t
 SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF1624 Algebra och geometri Bedömningskriterier till tentamen Tisdagen den 15 december, 2009
 SF1624 Algebra och geometri Bedömningskriterier till tentamen Tisdagen den 15 december, 2009 Allmänt gäller följande: Om lösningen helt saknar förklarande text till beräkningar och formler ges högst två
SF1624 Algebra och geometri Bedömningskriterier till tentamen Tisdagen den 15 december, 2009 Allmänt gäller följande: Om lösningen helt saknar förklarande text till beräkningar och formler ges högst två
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
x 1(t) = x 2 (t) x 2(t) = x 1 (t)
 Differentialekvationer II Modellsvar till räkneövning 4 16.4. 218 (kl 12-14 B222) 1. Lös det linjära homogena DE-systemet x 1(t) = x 2 (t) x 2(t) = x 1 (t) med matrismetoden. Påminnelse: egenvärden och
Differentialekvationer II Modellsvar till räkneövning 4 16.4. 218 (kl 12-14 B222) 1. Lös det linjära homogena DE-systemet x 1(t) = x 2 (t) x 2(t) = x 1 (t) med matrismetoden. Påminnelse: egenvärden och
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
P Q = ( 2, 1, 1), P R = (0, 1, 0) och QR = (2, 2, 1). arean = 1 2 P Q P R
 1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
1 Matematiska Institutionen KTH Lösningar till några övningar på geometri och vektorer inför lappskrivning nummer 2 på kursen Linjär algebra II, SF1604, vt11. 1. En triangel har hörn i punkterna (1, 2,
Multiplicera 7med A λ 1 I från vänster: c 1 (Av 1 λ 1 v 1 )+c 2 (Av 2 λ 1 v 2 )+c 3 (Av 3 λ 1 v 3 ) = 0
 Diagonalisering Anm. Begreppet diagonaliserbarhet är relevant endast för linjära avbildningar mellan rum av samma dimension, d.v.s. sådana som representeras av kvadratiska matriser. När vi i fortsättningen
Diagonalisering Anm. Begreppet diagonaliserbarhet är relevant endast för linjära avbildningar mellan rum av samma dimension, d.v.s. sådana som representeras av kvadratiska matriser. När vi i fortsättningen
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
Lösningar till utvalda uppgifter i kapitel 1
 Lösningar till utvalda uppgifter i kapitel.3 Vi utnyttjar definitionen av skalärprodukt som ger att cos α = u v u v, där α är (minsta vinkeln mellan u och v. I vårt fall så får vi cos α = 7 4 4 =. Alltså
Lösningar till utvalda uppgifter i kapitel.3 Vi utnyttjar definitionen av skalärprodukt som ger att cos α = u v u v, där α är (minsta vinkeln mellan u och v. I vårt fall så får vi cos α = 7 4 4 =. Alltså
