Dagens Teori. Figur 12.1:

Transkript

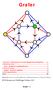
1 Dagens Teori 12.1 Grafer Del II Grafer i Mathematica Definition Genom paketen Combinatorica och GraphUtilities får vi tillgång till en mängd rutiner och fördefinierade grafer för lösandet av problem i grafteorin. En Graph definierad i Combinatorica är en struktur vi först ska titta närmare på. Vi startar med att skapa en slumpmässig graf med 5 moder. Sannolikheten att en bestämd båge mellan två noder ska finnas med är 0.5. m = RandomGraph[5, 0.5 ShowGraph[m Resultatet ser vi i figur 12.1 Figur 12.1: m[[1 {{{1,2}},{{1,3}},{{1,4}},{{2,4}},{{3,4}},{{1,5}},{{2,5}}} m[[2 {{{ , }},{{ , }},{{ , }} {{ , }},{{1.,0}}} m[[1 ger en lista över bågarna och m[[2 en lista över de fem noderna med framslumpade koordinater. Genom följande satser kan vi tilldela grafen m olika egenskaper Håkan Strömberg 1 KTH STH

2 12.1. GRAFER DEL II m = SetEdgeWeights[m, 10*Range[Length[m[[1 m = SetEdgeLabels[m, GetEdgeWeights[m m = SetVertexWeights[m, 100*Range[5 m = SetVertexLabels[m, {"A", "B", "C", "D", "E"} ShowGraph[m, EdgeLabel -> True, VertexLabel -> True Varje båge får en vikt, här 10,20,...70 Varje båge får en etikett som här överensstämmer med vikten Varje nod får en vikt, här 100,200,...,500 Varje nod får en etikett, här A,B,C,D,E När vi nu plottar grafen får vi Figur 12.2: Efter dessa tilldelningar har m följande innehåll: m[[1 {{{1, 2}, EdgeWeight->10, EdgeLabel->10}, {{1, 3}, EdgeWeight->20, EdgeLabel->20}, {{1, 4}, EdgeWeight->30, EdgeLabel->30}, {{2, 4}, EdgeWeight->40, EdgeLabel->40}, {{3, 4}, EdgeWeight->50, EdgeLabel->50}, {{1, 5}, EdgeWeight->60, EdgeLabel->60}, {{2, 5}, EdgeWeight->70, EdgeLabel->70}} m[[2 {{{ , },VertexWeight->100,VertexLabel->"A"}, {{ , },VertexWeight->200,VertexLabel->"B"}, {{ , },VertexWeight->300,VertexLabel->"C"}, {{ , },VertexWeight->400,VertexLabel->"D"}, {{1., 0}, VertexWeight->500,VertexLabel->"E"}} Med hjälp av s = RandomGraph[8, 0.5, Type->Directed UndirectedQ[s False kan vi se till att vi får en riktad graf. Med denna introduktion har vi nu en uppfattning om de data en graf kan innehålla. Håkan Strömberg 2 KTH STH

3 Fördefinierade grafer I Mathematica, finns en mängd fördefinierade grafer. Genom kommandot GraphData[ Classes får man en lista över de olika klasserna av grafer som finns i databasen. Väljer vi till exempel Paulus och skriver GraphData[ Paulus får vi en lista över de 25 graferna som i denna klass. Vill vi se till exempel Paulus {25,1} skriver man GraphData[{ Paulus, {25,1}} Figur 12.3: Graferna kan kombineras med en mängd olika egenskaper och data. De olika egenskaperna listas genom GraphData[ Properties. Genom g = GraphData[{ Paulus, {25, 1}}, VertexCount 25 g = GraphData[{ Paulus, {25, 1}}, EdgeCount 150 Vi får reda på att grafen har 25 noder och 150 bågar. Googlar vi på Paulus Graph får vi reda på att denna graf med 25 noder är en strongly regular graf. En graf där varje nod har 12 grannar. Varje grannpar har 5 gemensamma grannar och alla par av noder som inte är grannar har 6 gemensamma grannar. Så när vi skriver GraphData[{ Paulus, {25, 1}}, StronglyRegular True får vi det förväntade svaret. Eulersk graf En eulersk graf är en graf G som har en krets som går genom varje båge i grafen exakt en gång. En graf kan också ha en väg som går genom varje båge i grafen exakt en gång utan att för den skull behöva börja och sluta i samma nod. Till vänster i figur 12.5 ser vi en graf som varken har en eulersk krets eller eulersk väg. Grafen mitt i figuren har en eulersk väg men inte krets. Grafen till höger har en eulersk krets och därmed en eulersk väg. Håkan Strömberg 3 KTH STH

4 12.1. GRAFER DEL II Figur 12.4: Det var så den började grafteorin med sju broar i Königsberg Är det möjligt att gå över de sju broarna utan att gå över samma bro mer än en gång. Du får starta var du vill! Figur 12.5: Skriver vi Length[GraphData[All får vi reda på att det finns 3203 grafer i databasen. Genom b = GraphData[All, "Eulerian"; Count[b, True får vi reda på att 1449 är eulerska. Följande måste gälla för att en graf ska ha en eulerväg eller eulerkrets: En graf har en eulerkrets om och endast om grafen är sammanhängande och alla noder har jämnt gradtal. En graf har en eulerväg om och endast om grafen är sammanhängande och högst två noder har udda grad. Med denna kunskap ser vi direkt resultatet i figur Om vi slumpar fram grafer med givna data, kan vi ta reda på hur många av dem som eulerska n = 0; For[i = 1, i <= 1000, i++, g = RandomGraph[7, 0.4; If[EulerianQ[g, n++ n Håkan Strömberg 4 KTH STH

5 Endast 11 av 1000 framslumpade grafer hade denna egenskap. Byter vi ut 0.4 mot 1 ovan kommer alla grafer att vara eulerska. Men skriver vi RandomGraph[6, 1 kommer inte en enda en att vara eulersk. Vad beror det på? Hamiltonisk graf En graf sägs vara hamiltonisk om den har en krets som går genom varje nod i grafen exakt en gång. En graf kan också ha en hamiltonisk väg. En väg som går genom samtliga noder exakt en gång, men inte behöver sluta i den nod den börjar. Hur många av graferna i databasen är hamiltoniska? b = GraphData[All, "Hamiltonian"; Count[b, True 4448, visar det sig. Men är det verkligen vanligare med hamiltoniska grafer än eulerska. Vi gör ett nytt slumpförsök f[n_:=block[{he=0, nenh=0, neh=0, enh=0, i, ok, g, s1, s2}, For[i = 1, i <= n, i++, ok = False; While[! ok, g = RandomGraph[7, 0.5; ok = ConnectedQ[g; ; s1 = EulerianQ[g; s2 = HamiltonianQ[g; If[s1 && s2, he++, If[! s1 &&! s2, nenh++, If[! s1 && s2, neh++, If[s1 &&! s2, enh++ ; {he, nenh, neh, enh} Simuleringen ger 9 som är både och, 522 som är varken eller, 462 som inte är eulerska men hamiltoniska och 7 stycken som är eulerska men inte hamiltoniska. Om det inte räcker med att veta att en graf är hamiltonisk kan man få en av lösningarna utritad som i figur 12.6, med hjälp av denna sekvens. Håkan Strömberg 5 KTH STH

6 12.1. GRAFER DEL II b = HamiltonianCycle[g {1, 2, 6, 4, 3, 7, 5, 1} b1 = Partition[b, 2, 1 {{1,2}, {2,6}, {6,4}, {4,3}, {3,7}, {7,5}, {5,1}} ShowGraph[Highlight[g,{b1},HighlightedEdgeColors->{Blue} Lägg märke till hur Partition fungerar här Figur 12.6: Graffärgning Figur 12.7: Fyra färger har använts till vänster, men det räcker med tre som till höger Att färga en graf innebär i första hand att ge noderna färger så att inga intilliggande noder får samma färg. Detta är genomfört i Men skulle det gå att använda färre färger? Vi frågar Mathematica g = FromOrderedPairs[{{1,2},{2,3},{3,4},{4,5},{5,6},{6,7},{7,1}, {3,5},{8,1},{8,2},{8,3},{8,6},{8,7}} ChromaticNumber[g 3 MinimumVertexColoring[g {1, 2, 1, 2, 2, 1, 3} Vi startar med att ge datorn en lista över bågarna och skapar grafen grafen g. Med ChromaticNumber får vi reda på det minsta antalet färger som behövs. Det visar sig att det räcker med tre färger. g har det kromatiska talet, χ(g) = 3. Vi kan dessutom ta reda på vilka noder som ska ha samma färg. Genom MinimumVertexColoring får vi förslag till hur noderna kan målas. Som vi ser finns det flera lösningar. Håkan Strömberg 6 KTH STH

7 Nedan ser Du en karta, med åtföljande graf. Ser du analogin? Varje nod motsvarar ett land och vare båge en gräns. Figur 12.8: Ett mycket välkänt problem: Hur många färger behövs det minst för att måla länderna på en karta, så att två länder som gränsar till varandra inte får samma färg? Motsvarande graf är alltid plan, kan ritas utan korsande bågar. Detta är ett 150 år gammalt problem. Det bevisades på 1970-talet att det alltid räcker med fyra färger. Detta var det första bevis som godtagits, där en dator använts. Man kan även tala om färgning av bågar, så att två bågar förbundna med samma nod får skilda färger. Kortaste avståndet Figur 12.9: För att bestämma kortaste vägen mellan två noder är Dijkstras algorithm ett lämpligt val. Med grafen vi ser i figur 12.9 vill vi ta reda på kortaste vägen mellan 5 och 15. ShortestPath[u, 5, 15 tab = AllPairsShortestPath[u; tab[[5, får vi resvägen Med hjälp av AllPairsShortestPath får man en matris där tab[[5,15 ger den efterlängtade sträckan, som verkar stämma när vi summerar = Håkan Strömberg 7 KTH STH

8 12.1. GRAFER DEL II Genom kommandot Diameter får vi reda på det längsta kortaste avståndet, här Tyvärr får vi inte reda på mellan vilka noder detta avstånd uppmätts. For[i = 1, i <= 23, i++, For[j = i + 1, j <= 24, j++, If[tab[[i, j == 1835, Print[i, " ", j Vi får att det längsta kortaste avståndet är mellan 1 och 22. Handelsresandeproblemet Detta är ett klassiskt problem, som har en mängd forskning bakom sig. En handelsresande ska besöka var och en av n städer och sedan återvända hem. Samtliga städer är förbundna med flyglinjer. Biljettkostnaderna varierar. Problemet består i att finna den billigaste rundturen. Här följer Mathematica-koden för ett exempel. Tabellen nedan skulle kunna vara en avståndsmatris, men är här en prismatris, där aktuellt tal anger biljettkostnaden i 100- tals kronor mellan ett par av städer TravelingSalesman[g {1, 5, 7, 3, 4, 8, 2, 6, 1} CostOfPath[g, {1, 5, 7, 3, 4, 8, 2, 6, 1} 237 g är en komplett graf med 8 noder (städer). Att den är komplett innebär att grafen har 28 bågar (flyglinjer). Med funktionen TravelingSalesman bestäms den lägsta totalkostnaden. Listan anger den ordning i vilka städerna ska besökas. Resultatet får vi = 237. Uppspännande träd Vi har en oriktad, viktad graf G, där vi vill ta bort så många bågar som möjligt, men behålla grafen sammanhängande. Den totala vikten hos de bågar som återstår vill vi minimera. När vi funnit detta minimum har vi funnit det minsta uppspännande trädet. Håkan Strömberg 8 KTH STH

9 Det finns en algoritm, ganska enkel att implementera som ett program: Välj en nod A, vilken som helst. Sök reda på den nod B, som ligger närmast A (lägsta vikten). Förbind A och B med en båge. Sök upp den nod C, som ligger närmast någon av noderna A och B. Förbind C med en båge till närmaste nod, A eller B. Nu består vägnätet av tre noder och två bågar. Nästa nod som ska förbindas är den som ligger närmast någon av de tre noderna A, B eller C. Fortsätt denna procedur tills alla noder är anslutna. Här några rader över hur man utför det hela i Mathematica g = RandomGraph[12, 0.4 ShowGraph[g g = SetEdgeWeights[h, WeightingFunction -> Euclidean h = MinimumSpanningTree[g ShowGraph[h Till vänster ser vi den viktade grafen och till höger det träd som ger det minsta summan av vikterna Plan graf Figur 12.10: Håkan Strömberg 9 KTH STH

10 12.1. GRAFER DEL II Ett klassiskt problem i figur 12.10: Kan man dra ledningar från gasverket (G), elverket (E) och vattenverket (V) till vart och ett av de tre husen utan att någon av de nio ledningarna korsar någon annan? Om man lyckas med det har man konstruerat en plan graf, det vill säga en graf där inga noder skär varandra. Det visar sig omöjligt i vårt exempel. Vi testar det med Mathematica: g=fromorderedpairs[{{1,4},{1,5},{1,6},{2,4},{2,5}, {2,6},{3,4},{3,5},{3,6}} PlanarQ[g False Laboration Laborationsuppgift 1. (2) Bestäm en formel som bestämmer summan av den aritmetiska serien som bestäms av a, b och c på följande sätt a+(a+b)+(a+2b)+(a+3b)+...+(a+(c 1)b)+(a+cb) Använd sedan formeln till att bestämma följande summor a b c Laborationsuppgift 2. (2) Konstruera en graf som är en eulergraf men inte en hamiltongraf. Laborationsuppgift 3. (2) Bestäm det minimala uppspännade trädet till grafen i figur Figur 12.11: Håkan Strömberg 10 KTH STH

11 Laborationsuppgift 4. (2) Hur många färger behövs det för att färglägga Sydamerika, så att inga intilliggande länder från samma färg? Figur 12.12: Laborationsuppgift 5. (2) Skriv en funktion i Mathematica som tar emot en graf G producerar en tabell över alla kortaste avstånden i grafen. Testa din funktion genom att generera en viktad slumpgraf med cirka 10 noder. Laborationsuppgift 6. (2) Använd GraphPlot och GraphPlot3D för att ta reda på vad grafen i filen Graf1Ma.txt föreställer. Håkan Strömberg 11 KTH STH

12 12.1. GRAFER DEL II Teoriuppgifter Till uppgifterna finns grafer.zip i vilken Du hittar filer som beskriver graferna. Använd cut and paste för att föra över dem till Mathematica Figur 12.13: Problem 1 Adam har haft sommarjobb som brevbärare på det distrikt som kartan visar. Mot slutet av sommaren hittade han en rutt som gjorde att han inte behövde besöka någon av de 17 postlådorna mer än en gång. Postkontoret ligger i huset märkt nummer 1 dit han också återvänder efter dagens arbete. Alla möjliga vägar är utritade. Ange en följd av nummer som startar och slutar med 1 och som innehåller numren på postlådorna i den ordning han besökte dem. För att underlätta arbetet finns en beskrivning av kartan i filen uppgift1.txt för cut and paste. Svar: Problemet handlar förstås om en hamiltonsk krets, som vi får fram genom följande kod: e={{2,3},{1,2},{1,7},{2,12},{5,11},{6,18},{6,11}, {7,8},{8,14},{8,13},{9,16},{9,15},{10,11},{10,16}, {11,17},{13,18},{14,15},{14,18},{15,17},{6,12},{2,8}, {3,4},{3,7},{3,9},{3,8},{4,5},{4,10},{9,14},{2,7}, {4,11},{9,10}}; g = FromOrderedPairs[e, Type -> Undirected HamiltonianQ[g HamiltonianCycle[g, All {{1,2,12,6,18,13,8,14,15,17,11,5,4,10,16,9,3,7,1}, {1,7,3,9,16,10,4,5,11,17,15,14,8,13,18,6,12,2,1}} Självklart finns två lösningar. Håkan Strömberg 12 KTH STH

13 Figur 12.14: Observera att de tre vägkorsningarna ligger i olika plan och att man till exempel inte kan resa direkt från 2 till 7 eller från 14 till 19 Problem 2 Adam, som bor i 1, ska företa en resa där han ska besöka varje stad precis en gång och därefter återvända till hemstaden. Ta reda på hur resan går från stad till stad. På filen uppgift2.txt finns grafen i figuren översatt till en mängd av bågar. Svar: Åter ett problem som syftar till att hitta en hamiltonsk krets. e={{1,2},{2,3},{3,4},{4,5},{1,6},{2,12},{4,9}, {5,10},{6,7},{7,8},{8,9},{9,10},{6,11},{7,13}, {8,19},{9,14},{10,15},{11,12},{12,13},{13,14}, {14,15},{11,16},{13,18},{15,21},{16,17},{17,18}, {18,19},{19,20},{20,21},{16,22},{17,28},{18,23}, {20,25},{21,26},{22,23},{23,24},{25,26},{22,27}, {23,29},{24,30},{26,31},{27,28},{28,29},{29,30}, {30,31}}; g = FromOrderedPairs[e, Type -> Undirected; HamiltonianQ[g HamiltonianCycle[g, Allend{verbatim} {{1,2,3,4,5,10,9,14,15,21,20,25,26,31,30,24,23,29, 28,27,22,16,17,18,19,8,7,13,12,11,6,1}, {1,6,11,12,13,7,8,19,18,17,16,22,27,28,29,23,24, 30,31,26,25,20,21,15,14,9,10,5,4,3,2,1}} Även detta problem har endast två lösningar, eller en om man så vill. Håkan Strömberg 13 KTH STH

14 12.1. GRAFER DEL II Problem 3 A B C D E F G H A B C D E F G 16 H Adam, som bor i A, har tänkt besöka städerna B,C,D,E,F,G och H. Han kan välja att besöka dem i vilken ordning som helst och sedan återvända hem till A. I tabellen ovan anges avståndet i mil mellan alla par av städer. Bestäm i vilken ordning han ska besöka städerna för att minimera resvägen och hur lång den blir. (På filen uppgift3.txt finns data som genom cut and paste kan underlätta lösandet av problemet) Svar: Vi får Adams kortaste tripp genom att lösa problemet med TravelingSalesman. g=completegraph[8 v1={12,55,43,38,6,21,36,42,52,47,16,34,47,80, 76,59,75,85,5,48,32,21,43,27,19,21,37,16}; g=setedgeweights[g,v1 p=travelingsalesman[g {1,2,3,5,4,8,7,6,1} CostOfPath[g,p 199 Han startar och slutar i 1 och besöker städerna i ordning {1,2,3,5,4,8,7,6,1}. Totalt har resan en längd av 199 mil. Håkan Strömberg 14 KTH STH

15 Figur 12.15: Problem 4 7 jobbsökande söker lika många lediga jobb A...G. Bågarna visar vilka jobb de sökande är kvalificerade för. Finns det möjlighet att tillsätta jobben så att alla blir anställda? I så fall vilka jobb kommer de sökande att få? Filen som beskriver grafen heter uppgift4.txt Svar: e={{1,8},{1,10},{2,8},{2,11},{3,8},{4,10},{4,13}, {5,8},{5,9},{6,9},{6,11},{6,12},{6,13},{7,12}, {7,13},{7,14}}; g=fromorderedpairs[e,type->undirected; BipartiteMatching[g {{1,10},{2,11},{3,8},{4,13},{5,9},{6,12},{7,14}} Alla 7 jobbsökande kan tilldelas ett jobb. Det finns bara en lösning. Man klarar sig förresten utan programvara. Om alla ska ha jobb måste 3 A. leder till 1 C och då 4 F. 5 B och 7 G. 2 D och därmed 6 E. Håkan Strömberg 15 KTH STH

16 12.1. GRAFER DEL II Problem 5 Genom Förbifart Stockholm har anlagts en väg, som en cirkel runt staden, se figur, för att på det sättet avlasta trafiken i innerstaden (1). Mellan två intilliggande trafikplatser ( ) och mellan vissa trafikplatser och innerstaden finns beräknad körtid angiven. Trots det tjänar man ibland att ta vägen genom staden. Ta reda på för vilka par av trafikplatser (angivna som [tp 1,tp 2 ) man vinner tid, om man åker genom innerstaden. Grafen finns att på filen uppgift5.txt. Svar: f[:=block[{i,j,e,v,g,p,t,l={}}, e={{1,2},{1,4},{1,6},{1,8},{1,9},{2,3},{2,10}, {3,4},{4,5},{5,6},{6,7},{7,8},{8,9},{9,10}}; v={180,165,146,116,174,110,64,106,138,88,78,110,97,72}; g=fromorderedpairs[e,type->undirected; g=setedgeweights[g,v; t=allpairsshortestpath[g; For[i=2,i<=8,i++, For[j=i+1,j<=9,j++, p=shortestpath[g,i,j; If[Position[p,1!={}, AppendTo[l,{i,j,t[[i,j} ; l f[ Vi får genom funktionen reda på att mellan (2,6),(4,8) och (4,9) bör färden gå genom innerstaden. Håkan Strömberg 16 KTH STH

17 Figur 12.16: Problem 6 Figur visar en karta över ett område med 21 kolonistugor. På kartan är inritade de gångstigar som finns idag. Man önskar nu bredda en del av stigarna så att de blir framkomliga med bil. Målet är att man, med bil, ska kunna ta sig från viken stuga som helst till vilken annan som helst. Man vill dock minimera den totala sträckan av stigar som ska byggas om. Ta, med hjälp av den information om grafen, som finns på filen uppgift6.txt reda på det eftersökta sträckan. Svar: Figur 12.17: Tyvärr kommer inte grafen att se ut så här när vi plottar den från Mathematica e={{1,2},{1,5},{1,6},{1,9},{1,10},{2,6},{3,4},{3,15}, {3,19},{3,20},{4,6},{4,7},{4,15},{5,6},{5,7},{5,8}, {5,9},{6,7},{7,8},{7,14},{7,15},{7,18},{8,9},{8,10}, {8,13},{8,14},{9,10},{10,13},{11,12},{11,13},{11,17}, {12,13},{12,14},{12,17},{12,18},{14,18},{15,18}, {15,19},{16,17},{16,18},{16,19},{16,21},{17,18}, {19,20},{19,21},{20,21}}; v={1099,962,1085,1003,1641,494,748,1225,1044,667,661,679, 683,555,709,1039,547,900,919,506,628,682,759,800,488, 646,837,880,916,819,1014,896,506,945,610,533,456,846, 995,837,1186,489,1268,698,1006,1678}; g=fromorderedpairs[e,type->undirected; g=setedgeweights[g,v; h=minimumspanningtree[g Apply[Plus,GetEdgeWeights[g,Edges[h Den eftersökta sträckan är meter. Att grafen h inte kommer att se ut som vi förväntar oss, beror på att nodernas koordinater är slumpmässiga. Håkan Strömberg 17 KTH STH

18 12.1. GRAFER DEL II Figur 12.18: Problem 7 Adam och Bertil är på cykelsemester. De har bestämt sig för att besöka de de 23 platserna på kartan, i figur 12.18, men ingen av platserna ska besökas fler än än gång, utom plats 1, där de befinner sig just nu och där resan ska starta och sluta. Nu finns det flera möjliga rundturer som uppfyller villkoren och herrarna är därför intresserade av den kortaste. På filen uppgift7.txt finns en graf definierad, som motsvarar kartan. Hur lång är den kortaste rundturen? Svar: g = Graph[{{{1, 2},EdgeWeight->9740},{{1,20},EdgeWeight->31950}, {{1, 12},EdgeWeight->14280},{{1, 13},EdgeWeight->17790}, {{1, 7},EdgeWeight->11220},{{2, 7},EdgeWeight->6680}, {{2, 3}, EdgeWeight->7240},{{2, 9},EdgeWeight->9310}, {{2, 5}, EdgeWeight->19530},{{3, 13}, EdgeWeight->8180}, {{3, 14}, EdgeWeight -> 11610}, {{3, 8},EdgeWeight->5250}, {{4, 5},EdgeWeight ->7450},{{4, 16},EdgeWeight->11260}, {{4, 10},EdgeWeight->6880},{{4, 8},EdgeWeight->8860}, {{5, 9},EdgeWeight->12560},{{5, 11},EdgeWeight->8590}, {{5, 16},EdgeWeight->13860},{{6, 12},EdgeWeight->4420}, {{27, 13},EdgeWeight->7590},{{8, 9},EdgeWeight->5380}, {{8, 15},EdgeWeight->9020},{{8, 14},EdgeWeight->8480}, {{10, 15},EdgeWeight->6350},{{10, 23},EdgeWeight->19150}, {{10, 19},EdgeWeight->5050},{{11, 16},EdgeWeight->6520}, {{6, 20},EdgeWeight->20230},{{16, 23},EdgeWeight->16840}, {{16, 19},EdgeWeight->4680},{{13, 17},EdgeWeight->9430}, {{14, 15},EdgeWeight->7220},{{14, 18},EdgeWeight->5680}, {{14, 17},EdgeWeight->7080},{{15, 23},EdgeWeight->15350}, {{15, 22},EdgeWeight->9250},{{20, 21},EdgeWeight->10640}, {{20, 23},EdgeWeight->30260},{{17, 21},EdgeWeight->5100}, {{21, 22},EdgeWeight->11090},{{22, 23},EdgeWeight->9380}, {{18, 22},EdgeWeight->7870},{{6, 17},EdgeWeight->14440}}, {{{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }}, Håkan Strömberg 18 KTH STH

19 {{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }}, {{ , }} } c = HamiltonianCycle[g, All Length[c Min[Map[CostOfPath[g, # &, c Det finns 38 hamiltonska kretsar, där den kortaste är mil Håkan Strömberg 19 KTH STH

20 12.1. GRAFER DEL II A B C D Problem 8 De fyra graferna i figuren är egentligen två par av identiska grafer, de är isomorfa. Para ihop dem! Här får du inga filer utan får bygga upp de fyra graferna för hand. Svar: Genom koden nedan får vi reda på att A och D respektive B och C är isomorfa, eftersom utskriften blir i tur och ordning: False,False,True,True,False,False a=fromorderedpairs[{{1,2},{1,3},{2,3},{1,5},{3,5},{4,5}, {2,6},{3,6},{4,6},{5,6}},Type->Undirected; b=fromorderedpairs[{{1,2},{2,3},{2,4},{1,5},{3,5},{4,5}, {1,6},{2,6},{3,6},{5,6}},Type->Undirected; c=fromorderedpairs[{{1,3},{2,3},{1,4},{2,4},{3,5},{4,5}, {2,6},{3,6},{4,6},{5,6}},Type->Undirected; d=fromorderedpairs[{{1,3},{1,4},{2,4},{3,4},{1,5},{3,5}, {1,6},{2,6},{4,6},{5,6}},Type->Undirected; IsomorphicQ[a,b IsomorphicQ[a,c IsomorphicQ[a,d IsomorphicQ[b,c IsomorphicQ[b,d IsomorphicQ[c,d Utskriften blir i tur och ordning: False,False,True,True,False,False Håkan Strömberg 20 KTH STH

21 Figur 12.19: Problem 9 Figur visar kartan över en djurpark. De gula cirklarna visar var man kan se djur och de svarta strecken markerar vägar. Man är nu intresserad av att ordna en guidad tur genom samtliga 10 platser i parken, där man kan starta var som helst och återvända till denna plats utan att behöva besöka samma plats fler än en gång. Man kan inte åstadkomma detta utan att lägga till en väg. Vägen ska vara rak och får inte korsa någon annan väg. Vilka är de två möjligheterna? Grafen finns på filen uppgift9.txt Svar: g=graph[{{{1,6}},{{1,7}},{{4,8}},{{8,10}},{{4,7}},{{4,6}}, {{5,9}},{{5,10}},{{4,10}},{{3,4}},{{3,9}},{{3,10}}, {{2,6}},{{2,9}},{{2,10}},{{9,10}},{{6,9}}}, {{{ , }},{{ , }}, {{-1.25, }},{{ , }}, {{ , }},{{ , }}, {{ , }},{{ , }}, {{ , }},{{ , }}} lista = {}; For[i = 1, i <= 10, i++, For[j = i + 1, j <= 10, j++, b = g[[1; b = AppendTo[b, {{i, j}}; h = Graph[b, g[[2; If[HamiltonianQ[h, lista = AppendTo[lista, {i, j} ; lista Vi får följande förslag till vägbyggen {2,3}, {2,5}, {2,8}, {3,5}, {3,7}, {3,8}, {5,7}, {5,8}, {7,8} Från kartan ser vi så att endast vägar mellan 3 och 5 samt mellan 3 och 8 fungerar Håkan Strömberg 21 KTH STH