2 Bj rkfeltbjon d r k èk =;:::;pè betecknar A:s olika egenv rden och n k r den algebraiska multipliciteten hos egenv rdet k. Om multipliciteten hos et
|
|
|
- Roland Engström
- för 8 år sedan
- Visningar:
Transkript
1 7. Egenv rden och egenvektorer L t A beteckna en n=n-matris. I vissa riktningar x 6= beter sig matrisen A enkelt i den meningen att x och Ax r kar vara parallella: Denition 7.. Talet s gs vara ett egenv rde till A om Ax = x f r n gon vektor x 6=. Vektorn x s gs d vara en egenvektor till A som svarar mot egenv rdet. Observera att om x r en egenvektor till A som svarar mot ett visst egenv rde, s r f r varje c 6= ocks cx en egenvektor som svarar mot egenv rdet. L ngden av vektorn x r allts irrelevant, endast riktningen har n gon betydelse. Egenv rden och egenvektorer r karakteristika f r en matris A och ber ttar en hel del om matrisens egenskaper precis som t.ex. typen och rangen ocks g r det. Vi kommer att se att i m nga fall inneh ller egenv rdena och egenvektorerna t.o.m. all information om A. Exempel 7.. F r en enhetsmatris I g ller att Ix = x f r varje x. S ledes r talet ett egenv rde till I och varje x 6= r en motsvarande egenvektor. Om r ett egenv rde till A och x r en motsvarande egenvektor, s r Ax = x èè èa,ièx = fæor ngt x 6= fæor ngt x 6= S ledes g ller: èèa,i æar singulæar èè detèa, Iè =: Sats 7.. Om A r en n=n-matris, s f s A:s egenv rden genom att man l ser den s.k. karakteristiska ekvationen èocks kallad sekularekvationenè detèa, Iè =: D refter f s de egenvektorer, som svarar mot ett visst egenv rde, genom att man l ser den homogena ekvationen èa, Ièx =. D man utvecklar determinanten i den karakteristiska ekvationen, f s alltid en polynomekvation av n:te graden, i vilken koecienten f r n r è,è n. En s dan har ju alltid exakt n èreella eller komplexaè l sningar d multipliciteten beaktas. Den karakteristiska ekvationen kan allts skrivas i den ekvivalenta formen è, è n æææè, p è np =;
2 2 Bj rkfeltbjon d r k èk =;:::;pè betecknar A:s olika egenv rden och n k r den algebraiska multipliciteten hos egenv rdet k. Om multipliciteten hos ett egenv rde r, 2, 3 ::: s gs detta vara enkelt, dubbelt, tredubbelt :::. Denition 7.2. Egenrummet V èè till en n=n-matris A med egenv rdet r nollrummet N èa, Iè, dvs. l sningsm ngden till Ax = x. Egenrummet V èè r allts ett underrum av R n och best r av nollvektorn och alla egenvektorer till A som svarar mot egenv rdet. Eftersom N èa, æ Iè =NèAè,s r ett egenv rde till A om och endast om matrisen A r singul r. A = 2 2 Exempel 7.2. Den karakteristiska ekvationen f r matrisen r = æ2, 2,æ =è2,è2,: Ur denna l ser vi ut egenv rdena 3 och. De egenvektorer som svarar mot egenv rdet 3 f s nu genom att man l ser ekvationen èa, 3Ièx =: A,3I=,,!, L sningarna r allts x = t è è T och varje s dan vektor utom nollvektorn r en egenvektor som svarar mot egenv rdet 3. P samma s tt l ser vi èa, Ièx = med hj lp av r kneschemat A, I =! och f r fram de egenvektorer x = t è, è T èt6=è som svarar mot egenv rdet. Om matrisen A r reell och ett egenv rde inte r reellt èdvs. kta komplextè, s m ste tminstone n gon komponent av en motsvarande egenvektor x vara icke-reell f r att likheten Ax = x skall kunna g lla. Om d remot b de A och egenv rdet r reella, s kan motsvarande egenvektorer x v ljas reella. Exempel 7.3. Den karakteristiska ekvationen f r matrisen, r 2 + =, varf r egenv rdena r æi. De egenvektorer som svarar mot t.ex. egenv rdet i har formen t è,iè T, d r t 6= r ett reellt èeller komplextè tal. Eftersom reella matriser s ledes kan ha icke-reella egenv rden, s inser vi att teorin f r egenv rden och egenvektorer egentligen borde utformas f r komplexa matriser. I forts ttningen v ljer vi emellertid alltid som exempel bara s dana matriser, som har :
3 Egenv rden och egenvektorer 3 reella egenv rden. I m nga fall r egenv rdena t.o.m. alltid automatiskt reella, s som f ljande sats visar: Sats 7.2. Antag att A r en symmetrisk reell n=n-matris. D g ller: èiè Alla egenv rden till A r reella; èiiè Om och r olika egenv rden till A s r V èè? V èè. Bevis. èiè L t vara ett egenv rde och l t x è6= è vara en motsvarande egenvektor. H r m ste vi tempor rt acceptera att x kan ha icke-reella komponenter eftersom vi nnu inte vet att i sj lva verket m ste vara reellt. Om x = è x ::: x n è T, s tt x æ = è x ::: x n è, d r beteckningen c = a, ib st r f r konjugattalet till ett givet komplext tal c = a + ib. Om ekvationen Ax = x multipliceras fr n v nster med x æ f s x æ Ax = x æ x, dvs. = xæ Ax x æ x : N mnaren x æ x = jx j 2 + æææ + jx n j 2 6= r en summa av kvadrater av belopp av komplexa tal och r s ledes reell. T ljaren r ett komplext tal som sammanfaller med sitt eget konjugattal, ty eftersom A =èa ik è r reell och symmetrisk, r x æ Ax =X x i a ik x k =X x i a ik x k i;k =X i;k i;k x k a ki x i = x æ Ax : D d rmed b de t ljaren och n mnaren i uttrycket f r r reella, s r reellt. èiiè Vi skall visa att om vi tar godtyckliga èreellaè vektorer x 2 V èè och y 2 V èè, s r x? y: Ax = x =è yt Ax = y T x =è yt Ax = y T x Ay = y x T Ay = x T y y T Ax = y T x =è è, èy T x = =è x?y:í F r en matris A som inte r symmetrisk, beh ver det inte g lla att egenvektorer som svarar mot olika egenv rden r ortogonala. D remot m ste de nog vara linj rt oberoende: Sats 7.3. Antag att ;:::; p r olika egenv rden till en n=n-matris och l t x ;:::;x p vara en upps ttning motsvarande egenvektorer, s att Ax k = k x k èk =;:::;pè: D r x ;:::;x p linj rt oberoende. Bevis. Satsen bevisas enklast genom induktion. Vi konstaterar f rst att p st endet g ller om p =. Sedan antar vi att p st endet g ller om vi har p = k, egenvektorer x ;:::;x k, och skall bevisa att p st endet ocks g ller d antalet r p = k. Vi bildar d rf r en linj rkombination av dekegenvektorerna och s ttar denna lika med : èè c x + æææ+c k x k = :
4 4 Bj rkfeltbjon Vi multiplicera fr n v nster med A, beaktar att Ax i = i x i och f r: è2è c x + æææ+c k k x k =: Vektorn x k elimineras genom att vi bildar skillnaden mellan è2è och k g nger èè: c è, k èx + æææ+c k, è k,, k èx k, = : Nu f ljer att c = æææ = c k, =, eftersom x, :::, x k, r linj rt oberoende. Enligt èè r d rf r c k x k = och d rmed c k =. Allts r x,:::, x k linj rt oberoende. Induktionen ger att satsens p st ende g ller f r varje antal p av egenvektorer. í Exempel 7.4. Matrisen har den karakteristiska ekvationen = A = æ 4, , , =è2,è 2 æ,, 2 2 4, A æ = æ 2,,2+ 2,, , æ æ æ, =è2,è2, 2 6,æ =è2,è 2 æ,, 8,æ =è2,è2 è8, è : Matrisen A har allts egenv rdena 2 èdubbeltè och 8 èenkeltè. =2: En bas i egenrummet V è2è = N èa, 2Iè f s ur A, 2I = A! A ; och resulterer i fè, è T ; è, è T g. =8: En motsvarande kalkyl A, 8I =, , ,4 A!æææ!,A ger basen fè è T givè8è = N èa,8iè. Observera att vektorn è è T r ortogonal mot basvektorerna i V è2è men att basvektorerna i V è2è inte èautomatisktè beh ver bli ortogonala mot varandra èjfr. Sats 7.2è.
5 Egenv rden och egenvektorer 5 Exempel 7.5. Efter en stunds kalkylerande nner man att matrisen,2 A = 2 3 A har den karakteristiska ekvationen è, èè, 2è 2 =. =2: En bas i V è2è f s ur A, 2I = dvs. fè è T ; è, è T g. =: R kneschemat blir A, I =,2,2,,2 2 A! A ;,A : A! 2 En bas i V èè best r allts av en enda vektor è,2 è T, som uppenbarligen inte r ortogonal mot basvektorerna i V è2è. D remot bildar unionen av baserna i V è2è och V èè en linj rt oberoende m ngd èjfr. Sats 7.3è. P basen av de tv senaste exemplen kunde man f uppfattningen att om multipliciteten hos ett egenv rde r t.ex. 2, s inneh ller en bas i V èè precis 2 vektorer. Detta beh ver inte alltid vara fallet men f r symmetriska matriser r det s : Anm rkning. Man kan visa att om A r en symmetrisk n=n-matris med den karakteristiska ekvationen è, è n æææè, p è np =; d r ;:::; p r olika egenv rden och Pi n i = n, s r dim V è i è=n i : Vi ger ett exempel p en èicke-symmetriskè matris, som saknar denna egenskap: Exempel 7.6. Matrisen A = har den karakteristiska ekvationen = detèa,iè = 2,varf r det enda egenv rdet har multipliciteten 2. Matrisen r redan i reducerad echelonform, s vi kan direkt avl sa att fè èg r en bas i motsvarande egenrum V èè. Dimensionen hos V èè r s ledes bara, inte 2. Anm rkning. Matriserna i exemplen i denna kurs r s sm att det fortfarande r m jligt att utveckla determinanten i den karakteristiska ekvationen. Om matrisen r stor,
6 6 Bj rkfeltbjon blir detta oftast en uppgift som verstiger krafterna. Andra metoder kr vs d f r att man skall f fram egenv rdena till matrisen. Som ett exempel p en s dan metod n mner vi att koecienterna i den karakteristiska ekvationen B n + c n, n, + æææ+c +c = till en n=n-matris kan f s genom att man l ser ekvationen æææ S 2 æææ S 2 S 3 æææ,,,,,, S n, S n,2 S n,3 æææ S n CA B c n, c n,2 c n,3, c S S CA B 2 =, S 3, S n CA ; d r S k = trèa k è f r k = ; 2;:::;n r sp ret av potensen A k av matrisen A. Egenv rdena kan sedan best mmas genom att man l ser den karakteristiska ekvationen med numeriska metoder. vningsuppgifter. Finn alla egenv rden och motsvarande egenvektorer till matriserna èaè ; èbè ; ècè 3 A : 7 6 3, Best m egenv rden och baser i egenrummen till matriserna 2 6 6,2 èaè ; èbè ; 6,2 9 3 ècè,2 3,2A ; èdè 5,2 6, 5,A : 2 5,5 8,6 3. Best m egenv rden och baser i egenrummen f r A 62 d A r matrisen,, èaè,2 A ; èbè 2,4 4,2 4A : 2 2, Visa att den karakteristiska ekvationen f r en èreellè 2=2-matris A kan skrivas 2, trèaè + detèaè =: Best m villkoret f r att A skall ha enbart reella egenv rden samt veriera att detta villkor r uppfyllt f r alla symmetriska 2=2-matriser. 5. Visa att A och A T har samma egenv rden. Hur r tv egenvektorer x och y till A respektive A T som svarar mot olika egenv rden relaterade till varandra? 6. Visa att om A r en upp t èned tè triangul r matris eller en diagonalmatris, s r A:s egenv rden precis matriselementen i huvuddiagonalen i A. 7. En matris A s gs vara nilpotent om A k =f r n got positivt heltal k. Visa att en nilpotent matris bara har egenv rdet. 8. L t pètè =a +a t+æææ+a n t n vara ett polynom och s tt pèaè =a I+a A+æææ+ a n A n. Visa att om r ett egenv rde till A, s rpèèett egenv rde till pèaè.
x - Px U = R(A) = R(P)
 8. Ortogonala projektioner Antag att a (6= ) och b r tv vektorer i R n. Vi skall bilda den ortogonala projektionen av b p det endimensionella underrummet L = spn fag. Enligt resonemanget i beviset av Schwarz
8. Ortogonala projektioner Antag att a (6= ) och b r tv vektorer i R n. Vi skall bilda den ortogonala projektionen av b p det endimensionella underrummet L = spn fag. Enligt resonemanget i beviset av Schwarz
Vektorrum 43 Exempel 4.. M ngden E av alla m=n-matriser, f rsedd med vanlig matrisaddition och vanlig multiplikation av en matris med en skal r, r ett
 4. Vektorrum Tidigare har vi r knat upp en rad av r kneregler som g ller f r m=n-matriser. Dessa regler g ller inte bara f r varje matristyp m=n utan ocks f r m nga andra objekt som t.ex. funktioner, talf
4. Vektorrum Tidigare har vi r knat upp en rad av r kneregler som g ller f r m=n-matriser. Dessa regler g ller inte bara f r varje matristyp m=n utan ocks f r m nga andra objekt som t.ex. funktioner, talf
Egenvärden och egenvektorer
 Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
2 Bj rkfeltçbjon Exempel.2. Systemet 2x + x 2, x 3 + x 4 =5 x 2 + x 3, x 4 =3 3x 3 +6x 4 =6 r inte triangul rt èdet r ju inte kvadratisktè. Ger vi d r
 . Gausseliminering Vi skall till att b rja med s ka l sningen èl sningarnaè till ett s kallat linj rt ekvationssystem. Ett s dant system med m ekvationer och n obekanta èm; n 2 Z + è har formen a x + a
. Gausseliminering Vi skall till att b rja med s ka l sningen èl sningarnaè till ett s kallat linj rt ekvationssystem. Ett s dant system med m ekvationer och n obekanta èm; n 2 Z + è har formen a x + a
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
4 Bj rkfeltbjon Det andra elimineringssteget è3è! è3è, èè svarar enligt samma m nster mot multiplikation fr n v nster med E = I, J 3, E ; som ger
 3. Gausseliminering genom matrismultiplikation Vi skall visa att den omformning, som man f r genom att utf ra en basoperation p ett r kneschema, ocks kan f s genom att man multiplicerar r kneschemat fr
3. Gausseliminering genom matrismultiplikation Vi skall visa att den omformning, som man f r genom att utf ra en basoperation p ett r kneschema, ocks kan f s genom att man multiplicerar r kneschemat fr
Självkoll: Ser du att de två uttrycken är ekvivalenta?
 ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
ANTECKNINGAR TILL RÄKNEÖVNING 1 & - LINJÄR ALGEBRA För att verkligen kunna förstå och tillämpa kvantmekaniken så måste vi veta något om den matematik som ligger till grund för formuleringen av vågfunktionen
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
A = v 2 B = = (λ 1) 2 16 = λ 2 2λ 15 = (λ 5)(λ+3). E 5 = Span C =
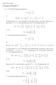 KTH Matematik Lösningar till Kapitel 7 A a Karakteristiska polynomet av detλi A det A λ λ λ b Egenvdena av A nollställen till karakteristiska polynomet alltså har A egenvdet λ c Motsvarande egenrum E lösningsrummet
KTH Matematik Lösningar till Kapitel 7 A a Karakteristiska polynomet av detλi A det A λ λ λ b Egenvdena av A nollställen till karakteristiska polynomet alltså har A egenvdet λ c Motsvarande egenrum E lösningsrummet
19. Spektralsatsen Spektralsatsen SPEKTRALSATSEN
 9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng.
 ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
A = x
 Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Determinanter. Exempel 1. Både (2, 1, 4, 3) och (4, 3, 1, 2) är permutationer av talen 1,...,4.
 Determinanter Innan vi slår fast en definition av begreppet determinant, behöver vi gå inpånågra förberedande förklaringar En permutation av talen 1,,n är en uppräkning (j 1,,j n ) av dessa samma tal inågon
Determinanter Innan vi slår fast en definition av begreppet determinant, behöver vi gå inpånågra förberedande förklaringar En permutation av talen 1,,n är en uppräkning (j 1,,j n ) av dessa samma tal inågon
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 2014
 SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner. 2? Det är komplicerat att
 Egensystem Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner Potens av matris 2 6 Ex Givet matrisen A =, vad är A 2? Det är komplicerat att beräkna högre
Egensystem Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner Potens av matris 2 6 Ex Givet matrisen A =, vad är A 2? Det är komplicerat att beräkna högre
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
Determinanter, egenvectorer, egenvärden.
 Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
Egenvärden, egenvektorer
 Egenvärden, egenvektorer Om en matris är kvadratisk (dvs n n) kan vi beräkna egenvärden och egenvektorer till matrisen. Polynomet p(λ) = det(a λi) kallas det karakterisktiska polynomet för A. Ett nollställe
Egenvärden, egenvektorer Om en matris är kvadratisk (dvs n n) kan vi beräkna egenvärden och egenvektorer till matrisen. Polynomet p(λ) = det(a λi) kallas det karakterisktiska polynomet för A. Ett nollställe
DN1230 Tillämpad linjär algebra Tentamen Onsdagen den 29 maj 2013
 TILLÄMPAD LINJÄR ALGEBRA, DN123 1 DN123 Tillämpad linjär algebra Tentamen Onsdagen den 29 maj 213 Skrivtid: 8-13 Tillåtna hjälpmedel: inga Examinator: Anna-Karin Tornberg Betygsgränser: Betyg A B C D E
TILLÄMPAD LINJÄR ALGEBRA, DN123 1 DN123 Tillämpad linjär algebra Tentamen Onsdagen den 29 maj 213 Skrivtid: 8-13 Tillåtna hjälpmedel: inga Examinator: Anna-Karin Tornberg Betygsgränser: Betyg A B C D E
9 Bj rkfeltçbjon Oftast anv nder man beteckningen f r determinanten detèaè. Exempel 6.4. Matrisen a a 2 a n a 2 a 22 a 2n,,,, a n a n2 a nn A =ç a a 2
 6. Determinanter Innan vi sl r fast en deçnition av begreppet determinant, beh ver vi vissa f rberedande f rklaringar En permutation av talen ;;n r en uppr kning èj ;;j n è av dessa samma tal i n gon ordning.
6. Determinanter Innan vi sl r fast en deçnition av begreppet determinant, beh ver vi vissa f rberedande f rklaringar En permutation av talen ;;n r en uppr kning èj ;;j n è av dessa samma tal i n gon ordning.
1 De fyra fundamentala underrummen till en matris
 Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
Krister Svanberg, mars 2012 1 De fyra fundamentala underrummen till en matris 1.1 Definition av underrum En given delmängd M av IR n säges vara ett underrum i IR n om följande gäller: För varje v 1 M,
6.1 Skalärprodukt, norm och ortogonalitet. TMV141 Linjär algebra E VT 2011 Vecka 6. Lärmål 6.1. Skalärprodukt. Viktiga begrepp
 6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Repetera hur man nner bas för rum som spänns upp av några vektorer Reptetera hur man nner bas för summa och snitt av delrum. Reptetera
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Repetera hur man nner bas för rum som spänns upp av några vektorer Reptetera hur man nner bas för summa och snitt av delrum. Reptetera
16.7. Nollrum, värderum och dimensionssatsen
 170 16 LINJÄRA AVBILDNINGAR 16.7. Nollrum, värderum och dimensionssatsen Definition 16.33. Låt F : V W vara en linjär avbildning. 1. Nollrummet till F definierar vi som mängden av alla u V, vilkas bild
170 16 LINJÄRA AVBILDNINGAR 16.7. Nollrum, värderum och dimensionssatsen Definition 16.33. Låt F : V W vara en linjär avbildning. 1. Nollrummet till F definierar vi som mängden av alla u V, vilkas bild
kretsen och terv nder, ges den terv ndande signalen av d1 = G p G c è,1èd. Men denna st rning g r i sin tur runt kretsen och terv nder, och den terv n
 Kapitel 5 Inst llning av regulatorer I detta avsnitt skall vi i korthet betrakta problemet att st lla in regulatorer s att den slutna kretsen f r nskade egenskaper. Situationen illustreras av reglerkretsen
Kapitel 5 Inst llning av regulatorer I detta avsnitt skall vi i korthet betrakta problemet att st lla in regulatorer s att den slutna kretsen f r nskade egenskaper. Situationen illustreras av reglerkretsen
Egenvärden och egenvektorer. Linjär Algebra F15. Pelle
 Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
SF1624 Algebra och geometri Tentamen Torsdag, 9 juni 2016
 SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
16.7. Nollrum, värderum och dimensionssatsen
 86 6 LINJÄRA AVBILDNINGAR 6.7. Nollrum, värderum och dimensionssatsen Definition 6.36. Låt F : V W vara en linjär avbildning.. Nollrummet till F definierar vi som mängden av alla u V som avbildas på nollvektorn,
86 6 LINJÄRA AVBILDNINGAR 6.7. Nollrum, värderum och dimensionssatsen Definition 6.36. Låt F : V W vara en linjär avbildning.. Nollrummet till F definierar vi som mängden av alla u V som avbildas på nollvektorn,
2 Bj rkfeltbjon Elementen a ii, i ;;n, i en kvadratisk matris bildar matrisens èhuvudèdiagonal. En enhetsmatris r en diagonalmatris med enbart ettor i
 2. Matriser och vektorer Denition 2.. En matris r ett rektangul rt schema A B a a 2 æææ a n a 2 a 22 æææ a 2n,,,, a m a m2 æææ a mn CA av reella tal, som kallas matriselement. Matrisen A har m rader och
2. Matriser och vektorer Denition 2.. En matris r ett rektangul rt schema A B a a 2 æææ a n a 2 a 22 æææ a 2n,,,, a m a m2 æææ a mn CA av reella tal, som kallas matriselement. Matrisen A har m rader och
UPPSALA UNIVERSITET Matematiska institutionen Styf. Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 2004
 UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Crash Course Algebra och geometri. Ambjörn Karlsson c januari 2016
 Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 017-05-09 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
MATRISTEORI. Pelle Pettersson MATRISER. En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens
 MATRISTEORI Pelle Pettersson ALLMÄN MATRISKUNSKAP MATRISER En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens element Exempel Matrisen 2 3 4 5 6 har två rader och
MATRISTEORI Pelle Pettersson ALLMÄN MATRISKUNSKAP MATRISER En matris är ett rektangulärt schema med tal, reella eller komplexa, vilka kallas matrisens element Exempel Matrisen 2 3 4 5 6 har två rader och
Lösningar till utvalda uppgifter i kapitel 8
 Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra, SF1604, den 15 mars 2012 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF604, den 5 mars 202 kl 08.00-3.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra, SF604, den 5 mars 202 kl 08.00-3.00. Examinator: Olof Heden. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen.
Version 0.82. Linjär algebra kapiltet från ett ODE-kompendium. Mikael Forsberg
 Version.8 Linjär algebra kapiltet från ett ODE-kompendium Mikael Forsberg 8 Den här boken är typsatt av författaren med hjälp av L A TEX. Alla illustrationer är utförda av Mikael Forsberg med hjälp av
Version.8 Linjär algebra kapiltet från ett ODE-kompendium Mikael Forsberg 8 Den här boken är typsatt av författaren med hjälp av L A TEX. Alla illustrationer är utförda av Mikael Forsberg med hjälp av
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
Lösningar till MVE021 Linjär algebra för I
 Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
1 Ortogonalitet. 1.1 Skalär produkt. Man kan tala om vinkel mellan vektorer.
 Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
1 Diagonalisering av matriser
 1 Diagonalisering av matriser Kan alla matriser diagonaliseras? Nej, det kan de inte. Exempel: ẋ 1 = x 1 + 2x 2, Integrerande faktor: e t x 2 = x 2 x 2 (t) = c 2 e t och ẋ 1 x 1 = 2c 2 e t. e t x 1 e t
1 Diagonalisering av matriser Kan alla matriser diagonaliseras? Nej, det kan de inte. Exempel: ẋ 1 = x 1 + 2x 2, Integrerande faktor: e t x 2 = x 2 x 2 (t) = c 2 e t och ẋ 1 x 1 = 2c 2 e t. e t x 1 e t
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
Tentamen i Linjär algebra (TATA31/TEN1) ,
 Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN) 7 8 9, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst
Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN) 7 8 9, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst
3 differensekvationer med konstanta koefficienter.
 Matematiska institutionen Carl-Henrik Fant 17 november 2000 3 differensekvationer med konstanta koefficienter 31 T Med en menar vi en av rella eller komplexa tal varje heltal ges ett reellt eller komplext
Matematiska institutionen Carl-Henrik Fant 17 november 2000 3 differensekvationer med konstanta koefficienter 31 T Med en menar vi en av rella eller komplexa tal varje heltal ges ett reellt eller komplext
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
1. (a) (1p) Undersök om de tre vektorerna nedan är linjärt oberoende i vektorrummet
 1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)
![A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p) A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)](/thumbs/93/112249032.jpg) SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v04, 7 augusti 05 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 05-08-7 kl 080-0 Hjälpmedel : Inga hjälpmedel
3. Lös det överbestämda systemet nedan på bästa sätt i minsta kvadratmening. x + y = 1 x + 2y = 3 x + 3y = 4 x + 4y = 6
 TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 734-433 kurser:: Linjär Algebra ma4a Matematik för ingenjörer ma3a 5 4 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och
TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 734-433 kurser:: Linjär Algebra ma4a Matematik för ingenjörer ma3a 5 4 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
SKRIVNING I VEKTORGEOMETRI 2018-04-24 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade. 1. Bestäm
y z 3 = 0 z 5 16 1 i )
 ATM-Matematik Mikael Forsberg 734-433 Sören Hector 7-46686 Rolf Källström 7-6939 Ingenjörer, Lantmätare och Distansstuderande, mfl. Linjär Algebra ma4a 4 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna
ATM-Matematik Mikael Forsberg 734-433 Sören Hector 7-46686 Rolf Källström 7-6939 Ingenjörer, Lantmätare och Distansstuderande, mfl. Linjär Algebra ma4a 4 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna
Linjär algebra I, vt 12 Vecko PM läsvecka 4
 Linjär algebra I, vt 12 Vecko PM läsvecka 4 Lay: 2.8-2.9, 4.1-4.6 Underrum i R n, dimension och rang. Vektorrum. Innehållet i avsnitten 2.8 och 2.9 täcks av kapitel 4, men presenterar begreppen på ett
Linjär algebra I, vt 12 Vecko PM läsvecka 4 Lay: 2.8-2.9, 4.1-4.6 Underrum i R n, dimension och rang. Vektorrum. Innehållet i avsnitten 2.8 och 2.9 täcks av kapitel 4, men presenterar begreppen på ett
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
ax + y + 4z = a x + y + (a 1)z = 1. 2x + 2y + az = 2 Ange dessutom samtliga lösningar då det finns oändligt många.
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
LUNDS TEKNISKA HÖGSKOLA MATEMATIK TENTAMENSSKRIVNING Linjär algebra 8 kl 4 9 INGA HJÄLPMEDEL. För alla uppgifterna, utom 3, förklara dina beteckningar och motivera lösningarna väl. Alla baser får antas
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
Algebrans fundamentalsats
 School of Science and Technology SE-701 8 Örebro, Sweden Algebrans fundamentalsats Ett linjäralgebraiskt bevis Andreas Thore Örebro Universitet Akademin för naturvetenskap och teknik Matematik C, 61 75
School of Science and Technology SE-701 8 Örebro, Sweden Algebrans fundamentalsats Ett linjäralgebraiskt bevis Andreas Thore Örebro Universitet Akademin för naturvetenskap och teknik Matematik C, 61 75
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
12. SINGULÄRA VÄRDEN. (u Av) u v
 . SINGULÄRA VÄRDEN Vårt huvudresultat sen tidigare är Sats.. Varje n n matris A kan jordaniseras, dvs det finns en inverterbar matris S sån att S AS J där J är en jordanmatris. Om u och v är två kolonnvektorer
. SINGULÄRA VÄRDEN Vårt huvudresultat sen tidigare är Sats.. Varje n n matris A kan jordaniseras, dvs det finns en inverterbar matris S sån att S AS J där J är en jordanmatris. Om u och v är två kolonnvektorer
1 Grundläggande kalkyler med vektorer och matriser
 Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Krister Svanberg, mars 2015 1 Grundläggande kalkyler med vektorer och matriser Trots att läsaren säkert redan behärskar grundläggande vektor- och matriskalkyler, ges här i Kapitel 1 en repetition om just
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Linjära avbildningar IV Innehåll Nollrum och
Tentamen i Linjär algebra (TATA31/TEN1) ,
 Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN) 7 9, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst
Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN) 7 9, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst
Diagonalisering och linjära system ODE med konstanta koe cienter.
 Diagonalisering och linjära system ODE med konstanta koe cienter. Variabelbyte i linjära system di erentialekvationer. Målet med det kapitlet i kursen är att lösa linjära system di erentialekvationer på
Diagonalisering och linjära system ODE med konstanta koe cienter. Variabelbyte i linjära system di erentialekvationer. Målet med det kapitlet i kursen är att lösa linjära system di erentialekvationer på
SF1624 Algebra och geometri Tentamen Onsdag, 13 januari 2016
 SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
Kapitel 4 Inst llning av regulatorer I detta avsnitt skall vi i korthet betrakta problemet att st lla in regulatorer s att den slutna kretsen f r nska
 Kapitel 4 Inst llning av regulatorer I detta avsnitt skall vi i korthet betrakta problemet att st lla in regulatorer s att den slutna kretsen f r nskade egenskaper. Situationen illustreras av reglerkretsen
Kapitel 4 Inst llning av regulatorer I detta avsnitt skall vi i korthet betrakta problemet att st lla in regulatorer s att den slutna kretsen f r nskade egenskaper. Situationen illustreras av reglerkretsen
SF1624 Algebra och geometri Tentamen Torsdag, 17 mars 2016
 SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
DIAGONALISERING AV EN MATRIS
 DIAGONALISERING AV EN MATRIS Definition ( Diagonaliserbar matris ) Låt A vara en kvadratisk matris dvs en matris av typ n n. Matrisen A är diagonaliserbar om det finns en inverterbar matris P och en diagonalmatris
DIAGONALISERING AV EN MATRIS Definition ( Diagonaliserbar matris ) Låt A vara en kvadratisk matris dvs en matris av typ n n. Matrisen A är diagonaliserbar om det finns en inverterbar matris P och en diagonalmatris
3 1 = t 2 2 = ( 1) ( 2) 1 2 = A(t) = t 1 10 t
 SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
1. (a) Bestäm alla värden på c som gör att matrisen A(c) saknar invers: 1 0 1. 1 c 1
 ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
3x + y z = 0 4x + y 2z = 0 2x + y = Lös det överbestämda systemet nedan på bästa sätt i minsta kvadratmening. x = 1 x + y = 1 x + 2y = 2
 TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 734-433 kurser:: Linjär Algebra ma4a Matematik för ingenjörer ma3a 3 7 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och
TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 734-433 kurser:: Linjär Algebra ma4a Matematik för ingenjörer ma3a 3 7 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och
Objective:: Linjärt beroende och oberoende version 1.0
 DEFINITIONEN AV LINJÄRT BEROENDE MED EXEMPEL Objective:: Linjärt beroende och oberoende version. Definitionen av linjärt beroende med exempel Vi börjar med ett inledande exempel för att motivera definitionen
DEFINITIONEN AV LINJÄRT BEROENDE MED EXEMPEL Objective:: Linjärt beroende och oberoende version. Definitionen av linjärt beroende med exempel Vi börjar med ett inledande exempel för att motivera definitionen
Linjär algebra kurs TNA002
 Linjär algebra kurs TNA002 Lektionsanteckningar klass ED1 I detta dokument finns ett utdrag av de tavelanteckningar som uppkommit under lektionstid under kursen TNA002. Alltså kan detta dokument långt
Linjär algebra kurs TNA002 Lektionsanteckningar klass ED1 I detta dokument finns ett utdrag av de tavelanteckningar som uppkommit under lektionstid under kursen TNA002. Alltså kan detta dokument långt
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
Del 1: Godkäntdelen. TMV142 Linjär algebra Z
 MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 130313 kl 0830 1230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV142 Linjär algebra Z Tentan
MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 130313 kl 0830 1230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV142 Linjär algebra Z Tentan
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
SKRIVNING I VEKTORGEOMETRI 2014-11-25 1400-1700 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas Baser i rummet kan dessutom antas vara positivt orienterade
TMV166 Linjär algebra för M, vt 2016
 TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
TMV166 Linjär algebra för M, vt 2016 Lista över alla lärmål Nedan följer en sammanfattning av alla lärmål i kursen, uppdelade enligt godkänt- och överbetygskriterier. Efter denna lista följer ytterligare
EXEMPEL OCH LÖSNINGAR I LINJÄR ALGEBRA II
 EXEMPEL OCH LÖSNINGAR I LINJÄR ALGEBRA II PER ALEXANDERSSON Sammanfattning. Detta är en samling kompletterande uppgifter till Linjär Algebra II för lärare. Exemplen är av varierande svårighetsgrad och
EXEMPEL OCH LÖSNINGAR I LINJÄR ALGEBRA II PER ALEXANDERSSON Sammanfattning. Detta är en samling kompletterande uppgifter till Linjär Algebra II för lärare. Exemplen är av varierande svårighetsgrad och
1 Positivt definita och positivt semidefinita matriser
 Krister Svanberg, april 1 1 Positivt definita och positivt semidefinita matriser Inom ickelinjär optimering, speciellt kvadratisk optimering, är det viktigt att på ett effektivt sätt kunna avgöra huruvida
Krister Svanberg, april 1 1 Positivt definita och positivt semidefinita matriser Inom ickelinjär optimering, speciellt kvadratisk optimering, är det viktigt att på ett effektivt sätt kunna avgöra huruvida
x 2y + z = 1 (1) 2x + y 2z = 3 (2) x + 3y z = 4 (3)
 TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 74-4 kurser:: Linjär Algebra ma4a Matematik för ingenjörer maa 8 5 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta
TM-Matematik Sören Hector :: 7-46686 Mikael Forsberg :: 74-4 kurser:: Linjär Algebra ma4a Matematik för ingenjörer maa 8 5 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta
2s + 3t + 5u = 1 5s + 3t + 2u = 1 3s 3u = 1
 ATM-Matematik Mikael Forsberg 074-4 För studenter på distans och campus Linjär algebra ma04a 04 0 5 Skrivtid: 09:00-4:00. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja
ATM-Matematik Mikael Forsberg 074-4 För studenter på distans och campus Linjär algebra ma04a 04 0 5 Skrivtid: 09:00-4:00. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja
TMV166 Linjär Algebra för M. Tentamen
 MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 3 6 kl. 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Tony Stillfjord,
MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 3 6 kl. 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Tony Stillfjord,
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
Del 1: Godkäntdelen. TMV141 Linjär algebra E
 Var god vänd! MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 26083 kl 0830 230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV4 Linjär algebra
Var god vänd! MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 26083 kl 0830 230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV4 Linjär algebra
Institutionen för Matematiska Vetenskaper TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F1/TM1, TMA671 2014-05-26
 Institutionen för Matematiska Vetenskaper Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F/TM, TMA67 4-5-6 DAG: Måndag 6 maj 4 TID: 4. - 8. SAL: V Ansvarig: Ivar Gustafsson, tel: 75-33545 Förfrågningar:
Institutionen för Matematiska Vetenskaper Göteborg TENTAMEN I LINJÄR ALGEBRA OCH NUMERISK ANALYS F/TM, TMA67 4-5-6 DAG: Måndag 6 maj 4 TID: 4. - 8. SAL: V Ansvarig: Ivar Gustafsson, tel: 75-33545 Förfrågningar:
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v7, 7 januari 6 Högskolan i Skövde Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 5--7 kl 43-93 Hjälpmedel : Inga hjälpmedel
