Effektivare dimensionering av en pålplatta
|
|
|
- Åke Berglund
- för 8 år sedan
- Visningar:
Transkript
1 ISRN UTH-INGUTB-EX-B-2016/23-SE Examensarbete 15 hp Juni 2016 Effektivare dimensionering av en pålplatta Björn Larsson
2
3 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA Ett fördtydligande av beräkningsgången enligt Eurokod Björn Larsson Institutionen för teknikvetenskaper, Tillämpad mekanik, Byggteknik, Uppsala Universitet Examensarbete 2016
4 Detta examensarbete är framställt vid Institutionen för teknikvetenskaper, Tillämpad mekanik, Byggteknik, Uppsala Universitet, Box 337, Uppsala Typsnitt: Times New Roman Copyright Björn Larsson Institutionen för teknikvetenskaper, Tillämpad mekanik, Byggteknik, Uppsala Universitet ii
5 Abstract Effective design of a pile cap Björn Larsson Teknisk- naturvetenskaplig fakultet UTH-enheten Besöksadress: Ångströmlaboratoriet Lägerhyddsvägen 1 Hus 4, Plan 0 Postadress: Box Uppsala Telefon: Telefax: Design of pile caps in accordance with SS-EN :2005 Eurocode 2 is a time-consuming work when calculations are performed by hand. This thesis intends to investigate whether it is possible to streamline the design of pile caps with a self-developed computational tool. The tool streamlines the design of new pile caps and performing a verification of existing pile caps. This thesis will also provide a clarification of the calculation of pile caps according to current standards. The possibility of streamlining the design of a pile cap is presented by a case study where an existing pile cap is controlled with the computational tool. A conclusion is drawn whether it is possible to increase the load on the column or not. The result of this work is the computational tool, and the report itself. The computational tool is considered to be a more efficient way of designing pile caps. Exactly how much time saved is not investigated. Hemsida: Handledare: Dario Muratagic Ämnesgranskare: Kristofer Gamstedt Examinator: Caroline Öhman Mägi ISRN UTH-INGUTB-EX-B-2016/23-SE Tryckt av: Polacksbackens Repro, Inst. för teknikvetenskaper, Uppsala Universitet
6 SAMMANFATTNING Detta examensarbete avser att undersöka om det går att effektivisera dimensionering av pålplattor då detta är ett tidsödande arbete. Inom ramen av arbetet utvecklas även ett beräkningsverktyg som effektiviserar dimensionering av nya, samt kontroll av befintliga pålplattor. Detta examensarbete ska även ge ett förtydligande av beräkningsgången för pålplattor enligt gällande norm, SS-EN :2005 Eurokod 2. Effektiviseringsmöjligheten redovisas med en fallstudie där en befintlig pålplatta kontrolleras med beräkningsverktyget och även en redogörelse kring om eventuell ökad pelarlast är tillåtet. Resultatet av arbetet är beräkningsverktyget, samt själva rapporten i sig. Slutsatsen som kan dras är att beräkningsverktyget anses effektivisera dimensioneringen av pålplattor. Exakt hur mycket tid som sparas är inte utrett. Nyckelord: Pålplatta, effektivisering, Eurokod, beräkningsverktyg, beräkningsgång iv
7 FÖRORD Detta arbete är min avslutning på Högskoleingenjörsprogrammet i byggteknik på Uppsala Universitet. Arbetet är skrivet på företaget Ramböll AB s Uppsala kontor. Jag vill passa på att rikta ett stort tack till min handledare Dario Muratagic för sitt engagemang och stöd under våren Uppsala, maj 2016 Björn Larsson v
8 vi
9 INNEHÅLL 1 INLEDNING BAKGRUNDSBESKRIVNING SYFTE MÅL OMFATTNING OCH AVGRÄNSNINGAR LITTERATURSTUDIE PÅLPLATTA BERÄKNINGSMETODER FACKVERKSMETODEN GRUNDPLATTAMETODEN DIMENSIONERING AV EN PÅLPLATTA BERÄKNING AV REAKTIONSKRAFTER I PÅLARNA BERÄKNING AV LASTEFFEKTER Dimensionerande moment Dimensionerande tvärkraft DIMENSIONERING AV BÖJARMERING KONTROLL AV TVÄRKRAFTSKAPACITET Tvärkraftskapacitet med avseende på skjuvglidbrott Tvärkraftskapacitet med avseende på livtryckbrott KONTROLL AV GENOMSTANSNING - PELARE Snitt för kontroll av genomstansning Dimensionerande genomstansningskraft - pelare Dimensionerande hållfasthet, genomstansning - pelare KONTROLL AV GENOMSTANSNING - PÅLE Dimensionerande genomstansningskraft - påle Dimensionerande hållfasthet, genomstansning - påle KONTROLL AV LOKALT TRYCK PRÄGLING...28 vii
10 5 FALLSTUDIE BAKGRUND KONTROLLBERÄKNING MED RÅDANDE PELARLAST Utformning: Resulterande pålkrafter Lasteffekter Utnyttjandegrad - tillgänglig armeringsarea RESULTAT SLUTSATS OCH DISKUSSION FÖRSLAG PÅ FORTSATTA STUDIER KÄLLFÖRTECKNING BILAGOR: BILAGA 1 - KONTROLLBERÄKNING AV BEFINTLIG PÅLPLATTA... B1.1 viii
11 1 INLEDNING Städernas ständiga expansion leder till att det blir vanligare med bebyggelse på mark med sämre markförhållanden. Anledningen är dels att det byggs mycket mer och dels att i större städer är mark med goda markförhållanden redan bebyggd. Vid sämre markförhållanden används grundläggningstekniken pålning. Även vid ombyggnationer uppstår situationer där konstruktören behöver kontrollera befintliga pålplattor. Dessa processer, både dimensionering av nya pålplattor samt kontroll av befintliga, är i dagsläget tidskrävande då det sker med handberäkningar. Dimensioneringen i dagens läge sker enligt Eurokod och i vissa avseenden finns vissa frånsteg från tidigare beräkningsnormer. Även vid kontrollberäkning av befintliga konstruktioner gäller Eurokod, vilket kan begränsa ombyggnationer av hus som dimensionerats enligt tidigare normer. 1.1 Bakgrundsbeskrivning För närvarande finns det ingen datorapplikation som enkelt och smidigt kontrollerar och dimensionerar pålplattor med godtyckligt antal pålar, samt pålplacering. Dimensionering och kontrollberäkning av pålplattor sker huvudsakligen genom handberäkningar med ett stort antal iterationer, vilket medför att beräkningarna blir mycket tidskrävande. Under produktion av nya pålplattor sker ibland även felslagning av pålar. Med felslagning menas att pålar slås ned med en placering och lutning som ligger utanför angivna toleranser. När detta sker har konstruktören ofta bara någon arbetsdag på sig att ge besked till pålkranföraren om hur problemet med felslagningen ska lösas. En av anledningarna till den korta svarstiden kan vara att pålkranföraren är uppbokad på andra arbeten. Lösningar till felslagningen kan vara en annan placering på kvarvarande pålar i pålplattan eller fler pålar, alternativt mer armering i betongen. Då det är omständligt att utföra beräkningar för hand så sker ingen större optimering av pålplattor vid nyproduktion. Vid större projekt kan exempelvis tre till fyra typ-plattor beräknas där konstruktören medvetet överdimensionerar pålplattor för att underlätta dimensionering vid eventuella felslagningar. 1
12 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA 1.2 Syfte Syftet med detta examensarbete är att undersöka om det går att effektivisera dimensionering i brottgränstillstånd för pålplattor med större antal pålar. Detta arbete ska även förtydliga beräkningsgången med gällande normer. Där eventuella skillnader mot tidigare beräkningsnormer finns skall dessa tydliggöras. 1.3 Mål Målet är att förtydliga beräkningsgången med gällande normer och upprätta ett beräkningsverktyg, MathCAD-program. Med hjälp av verktyget ska konstruktörer ges möjlighet att på ett smidigt sätt dimensionera och kontrollera pålplattor med godtyckligt antal pålar, godtycklig geometri och pålplacering. Programmet skall beakta påförda yttre laster och utföra snittkontroller för tvärkraft och moment i betongen, samt genomstansnings- och präglingskontroll. Även en föreslagen armeringsmängd skall ges i programmet. Med detta program skall förhoppningsvis konstruktörers arbete underlättas, samt spara tid i produktion vid eventuella felslagningar. Beräkningsverktyget skall utformas på ett sådant sätt att användaren av verktyget enkelt kan föra in olika ingående parametrar och sedan få ett snabbt resultat. 1.4 Omfattning och avgränsningar Detta arbete kommer belysa beräkning av pålplattor i brottgränstillstånd. Begränsningarna som valts vid utformningen av MathCAD-programmet är att det endast är betong och armering som kommer beaktas vid beräkning av pålplattan. Pålarnas dimensionerande hållfasthet, samt den geotekniska bärförmågan kommer inte beräknas. MathCAD är ett program som räknar med variabler med tilldelade värden och enheter. En ettårig licens för en ny användare kostar 1660 USD 1), vilket i dagens penningvärde motsvarar ca kr. Vidare tillkommer en årsvis avgift på ca kr för att bibehålla licensen. 1) PTC, Webshop - licenskostnad ( ) 2
13 Kap. 1 Inledning MathCAD valdes att användas vid utformningen av beräkningsverktyget, för att enligt nya tillämpningen av europeiska konstruktionsstandarder, 2) EKS 10 (BFS 2015:6), finns numera ett krav på redovisning och dokumentation av beräkningar. 3) Vid utformningen av beräkningsverktyget har följande avgränsningar gjorts: - Endast helt vertikala pålar. Detta beror på att i hus är det främst pelare som belastas med vertikal last, samt moment p.g.a. excentricitet. - Den geometriska formen på pålplattan kommer att begränsas till rektangulär. Det förekommer pålplattor med annan geometrisk form, dock beaktas inte detta. - Rektangulära betongpålar, SP1, SP2 samt SP3. Dessa pålar är kvadratiska och kommer endast att beaktas vid stansningsberäkningen av pålplattan. - Verktyget kommer inte ta hänsyn till kostnadsparametrar, t.ex. ökad betongmängd kontra ökad armeringsmängd. Det är upp till användaren av verktyget att utföra den kostnadsbedömningen. - Pelaren kommer vara placerad centriskt, d.v.s. i pålgruppens tyngdpunkt. 1.5 Litteraturstudie I den litteraturstudie som utförts har fokus lagts på litteratur som innefattar dimensionering av betongkonstruktioner och vilka brottmoder som bör beaktas. Främst är det den gällande normen Eurokod SS-EN , Dimensionering av betongkonstruktioner, som varit till grund i studien. Även den äldre normen BKR (Boverkets konstruktionsregler), samt böcker och artiklar som berör mekanik och beräkningsmetoder har studerats. Vad gäller information som inhämtats beträffande BKR är det Boverkets handbok om betongkonstruktioner - BBK 04, och Svensk Byggtjänst Betonghandbok - Konstruktion, som studerats. Det finns som tidigare nämnts inte någon datorapplikation som beräknar pålplattor. I Betonghandboken har beräkningsmetodiken för pålplattor inhämtats och sedan tillämpats med nu 2) Boverket, Om Boverkets konstruktionsregler, EKS, ( ) 3) Björn Mattsson, Ändrade konstruktionsregler, EKS 10, ( ) 3
14 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA gällande norm i det egenutvecklade beräkningsverktyget. Litteraturstudien har varit en viktig grund för att kunna tydliggöra beräkningar och antaganden som redovisas under beräkningsteorin i detta arbete. 4
15 2 PÅLPLATTA En pålplatta är en form av pålfundament som utbreder sig över en relativt stor yta och har ett stort antal pålar. Pålfundament är en betongkonstruktion, som har till uppgift att fördela lasten från överbyggnaden till de pålar som är nedslagna i marken. Då betongen har dålig draghållfasthet brukar fundamenten oftast behöva armering för att klara av dragspänningarna. Pålfundamenten armeras numera med armeringskorgar som sänks ned i en grop och därefter hälls betongen i. Ingjutningsdjupet för tryckta pålar bör minst vara mm, 4) samt att ett minsta täckande betongskikt mellan armering och påltoppar måste beaktas. Se Figur 2.1. FIGUR 2.1 Enkel bild på ett pålfundament av typen pålplatta. Jorden under byggnaden är den faktor som avgör vilken grundläggning som ska användas. Utformning av grundläggning med pålfundament sker i de fall som jorden har en sådan låg hållfasthet att en ytlig grundläggning, t.ex. en grundsula, inte kan uppfylla lastöverföringskraven. Vid pålning slås antingen 4) Svensk Byggtjänst, Betonghandbok Konstruktion utgåva 2,
16 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA pålarna ned till ett sådant djup att lasterna kan föras över via pålens mantelyta eller om så krävs ända ned till berg. Pålar som slås ned till berg är så kallade spetsburna pålar. Dessa överför hela lasten via dess spets ned till berget. En påle som inte slås ända ned till berg är en så kallad mantelburen påle. Den för över största delen av lasten via friktion kring sin mantelyta. Pålar finns i olika material, bl.a. betong, trä och stål. Det vanligaste förekommande pålmaterialet i dagens Sverige är betongpålar. 5 ) Idag finns tre standardutföranden på betongpålar, SP1, SP2 och SP3. SP1 har breddmåttet på minst 235 mm, medan SP2 och SP3 har breddmåtten 270 eller 275 mm. Skillnaden mellan SP2 och SP3 är mängden armering, en SP2 har armeringsjärn med dimensionen Ø12 medan en SP3 har armeringsjärn med dimensionen Ø16. 6) Dessa pålar förs ned i marken genom slagning. 5) Kennet Axelsson, Grundläggningsteknik, Uppsala Universitet, ) Pålkommisonen, Standardpålar av betong lastkapacitet och geotekniskbärförmåga, rapport 94,
17 3 BERÄKNINGSMETODER Vid dimensionering av pålfundament finns det främst två beräkningsmetoder som används, fackverksmetoden och grundplattametoden. Dessa två metoder har båda sina för- och nackdelar, samt vissa begränsningar. I detta avsnitt kommer begränsningarna, samt grunderna i dessa två beräkningsmetoder att redogöras. 3.1 Fackverksmetoden Vid en dimensionering av ett pålfundament med fackverksmetoden tänks att ett fackverk skapas. Dels av trycksträvorna, som är lokaliserade diagonalt från pelarens botten ned till påltopparna, samt armeringen som ligger i underkant pålfundament. Trycksträvorna tar hand om trycket från pelaren. I och med lutningen på trycksträvorna skapas en dragkraft som blir dimensionerande för armeringen, se Figur 3.1. Trycksträvorna tillåts ha en lutning på 45 θ 70, 7) därtill måste en felslagningsparameter på 100 mm beaktas. 8) I och med begränsningen på lutning på trycksträvorna blir kombinationen av höjden på fundamentet, samt avståndet mellan pålarna de parametrar som måste beaktas. FIGUR 3.1 Fackverk vid beräkning med fackverksmetoden 7) Betongföreningen, Betongrapport nr 15, Svenska Betongföreningens handbok till Eurokod 2 (Volym1), ) Svensk Byggtjänst, Betonghandbok Konstruktion utgåva 2,
18 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA Vid en stor pelarkraft blir behovet av antal pålar så stort att det blir svårt att med en rimlig höjd på fundamentet få pålarna att rymmas inom det tillåtna avståndet från pelarcentrum. Denna beräkningsmetod kan därför endast tillämpas där pålarna är inom ett visst avstånd från pelaren. Det tillåtna avståndets storlek beror på lutningen på trycksträvan, samt fundamentets höjd. Även höjden kan vara begränsande vid grundläggning för ett hus. Det är inte alltid det finns utrymme för allt för höga fundament. I och med avståndsbegränsningarna och behovet av höjd på fundamentet blir det fundamentstypen pålplintar som kan dimensioneras enligt fackverksmodellen, se Figur 3.1. Minsta avstånd för pålar redovisas i Tabell 3.1. TABELL 3.1 9) Minsta centrumavstånd för pålar Där: Förutsedd pållängd [m] Stödpåle och friktionspåle Kohesionspåle Cirkulär Kvadratisk Cirkulär Kvadratisk <10 3 D 3,4 d 4 D 4,5 d D 4,5 d 5 D 5,6 d >25 5 D 5,6 d 6 D 6,8 d D d är diametern på en cirkulär påle är sidomåttet på en kvadratisk påle 3.2 Grundplattametoden Vid denna beräkningsmetod analyseras fundamentet med balkteori som en konsolplatta. Betongen och armeringen dimensioneras på sådant sätt att tillräcklig skjuvkapacitet uppnås i kritiska snitt, samt att armeringsarean är tillräckligt stor för att klara av det böjande momentet som uppkommer i underkanten av plattan. Denna beräkningsmetod gör det möjligt att beräkna tunnare fundament med större area, samt ett större antal pålrader än fackverksmetoden. Redan vid fler än två pålrader är det svårt att använda sig av fackverksmetoden på p.g.a. kraven på minsta avstånd mellan respektive påle. Syftet med detta arbete är att just undersöka och förtydliga beräkningsgången för pålplattor och därmed kommer vidare beräkningar baseras på denna beräkningsmetod. 9) Statens planverk, Pålnormer Föreskrifter, råd och anvisningar angående grundläggning med pålar, Publikation nr 11 Svensk Byggnorm Supplement SBN-S- 23:6,
19 4 DIMENSIONERING AV EN PÅLPLATTA I detta kapitel kommer beräkningsgången för pålplattor belysas och förtydligas. Beräkningsstegen tas upp i den ordning som rekommenderas för att lättast dimensionera en pålplatta enligt SS-EN , Eurokod 2: Dimensionering av betongkonstruktioner. Där inte annat anges är informationen hämtad från Eurokod 2. 10) 4.1 Beräkning av reaktionskrafter i pålarna Enligt tidigare nämnda avgränsningar undersöks beräkningen för pålplattor med endast vertikala pålar, se Figur 2.1. Pålplattan antas vara oändligt styv, vilket leder till att alla pålar får en lika stor vertikalkraft p.g.a. pelarkraften. En pålplatta som endast är belastad med en vertikal kraft, får resulterande pålkrafter enligt Ekvation 4.1. P v = P d n (4.1) Där: n P d P v är antalet pålar är dimensionerande pelarkraft är dimensionerande vertikalkraft i respektive påle Om samma pålplatta teoretiskt endast belastas med momentet M x kring pålplattans x-axel kan reaktionskraften i pålen P i som är belägen med ett avstånd r yi från pelarens centrum beräknas enligt Ekvation 4.2. Se Figur 4.1. P i = M x r2 r yi (4.2) yi 10) Svensk Standard, SS-EN :2005 Eurokod 2: Dimensionering av betongkonstruktioner - Del 1-1: Allmänna regler och regler för byggnader. (Fastställd 2005, Publicerad 2008) 9
20 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA FIGUR 4.1 Pålplatta belastad med moment kring x-axeln Är pålplattan belastad med momentet M y kring y-axeln beräknas det med Ekvation 4.2 men med pålens avstånd i x-led istället. Om den blir belastad med en vertikalkraft och ett moment kring x-axeln samt ett moment kring y-axeln beräknas respektive pålkraft med Ekvation ) P i = P d + M x n r yi 2 r yi + M y 2 r xi (4.3) r xi Det gäller att vara noga med definitionen av momentets riktning samt pålens koordinater vid teckenbestämning. D.v.s. en påle kan antingen få reducerad eller ökad resulterande kraft beroende på riktning på moment. I Figur 4.1 illustreras att det vridande momentet M x skapar en dragpåkänning för pålarna placerade till vänster om pelaren. Medan momentet M x ger upphov till en tryckpåkänning, för pålarna belägna till höger om pelaren. En påle som påverkas av en dragpåkänning p.g.a. momentet får en minskad resulterande vertikalkraft och för en påle som påverkas av en tryckpåkänning ökas den resulterande vertikalkraften. 11) Bengt Langesten, Byggkonstruktion 1 Byggnadsstatik, Liber,
21 Kap.4 Dimensionering av en pålplatta 4.2 Beräkning av lasteffekter Pålplattan kommer få lasteffekter på grund av de yttre påförda lasterna. Såväl en dimensionerande tvärkraft som ett dimensionerande moment kommer att beräknas under denna del Dimensionerande moment Det dimensionerande momentet för en pålplatta beräknas vid ett snitt alldeles invid pelarens yttersida, se Figur 4.2. FIGUR 4.2 Planvy där snitt för moment redovisas Det dimensionerande momentet, M Ed, skall beräknas kring pålplattans x-axel och dess y-axel. Momentet räknas ut genom att pålplattan analyseras likt en konsolbalk där pålarnas krafter utanför snittet ger upphov till momentet, se Figur 4.3. Med hjälp av momentjämvikt kan snittmomentet i snittet A 1 räknas ut enligt Ekvation 4.4. FIGUR 4.3 Beräkning av snittmoment för en pålplatta M Ed = P 3 l 3 + P 4 l 4 (4.4) 11
22 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA Vid specialfallet där pålplattan inte är belastad med något yttre moment samt att pålarna är helt symmetriskt placerade, behöver endast en snittkontroll utföras. I övriga fall måste snittkontroller utföras i både x- och y-led. För oerfarna konstruktörer rekommenderas att utföra snittkontroller invid pelarens alla fyra sidor Dimensionerande tvärkraft Vid dimensionering med avseende på tvärkraft är det två brottmoder som skall kontrolleras, skjuvglidbrott och livtryckbrott Lasteffekt - dimensionering mot skjuvglidbrott Skjuvglidbrott är ett tvärkraftsbrott där betongen förskjuts längs en uppkommen spricka, så kallad skjuvglidning se Figur 4.4. FIGUR 4.4 Skjuvglidbrott i en konstruktion med endast böjarmering 12) Sprickorna uppkommer oftast av det böjande momentet. En pålplatta är normalt endast armerad med böjarmering, d.v.s. ingen extra tvärkraftsarmering i form av byglar brukar förekomma. Kapaciteten mot skjuvglidbrott för betongen beror på friktionen i sprickan, men även böjarmeringen påverkar kapaciteten. Böjarmeringen bidrar mestadels till tvärkraftskapaciteten genom att hålla ihop sprickan i den dragna zonen, men bidrar även till kapaciteten med en mothållande kraft som kallas dymlingsverkan. Dymlingsverkan är armeringens motvilja att böja sig vid de båda sidorna om sprickan. Därmed kan en ökad armering öka tvärkraftskapaciteten med avseende på skjuvglidbrott. Vid beräkning av dimensionerande tvärkraft med avseende på skjuvglidbrott finns det en del otydligheter i Eurokod. Enligt avsnitt (8) i Eurokod 2 behöver inte konstruktioner utsatta för huvudsakligen jämt fördelad last, t.ex. 12) Björn Engström, Chalmers, Beräkning av Betongkonstruktioner, Chalmers Tekniska Högskola,
23 Kap.4 Dimensionering av en pålplatta en utbredd last i form av nyttiglast, kontrolleras närmare än ett d ifrån pelarens periferi, där d är den effektiva höjden. Effektiva höjden är avståndet från konstruktionens överkant ned till armeringens centrumlinje. I detta fall är lasten i form av punktlaster, pålarnas reaktionskrafter. Det står inget i Eurokod 2 om hur nära snittkontrollen för tvärkraft skall ske vid en sådan utformning av last. Enligt en undersökning som Constin Pacoste (ELU, KTH) tillsammans med Mario Plos (CTH) och Morgan Johansson (Reinertsen) har utfört 13 ), behöver inte snittkontroller med avseende på skjuvglidbrott utföras närmare än ett d oavsett utformning på last. Dock har valet gjorts i detta arbete att utföra snittkontrollen enligt den gamla normen 14), vilket innebär att den skall utföras 0,5d från pelarens periferi, se Figur 4.5. Detta gör att beräkningarna är på den säkra sidan. FIGUR 4.5 Planvy där snitt för kontroll av skjuvglidbrott redovisas Tvärkraften i varje snitt är summan av reaktionskrafter från pålar som är belägna utanför snittet, se Ekvation 4.5. V i = P Utanförsnitt (4.5) 13) Costin Pacoste, Mario Plos, Morgan Johansson, Recommendations for finite element analysis for the design of reinforced concrete slabs, KTH Stockholm, Oktober ) Svensk Byggtjänst, Betonghandbok Konstruktion utgåva 2,
24 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA Det går om så önskas att minska tvärkraften med egentyngden av den del av pålplattan som är utanför snittet. Den dimensionerande tvärkraften i varje riktning är det största kraften V i i respektive riktning. Enligt avsnitt (6) i Eurokod 2 kan den dimensionerande tvärkraften nära upplag, V Ed, vid kontroll av skjuvglidbrott reduceras med faktorn β, se Ekvation 4.6. β = a v 2 d (4.6) Där: a v är avståndet från upplagets kant till kraften 0.5d a v 2d Vid dimensionering av en pålplatta är pelaren upplag. Dock måste bärverksdelen ha fullt upplag utmed hela dess bredd för att reduktion av tvärkraften skall vara tillåten. I och med detta krav, samt att pålplattan beaktas som en bred strimla med upplag endast vid pelaren, kan reduktion av tvärkraften endast ske i linje med pelaren. 15 ) Därför försummas denna reduktion Lasteffekt Dimensionering mot Livtryckbrott Livtryckbrott är ett tvärkraftsrelaterat brott där tryckspänningen i den sneda trycksträvan blir större än betongens tryckhållfasthet. Trycksträvan är lokaliserad precis invid pelarens periferi och antas ha en lutning på 45, se Figur 4.6. FIGUR 4.6 Krossning av trycksträva 15) Björn Engström, Chalmers, Beräkning av Betongkonstruktioner, Chalmers Tekniska Högskola,
25 Kap.4 Dimensionering av en pålplatta Den dimensionerande tvärkraften för livtryckbrott räknas ut, såsom för skjuvglidbrott med Ekvation 4.5. Skillnaden är att snittet skall läggas invid pelarens periferi, precis som för uträkningen av dimensionerande snittmomentet, se Figur 4.2. Även här bör tvärkraften kontrolleras invid pelarens alla yttersidor. 4.3 Dimensionering av böjarmering Vid dimensionering av böjarmeringen beaktas det dimensionerande momenten M Edx, momentet kring pålplattans x-axel, och M Edy, momentet kring pålplattans y-axel. M Edx är det som avgör vilken armering som behövs i pålplattans y- riktning och omvänt för M Edy. Vid dimensionering av böjarmering enligt SS-EN används rektangulär spänningsfördelning, eller förenklat tryckblock som Björn Engström benämner det 16), se Figur 4.7. FIGUR 4.7 Rektangulär spänningsfördelning Där: λ = 0.8 för betongklass C50/60 λ = 0.8 (f ck 50) 400 för C50/60 betongklass C90/105 η = 1.0 för betongklass C50/60 η = 1.0 (f ck 50 ) 200 för C50/60 betongklass C90/105 16) Björn Engström, Chalmers, Beräkning av Betongkonstruktioner, Chalmers Tekniska Högskola,
26 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA I vidare ekvationer ansätts betongklass C50/60. Utifrån den rektangulära spänningsfördelningen kan två jämviktsekvationer ställas upp, se Ekvation 4.8 och : F s = F c (4.7.a) Där: F s = σ s A s F c = f cd b 0.8x (4.7.b) (4.7.c) σ s A s x b f cd är stålspänningen är armeringsarean är tryckzonens höjd är betongtvärsnittets bredd, i detta fall pålplattans bredd är betongens dimensionerande tryckhållfasthet Ekvation 4.7.b och 4.7.c insatt i Ekvation 4.7.a ger: : σ s A s = f cd b 0.8x (4.8) Moment kring F c : : M = F s (d 0.8x 2 ) (4.9) Vilket kan skrivas om med hjälp av Ekvation 4.7.b till: : M = σ s A s (d 0.4x) (4.10) Jämviktsekvationerna 4.8 och 4.10 ger grunden till dimensionering av böjarmering. Om Ekvation 4.8 förlängs med f cd b d och Ekvation 4.10 förlängs med f cd b d 2 fås ekvationssystemet: M f cd b d 2 = σ s A s (d 0.4x) f cd b d 2 σ s A s f cd b d = 0.8x d 16
27 Kap.4 Dimensionering av en pålplatta Om sedan begrepp som relativt moment, mekaniskt armeringsinnehåll, samt geometrisk armeringsandel förs in. m = M f cd b d 2 ω = σ s A s f cd b d ρ = A s b d relativt moment mekaniskt armeringsinnehåll geometrisk armeringsandel Dessa begrepp möjliggör en omskrivning av ekvationssystemet. M m = f cd b d 2 ω = 0.8x d = ρ σ s f cd = m När ω beräknats måste värdet jämföras med ω bal, vilket räknas ut med Ekvation Där: ω bal = 0.8 ε cu ε cu +ε sy (4.11) ε sy = f yd E s E s = 200 GPa 17) ε cu = 3,5 18) stålets töjning vid sträckgränsen stålets elasticitetsmodul betongens brottstukning 17) Paul Johannesson, Bengt Vretblad, Byggformler och tabeller, Liber (2011) 18 ) Björn Engström, Chalmers, Beräkning av Betongkonstruktioner, Chalmers Tekniska Högskola,
28 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA Om ω ω bal är tvärsnittet balanserat/underarmerat och om ω > ω bal är tvärsnittet överarmerat. 19 ) Erforderlig armeringsmängd räknas ut enligt Ekvation 4.12.a. A s = M Ed σ s d (1 ω 2 ) (4.12.a) Där: σ s = f yd för ω ω bal σ s = ε s E s för ω > ω bal ε s = ε cu ( 0.8 ω 1) är stålets töjning Enligt SS-EN avsnitt skall kravet på minimiarmering uppfyllas. Minsta tillåtna armeringsmängd räknas ut enligt Ekvation 4.12.b. Där: A smin = 0,26 f ctm f yk b t d dock minst b t d (4.12.b) 3 f ctm = 0.3 (f ck ) 2 betongens medeldraghållfasthet f ck f yk b t är betongens karakteristiska tryckhållfasthet är stålets karakteristiska sträckgräns är betongtvärsnittets medelbredd 19) Tord Isaksson, Annika Mårtensson, Byggkonstruktion Regel och formelsamling, Studentlitteratur (2010) 18
29 Kap.4 Dimensionering av en pålplatta När erforderlig armeringsarea beräknats kan antalet stänger bestämmas enligt Ekvation Där: n = A s A (avrundas uppåt till närmsta heltal) (4.13) A = π ( 2 )2 är en armeringsstångs area är armeringsstångens diameter Armeringsstängernas centrumavstånd, så kallat s-avstånd, erhålls av Ekvation s = b [2c nom+2( 2 )] n 1 (4.14) Där: c nom är täckande betongskikt, vilket är avståndet från armeringens periferi till betongens ytterkant 20), se Figur 4.8. FIGUR 4.8 Täckande betongskikt 20) Svensk Standard, SS-EN :2005 Eurokod 2: Dimensionering av betongkonstruktioner - Del 1-1: Allmänna regler och regler för byggnader. (Fastställd 2005, Publicerad 2008) 19
30 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA 4.4 Kontroll av tvärkraftskapacitet Vid kontroll av tvärkraftskapacitet är det som tidigare nämnt mot skjuvglidbrott och livtryckbrott Tvärkraftskapacitet med avseende på skjuvglidbrott Vid kontroll av skjuvglidbrott utgår beräkningarna utifrån erforderlig böjarmering i respektive riktning. Vilket härleds i delavsnittet 4.3. Hur brottet uppkommer redovisas i delavsnitt Följande villkor gäller: Där: V Ed V Rd,c 100 % V Ed V Rd,c är dimensionerande tvärkraft i respektive riktning, se delavsnitt är dimensionerande tvärkraftskapacitet i respektive riktning Tvärkraftskapaciteten beräknas enligt SS-EN : 3 V Rd,c = C Rd,c k 100 ρ l f ck b w d (4.15.a) Dock minst: V Rd,c = υ min b w d (4.15.b) Där: C Rd,c = 0.18 γ C γ C = 1.5 är rekommenderat värde är betongens partialkoefficient k = d 2.0 är storleksfaktor ρ l = A s d 0.02 b w är armeringsinnehåll är tvärsnittets minsta bredd [mm] i dragzonen υ min = k (3 2 ) fck (4.16) 20
31 Kap.4 Dimensionering av en pålplatta Om villkoret, V Ed V Rd,c 100 %, inte uppfylls med den erforderliga böjarmeringen måste armeringsmängden ökas, d.v.s. minska s-avståndet eller öka armeringsstångens dimension, till villkoret uppfylls. Alternativt kan höjden på fundamentet ökas eller att en betongkvalité med högre tryckhållfasthet används Tvärkraftskapacitet med avseende på livtryckbrott Oavsett om tvärsnittet klarar sig med avseende på skjuvglidbrott måste tvärsnittet kontrolleras mot livtryckbrott. Hur brottet uppkommer redovisas i delavsnitt Kontroll av brott i trycksträvan sker enligt avsnitt (6) i SS-EN Följande villkor gäller: Där: V Edmax V Rdmax V Edmax V Rdmax är dimensionerande tvärkraft i respektive riktning, se delavsnitt är kapaciteten i trycksträvan vilket kan beräknas enligt Ekvation V Rdmax = 0.5 b w d υ f cd (4.17) Där: υ = 0.6 (1 f ck 250 ) Rekommenderat värde, f ck med enhet MPa Om villkoret inte uppfylls måste antingen höjden på fundamentet justeras, så att effektiva höjden d blir större och/eller välja en betongkvalité med högre tryckhållfasthet, alternativt öka bredden på pålplattan. 21
32 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA 4.5 Kontroll av genomstansning - pelare Vid dimensionering av en pålplatta måste en genomstansningskontroll utföras, den utförs enligt avsnitt 6.4 i Eurokod 2. Upphovet till genomstansning är att skjuvspänningen i ett eller flera snitt blir för stor. Pålplattor brukar dimensioneras utan extra ilagd skjuvarmering, då detta är kostnadsdrivande Snitt för kontroll av genomstansning Enligt SS-EN :2005 skall en bärverksdel kontrolleras för genomstansning i ett grundkontrollsnitt som är beläget 2d ifrån pelarens periferi, där d är den effektiva höjden, se Figur 4.9. FIGUR 4.9 Grundkontrollsnitt kring pelare Om den koncentrerade kraften, i detta fall pelarkraften, motverkas av reaktionskrafter som är belägna innanför 2d anses konstruktionen lämplig att kontrolleras i snitt närmre än 2d. Då pålar kan vara placerade innanför kontrollsnittet utförs snittkontroller i snitten, d, d, d, 1.5d och 2d. Se Figur FIGUR 4.10 Snittkontroller vid genomstansning 22
33 Kap.4 Dimensionering av en pålplatta Dimensionerande genomstansningskraft - pelare Vid stansning tänks att en cylinder med omkretsen u i och höjden d, stansas ut om skjuvspänningen blir för hög i ett eller flera snitt, se Figur 4.10 och Figur Den dimensionerande genomstansningskraften beräknas genom att pelarlasten minskas med summan av pålkrafter som verkar inom snittet, se Ekvation Där: V Edi = P d P iinnanför_snitt (4.18) V Edi P d P i är den dimensionerande genomstansningskraften i resp. snitt är den dimensionerande pelarlasten är respektive påles reaktionskraft Detta är för att pålarna inom stansningssnittet motverkar att cylindern ska stansas ut. D.v.s. att de minskar totala stansningskraften som skall tas upp av skjuvarean i snittet. I Figur 4.11 illustreras det att påle 2 och 3 motverkar stansningen av cylindern vid snittet 2d. I detta fall skall därmed P d minskas med dessa två pålars reaktionskrafter. FIGUR 4.11 Sektion av pålplatta vid genomstansningskontroll 23
34 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA Genomstansningskraft vid förekomst av excentricitet Vid förekomst av excentricitet, d.v.s. moment, skall en uppförstoring av genomstansningskraften utföras, se Ekvation Momentet som beaktas vid genomstansning är pelarens inspänningsmoment, vilket kan uppkomma vid snedställning av pelaren. Även horisontell belastning skapar inspänningsmoment, men enligt tidigare avgränsningar beaktas inte detta. V Edi_excent = β V Edi (4.19) Vid moment kring endast en axel erhålls β ur Ekvation Där: β = 1 + k M Ed_inspänning V Ed u i W i (4.20) k c 1 c 2 u i för rektangulära pelare fås ur Tabell 4.1 och beror på förhållande mellan c 1 och c 2. är pelartvärsnittets bredd parallellt med momentet är pelartvärsnittets bredd vinkelrätt momentet är omkretsen på respektive stansningssnitt, se Figur 4.9. Och erhålls ur Ekvation u i = 2 b pel + 2 h pel + 2 r π (4.21) r W i är avståndet till respektive snitt från pelarens ytterkant, d.v.s. antingen d, d, d, 1.5d eller 2d 4 2 är en fördelning av skjuvspänningarna i respektive snitt och räknas ut för en rektangulär pelare enligt Ekvation W i = c c 1 c r c 2 + r 8 d + r π c 1 (4.22) 24
35 Kap.4 Dimensionering av en pålplatta TABELL 4.1 Värde för faktor k 21), - linjär interpolation kan användas för kvoter mellan värden c c 2 k FIGUR 4.12 Definition av c 1 och c 2 22) För en pelare med moment kring båda axlarna erhålls excentricitetsfaktorn, β, ur Ekvation Där: β = ( b 2 x ) ( b y ) 2 (4.23) e y e x b x är totala bredden på stansningssnittet i x-led, se Figur 4.9 b y är totala bredden på stansningssnittet i y-led, se Figur 4.9 e är lastens excentricitet, e = M Ed P d. Där e y räknas ut med M Edx_inspänning och e x räknas ut med M Edy_inspänning 21) Svensk Standard, SS-EN :2005 Eurokod 2: Dimensionering av betongkonstruktioner - Del 1-1: Allmänna regler och regler för byggnader. (Fastställd 2005, Publicerad 2008) 22) Svensk Standard, SS-EN :2005 Eurokod 2: Dimensionering av betongkonstruktioner - Del 1-1: Allmänna regler och regler för byggnader. (Fastställd 2005, Publicerad 2008) 25
36 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA Dimensionerande hållfasthet, genomstansning - pelare Hållfastheten med avseende på genomstansning beräknas enligt Ekvation V Rdi = C Rd,c k 100 ρ l f ck χ i 2d r (4.24) Dock gäller att V Rdi minst är: V Rdi = υ min χ i 2d r (4.25) Där: C Rd,c är tidigare definierat i delavsnitt k är tidigare definierat i delavsnitt υ min är tidigare definierat i delavsnitt χ d är stansningsarean i respektive snitt, χ i = u i d är effektiva höjden u i är stansningssnittets längd, se Ekvation ρ l = ρ lx ρ l y 0.02 (4.26) Där: ρ l x ρ l y är armeringsinnehåll i x-riktningen är armeringsinnehåll i y-riktningen 26
37 Kap.4 Dimensionering av en pålplatta 4.6 Kontroll av genomstansning - påle Vid stora reaktionskrafter i pålarna kan även en genomstansning av en påle förekomma. Den påle som löper störst risk att stansa igenom pålplattan kommer alltid att vara en hörnpåle. Dels för att reaktionskraften, enligt Ekvation 4.3, kommer att vara störst hos en hörnpåle och dels för att skjuvarean är mindre för en hörnpåle, jämför Figur 4.10 och Figur FIGUR 4.13 Snittkontroller för en hörnpåle Dimensionerande genomstansningskraft - påle I och med att pålplattan ansätts vara oändligt styv och fritt upplagd på pålarna, samt att hörnpålens reaktionskraft verkar i påltvärsnittets tyngdpunkt, d.v.s. det förekommer ingen excentricitet. Därmed erhålls den dimensionerande stansningslasten ur Ekvation 4.27 Där: V Edpåle = P imax (4.27) P imax är den största pålkraften som erhålls med Ekvation
38 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA Dimensionerande hållfasthet, genomstansning - påle Hållfastheten med avseende på genomstansning för en hörnpåle erhålls precis som för genomstansning av en pelare, se Ekvation 4.24 samt Ekvation Skillnaden är längden på stansningssnittet, u i, jämför Figur 4.10 och Figur För att räkna på säkra sidan antas pålen vara placerad precis i hörnet på pålplattan, snittlängden blir då lite kortare än i det verkliga fallet. Även här utförs snittkontroller innanför grundkontrollsnittet 2d. Snittlängden för en hörnpåle erhålls ur Ekvation u i = 2 b påle + (2 r π) 4 (4.28) Där: b påle r är påltvärsnittets bredd, betongpålar är kvadratiska därmed faktor 2. är avståndet till respektive snitt från pålens ytterkant, d.v.s. antingen d, d, d, 1.5d eller 2d Kontroll av lokalt tryck prägling Väldigt stor pelarlast kan orsaka krossning av betongen direkt under pelaren, vilket kallas prägling. 23) Denna krossning kan orsaka en lokal sättning vilket i sin tur kan ha en åverkan på andra konstruktionsdelar i byggnaden. Kontroll av lokalt tryck utförs enligt avsnitt 6.7 i SS-EN :2005. Den dimensionerande tryckkraften är pelarlasten, P d, och bärförmågan med avseende på lokalt tryck kan beräknas enligt Ekvation F Rdu = A c0 f cd A c1 A c0 3.0 A c0 f cd (4.29) 23) Boverket, Boverkets handbok om betongkonstruktioner, BBK 04,(Boverket 2004) 28
39 Kap.4 Dimensionering av en pålplatta FIGUR ) Illustration av lokalt tryck med villkor Om villkoren i Figur 4.14 precis är uppfyllda erhålls en lastspridning på 1:2, se Figur Detta leder till att A c1 kan max vara 9 A c0, vilket härleds i Ekvation A c1 erhålls ur Ekvation A c1 3b 1 3d 1 = 9(b 1 d 1 ) = 9 A c0 (4.30) FIGUR 4.15 Lastspridning vid lokalt tryck där villkoren precis är uppfyllda 24) Svensk Standard, SS-EN :2005 Eurokod 2: Dimensionering av betongkonstruktioner - Del 1-1: Allmänna regler och regler för byggnader. (Fastställd 2005, Publicerad 2008) 29
40 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA Där: A c0 är pelarens area, se Figur 4.14 A c1 = (b h 2 ) (d h 2 ) (4.31) b 1 d 1 h är pelartvärsnittets bredd är pelartvärsnittets djup är pålplattans höjd Om A c1 9 A c0, blir den dimensionerande hållfastheten med avseende på lokalt tryck, F Rdu = 3.0 A c0 f cd. Detta innebär att när pålplattan når en viss tjocklek tillgodoräknas inte mer lastspridning i betongen. Se Figur 4.16 som illustrerar detta. FIGUR 4.16 Tillgodoräkning av lastspridning vid lokalt tryck 30
41 5 FALLSTUDIE I detta kapitel kommer en befintlig pålplatta att studeras och beräknas med det beräkningsverktyg som upprättats under detta examensarbete. Utnyttjandegrad för respektive del i Kapitel 4 kommer att redovisas. 5.1 Bakgrund Den befintliga pålplattan som skall studeras finns i en byggnad belägen i Stockholm. Den pelarlast som antas belasta pålplattan är 3600 kn. Pelarlasten har en konstruktör överslagsberäknat enligt Eurokod. Inga inspänningsmoment i pelaren förekommer och den påltyp som använts är SP3. Pålplattans befintliga utformning redovisas i Figur 5.1 och Figur 5.2. FIGUR 5.1 Armeringsritning för befintlig pålplatta 31
42 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA FIGUR 5.2 Måttritningar på befintlig pålplatta 32
43 Kap.5 Fallstudie Pålplattan kommer först analyseras med beräkningsverktyget med den rådande pelarlasten och sedan analyseras hur stor pelarlast som den kan uppnå. Det skall ske en ombyggnation, vilket leder till en ökad pelarlast till 6100 kn. Med hjälp av beräkningsverktyget skall det kontrolleras om det är tillåtet att öka belastningen eller om åtgärder, t.ex. en grundförstärkning, måste vidtas. Lasterna som belastar pålplattan innan ombyggnation är följande: P d = 3600 kn Dimensionerande pelarkraft, vertikal kraft M Edx = 0 knm M Edy = 0 knm Dimensionerande moment kring x-axeln Dimensionerande moment kring y-axeln Lasterna som pålplattan skulle utsättas för efter ombyggnation: P d = 6100 kn Dimensionerande pelarkraft, vertikal kraft M Edx = 0 knm M Edy = 0 knm Dimensionerande moment kring x-axeln Dimensionerande moment kring y-axeln 5.2 Kontrollberäkning med rådande pelarlast I detta delavsnitt studeras och beräknas utnyttjandegraden med pålplattans befintliga belastning. Geometriparametrar och pålkoordinater samt laster är det enda som behöver skrivas in för att kontrollera pålplattan, alla beräkningar sker per automatik. De ändringsbara värdena är de som är fetmarkerade med blå text under rubriken Indata i Bilaga 1. Då beräkningarna blir väldigt långa med många beräkningsoperationer redovisas endast utdrag av beräkningarna i några figurer i detta avsnitt. I Bilaga 1 redovisas den minimerade utformningen av beräkningsdokumentet, som fås i programmet. Om användaren av programmet önskar att redovisa alla beräkningar är det endast att förstora upp de minimerade områdena genom att dubbelklicka på pilen, se Figur 5.3. FIGUR 5.3 Öppning av minimerade områden 33
44 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA Utformning: Pålplattans fullständiga utformning finns under indata i Bilaga 1. Nedan följer en sammanfattning. Antal pålar: Pålplattans bredd: Pålplattans längd: Pålplattans höjd: 13 st 4.0 m 4.0 m 1.0 m Armeringens dimension: 20 mm Armeringens s-avstånd: 140 mm Först förs fullständig indata in i verktyget, såsom antal pålar, pålplacering, materialparametrar, dimensioner mm. I vidare delavsnitt följer en sammanställning av resultatet från beräkningsverktyget Resulterande pålkrafter De resulterande pålkrafterna blir lika stora då det endast är en vertikal pelarkraft som belastar pålplattan. Med Ekvation 4.3 fås följande resulterande pålkrafter: P i = r r yi + 0 yi 2 r r xi = kn xi Lasteffekter De dimensionerande lasteffekterna beräknas i enlighet med beräkningsmetodiken i delavsnitt Moment Det dimensionerande momentet beräknas med Ekvation 4.4. Pålar som är belägna utanför snittet redovisas i Figur 5.4. Det dimensionerande momentet blir följande. M Ed = = knm 34
45 Kap.5 Fallstudie FIGUR 5.4 Snitt för dimensionerande moment befintlig pålplatta Tvärkraft - skjuvglidbrott Den dimensionerande tvärkraften för skjuvglidbrott erhålls med Ekvation 4.5. Denna pålplatta är helt symmetrisk vad gäller pålplacering och är inte momentbelastad. Därmed blir tvärkraften lika stor i alla snitt. Det är 4 pålar som är belägna utanför snittet 0.5d, se Figur 5.5 FIGUR 5.5 Snitt för tvärkraft befintlig pålplatta 35
46 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA Med insatta värden i Ekvation 4.5 blir den dimensionerande tvärkraften med avseende på skjuvglidbrott följande: V Ed = P Utanförsnitt = kN = kn Tvärkraft - Livtryckbrott Enligt delavsnitt , Lasteffekt Dimensionering mot Livtryckbrott beräknas den dimensionerande tvärkraften med avseende på brottmodet i samma snitt som vid beräkning av moment. Därmed är det i detta fall 6 pålar, vilka är belägna utanför detta snitt, se Figur 5.4. Med insatta värden i Ekvation 4.5 erhålls. V Edmax = P Utanförsnitt = kN = kn Utnyttjandegrad - tillgänglig armeringsarea Pålplattans utnyttjandegrad med tillgänglig armering redovisas under rubrik 5.2 i Bilaga 1. Då pålplattan är symmetrisk, samt att ingen momentbelastning förekommer blir utnyttjandegraden i y- respektive x-led exakt lika. Alla beräkningar är utförda enligt beräkningsgången i Kapitel 4, Dimensionering av en pålplatta Moment Likt beräkningsgången i Kapitel 4 i detta arbete kontrolleras pålplattan först med avseende på moment. Momentlasteffekten beräknas och utifrån lasteffekten ger programmet en erforderlig armering. Om det är en befintlig pålplatta redovisar programmet utnyttjandegraden med tillgänglig böjarmering. I Figur 5.6 redovisas hur beräkningarna är upplagda i programmet. Följande villkor gäller: M Ed M Rdtill 100% Den tillgängliga momentbärförmågan beräknas genom en omskrivning av Ekvation M Rdtill = A stillgänglig f yd d (1 ω ) = knm 2 Där: A stillgänglig är tillgänglig armeringsarea ω är mekaniskt armeringsinnehåll, se delavsnitt 4.3 Dimensionering av böjarmering 36
47 Kap.5 Fallstudie Utnyttjandegraden med avseende på moment blir lika kring båda axlarna. M Edx M Rdx till = M Edy = = 43.8 % 100 % M Rdy till Ok, tillgänglig armering är tillräcklig FIGUR 5.6 Utdrag från beräkningsverktyg beräkning av böjarmering 37
48 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA Skjuvglidbrott Nästa steg är att kontrollera om pålplattan har tillräcklig tvärkraftskapacitet med avseende på skjuvglidbrott. Tvärkraftskapaciteten beräknas med Ekvation 4.15.a och Ekvation 4.15.b. Det maximala värdet av dessa två ekvationer är den dimensionerande tvärkraftskapaciteten. Vilket i detta fall erhålls av Ekvation 4.15.a. Där: 3 V Rd,c = C Rd,c k 100 ρ l f ck b w d = kn ρ l beräknas med tillgängliga armeringens s-avstånd Utnyttjandegraden med avseende på skjuvglidbrott blir enligt nedan. V Edx V Rdx till = V Edy = = 108 % > 100 % V Rdy till Detta innebär att den tillgängliga armeringsarean inte är tillräcklig utan pålplattan går i brott Livtryckbrott Redan i delavsnittet ges indikationer om att pelarlasten är för hög. Därmed är övriga kontroller oväsentliga, men i och med att programmet räknar ut dessa per automatik redovisas dessa. Med Ekvation 4.17 erhålls följande kapacitet: V Rdmax = 0.5 b w d υ f cd = kn Följande utnyttjandegrad med avseende på livtryckbrott blir enligt nedan V Edxmax = V Edy max = = 14.5 % 100 % V Rdxmax V Rdymax Ok, tillgänglig armering är tillräcklig. 38
49 Kap.5 Fallstudie Genomstansning av pelare Vid kontroll av genomstansning av pelare verifieras om det finns tillräcklig skjuvkapacitet i olika snitt. Då det inte förekommer något inspänningsmoment för pelaren beräknas den dimensionerande skjuvkraften med Ekvation 4.18 för respektive snitt. Hur många pålar som finns inom respektive snitt redovisas i Figur 5.7. FIGUR 5.7 Snitt för genomstansning befintlig pålplatta Dimensionerande skjuvkraft i varje snitt redovisas nedan. Den dimensionerande pelarlasten, P d, innan ombyggnation är som tidigare nämnts 3600 kn. V Ed ( d 4 ) = P d kn = 3323 kn V Ed ( d 2 ) = P d kn = 3323 kn V Ed (d) = P d kn = 3323 kn V Ed (1.5d) = P d kn = kn V Ed (2d) = P d kn = 0 kn Skjuvhållfastheten med avseende på genomstansning beräknas enligt Ekvation 4.24 och Ekvation 4.25 för varje snitt. Där det maximala värdet som erhålls av 39
50 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA dessa ekvationer blir den dimensionerande skjuvhållfastheten. I detta fall erhålls den dimensionerande hållfastheten för varje snitt med Ekvation Där: 3 V Rdi = C Rd,c k 100 ρ l f ck χ i 2d r χ i är stansningsarean i respektive snitt, se delavsnitt Dimensionerande hållfasthet, genomstansning - pelare r är avståndet till respektive snitt från pelarens ytterkant, d.v.s. antingen d, d, d, 1.5d eller 2d 4 2 Med insatta värden erhålls stansningshållfastheten för respektive snitt enligt nedan. V Rd ( d ) = kn 4 V Rd ( d ) = kn 2 V Rd (d) = 4162 kn V Rd (1.5d) = kn V Rd (2d) = kn Utnyttjandegraden för respektive snitt blir enligt nedan och redovisas i Figur 5.8. η ( d 4 ) = = 39.8% 100% η ( d 2 ) = 3323 = 59.8% 100% η(d) = 3323 = 79.8% 100% 4162 η(1.5d) = = 30% 100% η(2d) = 0 = 0% 100%
51 Kap.5 Fallstudie FIGUR 5.8 Utdrag från beräkningsverktyg enligt beräkningar i detta avsnitt -Diagram som redovisar utnyttjandegrad för genomstansning av pelare för respektive snittkontroll Genomstansning av påle Beräkningsmetodiken för kontroll av genomstansning av påle redogörs i delavsnitt 4.6 Kontroll av genomstansning - påle. Pålkraften som beaktas är den största av pålkrafterna, vilket enligt tidigare beräkningar är kn. Beräkningsgången är densamma som vid kontroll av genomstansning. Det som skiljer är storleken på kontrollsnittslängderna, vilket beräknas med Ekvation Därmed redovisas endast resultatet av kontroll utav stansningen. η påle ( d 4 ) = V Ed_påle = = 15.4% 100% V Rd_påle 1799 η påle ( d 2 ) = V Ed_påle = = 22.2% 100% V Rd_påle 1245 η påle (d) = V Ed_påle = = 28.6% 100% V Rd_påle 969 η påle (1.5d) = V Ed_påle = = 31.6% 100% V Rd_påle 877 η påle (2d) = V Ed_påle = = 33.3% 100% V Rd_påle
52 EFFEKTIVARE DIMENSIONERING AV EN PÅLPLATTA Lokalt tryck prägling Beräkningsmetodiken som används i beräkningsverktyget är redovisat i delavsnitt 4.7 Kontroll av lokalt tryck prägling. Den dimensionerande pelarlasten är den kraft som beaktas vid kontroll med avseende på lokalt tryck. Enligt tidigare är denna kraft 3600 kn. Hållfastheten beräknas enligt Ekvation I och med att höjden på pålplattan är inom villkoren, se Figur 4.14, blir den dimensionerande hållfastheten med avseende på lokalt tryck enligt nedan. F Rdu = A c0 f cd A c1 A c0 = kn Utnyttjandegraden med avseende på lokalt tryck blir därmed. η pragling = = 26.3% 42
53 Kap.5 Fallstudie 5.3 Resultat Enligt avsnittet ovan är den tillgängliga armeringen inte tillräcklig för att klara av snittkontrollen för tvärkraft, d.v.s. skjuvglidbrott riskerar att uppkomma med rådande pelarlast. Beräkningsverktyget räknar ut den erforderliga armeringsmängden, den redovisas under rubriken resultat i Bilaga 1. Nedan följer en sammanfattning gällande ökad armeringsmängd. Armeringens dimension: 20 mm Armeringens s-avstånd: 110 mm Utnyttjandegrad med avseende på skjuvglidbrott blir då följande: V x = V y = 99.8 % 100% Övriga utnyttjandegrader blir lägre än med den tillgängliga armeringen och redovisas under delavsnitt 5.1 i Bilaga 1. Då pålplattan inte klarar av den överslagsberäknade lasten på 3600 kn, utfördes en kontroll av vad den maximalt tillåtna pelarlasten är. Med befintlig utformning av pålplattan är den maximala belastningen 3300 kn, vilket är långt ifrån den önskade ökningen upp till 6100 kn. Den ökande lasten beror på som tidigare nämnts av en ombyggnation. Utnyttjandegraden med avseende på skjuvglidbrott blev 99,1 % med en last på 3300 kn. Detta visar på att den befintliga pålplattan inte överdimensionerades när byggnaden konstruerades. 43
Betongkonstruktion BYGC11 (7,5hp)
 Karlstads universitet 1(11) Betongkonstruktion BYGC11 (7,5hp) Tentamen Tid Fredag 17/01 2014 kl. 14.00 19.00 Plats Universitetets skrivsal Ansvarig Asaad Almssad tel 0736 19 2019 Carina Rehnström tel 070
Karlstads universitet 1(11) Betongkonstruktion BYGC11 (7,5hp) Tentamen Tid Fredag 17/01 2014 kl. 14.00 19.00 Plats Universitetets skrivsal Ansvarig Asaad Almssad tel 0736 19 2019 Carina Rehnström tel 070
 www.eurocodesoftware.se caeec230 Genomstansning Beräkningsprogram för analys av genomstansning av pelare i armerad betong. Programmet utför beräkningar enligt EN 1992-1-1 Kap. 6.4. Användarmanual Rev B
www.eurocodesoftware.se caeec230 Genomstansning Beräkningsprogram för analys av genomstansning av pelare i armerad betong. Programmet utför beräkningar enligt EN 1992-1-1 Kap. 6.4. Användarmanual Rev B
Dimensionering för tvärkraft Betong
 Dimensionering för tvärkraft Betong Tvärkrafter Huvudspänningar Skjuvsprickor Böjskjuvsprickorna initieras i underkant p.g.a. normalspänningar som överstiger draghållfastheten Livskjuvsprickor uppträder
Dimensionering för tvärkraft Betong Tvärkrafter Huvudspänningar Skjuvsprickor Böjskjuvsprickorna initieras i underkant p.g.a. normalspänningar som överstiger draghållfastheten Livskjuvsprickor uppträder
CAEBBK30 Genomstansning. Användarmanual
 Användarmanual Eurocode Software AB 1 Innehåll 1 INLEDNING...3 1.1 TEKNISK BESKRIVNING...3 2 INSTRUKTIONER...4 2.1 KOMMA IGÅNG MED CAEBBK30...4 2.2 INDATA...5 2.2.1 BETONG & ARMERING...5 2.2.2 LASTER &
Användarmanual Eurocode Software AB 1 Innehåll 1 INLEDNING...3 1.1 TEKNISK BESKRIVNING...3 2 INSTRUKTIONER...4 2.1 KOMMA IGÅNG MED CAEBBK30...4 2.2 INDATA...5 2.2.1 BETONG & ARMERING...5 2.2.2 LASTER &
caeec230 Genomstansning Användarmanual Eurocode Software AB
 caeec230 Genomstansning Beräkningsprogram för analys av genomstansning av pelare i armerad betong. Programmet utför beräkningar enligt EN 1992-1-1 Kap. 6.4. Användarmanual Rev C Eurocode Software AB caeec230
caeec230 Genomstansning Beräkningsprogram för analys av genomstansning av pelare i armerad betong. Programmet utför beräkningar enligt EN 1992-1-1 Kap. 6.4. Användarmanual Rev C Eurocode Software AB caeec230
Betongkonstruktion BYGC11 (7,5hp)
 Karlstads universitet 1(12) Betongkonstruktion BYGC11 (7,5hp) Tentamen Tid Torsdag 17/1 2013 kl 14.00 19.00 Plats Universitetets skrivsal Ansvarig Asaad Almssad tel 0736 19 2019 Carina Rehnström tel 070
Karlstads universitet 1(12) Betongkonstruktion BYGC11 (7,5hp) Tentamen Tid Torsdag 17/1 2013 kl 14.00 19.00 Plats Universitetets skrivsal Ansvarig Asaad Almssad tel 0736 19 2019 Carina Rehnström tel 070
 www.eurocodesoftware.se caeec241 Pålfundament Program för dimensionering av pålfundament. Användarmanual Rev C Eurocode Software AB caeec241 Pålfundament Sidan 2(14) Innehållsförteckning 1 Allmänt... 3
www.eurocodesoftware.se caeec241 Pålfundament Program för dimensionering av pålfundament. Användarmanual Rev C Eurocode Software AB caeec241 Pålfundament Sidan 2(14) Innehållsförteckning 1 Allmänt... 3
www.eurocodesoftware.se
 www.eurocodesoftware.se caeec220 Pelare betong Program för dimensionering av betongtvärsnitt belastade med moment och normalkraft. Resultat är drag-, tryckarmering och effektiv höjd. Användarmanual Rev
www.eurocodesoftware.se caeec220 Pelare betong Program för dimensionering av betongtvärsnitt belastade med moment och normalkraft. Resultat är drag-, tryckarmering och effektiv höjd. Användarmanual Rev
Dimensionering för moment Betong
 Dimensionering för moment Betong Böjmomentbelastning x Mmax Böjmomentbelastning stål och trä σmax TP M σmax W x,max z I y M I z max z z y max x,max M W z z Bärförmåga: M R f y W Betong - Låg draghållfasthet
Dimensionering för moment Betong Böjmomentbelastning x Mmax Böjmomentbelastning stål och trä σmax TP M σmax W x,max z I y M I z max z z y max x,max M W z z Bärförmåga: M R f y W Betong - Låg draghållfasthet
caeec209 Pelartopp Användarmanual Eurocode Software AB Program för dimensionering av pelartopp. Rev C
 caeec209 Pelartopp Program för dimensionering av pelartopp. Rev C Eurocode Software AB caeec209 Pelartopp Sidan 2(13) Innehållsförteckning 1 Inledning...3 1.1 Beteckningar...3 2 Teknisk beskrivning...3
caeec209 Pelartopp Program för dimensionering av pelartopp. Rev C Eurocode Software AB caeec209 Pelartopp Sidan 2(13) Innehållsförteckning 1 Inledning...3 1.1 Beteckningar...3 2 Teknisk beskrivning...3
 www.eurocodesoftware.se caeec241 Pålfundament Program för dimensionering av pålfundament. Användarmanual Version B Eurocode Software AB caeec241 Pålfundament Sidan 2(8) Innehållsförteckning 1 Allmänt...
www.eurocodesoftware.se caeec241 Pålfundament Program för dimensionering av pålfundament. Användarmanual Version B Eurocode Software AB caeec241 Pålfundament Sidan 2(8) Innehållsförteckning 1 Allmänt...
 www.eurocodesoftware.se caeec201 Armering Tvärsnitt Program för dimensionering av betongtvärsnitt belastade med moment och normalkraft. Resultat är drag-, tryckarmering och effektiv höjd. Användarmanual
www.eurocodesoftware.se caeec201 Armering Tvärsnitt Program för dimensionering av betongtvärsnitt belastade med moment och normalkraft. Resultat är drag-, tryckarmering och effektiv höjd. Användarmanual
caeec201 Armering Tvärsnitt Användarmanual Eurocode Software AB
 caeec201 Armering Tvärsnitt Program för dimensionering av betongtvärsnitt belastade med moment och normalkraft. Resultat är drag-, tryckarmering och effektiv höjd. Användarmanual Rev C Eurocode Software
caeec201 Armering Tvärsnitt Program för dimensionering av betongtvärsnitt belastade med moment och normalkraft. Resultat är drag-, tryckarmering och effektiv höjd. Användarmanual Rev C Eurocode Software
caeec240 Grundplatta betong Användarmanual Eurocode Software AB Program för dimensionering av grundplattor m h t stjälpning, marktryck och armering.
 www.eurocodesoftware.se caeec240 Grundplatta betong Program för dimensionering av grundplattor m h t stjälpning, marktryck och armering. Användarmanual Version 1.1 Eurocode Software AB caeec240 Grundplatta
www.eurocodesoftware.se caeec240 Grundplatta betong Program för dimensionering av grundplattor m h t stjälpning, marktryck och armering. Användarmanual Version 1.1 Eurocode Software AB caeec240 Grundplatta
Bromall: Tvärkraft. Innehåll. Bestämning av tvärkraft. Rev: A EN : 2004 EN : 2005
 Bestämning av tvärkraft. Rev: A EN 1992-1-1: 2004 EN 1992-2: 2005 Innehåll 1 Bärförmåga generellt 2 2 Bärförmåga utan tvärkraftsarmering 3 3 Dimensionering av tvärkraftsarmering 4 4 Avtrappning av armering
Bestämning av tvärkraft. Rev: A EN 1992-1-1: 2004 EN 1992-2: 2005 Innehåll 1 Bärförmåga generellt 2 2 Bärförmåga utan tvärkraftsarmering 3 3 Dimensionering av tvärkraftsarmering 4 4 Avtrappning av armering
caeec204 Sprickvidd Användarmanual Eurocode Software AB
 caeec204 Sprickvidd Program för beräkning av sprickvidd för betongtvärsnitt belastade med moment och normalkraft. Resultat är sprickvidd. Användarmanual Rev A Eurocode Software AB caeec204 Sprickvidd Sidan
caeec204 Sprickvidd Program för beräkning av sprickvidd för betongtvärsnitt belastade med moment och normalkraft. Resultat är sprickvidd. Användarmanual Rev A Eurocode Software AB caeec204 Sprickvidd Sidan
Betongbalkar. Böjning. UMEÅ UNIVERSITET Tillämpad fysik och elektronik Annika Moström. Räkneuppgifter
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Annika Moström Räkneuppgifter 2012-11-15 Betongbalkar Böjning 1. Beräkna momentkapacitet för ett betongtvärsnitt med bredd 150 mm och höjd 400 mm armerad
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Annika Moström Räkneuppgifter 2012-11-15 Betongbalkar Böjning 1. Beräkna momentkapacitet för ett betongtvärsnitt med bredd 150 mm och höjd 400 mm armerad
Rättelseblad 1 till Boverkets handbok om betongkonstruktioner, BBK 04
 Rättelseblad till Boverkets handbok om betongkonstruktioner, BBK 04 I den text som återger BBK 04 har det smugit sig in tryckfel samt några oklara formuleringar. Dessa innebär att handboken inte återger
Rättelseblad till Boverkets handbok om betongkonstruktioner, BBK 04 I den text som återger BBK 04 har det smugit sig in tryckfel samt några oklara formuleringar. Dessa innebär att handboken inte återger
Bromall: Prägling och spjälkning
 Kontroll av prägling och spjälkning. Erforderlig spjälkarmering bestäms genom fackverksmodell från BBK04. Rev: A EN 1992-1-1: 2004 BBK04 Innehåll 1 Prägling 3 2 Spjälkning 3 Sida 2 av 6 Förutsättningar/Begränsningar
Kontroll av prägling och spjälkning. Erforderlig spjälkarmering bestäms genom fackverksmodell från BBK04. Rev: A EN 1992-1-1: 2004 BBK04 Innehåll 1 Prägling 3 2 Spjälkning 3 Sida 2 av 6 Förutsättningar/Begränsningar
Moment och normalkraft
 Moment och normalkraft Betong Konstruktionsteknik LTH 1 Pelare Främsta uppgift är att bära normalkraft. Konstruktionsteknik LTH 2 Pelare Typer Korta stubbiga pelare: Bärförmågan beror av hållfasthet och
Moment och normalkraft Betong Konstruktionsteknik LTH 1 Pelare Främsta uppgift är att bära normalkraft. Konstruktionsteknik LTH 2 Pelare Typer Korta stubbiga pelare: Bärförmågan beror av hållfasthet och
Betongkonstruktion Facit Övningstal del 2 Asaad Almssad i samarbete med Göran Lindberg
 Pelare ÖVNING 27 Pelaren i figuren nedan i brottgränstillståndet belastas med en centriskt placerad normalkraft 850. Kontrollera om pelarens bärförmåga är tillräcklig. Betong C30/37, b 350, 350, c 50,
Pelare ÖVNING 27 Pelaren i figuren nedan i brottgränstillståndet belastas med en centriskt placerad normalkraft 850. Kontrollera om pelarens bärförmåga är tillräcklig. Betong C30/37, b 350, 350, c 50,
TENTAMEN I KURSEN DIMENSIONERING AV BYGGNADSKONSTRUKTIONER
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Byggteknik TENTAMEN I KURSEN DIMENSIONERING AV BYGGNADSKONSTRUKTIONER Datum: 011-1-08 Antal uppgifter: 4 Max poäng: 40 Lärare: Annika Moström Hjälpmedel:
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Byggteknik TENTAMEN I KURSEN DIMENSIONERING AV BYGGNADSKONSTRUKTIONER Datum: 011-1-08 Antal uppgifter: 4 Max poäng: 40 Lärare: Annika Moström Hjälpmedel:
Spännbetongkonstruktioner. Dimensionering i brottgränstillståndet
 Spännbetongkonstruktioner Dimensionering i brottgränstillståndet Spännarmering Introducerar tryckspänningar i zoner utsatta för dragkrafter q P0 P0 Förespänning kablarna spänns före gjutning Efterspänning
Spännbetongkonstruktioner Dimensionering i brottgränstillståndet Spännarmering Introducerar tryckspänningar i zoner utsatta för dragkrafter q P0 P0 Förespänning kablarna spänns före gjutning Efterspänning
caeec220 Pelare betong Användarmanual Eurocode Software AB
 caeec220 Pelare betong Program för dimensionering av betongtvärsnitt belastade med moment och normalkraft. Resultat är drag-, tryckarmering och effektiv höjd. Användarmanual Rev C Eurocode Software AB
caeec220 Pelare betong Program för dimensionering av betongtvärsnitt belastade med moment och normalkraft. Resultat är drag-, tryckarmering och effektiv höjd. Användarmanual Rev C Eurocode Software AB
1. En synlig limträbalk i tak med höjd 900 mm, i kvalitet GL32c med rektangulär sektion, belastad med snölast.
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Byggteknik Uppgifter 2016-08-26 Träkonstruktioner 1. En synlig limträbalk i tak med höjd 900 mm, i kvalitet GL32c med rektangulär sektion, belastad med snölast.
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Byggteknik Uppgifter 2016-08-26 Träkonstruktioner 1. En synlig limträbalk i tak med höjd 900 mm, i kvalitet GL32c med rektangulär sektion, belastad med snölast.
caeec205 Stadium I och II Användarmanual Eurocode Software AB
 caeec205 Stadium I och II Rutin för beräkning av spänningar och töjningar för olika typer av tvärsnitt, belastade med moment och normalkraft. Hänsyn tas till krympning och krypning. Rev C Eurocode Software
caeec205 Stadium I och II Rutin för beräkning av spänningar och töjningar för olika typer av tvärsnitt, belastade med moment och normalkraft. Hänsyn tas till krympning och krypning. Rev C Eurocode Software
TENTAMEN I KURSEN DIMENSIONERING AV BYGGNADSKONSTRUKTIONER
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Byggteknik TENTAMEN I KURSEN DIMENSIONERING AV BYGGNADSKONSTRUKTIONER Datum: 01-1-07 Tid: 9.00-15.00 Antal uppgifter: 4 Max poäng: 40 Lärare: Annika Moström
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Byggteknik TENTAMEN I KURSEN DIMENSIONERING AV BYGGNADSKONSTRUKTIONER Datum: 01-1-07 Tid: 9.00-15.00 Antal uppgifter: 4 Max poäng: 40 Lärare: Annika Moström
Exempel 11: Sammansatt ram
 Exempel 11: Sammansatt ram 11.1 Konstruktion, mått och dimensioneringsunderlag Dimensionera den sammansatta ramen enligt nedan. Sammansatt ram Tvärsnitt 8 7 6 5 4 3 2 1 Takåsar Primärbalkar 18 1,80 1,80
Exempel 11: Sammansatt ram 11.1 Konstruktion, mått och dimensioneringsunderlag Dimensionera den sammansatta ramen enligt nedan. Sammansatt ram Tvärsnitt 8 7 6 5 4 3 2 1 Takåsar Primärbalkar 18 1,80 1,80
www.eurocodesoftware.se
 www.eurocodesoftware.se caeec209 Pelartopp Program för dimensionering av pelartopp. Användarmanual Rev B Eurocode Software AB caeec209 Pelartopp Sidan 2(12) Innehållsförteckning 1 Inledning... 3 1.1 Beteckningar...
www.eurocodesoftware.se caeec209 Pelartopp Program för dimensionering av pelartopp. Användarmanual Rev B Eurocode Software AB caeec209 Pelartopp Sidan 2(12) Innehållsförteckning 1 Inledning... 3 1.1 Beteckningar...
Konstruktionsteknik 25 maj 2012 kl Gasquesalen
 Bygg och Miljöteknologi Avdelningen för Konstruktionsteknik Tentamen i Konstruktionsteknik 25 maj 2012 kl. 14.00 19.00 Gasquesalen Tillåtna hjälpmedel: Tabell & Formelsamlingar Räknedosa OBS! I vissa uppgifter
Bygg och Miljöteknologi Avdelningen för Konstruktionsteknik Tentamen i Konstruktionsteknik 25 maj 2012 kl. 14.00 19.00 Gasquesalen Tillåtna hjälpmedel: Tabell & Formelsamlingar Räknedosa OBS! I vissa uppgifter
Karlstads universitet 1(7) Byggteknik
 Karlstads universitet 1(7) Träkonstruktion BYGB21 5 hp Tentamen Tid Lördag 28 november 2015 kl 9.00-14.00 Plats Universitetets skrivsal Ansvarig Kenny Pettersson, tel 0738 16 16 91 Hjälpmedel Miniräknare
Karlstads universitet 1(7) Träkonstruktion BYGB21 5 hp Tentamen Tid Lördag 28 november 2015 kl 9.00-14.00 Plats Universitetets skrivsal Ansvarig Kenny Pettersson, tel 0738 16 16 91 Hjälpmedel Miniräknare
Program S3.21 SOFTWARE ENGINEERING AB BYGGTEKNISKA PROGRAM GENOMSTANSNING
 Program S3.21 SOFTWARE ENGINEERING AB BYGGTEKNISKA PROGRAM GENOMSTANSNING BYGGTEKNISKA PROGRAM Genomstansning Software Engineering AB Hisingsgatan 30 417 03 Göteborg Tel/Fax: 031-50 83 30/50 83 33 E-mail
Program S3.21 SOFTWARE ENGINEERING AB BYGGTEKNISKA PROGRAM GENOMSTANSNING BYGGTEKNISKA PROGRAM Genomstansning Software Engineering AB Hisingsgatan 30 417 03 Göteborg Tel/Fax: 031-50 83 30/50 83 33 E-mail
Tentamen i. Konstruktionsteknik. 26 maj 2009 kl
 Bygg och Miljöteknolo gi Avdelningen för Konstruktionsteknik Tentamen i Konstruktionsteknik 26 maj 2009 kl. 8.00 13.00 Tillåtna hjälpmedel: Tabell & Formelsamlingar Räknedosa OBS! I vissa uppgifter kan
Bygg och Miljöteknolo gi Avdelningen för Konstruktionsteknik Tentamen i Konstruktionsteknik 26 maj 2009 kl. 8.00 13.00 Tillåtna hjälpmedel: Tabell & Formelsamlingar Räknedosa OBS! I vissa uppgifter kan
Betongkonstruktion Facit Övningstal del 2 Asaad Almssad i samarbete med Göran Lindberg
 Pelare ÖVNING 7 LÖSNING Dimensionerande materialegenskaper Betong C30/37 f cc f cc 30 0 MMM γ c 1,5 E cc E cc 33 γ cc 1, 7,5GGG Armering f yy f k 500 435 MMM γ s 1,15 ε yy f yy 435. 106,17. 10 3 E s 00.
Pelare ÖVNING 7 LÖSNING Dimensionerande materialegenskaper Betong C30/37 f cc f cc 30 0 MMM γ c 1,5 E cc E cc 33 γ cc 1, 7,5GGG Armering f yy f k 500 435 MMM γ s 1,15 ε yy f yy 435. 106,17. 10 3 E s 00.
Dimensionering i bruksgränstillstånd
 Dimensionering i bruksgränstillstånd Kapitel 10 Byggkonstruktion 13 april 2016 Dimensionering av byggnadskonstruktioner 1 Bruksgränstillstånd Formändringar Deformationer Svängningar Sprickbildning 13 april
Dimensionering i bruksgränstillstånd Kapitel 10 Byggkonstruktion 13 april 2016 Dimensionering av byggnadskonstruktioner 1 Bruksgränstillstånd Formändringar Deformationer Svängningar Sprickbildning 13 april
)"-'&/ 4,+67"/,"3& )%# HDB 08 BETON G
 HDB 08 BETONG Skjuvankare HDB är en produkt som används som skjuv- och genomstansningsarmering. Systemet består av skenor med 2 eller 3 dubbelhuvade ankare. Dessa moduler kan kombineras för att få önskat
HDB 08 BETONG Skjuvankare HDB är en produkt som används som skjuv- och genomstansningsarmering. Systemet består av skenor med 2 eller 3 dubbelhuvade ankare. Dessa moduler kan kombineras för att få önskat
Betongkonstruktion Facit Övningstal del 1 Asaad Almssad i samarbete med Göran Lindberg
 Böjning ÖVNING 1 Bestäm M Rd Betong C30/37 XC3 vct ekv = 0,50 L100 Stenmax = 12 mm 4ϕ16 A s = 4 201 = 804 mm 2 Täckskikt: ϕ16 C nom = c min +Δc dev, Δc dev = 10 mm C min = max (c min,b, c min,dur, 10 mm)
Böjning ÖVNING 1 Bestäm M Rd Betong C30/37 XC3 vct ekv = 0,50 L100 Stenmax = 12 mm 4ϕ16 A s = 4 201 = 804 mm 2 Täckskikt: ϕ16 C nom = c min +Δc dev, Δc dev = 10 mm C min = max (c min,b, c min,dur, 10 mm)
Tentamen i Konstruktionsteknik
 Bygg och Miljöteknologi Avdelningen för Konstruktionsteknik Tentamen i Konstruktionsteknik 5 Juni 2015 kl. 14.00-19.00 Gasquesalen Tillåtna hjälpmedel: Tabell & Formelsamling Räknedosa OBS! I vissa uppgifter
Bygg och Miljöteknologi Avdelningen för Konstruktionsteknik Tentamen i Konstruktionsteknik 5 Juni 2015 kl. 14.00-19.00 Gasquesalen Tillåtna hjälpmedel: Tabell & Formelsamling Räknedosa OBS! I vissa uppgifter
Exempel 3: Bumerangbalk
 Exempel 3: Bumerangbalk 3.1 Konstruktion, mått och dimensioneringsunderlag Dimensionera bumerangbalken enligt nedan. Bumerangbalk X 1 600 9 R18 000 12 360 6 000 800 10 000 10 000 20 000 Statisk modell
Exempel 3: Bumerangbalk 3.1 Konstruktion, mått och dimensioneringsunderlag Dimensionera bumerangbalken enligt nedan. Bumerangbalk X 1 600 9 R18 000 12 360 6 000 800 10 000 10 000 20 000 Statisk modell
Innehållsförteckning. Bilagor. 1. Inledning 1
 Innehållsförteckning 1. Inledning 1 2. Beräkningsförutsättningar 1 2.1 Kantbalkelementets utseende 1 2.2 Materialparametrar 1 2.2.1 Betong 1 2.2.2 Armering 1 2.2.3 Cellplast 2 2.2.4 Mark 2 2.2.5 Friktionskoefficient
Innehållsförteckning 1. Inledning 1 2. Beräkningsförutsättningar 1 2.1 Kantbalkelementets utseende 1 2.2 Materialparametrar 1 2.2.1 Betong 1 2.2.2 Armering 1 2.2.3 Cellplast 2 2.2.4 Mark 2 2.2.5 Friktionskoefficient
Stålbyggnadsprojektering, SBP-N Tentamen 2015-03-12
 Godkända hjälpmedel till tentamen 2015 03 12 Allt utdelat kursmaterial samt lösta hemuppgifter Balktabell Miniräknare Aktuell EKS Standarden SS EN 1090 2 Eurokoder Lösningar på utdelade tentamensfrågor
Godkända hjälpmedel till tentamen 2015 03 12 Allt utdelat kursmaterial samt lösta hemuppgifter Balktabell Miniräknare Aktuell EKS Standarden SS EN 1090 2 Eurokoder Lösningar på utdelade tentamensfrågor
Exempel 2: Sadelbalk. 2.1 Konstruktion, mått och dimensioneringsunderlag. Exempel 2: Sadelbalk. Dimensionera sadelbalken enligt nedan.
 2.1 Konstruktion, mått och dimensioneringsunderlag Dimensionera sadelbalken enligt nedan. Sadelbalk X 1 429 3,6 360 6 000 800 10 000 10 000 20 000 Statisk modell Bestäm tvärsnittets mått enligt den preliminära
2.1 Konstruktion, mått och dimensioneringsunderlag Dimensionera sadelbalken enligt nedan. Sadelbalk X 1 429 3,6 360 6 000 800 10 000 10 000 20 000 Statisk modell Bestäm tvärsnittets mått enligt den preliminära
K-uppgifter Strukturmekanik/Materialmekanik
 K-uppgifter Strukturmekanik/Materialmekanik K 1 Bestäm resultanten till de båda krafterna. Ange storlek och vinkel i förhållande till x-axeln. y 4N 7N x K 2 Bestäm kraftens komposanter längs x- och y-axeln.
K-uppgifter Strukturmekanik/Materialmekanik K 1 Bestäm resultanten till de båda krafterna. Ange storlek och vinkel i förhållande till x-axeln. y 4N 7N x K 2 Bestäm kraftens komposanter längs x- och y-axeln.
Karlstads universitet 1(7) Byggteknik. Carina Rehnström
 Karlstads universitet 1(7) Träkonstruktion BYGB21 5 hp Tentamen Tid Tisdag 14 juni 2016 kl 8.15-13.15 Plats Ansvarig Hjälpmedel Universitetets skrivsal Kenny Pettersson Carina Rehnström Miniräknare Johannesson
Karlstads universitet 1(7) Träkonstruktion BYGB21 5 hp Tentamen Tid Tisdag 14 juni 2016 kl 8.15-13.15 Plats Ansvarig Hjälpmedel Universitetets skrivsal Kenny Pettersson Carina Rehnström Miniräknare Johannesson
Exempel 5: Treledstakstol
 5.1 Konstruktion, mått och dimensioneringsunderlag Dimensionera treledstakstolen enligt nedan. Beakta två olika fall: 1. Dragband av limträ. 2. Dragband av stål. 1. Dragband av limträ 2. Dragband av stål
5.1 Konstruktion, mått och dimensioneringsunderlag Dimensionera treledstakstolen enligt nedan. Beakta två olika fall: 1. Dragband av limträ. 2. Dragband av stål. 1. Dragband av limträ 2. Dragband av stål
TENTAMEN I KURSEN BYGGNADSMEKANIK 2
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Byggteknik TENTAMEN I KURSEN BYGGNADSMEKANIK Datum: 014-08-6 Tid: 9.00-15.00 Antal uppgifter: 4 Max poäng: 40 Lärare: Annika Moström och Fredrik Häggström
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Byggteknik TENTAMEN I KURSEN BYGGNADSMEKANIK Datum: 014-08-6 Tid: 9.00-15.00 Antal uppgifter: 4 Max poäng: 40 Lärare: Annika Moström och Fredrik Häggström
2016-04-01. SS-Pålen Dimensioneringstabeller Slagna Stålrörspålar
 2016-04-01 SS-Pålen Dimensioneringstabeller Slagna Stålrörspålar Dimensioneringstabeller slagna stålrörspålar 2016-05-10 1 (20) SCANDIA STEEL DIMENSIONERINGSTABELLER SLAGNA STÅLRÖRSPÅLAR, SS-PÅLEN RAPPORT
2016-04-01 SS-Pålen Dimensioneringstabeller Slagna Stålrörspålar Dimensioneringstabeller slagna stålrörspålar 2016-05-10 1 (20) SCANDIA STEEL DIMENSIONERINGSTABELLER SLAGNA STÅLRÖRSPÅLAR, SS-PÅLEN RAPPORT
Beräkningsstrategier för murverkskonstruktioner
 Beräkningsstrategier för murverkskonstruktioner Tomas Gustavsson TG konstruktioner AB 2017-06-08 Dimensionerande lastfall ofta endera av: 1. Vindlast mot fasad + min vertikallast 2. Max vertikallast +
Beräkningsstrategier för murverkskonstruktioner Tomas Gustavsson TG konstruktioner AB 2017-06-08 Dimensionerande lastfall ofta endera av: 1. Vindlast mot fasad + min vertikallast 2. Max vertikallast +
RAPPORT 2(10) Göteborg, 2010-04-07 70209 Upprättat av, telefon Reviderat den Arbetsnamn Simon Håkansson
 RAPPORT 1(10) Sverige AB Mats Larsson Dimensionering av borrade stålrörpålar för bro Referensobjekt Botorpström ELU Konsult AB Avdelning Anläggning/Göteborg Lilla Badhusgatan 2 411 21 Göteborg Växel: 031-339
RAPPORT 1(10) Sverige AB Mats Larsson Dimensionering av borrade stålrörpålar för bro Referensobjekt Botorpström ELU Konsult AB Avdelning Anläggning/Göteborg Lilla Badhusgatan 2 411 21 Göteborg Växel: 031-339
Bromallar Eurocode. Bromall: Omlottskarvning. Innehåll. Minimimått vid omlottskarvning av armeringsstänger samt beräkning av skarvlängd.
 Bromallar Eurocode Bromall: Omlottskarvning Minimimått vid omlottskarvning av armeringsstänger samt beräkning av skarvlängd. Rev: A EN 1992-1-1: 2004 Innehåll 1 Allmänt 2 2 Omlottskarvar 4 3 Skarvlängd
Bromallar Eurocode Bromall: Omlottskarvning Minimimått vid omlottskarvning av armeringsstänger samt beräkning av skarvlängd. Rev: A EN 1992-1-1: 2004 Innehåll 1 Allmänt 2 2 Omlottskarvar 4 3 Skarvlängd
GLH FÖRTAGNINGSSYSTEM FÖR BETONGKONSTRUKTIONER
 GLH FÖRTAGNINGSSYSTEM FÖR BETONGKONSTRUKTIONER Tillverkning och försäljning: GLH Byggdetaljer AB Stenhuggaregatan 21, 913 35 HOLMSUND Telefon 090-402 48, Telefax 090-14 92 00 PROJEKTERINGSHANDLING INNEHÅLLSFÖRTECKNING
GLH FÖRTAGNINGSSYSTEM FÖR BETONGKONSTRUKTIONER Tillverkning och försäljning: GLH Byggdetaljer AB Stenhuggaregatan 21, 913 35 HOLMSUND Telefon 090-402 48, Telefax 090-14 92 00 PROJEKTERINGSHANDLING INNEHÅLLSFÖRTECKNING
Belastningsanalys, 5 poäng Balkteori Deformationer och spänningar
 Spänningar orsakade av deformationer i balkar En från början helt rak balk antar en bågform under böjande belastning. Vi studerar bilderna nedan: För deformationerna gäller att horisontella linjer blir
Spänningar orsakade av deformationer i balkar En från början helt rak balk antar en bågform under böjande belastning. Vi studerar bilderna nedan: För deformationerna gäller att horisontella linjer blir
KONSTRUKTIONSTEKNIK 1
 KONSTRUKTIONSTEKNIK 1 TENTAMEN Ladokkod: 41B16B-20151-C76V5- NAMN: Personnummer: - Tentamensdatum: 17 mars 2015 Tid: 09:00 13.00 HJÄLPMEDEL: Formelsamling: Konstruktionsteknik I (inklusive här i eget skrivna
KONSTRUKTIONSTEKNIK 1 TENTAMEN Ladokkod: 41B16B-20151-C76V5- NAMN: Personnummer: - Tentamensdatum: 17 mars 2015 Tid: 09:00 13.00 HJÄLPMEDEL: Formelsamling: Konstruktionsteknik I (inklusive här i eget skrivna
caeec225 Skev böjning Användarmanual Eurocode Software AB
 caeec225 Skev böjning Programmet analyserar olika typer av tvärsnitt belastade med moment och normalkraft. Resultatet är utnyttjandegrad, spänningar och sprickvidder. Rav C Eurocode Software AB caeec225
caeec225 Skev böjning Programmet analyserar olika typer av tvärsnitt belastade med moment och normalkraft. Resultatet är utnyttjandegrad, spänningar och sprickvidder. Rav C Eurocode Software AB caeec225
(kommer inte till tentasalen men kan nås på tel )
 Karlstads universitet 1(7) Träkonstruktion BYGB21 5 hp Tentamen Tid Tisdag 13 januari 2015 kl 14.00-19.00 Plats Ansvarig Hjälpmedel Universitetets skrivsal Carina Rehnström (kommer inte till tentasalen
Karlstads universitet 1(7) Träkonstruktion BYGB21 5 hp Tentamen Tid Tisdag 13 januari 2015 kl 14.00-19.00 Plats Ansvarig Hjälpmedel Universitetets skrivsal Carina Rehnström (kommer inte till tentasalen
Boverkets författningssamling Utgivare: Förnamn Efternamn
 Boverkets författningssamling Utgivare: Förnamn Efternamn Boverkets föreskrifter om ändring i verkets föreskrifter och allmänna råd (2011:10) om tillämpning av europeiska konstruktionsstandarder (eurokoder);
Boverkets författningssamling Utgivare: Förnamn Efternamn Boverkets föreskrifter om ändring i verkets föreskrifter och allmänna råd (2011:10) om tillämpning av europeiska konstruktionsstandarder (eurokoder);
Oarmerade väggar utsatta för tvärkraft (skjuvväggar) Stomanalys
 Oarmerade väggar utsatta för tvärkraft (skjuvväggar) Stomanalys Generellt Beskrivs i SS-EN 1996-1-1, avsnitt 6.2 och avsnitt 5.5.3 I handboken Utformning av murverkskonstruktioner enligt Eurokod 6, beskrivs
Oarmerade väggar utsatta för tvärkraft (skjuvväggar) Stomanalys Generellt Beskrivs i SS-EN 1996-1-1, avsnitt 6.2 och avsnitt 5.5.3 I handboken Utformning av murverkskonstruktioner enligt Eurokod 6, beskrivs
Innehållsförteckning. Bilagor. 1. Inledning 1
 Innehållsförteckning 1. Inledning 1 2. Beräkningsförutsättningar 1 2.1 Kantbalkelementets utseende 1 2.2 Materialparametrar 1 2.2.1 Betong 1 2.2.2 Armering 1 2.2.3 Cellplast 2 2.2.4 Mark 2 2.2.5 Friktionskoefficient
Innehållsförteckning 1. Inledning 1 2. Beräkningsförutsättningar 1 2.1 Kantbalkelementets utseende 1 2.2 Materialparametrar 1 2.2.1 Betong 1 2.2.2 Armering 1 2.2.3 Cellplast 2 2.2.4 Mark 2 2.2.5 Friktionskoefficient
Svetsplåt PJL. Dimensionering. Pre Cast Technology AB Solbräckegatan 15, Kungälv
 Svetsplåt PJL Innehåll... 1 1 Dimensioner... 3 Materialegenskaper... 3 2 Kapaciteter och dimensioneringsförutsättningar... 4 2.1 Kombinerade belastningar... 4 2.2 KAPACITETSTABELLER... 5 PJL 15x15x25...
Svetsplåt PJL Innehåll... 1 1 Dimensioner... 3 Materialegenskaper... 3 2 Kapaciteter och dimensioneringsförutsättningar... 4 2.1 Kombinerade belastningar... 4 2.2 KAPACITETSTABELLER... 5 PJL 15x15x25...
P R O B L E M
 Tekniska Högskolan i Linköping, IEI /Tore Dahlberg TENTAMEN i Hållfasthetslära - Dimensioneringmetoder, TMHL09, 2008-08-14 kl 8-12 P R O B L E M med L Ö S N I N G A R Del 1 - (Teoridel utan hjälpmedel)
Tekniska Högskolan i Linköping, IEI /Tore Dahlberg TENTAMEN i Hållfasthetslära - Dimensioneringmetoder, TMHL09, 2008-08-14 kl 8-12 P R O B L E M med L Ö S N I N G A R Del 1 - (Teoridel utan hjälpmedel)
VSMA01 - Mekanik ERIK SERRANO
 VSMA01 - Mekanik ERIK SERRANO Innehåll Material Spänning, töjning, styvhet Dragning, tryck, skjuvning, böjning Stång, balk styvhet och bärförmåga Knäckning Exempel: Spänning i en stång x F A Töjning Normaltöjning
VSMA01 - Mekanik ERIK SERRANO Innehåll Material Spänning, töjning, styvhet Dragning, tryck, skjuvning, böjning Stång, balk styvhet och bärförmåga Knäckning Exempel: Spänning i en stång x F A Töjning Normaltöjning
Svetsplåt PBKL. Dimensionering
 Svetsplåt PBKL Innehåll... Dimensioner... Materialegenskaper... Kapaciteter och dimensioneringsförutsättningar.... Kombinerade belastningar.... KAPACITETSTABELLER... PBKL 5xx8... 5 PBKL xx8... 7 PBKL x5x...
Svetsplåt PBKL Innehåll... Dimensioner... Materialegenskaper... Kapaciteter och dimensioneringsförutsättningar.... Kombinerade belastningar.... KAPACITETSTABELLER... PBKL 5xx8... 5 PBKL xx8... 7 PBKL x5x...
Eurokod grundläggning. Eurocode Software AB
 Eurokod grundläggning Eurocode Software AB Eurokod 7 Kapitel 1 Allmänt Kapitel 2 Grunder för geotekniskdimensionering Kapitel 3 Geotekniska data Kapitel 4 Kontroll av utförande, uppföljning och underhåll
Eurokod grundläggning Eurocode Software AB Eurokod 7 Kapitel 1 Allmänt Kapitel 2 Grunder för geotekniskdimensionering Kapitel 3 Geotekniska data Kapitel 4 Kontroll av utförande, uppföljning och underhåll
Svetsplåt PKL. Dimensionering
 Svetsplåt PKL Innehåll... Dimensioner... Materialegenskaper... Kapaciteter och dimensioneringsförutsättningar.... Kombinerade belastningar.... KAPACITETSTABELLER... PKL 5xx8... 5 PKL xx8... 7 PKL x5x...
Svetsplåt PKL Innehåll... Dimensioner... Materialegenskaper... Kapaciteter och dimensioneringsförutsättningar.... Kombinerade belastningar.... KAPACITETSTABELLER... PKL 5xx8... 5 PKL xx8... 7 PKL x5x...
Tentamen i Hållfasthetslära AK2 för M Torsdag , kl
 Avdelningen för Hållfasthetslära Lunds Tekniska Högskola, LTH Tentamen i Hållfasthetslära AK2 för M Torsdag 2015-06-04, kl. 8.00-13.00 Tentand är skyldig att visa upp fotolegitimation. Om sådan inte medförts
Avdelningen för Hållfasthetslära Lunds Tekniska Högskola, LTH Tentamen i Hållfasthetslära AK2 för M Torsdag 2015-06-04, kl. 8.00-13.00 Tentand är skyldig att visa upp fotolegitimation. Om sådan inte medförts
BERÄKNING AV SKJUVBROTT I PELARUNDERSTÖDDA PLATTOR
 BERÄKNING AV SKJUVBROTT I PELARUNDERSTÖDDA PLATTOR En studie av kontrollen utanför påverkade zonen vid beräkning av genomstansning SEBASTIAN NYBERG Akademin för ekonomi, samhälle och teknik Kurs: Examensarbete
BERÄKNING AV SKJUVBROTT I PELARUNDERSTÖDDA PLATTOR En studie av kontrollen utanför påverkade zonen vid beräkning av genomstansning SEBASTIAN NYBERG Akademin för ekonomi, samhälle och teknik Kurs: Examensarbete
Tentamen i Konstruktionsteknik
 Bygg och Miljöteknologi Avdelningen för Konstruktionsteknik Tentamen i Konstruktionsteknik 2 Juni 2014 kl. 14.00-19.00 Gasquesalen Tillåtna hjälpmedel: Tabell & Formelsamlingar Räknedosa OBS! I vissa uppgifter
Bygg och Miljöteknologi Avdelningen för Konstruktionsteknik Tentamen i Konstruktionsteknik 2 Juni 2014 kl. 14.00-19.00 Gasquesalen Tillåtna hjälpmedel: Tabell & Formelsamlingar Räknedosa OBS! I vissa uppgifter
Eurokoder betong. Eurocode Software AB
 Eurokoder betong Eurocode Software AB 1.1.2 Eurokod 2 Kapitel 1 Allmänt Kapitel 2 Grundläggande dimensioneringsregler Kapitel 3 Material Kapitel 4 Beständighet och täckande betongskikt Kapitel 5 Bärverksanalys
Eurokoder betong Eurocode Software AB 1.1.2 Eurokod 2 Kapitel 1 Allmänt Kapitel 2 Grundläggande dimensioneringsregler Kapitel 3 Material Kapitel 4 Beständighet och täckande betongskikt Kapitel 5 Bärverksanalys
Exempel 13: Treledsbåge
 Exempel 13: Treledsbåge 13.1 Konstruktion, mått och dimensioneringsunderlag Dimensionera treledsbågen enligt nedan. Treledsbåge 84,42 R72,67 12,00 3,00 56,7º 40,00 80,00 40,00 Statisk modell Bestäm tvärsnittets
Exempel 13: Treledsbåge 13.1 Konstruktion, mått och dimensioneringsunderlag Dimensionera treledsbågen enligt nedan. Treledsbåge 84,42 R72,67 12,00 3,00 56,7º 40,00 80,00 40,00 Statisk modell Bestäm tvärsnittets
caeec301 Snittkontroll stål Användarmanual Eurocode Software AB
 caeec301 Snittkontroll stål Analys av pelarelement enligt SS-EN 1993-1-1:2005. Programmet utför snittkontroll för givna snittkrafter och upplagsvillkor. Rev: C Eurocode Software AB caeec301 Snittkontroll
caeec301 Snittkontroll stål Analys av pelarelement enligt SS-EN 1993-1-1:2005. Programmet utför snittkontroll för givna snittkrafter och upplagsvillkor. Rev: C Eurocode Software AB caeec301 Snittkontroll
TENTAMEN I FÖRDJUPNINGSKURS I BYGGKONSTRUKTION
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Byggteknik TENTAMEN I FÖRDJUPNINGSKURS I BYGGKONSTRUKTION Datum: 014-08-8 Tid: 9.00-15.00 Antal uppgifter: 4 Max poäng: 40 Lärare: Annika Moström Hjälpmedel:
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Byggteknik TENTAMEN I FÖRDJUPNINGSKURS I BYGGKONSTRUKTION Datum: 014-08-8 Tid: 9.00-15.00 Antal uppgifter: 4 Max poäng: 40 Lärare: Annika Moström Hjälpmedel:
Tekniska Högskolan i Linköping, IKP Tore Dahlberg TENTAMEN i Hållfasthetslära; grk, TMMI17, kl DEL 1 - (Teoridel utan hjälpmedel)
 Tekniska Högskolan i inköping, IK DE 1 - (Teoridel utan hjälpmedel) NAMN... 1. Vilken typ av ekvation är detta: ε = d u(x) d x Ange vad de ingående storheterna betyder, inklusive deras dimension i SI-enheter.
Tekniska Högskolan i inköping, IK DE 1 - (Teoridel utan hjälpmedel) NAMN... 1. Vilken typ av ekvation är detta: ε = d u(x) d x Ange vad de ingående storheterna betyder, inklusive deras dimension i SI-enheter.
CAEMRK12 Grundplatta. Användarmanual
 Användarmanual Eurocode Software AB 1 Innehåll 1 INLEDNING...3 1.1 TEKNISK BESKRIVNING...3 2 INSTRUKTIONER...4 2.1 KOMMA IGÅNG MED CAEMRK12...5 2.2 INDATA...5 2.2.1 GRUNDDATA...6 2.2.2 GEOMTERI...7 2.2.3
Användarmanual Eurocode Software AB 1 Innehåll 1 INLEDNING...3 1.1 TEKNISK BESKRIVNING...3 2 INSTRUKTIONER...4 2.1 KOMMA IGÅNG MED CAEMRK12...5 2.2 INDATA...5 2.2.1 GRUNDDATA...6 2.2.2 GEOMTERI...7 2.2.3
Självständigt arbete på grundnivå
 Självständigt arbete på grundnivå Independent degree project first cycle Byggnadsteknik Building Engineering Armeringsutformning Utformning av armeringsdetaljer i platsgjutna konstruktioner enligt Eurokod
Självständigt arbete på grundnivå Independent degree project first cycle Byggnadsteknik Building Engineering Armeringsutformning Utformning av armeringsdetaljer i platsgjutna konstruktioner enligt Eurokod
I figuren nedan visas en ritning över stommen till ett bostadshus. Stommen ska bestå av
 Uppgift 2 I figuren nedan visas en ritning över stommen till ett bostadshus. Stommen ska bestå av fackverkstakstol i trä, centrumavstånd mellan takstolarna 1200 mm, lutning 4. träreglar i väggarna, centrumavstånd
Uppgift 2 I figuren nedan visas en ritning över stommen till ett bostadshus. Stommen ska bestå av fackverkstakstol i trä, centrumavstånd mellan takstolarna 1200 mm, lutning 4. träreglar i väggarna, centrumavstånd
Projekteringsanvisning
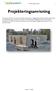 Projekteringsanvisning 1 Projekteringsanvisning Den bärande stommen i ett hus med IsoTimber dimensioneras av byggnadskonstruktören enligt Eurokod. Denna projekteringsanvisning är avsedd att användas som
Projekteringsanvisning 1 Projekteringsanvisning Den bärande stommen i ett hus med IsoTimber dimensioneras av byggnadskonstruktören enligt Eurokod. Denna projekteringsanvisning är avsedd att användas som
Bromall: Kontroll av sprickbredd
 Bromall: Kontroll av sprickbredd Beräkning av armeringsspänning för bestämning av sprickavstånd och sprickbredd. Rev: A EN 1992-1-1:2004 Svenska betongföreningens handbok till Eurokod 2 Volym 1: 2010 Innehåll
Bromall: Kontroll av sprickbredd Beräkning av armeringsspänning för bestämning av sprickavstånd och sprickbredd. Rev: A EN 1992-1-1:2004 Svenska betongföreningens handbok till Eurokod 2 Volym 1: 2010 Innehåll
Eurokod 3 del 1-2 Brandteknisk dimensionering av stålkonstruktioner
 Eurokod 3 del 1-2 Brandteknisk dimensionering av stålkonstruktioner Peter Karlström, Konkret Rådgivande Ingenjörer i Stockholm AB Allmänt EN 1993-1-2 (Eurokod 3 del 1-2) är en av totalt 20 delar som handlar
Eurokod 3 del 1-2 Brandteknisk dimensionering av stålkonstruktioner Peter Karlström, Konkret Rådgivande Ingenjörer i Stockholm AB Allmänt EN 1993-1-2 (Eurokod 3 del 1-2) är en av totalt 20 delar som handlar
Konstruktionsuppgift i byggnadsmekanik II. Flervåningsbyggnad i stål. Anders Andersson Malin Bengtsson
 Konstruktionsuppgift i byggnadsmekanik II Flervåningsbyggnad i stål Anders Andersson Malin Bengtsson SAMMANFATTNING Syftet med projektet har varit att dimensionera en flervåningsbyggnad i stål utifrån
Konstruktionsuppgift i byggnadsmekanik II Flervåningsbyggnad i stål Anders Andersson Malin Bengtsson SAMMANFATTNING Syftet med projektet har varit att dimensionera en flervåningsbyggnad i stål utifrån
caeec213 Strut and Tie Användarmanual Eurocode Software AB
 caeec213 Strut and Tie Beräkningsprogram för betong konstruktion hög balkar. Programmet innehåller lastgenerering enligt Ec2. Resultatet omfattar dimensionerande värden för Krafts spänningar, armeringersbehov.
caeec213 Strut and Tie Beräkningsprogram för betong konstruktion hög balkar. Programmet innehåller lastgenerering enligt Ec2. Resultatet omfattar dimensionerande värden för Krafts spänningar, armeringersbehov.
Svetsplåt PBKL. Dimensionering
 Svetsplåt PBKL Innehåll... Dimensioner... Materialegenskaper... Kapaciteter och dimensioneringsförutsättningar.... Kombinerade belastningar.... KAPACITETSTABELLER... PBKL 5xx8... 5 PBKL xx8... 7 PBKL x5x...
Svetsplåt PBKL Innehåll... Dimensioner... Materialegenskaper... Kapaciteter och dimensioneringsförutsättningar.... Kombinerade belastningar.... KAPACITETSTABELLER... PBKL 5xx8... 5 PBKL xx8... 7 PBKL x5x...
TENTAMEN I KURSEN TRÄBYGGNAD
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Byggteknik TENTAMEN I KURSEN TRÄBYGGNAD Datum: 013-05-11 Tid: 9.00-15.00 Antal uppgifter: 4 Max poäng: 40 Lärare: Annika Moström Hjälpmedel: Limträhandboken
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Byggteknik TENTAMEN I KURSEN TRÄBYGGNAD Datum: 013-05-11 Tid: 9.00-15.00 Antal uppgifter: 4 Max poäng: 40 Lärare: Annika Moström Hjälpmedel: Limträhandboken
SVENSK STANDARD SS-EN :2005/AC:2010
 SVENSK STANDARD SS-EN 1992-1-1:2005/AC:2010 Fastställd/Approved: 2010-11-18 Publicerad/Published: 2016-01-29 Utgåva/Edition: 1 Språk/Language: svenska/swedish ICS: 91.010.30; 91.070.02; 91.070.50; 91.070.60;
SVENSK STANDARD SS-EN 1992-1-1:2005/AC:2010 Fastställd/Approved: 2010-11-18 Publicerad/Published: 2016-01-29 Utgåva/Edition: 1 Språk/Language: svenska/swedish ICS: 91.010.30; 91.070.02; 91.070.50; 91.070.60;
TENTAMEN I FÖRDJUPNINGSKURS I BYGGKONSTRUKTION
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Byggteknik TENTAMEN I FÖRDJUPNINGSKURS I BYGGKONSTRUKTION Datum: 016-05-06 Tid: 9.00-15.00 Antal uppgifter: 4 Max poäng: 40 Lärare: Annika Moström Hjälpmedel:
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Byggteknik TENTAMEN I FÖRDJUPNINGSKURS I BYGGKONSTRUKTION Datum: 016-05-06 Tid: 9.00-15.00 Antal uppgifter: 4 Max poäng: 40 Lärare: Annika Moström Hjälpmedel:
VSMA01 - Mekanik ERIK SERRANO
 VSMA01 - Mekanik ERIK SERRANO Repetition Krafter Representation, komposanter Friläggning och jämvikt Friktion Element och upplag stång, lina, balk Spänning och töjning Böjning Knäckning Newtons lagar Lag
VSMA01 - Mekanik ERIK SERRANO Repetition Krafter Representation, komposanter Friläggning och jämvikt Friktion Element och upplag stång, lina, balk Spänning och töjning Böjning Knäckning Newtons lagar Lag
Förstudie till ramprojektet: Utvärdering av tillåten trafiklast. Vägverket 1(9) Avdelningen för bro och tunnel
 Vägverket 1(9) Förstudie till ramprojektet: Utvärdering av tillåten trafiklast Enheten för statlig väghållning 1998-12-17 Vägverket 1998-12-17 2(9) Förord Föreliggande förstudie till ramprojektet Utvärdering
Vägverket 1(9) Förstudie till ramprojektet: Utvärdering av tillåten trafiklast Enheten för statlig väghållning 1998-12-17 Vägverket 1998-12-17 2(9) Förord Föreliggande förstudie till ramprojektet Utvärdering
Beteende hos samverkansbjälklag med stål och betong utsatta för brand. Enkel dimensioneringsmetod
 Beteende hos med stål och betong utsatta brand Enkel dimensioneringsmetod Syftet med dimensioneringsmetoden 2 3 Presentationens innehåll Mekaniskt beteende hos armerade Modell betongbjälklaget Brottmoder
Beteende hos med stål och betong utsatta brand Enkel dimensioneringsmetod Syftet med dimensioneringsmetoden 2 3 Presentationens innehåll Mekaniskt beteende hos armerade Modell betongbjälklaget Brottmoder
PPU408 HT15. Beräkningar stål. Lars Bark MdH/IDT
 Beräkningar stål 1 Balk skall optimeras map vikt (dvs göras så lätt som möjligt) En i aluminium, en i höghållfast stål Mått: - Längd 180 mm - Tvärsnittets yttermått Höjd: 18 mm Bredd: 12 mm Lastfall: -
Beräkningar stål 1 Balk skall optimeras map vikt (dvs göras så lätt som möjligt) En i aluminium, en i höghållfast stål Mått: - Längd 180 mm - Tvärsnittets yttermått Höjd: 18 mm Bredd: 12 mm Lastfall: -
Grundläggande maskinteknik II 7,5 högskolepoäng
 Grundläggande maskinteknik II 7,5 högskolepoäng Provmoment: TEN 2 Ladokkod: TH081A Tentamen ges för: KENEP 15h TentamensKod: Tentamensdatum: 2016-01-15 Tid: 09:00 13:00 Hjälpmedel: Bifogat formelsamling,
Grundläggande maskinteknik II 7,5 högskolepoäng Provmoment: TEN 2 Ladokkod: TH081A Tentamen ges för: KENEP 15h TentamensKod: Tentamensdatum: 2016-01-15 Tid: 09:00 13:00 Hjälpmedel: Bifogat formelsamling,
Angående skjuvbuckling
 Sidan 1 av 6 Angående skjuvbuckling Man kan misstänka att liven i en sandwich med invändiga balkar kan haverera genom skjuvbuckling. Att skjuvbuckling kan uppstå kan man förklara med att en skjuvlast kan
Sidan 1 av 6 Angående skjuvbuckling Man kan misstänka att liven i en sandwich med invändiga balkar kan haverera genom skjuvbuckling. Att skjuvbuckling kan uppstå kan man förklara med att en skjuvlast kan
Geokonstruktion, BYGC13 7,5 hp Omtentamen
 Karlstads universitet Byggteknik Byggingenjörsprogrammet Geokonstruktion, BYGC13 7,5 hp Omtentamen Tid: måndag den 9/6 2014 kl 14.00-19.00 Plats: Universitetets skrivsal Ansvarig: Malin Olin 700 1590,
Karlstads universitet Byggteknik Byggingenjörsprogrammet Geokonstruktion, BYGC13 7,5 hp Omtentamen Tid: måndag den 9/6 2014 kl 14.00-19.00 Plats: Universitetets skrivsal Ansvarig: Malin Olin 700 1590,
Möjligheter med samverkanskonstruktioner. Stålbyggnadsdagen Jan Stenmark
 Möjligheter med samverkanskonstruktioner Stålbyggnadsdagen 2016 2016-10-26 Jan Stenmark Samverkanskonstruktioner Ofrivillig samverkan Uppstår utan avsikt eller till följd av sekundära effekter Samverkan
Möjligheter med samverkanskonstruktioner Stålbyggnadsdagen 2016 2016-10-26 Jan Stenmark Samverkanskonstruktioner Ofrivillig samverkan Uppstår utan avsikt eller till följd av sekundära effekter Samverkan
4.3. 498 Gyproc Handbok 7 Gyproc Teknik. Statik. Bärförmåga hos Gyproc GFR DUROnomic Regel. Dimensioneringsvärden för transversallast och axiallast
 .3 Dimensionering av Gyproc DUROnomic Bärförmåga hos Gyproc GFR DUROnomic Regel Dimensioneringsvärden för transversallast och axiallast Gyproc GFR Duronomic förstärkningsreglar kan uppta såväl transversallaster
.3 Dimensionering av Gyproc DUROnomic Bärförmåga hos Gyproc GFR DUROnomic Regel Dimensioneringsvärden för transversallast och axiallast Gyproc GFR Duronomic förstärkningsreglar kan uppta såväl transversallaster
Pålfundament EMELIE FAHLESON OCH KAJSA LINDBLADH. Examensarbete inom brobyggnad, avancerad nivå Stockholm, Sverige 2015
 i Pålfundament En studie med olika fackverksmodeller EMELIE FAHLESON OCH KAJSA LINDBLADH Examensarbete inom brobyggnad, avancerad nivå Stockholm, Sverige 2015 Pålfundament En studie med olika fackverksmodeller
i Pålfundament En studie med olika fackverksmodeller EMELIE FAHLESON OCH KAJSA LINDBLADH Examensarbete inom brobyggnad, avancerad nivå Stockholm, Sverige 2015 Pålfundament En studie med olika fackverksmodeller
Biomekanik Belastningsanalys
 Biomekanik Belastningsanalys Skillnad? Biomekanik Belastningsanalys Yttre krafter och moment Hastigheter och accelerationer Inre spänningar, töjningar och deformationer (Dynamiska påkänningar) I de delar
Biomekanik Belastningsanalys Skillnad? Biomekanik Belastningsanalys Yttre krafter och moment Hastigheter och accelerationer Inre spänningar, töjningar och deformationer (Dynamiska påkänningar) I de delar
Dimensionering för moment och normalkraft stål/trä KAPITEL 9 DEL 2
 Dimensionering för moment och normalkraft stål/trä KAPITEL 9 DEL 2 oment och normalkraft Laster Q (k) Snittkrafter och moment L q (k/m) max = ql 2 /8 max =Q Snittkrafterna jämförs med bärförmågan, t.ex.
Dimensionering för moment och normalkraft stål/trä KAPITEL 9 DEL 2 oment och normalkraft Laster Q (k) Snittkrafter och moment L q (k/m) max = ql 2 /8 max =Q Snittkrafterna jämförs med bärförmågan, t.ex.
Geoteknik? Geologi/berg. Hydrogeologi/Geohydrologi. Geoteknik c fu
 Geoteknik? Geologi/berg Hydrogeologi/Geohydrologi Geoteknik c fu E Geoteknik 1. Projekt Undersökningar/ utredningar Tolkning/ utvärdering 2. Geometrisk modell Bygghandlingar/ uppföljning Tolkning/ utvärdering
Geoteknik? Geologi/berg Hydrogeologi/Geohydrologi Geoteknik c fu E Geoteknik 1. Projekt Undersökningar/ utredningar Tolkning/ utvärdering 2. Geometrisk modell Bygghandlingar/ uppföljning Tolkning/ utvärdering
Beräkning av sprickbredd. för konstruktioner utsatta för tvångskrafter
 Beräkning av sprickbredd för konstruktioner utsatta för tvångskrafter Betonggolv är exempel på en konstruktionstyp där tvångskrafter kan leda till en oacceptabel sprickbildning (se figur 1), vilket inte
Beräkning av sprickbredd för konstruktioner utsatta för tvångskrafter Betonggolv är exempel på en konstruktionstyp där tvångskrafter kan leda till en oacceptabel sprickbildning (se figur 1), vilket inte
Väggar med övervägande vertikal- och viss transversallast
 Väggar med övervägande vertikal- och viss transversallast 1 Generellt Beskrivs i SS-EN 1996-1-1, avsnitt 6.1 och kapitel 5 I handboken Utformning av murverkskonstruktioner enligt Eurokod 6, beskrivs i
Väggar med övervägande vertikal- och viss transversallast 1 Generellt Beskrivs i SS-EN 1996-1-1, avsnitt 6.1 och kapitel 5 I handboken Utformning av murverkskonstruktioner enligt Eurokod 6, beskrivs i
PPU408 HT15. Beräkningar stål. Lars Bark MdH/IDT
 Beräkningar stål 1 Balk skall optimeras map vikt (dvs göras så lätt som möjligt) En i aluminium, en i höghållfast stål Mått: - Längd 180 mm - Tvärsnittets yttermått Höjd: 18 mm Bredd: 12 mm Lastfall: -
Beräkningar stål 1 Balk skall optimeras map vikt (dvs göras så lätt som möjligt) En i aluminium, en i höghållfast stål Mått: - Längd 180 mm - Tvärsnittets yttermått Höjd: 18 mm Bredd: 12 mm Lastfall: -
