Svar och lösningar Benjamin
|
|
|
- Roger Ström
- för 8 år sedan
- Visningar:
Transkript
1 Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A = Talet efter det största fyrsiffriga talet måste vara det minsta femsiffriga talet. 3: B 3 Emil tar 2 svarta och 1 vit kula från vänster och 3 svarta och 2 vita kulor från höger. Då har han 5 svarta, och dessutom 3 vita kulor lösa. 4: D När man ser bakifrån byter höger och vänster plats, liksom framför och bakom. Jenny ser den mörka ringen till vänster om den ljusa, den mörka ligger framför den vita upptill och bakom den vita nedtill vid ihopsättningen. 5: D 60 cm Sidorna på kvadraten är 12 cm. Den långa rektangeln består av 4 sådana sidor och dessutom två halva sådana sidor, dvs: 4 12 cm cm = 60 cm. 6: D 450 g Eftersom den största biten väger lika mycket som de andra tillsammans väger den hälften av 900 g, dvs 450 g. 7: E Det går inte att få lika stor area med någon av bitarna Den totala arean är 9 rutor, så hälften är 4,5 rutor. Redan nu är arean av de vita områdena 5 rutor och den kan inte bli mindre. 8: D 7 I övre lagret kan bara de 4 hörnbitarna vara kvar, dvs fem bitar tas bort. Dessutom måste ytterligare två bitar i mitten utefter ena sidan tas bort. 9: B 1 km mot norr Hannas väg Samirs väg 10: D 10 De som åt glass igår var de 7 barn som äter varje dag och 6 av dem som äter varannan dag. I dag är det de 7 och resten av varanndagsätarna, dvs 3 barn, som äter glass. Totalt 10 barn äter glass idag. 11: B Bella Om två grannar byter plats sitter de fortfarande bredvid varandra, men på andra sidan. Ari och Eli har bytt plats, liksom Cosmos och Dolly. Men Bella sitter inte bredvid någon av sina ursprungliga grannar. NCM & Kungl Vetenskapsakademien 2
2 Kängurutävlingen 2014 Benjamin, svar och lösningar 12: B D E A C 13: A = 36 platser finns vid bord med 6 platser. Det betyder att sex bord har plats för 6 personer. Det ska därför vara 16 6 = 10 bord med totalt 36 platser, fördelade på bord med 3 och bord med 4 platser. 36 uppdelat på multiplar av 3 och 4 ger = 36, så en lösning är fyra bord med 3 vid varje och sex bord med 4 vid varje. Någon annan lösning som uppfyller kravet på tio bord finns inte. 14: D 16 cm Vi vet att hela sträckan AF har längden 35 cm. A B C D E F 12 cm 11 cm 12 cm 16 cm Vi kan sedan söka längderna av AB och EF för att subtrahera dessa. Vi adderar längderna av BD och DF, 11 cm + 16 cm = 27 cm. Alltså är längden av AB 35 cm 27 cm = 8 cm. AC och CE är tillsammans 12 cm + 12 cm = 24 cm, alltså är EF 35 cm 24 cm = 11 cm. Sträckan BD är 35 cm 8 cm 11 cm = 16 cm. 15: A Hela loopen tar 13 minuter. Efter 60 minuter har musiken spelat 4 hela loopar och 8 minuter in på nästa. Om vi startar på C och går 8 minuter framåt hamnar vi på A, detta oberoende av var i C vi startade. 16: A 1 Två sidor med gemensam kant kallar vi grannar. Två grannar har alltid två gemensamma grannar (som är motstående sidor till varandra). 1 och 6 är grannar och deras gemensamma grannar är 2 och 5. Det finns alltså inga fler gemensamma grannar till 1 och 6. 4 är granne till 6, men inte en gemensam granne till 1 och 6, dvs inte granne till 1. Alltså ligger 4 mitt emot 1. 17: C 20 Mönstret kan delas in i grupper om 6 träd, eftersom rönnar och lindar står som vartannat och vart tredje träd. Det räcker därför att undersöka en sådan grupp: B, R, L, R, B, R Hela planteringen består av 10 grupper. I varje grupp finns 2 björkar, totalt 20 st. NCM & Kungl Vetenskapsakademien 3
3 Kängurutävlingen 2014 Benjamin, svar och lösningar 18: E 29 5 och 6 måste placeras som i bilden, för att summan av femmans grannar ska bli 9. Grannar till 6 blir då 5, 7, 8 och 9 med summan : B 7 eller 8 36 kan med tre faktorer, varav minst en ska vara 3, skrivas eller För att siffersumman ska bli 15 i första fallet måste 3 ersättas med 7. I andra fallet måste en av treorna ersättas med 8. 20: C 2 Vi ser först hur vi kan kombinera multiplar av 9 och multiplar av 4 för att få 30, dvs antalet morötter = 30 är enda möjligheten. Det betyder att Ville åt bara morötter i 2 dagar och morötter och kålrötter i 3 dagar. Under dessa 5 dagar åt han alltså 3 kålrötter. Övriga 6 kålrötter åt han under 3 dagar. De återstående 2 dagarna åt han bara gräs. Med en tabell ser vi det tydligare: Dagar totalt Morötter, 9 per dag 2 18 morötter Kålrötter, 2 per dag 3 6 kålrötter 1 kålrot och 4 morötter per dag 3 3 kålrötter 12 morötter Gräs kålrötter 30 morötter 21: E 13 Det antal stenar som Leo ska ha måste vara delbart med både 3 och 5, dvs med 15. Det antal han har får rest 2 om det delas med 15. Det innebär att det saknas 13 stenar. NCM & Kungl Vetenskapsakademien 4
4 Kängurutävlingen 2014 Arbeta vidare med Benjamin 2014 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta eleverna resonera sig fram till lösningarna i grupp. Låt alla först få möjlighet att lösa problemen på egen hand om de inte hann det i samband med tävlingen. Diskutera gruppernas lösningar i klassen och jämför idéer och angreppssätt. Låt också eleverna få granska kamraternas lösningar: Har de tagit hänsyn till alla förutsättningar? Är de tydliga? Är resonemanget korrekt? Fungerar lösningsmetoden på andra, liknande problem? Att analysera och diskutera varandras lösningar är bra, men det kräver förstås att man arbetar långsiktigt så att eleverna vänjer sig vid att både ge kritik på ett konstruktivt sätt och att ta emot kritik. Om de redan från början får uppleva att det är en del av undervisningen kan det bli en naturlig och uppskattad form av arbete med problem. Att presentera en lösning som andra kan följa och som är korrekt uppbyggd är något som eleverna måste få tid och möjlighet att utveckla med hjälp av lärare. Välj några av årets problem, arbeta igenom lösningarna noga och gör en riktigt genomarbetad redovisning. Alla problem kan naturligtvis diskuteras utifrån valda lösningsmetoder. De flesta problem kan lösas på olika sätt och det är alltid bra att jämföra dessa och se på likheter och skillnader. Det är också bra att beskriva lösningarna med hjälp av olika uttrycksformer, konkret material, bilder, muntligt eller skriftligt tal och med symboler. Jämför de olika formerna och se hur den konkreta representationen uttrycks i ord och med symboler. Några frågor att återkomma till när problemet är löst: Kontrollera att lösningen verkligen svarar mot frågan. Är det ett rimligt svar? Hur vet vi det? Påminner problemet om något annat problem vi har löst tidigare? Vilka kunskaper hade vi nytta av när vi löste problemet? Vilka nya frågor kan problemet väcka? Lärde vi oss något nytt av problemet? Gå också igenom de felaktiga svarsalternativen och resonera om varför dessa inte är riktiga. Låt eleverna göra förändringar i uppgiften så att de andra alternativen blir riktiga. Utmaningen kan vara att göra så små förändringar som möjligt. De felaktiga svarsalternativen kan också användas som utgångspunkt för diskussion om vad som skulle kunna leda fram till dessa svar: Hur tror ni att den som har fått alternativ a som svar har tänkt? Matematiskt arbete handlar mycket om resonemang. Elever behöver få resonera om både matematik innehållet och strategier för att utveckla sin matematiska kompetens. Låt dem också få argumentera för sina lösningar och sina val av metoder. I arbetet med alla problem bör förmågorna att resonera och argumentera vara centrala. I samband med diskussion av problemen kommer ett antal termer att aktualiseras. Gå igenom dem. Låt eleverna använda och själva få definiera olika begrepp och återkom till dem i olika sammanhang. För definitioner hänvisar vi till Matematiktermer för skolan (Kiselman & Mouwitz, 2008). Här har vi sorterat förslag under rubrikerna Problemlösning och logiska resonemang Tal, Tid, Geometri och Koordinatsystem. Naturligtvis kan flera av problemen också passa under andra rubriker. Många problemtyper återkommer år från år, i olika skepnader och i olika varianter. Vi hänvisar här till några gamla problem som kan användas i samband med arbetet med årets, men det finns många fler att hämta på Kängurusidan på nätet, ncm.gu.se/kanguru, där alla tidigare omgångar är samlade. Tidigare problem inom området geometri finns dessutom samlade i boken Geometri och rumsuppfattning med känguruproblem. Läs mer om den på ncm.gu.se/node/4742. NCM & Kungl Vetenskapsakademien 1
5 Problemlösning och logiska resonemang Textproblem uppfattas av många som svåra, speciellt om det är mycket information att hantera. Eleverna behöver få undervisning om hur de ska angripa den typen av uppgifter. Arbeta därför gemensamt med texterna. Gå igenom tillsammans och uppmuntra eleverna att sätta sig in i problemet, exempelvis med hjälp av stödjande frågor. Hjälp eleverna att strukturera informationen i texten. Att förstå vad problemet handlar om är en förutsättning för att kunna lösa det. Men att förstå vad det handlar om och vad som efterfrågas är inte detsamma som att veta vad man ska göra. Problemlösning handlar om att komma från att förstå situationen till att komma på hur man ska komma fram till svaret på den formulerade frågan. Det är denna process, som består av flera steg och ofta innebär både misslyckade och lyckade insatser, som är central i undervisning om problemlösning. I denna process är resonemang en viktig del. 3 Pärltråden Här gäller det att välja på ett smart sätt och att försäkra sig om att den väg man väljer är den bästa. Hur vet vi det? Låt eleverna motivera sina lösningar. Att inte bara hitta en lösning utan att undersöka om det är den enda eller den bästa lösningen är en del av problemlösningsförmågan. Gör egna liknande problem. Om eleverna får göra problem kommer de antagligen att göra dem mer komplexa. Det är bra. Benjamin 2009:4 var ett liknande problem. 10 Glassätare Beräkningarna i detta problem är enkla så här handlar det mer om att hantera information och att resonera logiskt. Arbeta gemensamt med texten och strukturera informationen. Låt eleverna beskriva situationen med egna ord och med hjälp av konkret material. Vad vet vi? Spelar det någon roll hur många barn det är på lägret? Diskutera gemensamt olika frågor som man kan ställa sig för att reda ut problemet, exempelvis: Vilket är det minst antalet glassätare idag? Hur många av varannandagsätarna åt glass igår? 11 Platsbyte Diskutera gemensamt hur eleverna har angripit problemet. Hur har de strukturerat informationen? Illustrera gärna situationen konkret. Undersök om det spelar någon roll om ordningen är medsols eller motsols. Benjamin 2011:10 handlar också om att byta platser. 13 Bordsplacering Problemet handlar om tal och hur tal kan delas upp. Illustrera problemet med konkret material och med en tabell. Vilken betydelse har informationen att restaurangen har 72 platser? Det finns två tänkbara sätt att dela upp 36 platser på tremannabord och fyrmannabord: = 36 och = 36. Den andra lösningen, 8 tremmannabord och 3 fyrmannabord stämmer dock inte med förutsättningen att det ska vara 10 bord. Att hantera flera förutsättningar samtidigt kan vara en utmaning för många elever. Diskutera betydelsen av att gå tillbaka till problemet och kontrollera mot förutsättningar och villkor. Pröva att göra andra exempel med andra kombinationer och andra villkor. Låt eleverna konstruera liknande problem själva. Problemet kan också uttryckas med ekvationer, eller med förenklade symboluttryck som är någonting mellan en beskrivande text och en korrekt ekvation, gärna flera olika. Hur formellt korrekt man uttrycker sambandet får bestämmas av elevernas tidigare erfarenheter. Ställ gemensamt upp ekvationerna eller uttrycken och låt eleverna beskriva vad dessa talar om. Jämför med den konkreta representationen och tabellen. Tidigare problem: Ecolier 2013:15 NCM & Kungl Vetenskapsakademien 2
6 14 Sträckor Här passar det bra att diskutera bildens roll som stöd i problemlösning. Bilden i detta problem kan ge oss ett stöd för resonemanget, men ger inte direkt de exakta värdena och man kan inte mäta sig fram till svaret. Bilden blir sannolikt inte korrekt vid första försöket och den behöver heller inte vara riktig beträffande längderna. Bilden i det här problemet är ett bra stöd för att diskutera innebörden av räknesättet subtraktion. I problemet handlar det om längder av sträckor, men det skulle också kunna handla om exempelvis åldrar. Låt eleverna formulera ett eget problem om årtal i stället. Observera och diskutera då skillnaden mellan en tidslinje och en tallinje. På en tallinje är varje tal en punkt, medan varje år (eller dag) på en tidslinje är en utsträckning. Benjamin 2008:13 20 Kaninmat I detta problem är det mycket att hålla reda på, förutom vad Ville äter varje dag måste man också ta antalet dagar i beaktande. Det finns olika sätt att kombinera Villys dagsransoner, men endast ett sätt som ger 30 morötter och 9 kålrötter på 10 dagar. Gå igenom problemet noga så att alla förstår innebörden av att Villy äter endera av de fyra möjligheterna. Diskutera problemlösningsstrategier. Har någon använt tabell? Undersök olika kombinationer: Hur ska han äta för att få så många morötter som möjligt? Hur många kan han som mest få under en vecka? Som minst? Hur många kålrötter kan han få som mest? Hur ska han planera sin mat om han vill ha jämn fördelning mellan kålrötter och morötter? Är det möjligt för honom att under en period äta lika många morötter som kålrötter? Hur många dagar skulle i så fall den perioden vara? Ett liknande något enklare problem finns på Ecolier, nr 15. Pröva gärna det också. Tidigare problem: Ecolier 2010: 14; Ecolier 2013:15; Benjamin 2009:5 Tal Med utgångspunkt i problem kan vi diskutera egenskaper hos tal. Elever i denna ålder kan resonera om bl a räknesättens innebörd, faktorisering och delbarhet. Problemen utmanar också barnen strategiska tänkande och förhoppningsvis väcker de frågor om tal. Uppmuntra därför eleverna att ställa fördjupande frågor. Hjälp dem också att se samband både inom matematiken och mellan matematiken och omvärlden. 1: Additionsuppställning Varför kan vi direkt se att summan måste vara 0? Gör olika exempel med villkoret att det är olika/samma siffra som är övertäckt Några tidigare problem av denna typ: Benjamin 2004:14; B2009:12; B 2010:1; B 2013:5; Ecolier 2013:2 NCM & Kungl Vetenskapsakademien 3
7 2 Största och minsta tal Gör motsvarande uppgift inom större och mindre talområden. Största femsiffriga och minsta sexsiffriga? Minsta fyrsiffriga och största femsiffriga etc. Se efter mönster och låt eleverna finna det generella sambandet. Anknyt gärna till trippmätaren i bilen eller andra räkneverk som eleverna har erfarenhet av. Tidigare problem: Benjamin 2011:12 6 Kakdelning Vad väger de andra bitarna? Variera villkoren för att få olika svar, exempelvis: Om alla väger lika? Om den största av de bitarna väger lika mycket som de andra tillsammans? Om den minsta biten väger 100 gram? Här finns möjlighet att variera öppenhetsgraden och anpassa problemet till olika elever. Tog eleverna kanske för givet att alla bitarna var lika stora? I så fall varför? Diskutera betydelsen av sätta sig in i problemet och inte lägga till villkor som inte finns. 7 Trädplantering Undersök om det spelar någon roll om vi bestämmer att det första eller det andra trädet ska vara en rönn. Diskutera tolkningen av vartannat och vart tredje och jämför med hur vi använder det i vardagen. Varför spelar det ingen roll hur vi placerar ut vartannat respektive vart tredje? Diskutera hur talen 2, 3 och 60 hör ihop. Varför räcker det att se på de 6 första träden? Låt eleverna konstruera ett liknande problem men inte med vartannat och vart tredje, utan med andra intervall, exempelvis vart annat och vart femte. Diskutera likheter och försök att komma fram till det generella i problemet. 18 Talrutor Låt eleverna få resonera sig fram till en lösning och hjälp dem att argumentera för varför 5 måste stå i rutan mellan 1 och 2. Se också nr 17 i årets Ecolier och nr 15 på Cadet, som båda är varianter på detta problem. Ecolier 2007:7; Benjamin 2010:10 och Ecolier 2011: Suddat tal Detta handlar om att faktorisera tal och om siffersumma. Gå igenom alla möjligheter att multiplicera tre ensiffriga tal och få 36. Låt eleverna argumentera för lösningen på problemet, varför duger inte de andra möjligheterna? Här är det viktigt att tänka på alla villkor: siffersumman i det ursprungliga talet var 15, minst en av siffrorna i det nya talet ska vara 3. Låt eleverna beräkna siffersumma på olika tal. Eftersom vi använder siffersumma för att bestämma delbarhet är det bra att kunna detta begrepp även om det inte används utanför matematiken. Att kunna faktorisera tal är användbart. Låt eleverna systematiskt faktorisera talen upp till hundra. Vilka tal har många faktorer? Vilka har få? Diskutera primtal, rika tal, fattiga tal och perfekta tal. Ett perfekt tal: Summan av talets delare (utom talet själv) ska vara lika med talet. Exempel: 6: och 28: Nästa perfekta tal är 496 och därefter Hittills har man upptäckt 48 perfekta tal, det senaste upptäcktes 2013 och består av siffror! Ett rikt tal: Summan av talets delare är större än talet. Exempel 24: = 36 De rika talen är lättare att finna, de första är: 12, 18, 20, 24, 30, 36. Fattiga tal: Summan av talets delare är mindre än talet. Exempel: 10: = 8. Alla primtal är fattiga liksom 4, 8, 9, 14, 15. Att låta eleverna leka med tal och undersöka deras egenskaper är bra för att de ska kunna utveckla god taluppfattning. NCM & Kungl Vetenskapsakademien 4
8 21 Stengruppering Här handlar det också om delbarhet, och om rest. Undersök vilka rester som kan komma ifråga om vi delar ett tal med 3, med 4 etc. Låt eleverna få förklara hur vi kan veta vilket den största möjliga resten blir. Det är inte säkert att de har reflekterat över detta samband. För att kunna undersöka rester behöver eleverna kunna utföra division manuellt. Behärskar de någon algoritm kan de göra intressanta undersökningar om decimalutveckling. 1/3 0, ? Varför upprepas trean och hur många decimaler måste vi beräkna för att inse att det bara blir treor? Tid 15 Musikslinga Varje år brukar det finnas något problem som handlar om tid och hur vi beräknar tid. Själva tideräkningen är troligen ingen svårighet i detta problem, att 60 sekunder är en minut och 60 minuter är en timme är de enda tidskunskaper som behövs. Men hur utnyttjar eleverna att varje loop är 13 minuter? Jämför elevernas olika lösningsstrategier hur går de vidare från att varje loop tar 13 minuter och en timme är 60 minuter. Börjar de från början och räknar upp, = 52 och sen saknas det 8? Eller arbetar de bakifrån? Delar de 60 med 13 och får 4 rest 8? Hur tolkar de i så fall det? Här finns goda möjligheter att se på räknesättens relation: addition och subtraktion som omvända operationer, division som upprepad subtraktion. Vad hade svaret blivit om det i stället hade stått: När Sofia gick hemifrån spelade låt C? Spelar det någon roll var i låt C slingan är? Vad händer om det är låt E som spelas? Undersök andra möjligheter med loopen. Varifrån känner eleverna igen ordet loop? Vad betyder det? Låt eleverna konstruera en egen spellista som har den egenskapen att om en speciell låt spelas så kommer det att vara samma låt som spelar efter en timme, oavsett var i låten man börjar. Geometri Geometri är ett område som lämpar sig väl för problemlösning. Att resonera sig fram till lösningen och att sedan kunna argumentera för den är väsentliga delar av problemlösningsförmågan. I geometri spelar också bilden en väsentlig roll, som underlag för kommunikation och som stöd för tanken. Med stigande ålder hos eleverna bör vi också ställa större krav på hur de använder bilder. Hur vet vi att vinklar är räta? Hur kan vi vara säkra på att en yta är hälften så stor som en annan? Att det ser så ut är inte ett tillräckligt starkt argument. 5 Kvadratdelning Upprepa delningen. Hur lång kan den smala rektangeln bli som längst? Vad händer med arean? Med omkretsen? Låt eleverna gemensamt formulera ett algebraiskt uttryck för omkretsen på den bildade rektangeln. Starta med en rektangel med olika långa sidor. Undersök upprepad delning åt båda hållen. Sök generella samband. Utgå från en figur med given omkrets och omforma figuren. Vad händer med arean? Eleverna behöver få många möjligheter att undersöka hur area och omkrets påverkas av att formen ändras men omkrets eller area hålls konstant. Många har uppfattningen att både area och omkrets behålls, oavsett hur formen ändras. Återkom därför till liknande undersökningar och låt eleverna få formulera sina iakttagelser och slutsatser Några tidigare problem: Benjamin 2007:12 och 14; Ecolier 2009:13; Ecolier 2006:9. NCM & Kungl Vetenskapsakademien 5
9 7 Svarta och vita plattor Varför räcker det att se på de enfärgade bitarna? Hur vet vi att de tvåfärgade bitarna är delade i halvor? Undersök hur diagonaler delar kvadrater, romber, rektanglar, parallellogrammer, godtyckliga fyrhörningar. I vilka fall får vi två lika stora delar? I vilka fall är diagonalen också en symmetrilinje? Hur skulle figuren kunna ändras för att det skulle bli möjligt att få lika stor mörk som vit area? Hur stor andel av figuren är mörk respektive vit? Uttryck arean av vitt och mörkt i varje bit i form av bråk där biten är helheten. Se sedan på arean i relation till hela figuren. Lägg till de olika svarsalternativen och se hur det påverkar andelen. Ecolier 2011:6; Ecolier 2012:7. 12: Buktiga bitar Jämför sidornas form, hur kan de hjälpa oss? De fem bitarna har sammanlagt 4 inbuktningar och 4 utbuktningar. Man bevarar balansen om man tar bort en bit med en inbuktning och en utbuktning. Undersök problemet konkret, klipp ut och rita av formerna. I tanken måste vi vrida bitarna och också se att det bildas räta vinklar i hörnen för att det ska bli en kvadrat. Om vi vet att de fyra bitarna ska bilda en kvadrat, vad vet vi då om sidlängderna? Diskutera vilka egenskaper en kvadrat har. Kan vi bygga en kvadrat med fyra bitar på ett annat sätt, om vi kan använda samma bit flera gånger? Undersök bitarnas former och storlek. Vilka är lika stora? Hur kan vi sluta oss till att inbuktningar och utbuktningar är lika stora? (Vi vet att det går att göra en kvadrat med fyra bitar, alltså måste detta gälla) Diskutera gärna att vi inte kan bygga vårt resonemang på hur något ser ut utan att vi måste ha mer stöd för våra utgångsantaganden. Graden av precision på resonemang beror naturligtvis på hur gamla eleverna är, för de allra yngsta kan man förstås utgå från hur bilden ser ut. I Benjaminåldern kan man däremot låta eleverna möta större krav på argumentationen. Fler problem som handlar om att sätta samman olika bitar är Benjamin 2011:3; B 2012:7; Ecolier 2013:11. Visualisering Flera problem tar elevernas förmåga att visualisera och att föreställa sig hur något ter sig från en annan synvinkel i anspråk. Denna förmåga utvecklas genom konkreta erfarenheter. För en del barn räcker det att de gör dessa erfarenheter, men många behöver hjälp med att dra slutsatser. Diskutera därför konkreta exempel och låt eleverna berätta vad de ser i den konkreta situationen och hur de tänker kring problem som de löser i huvudet. NCM & Kungl Vetenskapsakademien 6
10 4 Ringar från andra sidan Låt eleverna rita av föremål eller samlingar av föremål från olika håll och sedan byta papper med varandra. Var har den som ritat stått? Det går förstås också bra att fotografera eller att använda färdiga bilder och diskutera: Var har fotografen stått? Hur ser motivet ut från andra håll? Jenny och Amer står vända mot varandra så det som Amer ser till vänster ser Jenny till höger. Där ringen går framför sett från ena sidan går den bakom sett från den andra. Hur hade ringarna sett ut om Amer i stället hade sett på ringarna i en spegel bakom sig, eller om Jenny hade sett i en spegel bakom Amer? En aktivitet inom detta område är beskriven i Matematiken i bilden eller bilden i matematiken, Nämnaren 1996:2 Se också Uppslag: Fyren, kvarnen och tornet som finns på ArkivN på ncm.gu.se. Ecolier 4 i år är ett liknande problem, liksom Ecolier 2011:18. 8 Klossbygge Bygg kuber och se på den från olika håll. Gör andra vyer av kuber och bygg så att det motsvarar ritningen. Att överföra den konkreta upplevelsen av en verklig kropp till en tvådimensionell bild kräver erfarenhet och övning. Många barn får sådan träning i samband med lek men en del barn måste få göra sina erfarenheter i skolan. Ett steg mellan det konkreta och den tvådimensionella bilden kan vi numer ta med hjälp av digital teknik, med vars hjälp eleverna kan undersöka och laborera med virtuella kuber. Undersök också större kuber, 5 x 5, 7 x 7. Kubproblem och problem med att se byggen från olika håll har funnits i många Kängurutävlingar, bl a Benjamin 2011:2; Benjamin 2012:3; Benjamin 2013:15. I boken Geometri och rumsuppfattning med Känguruproblem finns ytterligare samlade och kommenterade exempel. 16 Kub med numrerade sidor Här står resonemanget i fokus. Med avsikt använder vi inte ordet tärning i formuleringen, då en korrekt tärning är konstruerad så att summan på de motstående sidorna är 7. Låt eleverna rita den utbredda kuben och undersöka om det finns olika sätt att placera siffrorna. Pröva också att rita utbredningen på olika sätt. Klipp ur och pröva. Ecolier 2008:18; Ecolier 2004:12; Cadet 2004:7; Ecolier 2005:13, Benjamin 2006: 6 handlar om hur en utbredd kub kan se ut. Se också Benjamin 2003:10, som handlar om ett utbrett hus. Problem med tärningar har förekommit flera gånger, ex: Benjamin 2002:21; Benjamin 2007:5; Benjamin 2011:20 och Ecolier 2011:18. Junior: 13 i årets tävling kan vara en spännande utmaning. I artikeln Rika tärningar i Nämnaren 2003:4 beskriver Barbara Clarke en intressant och utvecklingsbar aktivitet kring tärningar, som inte handlar om visualisering men om att se generella mönster. NCM & Kungl Vetenskapsakademien 7
11 Koordinatsystem Problem som inbegriper koordinatsystem är relativt ovanliga i Kängurusammanhang. Men de är ofta roliga och för eleverna i Benjaminåldern passar de speciellt bra med tanke på att de också arbetar en hel del med kartor under dessa skolår. 9 Orientering Rita in vägarna i problemet i ett koordinatsystem. Pröva att låta Hanna och Samir gå sina delsträckor i en annan ordning. Spelar ordningen någon roll? Vilket hade varit den kortaste vägen för var och en? Rita in den vägen. I vilket väderstreck har de gått? Jämför deras vägar, vem går längst totalt fågelvägen? Gör fler egna exempel på vägar och låt eleverna hitta olika vägar mellan två bestämda punkter Undersök vandring på klotet, om vi startar vid en pol. Detta kan fascinera barnen. Jämför med koordinatsystemet. Varför blir det inte likadant på klotet som i koordinatsystemet? Anknyt till elevernas erfarenhet av kartor över närområdet och världskartor. Vad händer med polområdena på en platt världskarta? Varför? Om kartor och kartprojektion kan man läsa i Ulf Perssons artikel Sfären i Nämnaren 2004:4. Cadet 16 i år är också ett problem i koordinatsystemet. Att läsa Gennow, S. & Wallby, K. (2010). Geometri och rumsuppfattning med Känguruproblem. NCM, Göteborgs universitet. Hagland, K., Hedrén, R. & Taflin, E. (2005). Rika matematiska problem inspiration till variation. Stockholm: Liber. Kiselman, C. & Mouwitz, L. (2008). Matematiktermer för skolan. NCM, Göteborgs universitet. McIntosh, A. (2008). Förstå och använda tal. NCM, Göteborgs universitet. Rystedt, E. &Trygg, L. (2010). Laborativ matematikundervisning vad vet vi? NCM, Göteborgs universitet. Wallby, K. m fl (red) (2014). NämnarenTema 10 Matematikundervisning i praktiken. NCM, Göteborgs universitet. Nämnaren. I varje nummer finns Problemavdelningen och Kängurusidan. Läs också tidigare artiklar kring problemlösning. Nämnarenartiklar publicerade finns fritt tillgängliga som pdf-dokument på Nämnaren på nätet, namnaren.ncm.gu.se. Du finner dem via artikeldatabasen. Under ArkivN finns alla publicerade Uppslag och Problemavdelningar samlade. Nämnaren på nätet presenterar varje månad nya problem under rubriken Månadens problem. Strävorna finns på ncm.gu.se/stravorna. Där finns aktiviteter, problem och artiklar samlade och ordnade efter kursplanens beskrivning av matematikämnets syfte och mål. Matematiklyftets lärportal matematiklyftet.skolverket.se. På lärportalen finns moduler om problemlösning för alla stadier. Dessa ingår i Matematiklyftet men finns fritt tillgängliga för alla. Modulerna innehåller teoritexter, underlag för lärares gemensamma fortbildning samt problem för eleverna. Om ni inte har och inte planerar att läsa problemlösningsmodulen inom Matematiklyftet, finns den alltså ändå tillgänglig. På lärportalen finns också andra moduler där problemlösning ingår. NCM & Kungl Vetenskapsakademien 8
1 I denna additionsuppställning har några siffror täckts över med. Vad är summan av de övertäckta siffrorna? A: 0 B: 1 C: 2 D: 3 E: 10
 Trepoängsproblem 1 I denna additionsuppställning har några siffror täckts över med. Vad är summan av de övertäckta siffrorna? 1 2 1 3 +1 4 3 0 9 A: 0 B: 1 C: 2 D: 3 E: 10 2 Hur stor är skillnaden mellan
Trepoängsproblem 1 I denna additionsuppställning har några siffror täckts över med. Vad är summan av de övertäckta siffrorna? 1 2 1 3 +1 4 3 0 9 A: 0 B: 1 C: 2 D: 3 E: 10 2 Hur stor är skillnaden mellan
Svar och lösningar Ecolier
 Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder till svaret 6.
 Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Svar och lösningar Benjamin
 Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Kängurutävlingen 2017 NCM 1
 Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Lösningsförslag Cadet 2014
 Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Arbeta vidare med Ecolier 2010
 Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Svar och arbeta vidare med Benjamin 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte.
 Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
Kängurun Matematikens hopp
 Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Svar och korta lösningar Benjamin 2006
 3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kortfattade lösningar med svar till Cadet 2006
 3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
Arbeta vidare med Milou 2008
 Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Arbeta vidare med Benjamin
 Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
5: D 3 23 kan bara fås på ett sätt: Här har man nytta av att känna igen 24 som ett tal i sexans tabell.
 Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Facit och kommentarer Ecolier 2019
 Facit och kommentarer Ecolier 2019 1 E 2 C 5+5+1+1 3 A tisdag Om det var söndag igår är det måndag idag. 4 D,, Det kvadratiska hålet kommer att hamna tre rutor från mittvikningen och då syns motorcykeln.
Facit och kommentarer Ecolier 2019 1 E 2 C 5+5+1+1 3 A tisdag Om det var söndag igår är det måndag idag. 4 D,, Det kvadratiska hålet kommer att hamna tre rutor från mittvikningen och då syns motorcykeln.
Svar och lösningar Benjamin
 Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer,
Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer,
3: A I den vita asken. Kolan ligger i den röda asken så chokladbiten måste ligga i den vita. Problemet kan lösas konkret och med en enkel bild.
 Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt.
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Svar och arbeta vidare med Cadet 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
4. A. 4, 6, 11 Viker man ihop till en kub, så kommer talet 1 mitt emot 3, 2 mitt emot 4 och 5 mitt emot 6. Det ger summorna 4, 6, 11.
 N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
5: B grön Någon har den gröna ryggsäcken och det är inte Anna (och inte Maja), så det måste vara Tom.
 Kängurutävlingen 2018 Ecolier, svar och kommentarer Facit Ecolier 1: E 6 2: B 6 Liam behöver 0, 1, 2, 3, 5 och 8. 3: C 18 Syskonen är 5 år, 6 år och 7 år, 5 + 6 + 7 = 18 4: E 5 Om skruv 5 hade varit lika
Kängurutävlingen 2018 Ecolier, svar och kommentarer Facit Ecolier 1: E 6 2: B 6 Liam behöver 0, 1, 2, 3, 5 och 8. 3: C 18 Syskonen är 5 år, 6 år och 7 år, 5 + 6 + 7 = 18 4: E 5 Om skruv 5 hade varit lika
Bagarmossens skolas kravnivåer beträffande tal och talens beteckningar som eleven ska ha uppnått efter:
 Matematik 1-5 Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och
Matematik 1-5 Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och
Svar och lösningar. Kängurutävlingen 2009 Cadet för gymnasiet
 Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Facit och kommentarer Benjamin 2019
 Facit och kommentarer Benjamin 2019 1 B 2 C 3 D 419 380 + 39 = 419 eller 380 + 20 + 19 = 419 4 C 5 E 1 Hälften av 26 barn är 13 barn. Eftersom det finns 12 pojkar i gruppen måste det som minst vara en
Facit och kommentarer Benjamin 2019 1 B 2 C 3 D 419 380 + 39 = 419 eller 380 + 20 + 19 = 419 4 C 5 E 1 Hälften av 26 barn är 13 barn. Eftersom det finns 12 pojkar i gruppen måste det som minst vara en
Kortfattade lösningar med svar till Gymnasiets Cadet 2006
 Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Arbeta vidare med Junior 2010
 Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Svar och arbeta vidare med Student 2008
 Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Ecolier. Avdelning 1. Trepoängsproblem. 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6.
 Ecolier Avdelning 1. Trepoängsproblem 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6 (Ryssland) 2 Gilda har 50 kr. Hon tänker köpa fem skrivböcker som
Ecolier Avdelning 1. Trepoängsproblem 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6 (Ryssland) 2 Gilda har 50 kr. Hon tänker köpa fem skrivböcker som
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 4 C: kvadrat Exempel på hur formerna kan konstrueras:
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
ARBETSPLAN MATEMATIK
 ARBETSPLAN MATEMATIK Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt värdera
ARBETSPLAN MATEMATIK Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt värdera
Kängurutävlingen 2017
 Kängurutävlingen 2017 Arbeta vidare med Ecolier 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. Låt alla först få
Kängurutävlingen 2017 Arbeta vidare med Ecolier 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. Låt alla först få
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2019, facit och kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Kängurun Matematikens hopp Milou 2019, facit och kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
1 B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3.
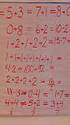 Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Matematik Steg: Bas. Mål att sträva mot Mål Målkriterier Omdöme Åtgärder/Kommentarer
 Matematik Steg: Bas ha en grundläggande taluppfattning som omfattar naturliga tal och enkla tal i talområdet 0-10 bråk- och decimalform ordningstal upp till 5 ha en grundläggande rumsuppfattning och kunna
Matematik Steg: Bas ha en grundläggande taluppfattning som omfattar naturliga tal och enkla tal i talområdet 0-10 bråk- och decimalform ordningstal upp till 5 ha en grundläggande rumsuppfattning och kunna
Om Lgr 11 och Favorit matematik 4 6
 Om Lgr 11 och Favorit matematik 4 6 TYDLIG OCH MEDVETEN MATEMATIKUNDERVISNING En stark koppling mellan läroplan/kunskaps mål, innehåll och bedömning finns för att medvetande göra eleverna om syftet med
Om Lgr 11 och Favorit matematik 4 6 TYDLIG OCH MEDVETEN MATEMATIKUNDERVISNING En stark koppling mellan läroplan/kunskaps mål, innehåll och bedömning finns för att medvetande göra eleverna om syftet med
Lokal studieplan Matematik 3 8 = 24. Centrum för tvåspråkighet Förberedelseklass
 Lokal studieplan Matematik 3 8 = 24 Centrum för tvåspråkighet Förberedelseklass 1 Mål att sträva mot Skolan skall i sin undervisning i matematik sträva efter att eleven S11 utvecklar intresse för matematik
Lokal studieplan Matematik 3 8 = 24 Centrum för tvåspråkighet Förberedelseklass 1 Mål att sträva mot Skolan skall i sin undervisning i matematik sträva efter att eleven S11 utvecklar intresse för matematik
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens
Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens
Lgr 11 matriser i Favorit matematik 4 6
 Lgr 11 matriser i Favorit matematik 4 6 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla förmågan att De matematiska förmågor
Lgr 11 matriser i Favorit matematik 4 6 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla förmågan att De matematiska förmågor
Anpassning av problem
 Modul: Problemlösning Del 7: Anpassning av problem Anpassning av problem Kerstin Hagland och Eva Taflin Detta är en något omarbetad text från boken: Hagland, K., Hedrén R., & Taflin, E. (2005). Rika matematiska
Modul: Problemlösning Del 7: Anpassning av problem Anpassning av problem Kerstin Hagland och Eva Taflin Detta är en något omarbetad text från boken: Hagland, K., Hedrén R., & Taflin, E. (2005). Rika matematiska
Bo skola 1 Matematikmål år F-3 Skriftligt omdöme/kunskapsinformation
 Bo skola Matematikmål år - Namn: Strävansmål: Vi strävar efter att varje elev ska Utveckla goda baskunskaper i de fyra räknesätten Utvecklar en god förståelse för matematik och matematiska begrepp att
Bo skola Matematikmål år - Namn: Strävansmål: Vi strävar efter att varje elev ska Utveckla goda baskunskaper i de fyra räknesätten Utvecklar en god förståelse för matematik och matematiska begrepp att
Matematik. Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret. Mål som eleverna skall ha uppnått i slutet av det femte skolåret
 Balderskolan, Uppsala musikklasser 2009 Matematik Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret läsa och skriva tal inom talområdet 0 10 000 räkna de fyra räknesätten med olika metoder
Balderskolan, Uppsala musikklasser 2009 Matematik Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret läsa och skriva tal inom talområdet 0 10 000 räkna de fyra räknesätten med olika metoder
Matematik. Ämnesprov, läsår 2013/2014. Bedömningsanvisningar Delprov B, C, D, E. Årskurs
 Ämnesprov, läsår 2013/2014 Matematik Bedömningsanvisningar Delprov B, C, D, E Årskurs 6 Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Ämnesprov, läsår 2013/2014 Matematik Bedömningsanvisningar Delprov B, C, D, E Årskurs 6 Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Kursplan för Matematik
 Sida 1 av 5 Kursplan för Matematik Inrättad 2000-07 SKOLFS: 2000:135 Ämnets syfte och roll i utbildningen Grundskolan har till uppgift att hos eleven utveckla sådana kunskaper i matematik som behövs för
Sida 1 av 5 Kursplan för Matematik Inrättad 2000-07 SKOLFS: 2000:135 Ämnets syfte och roll i utbildningen Grundskolan har till uppgift att hos eleven utveckla sådana kunskaper i matematik som behövs för
Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Kängurutävlingen Matematikens Hopp Cadet 2003 Lösningar, Arbeta vidare
 Kängurutävlingen Matematikens Hopp Lösningar, Arbeta vidare Arrangeras av Många problem kan lösas på flera sätt. Följande förslag ger inte någon heltäckande beskrivning. Diskutera olika lösningsförslag
Kängurutävlingen Matematikens Hopp Lösningar, Arbeta vidare Arrangeras av Många problem kan lösas på flera sätt. Följande förslag ger inte någon heltäckande beskrivning. Diskutera olika lösningsförslag
Södervångskolans mål i matematik
 Södervångskolans mål i matematik Mål som eleverna lägst ska ha uppnått i slutet av det första skolåret beträffande tal och taluppfattning kunna läsa av en tallinje mellan 0-20 kunna läsa och ramsräka tal
Södervångskolans mål i matematik Mål som eleverna lägst ska ha uppnått i slutet av det första skolåret beträffande tal och taluppfattning kunna läsa av en tallinje mellan 0-20 kunna läsa och ramsräka tal
Trepoängsproblem. Kängurutävlingen 2011 Cadet. 1 Vilket av följande uttryck har störst värde? 1 A: B: C: D: E: 2011
 Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
a) A = 3 B = 4 C = 9 D = b) A = 250 B = 500 C = a) Tvåhundrasjuttiotre b) Ettusenfemhundranittio
 Övningsblad 2.1 A Heltal 1 Skriv det tal som motsvaras av bokstaven på tallinjen. A B C D E F 0 10 0 50 A = B = C = D = E = F = G H I J K L 10 20 50 100 G = H = I = J = K = L = 2 Placera ut talen från
Övningsblad 2.1 A Heltal 1 Skriv det tal som motsvaras av bokstaven på tallinjen. A B C D E F 0 10 0 50 A = B = C = D = E = F = G H I J K L 10 20 50 100 G = H = I = J = K = L = 2 Placera ut talen från
jämföra/storleksordna talen jämföra/storleksordna talen Jag kan jämföra/storleksordna talen
 Utveckling A Taluppfattning 0-100 Jag kan ramsräkna 0-100. Jag kan jämföra/storleksordna talen 0-100. Jag kan markera ut tal 0-100 på en tallinje. Jag förstår tiotal och ental för talen 0-100. B Taluppfattning
Utveckling A Taluppfattning 0-100 Jag kan ramsräkna 0-100. Jag kan jämföra/storleksordna talen 0-100. Jag kan markera ut tal 0-100 på en tallinje. Jag förstår tiotal och ental för talen 0-100. B Taluppfattning
Utmanande uppgifter som utvecklar. Per Berggren och Maria Lindroth
 Utmanande uppgifter som utvecklar Per Berggren och Maria Lindroth 2014-11-12 Vilka förmågor ska utvecklas Problemlösning (Förstå frågan i en textuppgift, Använda olika strategier när jag löser ett problem,
Utmanande uppgifter som utvecklar Per Berggren och Maria Lindroth 2014-11-12 Vilka förmågor ska utvecklas Problemlösning (Förstå frågan i en textuppgift, Använda olika strategier när jag löser ett problem,
Delprov A Muntligt delprov
 Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning
 Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning Eleven skall år 1 Begrepp Jämförelse- och storleksord, t.ex. stor, större, störst. Positionssystemet
Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning Eleven skall år 1 Begrepp Jämförelse- och storleksord, t.ex. stor, större, störst. Positionssystemet
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Målkriterier Beskrivning Exempel Eleven kan tolka elevnära information med matematiskt innehåll.
 ÖREBRO MATEMATIK, ÅR 3 1(5) Eleven kan tolka elevnära information med matematiskt innehåll Eleven kan uttrycka sig muntligt, skriftligt och i handling på ett begripligt sätt med hjälp av vardagligt språk,
ÖREBRO MATEMATIK, ÅR 3 1(5) Eleven kan tolka elevnära information med matematiskt innehåll Eleven kan uttrycka sig muntligt, skriftligt och i handling på ett begripligt sätt med hjälp av vardagligt språk,
22,5 högskolepoäng. Provmoment: Ladokkod: Tentamen ges för: Matematik 3hp. Studenter i inriktningen GSME. TentamensKod:
 SMID Provmoment: Ladokkod: Tentamen ges för: TentamensKod: Matematik 3hp Studenter i inriktningen GSME 22,5 högskolepoäng Tentamensdatum: 12-08-30 Tid: 09.00-13.00 Hjälpmedel: Inga Totalt antal poäng på
SMID Provmoment: Ladokkod: Tentamen ges för: TentamensKod: Matematik 3hp Studenter i inriktningen GSME 22,5 högskolepoäng Tentamensdatum: 12-08-30 Tid: 09.00-13.00 Hjälpmedel: Inga Totalt antal poäng på
Ämnesplan i matematik för Häggenås, Bringåsen och Treälven
 Ämnesplan i matematik för Häggenås, Bringåsen och Treälven (2009-05-14) Namn Utarbetad under läsåret 08/09 Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik
Ämnesplan i matematik för Häggenås, Bringåsen och Treälven (2009-05-14) Namn Utarbetad under läsåret 08/09 Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik
Storvretaskolans Kursplan för Matematik F-klass- år 5
 2010-11-01 Storvretaskolans Kursplan för Matematik F-klass- år 5 Skolan skall i sin undervisning sträva efter att eleven : utvecklar intresse för matematik samt tilltro till det egna tänkandet och den
2010-11-01 Storvretaskolans Kursplan för Matematik F-klass- år 5 Skolan skall i sin undervisning sträva efter att eleven : utvecklar intresse för matematik samt tilltro till det egna tänkandet och den
Matematik. Mål att sträva mot. Mål att uppnå. År 1 Mål Kriterier Eleven ska kunna. Taluppfattning koppla ihop antal och siffra kan lägga rätt antal
 Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Enhet / skola: Lindens skola i Lanna Åk: 3
 Skolområde Väster Lokal Pedagogisk Planering Enhet / skola: Lindens skola i Lanna Åk: 3 Avsnitt / arbetsområde: Undersöka med Hedvig Ämnen som ingår: Svenska/svenska som andraspråk, matematik, bild, So,
Skolområde Väster Lokal Pedagogisk Planering Enhet / skola: Lindens skola i Lanna Åk: 3 Avsnitt / arbetsområde: Undersöka med Hedvig Ämnen som ingår: Svenska/svenska som andraspråk, matematik, bild, So,
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Per Berggren och Maria Lindroth 2014-11-19
 Varierad matematikundervisning Per Berggren och Maria Lindroth 2014-11-19 Luffarschack Med en utmaning! Sfinxen En rik laborativ matematikuppgift som tar sin början i de första skolåren och fortsätter
Varierad matematikundervisning Per Berggren och Maria Lindroth 2014-11-19 Luffarschack Med en utmaning! Sfinxen En rik laborativ matematikuppgift som tar sin början i de första skolåren och fortsätter
Lösningsförslag Junior 2014
 Kängurutävlingen 014 Junior, svar och lösningar Lösningsförslag Junior 014 1 E: c < b < a Längden av linje a är 16 l.e., linje b (8 + ) l.e. och linje c (8+4 p ) l.e. Alternativ lösning: Grundfiguren har
Kängurutävlingen 014 Junior, svar och lösningar Lösningsförslag Junior 014 1 E: c < b < a Längden av linje a är 16 l.e., linje b (8 + ) l.e. och linje c (8+4 p ) l.e. Alternativ lösning: Grundfiguren har
Arbeta vidare med aritmetik 2018
 Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Torskolan i Torsås Mars 2007. Matematik. Kriterier för betyget godkänd. Metoder: Arbetssätt. Muntligt. Problemlösning
 Torskolan i Torsås Mars 2007 Matematik Kriterier för betyget godkänd Metoder: Arbetssätt Ta ansvar för sin egen inlärning. Göra läxor. Utnyttja lektionstiden (lyssna, arbeta). Utnyttja den hjälp/stöd som
Torskolan i Torsås Mars 2007 Matematik Kriterier för betyget godkänd Metoder: Arbetssätt Ta ansvar för sin egen inlärning. Göra läxor. Utnyttja lektionstiden (lyssna, arbeta). Utnyttja den hjälp/stöd som
Per Berggren och Maria Lindroth 2012-10-30
 Varierad undervisning Per Berggren och Maria Lindroth 2012-10-30 Matematiska förmågor Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga
Varierad undervisning Per Berggren och Maria Lindroth 2012-10-30 Matematiska förmågor Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
BEDÖMNINGSSTÖD. till TUMMEN UPP! matte i årskurs 3
 BEDÖMNINGSSTÖD till TUMMEN UPP! matte i årskurs 3 Det här är ett BEDÖMNINGSSTÖD som hjälper dig att göra en säkrare bedömning av elevernas kunskaper i årskurs 3. Av tradition har man i den svenska skolan
BEDÖMNINGSSTÖD till TUMMEN UPP! matte i årskurs 3 Det här är ett BEDÖMNINGSSTÖD som hjälper dig att göra en säkrare bedömning av elevernas kunskaper i årskurs 3. Av tradition har man i den svenska skolan
Välkommen till Kängurutävlingen Matematikens hopp 17 mars Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Nationella strävansmål i matematik. Skolan skall i sin undervisning i matematik sträva efter att eleven
 Nationella strävansmål i matematik Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära
Nationella strävansmål i matematik Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära
Remissversion av kursplan i matematik i grundskolan. Matematik. Syfte
 Matematik Syfte Matematiken har en mångtusenårig historia med bidrag från många kulturer och har utvecklats ur människans praktiska behov och naturliga nyfikenhet. Matematiken är kreativ och problemlösande
Matematik Syfte Matematiken har en mångtusenårig historia med bidrag från många kulturer och har utvecklats ur människans praktiska behov och naturliga nyfikenhet. Matematiken är kreativ och problemlösande
Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna
Cadet. a: 1001 b: 11 c: 223 d: 191 e: 123 (Sverige) 2 Boris är född 1 januari 2002 och han är 1 år och 1 dag äldre än Irina. Vilken dag föddes Irina?
 Cadet Avdelning. Trepoängsproblem 2007 2 + 0 + 0 + 7 = a: 00 b: c: 223 d: 9 e: 23 (Sverige) 2 Boris är född januari 2002 och han är år och dag äldre än Irina. Vilken dag föddes Irina? a: 2 januari 2003
Cadet Avdelning. Trepoängsproblem 2007 2 + 0 + 0 + 7 = a: 00 b: c: 223 d: 9 e: 23 (Sverige) 2 Boris är född januari 2002 och han är år och dag äldre än Irina. Vilken dag föddes Irina? a: 2 januari 2003
ESN lokala kursplan Lgr11 Ämne: Matematik
 ESN lokala kursplan Lgr11 Ämne: Matematik Övergripande Mål: formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, använda och analysera matematiska begrepp och samband
ESN lokala kursplan Lgr11 Ämne: Matematik Övergripande Mål: formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, använda och analysera matematiska begrepp och samband
Kursplan för matematik År 1-5 Rösjöskolan TÄBY KOMMUN
 RUMSUPPFATTNING GEOMETRI OCH MÄTNING MATEMATIK REDOVISNING OCH MATEMATISKT SPRÅK TALUPPFATTNING, OCH RÄKNEMETODER STATISTIK Kursplan för matematik År 1-5 Rösjöskolan TÄBY KOMMUN Kursplan i matematik Lgr
RUMSUPPFATTNING GEOMETRI OCH MÄTNING MATEMATIK REDOVISNING OCH MATEMATISKT SPRÅK TALUPPFATTNING, OCH RÄKNEMETODER STATISTIK Kursplan för matematik År 1-5 Rösjöskolan TÄBY KOMMUN Kursplan i matematik Lgr
Vardagsord. Förstår ord som fler än, färre än osv. Har kunskap om hälften/dubbelt. Ex. Uppfattning om antal
 TALUPPFATTNING Mål som eleven ska ha uppnått i slutet av det femte skolåret: Eleven skall ha förvärvat sådana grundläggande kunskaper i matematik som behövs för att kunna beskriva och hantera situationer
TALUPPFATTNING Mål som eleven ska ha uppnått i slutet av det femte skolåret: Eleven skall ha förvärvat sådana grundläggande kunskaper i matematik som behövs för att kunna beskriva och hantera situationer
Magiska kvadrater. Material Nio kapsyler Material för att göra egna spelplaner eller spelpåsar, se separata beskrivningar.
 Strävorna 4A Magiska kvadrater... utvecklar sin förmåga att förstå, föra och använda logiska resonemang, dra slutsatser och generalisera samt muntligt och skriftligt förklara och argumentera för sitt tänkande....
Strävorna 4A Magiska kvadrater... utvecklar sin förmåga att förstå, föra och använda logiska resonemang, dra slutsatser och generalisera samt muntligt och skriftligt förklara och argumentera för sitt tänkande....
2. 1 L ä n g d, o m k r e t s o c h a r e a
 2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
Begrepps- och taluppfattning Du förstår sambandet mellan tal och antal, t.ex. genom att hämta rätt antal föremål till muntligt givna tal.
 MATEMATIK ÅR1 MÅL Begrepps- och taluppfattning Kunna talbildsuppfattning, 0-10 EXEMPEL Du förstår sambandet mellan tal och antal, t.ex. genom att hämta rätt antal föremål till muntligt givna tal. Kunna
MATEMATIK ÅR1 MÅL Begrepps- och taluppfattning Kunna talbildsuppfattning, 0-10 EXEMPEL Du förstår sambandet mellan tal och antal, t.ex. genom att hämta rätt antal föremål till muntligt givna tal. Kunna
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Matematik 92MA41 (15hp) Vladimir Tkatjev
 Matematik 92MA41 (15hp) Vladimir Tkatjev Med anledning av de nya kursplanerna har Strävorna reviderats. Formen, en matris med rutor, är densamma men istället för att som tidigare anknyta till mål att sträva
Matematik 92MA41 (15hp) Vladimir Tkatjev Med anledning av de nya kursplanerna har Strävorna reviderats. Formen, en matris med rutor, är densamma men istället för att som tidigare anknyta till mål att sträva
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant?
 En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
Under en forskningscirkel, som vi matematikutvecklare i Göteborg har
 Britt Holmberg Analysera mera i geometri Inom undervisningen i geometri behöver vi utmana elevernas nyfikenhet med frågeställningar och ge dem tid att undersöka geometriska objekt. Praktiskt arbete där
Britt Holmberg Analysera mera i geometri Inom undervisningen i geometri behöver vi utmana elevernas nyfikenhet med frågeställningar och ge dem tid att undersöka geometriska objekt. Praktiskt arbete där
