Kängurun Matematikens hopp
|
|
|
- Mona Eliasson
- för 7 år sedan
- Visningar:
Transkript
1 Kängurun Matematikens hopp Benjamin 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på nätet. Rätta elevernas lösningar och redovisa resultaten på webbadressen ncm.gu.se/kanguru/ Om du får problem med att redovisa via nätet, hör av dig till oss på eller på telefon Vi ber er redovisa era resultat senast 27 april. Uppmärksamma gärna goda prestationer i klassen och i skolan. Vi delar inte ut några priser, men namnen på de elever som fått bäst resultat, i varje årskurs, kommer att publiceras på webben. Där publiceras också lösningsfrekvenser på alla uppgifter liksom en sammanställning av hur elevernas resultat fördelar sig på olika poängintervall. Du kan sedan jämföra dina elevers resultat med övriga elever i samma åldersgrupp och du kan se om de problem som dina elever hade svårt för också var svåra för andra. Vi är medvetna om att redovisningen tar tid, men vi ber er ändå att redovisa resultaten. De är värdefulla för oss och förhoppningsvis ger en sammanställning av klassens resultat även er ett bra underlag för vidare arbete. Många efterfrågar också en sammanställning med lösningsfrekvenser och denna blir förstås bättre ju fler som redovisar. Vi har valt att inte ta några deltagaravgifter, vilket man gör i flera andra länder. Att låta er sköta rättning och redovisning av resultat är ett sätt att hålla kostnaderna nere. Låt eleverna få en ny chans att lösa de problem de inte hann med Endast några enstaka elever hinner att lösa alla problem under tävlingstillfället. Ordna därför gärna ett extra tillfälle utom tävlan, där klassen kan lösa problemen utan tidsbegränsning. Många skulle säkert utmanas av de svårare problemen. Arbeta vidare med lösningarna De flesta problem kan lösas på flera sätt och med olika representationsformer. Låt eleverna försöka hitta olika metoder, beskriva sina lösningar och jämför metoderna. Se efter både likheter och skillnader. Pröva om lösningsmetoden är generell, t ex genom att ändra de ingående talen. Låt eleverna få upptäcka, eller visa dem, hur samma lösning kan presenteras på olika sätt, t ex med ord och med symboler. Det är viktigt att eleverna får uttrycka sina lösningar på mer än ett sätt. Att kunna gå mellan olika representationsformer är viktigt för att utveckla förståelse. Arbeta vidare med problemen Efter redovisningssidorna i detta dokument följer förslag till hur ni kan arbeta vidare med problemen. Kungl Vetenskapsakademien & NCM/Nämnaren 1
2 Kängurutävlingen 2012 Svar och lösningar Benjamin 1: C 1,5 m När mittdelens 3 m tagits bort återstår 3 m att fördela lika på två sidor. 6 3 = 3; 3/2 = 1,5. 2: A 8 Varje sida blir dubbelt så lång. Om sidan blir dubbelt så lång blir arean fyra gånger så stor. 3: B De tärningar som ligger intill den dolda tärningen har bokstäverna C, D och A. 4: D 3 Från varje punkt (stad) ska det utgå 4 sträckor (vägar). Totalt finns det = 10 vägar. 7 är utritade, alltså saknas 3. 5: C Alternativen A, B och E är möjliga att skapa, men de mönstren är ofullständiga. I alternativ A och E används inte alla sexhörningarnas mittpunkter och i B är de inte sammanbundna. Alternativ D är inte konstruerat utifrån mittpunkterna i figuren. 6: A Det övre myntet ska rotera ett fjärdedels varv och förflyttar sig samtidigt ett fjärdedels varv utefter det undre myntet, som om de vore två kugghjul. 7: E 2, 3 och 6 Endast bit 2 passar i mitten och då ska bit 3 ligga till höger om den. Det ger att det är bit 6 som ska sitta i övre högra hörnet. 8. E 6 i morse Tidsskillnaden mellan Madrid och San Fransisco är 9 timmar. Madrid är 9 timmar före San Fransisco. 9: B 20 kg Om ballongerna lyfter varsin korg med innehåll klarar de 160 kg. Tillsammans klarar de 20 kg mer, vilket alltså är det som en extra korg skulle väga. Med ekvation: Antag att det som en ballong kan lyfta inklusive korg är M kg. och att korgen väger m kg. M = m + 80 och 2M = m M M = m (m + 80) M = 100 ger m = 20 10: C bara grön Ett rött och ett blått tal blir alltid en multipel av 3, dvs ett grönt tal. Alla röda tal kan uttryckas som ett grönt tal 2 och alla blå tal som ett grönt tal 1. Kungl Vetenskapsakademien & NCM/Nämnaren 2
3 Kängurutävlingen 2012 Benjamin, svar och lösningar 11: D Från start hoppar han 2 gånger 2 rutor rakt uppåt (på kartan). Andra hoppet går 2 gånger (4 rutor åt höger och 1 ruta uppåt). Tredje hoppet är 2 gånger (3 steg nedåt och två steg åt vänster). 12: D 20 cm Vi kan jämföra figurerna och räkna bort de sträckor som är lika. Vi ser då att den vänstra figuren har tre delsträckor som den högra saknar. Det är en sida som är 10 cm och två sidor som är vardera 5 cm. 13: B Det är mer olja än vinäger och vatten tillsammans Vi utgår från mängden vatten och kallar det för x. Vi får då att mängden olja är 3x och mängden vinäger är 1,5 x. Sen kan vi undersöka alternativen. eller: Mängden olja ska vara både dubbelt och tre gånger så stor som något. Vi väljer ett tal som enkelt kan delas i både 2 och 3, t ex 12. Låt oss anta att mängden olja är 12. Då får vi att mängden vinäger är 6 (hälften) och mängden vatten är 4 (en tredjedel). Utifrån dessa tal kan vi undersöka alternativen. Vi kan ersätta 12, 6 och 4 med vilka andra taltrippler som helst som har samma inbördes relation. 14: B 72 cm 2 Omkretsen består av 14 kvadratsidor. En sida är alltså 3 cm. Arean på varje kvadrat är då 9 cm 2, totalt 72 cm 2. 15: D 6 gånger Man kan se bollen då den faller första gången, därefter när den studsar upp mot 8 m ( 4 5 av 10) och när den är på väg ner igen. Nästa studs går till 4 5 av 8 m, m (6,4 m), och vi ser bollen på väg upp och på väg ner. Sen studsar bollen upp till 4 5 av 6,4 m, vilket är 5,12 m och då ser vi hur bollen vänder utanför fönstret. Det blir sammanlagt sex gånger. 10 m marken 8 m 6,4 m 5,12 m fönstrets höjd 16: D 7,5 Vi vet att 4 barn är 6 år och att minst 5 barn är 8 år. Det är 9 barn, vilket innebär att det är precis 5 barn som är 8 år och att de tre återstående måste vara 7, 9 och 10 år gamla. Vi får fördelningen: år antal Medelvärdet: = = 7,5. Medelvärdet är 7,5. Det betyder att barnen i genomsnitt var 7 år och 6 månader, dvs 7 och ett halvt år, förutsatt att åldersangivelsen är någorlunda exakt. Kungl Vetenskapsakademien & NCM/Nämnaren 3
4 Kängurutävlingen 2012 Benjamin, svar och lösningar 17: A 8 och 10 I ringarna på vardera sidan om 12 måste vi skriva 10 och 11. Intill 11 måste det på andra sidan stå 9, eftersom 10 redan står i ringen intill 12. I ringen på andra sidan 10 måste det därmed stå 8. 18: B 5 Eftersom vi vill ha så få kvadrater som möjligt gäller det att hitta så stora som möjligt. Den största möjliga, 6 x 6, ger dock sju småkvadrater dessutom. Även 5 x 5 ger flera småkvadrater. Men med kombinationen av en 4 x 4 och två 3 x 3 får vi bara två ytterligare kvadrater, två st 2 x 2. 19: E Alternativ A kan uteslutas därför att första kolumnen 2 har 0 samtidigt som översta raden har 4. 1 Summan av antalet markerade rutor i raderna måste vara 2 2 densamma som summan av antalet markerade rutor i kolumnerna. Det gör att alternativ B kan uteslutas. en möjlig lösning Alternativ C kan uteslutas då det inte ska vara några markeringar i de två nedre raderna vilket gör det omöjligt att få 3 i kolumnerna. Alternativ D ska ha en rad och en kolumn tom och två rader och två kolumner med 3 i varje, vilket inte går att kombinera med att en rad och kolumn endast ska ha 1. 20: D 16 cm 2 Med alla vikningar och sidor utritade ser vi att de båda rektanglarna tillsammans har lika stor area som 1 4 av den ursprungliga kvadraten, dvs 16 cm 2. Eller: Kvadratens sida är 8 cm och den första vikningen delar sidan mitt itu. Längden på de grå rektanglarna är lika med den halva sidan, alltså 4 cm. Den andra vikningen bildar en triangel som kan ses som en halv kvadrat med sidan 3 4 av den stora. Den korta sidan på den grå rektangeln är alltså 2 cm. Arean av en rektangel är 8 cm 2. 21: C 5 Tre ental C + C + C ska ge entalssiffran 2. Den enda möjligheten är C = 4. Det ger att B + B + 1 = 11 (21 går inte, det skulle innebära att B = 10 och 1 skulle innebära att B = 0 och att ett husnummer började med 0, vilket de inte gör, B är alltså 5. A= 8. Kungl Vetenskapsakademien & NCM/Nämnaren 4
5 Arbeta vidare med Benjamin 2012 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta eleverna resonera sig fram till lösningarna i grupp. Låt alla först få möjlighet att lösa problemen på egen hand om de inte hann det i samband med tävlingen. Diskutera gruppernas lösningar i klassen och jämför idéer och angreppssätt. Låt också eleverna få granska kamraternas lösningar: Har de tagit hänsyn till alla förutsättningar? Är de tydliga? Är resonemanget korrekt? Fungerar lösningsmetoden på andra, liknande problem? Att analysera och diskutera varandras lösningar är bra, men det kräver förstås att man arbetar lång siktigt så att eleverna vänjer sig vid att både ge kritik på ett konstruktivt sätt och att ta emot kritik. Om de redan från början får uppleva att det är en del av undervisningen kan det bli en naturlig och uppskattad form av arbete med problem. Att presentera en lösning som andra kan följa och som är korrekt uppbyggd är något som eleverna måste få tid och möjlighet att utveckla med hjälp av lärare. Välj några av årets problem och arbeta igenom lösningarna noga och gör en riktigt genomarbetad redovisning. Alla problem kan naturligtvis diskuteras utifrån valda lösningsmetoder. De flesta problem kan lösas på olika sätt och det är alltid bra att jämföra dessa och se på likheter och skillnader. Det är också bra att beskriva lösningarna med hjälp av olika representationsformer, konkret material, bilder, muntligt eller skriftligt tal och med symboler. Jämför de olika formerna och se hur det konkreta uttrycks i ord och med symboler. Några frågor att återkomma till när problemet är löst: Kontrollera att lösningen verkligen svarar mot frågan. Är det ett rimligt svar? Hur vet vi det? Påminner problemet om något annat problem vi löst tidigare? Vilka kunskaper hade vi nytta av när vi löste problemet? Vilka nya frågor kan problemet väcka? Lärde vi oss något nytt av problemet? Gå också igenom de felaktiga svarsalternativen och resonera om varför dessa inte är riktiga. Låt eleverna göra förändringar i uppgiften så att de andra alternativen blir riktiga. Utmaningen kan vara att göra så små förändringar som möjligt. Matematiskt arbete handlar mycket om resonemang. Elever behöver få resonera om både matematik innehållet och om strategier för att utveckla sin matematiska kompetens. Låt dem också få argumentera för sina lösningar och sina val av metoder. I arbetet med alla problem bör förmågorna att resonera och argumentera vara centrala. I samband med diskussion av problemen kommer ett antal termer att aktualiseras. Gå igenom dem. Låt eleverna använda och själva få definiera olika begrepp och återkom till dem i olika sammanhang. För definitioner hänvisar vi till Matematiktermer för skolan (Kiselman & Mouwitz, 2008) Här har vi sorterat förslag under några rubriker. Naturligtvis kan flera av problemen också passa under andra rubriker. Många problemtyper återkommer år från år, i olika skepnader och i olika varianter. Här har vi hänvisat till några gamla problem som kan användas i samband med arbetet med årets, men det finns många fler att hämta på Kängurusidan på nätet, ncm.gu.se/kanguru, där alla tidigare omgångar är samlade. Tidigare problem inom området geometri finns dessutom samlade i boken Geometri och rumsuppfattning med känguruproblem. Läs mer om den på ncm.gu.se/node/4742. Kungl Vetenskapsakademien & NCM/Nämnaren 1
6 Problemlösning resonemang 9. Ballongerna och korgen. Problemet är av en klassisk problemtyp, ett mer känt och gammalt exempel handlar om en flaska med en kork: En flaska med kork kostar 1 kr 10 öre. Flaskan kostar 1 kr mer än korken. Vad kostar flaskan och vad kostar korken? Variera problemet med andra vikter och med andra sammanhang. Diskutera med eleverna vad det är som gör problemet komplicerat. Låt eleverna konstruera liknande problem, då får de en bild av hur problemen är konstruerade. Tidigare problem: Cadet 2001: 16; Cadet 2003: 17, Adventskalendern Olja och vinäger. Här är de språkliga uttrycken viktiga. Diskutera vad uttrycken dubbelt så mycket som och tre gånger så mycket som innebär. Hur ska det uttryckas med symboler? Om vi har x dl vatten och dubbelt så mycket olja kan vi skriva: mängden olja = 2x. Det är alltså inte oljemängden som ska dubbleras. Detta är en nyckel för att förstå hur man skriver algebraiska uttryck. Gör många exempel gemensamt och låt eleverna formulera både muntligt och med symboler och genom att rita figurer. I den här typen av problem handlar det också om att se på relationen och hur många delar den totala mängden har. Om vi har dubbelt så mycket olja som vatten är relationen 2:1 och det är totalt tre delar det handlar om. Problemet passar bra för att visa olika lösningsmetoder. I avdelnngen svar och lösningar har vi visat en algebraisk och en resonerande lösning. Resonemang kan förstås se olika ut. Här är ett annat: Alternativ A är fel eftersom vi vet att det är dubbelt så mycket olja som vinäger. Alternativ D är fel eftersom vi vet att det är tre gånger så mycket olja som vatten. Alternativ E är fel eftersom vi vet att det är mer vinäger än vatten. Mängden olja är dubbelt så stor som mängden vinäger, men tre gånger mängden vatten. Alltså är det minst vatten. Återstår att undersöka alternativen B och C. Är det mer olja än vatten och vinäger tillsammans eller är det mer vinäger än olja och vatten tillsammans? Alternativ B: Mängden vatten är 1 3 och mängden vinäger är 1 2 av mängden olja, = 5 6. Det är alltså mer olja än vinäger och vatten tillsammans. Sant. Alternativ C: Vi vet att det är dubbelt så mycket olja som vinäger. För att mängden olja och vatten ska bli större än mängden vinäger måste mängden vatten vara minst lika stor som mängden vinäger. Vi vet att det är mindre vatten ( 1 3 av oljemängden) än vinäger ( 1 ). Alltså falskt. 2 Vi kan också rita en enkel bild där vi fördelar ingredienserna. Några tidigare problem: Cadet 2001: 4; Ecolier 2003: 16. vatten vatten olja olja olja olja olja olja vin. vin. vin. Kungl Vetenskapsakademien & NCM/Nämnaren 2
7 15. Den studsande bollen. När vi löser det här problemet har vi stor nytta av en bild. Vi måste både ha kontroll på vid vilken höjd bollen vänder och var fönstret är. Dessutom måste vi hålla räkning på antalet studsningar. Problemet handlar också om bråk. Många uttrycker nog gärna talen i decimalform, inte minst för att det handlar om mätetal. Passa på att jämföra formerna bråk decimalform procent. Diskutera när det kan vara bättre att använda en viss form. Här handlar det också om upprepade multiplikationer med samma tal, Det kan uttryckas i potensform( 4 5 )3. Vi kan också skriva decimalformen som en potens: 0,8 3. Om eleverna inte har arbetat med potenser kan detta vara en inledning. Förändra då problemet så att det handlar om något som hela tiden fördubblas, t ex antalet bakterier. Ett närliggande problem är det klassiska med riskornen på schackbrädet, med varianter: Kalle ska förhandla om en ersättning för disken under sommarlovet. Han föreslår antingen 1 kr första dagen, 2 kr andra dagen, 4 kr tredje dagen, 8 kr fjärde dagen och så vidare, eller 100 kr varje dag. Vilket alternativ ska föräldrarna föredra? Tycker du att hans föräldrar ska acceptera det? En intressant utveckling att studera och fundera över är vad som händer om vi upprepade gånger halverar något. Arbeta konkret med ett paper som ni delar mitt itu. Dela sedan ena halvan mitt itu etc. Resonera om vad närmar sig för tal och är exempel på geometriska serier. 19 Rutorna. För att lösa detta är det bra att kunna resonera logiskt. Logik handlar om vad som är nödvändigt, möjligt eller omöjligt utifrån vissa förutsättningar. Om en rad innehåller fyra röda rutor, så kan inte en kolumn innehålla noll röda rutor. Alltså kan det inte vara A. Försök att hitta flera möjliga sätt att färglägga, som ändå stämmer med markeringarna. Använd gärna konkret material. Diskutera de felaktiga alternativen och låt eleverna få justera dem så att de stämmer, med minsta möjliga förändringar. Vi kan också anknyta till Sudoku, som finns i olika svårighetsgrader och som många roas av. I båda problemtyperna måste man tänka på att det ska stämma både i rader och i kolumner. Några tidigare problem inom dessa områden: Ecolier 2011:16, Benjamin 2010:10, Student 2010:11; Cadet 2008:2; Ecolier 2007: 7; Cadet 2005:2; Ecolier 2004: 5 och Cadet 2004: 3. Grafteori, kombinatorik 4 Vägarna mellan städerna. Även här finns det olika sätt att tänka: Det ska gå fyra vägar från varje stad eller om jag drar fyra vägar från första staden behöver jag bara dra tre till från andra, osv. Jämför de olika metoderna. Uttryck dem också med symboler och gör exempel med olika antal städer. Hur ökar antalet vägar när städernas antal ökar? Kungl Vetenskapsakademien & NCM/Nämnaren 3
8 Problemet påminner om det som ofta kallas Handskakningsproblemet. Tolv gäster på ett kalas hälsar alla på varandra. Hur många handskakningar blir det sammanlagt? (Vi räknar det som en handskakning när två personer hälsar på varandra, även om de står och skakar sina händer en lång stund). Beroende på hur vi resonerar leder det fram till två sätt att beräkna antalet: 1: Den förste hälsar på 11 personer, nästa på 10 etc: , eller 2: 12 personer hälsar på 11 andra, men varje handskakning räknas två gånger, så vi måste dividera med 2: Problemtypen kan varieras på många sätt och illustreras med dramatisering, med konkret material och med bilder. Läs mer i Benjamin 2010: facit och att arbeta vidare med, som finns tillgängligt på Kängurusidan på nätet. I det här fallet gäller det att finna hur många sätt det finns att kombinera städer med varandra med hjälp av ett antal vägar, så det är en uppgift inom området kombinatorik. Det handlar också om grafteori, och då kallas knutpunkterna (städer i det här fallet) för noder och vägarna emellan kallas bågar. Det finns ett antal klassiska problem inom detta område, Königsbergs broar är kanske det mest kända. (Sök på Königsbergs broar i Nämnarens artikelregister). Den förste som löste det problemet var Leonard Euler. Vill man arbeta mer med Euler kan det passa att undersöka Eulers samband, som handlar om sambandet mellan antalet hörn, kanter och områden i polygoner (se NämnarenTEMA Uppslagsboken, 2E. Detta Uppslag finns också tillgängligt som pdf på Kängurusidan på nätet) Andra problem: Cadet 2004:11; Cadet 2001:8; Cadet 2001: 10. Läs också: Mikael Passare: Sesam öppna dig i Nämnaren nr 4, Geometri Som vanligt handlar flera problem om geometri. De lämpar sig att undersöka konkret och med bilder. Stimulera eleverna att berätta om sina lösningar, bilder etc med hjälp av korrekta termer, som ni gemensamt definierar. Samtala om formernas egenskaper och jämför olika former med varandra vad är lika och vad är olika? Här har vi några förslag på hur man kan arbeta med geometriproblem, och i tidigare års material finns mycket mer att hämta. Dessutom hänvisar vi till boken Geometri och rumsuppfattning med Känguruproblem. Flera problem handlar om grundläggande geometriska former, deras omkrets och area samt relationer mellan dessa. Resonera om formernas egenskaper, se på vinklar, sidor, hörn och diagonaler. 7. Pusslet. Diskutera olika strategier när man lägger pussel. Börjar alla med ramen? Utgår från färger? Vilka bitar är lättast att hitta? Låt eleverna beskriva uppgiftens pusselbitar med ord. Hur känner vi igen kantbitar? Hörnbitar? Vi säger kantbitar på ett pussel, men sidan på en rektangel. Gör eleverna uppmärksamma på termerna kant, sida och hörn och hur de används i olika sammanhang, matematiska och vardagliga. Pusselproblem har funnits många gånger i kängurun, bl a Benjamin 2003:5 och 14. I Geometri och rumsuppfattning med Känguruproblem finns flera sådana samlade och kommenterade. Se också Nämnaren Uppslaget, 2004:2,Visualisering i tysthet, som finns på ArkivN på Nämnaren på nätet. Kungl Vetenskapsakademien & NCM/Nämnaren 4
9 2. Mynten i kvadraten. Undersök rektanglar, som inte nödvändigtvis är kvadrater för olika antal mynt. Låt eleverna konstruera frågor till varandra, t ex: vilken omkrets skulle en rektangel (som inte är en kvadrat) få om den ska rymma 16 mynt? Undersök hur många olika rektanglar som kan byggas med ett visst antal stickor, t ex 24. Har två olika rektanglar med samma omkrets också samma area? Konstruera olika rektanglar med samma area. Hur vet vi att arean är densamma? Tidigare problem: Ecolier 2002: Sexhörningarna. Resonera utifrån alternativen, varför är de fel? Jämför med instruktionen. Låt eleverna rita alternativen i figuren. Ett kopieringsunderlag med figurer finns på nätet. Gå igenom vad månghörningarna heter, både oregelbundna och regelbundna. Jämför antalet sidor med antalet hörn. Det är inte säkert att eleverna har reflekterat över det. Undersök hur många trianglar av olika storlek som går att se i alternativen A, C och E. Arbeta med tesselleringar. Undersök med vilka regelbundna månghörningar kan vi täcka en yta, utan att överlappa och utan att det uppstår hål. Det finns bara tre: sexhörningar, kvadrater och liksidiga trianglar. Resonera om varför. Hur kan vi kombinera olika regelbundna månghörningar och täcka en yta? Undersök gärna golv och kakelmönster i verkligheten eller på bilder från t ex kyrkor. Läs Gunilla Borgefors: Tessellationer konsten att dela upp planet i regelbundna mönster i Människor och matematik, NCM. Sök också i Nämnarens artikelregister. 12. Den sammansatta figuren. Resonera om att omkretsen ändras men inte arean, och varför det är så. Att figurerna har olika omkrets beror bland annat på att i den andra figuren ligger fler pusselbitskanter (sidor på delarna) inne i figuren, så de räknas inte till omkretsen. Den enda pusselbit som förlänger omkretsen i den andra figuren är rektangeln, som ju i första figuren har alla sidor inne i figuren. Låt eleverna försöka göra egna liknande problem. Försök att konstruera en figur med delar som efter omflyttning har samma area och samma omkrets men ett annat utseende utseende. Ett problem som påminner om detta är årets Cadet 24, som kan vara en utmaning för en del elever. 24. Tre sträckor delar en triangel i fyra små trianglar och tre fyrhörningar (se figuren). Summan av fyrhörningarnas omkretsar är 25 cm och summan av de fyra små trianglarnas omkretsar är 20 cm. Omkretsen av den stora triangeln är 19 cm. Hur stor är de tre sträckornas sammanlagda längd? A: 11 B: 12 C: 13 D: 15 E: 16 Se också Benjamin 2007:20; Kungl Vetenskapsakademien & NCM/Nämnaren 5
10 14. Åtta kvadrater. Vilka olika omkretsar kan man få av kvadraterna? Vilken är den största möjliga och vilken är den minsta möjliga? Betrakta figuren som en utvikt ask. Hur stor blir volymen på asken när vi viker upp den? Låt eleverna undersöka en större kvadrat, t ex med sidan 20 cm. Klipp bort kvadrater i hörnen och vik upp sidorna så att det blir en ask. Hur ser den största möjliga lådan ut? Den minsta? Tidigare problem: Benjamin 2004: Vikt papperskvadrat. Även i problem 20 handlar det om vikningar. Arbeta laborativt och undersök relationen mellan olika delområden. Låt eleverna motivera sina svar med hjälp av vad de vet. Ge dem också i uppgift att med hjälp av vikning konstruera områden med en bestämd area eller omkrets, t ex vik så att arean blir hälften. Hur vet vi att det är precis hälften? Här passar det bra att anknyta till bråk och att uttrycka areorna som bråk. Nära till hands ligger också arbete med Tangram. Se tex Erkki Pehkonen: Uppslag: Övningar med Tangram i Nämnaren nr 3, 1994 och Tangrampussel som finns på Strävorna 2C och 2A. Mer finns att hitta på ncm.gu.se, skriv Tangram i sökrutan. Vikning och vinklar behandlas också i Cadet 2002:21 3. Klossbygget. Problem 3 handlar om att se en tvådimensionell bild som en tredimensionell form. Många elever behöver mycket träning i detta. Låt dem bygga efter ritningar och också rita av byggen de gör. Ställ frågor som får dem att uppmärksamma hur rätblocket är konstruerat: Ett plan är uppbyggt av ett antal klossar i ett antal rader och rätblocket består av ett antal sådana plan. Diskutera olika sätt att angripa problemet: någon kanske delar upp kuben i två plan, medan någon annan resonerar utifrån grannklossar. Låt eleverna rita planen och bygg på med ytterligare en våning. Problem med klossar har funnits många gånger i Kängurun, och i Geometri och rumsuppfattning med Känguruproblem finns de samlade, ordnade och kommenterade. 6. Myntrullning. I detta problem måste vi också rotera formen. Det är naturligtvis enklare om man får göra det konkret. Undersök med verkliga mynt. Här är det två slags rotationer: både myntets rotation på det andra myntet och den rotation som uppstår på grund av att banan är böjd. Låt eleverna få resonera om detta och beskriva rotationen med ord. Resonera om myntens inbördes läge. Jämför med kugghjul. Se också Cadet 2002: 2. Kungl Vetenskapsakademien & NCM/Nämnaren 6
11 11. Hipp och Happ. Låt eleverna beskriva Hipps hopp som antal steg och riktning. Finns det andra vägar att komma till samma punkt, om man inte tar steget i ett hopp? Hur skulle Hipp hoppa om han tog sig hela vägen i ett hopp? Gör likadant med Happs hopp. Låt eleverna rita månghörningar i ett rutnät. Med hjälp av riktning och antal steg kan de sedan beskriva sina figurer för en kamrat, som inte få se bilden. Kamratens uppgift är att följa instruktionen och rita motsvarande figur på ett eget rutpapper. Lägg in ett koordinatsystem i bilderna över Hipps och Happs hopp, och diskutera punkterna med hjälp av koordinater. Låt eleverna i par göra motsvarande övning som ovan, men med hjälp av koordinater. Anknyt gärna till kartor och GPS. Statistik 16. Födelsedagskalaset. Om vi vill behålla medeltalet när några går vilka ska bort? Om vi vill att det ska höjas? Sänkas? Variera villkoren, ändra exempelvis till att tre barn var 6 år och undersök vad som händer. Undersök hur olika förändringar påverkar medeltalet. Beräknar medeltalet av åldrarna i en familj (kan vara verklig eller fiktiv) och låt det födas ett barn. Vad händer? Jämför hur en persons ålder påverkar medeltalet i en stor familj, en släkt, stora populationer, hela landet? Studera befolkningsstatistik. På Statistiska centralbyråns webbplats, finns bland annat en tabell över Sveriges befolkning 31 dec Där kan vi se att det då fanns 3 personer som är 110 år eller äldre och 769 hundraåringar. Hur många barn föds det ungefär under ett år i Sverige? Behandla begreppet median, det mittersta värdet. Vilken är medianen på åldrarna i exemplet. Låt eleverna räkna om sina åldrar till månader (för att få bättre värden att arbeta med) och beräkna klassens medianålder. Jämför med medeltalet. I detta sammanhang passar det bra att diskutera varför vi inte kan skriva 12 år och 4 månader som 12,4 år. Det är ett skrivsätt som förekommer, men som inte är korrekt. Vad skulle 12,4 år innebära? Varför lämpar sig inte decimalform när vi skriver år? Motsvarande problem har vi när det handlar om timmar, minuter och sekunder. 1,12 timmar är inte detsamma som 1 timme och 12 min. Hur skulle 1 timme och 12 minuter skrivas i decimalform? Många elever i den här åldern tycker att det är roligt att göra på oväntade sätt. Låt dem undersöka hur vissa tider skulle uttryckas om de skrevs i decimalform. Kanske kan ni sedan ta rast i 0,25 timme. Tidigare problem: Cadet 2011: 12; Cadet 2004:16. Kungl Vetenskapsakademien & NCM/Nämnaren 7
12 Tid 8. Tidszoner. Att fundera över hur mycket klockan är på olika ställen på jorden just nu tycker många barn är spännande. Var har de just vaknat? Var går de och lägger sig nu? Var på jorden är det fortfarande igår? Redan i morgon? Många har telefoner med klockor där vi snabbt kan få reda på tiden på andra ställen. Varför har vi inte samma tid jorden runt? Undersök tidszonerna med hjälp av en karta. På några ställen ser vu tydligt att tidszonerna är en anpassning till människan, att de inte enbart beror på solens läge. Diskutera varför vi har detta system. I samband med årsskiftet bytte republiken Samoa tidszon. De strök 30 december ur almanackan och i stället för att tillhöra den sista tidszonen tillhör de nu den första. Orsaken var rent praktisk, det är mer lämpligt att ligga tre timmar före de viktigaste handelspartner än 21 timmar efter. Tal Några problem handlar förstås om tal. Att resonera om tal, undersöka och pröva, och att leka med tal hjälper eleverna att utveckla sin taluppfattning. Problem om tal är bra för att få igång resonemang och diskussion kring talens egenskaper. 1. Skrivtavlan. Problemet kan vid första anblick uppfattas som ett geometriproblem, men det handlar egentligen om tal, fast de är geometriskt representerade. För många elever är det ett stöd att kunna se talen som bilder, och det hjälper dem att förstå och tänka kring tal. Vad händer med den högra delen om vi förlänger eller förkortar den vänstra? Om vi förlänger den högra med 0,5? Om den högra är dubbelt så bred som den vänstra? vänstra delen högra delen 1,5 0,5 1,5 + 0,5 Gör en tabell och undersök systematiskt: 1,5 1 1,5 +1 1, ,5 1 gå över till algebra: 1,5 + a 1,5 a Hur stort kan a vara. 18. Fatimas kvadrater är ett bra exempel på sambandet mellan geometri och aritmetik. Vi kan se på talen geometriskt, här som rektanglar, men också behandla dem enbart som tal. Om vi formulerar om det: Uttryck talet 42 som summan av kvadrater, där sidan inte kan var större än 6. Vilka möjligheter finns det, om vi inte behöver tänka på att det ska vara så få som möjligt? Om vi inte behöver begränsa oss till att de ska finnas inom ramen 6 7? Försök att skriva alla positiva heltal som summan av så få kvadrater som möjligt. Det går att uttrycka alla naturliga tal med högst fyra kvadrattal. Satsen är bevisad av den franske matematikern Joseph-Louis Lagrange ( ). Diskutera varför svaret på problemet blir större än 4. Varför duger inte lösningarna 42 = eller 42 = ? Genom att ge problemet en geometrisk kontext har vi infört en begränsning, Se också: Benjamin 2003:19 Kungl Vetenskapsakademien & NCM/Nämnaren 8
13 10. Olikfärgade tal. I samband med problem 10 kan vi diskutera delbarhet och delbarhetsregler. Hur vet vi att ett tal är delbart med 3? Med 9? Med 5? 10? 21. Gatunumren. I originalversionen av problemen fanns alternativet 0 på problem 21. Vi beslöt att ändra det för att det inte skulle bli någon diskussion. 0 är en möjlig lösning på problemet, om man bortser från sammanhanget. Här handlar det om nummer på en gata, och sådana börjar aldrig med 0. Låt eleverna först försöka hitta en annan lösning än 5. Diskutera med eleverna om när vi sätter 0 först i ett tal, i matematiken och i verkligheten. Diskutera hur man kan resonera sig fram till lösningen. Gör egna liknande uppgifter, med olika antal siffror i talen. Försök att konstruera summor som har flera tänkbara lösningar. Kryptaritmer är en form av talpussel som passar bra för resonemang. Varje bokstav står för en siffra, samma bokstav är samma siffra. Här är några klassiker att a rbeta med: SEND + MORE = MONEY ETT + ETT = TVÅ TEN + TEN + FORT = SIXTY HALF + HALF = WHOLE En formell lösning bygger på att tal kan skriva på formen: 100a + 10b + c Skriv tal på det sättet och se hur vi har förenklat vårt skrivsätt: Tre hundratal + fem tiotal + nio ental = = 359 Tidigare problem: Benjamin 2004: 14 Att läsa Borgefors, G. (200?). Tessellationer konsten att dela upp planet i regelbundna mönster. I O. Helenius & K. Wallby (red) Människor och matematik läsebok för nyfikna. NCM, Göteborgs universitet. Gennow, S. & Wallby, K. (2010). Geometri och rumsuppfattning med Känguruproblem. NCM, Göteborgs universitet. Hagland, K., Hedrén, R. & Taflin, E. (2005). Rika matematiska problem inspiration till variation. Stockholm: Liber. Kiselman, C. & Mouwitz, L. (2008). Matematiktermer för skolan. NCM, Göteborgs universitet. McIntosh, A. (2008). Förstå och använda tal. NCM, Göteborgs universitet. Rystedt, E. &Trygg, L. (2010). Laborativ matematikundervisning vad vet vi? NCM, Göteborgs universitet. Nämnaren. I varje nummer finns Problemavdelningen och Kängurusidan. Läs också tidigare artiklar kring problemlösning. Nämnarenartiklar publicerade finns fritt tillgängliga som pdf-dokument på Nämnaren på nätet, namnaren.ncm.gu.se. Du finner dem via artikeldatabasen. Under ArkivN finns alla publicerade Uppslag och Problemavdelningar samlade. Nämnaren på nätet presenterar varje månad nya problem under rubriken Månadens problem. Strävorna finns på ncm.gu.se/stravorna. Där finns aktiviteter, problem och artiklar samlade och ordnade efter kursplanens beskrivning av matematikämnets syfte och mål. Kungl Vetenskapsakademien & NCM/Nämnaren 9
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. De flesta problem kan lösas på flera sätt och med olika representationsformer.
Kängurun Matematikens hopp Ecolier 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. De flesta problem kan lösas på flera sätt och med olika representationsformer.
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurutävlingen 2017 NCM 1
 Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Arbeta vidare med Ecolier 2010
 Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 017, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på
Kängurun Matematikens hopp Ecolier 017, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Arbeta vidare med Milou 2008
 Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder till svaret 6.
 Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Svar och arbeta vidare med Benjamin 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Svar och korta lösningar Benjamin 2006
 3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
Svar och lösningar Benjamin
 Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt.
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurun Matematikens hopp
 Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Lösningsförslag Cadet 2014
 Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Känguru 2012 Benjamin sid 1 / 8 (åk 6 och 7)
 Känguru 2012 Benjamin sid 1 / 8 NAMN KLASS Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara den frågan. Felaktigt
Känguru 2012 Benjamin sid 1 / 8 NAMN KLASS Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara den frågan. Felaktigt
3: A I den vita asken. Kolan ligger i den röda asken så chokladbiten måste ligga i den vita. Problemet kan lösas konkret och med en enkel bild.
 Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Svar och lösningar Ecolier
 Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte.
 Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens
Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens
Arbeta vidare med Benjamin
 Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Kortfattade lösningar med svar till Cadet 2006
 3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
Svar och lösningar Benjamin
 Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A 1 9999 + 1= 10 000. Talet
Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A 1 9999 + 1= 10 000. Talet
Svar och lösningar. Kängurutävlingen 2009 Cadet för gymnasiet
 Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Svar och arbeta vidare med Cadet 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Välkommen till Kängurutävlingen Matematikens hopp 17 mars Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
4. A. 4, 6, 11 Viker man ihop till en kub, så kommer talet 1 mitt emot 3, 2 mitt emot 4 och 5 mitt emot 6. Det ger summorna 4, 6, 11.
 N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Arbeta vidare med Junior 2010
 Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 4 C: kvadrat Exempel på hur formerna kan konstrueras:
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Kängurutävlingen Matematikens Hopp Cadet 2003 Lösningar, Arbeta vidare
 Kängurutävlingen Matematikens Hopp Lösningar, Arbeta vidare Arrangeras av Många problem kan lösas på flera sätt. Följande förslag ger inte någon heltäckande beskrivning. Diskutera olika lösningsförslag
Kängurutävlingen Matematikens Hopp Lösningar, Arbeta vidare Arrangeras av Många problem kan lösas på flera sätt. Följande förslag ger inte någon heltäckande beskrivning. Diskutera olika lösningsförslag
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant?
 En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Cadet 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Cadet 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Student 016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Kängurutävlingen Matematikens hopp Student 016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Trepoängsproblem. Kängurutävlingen 2011 Cadet. 1 Vilket av följande uttryck har störst värde? 1 A: B: C: D: E: 2011
 Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna
Sammanfattningar Matematikboken X
 Sammanfattningar Matematikboken X KAPITEL 1 TAL OCH RÄKNING Naturliga tal Med naturliga tal menas talen 0, 1,,, Jämna tal 0,,, 6, 8 Udda tal 1,,, 7 Tallinje Koordinater En tallinje kan t ex användas för
Sammanfattningar Matematikboken X KAPITEL 1 TAL OCH RÄKNING Naturliga tal Med naturliga tal menas talen 0, 1,,, Jämna tal 0,,, 6, 8 Udda tal 1,,, 7 Tallinje Koordinater En tallinje kan t ex användas för
Facit och kommentarer Ecolier 2019
 Facit och kommentarer Ecolier 2019 1 E 2 C 5+5+1+1 3 A tisdag Om det var söndag igår är det måndag idag. 4 D,, Det kvadratiska hålet kommer att hamna tre rutor från mittvikningen och då syns motorcykeln.
Facit och kommentarer Ecolier 2019 1 E 2 C 5+5+1+1 3 A tisdag Om det var söndag igår är det måndag idag. 4 D,, Det kvadratiska hålet kommer att hamna tre rutor från mittvikningen och då syns motorcykeln.
Svar och lösningar Benjamin
 Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer,
Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer,
Kortfattade lösningar med svar till Gymnasiets Cadet 2006
 Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Ecolier. Avdelning 1. Trepoängsproblem. 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6.
 Ecolier Avdelning 1. Trepoängsproblem 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6 (Ryssland) 2 Gilda har 50 kr. Hon tänker köpa fem skrivböcker som
Ecolier Avdelning 1. Trepoängsproblem 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6 (Ryssland) 2 Gilda har 50 kr. Hon tänker köpa fem skrivböcker som
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt
Kängurutävlingen Matematikens hopp Junior 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt
Södervångskolans mål i matematik
 Södervångskolans mål i matematik Mål som eleverna lägst ska ha uppnått i slutet av det första skolåret beträffande tal och taluppfattning kunna läsa av en tallinje mellan 0-20 kunna läsa och ramsräka tal
Södervångskolans mål i matematik Mål som eleverna lägst ska ha uppnått i slutet av det första skolåret beträffande tal och taluppfattning kunna läsa av en tallinje mellan 0-20 kunna läsa och ramsräka tal
1 B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3.
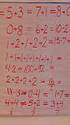 Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Lokal planering i Matematik, fskkl Moment Lokalt mål Strävansmål Metod
 Lokal planering i Matematik, fskkl. 080415 Grundläggande taluppfattning 1-10, talkamrater 1-10. Träna begrepp som före/efter, mer/mindre, hälften/dubbelt. Parbildning. Ordningstal Längd meter. Vikt kg.
Lokal planering i Matematik, fskkl. 080415 Grundläggande taluppfattning 1-10, talkamrater 1-10. Träna begrepp som före/efter, mer/mindre, hälften/dubbelt. Parbildning. Ordningstal Längd meter. Vikt kg.
Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Kängurutävlingen Matematikens hopp Junior 2016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Kängurutävlingen Matematikens hopp 2010 Benjamin för elever i åk 5, 6 och 7.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 200 Benjamin för elever i åk 5, 6 och 7. Kängurutävlingen genomförs den 8 mars. Om den dagen inte passar kan hela veckan 9 26 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 200 Benjamin för elever i åk 5, 6 och 7. Kängurutävlingen genomförs den 8 mars. Om den dagen inte passar kan hela veckan 9 26 mars användas,
5: D 3 23 kan bara fås på ett sätt: Här har man nytta av att känna igen 24 som ett tal i sexans tabell.
 Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Avdelning 1, trepoängsproblem
 Avdelning 1, trepoängsproblem 1. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Var är kängurun? A: I cirkeln och i triangeln, men inte i kvadraten. B: I cirkeln
Avdelning 1, trepoängsproblem 1. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Var är kängurun? A: I cirkeln och i triangeln, men inte i kvadraten. B: I cirkeln
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2019, facit och kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Kängurun Matematikens hopp Milou 2019, facit och kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Student 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Student 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Känguru 2013 Junior sida 1 / 8 (gymnasiet åk 1) i samarbete med Jan-Anders Salenius vid Brändö gymnasium
 Känguru 2013 Junior sida 1 / 8 NAMN KLASS / GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Felaktigt svar ger minus 1/4 poäng av uppgiftens totala
Känguru 2013 Junior sida 1 / 8 NAMN KLASS / GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Felaktigt svar ger minus 1/4 poäng av uppgiftens totala
Lösningsförslag Junior 2014
 Kängurutävlingen 014 Junior, svar och lösningar Lösningsförslag Junior 014 1 E: c < b < a Längden av linje a är 16 l.e., linje b (8 + ) l.e. och linje c (8+4 p ) l.e. Alternativ lösning: Grundfiguren har
Kängurutävlingen 014 Junior, svar och lösningar Lösningsförslag Junior 014 1 E: c < b < a Längden av linje a är 16 l.e., linje b (8 + ) l.e. och linje c (8+4 p ) l.e. Alternativ lösning: Grundfiguren har
Bagarmossens skolas kravnivåer beträffande tal och talens beteckningar som eleven ska ha uppnått efter:
 Matematik 1-5 Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och
Matematik 1-5 Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Välkommen till. Kängurutävlingen Matematikens hopp 2009 Student för elever på kurs D och E. Kängurutävlingen 2009 Student.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 009 Student för elever på kurs D och E. Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 0 7 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 009 Student för elever på kurs D och E. Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 0 7 mars användas, däremot
Matematik Steg: Bas. Mål att sträva mot Mål Målkriterier Omdöme Åtgärder/Kommentarer
 Matematik Steg: Bas ha en grundläggande taluppfattning som omfattar naturliga tal och enkla tal i talområdet 0-10 bråk- och decimalform ordningstal upp till 5 ha en grundläggande rumsuppfattning och kunna
Matematik Steg: Bas ha en grundläggande taluppfattning som omfattar naturliga tal och enkla tal i talområdet 0-10 bråk- och decimalform ordningstal upp till 5 ha en grundläggande rumsuppfattning och kunna
Svar och arbeta vidare med Student 2008
 Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Kängurutävlingen Matematikens Hopp Benjamin 2003 Uppgifter
 Kängurutävlingen Matematikens Hopp Uppgifter Arrangeras av Kungl. Vetenskapsakademien & NCM/Nämnaren 3-poängsuppgifter 1. Tomas har 9 hundrakronors-sedlar, 9 tiokronor och 10 enkronor. Hur mycket pengar
Kängurutävlingen Matematikens Hopp Uppgifter Arrangeras av Kungl. Vetenskapsakademien & NCM/Nämnaren 3-poängsuppgifter 1. Tomas har 9 hundrakronors-sedlar, 9 tiokronor och 10 enkronor. Hur mycket pengar
Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Om Lgr 11 och Favorit matematik 4 6
 Om Lgr 11 och Favorit matematik 4 6 TYDLIG OCH MEDVETEN MATEMATIKUNDERVISNING En stark koppling mellan läroplan/kunskaps mål, innehåll och bedömning finns för att medvetande göra eleverna om syftet med
Om Lgr 11 och Favorit matematik 4 6 TYDLIG OCH MEDVETEN MATEMATIKUNDERVISNING En stark koppling mellan läroplan/kunskaps mål, innehåll och bedömning finns för att medvetande göra eleverna om syftet med
Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning
 Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning Eleven skall år 1 Begrepp Jämförelse- och storleksord, t.ex. stor, större, störst. Positionssystemet
Lokala kursplaner i Matematik Fårösunds skolområde reviderad 2005 Lokala mål Arbetssätt Underlag för bedömning Eleven skall år 1 Begrepp Jämförelse- och storleksord, t.ex. stor, större, störst. Positionssystemet
Bedömning för lärande i matematik
 HANDLEDNING TILL Bedömning för lärande i matematik FÖR ÅRSKURS 1 9 1 Handledning I denna handledning ges förslag på hur du kan komma igång med materialet Bedömning för lärande i matematik åk 1 9. Du börjar
HANDLEDNING TILL Bedömning för lärande i matematik FÖR ÅRSKURS 1 9 1 Handledning I denna handledning ges förslag på hur du kan komma igång med materialet Bedömning för lärande i matematik åk 1 9. Du börjar
Facit och kommentarer Benjamin 2019
 Facit och kommentarer Benjamin 2019 1 B 2 C 3 D 419 380 + 39 = 419 eller 380 + 20 + 19 = 419 4 C 5 E 1 Hälften av 26 barn är 13 barn. Eftersom det finns 12 pojkar i gruppen måste det som minst vara en
Facit och kommentarer Benjamin 2019 1 B 2 C 3 D 419 380 + 39 = 419 eller 380 + 20 + 19 = 419 4 C 5 E 1 Hälften av 26 barn är 13 barn. Eftersom det finns 12 pojkar i gruppen måste det som minst vara en
Delprov A Muntligt delprov
 Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Skolverkets förslag till kursplan i matematik i grundskolan. Matematik
 Matematik Matematiken har en mångtusenårig historia med bidrag från många kulturer. Den har utvecklats ur människans praktiska behov och hennes naturliga nyfikenhet och lust att utforska. Matematisk verksamhet
Matematik Matematiken har en mångtusenårig historia med bidrag från många kulturer. Den har utvecklats ur människans praktiska behov och hennes naturliga nyfikenhet och lust att utforska. Matematisk verksamhet
ESN lokala kursplan Lgr11 Ämne: Matematik
 ESN lokala kursplan Lgr11 Ämne: Matematik Övergripande Mål: formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, använda och analysera matematiska begrepp och samband
ESN lokala kursplan Lgr11 Ämne: Matematik Övergripande Mål: formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, använda och analysera matematiska begrepp och samband
Arbeta vidare med aritmetik 2018
 Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Benjamin. Avdelning 1. Trepoängsproblem
 Avdelning 1. Trepoängsproblem Benjamin 1 Greta promenerar längs stigen från vänster till höger. När stigen delar sig måste hon välja den ena stigen. Hon vänder inte och går tillbaka. Längs stigen hittar
Avdelning 1. Trepoängsproblem Benjamin 1 Greta promenerar längs stigen från vänster till höger. När stigen delar sig måste hon välja den ena stigen. Hon vänder inte och går tillbaka. Längs stigen hittar
= A: 0 B: 1 C: 2013 D: 2014 E: 4028
 Trepoängsproblem 1. 2014 2014 2014 2014 = A: 0 B: 1 C: 2013 D: 2014 E: 4028 2. Kängurutävlingen hålls den tredje torsdagen i mars varje år. Vilket datum är det senaste som tävlingen kan hållas? A: 14 mars
Trepoängsproblem 1. 2014 2014 2014 2014 = A: 0 B: 1 C: 2013 D: 2014 E: 4028 2. Kängurutävlingen hålls den tredje torsdagen i mars varje år. Vilket datum är det senaste som tävlingen kan hållas? A: 14 mars
Lgr 11 matriser i Favorit matematik 4 6
 Lgr 11 matriser i Favorit matematik 4 6 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla förmågan att De matematiska förmågor
Lgr 11 matriser i Favorit matematik 4 6 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla förmågan att De matematiska förmågor
Junior för elever på kurs Ma 2 och Ma 3
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Junior för elever på kurs Ma 2 och Ma 3 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Junior för elever på kurs Ma 2 och Ma 3 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Trepoängsproblem. Kängurutävlingen 2012 Junior
 Trepoängsproblem 1. M och N är mittpunkterna på de lika långa sidorna i en likbent triangel. Hur stor är arean av fyrhörningen markerad med X? : 3 : 4 C: 5 D: 6 E: 7 M? X 3 3 6 N 2. När lice skickar ett
Trepoängsproblem 1. M och N är mittpunkterna på de lika långa sidorna i en likbent triangel. Hur stor är arean av fyrhörningen markerad med X? : 3 : 4 C: 5 D: 6 E: 7 M? X 3 3 6 N 2. När lice skickar ett
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Student 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Student 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Lokala mål i matematik
 Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
5: B grön Någon har den gröna ryggsäcken och det är inte Anna (och inte Maja), så det måste vara Tom.
 Kängurutävlingen 2018 Ecolier, svar och kommentarer Facit Ecolier 1: E 6 2: B 6 Liam behöver 0, 1, 2, 3, 5 och 8. 3: C 18 Syskonen är 5 år, 6 år och 7 år, 5 + 6 + 7 = 18 4: E 5 Om skruv 5 hade varit lika
Kängurutävlingen 2018 Ecolier, svar och kommentarer Facit Ecolier 1: E 6 2: B 6 Liam behöver 0, 1, 2, 3, 5 och 8. 3: C 18 Syskonen är 5 år, 6 år och 7 år, 5 + 6 + 7 = 18 4: E 5 Om skruv 5 hade varit lika
22,5 högskolepoäng. Provmoment: Ladokkod: Tentamen ges för: Matematik 3hp. Studenter i inriktningen GSME. TentamensKod:
 SMID Provmoment: Ladokkod: Tentamen ges för: TentamensKod: Matematik 3hp Studenter i inriktningen GSME 22,5 högskolepoäng Tentamensdatum: 12-08-30 Tid: 09.00-13.00 Hjälpmedel: Inga Totalt antal poäng på
SMID Provmoment: Ladokkod: Tentamen ges för: TentamensKod: Matematik 3hp Studenter i inriktningen GSME 22,5 högskolepoäng Tentamensdatum: 12-08-30 Tid: 09.00-13.00 Hjälpmedel: Inga Totalt antal poäng på
formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder,
 Arbetsområde: Huvudsakligt ämne: Matematik, åk 4-6 Läsår: Tidsomfattning: Ämnets syfte Undervisning i ämnet matematik syftar till: länk Följande syftesförmågor för ämnet ska utvecklas: formulera och lösa
Arbetsområde: Huvudsakligt ämne: Matematik, åk 4-6 Läsår: Tidsomfattning: Ämnets syfte Undervisning i ämnet matematik syftar till: länk Följande syftesförmågor för ämnet ska utvecklas: formulera och lösa
Välkommen till Kängurun Matematikens hopp 2008 Benjamin
 Till läraren Välkommen till Kängurun Matematikens hopp 2008 enjamin Kängurutävlingen genomförs april. Om den dagen inte passar går det bra 4 april eller veckan därpå, däremot inte tidigare. Se till att
Till läraren Välkommen till Kängurun Matematikens hopp 2008 enjamin Kängurutävlingen genomförs april. Om den dagen inte passar går det bra 4 april eller veckan därpå, däremot inte tidigare. Se till att
Trepoängsproblem. Kängurutävlingen 2011 Junior
 Trepoängsproblem 1 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen börjar och slutar med ett vitt streck. På Storgatan har ett övergångsställe totalt åtta vita
Trepoängsproblem 1 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen börjar och slutar med ett vitt streck. På Storgatan har ett övergångsställe totalt åtta vita
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2016, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2016, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Avdelning 1, trepoängsproblem
 Avdelning, trepoängsproblem. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Stjärnan i figuren har bildats av 2 identiska, liksidiga trianglar. Stjärnans omkrets
Avdelning, trepoängsproblem. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Stjärnan i figuren har bildats av 2 identiska, liksidiga trianglar. Stjärnans omkrets
Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas, däremot
