3: A I den vita asken. Kolan ligger i den röda asken så chokladbiten måste ligga i den vita. Problemet kan lösas konkret och med en enkel bild.
|
|
|
- Adam Berglund
- för 7 år sedan
- Visningar:
Transkript
1 Svar och lösningar 1: D Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett jämnt eller udda tal? Vilket grundläggande samband är det ett resultat av? 2: B I cirkeln och kvadraten, men inte i triangeln. Här handlar det dels om att benämna de tre geometriska formerna och att kunna se att kängurun är i både cirkeln och kvadraten. 3: A I den vita asken. Kolan ligger i den röda asken så chokladbiten måste ligga i den vita. Problemet kan lösas konkret och med en enkel bild. 4: C 3 Det finns flera sätt att få ett palindromtal, men alla kräver att vi tar bort åtminstone tre siffror: Vi kan få 12321, 13331, : D 8 Lös uppgiften konkret med klotsar eller markörer av något slag och gör en tabell över hur antalet ökar. Resonera om att det från början är 16 pojkar fler och att flickorna närmar sig pojkarnas antal med 2 i veckan, alltså tar det 8 veckor tills de blir lika många. 6: D 240 m Halva brons längd ligger på flodens stränder totala längden som är 240 m. = m är hälften av den 7: C 46 dm Om plattorna ligger kant mot kant är det lika långt mellan två mittpunkter som från kant till kant på en platta. Alltså 5 plattlängder och 4 plattbredder. Varför bara 4 bredder? 5 6 dm dm = 46 dm. Jämför med 10 3 dm dm. 8: E 65 cm 2 Den vita rektangeln, överlappningen, 80 cm 2 37 cm 2 = 43 cm cm 2 43 cm 2 = 65 cm 2. 9: D 6 cm Figurernas omkrets är 36 cm. Triangelns sida är därför 36 3 cm = 12cm. Rektangelns långsida är också 12 cm och därmed är kortsidan 6 cm. 12 cm + 6 cm = 18 cm, 2 18 cm= 36 cm. Kungl Vetenskapsakademien & NCM/Nämnaren 2
2 10: B Katterna är hälften så många som hundarna. Gör en tabell över ett antal katt-tassar och motsvarande hund nosar och se efter hur många katter respektive hundar det motsvarar. T ex så här: katt-tassar katter hundnosar hundar Man kan också resonera sig fram: Eftersom en katt har fyra gånger så många tassar som hunden har nos så hade katterna varit lika många om antalet tassar varit fyra gånger så stort som antalet nosar. Nu är antalet tassar bara dubbelt så stort, dvs hälften så mycket. Problemet kan ge upphov till diskussion kring hur mycket hälften av hälften är etc. 11: D David Tillsammans har de fyra pojkarna = 10 platspoäng. Det är alltså Carlo som blev nummer 4, eftersom de andra tre tillsammans får 6. Då = 6 är det Boris som blev tvåa. Boris var bättre än Anders, så det kan inte vara Anders som vann. Det måste vara David. 12: C 6 Vi kan jämföra summorna i raderna och kolumnerna: + + = = 9 Alltså är 2 mer än. + + = = 11 Alltså är 1 mer än Om vi byter ut i första raden får vi tre =12, alltså är =4 Sen kan vi lösa ut de andra figurerna: =3, = = 6 Ersätt figurerna med bokstäver: x, y och z och skriv ner samband, t ex: x + y + x = 11 och x + y + y = 10 innebär att y = x 1 x + y + x = 11 och x + z + x = 9 innebär att z = y 2 Problemet lämpar sig bra för att låta eleverna bekanta sig med lösningar av ekvationssystem. Kungl Vetenskapsakademien & NCM/Nämnaren 3
3 13: C 48 cm 2 Det vita området består av fyra småkvadrater om vardera 4 cm 2, dvs 16 cm 2, och en stor kvadrat med sidan 6 cm, dvs 36 cm 2. Den stora vita kvadraten får man genom att tänka sig en förflyttning av de fyra likbenta trianglarna så att de möts i en gemensam mittpunkt. Detta kan förstås utföras konkret. 16 cm cm 2 = 52 cm cm 2 52 cm 2 = 48 cm 2. 14: C 45 Den största kub vi kan använda har sidan 10 cm, eftersom det är den största gemensamma faktorn i 30 och 50. Använder vi sådana kuber behöver vi 3 x 3 x 5 st. Gör en bild eller illustrera konkret. Vi kan förstås använda kuber med sidan 5 och 1 cm också, men då går det åt flera. 15: C 48 cm 2 Fyrhörningen kan delas i två rätvinkliga trianglar ADB och DBC. Triangeln ADB har arean tillsammans 31,5 cm ,5 cm 2 =48 cm 2. cm 2 och triangeln DBC har arean cm2, 16: D Kort nummer 2 ligger i ask B Den totala summan på korten är 36, så summan i en ask ska vara 18. För att få summan 18 med tre kort kan vi inte använda korten 1 eller 2. Om vi tar kort 7 och kort 8 måste det tredje kortet vara 3, alltså ligger kort 2 i alla tänkbara fall i ask B. Det finns olika sätt att få summan 18: ; ; Undersök de andra alternativen också, inget av dem gäller alltid. 17: A A I rutan mellan B och C i övre raden kan vi antingen skriva D eller A. Oavsett vad vi väljer kommer vi att få A i den markerade rutan. 18: A 5 Här finns det flera strategier att använda. Resonera: Vi vet att det blir en 45 och en 36 över. Vi vet alltså att alla skostorlekar ligger inom detta intervall. För att få så få personer som möjligt utgår vi från att så många som möjligt att två storlekars skillnad, , , , och eller: , , , och Åtminstone en person har bara ett nummers skillnad (eftersom vi får över ett jämnt och ett udda nummer). Vi klarar att para ihop detta med 5 personer, vilket är det minsta alternativet Kungl Vetenskapsakademien & NCM/Nämnaren 4
4 19: C 17 För att summan av de tre talen på varje sidan ska bli densamma, måste talen vid hörnen runt mitten av kroppen vara desamma, dvs 5 och talen i topp- och bottenspetsen desamma, dvs 1. Pröva att sätta in andra tal det går inte, vilket kan bli uppenbart om man provar. 20: D 20 Ifylld kommer tabellen se ut så här: I tabellen framträder ett mönster med dubbleringar och halveringar. Vad beror dessa på? Kalla de första talen a respetive b. a a + b b a b (a + b) + (a b) = 2a (a + b) (a b) = 2b etc Sådana här överblickbara och lätt kontrollerbara samband är bra att använda som utgångspunkt för att visa styrkan i att använda generella uttryck. 21: C kan skrivas som vilket gör att de enda möjliga rektanglarna, dvs multiplikationer med två heltalsfaktorer, är (och ); (287 7) och (41 49), dvs 3 st. Alternativet 6 finns inte med, vi betraktar som samma rektangel som För att finna dessa faktorer kan man resonera, pröva sig fram och använda uteslutningsmetoden är inte delbart med 2, 3, 4, 5 eller 6. Det kan vi relativt enkelt konstatera. Det första tal vi behöver prova med är 7, och 7 är en faktor som ger 287 som den andra faktorn. Vi behöver då bara undersöka 287, där vi med samma resonemang kan utesluta 2, 3, 4, 5, och 6, så att 7 är det första vi behöver prova. 7 går fint och ger 41 som faktor. Nu har vi tre primtal och saken är klar. Kungl Vetenskapsakademien & NCM/Nämnaren 5
5 Kängurutävlingen 2009 Arbeta vidare med Benjamin Vi hoppas att arbetet med lösningarna har givit upphov till många bra diskussioner och också intressanta frågor. Kanske har ni tillsammans utvecklat frågeställningarna och gått vidare med liknande problem. Vi har i detta dokument samlat några förslag på hur man kan arbeta vidare med problemen. Dela också gärna med dig av era egna idéer, som du kan skicka till kanguru@ncm.gu.se eller på papper till Kängurun, NCM Göteborgs universitet, Box 160, Göteborg. I samband med det gemensamma arbetet kan det vara lämpligt att uppmärksamma terminologin och passa på att lyfta fram vad de olika termerna innebär. Låt också eleverna själva få definiera olika begrepp. För definitioner hänvisar vi till den nyutkomna Matematiktermer för skolan (Kiselman & Mouwitz, 2008). Många problem återkommer i olika skepnader år från år. Bland de gamla problemen finns också förslag till hur de kan utvecklas. Alla gamla problem och dessa förslag finns tillgängliga på Kängurusidan på ncm.gu.se och är helt fria att använda. Tal Några problem handlar om grundläggande talkunskaper, B 1, B 10, B 11, B 16. Udda och jämna tal B 1 behandlar udda och jämna tal. Betona att jämna tal är multiplar av 2. Vad får det för konsekvenser om ett tal är udda eller jämnt? Denna bakgrund kan man bygga vidare på för att utveckla elevernas förståelse för vilka entalssiffror som blir resultatet av olika multiplikationer. Sådan talkunskap är värdefull t ex när man ska pröva tals delbarhet. Hälften och dubbelt Problem 10 aktualiserar dubblering och halvering. Att dubblera och ta hälften har barn i den här åldern oftast inga problem med. Däremot kan språkliga formuleringar med hälften så många uppfattas som problematiska och svåra att hantera om det är okänt vad det är hälften av. Ex: Kalle har sparat hälften så mycket som Siv och tillsammans har de sparat ihop 474 kr. Hur mycket har Kalle sparat? Siv? Låt eleverna själva formulera liknande problem, då ser de hur delarna förhåller sig till helheten. Variera också med andra delar, tredjedelar, fjärdedelar etc, så att det blir tydligt hur relationen ser ut. Illustrera konkret. Successiv dubblering användes i gamla algoritmer för multiplikation, t ex i det som kallas egyptisk multiplikation och i den ryske bondens metod. Exempel = = = = = = , så = = 1472 Låt eleverna använda denna metod för att utföra multiplikationer. Kungl Vetenskapsakademien & NCM/Nämnaren 1
6 Börja på 1 och dubblera successivt: 1, 2, 4, 8, 16, 32, Den talföljden kommer eleverna att möta många gånger. Låt eleverna skriva talen som produkter av 2, och diskutera hur skrivsättet skulle kunna förenklas. Det kan vara ett lämpligt sammanhang för att introducera potensskrivning. Inte för att eleverna nu måste kunna det, utan för att de i ett sammanhang som de är engagerad i ser användningen. Nästa gång de ser det skrivsättet kanske de känner igen det. Det är bra att få möta procedurer, konventioner och begrepp innan man måste kunna dem. Börja på 1 och halvera successivt 1, 1 2, 1 4, 1 8, 1 Jämför dubbleringen och halveringen. 16 Vad skulle vi få om vi adderade alla dessa delar: ? Okända tal Att förbereda arbetet med ekvationslösning genom att ersätta tal med rutor eller figurer förekommer redan i de första skolåren. Det kan vi fortsätta med och göra parallellt med att använda bokstäver så att eleverna uppmärksammas på att det inte är bokstaven i sig som är det väsentliga. Många elever blir rädda så fort de ser ett x, men har inga problem med en ruta. Utgå från enkla ekvationssystem och ersätt inledningsvis bokstäverna med figurer och presentera dem på motsvarande sätt som i problem 12. Lägg sedan till några koefficienter. Ersätt sedan figurerna med bokstäver och presentera uttrycken så som vi vanligen skriver ett ekvationssystem. I det här problemet finns det tre obekanta och fyra olika ekvationer, men det hade räckt med tre ekvationer. Pröva att ta bort någon av ekvationerna och lös problemet. B 19 handlar också om att hitta ett okänt tal. Kalla de okända hörnen för a, b och c och lös ekvationssystemet. Faktorisering, primtal Problem 21 handlar om hur talet 2009 kan faktoriseras. Låt eleverna systematiskt faktorisera talen upp till t ex 150. Vilka faktorer behöver man pröva? Varför är det ingen idé att pröva med 2 om entalssiffran är 3? Med 5 om entalssiffran är 4 eller 7? Hur stora faktorer behöver man pröva? Varför räcker det med upp till 6 om talet är 35? Diskutera gemensamt efteråt vilka slutsatser man kan dra. Vad är det för speciellt med primtalen? Presentera Erathostenes såll för eleverna. Undersök och diskutera några av de vanliga delbarhetsreglerna, t ex delbarhet med 2, 3, 4, 5, 9, och 10, 100, Tals uppdelning Problem B 11 och B 16 leder in på diskussioner om heltals uppdelning. B 11 handlar om att dela upp talet 6 som en summa av tre olika tal och talet 10 som en summa av Vilka tal kan vi dela upp på detta sätt? Undersök triangeltalen, de är grundläggande och eleverna kommer att möta dem i olika sammanhang framöver. I problem B 16 är det summan som vi arbetar med. Se också E 8. Arbeta med att skriva tal som summor av olika ensiffriga tal, som summor av tre olika ensiffriga tal. Vilket är det största tal vi kan skriva som en summa av tre ensiffriga tal? Kungl Vetenskapsakademien & NCM/Nämnaren 2
7 Mönster i talserier I problem 20 ser vi ett intressant mönster. Att se efter mönster i talserier är ett lekfullt sätt att utveckla god taluppfattning. Presentera talserier, t ex: 1, 2, 4, 7, ; 0, 3, 8, 15, 24...; 1, 1, 2, 1, 3, 2, 5, 3, 8... Kan det finnas olika möjliga fortsättningar? Olika sätt att se som ger samma resultat? Låt eleverna göra egna serier att utmana varandra med. Be dem att själva skriva ner seriens regler innan de lämnar över till kamraten. Venndiagram Med utgångspunkt från problem 2 kan Venndiagram presenteras. Sådana arbetade man med under den tid som mängdläran hade en framskjuten roll inom matematikundervisningen, men Venndiagram är användbara och borde kunna användas mer för att t ex illustrera relationer inom och mellan olika mängder. Undersök talen upp till ca 30 och sortera dem i kategorier: udda tal, tal delbara med 3 och tal delbara med 7. Gör tre ringar, med blyertspenna eller med snöre och märk dem med dessa egenskaper. Placera ut talen på rätt plats. Hur ska ringarna överlappa varandra? Eventuellt kommer man att få rita om sin bild eller flytta sina snören. Var ska man placera 14? 6? 21? Se också Uppslaget i Nämnaren 3, Geometri Några grundläggande samband Vi behöver ha vissa grundläggande faktakunskaper, t ex att en rektangel är en fyrhörning där alla vinklar är räta, och alltså motstående sidor parallella (vilket också innebär att en kvadrat är en rektangel). För att eleverna ska lära sig att urskilja det som är väsentligt bör vi tänka på att orientera figuren åt olika håll. En kvadrat kan stå på ett hörn, det förändrar inte vinklarnas storlek eller sidornas längder. En triangel måste inte stå på sin bas och en trubbvinklig triangel kan ha en höjd som ligger utanför figuren. Undersök figuren i B 13 och hitta och namnge olika geometriska former. Beroende på hur områdena delas kan vi finna olika former, försök att hitta så många som möjligt. Hur kan vi fastställa att ett område är av en viss form, t ex en kvadrat, utan att mäta. Låt eleverna arbeta med att definiera andra geometriska figurer de känner till. Uppmuntra dem att vara så precisa och utförliga som möjligt. Ställ frågor som hjälper eleverna att se de avgörande skillnaderna och likheterna mellan olika former, t ex varför är inte detta en rektangel? För definitioner hänvisar vi till den nyutkomna Matematiktermer för skolan (Kiselman & Mouwitz, 2008). B 6 och B 7 rör mätning av sträckor. Ett liknande problem som B 7 fanns 2007, B 16. Centralt i dessa är mittpunkten. Som vanligt handlar några problem om enkla formers area och omkrets B 8, B 9, B 13 och B 15. Ge eleverna en given omkrets och låt dem konstruera en figur med så stor och en med så liten area som möjligt. Gör motsvarande undersökning med en given area. Kungl Vetenskapsakademien & NCM/Nämnaren 3
8 Grundläggande konstruktioner, Triangelns area, som hälften av en rektangel, är en del av lösningen i B 15. Den kan undersökas på geobräde. Då kan formen på triangeln lätt varieras när den grundläggande relationen gjorts trolig. Låt eleverna skapa egna trianglar och sedan försöka beräkna arean. Be dem att motivera lösningen med andra argument än att det ser man. Två- och tredimensionella konstruktioner Att kunna uppfatta de tre dimensionerna i en tvådimensionell bild, som i B 19, är förvånansvärt svårt för många elever. Det är en förmåga som måste bygga på konkreta erfarenheter och utvecklas med hjälp av samtal och att eleverna uppmärksammas på hur djupet vi kan se i verkligheten överförs till platta bilder. B 9 handlar om en tvådimensionell figur, som kallas ett torn. Vanligtvis är ett torn tredimensionellt. Hur skulle ett sådant torn kunna se ut? Diskutera kanter, sidoytor, antal hörn och beräkna byggets volym. Att kunna bedöma hur många klossar som finns i ett bygge, B 14, är en viktig grund för volymbegreppet. Hjälp eleverna att utveckla påbyggbara strategier för att beräkna antalet, så att de systematiserar sina beräkningar radvis och kolumnvis. Att räkna antalet på ett ostrukturerat vis leder inte till förståelse för de grundläggande formlerna för area och volym. Den måste bygga på konkret erfarenhet av att systematiskt räkna antalet. Låt eleverna bygga olika kroppar med kuber och rita dem från olika håll. Prata om vad man ser och hur det ser ut. En modell som kan användas är att bygga med multilink, olikfärgade kuber, och sen rita bygget från fyra håll: framifrån, bakifrån, från vänster och från höger. Varje bygge beskrivs alltså av fyra ritningar. Eleverna kan arbeta i par och sen byta ritningar med ett par kamrater, som får i uppgift att bygga efter ritningarna. Att rita tredimensionellt är inte lätt och eleverna behöver få ledning och stöd för det. Använd gärna ett isometriskt prickpapper, som finns att hämta på ncm.gu.se/node/2281 Låt eleverna rita av något i omgivningen från ett annat perspektiv än de kan se, t ex huset ovanifrån. Använd tidningsbilder och låt dem rita motivet så som det skulle sett ut från ett annat håll. (Se Nämnaren 2, Matematiken i bilden eller bilden i matematiken). Problem med klossbyggen har funnits i Kängurun varje år, i flera olika klasser. I årets omgång kan E 4 och S 9 vara intressanta att arbeta vidare med. I Milou finns också ett problem kring klossbygge. Det handlar om att tolka en speciell sorts ritning: Kungl Vetenskapsakademien & NCM/Nämnaren 4
9 Problemlösningstrategier Gör en bild och systematisera Problem 3 löser man lättare med en enkel skiss över de tre askarna. Liknande problem har varit med många gånger, och de har ofta relativt hög lösningsprocent. Kanske beror det på att eleverna systematiserar sin lösning. Här handlar det också om att verkligen läsa och förstå informationen i uppgiften, och för många är det nödvändigt att organisera denna information på ett överskådligt sätt. Det blir för mycket att hålla i huvudet. En del elever har stora svårigheter med läsningen och de kan behöva arbeta extra mycket med den här typen av uppgifter, och få stöd för hur de ska hantera informationen. Arbeta gärna gemensamt med liknande problem och diskutera allteftersom hur informationen som ges ska hanteras. För att lösa B 5 kan flera olika strategier komma till användning: t ex göra en tabell, föra resonemang, sätta upp en ekvation. Genom att lösa problem på olika sätt och jämföra resultatet kan eleverna få djupare förståelse. Ekvationens tal och symboler kan återfinnas i tabellen, och det resonemang man för kan ses i tabellen och i symbolerna. Lyft fram dessa samband så att det blir tydligt att det inte är olika lösningar utan olika sätt att genomföra och beskriva lösningen. B 10 aktualiserar frågor om proportionalitet, relationen mellan tassar och nosar är densamma hela tiden. Vilket skulle förhållandet mellan katt-tassar och hundnosar vara om de andra alternativen vore korrekta? Ett liknande problem, men med en annan frågeställning är E 14, som är en variant av det klassiska problemet med höns och får. B 17, B 18 och B 19 handlar alla om logiska resonemang. I B 17 behöver man inte fylla i alla rutor för att komma fram till ett svar. Hur kan man resonera? En något svårare variant är J 7. I B 19 kan man prova att flytta ettan till ett annat hörn. Byt plats på ettan och femman. Undersök under vilka förutsättningar som problemet är lösbart. Undersök en oktaeder på motsvarande sätt. Litteratur Hagland, K. (2007). Rita en bild. I Nämnaren 34(3), s Kiselmn, C. & Mouwitz, L. (2008). Matematiktermer för skolan. NCM, Göteborgs universitet. McIntosh, A. (2008). Förstå och använda tal. NCM, Göteborgs universitet. Nämnarenartiklar publicerade finns fritt tillgängliga som pdf-dokument på Nämnaren på nätet, namnaren.ncm.gu.se. Du finner dem via artikeldatabasen. Under ArkivN finns alla publicerade Uppslag och Problemavdelningar samlade. Alla tidigare Känguruproblem finns på Kängurusidan: ncm.gu.se/kanguru Kungl Vetenskapsakademien & NCM/Nämnaren 5
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
5: D 3 23 kan bara fås på ett sätt: Här har man nytta av att känna igen 24 som ett tal i sexans tabell.
 Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Avdelning 1, trepoängsproblem
 Avdelning 1, trepoängsproblem 1. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Var är kängurun? A: I cirkeln och i triangeln, men inte i kvadraten. B: I cirkeln
Avdelning 1, trepoängsproblem 1. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Var är kängurun? A: I cirkeln och i triangeln, men inte i kvadraten. B: I cirkeln
Arbeta vidare med Milou 2008
 Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Svar och arbeta vidare med Benjamin 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Svar och lösningar. Kängurutävlingen 2009 Cadet för gymnasiet
 Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Kängurutävlingen 2017 NCM 1
 Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Avdelning 1, trepoängsproblem
 Avdelning, trepoängsproblem. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Stjärnan i figuren har bildats av 2 identiska, liksidiga trianglar. Stjärnans omkrets
Avdelning, trepoängsproblem. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Stjärnan i figuren har bildats av 2 identiska, liksidiga trianglar. Stjärnans omkrets
Arbeta vidare med Ecolier 2010
 Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Svar och arbeta vidare med Cadet 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte.
 Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder till svaret 6.
 Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Lösningsförslag Cadet 2014
 Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Problem Svar
 Känguru Benjamin, svarsblankett Namn Klass/Grupp Poängsumman Känguruskuttet Ta lös svarsblanketten. Skriv ditt svarsalternativ under numret. Lämna rutan tom om du inte vet svaret. Gissa inte, felaktigt
Känguru Benjamin, svarsblankett Namn Klass/Grupp Poängsumman Känguruskuttet Ta lös svarsblanketten. Skriv ditt svarsalternativ under numret. Lämna rutan tom om du inte vet svaret. Gissa inte, felaktigt
Välkommen till Kängurutävlingen Matematikens hopp 17 mars Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt.
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
4. A. 4, 6, 11 Viker man ihop till en kub, så kommer talet 1 mitt emot 3, 2 mitt emot 4 och 5 mitt emot 6. Det ger summorna 4, 6, 11.
 N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
PLANGEOMETRI I provläxa med facit ht18
 PLANGEOMETRI I provläxa med facit ht18 På det här avsnittet kommer du i första hand att utveckla din begrepps metod och kommunikations förmåga. Det är nödvändigt att ha en linjal för att klara avsnittet.
PLANGEOMETRI I provläxa med facit ht18 På det här avsnittet kommer du i första hand att utveckla din begrepps metod och kommunikations förmåga. Det är nödvändigt att ha en linjal för att klara avsnittet.
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Svar och lösningar Benjamin
 Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt
Kängurutävlingen Matematikens hopp Junior 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt
Avdelning 1, trepoängsproblem
 Avdelning, trepoängsproblem. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Stjärnan i figuren har bildats av 2 identiska, liksidiga trianglar. Stjärnans omkrets
Avdelning, trepoängsproblem. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Stjärnan i figuren har bildats av 2 identiska, liksidiga trianglar. Stjärnans omkrets
Arbeta vidare med Benjamin
 Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Svar och korta lösningar Benjamin 2006
 3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant?
 En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
Kortfattade lösningar med svar till Cadet 2006
 3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. De flesta problem kan lösas på flera sätt och med olika representationsformer.
Kängurun Matematikens hopp Ecolier 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. De flesta problem kan lösas på flera sätt och med olika representationsformer.
Kängurun Matematikens hopp
 Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Trepoängsproblem. Kängurutävlingen 2011 Cadet. 1 Vilket av följande uttryck har störst värde? 1 A: B: C: D: E: 2011
 Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Arbeta vidare med Junior 2010
 Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Svar och lösningar Benjamin
 Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A 1 9999 + 1= 10 000. Talet
Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A 1 9999 + 1= 10 000. Talet
Svar och arbeta vidare med Student 2008
 Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 4 C: kvadrat Exempel på hur formerna kan konstrueras:
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Arbeta vidare med Milou
 Kängurutävlingen 2009 Arbeta vidare med Milou Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. När ni nu diskuterar lösningarna kan ni också kontrollera
Kängurutävlingen 2009 Arbeta vidare med Milou Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. När ni nu diskuterar lösningarna kan ni också kontrollera
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Student 016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Kängurutävlingen Matematikens hopp Student 016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
1 B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3.
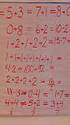 Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Matematik. Mål att sträva mot. Mål att uppnå. År 1 Mål Kriterier Eleven ska kunna. Taluppfattning koppla ihop antal och siffra kan lägga rätt antal
 Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas, däremot
Kortfattade lösningar med svar till Gymnasiets Cadet 2006
 Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Välkommen till. Kängurutävlingen Matematikens hopp 2016 Milou, för elever i förskoleklass åk 2. Till läraren. Lycka till med årets Känguru!
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Milou, för elever i förskoleklass åk 2 Syftet med Kängurun är att skapa intresse för matematik med hjälp av intressanta problem. Vår
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Milou, för elever i förskoleklass åk 2 Syftet med Kängurun är att skapa intresse för matematik med hjälp av intressanta problem. Vår
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Cadet 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Cadet 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Svar och lösningar Ecolier
 Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Trepoängsproblem. Kängurutävlingen 2011 Junior
 Trepoängsproblem 1 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen börjar och slutar med ett vitt streck. På Storgatan har ett övergångsställe totalt åtta vita
Trepoängsproblem 1 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen börjar och slutar med ett vitt streck. På Storgatan har ett övergångsställe totalt åtta vita
Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
2. 1 L ä n g d, o m k r e t s o c h a r e a
 2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
22,5 högskolepoäng. Provmoment: Ladokkod: Tentamen ges för: Matematik 3hp. Studenter i inriktningen GSME. TentamensKod:
 SMID Provmoment: Ladokkod: Tentamen ges för: TentamensKod: Matematik 3hp Studenter i inriktningen GSME 22,5 högskolepoäng Tentamensdatum: 12-08-30 Tid: 09.00-13.00 Hjälpmedel: Inga Totalt antal poäng på
SMID Provmoment: Ladokkod: Tentamen ges för: TentamensKod: Matematik 3hp Studenter i inriktningen GSME 22,5 högskolepoäng Tentamensdatum: 12-08-30 Tid: 09.00-13.00 Hjälpmedel: Inga Totalt antal poäng på
Välkommen till. Kängurutävlingen Matematikens hopp 2009 Student för elever på kurs D och E. Kängurutävlingen 2009 Student.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 009 Student för elever på kurs D och E. Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 0 7 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 009 Student för elever på kurs D och E. Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 0 7 mars användas, däremot
ARBETSPLAN MATEMATIK
 ARBETSPLAN MATEMATIK Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt värdera
ARBETSPLAN MATEMATIK Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt värdera
Matematik 92MA41 (15hp) Vladimir Tkatjev
 Matematik 92MA41 (15hp) Vladimir Tkatjev Med anledning av de nya kursplanerna har Strävorna reviderats. Formen, en matris med rutor, är densamma men istället för att som tidigare anknyta till mål att sträva
Matematik 92MA41 (15hp) Vladimir Tkatjev Med anledning av de nya kursplanerna har Strävorna reviderats. Formen, en matris med rutor, är densamma men istället för att som tidigare anknyta till mål att sträva
Delprov A Muntligt delprov
 Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
Kängurutävlingen Matematikens hopp 2010 Benjamin för elever i åk 5, 6 och 7.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 200 Benjamin för elever i åk 5, 6 och 7. Kängurutävlingen genomförs den 8 mars. Om den dagen inte passar kan hela veckan 9 26 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 200 Benjamin för elever i åk 5, 6 och 7. Kängurutävlingen genomförs den 8 mars. Om den dagen inte passar kan hela veckan 9 26 mars användas,
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Arbeta vidare med aritmetik 2018
 Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Svar och lösningar Benjamin
 Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer,
Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer,
Bedömning för lärande i matematik
 HANDLEDNING TILL Bedömning för lärande i matematik FÖR ÅRSKURS 1 9 1 Handledning I denna handledning ges förslag på hur du kan komma igång med materialet Bedömning för lärande i matematik åk 1 9. Du börjar
HANDLEDNING TILL Bedömning för lärande i matematik FÖR ÅRSKURS 1 9 1 Handledning I denna handledning ges förslag på hur du kan komma igång med materialet Bedömning för lärande i matematik åk 1 9. Du börjar
A: måndag B: tisdag C: onsdag D: torsdag E: fredag. Vilken av följande bitar behöver vi för att det ska bli ett rätblock?
 Trepoängsproblem 1 Doris gör en skylt till djurparken. På skylten ska det stå ordet KÄNGURUR. Hon målar en bokstav varje dag. Hon målar den första på en onsdag. Vilken dag kommer hon att måla den sista
Trepoängsproblem 1 Doris gör en skylt till djurparken. På skylten ska det stå ordet KÄNGURUR. Hon målar en bokstav varje dag. Hon målar den första på en onsdag. Vilken dag kommer hon att måla den sista
Studieplan och bedömningsgrunder i Matematik för åk 7 Moment Bedömningsgrunder för uppnåendemålen Begreppsbildning Tal och räkning
 Moment Begreppsbildning Mätningar och enheter Algebra och ekvationer Studieplan och bedömningsgrunder i Matematik för åk 7 Bedömningsgrunder för uppnåendemålen känna igen naturliga tal kunna positiva heltal:
Moment Begreppsbildning Mätningar och enheter Algebra och ekvationer Studieplan och bedömningsgrunder i Matematik för åk 7 Bedömningsgrunder för uppnåendemålen känna igen naturliga tal kunna positiva heltal:
Välkommen till Kängurutävlingen Matematikens hopp 2019 Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2019 Benjamin för elever i åk 5, 6 och 7 Tävlingen genomförs under perioden 21 mars 29 mars. Uppgifterna får inte användas tidigare. Sista
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2019 Benjamin för elever i åk 5, 6 och 7 Tävlingen genomförs under perioden 21 mars 29 mars. Uppgifterna får inte användas tidigare. Sista
Uppgifter till Första-hjälpen-lådan
 Uppgifter till Första-hjälpen-lådan Många Stockholmslärare har fått en första-hjälpen-låda i matematik då de deltagit i de kurser som letts av Karin Kairavuo, matematiklärare från Mattelandet i Helsingfors.
Uppgifter till Första-hjälpen-lådan Många Stockholmslärare har fått en första-hjälpen-låda i matematik då de deltagit i de kurser som letts av Karin Kairavuo, matematiklärare från Mattelandet i Helsingfors.
formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder,
 Arbetsområde: Huvudsakligt ämne: Matematik, åk 4-6 Läsår: Tidsomfattning: Ämnets syfte Undervisning i ämnet matematik syftar till: länk Följande syftesförmågor för ämnet ska utvecklas: formulera och lösa
Arbetsområde: Huvudsakligt ämne: Matematik, åk 4-6 Läsår: Tidsomfattning: Ämnets syfte Undervisning i ämnet matematik syftar till: länk Följande syftesförmågor för ämnet ska utvecklas: formulera och lösa
ESN lokala kursplan Lgr11 Ämne: Matematik
 ESN lokala kursplan Lgr11 Ämne: Matematik Övergripande Mål: formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, använda och analysera matematiska begrepp och samband
ESN lokala kursplan Lgr11 Ämne: Matematik Övergripande Mål: formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, använda och analysera matematiska begrepp och samband
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 017, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på
Kängurun Matematikens hopp Ecolier 017, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på
kan använda sig av matematiskt tänkande för vidare studier och i vardagslivet kan lösa problem och omsätta idéer i handling på ett kreativt sätt
 Lokal pedagogisk planering Matematik år 2 Syfte Undervisningen i matematikämnet ska syfta till att eleverna ska utveckla kunskaper om matematik och visa intresse och tilltro till sin förmåga att använda
Lokal pedagogisk planering Matematik år 2 Syfte Undervisningen i matematikämnet ska syfta till att eleverna ska utveckla kunskaper om matematik och visa intresse och tilltro till sin förmåga att använda
Kängurutävlingen 2017
 Kängurutävlingen 2017 Arbeta vidare med Ecolier 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. Låt alla först få
Kängurutävlingen 2017 Arbeta vidare med Ecolier 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. Låt alla först få
Ecolier. Avdelning 1. Trepoängsproblem. 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6.
 Ecolier Avdelning 1. Trepoängsproblem 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6 (Ryssland) 2 Gilda har 50 kr. Hon tänker köpa fem skrivböcker som
Ecolier Avdelning 1. Trepoängsproblem 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6 (Ryssland) 2 Gilda har 50 kr. Hon tänker köpa fem skrivböcker som
Lokala mål i matematik
 Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
Lokala mål i matematik År 6 År 7 År 8 År 9 Taluppfattning (aritmetik) förstår positionssystemets uppbyggnad med decimaler ex: kan skriva givna tal adderar decimaltal ex: 15,6 + 3,87 subtraherar decimaltal
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kvalificeringstävling den 30 september 2008
 SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
Avdelning 1, trepoängsproblem
 vdelning 1, trepoängsproblem 1. Hur många symmetrilinjer har figuren? : 0 : 1 : 2 D: 4 E: oändligt många 2. Robert arbetar på leksaksfabriken. Han ska packa kängurur som ska fraktas till affärerna. Varje
vdelning 1, trepoängsproblem 1. Hur många symmetrilinjer har figuren? : 0 : 1 : 2 D: 4 E: oändligt många 2. Robert arbetar på leksaksfabriken. Han ska packa kängurur som ska fraktas till affärerna. Varje
Detta prov består av del 1 och 2. Här finns också facit och förslag till poängsättning
 Allmänt om proven Detta prov består av del 1 och. Här finns också facit och förslag till poängsättning och bedömning. Provet finns på lärarwebben, dels som pdf-fil och dels som redigerbar Word-fil. Del
Allmänt om proven Detta prov består av del 1 och. Här finns också facit och förslag till poängsättning och bedömning. Provet finns på lärarwebben, dels som pdf-fil och dels som redigerbar Word-fil. Del
Gymnasiets Cadet. a: 2 b: 4 c: 5 d: 6 e: 11
 Gymnasiets Cadet Avdelning 1. Trepoängsproblem 1. I en klass finns 1 flickor och 9 pojkar. Hälften av eleverna i klassen är förkylda. Vilket är det minsta antalet flickor som är förkylda? a: 2 b: 4 c:
Gymnasiets Cadet Avdelning 1. Trepoängsproblem 1. I en klass finns 1 flickor och 9 pojkar. Hälften av eleverna i klassen är förkylda. Vilket är det minsta antalet flickor som är förkylda? a: 2 b: 4 c:
5: B grön Någon har den gröna ryggsäcken och det är inte Anna (och inte Maja), så det måste vara Tom.
 Kängurutävlingen 2018 Ecolier, svar och kommentarer Facit Ecolier 1: E 6 2: B 6 Liam behöver 0, 1, 2, 3, 5 och 8. 3: C 18 Syskonen är 5 år, 6 år och 7 år, 5 + 6 + 7 = 18 4: E 5 Om skruv 5 hade varit lika
Kängurutävlingen 2018 Ecolier, svar och kommentarer Facit Ecolier 1: E 6 2: B 6 Liam behöver 0, 1, 2, 3, 5 och 8. 3: C 18 Syskonen är 5 år, 6 år och 7 år, 5 + 6 + 7 = 18 4: E 5 Om skruv 5 hade varit lika
Skolverkets förslag till kursplan i matematik i grundskolan. Matematik
 Matematik Matematiken har en mångtusenårig historia med bidrag från många kulturer. Den har utvecklats ur människans praktiska behov och hennes naturliga nyfikenhet och lust att utforska. Matematisk verksamhet
Matematik Matematiken har en mångtusenårig historia med bidrag från många kulturer. Den har utvecklats ur människans praktiska behov och hennes naturliga nyfikenhet och lust att utforska. Matematisk verksamhet
Facit åk 6 Prima Formula
 Facit åk 6 Prima Formula Kapitel 1 Omkrets och area Sidan 7 1 A och C 2 D och E 3 a G, H och J b I och J c J Sidan 8 4 a 1 b 1 c 1 d 4 5 A = 0 B = 2 C = 4 D = 2 6 a 8 0 8 b 1 0 1 c 3 8 3 d 1 3 8 F7 A B
Facit åk 6 Prima Formula Kapitel 1 Omkrets och area Sidan 7 1 A och C 2 D och E 3 a G, H och J b I och J c J Sidan 8 4 a 1 b 1 c 1 d 4 5 A = 0 B = 2 C = 4 D = 2 6 a 8 0 8 b 1 0 1 c 3 8 3 d 1 3 8 F7 A B
7F Ma Planering v2-7: Geometri
 7F Ma Planering v2-7: Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
7F Ma Planering v2-7: Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
Eva Björklund Heléne Dalsmyr. matematik. Koll på. Skriva Facit
 Eva Björklund Heléne Dalsmyr 5A matematik Koll på Skriva Facit 1 Tal i decimalform,3 1 a) 0,5 b) 0,7 c) 0, a) 4, b),1 c) 9,4 3 a) 35,8 b) 41, c) 0,9 4 a) 1,1 b) 4, c) 7,3 5 a) 13,4 b) 3,5 c) 91,7 a) 40,8
Eva Björklund Heléne Dalsmyr 5A matematik Koll på Skriva Facit 1 Tal i decimalform,3 1 a) 0,5 b) 0,7 c) 0, a) 4, b),1 c) 9,4 3 a) 35,8 b) 41, c) 0,9 4 a) 1,1 b) 4, c) 7,3 5 a) 13,4 b) 3,5 c) 91,7 a) 40,8
Problem 1 2 3 4 5 6 7 Svar
 Känguru Cadet, svarsblankett Namn Klass/Grupp Poängsumman Känguruskuttet Ta lös svarsblanketten. Skriv ditt svarsalternativ under numret. Lämna rutan tom om du inte vet svaret. Gissa inte, felaktigt svar
Känguru Cadet, svarsblankett Namn Klass/Grupp Poängsumman Känguruskuttet Ta lös svarsblanketten. Skriv ditt svarsalternativ under numret. Lämna rutan tom om du inte vet svaret. Gissa inte, felaktigt svar
Avdelning 1, trepoängsproblem
 vdelning 1, trepoängsproblem 1. Hur många symmetrilinjer har figuren? : 0 : 1 : 2 : 4 E: oändligt många 2. Robert arbetar på leksaksfabriken. Han ska packa kängurur som ska fraktas till affärerna. Varje
vdelning 1, trepoängsproblem 1. Hur många symmetrilinjer har figuren? : 0 : 1 : 2 : 4 E: oändligt många 2. Robert arbetar på leksaksfabriken. Han ska packa kängurur som ska fraktas till affärerna. Varje
Högstadiets matematiktävling 2018/19 Finaltävling 19 januari 2019 Lösningsförslag
 Högstadiets matematiktävling 2018/19 Finaltävling 19 januari 2019 Lösningsförslag 1. Lösningsförslag: Vi börjar med att notera att delbarhet med 6 betyder att N är delbart med 2 och 3. Om N är delbart
Högstadiets matematiktävling 2018/19 Finaltävling 19 januari 2019 Lösningsförslag 1. Lösningsförslag: Vi börjar med att notera att delbarhet med 6 betyder att N är delbart med 2 och 3. Om N är delbart
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Geometri med fokus på nyanlända
 Geometri med fokus på nyanlända Borås 17 januari 2017 Madeleine Löwing Tala matematik Bygga och Begripa Begrepp i Geometri Använda förklaringsmodeller som hjälper eleven att bygga upp långsiktigt hållbara
Geometri med fokus på nyanlända Borås 17 januari 2017 Madeleine Löwing Tala matematik Bygga och Begripa Begrepp i Geometri Använda förklaringsmodeller som hjälper eleven att bygga upp långsiktigt hållbara
Välkommen till Kängurun Matematikens hopp 2008 Benjamin
 Till läraren Välkommen till Kängurun Matematikens hopp 2008 enjamin Kängurutävlingen genomförs april. Om den dagen inte passar går det bra 4 april eller veckan därpå, däremot inte tidigare. Se till att
Till läraren Välkommen till Kängurun Matematikens hopp 2008 enjamin Kängurutävlingen genomförs april. Om den dagen inte passar går det bra 4 april eller veckan därpå, däremot inte tidigare. Se till att
Matematik Steg: Bas. Mål att sträva mot Mål Målkriterier Omdöme Åtgärder/Kommentarer
 Matematik Steg: Bas ha en grundläggande taluppfattning som omfattar naturliga tal och enkla tal i talområdet 0-10 bråk- och decimalform ordningstal upp till 5 ha en grundläggande rumsuppfattning och kunna
Matematik Steg: Bas ha en grundläggande taluppfattning som omfattar naturliga tal och enkla tal i talområdet 0-10 bråk- och decimalform ordningstal upp till 5 ha en grundläggande rumsuppfattning och kunna
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
