Kängurun Matematikens hopp
|
|
|
- Anna Ellen Ek
- för 7 år sedan
- Visningar:
Transkript
1 Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på nätet. Rätta elevernas lösningar och redovisa resultaten på webbadressen ncm.gu.se/kanguru/ Om du får problem med att redovisa via nätet, hör av dig till oss på eller på telefon Vi ber er redovisa era resultat senast 7 april. Uppmärksamma gärna goda prestationer i klassen och i skolan. Vi delar inte ut några priser, men namnen på de elever som fått bäst resultat, i varje årskurs, kommer att publiceras på webben. Där publiceras också lösningsfrekvenser på alla uppgifter liksom en sammanställning av hur elevernas resultat fördelar sig på olika poängintervall. Du kan sedan jämföra dina elevers resultat med övriga elever i samma åldersgrupp och du kan se om de problem som dina elever hade svårt för också var svåra för andra. Vi är medvetna om att redovisningen tar tid, men vi ber er ändå att redovisa resultaten. De är värdefulla för oss och många lärare frågar efter sammanställningen med lösningsfrekvenser. Förhoppningsvis ger en översikt av klassens resultat även ett bra underlag för ert vidare arbete. Vi har valt att inte ta några deltagaravgifter, vilket man gör i flera andra länder. Att låta er sköta rättning och redovisning av resultat är ett sätt att hålla kostnaderna nere. Låt eleverna få en ny chans att lösa de problem de inte hann med Endast några enstaka elever hinner att lösa alla problem under tävlingstillfället. Ordna därför gärna ett extra tillfälle utom tävlan, där klassen kan lösa problemen utan tidsbegränsning. Många skulle säkert utmanas av de svårare problemen. Arbeta vidare med lösningarna De flesta problem kan lösas på flera sätt och med olika representationsformer. Låt eleverna försöka hitta olika metoder, beskriva sina lösningar och jämför metoderna. Se efter både likheter och skillnader. Pröva om lösningsmetoden är generell, t ex genom att ändra de ingående talen. Låt eleverna få upptäcka, eller visa dem, hur samma lösning kan presenteras på olika sätt, t ex med ord och med symboler. Det är viktigt att eleverna får uttrycka sina lösningar på mer än ett sätt. Att kunna gå mellan olika representationsformer är viktigt för att utveckla förståelse. Arbeta vidare med problemen Efter redovisningssidorna i detta dokument följer förslag till hur ni kan arbeta vidare med problemen. Där finns också ytterligare kommentarer till lösningarna i vissa fall. Kungl Vetenskapsakademien & NCM/Nämnaren
2 Kängurutävlingen 0 Svar och lösningar Ecolier : C 4 A B C D : B 0 Det behövs en klädnypa mer än antalet handdukar. : B 8 Nerifrån räknat + + grå plattor. 4: A Det är barn som har gömt sig. 5: C I tredje kolumnen andra raden uppifrån måste det stå. Det ger att tredje kolumnen fjärde raden måste vara 4. Då blir det i den färgade rutan. Det finns andra vägar att gå, men alla ger samma lösning. 6: E alla fyra 7: D Diagonaler delar rektanglar i lika stora delar. I alternativen A, B, C och E har varje mörkt område ett motsvarande lika stort vitt område, och omvänt. 8: B 5 Kattungarna, ankungarna och kycklingarna har tillsammans = 4 ben. Lammen har alltså sammanlagt 0 ben, vilket innebär att de är 5 st. 9: E 0 När farmor har lagt russin på 5 kakor har hon 5 kakor utan russin. Hon lägger sen nötter först på de 5 kakor som inga russin har, för att få så få kakor som möjligt med både russin och nötter. För att det ska bli 5 kakor med nötter måste hon sen lägga nötter på 0 av de kakor som redan hade russin. Hon får alltså 5 kakor med bara russin, 5 med bara nötter och 0 med både russin och nötter. 0: B 6 kr Tre ballonger är två fler än en ballong. De två ballongerna kostar kr, dvs 6 kr styck. : D Biten måste ha tre klossar i undre raden och en i mitten av den övre.. E 0 Antalet måste vara jämnt delbart med. Alla antal som är delbara med är möjliga, men bara ett, talet 0, finns bland svarsalternativen. Kungl Vetenskapsakademien & NCM/Nämnaren
3 Kängurutävlingen 0 Ecolier, svar och lösningar : D 7 För att få så stor summa som möjligt ska vi låta 5 och 6 vara hundratalssiffror, och 4 tiotalssiffror och och entalssiffror. Vi kan kombinera siffrorna på flera sätt: = = = etc. 4: C 4 På de brickor som ligger kvar ser vi sammanlagt prickar. Det saknas alltså st. På de brickor som saknas måste prickar finnas på den vänstra och prick på den högra, återstår 8 prickar att fördela på de två återstående bitarna, 4 prickar på varje. 5: B 4 Ebba och Leo kan stå antingen EL eller LE. Ina ska stå bredvid Leo vilket ger möjligheterna ELI och ILE. Viktor kan stå antingen till vänster eller till höger i båda fallen, dvs 4 möjligheter: VELI, ELIV, VILE, ILEV. 6: D Loppan ska hoppa ett visst antal hopp upp och ett visst antal hopp ner. Hon kan göra hoppen i olika ordning. Det gäller att få talet genom en kombination av multiplar av + och multiplar av =, dvs 0 hopp uppåt och nedåt. 7: D 7 Arbeta baklänges: 0/4 = 50; 50 = 500; 500/0 = 50; 50 = 49; 49 = : C 0 Vi vill hitta det största möjliga antalet förluster och räknar då med att de 80 poängen i så stor utsträckning som möjligt ska komma från segrar. 80/ ger 6 rest, dvs som mest kan laget ha vunnit 6 matcher och fått 78 poäng. De ytterligare poängen upp till 80 kommer från två oavgjorda matcher, totalt 8 matcher som givit poäng, vilket innebär 0 förlorade matcher. Laget kan förstås få 80 poäng på andra sätt. Då måste fler matcher ha blivit oavgjorda och färre vunna, men då blir också antalet förlorade matcher färre. Kungl Vetenskapsakademien & NCM/Nämnaren
4 Arbeta vidare med Ecolier 0 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta eleverna resonera sig fram till lösningarna i grupp. Låt alla först få möjlighet att lösa problemen på egen hand om de inte hann det i samband med tävlingen. Diskutera gruppernas lösningar i klassen och jämför idéer och angreppssätt. Låt också eleverna få granska kamraternas lösningar: Har de tagit hänsyn till alla förutsättningar? Är de tydliga? Är resonemanget korrekt? Fungerar lösningsmetoden på andra, liknande problem? Att analysera och diskutera varandras lösningar är bra, men det kräver förstås att man arbetar lång siktigt så att eleverna vänjer sig vid att både ge kritik på ett konstruktivt sätt och att ta emot kritik. Om de redan från början får uppleva att det är en del av undervisningen kan det bli en naturlig och uppskattad form av arbete med problem. Att presentera en lösning som andra kan följa och som är korrekt uppbyggd är något som eleverna måste få tid och möjlighet att utveckla med hjälp av lärare. Välj några av årets problem, arbeta igenom lösningarna noga och gör en riktigt genomarbetad redovisning. Alla problem kan naturligtvis diskuteras utifrån valda lösningsmetoder. De flesta problem kan lösas på olika sätt och det är alltid bra att jämföra dessa och se på likheter och skillnader. Det är också bra att beskriva lösningarna med hjälp av olika representationsformer, konkret material, bilder, muntligt eller skriftligt tal och med symboler. Jämför de olika formerna och se hur det konkreta uttrycks i ord och med symboler. Några frågor att återkomma till när problemet är löst: Kontrollera att lösningen verkligen svarar mot frågan. Är det ett rimligt svar? Hur vet vi det? Påminner problemet om något annat problem vi löst tidigare? Vilka kunskaper hade vi nytta av när vi löste problemet? Vilka nya frågor kan problemet väcka? Lärde vi oss något nytt av problemet? Gå också igenom de felaktiga svarsalternativen och resonera om varför dessa inte är riktiga. Låt eleverna göra förändringar i uppgiften så att de andra alternativen blir riktiga. Utmaningen kan vara att göra så små förändringar som möjligt. Matematiskt arbete handlar mycket om resonemang. Elever behöver få resonera om både matematik innehållet och om strategier för att utveckla sin matematiska kompetens. Låt dem också få argumentera för sina lösningar och sina val av metoder. I arbetet med alla problem bör förmågorna att resonera och argumentera vara centrala. I samband med diskussion av problemen kommer ett antal termer att aktualiseras. Gå igenom dem. Låt eleverna använda och själva få definiera olika begrepp och återkom till dem i olika sammanhang. För definitioner hänvisar vi till Matematiktermer för skolan (Kiselman & Mouwitz, 008). Här har vi sorterat förslag under några rubriker. Naturligtvis kan flera av problemen också passa under andra rubriker. Många problemtyper återkommer år från år, i olika skepnader och i olika varianter. Vi hänvisar här till några gamla problem som kan användas i samband med arbetet med årets, men det finns många fler att hämta på Kängurusidan på nätet, ncm.gu.se/kanguru, där alla tidigare omgångar är samlade. Tidigare problem inom området geometri finns dessutom samlade i boken Geometri och rumsuppfattning med känguruproblem. Läs mer om den på ncm.gu.se/node/474. Kungl Vetenskapsakademien & NCM/Nämnaren
5 Problemlösningsstrategier 4: Kurragömma. Ett problem där barnens erfarenheter kommer till användning. Man måste veta att den som står inte också gömmer sig och också tänka på det när man löser problemet. Många elever ser talen och 9 och gör snabbt en beräkning, utan att fundera på sammanhanget. Problemet passar bra som utgångspunkt för att diskutera nödvändigheten av att relatera situationen som beskrivs till beräkningen. I det här fallet att fundera på vilka de barnen är, hur många som gömde sig från början och att 9 hittade tillsammans med de som gömmer sig och Hektor ska bli. Problemet kan med fördel dramatiseras. Det passar också bra att illustrera det med hjälp av konkret material eller med en ritning. Jämför barnen/materialet/bilden med symbolerna i den tecknade uträkningen, t ex: 9 =. Gör barnen uppmärksamma på Hektors roll. Han är en av de, men han gömmer sig inte och är inte heller en av de 9 hittade. I just det här problemet är det nödvändigt att veta något om verkligheten. I andra problem fungerar verkligheten mer som kuliss och problemen går lika bra att lösa utan kunskaper om den. I vissa fall måste vi också bortse från kunskaper om omvärlden, eftersom sådana kunskaper gör att vi lägger till (eller tar bort) vissa förutsättningar som inte finns (eller finns) i problemet. Om verkligheten och problemlösning, se t ex: Torulf Palm: Problem med verkligheten att lösa tillämpade matematikuppgifter. I Nämnaren 00: Sudoku. I ett Sudoku måste både rader och kolumner stämma. För elever i den här åldern är det en mycket bra övning och för många är det fortfarande en stor utmaning. Diskutera gemensamt vilka rutor som det är bäst att börja med. Varför? Uppmana också eleverna att kontrollera att lösningen stämmer åt båda hållen. Låt dem konstruera egna rutor åt varandra. En typ av problem som påminner om detta finns i år på Benjamin. 9. Några av rutorna i tabellerna nedan färgades röda. Antalet röda rutor i varje rad och kolumn markerades vid sidan och nedanför. Sen togs färgen bort. Vilken av tabellerna kan vara riktig? A B C D E Det är mer komplicerat och kräver mer av elevernas problemlösnings- och resonemangsförmåga, men annars räcker det att kunna räkna till fyra. Låt eleverna resonera och pröva sig fram (använd gärna konkret material) till en lösning. Uppmana dem att kontrollera sin lösning och att dokumentera sin lösning på lämpligt sätt. Tidigare problem: Ecolier 0:6, Benjamin 00:0, Cadet 008:; Ecolier 007: 7; Ecolier 004: Kungl Vetenskapsakademien & NCM/Nämnaren
6 8. Barnens lantgård är en variation på ett klassiskt problem: Oskar och Anna besöker en lantgård med höns och lamm. Efteråt säger Anna att hon har sett 8 djur. Oskar vet inte hur många djur han har sett, men han är säker på att de hade 50 ben tillsammans. Hur många lamm och hur många höns hade de sett? Här är det mycket lämpligt att jämföra och diskutera olika strategier. Låt eleverna förklara hur de resonerar och redovisa resonemang och lösning på ett blädderblock eller liknande. Jämför de olika lösningsmetoderna och se på likheter och skillnader. Hur många olika lösningsmetoder har ni i klassen? Ett problem som har anknytning till detta är Student 004:. Även om det finns i en tävlingsklass för gymnasieelever är det möjligt att lösa för yngre barn, med andra metoder. Se också Adventskalendern 0, lucka (Nämnaren på nätet, ArkivN). 9. Farmor bakar kakor. Här är frågan: Vilket är det minsta antal kakor som fick både nötter och russin? Diskutera vad frågan innebär och låt barnen möta och använda ordet åtminstone. Vad betyder det att någon har åtminstone en bror? Det gäller alltså att hitta den lösning som ger så få kakor som möjligt med både russin och nötter Ofta handlar problem om att hitta mesta möjliga eller minsta möjliga. Vi ska då kunna visa både att det är möjligt och att det inte finns någon lösning med fler (eller färre). Det minsta antal kakor med både nötter och russin som farmor gör är 0 st: N N N N N N N N N N N N N N N R R R R R R R R R R R R R R R R Motsatt problem är kanske enklare: Farmor vill ha så många kakor som möjligt med både nötter och russin. 4. Unos dominobrickor är ett bra exempel på flerstegsproblem. Först måste vi beräkna hur många prickar som har försvunnit, st. Vi vet var det ska ligga en och en. Återstår 8 prickar som ska ligga på två rutor, samma antal på båda, dvs 8/=4 på vardera av de återstående. Låt gärna eleverna redovisa sin tankegång strukturerat, i de steg de tänker, så att kamraterna får följa resonemanget. Det är ett bra sätt att utveckla förmågan att föra och följa resonemang, och det kan hjälpa eleverna att hitta svagheter och felaktigheter i lösningen. 5. Hos fotografen är ett problem som kräver ett strategiskt angreppssätt. Det fungerar utmärkt att dramatisera och att lösa konkret med föremål. Låt eleverna inte bara placera ut sina föremål (eller sig själva) utan låt dem också motivera varför de placerar dem på just det sättet. Låt eleverna fundera över likheter och skillnader mellan de olika lösningarna och (förhoppningsvis) upptäcka att de är parvis spegelvända. Hur många sätt att placera barnen finns det om fotografen inte alls bryr sig om ordningen? Kungl Vetenskapsakademien & NCM/Nämnaren
7 Undersök olika kombinationer, med olika antal. Exempel: Portkoden i vårt hus har tre olika siffror mellan och 5. Hur många olika kombinationer är möjliga? Variera problemet med hjälp av antalet siffror i koden och antalet att välja bland. Isa ska köpa glass. Hon vill ha två kulor. Det finns vanilj-, choklad-, jordgubb- och nötglass att välja bland. Hur många olika möjligheter har hon? Hur många fler möjligheter blir det om hon får ta två kulor av samma sort, jämfört med om hon måste välja två smaker. En spännande sak att undersöka och fundera på är hur många olika bilregistreringsskyltar och telefonnummer vi kan ha. Detta är verkliga problem. Kanske kan barnen fråga någon äldre person om tidiga telefonnummer och registreringsskyltar. Hur gör vi när numren tar slut? Problem av det här slaget, som behandlar kombinatorik, finns i olika svårighetsgrad, från enkla problem som kan lösas konkret till komplicerade problem. Att eleverna vid upprepade tillfällen får arbeta med allt mer utmanande kombinationer hjälper dem att bygga upp förståelse för området. De behöver också få använda olika lösningsmetoder och uttrycksformer och också jämföra dessa: konkret, med laborativt material, med bild, med grafisk representation som träddiagram och symboliskt. Om de har utvecklat god förståelse för olika typer av lösningar har de en god grund att stå på då det är dags att formalisera. Se också kommentaren till problem. Tidigare problem: Benjamin 00:7; Ecolier 009:6. 8. Fotbollsserien. Diskutera formuleringen som mest ha förlorat. Det gäller alltså att få så många förlorade matcher som möjligt. Varför kan de inte ha förlorat alla matcher? Här passar det bra att rita upp en tabell och undersöka olika möjligheter. Vi kan också försöka resonera kring att lagets poäng helst ska komma från vunna matcher varför? Hur många vunna matcher kan det som mest ha spelat? 80/ = 6 rest. Laget kan ha fått sina poäng på 6 vinster och oavgjorda matcher. Talet 80 gick alltså inte att dela jämnt med, vi fick en rest. Undersök olika tals delbarhet. Vilka tal kan vi dela med? Med 5? Med 0? Låt barnen systematiskt gå igenom talen och skriva dem som produkter på alla möjliga sätt. Låt dem fundera över vad,, 5, 7,, etc har gemensamt. Begreppet primtal. Ett tidigare problem med anknytning till detta: Vilket tal står på plats 007 i det oändligt långa ordet KÄNGURUKÄNGURUKÄNG Hitta på egna liknande uppgifter av olika svårighet. Låt barnen göra egna utifrån sina namn eller namn på husdjur, idoler, etc Se också Benjamin 004: 9. Kungl Vetenskapsakademien & NCM/Nämnaren 4
8 Mönster. Tvätten på strecket. Hur många klädnypor behövs till 5 handdukar? Till 0? 57? 00? När barnen ser mönstret, det går åt en klädnypa fler än antalet handdukar, kan de skriva regeln med ord. Utifrån det skrivna kan ni sedan förenkla vidare, beroende på hur vana eleverna är, så att ni närmar er ett formellt sätt att skriva: Antalet klädnypor = antalet handdukar +. Gör fler liknande exempel, t ex sätt en klädnypa mitt på handduken också. Undersök vad som blir resultatet med andra regler: häng varje plagg med klädnypor, använd en klädnypa till varje par sockor etc. Låt eleverna först upptäcka vilken regel som gäller, därefter formulera den muntligt, sen skriftligt och därefter stegvis mer och mer symboliskt. Låt alla former, från vardagsspråk till symbolisk finnas på tavlan samtidigt så att eleverna kan jämföra de olika uttrycksformerna. Att hänga tvätt på klädstreck är kanske inte alla barns vardag, men bilden passar bra för att illustrera en klassisk problemformulering. Den kan också handla om antal mellanrum mellan ett bestämt antal stolpar, hur många knappar som behövs om de ska sitta med 7 cm mellanrum utefter en 50 cm kavajkant etc. Tidigare problem: Ecolier 007:4 och Benjamin 004:8 Tal 0. Ballongerna. Gå igenom texten i problemet noga och resonera om innebörden. Vilken information är nödvändig? Vilken information kan vi helt bortse från? Hur ska vi översätta texten till symboler? Begreppen mer än och mindre än är inte helt oproblematiska. Börja med enklare exempel. Ett päron kostar 5 kr. Ett äpple kostar kr mer än ett päron. Vad kostar ett äpple? 5kr + kr = 7 kr. Hur kan vi skriva detta uttryck om vi inte vet vad päronet kostar? Anta att päronet kostar x kr. Då kostar äpplet x kr + kr. Resonera om att det som äpplet kostar mer måste adderas till päronets pris, det är detta som kan vara svårt. Lyft fram likhetstecknets betydelse, det är avgörande i detta sammanhang. Gör flera exempel och använd också mindre än: En banan kostar kr mindre än ett äpple. Varifrån ska dras? Från äpplets pris eller bananens? Låt eleverna konstruera egna påståenden med mer än och mindre än och uttrycka dem skriftligt med ord och symboler. Diskutera gemensamt.. Nadjas klass. En annan språklig konstruktion som inte är helt lätt och som vi behöver arbeta med är dubbelt så många som. I problem är det dubbelt så många flickor som pojkar. Vad innebär det? Om vi vet antalet pojkar är det relativt enkelt att beräkna dubbelt. Men om den delen är okänd vet vi bara att relationen är :. Det innebär att hela gruppen måste delas i tre. Två delar flickor och en del pojkar. Låt eleverna undersöka detta konkret och med en bild. Undersök vilka antal som är möjliga att fördela på detta sätt. Vad har de gemensamt? Här återkommer begreppet delbarhet igen. Några tidigare problem: Ecolier 009:, Cadet 00:4. Kungl Vetenskapsakademien & NCM/Nämnaren 5
9 . Största summan. I problem ska vi bilda två tresiffriga tal med största möjliga summa med hjälp av siffrorna 6. Hur ska vi resonera för att finna den största? Vilken är den minsta? Kan vi få störst och minst summa på olika sätt? Varför? Låt eleverna finna alla tänkbara tresiffriga tal och sortera dem i storleksordning. Börja eventuellt med alla tresiffriga tal vi kan göra med siffrorna, och. Här krävs det systematik hur vet vi att vi har funnit alla tal? Hur många tal finns det? Även detta handlar om kombinatorik (se kommentaren till problem 5). Ett spel som passar i detta sammanhang är Tänk till tusen: Låt eleverna rita upp en spelplan som är x rutor: I de tre raderna ska det bildas tresiffrigt tal. De tre talen ska till slut adderas, och målet är att komma så nära 000 som möjligt. Spelledaren slår en tärning, eller slumpar fram en siffra på något annat sätt. Deltagarna ska skriva den siffran i valfri ruta. Efter nio slag/drag ska alla rutor vara ifyllda och talen kan summeras. Den som kommer närmast 000 vinner. Spelet stimulerar elevernas överslagsräkning, det gäller att snabbt avgöra var siffran passar bäst, och deras strategiska tänkande. Spelet går förstås att variera och andra tal än 00 kan väljas. Det går också att göra detta med nio tomplatser på rad, men det kan bli svårare att snabbt få en överblick då. + + Se också: Ecolier 006:4; Benjamin 00:. 6. Loppan i trappan. Här är trappan en bild av tallinjen och loppans hopp är treskutt uppåt, addition med, och fyrskutt nedåt, addition med -4 (eller subtraktion med 4). Undersök vilka steg loppan hamnar på om hon bara hoppar uppåt,, 6, 9 Diskutera vad det är för tal. Loppan kan alltså hamna på (för lite) och på 4 (för långt) om hon bara hoppar uppför och måste därför också hoppa nedåt också. Varför räcker det inte med ett nedåthopp? Spelar det någon roll var i serien loppan tar sin nedåthopp? Här finns det anledning att undersöka räknelagarna för addition och subtraktion. a + b = b + a men a b = b a, endast om a = b. a + (b + c) = (a+ b) + c Vad händer om vi låter loppan få en källare också? Låt eleverna undersöka problemet när loppan har möjlighet att hoppa till trappsteg -. Många barn har nog åkt i hissar där våning - och - är utsatta. Diskutera vad det innebär. Om ni inte redan har visat att tallinjen fortsätter både mot allt större tal och mot allt mindre passar det bra i detta sammanhang. Jämför loppans hopp i trappan med tallinjen. Låt eleverna få konstruera liknande problem till varandra. Uppmuntra dem att också hoppa ner i källaren dvs använda negativa tal. Kungl Vetenskapsakademien & NCM/Nämnaren 6
10 7. Talet. Problem 7 löser vi genom att arbeta baklänges. Det är nödvändigt att känna till räknesättens inbördes relation och att addition och subtraktion, liksom multiplikation och division är inversa räknesätt. Detta är en kunskap, som vi också kan använda för att kontrollera uträkningar. Det hjälper oss också att förstå samband, t ex varför det är omöjligt att dividera ett tal med 0. x 0 = a innebär att a 0 = x, och här har vi en motsägelse. Problemet kan också användas som förberedelse för algebra och ekvationslösning. Vi kan uttrycka texten med hjälp av symboler och kalla talet för talet (eller t, eller x) Börja gärna med ett enklare uttryck. Om vi ska uttrycka problemet med symboler måste vi ta hänsyn till prioriteringsregler och använda oss av parenteser. Här blir det alltså tydligt att dessa spelar roll. Se också: Benjamin 00:5. 008:7; 007: och Ecolier 007:8 Geometri. Rutmönstret. Geometri handlar också om lägesbestämningar. Koordinater är då mycket användbart och används ju i kartor. Ett tidigt möte får vi i problem. Rutorna är här numrerade på ett annat sätt än i ett vanligt koordinatsystem, så principen för hur man navigerar blir tydlig. Låt eleverna konstruera egna liknande problem. Studera alternativen och diskutera omkrets och area på de skuggade figurerna. Hur många rutor måste vi färga för att bilden ska bli symmetrisk. Var ligger symmetriaxeln? Finns det olika lösningar? Rutsystem kan också användas för en annan typ av problem, som i Milou 0 och Benjamin 9 i år. Pröva gärna dem. M 0. Det får bara finnas två mynt i varje rad och i varje kolumn. Hur många måste Julie ta bort? Se också: Ecolier 0:; Ecolier 009:6; Cadet 007: ; Ecolier 005:6; Cadet 004: och 7. Area och symmetri. Resonera om hur vi kan avgöra om de ljusa och mörka areorna är lika. Nöj er inte med argument av typen det ser man, utan låt eleverna använda sina kunskaper om formerna för att argumentera. Använd termer som gör argumentationen lätt att följa och entydig: diagonal, sida, hörn, kvadrat, cirkel, rektangel, parallelltrapets, triangel. Diskutera dessa begrepp. Hur stor area har de olika områdena? Varför kan vi inte bestämma arean av cirklarna (och omliggande område)? Uttryck areorna som bråk. Kungl Vetenskapsakademien & NCM/Nämnaren 7
11 Finns det någon möjlighet att de mörka och ljusa områdena i alternativ D skulle kunna vara lika stora? Hur stora skulle cirklarna i så fall vara? Se på symmetrierna i bilderna. Var finns symmetrilinjen? Har något alternativ mer än en symmetrilinje? Vilka alternativ är symmetriska om vi tar hänsyn till färgerna? Om vi inte tar hänsyn till färgerna? Låt eleverna konstruera liknande figurer, uttrycka areornas storlek och markera symmetrier. Detta problem kan med fördel följas upp i bild. 6 och. Pusselbitarna och Klossbygget, är av en typ som har förekommit många gånger i Kängurutävlingen. Förslag till hur man kan arbeta med sådana och ytterligare en mängd exempel i olika svårighetsgrad finns i boken Geometri och rumsuppfattning med Känguruproblem. Att läsa Gennow, S. & Wallby, K. (00). Geometri och rumsuppfattning med Känguruproblem. NCM, Göteborgs universitet. Kiselman, C. & Mouwitz, L. (008). Matematiktermer för skolan. NCM, Göteborgs universitet. McIntosh, A. (008). Förstå och använda tal. NCM, Göteborgs universitet. Rystedt, E. &Trygg, L. (00). Laborativ matematikundervisning vad vet vi? NCM, Göteborgs universitet. Nämnaren. I varje nummer finns Problemavdelningen och Kängurusidan. Läs också tidigare artiklar kring problemlösning. Nämnarenartiklar publicerade finns fritt tillgängliga som pdf-dokument på Nämnaren på nätet, namnaren.ncm.gu.se. Du finner dem via artikeldatabasen. Under ArkivN finns alla publicerade Uppslag och Problemavdelningar samlade. Där finns också alla Adventskalendrar. Nämnaren på nätet presenterar varje månad nya problem under rubriken Månadens problem. Strävorna finns på ncm.gu.se/stravorna. Där finns aktiviteter, problem och artiklar samlade och ordnade efter kursplanens beskrivningar av matematikeämnets syfte och mål. Kungl Vetenskapsakademien & NCM/Nämnaren 8
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 017, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på
Kängurun Matematikens hopp Ecolier 017, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. De flesta problem kan lösas på flera sätt och med olika representationsformer.
Kängurun Matematikens hopp Ecolier 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. De flesta problem kan lösas på flera sätt och med olika representationsformer.
Arbeta vidare med Ecolier 2010
 Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Arbeta vidare med Milou 2008
 Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Kängurutävlingen 2017 NCM 1
 Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte.
 Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Kängurun Matematikens hopp
 Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder till svaret 6.
 Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Svar och lösningar Ecolier
 Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Svar och lösningar Benjamin
 Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Ecolier. Avdelning 1. Trepoängsproblem. 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6.
 Ecolier Avdelning 1. Trepoängsproblem 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6 (Ryssland) 2 Gilda har 50 kr. Hon tänker köpa fem skrivböcker som
Ecolier Avdelning 1. Trepoängsproblem 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6 (Ryssland) 2 Gilda har 50 kr. Hon tänker köpa fem skrivböcker som
Arbeta vidare med Benjamin
 Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
5: D 3 23 kan bara fås på ett sätt: Här har man nytta av att känna igen 24 som ett tal i sexans tabell.
 Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Kängurutävlingen Matematikens hopp Junior 2016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Svar och arbeta vidare med Benjamin 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Kortfattade lösningar med svar till Cadet 2006
 3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Lösningsförslag Cadet 2014
 Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Svar och lösningar Benjamin
 Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A 1 9999 + 1= 10 000. Talet
Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A 1 9999 + 1= 10 000. Talet
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
1 B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3.
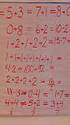 Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt.
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och korta lösningar Benjamin 2006
 3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
Kängurutävlingen Matematikens hopp 2010 Benjamin för elever i åk 5, 6 och 7.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 200 Benjamin för elever i åk 5, 6 och 7. Kängurutävlingen genomförs den 8 mars. Om den dagen inte passar kan hela veckan 9 26 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 200 Benjamin för elever i åk 5, 6 och 7. Kängurutävlingen genomförs den 8 mars. Om den dagen inte passar kan hela veckan 9 26 mars användas,
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Svar och lösningar Benjamin
 Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer,
Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer,
Arbeta vidare med aritmetik 2018
 Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas, däremot
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 4 C: kvadrat Exempel på hur formerna kan konstrueras:
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
5: B grön Någon har den gröna ryggsäcken och det är inte Anna (och inte Maja), så det måste vara Tom.
 Kängurutävlingen 2018 Ecolier, svar och kommentarer Facit Ecolier 1: E 6 2: B 6 Liam behöver 0, 1, 2, 3, 5 och 8. 3: C 18 Syskonen är 5 år, 6 år och 7 år, 5 + 6 + 7 = 18 4: E 5 Om skruv 5 hade varit lika
Kängurutävlingen 2018 Ecolier, svar och kommentarer Facit Ecolier 1: E 6 2: B 6 Liam behöver 0, 1, 2, 3, 5 och 8. 3: C 18 Syskonen är 5 år, 6 år och 7 år, 5 + 6 + 7 = 18 4: E 5 Om skruv 5 hade varit lika
Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
3: A I den vita asken. Kolan ligger i den röda asken så chokladbiten måste ligga i den vita. Problemet kan lösas konkret och med en enkel bild.
 Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
Kortfattade lösningar med svar till Gymnasiets Cadet 2006
 Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Arbeta vidare med Junior 2010
 Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2019, facit och kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Kängurun Matematikens hopp Milou 2019, facit och kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
Junior för elever på kurs Ma 2 och Ma 3
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Junior för elever på kurs Ma 2 och Ma 3 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Junior för elever på kurs Ma 2 och Ma 3 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Facit och kommentarer Ecolier 2019
 Facit och kommentarer Ecolier 2019 1 E 2 C 5+5+1+1 3 A tisdag Om det var söndag igår är det måndag idag. 4 D,, Det kvadratiska hålet kommer att hamna tre rutor från mittvikningen och då syns motorcykeln.
Facit och kommentarer Ecolier 2019 1 E 2 C 5+5+1+1 3 A tisdag Om det var söndag igår är det måndag idag. 4 D,, Det kvadratiska hålet kommer att hamna tre rutor från mittvikningen och då syns motorcykeln.
Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Kängurutävlingen Matematikens hopp 2010 Ecolier för elever i åk 3 och 4
 Välkommen till Kängurutävlingen Matematikens hopp 2010 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot får
Välkommen till Kängurutävlingen Matematikens hopp 2010 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot får
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Student 016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Kängurutävlingen Matematikens hopp Student 016, svar och lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till
Trepoängsproblem. Kängurutävlingen 2011 Cadet. 1 Vilket av följande uttryck har störst värde? 1 A: B: C: D: E: 2011
 Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Här är två korta exempel på situationer då vi tillämpar den distributiva lagen:
 Modul: Algebra Del 8: Avslutande reflektion och utvärdering Distributiva lagen Cecilia Kilhamn, Göteborgs Universitet Distributiva lagen a (b + c) = a b + a c Den distributiva lagen kallas den räknelag
Modul: Algebra Del 8: Avslutande reflektion och utvärdering Distributiva lagen Cecilia Kilhamn, Göteborgs Universitet Distributiva lagen a (b + c) = a b + a c Den distributiva lagen kallas den räknelag
Välkommen till Kängurutävlingen Matematikens hopp 17 mars Junior för elever på kurs Ma 2 och Ma 3
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Junior för elever på kurs Ma 2 och Ma 3 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Junior för elever på kurs Ma 2 och Ma 3 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Välkommen till Kängurutävlingen Matematikens hopp 17 mars Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Kängurutävlingen 2017
 Kängurutävlingen 2017 Arbeta vidare med Ecolier 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. Låt alla först få
Kängurutävlingen 2017 Arbeta vidare med Ecolier 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. Låt alla först få
Svar och lösningar. Kängurutävlingen 2009 Cadet för gymnasiet
 Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Lgr 11 matriser i Favorit matematik 4 6
 Lgr 11 matriser i Favorit matematik 4 6 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla förmågan att De matematiska förmågor
Lgr 11 matriser i Favorit matematik 4 6 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla förmågan att De matematiska förmågor
Om Lgr 11 och Favorit matematik 4 6
 Om Lgr 11 och Favorit matematik 4 6 TYDLIG OCH MEDVETEN MATEMATIKUNDERVISNING En stark koppling mellan läroplan/kunskaps mål, innehåll och bedömning finns för att medvetande göra eleverna om syftet med
Om Lgr 11 och Favorit matematik 4 6 TYDLIG OCH MEDVETEN MATEMATIKUNDERVISNING En stark koppling mellan läroplan/kunskaps mål, innehåll och bedömning finns för att medvetande göra eleverna om syftet med
4. A. 4, 6, 11 Viker man ihop till en kub, så kommer talet 1 mitt emot 3, 2 mitt emot 4 och 5 mitt emot 6. Det ger summorna 4, 6, 11.
 N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Svar och arbeta vidare med Student 2008
 Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant?
 En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
Välkommen till. Kängurutävlingen Matematikens hopp 2016 Milou, för elever i förskoleklass åk 2. Till läraren. Lycka till med årets Känguru!
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Milou, för elever i förskoleklass åk 2 Syftet med Kängurun är att skapa intresse för matematik med hjälp av intressanta problem. Vår
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Milou, för elever i förskoleklass åk 2 Syftet med Kängurun är att skapa intresse för matematik med hjälp av intressanta problem. Vår
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt
Kängurutävlingen Matematikens hopp Junior 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt
Per Berggren och Maria Lindroth 2014-11-19
 Varierad matematikundervisning Per Berggren och Maria Lindroth 2014-11-19 Luffarschack Med en utmaning! Sfinxen En rik laborativ matematikuppgift som tar sin början i de första skolåren och fortsätter
Varierad matematikundervisning Per Berggren och Maria Lindroth 2014-11-19 Luffarschack Med en utmaning! Sfinxen En rik laborativ matematikuppgift som tar sin början i de första skolåren och fortsätter
Statistik, sannolikhet, algebra och funktioner, 3 hp. Studenter i lärarprogrammet F-3 III, 12F380 ht17 Varberg
 Grundläggande matematik II 7,5 högskolepoäng Provmoment: Ladokkod: Tentamen ges för: Statistik, sannolikhet, algebra och funktioner, 3 hp Studenter i lärarprogrammet F-3 III, 12F380 ht17 Varberg TentamensKod:
Grundläggande matematik II 7,5 högskolepoäng Provmoment: Ladokkod: Tentamen ges för: Statistik, sannolikhet, algebra och funktioner, 3 hp Studenter i lärarprogrammet F-3 III, 12F380 ht17 Varberg TentamensKod:
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Cadet 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Cadet 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Välkommen till Kängurun Matematikens hopp 2008 Benjamin
 Till läraren Välkommen till Kängurun Matematikens hopp 2008 enjamin Kängurutävlingen genomförs april. Om den dagen inte passar går det bra 4 april eller veckan därpå, däremot inte tidigare. Se till att
Till läraren Välkommen till Kängurun Matematikens hopp 2008 enjamin Kängurutävlingen genomförs april. Om den dagen inte passar går det bra 4 april eller veckan därpå, däremot inte tidigare. Se till att
Bo skola 1 Matematikmål år F-3 Skriftligt omdöme/kunskapsinformation
 Bo skola Matematikmål år - Namn: Strävansmål: Vi strävar efter att varje elev ska Utveckla goda baskunskaper i de fyra räknesätten Utvecklar en god förståelse för matematik och matematiska begrepp att
Bo skola Matematikmål år - Namn: Strävansmål: Vi strävar efter att varje elev ska Utveckla goda baskunskaper i de fyra räknesätten Utvecklar en god förståelse för matematik och matematiska begrepp att
Arbeta vidare med Milou
 Kängurutävlingen 2009 Arbeta vidare med Milou Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. När ni nu diskuterar lösningarna kan ni också kontrollera
Kängurutävlingen 2009 Arbeta vidare med Milou Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. När ni nu diskuterar lösningarna kan ni också kontrollera
Bagarmossens skolas kravnivåer beträffande tal och talens beteckningar som eleven ska ha uppnått efter:
 Matematik 1-5 Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och
Matematik 1-5 Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och
Studenter i lärarprogrammet GF(11GF20) 46 p G: 28 p VG: 38 p
 11GF20 MaI Provmoment: Ladokkod: Tentamen ges för: Matematik 0,5 hp Studenter i lärarprogrammet GF(11GF20) 15 högskolepoäng TentamensKod: Tentamensdatum: 18-05-22 Tid: 09.00-13.00 Hjälpmedel: Inga hjälpmedel
11GF20 MaI Provmoment: Ladokkod: Tentamen ges för: Matematik 0,5 hp Studenter i lärarprogrammet GF(11GF20) 15 högskolepoäng TentamensKod: Tentamensdatum: 18-05-22 Tid: 09.00-13.00 Hjälpmedel: Inga hjälpmedel
mattetankar Reflektion kring de olika svaren
 Reflektion kring de olika svaren Taluppfattning och tals användning 15 Skriv trehundrasju Reflektion: 31007 tyder på att eleven tolkar talet som 3, 100, 7 3007 tyder på att eleven tolkar talet som 300,
Reflektion kring de olika svaren Taluppfattning och tals användning 15 Skriv trehundrasju Reflektion: 31007 tyder på att eleven tolkar talet som 3, 100, 7 3007 tyder på att eleven tolkar talet som 300,
Remissversion av kursplan i matematik i grundskolan. Matematik. Syfte
 Matematik Syfte Matematiken har en mångtusenårig historia med bidrag från många kulturer och har utvecklats ur människans praktiska behov och naturliga nyfikenhet. Matematiken är kreativ och problemlösande
Matematik Syfte Matematiken har en mångtusenårig historia med bidrag från många kulturer och har utvecklats ur människans praktiska behov och naturliga nyfikenhet. Matematiken är kreativ och problemlösande
Trepoängsproblem. Kängurutävlingen 2012 Junior
 Trepoängsproblem 1. M och N är mittpunkterna på de lika långa sidorna i en likbent triangel. Hur stor är arean av fyrhörningen markerad med X? : 3 : 4 C: 5 D: 6 E: 7 M? X 3 3 6 N 2. När lice skickar ett
Trepoängsproblem 1. M och N är mittpunkterna på de lika långa sidorna i en likbent triangel. Hur stor är arean av fyrhörningen markerad med X? : 3 : 4 C: 5 D: 6 E: 7 M? X 3 3 6 N 2. När lice skickar ett
Målet i sikte åk 1 3. Målet i sikte 1 3. kartläggning i matematik. Lgr11
 Må Målet i sikte åk Målet i sikte Målet i sikte är ett kopieringsmaterial som kartlägger elevernas kunskaper i matematik. Utgångspunkt är det centrala innehållet och kunskapskraven i Lgr. För varje område
Må Målet i sikte åk Målet i sikte Målet i sikte är ett kopieringsmaterial som kartlägger elevernas kunskaper i matematik. Utgångspunkt är det centrala innehållet och kunskapskraven i Lgr. För varje område
Lokal studieplan Matematik 3 8 = 24. Centrum för tvåspråkighet Förberedelseklass
 Lokal studieplan Matematik 3 8 = 24 Centrum för tvåspråkighet Förberedelseklass 1 Mål att sträva mot Skolan skall i sin undervisning i matematik sträva efter att eleven S11 utvecklar intresse för matematik
Lokal studieplan Matematik 3 8 = 24 Centrum för tvåspråkighet Förberedelseklass 1 Mål att sträva mot Skolan skall i sin undervisning i matematik sträva efter att eleven S11 utvecklar intresse för matematik
Svar och arbeta vidare med Cadet 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Enhet / skola: Lindens skola i Lanna Åk: 3
 Skolområde Väster Lokal Pedagogisk Planering Enhet / skola: Lindens skola i Lanna Åk: 3 Avsnitt / arbetsområde: Undersöka med Hedvig Ämnen som ingår: Svenska/svenska som andraspråk, matematik, bild, So,
Skolområde Väster Lokal Pedagogisk Planering Enhet / skola: Lindens skola i Lanna Åk: 3 Avsnitt / arbetsområde: Undersöka med Hedvig Ämnen som ingår: Svenska/svenska som andraspråk, matematik, bild, So,
kan använda sig av matematiskt tänkande för vidare studier och i vardagslivet kan lösa problem och omsätta idéer i handling på ett kreativt sätt
 Lokal pedagogisk planering Matematik år 2 Syfte Undervisningen i matematikämnet ska syfta till att eleverna ska utveckla kunskaper om matematik och visa intresse och tilltro till sin förmåga att använda
Lokal pedagogisk planering Matematik år 2 Syfte Undervisningen i matematikämnet ska syfta till att eleverna ska utveckla kunskaper om matematik och visa intresse och tilltro till sin förmåga att använda
22,5 högskolepoäng. Provmoment: Ladokkod: Tentamen ges för: Matematik 3hp. Studenter i inriktningen GSME. TentamensKod:
 SMID Provmoment: Ladokkod: Tentamen ges för: TentamensKod: Matematik 3hp Studenter i inriktningen GSME 22,5 högskolepoäng Tentamensdatum: 12-08-30 Tid: 09.00-13.00 Hjälpmedel: Inga Totalt antal poäng på
SMID Provmoment: Ladokkod: Tentamen ges för: TentamensKod: Matematik 3hp Studenter i inriktningen GSME 22,5 högskolepoäng Tentamensdatum: 12-08-30 Tid: 09.00-13.00 Hjälpmedel: Inga Totalt antal poäng på
Tränarguide del 2. Mattelek. www.flexprogram.se
 Tränarguide del 2 Mattelek www.flexprogram.se 1 ANTALSUPPFATTNING - MINST/STÖRST ANTAL Övningarna inom detta område tränar elevernas uppfattning av antal. Ett antal objekt presenteras i två separata rutor.
Tränarguide del 2 Mattelek www.flexprogram.se 1 ANTALSUPPFATTNING - MINST/STÖRST ANTAL Övningarna inom detta område tränar elevernas uppfattning av antal. Ett antal objekt presenteras i två separata rutor.
Målkriterier Beskrivning Exempel Eleven kan tolka elevnära information med matematiskt innehåll.
 ÖREBRO MATEMATIK, ÅR 3 1(5) Eleven kan tolka elevnära information med matematiskt innehåll Eleven kan uttrycka sig muntligt, skriftligt och i handling på ett begripligt sätt med hjälp av vardagligt språk,
ÖREBRO MATEMATIK, ÅR 3 1(5) Eleven kan tolka elevnära information med matematiskt innehåll Eleven kan uttrycka sig muntligt, skriftligt och i handling på ett begripligt sätt med hjälp av vardagligt språk,
Matematik. Mål att sträva mot. Mål att uppnå. År 1 Mål Kriterier Eleven ska kunna. Taluppfattning koppla ihop antal och siffra kan lägga rätt antal
 Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Student 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Student 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Lokal studieplan matematik åk 1-3
 Lokal studieplan matematik åk 1-3 Kunskaps område Taluppfat tning och tals användni ng Centralt Innehåll Kunskapskrav Moment Åk1 Moment Åk2 Moment Åk3 Naturliga tal och deras egenskaper samt hur talen
Lokal studieplan matematik åk 1-3 Kunskaps område Taluppfat tning och tals användni ng Centralt Innehåll Kunskapskrav Moment Åk1 Moment Åk2 Moment Åk3 Naturliga tal och deras egenskaper samt hur talen
Upprepade mönster kan talen bytas ut mot bokstäverna: A B C A B C eller mot formerna: Anna-Lena Ekdahl, Högskolan i Jönköping
 Algebra Del 1 Upprepade mönster Anna-Lena Ekdahl, Högskolan i Jönköping Det är välkänt att barn långt innan de börjat skolan utforskar och skapar mönster på olika sätt och med olika material. Ofta skapas
Algebra Del 1 Upprepade mönster Anna-Lena Ekdahl, Högskolan i Jönköping Det är välkänt att barn långt innan de börjat skolan utforskar och skapar mönster på olika sätt och med olika material. Ofta skapas
Matematik. Ämnesprov, läsår 2014/2015. Bedömningsanvisningar Delprov B, C, D, E. Årskurs
 Ämnesprov, läsår 2014/2015 Matematik Bedömningsanvisningar Delprov B, C, D, E Årskurs 6 Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Ämnesprov, läsår 2014/2015 Matematik Bedömningsanvisningar Delprov B, C, D, E Årskurs 6 Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
