Kängurun Matematikens hopp
|
|
|
- Niklas Larsson
- för 9 år sedan
- Visningar:
Transkript
1 Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare med problem i klassen. Kungl Vetenskapsakademien & NCM/Nämnaren 1
2 Svar och lösningar 1: C onsdag Åtta bokstäver kräver en vecka + en dag. 2: E 3: E Bitarna har tillsammans lika många inbuktningar som utbuktningar. Figuren i E har tre utbuktningar men bara en inbuktning, vilket inte går att få. 4: D 750 liter 1/4 av vattenmängden hamnar i behållare X och resten i behållare Y. 5: A kvadrat Alla andra är möjliga. En kvadrat är omöjlig att dela i två kvadrater med ett snitt eftersom snittet skulle behöva dela alla fyra sidor. 6: E 167 Summan måste vara 167 eller 96 (de tre termerna måste alla vara lägre än summan). Med överslag och kontroll av entalssiffrorna hittar vi = 96. 7: A 3 Om hon hade givit ett fel svar hade hon fått = 18 poäng, två felsvar ger = 16, tre felsvar = 14. Alla rätt hade givit 20 poäng, varje fel leder till 2 poäng färre, dels den förlorade pluspoängen och dels minuspoängen. Eller: Hon fick 4 poäng för 4 rätta svar. De övriga 6 fick hon ingenting för, därför att de var lika många rätt som fel, alltså tre rätt och tre fel. 8: B 13 Vi har ritat en väg som ger Fridolin 13 frön. Ett frö ligger i en återvändsgränd så det kan Fridolin inte plocka, för då skulle han fastna där eftersom han inte får passera samma ställe två gånger. Det finns flera möjliga vägar och Fridolin kan komma åt vilket frö som helst utom det i återvändsgränden, men inte fler än 13. Ett sätt att visa att 13 är det maximala antalet finns beskrivet i Arbeta vidare med problemen. Kungl Vetenskapsakademien & NCM/Nämnaren 2
3 9: A ; ; ; ; Det finns endast 12 månader, vilket utgör den första begränsningen. 10: C Disa, Sofia, Pia, Maja Arbeta baklänges. 11: D 56 Längs varje sida är det 5 svarta och 4 vita plattor, enligt mönstret. Totalt har golvet 9 9 = 81 rutor = : B 891 Talen på vardera sidan om 2011 är 1210 och = : C 64 Fyra kuber ligger utanför områdets sida, i hörnen. Det kvadratiska området får sidan 8. 14: B 3 0 Den match de förlorade måste vara den match då de släppte in ett mål. Den oavgjorda matchen blev alltså mållös. Återstår 3 mål till den match som de vann. 15: D D är den enda bit som kan spärra för de övriga, och bilden visar hur den gör det. 16: D 4 Punkterna mellan 1 och 2 och mellan 2 och 3 måste markeras med 4. Fortsätter vi undersöka ser vi att det måste bli fyra 4, varannan punkt. Vid den återstående punkten kan det dock stå 1, 2 eller 3, men inte 4. 17: C 3 Punkten ska sättas så att den utgör det fjärde hörnet i en parallellogram. Detta hörn ska ligga diagonalt mot ett av de andra hörnen vilket innebär att det finns tre möjligheter. 18: A fem onsdagar Eftersom det bara finns fyra fredagar och fyra måndagar måste månadens första dag infalla på den första lördagen. De följande lördagarna blir 8, 15, 22 och 29. Eftersom det inte finns fem måndagar är detta en månad med 30 dagar. Den första i följande månad är alltså en måndag. Alla månader med 30 dagar följs av en månad med 31 dagar vilket ger att den 31 är en onsdag. Det finns alltså fem måndagar, tisdagar och onsdagar i den följande månaden. Kungl Vetenskapsakademien & NCM/Nämnaren 3
4 19: C 2 Antag att Simba talar sanning. Då ljuger Murre, Puma talar sanning ochtiger ljuger. Antag att Simba ljuger. Då talar Murre sanning, Puma ljuger och Tiger talar sanning. I båda fallen är det två katter som ljuger och två som talar sanning. 20: E 6 Eftersom de sidor som möts ska ha summan 5 kan det bara vara 2, 3 eller 4 på den nedersta tärningens översida. På den nedersta tärningen kan det inte vara 4, för det skulle leda till att den mellersta tärningen hade 1 och 6 på de sidor som möter de andra tärningarna. Den nedersta tärningen har alltså 2 eller 3 uppåt. 3 leder till att den mellersta tärningen har 2 nedåt och 5 uppåt, det går inte. Om den nedersta tärningen har 2 uppåt får vi 3 och 4 på den mellersta tärningens sidor och 1 och 6 på den översta. Eller: Översidan på den nedersta tärningen och undersidan på den mellersta har tillsammans 5 prickar. Översidan på den mellersta tillsammans med undersidan har sammanlagt 7 prickar. Översidan på den mellersta har alltså två fler prickar än översidan på den nedersta. Samma resonemang ger att översidan på den översta tärningen (markerad med x) har två prickar fler än översidan av den mellersta, alltså fyra fler än översidan av den nedersta som har minst två eftersom ettan är på sidan. Alltså har den kryssmarkerade inte färre än sex. 21: D 56 cm 2 Den längre kateten är 14 cm. Två sådana + den korta kateten är 30 cm, så den korta kateten är 2 cm. Två trianglar har den sammanlagda arean 28 cm 2, alltså är den sammanlagda arean 56 cm 2. Kungl Vetenskapsakademien & NCM/Nämnaren 4
5 Arbeta vidare med Benjamin 2011 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta eleverna resonera sig fram till lösningarna i grupp. Låt alla först få möjlighet att lösa problemen på egen hand om de inte hann det i samband med tävlingen. Diskutera gruppernas lösningar i klassen och jämför idéer och angreppssätt. Låt också eleverna få granska kamraternas lösningar: Har de tagit hänsyn till alla förutsättningar? Är de tydliga? Är resonemanget korrekt? Fungerar lösningsmetoden på andra, liknande problem? Att analysera och diskutera varandras lösningar är bra, men det kräver förstås att man arbetar lång siktigt så att eleverna vänjer sig vid att både ge kritik på ett konstruktivt sätt och att ta emot kritik. Om de redan från början får uppleva att det är en del av undervisningen kan det bli en naturlig och uppskattad form av arbete med problem. Att presentera en lösning som andra kan följa och som är korrekt uppbyggd är något som eleverna måste få tid och möjlighet att utveckla med hjälp av lärare. Välj några av årets problem och arbeta igenom lösningarna noga och gör en riktigt genomarbetad redovisning. Alla problem kan naturligtvis diskuteras utifrån valda lösningsmetoder. De flesta problem kan lösas på olika sätt och det är alltid bra att jämföra dessa och se på likheter och skillnader. Det är också bra att beskriva lösningarna med hjälp av olika representationsformer, konkret material, bilder, muntligt eller skriftligt tal och med symboler. Jämför de olika formerna och se hur det konkreta uttrycks i ord och med symboler. Några frågor att återkomma till när problemet är löst: Kontrollera att lösningen verkligen svarar mot frågan. Är det ett rimligt svar? Hur vet vi det? Påminner problemet om något annat problem vi löst tidigare? Vilka kunskaper hade vi nytta av när vi löste problemet? Vilka nya frågor kan problemet väcka? Lärde vi oss något nytt av problemet? Gå också igenom de felaktiga svarsalternativen och resonera om varför dessa inte är riktiga. Låt eleverna göra förändringar i uppgiften så att de andra alternativen blir riktiga. Utmaningen kan vara att göra så små förändringar som möjligt. Matematiskt arbete handlar mycket om resonemang. Elever behöver få resonera om både matematik innehållet och om strategier för att utveckla sin matematiska kompetens. Låt dem också få argumentera för sina lösningar och sina val av metoder. I arbetet med alla problem bör förmågorna att resonera och argumentera vara centrala. I samband med diskussion av problemen kommer ett antal termer att aktualiseras. Gå igenom dem. Låt eleverna använda och själva få definiera olika begrepp och återkom till dem i olika sammanhang. Några exempel från årets Benjamin: rätblock, kub, parallellogram, rektangel, kvadrat, triangel, rätvinklig, likbent, area, heltal, addition. För definitioner hänvisar vi till Matematiktermer för skolan (Kiselman & Mouwitz, 2008) Här har vi sorterat förslag under några rubriker. Naturligtvis kan flera av problemen också passa under andra rubriker. Många problemtyper återkommer år från år, i olika skepnader och i olika varianter. Här har vi hänvisat till några gamla problem som kan användas i samband med arbetet med årets, men det finns många fler att hämta på Kängurusidan på nätet, ncm.gu.se/kanguru, där alla tidigare omgångar är samlade. Tidigare problem inom området geometri finns dessutom samlade i boken Geometri och rumsuppfattning med känguruproblem. Läs mer om den på ncm.gu.se/node/4742. Kungl Vetenskapsakademien & NCM/Nämnaren 1
6 Logiskt resonemang och problemlösningsstrategier Att välja en effektiv strategi är viktigt i alla problem, men i några av årets problem står valet av strategier och resonemang i centrum, t ex i 8, 10, 14, 16, 19 och Labyrinten. Det finns flera möjliga vägar för Fridolin, som kan komma åt vilket frö som helst utom det i återvändsgränden. Men han kan inte komma åt fler än 13. Ett sätt att visa detta: Ingång Vi markerar pumpafrön på så sätt att vart och ett av de 21 gångavsnitten (tunnlarna) förbinder ett markerat pumpafrö med ett omarkerat. Vi får 6 markerade fön. Fridolin börjar vid ingången. Där ligger det första fröet, omarkerat. Tunneln som börjar där, slutar vid ett markerat frö. Det blir det andra fröet. Därifrån kommer Fridolin till ett tredje frö som är omarkerat vilken riktning han än väljer. Så kommer det att fortsätta, det fjärde markerat, det femte omarkerat, det sjätte markerat osv. Vartannat är markerat och vartannat omarkerat. Det blir därför lika många markerade som omarkerade frön som Fridolin kan plocka på sin väg. Men han får också ett extra omarkerat eftersom vägen både börjar och slutar med ett sådant. Det kan ligga högst 6 markerade pumpafrön utefter Fridolins väg, eftersom det inte finns fler och högst alltså 7 omarkerade, tillsammans högst 13 pumpafrön. Finns det en väg från ingången till utgången med exakt 10 frön på? Vilka olika antal är det möjligt för Fridolin att få? Ecolier 10 är också ett problem med labyrint. På bilden ser du en labyrint. I varje liten ruta i labyrinten ligger en bit ost. Musen Kim går in i labyrinten och vill komma åt så många ostbitar som möjligt. Han kan inte gå i samma ruta mer än en gång. Vilket är det största antal ostbitar han kan få? A: 17 B: 33 C: 37 D: 41 E: 49 Hur kan man resonera där? Diskutera vilka rutor som Kim inte ska besöka. Varför ska han inte besöka några rutor markerade med kryss? Varför inte den ruta som är markerad med cirkel? Se också Ecolier 2010, 2. Utgång 10 Bänken. Här gäller det att finna ett sätt att angripa problemet och att hantera informationen på ett strukturerat vis. Det är förmågor som är bra att ha med sig. Arbeta gärna konkret med problemet. Visa att det går bra att arbeta baklänges för att komma fram till lösningen. Se också C 2005, 17; E 2007, 14; B 2007, 13; E 2008, 3; B 2008, 19 & E 2010, 17, som alla kräver att man strukturerar information. Kungl Vetenskapsakademien & NCM/Nämnaren 2
7 14 Fotbollsmatchen. Analysera de olika svarsalternativen och hur de stämmer med förutsättningarna. Låt eleverna konstruera liknande problem till varandra. Undersök resultattabeller i tidningen. För en del elever kan det vara motiverande att se att matematik används i för dem relevanta sammanhang. Undersök vilka konsekvenser det får med andra sätt att värdera vinst, oavgjort och förlust än de som används i tabellsammanhang. Skulle man kunna ha minuspoäng vid förlust? Jämför med problem 7, Frågesporten. 16 Åttahörningen. Om eleverna inte redan har upptäckt att det kan stå antingen 1, 2 eller 3 på en av punkterna kan de undersöka det. Ta bort 1, 2 eller 3 från ursprungsproblemet och undersök om det påverkar lösningen. Hur många olika siffror måste vi som minst använda? Junior 4 är ett liknande problem: Figuren visar en bild av grafén. Vid varje punkt ska ett tal skrivas. 4 Summan av talen vid två närliggande punkter ska vara densamma. Två av talen är redan inskrivna. x Vilket tal ska skrivas vid punkten märkt x? 1 A: 1 B: 3 C: 4 D: 5 E: mer information behövs 19 Katterna tillhör en typ av problem med lögnare och sanningssägare som ibland förekommer i Kängurun. Sådana problem ställer krav på resonemangsförmågan. Ett sätt att hantera sådana problem är att göra ett antagande och sedan undersöka vad det leder till. Tidigare problem C 2002, 12; C 2004, 18; J 2007, 10; C 2008, 17, C 2009, 13, B 2010, 21 och GyC 2010, Tärningarna. Låt eleverna pröva att ändra förutsättningarna, t ex så att summan av prickarna på de sidor som möts ska vara 7 eller 6. Vilket är den lägsta möjliga summan? Varför? Vilket är den största? Se också aktiviteten Rika tärningar som finns på Nämnarens webbplats, ncm.gu.se/namnaren, under artikelregister, sök på Rika tärningar. Tärningar kan användas för spatiala problem, som i det som finns på årets Ecolier, nummer 18. Där handlar det om att föreställa sig och resonera om hur ett tärningsbygge ser ut från andra sidan. Vi har samlat ett antal tidigare tärningsproblem i ett dokument som finns att hämta på ncm.gu.se/ media/namnaren/kanguru/2011/arb_tarningar_2011.pdf. Se också E 2007, 9; E 2009, 15; B 2001, 20; B 2010, 14 och 18. Mönster När vi i matematik talar om mönster menar vi något som upprepas efter en speciell regel. Det kan vara tal, former och förändringar. Mönster är centralt i matematiskt arbete. I skolan handlar problem ofta om att eleverna ska fortsätta ett figurativt mönster, så som i problem 11. Avsikten är bland annat att de ska utveckla sin förståelse för formler och generaliseringar. Den typen av problem passar mycket bra för att gå mellan olka representationer. Vi skapar mönstret konkret eller med bilder, uttrycker det muntligt och skriftligt med ord och med symboler, i text eller tabeller. Att uttrycka samband och begrepp med olika representationer är bra för att utveckla förståelsen. Nämnaren 2011, nr 2 behandlar mönster och undervisning om mönster på olika nivåer. Boken Rika matematiska problem (Hagland, Hedrén & Taflin, 2005) ger konkreta råd och stöd för undervisningen. 11 Golvplattorna är ett typiskt exempel på mönsterproblem. Bygg eller rita och undersök systematiskt. Gör en tabell över antalet svarta längs sidan, hela sidan, totalt antal svarta och antalet plattor totalt. Diskutera och jämför. Låt eleverna uttrycka mönstret skriftligt och muntligt och med symboler. Som ett steg i att utveckla formler kan de uttrycka mönstret med en blandning av skrivna ord och symboler. Kungl Vetenskapsakademien & NCM/Nämnaren 3
8 I en mycket tidig omgång av Kängurun förekom detta problem: Jan och Lars lägger ett kvadratiskt mönster av lika stora, kvadratiska brickor. Lars lägger en röd bricka i mitten. Sedan lägger Jan 8 gröna brickor runt omkring den, för att bygga en andra kvadrat. Lars fortsätter sedan och lägger 16 gula brickor runt dessa, för att bygga en tredje kvadrat. Hur många brickor kommer Lars att behöva för att bygga den femte kvadraten? a: 32 b: 64 c: 81 d: 121 e: 125 Några förslag på frågeställningar: Jämför antalet brickor i ramkvadraterna och antalet brickor i hela figuren. Vilka tal beskriver antalet i hela figuren? Varför? Hur många brickor finns på varje sida i de olika kvadraterna? Hur fortsätter det? Varför är det bara udda antal? Studera talserien som uppstår för ramkvadraterna: 1, 8, 16, 24, Hur fortsätter den? Varför? Problem 17 handlar om kvadrater, liksom problem 13, Ramen. Bygg ramen konkret eller rita. Resonera gemensamt om hörnens betydelse. Hur stort område finns innanför en ram med sidan 2? Varför? Fyll området i problemet med kuber och resonera om volymen. Undersök kvadraterna och låt gärna eleverna lära sig kvadraterna upp till Undersök talserien =. Bygg eller rita så att sambandet med kvadraterna blir tydligt och resonera med eleverna om det. Undersök också talserien = på motsvarande sätt. I Geometri och rumsuppfattning med känguruproblem finns ett kapitel med rubriken Mönster. Där finns ytterligare problem och förslag till hur man kan arbeta. Se också Benjamin 2002, 24; E 2006, 12 och 20; E 2007, 18; Benjamin 2007, 11; E 2008, 5. Kalenderproblem Problem 18, Fem lördagar och söndagar, aktualiserar kalendern. Att undersöka almanackan tycker många elever i den här åldern är intressant. Det är mycket som är lätt att ta för givet om man redan kan det, men för eleverna kan det vara nya upptäckter. Undersök hur året är indelat: kvartal, månader, veckor. Hur många veckor går det på ett år? Är det exakt 52 veckor? Är det alltid vecka 1 den 1 januari? Hur är det med elevernas kunskaper om antal dagar i respektive månad? Känner de till ramsan, 30 dagar har november, april, juni och september, 28 en allen, alla de övriga 31. Den stämmer om det inte är skottår, då har februari 29 dagar. Resonera om antal olika veckodagar i en månad med 28, 30 respektive 31 dagar. Låt eleverna markera innevarande månad i en tabell: måndag tisdag onsdag torsdag fredag lördag söndag Alla månader som har 30 dagar följs av en månad med 31 dagar, men en månad med 31 dagar kan följas av en månad med 28 (29), 30 eller 31 dagar. Vilket halvår har flest dagar? Är skolans vår- eller höst termin längst? Hur många söndagar kan en månad ha som mest? Som minst? Kungl Vetenskapsakademien & NCM/Nämnaren 4
9 Årets Junior 10 är också ett kalenderproblem: I en viss månad fanns det 5 måndagar, 5 tisdagar och 5 onsdagar. I den föregående månaden fanns det bara 4 söndagar. Vilket av följande gäller definitivt för den efterföljande månaden? Den har A: exakt 4 fredagar B: exakt 4 lördagar C: 5 lördagar D: 5 onsdagar E: situationen är omöjlig Problem kring almanackan har förekommit i flera tidigare Kängurutävlingar, t ex: B 2004, 15; C 2004, 10; C 2006, 11; Benjamin 2007, 7. Geometri Som vanligt handlar flera problem om geometri. Det är naturligtvis ibland lättast att lösa dem konkret, men syftet med problemen är inte att hitta det korrekta svaret i första hand. Det konkreta arbetet ska hjälpa eleverna att få förståelse. Därför är det också viktigt att samtala om det konkreta arbetet och lyfta fram de samband som ska illustreras. Under tävlingen har eleverna löst problemen utan hjälp medel. I efterarbetet kan eleverna jämföra hur de tänkt, dvs deras föreställning, med en konkret representation. Att tolka en tredimensionell bild exempelvis är inte lätt och många måste få återkommande möjligheter att jämföra bild och verklighet för att utveckla den förmågan. 2 Klossbygge. Låt eleverna konstruera det nästan fädiga bygget till de andra alternativen. De kan sedan göra liknande problem till varandra konkret, men där kamraten först får försöka lösa det utan att röra klossarna, bara titta. Bygg efter ritning och rita av byggen ur olika perspektiv. Diskutera hur de olika alternativen ska beskrivas. Låt eleverna arbeta i par där den ena bygger och beskriver sitt bygge för kamraten, som inte får se hur det ser ut. Kamraten ska försöka bygga efter beskrivningen. Tala om betydelsen av att uttrycka sig tydligt med termer som vi är överens om betydelsen av. Låt eleverna bestämma det totala antalet klossar i olika rätblock. Hjälp dem att upptäcka strukturen: antalet klossar i en rad, antalet rader i ett plan, antalet plan. Behandla olika volymenheter och diskutera när de används. I nästan alla tidigare Kängurutävlingar finns det problem med klossar. Se också i boken Geometri och rumsuppfattning där dessa klossproblem är samlade och kommenterade med förslag för undervisningen. 3 Pusselbitarna. Undersök alla möjligheter att pussla ihop de fyra bitarna och se om det stämmer att antalet utbuktningar och inbuktningar antingen är lika många eller tar ut varandra. Låt eleverna göra liknande problem till varandra. Liknande problem är E 2008, Kvadratiska pappret och 17 Hörnen i en parallellogram behandlar grundläggande geometriska objekt. Många elever känner igen och kan rätt benämna flera geometriska begrepp, men de behöver också få arbeta med definitioner. Diskutera egenskaper, se på antal sidor och antal hörn, på vinklar och symmetrier. Utgå från begreppet månghörning och gå sedan stegvis genom fyrhörningar, parallelltrapetser, parallellogram, rektanglar och till sist den speciella månghörningen kvadrat. Vilka egenskaper är gemensamma för alla? Vad är det som utmärker kvadraten och endast gäller för den? Vad är en romb? Är kvadraten en romb? Varför? Med en bild eller diagram kan man klargöra samband och illustrera att alla kvadrater är rektanglar, kvadraten är en delmängd av rektanglar, och att rektanglar är parallellogrammer etc. Kungl Vetenskapsakademien & NCM/Nämnaren 5
10 En form som saknar en svensk term är drake. Det är en fyrhörning som har två par av lika långa sidor, men där dessa sidor ligger intill varandra. Rita upp en drake och låt eleverna beskriva den utifrån dess egenskaper. Diskutera att bilder i geometri endast är idéskisser och kanske inte nödvändigtvis är perfekta bilder av de objekt de illustrerar. Visa hur vi med symboler kan markera egenskaper som har betydelse, t ex räta vinklar och lika långa sidor. Undersök hur de olika formerna i problem 5, Kvadratiska pappret, kan konstrueras. Låt eleverna få argumentera för att den form de skapat är just den de menar att det är. Hur vet du och hur kan du övertyga oss om att detta är en rektangel? Diskutera och jämför olika lösningar. Vad är lika? Vad är olika? Jämför arean av triangeln och kvadraten. Hur många räta linjer behövs för att vi ska kunna få en kvadrat? Tillåt vikningar och låt eleverna försöka att konstruera en kvadrat. Jämför storleken på den ursprungliga kvadraten och den nya. Arbeta vidare med den rätvinkliga, likbenta triangeln. Skapa ett mönster genom att i en stor sådan triangel successivt rita in mindre trianglar genom att dela sidorna mitt på: Jämför areorna av de olika trianglarna. Fortsätt att dela och att bygga på med större trianglar. Ge den inre trianglen arean 1. Hur stor är arean av de andra? Ge den största triangeln arean 1. Hur stor är arean av de andra? Variera vinkeln mellan de lika benen i triangeln och undersök vidare. Utveckla gärna till en bilduppgift och låt eleverna måla mönstret, eller till en slöjduppgift med lappar. Lek med andra geometriska former på motsvarande sätt. Att dela en form kan vara en bra utgångspunkt för resonmenag kring area. Inom detta område finns det många tidigare problematt välja bland. Några av dem är: B 2003, 15; B 2007, 14; E 2009, 2; B 2009, 2; B 2009, 9 och 13 samt C 2009, Pusslet. Undersök vilka av alternativen som kan placeras ut samtidigt, försök att få in så många som möjligt. Låt eleverna konstruera liknande problem till varandra. Resonera efteråt om hur de bitar som spärrar ska vara konstruerade. Pentomino är ett klassiskt pussel. Bitarna består av fem kvadrater, därav namnet (penta = fem på grekiska). Visa på ordlikheten och låt eleverna ta reda på vad pentagon, Pentagon (i Washington), pentagram är. På hur många sätt kan man sätta samman fem kvadrater, om de ska sättas sida mot sida? Låt eleverna undersöka. Bygg ihop bitarna på olika sätt. Om pentomino finns en mängd att läsa på webben. Se också problem i Geometri och rumsuppfattning. 21 Fyra trianglar i en rektangel. Här utnyttjar vi att arean av en triangel är hälften av en rektangel. Hur stort är det vita området? Diskutera vilka mått och förutsättningar som är viktiga i problemet. Ett tidigare problem är C 2007, 6. Kungl Vetenskapsakademien & NCM/Nämnaren 6
11 Tal 4 Vattenledningen. Här får vi en konkret illustration för bråkräkning. Diskutera vad hälften av hälften är. Kanske känner någon igen ett gammalt uttryck: En halv halv kalv och en fjärdedel därifrån. Se på andra språkliga uttryck, t ex hälften av en tredjedel, hälften av en sjättedel. Att förstå hälften av en fjärdedel är ofta lättare än 1/2 1/4. Resonera om kopplingen mellan dessa uttryckssätt. Variera mängden vatten i rören och dela upp vattenledningen i flera grenar. Se också B 2008, Tal i rutor. Låt eleverna göra flera liknande problem och använd dem för återkommande överslagsräkning. Diskutera strategier, t ex att först inse att inget av de tre minsta talen kan vara summan och sen att se på entalssiffrorna. 7 Frågesportsreglerna. Undersök andra poängtal. Vilka är möjliga? Variera problemet med olika poängtal. Diskutera varför det alltid blir ett jämnt tal med dessa regler. Se efter mönster. 9 Datumtal. Gör motsvarande med jämna tal. Är de fler, färre eller lika många? Varför? Lek med olika serier, t ex primtal, multiplar av 3, 4 och 5. Låt eleverna anteckna roliga datum och berätta varför de är speciella. Att leka med tal är ett sätt att bekanta sig med tal och på det sättet utveckla sin taluppfattning. Det är också ett sätt att se hur tal används i vår omvärld. i samband med detta problem är det lämpligt att resonera om hur tiden räknas, vad årtalet står för och hur man kan beräkna tidens gång. Det är inte självklart för alla elever i dessa åldrar att åldersskillnaden mellan två personer förblir densamma. Pigan Lina hos Emil i Lönneberga hade vissa problem med det. Läs gärna det avsnittet för eleverna, de flesta kommer säkert att förstå det roliga nu även om det gick dem förbi när de som små lyssnade på berättelsen. Även problem 12, Talet 2011 kan vi använda för att få undersöka och leka med tal. Vilka av de listade talen är primtal? Varför är inget av talen delbart med 3? Diskutera och undersök delbarhetsregler med 2, 5, 10, 3 och 4. Vilket är det största fyrsiffriga talet? Det minsta? Lista alla fyrsiffriga tal med siffersumman 4. Vilka andra tal har siffersumman 4? Ett dokument med flera problem kring talet 2011 att arbeta vidare med finns att hämta på: ncm.gu.se/ media/namnaren/kanguru/2011/arb_talet_2011.pdf. Att läsa Hagland, K., Hedrén, R. & Taflin, E. (2005). Rika matematiska problem inspiration till variation. Stockholm: Liber. Kiselman, C. & Mouwitz, L. (2008). Matematiktermer för skolan. NCM, Göteborgs universitet. McIntosh, A. (2008). Förstå och använda tal. NCM, Göteborgs universitet. Rystedt, E. &Trygg, L. (2010). Laborativ matematikundervisning vad vet vi? NCM, Göteborgs universitet. Nämnaren. I varje nummer finns Problemavdelningen och Kängurusidan. Läs också tidigare artiklar kring problemlösning. Nämnarenartiklar publicerade finns fritt tillgängliga som pdf-dokument på Nämnaren på nätet, namnaren.ncm.gu.se. Du finner dem via artikeldatabasen. Under ArkivN finns alla publicerade Uppslag och Problemavdelningar samlade. Nämnaren på nätet presenterar varje månad nya problem under rubriken Månadens problem. Strävorna finns på ncm.gu.se/stravorna. Där finns aktiviteter, problem och artiklar samlade och ordnade efter kursplanen. Kungl Vetenskapsakademien & NCM/Nämnaren 7
A: måndag B: tisdag C: onsdag D: torsdag E: fredag. Vilken av följande bitar behöver vi för att det ska bli ett rätblock?
 Trepoängsproblem 1 Doris gör en skylt till djurparken. På skylten ska det stå ordet KÄNGURUR. Hon målar en bokstav varje dag. Hon målar den första på en onsdag. Vilken dag kommer hon att måla den sista
Trepoängsproblem 1 Doris gör en skylt till djurparken. På skylten ska det stå ordet KÄNGURUR. Hon målar en bokstav varje dag. Hon målar den första på en onsdag. Vilken dag kommer hon att måla den sista
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Arbeta vidare med Ecolier 2010
 Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte.
 Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Lösningsförslag Cadet 2014
 Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder till svaret 6.
 Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Svar och lösningar Benjamin
 Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A 1 9999 + 1= 10 000. Talet
Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A 1 9999 + 1= 10 000. Talet
Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurutävlingen 2017 NCM 1
 Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt.
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
3: A I den vita asken. Kolan ligger i den röda asken så chokladbiten måste ligga i den vita. Problemet kan lösas konkret och med en enkel bild.
 Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
Kortfattade lösningar med svar till Cadet 2006
 3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
Arbeta vidare med Milou 2008
 Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Arbeta vidare med Junior 2010
 Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Svar och lösningar Ecolier
 Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt
Kängurutävlingen Matematikens hopp Junior 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt
Svar och arbeta vidare med Benjamin 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Trepoängsproblem. Kängurutävlingen 2011 Cadet. 1 Vilket av följande uttryck har störst värde? 1 A: B: C: D: E: 2011
 Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Svar och lösningar Benjamin
 Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant?
 En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
4. A. 4, 6, 11 Viker man ihop till en kub, så kommer talet 1 mitt emot 3, 2 mitt emot 4 och 5 mitt emot 6. Det ger summorna 4, 6, 11.
 N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 4 C: kvadrat Exempel på hur formerna kan konstrueras:
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Kängurun Matematikens hopp
 Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Kortfattade lösningar med svar till Gymnasiets Cadet 2006
 Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Svar och arbeta vidare med Cadet 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Svar och korta lösningar Benjamin 2006
 3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. De flesta problem kan lösas på flera sätt och med olika representationsformer.
Kängurun Matematikens hopp Ecolier 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. De flesta problem kan lösas på flera sätt och med olika representationsformer.
Svar och lösningar. Kängurutävlingen 2009 Cadet för gymnasiet
 Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Arbeta vidare med Benjamin
 Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Välkommen till Kängurutävlingen Matematikens hopp 17 mars Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2019, facit och kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Kängurun Matematikens hopp Milou 2019, facit och kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Avdelning 1, trepoängsproblem
 Avdelning, trepoängsproblem. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Stjärnan i figuren har bildats av 2 identiska, liksidiga trianglar. Stjärnans omkrets
Avdelning, trepoängsproblem. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Stjärnan i figuren har bildats av 2 identiska, liksidiga trianglar. Stjärnans omkrets
Avdelning 1, trepoängsproblem
 Avdelning 1, trepoängsproblem 1. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Var är kängurun? A: I cirkeln och i triangeln, men inte i kvadraten. B: I cirkeln
Avdelning 1, trepoängsproblem 1. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Var är kängurun? A: I cirkeln och i triangeln, men inte i kvadraten. B: I cirkeln
A: 111 B: 900 C: 909 D: 990 E: 999
 3-poängsproblem 1. 1000 100 + 10 1 =? A: 111 B: 900 C: 909 D: 990 E: 999 2. Miriam har 16 kort, fyra av varje färg: 4 spader, 4 klöver, 4 ruter och 4 hjärter. Hon vill lägga dem på rutnätet här bredvid
3-poängsproblem 1. 1000 100 + 10 1 =? A: 111 B: 900 C: 909 D: 990 E: 999 2. Miriam har 16 kort, fyra av varje färg: 4 spader, 4 klöver, 4 ruter och 4 hjärter. Hon vill lägga dem på rutnätet här bredvid
5: D 3 23 kan bara fås på ett sätt: Här har man nytta av att känna igen 24 som ett tal i sexans tabell.
 Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens
Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens
Svar och arbeta vidare med Student 2008
 Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Känguru 2018 Benjamin (åk 6 och 7)
 sida 0 / 8 NAMN KLASS Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Ett rätt svar ger 3, 4 eller 5 poäng. I varje uppgift är exakt ett svar korrekt.
sida 0 / 8 NAMN KLASS Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Ett rätt svar ger 3, 4 eller 5 poäng. I varje uppgift är exakt ett svar korrekt.
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Avdelning 1. A: måndag B: tisdag C: onsdag D: torsdag E: fredag. 2 Vi vill att vågen ska väga jämnt. Vilken sten ska vi lägga på den högra sidan?
 Avdelning 1 1 Doris gör en skylt till djurparken. På skylten ska det stå ordet KÄNGURUR. Hon målar en bokstav varje dag. Hon målar den första på en onsdag. Vilken dag kommer hon att måla den sista bokstaven?
Avdelning 1 1 Doris gör en skylt till djurparken. På skylten ska det stå ordet KÄNGURUR. Hon målar en bokstav varje dag. Hon målar den första på en onsdag. Vilken dag kommer hon att måla den sista bokstaven?
Matematikbokens Prio kapitel Kap 3,.,Digilär, NOMP
 Geometri Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, - använda och analysera begrepp
Geometri Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, - använda och analysera begrepp
Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Trepoängsproblem. Kängurutävlingen 2011 Junior
 Trepoängsproblem 1 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen börjar och slutar med ett vitt streck. På Storgatan har ett övergångsställe totalt åtta vita
Trepoängsproblem 1 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen börjar och slutar med ett vitt streck. På Storgatan har ett övergångsställe totalt åtta vita
Känguru 2011 Benjamin (Åk 6 och 7)
 sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara den frågan. Gissa inte, felaktigt
sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara den frågan. Gissa inte, felaktigt
Matematikbokens Prio kapitel Kap 3,.,Digilär, NOMP
 Geometri Syftet undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem hjälp av matematik samt värdera valda strategier och metoder, - använda och analysera begrepp och samband
Geometri Syftet undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem hjälp av matematik samt värdera valda strategier och metoder, - använda och analysera begrepp och samband
Kängurutävlingen Matematikens Hopp Benjamin 2003 Uppgifter
 Kängurutävlingen Matematikens Hopp Uppgifter Arrangeras av Kungl. Vetenskapsakademien & NCM/Nämnaren 3-poängsuppgifter 1. Tomas har 9 hundrakronors-sedlar, 9 tiokronor och 10 enkronor. Hur mycket pengar
Kängurutävlingen Matematikens Hopp Uppgifter Arrangeras av Kungl. Vetenskapsakademien & NCM/Nämnaren 3-poängsuppgifter 1. Tomas har 9 hundrakronors-sedlar, 9 tiokronor och 10 enkronor. Hur mycket pengar
Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
1 B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3.
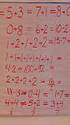 Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Känguru 2011 Cadet (Åk 8 och 9)
 sida 1 / 7 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara den frågan. Gissa inte, felaktigt
sida 1 / 7 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara den frågan. Gissa inte, felaktigt
Matematik. Mål att sträva mot. Mål att uppnå. År 1 Mål Kriterier Eleven ska kunna. Taluppfattning koppla ihop antal och siffra kan lägga rätt antal
 Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Matematik 92MA41 (15hp) Vladimir Tkatjev
 Matematik 92MA41 (15hp) Vladimir Tkatjev Med anledning av de nya kursplanerna har Strävorna reviderats. Formen, en matris med rutor, är densamma men istället för att som tidigare anknyta till mål att sträva
Matematik 92MA41 (15hp) Vladimir Tkatjev Med anledning av de nya kursplanerna har Strävorna reviderats. Formen, en matris med rutor, är densamma men istället för att som tidigare anknyta till mål att sträva
Ma7-Per: Geometri. Det tredje arbetsområdet handlar om geometri.
 Ma7-Per: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda
Ma7-Per: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda
Bagarmossens skolas kravnivåer beträffande tal och talens beteckningar som eleven ska ha uppnått efter:
 Matematik 1-5 Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och
Matematik 1-5 Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och
Gymnasiets Cadet. a: 2 b: 4 c: 5 d: 6 e: 11
 Gymnasiets Cadet Avdelning 1. Trepoängsproblem 1. I en klass finns 1 flickor och 9 pojkar. Hälften av eleverna i klassen är förkylda. Vilket är det minsta antalet flickor som är förkylda? a: 2 b: 4 c:
Gymnasiets Cadet Avdelning 1. Trepoängsproblem 1. I en klass finns 1 flickor och 9 pojkar. Hälften av eleverna i klassen är förkylda. Vilket är det minsta antalet flickor som är förkylda? a: 2 b: 4 c:
Välkommen till Kängurun Matematikens hopp 2008 Benjamin
 Till läraren Välkommen till Kängurun Matematikens hopp 2008 enjamin Kängurutävlingen genomförs april. Om den dagen inte passar går det bra 4 april eller veckan därpå, däremot inte tidigare. Se till att
Till läraren Välkommen till Kängurun Matematikens hopp 2008 enjamin Kängurutävlingen genomförs april. Om den dagen inte passar går det bra 4 april eller veckan därpå, däremot inte tidigare. Se till att
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Trepoängsproblem. Kängurutävlingen 2012 Junior
 Trepoängsproblem 1. M och N är mittpunkterna på de lika långa sidorna i en likbent triangel. Hur stor är arean av fyrhörningen markerad med X? : 3 : 4 C: 5 D: 6 E: 7 M? X 3 3 6 N 2. När lice skickar ett
Trepoängsproblem 1. M och N är mittpunkterna på de lika långa sidorna i en likbent triangel. Hur stor är arean av fyrhörningen markerad med X? : 3 : 4 C: 5 D: 6 E: 7 M? X 3 3 6 N 2. När lice skickar ett
Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
Svar och lösningar Benjamin
 Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer,
Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer,
Avdelning 1, trepoängsproblem
 Avdelning, trepoängsproblem. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Stjärnan i figuren har bildats av 2 identiska, liksidiga trianglar. Stjärnans omkrets
Avdelning, trepoängsproblem. Vilket är ett jämnt tal? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Stjärnan i figuren har bildats av 2 identiska, liksidiga trianglar. Stjärnans omkrets
Stavelsen Det talade ordet Läsa via skrivandet Strukturerad inlärning Vi arbetar i studiegrupper, dvs. ettor och tvåor tillsammans i mindre grupper.
 Stavelsen Det talade ordet Läsa via skrivandet Strukturerad inlärning Vi arbetar i studiegrupper, dvs. ettor och tvåor tillsammans i mindre grupper. Lokala mål Tala och lyssna: Jag kan lyssna och förstå
Stavelsen Det talade ordet Läsa via skrivandet Strukturerad inlärning Vi arbetar i studiegrupper, dvs. ettor och tvåor tillsammans i mindre grupper. Lokala mål Tala och lyssna: Jag kan lyssna och förstå
geometri och statistik
 Svikten geometri och statistik Innehåll Mönster Geometriska figurer Del av Matematiska ord Längd runt om Tredimensionella figurer Tabeller och diagram Problemlösning Kan du? Hur gick det? 2-3 4-5 6-7 8-9
Svikten geometri och statistik Innehåll Mönster Geometriska figurer Del av Matematiska ord Längd runt om Tredimensionella figurer Tabeller och diagram Problemlösning Kan du? Hur gick det? 2-3 4-5 6-7 8-9
Arbeta vidare med aritmetik 2018
 Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Känguru 2013 Ecolier sida 1 / 6 (åk 4 och 5) i samarbete med Pakilan ala-aste och Jan-Anders Salenius vid Brändö gymnasium
 Känguru 2013 Ecolier sida 1 / 6 NAMN KLASS Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Felaktigt svar ger minus 1/4 poäng av uppgiftens totala poängantal!
Känguru 2013 Ecolier sida 1 / 6 NAMN KLASS Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Felaktigt svar ger minus 1/4 poäng av uppgiftens totala poängantal!
Kängurutävlingen Matematikens hopp 2010 Benjamin för elever i åk 5, 6 och 7.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 200 Benjamin för elever i åk 5, 6 och 7. Kängurutävlingen genomförs den 8 mars. Om den dagen inte passar kan hela veckan 9 26 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 200 Benjamin för elever i åk 5, 6 och 7. Kängurutävlingen genomförs den 8 mars. Om den dagen inte passar kan hela veckan 9 26 mars användas,
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens Hopp Cadet 2003 Lösningar, Arbeta vidare
 Kängurutävlingen Matematikens Hopp Lösningar, Arbeta vidare Arrangeras av Många problem kan lösas på flera sätt. Följande förslag ger inte någon heltäckande beskrivning. Diskutera olika lösningsförslag
Kängurutävlingen Matematikens Hopp Lösningar, Arbeta vidare Arrangeras av Många problem kan lösas på flera sätt. Följande förslag ger inte någon heltäckande beskrivning. Diskutera olika lösningsförslag
Labora&v matema&k - för en varierad undervisning
 Labora&v matema&k - för en varierad undervisning Per Berggren & Maria Lindroth 2012-02- 23 Lgr11- Matema&ska förmågor Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar
Labora&v matema&k - för en varierad undervisning Per Berggren & Maria Lindroth 2012-02- 23 Lgr11- Matema&ska förmågor Genom undervisningen i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar
kan använda sig av matematiskt tänkande för vidare studier och i vardagslivet kan lösa problem och omsätta idéer i handling på ett kreativt sätt
 Lokal pedagogisk planering Matematik år 2 Syfte Undervisningen i matematikämnet ska syfta till att eleverna ska utveckla kunskaper om matematik och visa intresse och tilltro till sin förmåga att använda
Lokal pedagogisk planering Matematik år 2 Syfte Undervisningen i matematikämnet ska syfta till att eleverna ska utveckla kunskaper om matematik och visa intresse och tilltro till sin förmåga att använda
2. 1 L ä n g d, o m k r e t s o c h a r e a
 2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
2. 1 L ä n g d, o m k r e t s o c h a r e a Ett plan är en yta som inte är buktig och som är obegränsad åt alla håll. På ett plan kan man rita en linje som är rak (rät). En linje är obegränsad åt båda
Inledning. Polydronmaterialet. Tio områden. Lgr11-koppling
 Inledning Polydronmaterialet De färgglada bitarna i Polydronmaterialet har länge lockat till byggen av alla möjliga slag. Den geometriska funktionen är tydlig och möjligheterna till många matematiska upptäckter
Inledning Polydronmaterialet De färgglada bitarna i Polydronmaterialet har länge lockat till byggen av alla möjliga slag. Den geometriska funktionen är tydlig och möjligheterna till många matematiska upptäckter
Matematik. Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret. Mål som eleverna skall ha uppnått i slutet av det femte skolåret
 Balderskolan, Uppsala musikklasser 2009 Matematik Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret läsa och skriva tal inom talområdet 0 10 000 räkna de fyra räknesätten med olika metoder
Balderskolan, Uppsala musikklasser 2009 Matematik Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret läsa och skriva tal inom talområdet 0 10 000 räkna de fyra räknesätten med olika metoder
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
NAMN KLASS/GRUPP. Poängsumma: Känguruskutt: UPPGIFT 1 2 3 4 5 6 7 8 9 10 SVAR UPPGIFT 11 12 13 14 15 16 17 18 19 20 SVAR
 Känguru 2010 Junior (gymnasiet åk 1) sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara
Känguru 2010 Junior (gymnasiet åk 1) sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara
Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas, däremot
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 017, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på
Kängurun Matematikens hopp Ecolier 017, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på
= A: 0 B: 1 C: 2013 D: 2014 E: 4028
 Trepoängsproblem 1. 2014 2014 2014 2014 = A: 0 B: 1 C: 2013 D: 2014 E: 4028 2. Kängurutävlingen hålls den tredje torsdagen i mars varje år. Vilket datum är det senaste som tävlingen kan hållas? A: 14 mars
Trepoängsproblem 1. 2014 2014 2014 2014 = A: 0 B: 1 C: 2013 D: 2014 E: 4028 2. Kängurutävlingen hålls den tredje torsdagen i mars varje år. Vilket datum är det senaste som tävlingen kan hållas? A: 14 mars
Avdelning 1, trepoängsproblem
 vdelning 1, trepoängsproblem 1. Hur många symmetrilinjer har figuren? : 0 : 1 : 2 D: 4 E: oändligt många 2. Robert arbetar på leksaksfabriken. Han ska packa kängurur som ska fraktas till affärerna. Varje
vdelning 1, trepoängsproblem 1. Hur många symmetrilinjer har figuren? : 0 : 1 : 2 D: 4 E: oändligt många 2. Robert arbetar på leksaksfabriken. Han ska packa kängurur som ska fraktas till affärerna. Varje
Delprov A Muntligt delprov
 Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
9D Ma: Geometri VT 2018 Syftet med undervisningen är att du ska utveckla din förmåga att:
 9D Ma: Geometri VT 2018 Syftet med undervisningen är att du ska utveckla din förmåga att: formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, använda och analysera
9D Ma: Geometri VT 2018 Syftet med undervisningen är att du ska utveckla din förmåga att: formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, använda och analysera
7F Ma Planering v2-7: Geometri
 7F Ma Planering v2-7: Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
7F Ma Planering v2-7: Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Gruppledtrådar. Gruppledtrådarna ingår i lärarhandledningen till Prima Formula 6 Får kopieras! Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
 Gruppledtrådar Som hjälp för dina elevgrupper att utveckla sin förmåga att tala matematik, samarbeta och lära i grupp finns övningar som vi kallar Gruppledtrådar. Dessa går ut på att elever tillsammans
Gruppledtrådar Som hjälp för dina elevgrupper att utveckla sin förmåga att tala matematik, samarbeta och lära i grupp finns övningar som vi kallar Gruppledtrådar. Dessa går ut på att elever tillsammans
Cadet. 1. I en klass finns 13 flickor och 9 pojkar. Hälften av eleverna i klassen är förkylda. Vilket är det minsta antalet flickor som är förkylda?
 Cadet Avdelning 1. Trepoängsproblem 1. I en klass finns 1 flickor och 9 pojkar. Hälften av eleverna i klassen är förkylda. Vilket är det minsta antalet flickor som är förkylda? a: 2 b: 4 c: 5 d: 6 e: 11
Cadet Avdelning 1. Trepoängsproblem 1. I en klass finns 1 flickor och 9 pojkar. Hälften av eleverna i klassen är förkylda. Vilket är det minsta antalet flickor som är förkylda? a: 2 b: 4 c: 5 d: 6 e: 11
Välkommen till. Kängurutävlingen Matematikens hopp 2009 Student för elever på kurs D och E. Kängurutävlingen 2009 Student.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 009 Student för elever på kurs D och E. Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 0 7 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 009 Student för elever på kurs D och E. Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 0 7 mars användas, däremot
8F Ma Planering v2-7 - Geometri
 8F Ma Planering v2-7 - Geometri Arbetsform under en vecka: Tisdagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
8F Ma Planering v2-7 - Geometri Arbetsform under en vecka: Tisdagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
Kängurutävlingen Matematikens hopp 2010 Ecolier för elever i åk 3 och 4
 Välkommen till Kängurutävlingen Matematikens hopp 2010 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot får
Välkommen till Kängurutävlingen Matematikens hopp 2010 Ecolier för elever i åk 3 och 4 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot får
Uppsala Universitet Instutionen för pedagogik, didaktik och utbildningsstudier Matematik 2, Ht 2014 Tilde Henriksson, Hannah Kling, Linn Kristell
 Del 1: Pedagogisk planering a) Vi har gjort två lektionsplaneringar med fokus på tvådimensionella geometriska figurer för årskurs 1-3. Utifrån det centrala innehållet i Lgr11 för årskurs 1-3 ska eleverna
Del 1: Pedagogisk planering a) Vi har gjort två lektionsplaneringar med fokus på tvådimensionella geometriska figurer för årskurs 1-3. Utifrån det centrala innehållet i Lgr11 för årskurs 1-3 ska eleverna
