Svar och lösningar Benjamin
|
|
|
- Christer Åström
- för 5 år sedan
- Visningar:
Transkript
1 Kängurutävlingen 208 Benjamin, facit och kommentarer Svar och lösningar Benjamin : D: 3 2: E 3: B 8 Pilarna i den första omgången ger 7 poäng vardera. I den andra omgången ger den bästa pilen 2 poäng mer, dvs 9 poäng. Tredje omgången ger då 2 9 poäng = 8 poäng. 4: B B I punkt B har den långsamma snigeln gått 8 rutor och den snabba har gått 6 rutor. B är den enda punkt där sträckan är dubbelt så lång för den snabba snigeln. Eftersom förhållandet mellan de sträckor som sniglarna avverkar är :2 måste hela sträckan, dvs 24 rutor, delas i 3. En del till den långsamma och två delar till den snabba. 5: D 3 Den enda möjliga subtraktionen är = 25 som ger siffersumman = 3 6: E söndag Eftersom den första dagen är en onsdag så är 7, 4, 2 och 28 tisdagar = 26 och 28 2 =26, så den 26:e infaller på en söndag. Eller: Eftersom vi söker 26 så backar vi en vecka i taget tills vi kommer till datum där vi vet veckodagen: = 5, alltså söndag, eller tre veckor direkt 26 2 = 5. 7: C 7 Det sämsta tänkbara utfallet är att vi slår olika resultat sex gånger, men sen måste något upprepas. 8: C 2 cm Eftersom sidlängden på den minsta kvadraten är 6 cm är sidlängden på den mellanstora kvadraten = 8 cm. Den största kvadraten har då sidlängden 8cm + 6cm 2 cm = 2 cm. 9: A 2 Nationellt centrum för matematikutbildning & SKM 2
2 Kängurutävlingen 208 Benjamin, facit och kommentarer 0: B Om vi räknar hur många bilar som ska åt varje håll så finner vi rätt svar. : A dörr. Dörren har texten: Lejonet ligger inte bakom den här dörren. Eftersom upplysningen på dörr 3 är sann, är båda de andra osanna. 2: B 45 år Mormoderns ålder är nu 8 28 = 53 år. När Kate föddes var hon 53 8 = 45 år. 3: C 2 När alla trianglar är ifyllda ser det ut så här. Två rutor intill varandra har överallt summan 5. 4: E Två trianglar som har en gemensam sida kallar vi grannar. Det måste stå samma tal i alla trianglar som är grannar till en triangel, så alla grannar till en triangel med 2 måste ha samma tal och alla trianglar som är grannar till en triangel med 3 måste ha samma tal. Därför kan triangeln bara fyllas i på ett sätt. 5: A 0 Summa av två tresiffriga tal är alltid mindre än Alltså måste D vara och hela summan. Då ser vi att A + C har entalssiffran, så A + C är eller. Om A + C är skulle aldrig summan bli fyrsiffrig, alltså A + C =. Med B = 0 (och A + C = ) får vi summan, med B > 0 skulle vi få summan större än. 6: A Flyttingen kan visas så här: Flyttning vid den tredje visslingen Flyttning vid den fjärde visslingen Efter fjärde visslingen 7: C 2 Den enda möjligheten att få summan 7 med tre olika tal är Summan 8 kan vi få på två sätt: eller Båda dessa sätt ger att de har två gemensamma tal. Nationellt centrum för matematikutbildning & SKM 3
3 Kängurutävlingen 208 Benjamin, facit och kommentarer 8: C C A + D = B + C + E innebär att de fem vikterna ska delas i två grupper. Tillsammans väger kulorna 260 g, så varje grupp ska väga 30 g. Den tyngsta kulan kan alltså inte vara C, B eller E men den lättaste kulan, som väger 30 g, måste vara någon av dem. Eftersom B + E väger mer än A + C, måste det vara C som väger 30 g. Om A väger 50 g och C 30 gram och de två kulorna E och B väger 50 g vardera, så stämmer alla vågar: A, B och E väger 50 g vardera, C väger 30 g och D väger 80 g. 9: A Adam Oavsett om Adam kastar till Urban eller Isak så kommer den att vara hos Adam så att han får göra det femte kastet. Eva Adam Adam Isak/Urban Isak/Urban Urban/Isak Urban/Isak Adam 20: D 200 cm Kvadraten består av en bit som är 8 x 8 cm, 4 bitar som är 8 x 6 cm och fyra bitar som är 8 x 32 cm. Tillsammans är dessa bitar 8 cm + (4 6 cm) + (4 32 cm) = 200 cm 2: B 2 Varje 2 x 2 kvadrat ska innehålla både nollor och ettor, alltså minst en nolla. Hela tabellen innehåller 4 st 2 x 2 kvadrater som inte överlappar varandra (dessa kan väljas på olika sätt) alltså måste hela rutan innehålla minst 4 nollor. Den behöver inte innehålla fler än 4 nollor. Bilden visar det sätt som ger flest ettor Hur vi än väljer vår 2 x 2 ruta kommer den att innehålla en nolla. 22: C 30 cm 2 De tre kvadraterna har sidlängderna 3, 4 och 5 cm. Triangelns area är därför : D 24 Antal lästa böcker är totalt 52 st. 0 elever har läst 30 böcker tillsammans och 8 elever har läst 6, alltså har 8 elever läst 46 böcker. Då återstår 6 böcker till resten av klassen. Klassen består alltså av = 24 elever. cm 2. 0 elever läste som vi vet alla 3 böcker, men sen finns det flera möjligheter, t ex: 6 st har läst den blå och den gröna, 2 st har läst den blå och den gula, 2 bara den blå, 2 bara den gula och 2 bara den gröna. Nationellt centrum för matematikutbildning & SKM 4
4 Kängurutävlingen 208 Benjamin, facit och kommentarer 24: E 8 Summan av alla tal är 42, vilket är delbart med 3. 42/3=4. Eftersom talet i mitten ska ingå i alla tre summorna måste det vara delbart med 3. Det betyder att 3, 6 och 9 kan stå i mittcirkeln. De tre tvärsummorna ska vara lika och om vi tar bort mittentalet, som ju är detsamma för alla tre tvärsummor, kommer de summor som bildas av de två yttre cirklarna också att vara lika. Dessa tre lika summor är tillsammans ett tal som är delbart med 3. Därför måste också mittentalet vara delbart med 3 när totalsumman (42) är delbar med I första lösningen är summan av talen i de yttre cirklarna = 39 och = 42. I andra lösningen är summan = 36 och = 42 I tredje lösningen har vi på motsvarande sätt 3 = 33 och = 42. Nationellt centrum för matematikutbildning & SKM 5
5 Arbeta vidare med Benjamin 208 Efter tävlingen hoppas vi att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta eleverna arbeta med lösningarna i grupp. Uppmuntra dem att hitta så många olika lösningssätt som möjligt. Låt dock alla först få möjlighet att lösa problemen på egen hand om de inte hann det i samband med tävlingen. Diskutera gruppernas lösningar i klassen och jämför idéer och angreppssätt. Låt också eleverna få granska kamraternas lösningar: Har de tagit hänsyn till alla förutsättningar? Är de tydliga? Är resonemanget korrekt? Fungerar lösningsmetoden på andra, liknande problem? Att analysera och diskutera varandras lösningar är bra, men det kräver förstås att man arbetar långsiktigt så att eleverna vänjer sig vid att både ge kritik på ett konstruktivt sätt och att ta emot kritik. Om de redan från början får uppleva att det är en del av undervisningen kan det bli en naturlig och uppskattad form av arbete med problem. Att presentera en lösning som andra kan följa och som är korrekt uppbyggd är något som eleverna måste få tid och möjlighet att utveckla med hjälp av lärare. Välj några av årets problem, arbeta igenom lösningarna noga och gör en riktigt genomarbetad redovisning. Alla problem kan naturligtvis diskuteras utifrån valda lösningsmetoder. De flesta problem kan lösas på olika sätt och det är alltid bra att jämföra dessa och se på likheter och skillnader. Det är också bra att beskriva lösningarna med hjälp av olika uttrycksformer, konkret material, bilder, muntligt eller skriftligt tal och med symboler. Jämför de olika formerna och se hur den konkreta representationen uttrycks i ord och med symboler. Några frågor att återkomma till när problemet är löst: Kontrollera att lösningen verkligen svarar mot frågan. Är det ett rimligt svar? Hur vet vi det? Påminner problemet om något annat problem vi har löst tidigare? Vilka kunskaper hade vi nytta av när vi löste problemet? Vilka nya frågor kan problemet väcka? Lärde vi oss något nytt av problemet? Gå också igenom de felaktiga svarsalternativen och resonera om varför dessa inte är riktiga. Låt eleverna göra förändringar i uppgiften så att de andra alternativen blir riktiga. Utmaningen kan vara att göra så små förändringar som möjligt. De felaktiga svarsalternativen kan också användas som utgångspunkt för diskussion om vad som skulle kunna leda fram till dessa svar: Hur tror ni att den som har fått alternativ a som svar har tänkt? Matematiskt arbete handlar både om matematik innehållet och om strategier, vilket eleverna behöver få diskutera för att utveckla sin matematiska kompetens. Låt dem också få argumentera för sina lösningar och sina val av metoder. I arbetet med alla problem bör förmågorna att resonera och argumentera vara centrala. Om inte tydliga resonemang kommer fram i elevernas redovisningar kan du visa hur ett sådant kan föras. Eleverna behöver få se vad det innebär att föra ett resonemang. I samband med diskussion om problemen kommer ett antal termer att aktualiseras. Gå igenom dem. Låt eleverna använda och själva få definiera olika begrepp och återkom till dem i olika sammanhang. För definitioner hänvisar vi till Matematiktermer för skolan (Kiselman & Mouwitz, 2008). Här har vi sorterat förslag under rubrikerna Tal, Geometri och rumsuppfattning, Sannolikhet samt Problemlösning och resonemang. Vi ha rockså två problem som vi kommenterar under rubriken Matematik och programmering. Naturligtvis kan problemen också passa under en annan rubrik än den vi har valt, beroende på vad vi väljer att betrakta i problemet. Ett bra sätt att själv bilda sig en uppfattning om ett problems kvaliteter är att lösa det. Då blir vi medvetna om hur vi själva tänker och vilka samband vi använder. Lös därför gärna problemen själv och komplettera dessa förslag med egna idéer. Många problemtyper återkommer år från år, i olika skepnader och i olika varianter. Vi hänvisar här till några gamla problem som kan användas i samband med arbetet med årets, men det finns många fler att hämta på Kängurusidan på nätet, ncm.gu.se/kanguru, där alla tidigare omgångar är samlade. Där finns också förslag på hur man kan arbeta vidare med de problemen. Tidigare problem inom området geometri finns dessutom samlade i boken Geometri och rumsuppfattning med känguruproblem. Läs mer om den på ncm.gu.se/node/4742. Nationellt centrum för matematikutbildning & SKM
6 Tal Med utgångspunkt i problem kan vi diskutera egenskaper hos tal. Elever i denna ålder kan resonera om bl a räknesättens innebörd, faktorisering och delbarhet. Problemen utmanar också elevernas strategiska tänkande och förhoppningsvis väcker de frågor om tal. Uppmuntra därför eleverna att ställa fördjupande frågor. Hjälp dem också att se samband både inom matematiken och mellan matematiken och omvärlden. 3 Pilkastning Om ingen elev har använt sig av en tabell kan du visa, t ex: Omgång: 2 3 Ring (ytterst) Ring 2?+?? 0 Ring 3 0??+? Totalt 4 6 Fyll sedan i tabellen gemensamt och låt eleverna motivera sina förslag. Lägg till omgångar och utöka antalet pilar. Variera poängen så att eleverna får använda sina strategier på flera liknande problem. Ett liknande problem finns i år på både Milou och Ecolier. Tidigare problem: E 2008:9; E 20:7; E 204:8; B 2008:. 4 Snabba sniglar Problemet kan vid en ytlig betraktelse uppfattas som geometriskt, men handlar främst om hastighet och tal. Visa hur man i en grafisk lösning kan markera sträckan runt med ett eller två (dubbelt så snabbt) steg i taget och se var mötet sker. Undersök hur stor del av det totala antalet steg runt området som de två sniglarna kryper. Variera antalet rutor och se efter mönster. Om den ena snigeln kryper dubbelt så fort kommer den att tillryggalägga två tredjedelar av sträckan samtidigt som den andra snigeln kryper en tredjedel. Varför? Vilka olika antal rutor (eller snarare sidlängder längs kanten) ger en lösning där sniglarna möts i ett ruthörn? Om ett antal ska delas i två delar så att en del blir dubbelt så stor som den andra måste antalet vara delbart med 3. Varför? Vad krävs för att antalet ska kunna delas i två delar där den ena delen är tre gånger så stor som den andra? Generalisera. I originalversionen hade sniglarna hastigheterna m/h och 2 m/h. För in dessa värden i problemet och diskutera vad de betyder. Låt eleverna lösa problemet igen och motivera varför svaret blir detsamma. Ändra den ena snigelns hastighet och diskutera resultatet. Sätt en sidlängd på kvadraterna och låt eleverna beräkna när sniglarna befinner sig i de olika punkterna om de kryper med olika givna hastigheter, t ex 2 m/h och sidlängden m, 3 m/h och sidlängden m. I årets Milou är nr 6 ett besläktat problem: En sjörövare har två kistor. I den vänstra ligger det 0 guldmynt. Den andra är tom. I morgon ska sjörövaren lägga guldmynt i den vänstra kistan och 2 guldmynt i den andra. Sen fortsätter han så varje dag tills det är lika många mynt i båda kistorna. Hur många dagar tar det? Nationellt centrum för matematikutbildning & SKM 2
7 5 En övermålad subtraktion och 5 Addition med bokstäver Uppmärksamma terminologin: tusentalssiffra, hundratalssiffra, tiotalssiffra, entalssiffra och minnsessiffra. Jämför olika lösningsmetoder. Ett sätt är att pröva och utgå från en genomtänkt gissning. I problem 5 kan vi gissa att första termen är 53: = 33. Eftersom 33 är 8 för mycket måste vi ta bort ytterligare 8, dvs andra termen blir 28. Vilka tal är det meningsfullt att pröva med som första term? Varför? Ett annat sätt är att resonera sig fram till en lösning: Vad vet vi om entalssiffran i andra termen? Problem 5 kan också lösas genom att man prövar sig fram, men det passar här bra att föra ett resonemang om vilka möjligheter som finns. Vilken siffra måste D stå för? Varför? Vad vet vi om A + C? Vad vet vi om C + A? Alla siffror i svaret och minnessiffran =. Varför kan inte B vara 5? Diskutera när olika lösningsmetoder passar. Visa eleverna att de har stor nytta av att ha automatiserat tabellerna i addition och subtraktion. Låt eleverna konstruera liknande uppgifter till varandra för att öva dessa grundläggande kombinationer i ett lite mer kreativt sammanhang. Liknande problem från årets tävling: I Ecolier 2 saknas en siffra i vardera termen: = 57 I Cadet saknas en siffra i vardera faktor och en i produkten: 3 2 = 3 2 I Cadet 4 ska vi ersätta * med ett tal för att få ett korrekt uttryck: = 6 * 7 Tidigare problem: E 203:2; B 2003:9; B 2004:4; B 2005:; B 2007:6; B 200:; B 205:9; C 200:3; C 2003:22. 6 En fläckig kalender Diskutera hur man snabbt kan bestämma vilket datum det är om en vecka, två veckor om man vet dagens datum. Om onsdag är den sjätte dagen, vilken är den första? Vilken är den sjunde? Åttonde? Om :a är en onsdag, vilken veckodag är då 7:e? Undersök almanackan med avseende på veckodag och datum. Uppmärksamma att, + 7, 8 + 7, 5 + 7, är samma veckodagar (alltså inte, 7, etc). Vilka datum ligger på måndagar, tisdagar etc i kalendern i problemet? Hur många söndagar kan det som mest finnas i en månad? Som minst? Undersök hur ett visst datum infaller på veckodagar under ett antal på varandra följande år. Jag fyller år på en söndag i år, vilken veckodag fyller jag då år på nästa år? Varför? Blir det alltid så? Prata om skottårens betydelse. När fyller den som är född 29 februari år på rätt datum? Låt eleverna konstruera egna problem med kalendern. Tre problem i år, med olika svårighetsgrad, handlar om ett almanacksblad där de flesta datum är dolda av en stor fläck. Problemen är förutom detta i Benjamin också Ecolier nr 4, och Student nr. Tidigare problem med kalendrar och veckodagar: M 2008:3; E 20:; B 2006:9, C 2002:5. Nationellt centrum för matematikutbildning & SKM 3
8 2 Mormors ålder Illustrera åldrarna på en tallinje och se på skillnaden i ålder. När är Kate, mamma och mormor födda om Kate är 8 år i år? När fyller Kate 00 år? Vilken är summan av deras åldrar? Hur gammal var mormor när Kates mamma föddes? Hur gammal var Kates mamma när Kate föddes. Problemet går förstås att lösa med ekvation Här är K = Kates ålder, M = mammas ålder och B = mormors ålder: K = 8, M = 28, B =? M + B = 8 B = 8 28 B = 53 B:s ålder då K föddes = 53 8 = 45 år Låt eleverna göra liknande problem med sin egen familj, eller med någon fantasifamilj. Liknande problem: B 200:6, C 200:24. 7 Masha och Dasha summerar Vilken är den minsta summa man kan få om man väljer tre olika tal? Vilken är den största summan man kan få? Skriv upp alla möjliga summor av tre olika tal och jämför hur många gemensamma tal som ingår i två summor. Vilka summor kan man få om man väljer fyra olika tal ur den givna listan? Vilken är den minsta? Vilka summor kan man få om man väljer fem olika tal? Sex olika tal? Behandla triangeltal, + 2; ; ;. Förläng listan och räkna ut de följande triangeltalen. Visa att talen kan illustreras som trianglar. Visa att n = n(n + ) 2 Tidigare problem: E 2009:8; B 2007:9; B 2008:5, B 2009:6. 8 Kulvägning Även detta problem handlar om summor som vi kan få på olika sätt. Vilka olika summor kan vi få med tre kulor? Med två kulor? Diskutera elevernas olika strategier. Lyft fram sådana som bygger på ett resonemang om de ingående talen. Eleverna behöver få vara med om gemensamt resonemang, så att de får erfarenhet av hur ett sådant kan byggas upp. Ställ frågor som hjälper eleverna att bygga upp ett resonemang, t ex: Hur mycket väger kulorna tillsammans? Hur mycket finns det i vardera vågskålen i vågen längst till höger? Hur kan vi veta att det inte är A som väger 80 g? Hur vet vi att varken A eller D väger 30 g?. Nationellt centrum för matematikutbildning & SKM 4
9 Ecolier 20 i år är ett liknande problem, men något enklare. Använd det antingen som inledning och arbeta gemensamt med resonemanget eller låt eleverna försöka klara det på egen hand efter att ni har bearbetat Benjaminproblemet gemensamt. Även årets Milou 5 är ett liknande problem. En av kulorna väger 0 g, en väger 20 g, en 30 g och en väger 40 g. Vilken kula väger 30 g? A B C D B D C Tidigare problem: B 2006:8; B 202:9; B 205:9. 24 Tal i cirklar Vilken strategi kan man ha för att lösa ett sådant här problem? Det är alltid bra att börja med att summera talen. I det här problemet blir summan 42. Utifrån det kan vi resonera eller pröva oss fram. Årets Cadet 7 är ett liknande problem: Talen till 9 ska skrivas i rutorna, ett tal i varje ruta. Fem av de summor man får då varje rad och varje kolumn adderas är 2, 3, 5, 6 och 7 (ej nödvändigtvis i denna ordning). Vilken är den sjätte summan? A: 7 B: 6 C: 5 D: 4 E: 3 Även här börjar vi med att summera talen. Summan blir 45. När rader och kolumner adderas var för sig kommer varje tal att räknas två gånger. Alltså är summan av radsummor och kolumnsummor 90. Visa att det går att fylla i nätet så att summorna stämmer. Tidigare problem: B 2002:22, B 200:0. Geometri och rumsuppfattning Geometri är ett område som lämpar sig väl för problemlösning. Att resonera sig fram till lösningen och att sedan kunna argumentera för den är väsentliga delar av problemlösningsförmågan. I geometri spelar också bilden en väsentlig roll, som underlag för kommunikation och som stöd för tanken. Med stigande ålder hos eleverna bör vi också ställa större krav på hur de använder bilder och vilka slutsatser man kan dra av bilderna. Många problem går förstås att lösa konkret, men det konkreta arbetet, i samband med diskussion av lösningar, bör kombineras med samtal så att det konkreta ger stöd för tänkandet. Det är resonemanget som är centralt. Det konkreta arbetet kan också användas för att bekräfta lösningar och för att skapa nya erfarenheter att bygga vidare på. Att redovisa en lösning av ett geometriproblem kan vara svårt. Lösningen ska vara skriven så att läsaren förstå. Hur bör en lösning av ett geometriproblem se ut? Börja gärna med enklare problem. Finns det ingen figur bör lösningen inledas med att en tydlig figur ritas, beteckningar införs och att det som är givet markeras. Finns det en figur så är den ett underlag för redovisning. I den skriftliga redovisningen hänvisar man till beteckningarna i figuren. Hur markerar man t ex att en vinkel är rät eller att två vinklar är lika stora? Det går inte att hänvisa till att en vinkel är rät eller till att två vinklar ser lika stora ut om man inte har fått veta att det är så. Det kan vara lättare att förklara sina tankegångar muntligt. Låt eleverna göra en muntlig redovisning först och sedan formulera en skriftlig lösning. Nationellt centrum för matematikutbildning & SKM 5
10 Pilar mot ballonger Bilden kan vara utgångspunkt för en diskussion om både storlek och läge. Använd bilden för att diskutera längdskala och areaskala, och om det passar även volymskala. Hur många olika storlekar har ballongerna? Hur mycket större är den största ballongen jämfört med den minsta? Var ligger ballongerna i förhållande till varandra? Låt eleverna uttrycka ballongernas placering så noggrant som möjligt, med hjälp av ord. Be dem sedan att komma på ett annat sätt att beskriva läget. Om ni redan har arbetat med koordinatsystem så kommer de troligen på att de kan göra ett sådant i bilden, annars kan detta vara en introduktion. Använd bilden som en spelplan till ett sänka skepp -liknande spel. I vilka punkter kommer varje ballong att träffas? Det räcker med en träff för att ballongen ska spricka. 2 Konstruktion ur annat perspektiv Den här typen av problem har förekommit tidigare, inte minst i Milou och Ecolier. Låt eleverna först beskriva de tre klossarna och deras placering. För att diskutera bitarnas placering behöves flera begrepp, t ex mittpunkt, vänster, höger, kant, kortsida, långsida, cylinder, rätblock, kub, cirkel, rektangel, kub. För att utveckla språk och terminologi inom detta område kan eleverna arbeta i par, med en skärm emellan sig eller placerade så att de inte ser varandras arbeten. Den ena bygger av ett antal givna klossar eller föremål en konstruktion som den andra sedan ska kopiera, endast med hjälp av muntliga instruktioner. Uppgiften kan varieras i svårighetsgrad genom val av föremål, genom restriktioner om hur informationen får överföras det blir enklare om den som bygger får ställa frågor. Uppgiften blir svårare om eleverna sitter mitt emot varandra jämfört med om de sitter bredvid varandra. Motsvarande uppgift kan också göras utifrån en bild som den ena eleven ritar. Gör flera aktiviteter där en konstruktion ska beskrivas som en tvådimensionell bild. Låt eleverna bygga och göra beskrivningar åt varandra. Ett sätt att beskriva ett bygge med likadana klossar fanns i Milou 2009:2. Låt eleverna först få tolka bilden och sedan bygga och göra liknande ritningar I slöjden har eleverna troligen mött ritningar där man betraktar sin konstruktion framifrån, uppifrån och från sidan. Vad kan man se och vad kan man inte se? Hur ser något ut från baksidan? Utgå från ett fotografi och låt eleverna rita hur situationen ser ut från andra sidan eller uppifrån. Ett roligt problem, som visade sig vara mycket utmanande, var med i Kängurutävlingen Problemet presenterades sedan på Uppslaget i Nämnaren nummer 3, 2003, under rubriken Tänk, vik och se. Det finns fritt tillgängligt på ArkivN som du finner på ncm.gu.se. Fler problem: E 200:2; E 2002:5; E 2004:8; E 2006:2; E 2007:; E 2007:5; E 2009:4; B 200:23 & 24; B 2006:6; B 2008:8; B 20:2; B 203:2; B 204:8; B 206:6; B 207:4; C 2003:; C 204:6; C 206:2. 8 Tre kvadrater Diskutera hur de andra sidlängderna kan bestämmas. Här är det lämpligt att låta eleverna använda figuren för att redovisa sin lösning. Vilken omkrets har de tre kvadraterna? Vilken area? Vilken omkrets har hela figuren? Vilken area har figuren? Nationellt centrum för matematikutbildning & SKM 6
11 Vilken är den största omkrets vi kan få om de tre figurerna placeras på ett annat sätt? Vilken är den minsta möjliga omkretsen? Låt eleverna undersöka hur figuren och sidorna på kvadraten ändras om sträckan 2 cm ändras. Ändra till annan sidlängd på den minsta kvadraten. Låt den största kvadraten ha en given sidlängd och bestäm den minsta kvadratens sidlängd. Generalisera: Låt den minsta kvadraten ha sidan a cm. Behåll den markerade sträckan 2 cm. Låt eleverna skriva uttryck för sidorna i kvadraterna och även bestämma uttryck för kvadraternas areor. Ersätt även sträckan 2 cm med en variabel t ex b. Tidigare problem: B 2006:3; B 205:7, B 207:5. 4 En utvikt tärning Att i huvudet vika ihop en tärning kan vara utmanande för många. Vilka sidor hamnar intill varandra och vilka blir motstående? Låt eleverna beskriva vad som händer när de viker de olika alternativen. De får då anledning att använda ett antal relevanta termer som kant, sida eller sidoyta, motstående, närliggande. Vilken roll har de två utstickande bitarna på varje ritning? Var kommer de sidorna att hamna? Hur vet vi det? Gå igenom de olika alternativen och bestäm vilka sidor som är motstående. Försök att först göra uppgiften endast med hjälp av bild och resonemang, men gör den sedan konkret och jämför. Tidigare problem: E 2004:2; E 2008:8; E 205:7; B 2006:6; B 205:3; C 205:4. 20 En uppsågad träplanka Arbeta konkret med problemet: Ge eleverna en förstoring av bilden. Om du vill använda problemet för att också diskutera skala kan du anpassa förstoringen så att det blir enkelt att hantera måtten. Låt eleverna sen rita en pappersremsa med en bredd som ska motsvara 8 cm, och som ska passa in i den förstorade bilden. Här kan alltså begreppet skala komma in. Klipp ut den lilla kvadraten och placera den i bilden. Vilka sidor i rektanglarna har samma längd som kvadratens sida? Markera och sätt ut längderna. Låt eleverna klippa ut de rektanglar som har längden 6 cm. Hur många sådana rektanglar behövs? Lägg ut rektanglarna kring kvadraten. Vilken figur bildar kvadraten och de fyra rektanglarna? Hur lång är sidan på denna? Vilken längd har de rektanglar som nu saknas? Klipp ut dem och lägg klart kvadraten. Bestäm remsans längd genom att lägga ut alla delar efter varandra. Diskutera andra sätt att bestämma längden, utan att lägga kvadraten och rektanglarna efter varandra. Diskutera gemensamt hur vi kan bestämma storleken på den lilla kvadraten endast utifrån bilden. Vilka sidor i rektanglarna har samma längd som kvadratens sida? Hur kan vi använda den informationen för att bestämma längden av rektanglarna? Vilken area har den lilla och den stora kvadraten? Vilken omkrets har kvadraterna? Vilken omkrets har träplankan? Vilken area? Hur vi kan vi veta träplankans area utan att göra en ny beräkning om vi vet stora kvadratens area? Att arean inte ändras när vi delar ett område och flyttar bitarna är centralt för att förstå areabegreppet. Nationellt centrum för matematikutbildning & SKM 7
12 Om vi återgår till problemets kvadrat och ritar fyra nya rektanglar med samma bredd och placera dessa runt kvadraten kan vi konstruera en ännu större kvadrat. Vilket mått har de rektanglarna? Vilken sida får den nya kvadraten? Låt eleverna skriva numeriska uttryck för rektanglarnas längder för att se ett mönster. Kvadratens sida är 8 cm, de fyra inre rektanglarnas längd är 2 8 cm, de fyra yttre rektanglarnas längd är 4 8 cm. Plankans sammanlagda längd blir då ( ) cm = 25 8 cm = 200 cm. Generalisera: Sätt sidlängden på lilla kvadraten till och bestäm övriga längder. Ändra kvadratens sida till x cm och skriv uttryck om det är en kvadrat och fyra rektanglar, en kvadrat och åtta rektanglar osv. Två problem från grannklasserna påminner om detta problem: Ecolier 24 Den stora rektangeln är gjord av 7 kvadrater, av olika storlek. Det finns tre små kvadrater, som är lika stora. En sådan liten kvadrat har arean. Vilken area har hela den stora rektangeln? Låt eleverna arbeta med enhetskvadrater och konstruera rektangeln. Utgå från de tre givna enhetskvadraterna och rita enhetskvadrater så att nästa kvadrat bildas. Hur många enhetskvadrater är det sammanlagt? Vilken area har rektangeln som består av 2 enhetskvadrater? Fortsätt att rita fler enhetskvadrater så att figuren växer fram. Cadet 8: En stor rektangel är uppbyggd av nio identiska rektanglar vars längsta sida är 0 cm. Vilken omkrets har den stora rektangeln? Några ytterligare problem: B 2006:3; B 205:2, C 2006:6; C 20:22; C 206:9, 22 Area av en triangel Låt eleverna redovisa sina lösningsmetoder. Det finns åtminstone två skilda sätt att angripa problemet. Vi kan bestämma kvadraternas sidors längd: 3 cm, 4 cm och 5 cm. (3+4+5) 5 Den som kan formeln för triangelns area kan använda sig av den = 30 2 Den som inte kan denna kan tänka sig en större rektangel med ena sidan cm och den andra sidan 5 cm. Diagonalen i en rektangel delar den i två lika stora trianglar, så arean blir 30 cm 2. Detta är förstås samma idé som i formeln, så för elever som ännu inte har sett formeln kan detta vara ett sätt att möta den. Undersök hur diagonaler delar rektanglar. Låt eleverna motivera varför de två trianglarna är lika stora. Gör detsamma med andra parallellogrammer. Tidigare problem: B 2008:2. Nationellt centrum för matematikutbildning & SKM 8
13 Sannolikhet 7 Tärningskastet Här spelar formuleringen stor roll, vi behöver alltså inte ha ett visst utfall utan något utfall två gånger. Jämför med om formuleringen hade varit: Vi kastar en tärning och får en sexa. Hur många gånger måste vi kasta en tärning för att vara säkra på att få samma resultat igen? Hur många gånger måste vi kasta en tärning för att vara säker på att få exempelvis en trea två gånger? Varför kan vi vara säkra på att få två av något om vi kastar tärningen sju gånger? Låt eleverna förklara skillnaden mellan de tre frågeställningarna. Hur stor sannolikhet är det att vi får en sexa om vi slår en tärning? Att vi får en trea? Tidigare problem: B 2002:9; B 205:8; B 207:22; C 203:5. Problemlösning och resonemang Textproblem uppfattas av många som svåra, speciellt om det är mycket information att hantera. Eleverna behöver få undervisning om hur de ska angripa den typen av uppgifter. Arbeta därför gemensamt med texterna och hjälp eleverna att sätta sig in i problemet, exempelvis med stödjande frågor. Hjälp eleverna att strukturera informationen i texten. Att förstå vad problemet handlar om är en förutsättning för att kunna lösa det. Men att förstå vad det handlar om och vad som efterfrågas är inte detsamma som att veta vad man ska göra. Problemlösning handlar om att komma från att förstå situationen till att komma på hur man ska komma fram till svaret på den formulerade frågan. Det är denna process, som består av flera steg och ofta innebär både misslyckade och lyckade insatser, som är central i undervisning om problemlösning. I den processen är resonemang en viktig del. 9 Lysande knappar Undersök vad som händer om vi trycker på en knapp. Vilka knappar ger flest lysande grannknappar? Det är fyra knappar som är kopplade till tre andra knappar, men det finns ett bästa val, varför? Vad händer om varje knapp som tänds i sin tur tänder grannknappar? Låt eleverna konstruera liknande problem, både där så många knappar som möjligt ska tändas och där så få som möjligt ska tändas. Tidigare problem: B 207:4. Lejonet i rummet I problem av den här typen spelar texten en stor roll. Några hade uppfattat problemet så att frågan gällde vilken information som är sann. Gå igenom texten noga och låt eleverna få tala om vad frågan gäller. Gå sedan igenom och diskutera vilken information vi får. Arbeta systematiskt igenom texterna på dörrarna och jämför med bara en av dem är sann. Pröva sedan : Varför är inte alternativ E riktigt? Om lejonet ligger bakom dörr på hur många dörrar är då informationen sann? Om lejonet ligger bakom dörr 2 på hur många dörrar är då informationen sann? Om lejonet ligger bakom dörr 3 på hur många dörrar är då informationen sann? Nationellt centrum för matematikutbildning & SKM 9
14 Motsvarande problem fanns på årets Cadet 3. Jämför formuleringarna: Ett lejon har gömt sig i ett av tre rum. På första dörren kan man läsa: Lejonet är här, på den andra dörren kan man läsa Lejonet är inte här och på tredje dörren kan man läsa = 2 3. Endast en av de tre meningarna är korrekt. I vilket rum har lejonet gömt sig? Tidigare problem: B20:9; B203:20. 3 Tal i triangel och 2 Ettor och nollor Ett antal problem i årets Kängurutävling handlar om tal som ska skrivas in i nät av olika slag, rutor, trianglar, cirklar. Det finns några som liknar varandra men av olika svårighetsgrad. Låt eleverna börja med att lösa Ecolier 23 utan svarsalternativ: Lova ska skriva talen, 2, 3, 4, 5, 6 och 7 i figuren. Två tal som kommer efter varandra i talraden får inte stå i två rutor som möts i ett hörn eller längs en kant. Vad kan hon skriva i rutan med frågetecken? Hur många olika sätt finns det att fylla i rutnätet med de sju talen? Låt eleverna förklara hur de kommit fram till sitt svar. Är alla lösningar lika? Samla alla tänkbara sätt att sätta ut talen. Vad är lika? Vad är det för speciellt med talen och 7 i detta problem? Bygg ut hagen med en ruta nedåt och lägg till talet 8. Vilka tal kan då stå i rutan med frågetecken? I Benjamin 3 ska vi fylla i ett nät av nio trianglar. Låt eleverna motivera hur nätet ska fyllas i. Ändra 2 och 3 till andra tal och låt eleverna upptäcka att lösningen i princip är densamma, även om summan blir en annan. Gör egna trianglar och sätt ut två olika tal i två andra rutor. Hur måste rutorna väljas? Problem 2 är snarlikt, men troligen något svårare. Här behöver vi först identifiera var 2 x 2 kvadraterna finns, så att vi kan kontrollera att varje sådan innehåller 3 lika tal. Varför är det 3 st ettor vi vill ha? Hur många 2 x 2-kvadrater kan vi hitta i figuren? Hur många 3 x 3? 4 x 4? Att undersöka kvadrater på detta sätt kan vara en intressant utveckling av problemet. Vilket mönster finns där? I Uppslaget i Nämnaren 994:4 har Lillemor och Göran Emanuelsson beskrivit en aktivitet på detta tema. Tidigare problem: E 204;8; B 2009:2. 9 Bollek Detta problem passar bra för att jämföra lösningsmetoder. Kanske vill någon utföra lösningen konkret. Varför spelar det inte någon roll om Adam kastar bollen till Urban eller Isak. Hur påverkas lösningen av om vi i stället frågar Vem gör det sjätte kastet? Ändra förutsättningarna och undersök. Nationellt centrum för matematikutbildning & SKM 0
15 23 Bokläsning Diskutera olika lösningsstrategier. Börja med ett enklare fall och illustrera i en tabell: 3 st har läst alla tre böcker, här markerade med I 2 st har läst två av böckerna, markerade med I och I resten har läst en bok, markerade med I Gröna boken Röda boken Blå boken I I I I I I I I I I I I I I Undersök hur antalet lästa böcker påverkas av hur många resten är. Ändra sedan antalet som har läst alla tre böcker etc. Med en bild kan strukturen på problemet illustreras. Låt eleverna få konstruera liknande problem själva. Matematik och programmering Ett nytt innehåll i matematikundervisningen är programmering. I grundskolan handlar det främst om att lära sig att programmera, medan det på gymnasieskolan handlar om att använda programmering för att lösa matematiska problem. I årets tävling finns det (åtminstone) två problem som skulle kunna programmeras. Problemen kan lösas även på andra sätt och programmeringen kan ske även utan datorer. I detta material beskriver vi inte programmeringen, men vi hoppas att du som provar programmering delar med dig av erfarenheter så att vi kan publicera några sådana exempel, skriv till kanguru@ncm.gu.se. De två problemen är: 0 Korsvägen och 6 Skalbaggarna i rutan Dessa två problem påminner om varandra då de båda handlar om att tänka sig en förflyttning efter bestämda regler inom ett begränsat område. I problem 0 finns all information i bilden. Låt eleverna rita in en bil i taget, från startposition till den nya platsen. Hur ska bilarna svänga för att de andra svarsalternativen ska bli riktiga? Är alla alternativ möjliga? I problem 6 finns det mycket information i texten. Gå igenom den noga. Hur kan skalbaggarna krypa? De kan alltså inte krypa fram och tillbaka och på så sätt komma till den ruta de kom från, däremot kan de efter ett antal steg komma tillbaka till en ruta som de tidigare har stått i. Undersök hur många steg skalbaggen som minst måste ta för att komma tillbaka till sin ursprungsruta. Diskutera de olika svarsalternativen. På vilka andra sätt skulle resultatet efter fyra visslingar ha kunnat se ut? Hur kan resultatet se ut efter ytterligare en vissling? Hur många tänkbara lösningar finns det? Tidigare problem: E 2008:9; E 2008:7: E 20:7; E 204:8. Nationellt centrum för matematikutbildning & SKM
16 Att läsa Gennow, S. & Wallby, K. (200). Geometri och rumsuppfattning med Känguruproblem. NCM, Göteborgs universitet. Hagland, K., Hedrén, R. & Taflin, E. (2005). Rika matematiska problem inspiration till variation. Stockholm: Liber. Kiselman, C. & Mouwitz, L. (2008). Matematiktermer för skolan. NCM, Göteborgs universitet. McIntosh, A. (2008). Förstå och använda tal. NCM, Göteborgs universitet. Rystedt, E. & Trygg, L. (200). Laborativ matematikundervisning vad vet vi? NCM, Göteborgs universitet. Wallby, K. m fl (red) (204). NämnarenTema 0 Matematikundervisning i praktiken. NCM, Göteborgs universitet. Nämnaren. I varje nummer finns Problemavdelningen och Kängurusidan. Läs också tidigare artiklar kring problemlösning. Nämnarenartiklar äldre än ett år finns fritt tillgängliga som pdf-dokument på Nämnaren på nätet, namnaren.ncm.gu.se. Du finner dem via artikeldatabasen. Under ArkivN finns alla publicerade Uppslag och Problemavdelningar samlade. Nämnaren på nätet presenterar varje månad nya problem under rubriken Månadens problem. Strävorna finns på ncm.gu.se/stravorna. Där finns aktiviteter, problem och artiklar samlade och ordnade efter kursplanens beskrivning av matematikämnets syfte och mål. Matematiklyftets lärportal larportalen.skolverket.se. På lärportalen finns moduler om problemlösning för alla stadier. Dessa ingår i Matematiklyftet men finns fritt tillgängliga för alla. Modulerna innehåller teoritexter, underlag för lärares gemensamma fortbildning samt problem för eleverna. Matematiklyftets material finns alltså tillgängligt för alla. På Lärportalen finns också andra moduler där problemlösning ingår. Nationellt centrum för matematikutbildning & SKM 2
Kängurutävlingen Matematikens hopp 2018 Benjamin
 Kängurutävlingen Matematikens hopp 2018 Benjamin Trepoängsproblem 1 Bilden visar 3 pilar och 9 ballonger. När en pil träffar en ballong spricker ballongen, och pilen fortsätter vidare i samma riktning.
Kängurutävlingen Matematikens hopp 2018 Benjamin Trepoängsproblem 1 Bilden visar 3 pilar och 9 ballonger. När en pil träffar en ballong spricker ballongen, och pilen fortsätter vidare i samma riktning.
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Kängurutävlingen Matematikens hopp Arbeta vidare med Cadet 2017 Årets Känguruproblem kan direkt kopplas till innehållet i kursplanerna för åk 9 samt för Ma1. Få av problemen är direkta rutinuppgifter utan
Kängurutävlingen 2017 NCM 1
 Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Kängurutävlingen 2017 Arbeta vidare med Benjamin 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång
Svar och lösningar Benjamin
 Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
Kängurutävlingen 2015 Svar och lösningar Benjamin 1 B 2 C Det räcker att uppmärksamma att ett spegelvänt R inte förekommer på paraplyet. 3 A 2 svart En grå kvadrat som ska bli svart. En svart kvadrat som
2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder till svaret 6.
 Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Kängurutävlingen 2015 Ecolier, svar och lösningar Facit Ecolier 1 E 15 2 A Skenorna i A överlappar varandra minst. Det finns bara ett hål mellan skruvarna. 3 E 6 Bakom triangeln gömmer sig 3 vilket leder
Svar och lösningar Ecolier
 Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Kängurutävlingen 2014 Ecolier, svar och lösningar Svar och lösningar Ecolier 1: D mellan 1 och 4 Eftersom tre är mindre än fyra ska 3 placeras före 4. 2: A 1 och 4 Hus 2 har för liten huskropp och endast
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Ecolier 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Arbeta vidare med aritmetik 2018
 Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Arbeta vidare med aritmetik 2018 I det här materialet har vi samlat problem inom aritmetik från flera olika tävlingsklasser, från Ecolier till Student. Årtal Varje år förekommer det problem som utgår från
Lösningsförslag Cadet 2014
 Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Kängurutävlingen 2014 Cadet svar och korta lösningar Lösningsförslag Cadet 2014 1. A 0 2014 2014 2014 2014 = 0 2. D 21 mars Det blir torsdag senast om månaden börjar med en fredag. Då är det torsdag dag
Arbeta vidare med Milou 2008
 Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Arbeta vidare med Vi hoppas att problemen i Milou väckte intresse och lust att arbeta vidare. Nu kan ni kontrollera lösningarna genom att pröva konkret, klippa och bygga. Variera också problemen genom
Svar och lösningar Benjamin
 Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A 1 9999 + 1= 10 000. Talet
Kängurutävlingen 2014 Svar och lösningar Benjamin 1: A 0 Summerar vi entalen ger de 9, hundratalen ger 3 så det är inga minnessiffror att beakta. Summan av tiotalen är 0. 2: A 1 9999 + 1= 10 000. Talet
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Kängurun Matematikens hopp Milou 2018, svar och korta kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera
Svar och korta lösningar Benjamin 2006
 3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
3 poäng Svar och korta lösningar Benjamin 2006 1. B 2006 2005 + 2007 är lika mycket som 2 2006. 2. D 2 309 415 687 Det kort man lägger först längst till vänster, måste ha så litet tal till vänster som
Kängurun Matematikens hopp
 Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Kängurutävlingen 2016 Ecolier, svar och lösningar Kängurun Matematikens hopp Ecolier 2016, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Efter redovisningssidorna
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Ecolier 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Arbeta vidare med Ecolier 2010
 Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Arbeta vidare med Ecolier 2010 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2013, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens Hopp
 Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Kängurun Matematikens Hopp Cadet 2011 Här följer först svar och lösningar, samt rättningsmall och redovisningsblanketter. Vi ger förslag på lösningsmetod. Därefter följer förslag till hur ni kan arbeta
Arbeta vidare med Junior 2010
 Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Arbeta vidare med Junior 010 Känguruproblemen är kanske inte av samma karaktär som de problem eleverna möter i läroboken. De är inga rutinuppgifter utan bygger på förståelse och grundläggande kunskaper.
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Kängurutävlingen Matematikens hopp Cadet 2016, svar och korta lösningar Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Svar och arbeta vidare med Benjamin 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguru och problemen kan säkert ge idéer för undervisning under många lektioner. Här ger vi några förslag att arbeta vidare med. Problemen
5: B grön Någon har den gröna ryggsäcken och det är inte Anna (och inte Maja), så det måste vara Tom.
 Kängurutävlingen 2018 Ecolier, svar och kommentarer Facit Ecolier 1: E 6 2: B 6 Liam behöver 0, 1, 2, 3, 5 och 8. 3: C 18 Syskonen är 5 år, 6 år och 7 år, 5 + 6 + 7 = 18 4: E 5 Om skruv 5 hade varit lika
Kängurutävlingen 2018 Ecolier, svar och kommentarer Facit Ecolier 1: E 6 2: B 6 Liam behöver 0, 1, 2, 3, 5 och 8. 3: C 18 Syskonen är 5 år, 6 år och 7 år, 5 + 6 + 7 = 18 4: E 5 Om skruv 5 hade varit lika
Kortfattade lösningar med svar till Cadet 2006
 3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
3 poäng Kängurun Matematikens hopp Cadet 2006 Kortfattade lösningar med svar till Cadet 2006 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D Första siffran längst
Facit och kommentarer Benjamin 2019
 Facit och kommentarer Benjamin 2019 1 B 2 C 3 D 419 380 + 39 = 419 eller 380 + 20 + 19 = 419 4 C 5 E 1 Hälften av 26 barn är 13 barn. Eftersom det finns 12 pojkar i gruppen måste det som minst vara en
Facit och kommentarer Benjamin 2019 1 B 2 C 3 D 419 380 + 39 = 419 eller 380 + 20 + 19 = 419 4 C 5 E 1 Hälften av 26 barn är 13 barn. Eftersom det finns 12 pojkar i gruppen måste det som minst vara en
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Kängurun Matematikens hopp Benjamin 2009 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. De flesta problem kan lösas på flera sätt och
Facit och kommentarer Ecolier 2019
 Facit och kommentarer Ecolier 2019 1 E 2 C 5+5+1+1 3 A tisdag Om det var söndag igår är det måndag idag. 4 D,, Det kvadratiska hålet kommer att hamna tre rutor från mittvikningen och då syns motorcykeln.
Facit och kommentarer Ecolier 2019 1 E 2 C 5+5+1+1 3 A tisdag Om det var söndag igår är det måndag idag. 4 D,, Det kvadratiska hålet kommer att hamna tre rutor från mittvikningen och då syns motorcykeln.
4. A. 4, 6, 11 Viker man ihop till en kub, så kommer talet 1 mitt emot 3, 2 mitt emot 4 och 5 mitt emot 6. Det ger summorna 4, 6, 11.
 N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
N G A RA Kängurutävlingen 2015 Cadet svar och korta lösningar 1. B Betrakta de fem alternativen och jämför med paraplyet. (A) N är upp- och ner. (C) R är felvänd. (D) G är felvänd. (E) R ska inte stå mellan
1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte.
 Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
Svar och lösningar 1 D Linjerna på de plattorna går inte diagonalt. 2 E Båda djuren kommer ut, men vägarna möts inte. 3 C: 1 och 3 4 C: David 5 B: 2 Flytta myntet på toppen och myntet som ligger i mitten
3: A I den vita asken. Kolan ligger i den röda asken så chokladbiten måste ligga i den vita. Problemet kan lösas konkret och med en enkel bild.
 Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
Svar och lösningar 1: D 200 9 Alla de andra är udda. Undersök kombinationerna i multiplikationstabellen med avseende på jämna och udda tal. Hur kan man veta om resultatet av en multiplikation blir ett
Välkommen till Kängurutävlingen Matematikens hopp 17 mars Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Student för elever på kurs Ma 4 och Ma 5 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Milou 2019, facit och kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Kängurun Matematikens hopp Milou 2019, facit och kommentarer Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Svar och arbeta vidare med Cadet 2008
 Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
Svar och arbeta vidare med Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att arbeta vidare med. Känguruproblemen
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt.
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Kängurun Matematikens hopp Benjamin 2011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Därefter följer förslag till hur ni kan arbeta vidare
Arbeta vidare med Benjamin
 Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Arbeta vidare med Benjamin Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. I samband med genomgång passar det bra att låta
Svar och lösningar. Kängurutävlingen 2009 Cadet för gymnasiet
 Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Svar och lösningar 1: D 200 9 Ett tal är jämnt om entalssiffran är jämn. Det enda talet som uppfyller det villkoret är 200 9 = 1800 2: C 18 cm Stjärnans yttre består av 12 lika långa sidor med sammanlagd
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens
Kängurun Matematikens hopp Ecolier 0, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av klassens
Kängurutävlingen 2017
 Kängurutävlingen 2017 Arbeta vidare med Ecolier 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. Låt alla först få
Kängurutävlingen 2017 Arbeta vidare med Ecolier 2017 Nu är tävlingsdelen av Kängurun avslutad, men vi hoppas att problemen ska kunna vara underlag för många intressanta diskussioner. Låt alla först få
Kortfattade lösningar med svar till Gymnasiets Cadet 2006
 Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Kängurun Matematikens hopp Gymnasiets Cadet 2006 Kortfattade lösningar med svar till Gymnasiets Cadet 2006 3 poäng 1 B 2 0 0 6 + 2006 = 0 + 2006 2 A De tal som ger rest 2 är 8 och 38, summan är 46. 3 D
Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2009 Benjamin för elever i åk 5, 6 och 7 Kängurutävlingen genomförs 19 mars. Om den dagen inte passar kan hela veckan 20 27 mars användas,
Kängurutävlingen Matematikens Hopp Cadet 2003 Lösningar, Arbeta vidare
 Kängurutävlingen Matematikens Hopp Lösningar, Arbeta vidare Arrangeras av Många problem kan lösas på flera sätt. Följande förslag ger inte någon heltäckande beskrivning. Diskutera olika lösningsförslag
Kängurutävlingen Matematikens Hopp Lösningar, Arbeta vidare Arrangeras av Många problem kan lösas på flera sätt. Följande förslag ger inte någon heltäckande beskrivning. Diskutera olika lösningsförslag
Välkommen till Kängurutävlingen Matematikens hopp 2019 Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2019 Benjamin för elever i åk 5, 6 och 7 Tävlingen genomförs under perioden 21 mars 29 mars. Uppgifterna får inte användas tidigare. Sista
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2019 Benjamin för elever i åk 5, 6 och 7 Tävlingen genomförs under perioden 21 mars 29 mars. Uppgifterna får inte användas tidigare. Sista
Ecolier. Avdelning 1. Trepoängsproblem. 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6.
 Ecolier Avdelning 1. Trepoängsproblem 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6 (Ryssland) 2 Gilda har 50 kr. Hon tänker köpa fem skrivböcker som
Ecolier Avdelning 1. Trepoängsproblem 1 Hur många av bokstäverna i ordet KÄNGURU finns också i ordet TÄVLING? a: 2 b: 3 c: 4 d: 5 e: 6 (Ryssland) 2 Gilda har 50 kr. Hon tänker köpa fem skrivböcker som
Delprov A Muntligt delprov
 Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
Svar och arbeta vidare med Student 2008
 Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 16 mars 24 mars. Uppgifterna får inte användas tidigare.
2: E TOOT Bokstäverna O och T har en lodrät symmetriaxel, men inte R, B och L. Därför kommer endast ordet TOOT kunna skrivas på detta sätt.
 Kängurutävlingen 018 Cadet svar och kommentarer Facit Cadet 1: C 19 0 + 18 = 8 = 19 : E TOOT Bokstäverna O och T har en lodrät symmetriaxel, men inte R, B och L. Därför kommer endast ordet TOOT kunna skrivas
Kängurutävlingen 018 Cadet svar och kommentarer Facit Cadet 1: C 19 0 + 18 = 8 = 19 : E TOOT Bokstäverna O och T har en lodrät symmetriaxel, men inte R, B och L. Därför kommer endast ordet TOOT kunna skrivas
1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 4 C: kvadrat Exempel på hur formerna kan konstrueras:
 Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Svar och lösningar 1 C: 2 En vågrät och en lodrät symmetrilinje genom kvadratens mittpunkt. 2 D: 4 8 = 2 2 2, alltså finns det 2 2 = 4 boxar i bottenlagret. 3 E: 6a + 8b Sidorna är a + a + a = 3a och b
Känguru 2018 Benjamin (åk 6 och 7)
 sida 0 / 8 NAMN KLASS Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Ett rätt svar ger 3, 4 eller 5 poäng. I varje uppgift är exakt ett svar korrekt.
sida 0 / 8 NAMN KLASS Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Ett rätt svar ger 3, 4 eller 5 poäng. I varje uppgift är exakt ett svar korrekt.
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Cadet 2013 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Benjamin 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
Kängurun Matematikens hopp Benjamin 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring
5: D 3 23 kan bara fås på ett sätt: Här har man nytta av att känna igen 24 som ett tal i sexans tabell.
 Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Svar och lösningar 1: D 200 9 = 1800 Om eleverna inte redan kan multiplicera med 200 kan lösningen förklaras via 100 9 = 9 100 = 900. 200 9 är alltså dubbelt så mycket, 1800. Vi kan också utesluta de andra
Matematik 92MA41 (15hp) Vladimir Tkatjev
 Matematik 92MA41 (15hp) Vladimir Tkatjev Med anledning av de nya kursplanerna har Strävorna reviderats. Formen, en matris med rutor, är densamma men istället för att som tidigare anknyta till mål att sträva
Matematik 92MA41 (15hp) Vladimir Tkatjev Med anledning av de nya kursplanerna har Strävorna reviderats. Formen, en matris med rutor, är densamma men istället för att som tidigare anknyta till mål att sträva
Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Kängurutävlingen Matematikens hopp 2019 Benjamin
 Kängurutävlingen Matematikens hopp 2019 Benjamin Trepoängsproblem 1 Carrie har börjat att rita en katt. Hur kan hennes färdiga teckning se ut? (Norge) 2 Mayafolket skrev tal på ett annat sätt än vi gör.
Kängurutävlingen Matematikens hopp 2019 Benjamin Trepoängsproblem 1 Carrie har börjat att rita en katt. Hur kan hennes färdiga teckning se ut? (Norge) 2 Mayafolket skrev tal på ett annat sätt än vi gör.
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 017, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på
Kängurun Matematikens hopp Ecolier 017, svar och lösningar Här följer korta svar, rättningsmall och redovisningsblanketter. Ett underlag till hjälp för bokföring av klassens resultat finns att hämta på
Södervångskolans mål i matematik
 Södervångskolans mål i matematik Mål som eleverna lägst ska ha uppnått i slutet av det första skolåret beträffande tal och taluppfattning kunna läsa av en tallinje mellan 0-20 kunna läsa och ramsräka tal
Södervångskolans mål i matematik Mål som eleverna lägst ska ha uppnått i slutet av det första skolåret beträffande tal och taluppfattning kunna läsa av en tallinje mellan 0-20 kunna läsa och ramsräka tal
Kängurutävlingen Matematikens hopp 2018 Ecolier
 Kängurutävlingen Matematikens hopp 2018 Ecolier Trepoängsproblem 1 På bilden ser du 3 pilar som rör sig och 9 ballonger som sitter fast. När en pil träffar en ballong spricker ballongen. Pilen fortsätter
Kängurutävlingen Matematikens hopp 2018 Ecolier Trepoängsproblem 1 På bilden ser du 3 pilar som rör sig och 9 ballonger som sitter fast. När en pil träffar en ballong spricker ballongen. Pilen fortsätter
Känguru 2018 Cadet (åk 8 och 9)
 sida 0 / 8 NAMN KLASS Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Ett rätt svar ger 3, 4 eller 5 poäng. I varje uppgift är exakt ett svar korrekt.
sida 0 / 8 NAMN KLASS Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Ett rätt svar ger 3, 4 eller 5 poäng. I varje uppgift är exakt ett svar korrekt.
Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Student 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
1 B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3.
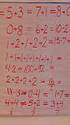 Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Svar och lösningar B: 3 Ta bort två trianglar på vardera sidan om likhetstecknet. Det ger två trianglar = 6, alltså en triangel = 3. C: 3 C: Skriv talen i ordning och räkna uppifrån. Diskutera med eleverna
Matematik. Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret. Mål som eleverna skall ha uppnått i slutet av det femte skolåret
 Balderskolan, Uppsala musikklasser 2009 Matematik Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret läsa och skriva tal inom talområdet 0 10 000 räkna de fyra räknesätten med olika metoder
Balderskolan, Uppsala musikklasser 2009 Matematik Mål som eleverna skall ha uppnått i slutet av det fjärde skolåret läsa och skriva tal inom talområdet 0 10 000 räkna de fyra räknesätten med olika metoder
= A: 0 B: 1 C: 2013 D: 2014 E: 4028
 Trepoängsproblem 1. 2014 2014 2014 2014 = A: 0 B: 1 C: 2013 D: 2014 E: 4028 2. Kängurutävlingen hålls den tredje torsdagen i mars varje år. Vilket datum är det senaste som tävlingen kan hållas? A: 14 mars
Trepoängsproblem 1. 2014 2014 2014 2014 = A: 0 B: 1 C: 2013 D: 2014 E: 4028 2. Kängurutävlingen hålls den tredje torsdagen i mars varje år. Vilket datum är det senaste som tävlingen kan hållas? A: 14 mars
Undersökande arbetssätt i matematik 1 och 2
 Matematik Gymnasieskola Modul: Matematikundervisning med digitala verktyg Del 6: Undersökande arbetssätt med matematisk programvara Undersökande arbetssätt i matematik 1 och 2 I texten Undersökande arbetssätt
Matematik Gymnasieskola Modul: Matematikundervisning med digitala verktyg Del 6: Undersökande arbetssätt med matematisk programvara Undersökande arbetssätt i matematik 1 och 2 I texten Undersökande arbetssätt
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Ecolier 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. De flesta problem kan lösas på flera sätt och med olika representationsformer.
Kängurun Matematikens hopp Ecolier 2010 Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. De flesta problem kan lösas på flera sätt och med olika representationsformer.
Känguru Student (gymnasiet åk 2 och 3) sida 1 / 6
 Känguru Student (gymnasiet åk 2 och 3) sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara
Känguru Student (gymnasiet åk 2 och 3) sida 1 / 6 NAMN KLASS/GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tom om du inte vill besvara
Benjamin. Avdelning 1. Trepoängsproblem
 Avdelning 1. Trepoängsproblem Benjamin 1 Greta promenerar längs stigen från vänster till höger. När stigen delar sig måste hon välja den ena stigen. Hon vänder inte och går tillbaka. Längs stigen hittar
Avdelning 1. Trepoängsproblem Benjamin 1 Greta promenerar längs stigen från vänster till höger. När stigen delar sig måste hon välja den ena stigen. Hon vänder inte och går tillbaka. Längs stigen hittar
kan använda sig av matematiskt tänkande för vidare studier och i vardagslivet kan lösa problem och omsätta idéer i handling på ett kreativt sätt
 Lokal pedagogisk planering Matematik år 2 Syfte Undervisningen i matematikämnet ska syfta till att eleverna ska utveckla kunskaper om matematik och visa intresse och tilltro till sin förmåga att använda
Lokal pedagogisk planering Matematik år 2 Syfte Undervisningen i matematikämnet ska syfta till att eleverna ska utveckla kunskaper om matematik och visa intresse och tilltro till sin förmåga att använda
Trepoängsproblem. Kängurutävlingen 2011 Cadet. 1 Vilket av följande uttryck har störst värde? 1 A: B: C: D: E: 2011
 Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
A: 111 B: 900 C: 909 D: 990 E: 999
 3-poängsproblem 1. 1000 100 + 10 1 =? A: 111 B: 900 C: 909 D: 990 E: 999 2. Miriam har 16 kort, fyra av varje färg: 4 spader, 4 klöver, 4 ruter och 4 hjärter. Hon vill lägga dem på rutnätet här bredvid
3-poängsproblem 1. 1000 100 + 10 1 =? A: 111 B: 900 C: 909 D: 990 E: 999 2. Miriam har 16 kort, fyra av varje färg: 4 spader, 4 klöver, 4 ruter och 4 hjärter. Hon vill lägga dem på rutnätet här bredvid
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
7F Ma Planering v2-7: Geometri
 7F Ma Planering v2-7: Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
7F Ma Planering v2-7: Geometri Arbetsform under en vecka: Måndagar (50 min): Genomgång av gemensamma svårigheter i begrepp och metoder. Arbete i grupp med begrepp och metoder. Läxa (30 min): Läsa på anteckningar
Benjamin för elever i åk 5, 6 och 7
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2016 Benjamin för elever i åk 5, 6 och 7 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Trepoängsproblem. Kängurutävlingen 2011 Junior
 Trepoängsproblem 1 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen börjar och slutar med ett vitt streck. På Storgatan har ett övergångsställe totalt åtta vita
Trepoängsproblem 1 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen börjar och slutar med ett vitt streck. På Storgatan har ett övergångsställe totalt åtta vita
a) 1 b) 4 a) b) c) c) 6 a) = 4 b) = 6 c) = 6 1. Hur många? Ringa in talet. 2. Vilket tal kommer efter? 4. Beräkna. 3. Hur många?
 1. Hur många? Ringa in talet. 2. Vilket tal kommer efter? Exempel a) 1 2 b) 4 5 a) b) c) c) 6 7 3. Hur många? 4. Beräkna. Exempel 1 + 2 = 3 a) 3 + 1 = 4 a) 4 b) 5 b) 4 + 2 = 6 c) 3 + 3 = 6 c) 3 d) 2 GILLA
1. Hur många? Ringa in talet. 2. Vilket tal kommer efter? Exempel a) 1 2 b) 4 5 a) b) c) c) 6 7 3. Hur många? 4. Beräkna. Exempel 1 + 2 = 3 a) 3 + 1 = 4 a) 4 b) 5 b) 4 + 2 = 6 c) 3 + 3 = 6 c) 3 d) 2 GILLA
Om LGR 11 FÖRMÅGOR CENTRALT INNEHÅLL. De matematiska förmågor som undervisningen i åk 1-9 syftar till att eleverna ska utveckla.
 Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Om LGR 11 FÖRMÅGOR FÖRMÅGOR Lgr 11: Genom undervisningen i matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att formulera och lösa problem med hjälp av matematik samt
Lösningsförslag Junior 2014
 Kängurutävlingen 014 Junior, svar och lösningar Lösningsförslag Junior 014 1 E: c < b < a Längden av linje a är 16 l.e., linje b (8 + ) l.e. och linje c (8+4 p ) l.e. Alternativ lösning: Grundfiguren har
Kängurutävlingen 014 Junior, svar och lösningar Lösningsförslag Junior 014 1 E: c < b < a Längden av linje a är 16 l.e., linje b (8 + ) l.e. och linje c (8+4 p ) l.e. Alternativ lösning: Grundfiguren har
Torskolan i Torsås Mars 2007. Matematik. Kriterier för betyget godkänd. Metoder: Arbetssätt. Muntligt. Problemlösning
 Torskolan i Torsås Mars 2007 Matematik Kriterier för betyget godkänd Metoder: Arbetssätt Ta ansvar för sin egen inlärning. Göra läxor. Utnyttja lektionstiden (lyssna, arbeta). Utnyttja den hjälp/stöd som
Torskolan i Torsås Mars 2007 Matematik Kriterier för betyget godkänd Metoder: Arbetssätt Ta ansvar för sin egen inlärning. Göra läxor. Utnyttja lektionstiden (lyssna, arbeta). Utnyttja den hjälp/stöd som
Problemlösning, utveckla förmågan att kommunicera matematik och använda matematikens uttrycksformer 5 F
 På jakt efter förmågor i undervisningen Problemlösning, utveckla förmågan att kommunicera matematik och använda matematikens uttrycksformer 5 F Aktivitetens namn: Triangelmatte Syfte Undervisningen ska
På jakt efter förmågor i undervisningen Problemlösning, utveckla förmågan att kommunicera matematik och använda matematikens uttrycksformer 5 F Aktivitetens namn: Triangelmatte Syfte Undervisningen ska
Målkriterier Beskrivning Exempel Eleven kan tolka elevnära information med matematiskt innehåll.
 ÖREBRO MATEMATIK, ÅR 3 1(5) Eleven kan tolka elevnära information med matematiskt innehåll Eleven kan uttrycka sig muntligt, skriftligt och i handling på ett begripligt sätt med hjälp av vardagligt språk,
ÖREBRO MATEMATIK, ÅR 3 1(5) Eleven kan tolka elevnära information med matematiskt innehåll Eleven kan uttrycka sig muntligt, skriftligt och i handling på ett begripligt sätt med hjälp av vardagligt språk,
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant?
 En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
En parallellogram har delats i två delar P och Q som figuren visar. Vilket av följande påståenden är säkert sant? P har större omkrets än Q. P har mindre omkrets än Q. P har mindre area än Q Q och P har
Matematik 92MA41 (15hp) Vladimir Tkatjev
 Matematik 92MA41 (15hp) Vladimir Tkatjev Lite inspiration Går det att konstruera 6 kvadrater av 12 tändstickor? Hur gör man då? (Nämnaren, Nr 2, 2005) Litet klurigt kanske, bygg en kub av stickorna: Uppgift
Matematik 92MA41 (15hp) Vladimir Tkatjev Lite inspiration Går det att konstruera 6 kvadrater av 12 tändstickor? Hur gör man då? (Nämnaren, Nr 2, 2005) Litet klurigt kanske, bygg en kub av stickorna: Uppgift
Cadet. a: 1001 b: 11 c: 223 d: 191 e: 123 (Sverige) 2 Boris är född 1 januari 2002 och han är 1 år och 1 dag äldre än Irina. Vilken dag föddes Irina?
 Cadet Avdelning. Trepoängsproblem 2007 2 + 0 + 0 + 7 = a: 00 b: c: 223 d: 9 e: 23 (Sverige) 2 Boris är född januari 2002 och han är år och dag äldre än Irina. Vilken dag föddes Irina? a: 2 januari 2003
Cadet Avdelning. Trepoängsproblem 2007 2 + 0 + 0 + 7 = a: 00 b: c: 223 d: 9 e: 23 (Sverige) 2 Boris är född januari 2002 och han är år och dag äldre än Irina. Vilken dag föddes Irina? a: 2 januari 2003
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Kängurutävlingen Matematikens hopp Junior 011 Här följer först svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Därefter följer förslag till hur ni
Känguru 2013 Junior sida 1 / 8 (gymnasiet åk 1) i samarbete med Jan-Anders Salenius vid Brändö gymnasium
 Känguru 2013 Junior sida 1 / 8 NAMN KLASS / GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Felaktigt svar ger minus 1/4 poäng av uppgiftens totala
Känguru 2013 Junior sida 1 / 8 NAMN KLASS / GRUPP Poängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Felaktigt svar ger minus 1/4 poäng av uppgiftens totala
Bagarmossens skolas kravnivåer beträffande tal och talens beteckningar som eleven ska ha uppnått efter:
 Matematik 1-5 Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och
Matematik 1-5 Skolan skall i sin undervisning i matematik sträva efter att eleven utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och
Kängurun Matematikens hopp
 Kängurun Matematikens hopp Cadet 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Kängurun Matematikens hopp Cadet 2012, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också lösningsförslag. Ett underlag till hjälp för bokföring av
Student för elever på kurs Ma 4 och Ma 5
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 16 mars 2017 Student för elever på kurs Ma 4 och Ma 5 Tävlingen genomförs under perioden 16 24 mars. Uppgifterna får inte användas tidigare.
Matematik. Ämnesprov, läsår 2013/2014. Bedömningsanvisningar Delprov B, C, D, E. Årskurs
 Ämnesprov, läsår 2013/2014 Matematik Bedömningsanvisningar Delprov B, C, D, E Årskurs 6 Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Ämnesprov, läsår 2013/2014 Matematik Bedömningsanvisningar Delprov B, C, D, E Årskurs 6 Prov som återanvänds av Skolverket omfattas av sekretess enligt 17 kap. 4 offentlighets- och sekretesslagen. Detta
Kängurutävlingen Matematikens hopp
 Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Kängurutävlingen Matematikens hopp Junior 2017, svar och lösningar Här följer svar, rättningsmall och redovisningsblanketter. Förutom svar ger vi också några olika lösningsförslag. Ett underlag till hjälp
Ma7-Per: Geometri. Det tredje arbetsområdet handlar om geometri.
 Ma7-Per: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda
Ma7-Per: Geometri Det tredje arbetsområdet handlar om geometri. Syftet med undervisningen är att du ska utveckla din förmåga att: - formulera och lösa problem med hjälp av matematik samt värdera valda
1. Det står KANGAROO på mitt paraply. Du kan se det på bilden. Vilken av följande bilder visar också mitt paraply? A: B: C: D: E:
 N G A RA Kängurutävlingen 2015 Cadet Trepoängsproblem 1. Det står KANGAROO på mitt paraply. Du kan se det på bilden. Vilken av följande bilder visar också mitt paraply? A: B: C: D: E: O O K 2. Rektangeln
N G A RA Kängurutävlingen 2015 Cadet Trepoängsproblem 1. Det står KANGAROO på mitt paraply. Du kan se det på bilden. Vilken av följande bilder visar också mitt paraply? A: B: C: D: E: O O K 2. Rektangeln
geometri och statistik
 Svikten geometri och statistik Innehåll Mönster Geometriska figurer Del av Matematiska ord Längd runt om Tredimensionella figurer Tabeller och diagram Problemlösning Kan du? Hur gick det? 2-3 4-5 6-7 8-9
Svikten geometri och statistik Innehåll Mönster Geometriska figurer Del av Matematiska ord Längd runt om Tredimensionella figurer Tabeller och diagram Problemlösning Kan du? Hur gick det? 2-3 4-5 6-7 8-9
Bedömning för lärande i matematik
 HANDLEDNING TILL Bedömning för lärande i matematik FÖR ÅRSKURS 1 9 1 Handledning I denna handledning ges förslag på hur du kan komma igång med materialet Bedömning för lärande i matematik åk 1 9. Du börjar
HANDLEDNING TILL Bedömning för lärande i matematik FÖR ÅRSKURS 1 9 1 Handledning I denna handledning ges förslag på hur du kan komma igång med materialet Bedömning för lärande i matematik åk 1 9. Du börjar
Matematik. Mål att sträva mot. Mål att uppnå. År 1 Mål Kriterier Eleven ska kunna. Taluppfattning koppla ihop antal och siffra kan lägga rätt antal
 Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c.
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2017 Cadet för elever i åk 8, 9 och för elever som läser kurs 1a, 1b eller 1c. Kängurutävlingen genomförs i år den 16 mars. Om den dagen inte
