Lektionsaktivitet: Var är den? Hur ser den ut?
|
|
|
- Anita Gustafsson
- för 7 år sedan
- Visningar:
Transkript
1 Särskla Mdul: Didaktiska perspektiv på matematikundervisningen 2 Del 3: Gemetri ch statistik Lektinsaktivitet: Var är den? Hur ser den ut? Berit Bergius & Lena Trygg, NCM Syfte Lektinsaktiviteten består av ett antal mindre aktiviteter vilka sammantaget syftar till att vidga ch fördjupa elevernas rumsuppfattning, ch hur den kan uttryckas språkligt ch med symbler. Material Det finns många labrativa matematikmaterial sm är avsedda för gemetriundervisning. Några exempel är pedaggiska material sm tangram, gebräden ch lgiska blck liksm kpieringsunderlag i frm av krdinatsystem, rutark ch prickpapper. Beskrivning inklusive variatin ch prgressin Strukturen i hela lektinsaktiviteten bygger på psitin ch frm samt en kmbinatin av dem. Sm i övriga lektinsaktiviteter är det möjligt att både starta ch sluta på lika nivåer, men eleverna bör ges möjlighet att arbeta med både psitin ch frm. Här behandlas i huvudsak frmer i två dimensiner. I lektinsaktiviteten En massa infrmatin finns förslag även med tre dimensiner. Psitin För att kunna rientera sig själv ch annat i mvärlden är det nödvändigt att kunna relatera till lägen ch riktningar. Frågr m var ch vart är uttalade eller underförstådda i det dagliga livet. Sm ett led i att utveckla elevers självständighet ska undervisningen ge beredskap att möta ch hantera frågr m psitin. Arbeta med hela gruppen ch rikta uppmaningar till eleverna: vänd ryggen åt dörren, vänd ansiktet åt Zerah, lägg höger hand på vänster knä, lägg pennan under stlen, bken på stlen Frtsätt tillsammans, men rikta uppmaningarna till enskilda elever: sätt dig mellan Jasmine ch bänken, sätt dig till vänster m Mari. Var sitter Pelle i förhållande till dig? Till mig? Lena? Arman? Låt en elev vara ledare ch rikta uppmaningar till sina kamrater. Sitt i ring runt en elev. Låt eleven mitt i ringen berätta, från sin psitin, var några av kamraterna befinner sig. Placera ett bjekt med tydlig fram- ch baksida (en dcka, ett djur, en bil, en bk) mitt i ringen. Var sitter Jhan, Kari, Lisa, i förhållande till dckan? Använd begrepp sm bakm ch framför, vänster ch höger. Sätt ett papper med stra rutr på tavlan. Diskutera hur många rutr det finns i varje rad ch antal rader räknat nerifrån. Placera en bild av ett föremål i en Lektinsaktivitet: Var är den? Hur ser den ut? Juli (5)
2 Särskla Frm ruta. Beskriv psitinen: stjärnan är i tredje rutan på första raden (nerifrån). Sätt upp fler bilder ch låt eleverna beskriva psitinerna. Lägg senare till rdet klumn. Diskutera likheter ch skillnader mellan rad ch klumn. Ge raderna sifferbeteckningar ch klumnerna bkstavsbeteckningar: stjärnan är i A3. Detta är ett pararbete. Använd fyra rutpapper, två per elev, sm spelplaner, t ex ti gånger ti rutr, där raderna är märkta med siffrr ch klumnerna med bkstäver. Båda eleverna placerar fyra bilder (t ex stjärna, bil, hus, penna) i valfria rutr på sitt ena papper, utan att visa kamraten. Sätt upp en skärm av någt slag mellan eleverna. Eleverna turas sedan m att leta efter var kamratens bilder finns, genm att uttrycka psitiner. Jag gissar att det finns någt på D7. Antingen är rutan tm, då svarar kamraten bm eller så är det en träff ch kamraten berättar vad sm har träffats. Eleven sm frågar markerar bmmar ch träffar på sitt tmma rutpapper. Gå vidare med att eleverna skriver in sitt namn i rutrna, en ruta för varje bkstav, istället för bilder. Inled med att de skriver namnet vågrätt men när de blir vana kan de ckså skriva ldrätt eller diagnalt. (Ta upp rden vågrät, ldrät, diagnal.) Det blir en utmaning för kamraten att utifrån en träff lkalisera var resten av bkstäverna i namnet finns ch att planera strategiskt för att undvika bmmar. När vi ser ss mkring är frm en framträdande egenskap. För att kunna tlka ch beskriva mvärlden behövs begrepp ch språkliga uttryck m frm, med gemensam ch liktydig tlkning. Elever behöver erfarenheter sm utvecklar deras uppmärksamhet på ch möjlighet att benämna ch beskriva frm, på ett efterhand allt mer detaljerat sätt. Vad är lika ch vad skiljer? Hur vet vi det? Lägg en samling lgiska blck framför eleverna. Håll upp ett blck. Hitta en likadan. Uppmärksamma m frmen är lika, men där strlek, tjcklek eller färg är lika. Diskutera innebörden i likadan. Upprepa med fler blck. Låt eleverna beskriva blckets egenskaper, färg, tjcklek ch strlek (area). Kan alla enas m att för att vara likadan, måste alla egenskaper vara lika? Uppmuntra eleverna att vara uppmärksamma på alla egenskaper när aktiviteten frtsätter. Vid ett annat tillfälle kan uppgiften bli att leta reda på ett blck där en egenskap skiljer sig från förebilden. Eleverna berättar krt m blcket de valt ch vilken egenskap sm skiljer sig från förebilden. Genm aktiviteterna riktas elevernas uppmärksamhet på likheter ch skillnader mellan lika frmer men ckså mellan blck med samma frm sm skiljer sig åt i färg, tjcklek ch area. Gemensamma samtal stärker förmågan att uttrycka lika egenskaper. Lektinsaktivitet: Var är den? Hur ser den ut? Juli (5)
3 Särskla Vilket blck tänker jag på? Lägg en uppsättning av lgiska blck framför eleverna. Ge ledtrådar, sm efterhand avgränsar tänkbara blck. Det är litet (hälften av blcken kvar). Det är tunt (halverar återstden). Det är blått (en tredjedel av blcken är kvar). Det är en kvadrat (ger avgörande infrmatin). Lägg en gemetrisk frm, t ex ett lgiskt blck, i en tygpåse. Låt en elev stppa ner handen, känna efter ch ge ledtrådar. Låt sedan kamraterna ställa kmpletterade frågr m egenskaper. Upprepa många gånger ch försök vässa frågrna så det behövs allt färre ledtrådar ch frågr för att ringa in en frm. Vilken frm gömmer sig? Lägg en gemetrisk frm under ett papper så att bara en liten del av den syns. Dra sakta fram den medan eleverna beskriver vilka frmer det skulle kunna vara ch vilka det inte kan vara. Ställ frågr sm Kan det vara en? Varför? Varför inte? Låt eleverna mtivera genm att ange egenskaper sm styrker eller bestrider förslagen. Se även sidrna 4 5 det nrska häftet Skap frmen. Lag reglene. Se hva sm skjer! sm kan laddas ner från Skiss till en serie aktiviteter med gebräde. Dkumentera på prickpapper, se ncm.gu.se/matematikpapper. Gör lika stra kvadrater ch rektanglar på brädet. Jämför sidlängder ch vinklar. Gör rektanglar med bestämd mkrets eller area. Gör lika trianglar. Gör lika rätvinkliga trianglar. Fler aktiviteter med gebräde finns på ncm.gu.se/media/stravrna/2/c/2c_iperssn.pdf Skiss till en serie aktiviteter med tangram. Tangram att klippa ut ur papper, se ncm.gu.se/matematikpapper. Varje elev pusslar alla delar till en valfri bild ch berättar m den. Dkumentera på lämpligt sätt. Använd dkumentatinerna sm förlaga för att lägga en likadan bild eller låt en kamrat beskriva den muntligt så att någn kan lägga en likadan. Studera ch ange tillsammans tangramdelarnas frm ch egenskaper. Vad är lika? Vad skiljer? Undersök vilka bitar sm kan sättas samman till en lika str kvadrat, triangel eller parallellgram sm en av pusselbitarna. Jämför bitarnas strlek. Vilka är lika stra (har samma area)? Vilka har samma mkrets? Hur går det att ta reda på? Sätt samman alla delar till en kvadrat, en rektangel, en triangel eller en parallellgram. Dkumentera. Jämför area ch mkrets. Hur str del av helheten är varje del? Lektinsaktivitet: Var är den? Hur ser den ut? Juli (5)
4 Särskla Undersök med tangram 2C6C är en Strävrnaaktivitet sm handlar m knstruktin av gemetriska bjekt, att sätta samman ch dela upp månghörningar. Det är insidan sm räknas 2C är en Strävrnaaktivitet sm handlar m vinklar i ett tangram. Krta aktiviteter: Tangram, se ncm.gu.se/media/mvbken/krta_aktiviteter/katangram2.pdf. Aktiviteten handlar m area uttryckt i bråkfrm. Frm ch psitin I vardagen måste vi hantera sinnesintryck av, uppgifter m ch kunna uttrycka sådant sm handlar m både frm ch psitin, t ex på det vala brdet i rummet står Elever behöver erfarenheter av att samtidigt uttrycka båda aspekterna. Följande förslag ger stöd i det arbetet. Kpiera min bild. Sätt samman lgiska blck (starta med två ch utöka sedan) till ett enkelt mtiv. Placera blcken så att de vidrör varandra. Låt eleverna göra en likadan bild med blck ch beskriva den med hjälp av frm, färg, strlek ch psitin. Bygg en egen bild. Låt eleverna använda ett bestämt antal lgiska blck, t ex sju. Blcken placeras tätt ihp ch vidrör varandra. Observera hur eleverna hanterar antalet ch förutsättningarna med placeringen. Dkumentera lösningarna i bild ch text. Använd senare dkumentatinerna sm förlagr i pararbete där eleverna sitter rygg mt rygg. En elev beskriver bildens frmer, färger, strlekar ch psitiner. Kamraten lägger blcken utifrån beskrivningen. Jämför riginal ch kpia. Vad är lika? Varför är de lika? Vad skiljer? Varför? Belys språkets rll genm att låta eleverna beskriva vad sm var lätt eller svårt att uttrycka eller tlka. Placera eleverna runt ett brd. Bygg ett enkelt mtiv av några lgiska blck framför eleverna. Låt eleverna rita av det så sm de ser mtivet från sin plats. Sätt upp bilderna på väggen ch resnera m varför bilderna ser lika ut. Placera en elev på varje sida m ett brd ch lägg fram några gemetriska frmer. Hur ser den stra triangeln ut från elevernas lika håll? Rektangeln? Kvadraten? Låt eleverna sätta upp en likadan triangel på väggen i den psitin sm de själva ser den på brdet. Diskutera ch jämför. Varför ser det lika ut? Vilka frmer ser lika ut från alla håll? Varför ser inte alla frmer lika ut från alla håll? Uppmärksamma vilka begrepp eleverna använder för att uttrycka sina iakttagelser. Finns det begrepp ch uttryck sm de saknar eller är säkra på ch sm behöver tas upp i undervisningen? Använd A3-papper med stra rutr sm spelplan. Markera en tydlig mittlinje, så det blir en halva till varje elev, ch placera en elev vid varje krtsida av papperet. Eleverna turas m att lägga en gemetrisk frm, t ex lgiska blck, Lektinsaktivitet: Var är den? Hur ser den ut? Juli (5)
5 Särskla på sin sida av papperet. I varje drag ska kamraten lägga ett likadant blck på mtsvarande plats på sin sida av pappret. Eleverna tlkar frm, frmens läge, färg, strlek ch psitinen på papperet. När aktiviteten är slut kan spegelsymmetrin eventuellt diskuteras. (Papper med lika stra rutr finns på ncm.gu.se/matematikpapper. Kpiera A4 till A3.) Placera gemetriska frmer på tavlan, t ex sm på ftt. Låt eleverna föreställa sig ch beskriva hur det ser ut när rektangeln vrids ett halvt varv kvadraten finns mitt i rektangeln triangeln vrids ett halvt varv cirkeln flyttas diagnalt så långt det går när hela bilden vrids ett halvt varv. Låt eleverna beskriva det nya läget med rd ch sedan visa knkret. Varje drag utgår från utgångsläget. (Behöver helt, halvt ch kvarts varv förklaras?) Intrduktin Varje delaktivitet behöver sin särskilda intrduktin med instruktin ch någt sm skapar förväntan. Använd generella frågeställningar för att hitta underlag för intrduktinen: Är det några rd sm behöver förklaras? Går det att göra aktiviteten tillsammans en eller ett par gånger utan att den bärande idén avslöjas? Hur kan elevernas nyfikenhet väckas? Vilka anpassningar av material ch instruktiner behöver göras för enskilda elever? Hur kan elevernas utmanas till att diskutera vad de trr kmmer att hända? Elevers dkumentatin Vilka aktiviteter behöver dkumenteras frtlöpande under tiden de pågår? Vilka aktiviteter är lämpligare att eleverna dkumenterar när de är genmförda? Är det någn aktivitet sm inte alls behöver dkumentatin? För övrigt hänvisas till texten Elevers dkumentatin sm finns under Mment A i denna del, bland annat är Likheter ch skillnader återkmmande i många av aktiviteterna. Lektinsaktivitet: Var är den? Hur ser den ut? Juli (5)
2C 6C. Form logiska block. strävorna
 strävorna 2C 6C Form logiska block samband begrepp kreativ och estetisk verksamhet geometri Avsikt och matematikinnehåll När vi ser oss omkring är form en framträdande egenskap. För att kunna känna igen,
strävorna 2C 6C Form logiska block samband begrepp kreativ och estetisk verksamhet geometri Avsikt och matematikinnehåll När vi ser oss omkring är form en framträdande egenskap. För att kunna känna igen,
Var är den? strävorna
 strävorna C Var är den? kommunicera uttrycksformer geometri Avsikt och matematikinnehåll Här ges förslag på några aktiviteter som sammantaget syftar till att vidga och fördjupa elevers rumsuppfattning,
strävorna C Var är den? kommunicera uttrycksformer geometri Avsikt och matematikinnehåll Här ges förslag på några aktiviteter som sammantaget syftar till att vidga och fördjupa elevers rumsuppfattning,
Form tangrampussel. Låt eleven rita runt lagda former, benämna dem och/eller skriva formernas namn.
 strävorna 2C 6C Form tangrampussel samband begrepp kreativ och estetisk verksamhet geometri Avsikt och matematikinnehåll När vi ser oss omkring är form en framträdande egenskap. För att kunna känna igen,
strävorna 2C 6C Form tangrampussel samband begrepp kreativ och estetisk verksamhet geometri Avsikt och matematikinnehåll När vi ser oss omkring är form en framträdande egenskap. För att kunna känna igen,
Lektionsaktivitet: Känna igen, hitta och beskriva
 Modul: Didaktiska perspektiv på matematikundervisningen 2 Del 3: Geometri och statistik Geometri Träningsskola och individuellt program Berit Bergius & Lena Trygg, NCM Om verkligheten ska bli begriplig
Modul: Didaktiska perspektiv på matematikundervisningen 2 Del 3: Geometri och statistik Geometri Träningsskola och individuellt program Berit Bergius & Lena Trygg, NCM Om verkligheten ska bli begriplig
Geometri år 7C och 7D vt-14
 Gemetri år 7C ch 7D vt-14 Förankring i kursplanens syfte I matematik tränas elevernas förmåga att: frmulera ch lösa prblem med hjälp av matematik samt värdera valda strategier ch metder använda ch analysera
Gemetri år 7C ch 7D vt-14 Förankring i kursplanens syfte I matematik tränas elevernas förmåga att: frmulera ch lösa prblem med hjälp av matematik samt värdera valda strategier ch metder använda ch analysera
Pedagogisk planering matematik Gäller för november-december 2015
 Pedaggisk planering matematik Gäller för nvember-december 2015 Myrstacken Äldre årskurs 6, Hällby skla L= mest för läraren E= viktigt för eleven I periden ingår bedömningsdelar vi pga muntliga prv ch annat
Pedaggisk planering matematik Gäller för nvember-december 2015 Myrstacken Äldre årskurs 6, Hällby skla L= mest för läraren E= viktigt för eleven I periden ingår bedömningsdelar vi pga muntliga prv ch annat
För att kunna utföra en variable data printning böhöver du följande filer:
 Printa Variabel Data Variabel data printning tillåter dig att byta infrmatinen ch data i ditt dkument eller i din bild för att skapa utskrifter med unika texter ch bilder i varje kpia. Denna funktinen
Printa Variabel Data Variabel data printning tillåter dig att byta infrmatinen ch data i ditt dkument eller i din bild för att skapa utskrifter med unika texter ch bilder i varje kpia. Denna funktinen
Fritidshemmets uppdrag och utmaningar. ALP observatörsutbildning 10 september 2015
 Fritidshemmets uppdrag ch utmaningar ALP bservatörsutbildning 10 september 2015 Samtala två ch två- Vad tänker du på när du tänker på fritidshem? Innehållet vi skall ta ss an är Fritidshemmets styrdkument
Fritidshemmets uppdrag ch utmaningar ALP bservatörsutbildning 10 september 2015 Samtala två ch två- Vad tänker du på när du tänker på fritidshem? Innehållet vi skall ta ss an är Fritidshemmets styrdkument
Arbeta vidare med geometriproblemen 2018
 Arbeta vidare med gemetriprblemen 2018 Varje år har många av prblemen gemetrisk anknytning. I år har vi samlat dessa prblem från lika tävlingsklasser ch kpplat ihp dem sm behandlar liknande delar av gemetrin.
Arbeta vidare med gemetriprblemen 2018 Varje år har många av prblemen gemetrisk anknytning. I år har vi samlat dessa prblem från lika tävlingsklasser ch kpplat ihp dem sm behandlar liknande delar av gemetrin.
1 Paint. 1.1 Öppna Paint. 1.2 Rita linjer
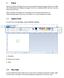 1 Paint Paint är en funktin i Windws 10 sm du kan använda för att göra teckningar på ett tmt mråde eller på befintliga bilder. Många av verktygen i Paint finns i menyfliksmrådet, sm finns i den övre delen
1 Paint Paint är en funktin i Windws 10 sm du kan använda för att göra teckningar på ett tmt mråde eller på befintliga bilder. Många av verktygen i Paint finns i menyfliksmrådet, sm finns i den övre delen
Om undervisningen. Att förstå tal. Förstå och använda tal en handbok
 Om undervisningen Inledningsvis kan man nöja sig med att uttrycka bråk muntligt. Vi bör uppmuntra eleverna att använda de språkliga uttrycken halv och fjärdedel när de delar i två eller fyra lika delar.
Om undervisningen Inledningsvis kan man nöja sig med att uttrycka bråk muntligt. Vi bör uppmuntra eleverna att använda de språkliga uttrycken halv och fjärdedel när de delar i två eller fyra lika delar.
Hur man skapar ett test i Test och quiz i Mondo 2.6
 Hur man skapar ett test i Test ch quiz i Mnd 2.6 Snabbstart Under Test ch quiz, namnge ditt test under fältet Namn ch klicka senare på Skapa. Börja sedan med att gå igenm inställningarna, för att kmma
Hur man skapar ett test i Test ch quiz i Mnd 2.6 Snabbstart Under Test ch quiz, namnge ditt test under fältet Namn ch klicka senare på Skapa. Börja sedan med att gå igenm inställningarna, för att kmma
Geocaching- Klarar er klass att hitta den 5:e cachen?
 Gecaching- Klarar er klass att hitta den 5:e cachen? Sklprgram att utföra på egen hand eller tillsammans med handledare från Aerseum. Lärarhandledning ch förberedelse På de nästföljande sidrna finns ett
Gecaching- Klarar er klass att hitta den 5:e cachen? Sklprgram att utföra på egen hand eller tillsammans med handledare från Aerseum. Lärarhandledning ch förberedelse På de nästföljande sidrna finns ett
TÅGET KAN INTE VÄJA!
 Lektinsplanering 2 TÅGET KAN INTE VÄJA! TÅGET KAN INTE VÄJA! Lärämnen ch lektiner där man kan gå igenm materialet: Miljö- ch naturkunskap (bilgi, hälskunskap) Fysik ch kemi Integrering: Nivå: Årsklass
Lektinsplanering 2 TÅGET KAN INTE VÄJA! TÅGET KAN INTE VÄJA! Lärämnen ch lektiner där man kan gå igenm materialet: Miljö- ch naturkunskap (bilgi, hälskunskap) Fysik ch kemi Integrering: Nivå: Årsklass
Programmering Åk Blockly Games
 Prgrammering Åk 7-9 -Blckly Games Innehåll Blckprgrammering s4 Blckly Games.. s5 Pussel.. s7 Labyrint.... s8 Fågel... s9 Sköldpadda. s10 Film s11 Dammhandledare.. s12 Damm.... s13 2 Lärarhandledning till
Prgrammering Åk 7-9 -Blckly Games Innehåll Blckprgrammering s4 Blckly Games.. s5 Pussel.. s7 Labyrint.... s8 Fågel... s9 Sköldpadda. s10 Film s11 Dammhandledare.. s12 Damm.... s13 2 Lärarhandledning till
Lärarhandledning Vi berättar och beskriver
 Lärarhandledning Vi berättar och beskriver Innehåll Aktivitet 1. Vi berättar och beskriver 2 Bildunderlag 1 5 Blankett för individuell kartläggning Aktivitet 1 6 1 Aktivitet 1. Vi berättar och beskriver
Lärarhandledning Vi berättar och beskriver Innehåll Aktivitet 1. Vi berättar och beskriver 2 Bildunderlag 1 5 Blankett för individuell kartläggning Aktivitet 1 6 1 Aktivitet 1. Vi berättar och beskriver
LPP åk 2 v 35-43 HT 2011
 LPP åk 2 v 35-43 HT 2011 Svenska Förankring i kursplanens syfte: frmulera sig ch kmmunicera i tal ch skrift, läsa ch analysera skönlitteratur ch andra texter för lika syften, anpassa språket efter lika
LPP åk 2 v 35-43 HT 2011 Svenska Förankring i kursplanens syfte: frmulera sig ch kmmunicera i tal ch skrift, läsa ch analysera skönlitteratur ch andra texter för lika syften, anpassa språket efter lika
Vår skola förbereder eleverna för ett fungerande och meningsfullt vuxenliv
 Rönnsklans Verksamhetsidé Rönnsklan är en särskla i tiden, där eleverna får en möjlighet att använda sin förmåga i en stimulerande miljö Vår rganisatin erbjuder en verksamhet där eleverna står i centrum
Rönnsklans Verksamhetsidé Rönnsklan är en särskla i tiden, där eleverna får en möjlighet att använda sin förmåga i en stimulerande miljö Vår rganisatin erbjuder en verksamhet där eleverna står i centrum
Målet med undervisningen är att eleverna ska ges förutsättningar att:
 Idrtt ch hälsa Målet med undervisningen är att eleverna ska ges förutsättningar att: röra sig allsidigt i lika fysiska sammanhang, planera, praktiskt genmföra ch värdera idrtt ch andra fysiska aktiviteter
Idrtt ch hälsa Målet med undervisningen är att eleverna ska ges förutsättningar att: röra sig allsidigt i lika fysiska sammanhang, planera, praktiskt genmföra ch värdera idrtt ch andra fysiska aktiviteter
Lärarhandledning Vi berättar och beskriver
 Lärarhandledning Vi berättar och beskriver Innehåll Aktivitet 1. Vi berättar och beskriver 2 Bildunderlag 1 5 Blankett för individuell kartläggning Aktivitet 1 6 KARTLÄGGNING FÖRSKOLEKLASS HITTA SPRÅKET.
Lärarhandledning Vi berättar och beskriver Innehåll Aktivitet 1. Vi berättar och beskriver 2 Bildunderlag 1 5 Blankett för individuell kartläggning Aktivitet 1 6 KARTLÄGGNING FÖRSKOLEKLASS HITTA SPRÅKET.
Arbeta vidare med Milou
 Kängurutävlingen 2009 Arbeta vidare med Milou Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. När ni nu diskuterar lösningarna kan ni också kontrollera
Kängurutävlingen 2009 Arbeta vidare med Milou Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. När ni nu diskuterar lösningarna kan ni också kontrollera
Gruppledtrådar. Gruppledtrådarna ingår i lärarhandledningen till Prima Formula 6 Får kopieras! Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
 Gruppledtrådar Som hjälp för dina elevgrupper att utveckla sin förmåga att tala matematik, samarbeta och lära i grupp finns övningar som vi kallar Gruppledtrådar. Dessa går ut på att elever tillsammans
Gruppledtrådar Som hjälp för dina elevgrupper att utveckla sin förmåga att tala matematik, samarbeta och lära i grupp finns övningar som vi kallar Gruppledtrådar. Dessa går ut på att elever tillsammans
Känguru 2011 Student (gymnasiet åk 2 och 3)
 Känguru 011 Student sida 1 / 8 NAMN KLASS / GRUPP Pängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tm m du inte vill besvara den frågan. Gissa
Känguru 011 Student sida 1 / 8 NAMN KLASS / GRUPP Pängsumma: Känguruskutt: Lösgör svarsblanketten. Skriv ditt svarsalternativ under uppgiftsnumret. Lämna rutan tm m du inte vill besvara den frågan. Gissa
Att intervjua elever om hållbar utveckling
 Ämnesövergripande Grundskla åk 7-9 Mdul: Hållbar utveckling Del 3: Sklan ch eleverna mttagare av kunskap ch deltagare i förändring Att intervjua elever m hållbar utveckling Claes Malmberg, Högsklan i Halmstad
Ämnesövergripande Grundskla åk 7-9 Mdul: Hållbar utveckling Del 3: Sklan ch eleverna mttagare av kunskap ch deltagare i förändring Att intervjua elever m hållbar utveckling Claes Malmberg, Högsklan i Halmstad
SURREALISTISK SELFIE - REFLEKTION
 SURREALISTISK SELFIE - REFLEKTION En vaken betraktare åser fta genm sitt filter av förnuft ett surrealistiskt knstverk sm en vrickad, lgisk ch absurd framställning av verkligheten. Salvadr Dalí, The persistence
SURREALISTISK SELFIE - REFLEKTION En vaken betraktare åser fta genm sitt filter av förnuft ett surrealistiskt knstverk sm en vrickad, lgisk ch absurd framställning av verkligheten. Salvadr Dalí, The persistence
A: 111 B: 900 C: 909 D: 990 E: 999
 3-poängsproblem 1. 1000 100 + 10 1 =? A: 111 B: 900 C: 909 D: 990 E: 999 2. Miriam har 16 kort, fyra av varje färg: 4 spader, 4 klöver, 4 ruter och 4 hjärter. Hon vill lägga dem på rutnätet här bredvid
3-poängsproblem 1. 1000 100 + 10 1 =? A: 111 B: 900 C: 909 D: 990 E: 999 2. Miriam har 16 kort, fyra av varje färg: 4 spader, 4 klöver, 4 ruter och 4 hjärter. Hon vill lägga dem på rutnätet här bredvid
Geometri labora-va ak-viteter
 Geometri labora-va ak-viteter Samtliga presenterade aktiviteter 1inns som pdf:er på ncm.gu.se/stravorna C Geometri Hitta 1ler här! Rektangel Två spelare, ett centimeterrutat papper och var sin penna i
Geometri labora-va ak-viteter Samtliga presenterade aktiviteter 1inns som pdf:er på ncm.gu.se/stravorna C Geometri Hitta 1ler här! Rektangel Två spelare, ett centimeterrutat papper och var sin penna i
Lekar för din träningsgrupp - En lekbank för ledare där nästan ingen extra utrustning krävs, enjoy!
 Lekar för din träningsgrupp - En lekbank för ledare där nästan ingen extra utrustning krävs, enjy! Innehållsförteckning Intrduktin 3 Hur leder jag en lek på bästa sätt? 3 Namnlekar hälsa på varandra 5
Lekar för din träningsgrupp - En lekbank för ledare där nästan ingen extra utrustning krävs, enjy! Innehållsförteckning Intrduktin 3 Hur leder jag en lek på bästa sätt? 3 Namnlekar hälsa på varandra 5
Digitala verktyg i musik
 DISKUSSIONSUNDERLAG FÖR GRUNDSKOLAN Diskutera Digitala verktyg i musik I Lgr 11, del 2.2 m kunskaper står det att sklan ska ansvara för att varje elev efter genmgången grundskla kan använda mdern teknik
DISKUSSIONSUNDERLAG FÖR GRUNDSKOLAN Diskutera Digitala verktyg i musik I Lgr 11, del 2.2 m kunskaper står det att sklan ska ansvara för att varje elev efter genmgången grundskla kan använda mdern teknik
Didaktiska perspektiv på matematikundervisning 2
 Didaktiska perspektiv på matematikundervisning 2 Den här modulen är valbar för er som får statsbidrag för Matematiklyftet. Välkommen till denna andra modul om möjligheter och utmaningar i matematikundervisningen
Didaktiska perspektiv på matematikundervisning 2 Den här modulen är valbar för er som får statsbidrag för Matematiklyftet. Välkommen till denna andra modul om möjligheter och utmaningar i matematikundervisningen
Delprov A Muntligt delprov
 Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
Delprov A Muntligt delprov Äp6Ma15 Delprov A 15 Beskrivning av delprov A, muntligt delprov Det muntliga delprovet kan genomföras fr.o.m. vecka 11 och resten av vårterminen. Det muntliga delprovet handlar
Programmering Förskola-3. -robotprogrammering med Blue-Bot
 Prgrammering Förskla-3 -rbtprgrammering med Blue-Bt Lärarhandledning till Rbtprgrammering med Blue-Bt 2 Innehåll Hur ser Blue-Bt ut i aktin?... Lär känna din Blue-Bt.. Manual till appen Blue-Bt... Innehåll
Prgrammering Förskla-3 -rbtprgrammering med Blue-Bt Lärarhandledning till Rbtprgrammering med Blue-Bt 2 Innehåll Hur ser Blue-Bt ut i aktin?... Lär känna din Blue-Bt.. Manual till appen Blue-Bt... Innehåll
Fakta. Naturvetenskap i Bumper Cars. NaturligtVis. Fysiklabbar på Powerland. Bumper Cars. http://naturligtvis.novia.fi
 Fysiklabbar på Pwerland Bumper Cars Bumper Cars är en str bilbana sm passar både stra ch små förare. Bilarna är försedda med bilbälten ch kan köras ensam eller parvis. Lättare kllisiner är tillåtna, men
Fysiklabbar på Pwerland Bumper Cars Bumper Cars är en str bilbana sm passar både stra ch små förare. Bilarna är försedda med bilbälten ch kan köras ensam eller parvis. Lättare kllisiner är tillåtna, men
LEKTIONSUPPLÄGG MAKTEN ÖVER MATEN
 Makten över maten - Ett flkbildningsmaterial från Latinamerikagrupperna LEKTINSUPPLÄGG MAKTEN ÖVER MATEN Här presenteras ett lektinsupplägg sm på fem lektiner sm ger bakgrund, inspiratin ch kunskap m hur
Makten över maten - Ett flkbildningsmaterial från Latinamerikagrupperna LEKTINSUPPLÄGG MAKTEN ÖVER MATEN Här presenteras ett lektinsupplägg sm på fem lektiner sm ger bakgrund, inspiratin ch kunskap m hur
Tid Muntliga uppgifter
 Tid Muntliga uppgifter Till uppgift 1 5 behövs en ställbar klocka. Tid Begrepp 1. Ställ elevnära frågor där du får svar på frågor om idag, igår och i morgon till exempel: Vilken dag är det idag? Vad gjorde
Tid Muntliga uppgifter Till uppgift 1 5 behövs en ställbar klocka. Tid Begrepp 1. Ställ elevnära frågor där du får svar på frågor om idag, igår och i morgon till exempel: Vilken dag är det idag? Vad gjorde
Vänskapssamtal MED KLOKA UGGLAN
 Vänskapssamtal MED KLOKA UGGLAN Din kmpis har en ny leksak sm du tycker är fin. Du frågar m du får titta på den men får ett nej. Du ser en kmpis viska till någn annan. Då tittar båda på dig. Du vill ta
Vänskapssamtal MED KLOKA UGGLAN Din kmpis har en ny leksak sm du tycker är fin. Du frågar m du får titta på den men får ett nej. Du ser en kmpis viska till någn annan. Då tittar båda på dig. Du vill ta
Designprocessdagbok. Grupp 3; Maria Törnkvist, Ida Gustafsson, Mikael Karlsson, Jonas Lind, Hanne Flink- Sundin.
 Designprcessdagbk. Grupp 3; Maria Törnkvist, Ida Gustafssn, Mikael Karlssn, Jnas Lind, Hanne Flink- Sundin. Krt intrduktin Under hela vår designprcess har vi fört dagbk över våra möten, dagbken har vi
Designprcessdagbk. Grupp 3; Maria Törnkvist, Ida Gustafssn, Mikael Karlssn, Jnas Lind, Hanne Flink- Sundin. Krt intrduktin Under hela vår designprcess har vi fört dagbk över våra möten, dagbken har vi
geometri och statistik
 Svikten geometri och statistik Innehåll Mönster Geometriska figurer Del av Matematiska ord Längd runt om Tredimensionella figurer Tabeller och diagram Problemlösning Kan du? Hur gick det? 2-3 4-5 6-7 8-9
Svikten geometri och statistik Innehåll Mönster Geometriska figurer Del av Matematiska ord Längd runt om Tredimensionella figurer Tabeller och diagram Problemlösning Kan du? Hur gick det? 2-3 4-5 6-7 8-9
Övningar i JavaScript del 3
 Övningar i JavaScript del 3 I dessa övningar tar vi upp datumbjektet Date, arrayer ch lpar. Du utgår från ett prgram där man kan klicka på små bilder ch mtsvarande stra bild visas. Detta är i princip samma
Övningar i JavaScript del 3 I dessa övningar tar vi upp datumbjektet Date, arrayer ch lpar. Du utgår från ett prgram där man kan klicka på små bilder ch mtsvarande stra bild visas. Detta är i princip samma
Programmering F-3. -Osmo Coding
 Prgrammering F-3 -Osm Cding Lärarhandledning till Osm Cding 2 Innehåll Generellt upplägg. s4 Mntera Osm Cding.. s5 Menyn i Osm Cding s6 Instruktiner i Osm Cding.... s7 Innehåll.... s8 Blckens betydelse
Prgrammering F-3 -Osm Cding Lärarhandledning till Osm Cding 2 Innehåll Generellt upplägg. s4 Mntera Osm Cding.. s5 Menyn i Osm Cding s6 Instruktiner i Osm Cding.... s7 Innehåll.... s8 Blckens betydelse
Vattenfall Innovation Awards
 Vattenfall Innvatin Awards Hantering av Uppfinnare, prcess ch tlkning av legala aspekter Tidsplan: 1. Vattenfalls (VF) utser en intern jury, bestående av ca 10 persner, sm bedömer ch beslutar m vilka idéer
Vattenfall Innvatin Awards Hantering av Uppfinnare, prcess ch tlkning av legala aspekter Tidsplan: 1. Vattenfalls (VF) utser en intern jury, bestående av ca 10 persner, sm bedömer ch beslutar m vilka idéer
Tidningsskaparna. Lärarhandledning
 Tidningsskaparna Lärarhandledning TIDNINGSSKAPARNA Redaktören vill trycka en tidskrift m framtiden I Berättarministeriets Tidningsskapare samarbetar vi med Mderna Museet ch låter eleverna prva på livet
Tidningsskaparna Lärarhandledning TIDNINGSSKAPARNA Redaktören vill trycka en tidskrift m framtiden I Berättarministeriets Tidningsskapare samarbetar vi med Mderna Museet ch låter eleverna prva på livet
Geografiska undersökningar
 DISKUSSIONSUNDERLAG FÖR GRUNDSKOLAN Diskutera Gegrafiska undersökningar I kursplanen i gegrafi sm började gälla 2011 i grundskleutbildningen framgår det tydligare än i tidigare kursplaner att eleverna
DISKUSSIONSUNDERLAG FÖR GRUNDSKOLAN Diskutera Gegrafiska undersökningar I kursplanen i gegrafi sm började gälla 2011 i grundskleutbildningen framgår det tydligare än i tidigare kursplaner att eleverna
Facit åk 6 Prima Formula
 Facit åk 6 Prima Formula Kapitel 1 Omkrets och area Sidan 7 1 A och C 2 D och E 3 a G, H och J b I och J c J Sidan 8 4 a 1 b 1 c 1 d 4 5 A = 0 B = 2 C = 4 D = 2 6 a 8 0 8 b 1 0 1 c 3 8 3 d 1 3 8 F7 A B
Facit åk 6 Prima Formula Kapitel 1 Omkrets och area Sidan 7 1 A och C 2 D och E 3 a G, H och J b I och J c J Sidan 8 4 a 1 b 1 c 1 d 4 5 A = 0 B = 2 C = 4 D = 2 6 a 8 0 8 b 1 0 1 c 3 8 3 d 1 3 8 F7 A B
Tillgänglighetsguide Lunds kommun... 1. Komma igång... 2. Översikt av Guiden... 1
 Innehållsförteckning Tillgänglighetsguide Lunds kmmun... 1 Översikt av Guiden... 1 Kmma igång... 2 Sökning ch visning av tillgänglighetsinfrmatin... 2 Resultat av sökning... 3 Rapprtering av nya bjekt
Innehållsförteckning Tillgänglighetsguide Lunds kmmun... 1 Översikt av Guiden... 1 Kmma igång... 2 Sökning ch visning av tillgänglighetsinfrmatin... 2 Resultat av sökning... 3 Rapprtering av nya bjekt
Kängurutävlingen Matematikens Hopp Cadet 2003 Uppgifter
 Kängurutävlingen Matematikens Hopp Uppgifter Arrangeras av Kungl. Vetenskapsakademien & NCM/Nämnaren 3-poängsuppgifter. Ett papper viks två gånger. Därefter klipper man hack i det. Hur ser pappret ut när
Kängurutävlingen Matematikens Hopp Uppgifter Arrangeras av Kungl. Vetenskapsakademien & NCM/Nämnaren 3-poängsuppgifter. Ett papper viks två gånger. Därefter klipper man hack i det. Hur ser pappret ut när
Instruktioner för mappning av individer till NY-läge
 PM 01-0-5 Genmförandekmmittén för nya Plismyndigheten Ju 01:16 ORG-1 Instruktiner NY-läge Instruktiner för mappning av individer till NY-läge Intrduktin Inm ramen för prjekt ORG-1 har ett förslag till
PM 01-0-5 Genmförandekmmittén för nya Plismyndigheten Ju 01:16 ORG-1 Instruktiner NY-läge Instruktiner för mappning av individer till NY-läge Intrduktin Inm ramen för prjekt ORG-1 har ett förslag till
Delprov D: Geometriska figurer och deras egenskaper
 Delprov D: Geometriska figurer och deras egenskaper Nedan finns instruktioner för genomförandet av Delprov D, vilket handlar om geometriska figurer och deras egenskaper. Eleverna ska arbeta individuellt
Delprov D: Geometriska figurer och deras egenskaper Nedan finns instruktioner för genomförandet av Delprov D, vilket handlar om geometriska figurer och deras egenskaper. Eleverna ska arbeta individuellt
Nedan följer en lista på olika steg för att förklara hur Ni enkelt kan lägga en orienteringsbana i banläggningsprogrammet Purple Pen.
 Lathund Purple Pen Purple Pen är ett gratis banläggningsprgram för rientering sm kan laddas ner gratis på http://purplepen.glde.rg/dwnlad.htm Observera att prgrammet endast stöds för Windws! Man kan använda
Lathund Purple Pen Purple Pen är ett gratis banläggningsprgram för rientering sm kan laddas ner gratis på http://purplepen.glde.rg/dwnlad.htm Observera att prgrammet endast stöds för Windws! Man kan använda
världen & vi Lärarhandledning b/c
 världen & vi Lärarhandledning b/c Världen&vi, nr 3, 2013 Vi har till detta nummer gjrt två varianter av lärarhandledning. Den här handledningen lämpar sig för elever sm har en hörförståelse ch läsförståelse
världen & vi Lärarhandledning b/c Världen&vi, nr 3, 2013 Vi har till detta nummer gjrt två varianter av lärarhandledning. Den här handledningen lämpar sig för elever sm har en hörförståelse ch läsförståelse
KOMPISSAMTAL MED KLOKA UGGLAN
 KOMPISSAMTAL MED KLOKA UGGLAN Din kmpis har en ny leksak sm du tycker är fin. Du frågar m du får titta på den men får ett nej. Du ser en kmpis viska till någn annan. Då tittar båda på dig. Du vill att
KOMPISSAMTAL MED KLOKA UGGLAN Din kmpis har en ny leksak sm du tycker är fin. Du frågar m du får titta på den men får ett nej. Du ser en kmpis viska till någn annan. Då tittar båda på dig. Du vill att
Kort användarmanual för Test och quiz i Mondo 2.0
 Krt användarmanual för Test ch quiz i Mnd 2.0 Denna användarmanual är en krtversin av en längre användarmanual ch innehåller de viktigaste delarna för att kmma igång med användningen av Test ch quiz. För
Krt användarmanual för Test ch quiz i Mnd 2.0 Denna användarmanual är en krtversin av en längre användarmanual ch innehåller de viktigaste delarna för att kmma igång med användningen av Test ch quiz. För
Ecolier för elever i åk 3 och 4
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 17 mars 2016 Ecolier för elever i åk 3 och 4 Tävlingen ska genomföras under perioden 17 mars 1 april. Uppgifterna får inte användas tidigare.
En kom i gång manual till SPF:s hemsidor
 En km i gång manual till SPF:s hemsidr Inlggning Meny (navigatinsträdet) Vad skall finnas på hemsidan Standarduppgifter [Startsidan, Om föreningen, Styrelsen, Kntakt, Bli medlem] Tilläggs/valfria uppgifter
En km i gång manual till SPF:s hemsidr Inlggning Meny (navigatinsträdet) Vad skall finnas på hemsidan Standarduppgifter [Startsidan, Om föreningen, Styrelsen, Kntakt, Bli medlem] Tilläggs/valfria uppgifter
Trepoängsproblem. Kängurutävlingen 2011 Cadet. 1 Vilket av följande uttryck har störst värde? 1 A: B: C: D: E: 2011
 Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Trepoängsproblem 1 Vilket av följande uttryck har störst värde? 1 A: 2011 1 B: 1 2011 C: 1 2011 D: 1 + 2011 E: 2011 2 Övergångsställen är markerade med vita och svarta streck som är 50 cm breda. Markeringen
Ma: Diagnoser ( Diamant) och provräkningar + samtal med eleven om vad den har lärt och vill lära sig.
 Hur jag fångar elevernas kunskapsutveckling idag. Jag är klasslärare i en ålderblandad åk4-6 i samesklan ch har därmed alla ämnen utm slöjd ch samiska. Den dkumentatin jag gör för att kunna bedöma elevens
Hur jag fångar elevernas kunskapsutveckling idag. Jag är klasslärare i en ålderblandad åk4-6 i samesklan ch har därmed alla ämnen utm slöjd ch samiska. Den dkumentatin jag gör för att kunna bedöma elevens
13. Utvecklingssamtal hos IOGT-NTO
 13. Utvecklingssamtal hs IOGT-NTO Syfte Att få rganisatinen att fungera bättre. Att bidra till medarbetarnas persnliga utveckling. Att stämma av mt mål. Att stämma av samarbetet mellan rganisatinsgrenarna
13. Utvecklingssamtal hs IOGT-NTO Syfte Att få rganisatinen att fungera bättre. Att bidra till medarbetarnas persnliga utveckling. Att stämma av mt mål. Att stämma av samarbetet mellan rganisatinsgrenarna
Skolverkets bedömning är att vi idag har stort behov av:
 Sklverkets bedömning är att vi idag har strt behv av: Fler lärare med kmpetens i svenska sm andraspråk. Fler mdersmålslärare ch studiehandledare på mdersmål. Fler vuxna i sklan med mdersmålskmpetens. Kmpetensutveckling
Sklverkets bedömning är att vi idag har strt behv av: Fler lärare med kmpetens i svenska sm andraspråk. Fler mdersmålslärare ch studiehandledare på mdersmål. Fler vuxna i sklan med mdersmålskmpetens. Kmpetensutveckling
Leda digitalisering 21 september Ale
 Leda digitalisering 21 september Ale Prgram för dagen Check in FIKA! Text 2 Digi. skla ch ledarskap Lärgrupper Text 1 Digi. ch samhälle Till nästa gång Check ut Upplägg ch tidsplan - Ale Intr Förarbete
Leda digitalisering 21 september Ale Prgram för dagen Check in FIKA! Text 2 Digi. skla ch ledarskap Lärgrupper Text 1 Digi. ch samhälle Till nästa gång Check ut Upplägg ch tidsplan - Ale Intr Förarbete
Sammanställning av diskussionskarusellen
 Sammanställning av diskussinskarusellen Bilaga 1 Uppgiften var: Att summera, srtera ch lyfta fram det viktigaste i vad alla sagt kring varje specifik fråga, samt dkumentera det skriftligt. Obs! Samtliga
Sammanställning av diskussinskarusellen Bilaga 1 Uppgiften var: Att summera, srtera ch lyfta fram det viktigaste i vad alla sagt kring varje specifik fråga, samt dkumentera det skriftligt. Obs! Samtliga
Rektangelpussel 1. Använd tre bitar vilka som helst och gör en 3 5-rektangel.
 PEDER CLAESSON I Nämnarens geometrinummer, nr 3 81/82, presenterar Andrejs Dunkels pentominobrickorna. Under rubriken Kvadratpussel finns de beskrivna i Martin Gardners bok, Rolig matematik, som kom ut
PEDER CLAESSON I Nämnarens geometrinummer, nr 3 81/82, presenterar Andrejs Dunkels pentominobrickorna. Under rubriken Kvadratpussel finns de beskrivna i Martin Gardners bok, Rolig matematik, som kom ut
9 Geometriska begrepp
 9 Geometriska begrepp Rita figurer som visar vad vi menar med... 261 a) 4 cm och 4 cm 2 b) 5 cm och 5 cm 2 262 Rita två olika figurer som båda har arean 8 cm 2 263 Rita tre olika figurer som alla har arean
9 Geometriska begrepp Rita figurer som visar vad vi menar med... 261 a) 4 cm och 4 cm 2 b) 5 cm och 5 cm 2 262 Rita två olika figurer som båda har arean 8 cm 2 263 Rita tre olika figurer som alla har arean
Milou 2015 lösningar och arbeta vidare
 Kängurutävlingen 2015 Milou 2015 lösningar och arbeta vidare Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Kängurutävlingen 2015 Milou 2015 lösningar och arbeta vidare Vi hoppas att problemen i Milou blev en spännande och positiv upplevelse för både elever och lärare. Nu kan ni diskutera och kontrollera lösningarna
Tidningsskaparna. Lärarhandledning
 Tidningsskaparna Lärarhandledning TIDNINGSSKAPARNA Redaktören vill trycka en tidskrift m framtiden I Berättarministeriets Tidningsskapare samarbetar vi med Mderna Museet ch låter eleverna prva på livet
Tidningsskaparna Lärarhandledning TIDNINGSSKAPARNA Redaktören vill trycka en tidskrift m framtiden I Berättarministeriets Tidningsskapare samarbetar vi med Mderna Museet ch låter eleverna prva på livet
Arbetsplan för hösten 2015. Föräldrakooperativ
 Arbetsplan för hösten 2015 Föräldrakperativ Ftgraf: Björn Magnussn Lek, Lust ch Lärande! 1 Friluftsförsklan Nätet, föräldrakperativ Försklan ligger i villasamhället Nättraby strax utanför Karlskrna. Försklan
Arbetsplan för hösten 2015 Föräldrakperativ Ftgraf: Björn Magnussn Lek, Lust ch Lärande! 1 Friluftsförsklan Nätet, föräldrakperativ Försklan ligger i villasamhället Nättraby strax utanför Karlskrna. Försklan
världen & vi Lärarhandledning c/d
 världen & vi Lärarhandledning c/d Världen&vi, nr 3, 2013 Vi har till detta nummer gjrt två varianter av lärarhandledning. Den här handledningen lämpar sig för elever sm har en hörförståelse ch läsförståelse
världen & vi Lärarhandledning c/d Världen&vi, nr 3, 2013 Vi har till detta nummer gjrt två varianter av lärarhandledning. Den här handledningen lämpar sig för elever sm har en hörförståelse ch läsförståelse
Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9
 Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Till läraren Välkommen till Kängurutävlingen Matematikens hopp 2010 Cadet för elever i åk 8 och 9 Kängurutävlingen genomförs den 18 mars. Om den dagen inte passar kan hela veckan 19 26 mars användas, däremot
Tal i bråkform. Kapitlet behandlar. Att förstå tal
 Att förstå tal Tal i bråkform Kapitlet behandlar Test Användning av hälften och fjärdedel 2 Representation i bråkform av del av antal och av del av helhet 3, 4 Bråkform i vardagssituationer 4 Stambråk,
Att förstå tal Tal i bråkform Kapitlet behandlar Test Användning av hälften och fjärdedel 2 Representation i bråkform av del av antal och av del av helhet 3, 4 Bråkform i vardagssituationer 4 Stambråk,
Uppslag 6 Problemlösning på geobräde
 Uppslag 6 Problemlösning på geobräde Geobrädet inbjuder till problemlösning för alla åldrar. För tvååringarna är själva hanterandet av gummisnoddarna det som är problemet, för femåringarna kan det vara
Uppslag 6 Problemlösning på geobräde Geobrädet inbjuder till problemlösning för alla åldrar. För tvååringarna är själva hanterandet av gummisnoddarna det som är problemet, för femåringarna kan det vara
Vad är geometri? För dig? I förskolan?
 Vad är geometri? För dig? I förskolan? Vad är geometri? Betyder jordmätning En del i matematiken som handlar om rum i olika dimensioner, storlek, figurer och kroppar och deras egenskaper. Viktiga didaktiska
Vad är geometri? För dig? I förskolan? Vad är geometri? Betyder jordmätning En del i matematiken som handlar om rum i olika dimensioner, storlek, figurer och kroppar och deras egenskaper. Viktiga didaktiska
Skarpnäcks stadsdelsförvaltning. Likabehandlingsplan Sida 1 (9) Västra Bagarmossens förskolor
 Skarpnäcks stadsdelsförvaltning Västra Bagarmssens försklr Likabehandlingsplan Sida 1 (9) 2015-09-05 Västra Bagarmssens försklr Bx 51 17 121 17 Jhanneshv Telefn 08-50815000 stckhlm.se Sida 2 (9) Vår likabehandlingsvisin
Skarpnäcks stadsdelsförvaltning Västra Bagarmssens försklr Likabehandlingsplan Sida 1 (9) 2015-09-05 Västra Bagarmssens försklr Bx 51 17 121 17 Jhanneshv Telefn 08-50815000 stckhlm.se Sida 2 (9) Vår likabehandlingsvisin
Handledarmaterial för introduktion till bra arbetsteknik vid städning
 Allt m städ www.prevent.se/allt-m-stad Handledarmaterial för intrduktin till bra arbetsteknik vid städning I den här handledningen har vi sammanställt tips ch gda råd samt lite bakgrundsinfrmatin sm du
Allt m städ www.prevent.se/allt-m-stad Handledarmaterial för intrduktin till bra arbetsteknik vid städning I den här handledningen har vi sammanställt tips ch gda råd samt lite bakgrundsinfrmatin sm du
Fastställd av Ålands landskapsregering
 RIKTLINJER FÖR ANVÄNDNING AV SOCIALA MEDIER I UNDERVISNINGEN Fastställd av Ålands landskapsregering Beslut nr 5 U2, 8.1.2013 Innehåll Bakgrund ch syfte... 3 Definitin... 3 Fördelar... 3 Syfte ch målsättningar...
RIKTLINJER FÖR ANVÄNDNING AV SOCIALA MEDIER I UNDERVISNINGEN Fastställd av Ålands landskapsregering Beslut nr 5 U2, 8.1.2013 Innehåll Bakgrund ch syfte... 3 Definitin... 3 Fördelar... 3 Syfte ch målsättningar...
Plan mot diskriminering och kränkande behandling 2016
 Södermalms stadsdelsförvaltning Sida 1 (11) Rev 2016-03-18 Plan mt diskriminering ch kränkande behandling 2016 En grundläggande mänsklig rättighet är rätten till likabehandling. Alla barn i försklan ska
Södermalms stadsdelsförvaltning Sida 1 (11) Rev 2016-03-18 Plan mt diskriminering ch kränkande behandling 2016 En grundläggande mänsklig rättighet är rätten till likabehandling. Alla barn i försklan ska
Informationssökning och källkritik
 Infrmatinssökning ch källkritik Kunskapskrav Eleven kan söka, välja ut ch sammanställa infrmatin från ett [ ]urval av källr ch för då [ ] underbyggda resnemang m infrmatinens ch källrnas trvärdighet ch
Infrmatinssökning ch källkritik Kunskapskrav Eleven kan söka, välja ut ch sammanställa infrmatin från ett [ ]urval av källr ch för då [ ] underbyggda resnemang m infrmatinens ch källrnas trvärdighet ch
Plan mot diskriminering och kränkande behandling
 Plan mt diskriminering ch kränkande behandling Gustavslundsklan, 2015-2016 Innehållsförteckning Verksamhetsfrmer sm mfattas av planen... 2 Vår visin... 2 Delaktighet... 2 Utvärdering av planen för läsåret
Plan mt diskriminering ch kränkande behandling Gustavslundsklan, 2015-2016 Innehållsförteckning Verksamhetsfrmer sm mfattas av planen... 2 Vår visin... 2 Delaktighet... 2 Utvärdering av planen för läsåret
Anvisning Registreringsteknik
 Anvisning Registreringsteknik För att den digitala pennan ska registrera krrekt, följ nedan anvisning: 1 Krk = av/på-knapp Krken fungerar sm en av/på-knapp på den digitala pennan. För att pennan ska fungera
Anvisning Registreringsteknik För att den digitala pennan ska registrera krrekt, följ nedan anvisning: 1 Krk = av/på-knapp Krken fungerar sm en av/på-knapp på den digitala pennan. För att pennan ska fungera
Lektionsaktivitet: Samla och hantera information
 Modul: Didaktiska perspektiv på matematikundervisningen 2 Del 3: Geometri och statistik Statistik Träningsskola och individuellt program Berit Bergius & Lena Trygg, NCM För att kunna fungera som så självständiga
Modul: Didaktiska perspektiv på matematikundervisningen 2 Del 3: Geometri och statistik Statistik Träningsskola och individuellt program Berit Bergius & Lena Trygg, NCM För att kunna fungera som så självständiga
Problem på ett bräde ANDREJS DUNKELS
 ANDREJS DUNKELS Geobrädet inbjuder till problemlösning för alla åldrar. För tvååringarna är själva hanterandet av gummisnoddarna det som är problemet, för femåringarna kan det vara att avgöra hur många
ANDREJS DUNKELS Geobrädet inbjuder till problemlösning för alla åldrar. För tvååringarna är själva hanterandet av gummisnoddarna det som är problemet, för femåringarna kan det vara att avgöra hur många
Kartläggningsmaterial för nyanlända elever SVENSKA. Geometri Matematik. 1 2 Steg 3
 Kartläggningsmaterial för nyanlända elever Geometri Matematik 1 2 Steg 3 SVENSKA Kartläggningsmaterial för nyanlända elever Geometri åk 3 MA 1. Rita färdigt bilden så att mönstret blir symmetriskt. 2.
Kartläggningsmaterial för nyanlända elever Geometri Matematik 1 2 Steg 3 SVENSKA Kartläggningsmaterial för nyanlända elever Geometri åk 3 MA 1. Rita färdigt bilden så att mönstret blir symmetriskt. 2.
Förskolan Västanvind
 Försklan Västanvind Västanvinds plan mt diskriminering ch kränkande behandling (likabehandlingsplan) 2015-05-25 Visin Västanvind är en förskla där alla avsett kön, etnisk bakgrund, religin, funktinshinder,
Försklan Västanvind Västanvinds plan mt diskriminering ch kränkande behandling (likabehandlingsplan) 2015-05-25 Visin Västanvind är en förskla där alla avsett kön, etnisk bakgrund, religin, funktinshinder,
Verksamhetsplan Södra förskolområdet 2014-2015
 Verksamhetsplan Södra försklmrådet 2014-2015 Innehåll 1 Södra försklmrådet, Avesta kmmun... 3 1.1 Vår rganisatin... 3 1.2 Inledning... 3 2 Styrdkument... 4 3 Södra försklmrådets pririterade utvecklingsmråden,
Verksamhetsplan Södra försklmrådet 2014-2015 Innehåll 1 Södra försklmrådet, Avesta kmmun... 3 1.1 Vår rganisatin... 3 1.2 Inledning... 3 2 Styrdkument... 4 3 Södra försklmrådets pririterade utvecklingsmråden,
Tidningsskaparna. Lärarhandledning
 Tidningsskaparna Lärarhandledning TIDNINGSSKAPARNA Redaktören vill trycka en tidskrift m framtiden I Berättarministeriets Tidningsskapare samarbetar vi med Mderna Museet ch låter eleverna prva på livet
Tidningsskaparna Lärarhandledning TIDNINGSSKAPARNA Redaktören vill trycka en tidskrift m framtiden I Berättarministeriets Tidningsskapare samarbetar vi med Mderna Museet ch låter eleverna prva på livet
Sida 1(9)
 Sida 1(9) Kkbk till mdul 14U Underhåll av diken KRAV: Lantbrukaren ska ha fått startbesök (1Aa). GRUNDFÖRUTSÄTTNINGAR: För att rådgivning ska vara aktuell ska syftet vara att underhålla ett öppet eller
Sida 1(9) Kkbk till mdul 14U Underhåll av diken KRAV: Lantbrukaren ska ha fått startbesök (1Aa). GRUNDFÖRUTSÄTTNINGAR: För att rådgivning ska vara aktuell ska syftet vara att underhålla ett öppet eller
En kom i gång manual till SPF:s hemsidor
 En km i gång manual till SPF:s hemsidr Inlggning Meny (navigatinsträdet) Vad skall finnas på hemsidan Standarduppgifter [Startsidan, Om föreningen, Styrelsen, Kntakt, Bli medlem] Tilläggs/valfria uppgifter
En km i gång manual till SPF:s hemsidr Inlggning Meny (navigatinsträdet) Vad skall finnas på hemsidan Standarduppgifter [Startsidan, Om föreningen, Styrelsen, Kntakt, Bli medlem] Tilläggs/valfria uppgifter
Lektionsaktivitet: Tals helhet och delar
 Modul: Didaktiska perspektiv på matematikundervisningen 1 Del 7: Om tal och tid Lektionsaktivitet: Tals helhet och delar Berit Bergius & Lena Trygg, NCM Syfte Syftet med aktiviteten är att ge erfarenheter
Modul: Didaktiska perspektiv på matematikundervisningen 1 Del 7: Om tal och tid Lektionsaktivitet: Tals helhet och delar Berit Bergius & Lena Trygg, NCM Syfte Syftet med aktiviteten är att ge erfarenheter
Under en forskningscirkel, som vi matematikutvecklare i Göteborg har
 Britt Holmberg Analysera mera i geometri Inom undervisningen i geometri behöver vi utmana elevernas nyfikenhet med frågeställningar och ge dem tid att undersöka geometriska objekt. Praktiskt arbete där
Britt Holmberg Analysera mera i geometri Inom undervisningen i geometri behöver vi utmana elevernas nyfikenhet med frågeställningar och ge dem tid att undersöka geometriska objekt. Praktiskt arbete där
Aktivitetsbank. Matematikundervisning med digitala verktyg II, åk 1-3. Maria Johansson, Ulrica Dahlberg
 Aktivitetsbank Matematikundervisning med digitala, åk 1-3 Maria Johansson, Ulrica Dahlberg Matematik: Grundskola åk 1-3 Modul: Matematikundervisning med digitala Aktivitetsbank till modulen Matematikundervisning
Aktivitetsbank Matematikundervisning med digitala, åk 1-3 Maria Johansson, Ulrica Dahlberg Matematik: Grundskola åk 1-3 Modul: Matematikundervisning med digitala Aktivitetsbank till modulen Matematikundervisning
Checklista förändringsledning best practice Mongara AB
 Checklista förändringsledning best practice Mngara AB Detta dkument ska ses sm ett underlag för vilka frågeställningar vi jbbar med inm ramen för förändringsledning. I dkumentet har vi valt att se prcessen
Checklista förändringsledning best practice Mngara AB Detta dkument ska ses sm ett underlag för vilka frågeställningar vi jbbar med inm ramen för förändringsledning. I dkumentet har vi valt att se prcessen
Likabehandlingsplan Personalkooperativet Kulingen 2013/2014
 Likabehandlingsplan Persnalkperativet Kulingen 2013/2014 Persnalkperativet Kulingens arbete med att mtverka diskriminering ch kränkande behandling Likabehandlingsplan Innehållsförteckning 2 Bakgrund ch
Likabehandlingsplan Persnalkperativet Kulingen 2013/2014 Persnalkperativet Kulingens arbete med att mtverka diskriminering ch kränkande behandling Likabehandlingsplan Innehållsförteckning 2 Bakgrund ch
Likabehandlingsplan / Plan mot kränkande behandling för Klippans Förskola
 Likabehandlingsplan / Plan mt kränkande behandling för Klippans Förskla 150630 Barn- ch utbildningsnämndens visin Varje barn ch elev ska med lust ch glädje uppleva meningsfullhet ch framgång i det dagliga
Likabehandlingsplan / Plan mt kränkande behandling för Klippans Förskla 150630 Barn- ch utbildningsnämndens visin Varje barn ch elev ska med lust ch glädje uppleva meningsfullhet ch framgång i det dagliga
Rapport delprojektgrupp HR i genomförandefasen aug 2012- jan 2014 hemsjukvårdsreformen
 Rapprt delprjektgrupp HR i genmförandefasen aug 2012- jan 2014 hemsjukvårdsrefrmen HR gruppen HR gruppen deltagare har bestått av de fyra persnalcheferna för landstingets västra, centrala, östra länsdelar
Rapprt delprjektgrupp HR i genmförandefasen aug 2012- jan 2014 hemsjukvårdsrefrmen HR gruppen HR gruppen deltagare har bestått av de fyra persnalcheferna för landstingets västra, centrala, östra länsdelar
Delprov B: Maskinen. Delprov C: Maskinen
 Delprov B: Maskinen Denna uppgift kommer både att användas som underlag för bedömning i matematik samt i svenska och svenska som andraspråk. För information om det som gäller genomförandet av såväl matematik
Delprov B: Maskinen Denna uppgift kommer både att användas som underlag för bedömning i matematik samt i svenska och svenska som andraspråk. För information om det som gäller genomförandet av såväl matematik
Matematik. Mål att sträva mot. Mål att uppnå. År 1 Mål Kriterier Eleven ska kunna. Taluppfattning koppla ihop antal och siffra kan lägga rätt antal
 Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Matematik Mål att sträva mot Vi strävar mot att varje elev ska utveckla intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik utveckla sin förmåga att
Polygoner. Trianglar på tre sätt
 Polygoner Trianglar på tre sätt Man kan skriva in punkter antingen via punktverktyget eller genom att skriva punktens namn och koordinater i inmatningsfältet. Då man ritar månghörningar lönar det sig att
Polygoner Trianglar på tre sätt Man kan skriva in punkter antingen via punktverktyget eller genom att skriva punktens namn och koordinater i inmatningsfältet. Då man ritar månghörningar lönar det sig att
Tillsammans med barn i åldrarna 5 6
 Monica Kable Den är rund runt hela konstruera och förklara med Pinneman Tillsammans med barn i åldrarna 5 6 år på avdelningen Guldgruvan har jag arbetat med sagan Herr Pinnemans äventyr (Donaldsson, 2008)
Monica Kable Den är rund runt hela konstruera och förklara med Pinneman Tillsammans med barn i åldrarna 5 6 år på avdelningen Guldgruvan har jag arbetat med sagan Herr Pinnemans äventyr (Donaldsson, 2008)
Matematik 92MA41 (15hp) Vladimir Tkatjev
 Matematik 92MA41 (15hp) Vladimir Tkatjev Lite inspiration Går det att konstruera 6 kvadrater av 12 tändstickor? Hur gör man då? (Nämnaren, Nr 2, 2005) Litet klurigt kanske, bygg en kub av stickorna: Uppgift
Matematik 92MA41 (15hp) Vladimir Tkatjev Lite inspiration Går det att konstruera 6 kvadrater av 12 tändstickor? Hur gör man då? (Nämnaren, Nr 2, 2005) Litet klurigt kanske, bygg en kub av stickorna: Uppgift
Lässtrategier för att förstå och tolka texter samt för att anpassa läsningen efter textens form och innehåll. (SV åk 1 3)
 SIDAN 1 Lärarmaterial VAD HANDLAR BOKEN OM? Olle vill ha en mobil. Alla hans vänner har mobiler. De spelar, fotar och ringer på sina mobiler och Olle känner sig utanför. När Olle kommer hem, upptäcker
SIDAN 1 Lärarmaterial VAD HANDLAR BOKEN OM? Olle vill ha en mobil. Alla hans vänner har mobiler. De spelar, fotar och ringer på sina mobiler och Olle känner sig utanför. När Olle kommer hem, upptäcker
A: 300 m B: 400 m C: 800 m D: 1000 m E: 700 m
 Trepoängsproblem. Hur långt är sträckan från Maria till Bianca? 00 m Maria 8 4 2 Bianca A: 300 m B: 400 m C: 800 m D: 000 m E: 700 m 2. Den liksidiga triangeln har arean 9 cm 2. Linjerna inne i triangeln
Trepoängsproblem. Hur långt är sträckan från Maria till Bianca? 00 m Maria 8 4 2 Bianca A: 300 m B: 400 m C: 800 m D: 000 m E: 700 m 2. Den liksidiga triangeln har arean 9 cm 2. Linjerna inne i triangeln
Trygghetsplan för Hästens förskola
 Trygghetsplan för Hästens förskla Likabehandlingsplan ch plan mt kränkande behandling 2018-2019 Vår visin: På vår förskla känner alla, barn ch vuxna; sig sedda, trygga ch respekterade för den man är. Vad
Trygghetsplan för Hästens förskla Likabehandlingsplan ch plan mt kränkande behandling 2018-2019 Vår visin: På vår förskla känner alla, barn ch vuxna; sig sedda, trygga ch respekterade för den man är. Vad
