Repetition Harmonisk svängning & vågor - Fy2 Heureka 2: kap. 7, 9, 13 version 2016
|
|
|
- Marianne Samuelsson
- för 6 år sedan
- Visningar:
Transkript
1 Repetition Harmonisk svängning & vågor - Fy2 Heureka 2: kap. 7, 9, 13 version 2016 Harmonisk svängning En svängning fram och tillbaka kring ett jämviktsläge, där den resulterande kraften på den svängande kroppen hela tiden är proportionell mot avståndet från jämviktsläget, kallas harmonisk. Kraften ska vara riktad så att kroppen hela tiden strävar efter att återvända till jämviktsläget. Exempel på harmoniska svängningar: gunga, pendel, vikt i fjäder, kula i rundad skål etc. Hastigheten är som störst i jämviktsläget. Accelerationen måste vara som störst vid vändlägena, eftersom kroppen där bromsas/accelereras mest. Fjäder När en fjäder sträcks Δx m från sitt jämviktsläge, åtgår kraften F. Denna beror, förutom på Δx även på en fjäderkonstant k som talar om hur styv fjädern är. Ett högre k-värde medför en styvare fjäder som det krävs en högre kraft att dra ut. Sambandet kallas Hookes lag och ges av: F = k Δx Observera att vi här talar om kraften i fjädern. Den resulterande kraften på den svängande vikten, blir: F res = ky (resulterande kraften är hela tiden riktad mot jämviktsläget) Δx Vinkelhastigheten på svängningen är relaterad till fjäderkonstanten enligt: k ω = där m är kroppens massa. m Svängningstiden (periodtiden) för den harmoniska svängningen i en fjäder är T = 2π m k Energi och harmonisk svängning När man sätter igång svängningen, genom att dra ner eller upp vikten, tillförs lägesenergi i den spända fjädern. Denna omvandlas sedan till rörelseenergi. Rörelseenergin är som störst i jämviktsläget, för att sedan vara helt omvandlad till lägesenergi i vändlägena. Summan av lägesenergin och rörelseenergin är således hela tiden konstant och ges av: E p + E k = E tot eller ky E = ka2 k 2 Observera att det gamla hederliga uttrycket för rörelseenergin: mv2 endast kan användas om man 2 känner till den svängande kroppens hastighet i just det ögonblick man räknar på.
2 Pendeln Med en del approximationer kan man få en enkel formel för svängningstiden: snöret är masslöst utslagsvinkeln är liten (under 10 ) kulan är liten i förhållande till snörets längd, l. Svängningstiden kan då ges av: T = 2π l g Resonans En svängande system som man har satt igång, svänger alltid med en egen naturlig frekvens (egenfrekvens). Om yttre krafter ( i form av en yttre svängning) påverkar systemet med samma frekvens, uppstår en kraftig amplitud i svängningen. Detta fenomen kallas för resonans. Några exempel är gitarrens kropp, vars hålrum kraftigt förstärker ljudet som kommer från de vibrerande strängarna. Obalanserade däck på en bil, där bilens och däckets svängningar förstärker varandra. Att sätta fart på en gunga när man sitter på den själv: man utför en pendelrörelse med sin kropp och denna svängning förstärker tillsammans med gungans svängning så att man får en snabb acceleration på sin gunga. Detta är samma princip som det vi senare kallar för interferens; två vågor som förstärker varandra. Här har vi två svängningar som förstärker varandra. Vågrörelse Om man har en lång fjäder kan man skicka iväg en puls. Skickar man kontinuerligt iväg pulser kallas det istället för en vågrörelse. Om vågrörelsen alstras vinkelrätt mot utbredningsriktningen kallas den transversell, och den alstras längs med fjädern kallas den longitudinell. På transversella vågrörelser talar man om vågtoppar och vågdalar, på de longitudinella talar man om förtätningar och förtunningar.
3 Vid reflektion mot ett tätare medium vänder pulsen och går tillbaka på motsatt sida om fjädern (inverteras). Vid reflektion mot tunnare medium vänder pulsen tillbaka på samma sida som den kom ifrån En del av vågrörelsen överförs till en vågrörelse i det tunnare mediet. Detta kallas transmission. En vågrörelse utbreder sig med hastigheten v = λ där λ kallas våglängd, och är en sträcka. T Tiden det tar för en våglängd att utbreda sig kallar vi för svängningstid eller period. Elongation är ett finare ord för avstånd från jämviktsläget ( y ). Superformeln Sambandet mellan hastighet, frekvens och våglängd ges av: v = f λ Superposition / Interferens När två vågor möts får man den resulterande vågen genom att i varje punkt addera deras elongation. Detta kallas för superposition. Man säger att vågorna interfererar (sammanblandas) med varandra.
4 Stående vågor En vågrörelse som interfererar med sig själv kan för vissa frekvenser ge upphov till en s.k. stående våg. Detta uppstår bl.a. i strängar, snören, samt för ljudvågor i pipor (rör) av olika slag. En stående våg innebär att den resulterande vågen hela tiden står stilla i sidled. Strängar Pipor Grundsvängningen: 1:a översvängningen: 2:a översvängningen: 3:e översvängningen: OBSERVERA! Beteckningarna på våglängden λ anger bara hur många våglängder som får plats. Våglängderna är olika långa! Reflektion Om vi tar vattenvågor som exempel så kan de utbreda sig cirkulärt och plant. Då de möter ett hinder reflekteras de enligt i=r där i är infallsvinkel och r är reflektionsvinkel.
5 Brytning (refraktion) När en mekanisk våg går från ett ämne till ett annat ändras riktningen hos vågorna om de faller in snett mot gränslinjen mellan ämnena. Ju tätare ett ämne är desto snabbare går vågorna (atomleken). Brytningslagen ger: v2 sini = v1 sin b λ2 sin i = λ1 sin b Det som är konstant i vågrörelsen i båda ämnena är frekvensen f. Totalreflektion Eftersom b inte kan bli mer än 90 så innebär det att det finns en gräns för hur stor i kan bli. Om man överstiger den gränsen kommer inte ljudvågen att brytas ner i vattnet utan bara reflekteras mot ytan upp i luften igen. Detta kallas för totalreflektion. Speciellt för vattenvågor: När vattendjupet sjunker, sjunker våghastigheten. Detta ger ett brytningsfenomen eftersom vågorna succesivt ändrar riktning på väg in mot stranden. Därför kommer vågorna alltid in parallellt med strandlinjen.
6 Diffraktion Vi illustrerar begreppet diffraktion med hjälp av vattenvågor. Om en plan våg infaller mot ett hinder i vilket det finns en öppning (spalt) som är av samma storleksordning som våglängden, kommer vågen att böjas av efter hindret. Denna böjning kallas med ett finare ord för diffraktion. Lägg märke till att den lilla öppningens (spaltens) bredd betecknas d. Interferens Om vågor från två vågkällor möts, interfererar de med varandra. De som då kan hända är att vågtopp möter vågtopp (eller vågdal möter vågdal). Detta kallas konstruktiv interferens och medför att det blir en kraftigare våg just där. Men en vågtopp kan även möta en vågdal. Resultatet kallas destruktiv interferens och innebär att vattnet i princip blir stillastående just där. Vad är det som avgör i vilka punkter det blir konstruktiv resp. destruktiv interferens? Vägskillnad Vägskillnaden = skillnaden i sträcka mellan avstånden från en punkt P till respektive vågkälla. Enligt figuren definierar vi vägskillnaden δ som: vågkälla 1 vågkälla 2 δ = s 1 s 2 (de raka strecken betyder absolutbeloppet av differensen. Absolutbeloppet är alltid positivt - d.v.s. vägskillnaden är alltid positiv) s 1 s 2 P
7 Interferensmönster 1. Två vågkällor alstrar vågor. De svarta ringarna utgör vågberg och de gråa vågdalar. 2. Vågorna möts och interfererar med varandra. På vissa ställen möter topp topp och dal möter dal, på andra ställen möter topp dal. 3. Vid en vägskillnad på ett helt antal våglängder blir det tydligen konstruktiv interferens, d.v.s. berg möter berg och dal möter dal. Resultatet blir kraftiga vågor längs de röda linjerna. Dessa linjer kallas därför buklinjer. Vid en vägskillnad på ett udda antal halva våglängder, d.v.s. 0,5, 1,5, 2,5 o.s.v. blir det destruktiv interferens, d.v.s. berg möter dal. Resultatet blir att vågorna tar ut varandra och vattnet står stilla längs de blåa linjerna. Dessa linjer kallas därför nodlinjer. 2 våglängders skillnad 1,5 våglängders skillnad 1 våglängds skillnad 0,5 våglängders skillnad centrallinjen 0,5 våglängders skillnad 1 våglängds skillnad 1,5 våglängders skillnad 2 våglängders skillnad Vi sammanfattar allt i formeln s 1 s 2 = nλ Den resulterande vågen ser ut så här: (Interferensmönster)
8 Egenskaper för ljudvågor Ljudet färdas med hastigheten m/s beroende på temperatur och tryck. Vi använder 340 m/s om inget annat anges i uppgifterna. Ljudet är en longitudinell mekanisk våg. Ljudet färdas, till skillnad från ljuset, snabbare i vatten och metall (och andra tätare medier än luft) Undantag är vissa mycket lätta gaser (ex. väte och helium) där ljudets hastighet också är mycket högre än i luft. Ljudintensitet och Ljudnivå Ljudintensitet definieras som den effekt som träffar en yta: I = P A. Enhet: 1 W/m2. Ljudnivå ges av L = 10log I Grundenheten där kallas för decibel (db) En ökning med 10 db uppfattas ungefär som dubbelt så starkt ljud av vårt öra. Dopplereffekt Alla har vi hört sirenerna från ett utryckningsfordon som passerar i hög fart. Frekvensen hos sirenerna tycks ändras vid passagen. Detta kallas dopplereffekt och beror på att man före passagen upplever att ljudvågorna trycks ihop, och därför blir våglängden kortare, d.v.s. frekvensen ökar. Efter att sirenen passerat upplever man att ljudvågorna dras isär, och därför blir våglängden längre, d.v.s. frekvensen minskar. I detta fallet befinner sig ljudkällan i rörelse och observatören i vila. Samma effekt uppstår när observatören rör sig förbi en stillastående ljudkälla (t.ex. när ett tåg passerar nedfällda bommar). Ett motsvarande fenomen finns för ljuset från en stjärna, där våglängden hos det utsända ljuset blir lite större eller mindre beroende på om stjärnan är på väg bort eller på väg mot oss på Jorden.
9 Övningsuppgifter Nivå 1 1. Ljudets hastighet är vid ett visst tillfälle 336 m/s. Hur stor är våglängden för en ljudvåg som har frekvensen 512 Hz? 2. Varför rör sig ljud långsammare i luft än i vatten? 3. En fjäder har längden 7,2 cm. När en 50 g vikt hängs i den förlängs fjädern till 9,8 cm. Beräkna fjäderkonstanten. 4. En vikt i en fjäder utför 10 hela svängningar på 18 s. Beräkna vinkelhastigheten. 5. I ett försök hängde man en 200 g vikt i en fjäder, som då sträcktes ut 8,4 cm. Därefter bytte man ut vikten mot en 50 g vikt. Hur stor blir den resulterande kraften till storlek och riktning på denna nya vikt om den dras ner till ett läge 5,0 cm under jämviktsläget? 6. Beräkna perioden för den harmoniska svängning som uppstår, om man släpper den nya vikten i föregående uppgift. 7. En stående våg med fem bukar uppkommer i ett spänt snöre med längden 1,50 m. a) Beräkna våglängden b) Beräkna våglängden för nästkommande stående våg i snöret. c) Vilken är den längsta våglängd som kan ge en stående våg i snöret? 8. Den övre figuren visar en triangulär puls, som rör sig mot ett fast hinder. Då pulsen når fram till hindret kommer den att reflekteras. Rita hur den reflekterade pulsen ser ut, i den nedre figuren.
10 9. Figuren visar två pulser som rör sig mot varandra i en tråd. Avståndet mellan två prickar i rutmönstret är 1,0 cm. Rita i den nedre delen av figuren hur den resulterande pulsen ser ut efter 2,0 s. 10. I figuren nedan är A och B två vågkällor som svänger i takt med varandra. De sänder ut transversella vågor med frekvensen 14,0 Hz på en vattenyta. Till följd av interferens uppstår nodlinjer på ytan. Punkten P ligger på tredje nodlinjen räknat från centralmaximum (som ligger lodrätt mitt emellan sträckan AB). Med vilken hastighet utbreder sig vågorna? Figuren är i naturlig storlek. P A B 11. A och B är två vågkällor som ger upphov till vattenvågor. Avståndet mellan A och B är 4,0 cm. I punkten M på mittpunktsnormalen till AB har vi centralmaximum. Om man förflyttar sig från M till P minskar först vågornas amplitud till ett minimum för att sedan åter öka. I punkten P registreras på nytt ett amplitudmaximum. Avståndet mellan A och P är 10,0 cm enligt figuren nedan. Vilket värde på våglängden ger dessa iakttagelser? A 10,0 cm P 4,0 cm M B
11 12. Det sägs ofta fiskare emellan att man måste vara tyst när man fiskar för att inte skrämma bort fisken. Oftast är det så att ljudet i själva verket totalreflekteras mot vattenytan. Beräkna gränsvinkeln α, när ljudet inte längre bryts utan totalreflekteras. Se figur nedan. α v = 340 m/s 1 v = 1490 m/s Utbredningshastigheten för transversella vågor i en gitarrsträng är 720 m/s.. Strängens längd är 40,0 cm. Vilken frekvens har den grundton strängen ger ifrån sig? 14. Ett gummibands båda ändar är fästa i ett stativ resp. i en vibrator. Gummibandet sträcks så att våghastigheten för transversella vågor blir 4,80 m/s. Då vibratorn ger svängningar med frekvensen 18 Hz uppstår en stående transversell våg i gummibandet med sammanlagt tre svängningsbukar. Bestäm gummibandets längd. Nivå En vikt hänger i en vertikal fjäder och utför svängningar med amplituden 10,0 cm. Då vikten passerar jämviktsläget är dess rörelseenergi 0,24 J. Hur stor är rörelseenergin i en punkt mitt emellan viktens jämviktsläge och viktens vändläge? 16. En liten kula med massan 15 g fästs i en tråd med längden 25 cm. Man låter kulan utföra en plan pendelrörelse. Då kulan släpps är vinkeln mellan lodlinjen och pendeltråden 50. a) Bestäm kulans maximala hastighet under pendelrörelsen. b) Efter ett antal svängningar har utslagsvinkeln minskat till 3,0. Beräkna tiden för en hel svängning (perioden). 17. En person har en 50 cm lång fjäder i vilken han hänger en vikt med massan 200 g. Härvid sträcks fjädern och får längden 80 cm. Sedan drar han ned vikten 20 cm och släpper. a) Bestäm svängningstiden. b) Bestäm lägesenergin då vikten befinner sig 5,0 cm från jämviktsläget. c) Bestäm viktens hastighet då den befinner sig 5,0 cm från jämviktsläget. d) Bestäm kraften från fjädern på vikten då den befinner sig i samma läge som i c).
12 18. Man sänder in ljud i ett rör som är öppet i båda ändar. Man får ett kraftigt ljud vid frekvensen 600 Hz. Ge ett förslag på hur långt röret kan vara. 19. Nedanstående figur föreställer infallande vattenvågor med våghastighet v 1, som närmar sig ett område med en annan våghastighet, v 2. Figuren är i naturlig storlek och kan utnyttjas för mätningar. Infallande vågfronter v = 3,0 cm/s 1 v 2 a) Bestäm infallsvinkeln och brytningsvinkeln. b) Bestäm våghastigheten v 2. c) Hur stor blir brytningsvinkeln om infallsvinkeln i stället är 5,0? 20. En transversell våg utbreder sig med hastigheten 12,5 m/s enligt figuren nedan. En partikel i det svängande mediet befinner sig vid ett visst tillfälle i punkten A. 12,5 m/s A 1 m a) Markera i figuren var partikeln vid A befinner sig efter en kvarts period. b) Beräkna den transversella vågens frekvens. c) Hur länge dröjer det innan partikeln åter befinner sig i punkten A? 21. Ett gummiband är fäst med sin ena ände i ett stativ och sin andra ände i en vibrator. Då vibratorn svängde med frekvensen 60 Hz iakttogs en stående transversell våg med 3 svängningsbukar. Vilken skall frekvensen vara för att man skall se en stående våg med 5 svängningsbukar?
13 22. Två små högtalare H 1 och H 2 sänder ut ljudvågor med frekvensen 0,90 khz. Högtalarnas membraner svänger i fas med varandra. Högtalaren H 1 är fast placerad medan H 2 kan förflyttas utmed linjen DE. En mikrofon är placerad i punkten A, 1,5 m rakt framför H 1. Högtalarna är från början placerade intill varandra. Då H 2 förflyttas från H 1 mot E minskar först ljudstyrkan i punkten A för att sedan öka till ett maximum då avståndet mellan högtalarna är s. Bestäm avståndet s. A 1,5 m D E H 1 s H 2 Nivå Figuren visar en träkloss med massan 0,52 kg som är fäst i en horisontell fjäder med fjäderkonstanten 35 N/m. Klossen kan glida friktionsfritt mot underlaget. Då man skjuter iväg en kula med massan 20 g mot klossen kommer kulan att fastna i klossen. Omedelbart före stöten rör sig kulan med hastigheten 55 m/s. Hur stor blir amplituden i den svängningsrörelse som kloss och kula därefter kommer att hamna i? 55 m/s 24. En sten släpps ned i en brunn. Man kan höra hur stenen träffar vattnet 3,00 s senare. a) Hur lång tid tar det för stenen att falla ned till vattnet och hur lång tar det för ljudet att färdas upp så vi kan höra plasket? b) På vilket djup finns vattnet i brunnen? 25. En 74 cm lång järnstav är infäst på mitten enligt figur. Genom att gnida staven kan man få fram longitudinella ljudvågor (ett gnälligt ljud). Våghastigheten för sådana vågor är 5180 m/s. Hur många övertoner kan ett mänskligt öra uppfatta, om man antar att örats känslighetsområde är 20 Hz - 20 khz?
14 26. Den övre figuren visar två triangulära pulser, som rör sig mot ett fast hinder med farten v = 2 cm/s. Rita pulsernas utseende 2 s senare i den nedre figuren. 27. Två fjädrar parallellkopplas som figuren visar. Var och en av fjädrarna har fjäderkonstanten 40 N/m. Fjädersystemet belastas med en vikt med massan 0,20 kg. Vikten dras ner 3,0 cm och släpps sedan. Den kommer då att utföra en harmonisk svängningsrörelse. a) Hur stor blir hela fjädersystemets fjäderkonstant? b) Hur många svängningar hinner vikten utföra på 60 sekunder? c) Vilken blir viktens största hastighet? 28. Vågor rör sig från ett medium till ett annat varvid vågornas hastighet blir dubbelt så stor. I figuren nedan visas en ögonblicksbild över situationen vid gränslinjen mellan de två medierna. Vågfronten A står närmast i tur att passera gränslinjen och vågfronten B är den senaste som passerat gränslinjen. Beräkna våglängden i översta mediet. Figuren är i naturlig storlek och kan utnyttjas för mätningar. gränslinje A B v 2v v
15 Svar till övningsuppgifterna 1. 65,6 cm 2. Ljud är en mekanisk våg som fortplantas genom att energi förs över till nästa atom. I luft är det längre mellan atomerna (molekylerna) än i vatten. Därför tar det längre tid att överföra energin N/m 4. 3,5 rad/s 5. 1,2 N, uppåt 6. 0,29 s 7a. 60 cm 7b. 50 cm 7c. 3,0 m 8. > 9. > cm/s 11. 0,77 cm 12. α 13, Hz 14. 0,40 m 15. 0,18 J 16. a) 1,3 m/s b) 1,0 s 17. a) 1,1 s b) 8,2 mj c) 1,1 m/s d) 2,3 N om vikten är under jvl och 1,6 N om vikten är ovanför jvl ,33 cm eller längder som är n 28, 33 cm, där n = 1, 2, a) Mätningar i figuren ger att infallsvinkeln i = 24 och brytningsvinkeln b = 75 b) 7,1 cm/s c) a) i övre vändläget b) 3,1 Hz c) 0,16 s Hz 22. 1,13 m 23. 0,25 m 24. a) Stenen faller i 2,88 s, och ljudet behöver 0,12 s för att komma upp. b) ca 41 m st (man hör grundtonen + två övertoner) a) 80 N/m b) 191 st c) 0,60 m/s 28. Våglängden i översta mediet är 1,75 cm.
Vågor. En våg är en störning som utbreder sig En våg överför energi från en plats till en annan. Det sker ingen masstransport
 Vågor En våg är en störning som utbreder sig En våg överför energi från en plats till en annan. Det sker ingen masstransport Vågtyper Transversella Mediets partiklar rör sig vinkelrätt mot vågens riktning.
Vågor En våg är en störning som utbreder sig En våg överför energi från en plats till en annan. Det sker ingen masstransport Vågtyper Transversella Mediets partiklar rör sig vinkelrätt mot vågens riktning.
3. Mekaniska vågor i 2 (eller 3) dimensioner
 3. Mekaniska vågor i 2 (eller 3) dimensioner Brytning av vågor som passerar gränsen mellan två material Eftersom utbredningshastigheten för en mekanisk våg med största sannolikhet ändras då den passerar
3. Mekaniska vågor i 2 (eller 3) dimensioner Brytning av vågor som passerar gränsen mellan två material Eftersom utbredningshastigheten för en mekanisk våg med största sannolikhet ändras då den passerar
1 Figuren nedan visar en transversell våg som rör sig åt höger. I figuren är en del i vågens medium markerat med en blå ring prick.
 10 Vågrörelse Vågor 1 Figuren nedan visar en transversell våg som rör sig åt höger. I figuren är en del i vågens medium markerat med en blå ring prick. y (m) 0,15 0,1 0,05 0-0,05 0 0,5 1 1,5 2 x (m) -0,1-0,15
10 Vågrörelse Vågor 1 Figuren nedan visar en transversell våg som rör sig åt höger. I figuren är en del i vågens medium markerat med en blå ring prick. y (m) 0,15 0,1 0,05 0-0,05 0 0,5 1 1,5 2 x (m) -0,1-0,15
Vågrörelselära. Christian Karlsson Uppdaterad: Har jag använt någon bild som jag inte får använda så låt mig veta så tar jag bort den.
 Vågrörelselära Christian Karlsson Uppdaterad: 161003 Har jag använt någon bild som jag inte får använda så låt mig veta så tar jag bort den. christian.karlsson@ckfysik.se [14] 1 Elasticitet (bl.a. fjädrar)
Vågrörelselära Christian Karlsson Uppdaterad: 161003 Har jag använt någon bild som jag inte får använda så låt mig veta så tar jag bort den. christian.karlsson@ckfysik.se [14] 1 Elasticitet (bl.a. fjädrar)
Vågrörelselära. Uppdaterad: [1] Elasticitet (bl.a. fjädrar) [15] Superposition / [2] Elastisk energi /
![Vågrörelselära. Uppdaterad: [1] Elasticitet (bl.a. fjädrar) [15] Superposition / [2] Elastisk energi / Vågrörelselära. Uppdaterad: [1] Elasticitet (bl.a. fjädrar) [15] Superposition / [2] Elastisk energi /](/thumbs/73/68930624.jpg) Vågrörelselära Har jag använt någon bild som jag inte får Uppdaterad: 171017 använda? Låt mig veta så tar jag bort den. christian.karlsson@ckfysik.se [1] Elasticitet (bl.a. fjädrar) [15] Superposition
Vågrörelselära Har jag använt någon bild som jag inte får Uppdaterad: 171017 använda? Låt mig veta så tar jag bort den. christian.karlsson@ckfysik.se [1] Elasticitet (bl.a. fjädrar) [15] Superposition
2. Mekaniska vågrörelser i en dimension
 2. Mekaniska vågrörelser i en dimension Reflexion Även om alla vågrörelser kan beskrivas med begreppen och, för de flesta naturligt förekommande vågorna, de matematiska uttrycken introducerade i kapitel
2. Mekaniska vågrörelser i en dimension Reflexion Även om alla vågrörelser kan beskrivas med begreppen och, för de flesta naturligt förekommande vågorna, de matematiska uttrycken introducerade i kapitel
2. Ljud. 2.1 Ljudets uppkomst
 2. Ljud 2.1 Ljudets uppkomst Ljud är en mekanisk vågrörelse som fortskrider i ett medium (t.ex. luft, vatten...) Någon typ av medium är ett krav; I vakuum kan ljudet inte fortskrida. I vätskor och gaser
2. Ljud 2.1 Ljudets uppkomst Ljud är en mekanisk vågrörelse som fortskrider i ett medium (t.ex. luft, vatten...) Någon typ av medium är ett krav; I vakuum kan ljudet inte fortskrida. I vätskor och gaser
= T. Bok. Fysik 3. Harmonisk kraft. Svängningsrörelse. Svängningsrörelse. k = = = Vågrörelse. F= -kx. Fjäder. F= -kx. massa 100 g töjer fjärder 4,0 cm
 Bok Vågrörelse Fysik 3 Fysik 3, Vågrörelse Mekanisk vågrörelse Ljud Ljus Harmonisk kraft Ex [ F] [ k ] N / m [ x] Fjäder F -kx F -kx [ F] k fjäderkonstanten [ k ] [ x] - kraften riktad mot jämviktsläget
Bok Vågrörelse Fysik 3 Fysik 3, Vågrörelse Mekanisk vågrörelse Ljud Ljus Harmonisk kraft Ex [ F] [ k ] N / m [ x] Fjäder F -kx F -kx [ F] k fjäderkonstanten [ k ] [ x] - kraften riktad mot jämviktsläget
Upp gifter. c. Hjälp Bengt att förklara varför det uppstår en stående våg.
 1. Bengt ska just demonstrera stående vågor för sin bror genom att skaka en slinkyfjäder. Han lägger fjädern på golvet och ber sin bror hålla i andra änden. Sen spänner han fjädern genom att backa lite
1. Bengt ska just demonstrera stående vågor för sin bror genom att skaka en slinkyfjäder. Han lägger fjädern på golvet och ber sin bror hålla i andra änden. Sen spänner han fjädern genom att backa lite
Svar och anvisningar
 160322 BFL102 1 Tenta 160322 Fysik 2: BFL102 Svar och anvisningar Uppgift 1 a) Centripetalkraften ligger i horisontalplanet, riktad in mot cirkelbanans mitt vid B. A B b) En centripetalkraft kan tecknas:
160322 BFL102 1 Tenta 160322 Fysik 2: BFL102 Svar och anvisningar Uppgift 1 a) Centripetalkraften ligger i horisontalplanet, riktad in mot cirkelbanans mitt vid B. A B b) En centripetalkraft kan tecknas:
Lösningar Heureka 2 Kapitel 7 Harmonisk svängningsrörelse
 Lösningar Heureka Kapitel 7 Harmonisk svängningsrörelse Andreas Josefsson Tullängsskolan Örebro Lo sningar Fysik Heureka Kapitel 7 7.1 a) Av figuren framgår att amplituden är 0,30 m. b) Skuggan utför en
Lösningar Heureka Kapitel 7 Harmonisk svängningsrörelse Andreas Josefsson Tullängsskolan Örebro Lo sningar Fysik Heureka Kapitel 7 7.1 a) Av figuren framgår att amplituden är 0,30 m. b) Skuggan utför en
1.3 Uppkomsten av mekanisk vågrörelse
 1.3 Uppkomsten av mekanisk vågrörelse För att en mekanisk vågrörelse skall kunna uppstå, behövs ett medium, något som rörelsen kan framskrida i. Det kan vara vatten, luft, ett bord, jordskorpan, i princip
1.3 Uppkomsten av mekanisk vågrörelse För att en mekanisk vågrörelse skall kunna uppstå, behövs ett medium, något som rörelsen kan framskrida i. Det kan vara vatten, luft, ett bord, jordskorpan, i princip
1. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (1p)
 Problem Energi. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (p) b) Ge en tydlig förklaring av hur frekvens, period, våglängd och våghastighet hänger
Problem Energi. a) I en fortskridande våg, vad är det som rör sig från sändare till mottagare? Svara med ett ord. (p) b) Ge en tydlig förklaring av hur frekvens, period, våglängd och våghastighet hänger
1. Allmänt vågrörelser mekaniska vågrörelser
 1. Allmänt vågrörelser mekaniska vågrörelser Definition En mekanisk vågrörelse utgörs av en regelbundet upprepad (periodisk) störning i en del av ett medium (material) som fortplantas (utbreder sig) genom
1. Allmänt vågrörelser mekaniska vågrörelser Definition En mekanisk vågrörelse utgörs av en regelbundet upprepad (periodisk) störning i en del av ett medium (material) som fortplantas (utbreder sig) genom
TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t s(x,t) =s 0 sin 2π T x. v = fλ =3 5 m/s = 15 m/s
 140528: TFEI02 1 TFEI02: Vågfysik Tentamen 140528: Svar och anvisningar Uppgift 1 a) En fortskridande våg kan skrivas på formen: t s(x,t) =s 0 sin 2π T x λ Vi ser att periodtiden är T =1/3 s, vilket ger
140528: TFEI02 1 TFEI02: Vågfysik Tentamen 140528: Svar och anvisningar Uppgift 1 a) En fortskridande våg kan skrivas på formen: t s(x,t) =s 0 sin 2π T x λ Vi ser att periodtiden är T =1/3 s, vilket ger
Hjälpmedel: Grafritande miniräknare, gymnasieformelsamling, linjal och gradskiva
 Fysik Bas 2 Provmoment: Ladokkod: Tentamen ges för: KBAST17h KBASX17h 9 högskolepoäng Tentamensdatum: 2018-05-28 Tid: 09:00-13:00 Hjälpmedel: Grafritande miniräknare, gymnasieformelsamling, linjal och
Fysik Bas 2 Provmoment: Ladokkod: Tentamen ges för: KBAST17h KBASX17h 9 högskolepoäng Tentamensdatum: 2018-05-28 Tid: 09:00-13:00 Hjälpmedel: Grafritande miniräknare, gymnasieformelsamling, linjal och
Svar och anvisningar
 170317 BFL10 1 Tenta 170317 Fysik : BFL10 Svar och anvisningar Uppgift 1 a) Den enda kraft som verkar på stenen är tyngdkraften, och den är riktad nedåt. Alltså är accelerationen riktad nedåt. b) Vid kaströrelse
170317 BFL10 1 Tenta 170317 Fysik : BFL10 Svar och anvisningar Uppgift 1 a) Den enda kraft som verkar på stenen är tyngdkraften, och den är riktad nedåt. Alltså är accelerationen riktad nedåt. b) Vid kaströrelse
Våglära och Optik Martin Andersson mading1977@gmail.com
 Våglära och Optik Martin Andersson mading1977@gmail.com A - Våglära (Kapitel 19-21) Innehåll: I - Beskrivning, Egenskaper hos vibrationer och vågor II - Mekaniska vågor ljud I - Beskrivning, egenskaper
Våglära och Optik Martin Andersson mading1977@gmail.com A - Våglära (Kapitel 19-21) Innehåll: I - Beskrivning, Egenskaper hos vibrationer och vågor II - Mekaniska vågor ljud I - Beskrivning, egenskaper
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 14 Harmonisk oscillator 1 Vågrörelselära och optik 2 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator:
Vågrörelselära och optik Kapitel 14 Harmonisk oscillator 1 Vågrörelselära och optik 2 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator:
1. Mekanisk svängningsrörelse
 1. Mekanisk svängningsrörelse Olika typer av mekaniska svängningar och vågrörelser möter oss överallt i vardagen allt från svajande höghus till telefoner med vibrationen påslagen hör till denna kategori.
1. Mekanisk svängningsrörelse Olika typer av mekaniska svängningar och vågrörelser möter oss överallt i vardagen allt från svajande höghus till telefoner med vibrationen påslagen hör till denna kategori.
Handledning laboration 1
 : Fysik 2 för tekniskt/naturvetenskapligt basår Handledning laboration 1 VT 2017 Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen
: Fysik 2 för tekniskt/naturvetenskapligt basår Handledning laboration 1 VT 2017 Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 15 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 : Kapitel 15.1 15.8 Ljud och
Vågrörelselära och optik Kapitel 15 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 : Kapitel 15.1 15.8 Ljud och
Tentamen i fysik B2 för tekniskt basår/termin VT 2014
 Tentamen i fysik B för tekniskt basår/termin VT 04 04-0-4 En sinusformad växelspänning u har amplituden,5 V. Det tar 50 μs från det att u har värdet 0,0 V till dess att u har antagit värdet,5 V. Vilken
Tentamen i fysik B för tekniskt basår/termin VT 04 04-0-4 En sinusformad växelspänning u har amplituden,5 V. Det tar 50 μs från det att u har värdet 0,0 V till dess att u har antagit värdet,5 V. Vilken
Lösningar till Tentamen i fysik B del 1 vid förutbildningar vid Malmö högskola
 Lösningar till Tentamen i fysik B del 1 vid förutbildningar vid Malmö högskola Tid: Måndagen 5/3-2012 kl: 8.15-12.15. Hjälpmedel: Räknedosa. Bifogad formelsamling. Lösningar: Lösningarna skall vara väl
Lösningar till Tentamen i fysik B del 1 vid förutbildningar vid Malmö högskola Tid: Måndagen 5/3-2012 kl: 8.15-12.15. Hjälpmedel: Räknedosa. Bifogad formelsamling. Lösningar: Lösningarna skall vara väl
BFL102/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik mars :00 12:00. Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
 Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL102/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik 2 17 mars 2017 8:00 12:00 Tentamen består av 6 uppgifter som vardera kan ge upp till 4
Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL102/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik 2 17 mars 2017 8:00 12:00 Tentamen består av 6 uppgifter som vardera kan ge upp till 4
Denna våg är. A. Longitudinell. B. Transversell. C. Något annat
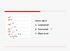 Denna våg är A. Longitudinell B. Transversell ⱱ v C. Något annat l Detta är situationen alldeles efter en puls på en fjäder passerat en skarv A. Den ursprungliga pulsen kom från höger och mötte en lättare
Denna våg är A. Longitudinell B. Transversell ⱱ v C. Något annat l Detta är situationen alldeles efter en puls på en fjäder passerat en skarv A. Den ursprungliga pulsen kom från höger och mötte en lättare
Lösningsförslag - tentamen. Fysik del B2 för tekniskt / naturvetenskapligt basår / bastermin BFL 122 / BFL 111
 Linköpings Universitet Institutionen för Fysik, Kemi, och Biologi Avdelningen för Tillämpad Fysik Mike Andersson Lösningsförslag - tentamen Torsdagen den 27:e maj 2010, kl 08:00 12:00 Fysik del B2 för
Linköpings Universitet Institutionen för Fysik, Kemi, och Biologi Avdelningen för Tillämpad Fysik Mike Andersson Lösningsförslag - tentamen Torsdagen den 27:e maj 2010, kl 08:00 12:00 Fysik del B2 för
BFL102/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik mars :00 12:00. Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
 Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL12/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik 2 22 mars 216 8: 12: Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL12/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik 2 22 mars 216 8: 12: Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
Laboration 1 Fysik
 Laboration 1 Fysik 2 2015 : Fysik 2 för tekniskt/naturvetenskapligt basår Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen på
Laboration 1 Fysik 2 2015 : Fysik 2 för tekniskt/naturvetenskapligt basår Laboration 1 Förberedelseuppgifter 1. För en våg med frekvens f och våglängd λ kan utbredningshastigheten skrivas: 2. Färgen på
Prov i vågrörelselära vt06 Lösningsförslag
 Prov i vågrörelselära vt06 Lösningsförslag Hjälpmedel: Formelsamling, fysikbok, miniräknare, linjal, sunt förnuft. 7 uppgifter vilka inlämnas på separat papper snyggt och välstrukturerat! Låt oss spela
Prov i vågrörelselära vt06 Lösningsförslag Hjälpmedel: Formelsamling, fysikbok, miniräknare, linjal, sunt förnuft. 7 uppgifter vilka inlämnas på separat papper snyggt och välstrukturerat! Låt oss spela
3. Ljus. 3.1 Det elektromagnetiska spektret
 3. Ljus 3.1 Det elektromagnetiska spektret Synligt ljus är elektromagnetisk vågrörelse. Det följer samma regler som vi tidigare gått igenom för mekanisk vågrörelse; reflexion, brytning, totalreflexion
3. Ljus 3.1 Det elektromagnetiska spektret Synligt ljus är elektromagnetisk vågrörelse. Det följer samma regler som vi tidigare gått igenom för mekanisk vågrörelse; reflexion, brytning, totalreflexion
BFL102/TEN1: Fysik 2 för basår (8 hp) Tentamen Fysik 2. 5 juni :00 12:00. Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
 Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL02/TEN: Fysik 2 för basår (8 hp) Tentamen Fysik 2 5 juni 205 8:00 2:00 Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
Institutionen för fysik, kemi och biologi (IFM) Marcus Ekholm BFL02/TEN: Fysik 2 för basår (8 hp) Tentamen Fysik 2 5 juni 205 8:00 2:00 Tentamen består av 6 uppgifter som vardera kan ge upp till 4 poäng.
Elektromagnetiska vågor (Ljus)
 Föreläsning 4-5 Elektromagnetiska vågor (Ljus) Ljus kan beskrivas som bestående av elektromagnetiska vågrörelser, d.v.s. ett tids- och rumsvarierande elektriskt och magnetiskt fält. Dessa ljusvågor följer
Föreläsning 4-5 Elektromagnetiska vågor (Ljus) Ljus kan beskrivas som bestående av elektromagnetiska vågrörelser, d.v.s. ett tids- och rumsvarierande elektriskt och magnetiskt fält. Dessa ljusvågor följer
Ljud. Låt det svänga. Arbetshäfte
 Ljud Låt det svänga Arbetshäfte Ljud När ljudvågorna träffar örat börjar trumhinnan svänga i takt vi hör ett ljud! Trumhinnan Ljud är en svängningsrörelse. När ett föremål börjar vibrera packas luftens
Ljud Låt det svänga Arbetshäfte Ljud När ljudvågorna träffar örat börjar trumhinnan svänga i takt vi hör ett ljud! Trumhinnan Ljud är en svängningsrörelse. När ett föremål börjar vibrera packas luftens
Tentamen i Mekanik II
 Institutionen för fysik och astronomi F1Q1W2 Tentamen i Mekanik II 30 maj 2016 Hjälpmedel: Mathematics Handbook, Physics Handbook och miniräknare. Maximalt 5 poäng per uppgift. För betyg 3 krävs godkänd
Institutionen för fysik och astronomi F1Q1W2 Tentamen i Mekanik II 30 maj 2016 Hjälpmedel: Mathematics Handbook, Physics Handbook och miniräknare. Maximalt 5 poäng per uppgift. För betyg 3 krävs godkänd
TFYA58, Fysik, 8 hp, 3 delar
 1. Vågrörelselära (mekaniska vågor, optik, diffraktion ) 7x2 tim föreläsning 6x2tim lektion 2. Experimentell problemlösning TFYA58, Fysik, 8 hp, 3 delar Ht 1 Ht 2 2x1 tim föreläsning 2 st Richardslabbar
1. Vågrörelselära (mekaniska vågor, optik, diffraktion ) 7x2 tim föreläsning 6x2tim lektion 2. Experimentell problemlösning TFYA58, Fysik, 8 hp, 3 delar Ht 1 Ht 2 2x1 tim föreläsning 2 st Richardslabbar
92FY27: Vågfysik teori och tillämpningar. Tentamen Vågfysik. 17 oktober :00 13:00
 Linköpings Universitet Institutionen för fysik, kemi och biologi Roger Magnusson 92FY27: Vågfysik teori och tillämpningar Tentamen Vågfysik 17 oktober 2016 8:00 13:00 Tentamen består av 6 uppgifter som
Linköpings Universitet Institutionen för fysik, kemi och biologi Roger Magnusson 92FY27: Vågfysik teori och tillämpningar Tentamen Vågfysik 17 oktober 2016 8:00 13:00 Tentamen består av 6 uppgifter som
Fysik (TFYA14) Fö 5 1. Fö 5
 Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Fysik (TFYA14) Fö 5 1 Fö 5 Kap. 35 Interferens Interferens betyder samverkan och i detta fall samverkan mellan elektromagnetiska vågor. Samverkan bygger (precis som för mekaniska vågor) på superpositionsprincipen
Vågfysik. Superpositionsprincipen
 Vågfysik Superposition Knight, Kap 21 Superpositionsprincipen Superposition = kombination av två eller fler vågor. Vågor partiklar Elongation = D 1 +D 2 D net = Σ D i Superpositionsprincipen 1 2 vågor
Vågfysik Superposition Knight, Kap 21 Superpositionsprincipen Superposition = kombination av två eller fler vågor. Vågor partiklar Elongation = D 1 +D 2 D net = Σ D i Superpositionsprincipen 1 2 vågor
λ = T 2 g/(2π) 250/6 40 m
 Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Problem. Utbredning av vattenvågor är komplicerad. Vågorna är inte transversella, utan vattnet rör sig i cirklar eller ellipser. Våghastigheten beror bland annat på hur djupt vattnet är. I grunt vatten
Final i Wallenbergs Fysikpris
 Final i Wallenbergs Fysikpris 26-27 mars 2010. Teoriprov Lösningsförslag 1. a) Vattens värmekapacitivitet: Isens värmekapacitivitet: Smältvärmet: Kylmaskinen drivs med spänningen och strömmen. Kylmaskinens
Final i Wallenbergs Fysikpris 26-27 mars 2010. Teoriprov Lösningsförslag 1. a) Vattens värmekapacitivitet: Isens värmekapacitivitet: Smältvärmet: Kylmaskinen drivs med spänningen och strömmen. Kylmaskinens
Lösningar till repetitionsuppgifter
 Lösningar till repetitionsuppgifter 1. Vågen antas röra sig i positiva x-axelns riktning dvs s = a sin(ω t k x +δ). Elongationen = +0,5 a för x = 0 vid t = 0 0,5 a = a sin(δ) sin(δ) = 0,5 δ 1 = π/6 och
Lösningar till repetitionsuppgifter 1. Vågen antas röra sig i positiva x-axelns riktning dvs s = a sin(ω t k x +δ). Elongationen = +0,5 a för x = 0 vid t = 0 0,5 a = a sin(δ) sin(δ) = 0,5 δ 1 = π/6 och
4. Allmänt Elektromagnetiska vågor
 Det är ett välkänt faktum att det runt en ledare som det flyter en viss ström i bildas ett magnetiskt fält, där styrkan hos det magnetiska fältet beror på hur mycket ström som flyter i ledaren. Om strömmen
Det är ett välkänt faktum att det runt en ledare som det flyter en viss ström i bildas ett magnetiskt fält, där styrkan hos det magnetiska fältet beror på hur mycket ström som flyter i ledaren. Om strömmen
1. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft.
 Problem. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft. (p) Det finns många förklaringar, till exempel Hewitt med insekten
Problem. Ge en tydlig förklaring av Dopplereffekt. Härled formeln för frekvens som funktion av källans hastighet i stillastående luft. (p) Det finns många förklaringar, till exempel Hewitt med insekten
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 35-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 35-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 16-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 16-1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Ljud, Hörsel. vågrörelse. och. Namn: Klass: 7A
 Ljud, Hörsel och vågrörelse Namn: Klass: 7A Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och samhället genomföra
Ljud, Hörsel och vågrörelse Namn: Klass: 7A Dessa förmågor ska du träna: använda fysikens begrepp, modeller och teorier för att beskriva och förklara fysikaliska samband i naturen och samhället genomföra
TFEI02: Vågfysik. Tentamen : Lösningsförslag
 160530: TFEI0 1 Uppgift 1 TFEI0: Vågfysik Tentamen 016-05-30: Lösningsförslag a) Ljudintensiteten, I, är ett mått på hur stor effekt, P eff, som transporteras per area. Om vi vet amplituden på vågen kan
160530: TFEI0 1 Uppgift 1 TFEI0: Vågfysik Tentamen 016-05-30: Lösningsförslag a) Ljudintensiteten, I, är ett mått på hur stor effekt, P eff, som transporteras per area. Om vi vet amplituden på vågen kan
5. Elektromagnetiska vågor - interferens
 Interferens i dubbelspalt A λ/2 λ/2 Dal för ena vågen möter topp för den andra och vice versa => mörkt (amplitud = 0). Dal möter dal och topp möter topp => ljust (stor amplitud). B λ/2 Fig. 5.1 För ljusvågor
Interferens i dubbelspalt A λ/2 λ/2 Dal för ena vågen möter topp för den andra och vice versa => mörkt (amplitud = 0). Dal möter dal och topp möter topp => ljust (stor amplitud). B λ/2 Fig. 5.1 För ljusvågor
Alla svar till de extra uppgifterna
 Alla svar till de extra uppgifterna Fö 1 1.1 (a) 0 cm 1.4 (a) 50 s (b) 4 cm (b) 0,15 m (15 cm) (c) 0 cm 1.5 2 m/s (d) 0 cm 1.6 1.2 (a) A nedåt, B uppåt, C nedåt, D nedåt 1.7 2,7 m/s (b) 1.8 Våglängd: 2,0
Alla svar till de extra uppgifterna Fö 1 1.1 (a) 0 cm 1.4 (a) 50 s (b) 4 cm (b) 0,15 m (15 cm) (c) 0 cm 1.5 2 m/s (d) 0 cm 1.6 1.2 (a) A nedåt, B uppåt, C nedåt, D nedåt 1.7 2,7 m/s (b) 1.8 Våglängd: 2,0
Läran om ljudet Ljud är egentligen tryckförändringar i något material. För att ett ljud ska uppstå måste något svänga eller vibrera.
 Akustik Läran om ljudet Ljud är egentligen tryckförändringar i något material. För att ett ljud ska uppstå måste något svänga eller vibrera. När en gitarrsträng vibrerar, rör den sig fram och tillbaka.
Akustik Läran om ljudet Ljud är egentligen tryckförändringar i något material. För att ett ljud ska uppstå måste något svänga eller vibrera. När en gitarrsträng vibrerar, rör den sig fram och tillbaka.
Tentamen. Fysik del B2 för tekniskt / naturvetenskapligt basår / bastermin BFL 120 / BFL 111
 Linköpings Universitet Institutionen för Fysik, Kemi, och Biologi Avdelningen för Tillämpad Fysik Mike Andersson Lösningsförslag Tentamen Tisdagen den 27:e maj 2008, kl 08:00 12:00 Fysik del B2 för tekniskt
Linköpings Universitet Institutionen för Fysik, Kemi, och Biologi Avdelningen för Tillämpad Fysik Mike Andersson Lösningsförslag Tentamen Tisdagen den 27:e maj 2008, kl 08:00 12:00 Fysik del B2 för tekniskt
Övningar Arbete, Energi, Effekt och vridmoment
 Övningar Arbete, Energi, Effekt och vridmoment G1. Ett föremål med massan 1 kg lyfts upp till en nivå 1,3 m ovanför golvet. Bestäm föremålets lägesenergi om golvets nivå motsvarar nollnivån. G10. En kropp,
Övningar Arbete, Energi, Effekt och vridmoment G1. Ett föremål med massan 1 kg lyfts upp till en nivå 1,3 m ovanför golvet. Bestäm föremålets lägesenergi om golvets nivå motsvarar nollnivån. G10. En kropp,
Tentamen i Fysik för M, TFYA72
 Tentamen i Fysik för M, TFYA72 Onsdag 2015-06-10 kl. 8:00-12:00 Tillåtna hjälpmedel: Bifogat formelblad Avprogrammerad räknedosa enlig IFM:s regler. Christopher Tholander kommer att besöka tentamenslokalen
Tentamen i Fysik för M, TFYA72 Onsdag 2015-06-10 kl. 8:00-12:00 Tillåtna hjälpmedel: Bifogat formelblad Avprogrammerad räknedosa enlig IFM:s regler. Christopher Tholander kommer att besöka tentamenslokalen
Repetitionsuppgifter i vågrörelselära
 Repetitionsuppgifter i vågrörelselära 1. En harmonisk vågrörelse med frekvensen 6, Hz och utbredningshastigheten 1 m/s har amplituden a. I en viss punkt och vid en viss tid är elongationen +,5a. Hur stor
Repetitionsuppgifter i vågrörelselära 1. En harmonisk vågrörelse med frekvensen 6, Hz och utbredningshastigheten 1 m/s har amplituden a. I en viss punkt och vid en viss tid är elongationen +,5a. Hur stor
Final i Wallenbergs fysikpris
 Final i Wallenbergs fysikpris 5-6 mars 011. Teoriprov. Lösningsförslag. 1) Fysikern Hilda leker med en protonstråle i en vakuumkammare. Hon accelererar protonerna från stillastående med en protonkanon
Final i Wallenbergs fysikpris 5-6 mars 011. Teoriprov. Lösningsförslag. 1) Fysikern Hilda leker med en protonstråle i en vakuumkammare. Hon accelererar protonerna från stillastående med en protonkanon
Vad är ljud? När man spelar på en gitarr så rör sig strängarna snabbt fram och tillbaka, de vibrerar.
 LJUD Vad är ljud? När man spelar på en gitarr så rör sig strängarna snabbt fram och tillbaka, de vibrerar. När strängen rör sig uppåt, pressar den samman luften på ovansidan om strängen => luftmolekylerna
LJUD Vad är ljud? När man spelar på en gitarr så rör sig strängarna snabbt fram och tillbaka, de vibrerar. När strängen rör sig uppåt, pressar den samman luften på ovansidan om strängen => luftmolekylerna
TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t 2π T x. s(x,t) = 2 cos [2π (0,4x/π t/π)+π/3]
![TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t 2π T x. s(x,t) = 2 cos [2π (0,4x/π t/π)+π/3] TFEI02: Vågfysik. Tentamen : Svar och anvisningar. t 2π T x. s(x,t) = 2 cos [2π (0,4x/π t/π)+π/3]](/thumbs/94/118804794.jpg) TFEI0: Vågfysik Tentamen 14100: Svar och anvisningar Uppgift 1 a) Vågen kan skrivas på formen: vilket i vårt fall blir: s(x,t) =s 0 sin t π T x + α λ s(x,t) = cos [π (0,4x/π t/π)+π/3] Vi ser att periodtiden
TFEI0: Vågfysik Tentamen 14100: Svar och anvisningar Uppgift 1 a) Vågen kan skrivas på formen: vilket i vårt fall blir: s(x,t) =s 0 sin t π T x + α λ s(x,t) = cos [π (0,4x/π t/π)+π/3] Vi ser att periodtiden
Kaströrelse. 3,3 m. 1,1 m
 Kaströrelse 1. En liten kula, som vi kallar kula 1, släpps ifrån en höjd över marken. Exakt samtidigt skjuts kula 2 parallellt med marken ifrån samma höjd som kula 1. Luftmotståndet som verkar på kulorna
Kaströrelse 1. En liten kula, som vi kallar kula 1, släpps ifrån en höjd över marken. Exakt samtidigt skjuts kula 2 parallellt med marken ifrån samma höjd som kula 1. Luftmotståndet som verkar på kulorna
Försättsblad Tentamen (Används även till tentamenslådan.) Måste alltid lämnas in. OBS! Eventuella lösblad måste alltid fästas ihop med tentamen.
 Försättsblad Tentamen (Används även till tentamenslådan.) Måste alltid lämnas in. OBS! Eventuella lösblad måste alltid fästas ihop med tentamen. Institution DFM Skriftligt prov i delkurs Vågrörelselära
Försättsblad Tentamen (Används även till tentamenslådan.) Måste alltid lämnas in. OBS! Eventuella lösblad måste alltid fästas ihop med tentamen. Institution DFM Skriftligt prov i delkurs Vågrörelselära
Svar och anvisningar
 15030 BFL10 1 Tenta 15030 Fysik : BFL10 Svar och anvisningar Uppgift 1 a) Enligt superpositionsprincipen ska vi addera elongationerna: y/cm 1 1 x/cm b) Reflektionslagen säger att reflektionsvinkeln är
15030 BFL10 1 Tenta 15030 Fysik : BFL10 Svar och anvisningar Uppgift 1 a) Enligt superpositionsprincipen ska vi addera elongationerna: y/cm 1 1 x/cm b) Reflektionslagen säger att reflektionsvinkeln är
Problem Vågrörelselära & Kvantfysik, FK november Givet:
 Räkneövning 3 Vågrörelselära & Kvantfysik, FK2002 29 november 2011 Problem 16.5 Givet: En jordbävning orsakar olika typer av seismiska vågor, bland annat; P- vågor (longitudinella primär-vågor) med våghastighet
Räkneövning 3 Vågrörelselära & Kvantfysik, FK2002 29 november 2011 Problem 16.5 Givet: En jordbävning orsakar olika typer av seismiska vågor, bland annat; P- vågor (longitudinella primär-vågor) med våghastighet
LÄRARHANDLEDNING Harmonisk svängningsrörelse
 LÄRARHANDLEDNING Harmonisk svängningsrörelse Utrustning: Dator med programmet LoggerPro LabQuest eller LabPro Avståndsmätare Kraftgivare Spiralfjäder En vikt Stativmateriel Kraftgivare Koppla mätvärdesinsamlaren
LÄRARHANDLEDNING Harmonisk svängningsrörelse Utrustning: Dator med programmet LoggerPro LabQuest eller LabPro Avståndsmätare Kraftgivare Spiralfjäder En vikt Stativmateriel Kraftgivare Koppla mätvärdesinsamlaren
TENTAMEN I TILLÄMPAD VÅGLÄRA FÖR M
 TENTAMEN I TILLÄMPAD VÅGLÄRA FÖR M 2012-01-13 Skrivtid: 8.00 13.00 Hjälpmedel: Formelblad och räknedosa. Uppgifterna är inte ordnade efter svårighetsgrad. Börja varje ny uppgift på ett nytt blad och skriv
TENTAMEN I TILLÄMPAD VÅGLÄRA FÖR M 2012-01-13 Skrivtid: 8.00 13.00 Hjälpmedel: Formelblad och räknedosa. Uppgifterna är inte ordnade efter svårighetsgrad. Börja varje ny uppgift på ett nytt blad och skriv
Lösningsförslag. Fysik del B2 för tekniskt / naturvetenskapligt basår / bastermin BFL 120 / BFL 111
 Linköpings Universitet Institutionen för Fysik, Kemi, och Biologi Avdelningen för Tillämpad Fysik Mike Andersson Lösningsförslag Fredagen den 29:e maj 2009, kl 08:00 12:00 Fysik del B2 för tekniskt / naturvetenskapligt
Linköpings Universitet Institutionen för Fysik, Kemi, och Biologi Avdelningen för Tillämpad Fysik Mike Andersson Lösningsförslag Fredagen den 29:e maj 2009, kl 08:00 12:00 Fysik del B2 för tekniskt / naturvetenskapligt
Laboration Svängningar
 Laboration Svängningar Laboranter: Fredrik Olsen Roger Persson Utförande datum: 2007-11-22 Inlämningsdatum: 2007-11-29 Fjäder Högtalarmembran Stativ Fjäder Ultraljudssensor Försökets avsikt Syftet med
Laboration Svängningar Laboranter: Fredrik Olsen Roger Persson Utförande datum: 2007-11-22 Inlämningsdatum: 2007-11-29 Fjäder Högtalarmembran Stativ Fjäder Ultraljudssensor Försökets avsikt Syftet med
Uppgifter 2 Grundläggande akustik (II) & SDOF
 Uppgifter Grundläggande akustik (II) & SDOF. Två partiklar rör sig med harmoniska rörelser. = 0 u ( Acos( där u ( Acos( t ) 6 a. Vad är frekvensen för de båda rörelserna? b. Vad är periodtiden? c. Den
Uppgifter Grundläggande akustik (II) & SDOF. Två partiklar rör sig med harmoniska rörelser. = 0 u ( Acos( där u ( Acos( t ) 6 a. Vad är frekvensen för de båda rörelserna? b. Vad är periodtiden? c. Den
Tentamen i Vågor och Optik 5hp F, Q, kandfys, gylärfys-programm, den 11. juni 2010
 Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 8-13 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
Uppsala Universitet Fysiska Institutionen Laurent Duda Tentamen i Vågor och Optik 5hp Skrivtid kl. 8-13 Hjälpmedel: Räknedosa, Physics Handbook eller motsvarande (även Mathematical Handbook är tillåten)
KOMIHÅG 12: Ekvation för fri dämpad svängning: x + 2"# n
 KOMIHÅG 1: ------------------------------------------------------ Ekvation för fri dämpad svängning: x + "# n x + # n x = a, Tre typer av dämpning: Svag, kritisk och stark. 1 ------------------------------------------------------
KOMIHÅG 1: ------------------------------------------------------ Ekvation för fri dämpad svängning: x + "# n x + # n x = a, Tre typer av dämpning: Svag, kritisk och stark. 1 ------------------------------------------------------
Vinkelupplösning, exempel hålkameran. Vinkelupplösning När är två punkter upplösta? FAF260. Lars Rippe, Atomfysik/LTH 1. Böjning i en spalt
 Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 10,5 högskolepoäng, FK4009 Tisdagen den 17 juni 2008 kl 9-15
 FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 1,5 högskolepoäng, FK49 Tisdagen den 17 juni 28 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare
FYSIKUM STOCKHOLMS UNIVERSITET Tentamensskrivning i Vågrörelselära och optik, 1,5 högskolepoäng, FK49 Tisdagen den 17 juni 28 kl 9-15 Hjälpmedel: Handbok (Physics handbook eller motsvarande) och räknare
INSTITUTIONEN FÖR FYSIK. Hej!
 Hej! Nedan finns de olika fysikaliska fenomen vi provade och försökte förklara under denna workshop. Har du frågor om någon av delarna så är du välkommen att höra av dig och jag hoppas du har nytta av
Hej! Nedan finns de olika fysikaliska fenomen vi provade och försökte förklara under denna workshop. Har du frågor om någon av delarna så är du välkommen att höra av dig och jag hoppas du har nytta av
Gauss Linsformel (härledning)
 α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
α α β β S S h h f f ' ' S h S h f S h f h ' ' S S h h ' ' f f S h h ' ' 1 ' ' ' f S f f S S S ' 1 1 1 S f S f S S 1 ' 1 1 Gauss Linsformel (härledning) Avbilding med lins a f f b Gauss linsformel: 1 a
E-strängen rör sig fyra gånger så långsamt vid samma transversella kraft, accelerationen. c) Hur stor är A-strängens våglängd?
 Problem. Betrakta en elgitarr. Strängarna är 660 mm långa. Stämningen är E-A-d-g-b-e, det vill säga att strängen som ger tonen e-prim (330 Hz) ligger två oktav högre i frekvens än E-strängen. Alla strängar
Problem. Betrakta en elgitarr. Strängarna är 660 mm långa. Stämningen är E-A-d-g-b-e, det vill säga att strängen som ger tonen e-prim (330 Hz) ligger två oktav högre i frekvens än E-strängen. Alla strängar
Observera att uppgifterna inte är ordnade efter svårighetsgrad!
 TENTAMEN I FYSIK FÖR n1, 19 DECEMBER 2003 Skrivtid: 14.00-19.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och försedda med svar. Kladdblad
TENTAMEN I FYSIK FÖR n1, 19 DECEMBER 2003 Skrivtid: 14.00-19.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och försedda med svar. Kladdblad
Mekaniska vågor. Emma Björk
 Mekaniska vågor Emma Björk Olika typer av vågfenomen finns överallt! Mekaniska vågor Ljudvågor Havsvågor Seismiska vågor Vågor på sträng Elektromagnetiska vågor Ljus Radiovågor Mikrovågor IR UV Röntgenstrålning
Mekaniska vågor Emma Björk Olika typer av vågfenomen finns överallt! Mekaniska vågor Ljudvågor Havsvågor Seismiska vågor Vågor på sträng Elektromagnetiska vågor Ljus Radiovågor Mikrovågor IR UV Röntgenstrålning
Gunga med Galileo matematik för hela kroppen
 Ann-Marie Pendrill Gunga med Galileo matematik för hela kroppen På en lekplats eller i en nöjespark finns möjlighet att påtagligt uppleva begrepp från fysik och matematik med den egna kroppen. Med hjälp
Ann-Marie Pendrill Gunga med Galileo matematik för hela kroppen På en lekplats eller i en nöjespark finns möjlighet att påtagligt uppleva begrepp från fysik och matematik med den egna kroppen. Med hjälp
Dopplerradar. Ljudets böjning och interferens.
 Dopplerradar. Ljudets böjning och interferens. Förberedelser Läs i vågläraboken om interferens (sid 60 70), svävning (sid 71 72), dopplereffekt (sid 83 86), ljudreflektioner i ett rum (sid 138 140), böjning
Dopplerradar. Ljudets böjning och interferens. Förberedelser Läs i vågläraboken om interferens (sid 60 70), svävning (sid 71 72), dopplereffekt (sid 83 86), ljudreflektioner i ett rum (sid 138 140), böjning
WALLENBERGS FYSIKPRIS
 WALLENBERGS FYSKPRS FNALTÄVLNG 3 maj 2014 SVENSKA FYSKERSAMFUNDET LÖSNNGSFÖRSLAG 1. a) Fasförskjutningen ϕ fås ur P U cosϕ cosϕ 1350 1850 ϕ 43,1. Ett visardiagram kan då ritas enligt figuren nedan. U L
WALLENBERGS FYSKPRS FNALTÄVLNG 3 maj 2014 SVENSKA FYSKERSAMFUNDET LÖSNNGSFÖRSLAG 1. a) Fasförskjutningen ϕ fås ur P U cosϕ cosϕ 1350 1850 ϕ 43,1. Ett visardiagram kan då ritas enligt figuren nedan. U L
Ex 1. En fjäder som belastas med en massa av 5 kg töjs ut 6 cm. Beräkna dess fjäderkonstant.
 1. Mekanisk svängningsrörelse Olika typer av mekaniska svängningar och vågrörelser möter oss överallt i vardagen allt från svajande höghus till telefoner med vibrationen påslagen hör till denna kategori.
1. Mekanisk svängningsrörelse Olika typer av mekaniska svängningar och vågrörelser möter oss överallt i vardagen allt från svajande höghus till telefoner med vibrationen påslagen hör till denna kategori.
WALLENBERGS FYSIKPRIS
 WALLENBERGS FYSIKPRIS KVALIFICERINGSTÄVLING 24 januari 2013 SVENSKA FYSIKERSAMFUNDET LÖSNINGSFÖRSLAG 1. (a) Ljudhastigheten i is är 180 m 55 10 3 s 3,27 103 m/s. Ur diagrammet avläser vi att det tar 1,95
WALLENBERGS FYSIKPRIS KVALIFICERINGSTÄVLING 24 januari 2013 SVENSKA FYSIKERSAMFUNDET LÖSNINGSFÖRSLAG 1. (a) Ljudhastigheten i is är 180 m 55 10 3 s 3,27 103 m/s. Ur diagrammet avläser vi att det tar 1,95
Övning 9 Tenta från Del A. Vägg på avståndet r = 2.0 m och med reflektansen R = 0.9. Lambertspridare.
 Övning 9 Tenta från 2016-08-24 Del A 1.) Du lyser med en ficklampa rakt mot en vit vägg. Vilken luminans får väggen i mitten av det belysta området? Ficklampan har en ljusstyrka på 70 cd och du står 2.0
Övning 9 Tenta från 2016-08-24 Del A 1.) Du lyser med en ficklampa rakt mot en vit vägg. Vilken luminans får väggen i mitten av det belysta området? Ficklampan har en ljusstyrka på 70 cd och du står 2.0
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
Datum: , , , ,
 RR:1 Instruktion till laborationen ROTERANDE REFERENSSYSTEM Författare: Lennart Selander, Svante Svensson Datum: 2000-02-21, 2004-12-02, 2006-12-01, 2012-02-03, 2013-01-22 Mål Att få erfarenhet av de fenomen
RR:1 Instruktion till laborationen ROTERANDE REFERENSSYSTEM Författare: Lennart Selander, Svante Svensson Datum: 2000-02-21, 2004-12-02, 2006-12-01, 2012-02-03, 2013-01-22 Mål Att få erfarenhet av de fenomen
Kapitel 33 The nature and propagation of light. Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion)
 Kapitel 33 The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Kapitel 33 The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Repetition Ljus - Fy2!!
 Repetition Ljus - Fy2 Egenskaper ör : Ljus är inte en mekanisk vågrörelse. Den tar sig ram utan problem även i vakuum och behöver alltså inget medium. Exakt vilken typ av vågrörelse är återkommer vi till
Repetition Ljus - Fy2 Egenskaper ör : Ljus är inte en mekanisk vågrörelse. Den tar sig ram utan problem även i vakuum och behöver alltså inget medium. Exakt vilken typ av vågrörelse är återkommer vi till
2. Spetsen på en symaskinsnål rör sig i en enkel harmonisk rörelse med frekvensen f = 5,0 Hz. Läget i y-led beskrivs alltså av uttrycket
 TENTAMEN I FYSIK FÖR n1, 14 JANUARI 2011 Skrivtid: 08.00-13.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och försedda med svar. Kladdblad
TENTAMEN I FYSIK FÖR n1, 14 JANUARI 2011 Skrivtid: 08.00-13.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och försedda med svar. Kladdblad
Miniräknare, formelsamling
 Umeå Universitet TENTAMEN Linje: Kurs: Hjälpmedel: Fysik B Miniräknare, formelsamling Lärare: Joakim Lundin Datum: 09-10-29 Tid: 9.00-15.00 Kod:... Grupp:... Poäng:... Betyg U G VG... Tentamen i Fysik
Umeå Universitet TENTAMEN Linje: Kurs: Hjälpmedel: Fysik B Miniräknare, formelsamling Lärare: Joakim Lundin Datum: 09-10-29 Tid: 9.00-15.00 Kod:... Grupp:... Poäng:... Betyg U G VG... Tentamen i Fysik
Föreläsning 7: Antireflexbehandling
 1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
1 Föreläsning 7: Antireflexbehandling När strålar träffar en yta vet vi redan hur de bryts (Snells lag) eller reflekteras (reflektionsvinkeln lika stor som infallsvinkeln). Nu vill vi veta hur mycket som
! = 0. !!!"ä !"! +!!!"##$%
 TENTAMEN I FYSIK FÖR n1 3 MAJ 2011 Skrivtid: 08.00-13.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och för- sedda med svar. Kladdblad
TENTAMEN I FYSIK FÖR n1 3 MAJ 2011 Skrivtid: 08.00-13.00 Hjälpmedel: Formelblad och räknare. Börja varje ny uppgift på nytt blad. Lösningarna ska vara väl motiverade och för- sedda med svar. Kladdblad
The nature and propagation of light
 Ljus Emma Björk The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
Ljus Emma Björk The nature and propagation of light Elektromagnetiska vågor Begreppen vågfront och stråle Reflektion och brytning (refraktion) Brytningslagen (Snells lag) Totalreflektion Polarisation Huygens
FYSIK ÅK 9 AKUSTIK OCH OPTIK. Fysik - Måldokument Lena Folkebrant
 Fysik - Måldokument Lena Folkebrant FYSIK ÅK 9 AKUSTIK OCH OPTIK Ljud är egentligen tryckförändringar i något material. För att ett ljud ska uppstå måste något svänga eller vibrera. När en gitarrsträng
Fysik - Måldokument Lena Folkebrant FYSIK ÅK 9 AKUSTIK OCH OPTIK Ljud är egentligen tryckförändringar i något material. För att ett ljud ska uppstå måste något svänga eller vibrera. När en gitarrsträng
Ämnesområde Hörselvetenskap A Kurs Akustik och ljudmiljö, 7 hp Kurskod: HÖ1015 Tentamenstillfälle 4
 IHM Kod: Ämnesområde Hörselvetenskap A Kurs Akustik och ljudmiljö, 7 hp Kurskod: HÖ115 Tentamenstillfälle 4 Datum 213-11-7 Tid 4 timmar Kursansvarig Susanne Köbler Tillåtna hjälpmedel Miniräknare Linjal
IHM Kod: Ämnesområde Hörselvetenskap A Kurs Akustik och ljudmiljö, 7 hp Kurskod: HÖ115 Tentamenstillfälle 4 Datum 213-11-7 Tid 4 timmar Kursansvarig Susanne Köbler Tillåtna hjälpmedel Miniräknare Linjal
Vinkelupplösning, exempel hålkameran. Vinkelupplösning När är två punkter upplösta? FAF260. Lars Rippe, Atomfysik/LTH 1. Böjning i en spalt
 Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Kursavsnitt Böjning och interferens Böjning i en spalt bsin m m 1,... 8 9 Böjning i en spalt Böjning i cirkulär öppning med diameter D Böjningsminimum då =m Första min: Dsin 1. 10 11 Vinkelupplösning,
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 33 - Ljus 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Vågrörelselära och optik Kapitel 33 - Ljus 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel
Mål med temat vad är ljud?
 Vad är ljud? När vi hör är det luftens molekyler som har satts i rörelse. När en mygga surrar och låter är det för att den med sina vingar puttar på luften. När en högtalare låter är det för att den knuffar
Vad är ljud? När vi hör är det luftens molekyler som har satts i rörelse. När en mygga surrar och låter är det för att den med sina vingar puttar på luften. När en högtalare låter är det för att den knuffar
Geometrisk optik reflektion och brytning. Optiska system F9 Optiska instrument. Elektromagnetiska vågor. Det elektromagnetiska spektrumet FAF260
 Geometrisk optik reflektion oh brytning Geometrisk optik F7 Reflektion oh brytning F8 Avbildning med linser Plana oh buktiga speglar Optiska system F9 Optiska instrument 1 2 Geometrisk optik reflektion
Geometrisk optik reflektion oh brytning Geometrisk optik F7 Reflektion oh brytning F8 Avbildning med linser Plana oh buktiga speglar Optiska system F9 Optiska instrument 1 2 Geometrisk optik reflektion
Laborationer i OPTIK och AKUSTIK (NMK10) Augusti 2003
 TEKNISKA HÖGSKOLAN I LINKÖPING Institutionen för teknik och naturvetenskap Campus Norrköping Igor Zozoulenko Laborationer i OPTIK och AKUSTIK (NMK10) Augusti 2003 Laboration 1: Ljudhastigheten i luft;
TEKNISKA HÖGSKOLAN I LINKÖPING Institutionen för teknik och naturvetenskap Campus Norrköping Igor Zozoulenko Laborationer i OPTIK och AKUSTIK (NMK10) Augusti 2003 Laboration 1: Ljudhastigheten i luft;
Tentamen i Fysik för π,
 KURSLABORATORET FYSK, LTH Tentamen i Fysik för π, 386 SKRVTD: 8 3 HJÄLPMEDEL: UTDELAT FORMELBLAD, GODKÄND RÄKNARE. LÖSNNGAR: BÖRJA VARJE NY UPPGFT PÅ NYTT BLAD OCH SKRV BARA PÅ EN SDA. LÖSNNGARNA SKA VARA
KURSLABORATORET FYSK, LTH Tentamen i Fysik för π, 386 SKRVTD: 8 3 HJÄLPMEDEL: UTDELAT FORMELBLAD, GODKÄND RÄKNARE. LÖSNNGAR: BÖRJA VARJE NY UPPGFT PÅ NYTT BLAD OCH SKRV BARA PÅ EN SDA. LÖSNNGARNA SKA VARA
