Detta är föreläsningsanteckningar från Jakob Nordströms föreläsning om Expandergrafer,
|
|
|
- Jonas Vikström
- för 7 år sedan
- Visningar:
Transkript
1 Detta är föreläsningsanteckningar från Jakob Nordströms föreläsning om Expandergrafer, torsdag 24 mars Introduktion På en intuitiv nivå är en expandergraf en gles men spretig graf, en graf med relativt få kanter men relativt korta stigar mellan varje par av hörn. Expandergrafer har väldigt många tillämpningsområden. Några av dessa är: Nätverksdesign Om man är intresserad av att konstruera robusta nätverk, där det finns stigar mellan varje par av noder även om vissa noder försvinner, är expandergrafer lämpliga. Slumpreduktion av algoritmer Mer om detta i Douglas anteckningar från en av Johans föreläsningar. Felrättande koder Mer om detta i avsnitt 4. Icke-approximation Expandergrafer är bl.a. användbara för att visa att det finns en konstant δ>0 så att överbestämda linjära ekvationssystem över de rationella talen med m ekvationer inte kan approximeras inom m δ (där måttet är antalet satisfierade ekvationer). Kryptografi Beviskomplexitet 2 Notation och definitioner Så länge inte annat uttryckligen sägs kommer G i dessa anteckningar att beteckna en d-reguljär oriktad graf G =(V,E) med hörnmängd resp. kantmängd V = V (G),E = E(G), där vi även tillåter multipla kanter och öglor (loopar). För en mängd S betecknar S = V (G) \ S komplementet av S i V (G). Såvida inget annat sägs kommer vi att reservera n för n = V (G). För två (inte nödvändigtvis disjunkta) mängder S, T betecknar vi mängden kanter mellan S och T som E(S, T )={ (u, v) E(G) u S, v T }. (1) Definition 1. Kantranden av S är kanterna som leder ut från S, d.v.s. Definition 2. G har kantexpansion (δ, ɛ) om S = E(S, S). (2) min S / S ɛ (3) S δn Med kantexpansionen h(g) för G åsyftar vi maximalt möjligt ɛ för δ =1/2, d.v.s. h(g) = min S / S, (4) S n/2 1/11
2 Figur 1: Petersengrafen Exempel 1. Den kompletta (n 1)-reguljära grafen K n har kantexpansion h(k n )= n/2. Exempel 2. Den 3-reguljära Petersengrafen (se figur 1) har kantexpansion h =1. Exempel 3. Den m-reguljära booleska hyperkuben C m på n =2 m hörn har också kantexpansion h(c m )=1. Exempel 4. Om G inte är sammanhängande gäller h(g) =0. Det vi är ute efter (expandergrafer), är grafer med hög kantexpansion, men med så få kanter (d.v.s. lågt värde på d) som möjligt. Definition 3. En familj av expandergrafer är en familj {G i } i N av grafer sådan att det finns d och ɛ>0 sådana att 1. G i är d-reguljär för alla i. 2. V (G i ) = n i för n i 1 <n i n 2 i 1, säg. 3. h(g i ) ɛ för alla i Observera att vi förvisso i exempel 1 och 3 hade oändliga familjer av grafer med stor kantexpansion, men att gradtalet d inte var konstant. Definition 4. En familj expandergrafer är explicit om varje G i kan konstrueras i tid polynomiell i n i (av en deterministisk Turingmaskin). Definition 5. En familj expandergrafer är jätteexplicit (eng. very explicit ) om vi i polylogaritmisk tid (med en deterministisk Turingmaskin) i n i kan beräkna den j:te (1 j d) grannen till en godtycklig nod v V (G i ). Exempel 5. Låt G i =(V i,e i ) med V i = Z i Z i.från[x, y] V i drar vi kanter till [x + y, y], [x y, y], [x, y + x], [x, y x]. Detta är en jättexplicit familj av d =4-reguljära expandergrafer. Exempel 6. För p primtal, låt G p =(V p,e p ) med V p = Z p.frånx V p drar vi kanter till x 1, x 1 och x 1, där operationerna och är addition och subtraktion i Z p 1 (representerat av talen 1 till p 1) ochx 1 är inversion. Detta är en jättexplicit familj av d =3-reguljära expandergrafer. Det är inte jättelätt att inse att dessa exempel faktiskt är expandergrafer. 2/11
3 2.1 Andramåttpåexpansion Det sätt på vilket vi hittills definierat expansion för en graf är på intet vis kanoniskt; det finns även andra rimliga sätt. Ett sådant är hörnexpansionen. Vi säger att G har hörnexpansion (δ, ɛ) om min N(S) / S ɛ, (5) S δ V (G) där N(S) ={ u finns kant från u till något hörn i S } är grannarna till S. En viktiga skillnad mot kantexpansionen är att vi i N(S) även inkluderar hörn vi kan nå med hjälp av kanter som går inom S. Detta har som följd att alla d-reguljära grafer har hörnexpansion ɛ 1 för alla δ. En graf med god hörnexpansion har också bra kantexpansion: Påstående 1. Om G (d-reguljär) har hörnexpansion (δ, 1+ɛ) så har den kantexpansion (δ, ɛ). Bevis. Om N(S) (1 + ɛ) S måste S ha kanter till åtminstone ɛ S hörn utanför S, d.v.s. E(S, S) ɛ S. En något svagare koppling från kantexpansion till hörnexpansion ges av: Påstående 2. Om G (d-reguljär) har kantexpansion (δ, ɛ), så har G hörnexpansion ( ) δ 2+ɛ/d, 1+ɛ/d. Bevis. Antag motsatsen, att det finns en mängd S V (G) sådan att S δ/(2 + ɛ/d) V och N(S) < (1 + ɛ/d) S. LåtT = S N(S) (notera S T δ V. Alla kanter mellan T och T måste komma från N(S). Det finns totalt d N(S) < (d + ɛ) S kanter med något hörn i N(S), mend S av dem måste ha andra hörnet i S, varför vi får att E(T,T ) < (d + ɛ) S d S = ɛ S, (6) med andra ord E(T,T ) <ɛ, (7) T vilket motsäger att G är en (δ, ɛ)-kantexpander. En trevlig användning av hörnexpansion är att visa att en graf har låg diameter (d.v.s. längsta kortaste avstånd mellan två hörn i grafen): om G har hörnexpansion (δ, ɛ) så är det enkelt att visa att diametern av G är högst 2logn +logδ +log(1 δ). (8) log ɛ Det finns naturligtvis även fler sätt att definiera expansion på, man kan t.ex. tänka sig att definiera hörnexpansionen som minumum av N(S) \ S / S (d.v.s. hur många nya hörn vi kommer till) istället. De flesta (alla?) rimliga sätt att definiera expansion på hänger mer eller mindre ihop (som illustreras av påståendena 1 och 2 ovan), det gäller bara att man tänker sig för lite och är på det klara med vilken definition man använder. 3/11
4 2.2 Lite linjär algebra Ett viktigt verktyg för att arbeta med expandergrafer är linjär algebra, och i synnerhet grundläggande spektralteori. Vi fräschar upp de grundläggande definitionerna. Låt A och B vara reella n n-matriser. Definition 6. Om det finns µ R och en nollskild vektor v sådan att Av = µv kallas µ ett egenvärde till A och v är en motsvarande egenvektor. Definition 7. Det karaktäristiska polynomet till A är den formella determinanten c A (x) =det(xi A) (9) Egenvärdena till A är precis rötterna till c A (x). Definition 8. Egenrummet E µ för egenvärdet µ består av alla egenvektorer v till egenvärdet µ, samt nollvektorn v =0. Det är enkelt att verifiera att egenrummet E µ är ett delrum till R n.oma är symmetrisk gäller dessutom följande trevliga egenskaper: alla rötter till c A (x) (och därmed alla egenvärden) är reella. egenvektorer svarande mot olika egenvärden är linjärt obereonde. dimensionen för egenrummet E µ är multipliciteten för egenvärdet µ. Definition 9. A och B är similära om det finns en inverterbar matris P sådan att B = P 1 AP. Definition 10. A är diagonaliserbar om den är similär med någon diagonalmatris. Definition 11. A är ortogonal om A 1 = A T. Definition 12. A är ortogonalt diagonaliserbar om det finns en ortogonal matris P sådan att P 1 AP är en diagonalmatris. Similära matriser har samma uppsättning egenvärden. Notera att en diagonalmatris har sina egenvärden på diagonalen. Sats (Reella spektralsatsen). Låt A vara en reell n n-matris. Följande villkor är ekvivalenta: A har en ortonormal mängd egenvektorer (som är en bas för R n ). A är ortogonalt diagonaliserbar. A är symmetrisk. 3 Grannmatriser och egenvärden Grannmatrisen A(G) för G är en n n-matris där elementet a ij på rad i kolumn j är antalet kanter mellan i och j. Notera att grannmatrisen är symmetrisk och att den för en d-reguljär graf har varje rad- och kolumnsumma lika med d. Låt µ 1 µ 2... µ n vara egenvärdena till A(G). Vi kallar dessa G:s spektrum. 4/11
5 Påstående 3. µ 1 = d. Bevis. Observera att 1-vektorn är en egenvektor till A = A(G) med motsvarande egenvärde d. Det räcker alltså att visa att alla egenvärden har absolutbelopp begränsat av d. Låtv vara någon egenvektor till A med egenvärde µ. Låtv i vara den koordinat i v som har högst belopp. Vi har att den i:te koordinaten i A v uppfyller µv i = (A v) i = a ij v j v i a ij = d v i (10) så µ d, som önskat. j Påstående 4. Multipliciteten för egenvärdet d i A(G) är antalet sammanhängande komponenter i G. Bevis. Tag en egenvektor v med motsvarande egenvärde µ = d. Antag utan inskränkning att v har något positivt element (titta på v annars). Låt r = max v i,ochlåti = { i v i = r }. För i I gäller d v i =(A v) i = a ij v j j=1 j a ij r = d r = d v i (11) Sålunda måste likhet gälla i olikheten, m.a.o. måste vi ha v j = r för alla j så att a ij 0. Detta ger att alla kanter från i även har sin andra ändpunkt i I, varför I består av en eller flera sammanhängande komponenter av G. Låt G bestå av k sammanhängande komponenter G 1,...,G k av storlek V (G i ) = n i. Genom en lämplig numrering av noderna i G kan A(G) skrivas som A A A = , (12) A k där A i = A(G i ) är n i n i -grannmatrisen till G i.ivarjea i har egenvärdet d multiplicitet ett, eftersom den enda uppsättningen sammanhängande komponenter som kan väljas är G i självt och alla egenvektorer med egenvärde d därmed måste vara multipler av 1-vektorn. Men det karaktäristiska polynomet till A kan skrivas som k det(xi n A) = det(xi ni A i ). (13) Så multipliciteten för egenvärdet d i A är summan av multipliciteterna för d i de olika komponenterna, d.v.s. precis antalet komponenter. Påstående 5. Multipliciteten för egenvärdet d i A(G) är antalet sammanhängande bipartita komponenter i G. j=1 5/11
6 Bevis. Antag att µ n = d, och tag en motsvarande egenvektor v. I samma anda som det föregående beviset, låt r =max v i, och definiera mängderna I L = { i v i = r } och I R = { i v i = r }. Föri I L har vi dv i =(A v) i = a ij v j j=1 a ij ( r) = d r = d v i (14) j=1 På samma sätt som förut måste vi ha likhet i olikheten, och vi inser att alla utgående kanter från i måste ha sin ändpunkt i I R. På samma sätt inses att utgående kanter från noder i I R har sin ändpunkt i I L. Alltså utgör I L I R en eller flera bipartita sammanhängande komponenter till G. Resten av beviset är analogt med slutklämmen i föregående bevis. Definition 13. Spektralgapet för G är µ 1 µ 2 = d µ 2. Vi kommer också att vara intresserade av absolutbeloppen av egenvärdena till A(G), och kommer att beteckna dessa som λ 1,λ 2,...,λ n i fallande storleksordning. Vi har alltså λ 1 = µ 1 = d, λ 2 =max( µ 2, µ n ), ochsåvidare. Sats 1. För en d-reguljär graf G gäller d µ 2 h(g) 2d(d µ 2 ), (15) 2 där µ 2 är det näst största egenvärdet till A(G). Bevis av denna sats (eller liknande) kommer levereras i senare anteckningar av Douglas från en av Johans föreläsningar. Intuitivt säger satsen att grafer där andra egenvärdet är litet har bra expansionsegenskaper. En annan koppling mellan den näst största egenvärdet och egenskapen att se slumpvis ut ges av följande lemma, som säger att ju mindre det näst största egenvärdet är, desto närmare kommer antalet kanter mellan två godtyckliga mängder att vara det förväntade antalet kanter mellan dessa två mängder i en slumpgraf. Lemma 1. För alla S, T V (G) gäller d S T E(S, T ) n λ 2 S T (16) Bevis. Låt A = A(G). Vikanskriva E(S, T ) som E(S, T ) = χ S Aχ T, (17) där χ U är den karaktäristiska vektorn för delmängden U (d.v.s. element i i χ U är 1 om i U och 0 annars). Eftersom A är symmetrisk finns en ortonormal bas v 1,v 2,...,v n av egenvektorer, där v i är en egenvektor till µ i, och se till att välja basen så att v 1 =(1/ n, 1/ n,...,1/ n). Skriv χ S = χ T = a i v i b i v i 6/11
7 Vi får vilket ger A χ T = b i Av i = b i µ i v i, (18) E(S, T ) = χ S A χ T = a i b j µ j (v i v j )= a i b i µ i, (19) j=1 där vi utnyttjar att {v i } n är en ortonormal bas, d.v.s. att v i v j = { 1 om i = j 0 om i j. Vi har a 1 = χ S v 1 = S / n, och på samma sätt b 1 = T / n. Utnyttjar vi µ 1 = d får vi E(S, T ) d S T = a i b i µ i (20) n i=2 Tar vi absolutbelopp på detta får vi E(S, T ) d S T n = a i b i µ i λ 2 i=2 n i=2 a i b i, (21) eftersom µ i λ 2 för i 2. Låta =(a 1,...,a n ), b =(b 1,...,b n ).Cauchy- Swartz olikhet ger att och vi är klara. a i b i a b = S T, (22) i=2 4 Tillämpning: felrättande koder Vi erinrar oss att en felrättande kod är en mängd C {0, 1} n. Definition 14. Det relativa avståndet för en kod C är min x,y C,x y där d H (x, y) är Hammingavståndet. d H (x, y), (23) n Definition 15. Informationskvoten för en felrättande kod C är log 2 C /n. Definition 16. En kodfamilj {C n } är asymptotisk bra om alla koder har relativt avstånd och informationskvot större än någon positiv konstant. Definition 17. En felrättande kod är linjär om den är ett delrum till {0, 1} n betraktat som ett vektorrum över Z 2. 7/11
8 Ett meddelande kan kodas med en linjär kod i polynomiell tid, men avkodning är generellt sett (för meddelanden som är så förstörda att vi inte längre har unik avkodning) NP-svårt. Vårt mål för stunden är att konstruera asymptotiskt bra koder där unikt avkodbara ord kan avkodas i linjär tid. Låt G =(V L V R,E) vara en vänster-c-reguljär bipartit graf, V L = {a 1,...,a n }, V R = {b 1,...,b m }, m<n. Vi konstruerar en felrättande kod C {0, 1} n bestående av alla {x 1,...,x n } sådana att x i 0 (mod 2) (24) {a i,b j} E för alla 1 j m. Vifårm stycken villkor på pariteten av olika c-delmängder av variablerna. Varje sådant villkor kan högst halvera mängden giltiga kodord, varför C 2 n m. Definition 18. En bipartit graf G =(V L V R,E) är en (n, m, c, δ, ɛ)-bipartit expander om V L = n, V R = m, G är vänster-c-reguljär och för alla S V L med S δn gäller N(S) > ɛ S. Notera att vi här använder en variant av hörnexpansion anpassad för bipartita grafer. Sats 2. Om G är en (n, n/2,c,δ,3c/4)-bipartit expander, så är C konstruerad som ovan en kod med informationskvot 1/2 och relativt avstånd δ. Meddelanden på avstånd δ/2 från C kan avkodas i linjär tid. Bevis. Informationskvoten torde vara uppenbar. För att visa det relativa avståndet, antag motsatsen och tag x, y C med Hammingavstånd d H (x, y) <δn. Låt S = { i x i y i }.Dåbådex och y är kodord måste x i + y i 0 (mod 2) (25) {a i,b j} E för varje b j V R,menx i + y i 1 om och endast om a i S, varförviför b j V R måste ha 1 0 (mod 2). (26) a i S,(a i,b j) E För varje b j N(S) är summan ovan icke-tom, varför det för varje b j N(S) måste gå minst två kanter till noder i S. Sålunda har vi E(S, N(S)) 2N(S), vilket tack vare G:s expansionsegenskaper är åtminstone 3c S /2. Men detta motsäger att G är vänster-c-reguljär (vi borde ha E(S, N(S)) = c S ), varför vi drar slutsatsen att x, y C med d H (x, y) <δninte kan existera. Avkodningsalgoritmen går vi inte igenom i detalj. Huvudidén är att köra följande procedur: så länge det finns a i med en majoritet av icke-satisfierade grannar b j, flippa x i. Detta klarar indata på relativt avstånd δ/2 från C. Att inse att det kan implementeras i linjär tid är lite pyssligare, men detta är alltså möjligt. Med anledning av denna sats ovan känner vi oss motiverade att leta reda på en bra bipartit expander. Sats 3. För c>4 och lämpligt val av δ>0 är en slumpvis vald graf G en (n, n/2,c,δ,3c/4)-bipartit expander för alla tillräckligt stora n. 8/11
9 Bevis. Låt G vara en slumpgraf på hörmängden V L V R där vi för varje v V L väljer grannmängden N(v) V R oberoende och likformigt bland alla c- delmängder till V R. Låt P (S, M) =Pr G [N(S) M]. Enligt definitionen av bipartit expander gäller att G inte är en bipartit expander om det existerar en delmängd S V L sådan att S δn och N(S) ɛ S. Använder vi unionsgränsen för sannolikheter får vi Pr[G inte (n, n/2,c,δ,ɛ)-expander] P (S, M) (27) 1 s δn S V L M V R S =s M =ɛs Fixera S V L och M V R sådant att S = s och M = ɛs, ochnoteraatt ɛs < V R = n/2. Dåharvi (( ) ( )) s ( ) cs ɛs n/2 ɛs P (S, M) = /, (28) c c n/2 eftersom ( ) ( m k / n k) < (m/n) k för n>m>k. Pluggar vi in detta i ekvation (27) och uttnyttjar ɛ =3c/4 får vi ( )( )( ) cs n n/2 3cs (29) s 3cs/4 2n 1 s δn Varje term kan begränsas med hjälp av ( n k )( ) cs 3cs ( ne ( )( n n/2 s 3cs/4 2n = = ) ( ne ) k,ochvifår k ) ( ) s 3cs/4 ( ) cs ne/2 3cs s 3cs/4 2n [ ( ) 3c/4 ( ) ] c s ne 2ne 3cs s 3cs 2n [(n/s) 1 c/4 e 1+3c/4 (3c/2) c/4] s Då c>4 och s δn får vi att basen i ekvation (30) kan begränsas av (n/s) 1 c/4 e 1+3c/4 (3c/2) c/4 δ c/4 1 e 1+3c/4 (3c/2) c/4 (30) = K = K(δ, c) < 1, (31) om δ väljs tillräckligt litet. Stoppar vi in ekvationerna (30) och (31) i ekvation (29) erhåller vi till slut Pr[G inte (n, n/2,c,δ,ɛ)-expander] δ [(n/s) 1 c/4 e 1+3c/4 (3c/2) c/4] s n 1 c/4 e 1+3c/4 (3c/2) c/4 = n 1 c/4 e1+3c/4 (3c/2) c/4, (32) 1 K vilket går mot 0 då n går mot. Sålunda drar vi slutsatsen att en bipartit slumpgraf G med n+n/2 hörn och vänstergrad c>4 nästan säkert är en (n, n/2,c,δ,3c/4)-expander när n och δ tillräckligt litet (väldigt litet). i=0 K s 9/11
10 5 Deterministisk konstruktion av bra expander Ett problem med den bipartita expander vi konstruerade i föregående avsnitt är att vi med en viss (förvisso försumbart liten) sannolikhet kunde få en graf som inte är en expander, och att det inte finns något känt effektivt sätt att upptäcka detta. I detta avsnitt ger vi oss på att deterministiskt konstruera bra expandergrafer. Definition 19. En d-reguljär graf G är en Ramanujangraf om λ 2 2 d 1. Sats 4. För alla d>0, ɛ>0 gäller Pr G [λ 2 2 ] d 1+ɛ 1 n Ω( d) (33) Å ena sidan gör denna sats oss väldigt glada; nästan alla grafer är nästan Ramanujangrafer (och därmed bra expandergrafer enligt sats 1). Å andra sidan är vi inte ett dugg lyckligare, då detta precis som i föregående avsnitt bara ger oss möjlighet att konstruera grafer som med väldigt hög sannolikhet har bra expansionsegenskaper. Definition 20. Den normaliserade grannmatrisen för G är Â(G), därâ i,j är antalet kanter mellan i och j delat med valensen för v j. För en d-reguljärgrafgällerattâ(g) =A(G)/d, och att alla egenvärden skalats med en faktor 1/d, eftersom alla valenser är d.  kansessomenövergångsmatrisförenslumpvandringpåg: omp R n är en sannolikhetsfördelning så är  p fördelningen efter ett steg längs en slumpvis vald kant. Definition 21. En graf G är en [n, d, α]-expander om 1. n = V (G) 2. G är d-reguljär 3. λ 2 (Â) α Kopplingen till vår ursprungliga definition av expandergrafer (definition 3) ges av sats 1: vi har µ 2 (A) λ 2 (A) αd, varfören[n, d, α]-expander har h(g) (1 α) d 2. Definition 22. Kvadraten av en graf G är en ny graf G 2 =(V (G),E ),där u V har kanter till alla noder som kan nås i två steg i G, d.v.s. E = { (u, v) w s.a. (u, w), (w, v) E(G) } (34) Vi har A(G 2 )=A(G) 2, vilket ger att om G är en [n, d, α]-expander gäller att G 2 är en [n, d 2,α 2 ]-expander. 5.1 Sicksackprodukt Som vi såg i förra avsnittet kan vi på ett enkelt sätt från en expandergraf konstruera en ny expandergraf med bättre expansionegenskaper men mycket fler kanter genom en lämplig och naturlig definition av produkten av två grafer. 10 / 11
11 Vårt mål är nu att definiera en annan (ännu lämpligare men mindre naturlig) produkt på grafer, som rätt utnyttjad också kommer att hjälpa oss förbättra expansionen av en graf, men till mindre kostnad i antal kanter. Vi kommer att definiera sicksackprodukten G z H på grafer G och H som uppfyller G är V (H) -reguljär H är d-reguljär Definitionen av sicksackprodukten är en smula invecklad, så vi nämner först vad man kan använda den till. Sats (Sicksacksatsen). Låt G vara en [n, m, α]-expander och H en [m, d, β]- expander. Då är sicksackprodukten G z H en [nm, d 2,α+ β]-expander. Bevis av sicksacksatsen kommer att finnas i Gustavs anteckningar från Jakobs nästa föreläsning. Sicksacksatsen hjälper oss att hitta bra expandergrafer: Sats 5. Låt H vara en [d 4,d,1/4]-expander, och definiera G 1 = H 2 G i+1 = G 2 i z H. Då är G i en [d 4i,d 2, 1/2]-expander för alla i 1. Bevis. G 1 = H 2 är en [d 4,d 2, 1/16]-expander, och därmed även en [d 4,d 2, 1/2]- expander. Antag via induktion att G i är en [d 4i,d 2, 1/2]-expander. Då är G 2 i en [d 4i,d 4, 1/4]-expander. Antalet hörn i H är lika med valensen för G 2 i och vi får enligt sicksacksatsen att G i+1 är en [d 4i d 4,d 2, 1/4 +1/4]-expander, som önskat. Med detta trevliga resultat i bakhuvudet känner vi oss förhoppningsvis tillräckligt modiga för att definiera sicksackprodukten. Definition (Sicksackprodukt). Låt G vara en m-reguljär graf med n = V (G). Ordna kanterna ut från v V (G) som e 1 v,e 2 v,...,e m v (på något kanoniskt sätt). Låt H vara en d-reguljär graf med V (H) =[m]. Vi definierar sicksackprodukten G z H =(V [m],e ),där E = { ([v, i], [u, j]) k, l (i, k), (l, j) E(H) e k v = e l } u (35) Intuitivt ersätter vi varje nod v i G meden minikopia H v av H, ochdraren kant från ett hörn i i H v till ett hörn j i H u om (v, u) är en kant i G och det finns k i H v så att (i, k) är en kant i H v och den k:te kanten från v i G är (v, u), och det finns motsvarande l H u. 11 / 11
MVE022 Urval av bevis (på svenska)
 MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
MVE22 Urval av bevis (på svenska) J A S, VT 218 Sats 1 (Lay: Theorem 7, Section 2.2.) 1. En n n-matris A är inverterbar precis när den är radekvivalent med indentitesmatrisen I n. 2. När så är fallet gäller
Crash Course Algebra och geometri. Ambjörn Karlsson c januari 2016
 Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
Crash Course Algebra och geometri Ambjörn Karlsson c januari 2016 ambjkarlsson@gmail.com 1 Contents 1 Projektion och minsta avstånd 4 2 Geometriska avbildningar och avbildningsmatriser 5 3 Kärnan 6 3.1
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A. (1 p) (c) Bestäm avståndet mellan A och linjen l.
 SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF64 Algebra och geometri Lösningsförslag till tentamen 5.6. DEL A. Betrakta följande punkter i rummet: A = (,, ), B = (,, ) och C = (,, ). (a) Ange en parametrisk ekvation för linjen l som går genom B
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SF1624 Algebra och geometri Lösningsförslag till tentamen 14129 DEL A 1 (a) Bestäm linjen genom punkterna A = (,, 1) och B = (2, 4, 1) (1 p) (b) Med hjälp av projektion kan man bestämma det kortaste avståndet
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
SF1624 Algebra och geometri Lösningsförslag till tentamen 2013-10-28 DEL A 1. Vi har matriserna 1 1 1 1 1 0 3 0 A = 1 1 1 1 1 1 1 1 och E = 0 0 0 1 0 0 1 0. 1 0 0 1 0 1 0 0 (a) Bestäm vilka elementära
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
SF64 Algebra och geometri Lösningsförslag till tentamen 04-05-0 DEL A. Planet P innehåller punkterna (,, 0), (0, 3, ) och (,, ). (a) Bestäm en ekvation, på formen ax + by + cz + d = 0, för planet P. (
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng.
 ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
ATM-Matematik Mikael Forsberg 34-4 3 3 Matematik med datalogi, mfl. Linjär algebra mag4 6 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift
Lösningar till utvalda uppgifter i kapitel 8
 Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
Lösningar till utvalda uppgifter i kapitel 8 8. Alla vektorer som är normaler till planet, d v s vektorer på formen (0 0 z) t, avbildas på nollvektorn. Dessa kommer därför att vara egenvektorer med egenvärdet
SF1624 Algebra och geometri Tentamen Torsdag, 17 mars 2016
 SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
SF4 Algebra och geometri Tentamen Torsdag, 7 mars Skrivtid: 8:-: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på tentamen
Övningar. MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik. Linjär algebra 2. Senast korrigerad:
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Avd. Matematik Linjär algebra 2 Senast korrigerad: 2006-02-10 Övningar Linjära rum 1. Låt v 1,..., v m vara vektorer i R n. Ge bevis eller motexempel till
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
SF64 Algebra och geometri Lösningsförslag till tentamen 533 DEL A Planet H ges av ekvationen 3x y + 5z + a) Bestäm en linje N som är vinkelrät mot H ( p) b) Bestäm en linje L som inte skär planet H ( p)
PCP-satsen på kombinatoriskt manér
 austrin@kth.se Teorigruppen Skolan för Datavetenskap och Kommunikation 2005-10-24 Agenda 1 Vad är ett bevis? Vad är ett PCP? PCP-satsen 2 Vad, hur och varför? Lite definitioner Huvudresultatet 3 Ännu mer
austrin@kth.se Teorigruppen Skolan för Datavetenskap och Kommunikation 2005-10-24 Agenda 1 Vad är ett bevis? Vad är ett PCP? PCP-satsen 2 Vad, hur och varför? Lite definitioner Huvudresultatet 3 Ännu mer
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA702) måndagen den 30 maj 2005 Uppgift. Bestäm samtliga vektorer
1. (Dugga 1.1) (a) Bestäm v (3v 2u) om v = . (1p) and u =
 Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, 5 eller underkänd, där 5 är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
SF1624 Algebra och geometri Lösningsförslag till tentamen 2010-10-22 DEL A (1) Uttrycket (x, y, z) (1, 1, 1) + s(1, 3, 0) + t(0, 5, 1) definierar ett plan W i rummet där s och t är reella parametrar. (a)
Basbyten och linjära avbildningar
 Föreläsning 11, Linjär algebra IT VT2008 1 Basbyten och linjära avbildningar Innan vi fortsätter med egenvärden så ska vi titta på hur matrisen för en linjär avbildning beror på vilken bas vi använder.
Föreläsning 11, Linjär algebra IT VT2008 1 Basbyten och linjära avbildningar Innan vi fortsätter med egenvärden så ska vi titta på hur matrisen för en linjär avbildning beror på vilken bas vi använder.
Egenvärden och egenvektorer
 Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Föreläsning 10, Linjär algebra IT VT2008 1 Egenvärden och egenvektorer Denition 1 Antag att A är en n n-matris. En n-vektor v 0 som är sådan att A verkar som multiplikation med ett tal λ på v, d v s Av
Övningar. c) Om någon vektor i R n kan skrivas som linjär kombination av v 1,..., v m på precis ett sätt så. m = n.
 Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Övningar Linjära rum 1 Låt v 1,, v m vara vektorer i R n Ge bevis eller motexempel till följande påståenden Satser ur boken får användas a) Om varje vektor i R n kan skrivas som linjär kombination av v
Diagonalisering och linjära system ODE med konstanta koe cienter.
 Diagonalisering och linjära system ODE med konstanta koe cienter. Variabelbyte i linjära system di erentialekvationer. Målet med det kapitlet i kursen är att lösa linjära system di erentialekvationer på
Diagonalisering och linjära system ODE med konstanta koe cienter. Variabelbyte i linjära system di erentialekvationer. Målet med det kapitlet i kursen är att lösa linjära system di erentialekvationer på
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A
 SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till tentamen Fredagen den 23 oktober, 2009 DEL A (1) (a) Bestäm de övriga rötterna till ekvationen z 3 11z 2 + 43z 65 = 0 när det är känt att en av rötterna
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A (1) Vid lösningen av ekvationssystemet x 1 3x 2 +3x 3 4x 4 = 1, x 2 +x 3 x 4 = 0, 4x 1 +x 2 x 3 2x 4 = 5, kommer man genom Gausselimination
November 24, Egenvärde och egenvektor. (en likformig expansion med faktor 2) (en rotation 30 grader moturs)
 Fö : November 4, 7 Egenvärde och egenvektor Definition s 9: Låt A resp T : R n R n vara en n n-matris resp en linjär avbildning En icke-trivial vektor v R n kallas en egenvektor till A resp till T med
Fö : November 4, 7 Egenvärde och egenvektor Definition s 9: Låt A resp T : R n R n vara en n n-matris resp en linjär avbildning En icke-trivial vektor v R n kallas en egenvektor till A resp till T med
6.1 Skalärprodukt, norm och ortogonalitet. TMV141 Linjär algebra E VT 2011 Vecka 6. Lärmål 6.1. Skalärprodukt. Viktiga begrepp
 6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
6.1 Skalärprodukt, norm och ortogonalitet TMV141 Linjär algebra E VT 2011 Vecka 6 Skalärprodukt Norm/längd Normerad vektor/enhetsvektor Avståndet mellan två vektorer Ortogonala vektorer Ortogonala komplementet
Lösningsförslag till skrivningen i Vektorgeometri (MAA702) Måndagen den 13 juni 2005
 VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
VÄXJÖ UNIVERSITET Matematiska och systemtekniska institutionen Per-Anders Svensson Lösningsförslag till skrivningen i Vektorgeometri (MAA70) Måndagen den 13 juni 005 Uppgift 1. Lös ekvationssystemet AX
Egenvärden, egenvektorer
 Egenvärden, egenvektorer Om en matris är kvadratisk (dvs n n) kan vi beräkna egenvärden och egenvektorer till matrisen. Polynomet p(λ) = det(a λi) kallas det karakterisktiska polynomet för A. Ett nollställe
Egenvärden, egenvektorer Om en matris är kvadratisk (dvs n n) kan vi beräkna egenvärden och egenvektorer till matrisen. Polynomet p(λ) = det(a λi) kallas det karakterisktiska polynomet för A. Ett nollställe
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
SF64 Algebra och geometri Lösningsförslag till tentamen 0-0-0 DEL A De tre totalmatriserna 0 3 3 4 0 3 0 0 0 0, 0 3 0 4 4 0 3 0 3 0 0 0 0 och 0 3 0 4 0 3 3 0 0 0 0 0 svarar mot linjära ekvationssystem
Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA
 UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
UPPSALA UNIVERSITET Matematiska institutionen Volodymyr Mazorchuk Ryszard Rubinsztein Prov i matematik Civilingenjörsprogrammen EL, IT, K, X, ES, F, Q, W, Enstaka kurs LINJÄR ALGEBRA 007 08 16 Skrivtid:
SF1624 Algebra och geometri Lösningsförslag till modelltentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
SF624 Algebra och geometri Lösningsförslag till modelltentamen DEL A () (a) Använd Gauss-Jordans metod för att bestämma lösningsmängden till ekvationssystemet 2x + 4x 2 + 2x 3 + 2x 4 = 2, 3x + 6x 2 x 3
UPPSALA UNIVERSITET Matematiska institutionen Styf. Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 2004
 UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
UPPSALA UNIVERSITET Matematiska institutionen Styf Exempeltenta med lösningar Programmen EI, IT, K, X Linjär algebra juni 24 Skrivtid: Fem timmar. Tillåtna hjälpmedel: Skrivdon. Lösningarna skall vara
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Föreläsning I Timme I: Repetition av matriser, linjära ekvationssystem Linjärt ekvationssystem: x + y + z 3w = 3 2x + y + z 4w =
A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)
![A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p) A = (3 p) (b) Bestäm alla lösningar till Ax = [ 5 3 ] T.. (3 p)](/thumbs/93/112249032.jpg) SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
SF1624 Algebra och geometri Tentamen med lösningsförslag fredag, 21 oktober 216 1 Låt A = [ ] 4 2 7 8 3 1 (a) Bestäm alla lösningar till det homogena systemet Ax = [ ] T (3 p) (b) Bestäm alla lösningar
Preliminärt lösningsförslag
 Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
Preliminärt lösningsförslag v4, 9 augusti 4 Högskolan i Skövde (SK) Tentamen i matematik Kurs: MA4G Linjär algebra MAG Linjär algebra för ingenjörer Tentamensdag: 4-8-6 kl 43-93 Hjälpmedel : Inga hjälpmedel
3 1 = t 2 2 = ( 1) ( 2) 1 2 = A(t) = t 1 10 t
 SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
SF624 Algebra och geometri Tentamen med lösningsförslag måndag, 3 mars 207 Betrakta vektorerna P =, Q = 3, u = Låt l vara linjen som går genom 2 0 P och Q och låt l 2 vara linjen som är parallell med u
Uppgifter, 2015 Tillämpad linjär algebra
 Geometri. Uppgifter, 25 Tillämpad linjär algebra. Uppgift. Låt (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av linjära
Geometri. Uppgifter, 25 Tillämpad linjär algebra. Uppgift. Låt (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av linjära
Grafer och grannmatriser
 Föreläsning 2, Linjär algebra IT VT2008 Som avslutning på kursen ska vi knyta samman linjär algebra med grafteori och sannolikhetsteori från första kursen. Resultatet blir så kallade slumpvandringar på
Föreläsning 2, Linjär algebra IT VT2008 Som avslutning på kursen ska vi knyta samman linjär algebra med grafteori och sannolikhetsteori från första kursen. Resultatet blir så kallade slumpvandringar på
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Egenvärden och egenvektorer. Linjär Algebra F15. Pelle
 Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
Egenvärden och egenvektorer Linjär Algebra F1 Egenvärden och egenvektorer Pelle 2016-03-07 Egenvärde och egenvektor Om A är en n n matris så kallas ett tal λ egenvärde och en kolonnvektor v 0 egenvektor
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
SF624 Algebra och geometri Lösningsförslag till tentamen 202-2-3 DEL A Betrakta punkterna A = (2, 2) och B = (6, 4) och linjen (, 3) + t(2, ) i planet (a) Det finns exakt en punkt P på linjen så att triangeln
TAMS79: Föreläsning 10 Markovkedjor
 TAMS79: Föreläsning 0 Markovkedjor Johan Thim december 08 0. Markovkedjor Vi ska nu betrakta en speciell tidsdiskret diskret stokastisk process, nämligen Markovkedjan. Vi börjar med en definition Definition.
TAMS79: Föreläsning 0 Markovkedjor Johan Thim december 08 0. Markovkedjor Vi ska nu betrakta en speciell tidsdiskret diskret stokastisk process, nämligen Markovkedjan. Vi börjar med en definition Definition.
SF1624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 2010 DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen Lördagen den 5 juni, 200 DEL A ( Betrakta det komplexa talet w = i. (a Skriv potenserna w n på rektangulär form, för n = 2,, 0,, 2. ( (b Bestäm
Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner. 2? Det är komplicerat att
 Egensystem Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner Potens av matris 2 6 Ex Givet matrisen A =, vad är A 2? Det är komplicerat att beräkna högre
Egensystem Vi skalla främst utnyttja omskrivning av en matris för att löas ett system av differentialekvaioner Potens av matris 2 6 Ex Givet matrisen A =, vad är A 2? Det är komplicerat att beräkna högre
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet
 Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Repetera hur man nner bas för rum som spänns upp av några vektorer Reptetera hur man nner bas för summa och snitt av delrum. Reptetera
Föreläsningsanteckningar Linjär Algebra II Lärarlyftet Per Alexandersson Repetera hur man nner bas för rum som spänns upp av några vektorer Reptetera hur man nner bas för summa och snitt av delrum. Reptetera
Multiplicera 7med A λ 1 I från vänster: c 1 (Av 1 λ 1 v 1 )+c 2 (Av 2 λ 1 v 2 )+c 3 (Av 3 λ 1 v 3 ) = 0
 Diagonalisering Anm. Begreppet diagonaliserbarhet är relevant endast för linjära avbildningar mellan rum av samma dimension, d.v.s. sådana som representeras av kvadratiska matriser. När vi i fortsättningen
Diagonalisering Anm. Begreppet diagonaliserbarhet är relevant endast för linjära avbildningar mellan rum av samma dimension, d.v.s. sådana som representeras av kvadratiska matriser. När vi i fortsättningen
Inför tentamen i Linjär algebra TNA002.
 Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
Inför tentamen i Linjär algebra TNA002. 1. Linjära ekvationssytem (a) Omskrivningen av ekvationssystem på matrisform samt utföra radoperationer. (b) De 3 typer av lösningar som dyker upp vid lösning av
. b. x + 2 y 3 z = 1 3 x y + 2 z = a x 5 y + 8 z = 1 lösning?
 Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Repetition, Matematik 2, linjär algebra 10 Lös ekvationssystemet 5 x + 2 y + 2 z = 7 a x y + 3 z = 8 3 x y 3 z = 2 b 11 Ange för alla reella a lösningsmängden till ekvationssystemet 2 x + 3 y z = 3 x 2
Lösningar till MVE021 Linjär algebra för I
 Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
Lösningar till MVE Linjär algebra för I 7-8-9 (a Vektorer är ortogonala precis när deras skalärprodukt är Vi har u v 8 5h + h h 5h + 6 (h (h När h och när h (b Låt B beteckna basen {v, v } Om vi sätter
Frågorna 1 till 6 ska svaras med ett kryss för varje korrekt påstående. Varje uppgift ger 1 poäng. Använd bifogat formulär för dessa 6 frågor.
 TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
TM-Matematik Mikael Forsberg 74-4 Matematik med datalogi, mfl. Linjär algebra ma4a 6 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje ny uppgift på
Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 9 juni 2011 kl 08.00-1.00. OBS: Inga hjälpmedel är tillåtna på tentamensskrivningen. Bonuspoäng
1 Linjära ekvationssystem. 2 Vektorer
 För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
För. 1 1 Linjära ekvationssystem Gaußelimination - sriv om systemet för att få ett trappformat system genom att: byta ordningen mellan ekvationer eller obekanta; multiplicera en ekvation med en konstant
Avsnitt 6, Egenvärden och egenvektorer. Redan första produktelementet avslöjar att matrisen inte är en ortogonal matris. En matris 1 0.
 Avsnitt Egenvärden och egenvektorer W Vilka av följande matriser är ortogonala? b d En matris A a a a n a a a n a a a n a m a m a mn är en ortogonal matris om dess kolumner bildar en ON-bas för rummet
Avsnitt Egenvärden och egenvektorer W Vilka av följande matriser är ortogonala? b d En matris A a a a n a a a n a a a n a m a m a mn är en ortogonal matris om dess kolumner bildar en ON-bas för rummet
SKRIVNING I VEKTORGEOMETRI
 SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
SKRIVNING I VEKTORGEOMETRI 201-0-0 14.00-17.00 Om inget annat uttryckligen sägs, kan koordinaterna för en vektor i antas vara givna i en ON-bas. Baser i rummet kan dessutom antas vara positivt orienterade.
Uppgifter, 2014 Tillämpad linjär algebra
 Geometri. Uppgifter, 24 Tillämpad linjär algebra. Uppgift. Låt A = (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av
Geometri. Uppgifter, 24 Tillämpad linjär algebra. Uppgift. Låt A = (,, ), B = (, 2, 3), C = (,, ) vara punkter i R 3. () Beskriva på parameter form alla plan som innehåler A, B och C. Ger ett system av
x 1(t) = x 2 (t) x 2(t) = x 1 (t)
 Differentialekvationer II Modellsvar till räkneövning 4 16.4. 218 (kl 12-14 B222) 1. Lös det linjära homogena DE-systemet x 1(t) = x 2 (t) x 2(t) = x 1 (t) med matrismetoden. Påminnelse: egenvärden och
Differentialekvationer II Modellsvar till räkneövning 4 16.4. 218 (kl 12-14 B222) 1. Lös det linjära homogena DE-systemet x 1(t) = x 2 (t) x 2(t) = x 1 (t) med matrismetoden. Påminnelse: egenvärden och
Uppsala Universitet Matematiska Institutionen Bo Styf. Sammanfattning av föreläsningarna
 Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
Uppsala Universitet Matematiska Institutionen Bo Styf LAoG I, 5 hp ES, KandMa, MatemA -9-6 Sammanfattning av föreläsningarna 3-7 Föreläsningarna 3 7, 8/ 5/ : Det viktigaste är här att du lär dig att reducera
A = v 2 B = = (λ 1) 2 16 = λ 2 2λ 15 = (λ 5)(λ+3). E 5 = Span C =
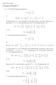 KTH Matematik Lösningar till Kapitel 7 A a Karakteristiska polynomet av detλi A det A λ λ λ b Egenvdena av A nollställen till karakteristiska polynomet alltså har A egenvdet λ c Motsvarande egenrum E lösningsrummet
KTH Matematik Lösningar till Kapitel 7 A a Karakteristiska polynomet av detλi A det A λ λ λ b Egenvdena av A nollställen till karakteristiska polynomet alltså har A egenvdet λ c Motsvarande egenrum E lösningsrummet
SF1624 Algebra och geometri Tentamen Torsdag, 9 juni 2016
 SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
SF624 Algebra och geometri Tentamen Torsdag, 9 juni 26 Skrivtid: 8: 3: Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del A på
Determinanter, egenvectorer, egenvärden.
 Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Determinanter, egenvectorer, egenvärden. Determinanter av kvadratiska matriser de nieras recursivt: först för matriser, sedan för matriser som är mest användbara. a b det = ad bc c d det a a a a a a a
Stöd inför omtentamen i Linjär algebra TNA002.
 LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
LINKÖPINGS UNIVERSITET ITN, Campus Norrköping Univ lekt George Baravdish Stöd inför omtentamen i Linjär algebra TNA002. Läsråd: Detta är ett stöd för dig som vill repetera inför en omtentamen. 1. Börja
y z 3 = 0 z 5 16 1 i )
 ATM-Matematik Mikael Forsberg 734-433 Sören Hector 7-46686 Rolf Källström 7-6939 Ingenjörer, Lantmätare och Distansstuderande, mfl. Linjär Algebra ma4a 4 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna
ATM-Matematik Mikael Forsberg 734-433 Sören Hector 7-46686 Rolf Källström 7-6939 Ingenjörer, Lantmätare och Distansstuderande, mfl. Linjär Algebra ma4a 4 3 Skrivtid: 9:-4:. Inga hjälpmedel. Lösningarna
Lite Linjär Algebra 2017
 Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
Lite Linjär Algebra 2017 Lektionsanteckningar och sammanfattning Johan Thim, MAI (johan.thim@liu.se) ū ū O z y ū // L : OP + t v x Ortogonalprojektion: ū // = ū v v v v, ū = ū ū //. Innehåll 1 Bakgrund
SF1624 Algebra och geometri Tentamen Onsdag, 13 januari 2016
 SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
SF624 Algebra och geometri Tentamen Onsdag, 3 januari 206 Skrivtid: 08:00 3:00 Tillåtna hjälpmedel: inga Examinator: Tilman Bauer Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. Del
SF1624 Algebra och geometri Lösningsförslag till tentamen DEL A
 SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
SF624 Algebra och geometri Lösningsförslag till tentamen 22--6 DEL A Planet H ges av ekvationen x + 2y + z =, och planet W ges på parameterform som 2t 4s, t + 2s där s och t är reella parametrar (a) Bestäm
1. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x 1 = (2, 3, 5), x 2 = (3, 1, 1) och x 3 = (1, 3, 0).
 N-institutionen Mikael Forsberg 06-64 89 6 Prov i matematik Matematik med datalogi, mfl. Linjär algebra mk06a Testtenta. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x = (,, 5),
N-institutionen Mikael Forsberg 06-64 89 6 Prov i matematik Matematik med datalogi, mfl. Linjär algebra mk06a Testtenta. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x = (,, 5),
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 2010 kl
 1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
1 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 15 mars 010 kl 14.00-19.00. Hjälpmedel: Inga hjälpmedel är tillåtna på tentamensskrivningen. Betygsgränser:
Vektorerna är parallella med planet omm de är vinkelräta mot planets normal, dvs mot
 Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
Kursen bedöms med betyg,, eller underkänd, där är högsta betyg. För godkänt betyg krävs minst poäng från uppgifterna -7. Var och en av dessa sju uppgifter kan ge maximalt poäng. För var och en av uppgifterna
DEL I 15 poäng totalt inklusive bonus poäng.
 Matematiska Institutionen KTH TENTAMEN i Linjär algebra, SF604, den 5 december, 2009. Kursexaminator: Sandra Di Rocco Svaret skall motiveras och lösningen skrivas ordentligt och klart. Inga hjälpmedel
Matematiska Institutionen KTH TENTAMEN i Linjär algebra, SF604, den 5 december, 2009. Kursexaminator: Sandra Di Rocco Svaret skall motiveras och lösningen skrivas ordentligt och klart. Inga hjälpmedel
Föreläsning 5: Grafer Del 1
 2D1458, Problemlösning och programmering under press Föreläsning 5: Grafer Del 1 Datum: 2006-10-02 Skribent(er): Henrik Sjögren, Patrik Glas Föreläsare: Gunnar Kreitz Den här föreläsningen var den första
2D1458, Problemlösning och programmering under press Föreläsning 5: Grafer Del 1 Datum: 2006-10-02 Skribent(er): Henrik Sjögren, Patrik Glas Föreläsare: Gunnar Kreitz Den här föreläsningen var den första
1. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x 1 = (2, 3, 5), x 2 = (3, 1, 1) och x 3 = (1, 3, 0).
 TM-Matematik Mikael Forsberg Linjär algebra mk4a Övningstenta LA-. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x = (,, ), x = (,, ) och x = (,, ).. För alla värden på parametern
TM-Matematik Mikael Forsberg Linjär algebra mk4a Övningstenta LA-. Bestäm volymen för den parallellepiped som ges av de tre vektorerna x = (,, ), x = (,, ) och x = (,, ).. För alla värden på parametern
SF1624 Algebra och geometri Lösningsförsag till modelltentamen
 SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
SF1624 Algebra och geometri Lösningsförsag till modelltentamen DEL A (1) a) Definiera begreppen rektangulär form och polär form för komplexa tal och ange sambandet mellan dem. (2) b) Ange rötterna till
. (2p) 2x + 2y + z = 4 y + 2z = 2 4x + 3y = 6
 Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Kursen bedöms med betyg, 4, 5 eller underkänd, där 5 är högsta betyg För godkänt betyg krävs minst 4 poäng från uppgifterna -7 Var och en av dessa sju uppgifter kan ge maximalt poäng För var och en av
Lösningsförslag till Tentamen i 5B1118 Diskret matematik 5p 14 augusti, 2002
 Institutionen för matematik, KTH Mats Boij och Niklas Eriksen Lösningsförslag till Tentamen i 5B1118 Diskret matematik 5p 14 augusti, 2002 1. Använd induktion för att visa att 8 delar (2n + 1 2 1 för alla
Institutionen för matematik, KTH Mats Boij och Niklas Eriksen Lösningsförslag till Tentamen i 5B1118 Diskret matematik 5p 14 augusti, 2002 1. Använd induktion för att visa att 8 delar (2n + 1 2 1 för alla
Material till kursen SF1679, Diskret matematik: Lite om kedjebråk. 0. Inledning
 Matematik, KTH Bengt Ek november 207 Material till kursen SF679, Diskret matematik: Lite om kedjebråk 0 Inledning Talet π (kvoten mellan en cirkels omkrets och dess diameter) är inte ett rationellt tal
Matematik, KTH Bengt Ek november 207 Material till kursen SF679, Diskret matematik: Lite om kedjebråk 0 Inledning Talet π (kvoten mellan en cirkels omkrets och dess diameter) är inte ett rationellt tal
Linjär algebra på 2 45 minuter
 Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
Linjär algebra på 2 45 minuter π n x F(x) Förberedelser inför skrivningen Den här genomgången täcker förstås inte hela kursen. Bra sätt att lära sig kursen: läs boken, diskutera med kompisar, gå igenom
1. (a) (1p) Undersök om de tre vektorerna nedan är linjärt oberoende i vektorrummet
 1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
1 Matematiska Institutionen, KTH Lösningar till tentamensskrivning på kursen Linjär algebra, SF1604, för CDA- TE, CTFYS och vissa CL, fredagen den 13 mars 015 kl 08.00-13.00. Examinator: Olof Heden. OBS:
LINJÄR ALGEBRA II LEKTION 6
 LINJÄR ALGEBRA II LEKTION 6 JOHAN ASPLUND INNEHÅLL 1 Inre produktrum 1 2 Cauchy-Schwarz olikhet 3 3 Ortogonala projektioner och Gram-Schmidts process 3 4 Uppgifter 4 61:13(a) 4 61:23(a) 4 61:29 5 62:7
LINJÄR ALGEBRA II LEKTION 6 JOHAN ASPLUND INNEHÅLL 1 Inre produktrum 1 2 Cauchy-Schwarz olikhet 3 3 Ortogonala projektioner och Gram-Schmidts process 3 4 Uppgifter 4 61:13(a) 4 61:23(a) 4 61:29 5 62:7
Del 1: Godkäntdelen. TMV142 Linjär algebra Z
 MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 130313 kl 0830 1230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV142 Linjär algebra Z Tentan
MATEMATIK Hjälpmedel: ordlistan från kurswebbsidan, ej räknedosa Chalmers tekniska högskola Datum: 130313 kl 0830 1230 Tentamen Telefonvakt: Christoffer Standar 0703-088304 TMV142 Linjär algebra Z Tentan
SF1624 Algebra och geometri
 SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
SF1624 Algebra och geometri Tjugofemte föreläsningen Mats Boij Institutionen för matematik KTH 10 december, 2009 Tentamens struktur Tentamen består av tio uppgifter uppdelade på två delar, Del A och Del
Modul 1: Komplexa tal och Polynomekvationer
 Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
Modul : Komplexa tal och Polynomekvationer. Skriv på formen a + bi, där a och b är reella, a. (2 + i)( 2i) 2. b. + 2i + 3i 3 4i + 2i 2. Lös ekvationerna a. (2 i)z = 3 + i. b. (2 + i) z = + 3i c. ( 2 +
ALA-c Innehåll. 1 Linearization and Stability Uppgift Uppgift Egenvärdesproblemet Uppgift
 Vecka ALA-c 6 Innehåll Linearization and Stability RÄKNEÖVNING VECKA. Uppgift 9........................................ Uppgift 9.5...................................... 5 Egenvärdesproblemet 9. Uppgift
Vecka ALA-c 6 Innehåll Linearization and Stability RÄKNEÖVNING VECKA. Uppgift 9........................................ Uppgift 9.5...................................... 5 Egenvärdesproblemet 9. Uppgift
Tentamen i Linjär algebra (TATA31/TEN1) ,
 Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN) 7 8 9, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst
Linköpings universitet Matematiska institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN) 7 8 9, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst
TMV206: Linjär algebra
 Matematiska vetenskaper Lösningsförslag till tentamen Chalmers tekniska högskola 2018-06-07, 14:00 18:00 TMV206: Linjär algera Uppgift 1 Linjerna skär varandra om det finns någon punkt (x,y, z) som uppfyller
Matematiska vetenskaper Lösningsförslag till tentamen Chalmers tekniska högskola 2018-06-07, 14:00 18:00 TMV206: Linjär algera Uppgift 1 Linjerna skär varandra om det finns någon punkt (x,y, z) som uppfyller
12. SINGULÄRA VÄRDEN. (u Av) u v
 . SINGULÄRA VÄRDEN Vårt huvudresultat sen tidigare är Sats.. Varje n n matris A kan jordaniseras, dvs det finns en inverterbar matris S sån att S AS J där J är en jordanmatris. Om u och v är två kolonnvektorer
. SINGULÄRA VÄRDEN Vårt huvudresultat sen tidigare är Sats.. Varje n n matris A kan jordaniseras, dvs det finns en inverterbar matris S sån att S AS J där J är en jordanmatris. Om u och v är två kolonnvektorer
1. (a) Bestäm alla värden på c som gör att matrisen A(c) saknar invers: 1 0 1. 1 c 1
 ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734-4 3 3 För ingenjörs- och distansstudenter Linjär Algebra ma4a 5 4 Skrivtid: :-4:. Inga hjälpmedel. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
Matrisexponentialfunktionen
 U.U.D.M. Project Report 206:2 Matrisexponentialfunktionen Neda Farzaneh Examensarbete i matematik, 5 hp Handledare: Martin Herschend Examinator: Jörgen Östensson Juni 206 Department of Mathematics Uppsala
U.U.D.M. Project Report 206:2 Matrisexponentialfunktionen Neda Farzaneh Examensarbete i matematik, 5 hp Handledare: Martin Herschend Examinator: Jörgen Östensson Juni 206 Department of Mathematics Uppsala
x + y z = 2 2x + 3y + z = 9 x + 3y + 5z = Gauss-Jordan elemination ger: Area = 1 2 AB AC = 4. Span(1, 1 + x, x + x 2 ) = P 2.
 1 Matematiska Institutionen KTH Exam for the course Linjär algebra, 5B1307, Januari 14, 008, 14:00-19:00 Kursexaminator: Sandra Di Rocco Minst 15 poäng ger betyg 3, minst poäng ger betyg 4 och mins 8 poäng
1 Matematiska Institutionen KTH Exam for the course Linjär algebra, 5B1307, Januari 14, 008, 14:00-19:00 Kursexaminator: Sandra Di Rocco Minst 15 poäng ger betyg 3, minst poäng ger betyg 4 och mins 8 poäng
LÖSNINGAR LINJÄR ALGEBRA LUNDS TEKNISKA HÖGSKOLA MATEMATIK
 LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
LUNDS TEKNISKA HÖGSKOLA MATEMATIK LÖSNINGAR LINJÄR ALGEBRA 2017-10-2 1 Om vi skriver ekvationssystemet på matrisform AX = Y, så vet vi att systemet har en entydig lösning X = A 1 Y då det A 0 Om det A
TMV142/186 Linjär algebra Z/TD
 MATEMATIK Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Chalmers tekniska högskola Datum: 2018-08-27 kl 1400 1800 Tentamen Telefonvakt: Anders Hildeman ank 5325 TMV142/186 Linjär algebra Z/TD Skriv
MATEMATIK Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Chalmers tekniska högskola Datum: 2018-08-27 kl 1400 1800 Tentamen Telefonvakt: Anders Hildeman ank 5325 TMV142/186 Linjär algebra Z/TD Skriv
19. Spektralsatsen Spektralsatsen SPEKTRALSATSEN
 9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
9 SPEKTRALSATSEN 9. Spektralsatsen 9.. Spektralsatsen Symmetriska avbildningar är en viktig klass av linjära avbildningar. Vi kommer nedan att formulera ett antal viktiga resultat för dessa avbildningar
DEL I. Matematiska Institutionen KTH. Lösning till tentamensskrivning på kursen Linjär algebra II, SF1604, den 17 april 2010 kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Matematiska Institutionen KTH Lösning till tentamensskrivning på kursen Linjär algebra II, SF604, den 7 april 200 kl 09.00-4.00. DEL I. En triangel i den tredimensionella rymden har sina hörn i punkterna
Föreläsning 9: NP-fullständighet
 Föreläsning 9: NP-fullständighet Olika typer av problem: 1. Beslutsproblem: A(x) =Ja. 2. Optimeringsproblem: A(x) =m Vanligen max/min. 3. Konstruktionsproblem: A(x) =En struktur. Vanligen lösningen till
Föreläsning 9: NP-fullständighet Olika typer av problem: 1. Beslutsproblem: A(x) =Ja. 2. Optimeringsproblem: A(x) =m Vanligen max/min. 3. Konstruktionsproblem: A(x) =En struktur. Vanligen lösningen till
SF1624 Algebra och geometri
 Föreläsning 16 Institutionen för matematik KTH 5 december 2017 Modul 6 Veckans arbete 1. Idag: Ortonormalt, kap 7.1-7.2 a. Ortogonala och ortonormala baser b. Gram-Schmidts metod c. Ortogonala matriser
Föreläsning 16 Institutionen för matematik KTH 5 december 2017 Modul 6 Veckans arbete 1. Idag: Ortonormalt, kap 7.1-7.2 a. Ortogonala och ortonormala baser b. Gram-Schmidts metod c. Ortogonala matriser
Linjär algebra på några minuter
 Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
Linjär algebra på några minuter Linjära ekvationssystem Ekvationssystem: { Löses på matrisform: ( ) ( ) I det här fallet finns en entydig lösning, vilket betyder att determinanten av koefficientmatrisen
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 2014
 SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
SF1624 Algebra och geometri Tentamen Onsdagen 29 oktober, 214 Skrivtid: 14.-19. Tillåtna hjälpmedel: inga Examinator: Roy Skjelnes Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng.
kvivalenta. Ange rangen för A samt en bas för kolonnrummet för A. och U =
 MATEMATIK Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola Datum: 9-- kl 8 Tentamen Telefonvakt: Aron Lagerberg tel 76-786 Linjär Algebra Z (tmv4) Skriv tentamenskod tydligt på samtliga
MATEMATIK Hjälpmedel: utdelad ordlista, ej räknedosa Chalmers tekniska högskola Datum: 9-- kl 8 Tentamen Telefonvakt: Aron Lagerberg tel 76-786 Linjär Algebra Z (tmv4) Skriv tentamenskod tydligt på samtliga
TMV166 Linjär Algebra för M. Tentamen
 MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 3 6 kl. 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Tony Stillfjord,
MATEMATISKA VETENSKAPER TMV66 6 Chalmers tekniska högskola 6 3 6 kl. 8:3 :3 (SB Multisal) Examinator: Tony Stillfjord Hjälpmedel: ordlistan från kurshemsidan, ej räknedosa Telefonvakt: Tony Stillfjord,
Chalmers tekniska högskola Datum: kl Telefonvakt: Linnea Hietala MVE480 Linjär algebra S
 MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
MATEMATIK Hjälpmedel: inga Chalmers tekniska högskola Datum: 69 kl 4-8 Tentamen Telefonvakt: Linnea Hietala 55 MVE48 Linjär algebra S Tentan rättas och bedöms anonymt Skriv tentamenskoden tydligt på placeringlista
Linjär Algebra, Föreläsning 9
 Linjär Algebra, Föreläsning 9 Tomas Sjödin Linköpings Universitet Euklidiska rum Vi ska nu införa en extra struktur på vektorrum, en så kallad skalärprodukt, vilken vi kan använda för att definiera längd
Linjär Algebra, Föreläsning 9 Tomas Sjödin Linköpings Universitet Euklidiska rum Vi ska nu införa en extra struktur på vektorrum, en så kallad skalärprodukt, vilken vi kan använda för att definiera längd
A = x
 Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Matematiska Institutionen KTH Lösningar till några övningar på linjära avbildningar och egenvärden och ehenvektorer inför lappskrivning nummer 5 på kursen linjär algebra SF604, ht 07.. (a) A(2,, 0) A(2(,
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar I Innehåll
Linjär algebra Föreläsning 10
 Linjär algebra Föreläsning 10 IT-programmet, Chalmers 2006 Samuel Bengmark Repetition Handlade om kvadratiska matriser. Kvadratiska ekvationssystem har: Unik lösning omm Det(A) 0. Har oändligt antal lösningar
Linjär algebra Föreläsning 10 IT-programmet, Chalmers 2006 Samuel Bengmark Repetition Handlade om kvadratiska matriser. Kvadratiska ekvationssystem har: Unik lösning omm Det(A) 0. Har oändligt antal lösningar
