RÄKNEÖVNINGAR. Elementär akustik
|
|
|
- Sven Åberg
- för 9 år sedan
- Visningar:
Transkript
1 DT75 Ljud Räkneövningar RÖ sid RÄKNEÖVNINGAR Ta med detta häfte till räkneövningstillfällena. Ta också med en fickräknare med log och trig. Lösningarna börjar på sidan. Elementär akustik. Beräkna skillnaden i ljudhastighet mellan tropikerna +4 ºC och svensk höst + ºC. Ange svaret i procent.. Hur förhåller sig partikelhastigheten v till ljudhastigheten c? Ställ upp formeln och förklara med ord.. Ett typiskt värde på Z i luft är 4 Ns/m³. Hur stor är partikelhastigheten om ljudtrycket är Pa (effektivvärden)? Jämför med ljudhastigheten. 4. Vågtalet är en frekvens i rummet snarare än i tiden, närmare bestämt rumsvinkelfrekvens. En LP-skiva av vinyl har diametern cm. Över vilken frekvens börjar skivan få betydelse som akustisk reflektor? 5. Om ljudtrycket är Pa, vad är då ljudtrycksnivån? Antag den vanliga definitionen av referensnivån. 6. Intensiteten J från en rundstrålande källa i fri rymd är µw/m² på 5 meters håll. Beräkna a) ljudintensitetsnivån L J b) den av källan utstrålade effekten W (sid -6) 7. Hur stor effekt behövs i slutförstärkaren, om ljudnivån på 5 meters håll ska vara 85 db? Antag att högtalaren är rundstrålande, står nära marken, och dess verkningsgrad är %. 8. Publiken på en fotbollsmatch vrålar när det görs mål. 4 personer hejar på hemmalaget, och personer hejar på bortalaget. a) Hur många db starkare blir vrålet för hemmalaget? b) Låter detta som mer eller mindre än dubbelt så starkt? 9. En oktav är en musikalisk beteckning på frekvensförhållandet :. Denna term är vanlig inom ljudtekniken. Över hur många oktaver sträcker sig det hörbara frekvensområdet Hz khz? Ange svaret med två decimaler.. Beräkna effektivvärdet för en signal med toppamplituden ± Pa, om vågformen är a) en sinusvåg, b) en symmetrisk fyrkantvåg, c) en symmetrisk triangelvåg.
2 DT75 Ljud Räkneövningar RÖ sid Hörsel. Vid vilken ljudnivå måste en ton på 5 Hz presenteras, om den ska låta lika stark som en ton på Hz som presenteras vid db ljudnivå? Vad blir tonernas hörnivå i fon?. Orkestermusik har mest energi i området omkring 5 Hz. Om man repeterar tre timmar per dag, vilken skulle vara den högsta ihållande ljudnivå som ger en tillåten bullerdos enligt arbetarskyddsnormen?. Man har en störton på Hz med en ljudnivå om 9 db. Hur stark måste då en mätton vid 5 Hz vara för att inte maskeras? 4. Exempel på tentamensuppgift. För en experimentell radioteater ska du framställa en binaural inspelning (endast för återgivning i hörlurar) som ger illusionen av att en talare står 45 grader till höger om lyssnaren. Råmaterialet är en ljudfil med en högklassig monoinspelning av talaren, gjord i studio utan rumsklang. Verktyget är ett ordinärt flerkanaligt ljudredigeringsprogram med mixning och några enkla filter. a) Huvudets ljudskugga har i verkligheten en lågpass-karakteristik som är litet mer komplicerad än ett första ordningens lågpassfilter, men det är den enda filtertyp som finns i ditt ljudredigeringsprogram. Ungefär vilken brytfrekvens bör väljas på detta filter? Motivera. ( p) b) Beskriv steg för steg hur du manipulerar signalen för att åstadkomma ett så illusoriskt resultat som möjligt. Endast direktljudet behöver simuleras. (5 p) c) Regissören vill nu ge intryck av att lyssnaren och talaren står utomhus på hård plan mark, på 4 meters avstånd från varandra, utan andra väggar eller föremål i närheten. Antag att huvudena är,5 m över marken. Beskriv steg för steg hur du simulerar markreflexen. Tips: Rita strålgången. (4 p) d) Tror du att det spelar någon roll om man lägger till markreflexen innan eller efter man gör om monoinspelningen till stereo; och hur skulle du göra? Motivera. ( p) Rumsakustik 5. Beräkna efterklangstiderna vid 5, 5 och Hz i ett rektangulärt rum med tegelväggar och med betong i tak och golv. Rummets dimensioner är l x, l y 4,7 l z,5 [m]. 6. En tom sal med måtten 8 7 meter har en efterklangstid på,6 sekunder vid 5 Hz. a) Vad blir efterklangstiden om man monterar upp tunga draperier med en area på m som hänger fritt i rummet, så att båda sidorna exponeras? b) Vad blir efterklangstiden om dessutom 4 vuxna studenter sitter som publik i salen? c) Vad är efterklangsradien i den tomma salen? d) Vad är efterklangsradien i salen med både draperier och studenter? e) Hur långt från en talare kan man anse ha goda lyssningsförhållanden i fallet med både draperier och elever? f) Skvalmusik spelas upp i en högtalare i den tomma salen och ger då en genomsnittlig ljudintensitetsnivå på 78 db i det diffusa fältet. Hur mycket akustisk effekt strålas då ut av högtalaren? g) Vad blir diffusa ljudintensitetsnivån från högtalaren i föregående uppgift när draperierna är monterade?
3 DT75 Ljud Räkneövningar RÖ sid 7. En rektangulär hytt ska användas för akustisk inspelning av en elbas (med egen förstärkare+högtalare) på en musikstudio. Hytten har invändigt måtten 4,, m. a) Beräkna frekvenserna för de tre lägsta rumsresonanserna i hytten. Antag c 4 m/s. b) Var i rummet finns trycknoder där man kan placera högtalaren för att i möjligaste mån undvika att excitera dessa resonanser? Rita. 8. Akustikerlärlingen Johan har genom en mätning kommit fram till följande rumsakustiska storheter i ett vardagsrum, vars volym är 5 m³. Ett av resultaten är fel med mer än %. T.8 s (efterklangstiden) A.4 m² (ekvivalenta absorptionsarean) r r.47 m (efterklangsradien) f s 5 Hz (Schröders gränsfrekvens) (a) Vilket mått är fel, och vilket värde borde det ha? (b) Johan har tillgång till en effektkalibrerad ljudkälla med sinus och brus, en ljudnivåmätare, en kurvskrivare till nivåmätaren, och en startpistol med knallskott. På vilka sätt kan han ha använt dessa för sin mätning? Placering av mikrofoner och högtalare 9. Kamfiltereffekt och mikplacering Om en stark reflex t.ex. via golvet når mikrofonen strax efter direktljudet, kan interferensen mellan direktljud och reflex bli hörbar. För vissa frekvenser blir nivån 6 db högre, för andra kan ljudet släckas ut nästan helt. (a) Givet ett hårt golv, en höjd h över golvet för både källa och mikrofon, samt ett avstånd l mellan källa och mikrofon, ställ upp det uttryck som behövs för att beräkna de tysta respektive de mest förstärkta frekvenserna. Rita strålgången så blir det lättare. (b) Rita upp en skiss av frekvensgången (nivå som funktion av frekvens), med maxima och minima på rätt ställen, om l 4 m och h,5 m. (c) Med bara en reflekterande yta så kan man aldrig få total utsläckning, eftersom reflexen har gått en längre väg, och därför är något svagare än direktljudet. Men kan man få total utsläckning om man har flera reflexer?
4 DT75 Ljud Räkneövningar RÖ sid 4 Flera ljudkällor Bakgrund: (jfr också avsnitt.. samt.. i kompendiet) Betrakta fallet med en högtalare nära ett oändligt plant golv, dvs i s.k. fri halvrymd. Vi får då endast en spegelkälla. Spegelkällans bidrag till den totala ljudnivån beror av i vilken mån direktljudet och det reflekterade ljudet är korrelerade med varandra. Eftersom det reflekterade ljudet är detsamma som en fördröjd version av direktljudet, blir frågan därför hur mycket signalen liknar sig själv som den var innan fördröjningen. Man brukar använda en korrelationskoefficient, som kan variera från + (positivt korrelerad, i fas) till (okorrelerad) till (negativt korrelerad, i motfas). För musik och tal, som hela tiden varierar, kan vi oftast anta att korrelationen är nära, om bara fördröjningen motsvarar flera våglängder. Detsamma gäller dock inte för periodiska testtoner. Om källan och spegelkällan är mycket nära varandra (i förhållande till våglängden!), blir reflexens fördröjning mycket liten, och korrelationen blir nära +. För helt okorrelerade signaler ska effekterna adderas, medan för helt korrelerade signaler ska trycken adderas. Delvis korrelerade signaler måste behandlas mer ingående, men det gör vi inte i denna kurs.. Nivå från flera ljudkällor (a) Om ljudnivån med en viss ljudkälla väljs till referens, db, hur hög blir då ljudnivån om flera likadana men okorrelerade ljudkällor tillkommer? Beräkna för fallen med,, 4, 5, 8 och ljudkällor. (b) Om ljudnivån med en viss ljudkälla väljs till referens, db, hur hög blir då ljudnivån om flera likadana och helt korrelerade ljudkällor tillkommer? Beräkna för fallen med,, 4, 5, 8 och ljudkällor.. Inverkan av högtalares placering i rum (a) Förklara varför man får störst nivåökning i basområdet, när en högtalare ställs intill väggen, riktad mot rummets mitt (två orsaker). (b) Beräkna ljudnivåökningen när en rundstrålande högtalare ställs mycket nära en, två och tre väggar som är vinkelräta mot varandra. Om vi har mer än tre väggar (sex väggar är vanligast) så blir det väldigt många spegelkällor. De flesta är dock så långt isär att korrelationen mellan dem blir liten för vanliga signaler. Men i små rum eller för låga frekvenser eller för stationära signaler har spegelkällorna alltid betydelse.
5 DT75 Ljud Räkneövningar RÖ sid 5 Signalers representation och distorsion Distorsion. En sinuston går igenom ett litet förstärkarsteg för ljud. Förstärkaren är dock inte helt linjär. Figuren till höger visar förstärkarens beteende: Utsignal som funktion av insignal. Vore förstärkaren linjär så skulle insignalen vara direkt proportionell mot utsignalen..8 Icke linjär förstärkare Linjär referens.6 UTSIGNAL INSIGNAL.5 När insignalen utnyttjar hela området från till fås följande effektspektrum för utsignalen (dvs. effekten som funktion av frekvensen). (Figur nedan) FÖRSTORING: Effektnivå [db] Effektnivå [db] Frekvens [Hz] Frekvens [Hz] a) Vilken är insignalens frekvens? b) Vilken typ av distorsion rör det sig om? Motivera. c) Distorsionen d hos en distorderad sinuston (en summa av sinustoner n) kan beräknas med formeln d U d U tot U n n U n n där Un är amplituden för delton nummer n. Distorsion anges av konvention som ett förhållande mellan spänningar. Beräkna distorsionshalten i förstärkarens utsignal. Ange svaret i procent. c) Beskriv hur nivåerna för de två topparna i effektspektrum ändras om vi minskar insignalens amplitud till en tiondel. Någon beräkning behövs ej, men motivera svaret.
6 DT75 Ljud Räkneövningar RÖ sid 6. I en ljudstudio har man gjort en inspelning med flera instrument på separata kanaler. Inspelningen sparas digitalt på hårddisk. D/A-omvandlarna arbetar med en samplingsfrekvens på 96 khz samt en upplösning av 4 bitar. Inspelningen krävde 5 kanaler. Hur många byte/s går åt vid inspelningen? 4. Om vi vill säkerhetskopiera multikanalsinspelningen till en vanlig CD-skiva, hur lång inspelning får då ungefär plats i ovanstående fall på en vanlig CD-skiva. Antag att alla kanalerna används hela tiden, samt att en CD-skiva rymmer 65 Mbyte. 5. Vad är den teoretiska skillnaden i signal-störförhållande (SNR, i db) mellan ett 6 bitarssystem och ett 4 bitars-system? 6. En sinuston med frekvensen F skall samplas. Rita en tänkbar följd av sampelvärden om samplingsfrekvensen är (a) 5F (b) F (c) F (d),6f (e),5f a) Rita så många perioder som behövs för att följden ska repetera. b) Hur kommer den resulterande samplade vågformen att låta i respektive fall när den spelas upp? 7. Ett filter gör en medelvärdesbildning av 4 på varandra följande sampel. Om filtret matas med en sinussignal med toppvärdet, hur stark blir då signalen ut från filtret om signalens frekvens är Hz, f s /8, f s /4, f s /8, eller f s /. Skissa filtrets tonkurva. 8. a) Räkna ut impulssvaret för nedanstående två filter: b) Om man kopplar de två filtren efter varandra, vad blir det då för impulssvar? Spelar ordningen någon roll?
7 DT75 Ljud Räkneövningar RÖ sid 7 Ljudnivåmätning 9. A-vägning Ett medelspektrum av ljudet i en fabrikslokal hade två tydliga toppar: en vid Hz och 88 db, och en annan vid Hz och 7 db. Ungefär hur mycket visar en nivåmätare om den är inställd på A-vägning resp. C-vägning?. Ekvivalentnivån (Tentamensuppgift från 7 - hela extentor finns på kursens hemsida) Bakgrund: Risken för hörselskador anses vara proportionell mot den totala energi som örat utsätts för, alltså effekt tid (eller, om effekten varierar, integralen av effekten över tiden). Om bullernivån varierar under en mätning så förenklar man därför till ett enda mätetal genom att ange den s.k. ekvivalentnivån, L eq. Den beräknas genom att ta medelvärdet av intensiteten över det givna tidsintervallet, och sedan uttrycka den erhållna medelintensiteten som en nivå i decibel. Ekvivalentnivån blir på så vis den konstanta nivå som skulle ha resulterat i samma totala energi som den varierande nivån. Märk att L eq alltså inte är tidsmedelvärdet av intensitetsnivån, som ger ett annat resultat. Ekvivalentnivå T J ( t) dt T log J ref Leq L J Medelnivå T T L ( t) dt J Uppgift: Inspektören från hälsovårdsnämnden har ålagt en discoägare att minska ekvivalentnivån på dansgolvet från till 99 db. Discoägaren tänker då (felaktigt) att detta är en minskning med %, och han lägger därför in minuters tyst drinkpaus, var tjugonde minut utan att ändra volymen på ljudet under de 8-minuters perioder som musiken pågår.
8 DT75 Ljud Räkneövningar RÖ sid 8 a) Beräkna med hur många decibel L eq minskar, om man gör som discoägaren. Discomusikens nivå kan antas vara konstant. ( p) b) Beräkna hur mycket paus (i procent av hela tiden) som man egentligen måste lägga in för att L eq verkligen ska minska till 99 db, om ljudanläggningen fortfarande spelar med db när den spelar. ( p) c) Enligt skyddsnormerna, hur länge får man dagligen vistas på dansgolvet om ljudnivån vid 5 Hz är db? ( p) d) Om man trots allt skulle räkna ut tidsmedelvärdet av intensitetsnivån ( medelnivån i tabellen ovan), skulle detta ge ett högre eller lägre värde än ekvivalentnivån? Motivera, eventuellt med ett exempel. ( p) Ledning: Ingen integralkalkyl behövs för att lösa uppgiften. Utnyttja att decibel uttrycker förhållanden.. Vilket ger högst ekvivalentnivå? Beräkna. () En larmklocka som på det givna avståndet ger intensitetsnivån 96 db, om den ljuder tolv sekunder var tjugonde minut, () Ett ihållande bakgrundsbuller med 74 db i korttidsmedelvärde. Fler sammansatta problem Dessa problem är representativa för tentamensuppgifterna, de brukar ge ca p på tentan. Uppgift. På hög nivå. (a) Osannolikt svaga ljud: beräkna den ljudtrycksnivå som råder när ljudtrycket är -6 Pa. (b) Osannolikt starka ljud: Tryckförändringar i det statiska atmosfärstrycket, normalt ca hpa, orsakas av hög- och lågtryck i vädret, mellan extremerna 97 och 5 hpa. Om man ser dessa tryckförändringar som ett extremt lågfrekvent ljud, vad är då dess ljudtrycksnivå? Antag en sinusformad variation. (c) Visa, med hänvisning till relevanta relationer ur kompendiet, att de tunna diagonala strecken för den av källan avgivna effekten har rätt läge, rätt lutning och rätt inbördes avstånd (fig - i boken). Uppgift. Mysteriet med den vandrande talaren. (a) När hörseln lokaliserar en ljudkälla sker det på flera sätt. Dels bestäms ljudets infallsriktning mot lyssnaren (A), dels avgör hörseln om det uppfattade ljudet är ett direktljud eller en reflex (B). Har precedenseffekten att göra med (A) eller (B)? Motivera. (b) Vilken av delfigurerna på sidan -4 i kompendiet är mest relevant för att beskriva inverkan av en panoreringsratt på en mixer? Motivera. (c) För en radioteaterproduktion ska du skapa en illusion av att en talare börjar tala helt nära lyssnaren, och sedan gradvis förflyttar sig allt längre bort i en stor tom hangar. Talarens röst finns studio-inspelad i mono med konstant nivå och utan efterklang. Diskutera i detalj vilka ljudmanipulationer som skulle kunna bidra till illusionen.
9 DT75 Ljud Räkneövningar RÖ sid 9 Uppgift 4. Ljud eller oljud på dagis. a) Kvinnliga förskollärare är påtagligt överrepresenterade bland dem som söker hjälp vid landets talvårdskliniker för röstproblem. Röstforskare har funnit att förskollärare talar eller ropar under upp till 5% av tiden under en arbetsdag från 8. till 6.. Till forskningsresultaten hör också att det genomsnittliga taltonläget (grundtonsfrekvensen) under denna tid är 5% högre än i normal samtalston. Beräkna ungefär hur många gånger under hela arbetsdagen stämbanden slår ihop hos en kvinnlig förskollärare, under de givna betingelserna. b) Ljudnivån på ett visst dagis varierar med aktiviteten (lek, rast, lunch), men är i genomsnitt 78 db, med den huvudsakliga energin vid frekvenser runt 5 Hz. Kan denna miljö utgöra en fara för de vuxnas hörsel, enligt bullernormen för arbetarskydd? c) Allrummet på ett dagis i ett äldre stenhus befinns ha för hög ljudnivå. Personalen menar att barngruppen har blivit för stor, med % fler barn än det var tänkt från början. Akustikkonsulten menar istället att det är rummets inredning det är fel på. Genom att byta till bättre akustik-plattor i taket kan man sänka ljudnivån med db, hävdar hon. Skulle nya plattor innebära en större förbättring än att återställa barngruppens storlek? Motivera, under antagandet att barnens röstlägen inte påverkas av åtgärderna (egentligen påverkas de, men det blir så krångligt då). Uppgift 5. Rumsakustik. Vid planeringen av en konferens för 4 deltagare befarar man att den kala gamla aulan som ska användas för en av sessionerna kanske har för lång efterklangstid. Salens volym är knepig att uppskatta direkt p g a av dess oregelbundna form. Dock lyckas man konstatera att dess efterklangstid sjunker från,7 (tom aula) till, sekunder när 4 personer finns i salen. (a) Beräkna salens volym (b) Hur kort blir efterklangstiden när alla 4 anländer? (c) När väldigt många kommer in, minskar ju faktiskt salens akustiska volym också något. Gör ett rimligt antagande om människokroppars volym och beräkna huruvida denna effekt kan vara något att bry sig om i detta fall. (d) Om man i den fullsatta salen vill spela ljudexempel med 75 db ljudnivå på åhörarplats, hur många akustiska watt måste den rundstrålande högtalaren på podiet då kunna avge?
10 DT75 Ljud Räkneövningar RÖ sid Uppgift 6. Rumsakustik Rita av diagrammet nedan och rita sedan in enkla, raka pilar som visar i vilken riktning följande storheter ökar, dvs någon av. Skriv också en kort motivering för varje svar, med gjorda antaganden om så behövs (t ex att större rumsvolym V också medför en större total väggyta S.) Efterklangstiden EKT a) Efterklangsradien EKR b) Genomsnittliga tiden T refl till första ordningens reflexer (dvs ljud som har studsat precis en gång) c) Ekvivalenta absorptionsytan A d) Den diffusa intensiteten J diff e) Schroeders gränsfrekvens f S
11 DT75 Ljud Räkneövningar RÖ sid LÖSNINGAR Uppgift. T c.4 7 ctropikerna c 7 HÖST SVAR: Skillnaden i ljudhastigheten är 7,%. Uppgift. p p Z ρ c v. v ρ c Partikelhastigheten är proportionell mot ljudtrycket och omvänt proportionell mot både ljudhastigheten och luftens densitet. Uppgift. v p Z 4 [ N m ] [ Ns m ].5 SVAR: Partikelhastigheten är.5 - m/s. Uppgift 4. Vågtalet k, om kr << akustiskt litet, våglängden >> föremålet om kr >> akustiskt stort, våglängden << föremålet r,5 m kr (Rund skiva, våglängden omkretsen). k /r. k ω/cπ f/c f kc/π [&] fc/πr 4/(π*.5) 6 Hz SVAR: Skivan börjar få betydelse som akustisk reflektor vid 6 Hz. Uppgift 5. Eftersom det är tryck vi jämför så ska vi multiplicera logaritmen med : P L log log. db p P 5 5 ref Svar ljudtrycksnivån är.5 db Uppgift 6. J 5 W / m m J a) Lj log log J ref b) S 4π r 4π 5m 5 W J S π.4mw s 5 7dB Här handlar det om ett förhållande mellan intensiteter (effekt/ytenhet), således ska logaritmen multipliceras med. Svar: Ljudintensitetsnivån är 7 db, och källan strålar ut en effekt av.4 mw.
12 DT75 Ljud Räkneövningar RÖ sid Uppgift 7. Vi antar att ljudet sprider sig likformigt över en halvrymd, dvs att högtalarna står på marken. J L j log J ref J J S ref Lj Halvsfär 8.5 π r W / m 5π m.5 W J S 5π.4W Wut Win.4/. 4W η.5 SVAR: Slutsteget behöver leverera 4 W. Uppgift 8. a) Källorna är icke koherenta, dvs har inte samhörande frekvens och fas. De ska därför adderas på effektbasis. En fördubbling av effekten motsvarar ca db. Två fördubblingar ger ca 6 db. SVAR: Hemmalagets vrål blir 6 db starkare Uppgift 9. b) Det låter mindre än dubbelt så starkt, se avsnitt.4. En oktav motsvarar en fördubbling av frekvensen. Logaritmlagarna ger a log x b log x / b log a n n log log 9.97 log SVAR: Knappt oktaver ryms inom det hörbara området. Uppgift. a) t π / π t sin( t) π dt t sin ( ) t dt π ( Svar: Effektivvärdet är / Pa för sinusvågen. cos(t) t + sin(t) π dt π π 4 t t b) dt t Svar: Effektivvärdet är Pa för fyrkantvågen. t t c) t dt t t dt Svar: Effektivvärdet är / Pa för triangelvågen.
13 DT75 Ljud Räkneövningar RÖ sid Uppgift. ca 57 db ljudnivå, phon hörnivå. Uppgift. ca 94 db. Uppgift. 4 db Uppgift 4. Exempel på lösning: Simulering av en binaural inspelning (a) Huvudets radie r kan uppskattas till ca. m, k πf / c, kr, ger f c k /π 4 /π 54 Hz 5 Hz duger som närmevärde. (b) En binaural inspelning består av två kanaler som ska levereras helt åtskilda, i hörlurar, till vänster och höger öra.. Kopiera talsignalen till en ytterligare kanal. Vi har nu det som ska bli Vänster och Höger signal i varsin kanal.. Lågpassfiltrera Vänster vid 5 Hz enligt ovan. Vänster är nu skuggad av huvudet.. Simulera löptidsskillnaden mellan öronen t ex genom att fördröja Vänster med,5 ms (ur figur - övre vänster). Man kan förslagsvis infoga,5 ms tystnad i början av Vänster kanal. 4. Höj nivån på Höger med 4 db och sänk nivån på Vänster med 4 db (ur figur - nedre höger, för talsignal). 5. [Finess, ej krav] Filtreringen av Vänster ger i sig en viss nivåsänkning. Mät den och kompensera för den. (c) 4 m,5,5,5,5,, Nu ska vi mixa in en signal till, nämligen markreflexen. Den är en kopia av originalet men ska vara lite svagare och senare eftersom den ska ha gått 5 meter istället för 4, se de s k egyptiska trianglarna ovan (med proportionerna :4:5). Antag att den hårda marken inte absorberar något alls. (Förlusten genom absorption mot marken är i nog alla fall försumbar jämfört med avståndsökningen.) Ljudtrycket är omvänt proportionellt mot avståndet, så reflexens amplitud ska multipliceras med 4/5 (eller minskas i nivå med,9 db). Vägskillnaden är meter vilket motsvarar ms fördröjning. Detta ska anbringas var för sig på både Vänster och Höger. (Man kan också tänka sig att sänka den totala ljudnivån litet för att simulera fyra meters avstånd, men vi vet inte på vilket avstånd originalet är inspelat och vi har ingen ljudtryckskalibrering av originalet.) (d) Nej, det blir nog väldigt lite skillnad, som i så fall skulle bero på att reflexen kommer snett nedifrån istället för rakt från sidan. Det blir samma löptidsskillnader och i stort sett samma ljudskugga för reflexen som för direktljudet. Det är därför antagligen smartare att först lägga på en reflex på den ursprungliga talsignalen i mono, och sedan simulera binaural stereo. Annars måste man ju tillverka även reflexljudet i stereo och sedan mixa ihop det med direktljudet i stereo.
14 DT75 Ljud Räkneövningar RÖ sid 4 Uppgift 5. absorptionsfaktor alfa area S [m²] 5 Hz 5 Hz Hz bredd [m] 8, tak och golv, betong,,, längd 4,7 [m],5 (långväggar) höjd,5 [m] 5, (kortväggar) 8,5 alla väggar, tegel,,,5 Volym 5,5 [m³] Absorptionsytor S*alfa tak och golv,8,564,564 [m²] väggar,77,55,95 [m²] Total absorptionsyta,5,79,489 [m²] 5 Hz 5 Hz Hz T6,6*V/A 5,6,8,7 [s] Uppgift 6. a) V RUM m Tom sals absorptionsyta > A.6 V T RUM TOM 6.8m Antag nu det enklaste fallet, att draperierna exponerar hela sin yta utan att skärma av någon vägg i rummet. Absorptionsyta för tunga draperier A α S.5 m Ny total absorptionsyta A m Ny efterklangstid.6 V.6 68 T. s A 6.8 b) Varje person har absorptionsytan. m (Se sida -4 i kurslitt.)> A.*4 m Ny total absorptionsyta A m Ny efterklangstid.6 V.6 68 T. 7s A 8.8 c) Efterklangsradien r A m 6π 6π d) Efterklangsradien r A m 6π 6π e) Sida -7 Taluppfattbarhetsprov.5 ggr efterklangsradien. >. meter.
15 DT75 Ljud Räkneövningar RÖ sid 5 f) J DIFFUS J J ref 4W A Lj W / m 4. J DIFFUS A 6.8 W.7mW mw akustisk effekt utstrålas från högtalaren. g) 4W 4.7 J DIFFUS 4.mW / m A 6. 6 Lj log 4. 76dB Med draperierna blir ljudintensitetsnivån 76 db. Uppgift 7. f x, y, z c n n x y nz c n n x y nz l x l y l z 4.. De tre lägsta frekvenserna hittas för (n x n y n z ) ( ), ( ), ( ) vilket motsvarar 4 Hz, 57 Hz samt 69 Hz. b) Vi söker en eller flera platser i rummet som utgör en trycknod i alla tre moderna. ( ) är moden som svarar mot en halv våglängd längs rummets längsta dimension (4, m) Den har en trycknodlinje som delar rummet i två halvor på längden, 4, / m. ( ) har en trycknodlinje som delar rummet i två halvor på bredden, / m. Moden ( ) har två trycknodlinjer som sammanfaller med de två första. För att undvika två av resonanserna kan man ställa bashögtalaren var som helst på de mittlinjer som är parallella med rummets väggar. För att undvika alla tre måste högtalaren ställas i mittpunkten. Sett uppifrån: Uppgift 8. a) Genom att sätta in värdena i bokens formler upptäcker man så småningom att värdet för T ska vara,7 s istället. a) Med en effektkalibrerad källa och en ljudnivåmätare kan man använda sambandet J 4W/A för att räkna ut A. Alternativt kan man uppskatta efterklangsradien genom att se hur långt ut från ljudkällan som ljudnivån slutar falla. Med knallskott och kurvskrivare kan man mäta efterklangstiden direkt ur lutningen på den avklingande nivåkurvan. b)
16 DT75 Ljud Räkneövningar RÖ sid 6 Uppgift 9. a) När skillnaden l i väg mellan direkt och reflekterat ljud är lika med n hela våglängder får vi förstärkning. När l är en halv våglängd kortare får vi (nästan) utsläckning. c l Vi har allmänt att f, samt i detta fall att l, och får därför λ n n c n c f n respektive f n l l Vi söker uttrycket för l. Låt l R vara vägen för den reflekterade vågen. Pytagoras sats ger och eftersom D l l R l får vi D f n ld R + l h ld k n c + h l D där k n n för förstärkning och n+½ för utsläckning, n [,,,,...[ Fallet n gäller Hz ( låga frekvenser ) med +6 db nära golvet. b) Insättning av l 4 och h,5 i uttrycket för l ger l m. Med c 4 m/s erhålls maxima på multiplar av 4 Hz och minima på 7 + n 4 Hz. Trycken av det direkta och det reflekterade ljudet adderas vid mikrofonen. Eftersom det reflekterade ljudet har gått 5 m istället för 4 m, gör avståndslagen att det reflekterade ljudets tryck är 8% av direktljudets (komp..5.). Amplituden på maxima blir % + 8% relativt direktljudet ensamt. Den totala nivån, relativt direktljudet ensamt, blir då log(,8) +5, db. För minima ligger ljuden i motfas och amplituden blir % minus 8%. Den totala nivån blir log(,) -4, db. d) Eftersom trycken adderas, kan vi tänka oss att vi t ex har två väggar som ger två samtidiga reflexer, vardera med 5% av direktljudets amplitud, och i motfas. Då blir det - 5 % dvs helt tyst på vissa frekvenser enligt ovan.
17 DT75 Ljud Räkneövningar RÖ sid 7 Uppgift. a) Om ljudkällorna är okorrelerade ska de adderas på effektbasis. Vi använder alltså faktorn framför logaritmen och får log(), log(), log(4), osv. Svar:, 4,77 6, 6,99 9,, db. Uppgift. Uppgift. b) Om ljudkällorna är helt korrelerade (endast amplituden kan skilja) ska de adderas på tryckbasis. Vi använder alltså faktorn framför logaritmen och får log(), log(), log(4), osv. Svar: 6, 9,54,4,98 8,6, db. a) Vid låga frekvenser är högtalarna rundstrålande och nära väggen, jämfört med våglängden. Därför blir korrelationen hög mellan källan och spegelkällan. Vidare är högtalaren akustiskt stor vid höga frekvenser och därför inte rundstrålande. Diskanten går rakt fram och påverkas inte nämnvärt av väggen. b) Varje ny vägg fördubblar antalet källor. Med en vägg har vi två källor (originalet och reflexen), med två väggar har vi fyra källor, och med tre väggar har vi åtta. Eftersom källorna är mycket nära varandra betraktar vi signalerna som korrelerade. Svaren finns då i lösningen till uppgift 6b: +6, + och +8 db. a) 75 Hz (Överton*755 Hz) b) Harmonisk distorsion, tredjetonsdistorsion c) L db, L -6.5 db > log (U /U ) 6,5 L U U L d U d U tot n U n n U n U Ú + U U U + U U + U U U + + L.47 5% d) När IN-amplituden minskar kommer vi att använda ett mindre område av förstärkarens arbetsområde. Det lilla området kommer att bete sig mer linjärt än det stora området (se figuren överst i uppgiften). Därför kommer distorsionen att minska, dvs. nivådifferensen mellan grundton och överton kommer att minska. Dessutom minskar den absoluta nivån eftersom insignalen har blivit db svagare. Således, grundtonen kommer att minska, men övertonen kommer att minska ännu mera.
18 DT75 Ljud Räkneövningar RÖ sid 8 En exakt beräkning visar att grundtonen minskar med 9 db och övertonen med 6 db. EXAKT BERÄKNING: (Inte nödvändigt, men bra för förståelsen) UT(IN) A IN - B IN A sin(ωt) - B sin (ωt) (A - /4 B) sin(ωt) + B/4 sin(ωt) (A - /4 B) / (B/4) > 4A-BB > A6 B Dessutom ger UT() > A-B 6B-B >B. A. SVAR: UT(IN). IN -. IN Amplitud :, sin(ωt), sin (ωt) (/ ) sin(ωt),5 sin(ωt) Amplitud,:, sin(ωt) - -4 sin (ωt) (,,5-4 ) sin(ωt) sin(ωt) Grundtonen minskar med en faktor (/) / (, -,5-4 ) 8,76 ggr > 9 db Övertonen minskar med en faktor > 6 db Uppgift. 96k*4/8*54. Mbyte/s. Svar: 4. Mbyte/s Uppgift 4. 65/4./6.577 min. En CD-skiva rymmer då ½ minuts inspelning. Uppgift 5. För varje bit vi lägger till, så får vi dubbelt så många kvantiseringsnivåer > Fördubblar det användbara amplitudområdet. Fördubbling av amplitud motsvarar ca 6 db. 8 bitars skillnad ger 8 fördubblingar > 8 6 db 48 db. Alternativ exakt lösning: log ( 4 / 6 ) 48. db Uppgift 6. Se figur på nästa sida. Uppgift 7. Innehållet i de tre fördröjningarna är okänt när beräkningen startar. Därför går det inte att räkna ut utsignalen förrän vi har kommit till fjärde samplet i insignalen. Om vi först antar att förstärkarblocken har en förstärkning på blir utsamplen summan av fyra på varandra följande sampel: Sampel nr f s/8 f s/4 f s/8 f s/ In Ut In Ut In Ut In Ut In Ut,?,?,?,?,?,?,7?,? -,7? -,?,?,? -,?,?,?, 4, -,7,,,,7, -,, 4, 4, -, -,,, -, -,,, 5, 4, -,7 -,4,,,7,4 -,, 6, 4,, -,4 -,,,,4,, 7, 4,,7 -,,, -,7 -, -,, 8, 4,,,,,,,,, 9, 4,,7,4,, -,7 -,4 -,,, 4,,,4 -,,, -,4,, Eftersom filtret ska vara medelvärdesbildande, blir utsignalen ¼ av tabellvärdena.
19 DT75 Ljud Räkneövningar RÖ sid 9 (Uppgift 6, figur) Låter lika F Ett gränsfall. Låter lika, men bara i det undantagsfallet att samplingen inträffar som i bilden. Låter inte alls. ( Hz) F F Låter med en lägre frekvens. Observera att den nya tonen fortfarande är en sinus. Låter inte alls. ( Hz) F F
20 DT75 Ljud Räkneövningar RÖ sid (uppgift 7, fortsättning) Man ser att frekvensgången har nollställen vid f s / och f s /4. Däremellan är beloppet större än noll och starkare mot låga frekvenser. De exakta amplituderna kan bestämmas, men uppgiften var att skissa frekvensgången så vi nöjer oss med en figur liknande den nedan. frekvensgång f/fs,,5,5,75,5 5,, nivå [db] -5, -, -5, -, Uppgift 8. Impulssvaren blir: (a) x z yx+,5 z +,5 +,5,5,5 +,5,5,5,5 +,5,5,5 4,5 +,5,5,65 5,65 +,5,65,5 (b) x z yx-,5 z -,5 -,5 -,5 -,5 -,5 4 -,5 5 -,5 (c) x z yx+,5 z z yy-,5 z +,5 -,5 +,5,5,5-,5,5 +,5,5,5,5,5-,5,5,5 +,5,5,5,5,5-,5,5 4,5 +,5,5,65,5,5-,5,5 5,65 +,5,65,5,65,65-,5,5
21 DT75 Ljud Räkneövningar RÖ sid (d) x z yx-,5 z z4 y4y+,5 z4 -,5 +,5 -,5 -,5 -,5+,5 -,5 +,5 -,5 +,5 4 -,5 +,5 5 -,5 +,5 Dvs impulssvaren för de två seriekopplade filtren är likadana. De är dessutom en impuls, vilket betyder att filtren råkar vara varandras invers; deras överföringsfunktioner tar ut varandra. Uppgift 9. Svar: A-vägning 7 db. Toppen vid Hz dämpas så kraftigt av A-vägningen att den kan försummas. C-vägning: 8 db (88-5) C-kurvan dämpar 5 db vid Hz, och toppen vid Hz är så mycket svagare att den kan försummas. Uppgift. Det svåra med det här problemet är att inse hur enkelt det egentligen är. Man behöver förstå sambanden mellan effekt, intensitet och energi, och att nivåer i db uttrycker kvoter. 8 a) Totala energin och därmed också medelvärdet av intensiteten minskar till av vad de 8 var innan. L blir alltså log, 45 db. Svaret kan lämpligen avrundas:,5 db lägre. b) Vi söker den faktor som motsvarar en minskning med -99 db. ( ),79 eller ca 8%. Man måste alltså ha paus 9% av tiden för att få db minskning av ekvivalentnivån. Då blir tidsmedelvärdet av intensiteten 8% av vad den är om musiken spelar oavbrutet. c) I kompendiets figur - ser vi att punkten db, 5 Hz ligger mellan kurvorna för < minuter och <5 minuter, och enligt texten är det kurvan närmast ovanför som gäller. Svaret är alltså högst 5 minuter. d) Om man t ex har ett ljud som halva tiden ligger på db och halva tiden ligger på 9 db så blir medelnivån 95 db. Eftersom db minskning innebär att intensiteten sjunker med en faktor, så ändras medelintensiteten (jämfört med oförändrade db) med en faktor (forts.)
22 DT75 Ljud Räkneövningar RÖ sid,5,5 +,55. L blir då log(,55), 6 db, och ekvivalentnivån blir -,697,4 db vilket är mer än 95 db. Medelnivån är alltid lägre än ekvivalentnivån. (Därför hade den passat discoägaren bättre...) Uppgift. minuter är 6 sekunder, så tolv sekunder är % av den tiden. Den ekvivalenta intensiteten blir då % av larmets intensitet när det ljuder. log (,) - db , vilket fortfarande är högre än 74 db. Svar: () ger högst ekvivalentnivå. Uppgift. 6 (a) log p L P log 5 db pref (b) Topp-amplituden p topp (5-97)/ 4 hpa. Sinusformad svängning ger att effektivärdet är ptopp. 4 log p L P log 6 5 db pref (c) Streckens lutning: Trycket är omvänt proportionellt mot avståndet, tio gånger avståndet ska ge tio gånger mindre tryck eller db. Bekräftas genom mätning i figuren. Streckens läge: enligt figuren ger µw på m avstånd en ljudnivå om 49 db. Antag att det är intensitetsnivån. Kontrollera intensiteten: 6 W 8 J 7,96 4πr 4π 8 8 log J L J 49 db J ref Streckens inbördes avstånd: från en diagonal till nästa ökar effekten tusen ggr, dvs log() db, vilket stämmer med figuren. Uppgift. (a) Precedenseffekten har med (B) att göra. Reflexer anländer alltid något senare än direktljudet och undertrycks av hörselsinnet. Det är det först anlända ljudet (det som har precedens) som vi varseblir. (b) Panoreringsratten inverkar endast på signalnivåerna i vänster och höger kanal. Det är den vänstra delen av figur - (Subjektivt uppfattad infallsvinkel) på sidan -4 som är mest relevant. (c) Ljudnivån för direktljudet skall avta med 6 db för varje fördubbling av det skenbara avståndet. Efterklangsljudets nivå skall vara konstant. Diskanten i direktljudet skall sjunka något litet snabbare än hela ljudets nivå (sträckdämpning). Golvet i en hangar är antagligen hårt
23 DT75 Ljud Räkneövningar RÖ sid och plant. En simulerad golvreflex, vars fördröjning och nivåskillnad relativt direktljudet blir allt mindre med ökande avstånd kommer därför att bidra till illusionen (kamfiltereffekt). En hangar är stor, även hörbara ekon kan förekomma. Uppgift 4. a) Kvinnors medelgrundtonsfrekvens ( Hz,5) i (8 timmar,5) ger 5 8,5 6,8 6 b) Figur -, 78 db vid 5 Hz ligger under riskgränsen. Svar: nej. c) % fler barn innebär att nivån i snitt har ökat med log(,),8 db. Nya plattor skulle innebära en större förbättring. (I praktiken hjälper nog en minskning av barngruppens storlek mer, eftersom party-effekten avtar och de enskilda barnens röstnivå sjunker.) Uppgift 5. V T,6 A V V T4,6,6 A4 A + 4Am T A + 4Am 4Am + T4 A A 4Am 4, A 69m T,7 T4, T A,7 69 V 64m,6,6 V 64 T4,6,6,s A + 4Am , mm 8 Vm,8m ρ 4V m m J A W 4 9,m 4 << 64m 75 / ( ,) 4, mw Två fall med samma V men olika A. Vi vet skillnaden i A och kan efter en stund lösa ut A som i sin tur ger V och nya värdet på T. Kroppens densitet kg/m³ på åhörarplats utanför r r diffus intensitet
24 DT75 Ljud Räkneövningar RÖ sid 4 Uppgift 6. För att reda ut sammansatta beroenden av rumsvolymen, konstaterar vi först, att om rummets volym V är proportionell mot rummets radie (eller sidolängd) i kubik R³, så är väggytan (och under konstant α även absorptionsytan A ) proportionell mot R². Vi får då proportionaliteterna nedan till vänster (här angivna med symbolen ). V R T,6 T R A R ½ V R rr,56 rr R T R A ½ rr rr ( R ) R 6π f S 9 T V f s ½ R R R Dvs T och r r ökar båda om rummets storlek ökar, medan f S minskar. c) absorptionen påverkar inte löptiden e) J absorberad : intensitet är effekt per ytenhet, dvs den totala arean spelar ingen roll. Märk också att J absorberad inte är riktigt samma sak som den diffusa intensiteten. Kombinerat med beroendena av absorptionen i standardformlerna får vi då att (a) EKT ökar när rumsvolymen ökar och absorptionsfaktorn minskar, alltså. Och så vidare. Om man istället antar att väggytan och volymen inte samvarierar, så måste man vara konsekvent i alla deluppgifter för att få full poäng. Många förvillas av att α ökar nedåt i figuren. I (e) får man poäng för om man konstaterar att för minskande volym så koncentreras en konstant källeffekt på en mindre A. Annars.
DT1175 Ljud Räkneövningar RÖ sid 1
 DT1175 Ljud Räkneövningar RÖ sid 1 RÄKNEÖVNINGAR Ta med detta häfte till räkneövningstillfällena. Ta också med en fickräknare med log och trig. Lösningarna börjar på sidan 11. Elementär akustik 1. Beräkna
DT1175 Ljud Räkneövningar RÖ sid 1 RÄKNEÖVNINGAR Ta med detta häfte till räkneövningstillfällena. Ta också med en fickräknare med log och trig. Lösningarna börjar på sidan 11. Elementär akustik 1. Beräkna
Vad är ljud? Ljud skapas av vibrationer
 Vad är ljud? Ljud skapas av vibrationer När en gitarrist spelar på en sträng börjar den att svänga snabbt fram och tillbaka - den vibrerar och du hör ett ljud. När du sjunger är det dina stämband som vibrerar
Vad är ljud? Ljud skapas av vibrationer När en gitarrist spelar på en sträng börjar den att svänga snabbt fram och tillbaka - den vibrerar och du hör ett ljud. När du sjunger är det dina stämband som vibrerar
2010-02-10. F8 Rumsakustik, ljudabsorption. Hur stoppar vi ljudet? Rumsakustik 3 förklaringsmodeller. Isolering. Absorption. Statistisk rumsakustik
 F8 Rumsakustik, ljudabsorption Hur stoppar vi ljudet? Isolering Blockera ljudvägen ingen energiförlust Absorption Omvandla ljud till värme energiförlust Rumsakustik 3 förklaringsmodeller Statistisk rumsakustik
F8 Rumsakustik, ljudabsorption Hur stoppar vi ljudet? Isolering Blockera ljudvägen ingen energiförlust Absorption Omvandla ljud till värme energiförlust Rumsakustik 3 förklaringsmodeller Statistisk rumsakustik
Lathund, procent med bråk, åk 8
 Lathund, procent med bråk, åk 8 Procent betyder hundradel, men man kan också säga en av hundra. Ni ska kunna omvandla mellan bråkform, decimalform och procentform. Nedan kan ni se några omvandlingar. Bråkform
Lathund, procent med bråk, åk 8 Procent betyder hundradel, men man kan också säga en av hundra. Ni ska kunna omvandla mellan bråkform, decimalform och procentform. Nedan kan ni se några omvandlingar. Bråkform
4-6 Trianglar Namn:..
 4-6 Trianglar Namn:.. Inledning Hittills har du arbetat med parallellogrammer. En sådan har fyra hörn och motstående sidor är parallella. Vad händer om vi har en geometrisk figur som bara har tre hörn?
4-6 Trianglar Namn:.. Inledning Hittills har du arbetat med parallellogrammer. En sådan har fyra hörn och motstående sidor är parallella. Vad händer om vi har en geometrisk figur som bara har tre hörn?
Modul 6: Integraler och tillämpningar
 Institutionen för Matematik SF65 Envariabelanalys Läsåret 5/6 Modul 6: Integraler och tillämpningar Denna modul omfattar kapitel 6. och 6.5 samt kapitel 7 i kursboken Calculus av Adams och Essex och undervisas
Institutionen för Matematik SF65 Envariabelanalys Läsåret 5/6 Modul 6: Integraler och tillämpningar Denna modul omfattar kapitel 6. och 6.5 samt kapitel 7 i kursboken Calculus av Adams och Essex och undervisas
Facit med lösningsförslag kommer att anslås på vår hemsida www.ebersteinska.norrkoping.se. Du kan dessutom få dem via e-post, se nedan.
 Detta häfte innehåller uppgifter från fyra olika områden inom matematiken. Meningen är att de ska tjäna som en självtest inför gymnasiet. Klarar du dessa uppgifter så är du väl förberedd inför gymnasiestudier
Detta häfte innehåller uppgifter från fyra olika områden inom matematiken. Meningen är att de ska tjäna som en självtest inför gymnasiet. Klarar du dessa uppgifter så är du väl förberedd inför gymnasiestudier
Erfarenheter från ett pilotprojekt med barn i åldrarna 1 5 år och deras lärare
 Erfarenheter från ett pilotprojekt med barn i åldrarna 1 5 år och deras lärare I boken får vi följa hur barn tillsammans med sina lärare gör spännande matematikupptäckter - i rutinsituationer - i leken
Erfarenheter från ett pilotprojekt med barn i åldrarna 1 5 år och deras lärare I boken får vi följa hur barn tillsammans med sina lärare gör spännande matematikupptäckter - i rutinsituationer - i leken
Mätningar på op-förstärkare. Del 3, växelspänningsförstärkning med balanserad ingång.
 Mätningar på op-förstärkare. Del 3, växelspänningsförstärkning med balanserad ingång. Denna gång skall vi titta närmare på en förstärkare med balanserad ingång och obalanserad utgång. Normalt använder
Mätningar på op-förstärkare. Del 3, växelspänningsförstärkning med balanserad ingång. Denna gång skall vi titta närmare på en förstärkare med balanserad ingång och obalanserad utgång. Normalt använder
Snabbslumpade uppgifter från flera moment.
 Snabbslumpade uppgifter från flera moment. Uppgift nr Ställ upp och dividera utan hjälp av miniräknare talet 48 med 2 Uppgift nr 2 Skriv talet 3 8 00 med hjälp av decimalkomma. Uppgift nr 3 Uppgift nr
Snabbslumpade uppgifter från flera moment. Uppgift nr Ställ upp och dividera utan hjälp av miniräknare talet 48 med 2 Uppgift nr 2 Skriv talet 3 8 00 med hjälp av decimalkomma. Uppgift nr 3 Uppgift nr
Vi skall skriva uppsats
 Vi skall skriva uppsats E n vacker dag får du höra att du skall skriva uppsats. I den här texten får du veta vad en uppsats är, vad den skall innehålla och hur den bör se ut. En uppsats är en text som
Vi skall skriva uppsats E n vacker dag får du höra att du skall skriva uppsats. I den här texten får du veta vad en uppsats är, vad den skall innehålla och hur den bör se ut. En uppsats är en text som
SF1620 Matematik och modeller
 KTH Teknikvetenskap, Institutionen för matematik 1 SF160 Matematik och modeller 007-09-10 Andra veckan Trigonometri De trigonometriska funktionerna och enhetscirkeln Redan vid förra veckans avsnitt var
KTH Teknikvetenskap, Institutionen för matematik 1 SF160 Matematik och modeller 007-09-10 Andra veckan Trigonometri De trigonometriska funktionerna och enhetscirkeln Redan vid förra veckans avsnitt var
Pesach Laksman är lärarutbildare i matematik och matematikdidaktik vid Malmö högskola.
 111a Geometri med snöre Pesach Laksman är lärarutbildare i matematik och matematikdidaktik vid Malmö högskola. Areabegreppet När elever får frågan vad area betyder ges mestadels svar som antyder hur man
111a Geometri med snöre Pesach Laksman är lärarutbildare i matematik och matematikdidaktik vid Malmö högskola. Areabegreppet När elever får frågan vad area betyder ges mestadels svar som antyder hur man
konstanterna a och b så att ekvationssystemet x 2y = 1 2x + ay = b 2 a b
 Tentamen i Inledande matematik för V och AT, (TMV25), 20-0-26. Till denna uppgift skulle endast lämnas svar, men här ges kortfattade lösningar. a) Bestäm { konstanterna a och b så att ekvationssystemet
Tentamen i Inledande matematik för V och AT, (TMV25), 20-0-26. Till denna uppgift skulle endast lämnas svar, men här ges kortfattade lösningar. a) Bestäm { konstanterna a och b så att ekvationssystemet
Algebra, polynom & andragradsekvationer en pampig rubrik på ett annars relativt obetydligt dokument
 Algebra, polynom & andragradsekvationer en pampig rubrik på ett annars relativt obetydligt dokument Distributiva lagen a(b + c) = ab + ac 3(x + 4) = 3 x + 3 4 = 3x + 12 3(2x + 4) = 3 2x + 3 4 = 6x + 12
Algebra, polynom & andragradsekvationer en pampig rubrik på ett annars relativt obetydligt dokument Distributiva lagen a(b + c) = ab + ac 3(x + 4) = 3 x + 3 4 = 3x + 12 3(2x + 4) = 3 2x + 3 4 = 6x + 12
Kvalitetsrapport Så här går det
 Kvalitetsrapport Så här går det Uppföljning av det systematiska kvalitetsarbetet på Lärkan förskola, Öja Verksamhetsåret 2013/2014 Kort sammanfattning av enhetens kvalitetsarbete under verksamhetsåret
Kvalitetsrapport Så här går det Uppföljning av det systematiska kvalitetsarbetet på Lärkan förskola, Öja Verksamhetsåret 2013/2014 Kort sammanfattning av enhetens kvalitetsarbete under verksamhetsåret
3.1 Linjens ekvation med riktningskoefficient. y = kx + l.
 Kapitel Analytisk geometri Målet med detta kapitel är att göra läsaren bekant med ekvationerna för linjen, cirkeln samt ellipsen..1 Linjens ekvation med riktningskoefficient Vi utgår från ekvationen 1
Kapitel Analytisk geometri Målet med detta kapitel är att göra läsaren bekant med ekvationerna för linjen, cirkeln samt ellipsen..1 Linjens ekvation med riktningskoefficient Vi utgår från ekvationen 1
Föreläsning 8 och 9. insignal. utsignal. Tvåport. Hambley avsnitt 5.5-6.1
 1 Föreläsning 8 och 9 Hambley avsnitt 5.56.1 Tvåport En tvåport är en krets med en ingångsport och en gångsport. Dess symbol är en rektangel med ingångsporten till vänster och gångsporten till höger. Tvåporten
1 Föreläsning 8 och 9 Hambley avsnitt 5.56.1 Tvåport En tvåport är en krets med en ingångsport och en gångsport. Dess symbol är en rektangel med ingångsporten till vänster och gångsporten till höger. Tvåporten
SKOGLIGA TILLÄMPNINGAR
 STUDIEAVSNITT 3 SKOGLIGA TILLÄMPNINGAR I detta avsnitt ska vi titta på några av de skogliga tillämpningar på geometri som finns. SKOGSKARTAN EN MODELL AV VERKLIGHETEN Arbetar man i skogen klarar man sig
STUDIEAVSNITT 3 SKOGLIGA TILLÄMPNINGAR I detta avsnitt ska vi titta på några av de skogliga tillämpningar på geometri som finns. SKOGSKARTAN EN MODELL AV VERKLIGHETEN Arbetar man i skogen klarar man sig
Svenska Du kan med flyt läsa texter som handlar om saker du känner till. Du använder metoder som fungerar. Du kan förstå vad du läser.
 Svenska Du kan med flyt läsa texter som handlar om saker du känner till. Du använder metoder som fungerar. Du kan förstå vad du läser. Du berättar på ett enkelt sätt om det du tycker är viktigt i texten.
Svenska Du kan med flyt läsa texter som handlar om saker du känner till. Du använder metoder som fungerar. Du kan förstå vad du läser. Du berättar på ett enkelt sätt om det du tycker är viktigt i texten.
Övningshäfte Algebra, ekvationssystem och geometri
 Stockholms Tekniska Gmnasium --9 Övningshäfte Algebra, ekvationssstem och geometri Nivå: rätt svårt Fråga : f är ett polnom. Beräkna värdet av f, f och fπ Fråga : Ingångslönen på företaget Börjes Gurkinläggning
Stockholms Tekniska Gmnasium --9 Övningshäfte Algebra, ekvationssstem och geometri Nivå: rätt svårt Fråga : f är ett polnom. Beräkna värdet av f, f och fπ Fråga : Ingångslönen på företaget Börjes Gurkinläggning
Får nyanlända samma chans i den svenska skolan?
 Får nyanlända samma chans i den svenska skolan? Sammanställning oktober 2015 De nyanlända eleverna (varit här högst fyra år) klarar den svenska skolan sämre än andra elever. Ett tydligt tecken är att för
Får nyanlända samma chans i den svenska skolan? Sammanställning oktober 2015 De nyanlända eleverna (varit här högst fyra år) klarar den svenska skolan sämre än andra elever. Ett tydligt tecken är att för
Avsikt På ett lekfullt sätt färdighetsträna, utveckla elevers känsla för hur vårt talsystem är uppbyggt samt hitta mönster som uppkommer.
 Strävorna 4A 100-rutan... förmåga att förstå, föra och använda logiska resonemang, dra slutsatser och generalisera samt muntligt och skriftligt förklara och argumentera för sitt tänkande.... grundläggande
Strävorna 4A 100-rutan... förmåga att förstå, föra och använda logiska resonemang, dra slutsatser och generalisera samt muntligt och skriftligt förklara och argumentera för sitt tänkande.... grundläggande
Övningshäfte i matematik för. Kemistuderande BL 05
 Övningshäfte i matematik för Kemistuderande BL 05 Detta häfte innehåller några grundläggande övningar i de delar av matematiken som man har användning för i de tidiga kemistudierna. Nivån är gymnasiematematik,
Övningshäfte i matematik för Kemistuderande BL 05 Detta häfte innehåller några grundläggande övningar i de delar av matematiken som man har användning för i de tidiga kemistudierna. Nivån är gymnasiematematik,
för M Skrivtid utbreder sig (0,5 p)
 Tentamen i tillämpad Våglära FAF260, 2015 06 05 för M Skrivtid 08.00 13.00 Hjälpmedel: Formelblad och miniräknare Uppgifterna är inte sorteradee i svårighetsgrad Börja varje ny uppgift på ett nytt blad
Tentamen i tillämpad Våglära FAF260, 2015 06 05 för M Skrivtid 08.00 13.00 Hjälpmedel: Formelblad och miniräknare Uppgifterna är inte sorteradee i svårighetsgrad Börja varje ny uppgift på ett nytt blad
Datorövning 2 Statistik med Excel (Office 2007, svenska)
 Datorövning 2 Statistik med Excel (Office 2007, svenska) Denna datorövning fokuserar på att upptäcka samband mellan två variabler. Det görs genom att rita spridningsdiagram och beräkna korrelationskoefficienter
Datorövning 2 Statistik med Excel (Office 2007, svenska) Denna datorövning fokuserar på att upptäcka samband mellan två variabler. Det görs genom att rita spridningsdiagram och beräkna korrelationskoefficienter
Kapitel 6. f(x) = sin x. Figur 6.1: Funktionen sin x. 1 Oinas-Kukkonen m.fl. Kurs 6 kapitel 1
 Kapitel 6 Gränsvärde 6. Definition av gränsvärde När vi undersöker gränsvärdet av en funktion undersöker vi vad som händer med funktionsvärdet då variabeln, x, går mot ett visst värde. Frågeställningen
Kapitel 6 Gränsvärde 6. Definition av gränsvärde När vi undersöker gränsvärdet av en funktion undersöker vi vad som händer med funktionsvärdet då variabeln, x, går mot ett visst värde. Frågeställningen
Omvandla Vinklar. 1 Mattematiskt Tankesätt
 Omvandla Vinklar 1 Mattematiskt Tankesätt (Kan användas till mer än bara vinklar) 2 Omvandla med hjälp av Huvudräkning (Snabbmetod i slutet av punkt 2) 3 Omvandla med Miniräknare (Casio) Läs denna Först
Omvandla Vinklar 1 Mattematiskt Tankesätt (Kan användas till mer än bara vinklar) 2 Omvandla med hjälp av Huvudräkning (Snabbmetod i slutet av punkt 2) 3 Omvandla med Miniräknare (Casio) Läs denna Först
vägtrafiken? Hur mycket bullrar
 Hur mycket bullrar vägtrafiken? Information från Boverket och Sveriges Kommuner och Landsting om hur du enkelt och snabbt kan beräkna utbredningen av buller från vägtrafik Foto: Hans Ekestang Översiktlig
Hur mycket bullrar vägtrafiken? Information från Boverket och Sveriges Kommuner och Landsting om hur du enkelt och snabbt kan beräkna utbredningen av buller från vägtrafik Foto: Hans Ekestang Översiktlig
Tentamen i Fysik A, Tekniskt-Naturvetenskapligt basår
 Tentamen i Fysik A, Tekniskt-Naturvetenskapligt basår Datum: 05-01-20 Skrivtid: 16.00-22.00 Hjälpmedel: Räknare, formelsamling Lärare: A. Gustafsson, M. Hamrin, L. Lundmark och L-E. Svensson Namn: Grupp:
Tentamen i Fysik A, Tekniskt-Naturvetenskapligt basår Datum: 05-01-20 Skrivtid: 16.00-22.00 Hjälpmedel: Räknare, formelsamling Lärare: A. Gustafsson, M. Hamrin, L. Lundmark och L-E. Svensson Namn: Grupp:
Elektronen och laddning
 Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Träning i bevisföring
 KTHs Matematiska Cirkel Träning i bevisföring Andreas Enblom Institutionen för matematik, 2005 Finansierat av Marianne och Marcus Wallenbergs Stiftelse 1 Mängdlära Här kommer fyra tips på hur man visar
KTHs Matematiska Cirkel Träning i bevisföring Andreas Enblom Institutionen för matematik, 2005 Finansierat av Marianne och Marcus Wallenbergs Stiftelse 1 Mängdlära Här kommer fyra tips på hur man visar
Volymer av n dimensionella klot
 252 Volymer av n dimensionella klot Mikael Passare Stockholms universitet Ett klot med radien r är mängden av punkter vars avstånd till en given punkt (medelpunkten) är högst r. Låt oss skriva B 3 (r)
252 Volymer av n dimensionella klot Mikael Passare Stockholms universitet Ett klot med radien r är mängden av punkter vars avstånd till en given punkt (medelpunkten) är högst r. Låt oss skriva B 3 (r)
När jag har arbetat klart med det här området ska jag:
 Kraft och rörelse När jag har arbetat klart med det här området ska jag: kunna ge exempel på olika krafter och kunna använda mina kunskaper om dessa när jag förklarar olika fysikaliska fenomen, veta vad
Kraft och rörelse När jag har arbetat klart med det här området ska jag: kunna ge exempel på olika krafter och kunna använda mina kunskaper om dessa när jag förklarar olika fysikaliska fenomen, veta vad
Nämnarens adventskalendern 2007
 Nämnarens adventskalendern 2007 1 När det närmar sig jul är det kallt. Då behöver de tre tomtenissarna både halsduk och mössa när de leker i snön. I korgen ligger en röd, en blå och en randig halsduk.
Nämnarens adventskalendern 2007 1 När det närmar sig jul är det kallt. Då behöver de tre tomtenissarna både halsduk och mössa när de leker i snön. I korgen ligger en röd, en blå och en randig halsduk.
Väga paket och jämföra priser
 strävorna 2AC 3AC Väga paket och jämföra priser begrepp rutinuppgifter tal geometri Avsikt och matematikinnehåll Den huvudsakliga avsikten med denna aktivitet är att ge elever möjlighet att utveckla grundläggande
strävorna 2AC 3AC Väga paket och jämföra priser begrepp rutinuppgifter tal geometri Avsikt och matematikinnehåll Den huvudsakliga avsikten med denna aktivitet är att ge elever möjlighet att utveckla grundläggande
Ämnesområde Hörselvetenskap A Kurs Akustik och ljudmiljö, 7 hp Kurskod: HÖ1015 Tentamenstillfälle 1
 Hälsoakademin Kod: Ämnesområde Hörselvetenskap A Kurs Akustik och ljudmiljö, 7 hp Kurskod: HÖ115 Tentamenstillfälle 1 Datum 211 11 3 Tid 4 timmar Kursansvarig Susanne Köbler Tillåtna hjälpmedel Miniräknare
Hälsoakademin Kod: Ämnesområde Hörselvetenskap A Kurs Akustik och ljudmiljö, 7 hp Kurskod: HÖ115 Tentamenstillfälle 1 Datum 211 11 3 Tid 4 timmar Kursansvarig Susanne Köbler Tillåtna hjälpmedel Miniräknare
I den här delen används inte räknare. Motivera alltid din slutsats med matematiska uttryck, figurer, förklaring el.dyl.
 DEL 1 Tid 30 min Poängantal 20 I den här delen används inte räknare. Motivera alltid din slutsats med matematiska uttryck, figurer, förklaring el.dyl. 1. Vilket är det största heltalet, som uppfyller följande
DEL 1 Tid 30 min Poängantal 20 I den här delen används inte räknare. Motivera alltid din slutsats med matematiska uttryck, figurer, förklaring el.dyl. 1. Vilket är det största heltalet, som uppfyller följande
Laborativ matematik som bedömningsform. Per Berggren och Maria Lindroth 2016-01-28
 Laborativ matematik som bedömningsform Per Berggren och Maria Lindroth 2016-01-28 Kul matematik utan lärobok Vilka förmågor tränas Problemlösning (Förstå frågan i en textuppgift, Använda olika strategier
Laborativ matematik som bedömningsform Per Berggren och Maria Lindroth 2016-01-28 Kul matematik utan lärobok Vilka förmågor tränas Problemlösning (Förstå frågan i en textuppgift, Använda olika strategier
2005-01-31. Hävarmen. Peter Kock
 2005-01-31 Hävarmen Kurs: WT0010 Peter Kock Handledare: Jan Sandberg Sammanfattning Om man slår upp ordet hävarm i ett lexikon så kan man läsa att hävarm är avståndet mellan kraften och vridningspunkten.
2005-01-31 Hävarmen Kurs: WT0010 Peter Kock Handledare: Jan Sandberg Sammanfattning Om man slår upp ordet hävarm i ett lexikon så kan man läsa att hävarm är avståndet mellan kraften och vridningspunkten.
Facit åk 6 Prima Formula
 Facit åk 6 Prima Formula Kapitel 3 Algebra och samband Sidan 95 1 a 12 cm (3 4 cm) b Han vet inte att uttrycket 3s betyder 3 s eller s + s + s 2 a 5x b 6y c 12z 3 a 30 cm (5 6 cm) b 30 cm (6 5 cm) Sidan
Facit åk 6 Prima Formula Kapitel 3 Algebra och samband Sidan 95 1 a 12 cm (3 4 cm) b Han vet inte att uttrycket 3s betyder 3 s eller s + s + s 2 a 5x b 6y c 12z 3 a 30 cm (5 6 cm) b 30 cm (6 5 cm) Sidan
Repetitivt arbete ska minska
 Repetitivt arbete ska minska Ett repetitivt arbete innebär att man upprepar en eller några få arbetsuppgifter med liknande arbetsrörelser om och om igen. Ofta med ett högt arbetstempo. Ett repetitivt arbete
Repetitivt arbete ska minska Ett repetitivt arbete innebär att man upprepar en eller några få arbetsuppgifter med liknande arbetsrörelser om och om igen. Ofta med ett högt arbetstempo. Ett repetitivt arbete
Texturbild. Lagerpaletten du kommer arbeta med ser du till höger. 1. Kopiera bakgrunden till ett nytt lager och gör den svartvit.
 Texturbild En guide om hur man skapar en bild med matta färger och texturiserad yta. Guiden innehåller moment där man får pröva sig fram och resultatet kanske inte blir det man tänkt sig direkt, men med
Texturbild En guide om hur man skapar en bild med matta färger och texturiserad yta. Guiden innehåller moment där man får pröva sig fram och resultatet kanske inte blir det man tänkt sig direkt, men med
ATT KUNNA TILL. MA1050 Matte Grund. 2011-06-14 Vuxenutbildningen Dennis Jonsson
 ATT KUNNA TILL MA1050 Matte Grund 2011-06-14 Vuxenutbildningen Dennis Jonsson Sida 2 av 5 Att kunna till prov G1 Kunna ställa upp och beräkna additions-, subtraktions-, multiplikations- och divisuionsuppgifter
ATT KUNNA TILL MA1050 Matte Grund 2011-06-14 Vuxenutbildningen Dennis Jonsson Sida 2 av 5 Att kunna till prov G1 Kunna ställa upp och beräkna additions-, subtraktions-, multiplikations- och divisuionsuppgifter
Boken om Teknik. Boken om Teknik är en grundbok i Teknik för åk 4 6.
 Boken om Teknik Boken om Teknik är en grundbok i Teknik för åk 4 6. PROVLEKTION: Teknikens arbetssätt att göra på riktigt Följande provlektion är ett utdrag ur Boken om Teknik. Uppslaget som är hämtat
Boken om Teknik Boken om Teknik är en grundbok i Teknik för åk 4 6. PROVLEKTION: Teknikens arbetssätt att göra på riktigt Följande provlektion är ett utdrag ur Boken om Teknik. Uppslaget som är hämtat
D A B A D B B D. Trepoängsproblem. Kängurutävlingen 2012 Benjamin
 Kängurutävlingen enjamin Trepoängsproblem. Skrivtavlan i klassrummet är 6 meter bred. Mittdelen är m bred. De båda yttre delarna är lika breda. Hur bred är den högra delen? A: m :,5 m C:,5 m D:,75 m E:
Kängurutävlingen enjamin Trepoängsproblem. Skrivtavlan i klassrummet är 6 meter bred. Mittdelen är m bred. De båda yttre delarna är lika breda. Hur bred är den högra delen? A: m :,5 m C:,5 m D:,75 m E:
En gemensam bild av verkligheten
 En gemensam bild av verkligheten En meningsfull diskussion om Sveriges framtid förutsätter en gemensam bild av var vi står i dag. Hur ser verkligheten egentligen ut och vilka fakta beskriver den bäst?
En gemensam bild av verkligheten En meningsfull diskussion om Sveriges framtid förutsätter en gemensam bild av var vi står i dag. Hur ser verkligheten egentligen ut och vilka fakta beskriver den bäst?
Ha det kul med att förmedla och utveckla ett knepigt område!
 Kul med pizzabitar Första gången eleverna får materialet i handen bör dem få sin egen tid till att undersöka det på det viset blir dem bekanta med dess olika delar. Det kan också vara en god idé att låta
Kul med pizzabitar Första gången eleverna får materialet i handen bör dem få sin egen tid till att undersöka det på det viset blir dem bekanta med dess olika delar. Det kan också vara en god idé att låta
1 Navier-Stokes ekvationer
 Föreläsning 5. 1 Navier-Stokes ekvationer I förra föreläsningen härledde vi rörelsemängdsekvationen Du j Dt = 1 τ ij + g j. (1) ρ x i Vi konstaterade också att spänningstensorn för en inviskös fluid kan
Föreläsning 5. 1 Navier-Stokes ekvationer I förra föreläsningen härledde vi rörelsemängdsekvationen Du j Dt = 1 τ ij + g j. (1) ρ x i Vi konstaterade också att spänningstensorn för en inviskös fluid kan
Sammanfattning av kursdag 2, 2013-03-07 i Stra ngna s och 2013-03-12 Eskilstuna
 Sammanfattning av kursdag 2, 2013-03-07 i Stra ngna s och 2013-03-12 Eskilstuna Sammanfattning och genomgång av lektion 1 samt hemläxa. -Hur ta ut en position i sjökortet? Mät med Passaren mellan positionen
Sammanfattning av kursdag 2, 2013-03-07 i Stra ngna s och 2013-03-12 Eskilstuna Sammanfattning och genomgång av lektion 1 samt hemläxa. -Hur ta ut en position i sjökortet? Mät med Passaren mellan positionen
Bruksanvisning - Spisvakt Prefi 2.3
 Bruksanvisning - Spisvakt Prefi 2.3 Försäljning och support Rutab AB Tel: 0380-55 50 60 Lerbacksgatan 2 571 38 Nässjö order@rutab.se http://www.rutab.se Utvecklad och tillverkad av: Cabinova AB Verkstadsvägen
Bruksanvisning - Spisvakt Prefi 2.3 Försäljning och support Rutab AB Tel: 0380-55 50 60 Lerbacksgatan 2 571 38 Nässjö order@rutab.se http://www.rutab.se Utvecklad och tillverkad av: Cabinova AB Verkstadsvägen
Särskilt stöd i grundskolan
 Enheten för utbildningsstatistik 15-1-8 1 (1) Särskilt stöd i grundskolan I den här promemorian beskrivs Skolverkets statistik om särskilt stöd i grundskolan läsåret 1/15. Sedan hösten 1 publicerar Skolverket
Enheten för utbildningsstatistik 15-1-8 1 (1) Särskilt stöd i grundskolan I den här promemorian beskrivs Skolverkets statistik om särskilt stöd i grundskolan läsåret 1/15. Sedan hösten 1 publicerar Skolverket
Projekt benböj på olika belastningar med olika lång vila
 Projekt benböj på olika belastningar med olika lång vila Finns det några skillnader i effektutveckling(kraft x hastighet) mellan koncentriskt och excentriskt arbete på olika belastningar om man vilar olika
Projekt benböj på olika belastningar med olika lång vila Finns det några skillnader i effektutveckling(kraft x hastighet) mellan koncentriskt och excentriskt arbete på olika belastningar om man vilar olika
Kängurun Matematikens hopp Benjamin 2006 A: B: C: D: E:
 3-poängsproblem : = + + Vilket tal ska frågetecknet ersättas med A: B: C: D: E: : Sex tal står skrivna på korten här intill. Vilket är det minsta tal man kan bilda genom att lägga korten efter varandra
3-poängsproblem : = + + Vilket tal ska frågetecknet ersättas med A: B: C: D: E: : Sex tal står skrivna på korten här intill. Vilket är det minsta tal man kan bilda genom att lägga korten efter varandra
Varför är det så viktigt hur vi bedömer?! Christian Lundahl!
 Varför är det så viktigt hur vi bedömer?! Christian Lundahl! Fyra olika aspekter! Rättvisa! Reflektion och utvärdering av vår egen undervisning! Motivation för lärande! Metalärande (kunskapssyn)! 1. Rättvisa!
Varför är det så viktigt hur vi bedömer?! Christian Lundahl! Fyra olika aspekter! Rättvisa! Reflektion och utvärdering av vår egen undervisning! Motivation för lärande! Metalärande (kunskapssyn)! 1. Rättvisa!
Stockholms Tekniska Gymnasium 2014-11-19. Prov Fysik 2 Mekanik
 Prov Fysik 2 Mekanik För samtliga uppgifter krävs om inte annat står antingen en tydlig och klar motivering eller fullständig lösning och att det går att följa lösningsgången. Fråga 1: Keplers tredje lag
Prov Fysik 2 Mekanik För samtliga uppgifter krävs om inte annat står antingen en tydlig och klar motivering eller fullständig lösning och att det går att följa lösningsgången. Fråga 1: Keplers tredje lag
3. Värmeutvidgning (s. 49 57)
 3. Värmeutvidgning (s. 49 57) Om du vill öppna ett burklock som har fastnat kan du värma det under varmt vatten en stund och sedan lossnar det enklare. Detta beror på att värmen får locket att utvidga
3. Värmeutvidgning (s. 49 57) Om du vill öppna ett burklock som har fastnat kan du värma det under varmt vatten en stund och sedan lossnar det enklare. Detta beror på att värmen får locket att utvidga
David Wessman, Lund, 30 oktober 2014 Statistisk Termodynamik - Kapitel 5. Sammanfattning av Gunnar Ohléns bok Statistisk Termodynamik.
 Sammanfattning av Gunnar Ohléns bok Statistisk Termodynamik. 1 Jämviktsvillkor Om vi har ett stort system som består av ett litet system i kontakt med en värmereservoar. Storheter för det lilla systemet
Sammanfattning av Gunnar Ohléns bok Statistisk Termodynamik. 1 Jämviktsvillkor Om vi har ett stort system som består av ett litet system i kontakt med en värmereservoar. Storheter för det lilla systemet
Mätning av effekter. Vad är elektrisk effekt? Vad är aktiv-, skenbar- reaktiv- medel- och direkteffekt samt effektfaktor?
 Mätning av effekter Vad är elektrisk effekt? Vad är aktiv-, skenbar- reaktiv- medel- och direkteffekt samt effektfaktor? Denna studie ger vägledning om de grundläggande parametrarna för 3-fas effektmätning.
Mätning av effekter Vad är elektrisk effekt? Vad är aktiv-, skenbar- reaktiv- medel- och direkteffekt samt effektfaktor? Denna studie ger vägledning om de grundläggande parametrarna för 3-fas effektmätning.
Linjära system av differentialekvationer
 CTH/GU LABORATION MVE0-0/03 Matematiska vetenskaper Linjära system av differentialekvationer Inledning Vi har i envariabelanalysen sett på allmäna system av differentialekvationer med begynnelsevillkor
CTH/GU LABORATION MVE0-0/03 Matematiska vetenskaper Linjära system av differentialekvationer Inledning Vi har i envariabelanalysen sett på allmäna system av differentialekvationer med begynnelsevillkor
Föreläsning 8: Räkning. Duvhålsprincipen. Kombinatorik
 Föreläsning 8: Räkning. Duvhålsprincipen. Kombinatorik Summaregeln Om och B är disjunkta mängder så B = + B, ty innehåller inga upprepningar Produktregeln Om och B är disjunkta mängder så är B = B Exempel:
Föreläsning 8: Räkning. Duvhålsprincipen. Kombinatorik Summaregeln Om och B är disjunkta mängder så B = + B, ty innehåller inga upprepningar Produktregeln Om och B är disjunkta mängder så är B = B Exempel:
Tentamen i matematisk statistik (9MA241/9MA341/LIMAB6, STN2) 2012-01-09 kl 08-13
 LINKÖPINGS UNIVERSITET MAI Johan Thim Tentamen i matematisk statistik (9MA241/9MA341/LIMAB6, STN2) 212-1-9 kl 8-13 Hjälpmedel är: miniräknare med tömda minnen och formelbladet bifogat. Varje uppgift är
LINKÖPINGS UNIVERSITET MAI Johan Thim Tentamen i matematisk statistik (9MA241/9MA341/LIMAB6, STN2) 212-1-9 kl 8-13 Hjälpmedel är: miniräknare med tömda minnen och formelbladet bifogat. Varje uppgift är
Företagsamhetsmätning Kronobergs län JOHAN KREICBERGS HÖSTEN 2010
 Företagsamhetsmätning Kronobergs län JOHAN KREICBERGS HÖSTEN 2010 Företagsamheten Kronobergs län Inledning Svenskt Näringslivs företagsamhetsmätning presenteras varje halvår. Syftet är att studera om antalet
Företagsamhetsmätning Kronobergs län JOHAN KREICBERGS HÖSTEN 2010 Företagsamheten Kronobergs län Inledning Svenskt Näringslivs företagsamhetsmätning presenteras varje halvår. Syftet är att studera om antalet
Presentationsövningar
 Varje möte då temadialog används bör inledas med en presentationsövning. har flera syften. Både föräldrar och ledare har nytta av att gå igenom samtliga deltagares namn och dessutom få en tydlig bild av
Varje möte då temadialog används bör inledas med en presentationsövning. har flera syften. Både föräldrar och ledare har nytta av att gå igenom samtliga deltagares namn och dessutom få en tydlig bild av
Om erbjudandet för din pensionsförsäkring med traditionell förvaltning.
 Om erbjudandet för din pensionsförsäkring med traditionell förvaltning. Reflex Pensionsförsäkring Pensionsförsäkring Fakta om erbjudandet att ändra villkor till vår nya traditionella förvaltning Nya Trad
Om erbjudandet för din pensionsförsäkring med traditionell förvaltning. Reflex Pensionsförsäkring Pensionsförsäkring Fakta om erbjudandet att ändra villkor till vår nya traditionella förvaltning Nya Trad
4-9 Rymdgeometri Namn:.
 4-9 Rymdgeometri Namn:. Inledning Rymden har alltid fascinerat. Men vad menas med rymd i matematisk eller geometrisk mening? Här skall du få studera 3- dimensionella figurer och hur man beräknar volymen
4-9 Rymdgeometri Namn:. Inledning Rymden har alltid fascinerat. Men vad menas med rymd i matematisk eller geometrisk mening? Här skall du få studera 3- dimensionella figurer och hur man beräknar volymen
Tentamen i SG1102 Mekanik, mindre kurs
 Tentamen i SG1102 Mekanik, mindre kurs 2014-03-20 Var noga med att skilja på skalärer och vektorer. Rita tydliga figurer och motivera lösningarna väl. Enda tillåtna hjälpmedel är papper, penna, linjal
Tentamen i SG1102 Mekanik, mindre kurs 2014-03-20 Var noga med att skilja på skalärer och vektorer. Rita tydliga figurer och motivera lösningarna väl. Enda tillåtna hjälpmedel är papper, penna, linjal
Ekvationssystem, Matriser och Eliminationsmetoden
 Matematiska institutionen Göteborgs universitet och Chalmers tekniska högskola Version 359 Ekvationssystem, Matriser och Eliminationsmetoden - En inledning Ekvationssystem - matrisformulering Vi såg att
Matematiska institutionen Göteborgs universitet och Chalmers tekniska högskola Version 359 Ekvationssystem, Matriser och Eliminationsmetoden - En inledning Ekvationssystem - matrisformulering Vi såg att
Tentamen i Linjär algebra (TATA31/TEN1) 2013 08 24, 14 19.
 LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
LINKÖPINGS UNIVERSITET Matematiska Institutionen Ulf Janfalk Kurskod: TATA Provkod: TEN Tentamen i Linjär algebra (TATA/TEN 8, 9. Inga hjälpmedel. Ej räknedosa. För godkänt räcker 9 poäng och minst uppgifter
Institutionen för matematik Envariabelanalys 1. Jan Gelfgren Datum: Fredag 9/12, 2011 Tid: 9-15 Hjälpmedel: Inga (ej miniräknare)
 Umeå universitet Dugga i matematik Institutionen för matematik Envariabelanalys 1 och matematisk statistik IE, ÖI, Stat. och Frist. Jan Gelfgren Datum: Fredag 9/12, 2011 Tid: 9-15 Hjälpmedel: Inga (ej
Umeå universitet Dugga i matematik Institutionen för matematik Envariabelanalys 1 och matematisk statistik IE, ÖI, Stat. och Frist. Jan Gelfgren Datum: Fredag 9/12, 2011 Tid: 9-15 Hjälpmedel: Inga (ej
1. Frekvensfunktionen nedan är given. (3p)
 TENTAMEN I MATEMATIK MED MATEMATISK STATISTIK HF14 TEN 11 kl 1.15-.15 Hjälpmedel: Formler och tabeller i statistik, räknedosa Fullständiga lösningar erfordras till samtliga uppgifter. Lösningarna skall
TENTAMEN I MATEMATIK MED MATEMATISK STATISTIK HF14 TEN 11 kl 1.15-.15 Hjälpmedel: Formler och tabeller i statistik, räknedosa Fullständiga lösningar erfordras till samtliga uppgifter. Lösningarna skall
Så kan du arbeta med medarbetarenkäten. Guide för chefer i Göteborgs Stad
 Så kan du arbeta med medarbetarenkäten Guide för chefer i Göteborgs Stad Till dig som är chef i Göteborgs Stad Medarbetarenkäten är ett redskap för dig som chef. Resultaten levererar förstås inte hela
Så kan du arbeta med medarbetarenkäten Guide för chefer i Göteborgs Stad Till dig som är chef i Göteborgs Stad Medarbetarenkäten är ett redskap för dig som chef. Resultaten levererar förstås inte hela
x 2 + px = ( x + p 2 x 2 2x = ( x + 2
 Inledande kurs i matematik, avsnitt P.3 P.3. Bestäm en ekvation för cirkeln med mittpunkt i (0, 0) och radie 4. Med hjälp av kvadratkompletteringsformeln + p = ( + p ) ( p ) En cirkel med mittpunkt i (
Inledande kurs i matematik, avsnitt P.3 P.3. Bestäm en ekvation för cirkeln med mittpunkt i (0, 0) och radie 4. Med hjälp av kvadratkompletteringsformeln + p = ( + p ) ( p ) En cirkel med mittpunkt i (
Effekt av balansering 2010 med hänsyn tagen till garantipension och bostadstillägg
 Effekt av balansering 2010 med hänsyn tagen till garantipension och bostadstillägg Balanseringen inom pensionssystemet påverkar pensionärer med inkomstpension och tilläggspension. Balanseringen innebär
Effekt av balansering 2010 med hänsyn tagen till garantipension och bostadstillägg Balanseringen inom pensionssystemet påverkar pensionärer med inkomstpension och tilläggspension. Balanseringen innebär
NATIONELLA MATEMATIKTÄVLING
 NATIONELLA MATEMATIKTÄVLING PRATA OM SPELS EN KURS I SANNOLIKHET 1 INLEDNING Sannolikhetskursen består av sju olika steg där det sista steget utgörs av själva tävlingsmomentet. Det är upp till pedagogen
NATIONELLA MATEMATIKTÄVLING PRATA OM SPELS EN KURS I SANNOLIKHET 1 INLEDNING Sannolikhetskursen består av sju olika steg där det sista steget utgörs av själva tävlingsmomentet. Det är upp till pedagogen
4-3 Vinklar Namn: Inledning. Vad är en vinkel?
 4-3 Vinklar Namn: Inledning I det här kapitlet skall du lära dig allt om vinklar: spetsiga, trubbiga och räta vinklar. Och inte minst hur man mäter vinklar. Att mäta vinklar och sträckor är grundläggande
4-3 Vinklar Namn: Inledning I det här kapitlet skall du lära dig allt om vinklar: spetsiga, trubbiga och räta vinklar. Och inte minst hur man mäter vinklar. Att mäta vinklar och sträckor är grundläggande
Antal grodor i varje familj Antal hopp tills alla bytt plats Ökning 1 3 5 2 8 7 3 15 9 4 24
 strävorna 1AB Grodhopp problemlösning taluppfattning algebra Avsikt och matematikinnehåll Elever behöver få möta många aktiviteter där de kan se att algebra bland annat är generaliserad aritmetik. För
strävorna 1AB Grodhopp problemlösning taluppfattning algebra Avsikt och matematikinnehåll Elever behöver få möta många aktiviteter där de kan se att algebra bland annat är generaliserad aritmetik. För
Rallylydnad Nybörjarklass
 Rallylydnad_Mom_Nyborjarklass.doc Remiss på Nya beskrivningar, börjar gälla 2017-01-01 Sida 1 (5) Mom nr Skylt Rallylydnad Nybörjarklass Beskrivning Start Här börjar banan. Startpositionen vid skylten
Rallylydnad_Mom_Nyborjarklass.doc Remiss på Nya beskrivningar, börjar gälla 2017-01-01 Sida 1 (5) Mom nr Skylt Rallylydnad Nybörjarklass Beskrivning Start Här börjar banan. Startpositionen vid skylten
Individuellt Mjukvaruutvecklingsprojekt
 Individuellt Mjukvaruutvecklingsprojekt RPG-spel med JavaScript Författare Robin Bertram Datum 2013 06 10 1 Abstrakt Den här rapporten är en post mortem -rapport som handlar om utvecklandet av ett RPG-spel
Individuellt Mjukvaruutvecklingsprojekt RPG-spel med JavaScript Författare Robin Bertram Datum 2013 06 10 1 Abstrakt Den här rapporten är en post mortem -rapport som handlar om utvecklandet av ett RPG-spel
DOP-matematik Copyright Tord Persson. Bråktal -3-2 -1 0 1 2 3. Läs av vilka tal på tallinjen, som pilarna pekar på. Uppgift nr 10 -3-2 -1 0 1 2 3
 Bråktal Uppgift nr En limpa delas i 4 lika stora delar. Hur stor del av limpan blir varje del? Uppgift nr 2 Hur många tiondelar behövs för att det skall räcka till en hel? Uppgift nr Hur läser man ut bråket
Bråktal Uppgift nr En limpa delas i 4 lika stora delar. Hur stor del av limpan blir varje del? Uppgift nr 2 Hur många tiondelar behövs för att det skall räcka till en hel? Uppgift nr Hur läser man ut bråket
10.03.2010. Översikt. Rapport från skolverket. Förändring av matematikprestationerna 1995 2003-2007. Grundtankar bakom Pixel
 Översikt Hur är situationen i Sverige och Norge när det gäller matematik-kompetensen? Är det nödvändigt att undervisa på andra sätt än vi gjort tidigare? Förändring av matematikprestationerna 1995 2003-2007
Översikt Hur är situationen i Sverige och Norge när det gäller matematik-kompetensen? Är det nödvändigt att undervisa på andra sätt än vi gjort tidigare? Förändring av matematikprestationerna 1995 2003-2007
Tentamen. Makroekonomi NA0133. Juni 2016 Skrivtid 3 timmar.
 Jag har svarat på följande fyra frågor: 1 2 3 4 5 6 Min kod: Institutionen för ekonomi Rob Hart Tentamen Makroekonomi NA0133 Juni 2016 Skrivtid 3 timmar. Regler Svara på 4 frågor. (Vid svar på fler än
Jag har svarat på följande fyra frågor: 1 2 3 4 5 6 Min kod: Institutionen för ekonomi Rob Hart Tentamen Makroekonomi NA0133 Juni 2016 Skrivtid 3 timmar. Regler Svara på 4 frågor. (Vid svar på fler än
FRÅN A TILL Ö LäraMera Ab / www.laramera.se och Allemansdata Ab / www.allemansdata.se FRÅN A TILL Ö
 I programmet finns 11 olika aktiviteter för att träna varje bokstav och på att känna igen ord. För varje bokstav kan olika övningsblad skrivas ut: Inledningsvis väljer du vilken bokstav du vill öva på.
I programmet finns 11 olika aktiviteter för att träna varje bokstav och på att känna igen ord. För varje bokstav kan olika övningsblad skrivas ut: Inledningsvis väljer du vilken bokstav du vill öva på.
Grundläggande Akustik
 Läran om ljud och ljudutbredning Ljud i fritt fält Ljudet utbreder sig som tryckväxlingar kring atmosfärstrycket Våglängden= c/f I luft, ljudhastigheten c= 344 m/s eller 1130 ft/s 1ft= 0.3048 m Intensiteten
Läran om ljud och ljudutbredning Ljud i fritt fält Ljudet utbreder sig som tryckväxlingar kring atmosfärstrycket Våglängden= c/f I luft, ljudhastigheten c= 344 m/s eller 1130 ft/s 1ft= 0.3048 m Intensiteten
Tentamen SSY041 Sensorer, Signaler och System, del A, Z2
 Tentamen SSY4 Sensorer, Signaler och System, del A, Z Examinator: Ants R. Silberberg 6 Dec kl. 8.3-.3, sal: Hörsalsvägen Förfrågningar: Ants Silberberg, tel. 88 Lösningar: Anslås måndag december på institutionens
Tentamen SSY4 Sensorer, Signaler och System, del A, Z Examinator: Ants R. Silberberg 6 Dec kl. 8.3-.3, sal: Hörsalsvägen Förfrågningar: Ants Silberberg, tel. 88 Lösningar: Anslås måndag december på institutionens
Handledning för digitala verktyg Talsyntes och rättstavningsprogram. Vital, StavaRex och SpellRight
 Handledning för digitala verktyg Talsyntes och rättstavningsprogram Vital, StavaRex och SpellRight Elevens namn:.. Skola: Datum:.. Varför behövs en handledning? Denna handledning är tänkt att användas
Handledning för digitala verktyg Talsyntes och rättstavningsprogram Vital, StavaRex och SpellRight Elevens namn:.. Skola: Datum:.. Varför behövs en handledning? Denna handledning är tänkt att användas
Logga in. Gå in på: www.t-d.se. Klicka på Logga in. Klicka på den region, kommun eller organisation där din verksamhet finns
 Registrera I TD Logga in Gå in på: www.t-d.se Klicka på Logga in. Klicka på den region, kommun eller organisation där din verksamhet finns inventerad och registrerad. Skriv in ditt användarnamn och lösenord.
Registrera I TD Logga in Gå in på: www.t-d.se Klicka på Logga in. Klicka på den region, kommun eller organisation där din verksamhet finns inventerad och registrerad. Skriv in ditt användarnamn och lösenord.
Sannolikhet och Odds
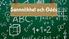 Sannolikhet och Odds Sannolikhet Tärning (Orange) och (Blå) 0 0 0 Om man satsat sina pengar på rätt summa multipliceras oddset med insatsen (pengarna man satsar) Odds Utfall (summan av två tärningar) Sannolikhet
Sannolikhet och Odds Sannolikhet Tärning (Orange) och (Blå) 0 0 0 Om man satsat sina pengar på rätt summa multipliceras oddset med insatsen (pengarna man satsar) Odds Utfall (summan av två tärningar) Sannolikhet
Begränsad uppräkning av den nedre skiktgränsen för statlig inkomstskatt för 2017
 Finansdepartementet Skatte- och tullavdelningen Begränsad uppräkning av den nedre skiktgränsen för statlig inkomstskatt för 2017 Februari 2016 Innehållsförteckning 1 Sammanfattning... 3 2 Förslag till
Finansdepartementet Skatte- och tullavdelningen Begränsad uppräkning av den nedre skiktgränsen för statlig inkomstskatt för 2017 Februari 2016 Innehållsförteckning 1 Sammanfattning... 3 2 Förslag till
a n = A2 n + B4 n. { 2 = A + B 6 = 2A + 4B, S(5, 2) = S(4, 1) + 2S(4, 2) = 1 + 2(S(3, 1) + 2S(3, 2)) = 3 + 4(S(2, 1) + 2S(2, 2)) = 7 + 8 = 15.
 1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D och F, SF161 och SF160, den juni 008 kl 08.00-1.00. DEL I 1. (p) Lös rekursionsekvationen
1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D och F, SF161 och SF160, den juni 008 kl 08.00-1.00. DEL I 1. (p) Lös rekursionsekvationen
Tentamen SSY040/041, del B Sensorer, Signaler och System, Z2
 Tentamen SSY4/41, del B Sensorer, Signaler och System, Z2 Examinator: Ants R. Silberberg / Gunnar Elgered 9 mars 21 kl. 8.3-12.3 sal: V Förfrågningar: Ants Silberberg, tel. 188 Lösningar: Anslås onsdag
Tentamen SSY4/41, del B Sensorer, Signaler och System, Z2 Examinator: Ants R. Silberberg / Gunnar Elgered 9 mars 21 kl. 8.3-12.3 sal: V Förfrågningar: Ants Silberberg, tel. 188 Lösningar: Anslås onsdag
Index vid lastbilstransporter
 index vid lastbilstransporter Matematiken Snabbhjälpen för att räkna rätt Index vid lastbilstransporter Innehåll A. Tre steg för att räkna rätt Sidan 1 B. Förändring enligt index 2 C. Andelskorrigering
index vid lastbilstransporter Matematiken Snabbhjälpen för att räkna rätt Index vid lastbilstransporter Innehåll A. Tre steg för att räkna rätt Sidan 1 B. Förändring enligt index 2 C. Andelskorrigering
Friskoleurval med segregation som resultat
 Friskoleurval med segregation som resultat Rapport februari 2016 Sammanfattning och slutsatser Denna undersökning har tagits fram som en del av projektet Ge alla elever samma chans som är ett samarbete
Friskoleurval med segregation som resultat Rapport februari 2016 Sammanfattning och slutsatser Denna undersökning har tagits fram som en del av projektet Ge alla elever samma chans som är ett samarbete
Bruksanvisning UCR-100
 381R912-A Bruksanvisning S UCR-100 Introduktion Läs alltid noggrant igenom bruksanvisningen innan ni använder enheten för första gången. Följ alla instruktioner och varningar. Enheten får ej utsättas för
381R912-A Bruksanvisning S UCR-100 Introduktion Läs alltid noggrant igenom bruksanvisningen innan ni använder enheten för första gången. Följ alla instruktioner och varningar. Enheten får ej utsättas för
Föreläsning 3: Radiometri och fotometri
 Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
Föreläsning 3: Radiometri och fotometri Radiometri att mäta strålning Fotometri att mäta synintrycket av strålning (att mäta ljus) Radiometri används t.ex. för: Effekt på lasrar Gränsvärden för UV Gränsvärden
L(9/G)MA10 Kombinatorik och geometri Gruppövning 1
 L(9/G)MA10 Kombinatorik och geometri Gruppövning 1 Lisa och Pelle leker med svarta och vita byggklossar. Deras pedagogiska föräldrar vill att de lär sig matematik samtidigt som de håller på och leker.
L(9/G)MA10 Kombinatorik och geometri Gruppövning 1 Lisa och Pelle leker med svarta och vita byggklossar. Deras pedagogiska föräldrar vill att de lär sig matematik samtidigt som de håller på och leker.
Möbiustransformationer.
 224 Om Möbiustransformationer Torbjörn Kolsrud KTH En Möbiustransformation är en komplexvärd funktion f av en komplex variabel z på formen f(z) = az + b cz + d. Här är a b c och d komplexa tal. Ofta skriver
224 Om Möbiustransformationer Torbjörn Kolsrud KTH En Möbiustransformation är en komplexvärd funktion f av en komplex variabel z på formen f(z) = az + b cz + d. Här är a b c och d komplexa tal. Ofta skriver
Systematiskt kvalitetsarbete
 Systematiskt kvalitetsarbete Rapport År: 2016 Organisationsenhet: NYEFSK/FSK Nye Förskola Fokusområde: Demokrati och värdegrund Övergripande mål: Normer och värden Deluppgift: Klassens kvalitetsrapport
Systematiskt kvalitetsarbete Rapport År: 2016 Organisationsenhet: NYEFSK/FSK Nye Förskola Fokusområde: Demokrati och värdegrund Övergripande mål: Normer och värden Deluppgift: Klassens kvalitetsrapport
Två konstiga klockor
 strävorna C Två konstiga klockor resonemang geometri Avsikt och matematikinnehåll Det som kan göra det svårt för barn att avläsa en analog klocka är att förstå att den består av två skalor som är beroende
strävorna C Två konstiga klockor resonemang geometri Avsikt och matematikinnehåll Det som kan göra det svårt för barn att avläsa en analog klocka är att förstå att den består av två skalor som är beroende
Manual Gamla Akka-plattan
 Manual Gamla Akka-plattan Manual för Akkaplattan Figur 1 1. 1. Uttag för laddare. Akkaplattan bör stå på laddning när den inte används men inte under för långa perioder dvs. flera veckor i sträck. Figur
Manual Gamla Akka-plattan Manual för Akkaplattan Figur 1 1. 1. Uttag för laddare. Akkaplattan bör stå på laddning när den inte används men inte under för långa perioder dvs. flera veckor i sträck. Figur
