NATIONELLA MATEMATIKTÄVLING
|
|
|
- Klara Ström
- för 9 år sedan
- Visningar:
Transkript
1 NATIONELLA MATEMATIKTÄVLING PRATA OM SPELS EN KURS I SANNOLIKHET 1
2 INLEDNING Sannolikhetskursen består av sju olika steg där det sista steget utgörs av själva tävlingsmomentet. Det är upp till pedagogen att välja vilka steg han eller hon vill använda eller gå igenom. Man kan välja att endast använda vissa delar eller alla steg, beroende på den tid som finns tillgänglig. GENOMGÅNG AV SANNOLIKHETSKURSEN: STARTUPPGIFT INTRODUKTION TILL SANNOLIKHET Del 1 är en Inledning till begreppet sannolikhet. Eleverna får titta på en animerad film till filmen hör ett antal diskussionsfrågor. SATSA PENGAR OCH FÖRSTÅELSE FÖR ODDS Del 2 är en elevaktiv uppgift, där eleverna satsar fiktiva pengar. Eleverna ska efter varje omgång räkna ut eventuell vinst eller förlust samt arbeta med procent. SANNOLIKHET MED 2 TÄRNINGAR Del 3 är en intro-uppgift till del 7. Här gäller det att räkna ut sannolikheten för att en viss summa av två tärningar visas. TRISS-LOTTER, VINST ELLER FÖRLUSTAFFÄR Del 4 låter eleverna med hjälp av trisslotter arbeta med sannolikhet och hur man på ett vanligt sätt kan räkna ut procent och promille. SANNOLIKHETEN ATT VINNA PÅ LOTTO Del 5 låter eleverna räkna ut hur stor sannolikheten är att få sju rätt på Lotto. Dessutom får de själva spela Lotto (fiktivt), för att få känna på hur svårt det egentligen är att vinna. I uppgiftens fördjupning introduceras även begreppen oberoende och beroende händelser. OBEROENDE OCH BEROENDE HÄNDELSER MED HJÄLP AV ETT MYNT Del 6 låter eleverna fortsätta med oberoende och beroende händelser. Eleverna får förklara de olika begreppen och även rita egna träddiagram samt arbeta med decimaltal och bråktal. SKAPA ODDS OCH TA FRAM TÄVLINGSUNDERLAG Del 7 består av själva tävlingsmomentet. Delen inleds med att eleverna själva ska sätta olika odds och fundera över sannolikheten med hjälp av två tärningar. I tävlingsmomentet skapar de en egen redovisning där de ska förklara ett antal olika begrepp och modeller. 2
3 Med hjälp av de olika stegen täcks följande centrala innehåll in: Likformig sannolikhet och metoder för att beräkna sannolikheten i vardagliga situationer. Hur kombinatoriska principer kan användas i enkla vardagliga och matematiska problem. Tabeller, diagram och grafer samt hur de kan tolkas och användas för att beskriva resultat av egna och andras undersökningar, till exempel med hjälp av digitala verktyg. Hur lägesmått och spridningsmått kan användas för bedömning av resultat vid statistiska undersökningar. Bedömningar av risker och chanser utifrån statistiskt material. FÖLJANDE BEGREPP KOMMER ATT BEHANDLAS I DE OLIKA STEGEN: Bråkform Decimalform Procentform Promille Oberoende händelser Beroende händelser Förkorta/förlänga bråk Bokstaven P Delen/Hela Utfall Odds 3
4 1 STARTUPPGIFT INTRODUKTION TILL SANNOLIKHET I den här uppgiften får ni bekanta er med begreppet sannolikhet genom att titta på en film. Läraren visar följande film från TEDed och stannar efter 36 sekunder. Eleverna ska sedan välja vem de vill vara; spelare 1 eller spelare 2. Se klart filmen. UPPGIFT UTIFRÅN FILM Hur skulle det bli om: Spelare 1 vann på siffrorna 1, 2 och 3? Spelare 2 vann på siffrorna 4, 5 och 6? Skulle utfallet ändras jämfört med filmen? Ja Nej Oförändrat Glöm inte att motivera ditt svar med uträkningar och förklaringar. Visa gärna att du behärskar både tabell och bråkräkning (som de visar i filmen). URL Filmlänk: 4
5 2 SATSA PENGAR OCH FÖRSTÅELSE FÖR ODDS I den här övningen arbetar vi med odds och sannolikhet. Läraren behöver en sexsidig tärning och eleverna nedanstående tabell. Du ska nu satsa på det alternativ (av de som finns i tabellen), som du tror tärningens prickar kommer att visa. Till exempel: Du satsar 10 kronor på utfall 1, det vill säga att tärningen visar en etta (1). Tärningen kastas. Den visar en etta (en prick)! Du vann! Hur mycket vann du? Insatsen multiplicerat med odds. Alltså 10 x 6 = 60 kronor. Men hur mycket hade du vunnit om du spelat på spelbolagets odds? Jo, 10 x 5,4 = 54 kronor. Men om du satsar på att tärningen kommer att visa en etta, och tärningen visar en tvåa. Då har du förlorat. Och då fyller du i 10 kronor i kolumnen Eventuell förlust. STEG 1 ODDS OCH SANNOLIKHET Förutsättningar: 1. Varje elev har 100 kronor att spela för. 2. Odds = 1/sannolikhet. Man har alltså räknat ut oddset genom att dividera 1 med sannolikheten. 3. Gå igenom tabellen tillsammans. Spelbolagen har sänkt oddsen med 10 procent, varför tror du de har gjort det? Utfall Sannolikhet Odds Spelbolagsodds 1 1/6 6 5,4 1 eller 2 1/3 3 2,7 1 till 3 1/2 2 1,8 1 till 4 2/3 1,5 1,35 1 till 5 5/6 1,2 1,08 4. Läraren ansvarar för att slå tärningen. 5. Eleverna satsar på något av ovanstående alternativ (de får högst satsa 10 kronor av sin 100-lapp). 6. Läraren slår. 7. Upprepa 25 gånger. 8. Efter varje slag räknar du ut eventuell vinst och eventuell förlust. 5
6 ELEVTABELL Omgång Vilket utfall satsar du på? Eventuell vinst, enligt odds Eventuell förlust Eventuell vinst enligt spelbolags odds STEG 2 RÄKNEUPPGIFT Räkna ut följande: Hur mycket vann du enligt det vanliga oddset? Hur mycket förlorade du? Kunde du vara med i alla 25 omgångar, eller tog pengarna slut? Hur mycket har spelbolaget tjänat på dig? På hela klassen? 6
7 3 STEG 1 SANNOLIKHET MED TVÅ TÄRNINGAR VILKEN SUMMA BLIR DEN MEST FÖREKOMMANDE? I den här övningen ska du kasta två tärningar. Tabellen läser du av så här: Visar tärning 1 (de gröna fälten) en tvåa (2) sätter du fingret på siffran 2 (grön). Sedan drar du fingret till den kolumnen som tärning nummer 2 visar. Genomför 25 kast och sätt en markering i rätt ruta för varje kast du gör. Att fundera över: Vilken summa kommer att bli den mest vanligt förekommande? Hur kan det komma sig att det blir så? STEG 2 BERÄKNA SANNOLIKHETEN FÖR TVÅ OLIKA UTFALL När man vill ta reda på sannolikheten av ett utfall skriver man följande: p(summa 4), det betyder att man ska ta reda på hur stor sannolikhet det är att få summan 4 när man slår två tärningar. Din uppgift är nu att beräkna sannolikheterna för: P(summa 4). P(summa 7). Använd tabellen och svara i enklaste bråkform, förkorta bråken så långt det går. Tärning 1 (grön) och 2 (blå) EXEMPEL Hur stor är sannolikheten att, om man slår två tärningar, får p(summa 5), alltså hur stor är sannolikheten att tärningarna tillsammans (addition) visar summan 5. Hur många 5:or finns det i tabellen här ovan? Jo, fyra stycken. För att: = = = = 5 7
8 4 TRISS-LOTTER, VINST ELLER FÖRLUSTAFFÄR? Plötsligt händer det hävdar Triss-reklamen. Nu ska vi ta reda på stor chansen är att vinna på en Trisslott. TIPS: Den här övningen handlar om ett vanligt sätt att räkna ut procent och promille på, nämligen delen delat med det hela (delen/hela). Räkneuppgift: Av 2 miljoner ( ) Trisslotter är det vinst på lotter. Hur räknar man ut hur stor sannolikheten är att vinna på triss? På två miljoner Trisslotter finns det 380 vinster som är över 1000 kronor. Hur stor är då chansen att vinna över 1000 kronor på trisslotter? Svara i procent och i promille. Hur stor är risken att du inte vinner 1000 kronor eller mer? Svara i procent och promille. 8
9 5 SANNOLIKHETEN ATT VINNA PÅ LOTTO I den här uppgiften ska ni testa att spela Lotto. I spelet Lotto ska man pricka in 7 av 35 nummer (1-35) för att vinna högsta vinsten. Hur stor är sannolikheten att få sju rätt på Lotto? Använd miniräknare. TIPS: Kom ihåg att när ett nummer har försvunnit finns det bara 34 siffror kvar och så vidare. 1:a numret: 7/35 2:a numret: 6/34 3:e numret: 5/33 Till läraren: Skriv ut denna spelplan. Klipp den så att du har 35 rektanglar med ett nummer i varje rektangel. Dra ett nummer. Visa klassen vilket nummer du drog. Släng den dragna lappen/numret. Till eleven: Ringa in sju stycken valfria nummer på spelplanen som du tror kan ge dig vinst. Kryssa sedan över de nummer som läraren drar. Hur många rätt fick du? LOTTO Vi testar att spela Lotto. Kryssa för 7 nummer Diskutera: Vem tjänar mest pengar, spelaren eller spelbolaget? Förklara varför! Varför väljer många att spela på Lotto? Hur kan spelbolagen erbjuda så höga vinster för sju rätt? 9
10 FÖRDJUPNING 01 OBEROENDE HÄNDELSER VI ANVÄNDER OSS AV TRÄDDIAGRAM Här nedan följer två förklarande exempel på oberoende och beroende händelser. OBEROENDE HÄNDELSER Vi använder oss av ett exempel med en urna där det ligger tre kulor med orange färg och två med svart färg. Om vi tänker oss att du nu ska beräkna sannolikheten att plocka två orange kulor i rad om du efter att ha dragit den första kulan lägger tillbaka den igen och sedan drar på nytt. När du plockar en kula och sedan lägger tillbaka den kommer inte sannolikheten att förändras mellan första och andra försöket. Detta innebär att båda händelserna är oberoende av varandra, alltså oberoende händelser. UPPGIFT: Hur stor är sannolikheten att vi drar två orange kulor i rad? Uppgiften kan också tecknas så här: P(2 orange). Vi gör ett träddiagram för att lösa uppgiften. 2/5 FÖRSTA DRAGNINGEN 3/5 ANDRA DRAGNINGEN 2/5 3/5 2/5 3/5 FÖR ATT RÄKNA UT DETTA GÖR VI FÖLJANDE: P(2 orange) = P(orange) x P(orange) = 3/5 x 3/5 = 9/25 9/25 = 0,36 0,36 = 36 % 10
11 FÖRDJUPNING 02 BEROENDE HÄNDELSER BEROENDE HÄNDELSER Även denna gång ska vi räkna ut sannolikheten för att ta två orange kulor. P(2 orange), men nu ska vi INTE lägga tillbaka den första kulan vi tog. Detta kallas för dragning utan återläggning. Och då kallas det för beroende händelser, eftersom det nu spelar roll vilken kula vi tog första gången. UPPGIFT: P(2 orange) 2/5 FÖRSTA DRAGNINGEN 3/5 1/4 3/4 ANDRA DRAGNINGEN 2/4 2/4 SVAR: P(2 orange) = P(orange) x P(orange) 3/5 x 2/4 = 6/20 6/20 = 3/10 3/10 = 30 % 11
12 6 OBEROENDE OCH BEROENDE HÄNDELSER MED HJÄLP AV ETT MYNT Nu har du läst om beroende- och oberoende händelser och träddiagram. I den här uppgiften ska du använda dig av de kunskaperna. UPPGIFT: När man kastar ett mynt kan det bli antingen krona eller klave. Du kastar myntet två gånger. Är händelserna oberoende eller beroende av varandra? Rita ett träddiagram och skriv dit de olika sannolikheterna som decimaltal och som bråktal. Hur stor är sannolikheten att det blir krona två gånger i rad? Kasta myntet två gånger. Hur stor är sannolikheten att det första kastet visar krona, och det andra kastet klave? 12
13 7 STEG 1 SKAPA ODDS OCH TA FRAM TÄVLINGSUNDERLAG Den här uppgiften är uppdelad i två delar. I del 1 ska du skapa odds och ta reda på sannolikheten för de olika summorna för två tärningar. I del 2 ska du skapa en redovisning av hur du/ni har tänkt. SANNOLIKHET MED HJÄLP AV TVÅ TÄRNINGAR ARBETA I PAR ELLER I GRUPPER OM TRE Nu är det dags att spela ett spel med två tärningar. Men nu är det NI som sätter oddsen och sannolikheten. SANNOLIKHET: Skriv i bråkform (använd tabellen nedan). ODDS: Här kan ni sätta odds för varje summa. Hur troligt är det att få summan 1 med två tärningar? Den sannolikheten är obefintlig, och därför bör oddset bli 100 på summan 1. SPELBOLAGSODDS: Tänk dig att du driver ett spelbolag, och ska sätta ett odds på varje utfall. Du ska tjäna pengar, men samtidigt se till att folk vill spela. Hur skulle du sätta dessa odds? Utfall (summan av två tärningar) Sannolikhet Odds Era odds
14 STEG 2 SKAPA EGEN REDOVISNING Ni ska nu skapa en redovisning (film, digital presentation) där ni/gruppen: Förklara varför ni har satt de oddsen ni har satt. Berätta vilka siffror som kommer att vara mest förekommande och varför de är mest förekommande. Berätta hur man omvandlar från decimalform till procentform. Berätta hur man förkortar ett tal i bråkform. Berätta varför alltid spelbolagen vinner i längden. Inkludera även den ifyllda tabellen ovan (under del 7) i tävlingsbidraget som ni skickar in enligt instruktionerna som ni finner i tävlingsinformationen. MÅLGRUPP FÖR ER PRESENTATION Tänk er att målgruppen för er presentation är någon från årskurs fem eller sex (och uppåt). Det är viktigt att en elev i årskurs fem eller sex kan förstå er presentation. Hämta gärna inspiration från filmen som ingår i del 1. 14
Sannolikhet och Odds
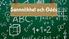 Sannolikhet och Odds Sannolikhet Tärning (Orange) och (Blå) 0 0 0 Om man satsat sina pengar på rätt summa multipliceras oddset med insatsen (pengarna man satsar) Odds Utfall (summan av två tärningar) Sannolikhet
Sannolikhet och Odds Sannolikhet Tärning (Orange) och (Blå) 0 0 0 Om man satsat sina pengar på rätt summa multipliceras oddset med insatsen (pengarna man satsar) Odds Utfall (summan av två tärningar) Sannolikhet
SANNOLIKHET. Sannolikhet är: Hur stor chans (eller risk) att något inträffar.
 SANNOLIKHET Sannolikhet är: Hur stor chans (eller risk) att något inträffar. [email protected] SANNOLIKHET Grundpremisser: Ju fler möjliga händelser, desto mindre sannolikhet att en viss händelse
SANNOLIKHET Sannolikhet är: Hur stor chans (eller risk) att något inträffar. [email protected] SANNOLIKHET Grundpremisser: Ju fler möjliga händelser, desto mindre sannolikhet att en viss händelse
Väga paket och jämföra priser
 strävorna 2AC 3AC Väga paket och jämföra priser begrepp rutinuppgifter tal geometri Avsikt och matematikinnehåll Den huvudsakliga avsikten med denna aktivitet är att ge elever möjlighet att utveckla grundläggande
strävorna 2AC 3AC Väga paket och jämföra priser begrepp rutinuppgifter tal geometri Avsikt och matematikinnehåll Den huvudsakliga avsikten med denna aktivitet är att ge elever möjlighet att utveckla grundläggande
DOP-matematik Copyright Tord Persson. Bråktal -3-2 -1 0 1 2 3. Läs av vilka tal på tallinjen, som pilarna pekar på. Uppgift nr 10 -3-2 -1 0 1 2 3
 Bråktal Uppgift nr En limpa delas i 4 lika stora delar. Hur stor del av limpan blir varje del? Uppgift nr 2 Hur många tiondelar behövs för att det skall räcka till en hel? Uppgift nr Hur läser man ut bråket
Bråktal Uppgift nr En limpa delas i 4 lika stora delar. Hur stor del av limpan blir varje del? Uppgift nr 2 Hur många tiondelar behövs för att det skall räcka till en hel? Uppgift nr Hur läser man ut bråket
Avsikt På ett lekfullt sätt färdighetsträna, utveckla elevers känsla för hur vårt talsystem är uppbyggt samt hitta mönster som uppkommer.
 Strävorna 4A 100-rutan... förmåga att förstå, föra och använda logiska resonemang, dra slutsatser och generalisera samt muntligt och skriftligt förklara och argumentera för sitt tänkande.... grundläggande
Strävorna 4A 100-rutan... förmåga att förstå, föra och använda logiska resonemang, dra slutsatser och generalisera samt muntligt och skriftligt förklara och argumentera för sitt tänkande.... grundläggande
Lathund, procent med bråk, åk 8
 Lathund, procent med bråk, åk 8 Procent betyder hundradel, men man kan också säga en av hundra. Ni ska kunna omvandla mellan bråkform, decimalform och procentform. Nedan kan ni se några omvandlingar. Bråkform
Lathund, procent med bråk, åk 8 Procent betyder hundradel, men man kan också säga en av hundra. Ni ska kunna omvandla mellan bråkform, decimalform och procentform. Nedan kan ni se några omvandlingar. Bråkform
Mål Blå kurs Röd kurs
 Bråk Mål När eleverna har arbetat med det här kapitlet ska de kunna läsa och skriva bråk veta vad som menas med täljare och nämnare känna till och kunna använda begreppen bråkform och blandad form kunna
Bråk Mål När eleverna har arbetat med det här kapitlet ska de kunna läsa och skriva bråk veta vad som menas med täljare och nämnare känna till och kunna använda begreppen bråkform och blandad form kunna
Snabbslumpade uppgifter från flera moment.
 Snabbslumpade uppgifter från flera moment. Uppgift nr Ställ upp och dividera utan hjälp av miniräknare talet 48 med 2 Uppgift nr 2 Skriv talet 3 8 00 med hjälp av decimalkomma. Uppgift nr 3 Uppgift nr
Snabbslumpade uppgifter från flera moment. Uppgift nr Ställ upp och dividera utan hjälp av miniräknare talet 48 med 2 Uppgift nr 2 Skriv talet 3 8 00 med hjälp av decimalkomma. Uppgift nr 3 Uppgift nr
Laborativ matematik som bedömningsform. Per Berggren och Maria Lindroth 2016-01-28
 Laborativ matematik som bedömningsform Per Berggren och Maria Lindroth 2016-01-28 Kul matematik utan lärobok Vilka förmågor tränas Problemlösning (Förstå frågan i en textuppgift, Använda olika strategier
Laborativ matematik som bedömningsform Per Berggren och Maria Lindroth 2016-01-28 Kul matematik utan lärobok Vilka förmågor tränas Problemlösning (Förstå frågan i en textuppgift, Använda olika strategier
Ha det kul med att förmedla och utveckla ett knepigt område!
 Kul med pizzabitar Första gången eleverna får materialet i handen bör dem få sin egen tid till att undersöka det på det viset blir dem bekanta med dess olika delar. Det kan också vara en god idé att låta
Kul med pizzabitar Första gången eleverna får materialet i handen bör dem få sin egen tid till att undersöka det på det viset blir dem bekanta med dess olika delar. Det kan också vara en god idé att låta
Svenska Du kan med flyt läsa texter som handlar om saker du känner till. Du använder metoder som fungerar. Du kan förstå vad du läser.
 Svenska Du kan med flyt läsa texter som handlar om saker du känner till. Du använder metoder som fungerar. Du kan förstå vad du läser. Du berättar på ett enkelt sätt om det du tycker är viktigt i texten.
Svenska Du kan med flyt läsa texter som handlar om saker du känner till. Du använder metoder som fungerar. Du kan förstå vad du läser. Du berättar på ett enkelt sätt om det du tycker är viktigt i texten.
DEN LILLA RÖDA HÖNAN
 1 DEN LILLA RÖDA HÖNAN 1 2 3 4 5 6 4 Sagan används för begreppsinlärning, problemlösning och för att tala matematik. Se lhdl s. 96-99. 7 8 9 10 Den som är lat får ingen mat. Problemlösning 1 Arbeta två
1 DEN LILLA RÖDA HÖNAN 1 2 3 4 5 6 4 Sagan används för begreppsinlärning, problemlösning och för att tala matematik. Se lhdl s. 96-99. 7 8 9 10 Den som är lat får ingen mat. Problemlösning 1 Arbeta två
Procent - procentenheter
 Procent - procentenheter Uppgift nr 1 Hur skriver man i matematiken tecknet för procent och vad betyder ordet procent? Uppgift nr 2 Av 100 mopeder på en parkering är 16 vita. Hur många procent av mopederna
Procent - procentenheter Uppgift nr 1 Hur skriver man i matematiken tecknet för procent och vad betyder ordet procent? Uppgift nr 2 Av 100 mopeder på en parkering är 16 vita. Hur många procent av mopederna
10.03.2010. Översikt. Rapport från skolverket. Förändring av matematikprestationerna 1995 2003-2007. Grundtankar bakom Pixel
 Översikt Hur är situationen i Sverige och Norge när det gäller matematik-kompetensen? Är det nödvändigt att undervisa på andra sätt än vi gjort tidigare? Förändring av matematikprestationerna 1995 2003-2007
Översikt Hur är situationen i Sverige och Norge när det gäller matematik-kompetensen? Är det nödvändigt att undervisa på andra sätt än vi gjort tidigare? Förändring av matematikprestationerna 1995 2003-2007
FRÅN A TILL Ö LäraMera Ab / www.laramera.se och Allemansdata Ab / www.allemansdata.se FRÅN A TILL Ö
 I programmet finns 11 olika aktiviteter för att träna varje bokstav och på att känna igen ord. För varje bokstav kan olika övningsblad skrivas ut: Inledningsvis väljer du vilken bokstav du vill öva på.
I programmet finns 11 olika aktiviteter för att träna varje bokstav och på att känna igen ord. För varje bokstav kan olika övningsblad skrivas ut: Inledningsvis väljer du vilken bokstav du vill öva på.
Det är bra om även distriktsstyrelsen gör en presentation av sig själva på samma sätt som de andra.
 Modul: Föreningspresentation Ett stort blädderblocksblad delas upp i fyra rutor. Deltagarna, som under detta pass är indelade föreningsvis, får i uppgift att rita följande saker i de fyra rutorna: Föreningsstyrelsen
Modul: Föreningspresentation Ett stort blädderblocksblad delas upp i fyra rutor. Deltagarna, som under detta pass är indelade föreningsvis, får i uppgift att rita följande saker i de fyra rutorna: Föreningsstyrelsen
Diskussionsfrågor till version 1 och 2
 Diskussionsfrågor till version 1 och 2 Version 1 Tillgång till internet i hemmet A. Vilken åldersgrupp har haft den största ökningen av tillgång till internet under perioden? B. Kan man med hjälp av de
Diskussionsfrågor till version 1 och 2 Version 1 Tillgång till internet i hemmet A. Vilken åldersgrupp har haft den största ökningen av tillgång till internet under perioden? B. Kan man med hjälp av de
ÄT RÄTT NÄR DU TRÄNAR
 ÄT RÄTT NÄR DU TRÄNAR Lärgruppsplan Lärgruppsplan Hur mycket, och vad, du äter spelar en stor roll för förmågan att prestera, såväl fysiskt som psykiskt. Vill du optimera din prestation kan det till och
ÄT RÄTT NÄR DU TRÄNAR Lärgruppsplan Lärgruppsplan Hur mycket, och vad, du äter spelar en stor roll för förmågan att prestera, såväl fysiskt som psykiskt. Vill du optimera din prestation kan det till och
Utveckla arbetsmiljö och verksamhet genom samverkan
 DEL 1: Utveckla arbetsmiljö och verksamhet genom samverkan Modulen inleds med det övergripande målet för modul 6 och en innehållsförteckning över utbildningens olika delar. Börja med att sätta ramarna
DEL 1: Utveckla arbetsmiljö och verksamhet genom samverkan Modulen inleds med det övergripande målet för modul 6 och en innehållsförteckning över utbildningens olika delar. Börja med att sätta ramarna
Gemensam problemlösning. Per Berggren och Maria Lindroth 2013-03-12
 Gemensam problemlösning 2013-03-12 Strategispel Hur ska du spela för att vinna dessa strategispel? Nim Tactical Att arbeta som en matematiker Först vill matematiker ha ett intressant problem. Matematiker
Gemensam problemlösning 2013-03-12 Strategispel Hur ska du spela för att vinna dessa strategispel? Nim Tactical Att arbeta som en matematiker Först vill matematiker ha ett intressant problem. Matematiker
Vi skall skriva uppsats
 Vi skall skriva uppsats E n vacker dag får du höra att du skall skriva uppsats. I den här texten får du veta vad en uppsats är, vad den skall innehålla och hur den bör se ut. En uppsats är en text som
Vi skall skriva uppsats E n vacker dag får du höra att du skall skriva uppsats. I den här texten får du veta vad en uppsats är, vad den skall innehålla och hur den bör se ut. En uppsats är en text som
Två konstiga klockor
 strävorna C Två konstiga klockor resonemang geometri Avsikt och matematikinnehåll Det som kan göra det svårt för barn att avläsa en analog klocka är att förstå att den består av två skalor som är beroende
strävorna C Två konstiga klockor resonemang geometri Avsikt och matematikinnehåll Det som kan göra det svårt för barn att avläsa en analog klocka är att förstå att den består av två skalor som är beroende
Matematikboken. alfa. Lennart Undvall Christina Melin Jenny Ollén
 Matematikboken alfa Lennart Undvall Christina Melin Jenny Ollén Matematikboken Alfa ISBN 978-91-47-10193-1 Författare: Lennart Undvall, Christina Melin och Jenny Ollén 2011 författarna och Liber AB Illustrationer:
Matematikboken alfa Lennart Undvall Christina Melin Jenny Ollén Matematikboken Alfa ISBN 978-91-47-10193-1 Författare: Lennart Undvall, Christina Melin och Jenny Ollén 2011 författarna och Liber AB Illustrationer:
DEMOKRATI 3 DEMOKRATINS VILLKOR
 SIDA 1/8 WORKSHOP I KLASSRUMMET TEMA: DEMOKRATI LÄRARMANUAL I det här dokumentet finns allt du behöver veta för att hålla workshopen. Här ser du också tydligt i vilka moment du använder det arbets- och
SIDA 1/8 WORKSHOP I KLASSRUMMET TEMA: DEMOKRATI LÄRARMANUAL I det här dokumentet finns allt du behöver veta för att hålla workshopen. Här ser du också tydligt i vilka moment du använder det arbets- och
Jörgen Lagnebo PLANERING OCH BEDÖMNING MATEMATIK ÅK 7
 PLANERING OCH BEDÖMNING MATEMATIK ÅK 7 TERMINSPLAN HÖSTTERMINEN ÅK 7: 1 FÖRDIAGNOS 2 FYRA RÄKNESÄTT 3 FYRA RÄKNESÄTT 4 1.1 NATURLIGA TAL 5 1.2 NEGATIVA HELA TAL 6 1.3 TAL I BRÅKFORM 7 FORTS. 1.3 TAL I
PLANERING OCH BEDÖMNING MATEMATIK ÅK 7 TERMINSPLAN HÖSTTERMINEN ÅK 7: 1 FÖRDIAGNOS 2 FYRA RÄKNESÄTT 3 FYRA RÄKNESÄTT 4 1.1 NATURLIGA TAL 5 1.2 NEGATIVA HELA TAL 6 1.3 TAL I BRÅKFORM 7 FORTS. 1.3 TAL I
Elektronen och laddning
 Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
Detta är en något omarbetad version av Studiehandledningen som användes i tryckta kursen på SSVN. Sidhänvisningar hänför sig till Quanta A 2000, ISBN 91-27-60500-0 Där det har varit möjligt har motsvarande
VÄRDERINGSÖVNINGAR. Vad är Svenskt?
 VÄRDERINGSÖVNINGAR Vad är Svenskt? Typ av övning: Avstamp till diskussion. Övningen belyser hur svårt det är att säga vad som är svenskt och att normen vad som anses vara svenskt ändras med tiden och utifrån
VÄRDERINGSÖVNINGAR Vad är Svenskt? Typ av övning: Avstamp till diskussion. Övningen belyser hur svårt det är att säga vad som är svenskt och att normen vad som anses vara svenskt ändras med tiden och utifrån
ATT KUNNA TILL. MA1050 Matte Grund. 2011-06-14 Vuxenutbildningen Dennis Jonsson
 ATT KUNNA TILL MA1050 Matte Grund 2011-06-14 Vuxenutbildningen Dennis Jonsson Sida 2 av 5 Att kunna till prov G1 Kunna ställa upp och beräkna additions-, subtraktions-, multiplikations- och divisuionsuppgifter
ATT KUNNA TILL MA1050 Matte Grund 2011-06-14 Vuxenutbildningen Dennis Jonsson Sida 2 av 5 Att kunna till prov G1 Kunna ställa upp och beräkna additions-, subtraktions-, multiplikations- och divisuionsuppgifter
Hur du arbetar med VFU-portfölj i Mondo. en lathund för student
 Hur du arbetar med VFU-portfölj i Mondo en lathund för student Du skapar din VFU-portfölj På ingångssidan mondo.su.se ligger i högerspalten, innan du loggar in, en länk till en manual för hur du skapar
Hur du arbetar med VFU-portfölj i Mondo en lathund för student Du skapar din VFU-portfölj På ingångssidan mondo.su.se ligger i högerspalten, innan du loggar in, en länk till en manual för hur du skapar
Boll-lek om normer. Nyckelord: likabehandling, hbt, normer/stereotyper, skolmiljö. Innehåll
 1 Boll-lek om normer Nyckelord: likabehandling, hbt, normer/stereotyper, skolmiljö Innehåll Materialet bygger på en övning där eleverna, genom en lek med bollar, får utmana sin förmåga att kommunicera
1 Boll-lek om normer Nyckelord: likabehandling, hbt, normer/stereotyper, skolmiljö Innehåll Materialet bygger på en övning där eleverna, genom en lek med bollar, får utmana sin förmåga att kommunicera
Upplägg och genomförande - kurs D
 Upplägg och genomförande - kurs D Provet består av fyra delprov: Läsa A och B Höra Skriva Tala Läsförståelse Hörförståelse Skriftlig produktion Muntlig produktion och interaktion Tid på respektive provdel
Upplägg och genomförande - kurs D Provet består av fyra delprov: Läsa A och B Höra Skriva Tala Läsförståelse Hörförståelse Skriftlig produktion Muntlig produktion och interaktion Tid på respektive provdel
Erfarenheter från ett pilotprojekt med barn i åldrarna 1 5 år och deras lärare
 Erfarenheter från ett pilotprojekt med barn i åldrarna 1 5 år och deras lärare I boken får vi följa hur barn tillsammans med sina lärare gör spännande matematikupptäckter - i rutinsituationer - i leken
Erfarenheter från ett pilotprojekt med barn i åldrarna 1 5 år och deras lärare I boken får vi följa hur barn tillsammans med sina lärare gör spännande matematikupptäckter - i rutinsituationer - i leken
Handledning för digitala verktyg Talsyntes och rättstavningsprogram. Vital, StavaRex och SpellRight
 Handledning för digitala verktyg Talsyntes och rättstavningsprogram Vital, StavaRex och SpellRight Elevens namn:.. Skola: Datum:.. Varför behövs en handledning? Denna handledning är tänkt att användas
Handledning för digitala verktyg Talsyntes och rättstavningsprogram Vital, StavaRex och SpellRight Elevens namn:.. Skola: Datum:.. Varför behövs en handledning? Denna handledning är tänkt att användas
Tränarguide del 1. Mattelek. www.mv-nordic.se
 Tränarguide del 1 Mattelek www.mv-nordic.se 1 ATT TRÄNA MED MATTELEK Mattelek är ett adaptivt träningsprogram för att träna centrala matematiska färdigheter såsom antalsuppfattning, den inre mentala tallinjen
Tränarguide del 1 Mattelek www.mv-nordic.se 1 ATT TRÄNA MED MATTELEK Mattelek är ett adaptivt träningsprogram för att träna centrala matematiska färdigheter såsom antalsuppfattning, den inre mentala tallinjen
Samtals- och dokumentationsunderlag Språk och erfarenheter
 Kartläggningsmaterial för nyanlända elever Samtals- och dokumentationsunderlag Språk och erfarenheter Steg 1 2 3 Samtals- och dokumentationsunderlag Steg 1 Information till elev och vårdnadshavare före
Kartläggningsmaterial för nyanlända elever Samtals- och dokumentationsunderlag Språk och erfarenheter Steg 1 2 3 Samtals- och dokumentationsunderlag Steg 1 Information till elev och vårdnadshavare före
Bilaga B Kartläggningsmaterial - Litteracitet Samtals- och dokumentationsunderlag avkodning, läsning, läsförståelse och skrivning
 Bilaga B Kartläggningsmaterial - Litteracitet Samtals- och dokumentationsunderlag avkodning, läsning, läsförståelse och skrivning Förberedelser och instruktioner Tid max: 70 min. Testledaren bör vara undervisande
Bilaga B Kartläggningsmaterial - Litteracitet Samtals- och dokumentationsunderlag avkodning, läsning, läsförståelse och skrivning Förberedelser och instruktioner Tid max: 70 min. Testledaren bör vara undervisande
4-6 Trianglar Namn:..
 4-6 Trianglar Namn:.. Inledning Hittills har du arbetat med parallellogrammer. En sådan har fyra hörn och motstående sidor är parallella. Vad händer om vi har en geometrisk figur som bara har tre hörn?
4-6 Trianglar Namn:.. Inledning Hittills har du arbetat med parallellogrammer. En sådan har fyra hörn och motstående sidor är parallella. Vad händer om vi har en geometrisk figur som bara har tre hörn?
Kampanj kommer från det franska ordet campagne och innebär att man under en tidsbegränsad period bedriver en viss verksamhet.
 EN LITEN KAMPANJSKOLA Kampanj kommer från det franska ordet campagne och innebär att man under en tidsbegränsad period bedriver en viss verksamhet. Finns det något man kan tänka på när man ska sprida ett
EN LITEN KAMPANJSKOLA Kampanj kommer från det franska ordet campagne och innebär att man under en tidsbegränsad period bedriver en viss verksamhet. Finns det något man kan tänka på när man ska sprida ett
Sammanfatta era aktiviteter och effekten av dem i rutorna under punkt 1 på arbetsbladet.
 Guide till arbetsblad för utvecklingsarbete Arbetsbladet är ett verktyg för dig och dina medarbetare/kollegor när ni analyserar resultatet från medarbetarundersökningen. Längst bak finns en bilaga med
Guide till arbetsblad för utvecklingsarbete Arbetsbladet är ett verktyg för dig och dina medarbetare/kollegor när ni analyserar resultatet från medarbetarundersökningen. Längst bak finns en bilaga med
Föräldrabroschyr. Björkhagens skola - en skola med kunskap och hjärta. Vad ska barnen lära sig i skolan?
 Föräldrabroschyr Björkhagens skola - en skola med kunskap och hjärta. Vad ska barnen lära sig i skolan? Vad ska barnen lära sig i skolan? Tanken med den här broschyren är att ge Er föräldrar en bild av
Föräldrabroschyr Björkhagens skola - en skola med kunskap och hjärta. Vad ska barnen lära sig i skolan? Vad ska barnen lära sig i skolan? Tanken med den här broschyren är att ge Er föräldrar en bild av
När jag har arbetat klart med det här området ska jag:
 Kraft och rörelse När jag har arbetat klart med det här området ska jag: kunna ge exempel på olika krafter och kunna använda mina kunskaper om dessa när jag förklarar olika fysikaliska fenomen, veta vad
Kraft och rörelse När jag har arbetat klart med det här området ska jag: kunna ge exempel på olika krafter och kunna använda mina kunskaper om dessa när jag förklarar olika fysikaliska fenomen, veta vad
Tankar om elevtankar. HÖJMA-projektet
 Tankar om elevtankar HÖJMA-projektet JAN UNENGE I förra numret av NÄMNAREN påbörjades en redogörelse från ett intressant forsknings- och utvecklingsarbete vid Lärarhögskolan i Jönköping. Den artikeln behandlade
Tankar om elevtankar HÖJMA-projektet JAN UNENGE I förra numret av NÄMNAREN påbörjades en redogörelse från ett intressant forsknings- och utvecklingsarbete vid Lärarhögskolan i Jönköping. Den artikeln behandlade
Presentationsövningar
 Varje möte då temadialog används bör inledas med en presentationsövning. har flera syften. Både föräldrar och ledare har nytta av att gå igenom samtliga deltagares namn och dessutom få en tydlig bild av
Varje möte då temadialog används bör inledas med en presentationsövning. har flera syften. Både föräldrar och ledare har nytta av att gå igenom samtliga deltagares namn och dessutom få en tydlig bild av
TIMREDOVISNINGSSYSTEM
 TIMREDOVISNINGSSYSTEM Företagsekonomiska Institutionen Inledning med begreppsförklaring Huvudmeny Budgethantering Planering Rapportering Signering Utskrifter/Rapporter Byt lösenord Logga ut 1 Inledning
TIMREDOVISNINGSSYSTEM Företagsekonomiska Institutionen Inledning med begreppsförklaring Huvudmeny Budgethantering Planering Rapportering Signering Utskrifter/Rapporter Byt lösenord Logga ut 1 Inledning
L(9/G)MA10 Kombinatorik och geometri Gruppövning 1
 L(9/G)MA10 Kombinatorik och geometri Gruppövning 1 Lisa och Pelle leker med svarta och vita byggklossar. Deras pedagogiska föräldrar vill att de lär sig matematik samtidigt som de håller på och leker.
L(9/G)MA10 Kombinatorik och geometri Gruppövning 1 Lisa och Pelle leker med svarta och vita byggklossar. Deras pedagogiska föräldrar vill att de lär sig matematik samtidigt som de håller på och leker.
SVENSKA ÖVERGRIPANDE MÅL FÖR ÅR 6, 7, 8, 9: LYSSNA
 SVENSKA ÖVERGRIPANDE MÅL FÖR ÅR 6, 7, 8, 9: Att DU kan LYSSNA, och förstå vad du hör. Att DU kan TALA, så man förstår vad du säger. Att DU kan LÄSA, och förstå vad du läser. Att DU kan SKRIVA, så man förstår
SVENSKA ÖVERGRIPANDE MÅL FÖR ÅR 6, 7, 8, 9: Att DU kan LYSSNA, och förstå vad du hör. Att DU kan TALA, så man förstår vad du säger. Att DU kan LÄSA, och förstå vad du läser. Att DU kan SKRIVA, så man förstår
Har vi lösningen för en bättre hemtjänst? Självklart.
 Har vi lösningen för en bättre hemtjänst? Självklart. Låt oss prata om Självklarhetsmetoden. Låt oss prata om Självklarhetsmetoden! 164 000 äldre är beroende av hemtjänsten i sin vardag. Och det är du
Har vi lösningen för en bättre hemtjänst? Självklart. Låt oss prata om Självklarhetsmetoden. Låt oss prata om Självklarhetsmetoden! 164 000 äldre är beroende av hemtjänsten i sin vardag. Och det är du
För dig som är valutaväxlare. Så här följer du reglerna om penningtvätt i din dagliga verksamhet INFORMATION FRÅN FINANSINSPEKTIONEN
 För dig som är valutaväxlare Så här följer du reglerna om penningtvätt i din dagliga verksamhet INFORMATION FRÅN FINANSINSPEKTIONEN MARS 2016 DU MÅSTE FÖLJA LAGAR OCH REGLER Som valutaväxlare ska du följa
För dig som är valutaväxlare Så här följer du reglerna om penningtvätt i din dagliga verksamhet INFORMATION FRÅN FINANSINSPEKTIONEN MARS 2016 DU MÅSTE FÖLJA LAGAR OCH REGLER Som valutaväxlare ska du följa
Modul 6: Integraler och tillämpningar
 Institutionen för Matematik SF65 Envariabelanalys Läsåret 5/6 Modul 6: Integraler och tillämpningar Denna modul omfattar kapitel 6. och 6.5 samt kapitel 7 i kursboken Calculus av Adams och Essex och undervisas
Institutionen för Matematik SF65 Envariabelanalys Läsåret 5/6 Modul 6: Integraler och tillämpningar Denna modul omfattar kapitel 6. och 6.5 samt kapitel 7 i kursboken Calculus av Adams och Essex och undervisas
Datorövning 2 Statistik med Excel (Office 2007, svenska)
 Datorövning 2 Statistik med Excel (Office 2007, svenska) Denna datorövning fokuserar på att upptäcka samband mellan två variabler. Det görs genom att rita spridningsdiagram och beräkna korrelationskoefficienter
Datorövning 2 Statistik med Excel (Office 2007, svenska) Denna datorövning fokuserar på att upptäcka samband mellan två variabler. Det görs genom att rita spridningsdiagram och beräkna korrelationskoefficienter
Från min. klass INGER BJÖRNELOO
 Från min klass INGER BJÖRNELOO Vi har nu följt Inger Björneloos klass under två år. Klassen börjar i höst på sitt sista lågstadieår, åk 3. Denna årgång av NÄMNAREN kommer att följa upp vad de gör och hur
Från min klass INGER BJÖRNELOO Vi har nu följt Inger Björneloos klass under två år. Klassen börjar i höst på sitt sista lågstadieår, åk 3. Denna årgång av NÄMNAREN kommer att följa upp vad de gör och hur
BibliotekMitt.se. Riktlinjer för Boktips, Artiklar, Arrangemang, Utställningar Arrangemang mm
 BibliotekMitt.se Riktlinjer för Boktips, Artiklar, Arrangemang, Utställningar Arrangemang mm Här hittar du speciella riktlinjer för BibliotekMitt. Vill du ha mer detaljerat om varje funktion så finns en
BibliotekMitt.se Riktlinjer för Boktips, Artiklar, Arrangemang, Utställningar Arrangemang mm Här hittar du speciella riktlinjer för BibliotekMitt. Vill du ha mer detaljerat om varje funktion så finns en
P-02/03 säsongen 2016
 P-02/03 säsongen 2016 AGENDA DU ÄR VÄRDEFULL IDROTTENS VÄRDEGRUND LAGANDA = VI TILLSAMMANS VINNARE I LÄNGDEN DU ÄR VÄRDEFULL 1. VARFÖR ÄR VI TRÄNARE & VARFÖR SPELAR NI FOTBOLL? (grupperna skriver varsin
P-02/03 säsongen 2016 AGENDA DU ÄR VÄRDEFULL IDROTTENS VÄRDEGRUND LAGANDA = VI TILLSAMMANS VINNARE I LÄNGDEN DU ÄR VÄRDEFULL 1. VARFÖR ÄR VI TRÄNARE & VARFÖR SPELAR NI FOTBOLL? (grupperna skriver varsin
Sid. 87-99 i boken Rekrytering. Författare Annica Galfvensjö, Jure Förlag
 Sid. 87-99 i boken Rekrytering Författare Annica Galfvensjö, Jure Förlag Nedan finner du en intervjuguide med förslag på frågor som du kan använda under intervjun. Det är många frågor så välj de du tycker
Sid. 87-99 i boken Rekrytering Författare Annica Galfvensjö, Jure Förlag Nedan finner du en intervjuguide med förslag på frågor som du kan använda under intervjun. Det är många frågor så välj de du tycker
Kriterium Kvalitet 1 Kvalitet 2 Kvalitet 3 Kvalitet 4 Använda, Utveckla och uttrycka
 Matematik Enheter - Tid Utveckla och Känner till några enheter och enstaka mätinstrument. Utför enkla mätningar. Avläser analoga och digitala tider.använder både muntliga och skriftliga metoder samt tekniska
Matematik Enheter - Tid Utveckla och Känner till några enheter och enstaka mätinstrument. Utför enkla mätningar. Avläser analoga och digitala tider.använder både muntliga och skriftliga metoder samt tekniska
Kursplan i svenska. Därför tränar vi följande färdigheter under elevens skoltid i ämnet svenska: Tala, lyssna och samtala. År 1
 Kursplan i svenska Språket är människans främsta redskap för att tänka, kommunicera och lära. Genom språket kan människor utveckla sin identitet, uttrycka känslor och tankar och förstå hur andra känner
Kursplan i svenska Språket är människans främsta redskap för att tänka, kommunicera och lära. Genom språket kan människor utveckla sin identitet, uttrycka känslor och tankar och förstå hur andra känner
Kunskapskrav för godtagbara kunskaper i matematik - slutet av åk 3
 Kunskapskraven åk k 3 - matematik 20 Kunskapskrav för godtagbara kunskaper i matematik - slutet av åk 3 Eleven kan lösa enkla problem i elevnära situationer genom att välja och använda någon strategi med
Kunskapskraven åk k 3 - matematik 20 Kunskapskrav för godtagbara kunskaper i matematik - slutet av åk 3 Eleven kan lösa enkla problem i elevnära situationer genom att välja och använda någon strategi med
2005-01-31. Hävarmen. Peter Kock
 2005-01-31 Hävarmen Kurs: WT0010 Peter Kock Handledare: Jan Sandberg Sammanfattning Om man slår upp ordet hävarm i ett lexikon så kan man läsa att hävarm är avståndet mellan kraften och vridningspunkten.
2005-01-31 Hävarmen Kurs: WT0010 Peter Kock Handledare: Jan Sandberg Sammanfattning Om man slår upp ordet hävarm i ett lexikon så kan man läsa att hävarm är avståndet mellan kraften och vridningspunkten.
Läraren som moderator vid problemlösning i matematik
 Läraren som moderator vid problemlösning i matematik Cecilia Christiansen 9 oktober 2012 Kursplanen för matematik: matematisk verksamhet är till sin art en kreativ, reflekterande och problemlösande aktivitet
Läraren som moderator vid problemlösning i matematik Cecilia Christiansen 9 oktober 2012 Kursplanen för matematik: matematisk verksamhet är till sin art en kreativ, reflekterande och problemlösande aktivitet
Läsfixarna. Idrott inne. Melinda får ta med en bok eller en sak hemifrån att visa och berätta om.
 Kom ihåg vecka 15 Förskoleklassen Läsfixarna. Idrott inne. Melinda får ta med en bok eller en sak hemifrån att visa och berätta om. Kul att träffa alla barn igen. Det verkar dock vara lite vårkänslor i
Kom ihåg vecka 15 Förskoleklassen Läsfixarna. Idrott inne. Melinda får ta med en bok eller en sak hemifrån att visa och berätta om. Kul att träffa alla barn igen. Det verkar dock vara lite vårkänslor i
Gruppenkät. Lycka till! Kommun: Stadsdel: (Gäller endast Göteborg)
 Gruppenkät Du har deltagit i en gruppaktivitet! Det kan ha varit en tjej- / killgrupp, ett läger eller ett internationellt ungdomsutbyte. Eller så har ni kanske ordnat ett musikarrangemang, skött ett café,
Gruppenkät Du har deltagit i en gruppaktivitet! Det kan ha varit en tjej- / killgrupp, ett läger eller ett internationellt ungdomsutbyte. Eller så har ni kanske ordnat ett musikarrangemang, skött ett café,
Boken om Teknik. Boken om Teknik är en grundbok i Teknik för åk 4 6.
 Boken om Teknik Boken om Teknik är en grundbok i Teknik för åk 4 6. PROVLEKTION: Teknikens arbetssätt att göra på riktigt Följande provlektion är ett utdrag ur Boken om Teknik. Uppslaget som är hämtat
Boken om Teknik Boken om Teknik är en grundbok i Teknik för åk 4 6. PROVLEKTION: Teknikens arbetssätt att göra på riktigt Följande provlektion är ett utdrag ur Boken om Teknik. Uppslaget som är hämtat
HT 2011 FK2004 Tenta Lärare delen 4 problem 6 poäng / problem
 HT 2011 FK2004 Tenta Lärare delen 4 problem 6 poäng / problem Problem 1 (6p) En undersökning utfördes med målet att besvara frågan Hur stor andel av den vuxna befolkningen i Sverige äger ett skjutvapen?.
HT 2011 FK2004 Tenta Lärare delen 4 problem 6 poäng / problem Problem 1 (6p) En undersökning utfördes med målet att besvara frågan Hur stor andel av den vuxna befolkningen i Sverige äger ett skjutvapen?.
Uppdrag: Huset. Fundera på: Vilka delar i ditt hus samverkar för att elen ska fungera?
 Uppdrag: Huset Praktiskt arbete: (Krav) Göra en skiss över ditt hus. Bygga en modell av ett hus i en kartong med minst två rum. Koppla minst tre lampor och två strömbrytare till ditt hus. Visa både parallellkoppling
Uppdrag: Huset Praktiskt arbete: (Krav) Göra en skiss över ditt hus. Bygga en modell av ett hus i en kartong med minst två rum. Koppla minst tre lampor och två strömbrytare till ditt hus. Visa både parallellkoppling
Föräldrar i Skola24. Schema
 Föräldrar i Skola24 Schema Ett textschema kan ses på startsidan om skolan har valt att aktivera funktionen. Passerade lektioner visas i grått, nuvarande eller nästkommande lektion är blåmarkerad och kommande
Föräldrar i Skola24 Schema Ett textschema kan ses på startsidan om skolan har valt att aktivera funktionen. Passerade lektioner visas i grått, nuvarande eller nästkommande lektion är blåmarkerad och kommande
Statistik, sannolikhet, algebra och funktioner, 3 hp. Studenter i lärarprogrammet F-3 III
 Grundläggande matematik II 7,5 högskolepoäng Provmoment: Ladokkod: Tentamen ges för: Statistik, sannolikhet, algebra och funktioner, 3 hp Studenter i lärarprogrammet F-3 III TentamensKod: Tentamensdatum:
Grundläggande matematik II 7,5 högskolepoäng Provmoment: Ladokkod: Tentamen ges för: Statistik, sannolikhet, algebra och funktioner, 3 hp Studenter i lärarprogrammet F-3 III TentamensKod: Tentamensdatum:
Drottningens gåta Lärarmaterial
 Lärarmaterial sidan 1 Författare: Cecilie Eken Vad handlar boken om? Boken är den spännande fortsättningen i serien Den Svarta Safiren. Sif har blivit biten av en hund och är svårt skadad. De ser män som
Lärarmaterial sidan 1 Författare: Cecilie Eken Vad handlar boken om? Boken är den spännande fortsättningen i serien Den Svarta Safiren. Sif har blivit biten av en hund och är svårt skadad. De ser män som
Fakta om Malala Yousafzai
 SIDAN 1 Elevmaterial Namn: Klicka HÄR för att skriva ut arbetsmaterialet. Klicka HÄR för att skicka ditt färdiga arbetsmaterial till din pedagog. LÄSFÖRSTÅELSE Skottet 1. Vart var Malala på väg när hon
SIDAN 1 Elevmaterial Namn: Klicka HÄR för att skriva ut arbetsmaterialet. Klicka HÄR för att skicka ditt färdiga arbetsmaterial till din pedagog. LÄSFÖRSTÅELSE Skottet 1. Vart var Malala på väg när hon
Texturbild. Lagerpaletten du kommer arbeta med ser du till höger. 1. Kopiera bakgrunden till ett nytt lager och gör den svartvit.
 Texturbild En guide om hur man skapar en bild med matta färger och texturiserad yta. Guiden innehåller moment där man får pröva sig fram och resultatet kanske inte blir det man tänkt sig direkt, men med
Texturbild En guide om hur man skapar en bild med matta färger och texturiserad yta. Guiden innehåller moment där man får pröva sig fram och resultatet kanske inte blir det man tänkt sig direkt, men med
Det flippade klassrummet hur uppfattas det av eleverna?
 Det flippade klassrummet hur uppfattas det av eleverna? Vi och vår skola Undervisningslyftet Samarbete Karlskrona kommun och Högskolan i Jönköping Föreläsningar, seminarier, handledning Möjlighet att ta
Det flippade klassrummet hur uppfattas det av eleverna? Vi och vår skola Undervisningslyftet Samarbete Karlskrona kommun och Högskolan i Jönköping Föreläsningar, seminarier, handledning Möjlighet att ta
Antal grodor i varje familj Antal hopp tills alla bytt plats Ökning 1 3 5 2 8 7 3 15 9 4 24
 strävorna 1AB Grodhopp problemlösning taluppfattning algebra Avsikt och matematikinnehåll Elever behöver få möta många aktiviteter där de kan se att algebra bland annat är generaliserad aritmetik. För
strävorna 1AB Grodhopp problemlösning taluppfattning algebra Avsikt och matematikinnehåll Elever behöver få möta många aktiviteter där de kan se att algebra bland annat är generaliserad aritmetik. För
Schlagerhjältar funderingsfrågor och presentationsövning
 en lektion från Lärarrummet för lättläst - www.lattlast.se/lararrum Schlagerhjältar funderingsfrågor och presentationsövning Ämne: Svenska, SVA, SFI Årskurs: 4-6, 7-9, Särgymn, Särvux, Gym, Vux Lektionstyp:
en lektion från Lärarrummet för lättläst - www.lattlast.se/lararrum Schlagerhjältar funderingsfrågor och presentationsövning Ämne: Svenska, SVA, SFI Årskurs: 4-6, 7-9, Särgymn, Särvux, Gym, Vux Lektionstyp:
Sveriges Trafikskolors Riksförbund Film om körkort för nysvenskar Speakertext - Svensk
 Sveriges Trafikskolors Riksförbund Film om körkort för nysvenskar Speakertext - Svensk Vägen till svenskt körkort Funderar du på att skaffa svenskt körkort för personbil? I den här filmen får du reda på
Sveriges Trafikskolors Riksförbund Film om körkort för nysvenskar Speakertext - Svensk Vägen till svenskt körkort Funderar du på att skaffa svenskt körkort för personbil? I den här filmen får du reda på
Varför är det så viktigt hur vi bedömer?! Christian Lundahl!
 Varför är det så viktigt hur vi bedömer?! Christian Lundahl! Fyra olika aspekter! Rättvisa! Reflektion och utvärdering av vår egen undervisning! Motivation för lärande! Metalärande (kunskapssyn)! 1. Rättvisa!
Varför är det så viktigt hur vi bedömer?! Christian Lundahl! Fyra olika aspekter! Rättvisa! Reflektion och utvärdering av vår egen undervisning! Motivation för lärande! Metalärande (kunskapssyn)! 1. Rättvisa!
Laganmälan & Laghantering
 203 Svenska Motorcykel- och Snöskoterförbundet Box 234 600 02 NORRKÖPING Tel. 0-23 0 80 www.svemo.se Laganmälan & Laghantering [En enkel guide för hur du anmäler ett lag i SVEMO TA.] Innehåll Innehåll...
203 Svenska Motorcykel- och Snöskoterförbundet Box 234 600 02 NORRKÖPING Tel. 0-23 0 80 www.svemo.se Laganmälan & Laghantering [En enkel guide för hur du anmäler ett lag i SVEMO TA.] Innehåll Innehåll...
Intervjumall. Datum: Intervjuare: Kandidatens namn: Kandidatens uppgifter: www.roirekrytering.se [email protected] Växel: 0770 110 177 1 (5)
 Intervjumall Datum: Intervjuare: Kandidatens namn: Kandidatens uppgifter: www.roirekrytering.se [email protected] Växel: 0770 110 177 1 (5) Intervju Att hålla i en anställningsintervju kan vara svårt.
Intervjumall Datum: Intervjuare: Kandidatens namn: Kandidatens uppgifter: www.roirekrytering.se [email protected] Växel: 0770 110 177 1 (5) Intervju Att hålla i en anställningsintervju kan vara svårt.
LÄSFÖRSTÅELSE PROVKAPITEL. Katarina Neiman Hedensjö
 LÄSFÖRSTÅELSE PROVKAPITEL Katarina Neiman Hedensjö Hej! Cirkus Ungefär och Cirkus Exakt Det är första veckan på sommarlovet och Julia ska gå i cirkusskola. Julia älskar allt som har med cirkus att göra.
LÄSFÖRSTÅELSE PROVKAPITEL Katarina Neiman Hedensjö Hej! Cirkus Ungefär och Cirkus Exakt Det är första veckan på sommarlovet och Julia ska gå i cirkusskola. Julia älskar allt som har med cirkus att göra.
Skriva B gammalt nationellt prov
 Skriva B gammalt nationellt prov Skriva B.wma Då fortsätter vi skrivträningen. Detta avsnitt handlar om att anpassa sin text till en särskild situation, en speciell texttyp och särskilda läsare. Nu ska
Skriva B gammalt nationellt prov Skriva B.wma Då fortsätter vi skrivträningen. Detta avsnitt handlar om att anpassa sin text till en särskild situation, en speciell texttyp och särskilda läsare. Nu ska
ELEV- HANDLEDNING (Ansökan via webben) www.orebro.se/gymnasieantagningen
 ELEV- HANDLEDNING (Ansökan via webben) www.orebro.se/gymnasieantagningen Gymnasieantagningen i Örebro län På Gymnasieantagningens hemsida www.orebro.se/gymnasieantagningen hittar du information om vad
ELEV- HANDLEDNING (Ansökan via webben) www.orebro.se/gymnasieantagningen Gymnasieantagningen i Örebro län På Gymnasieantagningens hemsida www.orebro.se/gymnasieantagningen hittar du information om vad
Flera nyanser av diskriminering
 ÖVNING: Flera nyanser av diskriminering I den här diskussionsövningen belyser vi diskriminerande strukturer, diskriminerande bemötande och fördomar. Så gör ni: 1 Läs noggrant igenom hela instruktionen
ÖVNING: Flera nyanser av diskriminering I den här diskussionsövningen belyser vi diskriminerande strukturer, diskriminerande bemötande och fördomar. Så gör ni: 1 Läs noggrant igenom hela instruktionen
Menys webbaserade kurser manual för kursdeltagare. Utbildningsplattform: Fronter
 Menys webbaserade kurser manual för kursdeltagare Utbildningsplattform: Fronter Innehållsförteckning Introduktion 3 Inloggning & Lösenordsbyte 4 Idagsidan 6 Kursens rum (startsida) 7 Webblektion 8 Inlämning
Menys webbaserade kurser manual för kursdeltagare Utbildningsplattform: Fronter Innehållsförteckning Introduktion 3 Inloggning & Lösenordsbyte 4 Idagsidan 6 Kursens rum (startsida) 7 Webblektion 8 Inlämning
Natur och samhälle Människans beroende av och påverkan på naturen och vad detta innebär för en hållbar utveckling.
 Ämne: Biologi, Matematik, Svenska, Hem- och konsumentkunskap, Årskurs: 4-6 SYFTE Syftet med övningen är att eleverna får undersöka hur mycket mat som kastas i skolrestaurangen. Eleverna får också arbeta
Ämne: Biologi, Matematik, Svenska, Hem- och konsumentkunskap, Årskurs: 4-6 SYFTE Syftet med övningen är att eleverna får undersöka hur mycket mat som kastas i skolrestaurangen. Eleverna får också arbeta
4-3 Vinklar Namn: Inledning. Vad är en vinkel?
 4-3 Vinklar Namn: Inledning I det här kapitlet skall du lära dig allt om vinklar: spetsiga, trubbiga och räta vinklar. Och inte minst hur man mäter vinklar. Att mäta vinklar och sträckor är grundläggande
4-3 Vinklar Namn: Inledning I det här kapitlet skall du lära dig allt om vinklar: spetsiga, trubbiga och räta vinklar. Och inte minst hur man mäter vinklar. Att mäta vinklar och sträckor är grundläggande
Enkätresultat för elever i år 2 i Nösnäsgymnasiet 2 i Stenungsund våren 2014
 Enkätresultat för elever i år 2 i Nösnäsgymnasiet 2 i Stenungsund våren 2014 Antal elever: 47 Antal svarande: 40 Svarsfrekvens: 85% Klasser: 12BAa, 12BAb, 12LL Skolenkäten Skolenkäten går ut en gång per
Enkätresultat för elever i år 2 i Nösnäsgymnasiet 2 i Stenungsund våren 2014 Antal elever: 47 Antal svarande: 40 Svarsfrekvens: 85% Klasser: 12BAa, 12BAb, 12LL Skolenkäten Skolenkäten går ut en gång per
Index vid lastbilstransporter
 index vid lastbilstransporter Matematiken Snabbhjälpen för att räkna rätt Index vid lastbilstransporter Innehåll A. Tre steg för att räkna rätt Sidan 1 B. Förändring enligt index 2 C. Andelskorrigering
index vid lastbilstransporter Matematiken Snabbhjälpen för att räkna rätt Index vid lastbilstransporter Innehåll A. Tre steg för att räkna rätt Sidan 1 B. Förändring enligt index 2 C. Andelskorrigering
Enkätresultat för elever i år 2 i Mega Musik gymnasium hösten 2014. Antal elever: 47 Antal svarande: 46 Svarsfrekvens: 98% Klasser: MM13
 Enkätresultat för elever i år 2 i Mega Musik gymnasium hösten 2014 Antal elever: 47 Antal svarande: 46 Svarsfrekvens: 98% Klasser: MM13 Skolenkäten Skolenkäten går ut en gång per termin till de skolor
Enkätresultat för elever i år 2 i Mega Musik gymnasium hösten 2014 Antal elever: 47 Antal svarande: 46 Svarsfrekvens: 98% Klasser: MM13 Skolenkäten Skolenkäten går ut en gång per termin till de skolor
D A B A D B B D. Trepoängsproblem. Kängurutävlingen 2012 Benjamin
 Kängurutävlingen enjamin Trepoängsproblem. Skrivtavlan i klassrummet är 6 meter bred. Mittdelen är m bred. De båda yttre delarna är lika breda. Hur bred är den högra delen? A: m :,5 m C:,5 m D:,75 m E:
Kängurutävlingen enjamin Trepoängsproblem. Skrivtavlan i klassrummet är 6 meter bred. Mittdelen är m bred. De båda yttre delarna är lika breda. Hur bred är den högra delen? A: m :,5 m C:,5 m D:,75 m E:
Enkätresultat för elever i år 2 i Praktiska Skövde i Praktiska Sverige AB hösten 2014
 Enkätresultat för elever i år 2 i Praktiska Skövde i Praktiska Sverige AB hösten 2014 Antal elever: 18 Antal svarande: 13 Svarsfrekvens: 72% Klasser: År 2 Skolenkäten Skolenkäten går ut en gång per termin
Enkätresultat för elever i år 2 i Praktiska Skövde i Praktiska Sverige AB hösten 2014 Antal elever: 18 Antal svarande: 13 Svarsfrekvens: 72% Klasser: År 2 Skolenkäten Skolenkäten går ut en gång per termin
Lokal kursplan för Ängkärrskolan år 9 Rev. 2009-09-22. -Positionssystemet. -Multiplikation och division. (utan miniräknare).
 Lokal kursplan för Ängkärrskolan år 9 Rev. 009-09- Matematik år 9 MOMENT MÅL KRITERIER/EXEMPELl Taluppfattning, aritmetik Repetition av: Skriv med siffror tolv -Positionssystemet. hundradelar. 0,, 0,7
Lokal kursplan för Ängkärrskolan år 9 Rev. 009-09- Matematik år 9 MOMENT MÅL KRITERIER/EXEMPELl Taluppfattning, aritmetik Repetition av: Skriv med siffror tolv -Positionssystemet. hundradelar. 0,, 0,7
Regler för onlinespel Bingo
 Regler för onlinespel Bingo 2012-11-05 Innehållsförteckning 1 INLEDNING 3 1.1 TILLÄMPLIGA VILLKOR 3 1.2 ALLMÄNT OM BINGO 3 1.3 GILTIGHETSTID FÖR REGLER FÖR ONLINESPEL BINGO 3 1.4 DEFINITIONER 3 1.4.1 GEMENSAMMA
Regler för onlinespel Bingo 2012-11-05 Innehållsförteckning 1 INLEDNING 3 1.1 TILLÄMPLIGA VILLKOR 3 1.2 ALLMÄNT OM BINGO 3 1.3 GILTIGHETSTID FÖR REGLER FÖR ONLINESPEL BINGO 3 1.4 DEFINITIONER 3 1.4.1 GEMENSAMMA
Kärnan. Halmstad 29 augusti 2014. Hej!
 Kärnan Halmstad 29 augusti 2014 Hej! Här kommer information ifrån oss på Kärnan (F-2). Varannan vecka berättar vi lite om hur vi har det på skolan, vad vi har arbetat med och vad som händer de kommande
Kärnan Halmstad 29 augusti 2014 Hej! Här kommer information ifrån oss på Kärnan (F-2). Varannan vecka berättar vi lite om hur vi har det på skolan, vad vi har arbetat med och vad som händer de kommande
7. SAMHÄLLSORIENTERING ÅK 5
 7. SAMHÄLLSORIENTERING ÅK 5 7.2. Elevhäfte 2 7.2.1. Livsfrågor Eva och Micke går båda i 5:an. De träffas ofta efter skolan och lyssnar på musik eller gör hemläxan tillsammans. Ibland funderar de på frågor
7. SAMHÄLLSORIENTERING ÅK 5 7.2. Elevhäfte 2 7.2.1. Livsfrågor Eva och Micke går båda i 5:an. De träffas ofta efter skolan och lyssnar på musik eller gör hemläxan tillsammans. Ibland funderar de på frågor
Syftet är att fördjupa diskussionen om vem som ansvarar för vad.
 ÖVNING: Roller och ansvar Syftet är att fördjupa diskussionen om vem som ansvarar för vad. Deltagarna får med utgångspunkt från olika arbetsmiljöutmaningar diskutera vilket ansvar rollen som chef och skyddsombud
ÖVNING: Roller och ansvar Syftet är att fördjupa diskussionen om vem som ansvarar för vad. Deltagarna får med utgångspunkt från olika arbetsmiljöutmaningar diskutera vilket ansvar rollen som chef och skyddsombud
Bygg ditt eget dataspel på sommarlovet!
 Bygg ditt eget dataspel Spelutveckling Finns det något roligare än att spela dataspel? Ja, att bygga sitt eget! Under en vecka i sommar får du lära dig mer om hur data - spel fungerar och dessutom designa
Bygg ditt eget dataspel Spelutveckling Finns det något roligare än att spela dataspel? Ja, att bygga sitt eget! Under en vecka i sommar får du lära dig mer om hur data - spel fungerar och dessutom designa
De två första korten Tidig position
 De två första korten Tidig position Hold em är ett positionsspel, och förmodligen mer än någon annan form av poker. Det beror på att knappen anger spelarnas turordning under satsningsrundorna. (Enda undantaget
De två första korten Tidig position Hold em är ett positionsspel, och förmodligen mer än någon annan form av poker. Det beror på att knappen anger spelarnas turordning under satsningsrundorna. (Enda undantaget
INSTUDERINGSFRÅGOR TILL PROVET
 INSTUDERINGSFRÅGOR TILL PROVET Svara så utförligt som möjligt på alla frågor. Skriv inte av exakt från boken utan försök formulera dina svar med egna ord. PowerPointen finns på bloggen. LYCKA TILL! /Therese
INSTUDERINGSFRÅGOR TILL PROVET Svara så utförligt som möjligt på alla frågor. Skriv inte av exakt från boken utan försök formulera dina svar med egna ord. PowerPointen finns på bloggen. LYCKA TILL! /Therese
Lokal pedagogisk planering i matematik för årskurs 8
 Lokal pedagogisk planering i matematik för årskurs 8 Arbetsområde 2. Algebra Syfte formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder. reflektera över matematikens
Lokal pedagogisk planering i matematik för årskurs 8 Arbetsområde 2. Algebra Syfte formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder. reflektera över matematikens
Facit med lösningsförslag kommer att anslås på vår hemsida www.ebersteinska.norrkoping.se. Du kan dessutom få dem via e-post, se nedan.
 Detta häfte innehåller uppgifter från fyra olika områden inom matematiken. Meningen är att de ska tjäna som en självtest inför gymnasiet. Klarar du dessa uppgifter så är du väl förberedd inför gymnasiestudier
Detta häfte innehåller uppgifter från fyra olika områden inom matematiken. Meningen är att de ska tjäna som en självtest inför gymnasiet. Klarar du dessa uppgifter så är du väl förberedd inför gymnasiestudier
Omvandla Vinklar. 1 Mattematiskt Tankesätt
 Omvandla Vinklar 1 Mattematiskt Tankesätt (Kan användas till mer än bara vinklar) 2 Omvandla med hjälp av Huvudräkning (Snabbmetod i slutet av punkt 2) 3 Omvandla med Miniräknare (Casio) Läs denna Först
Omvandla Vinklar 1 Mattematiskt Tankesätt (Kan användas till mer än bara vinklar) 2 Omvandla med hjälp av Huvudräkning (Snabbmetod i slutet av punkt 2) 3 Omvandla med Miniräknare (Casio) Läs denna Först
