Inlämning 1: Bedömning och kommentarer
|
|
|
- Fredrik Ivarsson
- för 6 år sedan
- Visningar:
Transkript
1 Inlämning 1: Bedömning och kommentarer Inledning. Här är vår bedömning av era lösningar till inlämningsuppgift 1. Därmed kommer vi till en viktig del av kursen återkopplingen. De som inte har fått godkänd och det är de flesta får nu möjlighet att bearbeta texten ännu en gång och därmed förbättre lösningen ytterligare; med avseende på matematisk stringens, disposition och grafisk utförande. Bearbetningen ska ske med utgångspunkt i de kommentarer om era lösningar som finns i detta papper. Förutom namnen på de som är godkända eller nästan godkända, finns nedan en lista med typiska fel som förekommer i era lösningar. Att felen är typiska betyder i detta sammanhang att alla som inte fått godkänt har gjort minns ett av dessa fel (eller en variant av samma). Listan är uppdelat tematiskt i fem kategorier efter feltyper: 1) Logiska fel och brister, 2) Disposition och det matematiska språket, 3) Den matematiska framställningen, 4) språket i allmänhet och 5) LATEX. Glädjande nog har det vist sig att majoriteten av lösningarna är matematiskt korrekta om man bortser från at det från tid till annan kan finnas någon liten lucka kvar i vissa bevis. Bedömning. Det finns tre kategorier: Godkända, nästan godkända och rest. Godkända lösningar är nästan eller helt perfekta och ingen uppdatering behövs. Nästan godkända lösningar innehåller bara fel av enklare karakter (aldrig logiska fel förutom rena felsägningar), oftast i framställning och typografi, och uppdatering behövs eftersom att det skulle förbättre slutprodukten märkbart. Rest i denna kategorin finns lösningar med logiska fel (som nämnt ovan, enbart smärre sådana i år) och något mera omfattande problem i framställningen. Dessa lösningar behöver naturligtvis uppdateras. Godkända. Erik Olsson, Anton Tuvegård, Joel Henriksson. Nästan godkända. Lukas Gardberg, Kåre von Geijer, Heidar Gergis, Rasmus Johansson, Lukas Karlsson, Axel Kärrholm, Oskar Hellsén Palmqvist, Mika Persson, Linus Rickman, Samuel Selleck, Elias Sjöberg, Tove Thunborg, Alex Uhlman Rest. Alla övriga. Godkända och nästan godkända får tillbaka sina lösningar direkt 1 (se Vita hyllan mittemot MH:333 i facket märkt Matematisk kommunikation), de med rest får uppdatera deras lösningar enbart med utgångspunkt i kommentarerna som ges här. 1 Nästan godkända lösningar återlämnas direkt eftersom att de, förutom att vara matematisk korrekta, oftast enbart innehåller småfel som inte ens är av standartyp.
2 Innan ni sätter i gång med att rätta: Läs igenom er egen lösning påny och se den med friska ögon. Förstår ni fortfarande er egen text? Deadline för inlämning av uppdaterad version av lösningen: Tisdag 12 december 2017.(Gäller Rest och Nästan godkända.) 1. Logiska fel och brister. I vissa lösningar referarar man till faktorssatsen istället för till allmänna konjugatregeln: Man säger t.ex. att a n 1 = (a 1)q(a) för något polynom q(a). Gör man så bör man bevisa att q(a) blir ett heltal, annars kan man inte dra slutsatsen att (a 1) (a n 1). (Det finns även de som refererar till faktorssatsen när det i själva verket menar allmänna konjugatregeln!) I beviset för att a = 2 förekommer lösningar där man direkt drar slutsatsen att om p = a n 1 är ett primtal så måste a 1 = 1 utan att utesluta fallet a 1 = p. Liknande fel förekommer ibland vid beviset av att n är ett primtal. Man påstår att 2 n 1 blir ett sammansatt tal utan att ens nämna att de funna faktorerna är skilda från 1. I en del lösningar förekommer det att man antar att n är ett sammansatt tal, n = ab, men glömmer att ange villkor på faktorerna a, b, alltså att 1 < a, b < n. 2. Disposition och det matematiska språket. I år har vi sett en antal lösningar där man har delat in beviset för a = 2 i två delar, ett där a antas vara ett jämnt tal, a = 2k, och ett annat där a antas udda, a = 2k 1. Dessa två fall behandlas var för sig och leder till ett korrekt bevis. Men indelningen i udda-jämn har inget med problemställningen i sig att göra och behövs alltså inte. Man får ett kortare och tydligare bevis för sammma slutsats om man inte gör den. Det kan ofta vara en fördel att definiera begreppet sammansatt tal i samband med att begreppet primtal introduceras. Sammansatta tal heter just så på svenska. Använd inte ordet komposit tal. I år refererar många till höger- och vänsterled i en ekvation med HL respektive VL. Det förekommer speciellt i samband med bevis för allmänna konjugatregeln. I 99% av alla fall (utom möjligen i vissa induktionsbevis) är det en helt onödig symbolik. Varför inte bara säga
3 t.ex. Vi börjar med att utveckla högerledet i ekvationen ovan och får varpå följer en beräkning (nu utan HL =...). På samma sätt kan man avsluta ett bevis med meningen vilket är lika med vänsterledet i ekvationen ovan. Alltså, binda ihop dina beräkningar till en sammanhängande text med hjälp av ord, inte med ännu fler symboler. Säg explicit med ord varför man kan välja a = 2 i bevisets andra del, n är ett primtal. (Om man använder detta i sitt bevis, såklart.) Vissa använder egenuppfunna ord som delsats och undersats och liknande. Var vänlig att använda standard terminologi. När man ska formulera en sats eller ett lemma, skriv då antagandet först (Om...) och konklusionen sen (så är...). Mönstret kan brytas, men inte gärna utan anledning eller medveten intention. Använd korrekt interpunktion: punkt eller komma även efter formler om grammatiken kräver så. Inleda aldrig en mening med en matematisk symbol eller ett variabelnamn. Formulera problemet/satsen inuti texten inte på textens omslag eller försatsblad. Använder man allmänna konjugatregeln flera gångar under bevisets gång så tycker jag det är bäst att formulera denna, med alla relevanta förutsättningar, redan innan beviset börjar. Resultatet kan formuleras i ett lemma eller i löpande text, det kvittar så länge påståendet är korrekt. Man kan ge ett bevis eller man kan referera till att resultatet är välkänt, om man vill. Iövrigt, upprepa inte argumentet för allmänna konjugatregeln (eller för andra elementära resultat) två eller flera gångar. I vissa formuleringar av allmänna konjugatregeln skrivs a n 1 n = (a 1) n a n k 1 k 1, eller motsvarande. Jag tycker inte man ska skriva ut de onödiga ettorna som i 1 k 1. Det är även osäkert om man behöver skriva 1 n istället för 1. (Allt detta gäller givetvis inte om man har med ettorna för att förtydliga ett steg i argumentet!) Ett annat exempel är uttrycket a 1 1 där exponenten 1 känns onödig. Bättre att bara skriva a 1. En del lösningar innehåller formler eller uttryck med överflödiga eller onödiga parenteser. Här är ett exempel: talet (a n 1) är delbart med (a 1). Parenteserna i sista uttrycket tjäner ingenting till. Parenteser k=1
4 används ju för att håll ihop uttryck som står intill andra uttryck. Det är inte fallet i exemplet innan och man kunne likaväl (eller bättre) ha skrivit talet a n 1 är delbart med a 1. Vi arbetar i denna uppgift bara med icke-negativa tal och positiva primtal. Därför behöver man bara referera till positiva delare när man t.ex. definierar primtal och sammansatta tal. Man behöver med andra ord inte ta med minustecknet när man skriver talet p kallas ett primtal om det endast kan delas med ±1 eller med ±p. En annan viktig sak är att ge definitionen så tidigt som möjligt i texten. Antingen under rubriken definition eller i löpande text, det är likvärdigt här. Kom ihåg att ordet primtal faktiskt finns med redan i problemet, och därför bör förklaras i anslutning till formuleringen av problemet. Använd ej symboler, t.ex. P, P + eller a b, innan dessa har introducerats formellt. Definition av ny symbol bör göras innan eller i anslutning till att symbolen används första gången. 3. Den matematiska framställningen En del lösningar innehåller formler eller uttryck met överflödiga eller onödiga parenteser. Här är ett exempel: talet a n 1 är delbart med (a 1). Parenteserna i sista uttrycket tjäner inget till. Parenteser används ju för att håll ihop uttryck som står intill andra uttryck. Det är inte fallet i exemplet innan och man kunne likaväl (eller bättre) ha skrivit talet a n 1 är delbart med a 1. Ett annat exempel vi har sett är en parentetisk anmärkning: ((a 1) eller (a n 1 +a n a+1)) där antalet parenteser blir överväldigande. Det finns gott om exempel av liknande karaktär där parenteser kan tas bort och texten därmed förbättras. I ett indirekt bevise för att n är ett primtal antas det först att n är sammansatt, alltså att n = bc där 1 < b < n, 1 < c < n. Sen säger texten Vi definierade c som ett heltal större än ett. Jag tycker att definierade är fel ord och rekommenderar att man skriver Vi antog att c är ett heltal större än ett. (En definition beskriver ett nytt begrepp i termer av redan kända begrepp. Ett antagande handler om objekts egenskaper.) Observera: ovanstående fel finns i flera snarlika varianter. I en definition står det Definition av ett primtal. Skriv hellre Definition av primtal, eftersom att man avser att definiera en hel klass av naturliga tal, inte bara ett enda.
5 Ytterligare ett språkexempel där vi citerar från en lösning: Med hjälp av lemma 1 kan vi skriva om a n 1 som två faktorer. n a n 1 = (a 1) a n k k=1 Enligt satsen så är detta ett primtal. Här förekommer flera småfel (sex stycken!): 1) Första meningen avslutas med en punkt innan formeln (korrekt) som egentligen är en del av samma mening. 2) Det ska vara produkten av två faktorer, 3) Ingen punkt efter formeln, men ändå påbörjas ny mening i raden därpå. 4) Otillsiktat textindragning i raden efter formeln (pga. extra mellanslag) 5) Enligt satsen refererar inte till satsens utsaga utan till dess hypotes. Därför bör man skriva Enligt antagandet i satsen. 6) Oklart vad detta i sista meningen refererar till. Bättre är: Med hjälp av lemma 1 kan vi skriva om a n 1 som en produkt av två faktorer a n 1 = (a 1) n a n k. k=1 Enligt antagandet i satsen så är vänsterledet ett primtal. Mycket enkla observationer som t.ex. a n 1 är varken ett primtal eller ett sammansatt tal då a = 1 bör inte anges som ett lemma eller liknande, men är just bara en observation. (Har i mitt tycke inte samma dignintet som ett lemma bör ha.) Skriver man för att formeln a n 1 = p ska stämma... menar man snarare För att a n 1 skulle kunne vara ett primtal.... Använd ej, eller. för multiplikation. Om ett tecken för multiplikation behövs kan man använda kommandot \cdot som t.ex. i 20 = Språket iövrigt. Det är ovanligt att använda personliga pronomen jag i matematisk prosa. Det gängse sättet är att använda vi (på det inkluderande sättet du, läsaren, och jag, författaren ) eller att använda passivform.
6 Använd heller kursiverad text för att framhäva ord eller fraser istället för understrykning, som är så fult! Ofta delas texten in i onödigt många avsnitt som var och en ges båda rubrik och nummer. Det ger ett splittrat intryck. Det är bättre att använda styckindelning istället. Speciellt i korta texter som denna behöver man verkligen inte numreringar av annat än t.ex. ekvationer. Läsaren kan i de flesta fallen hålla all nödvändig information i huvudet. (Senare, i projektrapporten, blir det en annan sak.) Kom ihåg att använda komma, punkt och kolon efter formler (även formler i fritstående läge) om svensk grammatik kräver så. (Tänk dig att du läser texten högt och alltså ersätter formeluttryck med ord.) Börja aldrig en ny mening med en matematisk symbol eller en formel. Omformulera istället så att meningen inleds med ett vanligt ord. Det finns även exempel på olyckligt valda rubriker, t.ex. Del 1 a = 2, där tankestrecket kan misstolkas som ett minustecken. Håll textens utseende enkel. Avstå från att använda fetstilt text om det inte är i en rubrik (eller en matematisk symbol). Många radbrytningar och nya stycken ger ett stökigt intryck. Ibland ser man att en rubrik, t.ex. Lemma, återföljs utan mellanliggande text av en sats-miljö Lemma. Det ser knasigt ut. Antingen behövs inte avsnitten och deras rubriker eller också behövs det mer text i varje avsnitt. 5. LATEX-tips. Formler, symboler och variabler skrivna i löpande text ska också skrivas i LATEX s formelmiljö. Exempelvis x = 1 istället för x=1, där man använder kommandot $x=1$. Akta er för (ofrivilliga) textindragningar precis efter formler i fristående läge! Lämna inte mellenrum efter \[...\] eller $$...$$, beroende på vad man föredrar att använda. Använd istället för, dvs. \Longleftrightarrow med stort L istället för \longleftrightarrow. (Var förövrigt försiktig med symboler i rubriker. Det är inte alltid det ser bra ut.) För att skriva en sats, t.ex.
7 Sats. Låt n beteckna ett udda heltal som är större än ett. Då har ekvationen x 2 y 2 = n (1) precis en lösning (x, y), där x, y N 0, om och endast om n är ett primtal. har jag använt följande LATEX-kommandon: \begin{sats} Låt $n$ beteckna ett udda heltal som är större än ett. Då har ekvationen \begin{equation}\label{ekv} x^2-y^2 = n \end{equation} precis en lösning $(x,y)$, där $x,y\in\boldsymbol{n}_0$, om och endast om $n$ är ett primtal. \end{sats} I preamble läggs det nödvändiga \newtheorem*{sats}{sats}, som skapar en sats-miljö med titeln Sats istället för Theorem. En motsvarande miljö för lemman kan skapas med \newtheorem*{sats}{lemma}. Här numreras lemman tillsammans med satserna (även om * efter \newtheorem gör så att man inte skriver ut satsnummer. Numrering fås genom att ta bort *.) En bevismiljö som här Bevis. Konjugatregeln ger (x y)(x + y) = n och eftersom att n är ett primtal och 0 < x y < x + y följer det att x y = 1 och x + y = n, et ekvationssystem med två ekvationer och två obekanta.... vilket skulle bevisas. fås genom kommandot \begin{proof} Konjugatregeln ger $(x-y)(x+y)=n$ och eftersom att $n$ är ett primtal och $0 <x-y<x+y$ följer det att $x-y=1$ och $x+y=n$, et ekvationssystem med två ekvationer och två obekanta.... vilket skulle bevisas. \end{proof}
8 Använd \cdots vid summor, som i a n 1 = (a 1)(a n 1 + a n a + 1), med centrerade punkter, vilket är bättre än \ldots som ger a n 1 = (a 1)(a n 1 + a n a + 1). Det senare kommandot används med fördel här: k = 1,2,..., N. De typografiskt passar ihop med placeringen av kommatecknen. Slutligen ett exempel på hur man kan förbättre utseendet på en längre beräkning. I en lösning finner vi följande: Högerledet kan omformas till att utgöra vänsterleder: HL = (a 1)(a n 1 + a n a + 1) = (a n + a n a 2 + a) (a n 1 + a n a + 1) = a n + (a n a 2 + a) (a n a 2 + a) 1 = vilket bevisar lemmat. Här har multline-miljön troligtvis använts. Bättre: Utveckling av högerledet ger (a 1)(a n 1 + a n a + 1) a n 1 = VL = (a n + a n a 2 + a) (a n 1 + a n a + 1) = a n + (a n a 2 + a) (a n a 2 + a) 1 = a n 1 vilket är vänsterledet i vår ekvation, vilket bevisar lemmat. Här har vi även tagit bort de onödiga beteckningarna HL och VL samt likhetstecknen till höger i beräkningen. Koden som använts är: \begin{align*} (a-1)&(a^{n-1}+a^{n-2}+\cdots+a+1)\\ &=(a^{n}+a^{n-1}+\cdots+a^2+a) -(a^{n-1}+a^{n-2}+\cdots+a+1)\\ &=a^n +(a^{n-1}+\cdots+a^2+a) -(a^{n-1}+\cdots+a^2+a)-1\\ &= a^n-1 \end{align*} Ampersan (&) anger hur texten riktas in i vertikal led och \\ ger radbrytning.
Kommentarer till inlämningsuppgift 1.
 Kommentarer till inlämningsuppgift 1. Inledning. Inlämningsuppgift 1 i Matematisk kommunikation rättas genom att ge ut en lista med typfel. Har man fått godkänt sin lösning, får man tillbaka pappersversionen
Kommentarer till inlämningsuppgift 1. Inledning. Inlämningsuppgift 1 i Matematisk kommunikation rättas genom att ge ut en lista med typfel. Har man fått godkänt sin lösning, får man tillbaka pappersversionen
inte följa någon enkel eller fiffig princip, vad man nu skulle mena med det. All right, men
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Christian Gottlieb Gymnasieskolans matematik med akademiska ögon Induktion Dag 2. Explicita formler och rekursionsformler. Dag mötte vi flera talföljder,
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Christian Gottlieb Gymnasieskolans matematik med akademiska ögon Induktion Dag 2. Explicita formler och rekursionsformler. Dag mötte vi flera talföljder,
Hur man skriver matematik
 Hur man skriver matematik Niels Chr. Overgaard 2018-10-01 N. Chr. Overgaard Skriva matematik 2018-10-01 1 / 12 Information: Opposition och kompisgranskning En del av inlämningsuppgift går ut på att man
Hur man skriver matematik Niels Chr. Overgaard 2018-10-01 N. Chr. Overgaard Skriva matematik 2018-10-01 1 / 12 Information: Opposition och kompisgranskning En del av inlämningsuppgift går ut på att man
Matematisk kommunikation (FMA085 4,5hp) Läsperiod 2, HT 2017
 Matematisk kommunikation (FMA085 4,5hp) Läsperiod 2, HT 2017 Kurschef: Niels Chr. Overgaard (NCO), tel. 046-222 85 32, epost nco@maths.lth.se, rum MH:551B. Föreläsningar: NCO Må 8 10 E:C läsvecka 1, 2,
Matematisk kommunikation (FMA085 4,5hp) Läsperiod 2, HT 2017 Kurschef: Niels Chr. Overgaard (NCO), tel. 046-222 85 32, epost nco@maths.lth.se, rum MH:551B. Föreläsningar: NCO Må 8 10 E:C läsvecka 1, 2,
TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor
 TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor Johan Thim 22 augusti 2018 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför Q
TATM79: Föreläsning 1 Notation, ekvationer, polynom och summor Johan Thim 22 augusti 2018 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför Q
Övningshäfte 2: Induktion och rekursion
 GÖTEBORGS UNIVERSITET MATEMATIK 1, MMG200, HT2017 INLEDANDE ALGEBRA Övningshäfte 2: Induktion och rekursion Övning D Syftet är att öva förmågan att utgående från enkla samband, aritmetiska och geometriska,
GÖTEBORGS UNIVERSITET MATEMATIK 1, MMG200, HT2017 INLEDANDE ALGEBRA Övningshäfte 2: Induktion och rekursion Övning D Syftet är att öva förmågan att utgående från enkla samband, aritmetiska och geometriska,
1. Inledning, som visar att man inte skall tro på allt man ser. Betrakta denna följd av tal, där varje tal är dubbelt så stort som närmast föregående
 MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Christian Gottlieb Gymnasieskolans matematik med akademiska ögon Induktion Dag 1 1. Inledning, som visar att man inte skall tro på allt man ser. Betrakta
MATEMATISKA INSTITUTIONEN STOCKHOLMS UNIVERSITET Christian Gottlieb Gymnasieskolans matematik med akademiska ögon Induktion Dag 1 1. Inledning, som visar att man inte skall tro på allt man ser. Betrakta
TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter
 TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter Johan Thim 15 augusti 2015 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför
TATM79: Föreläsning 1 Notation, ekvationer, polynom och olikheter Johan Thim 15 augusti 2015 1 Vanliga symboler Lite logik Implikation: P Q. Detta betyder att om P är sant så är Q sant. Utläses P medför
Inlämningsuppgift, LMN100
 Inlämningsuppgift, LMN100 Delkurs 3 Matematik Lösningar och kommentarer 1 Delbarhetsegenskaper (a) Påstående: Ett heltal är delbart med fyra om talet som bildas av de två sista siffrorna är delbart med
Inlämningsuppgift, LMN100 Delkurs 3 Matematik Lösningar och kommentarer 1 Delbarhetsegenskaper (a) Påstående: Ett heltal är delbart med fyra om talet som bildas av de två sista siffrorna är delbart med
Hela tal LCB 1999/2000
 Hela tal LCB 1999/2000 Ersätter Grimaldi 4.3 4.5 1 Delbarhet Alla förekommande tal i fortsättningen är heltal. DEFINITION 1. Man säger att b delar a om det finns ett heltal n så att a Man skriver b a när
Hela tal LCB 1999/2000 Ersätter Grimaldi 4.3 4.5 1 Delbarhet Alla förekommande tal i fortsättningen är heltal. DEFINITION 1. Man säger att b delar a om det finns ett heltal n så att a Man skriver b a när
Hur man skriver matematik
 Hur man skriver matematik Niels Chr. Overgaard 2015-09-28 1 / 8 Opposition och kompisgranskning En del av inlämningsuppgift går ut på att man granskar och opponerar på en annan kursdeltagares lösning.
Hur man skriver matematik Niels Chr. Overgaard 2015-09-28 1 / 8 Opposition och kompisgranskning En del av inlämningsuppgift går ut på att man granskar och opponerar på en annan kursdeltagares lösning.
Explorativ övning 5 MATEMATISK INDUKTION
 Explorativ övning 5 MATEMATISK INDUKTION Syftet med denna övning är att introducera en av de viktigaste bevismetoderna i matematiken matematisk induktion. Termen induktion är lite olycklig därför att matematisk
Explorativ övning 5 MATEMATISK INDUKTION Syftet med denna övning är att introducera en av de viktigaste bevismetoderna i matematiken matematisk induktion. Termen induktion är lite olycklig därför att matematisk
Lösningar till utvalda uppgifter i kapitel 5
 Lösningar till utvalda uppgifter i kapitel 5 5.3. Vi använder Euklides algoritm och får 4485 = 1 3042 + 1443 3042 = 2 1443 + 156 1443 = 9 156 + 39 156 = 4 39. Alltså är sgd(3042, 4485) = 39. Om vi startar
Lösningar till utvalda uppgifter i kapitel 5 5.3. Vi använder Euklides algoritm och får 4485 = 1 3042 + 1443 3042 = 2 1443 + 156 1443 = 9 156 + 39 156 = 4 39. Alltså är sgd(3042, 4485) = 39. Om vi startar
Sidor i boken 110-113, 68-69 2, 3, 5, 7, 11,13,17 19, 23. Ett andragradspolynom Ett tiogradspolynom Ett tredjegradspolynom
 Sidor i boken 110-113, 68-69 Räkning med polynom Faktorisering av heltal. Att primtalsfaktorisera ett heltal innebär att uppdela heltalet i faktorer, där varje faktor är ett primtal. Ett primtal är ett
Sidor i boken 110-113, 68-69 Räkning med polynom Faktorisering av heltal. Att primtalsfaktorisera ett heltal innebär att uppdela heltalet i faktorer, där varje faktor är ett primtal. Ett primtal är ett
Mer om analytisk geometri
 1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
1 Onsdag v 5 Mer om analytisk geometri Determinanter: Då man har en -matris kan man till den associera ett tal determinanten av som också skrivs Determinanter kommer att repeteras och studeras närmare
Explorativ övning 5 MATEMATISK INDUKTION
 Explorativ övning 5 MATEMATISK INDUKTION Syftet med denna övning är att introducera en av de viktigaste bevismetoderna i matematiken matematisk induktion. Termen induktion är lite olycklig därför att matematisk
Explorativ övning 5 MATEMATISK INDUKTION Syftet med denna övning är att introducera en av de viktigaste bevismetoderna i matematiken matematisk induktion. Termen induktion är lite olycklig därför att matematisk
MATEMATIKENS SPRÅK. Avsnitt 1
 Avsnitt 1 MATEMATIKENS SPRÅK Varje vetenskap, liksom varje yrke, har sitt eget språk som ofta är en blandning av vardagliga ord och speciella termer. En instruktionshandbok för ett kylskåp eller för en
Avsnitt 1 MATEMATIKENS SPRÅK Varje vetenskap, liksom varje yrke, har sitt eget språk som ofta är en blandning av vardagliga ord och speciella termer. En instruktionshandbok för ett kylskåp eller för en
Kvalificeringstävling den 30 september 2008
 SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
SKOLORNAS MATEMATIKTÄVLING Svenska Matematikersamfundet Kvalificeringstävling den 30 september 2008 Förslag till lösningar Problem 1 Tre rader med tal är skrivna på ett papper Varje rad innehåller tre
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson LÄSANVISNINGAR VECKA 36 VERSION 1. ARITMETIK FÖR RATIONELLA OCH REELLA TAL, OLIKHETER, ABSOLUTBELOPP ADAMS P.1 Real Numbers and the Real
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson LÄSANVISNINGAR VECKA 36 VERSION 1. ARITMETIK FÖR RATIONELLA OCH REELLA TAL, OLIKHETER, ABSOLUTBELOPP ADAMS P.1 Real Numbers and the Real
Svar till vissa uppgifter från första veckan.
 Svar till vissa uppgifter från första veckan. Svar till kortuppgifter F:. Ja! Förhoppningsvis så ser man direkt att g fx) är ett polynom. Vidare så gäller det att g fα) = gfα)) = gβ) = 0. Använd faktorsatsen!
Svar till vissa uppgifter från första veckan. Svar till kortuppgifter F:. Ja! Förhoppningsvis så ser man direkt att g fx) är ett polynom. Vidare så gäller det att g fα) = gfα)) = gβ) = 0. Använd faktorsatsen!
Sanningsvärdet av ett sammansatt påstående (sats, utsaga) beror av bindeord och sanningsvärden för ingående påståenden.
 MATEMATISK LOGIK Matematisk logik formaliserar korrekta resonemang och definierar formellt bindeord (konnektiv) mellan påståenden (utsagor, satser) I matematisk logik betraktar vi påståenden som antingen
MATEMATISK LOGIK Matematisk logik formaliserar korrekta resonemang och definierar formellt bindeord (konnektiv) mellan påståenden (utsagor, satser) I matematisk logik betraktar vi påståenden som antingen
Algebra och rationella uttryck
 Algebra och rationella uttryck - 20 Uppgift nr Förenkla x0 y 6 z 5 25 y 2 Uppgift nr 2 Uppgift nr 3 ab b 5a - a² 9a där a 0. där b 0. Uppgift nr 4 Multiplicera in i parentesen 2x(4 + 2x 3 ) Uppgift nr
Algebra och rationella uttryck - 20 Uppgift nr Förenkla x0 y 6 z 5 25 y 2 Uppgift nr 2 Uppgift nr 3 ab b 5a - a² 9a där a 0. där b 0. Uppgift nr 4 Multiplicera in i parentesen 2x(4 + 2x 3 ) Uppgift nr
Introduktion till L A TEX
 Introduktion till L A TEX Niels Chr. Overgaard 2012-09-18 N. Chr. Overgaard Intro. LATEX 2012-09-18 1 / 12 Varför L A TEX? Syftet med dokumentpreparationssystemet L A TEX är att generera välstrukturerade
Introduktion till L A TEX Niels Chr. Overgaard 2012-09-18 N. Chr. Overgaard Intro. LATEX 2012-09-18 1 / 12 Varför L A TEX? Syftet med dokumentpreparationssystemet L A TEX är att generera välstrukturerade
Lösningar och kommentarer till uppgifter i 1.1
 Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
Lösningar och kommentarer till uppgifter i 1.1 1106 d) 1107 d) 5t(t t 1) t (t 3) + t 3 5t 3 10t 5t (t 3 3t ) + t 3 5t 3 10t 5t t 3 + 3t + t 3 6t 3 7t 5t Kommentarer: Starta med att multiplicera in faktorerna
Induktion, mängder och bevis för Introduktionskursen på I
 Induktion, mängder och bevis för Introduktionskursen på I J A S, ht 04 1 Induktion Detta avsnitt handlar om en speciell teknik för att försöka bevisa riktigheten av påståenden eller formler, för alla heltalsvärden
Induktion, mängder och bevis för Introduktionskursen på I J A S, ht 04 1 Induktion Detta avsnitt handlar om en speciell teknik för att försöka bevisa riktigheten av påståenden eller formler, för alla heltalsvärden
INDUKTION OCH DEDUKTION
 Explorativ övning 3 INDUKTION OCH DEDUKTION Syftet med övningen är att öka Din problemlösningsförmåga och bekanta Dig med olika bevismetoder. Vårt syfte är också att öva skriftlig framställning av matematisk
Explorativ övning 3 INDUKTION OCH DEDUKTION Syftet med övningen är att öka Din problemlösningsförmåga och bekanta Dig med olika bevismetoder. Vårt syfte är också att öva skriftlig framställning av matematisk
Delbarhet och primtal
 Talet 35 är delbart med 7 eftersom 35 = 5 7 Delbarhet och primtal 7 är en faktor i 35 kan skrivas 7 35 7 är en delare (divisor) till 35 35 är en multipel av 7 De hela talen kan delas in i jämna och udda
Talet 35 är delbart med 7 eftersom 35 = 5 7 Delbarhet och primtal 7 är en faktor i 35 kan skrivas 7 35 7 är en delare (divisor) till 35 35 är en multipel av 7 De hela talen kan delas in i jämna och udda
Introduktion till L A TEX
 Introduktion till L A TEX Niels Chr. Overgaard 2018-09-17 N. Chr. Overgaard Intro. LATEX 2018-09-17 1 / 14 Varför L A TEX? Syftet med dokumentpreparationssystemet L A TEX är att generera välstrukturerade
Introduktion till L A TEX Niels Chr. Overgaard 2018-09-17 N. Chr. Overgaard Intro. LATEX 2018-09-17 1 / 14 Varför L A TEX? Syftet med dokumentpreparationssystemet L A TEX är att generera välstrukturerade
Sidor i boken V.L = 8 H.L. 2+6 = 8 V.L. = H.L.
 Sidor i boken 119-11 Andragradsekvationer Dagens tema är ekvationer, speciellt andragradsekvationer. Men först några ord om ekvationer i allmänhet. En ekvation är en likhet som innehåller ett (möjligen
Sidor i boken 119-11 Andragradsekvationer Dagens tema är ekvationer, speciellt andragradsekvationer. Men först några ord om ekvationer i allmänhet. En ekvation är en likhet som innehåller ett (möjligen
TATA42: Föreläsning 2 Tillämpningar av Maclaurinutvecklingar
 TATA42: Föreläsning 2 Tillämpningar av Maclaurinutvecklingar Johan Thim 24 mars 29 Entydighet Om vi har ett polynom som approimerar en snäll funktion bra, kan vi då vara säkra på att koefficienterna i
TATA42: Föreläsning 2 Tillämpningar av Maclaurinutvecklingar Johan Thim 24 mars 29 Entydighet Om vi har ett polynom som approimerar en snäll funktion bra, kan vi då vara säkra på att koefficienterna i
Kapitel 2: De hela talen
 Kapitel 2: De hela talen Divisionsalgoritmen ( a a Z, d Z\{0} q, r Z : d = q + r ) d, 0 r d c 2005 Eric Järpe Högskolan i Halmstad där q kallas kvoten och r kallas principala resten vid heltalsdivision.
Kapitel 2: De hela talen Divisionsalgoritmen ( a a Z, d Z\{0} q, r Z : d = q + r ) d, 0 r d c 2005 Eric Järpe Högskolan i Halmstad där q kallas kvoten och r kallas principala resten vid heltalsdivision.
Högstadiets matematiktävling 2016/17 Finaltävling 21 januari 2017 Lösningsförslag
 Högstadiets matematiktävling 2016/17 Finaltävling 21 januari 2017 Lösningsförslag 1. Lösningsförslag: Låt oss först titta på den sista siffran i 2 0 1 7. Ett tal som är delbart med 2 och 5 är då också
Högstadiets matematiktävling 2016/17 Finaltävling 21 januari 2017 Lösningsförslag 1. Lösningsförslag: Låt oss först titta på den sista siffran i 2 0 1 7. Ett tal som är delbart med 2 och 5 är då också
Tisdag v. 2. Speglingar, translationer och skalningar
 1 Tisdag v 2 Speglingar, translationer och skalningar Ofta i matematik och i matematiska kurser är det så att man måste kunna några grundläggande exempel utantill och man måste kunna några regler som säger
1 Tisdag v 2 Speglingar, translationer och skalningar Ofta i matematik och i matematiska kurser är det så att man måste kunna några grundläggande exempel utantill och man måste kunna några regler som säger
18 juni 2007, 240 minuter Inga hjälpmedel, förutom skrivmateriel. Betygsgränser: 15p. för Godkänd, 24p. för Väl Godkänd (av maximalt 36p.
 HH / Georgi Tchilikov DISKRET MATEMATIK,5p. 8 juni 007, 40 minuter Inga hjälpmedel, förutom skrivmateriel. Betygsgränser: 5p. för Godkänd, 4p. för Väl Godkänd (av maximalt 36p.). Förenkla (så mycket som
HH / Georgi Tchilikov DISKRET MATEMATIK,5p. 8 juni 007, 40 minuter Inga hjälpmedel, förutom skrivmateriel. Betygsgränser: 5p. för Godkänd, 4p. för Väl Godkänd (av maximalt 36p.). Förenkla (så mycket som
Bonusmaterial till Lära och undervisa matematik från förskoleklass till åk 6. Ledning för att lösa problemen i Övningar för kapitel 5, sid 138-144
 Bonusmaterial till Lära och undervisa matematik från förskoleklass till åk 6 Ledning för att lösa problemen i Övningar för kapitel 5, sid 138-144 Avsikten med de ledtrådar som ges nedan är att peka på
Bonusmaterial till Lära och undervisa matematik från förskoleklass till åk 6 Ledning för att lösa problemen i Övningar för kapitel 5, sid 138-144 Avsikten med de ledtrådar som ges nedan är att peka på
Repetitionsuppgifter inför Matematik 1. Matematiska institutionen Linköpings universitet 2013
 Repetitionsuppgifter inför Matematik Matematiska institutionen Linköpings universitet 0 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Facit 4 Repetitionsuppgifter inför Matematik Repetitionsuppgifter
Repetitionsuppgifter inför Matematik Matematiska institutionen Linköpings universitet 0 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Facit 4 Repetitionsuppgifter inför Matematik Repetitionsuppgifter
Ekvationer och system av ekvationer
 Modul: Undervisa matematik utifrån problemlösning Del 4. Strategier Ekvationer och system av ekvationer Paul Vaderlind, Stockholms universitet Ekvationslösning är ett av de viktiga målen i skolmatematiken.
Modul: Undervisa matematik utifrån problemlösning Del 4. Strategier Ekvationer och system av ekvationer Paul Vaderlind, Stockholms universitet Ekvationslösning är ett av de viktiga målen i skolmatematiken.
Polynomekvationer (Algebraiska ekvationer)
 Polynomekvationer (Algebraiska ekvationer) Faktorsatsen 1. Pettersson: teori och exempel på sid. 21-22 Det intressanta är följande idé: Om man på något sätt (Vilket det är en annan fråga, se nedan!) har
Polynomekvationer (Algebraiska ekvationer) Faktorsatsen 1. Pettersson: teori och exempel på sid. 21-22 Det intressanta är följande idé: Om man på något sätt (Vilket det är en annan fråga, se nedan!) har
Repetitionsuppgifter inför Matematik 1-973G10. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter inför Matematik - 7G0 Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 4 Facit Repetitionsuppgifter inför
Repetitionsuppgifter inför Matematik - 7G0 Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 4 Facit Repetitionsuppgifter inför
Linjär Algebra M/TD Läsvecka 3
 bild 1 Linjär Algebra M/TD Läsvecka 3 Omfattning och Innehåll Lay: 3.1-3.3 Determinanter. Definition, räkneregler och ett par viktiga satser. Huitfeldt: Om lösningsnoggrannhet: vektornorm, matrisnorm bild
bild 1 Linjär Algebra M/TD Läsvecka 3 Omfattning och Innehåll Lay: 3.1-3.3 Determinanter. Definition, räkneregler och ett par viktiga satser. Huitfeldt: Om lösningsnoggrannhet: vektornorm, matrisnorm bild
Talteori (OBS en del frågor gäller diofantiska ekvationer och de tas inte upp från och med hösten 2012)
 Talteori (OBS en del frågor gäller diofantiska ekvationer och de tas inte upp från och med hösten 2012) T4.4-T4.7, 4.3, 4.7,T4.13-T4.14 S: Jag har svårt för visa-uppgifter. i kapitel 4 Talteori. Kan du
Talteori (OBS en del frågor gäller diofantiska ekvationer och de tas inte upp från och med hösten 2012) T4.4-T4.7, 4.3, 4.7,T4.13-T4.14 S: Jag har svårt för visa-uppgifter. i kapitel 4 Talteori. Kan du
Övningshäfte 6: 2. Alla formler är inte oberoende av varandra. Försök att härleda ett par av de formler du fann ur några av de övriga.
 GÖTEBORGS UNIVERSITET MATEMATIK 1, MAM100, HT2005 MATEMATISK BASKURS Övningshäfte 6: Syftet med övningen är att utforska strukturen hos talsystemen under addition respektive multiplikation samt sambandet
GÖTEBORGS UNIVERSITET MATEMATIK 1, MAM100, HT2005 MATEMATISK BASKURS Övningshäfte 6: Syftet med övningen är att utforska strukturen hos talsystemen under addition respektive multiplikation samt sambandet
Sats 2.1 (Kinesiska restsatsen) Låt n och m vara relativt prima heltal samt a och b två godtyckliga heltal. Då har ekvationssystemet
 Avsnitt 2 Tillägg om kongruensräkning Detta avsnitt handlar om två klassiska satser som används för att förenkla kongruensräkning: Kinesiska restsatsen och Fermats lilla sats. Den första satsen används
Avsnitt 2 Tillägg om kongruensräkning Detta avsnitt handlar om två klassiska satser som används för att förenkla kongruensräkning: Kinesiska restsatsen och Fermats lilla sats. Den första satsen används
Abstrakt algebra för gymnasister
 Abstrakt algebra för gymnasister Veronica Crispin Quinonez Sammanfattning. Denna text är föreläsningsanteckningar från föredraget Abstrakt algebra som hölls under Kleindagarna på Institutet Mittag-Leffler
Abstrakt algebra för gymnasister Veronica Crispin Quinonez Sammanfattning. Denna text är föreläsningsanteckningar från föredraget Abstrakt algebra som hölls under Kleindagarna på Institutet Mittag-Leffler
, S(6, 2). = = = =
 1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D2 och F, SF161 och SF160, den 17 april 2010 kl 09.00-14.00. Examinator: Olof Heden. DEL I 1.
1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D2 och F, SF161 och SF160, den 17 april 2010 kl 09.00-14.00. Examinator: Olof Heden. DEL I 1.
Matematisk kommunikation för Π Problemsamling
 Problemsamling Niels Chr. Overgaard & Johan Fredriksson 3 september 205 Problem 0. Skriv följande summor mha summationstecken. ( Dvs på formen q k=p a k där k är en räknare som löper med heltalssteg mellan
Problemsamling Niels Chr. Overgaard & Johan Fredriksson 3 september 205 Problem 0. Skriv följande summor mha summationstecken. ( Dvs på formen q k=p a k där k är en räknare som löper med heltalssteg mellan
4. Bestäm alla trippler n 2, n, n + 2 av heltal som samtliga är primtal. 5. Skriv upp additions- och multiplikationstabellen för räkning modulo 4.
 Uppvärmningsproblem. Hur kan man se på ett heltal om det är delbart med, 2, 3, 4, 5, 6, 7, 8, 9, 0 respektive? Varför? 2. (a) Tänk på ett tresiffrigt tal abc, a 0. Bilda abcabc genom att skriva talet två
Uppvärmningsproblem. Hur kan man se på ett heltal om det är delbart med, 2, 3, 4, 5, 6, 7, 8, 9, 0 respektive? Varför? 2. (a) Tänk på ett tresiffrigt tal abc, a 0. Bilda abcabc genom att skriva talet två
Avsnitt 3, introduktion.
 KTHs Sommarmatematik Introduktion 3:1 3:1 Avsnitt 3, introduktion. Teckenstudium Här tränas teckenstudium av polynom och rationella funktioner (som är kvoter av polynom). Metoden går ut på att man faktoriserar
KTHs Sommarmatematik Introduktion 3:1 3:1 Avsnitt 3, introduktion. Teckenstudium Här tränas teckenstudium av polynom och rationella funktioner (som är kvoter av polynom). Metoden går ut på att man faktoriserar
2 (6) k 0 2 (7) n 1 F k F n. k F k F n F k F n F n 1 2 (8)
 De naturliga talen. Vi skall till att börja med stanna kvar i världen av naturliga tal, N 3. Vi har redan använt (i beviset av Euklides primtalssats) att de naturliga talen är uppbyggda (genom multiplikation)
De naturliga talen. Vi skall till att börja med stanna kvar i världen av naturliga tal, N 3. Vi har redan använt (i beviset av Euklides primtalssats) att de naturliga talen är uppbyggda (genom multiplikation)
1, 2, 3, 4, 5, 6,...
 Dagens nyhet handlar om talföljder, ändliga och oändliga. Talföljden 1,, 3, 4, 5, 6,... är det första vi, som barn, lär oss om matematik över huvud taget. Så småningom lär vi oss att denna talföljd inte
Dagens nyhet handlar om talföljder, ändliga och oändliga. Talföljden 1,, 3, 4, 5, 6,... är det första vi, som barn, lär oss om matematik över huvud taget. Så småningom lär vi oss att denna talföljd inte
29 Det enda heltalet n som satisfierar båda dessa villkor är n = 55. För detta värde på n får vi x = 5, y = 5.
 Tentamenskrivning MATA15 Algebra: delprov 1, 6hp Lördagen den 3 november 01 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1 a) Lös den diofantiska ekvationen 9x + 11y 00 b) Ange alla lösningar x, y) sådana
Tentamenskrivning MATA15 Algebra: delprov 1, 6hp Lördagen den 3 november 01 Matematikcentrum Matematik NF LÖSNINGSFÖRSLAG 1 a) Lös den diofantiska ekvationen 9x + 11y 00 b) Ange alla lösningar x, y) sådana
LMA033/LMA515. Fredrik Lindgren. 4 september 2013
 LMA033/LMA515 Fredrik Lindgren Matematiska vetenskaper Chalmers tekniska högskola och Göteborgs universitet 4 september 2013 F. Lindgren (Chalmers&GU) Matematik 4 september 2013 1 / 25 Outline 1 Föreläsning
LMA033/LMA515 Fredrik Lindgren Matematiska vetenskaper Chalmers tekniska högskola och Göteborgs universitet 4 september 2013 F. Lindgren (Chalmers&GU) Matematik 4 september 2013 1 / 25 Outline 1 Föreläsning
Matematisk kommunikation för Π Problemsamling
 Problemsamling Charlotte Soneson & Niels Chr. Overgaard september 200 Problem. Betrakta formeln n k = k= n(n + ). 2 Troliggör den först genom att exempelvis i summan +2+3+4+5+6 para ihop termer två och
Problemsamling Charlotte Soneson & Niels Chr. Overgaard september 200 Problem. Betrakta formeln n k = k= n(n + ). 2 Troliggör den först genom att exempelvis i summan +2+3+4+5+6 para ihop termer två och
Block 1 - Mängder och tal
 Block 1 - Mängder och tal Mängder Mängder och element Venndiagram Delmängder och äkta delmängder Union och snittmängd Talmängder Heltalen Z Rationella talen Q Reella talen R Räkning med tal. Ordning av
Block 1 - Mängder och tal Mängder Mängder och element Venndiagram Delmängder och äkta delmängder Union och snittmängd Talmängder Heltalen Z Rationella talen Q Reella talen R Räkning med tal. Ordning av
LABBA MED PRIMTAL OCH DELBARHET. Andreas Wannebo
 LABBA MED PRIMTAL OCH DELBARHET Andreas Wannebo Vi ska studera egenskaper för heltalen. Det finns heltal såsom 1,2,3,4,... De är de positiva heltalen och det är dem vi vill studera. Först kan man ställa
LABBA MED PRIMTAL OCH DELBARHET Andreas Wannebo Vi ska studera egenskaper för heltalen. Det finns heltal såsom 1,2,3,4,... De är de positiva heltalen och det är dem vi vill studera. Först kan man ställa
8-3 Kvadreringsreglerna och konjugatregeln. Namn:
 8-3 Kvadreringsreglerna och konjugatregeln. Namn: Inledning I kapitlet med matematiska uttryck lärde du dig hur man förenklade ett uttryck med en faktor framför en parentes genom att multiplicera varje
8-3 Kvadreringsreglerna och konjugatregeln. Namn: Inledning I kapitlet med matematiska uttryck lärde du dig hur man förenklade ett uttryck med en faktor framför en parentes genom att multiplicera varje
Algebra I, 1MA004. Lektionsplanering
 UPPSALA UNIVERSITET Matematiska Institutionen Dan Strängberg HT2016 Fristående, IT, KandDv, KandMa, Lärare 2016-11-02 Algebra I, 1MA004 Lektionsplanering Här anges rekommenderade uppgifter ur boken till
UPPSALA UNIVERSITET Matematiska Institutionen Dan Strängberg HT2016 Fristående, IT, KandDv, KandMa, Lärare 2016-11-02 Algebra I, 1MA004 Lektionsplanering Här anges rekommenderade uppgifter ur boken till
Repetitionsuppgifter i Matematik inför Basår. Matematiska institutionen Linköpings universitet 2014
 Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Repetitionsuppgifter i Matematik inför Basår Matematiska institutionen Linköpings universitet 04 Innehåll De fyra räknesätten Potenser och rötter 7 Algebra 0 4 Funktioner 7 Logaritmer 9 6 Facit 0 Repetitionsuppgifter
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 4. b) = 3 1 = 2
 Kapitel.1 101, 102 Exempel som löses i boken 10 a) x= 1 11+ x= 11+ 1 = 2 c) x= 11 7 x= 7 11 = 77 b) x= 5 x 29 = 5 29 = 6 d) x= 2 26 x= 26 2= 1 10 a) x= 6 5+ 9 x= 5+ 9 6= 5+ 5= 59 b) a = 8a 6= 8 6= 2 6=
Kapitel.1 101, 102 Exempel som löses i boken 10 a) x= 1 11+ x= 11+ 1 = 2 c) x= 11 7 x= 7 11 = 77 b) x= 5 x 29 = 5 29 = 6 d) x= 2 26 x= 26 2= 1 10 a) x= 6 5+ 9 x= 5+ 9 6= 5+ 5= 59 b) a = 8a 6= 8 6= 2 6=
TATM79: Föreläsning 2 Absolutbelopp, summor och binomialkoefficienter
 TATM79: Föreläsning Absolutbelopp, summor och binomialkoefficienter Johan Thim 15 augusti 015 1 Absolutbelopp Absolutbelopp Definition. För varje reellt x definieras absolutbeloppet x enligt { x, x 0 x
TATM79: Föreläsning Absolutbelopp, summor och binomialkoefficienter Johan Thim 15 augusti 015 1 Absolutbelopp Absolutbelopp Definition. För varje reellt x definieras absolutbeloppet x enligt { x, x 0 x
Lösa ekvationer på olika sätt
 Lösa ekvationer på olika sätt I denna aktivitet ska titta närmare på hur man kan lösa ekvationer på olika sätt. I kurserna lär du dig att lösa första- och andragradsekvationer exakt med algebraiska metoder.
Lösa ekvationer på olika sätt I denna aktivitet ska titta närmare på hur man kan lösa ekvationer på olika sätt. I kurserna lär du dig att lösa första- och andragradsekvationer exakt med algebraiska metoder.
Block 1 - Mängder och tal
 Block 1 - Mängder och tal Mängder Mängder och element Venndiagram Talmängder Heltalen Z Rationella talen Q Reella talen R Räkning med tal. Ordning av talen i R Intervall Absolutbelopp Olikheter 1 Prepkursen
Block 1 - Mängder och tal Mängder Mängder och element Venndiagram Talmängder Heltalen Z Rationella talen Q Reella talen R Räkning med tal. Ordning av talen i R Intervall Absolutbelopp Olikheter 1 Prepkursen
ÄNDLIGT OCH OÄNDLIGT AVSNITT 4
 VSNITT ÄNDLIGT OCH OÄNDLIGT Är det möjligt att jämföra storleken av olika talmängder? Har det någon mening om man säger att det finns fler irrationella tal än rationella? Är det överhuvudtaget möjligt
VSNITT ÄNDLIGT OCH OÄNDLIGT Är det möjligt att jämföra storleken av olika talmängder? Har det någon mening om man säger att det finns fler irrationella tal än rationella? Är det överhuvudtaget möjligt
Övningshäfte 1: Induktion, rekursion och summor
 LMA100 VT2006 ARITMETIK OCH ALGEBRA DEL 2 Övningshäfte 1: Induktion, rekursion och summor Övning A 1. Kan ni fortsätta följden 1,3,5,7,9,11,...? 2. Vilket är det 7:e talet i följden? Vilket är det 184:e?
LMA100 VT2006 ARITMETIK OCH ALGEBRA DEL 2 Övningshäfte 1: Induktion, rekursion och summor Övning A 1. Kan ni fortsätta följden 1,3,5,7,9,11,...? 2. Vilket är det 7:e talet i följden? Vilket är det 184:e?
a = a a a a a a ± ± ± ±500
 4.1 Felanalys Vill man hårddra det hela, kan man påstå att det inte finns några tal i den tillämpade matematiken, bara intervall. Man anger till exempel inte ett uppmätt värde till 134.78 meter utan att
4.1 Felanalys Vill man hårddra det hela, kan man påstå att det inte finns några tal i den tillämpade matematiken, bara intervall. Man anger till exempel inte ett uppmätt värde till 134.78 meter utan att
Lösning till tentamensskrivning i Diskret Matematik för CINTE, CL2 och Media 1, SF1610 och 5B1118, onsdagen den 17 augusti 2011, kl
 Matematiska Institutionen KTH Lösning till tentamensskrivning i Diskret Matematik för CINTE, CL och Media, SF60 och 5B8, onsdagen den 7 augusti 0, kl 4.00-9.00. Examinator: Olof Heden Hjälpmedel: Inga
Matematiska Institutionen KTH Lösning till tentamensskrivning i Diskret Matematik för CINTE, CL och Media, SF60 och 5B8, onsdagen den 7 augusti 0, kl 4.00-9.00. Examinator: Olof Heden Hjälpmedel: Inga
Algebra och talteori MMGL31. Repetition. Idag. Föreläsning 9 VT FLS och primtalstestning. Carmichaeltal. Rabin-Miller test.
 Algebra och talteori MMGL Föreläsning 9 VT 008 Samuel Bengmark Repetition FLS och primtalstestning Carmichaeltal Rabin-Miller test F-funktionen Idag Ordning av ett element i Z m Primitiv rot Index (diskret
Algebra och talteori MMGL Föreläsning 9 VT 008 Samuel Bengmark Repetition FLS och primtalstestning Carmichaeltal Rabin-Miller test F-funktionen Idag Ordning av ett element i Z m Primitiv rot Index (diskret
Algebra, kvadreringsregler och konjugatregeln
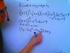 Algebra, kvadreringsregler och Uppgift nr 1 Multiplicera in i parentesen x(9 + 2y) Uppgift nr 2 Multiplicera in i parentesen 3x(7 + 5y) Uppgift nr 3 x² + 3x Uppgift nr 4 xy + yz Uppgift nr 5 5yz + 2xy
Algebra, kvadreringsregler och Uppgift nr 1 Multiplicera in i parentesen x(9 + 2y) Uppgift nr 2 Multiplicera in i parentesen 3x(7 + 5y) Uppgift nr 3 x² + 3x Uppgift nr 4 xy + yz Uppgift nr 5 5yz + 2xy
INDUKTION OCH DEDUKTION
 AVSNITT 3 INDUKTION OCH DEDUKTION Med induktion menar man vanligen en mycket vanlig resonemangsmetod: man gör flera observationer, upptäcker ett mönster (eller något som man tror är ett mönster) och därefter
AVSNITT 3 INDUKTION OCH DEDUKTION Med induktion menar man vanligen en mycket vanlig resonemangsmetod: man gör flera observationer, upptäcker ett mönster (eller något som man tror är ett mönster) och därefter
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem.
 Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
Vectorer, spannet av vektorer, lösningsmängd av ett ekvationssystem. Begrepp som diskuteras i det kapitlet. Vektorer, addition och multiplikation med skalärer. Geometrisk tolkning. Linjär kombination av
ÖVN 6 - DIFFERENTIALEKVATIONER OCH TRANSFORMMETODER - SF Nyckelord och innehåll. a n (x x 0 ) n.
 ÖVN 6 - DIFFERENTIALEKVATIONER OCH TRANSFORMMETODER - SF683 HTTP://KARLJODIFFTRANS.WORDPRESS.COM KARL JONSSON Nyckelord och innehåll Potensserielösningar Analytiska funktioner Konvergensradie Rot- och
ÖVN 6 - DIFFERENTIALEKVATIONER OCH TRANSFORMMETODER - SF683 HTTP://KARLJODIFFTRANS.WORDPRESS.COM KARL JONSSON Nyckelord och innehåll Potensserielösningar Analytiska funktioner Konvergensradie Rot- och
Algebraiska egenskaper hos R n i)u + v = v + U
 Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Underrum till R n, nollrum, kolonnrum av en matris, rank, bas, koordinater, dimension. Påminnelse om R n s egenskaper: Algebraiska egenskaper hos R n i)u + v = v + U v) c(u + v) = cu + cv ii) ( u + v)
Talmängder. Målet med första föreläsningen:
 Moment 1..1, 1.., 1..4, 1..5, 1.. 1..5, 1..6 Viktiga exempel 1.7, 1.8, 1.8,1.19,1. Handräkning 1.7, 1.9, 1.19, 1.4, 1.9 b,e 1.0 a,b Datorräkning 1.6-1.1 Målet med första föreläsningen: 1 En första kontakt
Moment 1..1, 1.., 1..4, 1..5, 1.. 1..5, 1..6 Viktiga exempel 1.7, 1.8, 1.8,1.19,1. Handräkning 1.7, 1.9, 1.19, 1.4, 1.9 b,e 1.0 a,b Datorräkning 1.6-1.1 Målet med första föreläsningen: 1 En första kontakt
Övning log, algebra, potenser med mera
 Övning log, algebra, potenser med mera Uppgift nr 1 Förenkla uttrycket x 3 + x 3 + x 3 + x 3 + x 3 Uppgift nr 2 Förenkla x x x+x x x Uppgift nr 3 Skriv på enklaste sätt x 2 x x x 8 x x x Uppgift nr 4 Förenkla
Övning log, algebra, potenser med mera Uppgift nr 1 Förenkla uttrycket x 3 + x 3 + x 3 + x 3 + x 3 Uppgift nr 2 Förenkla x x x+x x x Uppgift nr 3 Skriv på enklaste sätt x 2 x x x 8 x x x Uppgift nr 4 Förenkla
LOGIK, MÄNGDER OCH FUNKTIONER
 LOGIK, MÄNGDER OCH FUNKTIONER KOMPLETTERANDE STUDIEMATERIAL TILL MMA121 MATEMATISK GRUNDKURS VÅRTERMINEN 2014 ERIK DARPÖ 1. Utsagor, implikation och ekvivalens En utsaga är en påstående, formulerat med
LOGIK, MÄNGDER OCH FUNKTIONER KOMPLETTERANDE STUDIEMATERIAL TILL MMA121 MATEMATISK GRUNDKURS VÅRTERMINEN 2014 ERIK DARPÖ 1. Utsagor, implikation och ekvivalens En utsaga är en påstående, formulerat med
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson
 Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
Uppsala Universitet Matematiska Institutionen Thomas Erlandsson MATRISER MED MERA VEKTORRUM DEFINITION Ett vektorrum V är en mängd av symboler u som vi kan addera samt multiplicera med reella tal c så
(A B) C = A C B C och (A B) C = A C B C. Bevis: (A B) C = A C B C : (A B) C = A C B C : B C (A B) C A C B C
 Sats 1.3 De Morgans lagar för mängder För alla mängder A och B gäller att (A B) C = A C B C och (A B) C = A C B C. (A B) C = A C B C : A B A C (A B) C B C A C B C (A B) C = A C B C : A B A C (A B) C B
Sats 1.3 De Morgans lagar för mängder För alla mängder A och B gäller att (A B) C = A C B C och (A B) C = A C B C. (A B) C = A C B C : A B A C (A B) C B C A C B C (A B) C = A C B C : A B A C (A B) C B
MATEMATISK INDUKTION. Syftet med denna övning är att introducera en av de viktigaste bevismetoderna i matematiken
 Explorativ övning LMA100 ht 2002 MATEMATIS INDUTION Syftet med denna övning är att introducera en av de viktigaste bevismetoderna i matematiken matematisk induktion. Termen induktion är lite olycklig därför
Explorativ övning LMA100 ht 2002 MATEMATIS INDUTION Syftet med denna övning är att introducera en av de viktigaste bevismetoderna i matematiken matematisk induktion. Termen induktion är lite olycklig därför
TALTEORI FÖR ALLA 1 Juliusz Brzezinski
 TALTEORI FÖR ALLA 1 Juliusz Brzezinski För exakt 10 år sedan publicerade Andrew Wiles sitt bevis av Fermats Stora Sats. Nyheten om hans resultat väckte enorm uppmärksamhet i hela världen. Vägen till lösningen
TALTEORI FÖR ALLA 1 Juliusz Brzezinski För exakt 10 år sedan publicerade Andrew Wiles sitt bevis av Fermats Stora Sats. Nyheten om hans resultat väckte enorm uppmärksamhet i hela världen. Vägen till lösningen
Konsten att lösa icke-linjära ekvationssystem
 Konsten att lösa icke-linjära ekvationssystem Andreas Axelsson Vi beskriver här de grundläggande teknikerna för att lösa icke-linjära ekvationssystem. Detta är en nödvändig kunskap för att kunna lösa diverse
Konsten att lösa icke-linjära ekvationssystem Andreas Axelsson Vi beskriver här de grundläggande teknikerna för att lösa icke-linjära ekvationssystem. Detta är en nödvändig kunskap för att kunna lösa diverse
MATEMATIK. Ämnets syfte
 MATEMATIK Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas, såväl ur praktiska behov som ur människans nyfikenhet och lust att utforska matematiken som sådan. Kommunikation
MATEMATIK Matematiken har en flertusenårig historia med bidrag från många kulturer. Den utvecklas, såväl ur praktiska behov som ur människans nyfikenhet och lust att utforska matematiken som sådan. Kommunikation
Lösningar till udda övningsuppgifter
 Lösningar till udda övningsuppgifter Övning 1.1. (i) {, } (ii) {0, 1,, 3, 4} (iii) {0,, 4, 6, 8} Övning 1.3. Påståendena är (i), (iii) och (v), varav (iii) och (v) är sanna. Övning 1.5. andra. (i) Nej.
Lösningar till udda övningsuppgifter Övning 1.1. (i) {, } (ii) {0, 1,, 3, 4} (iii) {0,, 4, 6, 8} Övning 1.3. Påståendena är (i), (iii) och (v), varav (iii) och (v) är sanna. Övning 1.5. andra. (i) Nej.
Allmänna Tredjegradsekvationen - version 1.4.0
 Allmänna Tredjegradsekvationen - version 1.4.0 Lars Johansson 0 april 017 Vi vet hur man med rotutdragning löser en andragradsekvation med reella koecienter: x + px + 0 1) Men hur gör man för att göra
Allmänna Tredjegradsekvationen - version 1.4.0 Lars Johansson 0 april 017 Vi vet hur man med rotutdragning löser en andragradsekvation med reella koecienter: x + px + 0 1) Men hur gör man för att göra
TATM79: Föreläsning 2 Absolutbelopp, summor och binomialkoefficienter
 TATM79: Föreläsning 2 Absolutbelopp, summor och binomialkoefficienter Johan Thim 2 augusti 2016 1 Absolutbelopp Absolutbelopp Definition. För varje reellt x definieras absolutbeloppet x enligt { x, x 0
TATM79: Föreläsning 2 Absolutbelopp, summor och binomialkoefficienter Johan Thim 2 augusti 2016 1 Absolutbelopp Absolutbelopp Definition. För varje reellt x definieras absolutbeloppet x enligt { x, x 0
Vektorgeometri för gymnasister
 Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Vektorgeometri för gymnasister Per-Anders Svensson http://homepage.lnu.se/staff/psvmsi/vektorgeometri/gymnasiet.html Fakulteten för teknik Linnéuniversitetet Diagonalisering av linjära avbildningar III
Föreläsning 3: Ekvationer och olikheter
 Föreläsning 3: Ekvationer och olikheter En ekvation är en likhet som innehåller en flera obekanta storheter. Exempel: x = 9, x är okänd. t + t + 1 = 7, t är okänd. Vi säger att ett värde på den obekanta
Föreläsning 3: Ekvationer och olikheter En ekvation är en likhet som innehåller en flera obekanta storheter. Exempel: x = 9, x är okänd. t + t + 1 = 7, t är okänd. Vi säger att ett värde på den obekanta
Relationer. 1. Relationer. UPPSALA UNIVERSITET Matematiska institutionen Erik Melin. Specialkursen HT07 23 oktober 2007
 UPPSALA UNIVERSITET Matematiska institutionen Erik Melin Specialkursen HT07 23 oktober 2007 Relationer Dessa blad utgör skissartade föreläsningsanteckningar kombinerat med övningar. Framställningen är
UPPSALA UNIVERSITET Matematiska institutionen Erik Melin Specialkursen HT07 23 oktober 2007 Relationer Dessa blad utgör skissartade föreläsningsanteckningar kombinerat med övningar. Framställningen är
Om a 2 är ett jämnt tal, så är också a ett jämt tal sant. = 4n 2 + 4n + 1
 1127 Påstående betecknas med P Motsatsen till påsteåendet betecknas P = icke P = inte P = ej P P n är ett udda tal P n är ett jämnt tal Kommentar: n kan enbart vara udda eller jämnt, P a + 2b 15 P a +
1127 Påstående betecknas med P Motsatsen till påsteåendet betecknas P = icke P = inte P = ej P P n är ett udda tal P n är ett jämnt tal Kommentar: n kan enbart vara udda eller jämnt, P a + 2b 15 P a +
Svar och arbeta vidare med Student 2008
 Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
Student 008 Svar och arbeta vidare med Student 008 Det finns många intressanta idéer i årets Känguruaktiviteter. Problemen kan inspirera undervisningen under flera lektioner. Här ger vi några förslag att
MMA132: Laboration 2 Matriser i MATLAB
 MMA132: Laboration 2 Matriser i MATLAB Introduktion I den här labben skall vi lära oss hur man använder matriser och vektorer i MATLAB. Det är rekommerad att du ser till att ha laborationshandledningen
MMA132: Laboration 2 Matriser i MATLAB Introduktion I den här labben skall vi lära oss hur man använder matriser och vektorer i MATLAB. Det är rekommerad att du ser till att ha laborationshandledningen
Sidor i boken f(x) = a x 2 +b x+c
 Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
Sidor i boken 18-151 Andragradsfunktioner Här ska vi studera andragradsfunktionen som skrivs f(x) = ax +bx+c där a, b, c är konstanter (reella tal) och där a 0. Grafen (kurvan) till f(x), y = ax + bx +
2 Tillämpad Matematik I, Övning 1 HH/ITE/BN. De objekt som finns G men inte i H.
 HH/ITE/BN Tillämpad Matematik I, Övning 0 3 Tillämpad Matematik I Övning Allmänt 0 Övningsuppgifterna, speciellt Typuppgifter i första hand, är exempel på uppgifter du kommer att möta på tentamen. På denna
HH/ITE/BN Tillämpad Matematik I, Övning 0 3 Tillämpad Matematik I Övning Allmänt 0 Övningsuppgifterna, speciellt Typuppgifter i första hand, är exempel på uppgifter du kommer att möta på tentamen. På denna
PRIMTALEN, MULTIPLIKATION OCH DIOFANTISKA EKVATIONER
 Explorativ övning 4 PRIMTALEN, MULTIPLIKATION OCH DIOFANTISKA EKVATIONER Syftet med detta avsnitt är att bekanta sig med delbarhetsegenskaper hos heltalen. De viktigaste begreppen är Aritmetikens fundamentalsats
Explorativ övning 4 PRIMTALEN, MULTIPLIKATION OCH DIOFANTISKA EKVATIONER Syftet med detta avsnitt är att bekanta sig med delbarhetsegenskaper hos heltalen. De viktigaste begreppen är Aritmetikens fundamentalsats
5B1147. Envariabelanalys. MATLAB Laboration. Laboration 1. Gränsvärden och Summor
 5B47 MATLAB Laboration Laboration Gränsvärden och Summor joycew@kth.se uvehag@kth.se Innehåll Uppgift a... Problem... Lösning... Grafisk bestämning av gränsvärden... Beräkning av gränsvärden...2 Uppgift
5B47 MATLAB Laboration Laboration Gränsvärden och Summor joycew@kth.se uvehag@kth.se Innehåll Uppgift a... Problem... Lösning... Grafisk bestämning av gränsvärden... Beräkning av gränsvärden...2 Uppgift
Linjära ekvationssystem. Avsnitt 1. Vi ska lära oss en metod som på ett systematiskt sätt löser alla linjära ekvationssystem. Linjära ekvationssystem
 Avsnitt Linjära ekvationssystem Elementära radoperationer Gausseliminering Exempel Räkneschema Exempel med exakt en lösning Exempel med parameterlösning Exempel utan lösning Slutschema Avläsa lösningen
Avsnitt Linjära ekvationssystem Elementära radoperationer Gausseliminering Exempel Räkneschema Exempel med exakt en lösning Exempel med parameterlösning Exempel utan lösning Slutschema Avläsa lösningen
INLEDNING. Andreas Rahim
 INLEDNING Många tycker att matten på högskoleprovet är svår. Ibland blir man frustrerad för att man inte förstår. Frustrationen gör ibland att man ger upp. Man övertygar sig själv att det är omöjligt.
INLEDNING Många tycker att matten på högskoleprovet är svår. Ibland blir man frustrerad för att man inte förstår. Frustrationen gör ibland att man ger upp. Man övertygar sig själv att det är omöjligt.
Förslag på instruktioner och arbete med bedömning av muntlig presentation, från MMT-utredning 2003
 Förslag på instruktioner och arbete med bedömning av muntlig presentation, från MMT-utredning 2003 Instruktioner för muntlig redovisning: Uppgift Håll ett kort föredrag (15-20 minuter presentation + 10
Förslag på instruktioner och arbete med bedömning av muntlig presentation, från MMT-utredning 2003 Instruktioner för muntlig redovisning: Uppgift Håll ett kort föredrag (15-20 minuter presentation + 10
Datorlaboration :: 1 Problembeskrivning ::
 Datorlaboration :: Ett hyrbilsföretags problem Laborationen går ut på att lösa Labbuppgift 1 till 5. Laborationen redovisas individuellt genom att skicka laborationens Mathematicafil till Mikael Forsberg
Datorlaboration :: Ett hyrbilsföretags problem Laborationen går ut på att lösa Labbuppgift 1 till 5. Laborationen redovisas individuellt genom att skicka laborationens Mathematicafil till Mikael Forsberg
Blandade uppgifter om tal
 Blandade uppgifter om tal Uppgift nr A/ Beräkna värdet av (-3) 2 B/ Beräkna värdet av - 3 2 Uppgift nr 2 Skriv (3x) 2 utan parentes Uppgift nr 3 Multiplicera de de två talen 2 0 4 och 4 0 med varandra.
Blandade uppgifter om tal Uppgift nr A/ Beräkna värdet av (-3) 2 B/ Beräkna värdet av - 3 2 Uppgift nr 2 Skriv (3x) 2 utan parentes Uppgift nr 3 Multiplicera de de två talen 2 0 4 och 4 0 med varandra.
