LABORATION 2 MAGNETISKA FÄLT
|
|
|
- Rebecka Johansson
- för 9 år sedan
- Visningar:
Transkript
1 Fysikum FK Elektromagnetism Laborationsinstruktion (15 november 2013) LABORATION 2 MAGNETISKA FÄLT Mål I denna laboration skall du studera sambandet mellan B- och H- fälten i en toroidformad järnkärna med strömspole. De fenomen som skall studeras är komplexa och du måste förbereda övningen genom att sätta dig in i en del relevant teoretisk information före laborations- tillfället. Redovisningen sker i form av en labrapport.
2 1 Inledande kommentarer Denna laboration gäller en spole med järnkärna. De fenomen som studeras är mycket komplexa och det är därför inte möjligt att ge några kvantitativa förutsägelser. Det gäller istället att utnyttja teorin för att tolka mätningarna i termer av egenskaperna hos spolen. Det saknas ibland anvisningar som talar om exakt hur mätningarna ska gå till. Istället anges vad som skall mätas och hur mätningarna ska redovisas. Detta gör att laborationen kan ta ganska lång tid att genomföra om du inte tänkt igenom i förväg hur du ska arbeta. Planera därför mätningarna och gör de beräkningar du kan i förväg. Instruktionen innehåller en hel del relevanta teoretiska diskussioner som kan vara till hjälp när du skall tolka resultaten av dina mätningar under redovisningen. Ägna gärna tid åt att diskutera uppgifterna med dina kamrater, med labassistenten och med din gruppundervisare. Koncentrera dig på frågor av typen Varför blir det så här? och Hur gör man för att ta reda på det här?. Undvik ointressanta frågor av typ Vad ska det bli?. Det som avgör en mätnings kvalitet är storleken på felet i mätningen, och man skall alltså sträva efter att minimera detta, samt ange värden med feluppskattningar. Det är viktigt att du när du gör en mätning avgör vilka felkällor som finns och hur stora felen är, samt gör vad du kan för att minska dem. För att bedöma kvaliteten på någon annans mätning krävs också att man får klart för sig huruvida de fel och de värden som anges har härletts på ett korrekt sätt och att rådata är tillförlitliga. Det är därför också viktigt att redovisa sina mätningar och beräkningar på ett övertygande sätt. 2 Begrepp och definitioner Man beskriver ofta det magnetiska fältet B genom fältlinjer. Antalet fältlinjer som passerar en yta är proportionellt mot flödet genom ytan, dvs fältstyrkan eller flödestätheten, B, ges av antalet linjer per ytenhet. Eftersom B- fältet saknar källor (är divergensfritt) är fältlinjerna slutna. Enheten för magnetisk fältstyrka i SI- systemet är tesla, T. Andra vanliga beteckningar för samma enhet är Wb/m 2 (weber/m 2 ) och Vs/m 2 (voltsekunder/m 2 ). Det är ibland praktiskt att tänka sig att en elektrisk ström ger ett magnetiserande fält, H (mäts i enheten A/m), som i sin tur ger upphov till B, dels direkt i vakuum, dels genom att magnetisera eventuellt material. Olyckligtvis påverkas också H av det magnetiserade materialet, vilket gör det besvärligt att bestämma fältkonfigurationer för godtyckliga fall. Om magnetiseringen (dipolmomentet/volymenhet) är källfri bidrar materialet emellertid inte till H. Detta blir fallet i en magnetiserad torus där magnetiseringen beskrivs av slutna, cirkulära, fältlinjer. I en spole, tätt lindad runt en sådan torus, (toroidspole) samverkar strömmen i de olika lindningsvarven och det magnetiserande fältet blir proportionellt mot NI, där N är antalet varv och I är strömmen. Om torusen har ett tunt luftgap bidrar det magnetiserade materialet till H endast i luftgapet, medan B- fältet blir detsamma i luftgapet som i järnet. Sambandet mellan H och B- fält skrivs ofta på formen 2
3 Här är μ 0 den magnetiska permeabiliteten i vakuum, vars värde definieras som 4π 10 7 Vs/Am. Den relativa permeabiliteten, μ, karaktäriserar materialets magnetiska egenskaper. I vakuum är μ = 1. Det åtgår energi för att bygga upp ett magnetfält. Denna energi lagras i magnetfältet och kan återvinnas, med undantag för de energiförluster som kan uppstå då magnetiseringen av materiella medier ändras. Hur mycket energi som krävs för att öka strömmen i spolen beror på spolens självinduktans. Självinduktansen anger sambandet mellan strömmen genom spolen och det magnetiska flödet i spolen som denna ström ger upphov till. Om sambandet mellan ström och magnetfält är linjärt (som i vakuum), är självinduktansen L en konstant som ges av Om sambandet mellan strömmen och det magnetiska flödet inte är linjärt (om vi t.ex. har järn i spolen), definierar vi induktansen som flödesändring per strömändring: Anledningen till denna definition är att den inducerade spänningen i spolen ges av Faradays lag som så att vi kan skriva. Spänningen över spolen är, dvs När strömmen i spolen ändras uppstår alltså en spänning V L över spolen och strömkällan avkrävs ett arbete per tidsenhet (effekt) som är V L I. Detta arbete måste uföras mot det elektriska fält som Faradays lag ger, och det går dels till att öka den magnetiska fältenergin och dels till värmeförluster i järnkärnan (om vi har en sådan!). Om μ är konstant (t.ex. i vakuum) gäller att den energi som krävs för att bygga upp strömmen I i en spole är 3
4 Detta är ekvivalent med att tillskriva det magnetiska fältet en energi per volymsenhet som är Dessa båda formler gäller alltså när man kan försumma att μ beror på den magnetiska fältstyrkan och är en god approximation utom för ferri- och ferromagnetiska ämnen, t.ex. järn 1. Järn intill eller inuti en spole blir magnetiserat och bidrar då till spolens magnetfält. Järn, liksom andra ferro- och ferrimagnetiska material, ökar alltså spolens induktans vilket ofta är önskvärt. Järn har emellertid dessutom egenskapen att permeabiliteten varierar med den magnetiska fältstyrkan och att sambandet mellan B och H inte är entydigt. Detta gör att formeln ovan för energin i spolen inte är tillämplig. Istället måste man tillgripa en mer allmän formel för den energitillförsel som krävs för att ändra B och H, nämligen där den yttre integralen beräknas över det område där den inre integralen är skild från noll. Den inre integralen representerar alltså energiåtgång per volymsenhet. Uttrycken för W kan alltså härledas (se t.ex. Grant & Phillips sid 245) m.h.a. Faradays lag. W är det totala arbetet som krävs (bortsett från värmeförluster i ledningarna). Detta arbete går delvis till värmeutveckling i det magnetiserade materialet, delvis till energi som lagras i B- fältet. Det finns i den makroskopiska teorin för elektromagnetism inget sätt att skilja dessa båda bidrag åt. Den inre integralen ovan specificerar alltså den energi per volymsenhet som krävs för att variera B och H längs en kurva i den sexdimensionella (B,H)- rymden mellan punkterna (B 1,H 1 ) och (B 2,H 2 ). Denna integral är i allmänhet inte oberoende av kurvan. Om B och H är parallella blir naturligtvis H db = H db, och integralen ovan blir entydigt definierad av B 1 och B 2 om H är en entydig funktion av B. Detta innebär att den energi som krävs för att ändra fältet från B 1 till B 2 återfås om man går tillbaka till B 1, dvs man kan tillskriva det magnetiska fältet en lagrad energitäthet. Däremot kan man alltså inte definera ett entydigt energiinnehåll hos det makroskopiska fältet när man har värmeförluster. I det enklaste fallet, nämligen att med konstant μ, följer som redan nämnts att energitätheten blir. I det något mer komplicerade fallet som här studeras är B och H parallella eller antiparallella (se fig. 1), men sambandet mellan dem är inte entydigt. I detta fall kan B och H ersättas med B resp. H, dvs fältens komponenter moturs (eller medurs) i toroiden. Integralen ovan blir i så fall lika med den magnetiserade volymen gånger en integral i (B,H)- planet (observera att integrationsvariabeln är B): 1 Alla ämnen är antingen dia- eller paramagnetiska. Bland dessa finns vissa vars atomära magnetiskamoment, pga regelbunden gitterstruktur, sammansätter sig till en förhållandevis kraftigmagnetisering. Det är dessa som kallas ferro- och ferrimagnetiska. 4
5 Det faktum att sambandet mellan B och H inte är entydigt betyder också att den relativa permeabiliteten, μ, vare sig är konstant eller entydigt definierad. För små fält kan man dock, även för ett ferromagnetiskt material, ofta approximera sambandet mellan B och H med en proportionalitet. Figur 1: B- och H- fältlinjer i en toroidspole med luftgap 3 Toroidspolen En toroidspole med N varv är lindad på en järnkärna som har tvärsnittsytan A, medelomkretsen l och ett smalt luftgap. Det magnetiska fältet B i luftgapet kan mätas och användas för att beräkna fältstyrkan inuti toroidens järnkärna. Den toroid som används vid laborationen har ett ganska smalt luftgap och vi kan därför tillåta oss approximationen att försumma det läckflöde som luftgapet orsakar. Amperes lag kan användas för att beräkna det magnetiska fältet i en toroidspole. Den kan skrivas där I tot är den totala strömmen, som har en komponent, NI, från strömmen genom lindningsvarven, men domineras av magnetiseringsströmmen när spolen har en järnkärna. Magnetiseringsströmmen bidrar däremot inte till integralen av H: Om man integrerar runt en cirkel som sammanfaller med en B- fältlinje i figur 1 ovan får man, 5
6 där index j och l betecknar järn respektive luft och d är luftgapets tjocklek. Eftersom B- fältlinjerna är slutna innebär antagandet att man kan försumma läckflödet på grund av luftgapet att fältstyrkan B j i järnet måste vara lika stor som fältstyrkan B l i luftgapet. Sätt B j = B l = B. I luftgapet är sambandet mellan B och H entydigt bestämt: Insättning ger sambandet Det är alltså möjligt att samtidigt bestämma fälten B och H i järnet genom att a) Sända en bestämd ström I genom toroidspolen. b) Mäta fältstyrkan B i luftgapet. c) Beräkna det H j som svarar mot strömmen I och fältet B. Formellt kan man fortfarande skriva, men man måste då komma ihåg att den relative permeabiliteten, μ, inte längre är en konstant utan beror på järnets magnetisering. Sambandet mellan B och H i några olika magnetiska material finns angivna i t.ex. Physics Handbook. I figuren nedan återges en s.k. hystereskurva som grafiskt illustrerar sambandet mellan de två fältstyrkorna. Figur 2: Ett exempel på en hystereskurva. B m och B r är mättnadsvärdet av B- fältet resp. remanensen. Mättnadsfältet svarar mot att magnetiseringen nått sitt maximala värde. Om strömmen ökas ytterligare ökar B endast mycket långsamt eftersom endast strömmen i lindningen bidrar till ökningen. 6
7 3.1 Sambandet mellan B och H- fälten i toroidspolens järnkärna Här är det meningen att du skall undersöka sambandet mellan B och H i järnet för likström. Detta är inget entydigt funktionssamband, utan hysteres förekommer, dvs värdet på B för ett givet H beror på de föregående värdena. Detta har viss betydelse när du ställer in de värden på strömmen som du vill mäta vid. Uppgifter: a) Avmagnetisera järnet i toroidspolen med hjälp av växelström av minskande amplitud från en vridtransformator. Var försiktig när du handskas med transformatorn så att du inte får en stöt! Du bör kunna komma ned till några Gauss. b) Anslut spolen till en likspänningskälla som ger minst 6A och med kontinuerligt varierbar spänning upp till minst 20V. Mät B i toroidspolens luftgap med en gaussmeter (hallplatta) och jämför hystereskurvorna vid låg ström och vid hög ström. Låg ström: Mät ström och magnetfält för ström mellan - 100mA och +100mA i steg av ungefär 25 ma. Börja med I=0. Hög ström: Mät därefter ström och magnetfält i området I = - 6A till +6A. Börja med I = 0. Redovisa: 1. Spolens nummer och karaktäristika. 2. Diagram över B som funktion av strömmen I. 3. Diagram över B som funktion av H j. 4. Ett värde på μ i järnet som kan användas för att approximera hystereskurvan vid låg ström med en rät linje (skall senare användas för att beräkna L för spolen). Felet skall inkludera effekten av icke- linjäriteter och hysteres. Man anpassar lämpligen en rät linje till samtliga mätpunkter för låg ström så att avvikelserna från ett rätlinjigt samband bidrar till det beräknade felet i μ. 3.2 Toroidspolen som kretselement En ideal spole är resistanslös och karaktäriseras av självinduktansen som är en konstant (dvs sambandet mellan I och B är linjärt. Med en halvideal spole menar vi här en spole som är ideal i alla avseenden utom att lindningen har en viss resistans. Denna resistans kan enkelt representeras av en seriekopplad resistor då man gör beräkningar. Egenskaperna hos en halvideal spole bestäms alltså av två konstanter, induktansen L och resistansen r. Spänningen över en halvideal spole blir t.ex.. Idealet är svårt att uppnå, även när det gäller spolar. Mätningarna ovan visar tydligt att sambandet mellan I och B för vår toroidspole är icke- linjärt. Det är ju inte ens entydigt! Enligt 7
8 resonemanget i avsnitt 2 ovan innebär detta en viss energiförlust i järnet för varje period, dvs energiförlusten är för konstant ström proportionell mot vinkelfrekvensen ω. Dessutom är järnkärnan homogen, vilket innebär att det varierande magnetiska flödet lätt kan inducera strömmar i järnet (s.k. virvelströmmar), vilka leder till värmeförluster som beror på frekvensen. Det inducerade elektriska fältet som driver virvelströmmarna är proportionellt mot, dvs mot om amplituden hos - variationerna är konstant. Den utvecklade medeleffekten blir därför proportionell mot använda laminerade järnkärnor). (För att undvika virvelströmmar brukar man Syftet med denna övning är att studera hur avvikelserna från en ideal spole visar sig då du kopplar in spolen i en växelströmskrets, samt att du skall ge en kvalitativ tolkning av resultaten. Uppgifter: a) Mät lindningens resistens (för likström). b) Visa att om vi antar att järnets permeabilitet, μ j, är konstant ges toroidens induktans L av uttrycket, och beräkna värdet på L. Använd ditt värde på μ j från avsnitt 3.1. c) Avmagnetisera spolen igen. d) Koppla spolen i serie med ett lämpligt motstånd och mät med oscilloskop spänningen V 1 över kombinationen, och V 2 över seriemotståndet. Använd tongeneratorns sinussignaler vid mätningarna. Visa att, om man antar en halvideal spole, ges dess induktans och inre resistans (som naturligtvis båda är konstanter) av, där ω är vinkelfrekvensen och fasförskjutningen mellan spänningarna. För en halvideal spole är alltså L och r konstanter, och om vi mäter på en sådan ger alltså uttrycken ovan samma L och r för olika ω. (För L blir t.ex. proportionellt mot ω ). Hur tolkar du L och r som fås enligt ovan när spolen inte är (halv)ideal? Fundera över hur virvelströmmar och hysteres effekterkan tänkas påverka de mätta värdena på L och r för olika frekvenser. Finns det några andra effekter som kan spela en roll? Använd sambanden ovan för att bestämma L och r vid ett antal olika frekvenser, däribland 50Hz, 1500 Hz och 75 khz. 8
9 Redovisa: 1. Lindningens resistans. 2. Den beräknade induktansen. 3. L och r för växelström som funktioner av frekvensen och en jämförelse med lindningens resistans och den beräknade induktansen. (Tänk efter ordentligt när du beräknar felen på L och r. Undvik korrelerade fel.) Kommentera (de kraftiga!) avvikelserna från en ideal växelströmskrets. 3.3 Energiomsättningen i toroidspolen När toroidspolen kopplas till en växelströmskälla förbrukas elektrisk energi dels genom värmeutvecklingen i lindningens resistans (kopparförluster) och dels genom värmeutveckling i järnkärnan på grund av hysteres och virvelströmmar (järnförluster). Använd redan gjorda mätningar (avsnitt 3.1) för att lösa nedanstående beräkningsuppgifter (se avsnitt 2 och 3.2). I ett par av uppgifterna måste du numeriskt bestämma ytor som begränsas helt eller delvis av din hystereskurva. Beräkna: 1. Medeleffekten som utvecklas i järnkärnan då spolen genomflyts av en växelström med toppvärdet 6A och frekvensen 50Hz (antag att hystereskurvan blir den du mätt upp). Hur beror effekten på frekvensen? (Bortse från virvelströmmar!) 2. Motsvarande effektutveckling i spolens lindningar. Hur beror denna effekt på frekvensen? 3. Den energi som åtgår för att bygga upp det magnetiska fältet i spolens järnkärna då strömmen ökas från 0A till 6A och järnet från början är omagnetiserat. Håll reda på axlarna! 4. Motsvarande energi för det magnetiska fältet i spolens luftgap. 4 Enkla mätningar på en krets som innehåller en inducerad elektromotorisk spänning Syftet med denna övning är att använda toroidspolen och ett oscilloskop för att på ett handgripligt sätt övertyga sig om hur förträfflig Faradays lag är. Lagen ger ett samband mellan ett varierande magnetiskt flöde och vägintegralen av det elektriska fältet runt en sluten kurva i rymden: 9
10 Eftersom vägintegralen av E runt en sluten kurva inte är noll om B- fältet är tidsberoende kan man i det fallet inte definiera någon elektrisk potential, dvs spänningsskillnaden mellan två punkter blir odefinierad (vägintegralen av E mellan punkterna beror på vilken väg vi väljer). I detta sammanhang kan man betrakta ett oscilloskop eller en voltmeter som ett instrument som mäter vägintegralen inuti instrumentet mellan de två anslutningspolerna. Du bör innan laborationstillfället vara säker på att du förstår och kan redogöra för ovanstående resonemang. Toroidspolen matas med en sinusformad spänning från en tongenerator. Uppgifter: Dra en sladd genom toroiden och anslut ändpunkterna till ett oscilloskop. Sladden (en vanlig labsladd med banankontakter är lämplig) och ingångsimpedansen till oscilloskopet ska bilda en sluten strömkrets, som omsluter magnetiska fältet i toroidens järnkärna. Undersök om den inducerade spänningen är känslig för slingans form, avstånd till järnet etc. Pröva också att linda sladden flera varv kring järnkärnan. Koppla upp en krets enligt figur 3 så att R 1 och R 2 ingår i en slinga som omsluter toroidens järnkärna. De två ingångarna till ett dubbelstråleoscilloskop ansluts som figuren visar till samma punkter, A och B. Här betyder samma punkter verkligen just det! Figur 3: Koppling för induktionsförsök. Järnkärnan i mitten. Anordningen kan ses som en transformator där sekundärkretsen visas i figuren. Strömmarna genom oscilloskopen kan försummas (hög in- impedans), så strömmen i kretsen flyter enbart genom motstånden och deras anslutningsledningar. Mät signalerna (amplitud och fas) över ingångarna Y 1 och Y 2 för följande kombinationer av resistanser: 10
11 a) R 1 = R 2 = 100 b) R 1 = 100 och R 2 = 200 c) R 1 kortsluten med en labsladd och R 2 = 200 d) Både R 1 och R 2 kortslutna med var sin labsladd (likadana). Tänk före varje mätning igenom hur resultatet av denna rimligen borde bli och kontrollera sedan att du tänkt rätt. Hur kan de två oscilloskop- ingångarna ge olika utslag trots att de verkar mäta spänningen mellan samma punkter? Hur kan ett oscilloskop som mäter inuti sig självt (och inget annat!), och är på stort avstånd från spolen och motstånden veta vilket motstånd det skall visa spänningen över? För att ge en korrekt beskrivning är det enklast ansätta en ström I i kretsen och sedan utgå direkt från Faradays lag och tillämpa den på ett antal slutna kurvor, vilket ger ett ekvationssystem. Det gäller då att se till att man väljer en väg där man kan uttrycka det elektriska fältet i termer av I, Y 1, Y 2, R 1 och R 2. Det är bl.a. värt att notera att det elektriska fältet inuti ledningstrådarna oftast (men inte alltid!) kan försummas. Redovisa mätresultaten och en kort jämförelse med det förväntade utfallet. (Här räcker det med att ange värden utan fel.) Sammanställningen För att underlätta den sammanställning av resultat som skall inlämnas som en labrapport, ges här en sammanfattning av vad den ska innehålla. Gruppera materialet enligt punkterna nedan: 1. Data för toroidspolen (N, d, l, A, likströmsresistans), med fel, samt spolens nummer. 2. Mätvärden för I och B (med fel), samt motsvarande beräknade värden på H (med fel) i tabell- och grafisk form. 3. Värdet på för svag ström med fel som tar hänsyn till att sambandet inte är linjärt eller entydigt. Motsvarande beräknade värde på L för likström (med fel). 4. Härledningar av uttrycken för L och r som ges i avsnitt Värden (med fel) på L och r för olika ω. (Tänk på att beräkna felen korrekt utgående från mätta storheter som kan anses ha oberoende fel.) 6. Stolpvis uppräkning (max tre rader vanlig text) av effekter som bidrar till det observerade frekvensberoendet för L och r. 7. Resultatet av beräkningsuppgifterna i avsnitt 3.3. (Två effekter och två energier 11
12 utan fel.) 8. De uppmätta amplituderna och relativa faserna för Y 1 och Y 2 i kopplingarna a) till d) i avsnitt 4 (utan fel). 9. Härledningar av de förväntade resultaten för kopplingarna a) till d) för ett givet varierande magnetiskt flöde,, i toroidens järnkärna. 12
Kompletterande instruktioner, tips samt principer för bedömning av Laboration 2 Magnetiska fält (Elektromagnetism 12 hp)
 Kompletterande instruktioner, tips samt principer för bedömning av Laboration 2 Magnetiska fält (Elektromagnetism 12 hp) I. Allmänt. 1. Du studerar noggrant labinstruktionen för att förstå den, och löser
Kompletterande instruktioner, tips samt principer för bedömning av Laboration 2 Magnetiska fält (Elektromagnetism 12 hp) I. Allmänt. 1. Du studerar noggrant labinstruktionen för att förstå den, och löser
Sensorer, effektorer och fysik. Grundläggande fysikaliska begrepp som är viktiga inom mättekniken
 Sensorer, effektorer och fysik Grundläggande fysikaliska begrepp som är viktiga inom mättekniken Innehåll Grundläggande begrepp inom mekanik. Elektriskt fält och elektrisk potential. Gauss lag Dielektrika
Sensorer, effektorer och fysik Grundläggande fysikaliska begrepp som är viktiga inom mättekniken Innehåll Grundläggande begrepp inom mekanik. Elektriskt fält och elektrisk potential. Gauss lag Dielektrika
Elektricitetslära och magnetism - 1FY808. Lab 3 och Lab 4
 Linnéuniversitetet Institutionen för fysik och elektroteknik Elektricitetslära och magnetism - 1FY808 Lab 3 och Lab 4 Ditt namn:... eftersom labhäften far runt i labsalen. 1 Laboration 3: Likström och
Linnéuniversitetet Institutionen för fysik och elektroteknik Elektricitetslära och magnetism - 1FY808 Lab 3 och Lab 4 Ditt namn:... eftersom labhäften far runt i labsalen. 1 Laboration 3: Likström och
 IN Inst. för Fysik och materialvetenskap ---------------------------------------------------------------------------------------------- INSTRUKTION TILL LABORATIONEN INDUKTION ---------------------------------------------------------------------------------------------
IN Inst. för Fysik och materialvetenskap ---------------------------------------------------------------------------------------------- INSTRUKTION TILL LABORATIONEN INDUKTION ---------------------------------------------------------------------------------------------
Rep. Kap. 27 som behandlade kraften på en laddningar från ett B-fält.
 Rep. Kap. 7 som behandlade kraften på en laddningar från ett -fält. Kraft på laddning i rörelse Kraft på ström i ledare Gauss sats för -fältet Inte så användbar som den för E-fältet, eftersom flödet här
Rep. Kap. 7 som behandlade kraften på en laddningar från ett -fält. Kraft på laddning i rörelse Kraft på ström i ledare Gauss sats för -fältet Inte så användbar som den för E-fältet, eftersom flödet här
Elektromagnetism. Kapitel , 18.4 (fram till ex 18.8)
 Elektromagnetism Kapitel 8.-8., 8.4 (fram till ex 8.8) Varför magnetism? Energiomvandling elektrisk magnetisk mekanisk Elektriska maskiner Reversibla processer (de flesta) Motor Generator Elektromagneter
Elektromagnetism Kapitel 8.-8., 8.4 (fram till ex 8.8) Varför magnetism? Energiomvandling elektrisk magnetisk mekanisk Elektriska maskiner Reversibla processer (de flesta) Motor Generator Elektromagneter
Bra tabell i ert formelblad
 Bra tabell i ert formelblad Vi har gått igenom hur magnetfält alstrar krafter, kap. 7. Vi har gått igenom hur strömmar alstrar magnetfält, kap. 8. Återstår att lära sig hur strömmarna alstras. Tidigare
Bra tabell i ert formelblad Vi har gått igenom hur magnetfält alstrar krafter, kap. 7. Vi har gått igenom hur strömmar alstrar magnetfält, kap. 8. Återstår att lära sig hur strömmarna alstras. Tidigare
4. Elektromagnetisk svängningskrets
 4. Elektromagnetisk svängningskrets L 15 4.1 Resonans, resonansfrekvens En RLC krets kan betraktas som en harmonisk oscillator; den har en egenfrekvens. Då energi tillförs kretsen med denna egenfrekvens
4. Elektromagnetisk svängningskrets L 15 4.1 Resonans, resonansfrekvens En RLC krets kan betraktas som en harmonisk oscillator; den har en egenfrekvens. Då energi tillförs kretsen med denna egenfrekvens
FK Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (1:a omtentan), tisdag 17 juni 2014, kl 9:00-14:00
 FK4010 - Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (1:a omtentan), tisdag 17 juni 2014, kl 9:00-14:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror
FK4010 - Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (1:a omtentan), tisdag 17 juni 2014, kl 9:00-14:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror
Sammanfattning av likströmsläran
 Innehåll Sammanfattning av likströmsläran... Testa-dig-själv-likströmsläran...9 Felsökning.11 Mätinstrument...13 Varför har vi växelström..17 Växelspännings- och växelströmsbegrepp..18 Vektorräknig..0
Innehåll Sammanfattning av likströmsläran... Testa-dig-själv-likströmsläran...9 Felsökning.11 Mätinstrument...13 Varför har vi växelström..17 Växelspännings- och växelströmsbegrepp..18 Vektorräknig..0
Införa begreppen ström, strömtäthet och resistans Ohms lag Tillämpningar på enkla kretsar Energi och effekt i kretsar
 Kapitel: 25 Ström, motstånd och emf (Nu lämnar vi elektrostatiken) Visa under vilka villkor det kan finnas E-fält i ledare Införa begreppet emf (electromotoric force) Beskriva laddningars rörelse i ledare
Kapitel: 25 Ström, motstånd och emf (Nu lämnar vi elektrostatiken) Visa under vilka villkor det kan finnas E-fält i ledare Införa begreppet emf (electromotoric force) Beskriva laddningars rörelse i ledare
FK Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (2:a omtentan), fredag 30 augusti 2013, kl 9:00-14:00
 FK4010 - Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (2:a omtentan), fredag 30 augusti 2013, kl 9:00-14:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror
FK4010 - Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (2:a omtentan), fredag 30 augusti 2013, kl 9:00-14:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror
2.7 Virvelströmmar. Om ledaren är i rörelse kommer den att bromsas in, eftersom det inducerade magnetfältet och det yttre fältet är motsatt riktade.
 2.7 Virvelströmmar L8 Induktionsfenomenet uppträder för alla metaller. Ett föränderligt magnetfält inducerar en spänning, som i sin tur åstadkommer en ström. Detta kan leda till problem,men det kan också
2.7 Virvelströmmar L8 Induktionsfenomenet uppträder för alla metaller. Ett föränderligt magnetfält inducerar en spänning, som i sin tur åstadkommer en ström. Detta kan leda till problem,men det kan också
Att välja rätt strömtång (tångamperemeter) Börja med att besvara följande;
 Att välja rätt strömtång (tångamperemeter) Börja med att besvara följande; Är det AC eller DC ström som ska mätas? (DC tänger är kategoriserade som AC/DC tänger eftersom de mäter både lik- och växelström.)
Att välja rätt strömtång (tångamperemeter) Börja med att besvara följande; Är det AC eller DC ström som ska mätas? (DC tänger är kategoriserade som AC/DC tänger eftersom de mäter både lik- och växelström.)
Svaren på förståelsedelen skall ges på tesen som skall lämnas in.
 Dugga i Elektromagnetisk fältteori F. för F2. EEF031 2005-11-19 kl. 8.30-12.30 Tillåtna hjälpmedel: BETA, Physics Handbook, Formelsamling i Elektromagnetisk fältteori, Valfri kalkylator men inga egna anteckningar
Dugga i Elektromagnetisk fältteori F. för F2. EEF031 2005-11-19 kl. 8.30-12.30 Tillåtna hjälpmedel: BETA, Physics Handbook, Formelsamling i Elektromagnetisk fältteori, Valfri kalkylator men inga egna anteckningar
Motorprincipen. William Sandqvist
 Motorprincipen En strömförande ledare befinner sig i ett magnetfält B (längden l är den del av ledaren som befinner sig i fältet). De magnetiska kraftlinjerna får inte korsa varandra. Fältet förstärks
Motorprincipen En strömförande ledare befinner sig i ett magnetfält B (längden l är den del av ledaren som befinner sig i fältet). De magnetiska kraftlinjerna får inte korsa varandra. Fältet förstärks
Magnetiska fält. Magnetiska fält. Magnetiska fält. Magnetiska fält. Två strömförande ledningar kraftpåverkar varandra!
 38! 39! Två strömförande ledningar kraftpåverkar varandra! i 1! i 2! Krafterna beror av i 1 och i 2 och av geometrin! 40! Likaså kraftpåverkas en laddning Q som rör sig i närheten av en strömförande ledning!
38! 39! Två strömförande ledningar kraftpåverkar varandra! i 1! i 2! Krafterna beror av i 1 och i 2 och av geometrin! 40! Likaså kraftpåverkas en laddning Q som rör sig i närheten av en strömförande ledning!
Förståelsefrågorna besvaras genom att markera en av rutorna efter varje påstående till höger. En och endast en ruta på varje rad skall markeras.
 Dugga i Elektromagnetisk fältteori för F2. EEF031 2006-11-25 kl. 8.30-12.30 Tillåtna hjälpmedel: BETA, Physics Handbook, Formelsamling i Elektromagnetisk fältteori, Valfri kalkylator men inga egna anteckningar
Dugga i Elektromagnetisk fältteori för F2. EEF031 2006-11-25 kl. 8.30-12.30 Tillåtna hjälpmedel: BETA, Physics Handbook, Formelsamling i Elektromagnetisk fältteori, Valfri kalkylator men inga egna anteckningar
Kommentarer till målen inför fysikprovet. Magnetism & elektricitet
 Kommentarer till målen inför fysikprovet Magnetism & elektricitet Skillnaden mellan spänning, ström och resistans Spänningen är själva drivkraften av strömmen och mäts i enheten volt, V. Finns ingen spänning
Kommentarer till målen inför fysikprovet Magnetism & elektricitet Skillnaden mellan spänning, ström och resistans Spänningen är själva drivkraften av strömmen och mäts i enheten volt, V. Finns ingen spänning
1( ), 2( ), 3( ), 4( ), 5( ), 6( ), 7( ), 8( ), 9( )
 Inst. för Fysik och materialvetenskap Ola Hartmann Tentamen i ELEKTROMAGNETISM I 2008-10-08 Skrivtid: 5 tim. för Kand_Fy 2 och STS 3. Hjälpmedel: Physics Handbook, formelblad i Elektricitetslära, räknedosa
Inst. för Fysik och materialvetenskap Ola Hartmann Tentamen i ELEKTROMAGNETISM I 2008-10-08 Skrivtid: 5 tim. för Kand_Fy 2 och STS 3. Hjälpmedel: Physics Handbook, formelblad i Elektricitetslära, räknedosa
LNB727, Transformatorn. Jimmy Ehnberg, Examinator Avd. för Elkraftteknik Inst. för Elektroteknik
 LNB727, Transformatorn Jimmy Ehnberg, Examinator Avd. för Elkraftteknik Inst. för Elektroteknik Innehåll Vad är en transformator och varför behövs den Magnetisk koppling Kopplingsfaktor Ideal transformatorn
LNB727, Transformatorn Jimmy Ehnberg, Examinator Avd. för Elkraftteknik Inst. för Elektroteknik Innehåll Vad är en transformator och varför behövs den Magnetisk koppling Kopplingsfaktor Ideal transformatorn
Tentamen i El- och vågrörelselära,
 Tentamen i El- och vågrörelselära, 23 2 8 Hjälpmedel: Physics Handbook, räknare. Ensfäriskkopparkulamedradie = 5mmharladdningenQ = 2.5 0 3 C. Beräkna det elektriska fältet som funktion av avståndet från
Tentamen i El- och vågrörelselära, 23 2 8 Hjälpmedel: Physics Handbook, räknare. Ensfäriskkopparkulamedradie = 5mmharladdningenQ = 2.5 0 3 C. Beräkna det elektriska fältet som funktion av avståndet från
Magnetiska fält laboration 1FA514 Elektimagnetism I
 Magnetiska fält laboration 1FA514 Elektimagnetism I Utförs av: William Sjöström 19940404 6956 Oskar Keskitalo 19941021 4895 Uppsala 2015 05 09 Sammanfattning När man leder ström genom en spole så bildas
Magnetiska fält laboration 1FA514 Elektimagnetism I Utförs av: William Sjöström 19940404 6956 Oskar Keskitalo 19941021 4895 Uppsala 2015 05 09 Sammanfattning När man leder ström genom en spole så bildas
Elektricitetslära och magnetism - 1FY808
 Linnéuniversitetet Institutionen för datavetenskap, fysik och matematik Laborationshäfte för kursen Elektricitetslära och magnetism - 1FY808 Ditt namn:... eftersom labhäften far runt i labsalen. 1 1. Instrumentjämförelse
Linnéuniversitetet Institutionen för datavetenskap, fysik och matematik Laborationshäfte för kursen Elektricitetslära och magnetism - 1FY808 Ditt namn:... eftersom labhäften far runt i labsalen. 1 1. Instrumentjämförelse
Elektriska drivsystem Föreläsning 2 - Transformatorer
 Elektriska drivsystem Föreläsning 2 - Transformatorer Mattias Krysander Institutionen för systemteknik Linköpings universitet matkr@isy.liu.se 2010-09-23 1/36 Dagens föreläsning Använda kunskapen om magnetiska
Elektriska drivsystem Föreläsning 2 - Transformatorer Mattias Krysander Institutionen för systemteknik Linköpings universitet matkr@isy.liu.se 2010-09-23 1/36 Dagens föreläsning Använda kunskapen om magnetiska
Solar cells. 2.0 Inledning. Utrustning som används i detta experiment visas i Fig. 2.1.
 Solar cells 2.0 Inledning Utrustning som används i detta experiment visas i Fig. 2.1. Figure 2.1 Utrustning som används i experiment E2. Utrustningslista (se Fig. 2.1): A, B: Två solceller C: Svart plastlåda
Solar cells 2.0 Inledning Utrustning som används i detta experiment visas i Fig. 2.1. Figure 2.1 Utrustning som används i experiment E2. Utrustningslista (se Fig. 2.1): A, B: Två solceller C: Svart plastlåda
FK Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (1:a omtentan), tisdag 16 juni 2015, kl 9:00-14:00
 FK4010 - Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (1:a omtentan), tisdag 16 juni 2015, kl 9:00-14:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror
FK4010 - Elektromagnetism, Fysikum, Stockholms universitet Tentamensskrivning (1:a omtentan), tisdag 16 juni 2015, kl 9:00-14:00 Läs noggrant genom hela tentan först. Börja med uppgifterna som du tror
Räkneuppgifter på avsnittet Fält Tommy Andersson
 Räkneuppgifter på avsnittet Fält Tommy Andersson 1. En negativt laddad pappersbit befinner sig nära en oladdad metallplåt. Får man attraktion, repulsion eller ingen kraftpåverkan? Motivera! 2. På ett mönsterkort
Räkneuppgifter på avsnittet Fält Tommy Andersson 1. En negativt laddad pappersbit befinner sig nära en oladdad metallplåt. Får man attraktion, repulsion eller ingen kraftpåverkan? Motivera! 2. På ett mönsterkort
LABORATION 3. Växelström
 Chalmers Tekniska Högskola november 01 Fysik 14 sidor Kurs: Elektrisk mätteknik och vågfysik. FFY616 LABORATION 3 Växelström Växelströmskretsar (seriekoppling), Serieresonans. Förberedelse: i) Läs noggrant
Chalmers Tekniska Högskola november 01 Fysik 14 sidor Kurs: Elektrisk mätteknik och vågfysik. FFY616 LABORATION 3 Växelström Växelströmskretsar (seriekoppling), Serieresonans. Förberedelse: i) Läs noggrant
Tentamen ellära 92FY21 och 27
 Tentamen ellära 92FY21 och 27 2014-06-04 kl. 8 13 Svaren anges på separat papper. Fullständiga lösningar med alla steg motiverade och beteckningar utsatta ska redovisas för att få full poäng. Poängen för
Tentamen ellära 92FY21 och 27 2014-06-04 kl. 8 13 Svaren anges på separat papper. Fullständiga lösningar med alla steg motiverade och beteckningar utsatta ska redovisas för att få full poäng. Poängen för
Rättningstiden är i normalfall 15 arbetsdagar, till detta tillkommer upp till 5 arbetsdagar för administration.
 A135TG Elektrisk Kraftgenerering 7,5 högskolepoäng Provmoment: Skriftlig tentamen Ladokkod: A135TG Tentamen ges för: Energiingenjörsprogrammet Åk3 Tentamenskod: Tentamensdatum: 2017-01-12 Tid: 2017-01-12
A135TG Elektrisk Kraftgenerering 7,5 högskolepoäng Provmoment: Skriftlig tentamen Ladokkod: A135TG Tentamen ges för: Energiingenjörsprogrammet Åk3 Tentamenskod: Tentamensdatum: 2017-01-12 Tid: 2017-01-12
Strålningsfält och fotoner. Kapitel 23: Faradays lag
 Strålningsfält och fotoner Kapitel 23: Faradays lag Faradays lag Tidsvarierande magnetiska fält inducerar elektriska fält, eller elektrisk spänning i en krets. Om strömmen genom en solenoid ökar, ökar
Strålningsfält och fotoner Kapitel 23: Faradays lag Faradays lag Tidsvarierande magnetiska fält inducerar elektriska fält, eller elektrisk spänning i en krets. Om strömmen genom en solenoid ökar, ökar
EJ1200 ELEFFEKTSYSTEM. ENTR: En- och trefastransformatorn
 1 EJ1200 ELEFFEKTSYSTEM PM för laboration ENTR: En- och trefastransformatorn Syfte: Att skapa förståelse för principerna för växelspänningsmagnetisering och verkningssätt och fundamentala egenskaper hos
1 EJ1200 ELEFFEKTSYSTEM PM för laboration ENTR: En- och trefastransformatorn Syfte: Att skapa förståelse för principerna för växelspänningsmagnetisering och verkningssätt och fundamentala egenskaper hos
3.4 RLC kretsen. 3.4.1 Impedans, Z
 3.4 RLC kretsen L 11 Växelströmskretsar kan ha olika utsende, men en av de mest använda är RLC kretsen. Den heter så eftersom den har ett motstånd, en spole och en kondensator i serie. De tre komponenterna
3.4 RLC kretsen L 11 Växelströmskretsar kan ha olika utsende, men en av de mest använda är RLC kretsen. Den heter så eftersom den har ett motstånd, en spole och en kondensator i serie. De tre komponenterna
9. Magnetisk energi Magnetisk energi för en isolerad krets
 9. Magnetisk energi [RMC] Elektrodynamik, ht 005, Krister Henriksson 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
9. Magnetisk energi [RMC] Elektrodynamik, ht 005, Krister Henriksson 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
Övningsuppgifter/repetition inom elektromagnetism + ljus (OBS: ej fullständig)
 Övningsuppgifter/repetition inom elektromagnetism + ljus (OBS: ej fullständig) Elektrostatik 1. Ange Faradays lag i elektrostatiken. 2. Vad är kravet för att ett vektorfält F är konservativt? 3. En låda
Övningsuppgifter/repetition inom elektromagnetism + ljus (OBS: ej fullständig) Elektrostatik 1. Ange Faradays lag i elektrostatiken. 2. Vad är kravet för att ett vektorfält F är konservativt? 3. En låda
Vecka 4 INDUKTION OCH INDUKTANS (HRW 30-31) EM-OSCILLATIONER OCH VÄXELSTRÖMSKRETSAR
 Vecka 4 INDUKTION OCH INDUKTANS (HRW 30-31) EM-OSCILLATIONER OCH VÄXELSTRÖMSKRETSAR Inlärningsmål Induktion och induktans Faradays lag och inducerad källspänning Lentz lag Energiomvandling vid induktion
Vecka 4 INDUKTION OCH INDUKTANS (HRW 30-31) EM-OSCILLATIONER OCH VÄXELSTRÖMSKRETSAR Inlärningsmål Induktion och induktans Faradays lag och inducerad källspänning Lentz lag Energiomvandling vid induktion
isolerande skikt positiv laddning Q=CV negativ laddning -Q V V
 1 Föreläsning 5 Hambley avsnitt 3.1 3.6 Kondensatorn och spolen [3.1 3.6] Kondensatorn och spolen är två mycket viktiga kretskomponenter. Kondensatorn kan lagra elektrisk energi och spolen magnetisk energi.
1 Föreläsning 5 Hambley avsnitt 3.1 3.6 Kondensatorn och spolen [3.1 3.6] Kondensatorn och spolen är två mycket viktiga kretskomponenter. Kondensatorn kan lagra elektrisk energi och spolen magnetisk energi.
Laboration 2 Elektriska kretsar Online fjärrstyrd laborationsplats Blekinge Tekniska Högskola (BTH)
 Laboration 2 Elektriska kretsar Online fjärrstyrd laborationsplats Blekinge Tekniska Högskola (BTH) Växelspänningsexperiment Namn: Elektriska kretsar Online fjärrstyrd laborationsplats Blekinge Tekniska
Laboration 2 Elektriska kretsar Online fjärrstyrd laborationsplats Blekinge Tekniska Högskola (BTH) Växelspänningsexperiment Namn: Elektriska kretsar Online fjärrstyrd laborationsplats Blekinge Tekniska
FK Elektromagnetism och vågor, Fysikum, Stockholms Universitet Tentamensskrivning, måndag 21 mars 2016, kl 9:00-14:00
 FK5019 - Elektromagnetism och vågor, Fysikum, Stockholms Universitet Tentamensskrivning, måndag 21 mars 2016, kl 9:00-14:00 Läs noggrant igenom hela tentan först Tentan består av 5 olika uppgifter med
FK5019 - Elektromagnetism och vågor, Fysikum, Stockholms Universitet Tentamensskrivning, måndag 21 mars 2016, kl 9:00-14:00 Läs noggrant igenom hela tentan först Tentan består av 5 olika uppgifter med
Sammanfattning av kursen ETIA01 Elektronik för D, Del 1 (föreläsning 1-10)
 Sammanfattning av kursen ETIA0 Elektronik för D, Del (föreläsning -0) Kapitel : sid 37 Definitioner om vad laddning, spänning, ström, effekt och energi är och vad dess enheterna är: Laddningsmängd q mäts
Sammanfattning av kursen ETIA0 Elektronik för D, Del (föreläsning -0) Kapitel : sid 37 Definitioner om vad laddning, spänning, ström, effekt och energi är och vad dess enheterna är: Laddningsmängd q mäts
Kandidatprogrammet FK VT09 DEMONSTRATIONER INDUKTION I. Induktion med magnet Elektriska stolen Självinduktans Thomsons ring
 DEMONSTRATIONER INDUKTION I Induktion med magnet Elektriska stolen Självinduktans Thomsons ring Introduktion I litteraturen och framför allt på webben kan du enkelt hitta ett stort antal experiment som
DEMONSTRATIONER INDUKTION I Induktion med magnet Elektriska stolen Självinduktans Thomsons ring Introduktion I litteraturen och framför allt på webben kan du enkelt hitta ett stort antal experiment som
Laborationsrapport. Kurs Elinstallation, begränsad behörighet. Lab nr 2. Laborationens namn Växelströmskretsar. Kommentarer. Utförd den.
 Laborationsrapport Kurs Elinstallation, begränsad behörighet Lab nr 2 version 3.1 Laborationens namn Växelströmskretsar Namn Kommentarer Utförd den Godkänd den Sign 1 Inledning I denna laboration skall
Laborationsrapport Kurs Elinstallation, begränsad behörighet Lab nr 2 version 3.1 Laborationens namn Växelströmskretsar Namn Kommentarer Utförd den Godkänd den Sign 1 Inledning I denna laboration skall
Vi börjar med en vanlig ledare av koppar.
 Vi börjar med en vanlig ledare av koppar. [Från Wikipedia] Skineffekt är tendensen hos en växelström (AC) att omfördela sig inom en elektrisk ledare så att strömtätheten är störst nära ledarens yta, och
Vi börjar med en vanlig ledare av koppar. [Från Wikipedia] Skineffekt är tendensen hos en växelström (AC) att omfördela sig inom en elektrisk ledare så att strömtätheten är störst nära ledarens yta, och
TSFS04, Elektriska drivsystem, 6 hp Föreläsning 1 - Introduktion, magnetiska kretsar och material
 TSFS04, Elektriska drivsystem, 6 hp Föreläsning 1 - Introduktion, magnetiska kretsar och material Mattias Krysander Institutionen för systemteknik Linköpings universitet mattias.krysander@liu.se 2016-01-18
TSFS04, Elektriska drivsystem, 6 hp Föreläsning 1 - Introduktion, magnetiska kretsar och material Mattias Krysander Institutionen för systemteknik Linköpings universitet mattias.krysander@liu.se 2016-01-18
Laboration 2: Konstruktion av asynkronmotor
 Laboration 2: Konstruktion av asynkronmotor Laboranter: Henrik Bergman, Henrik Bergvall Berglund, William Sjöström, Georgios Davakos Plats och datum: Uppsala 2016-11-09 Kurs: Elektromagnetism 2 Handledare:
Laboration 2: Konstruktion av asynkronmotor Laboranter: Henrik Bergman, Henrik Bergvall Berglund, William Sjöström, Georgios Davakos Plats och datum: Uppsala 2016-11-09 Kurs: Elektromagnetism 2 Handledare:
Föreläsning 8. Ohms lag (Kap. 7.1) 7.1 i Griffiths
 1 Föreläsning 8 7.1 i Griffiths Ohms lag (Kap. 7.1) i är bekanta med Ohms lag i kretsteori som = RI. En mer generell framställning är vårt mål här. Sambandet mellan strömtätheten J och den elektriska fältstyrkan
1 Föreläsning 8 7.1 i Griffiths Ohms lag (Kap. 7.1) i är bekanta med Ohms lag i kretsteori som = RI. En mer generell framställning är vårt mål här. Sambandet mellan strömtätheten J och den elektriska fältstyrkan
Elektro och Informationsteknik LTH. Laboration 3 RC- och RL-nät i tidsplanet. Elektronik för D ETIA01
 Elektro och Informationsteknik LTH Laboration 3 R- och RL-nät i tidsplanet Elektronik för D ETIA01??? Telmo Santos Anders J Johansson Lund Februari 2008 Laboration 3 Mål Efter laborationen vill vi att
Elektro och Informationsteknik LTH Laboration 3 R- och RL-nät i tidsplanet Elektronik för D ETIA01??? Telmo Santos Anders J Johansson Lund Februari 2008 Laboration 3 Mål Efter laborationen vill vi att
Strömförsörjning. Transformatorns arbetssätt
 Strömförsörjning Transformatorns arbetssätt Transformatorn kan omvandla växelspänningar och växelströmmar. En fulltransformators in och utgångar är galvaniskt skilda från varandra. Att in- och utgångarna
Strömförsörjning Transformatorns arbetssätt Transformatorn kan omvandla växelspänningar och växelströmmar. En fulltransformators in och utgångar är galvaniskt skilda från varandra. Att in- och utgångarna
RC-kretsar, transienta förlopp
 13 maj 2013 Labinstruktion: RC-kretsar, magnetiska fält och induktion Ellära, 92FY21/27 1(5) RC-kretsar, transienta förlopp I den här laborationen kommer du att titta på urladdning av en RC-krets och hur
13 maj 2013 Labinstruktion: RC-kretsar, magnetiska fält och induktion Ellära, 92FY21/27 1(5) RC-kretsar, transienta förlopp I den här laborationen kommer du att titta på urladdning av en RC-krets och hur
Induktans Induktans Induktans Induktans
 71! 72! Spole med resistans R och med N varv! i! N v! För ett varv gäller! v ett varv = R ett varv " i + d# Seriekoppling ger! v = R " i + d#! är det sammanlänkade flödet och är summan av flödena genom
71! 72! Spole med resistans R och med N varv! i! N v! För ett varv gäller! v ett varv = R ett varv " i + d# Seriekoppling ger! v = R " i + d#! är det sammanlänkade flödet och är summan av flödena genom
Elektriska komponenter och kretsar. Emma Björk
 Elektriska komponenter och kretsar Emma Björk Elektromotorisk kraft Den mekanism som alstrar det E-fält som driver runt laddningarna i en sluten krets kallas emf(electro Motoric Force trots att det ej
Elektriska komponenter och kretsar Emma Björk Elektromotorisk kraft Den mekanism som alstrar det E-fält som driver runt laddningarna i en sluten krets kallas emf(electro Motoric Force trots att det ej
9. Magnetisk energi Magnetisk energi för en isolerad krets
 9. Magnetisk energi [RM] Elektrodynamik, vt 013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets anod
9. Magnetisk energi [RM] Elektrodynamik, vt 013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets anod
9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1
![9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1](/thumbs/61/46243221.jpg) 9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
Tentamen: Baskurs B i Fysik, del1, 4p 2007-03-23 kl. 08.00-13.00
 Institutionen för teknik, fysik och matematik Nils Olander och Herje Westman Tentamen: Baskurs B i Fysik, del1, 4p 2007-03-23 kl. 08.00-13.00 Max: 30 p A-uppgifterna 1-8 besvaras genom att ange det korrekta
Institutionen för teknik, fysik och matematik Nils Olander och Herje Westman Tentamen: Baskurs B i Fysik, del1, 4p 2007-03-23 kl. 08.00-13.00 Max: 30 p A-uppgifterna 1-8 besvaras genom att ange det korrekta
Växelström och reaktans
 Växelström och reaktans Magnus Danielson 6 februari 2017 Magnus Danielson Växelström och reaktans 6 februari 2017 1 / 17 Outline 1 Växelström 2 Kondensator 3 Spolar och induktans 4 Resonanskretsar 5 Transformator
Växelström och reaktans Magnus Danielson 6 februari 2017 Magnus Danielson Växelström och reaktans 6 februari 2017 1 / 17 Outline 1 Växelström 2 Kondensator 3 Spolar och induktans 4 Resonanskretsar 5 Transformator
Laboration 1: Likström
 1. Instrumentjämförelse Laboration 1: Likström Syfte och metod Vi undersöker hur ett instruments inre resistans påverkar mätresultatet. Vi mäter spänningar med olika instrument och inställningar, och undersöker
1. Instrumentjämförelse Laboration 1: Likström Syfte och metod Vi undersöker hur ett instruments inre resistans påverkar mätresultatet. Vi mäter spänningar med olika instrument och inställningar, och undersöker
Prov 3 2014-10-13. (b) Hur stor är kraften som verkar på en elektron mellan plattorna? [1/0/0]
![Prov 3 2014-10-13. (b) Hur stor är kraften som verkar på en elektron mellan plattorna? [1/0/0] Prov 3 2014-10-13. (b) Hur stor är kraften som verkar på en elektron mellan plattorna? [1/0/0]](/thumbs/25/5742088.jpg) Namn: Område: Elektromagnetism Datum: 13 Oktober 2014 Tid: 100 minuter Hjälpmedel: Räknare och formelsamling. Betyg: E: 25. C: 35, 10 på A/C-nivå. A: 45, 14 på C-nivå, 2 på A-nivå. Tot: 60 (34/21/5). Instruktioner:
Namn: Område: Elektromagnetism Datum: 13 Oktober 2014 Tid: 100 minuter Hjälpmedel: Räknare och formelsamling. Betyg: E: 25. C: 35, 10 på A/C-nivå. A: 45, 14 på C-nivå, 2 på A-nivå. Tot: 60 (34/21/5). Instruktioner:
Fysikum Kandidatprogrammet FK VT16 DEMONSTRATIONER MAGNETISM II. Helmholtzspolen Elektronstråle i magnetfält Bestämning av e/m
 DEMONSTRATIONER MAGNETISM II Helmholtzspolen Elektronstråle i magnetfält Bestämning av e/m Uppdaterad den 10 november 015 Introduktion I litteraturen och framför allt på webben kan du enkelt hitta ett
DEMONSTRATIONER MAGNETISM II Helmholtzspolen Elektronstråle i magnetfält Bestämning av e/m Uppdaterad den 10 november 015 Introduktion I litteraturen och framför allt på webben kan du enkelt hitta ett
Fysik TFYA86. Föreläsning 8/11
 Fysik TFYA86 Föreläsning 8/11 1 nduktion och elektromotorisk kraft (emk) University Physics: Kapitel 29, 30.1, (30.2 självinduktion) 2 ntroduktion Tidigare i kursen: Tidsberoende förändring, dynamik Elektrostatik
Fysik TFYA86 Föreläsning 8/11 1 nduktion och elektromotorisk kraft (emk) University Physics: Kapitel 29, 30.1, (30.2 självinduktion) 2 ntroduktion Tidigare i kursen: Tidsberoende förändring, dynamik Elektrostatik
Att fjärrstyra fysiska experiment över nätet.
 2012-05-11 Att fjärrstyra fysiska experiment över nätet. Komponenter, t ex resistorer Fjärrstyrd labmiljö med experiment som utförs i realtid Kablar Likspänningskälla Lena Claesson, Katedralskolan/BTH
2012-05-11 Att fjärrstyra fysiska experiment över nätet. Komponenter, t ex resistorer Fjärrstyrd labmiljö med experiment som utförs i realtid Kablar Likspänningskälla Lena Claesson, Katedralskolan/BTH
~ växelström. växelström 1. Heureka B Natur och Kultur 91-27-56722-2
 ~ växelström Det flyter växelström och inte likström i de flesta elnät världen över! Skälen är många. Hittills har det varit enklare att bygga generatorer som levererar växelspänning. Transport av elenergi
~ växelström Det flyter växelström och inte likström i de flesta elnät världen över! Skälen är många. Hittills har det varit enklare att bygga generatorer som levererar växelspänning. Transport av elenergi
IF1330 Ellära KK1 LAB1 KK2 LAB2 KK4 LAB4. tentamen
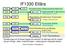 F330 Ellära F/Ö F/Ö4 F/Ö F/Ö5 F/Ö3 Strömkretslära Mätinstrument Batterier Likströmsnät Tvåpolsatsen KK LAB Mätning av och F/Ö6 F/Ö7 Magnetkrets Kondensator Transienter KK LAB Tvåpol mät och sim F/Ö8 F/Ö9
F330 Ellära F/Ö F/Ö4 F/Ö F/Ö5 F/Ö3 Strömkretslära Mätinstrument Batterier Likströmsnät Tvåpolsatsen KK LAB Mätning av och F/Ö6 F/Ö7 Magnetkrets Kondensator Transienter KK LAB Tvåpol mät och sim F/Ö8 F/Ö9
Där r är ortsvektorn mellan den punkt där fältet beräknas och den punkt där linjeelementet dl av strömbanan finns.
 1 Allmänt om magnetiska mtrl och tillämpningar; transformatorer, generatorer, motorer, magnetiska lagringsmedia (media + läs/skriv) NOBEL-PRI 27, magnetiska sensorer, drug carrier, magnetisk kylning Lektion
1 Allmänt om magnetiska mtrl och tillämpningar; transformatorer, generatorer, motorer, magnetiska lagringsmedia (media + läs/skriv) NOBEL-PRI 27, magnetiska sensorer, drug carrier, magnetisk kylning Lektion
Introduktion till fordonselektronik ET054G. Föreläsning 3
 Introduktion till fordonselektronik ET054G Föreläsning 3 1 Elektriska och elektroniska fordonskomponenter Att använda el I Sverige Fas: svart Nolla: blå Jord: gröngul Varför en jordkabel? 2 Jordning och
Introduktion till fordonselektronik ET054G Föreläsning 3 1 Elektriska och elektroniska fordonskomponenter Att använda el I Sverige Fas: svart Nolla: blå Jord: gröngul Varför en jordkabel? 2 Jordning och
LTK010, vt 2017 Elektronik Laboration
 Reviderad: 20 december 2016 av Jonas Enger jonas.enger@physics.gu.se Förberedelse: Du måste känna till följande Kirchoffs ström- och spänningslagar Ström- och spänningsriktig koppling vid resistansmätning
Reviderad: 20 december 2016 av Jonas Enger jonas.enger@physics.gu.se Förberedelse: Du måste känna till följande Kirchoffs ström- och spänningslagar Ström- och spänningsriktig koppling vid resistansmätning
4:3 Passiva komponenter. Inledning
 4:3 Passiva komponenter. Inledning I det här kapitlet skall du gå igenom de tre viktigaste passiva komponenterna, nämligen motståndet, kondensatorn och spolen. Du frågar dig säkert varför de kallas passiva
4:3 Passiva komponenter. Inledning I det här kapitlet skall du gå igenom de tre viktigaste passiva komponenterna, nämligen motståndet, kondensatorn och spolen. Du frågar dig säkert varför de kallas passiva
Kaströrelse. 3,3 m. 1,1 m
 Kaströrelse 1. En liten kula, som vi kallar kula 1, släpps ifrån en höjd över marken. Exakt samtidigt skjuts kula 2 parallellt med marken ifrån samma höjd som kula 1. Luftmotståndet som verkar på kulorna
Kaströrelse 1. En liten kula, som vi kallar kula 1, släpps ifrån en höjd över marken. Exakt samtidigt skjuts kula 2 parallellt med marken ifrån samma höjd som kula 1. Luftmotståndet som verkar på kulorna
Laboration 1 Elektriska kretsar Online fjärrstyrd laborationsplats Blekinge Tekniska Högskola (BTH)
 Laboration 1 Elektriska kretsar Online fjärrstyrd laborationsplats Blekinge Tekniska Högskola (BTH) Likspänningsexperiment Namn: Elektriska kretsar Online fjärrstyrd laborationsplats Blekinge Tekniska
Laboration 1 Elektriska kretsar Online fjärrstyrd laborationsplats Blekinge Tekniska Högskola (BTH) Likspänningsexperiment Namn: Elektriska kretsar Online fjärrstyrd laborationsplats Blekinge Tekniska
Demonstration: De magnetiska grundfenomenen. Utrustning: Tre stavmagneter, metallkulor, mynt, kompass.
 1. Magnetism Magnetismen som fenomen upptäcktes redan under antiken, då man märkte att vissa malmarter attraherade vissa metaller. Nuförtiden vet vi att magneter också kan skapas på konstgjord väg. 1.1
1. Magnetism Magnetismen som fenomen upptäcktes redan under antiken, då man märkte att vissa malmarter attraherade vissa metaller. Nuförtiden vet vi att magneter också kan skapas på konstgjord väg. 1.1
Elektroteknikens grunder Laboration 1
 Elektroteknikens grunder Laboration 1 Grundläggande ellära Elektrisk mätteknik Elektroteknikens grunder Laboration 1 1 Mål Du skall i denna laboration få träning i att koppla elektriska kretsar och att
Elektroteknikens grunder Laboration 1 Grundläggande ellära Elektrisk mätteknik Elektroteknikens grunder Laboration 1 1 Mål Du skall i denna laboration få träning i att koppla elektriska kretsar och att
TSFS04, Elektriska drivsystem, 6 hp Föreläsning 4 - Grundläggande principer för elmaskiner
 TSFS04, Elektriska drivsystem, 6 hp Föreläsning 4 - Grundläggande principer för elmaskiner Mattias Krysander Institutionen för systemteknik Linköpings universitet mattias.krysander@liu.se 2017-01-25 1/35
TSFS04, Elektriska drivsystem, 6 hp Föreläsning 4 - Grundläggande principer för elmaskiner Mattias Krysander Institutionen för systemteknik Linköpings universitet mattias.krysander@liu.se 2017-01-25 1/35
Svaren på förståelsedelen skall ges direkt på tesen som ska lämnas in
 Dugga i Elektromagnetisk fältteori för F2. EEF031 2013-11-23 kl. 8.30-12.30 Tillåtna hjälpmedel: BETA, Physics Handbook, Formelsamling i Elektromagnetisk fältteori. Valfri kalkylator, minnet måste raderas
Dugga i Elektromagnetisk fältteori för F2. EEF031 2013-11-23 kl. 8.30-12.30 Tillåtna hjälpmedel: BETA, Physics Handbook, Formelsamling i Elektromagnetisk fältteori. Valfri kalkylator, minnet måste raderas
Svaren på förståelsedelen skall ges direkt på tesen som ska lämnas in
 Övningstenta i Elektromagnetisk fältteori, 2015-11-28 kl. 8.30-12.30 Kurskod EEF031 Tillåtna hjälpmedel: BETA, Physics Handbook, Formelsamling i Elektromagnetisk fältteori. Valfri kalkylator, minnet måste
Övningstenta i Elektromagnetisk fältteori, 2015-11-28 kl. 8.30-12.30 Kurskod EEF031 Tillåtna hjälpmedel: BETA, Physics Handbook, Formelsamling i Elektromagnetisk fältteori. Valfri kalkylator, minnet måste
Elektromagnetism. Laboration 2. Utfördes av: Henrik Bergman Muzammil Kamaly. Uppsala
 Elektromagnetism Laboration 2 1 Utfördes av: Henrik Bergman Muzammil Kamaly Uppsala 2015-05-17 1 Tagen Från Kelvin Ramirez Q1.B Henrik Bergman 941120-0190 1 0. Historik Sammandrag 2. Introduktion 3. Syftet
Elektromagnetism Laboration 2 1 Utfördes av: Henrik Bergman Muzammil Kamaly Uppsala 2015-05-17 1 Tagen Från Kelvin Ramirez Q1.B Henrik Bergman 941120-0190 1 0. Historik Sammandrag 2. Introduktion 3. Syftet
Strålningsfält och fotoner. Våren 2013
 Strålningsfält och fotoner Våren 2013 1. Fält i rymden Vi har lärt oss att beräkna elektriska fält utgående från laddningarna som orsakar dem Kan vi härleda nånting åt andra hållet? 2 1.1 Gauss lag Låt
Strålningsfält och fotoner Våren 2013 1. Fält i rymden Vi har lärt oss att beräkna elektriska fält utgående från laddningarna som orsakar dem Kan vi härleda nånting åt andra hållet? 2 1.1 Gauss lag Låt
Tentamen eem076 Elektriska Kretsar och Fält, D1
 Tentamen eem076 Elektriska Kretsar och Fält, D1 Examinator: Ants R. Silberberg 21 maj 2012 kl. 08.30-12.30, sal: M Förfrågningar: Ants Silberberg, tel. 1808 Lösningar: Anslås tisdagen den 22 maj på institutionens
Tentamen eem076 Elektriska Kretsar och Fält, D1 Examinator: Ants R. Silberberg 21 maj 2012 kl. 08.30-12.30, sal: M Förfrågningar: Ants Silberberg, tel. 1808 Lösningar: Anslås tisdagen den 22 maj på institutionens
ETE115 Ellära och elektronik, tentamen oktober 2006
 (2) 9 oktober 2006 Institutionen för elektrovetenskap Daniel Sjöberg ETE5 Ellära och elektronik, tentamen oktober 2006 Tillåtna hjälpmedel: formelsamling i kretsteori. Observera att uppgifterna inte är
(2) 9 oktober 2006 Institutionen för elektrovetenskap Daniel Sjöberg ETE5 Ellära och elektronik, tentamen oktober 2006 Tillåtna hjälpmedel: formelsamling i kretsteori. Observera att uppgifterna inte är
Växelström K O M P E N D I U M 2 ELEKTRO
 MEÅ NIVERSITET Tillämpad fysik och elektronik Sverker Johansson Johan Pålsson 999-09- Rev.0 Växelström K O M P E N D I M ELEKTRO INNEHÅLL. ALLMÄNT OM LIK- OCH VÄXELSPÄNNINGAR.... SAMBANDET MELLAN STRÖM
MEÅ NIVERSITET Tillämpad fysik och elektronik Sverker Johansson Johan Pålsson 999-09- Rev.0 Växelström K O M P E N D I M ELEKTRO INNEHÅLL. ALLMÄNT OM LIK- OCH VÄXELSPÄNNINGAR.... SAMBANDET MELLAN STRÖM
IE1206 Inbyggd Elektronik
 IE1206 Inbyggd Elektronik F1 F3 F4 F2 Ö1 Ö2 PIC-block Dokumentation, Seriecom Pulsgivare I, U, R, P, serie och parallell KK1 LAB1 Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchoffs
IE1206 Inbyggd Elektronik F1 F3 F4 F2 Ö1 Ö2 PIC-block Dokumentation, Seriecom Pulsgivare I, U, R, P, serie och parallell KK1 LAB1 Pulsgivare, Menyprogram Start för programmeringsgruppuppgift Kirchoffs
Laborationshandledning för mätteknik
 Laborationshandledning för mätteknik - digitalteknik och konstruktion TNE094 LABORATION 1 Laborant: E-post: Kommentarer från lärare: Institutionen för Teknik och Naturvetenskap Campus Norrköping, augusti
Laborationshandledning för mätteknik - digitalteknik och konstruktion TNE094 LABORATION 1 Laborant: E-post: Kommentarer från lärare: Institutionen för Teknik och Naturvetenskap Campus Norrköping, augusti
Strålningsfält och fotoner. Våren 2016
 Strålningsfält och fotoner Våren 2016 1. Fält i rymden Vi har lärt oss att beräkna elektriska fält utgående från laddningarna som orsakar dem Kan vi härleda nånting åt andra hållet? 2 1.1 Gauss lag Låt
Strålningsfält och fotoner Våren 2016 1. Fält i rymden Vi har lärt oss att beräkna elektriska fält utgående från laddningarna som orsakar dem Kan vi härleda nånting åt andra hållet? 2 1.1 Gauss lag Låt
Tentamen i : Vågor,plasmor och antenner. Totala antalet uppgifter: 6 Datum:
 Tentamen i : Vågor,plasmor och antenner Kurs: MTF108 Totala antalet uppgifter: 6 Datum: 2006-05-27 Examinator/Tfn: Hans Åkerstedt/491280/Åke Wisten070/5597072 Skrivtid: 9.00-15.00 Jourhavande lärare/tfn:
Tentamen i : Vågor,plasmor och antenner Kurs: MTF108 Totala antalet uppgifter: 6 Datum: 2006-05-27 Examinator/Tfn: Hans Åkerstedt/491280/Åke Wisten070/5597072 Skrivtid: 9.00-15.00 Jourhavande lärare/tfn:
1 Grundläggande Ellära
 1 Grundläggande Ellära 1.1 Elektriska begrepp 1.1.1 Ange för nedanstående figur om de markerade delarna av kretsen är en nod, gren, maska eller slinga. 1.2 Kretslagar 1.2.1 Beräknar spänningarna U 1 och
1 Grundläggande Ellära 1.1 Elektriska begrepp 1.1.1 Ange för nedanstående figur om de markerade delarna av kretsen är en nod, gren, maska eller slinga. 1.2 Kretslagar 1.2.1 Beräknar spänningarna U 1 och
1.1 Mätning av permittiviteten i vakuum med en skivkondensator
 PERMITTIVITET Inledning Låt oss betrakta en skivkondensator som består av två parallella metalskivor. Då en laddad partikel förflyttas från den ena till den andra skivan får skivorna laddningen +Q och
PERMITTIVITET Inledning Låt oss betrakta en skivkondensator som består av två parallella metalskivor. Då en laddad partikel förflyttas från den ena till den andra skivan får skivorna laddningen +Q och
IF1330 Ellära KK1 LAB1 KK2 LAB2. tentamen
 F330 Ellära F/Ö F/Ö4 F/Ö F/Ö5 F/Ö3 Strömkretslära Mätinstrument Batterier Likströmsnät Tvåpolsatsen KK LAB Mätning av och F/Ö6 F/Ö7 Magnetkrets Kondensator Transienter KK LAB Tvåpol mät och sim F/Ö0 F/Ö9
F330 Ellära F/Ö F/Ö4 F/Ö F/Ö5 F/Ö3 Strömkretslära Mätinstrument Batterier Likströmsnät Tvåpolsatsen KK LAB Mätning av och F/Ö6 F/Ö7 Magnetkrets Kondensator Transienter KK LAB Tvåpol mät och sim F/Ö0 F/Ö9
A156TG Elkrafttekniska beräkningar och elkvalitet. 7,5 högskolepoäng. Lycka till!
 A156TG Elkrafttekniska beräkningar och elkvalitet 7,5 högskolepoäng Provmoment: Skriftlig tentamen Ladokkod: A135TG Tentamen ges för: Energiingenjörsprogrammet Åk3 Tentamenskod: Tentamensdatum: 2018-01-11
A156TG Elkrafttekniska beräkningar och elkvalitet 7,5 högskolepoäng Provmoment: Skriftlig tentamen Ladokkod: A135TG Tentamen ges för: Energiingenjörsprogrammet Åk3 Tentamenskod: Tentamensdatum: 2018-01-11
Magnetostatik och elektromagnetism
 Magnetostatik och elektromagnetism Magnetostatik eskriver hur magneter med konstanta magnetfält, t.ex. permanentmagneter, växelverkar med varandra och med externa magnetfält. Vi känner till följande effekter:
Magnetostatik och elektromagnetism Magnetostatik eskriver hur magneter med konstanta magnetfält, t.ex. permanentmagneter, växelverkar med varandra och med externa magnetfält. Vi känner till följande effekter:
Koppla spänningsproben till spolen.
 LÄRARHANDLEDNING Induktion Materiel: Utförande: Dator med programmet LoggerPro Mätinterfacet LabQuest eller LabPro spänningsprobe spolar (300, 600 och 1200 varv), stavmagnet plaströr och kopparrör (ca
LÄRARHANDLEDNING Induktion Materiel: Utförande: Dator med programmet LoggerPro Mätinterfacet LabQuest eller LabPro spänningsprobe spolar (300, 600 och 1200 varv), stavmagnet plaströr och kopparrör (ca
Laboration - Va xelstro mskretsar
 Laboration - Va xelstro mskretsar 1 Introduktion och redovisning I denna laboration simuleras spänning och ström i enkla växelströmskretsar bestående av komponenter som motstånd, kondensator, och spole.
Laboration - Va xelstro mskretsar 1 Introduktion och redovisning I denna laboration simuleras spänning och ström i enkla växelströmskretsar bestående av komponenter som motstånd, kondensator, och spole.
Strömdelning på stamnätets ledningar
 Strömdelning på stamnätets ledningar Enkel teori och varför luftledning ungefär halva sträckan Överby-Beckomberga är nödvändigt 1 Inledning Teorin bakom strömdelning beskriver varför och hur flödet av
Strömdelning på stamnätets ledningar Enkel teori och varför luftledning ungefär halva sträckan Överby-Beckomberga är nödvändigt 1 Inledning Teorin bakom strömdelning beskriver varför och hur flödet av
Tentamen i Elektronik, ESS010, del 1 den 18 oktober, 2010, kl
 Institutionen för Elektro och informationsteknik, LTH Tentamen i Elektronik, ESS00, del den 8 oktober, 00, kl. 08.00.00 Ansvariga lärare: Anders Karlsson, tel. 40 89, 07 98 (kursexp. 90 0). arje uppgift
Institutionen för Elektro och informationsteknik, LTH Tentamen i Elektronik, ESS00, del den 8 oktober, 00, kl. 08.00.00 Ansvariga lärare: Anders Karlsson, tel. 40 89, 07 98 (kursexp. 90 0). arje uppgift
Extra kursmaterial om. Elektriska Kretsar. Lasse Alfredsson. Linköpings universitet November 2015
 Extra kursmaterial om Elektriska Kretsar asse lfredsson inköpings universitet asse.lfredsson@liu.se November 205 Får kopieras fritt av ith-studenter för användning i kurserna TSDT8 Signaler & System och
Extra kursmaterial om Elektriska Kretsar asse lfredsson inköpings universitet asse.lfredsson@liu.se November 205 Får kopieras fritt av ith-studenter för användning i kurserna TSDT8 Signaler & System och
Vågrörelselära och optik
 Vågrörelselära och optik Kapitel 32 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Vågrörelselära och optik Kapitel 32 1 Vågrörelselära och optik Kurslitteratur: University Physics by Young & Friedman (14th edition) Harmonisk oscillator: Kapitel 14.1 14.4 Mekaniska vågor: Kapitel 15.1
Gemensamt projekt: Matematik, Beräkningsvetenskap, Elektromagnetism. Inledning. Fysikalisk bakgrund
 Gemensamt projekt: Matematik, Beräkningsvetenskap, Elektromagnetism En civilingenjör ska kunna idealisera ett givet verkligt problem, göra en adekvat fysikalisk modell och behandla modellen med matematiska
Gemensamt projekt: Matematik, Beräkningsvetenskap, Elektromagnetism En civilingenjör ska kunna idealisera ett givet verkligt problem, göra en adekvat fysikalisk modell och behandla modellen med matematiska
4:2 Ellära: ström, spänning och energi. Inledning
 4:2 Ellära: ström, spänning och energi. Inledning Det samhälle vi lever i hade inte utvecklats till den höga standard som vi ser nu om inte vi hade lärt oss att utnyttja elektricitet. Därför är det viktigt
4:2 Ellära: ström, spänning och energi. Inledning Det samhälle vi lever i hade inte utvecklats till den höga standard som vi ser nu om inte vi hade lärt oss att utnyttja elektricitet. Därför är det viktigt
Tentamen i ELEKTROMAGNETISM I, för W2 och ES2 (1FA514)
 Uppsala universitet Institutionen för fysik och astronomi Kod: Program: Tentamen i ELEKTROMAGNETISM I, 2016-03-19 för W2 och ES2 (1FA514) Kan även skrivas av studenter på andra program där 1FA514 ingår
Uppsala universitet Institutionen för fysik och astronomi Kod: Program: Tentamen i ELEKTROMAGNETISM I, 2016-03-19 för W2 och ES2 (1FA514) Kan även skrivas av studenter på andra program där 1FA514 ingår
