INNEHÅLL. Inledning...1. Talsystem...2. Logiska funktioner Logiska kretsar i praktiken Elektrostatisk urladdning (ESD)...
|
|
|
- Björn Svensson
- för 9 år sedan
- Visningar:
Transkript
1 INNEHÅLL Inledning... Talsystem...2 Logiska funktioner...2 Logiska kretsar i praktiken...9 Elektrostatisk urladdning (ESD) Introduktion övningsmoduler NOT-grind ND-grind OR-grind Ekvivalenta symboler...27 Grindnät Reaktionstest...3 Fler logiska grindar NND-grind NOR-grind NOR och NND-grindar...34 Kretsar med enbart NND eller NOR-grindar ND och OR med NND-grindar SR låskrets med NOR grindar SR låskrets med NND grindar...39 Kodare / vkodare Kodare / vkodare BCD 7-segmentavkodare...42 Vippor...44 Räknare Räknare (4-räknare) Räknare (6-räknare)...52 Serie och parallellöverföring...53 D/ och /D omvandlare...54 Repetitionsuppgifter...55
2 Om innehållet... Denna läro- arbets- och övningsbok är avsedd för kursen Digitalteknik i Elektronik för gymnasieskolan. Läromedlet är i huvudsak självinstruerande och kräver inga förkunskaper i elektronik. I avsnitt som eleven finner svåra bör dock läraren ge kompletterande undervisning. I boken behandlas först grundläggande talsystem och de logiska funktionerna NOT, ND och OR, åtföljt av ett antal teoriuppgifter. Efter avsnitt som beskriver logiska kretsar i praktiken och faran med elektrostatisk laddning följer ett antal praktiska övningar skrivna för laborationssystemet Modulab. Här ges också exempel på sökning av information och data på INTERNET. Därefter behandlas grindnät och övriga grundläggande grindfunktioner, NND, NOR, XNOR och XOR, blandat med teoriuppgifter och praktiska uppgifter. Eftersom det är vanligt att man bygger upp kretsar med enbart NND eller NOR grindar behandlas detta med både teori och praktik, där även SR låskretsar byggs upp med med denna teknik. Vi beskriver enkelt hur kodare och avkodare omvandlar decimalt/binärt och binärt/decimalt både teoretiskt och praktiskt. Vippor/räknare utgör ett stort kapitel som i teori och praktik på ett enkelt sätt visar utveckling från SR vippan till JK vippan och slutligen räknare med JK vippor. Boken avslutas med avsnitt som behandlar principer för serie och parallell dataöverföring samt analog till digital (/D) och digital till analog (D/) omvandling. Fyren indikerar huvudavsnitt med upplysande text, medan pilen förtydligar underrubriker. Handen med pennan påminner om ifyllnadsuppgifter. Uppgifter där miniräknare skall användas markeras med en miniräknare och en dator illustrerar internetuppgifter. De praktiska övningarna är skrivna för laborationssystemet Modulab, men kan också kopplas upp på valfritt laborationsdäck. Modulab säljs av: MODUL i Linköping B Lispundgatan LINKÖPING Tel/Fax: paul.hall@telia.com ll kopiering av delar eller hela boken förbjuds. Roger ndersson, Jerry Grahn, Per-Ola Johansson, OraSoft HB 22 ISBN nummer
3 Talsystem Decimala talsystemet Det decimala talsystemet är det system vi dagligen använder och är vana vid. Därför tänker vi vanligtvis inte på att detta är ett positionssystem där siffrans position (placering) i talet bestämmer dess värde (vikt). Normalt skriver man decimala tal utan index exempelvis 237. Man förutsätter att det är ett decimalt tal. När man arbetar med olika talsystem måste man dock ange vilket system man menar. Det decimala talet bör då skrivas 237. Basen i alla positionssystem är lika med antalet siffror i talsystemet. Det decimala talsystemet har tio siffror,,2,3,4,5,6,7,8 och 9. Basen är således. I det decimala talsystemet - liksom i andra talsystem - multiplicerar man siffran i respektive position med positionens vikt. Siffran längst till höger är minst betydelsefull (position ) och den längst till vänster mest betydelsefull. Vikten i en viss position är alltid basen upphöjt i positionsnummer. Till exempel är vikten i position alltid. ntalet fingrar är förmodligen anledningen till att vi valt decimalsystemet. Decimala positionssystemet Basen. Siffrorna,, 2, 3, 4, 5, 6, 7, 8 och 9. Tabellen nedan visar att de tre tvåorna i det decimala talet 222 ger olika värden beroende på siffrans placering (position) i talet. Position 2 2 Positionsvikt = = = Decimalt tal Siffra * vikt 2 * 2 * 2 * Summa: = 222 Basen upphöjt till är alltid oavsett vilket värde basen har ( =, 2 =, 8 =, 6 =) I det decimala talet 2356 kallas siffran (2) längst till vänster MSD (Most Significant Digit), på svenska mest betydelsefulla siffra. Siffran längst till höger (6) kallas LSD ( Least Significant Digit), på svenska minst betydelsefulla siffra.
4 Logiska funktioner Engelsmannen George Boole beskrev redan 854 matematiska teorier för logik och sannolikhet. Det var lagar för korrekt logiskt tänkande där varje påstående kunde vara antingen sant eller falskt. Den Booleska algebran föll i glömska, men på 93 talet upptäcktes att Booles teorier gick att tillämpa tekniskt i kontakt- och relänät. Eftersom den Booleska algebran bygger på principen att ett påstående är falskt eller sant passar det exakt till de elektriska kretsarnas tillstånd TILL / FRÅN. I och med transistorernas och senare de integrerade kretsarnas (IC kretsar) tillkomst kunde Boolesk algebra tillämpas i nya digitala system som t.ex telekommunikationssystem, digitala mätinstrument, videospel, kalkylatorer och datorer. Det gemensamma för alla dessa system är de så kallade grindarna. Dessa följer de elementära lagar som Boole en gång angav i sin algebra. I varje grind fattas beslut av typen sant eller falskt. Grindarna har gjort den logiska algebran praktiskt användbar. En GRIND (GTE) är en krets som kan utföra logiska operationer. De grundläggande logiska funktionerna är NOT, ND och OR. Grinden har ett antal ingångar men endast en utgång. Ingångarna brukar man beteckna med, B, C osv. och utgången med. Beroende på om ingångsvärdena är sanna eller falska fattar grinden ett logiskt beslut och resultatet presenteras på utgången. För att kunna beskriva en grinds funktion matematiskt och utföra beräkningar med Boolesk algebra låter man det binära talsystemets etta symbolisera sanna påståenden och nolla falska påståenden. Sant =. Falskt =. NOT grind (ICKE eller INVERS) Grinden har bara en ingång. NOT-grinden inverterar alltid insignalen. D.v.s om insignalen är en etta så blir utsignalen en nolla och omvänt. Nedan visas en elektrisk krets med NOT funktion IEC symbol *) + - Brytaren opåverkad () - lampan tänd. Brytaren påverkad () - lampan släckt. merikansk En ring i grindsymbolerna betyder att signalen inverteras. Ringen på NOT symbolens utgång illustrerar att inverteringen sker just där. = *) International Electrotechnical Commission (IEC) Internationella Elektrotekniska Kommissionen är en organisation som handlägger standardisering inom elektroteknikområdet. Svensk kommitté för IEC är Svenska Elektriska Kommissionen (SEK), som överför de internationella resultaten till svenska normer. Trots detta regelverk ritas symbolerna olika och beteckningen IEC är i detta fall svensk standard.
5 Logiska kretsar i praktiken En digital grind kan som tidigare visats kopplas upp med hjälp av dioder och transistorer. Vanligare är att man bygger in fl era grindar i samma hölje och får då så kallade integrerade kretsar (IC kretsar). Bilden visar IC kretsen SN74LS8, som innehåller fyra ND grindar, kopplade enligt figuren. Vcc 4 4B 4Y 3 3B 3Y B Y 2 2B 2Y GND Den engelska beteckningen för IC kretsen är uad 2-input ND gate vilket kan översättas till 4 stycken 2-ingångars ND grind. Man ser också att utgångarna kallas Y, vi använder för utgångar. Vcc och GND är anslutning för spänningsmatningen till kretsen, där GND är minusanslutningen (jord). Standardlogikkretsar indelas i två huvudgrupper, bipolära och CMOS kretsar. De vanligaste bipolära kretsarna är TTL (Transistor Transistor Logik). De har ofta en beteckning som börjar med SN74. TTL kretsar har matningsspänningen 5 volt. 748 I beteckning SN74LS32 betyder SN Semiconductor Network 74 Temperaturområde (74 Standard C - +7C) (54 Militär -55C - +25C) LS Speciella egenskaper (se nedan) 32 Funktion (OR) 4 Denna benkonfiguration kallas DUL IN LINE och är den vanligaste. 7 Kretsen märks så att man kan se tillverkningsår/månad. Dessutom finns någon form av markering för att man skall kunna identifiera benens numrering. Med markeringen till vänster blir numreringen enligt figuren. Tillverkad 996, vecka SN74S2 Exempel på speciella egenskaper Pricken markerar pin- 7 SN 742 H SN 742 L SN 742 S SN 742 LS SN 742S SN 742LS SN 742 F High Speed, snabb, hög effektförbrukning Low Power, långsam, låg effektförbrukning Schottky, snabb, hög effektförbrukning Schottky, extra snabb, låg effektförbrukning Schottky dvanced, hög effektförbrukning Schottky dvanced, låg effektförbrukning Fast (snabb), 22 mw/grind mw/grind 2 mw/grind 2 mw/grind 22 mw/grind mw/grind 4 mw/grind Förkortningar : L=Low power, S=Schottky, H=High speed, =dvanced, F=Fast Beroende på antalet funktioner har kretsen olika förkortningar : SSI MSI LSI VLSI VV- Small Scale Integration funktioner Medium Scale Integation > funktioner Large Scale Integration > funktioner Very Large Scale Integration > funktioner Very Very Scale Integration > funktioner
6 ÖVNING 3 Grundläggande logiska funktioner ND grind Vcc 4 4B 4Y 3 3B 3Y IC kretsen 748 innehåller 4 st ND grindar. Kretsschema: +5V B 2 3 F Övning 3. Rita förbindningsschema, följ det i schemat angivna beteckningarna och pin numreringarna. IC-D D C B F E D C B U +5V U U 748 Drivsteg IC-D6 F E D C B Övning 3.2 Montera modulerna på kopplingsbordet, gör en uppkoppling och testa. Vänd IC kretsen rätt i kapseln. Komplettera sanningstabellen och signaldiagrammet samt ange logiskt uttryck för kretsen. Sanningstabell B B Signaldiagram Logiskt uttryck = OBS! Behåll uppkopplingen för nästa övning!
7 Kretsar med enbart NND eller NOR grindar ND-OR-INVERS logik med NND grindar Vid närmare studier kan man se att man enbart med NND grindar kan konstruera ND-OR och INVERS funktioner. Nackdelen är att det åtgår fl era grindar. NND grind som NOT funktion Om man kopplar samman ingångarna på NND grinden kommer den att fungera som en NOTgrind (INVERTERRE). = * = NND grindar som ND funktion Om man kopplar en inversfunktionen från föregående exempel till en NND grinds utgång erhålls en ND funktion på -utgången. = *B. B *B = *B = *B NND grindar som OR funktion Dubbla inverteringar tar ut varandra. Genom att invertera ingångarna till en NND grind med hjälp av NND grindar i INVERS koppling får man på utgången en OR funktion. Enligt de Morgans teorem gäller följande regler om vill invertera ett helt uttryck :. lla variabler inverteras 2. lla + byts mot * och * byts mot +. I detta fall ( * B) innebär det att i uttrycket * B skall alla variabler inverteras = * B och * byts mot +. Detta ger + B, vilket motsvarar OR funktionen. B B = *B +B Dessa räknelagar är utvecklade av den engelske matematikern de Morgan och kallas därför de Morgans teorem. v ovanstående följer att om ett logiskt problem går att lösa med ND, OR eller INVERS grindar, så kan samma logiska problem också lösas, enbart med hjälp av samma typ av grindar = NND grindar. ND-OR-INVERS logik med NOR grindar På motsvarande sätt kan man också med enbart NOR grindar konstruera ND-OR och INVERS funktioner. Nackdelen även här är att det åtgår fl era grindar. NOR grind som NOT funktion Om man kopplar samman ingångarna på NOR grinden kommer den att fungera som en NOTgrind (INVERTERRE). > = + =
8 Logiska kretsar ÖVNING SR-låskrets (latch) med NOR-grindar Låskretsen (latchen) är en variant av den så kallade bistabila vippan. Bistabila vippor behandlas utförligare längre fram i boken. SR-låskretsen finns att få som färdig krets, men i denna övning skall vi bygga upp den med hjälp av NOR-grindar. Kretsen har två ingångar S (set) och R (reset). S och R kommer från det engelskans set (sätta) och reset (återställa). Utgången har två stabila lägen, ett eller noll. En etta på S ettställer utgången. En etta på R nollställer utgången. I kretsschemat ser man att utsignalerna återkopplas till grindarnas ingångar, denna återkoppling gör att kretsen minns det tidigare tillståndet. Kretsen innehåller en minnesfunktion. 742 S > Symbol S R R > Övning. Rita in förbindningar enligt ovanstående schema. Skriv in pin nummer och beteckningar för omkopplare och lysdioder. Låt lysdiod indikera utgång och lysdiod B utgång -invers. + > Övning.2 > Gör en uppkoppling efter förbindningsschemat. Undersök sedan hur låskretsen fungerar om du ger insignaler i den turordning som visas i funktionstabellen. Du behöver bara ge korta spänningspulser till S och R ingångarna för att låskretsen skall vippa om. Enligt tidigare skall ju utgångarna vara varandras inverser dvs. om = så är -invers =. Om båda ingångarna S och R är kommer de båda utgångarna och -invers att bli. För låskretsen är detta en otillåten kombination, eftersom den ger en felfunktion. Starta undersökningen med S,R och =. Funktionstabell S R
9 Vippor Vippan är en elektronisk koppling där utgången kan anta två lägen. ntingen logisk eller logisk. stabil vippa (stable multivibrator) har som namnet anger inget stabilt läge utan utgången växlar alltid mellan och. Vippan används för att generera klockpulser. Monostabil vippa (Monostable multivibrator) har ett stabilt läge där utgången antingen är eller. Bistabil vippa (Bistable multivibrator) har två stabila lägen och. SR vippa Den bistabila vippan användes i digitala kopplingar som låskrets (latch) och kallas då SR låskrets eller SR vippa. S:et är en förkortning för SET d.v.s ettställ vippans utgång och R står för RESET, nollställ vippans utgång. (Se Övning 2) Symbol Signaldiagram Funktionstabell S R S R S R X X T T Då SR = sker ingen ändring på utgångarna och invers. (behåller sina tidigare värden Tidigare ) Då SR =, noll-ställs utgången. (Reset) Då SR =, ett-ställs utgången. (Set) SR = är en otillåten kombination som ej får förekomma. Klockad (grindad) SR vippa I de fl esta sammanhang använder man en puls för att verkställa (trigga) ett- respektive nollställningen av SR vippans utgång. Denna verkställande puls kallas klockpuls och har många förkortningar exempelvis Cp, G (grindpuls) eller C. ntag SR =. Den första klockpulsen ettställer då vippans utgång. Om SR ändras till, behåller utgången sitt värde, oavsett klockpulser. För att nollställa vippans utgång krävs en klockpuls efter att resetingången får d.v.s SR =. Den klockade SR vippan påverkas endast under den tid då klockpulsen (C) är etta och C kallas därför verkställande ingång. S och R ingångarna är underställda C och kallas förberedande ingångar. Symbol Klockad SR vippa Signaldiagram S C R Cp S R
10 Denna läro-, arbets- och övningsbok är avsedd för kursen Digitalteknik i Elektronik för gymnasieskolan. (ISBN ) Läromedlet är i huvudsak självinstruerande och kräver inga förkunskaper i elektronik. I avsnitt som eleven finner svåra bör dock läraren ge kompletterande undervisning. I boken behandlas först grundläggande talsystem och de logiska funktionerna NOT, ND och OR, åtföljt av ett antal teoriuppgifter. Efter avsnitt som beskriver logiska kretsar i praktiken och faran med elektrostatisk laddning följer ett antal praktiska övningar skrivna för laborationssystemet Modulab. Här ges också exempel på sökning av information och data med hjälp av INTERNET. Därefter behandlas grindnät och övriga grundläggande grindfunktioner, NND, NOR, XNOR och XOR, blandat med teoriuppgifter och praktiska uppgifter. Eftersom det är vanligt att man bygger upp kretsar med enbart NND eller NOR grindar behandlas detta med både teori och praktik, där även SR låskretsar byggs upp med med denna teknik. Vi beskriver enkelt hur kodare och avkodare omvandlar decimalt/binärt och binärt/ decimalt både teoretiskt och praktiskt. Vippor/räknare utgör ett stort kapitel som i teori och praktik på ett enkelt sätt visar utveckling från SR vippan till JK vippan och slutligen räknare med JK vippor. Boken avslutas med avsnitt som behandlar principer för seriell och parallell dataöverföring samt analog till digital (/D) och digital till analog (D/) omvandling. Övriga läroböcker: Läromedelspaketet Ellära och B (ISBN ) innehåller fakta- arbetsbok och laborationer samt en laborationsenhet för alla laborationer. Laborationerna kan också utföras i Electronics Workbench. Till läromedelspaketet hör också ett häftat Kunskapstest med över 2 uppgifter. Förfrågningar ring: OraSoft HB rmévägen BODEN E-post: orasoft@telia.com jerry.grahn@jerryg.se perola.johansson@lulea.riksnet.se
F5 Introduktion till digitalteknik
 Exklusiv eller XOR F5 Introduktion till digitalteknik EDAA05 Roger Henriksson Jonas Wisbrant På övning 2 stötte ni på uttrycket x = (a b) ( a b) som kan utläsas antingen a eller b, men inte både a och
Exklusiv eller XOR F5 Introduktion till digitalteknik EDAA05 Roger Henriksson Jonas Wisbrant På övning 2 stötte ni på uttrycket x = (a b) ( a b) som kan utläsas antingen a eller b, men inte både a och
Laboration D181. ELEKTRONIK Digitalteknik. Kombinatoriska kretsar, HCMOS. 2008-01-24 v 2.1
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Christer Ardlin/Lars Wållberg/ Dan Weinehall/Håkan Joëlson 2008-01-24 v 2.1 ELEKTRONIK Digitalteknik Laboration D181 Kombinatoriska kretsar,
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Christer Ardlin/Lars Wållberg/ Dan Weinehall/Håkan Joëlson 2008-01-24 v 2.1 ELEKTRONIK Digitalteknik Laboration D181 Kombinatoriska kretsar,
F5 Introduktion till digitalteknik
 George Boole och paraplyet F5 Introduktion till digitalteknik EDAA05 Roger Henriksson Jonas Wisbrant p = b! (s " r) George Boole (1815-1864) Professor i Matematik, Queens College, Cork, Irland 2 Exklusiv
George Boole och paraplyet F5 Introduktion till digitalteknik EDAA05 Roger Henriksson Jonas Wisbrant p = b! (s " r) George Boole (1815-1864) Professor i Matematik, Queens College, Cork, Irland 2 Exklusiv
5:2 Digitalteknik Boolesk algebra. Inledning OCH-funktionen
 5:2 Digitalteknik Boolesk algebra. Inledning I en dator representeras det binära talsystemet med signaler i form av elektriska spänningar. 0 = 0 V (låg spänning), 1 = 5 V(hög spänning). Datorn kombinerar
5:2 Digitalteknik Boolesk algebra. Inledning I en dator representeras det binära talsystemet med signaler i form av elektriska spänningar. 0 = 0 V (låg spänning), 1 = 5 V(hög spänning). Datorn kombinerar
Laboration i digitalteknik Introduktion till digitalteknik
 Linköpings universitet Institutionen för systemteknik Laborationer i digitalteknik Datorteknik 6 Laboration i digitalteknik Introduktion till digitalteknik TSEA Digitalteknik D TSEA5 Digitalteknik Y TDDC75
Linköpings universitet Institutionen för systemteknik Laborationer i digitalteknik Datorteknik 6 Laboration i digitalteknik Introduktion till digitalteknik TSEA Digitalteknik D TSEA5 Digitalteknik Y TDDC75
T1-modulen Lektionerna 10-12. Radioamatörkurs OH6AG - 2011 OH6AG. Bearbetning och översättning: Thomas Anderssén, OH6NT Heikki Lahtivirta, OH2LH
 T1-modulen Lektionerna 10-12 Radioamatörkurs OH6AG - 2011 Bearbetning och översättning: Thomas Anderssén, OH6NT Original: Heikki Lahtivirta, OH2LH 1 Logikkretsar Logikkretsarna är digitala mikrokretsar.
T1-modulen Lektionerna 10-12 Radioamatörkurs OH6AG - 2011 Bearbetning och översättning: Thomas Anderssén, OH6NT Original: Heikki Lahtivirta, OH2LH 1 Logikkretsar Logikkretsarna är digitala mikrokretsar.
DIGITALTEKNIK I. Laboration DE2. Sekvensnät och sekvenskretsar
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Håkan Joëlson, John Berge 203 DIGITALTEKNIK I Laboration DE2 Sekvensnät och sekvenskretsar Namn... Personnummer... Epost-adress... Datum för
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Håkan Joëlson, John Berge 203 DIGITALTEKNIK I Laboration DE2 Sekvensnät och sekvenskretsar Namn... Personnummer... Epost-adress... Datum för
Digital Design IE1204
 Digital Design IE24 F2 : Logiska Grindar och Kretsar, Boolesk Algebra william@kth.se IE24 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska
Digital Design IE24 F2 : Logiska Grindar och Kretsar, Boolesk Algebra william@kth.se IE24 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska
Digital elektronik CL0090
 Digital elektronik CL0090 Föreläsning 2 2007-0-25 08.5 2.00 Naos De logiska unktionerna implementeras i grindar. Här visas de vanligaste. Svenska IEC standard SS IEC 87-2 Amerikanska ANSI/IEEE Std.9.984
Digital elektronik CL0090 Föreläsning 2 2007-0-25 08.5 2.00 Naos De logiska unktionerna implementeras i grindar. Här visas de vanligaste. Svenska IEC standard SS IEC 87-2 Amerikanska ANSI/IEEE Std.9.984
DIGITALA TAL OCH BOOLESK ALGEBRA
 DIGITALA TAL OCH BOOLESK ALGEBRA Innehåll Talsystem och koder Aritmetik för inära tal Grundläggande logiska operationer Logiska grindar Definitioner i Boolesk algera Räknelagar BINÄRA TALSYSTEMET Binärt
DIGITALA TAL OCH BOOLESK ALGEBRA Innehåll Talsystem och koder Aritmetik för inära tal Grundläggande logiska operationer Logiska grindar Definitioner i Boolesk algera Räknelagar BINÄRA TALSYSTEMET Binärt
Moment 2 - Digital elektronik. Föreläsning 1 Binära tal och logiska grindar
 Moment 2 - Digital elektronik Föreläsning 1 Binära tal och logiska grindar Jan Thim 1 F1: Binära tal och logiska grindar Innehåll: Introduktion Talsystem och koder Räkna binärt Logiska grindar Boolesk
Moment 2 - Digital elektronik Föreläsning 1 Binära tal och logiska grindar Jan Thim 1 F1: Binära tal och logiska grindar Innehåll: Introduktion Talsystem och koder Räkna binärt Logiska grindar Boolesk
D0013E Introduktion till Digitalteknik
 D0013E Introduktion till Digitalteknik Slides : Per Lindgren EISLAB per.lindgren@ltu.se Ursprungliga slides : Ingo Sander KTH/ICT/ES ingo@kth.se Vem är Per Lindgren? Professor Inbyggda System Från Älvsbyn
D0013E Introduktion till Digitalteknik Slides : Per Lindgren EISLAB per.lindgren@ltu.se Ursprungliga slides : Ingo Sander KTH/ICT/ES ingo@kth.se Vem är Per Lindgren? Professor Inbyggda System Från Älvsbyn
Digital elektronik CL0090
 Digital elektronik CL9 Föreläsning 3 27--29 8.5 2. My Talsystem Binära tal har basen 2 Exempel Det decimala talet 9 motsvarar 2 Den första ettan är MSB, Most Significant Bit, den andra ettan är LSB Least
Digital elektronik CL9 Föreläsning 3 27--29 8.5 2. My Talsystem Binära tal har basen 2 Exempel Det decimala talet 9 motsvarar 2 Den första ettan är MSB, Most Significant Bit, den andra ettan är LSB Least
Du har följande material: 1 Kopplingsdäck 2 LM339 4 komparatorer i vardera kapsel. ( ELFA art.nr datablad finns )
 Projektuppgift Digital elektronik CEL08 Syfte: Det här lilla projektet har som syfte att visa hur man kan konverterar en analog signal till en digital. Här visas endast en metod, flash-omvandlare. Uppgift:
Projektuppgift Digital elektronik CEL08 Syfte: Det här lilla projektet har som syfte att visa hur man kan konverterar en analog signal till en digital. Här visas endast en metod, flash-omvandlare. Uppgift:
Styrteknik: Grundläggande logiska funktioner D2:1
 Styrteknik: Grundläggande logiska funktioner D2:1 Digitala kursmoment D1 Boolesk algebra D2 Grundläggande logiska funktioner D3 Binära tal, talsystem och koder Styrteknik: Grundläggande logiska funktioner
Styrteknik: Grundläggande logiska funktioner D2:1 Digitala kursmoment D1 Boolesk algebra D2 Grundläggande logiska funktioner D3 Binära tal, talsystem och koder Styrteknik: Grundläggande logiska funktioner
Översikt, kursinnehåll
 Översikt, kursinnehåll Specifikation av digitala funktioner och system Digitala byggelement Kombinatoriska system Digital Aritmetik Synkrona system och tillståndsmaskiner Asynkrona system och tillståndsmaskiner
Översikt, kursinnehåll Specifikation av digitala funktioner och system Digitala byggelement Kombinatoriska system Digital Aritmetik Synkrona system och tillståndsmaskiner Asynkrona system och tillståndsmaskiner
Kombinationskretsar. Föreläsning 4 Digitalteknik Mattias Krysander Institutionen för systemteknik
 Kombinationskretsar Föreläsning 4 Digitalteknik Mattias Krysander Institutionen för systemteknik Dagens föreläsning Laboration 1 Adderare Konstruktion med minne 3 Laborationsinformation TSEA51/52: Deadline
Kombinationskretsar Föreläsning 4 Digitalteknik Mattias Krysander Institutionen för systemteknik Dagens föreläsning Laboration 1 Adderare Konstruktion med minne 3 Laborationsinformation TSEA51/52: Deadline
Digital elektronik CL0090
 Digital elektronik CL9 Föreläsning 5 27-2-2 8.5 2. Naxos Demonstration av uartus programvara. Genomgång av uartus flödesschema. Detta dokument finns på kurshemsidan. http://www.idt.mdh.se/kurser/cl9/ VHDL-kod
Digital elektronik CL9 Föreläsning 5 27-2-2 8.5 2. Naxos Demonstration av uartus programvara. Genomgång av uartus flödesschema. Detta dokument finns på kurshemsidan. http://www.idt.mdh.se/kurser/cl9/ VHDL-kod
Minneselement,. Styrteknik grundkurs. Digitala kursmoment. SR-latch med logiska grindar. Funktionstabell för SR-latchen R S Q Q ?
 Styrteknik grundkurs Digitala kursmoment Binära tal, talsystem och koder Boolesk Algebra Grundläggande logiska grindar Minneselement, register, enkla räknare Analog/digital omvandling SR-latch med logiska
Styrteknik grundkurs Digitala kursmoment Binära tal, talsystem och koder Boolesk Algebra Grundläggande logiska grindar Minneselement, register, enkla räknare Analog/digital omvandling SR-latch med logiska
Laboration D151. Kombinatoriska kretsar, HCMOS. Namn: Datum: Epostadr: Kurs:
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Christer Ardlin/Lars Wållberg/ Håkan Joëlson 2000-01-28 v 2.3 ELEKTRONIK Digitalteknik Laboration D151 Kombinatoriska kretsar, HCMOS Namn:
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Christer Ardlin/Lars Wållberg/ Håkan Joëlson 2000-01-28 v 2.3 ELEKTRONIK Digitalteknik Laboration D151 Kombinatoriska kretsar, HCMOS Namn:
Introduktion till logik
 Introduktion till logik Av Johan Johansson Johan.johansson@guldstadsgymnasiet.se Logik sägs som många andra saker komma från de grekiska filosoferna, och ordet kommer också därifrån. Grekerna kallade det
Introduktion till logik Av Johan Johansson Johan.johansson@guldstadsgymnasiet.se Logik sägs som många andra saker komma från de grekiska filosoferna, och ordet kommer också därifrån. Grekerna kallade det
Sanningstabell. En logisk funktion kan också beskrivas genom en sanningstabell (truth table) 1 står för sann (true) 0 står för falsk (false)
 Sanningstabell En logisk funktion kan också beskrivas genom en sanningstabell (truth table) 1 står för sann (true) 0 står för falsk (false) ND OR Logiska grindar ND-grinden (OCH) IEC Symbol (International
Sanningstabell En logisk funktion kan också beskrivas genom en sanningstabell (truth table) 1 står för sann (true) 0 står för falsk (false) ND OR Logiska grindar ND-grinden (OCH) IEC Symbol (International
2-14 Binära talsystemet-fördjupning Namn:
 2-14 Binära talsystemet-fördjupning Namn: Inledning I detta kapitel skall du få lära dig lite mer om det talsystem som datorerna arbetar med. Du skall lära dig att omvandla decimala tal till binära samt
2-14 Binära talsystemet-fördjupning Namn: Inledning I detta kapitel skall du få lära dig lite mer om det talsystem som datorerna arbetar med. Du skall lära dig att omvandla decimala tal till binära samt
PARITETSKONTROLL. Om generatorn i vidstående exempel avkänner ett jämt antal ettor ger den en nolla ut. Detta innebär att överföringen
 PARITETSKONTROLL Paritetskontroll (likhetskontroll) användes för att kontrollera att dataordet inte förändrats på sin väg via överföringsledningarna, från ett ställe till ett annat. Antag att man vill
PARITETSKONTROLL Paritetskontroll (likhetskontroll) användes för att kontrollera att dataordet inte förändrats på sin väg via överföringsledningarna, från ett ställe till ett annat. Antag att man vill
Grundläggande digitalteknik
 Grundläggande digitalteknik Jan Carlsson Inledning I den verkliga världen vet vi att vi kan få vilka värden som helst när vi mäter på något. En varm sommardag visar termometern kanske 6, 7 C. Men när det
Grundläggande digitalteknik Jan Carlsson Inledning I den verkliga världen vet vi att vi kan få vilka värden som helst när vi mäter på något. En varm sommardag visar termometern kanske 6, 7 C. Men när det
Struktur: Elektroteknik A. Digitalteknik 3p, vt 01. F1: Introduktion. Motivation och målsättning för kurserna i digital elektronik
 Digitalteknik 3p, vt 01 Struktur: Elektroteknik A Kurslitteratur: "A First Course in Digital Systems Design - An Integrated Approach" Antal föreläsningar: 11 (2h) Antal laborationer: 4 (4h) Examinationsform:
Digitalteknik 3p, vt 01 Struktur: Elektroteknik A Kurslitteratur: "A First Course in Digital Systems Design - An Integrated Approach" Antal föreläsningar: 11 (2h) Antal laborationer: 4 (4h) Examinationsform:
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #9 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola ekvensnät Vad kännetecknar ett sekvensnät? I ett sekvensnät
Digital- och datorteknik Föreläsning #9 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola ekvensnät Vad kännetecknar ett sekvensnät? I ett sekvensnät
Ett minneselements egenskaper. F10: Minneselement. Latch. SR-latch. Innehåll:
 F: Minneselement Innehåll: - Latchar - Flip-Flops - egister - Läs- och skrivminne (andom-access Memory AM) - Läsminne (ead Only Memory OM) Ett minneselements egenskaper Generellt sett så kan följande operationer
F: Minneselement Innehåll: - Latchar - Flip-Flops - egister - Läs- och skrivminne (andom-access Memory AM) - Läsminne (ead Only Memory OM) Ett minneselements egenskaper Generellt sett så kan följande operationer
Lösningförslag till Exempel på tentamensfrågor Digitalteknik I.
 Lösningförslag till Exempel på tentamensfrågor Digitalteknik I.. Uttryckt i decimal form: A=28+32+8 + 2 =70 B=59 C=7 A+B+C=246 2. Jag låter A' betyda "icke A" A'B'C'D'+ABC'D'+A'BCD'+AB'CD'=D'(A'(B'C'+BC)+A(BC'+B'C))=
Lösningförslag till Exempel på tentamensfrågor Digitalteknik I.. Uttryckt i decimal form: A=28+32+8 + 2 =70 B=59 C=7 A+B+C=246 2. Jag låter A' betyda "icke A" A'B'C'D'+ABC'D'+A'BCD'+AB'CD'=D'(A'(B'C'+BC)+A(BC'+B'C))=
Introduktion till digitalteknik
 Inledning Introduktion till digitalteknik Stefan Gustavson 997, lätt uppdaterat 2004-09-06 Digitalteknik är grunden till alla moderna datorer. I datorernas barndom förekom visserligen så kallade analogimaskiner,
Inledning Introduktion till digitalteknik Stefan Gustavson 997, lätt uppdaterat 2004-09-06 Digitalteknik är grunden till alla moderna datorer. I datorernas barndom förekom visserligen så kallade analogimaskiner,
Digitalteknik. Talsystem Grindlogik Koder Booles algebra Tillämpningar Karnaughdiagram. A.Lövdahl
 Digitalteknik Talsystem Grindlogik Koder ooles algebra Tillämpningar Karnaughdiagram.Lövdahl 1001001100101100000001011010010 TLSYSTEM Talsystem är en angivelse på en viss position. De vanligaste talsystemen
Digitalteknik Talsystem Grindlogik Koder ooles algebra Tillämpningar Karnaughdiagram.Lövdahl 1001001100101100000001011010010 TLSYSTEM Talsystem är en angivelse på en viss position. De vanligaste talsystemen
Hambley avsnitt 12.7 (7.3 för den som vill läsa lite mer om grindar) sann 1 falsk 0
 1 Föreläsning 2 ht2 Hambley avsnitt 12.7 (7.3 för den som vill läsa lite mer om grindar) Lite om logiska operationer Logiska variabler är storheter som kan anta två värden; sann 1 falsk 0 De logiska variabler
1 Föreläsning 2 ht2 Hambley avsnitt 12.7 (7.3 för den som vill läsa lite mer om grindar) Lite om logiska operationer Logiska variabler är storheter som kan anta två värden; sann 1 falsk 0 De logiska variabler
Tentamen i IE1204/5 Digital Design onsdagen den 5/
 Tentamen i IE1204/5 Digital Design onsdagen den 5/6 2013 9.00-13.00 Tentamensfrågor med lösningsförslag Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista
Tentamen i IE1204/5 Digital Design onsdagen den 5/6 2013 9.00-13.00 Tentamensfrågor med lösningsförslag Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista
DIGITALTEKNIK I. Laboration DE1. Kombinatoriska nät och kretsar
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Björne Lindberg/Håkan Joëlson John Berge 2013 DIGITALTEKNIK I Laboration DE1 Kombinatoriska nät och kretsar Namn... Personnummer... Epost-adress...
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Björne Lindberg/Håkan Joëlson John Berge 2013 DIGITALTEKNIK I Laboration DE1 Kombinatoriska nät och kretsar Namn... Personnummer... Epost-adress...
Tentamen i Grundläggande ellära och digitalteknik ETA 013 för D
 Lars-Erik ederlöf Tentamen i Grundläggande ellära och digitalteknik ET 03 för D 000-03-3 Tentamen omfattar 40 poäng, poäng för varje uppgift. 0 poäng ger godkänd tentamen. Tillåtet hjälpmedel är räknedosa.
Lars-Erik ederlöf Tentamen i Grundläggande ellära och digitalteknik ET 03 för D 000-03-3 Tentamen omfattar 40 poäng, poäng för varje uppgift. 0 poäng ger godkänd tentamen. Tillåtet hjälpmedel är räknedosa.
Föreläsning 4/11. Lite om logiska operationer. Hambley avsnitt 12.7, 14.1 (7.3 för den som vill läsa lite mer om grindar)
 1 Föreläsning 4/11 Hambley avsnitt 12.7, 14.1 (7.3 för den som vill läsa lite mer om grindar) Lite om logiska operationer Logiska variabler är storheter som kan anta två värden; sann 1 falsk 0 De logiska
1 Föreläsning 4/11 Hambley avsnitt 12.7, 14.1 (7.3 för den som vill läsa lite mer om grindar) Lite om logiska operationer Logiska variabler är storheter som kan anta två värden; sann 1 falsk 0 De logiska
Exempel på tentamensfrågor Digitalteknik
 Exempel på tentamensfrågor Digitalteknik Till dessa frågor (som kommer från lite olika tidgare tentor) gällde förutsättningen: Hjälpmedel: Kurslitteratur, föreläsningsantecknigar lab. med mätresultat,
Exempel på tentamensfrågor Digitalteknik Till dessa frågor (som kommer från lite olika tidgare tentor) gällde förutsättningen: Hjälpmedel: Kurslitteratur, föreläsningsantecknigar lab. med mätresultat,
SMD033 Digitalteknik. Digitalteknik F1 bild 1
 SMD033 Digitalteknik Digitalteknik F1 bild 1 Vi som undervisar Anders Hansson A3209 91 230 aha@sm.luth.se Digitalteknik F1 bild 2 Registrering Registrering via email till diglabs@luth.se Digitalteknik
SMD033 Digitalteknik Digitalteknik F1 bild 1 Vi som undervisar Anders Hansson A3209 91 230 aha@sm.luth.se Digitalteknik F1 bild 2 Registrering Registrering via email till diglabs@luth.se Digitalteknik
IE1205 Digital Design. F2 : Logiska Grindar och Kretsar, Boolesk Algebra. Fredrik Jonsson KTH/ICT/ES
 IE1205 Digital Design F2 : Logiska Grindar och Kretsar, oolesk Algebra Fredrik Jonsson KTH/ICT/ES fjon@kth.se Switch En switch har två lägen Sluten/Till (Closed/On) Öppen/Från (Open/Off) Sluten Öppen x
IE1205 Digital Design F2 : Logiska Grindar och Kretsar, oolesk Algebra Fredrik Jonsson KTH/ICT/ES fjon@kth.se Switch En switch har två lägen Sluten/Till (Closed/On) Öppen/Från (Open/Off) Sluten Öppen x
Switch. En switch har två lägen. Sluten/Till (Closed/On) Öppen/Från (Open/Off) Sluten. Öppen. Symbol. William Sandqvist
 Switch En switch har två lägen Sluten/Till (Closed/On) Öppen/Från (Open/Off) Sluten Öppen = = Symbol S Implementering av logiska funktioner Switchen kan användas för att implentera logiska funktioner Power
Switch En switch har två lägen Sluten/Till (Closed/On) Öppen/Från (Open/Off) Sluten Öppen = = Symbol S Implementering av logiska funktioner Switchen kan användas för att implentera logiska funktioner Power
Digitala system EDI610 Elektro- och informationsteknik
 Digitala system EDI610 Elektro- och informationsteknik Digitala System EDI610 Aktiv under hela första året, höst- och vår-termin Poäng 15.0 Godkännande; U,3,4,5 Under hösten i huvudsak Digitalteknik Under
Digitala system EDI610 Elektro- och informationsteknik Digitala System EDI610 Aktiv under hela första året, höst- och vår-termin Poäng 15.0 Godkännande; U,3,4,5 Under hösten i huvudsak Digitalteknik Under
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #3 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Logikgrindar Från data till digitala byggblock: Kursens
Digital- och datorteknik Föreläsning #3 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Logikgrindar Från data till digitala byggblock: Kursens
Låskretsar och Vippor
 Låskretsar och Vippor Låskretsar (latch) och vippor (flip-flop) är kretsar med minnesfunktion. De ingår i datorns minnen och i processorns register. SR-låskretsen är i princip datorns minnescell Q=1 Q=0
Låskretsar och Vippor Låskretsar (latch) och vippor (flip-flop) är kretsar med minnesfunktion. De ingår i datorns minnen och i processorns register. SR-låskretsen är i princip datorns minnescell Q=1 Q=0
Hur implementera algoritmerna på maskinnivå - datorns byggstenar
 Hur implementera algoritmerna på maskinnivå - datorns byggstenar Binära tal Boolesk logik grindar och kretsar A A extern representation intern representation minnet i datorn extern representation 1000001
Hur implementera algoritmerna på maskinnivå - datorns byggstenar Binära tal Boolesk logik grindar och kretsar A A extern representation intern representation minnet i datorn extern representation 1000001
Tentamen med lösningar i IE1204/5 Digital Design Måndag 27/
 Tentamen med lösningar i IE04/5 Digital Design Måndag 7/0 04 9.00-3.00 Allmän information Examinator: Ingo Sander. Ansvarig lärare: Elena Dubrova /William Sandvist, tel 08-7904487 Tentamensuppgifterna
Tentamen med lösningar i IE04/5 Digital Design Måndag 7/0 04 9.00-3.00 Allmän information Examinator: Ingo Sander. Ansvarig lärare: Elena Dubrova /William Sandvist, tel 08-7904487 Tentamensuppgifterna
Laborationshandledning för mätteknik
 Laborationshandledning för mätteknik - digitalteknik och konstruktion TNE094 LABORATION 2 Laborant: E-post: Kommentarer från lärare: Institutionen för Teknik och Naturvetenskap Campus Norrköping, augusti
Laborationshandledning för mätteknik - digitalteknik och konstruktion TNE094 LABORATION 2 Laborant: E-post: Kommentarer från lärare: Institutionen för Teknik och Naturvetenskap Campus Norrköping, augusti
Tentamen i IE1204/5 Digital Design onsdagen den 5/
 Tentamen i IE1204/5 Digital Design onsdagen den 5/6 2013 9.00-13.00 Allmän information Exaator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista IE1204) Tentamensuppgifterna behöver
Tentamen i IE1204/5 Digital Design onsdagen den 5/6 2013 9.00-13.00 Allmän information Exaator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista IE1204) Tentamensuppgifterna behöver
IE1204 Digital Design
 IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM
IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM
TSEA22 Digitalteknik 2019!
 1(39) 2019 Mattias Krysander Ingemar Ragnemalm 1(39) Föreläsning 5. Sekv1. enna föreläsning: Vippor Sekvensnät Moore och Mealy 2(39)2(39) Förra föreläsningen: Labb 1. Adderare. Carryaccelerator Och ännu
1(39) 2019 Mattias Krysander Ingemar Ragnemalm 1(39) Föreläsning 5. Sekv1. enna föreläsning: Vippor Sekvensnät Moore och Mealy 2(39)2(39) Förra föreläsningen: Labb 1. Adderare. Carryaccelerator Och ännu
Sekvensnät. William Sandqvist
 Sekvensnät Om en och samma insignal kan ge upphov till olika utsignal, är logiknätet ett sekvensnät. Det måste då ha ett inre minne som gör att utsignalen påverkas av både nuvarande och föregående insignaler!
Sekvensnät Om en och samma insignal kan ge upphov till olika utsignal, är logiknätet ett sekvensnät. Det måste då ha ett inre minne som gör att utsignalen påverkas av både nuvarande och föregående insignaler!
Tentamen i Grundläggande ellära och digitalteknik ETA 013 för D
 Lars-Erik ederlöf Per Liljas Tentamen i Grundläggande ellära och digitalteknik ET 03 för D 200-08-20 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet hjälpmedel
Lars-Erik ederlöf Per Liljas Tentamen i Grundläggande ellära och digitalteknik ET 03 för D 200-08-20 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet hjälpmedel
Grundläggande Datorteknik Digital- och datorteknik
 Grundläggande Datorteknik Digital- och datorteknik Kursens mål: Fatta hur en dator är uppbggd (HDW) Fatta hur du du programmerar den (SW) Fatta hur HDW o SW samverkar Digital teknik Dator teknik Grundläggande
Grundläggande Datorteknik Digital- och datorteknik Kursens mål: Fatta hur en dator är uppbggd (HDW) Fatta hur du du programmerar den (SW) Fatta hur HDW o SW samverkar Digital teknik Dator teknik Grundläggande
Försättsblad till skriftlig tentamen vid Linköpings universitet
 Försättsblad till skriftlig tentamen vid Linköpings universitet Datum för tentamen 08-03-3 Sal (5) Tid 8- Kurskod TSEA Provkod TEN Kursnamn/benämning Provnamn/benämning Institution Antal uppgifter som
Försättsblad till skriftlig tentamen vid Linköpings universitet Datum för tentamen 08-03-3 Sal (5) Tid 8- Kurskod TSEA Provkod TEN Kursnamn/benämning Provnamn/benämning Institution Antal uppgifter som
Högskolan i Halmstad Digital- och Mikrodatorteknik 7.5p. Lista på registeruppsättningen i PIC16F877A Datablad TTL-kretsar 74-serien
 DIGITAL- OCH MIKRODATORTEKNIK, U2 09.00 13.00 Tillåtna hjälpmedel: Instruktionslista PIC16F877A Lista på registeruppsättningen i PIC16F877A Datablad TTL-kretsar 74-serien Fullständiga lösningar skall inlämnas.
DIGITAL- OCH MIKRODATORTEKNIK, U2 09.00 13.00 Tillåtna hjälpmedel: Instruktionslista PIC16F877A Lista på registeruppsättningen i PIC16F877A Datablad TTL-kretsar 74-serien Fullständiga lösningar skall inlämnas.
DIGITALTEKNIK. Laboration D161. Kombinatoriska kretsar och nät
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik jörne Lindberg/Håkan Joëlson 2003-09-15 v 2.2 DIGITALTEKNIK Laboration D161 Kombinatoriska kretsar och nät Innehåll Uppgift 1...Grundläggande
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik jörne Lindberg/Håkan Joëlson 2003-09-15 v 2.2 DIGITALTEKNIK Laboration D161 Kombinatoriska kretsar och nät Innehåll Uppgift 1...Grundläggande
Laborationshandledning
 Laborationshandledning Utbildning: ED Ämne: TNE094 Digitalteknik och konstruktion Laborationens nummer och titel: Nr 5 Del A: Schmittrigger Del B: Analys av sekvensnät Laborant: E-mail: Medlaboranters
Laborationshandledning Utbildning: ED Ämne: TNE094 Digitalteknik och konstruktion Laborationens nummer och titel: Nr 5 Del A: Schmittrigger Del B: Analys av sekvensnät Laborant: E-mail: Medlaboranters
Mattias Wiggberg Collaboration
 Informationsteknologi sommarkurs 5p, 24 Mattias Wiggberg Dept. of Information Technology Box 337 SE75 5 Uppsala +46 847 3 76 Collaboration Jakob Carlström Binära tal Slideset 5 Agenda Binära tal Talbaser
Informationsteknologi sommarkurs 5p, 24 Mattias Wiggberg Dept. of Information Technology Box 337 SE75 5 Uppsala +46 847 3 76 Collaboration Jakob Carlström Binära tal Slideset 5 Agenda Binära tal Talbaser
Styrteknik distans: Minneselement, register, räknare, AD-omv D4:1
 Styrteknik distans: Minneselement, register, räknare, AD-omv D4:1 Digitala kursmoment D1 Binära tal, talsystem och koder D2 Boolesk Algebra D3 Grundläggande logiska grindar D4 Minneselement, register,
Styrteknik distans: Minneselement, register, räknare, AD-omv D4:1 Digitala kursmoment D1 Binära tal, talsystem och koder D2 Boolesk Algebra D3 Grundläggande logiska grindar D4 Minneselement, register,
Experiment med schmittrigger
 dlab00a Experiment med schmittrigger Namn Datum Handledarens sign. Varför denna laboration? Schmittriggern är en mycket användbar koppling inom såväl analog- som digitaltekniken. Ofta används den för att
dlab00a Experiment med schmittrigger Namn Datum Handledarens sign. Varför denna laboration? Schmittriggern är en mycket användbar koppling inom såväl analog- som digitaltekniken. Ofta används den för att
Repetition TSIU05 Digitalteknik Di/EL. Michael Josefsson
 Repetition TSIU05 Digitalteknik Di/EL Michael Josefsson Här kommer några frågeställningar och uppgifter du kan använda för att använda som egenkontroll på om du förstått huvudinnehållet i respektive föreläsning.
Repetition TSIU05 Digitalteknik Di/EL Michael Josefsson Här kommer några frågeställningar och uppgifter du kan använda för att använda som egenkontroll på om du förstått huvudinnehållet i respektive föreläsning.
Laborationshandledning
 Laborationshandledning Utbildning: ED Ämne: TNGE11 Digitalteknik Laborationens nummer och titel: Nr 5 Del A: Schmittrigger Del B: Analys av sekvensnät Laborant: E-mail: Medlaboranters namn: Handledarens
Laborationshandledning Utbildning: ED Ämne: TNGE11 Digitalteknik Laborationens nummer och titel: Nr 5 Del A: Schmittrigger Del B: Analys av sekvensnät Laborant: E-mail: Medlaboranters namn: Handledarens
Det finns en hemsida. Adressen är http://www.idt.mdh.se/kurser/ct3760/
 CT3760 Mikrodatorteknik Föreläsning 1 Torsdag 2005-08-25 Upprop. Det finns en hemsida. Adressen är http://www.idt.mdh.se/kurser/ct3760/ Kurslitteratur är Per Foyer Mikroprocessorteknik. Finns på bokhandeln.
CT3760 Mikrodatorteknik Föreläsning 1 Torsdag 2005-08-25 Upprop. Det finns en hemsida. Adressen är http://www.idt.mdh.se/kurser/ct3760/ Kurslitteratur är Per Foyer Mikroprocessorteknik. Finns på bokhandeln.
Laboration 6. A/D- och D/A-omvandling. Lunds universitet / Fakultet / Institution / Enhet / Dokument / Datum
 Laboration 6 A/D- och D/A-omvandling A/D-omvandlare Digitala Utgång V fs 3R/2 Analog Sample R R D E C O D E R P/S Skiftregister R/2 2 N-1 Komparatorer Digital elektronik Halvledare, Logiska grindar Digital
Laboration 6 A/D- och D/A-omvandling A/D-omvandlare Digitala Utgång V fs 3R/2 Analog Sample R R D E C O D E R P/S Skiftregister R/2 2 N-1 Komparatorer Digital elektronik Halvledare, Logiska grindar Digital
De grundläggande logiska grindarna
 dlab00a Namn Datum Handledarens sign. Laboration De grundläggande logiska grindarna Varför denna laboration? Till de grundläggande digitala kretsarna brukar man räkna kretsar som innehåller NND- och NORgrindar.
dlab00a Namn Datum Handledarens sign. Laboration De grundläggande logiska grindarna Varför denna laboration? Till de grundläggande digitala kretsarna brukar man räkna kretsar som innehåller NND- och NORgrindar.
2-13 Binära talsystemet Namn:
 2-13 Binära talsystemet Namn: Inledning Det finns inte bara olika taltyper som hela tal, decimaltal, bråktal osv. Det finns olika talsystem också. I det här kapitlet skall du lära dig lite om det talsystem
2-13 Binära talsystemet Namn: Inledning Det finns inte bara olika taltyper som hela tal, decimaltal, bråktal osv. Det finns olika talsystem också. I det här kapitlet skall du lära dig lite om det talsystem
TSIU05 Digitalteknik. LAB1 Kombinatorik LAB2 Sekvensnät LAB3 System
 1 TSIU05 Digitalteknik LAB1 Kombinatorik LAB2 Sekvensnät LAB3 System Sammanställning september 2013 Läs detta först Läs igenom hela laborationen så du vet vad du skall göra på laborationspasset. Hela
1 TSIU05 Digitalteknik LAB1 Kombinatorik LAB2 Sekvensnät LAB3 System Sammanställning september 2013 Läs detta först Läs igenom hela laborationen så du vet vad du skall göra på laborationspasset. Hela
TSEA22 Digitalteknik 2019!
 1(45) 2019 Mattias Krysander Ingemar Ragnemalm D D 1(45) Föreläsning 4. Komb2. Denna föreläsning: Labb 1 Adderare Lite mer om kombinationskretsar 2(45)2(45) Förra föreläsningen: Några kombinationskretsar.
1(45) 2019 Mattias Krysander Ingemar Ragnemalm D D 1(45) Föreläsning 4. Komb2. Denna föreläsning: Labb 1 Adderare Lite mer om kombinationskretsar 2(45)2(45) Förra föreläsningen: Några kombinationskretsar.
DIGITALTEKNIK. Laboration D173. Grundläggande digital logik
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Håkan Joëlson 2007-11-19 v 1.1 DIGITALTEKNIK Laboration D173 Grundläggande digital logik Innehåll Mål. Material.... Uppgift 1...Sanningstabell
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Håkan Joëlson 2007-11-19 v 1.1 DIGITALTEKNIK Laboration D173 Grundläggande digital logik Innehåll Mål. Material.... Uppgift 1...Sanningstabell
Tentamen i Digital Design
 Kungliga Tekniska Högskolan Tentamen i Digital Design Kursnummer : Kursansvarig: 2B56 :e fo ingenjör Lars Hellberg tel 79 7795 Datum: 27-5-25 Tid: Kl 4. - 9. Tentamen rättad 27-6-5 Klagotiden utgår: 27-6-29
Kungliga Tekniska Högskolan Tentamen i Digital Design Kursnummer : Kursansvarig: 2B56 :e fo ingenjör Lars Hellberg tel 79 7795 Datum: 27-5-25 Tid: Kl 4. - 9. Tentamen rättad 27-6-5 Klagotiden utgår: 27-6-29
DIGITALTEKNIK. Laboration D164. Logiska funktioner med mikroprocessor Kombinatoriska funktioner med PIC16F84 Sekvensfunktioner med PIC16F84
 UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Björne Lindberg Håkan Joëlson 2007-11-22 v 2.3 DIGITALTEKNIK Laboration D164 Logiska funktioner med mikroprocessor Kombinatoriska funktioner
UMEÅ UNIVERSITET Tillämpad fysik och elektronik Digitalteknik Björne Lindberg Håkan Joëlson 2007-11-22 v 2.3 DIGITALTEKNIK Laboration D164 Logiska funktioner med mikroprocessor Kombinatoriska funktioner
Vad är en UART? Universal Asynchronous Receiver Transmitter parallella seriella parallell åttabitars signal mest signifikant bit
 Vad är en UART? Beteckningen UART är en förkortning för det engelska uttrycket Universal Asynchronous Receiver Transmitter, vilket översatt till svenska blir ungefär Universell Asynkron Mottagare/Sändare.
Vad är en UART? Beteckningen UART är en förkortning för det engelska uttrycket Universal Asynchronous Receiver Transmitter, vilket översatt till svenska blir ungefär Universell Asynkron Mottagare/Sändare.
Tentamen i IE1204/5 Digital Design måndagen den 15/
 Tentamen i IE1204/5 Digital Design måndagen den 15/10 2012 9.00-13.00 Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista IE1204), Tentamensuppgifterna
Tentamen i IE1204/5 Digital Design måndagen den 15/10 2012 9.00-13.00 Allmän information Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist, tel 08-790 4487 (Kista IE1204), Tentamensuppgifterna
Sekvensnät vippor, register och bussar
 ekvensnät vippor, register och bussar agens föreläsning: Lärobok kap.5 Arbetsbok kap 8,9,10 Ur innehållet: Hur fungerar en -latch? Hur konstrueras JK-, - och T-vippor? er och excitationstabeller egister
ekvensnät vippor, register och bussar agens föreläsning: Lärobok kap.5 Arbetsbok kap 8,9,10 Ur innehållet: Hur fungerar en -latch? Hur konstrueras JK-, - och T-vippor? er och excitationstabeller egister
Digitalteknik 7.5 hp distans: 5.1 Generella sekvenskretsar 5.1.1
 Digitalteknik 7.5 hp distans: 5.1 Generella sekvenskretsar 5.1.1 Från Wikipedia: Sekvensnät Ett sekvensnäts utgångsvärde beror inte bara på indata, utan även i vilken ordning datan kommer (dess sekvens).
Digitalteknik 7.5 hp distans: 5.1 Generella sekvenskretsar 5.1.1 Från Wikipedia: Sekvensnät Ett sekvensnäts utgångsvärde beror inte bara på indata, utan även i vilken ordning datan kommer (dess sekvens).
Tentamen i Grundläggande ellära och digitalteknik ETA 013 för D
 Lars-Erik Cederlöf Tentamen i Grundläggande ellära och digitalteknik ETA 03 för D 2000-05-03 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet hjälpmedel är
Lars-Erik Cederlöf Tentamen i Grundläggande ellära och digitalteknik ETA 03 för D 2000-05-03 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet hjälpmedel är
EDA451 - Digital och Datorteknik 2010/2011. EDA Digital och Datorteknik 2010/2011
 EDA 451 - Digital och Datorteknik 2010/2011 Ur innehållet: Vi repeterar kursens lärandemål Diskussion i kring övningstentor t Övriga frågor 1 Lärandemål Det övergripande målet är att den studerande ska
EDA 451 - Digital och Datorteknik 2010/2011 Ur innehållet: Vi repeterar kursens lärandemål Diskussion i kring övningstentor t Övriga frågor 1 Lärandemål Det övergripande målet är att den studerande ska
Lösningsföslag till Exempel på tentamensuppgifter i Digitalteknik I
 Lösningsföslag till Exempel på tentamensuppgifter i Digitalteknik I Flervalsfrågor. A 2. C 3. B 4. D 5. A 6. B 7. C 8. D 9. C 0. B. B 2. C 3. A 4. C 5. A Problemuppgifter. Uttryckt i decimal form: A=28+32+8
Lösningsföslag till Exempel på tentamensuppgifter i Digitalteknik I Flervalsfrågor. A 2. C 3. B 4. D 5. A 6. B 7. C 8. D 9. C 0. B. B 2. C 3. A 4. C 5. A Problemuppgifter. Uttryckt i decimal form: A=28+32+8
Digital- och datorteknik
 Digital- och datorteknik Föreläsning #13 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Vad kännetecknar en tillståndsmaskin? En synkron tillståndsmaskin
Digital- och datorteknik Föreläsning #13 Biträdande professor Jan Jonsson Institutionen för data- och informationsteknik Chalmers tekniska högskola Vad kännetecknar en tillståndsmaskin? En synkron tillståndsmaskin
Övningar och datorlaborationer, Datorer i system
 LUNDS TEKNISKA HÖGSKOLA Datorer i system Institutionen för datavetenskap 2013/14 Övningar och datorlaborationer, Datorer i system Kursen Datorer i system inkluderar under läsperiod HT1 två övningar i seminariesal
LUNDS TEKNISKA HÖGSKOLA Datorer i system Institutionen för datavetenskap 2013/14 Övningar och datorlaborationer, Datorer i system Kursen Datorer i system inkluderar under läsperiod HT1 två övningar i seminariesal
Tenta i Digitalteknik
 Tenta i Digitalteknik Kurskod D0011E Tentamensdatum 2011-08-26 Skrivtid 9.00-14.00 Maximalt resultat 50 poäng Godkänt resultat 25 poäng Jourhavande lärare Per Lindgren Tel 070 376 8150 Tillåtna hjälpmedel
Tenta i Digitalteknik Kurskod D0011E Tentamensdatum 2011-08-26 Skrivtid 9.00-14.00 Maximalt resultat 50 poäng Godkänt resultat 25 poäng Jourhavande lärare Per Lindgren Tel 070 376 8150 Tillåtna hjälpmedel
Talsystem Teori. Vad är talsystem? Av Johan Johansson
 Talsystem Teori Av Johan Johansson Vad är talsystem? Talsystem är det sätt som vi använder oss av när vi läser, räknar och skriver ner tal. Exempelvis hade romarna ett talsystem som var baserat på de romerska
Talsystem Teori Av Johan Johansson Vad är talsystem? Talsystem är det sätt som vi använder oss av när vi läser, räknar och skriver ner tal. Exempelvis hade romarna ett talsystem som var baserat på de romerska
Lista på registeruppsättningen i PIC16F877A Datablad TTL-kretsar 74-serien
 DIGITAL- OCH MIKRODATORTEKNIK, U2 11-01-12 09.00 13.00 Tillåtna hjälpmedel: Instruktionslista PIC16F877A Lista på registeruppsättningen i PIC16F877A Datablad TTL-kretsar 74-serien Fullständiga lösningar
DIGITAL- OCH MIKRODATORTEKNIK, U2 11-01-12 09.00 13.00 Tillåtna hjälpmedel: Instruktionslista PIC16F877A Lista på registeruppsättningen i PIC16F877A Datablad TTL-kretsar 74-serien Fullständiga lösningar
Tentamen i Grundläggande ellära och digitalteknik ETA 013 för D
 Lars-Erik Cederlöf Per Liljas Tentamen i Grundläggande ellära och digitalteknik ETA 013 för D1 2001-05-28 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet
Lars-Erik Cederlöf Per Liljas Tentamen i Grundläggande ellära och digitalteknik ETA 013 för D1 2001-05-28 Tentamen omfattar 40 poäng, 2 poäng för varje uppgift. 20 poäng ger godkänd tentamen. Tillåtet
Laborationshandledning
 Laborationshandledning Utbildning: ED Ämne: TNE094 Digitalteknik och konstruktion Laborationens nummer och titel: Nr 3 Kombinatoriska nät Laborant: E-mail: Medlaboranters namn: Handledarens namn: Kommentarer
Laborationshandledning Utbildning: ED Ämne: TNE094 Digitalteknik och konstruktion Laborationens nummer och titel: Nr 3 Kombinatoriska nät Laborant: E-mail: Medlaboranters namn: Handledarens namn: Kommentarer
Laboration 1: Styrning av lysdioder med en spänning
 TSTE20 Elektronik Laboration 1: Styrning av lysdioder med en spänning v0.3 Kent Palmkvist, ISY, LiU Laboranter Namn Personnummer Godkänd Översikt I denna labroation ska en enkel Analog till Digital (A/D)
TSTE20 Elektronik Laboration 1: Styrning av lysdioder med en spänning v0.3 Kent Palmkvist, ISY, LiU Laboranter Namn Personnummer Godkänd Översikt I denna labroation ska en enkel Analog till Digital (A/D)
Tentamen. TSEA22 Digitalteknik 5 juni, 2015, kl
 Tentamen TSEA22 Digitalteknik 5 juni, 2015, kl. 08.00-12.00 Tillåtna hjälpmedel: Inga. Ansvarig lärare: Mattias Krysander Visning av skrivningen sker mellan 10.00-10.30 den 22 juni på Datorteknik. Totalt
Tentamen TSEA22 Digitalteknik 5 juni, 2015, kl. 08.00-12.00 Tillåtna hjälpmedel: Inga. Ansvarig lärare: Mattias Krysander Visning av skrivningen sker mellan 10.00-10.30 den 22 juni på Datorteknik. Totalt
Digitalteknik EIT020. Lecture 15: Design av digitala kretsar
 Digitalteknik EIT020 Lecture 15: Design av digitala kretsar November 3, 2014 Digitalteknikens kopplingar mot andra områden Mjukvara Hårdvara Datorteknik Kretskonstruktion Digitalteknik Elektronik Figure:,
Digitalteknik EIT020 Lecture 15: Design av digitala kretsar November 3, 2014 Digitalteknikens kopplingar mot andra områden Mjukvara Hårdvara Datorteknik Kretskonstruktion Digitalteknik Elektronik Figure:,
Lösningsförslag till tentamen i Digitalteknik, TSEA22
 Försättsblad till skriftlig tentamen vid Linköpings universitet, Datorteknik, ISY (4) Lösningsförslag till tentamen i Digitalteknik, TSEA Datum för tentamen 3009 Salar U4, U7, U0 Tid 4.00-8.00 Kurskod
Försättsblad till skriftlig tentamen vid Linköpings universitet, Datorteknik, ISY (4) Lösningsförslag till tentamen i Digitalteknik, TSEA Datum för tentamen 3009 Salar U4, U7, U0 Tid 4.00-8.00 Kurskod
Kodlås. Kopplingsschema över kodlåset PAL-18
 Kodlås I den här uppgiften skall du konstruera ett kodlås med hjälp av ett litet tangentbord. Varje gång man trycker på en tangent skall det pipa i summern och när man tryckt in den rätta fyrsiffriga koden
Kodlås I den här uppgiften skall du konstruera ett kodlås med hjälp av ett litet tangentbord. Varje gång man trycker på en tangent skall det pipa i summern och när man tryckt in den rätta fyrsiffriga koden
Laboration i digitalteknik Allmänna anvisningar
 Linköpings universitet Institutionen för systemteknik Laborationer i digitalteknik Datorteknik 206 Laboration i digitalteknik Allmänna anvisningar TSEA22 Digitalteknik D TSEA5 Digitalteknik Y TDDC75 Diskreta
Linköpings universitet Institutionen för systemteknik Laborationer i digitalteknik Datorteknik 206 Laboration i digitalteknik Allmänna anvisningar TSEA22 Digitalteknik D TSEA5 Digitalteknik Y TDDC75 Diskreta
Följddiagram för händelsestyrda rörelser
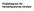 Följddiagram för händelsestyrda rörelser 2 STYROBJEKT UNIKA FASER Två arbetscylindrar ska röra sig i följande ordning. När man ger startkommando ska kolvstången i cylinder gå ut. När den har nått sitt
Följddiagram för händelsestyrda rörelser 2 STYROBJEKT UNIKA FASER Två arbetscylindrar ska röra sig i följande ordning. När man ger startkommando ska kolvstången i cylinder gå ut. När den har nått sitt
Ladderprogrammering steg för steg
 Ladderprogrammering steg för steg En introduktion till LD-programmering för kursen MIE 012 Elektroteknikens Grunder vid LTH. Gunnar Lindstedt Introduktion Den dominerande typen av styrsystem för binära
Ladderprogrammering steg för steg En introduktion till LD-programmering för kursen MIE 012 Elektroteknikens Grunder vid LTH. Gunnar Lindstedt Introduktion Den dominerande typen av styrsystem för binära
IE1205 Digital Design: F8: Minneselement: Latchar och Vippor. Räknare
 IE1205 Digital Design: F8: Minneselement: Latchar och Vippor. Räknare IE1205 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska
IE1205 Digital Design: F8: Minneselement: Latchar och Vippor. Räknare IE1205 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska
Tentamen i Grundläggande ellära och digitalteknik ETA 013 för D
 Lars-Erik Cederlöf Tentamen i Grundläggande ellära och digitalteknik ET 3 för D 999-3-5 Tentamen omfattar 4 poäng, 2 poäng för varje uppgift. 2 poäng ger godkänd tentamen. Tillåtet hjälpmedel är räknedosa.
Lars-Erik Cederlöf Tentamen i Grundläggande ellära och digitalteknik ET 3 för D 999-3-5 Tentamen omfattar 4 poäng, 2 poäng för varje uppgift. 2 poäng ger godkänd tentamen. Tillåtet hjälpmedel är räknedosa.
Digital Design IE1204
 Digital Design IE1204 F10 Tillståndsautomater del II william@kth.se IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska
Digital Design IE1204 F10 Tillståndsautomater del II william@kth.se IE1204 Digital Design F1 F3 F2 F4 Ö1 Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK1 LAB1 Kombinatoriska
Tentamen i IE1204/5 Digital Design Torsdag 29/
 Tentamen i IE1204/5 Digital Design Torsdag 29/10 2015 9.00-13.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist
Tentamen i IE1204/5 Digital Design Torsdag 29/10 2015 9.00-13.00 Allmän information ( TCOMK, Ask for an english version of this exam if needed ) Examinator: Ingo Sander. Ansvarig lärare: William Sandqvist
TSEA22 Digitalteknik 2019!
 1(43) 2019 Mattias Krysander Ingemar Ragnemalm 1(43) Föreläsning 7. Sekv3. enna föreläsning: Lösningar närmare verkligheten Synkronisering Enpulsare Problem till design 2(43)2(43) Förra föreläsningen:
1(43) 2019 Mattias Krysander Ingemar Ragnemalm 1(43) Föreläsning 7. Sekv3. enna föreläsning: Lösningar närmare verkligheten Synkronisering Enpulsare Problem till design 2(43)2(43) Förra föreläsningen:
Grindar och transistorer
 Föreläsningsanteckningar Föreläsning 17 - Digitalteknik I boken: nns ej med Grindar och transistorer Vi ska kort beskriva lite om hur vi kan bygga upp olika typer av grindar med hjälp av transistorer.
Föreläsningsanteckningar Föreläsning 17 - Digitalteknik I boken: nns ej med Grindar och transistorer Vi ska kort beskriva lite om hur vi kan bygga upp olika typer av grindar med hjälp av transistorer.
IE1204 Digital Design
 IE204 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM F0 F
IE204 Digital Design F F3 F2 F4 Ö Booles algebra, Grindar MOS-teknologi, minimering F5 F6 Ö2 Aritmetik Ö3 KK LAB Kombinatoriska kretsar F7 F8 Ö4 F9 Ö5 Multiplexor KK2 LAB2 Låskretsar, vippor, FSM F0 F
Systemkonstruktion LABORATION LOGIK
 Systemkonstruktion LABORATION LOGIK Laborationsansvarig: Anders Arvidsson Utskriftsdatum: 2005-04-26 Syfte Denna laboration syftar till att visa några av logikkretsarnas analoga egenskaper. Genom att experimentera
Systemkonstruktion LABORATION LOGIK Laborationsansvarig: Anders Arvidsson Utskriftsdatum: 2005-04-26 Syfte Denna laboration syftar till att visa några av logikkretsarnas analoga egenskaper. Genom att experimentera
