Summan av två tal är 38 och differensen mellan dem är 14. Vilka är talen? 2/0/0
|
|
|
- Jan Karlsson
- för 9 år sedan
- Visningar:
Transkript
1 Del A: Digitala verktyg är tillåtna. Skriv dina lösningar på separat papper. 1) Summan av två tal är 38 och differensen mellan dem är 14. Vilka är talen? 2/0/0 2) Ställ upp ett ekvationssystem för situationen nedan och bestäm hur mycket Dita väger? 2/0/0 3) Johanna och ichael köper CD skivor i London. CD skivorna har färgmarkeringar som kod för priset. Johanna betalar 32 pund för två röda och en blå skiva. ichael betalar 36 pund för en röd och tre blå skivor. Johannas köp kan beskrivas med ekvationen. 2x + y = 32 a) Beskriv ichaels köp med en liknande ekvation. b) Använd ekvationerna för att beräkna priset på en röd respektive en blå skiva. 3/0/0
2 4) Yamal ska köpa 100 fiskar till sitt nya akvarium. Han vill köpa blåtetror, slöjstjärtar och ciklider, se bilder. Blåtetrorna kostar 10 kr/st, slöjstjärtarna 50 kr/st och cikliderna 200 kr/st. Yamal funderar över om det är möjligt att köpa totalt 100 fiskar för exakt 3000 kr om 4 av de 100 fiskarna han köper är ciklider. Yamal ställer upp följande ekvationssystem: 4 + x + y = x + 10 y = 3000 a) Förklara vad y står för i ekvationssystemet. Endast svar krävs b) Bestäm hur många blåtetror och slöjstjärtar Yamal kan köpa om han köper 4 ciklider och totalt ska köpa 100 fiskar för 3000 kr. 3/0/0 5) En liten camping har 9 stugor, fördelade på trebäddsstugor och fembäddsstugor. Totalt har campingen 35 bäddar. Efter att ha läst texten ovanför ställde en elev upp följande ekvationssystem: x + y = 9 3x + 5y = 35 a) Vad står x respektive y för? b) Välj en av ekvationerna i ekvationssystemet och förklara vad ekvationen beskriver. c) Lös ekvationssystemet och förklara innebörden av din lösning. 4/0/0
3 6) En år gammal kinesisk gåta: I en bur finns fasaner och kaniner. De har tillsammans 35 huvuden och 94 ben. Hur många fasaner och hur många kaniner finns det i buren? 0/2/0 7) Ett företag tillverkar kepsar i en herr och en dammodell. Tabellen visar produktionskostnaden för en keps. I januari månad var materialkostnaden för de båda modellerna 9000 kr och arbetskostnaden kr. Hur många kepsar av varje modell tillverkade man den månaden? 1/3/0 8) Två linjer, och y = kx + m, skär varandra i en enda punkt. Den punkten ligger på y axeln. y = 2x + 5 Vilka värden kan riktningskoefficienten k ha? otivera ditt svar! 0/1/1 9) Anna adderade längderna på tre sidor av en rektangel och fick 44 cm. Heather adderade också tre sidor av samma rektangel och fick 40 cm. Vilken omkrets har rektangeln? 0/1/2
4 Bedömningsanvisningar 1) Talen är 26 och 12. Sätter upp ett korrekt ekvationssystem. samt löser ekvationssystemet rätt. Ev tar reda på det talen utan ett ekvationssystem. 2) 5 kg Korrekt ekvationssystem t ex. Variablerna definieras ed korrekt svar R + D = 8 R + 2 = D 3) a) x + 3y = 36 Korrekt uttryck. b) Röd skiva kostar 12 pund, blå skiva kostar 8 pund. Godtagbar metod med korrekt svar. L 4) a) Antal blåtetror Korrekt svar. b) 31 slöjstjärtar och 65 blåtetror Godtagbar ansats, bestämmer ett korrekt värde på minst en av variablerna med i övrigt godtagbar lösning med korrekt svar. L
5 5) a) x = antal trebäddsstugor och y = antal fembäddsstugor. Godtagbara svar. b) x + y = 9 Trebäddsstugorna tillsammans med fembäddsstugorna är totalt 9 stycken. 3x + 5y = 35 I varje trebäddsstuga finns tre sängar och i varje fembäddsstuga finns 5 sängar, sammanlagt finns det 35 sängar. Godtagbart svar. L c) x = 5 och y = 4 Svar: Det finns 5 st trebäddsstugor och 4 st fembäddsstugor Redovisad godtagbar metod med godtagbart svar. 6) 12 kaniner och 23 fasaner Godtagbar ansats, tex ställer upp ekvationssystemet x + y = 35 2x + 4y = 94 med korrekt svar. L 7) Det tillverkades 100 dammodeller och 50 herrmodeller. Förslag på ekvationssystem: Anger en korrekt ekvation. Anger två korrekta ekvationer. Använder sig av korrekt metod för att lösa ekvationssystemet. Korrekt lösning med korrekt svar. 55x + 70y = x + 90y = K
6 8) och m = 5; om k = 2 sammanfaller linjerna och ekvationssystemet har oändligt många lösningar k 2 Eleven drar slutsatsen att k värdena för de båda linjerna måste vara olika för att ekvationssystemet ska ha en lösning. R ed godtagbart välgrundat och nyanserat resonemang med korrekt svar. T ex Eftersom m = 5 kommer linjerna att sammanfalla (vara samma linje) om k = 2. Det innebär att ekvationssystemet har oändligt många lösningar när k = 2. För att ekvationssystemet ska ha en lösning kan k anta alla värden utom 2, alltså." + A k 2 R 9) 56 cm Konstaterar att eftersom Anna fick en större summa än Heather måste hon ha adderat två långsidor och en kortsida samtidigt som Heather adderat en långsida och två kortsidor. Godtagbar och effektiv lösningsstrategi, t ex ställer upp ekvationssystem 2a + b = 44 a + 2b = 40 Korrekt svar., där långsidan är a och kortsidan är b. + A + A R
a) Ange ekvationen för den räta linjen L. (1/0/0) Varje tal nedan motsvaras av en markerad punkt på tallinjen.
 Delprov B: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet. 1. Ange det uttryck som ska stå i parentesen för att likheten ska gälla. ( ) ( x 5) = x 5 (1/0/0).
Delprov B: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet. 1. Ange det uttryck som ska stå i parentesen för att likheten ska gälla. ( ) ( x 5) = x 5 (1/0/0).
ATT KUNNA TILL. MA1050 Matte Grund. 2011-06-14 Vuxenutbildningen Dennis Jonsson
 ATT KUNNA TILL MA1050 Matte Grund 2011-06-14 Vuxenutbildningen Dennis Jonsson Sida 2 av 5 Att kunna till prov G1 Kunna ställa upp och beräkna additions-, subtraktions-, multiplikations- och divisuionsuppgifter
ATT KUNNA TILL MA1050 Matte Grund 2011-06-14 Vuxenutbildningen Dennis Jonsson Sida 2 av 5 Att kunna till prov G1 Kunna ställa upp och beräkna additions-, subtraktions-, multiplikations- och divisuionsuppgifter
3.1 Linjens ekvation med riktningskoefficient. y = kx + l.
 Kapitel Analytisk geometri Målet med detta kapitel är att göra läsaren bekant med ekvationerna för linjen, cirkeln samt ellipsen..1 Linjens ekvation med riktningskoefficient Vi utgår från ekvationen 1
Kapitel Analytisk geometri Målet med detta kapitel är att göra läsaren bekant med ekvationerna för linjen, cirkeln samt ellipsen..1 Linjens ekvation med riktningskoefficient Vi utgår från ekvationen 1
3. Pappa hade köpt hem 16 clementiner. Karin åt upp hälften av dem. Eva åt två och David åt upp resten. Hur många clementiner åt David?
 Avdelning 1 1. Vilket av dessa tal är jämnt? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Var är kängurun? A: I cirkeln och i triangeln, men inte i kvadraten B: I cirkeln och i kvadraten,
Avdelning 1 1. Vilket av dessa tal är jämnt? A: 2009 B: 2 + 0 + 0 + 9 C: 200 9 D: 200 9 E: 200 + 9 Frankrike 2. Var är kängurun? A: I cirkeln och i triangeln, men inte i kvadraten B: I cirkeln och i kvadraten,
Laborativ matematik som bedömningsform. Per Berggren och Maria Lindroth 2016-01-28
 Laborativ matematik som bedömningsform Per Berggren och Maria Lindroth 2016-01-28 Kul matematik utan lärobok Vilka förmågor tränas Problemlösning (Förstå frågan i en textuppgift, Använda olika strategier
Laborativ matematik som bedömningsform Per Berggren och Maria Lindroth 2016-01-28 Kul matematik utan lärobok Vilka förmågor tränas Problemlösning (Förstå frågan i en textuppgift, Använda olika strategier
NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN 1998. Tidsbunden del
 Nationellt kursprov i Matematik kurs B ht 1998 sida 1 (av 7) Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap. 3 sekretesslagen. För detta material gäller sekretessen
Nationellt kursprov i Matematik kurs B ht 1998 sida 1 (av 7) Skolverket hänvisar generellt beträffande provmaterial till bestämmelsen om sekretess i 4 kap. 3 sekretesslagen. För detta material gäller sekretessen
3. Olle skriver ned ett visst antal heltal mellan 10 och 25. Talens medelvärde är 18. Hur många är talen? (1) Medelvärdet av de tre första talen som O
 2 1. Familjen Berg, som består av två vuxna och tre barn, har beställt en resa till Cypern. Barnen är 1, 7 och 10 år gamla. Med barnrabatter kostar hela familjens resa 18 000 kr. Hur mycket kostar resan
2 1. Familjen Berg, som består av två vuxna och tre barn, har beställt en resa till Cypern. Barnen är 1, 7 och 10 år gamla. Med barnrabatter kostar hela familjens resa 18 000 kr. Hur mycket kostar resan
Två konstiga klockor
 strävorna C Två konstiga klockor resonemang geometri Avsikt och matematikinnehåll Det som kan göra det svårt för barn att avläsa en analog klocka är att förstå att den består av två skalor som är beroende
strävorna C Två konstiga klockor resonemang geometri Avsikt och matematikinnehåll Det som kan göra det svårt för barn att avläsa en analog klocka är att förstå att den består av två skalor som är beroende
Exempel på tentamensuppgifter i LMA100, del 1
 Exempel på tentamensuppgifter i LMA100, del 1 Diskret matematik 1. Givet är de 7 bokstäverna i ordet APPARAT. Hur många olika ord (= bokstavspermutationer) kan man bilda av dem med (a) 7 bokstäver (b)
Exempel på tentamensuppgifter i LMA100, del 1 Diskret matematik 1. Givet är de 7 bokstäverna i ordet APPARAT. Hur många olika ord (= bokstavspermutationer) kan man bilda av dem med (a) 7 bokstäver (b)
Ekvationssystem, Matriser och Eliminationsmetoden
 Matematiska institutionen Göteborgs universitet och Chalmers tekniska högskola Version 359 Ekvationssystem, Matriser och Eliminationsmetoden - En inledning Ekvationssystem - matrisformulering Vi såg att
Matematiska institutionen Göteborgs universitet och Chalmers tekniska högskola Version 359 Ekvationssystem, Matriser och Eliminationsmetoden - En inledning Ekvationssystem - matrisformulering Vi såg att
Väga paket och jämföra priser
 strävorna 2AC 3AC Väga paket och jämföra priser begrepp rutinuppgifter tal geometri Avsikt och matematikinnehåll Den huvudsakliga avsikten med denna aktivitet är att ge elever möjlighet att utveckla grundläggande
strävorna 2AC 3AC Väga paket och jämföra priser begrepp rutinuppgifter tal geometri Avsikt och matematikinnehåll Den huvudsakliga avsikten med denna aktivitet är att ge elever möjlighet att utveckla grundläggande
Observera att alla funktioner kan ritas, men endast linjära funktioner blir räta linjer.
 1 Matematik som verktyg Antag att vi har en funktion som är en rät linje, y = 1 3x. Eftersom relationen mellan x och y är linjär räcker det med att vi hittar två punkter (två talpar) på linjen för att
1 Matematik som verktyg Antag att vi har en funktion som är en rät linje, y = 1 3x. Eftersom relationen mellan x och y är linjär räcker det med att vi hittar två punkter (två talpar) på linjen för att
Snabbslumpade uppgifter från flera moment.
 Snabbslumpade uppgifter från flera moment. Uppgift nr Ställ upp och dividera utan hjälp av miniräknare talet 48 med 2 Uppgift nr 2 Skriv talet 3 8 00 med hjälp av decimalkomma. Uppgift nr 3 Uppgift nr
Snabbslumpade uppgifter från flera moment. Uppgift nr Ställ upp och dividera utan hjälp av miniräknare talet 48 med 2 Uppgift nr 2 Skriv talet 3 8 00 med hjälp av decimalkomma. Uppgift nr 3 Uppgift nr
Kängurun Matematikens hopp Benjamin 2006 A: B: C: D: E:
 3-poängsproblem : = + + Vilket tal ska frågetecknet ersättas med A: B: C: D: E: : Sex tal står skrivna på korten här intill. Vilket är det minsta tal man kan bilda genom att lägga korten efter varandra
3-poängsproblem : = + + Vilket tal ska frågetecknet ersättas med A: B: C: D: E: : Sex tal står skrivna på korten här intill. Vilket är det minsta tal man kan bilda genom att lägga korten efter varandra
Lathund, procent med bråk, åk 8
 Lathund, procent med bråk, åk 8 Procent betyder hundradel, men man kan också säga en av hundra. Ni ska kunna omvandla mellan bråkform, decimalform och procentform. Nedan kan ni se några omvandlingar. Bråkform
Lathund, procent med bråk, åk 8 Procent betyder hundradel, men man kan också säga en av hundra. Ni ska kunna omvandla mellan bråkform, decimalform och procentform. Nedan kan ni se några omvandlingar. Bråkform
TT091A, TVJ22A, NVJA02 By, Pu, Ti. 50 poäng
 Matematisk statistik Provmoment: Ladokkod: Tentamen ges för: TT091A, TVJ22A, NVJA02 By, Pu, Ti 7,5 högskolepoäng Namn: (Ifylles av student) Personnummer: (Ifylles av student) Tentamensdatum: 2012-01-11
Matematisk statistik Provmoment: Ladokkod: Tentamen ges för: TT091A, TVJ22A, NVJA02 By, Pu, Ti 7,5 högskolepoäng Namn: (Ifylles av student) Personnummer: (Ifylles av student) Tentamensdatum: 2012-01-11
4-6 Trianglar Namn:..
 4-6 Trianglar Namn:.. Inledning Hittills har du arbetat med parallellogrammer. En sådan har fyra hörn och motstående sidor är parallella. Vad händer om vi har en geometrisk figur som bara har tre hörn?
4-6 Trianglar Namn:.. Inledning Hittills har du arbetat med parallellogrammer. En sådan har fyra hörn och motstående sidor är parallella. Vad händer om vi har en geometrisk figur som bara har tre hörn?
Värt att veta om högstadiets matematik
 Värt att veta om högstadiets matematik Av: Thomas Sundell Dessa uppgifter är övningsexempel gjorda för godkänd nivå. Upprepa gärna övningar inför varje prov. Aritmetik sid Jämförelsepris Sid Bråk Sid Procent
Värt att veta om högstadiets matematik Av: Thomas Sundell Dessa uppgifter är övningsexempel gjorda för godkänd nivå. Upprepa gärna övningar inför varje prov. Aritmetik sid Jämförelsepris Sid Bråk Sid Procent
Kurs: HF1012, Matematisk statistik Lärare: Armin Halilovic Datum: Måndag 30 mars 2015 Skrivtid: 8:15-10:00
 KONTROLLSKRIVNING 1 version A Kurs: HF1012, Matematisk statistik Lärare: Armin Halilovic Datum: Måndag 30 mars 2015 Skrivtid: 8:15-10:00 Tillåtna hjälpmedel: Miniräknare av vilken typ som helst. Förbjudna
KONTROLLSKRIVNING 1 version A Kurs: HF1012, Matematisk statistik Lärare: Armin Halilovic Datum: Måndag 30 mars 2015 Skrivtid: 8:15-10:00 Tillåtna hjälpmedel: Miniräknare av vilken typ som helst. Förbjudna
Delprov B: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet.
 Delprov B: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet. 1. Ange det uttryck som ska stå i parentesen för att likheten ska gälla. ( ) ( x 5) x 5 (1/0/0). Koordinatsystemet
Delprov B: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv dina svar direkt i provhäftet. 1. Ange det uttryck som ska stå i parentesen för att likheten ska gälla. ( ) ( x 5) x 5 (1/0/0). Koordinatsystemet
Facit med lösningsförslag kommer att anslås på vår hemsida www.ebersteinska.norrkoping.se. Du kan dessutom få dem via e-post, se nedan.
 Detta häfte innehåller uppgifter från fyra olika områden inom matematiken. Meningen är att de ska tjäna som en självtest inför gymnasiet. Klarar du dessa uppgifter så är du väl förberedd inför gymnasiestudier
Detta häfte innehåller uppgifter från fyra olika områden inom matematiken. Meningen är att de ska tjäna som en självtest inför gymnasiet. Klarar du dessa uppgifter så är du väl förberedd inför gymnasiestudier
Kursplan i Matematik för Alsalamskolan
 Kursplan i Matematik för Alsalamskolan Vi kommer att använda oss av följande nyanserade ord, Känna till, Kunna och Förstå. Att känna till är att ha hört talas om, att kunna är att kunna använda och förstå
Kursplan i Matematik för Alsalamskolan Vi kommer att använda oss av följande nyanserade ord, Känna till, Kunna och Förstå. Att känna till är att ha hört talas om, att kunna är att kunna använda och förstå
Övningshäfte Algebra, ekvationssystem och geometri
 Stockholms Tekniska Gmnasium --9 Övningshäfte Algebra, ekvationssstem och geometri Nivå: rätt svårt Fråga : f är ett polnom. Beräkna värdet av f, f och fπ Fråga : Ingångslönen på företaget Börjes Gurkinläggning
Stockholms Tekniska Gmnasium --9 Övningshäfte Algebra, ekvationssstem och geometri Nivå: rätt svårt Fråga : f är ett polnom. Beräkna värdet av f, f och fπ Fråga : Ingångslönen på företaget Börjes Gurkinläggning
Bedömningsanvisningar Del I vt 2010 Skolverket har den 2010-12-07 beslutat att provet i matematik A för vt 2010 inte ska återanvändas.
 Bedömningsanvisningar Del I vt 2010 Skolverket har den 2010-12-07 beslutat att provet i matematik A för vt 2010 inte ska återanvändas. Innehåll Inledning... 4 Bedömningsanvisningar... 4 Allmänna bedömningsanvisningar...
Bedömningsanvisningar Del I vt 2010 Skolverket har den 2010-12-07 beslutat att provet i matematik A för vt 2010 inte ska återanvändas. Innehåll Inledning... 4 Bedömningsanvisningar... 4 Allmänna bedömningsanvisningar...
URVALSSAMARBETET INOM NATURBRUK OCH MILJÖOMRÅDET I YRKESHÖGSKOLORNA URVALSPROV 2004. Provet i matematik 8.6.2004
 1 URVALSSAMARBETET INOM NATURBRUK OCH MILJÖOMRÅDET I YRKESHÖGSKOLORNA URVALSPROV 2004 Provet i matematik 8.6.2004 Uppgift 1 a) Farfar ger sitt barnbarn följande problem: Ett bröd väger ett kilogram plus
1 URVALSSAMARBETET INOM NATURBRUK OCH MILJÖOMRÅDET I YRKESHÖGSKOLORNA URVALSPROV 2004 Provet i matematik 8.6.2004 Uppgift 1 a) Farfar ger sitt barnbarn följande problem: Ett bröd väger ett kilogram plus
Facit åk 6 Prima Formula
 Facit åk 6 Prima Formula Kapitel 3 Algebra och samband Sidan 95 1 a 12 cm (3 4 cm) b Han vet inte att uttrycket 3s betyder 3 s eller s + s + s 2 a 5x b 6y c 12z 3 a 30 cm (5 6 cm) b 30 cm (6 5 cm) Sidan
Facit åk 6 Prima Formula Kapitel 3 Algebra och samband Sidan 95 1 a 12 cm (3 4 cm) b Han vet inte att uttrycket 3s betyder 3 s eller s + s + s 2 a 5x b 6y c 12z 3 a 30 cm (5 6 cm) b 30 cm (6 5 cm) Sidan
Nämnarens adventskalendern 2007
 Nämnarens adventskalendern 2007 1 När det närmar sig jul är det kallt. Då behöver de tre tomtenissarna både halsduk och mössa när de leker i snön. I korgen ligger en röd, en blå och en randig halsduk.
Nämnarens adventskalendern 2007 1 När det närmar sig jul är det kallt. Då behöver de tre tomtenissarna både halsduk och mössa när de leker i snön. I korgen ligger en röd, en blå och en randig halsduk.
Övningshäfte i matematik för. Kemistuderande BL 05
 Övningshäfte i matematik för Kemistuderande BL 05 Detta häfte innehåller några grundläggande övningar i de delar av matematiken som man har användning för i de tidiga kemistudierna. Nivån är gymnasiematematik,
Övningshäfte i matematik för Kemistuderande BL 05 Detta häfte innehåller några grundläggande övningar i de delar av matematiken som man har användning för i de tidiga kemistudierna. Nivån är gymnasiematematik,
DOP-matematik Copyright Tord Persson. Bråktal -3-2 -1 0 1 2 3. Läs av vilka tal på tallinjen, som pilarna pekar på. Uppgift nr 10 -3-2 -1 0 1 2 3
 Bråktal Uppgift nr En limpa delas i 4 lika stora delar. Hur stor del av limpan blir varje del? Uppgift nr 2 Hur många tiondelar behövs för att det skall räcka till en hel? Uppgift nr Hur läser man ut bråket
Bråktal Uppgift nr En limpa delas i 4 lika stora delar. Hur stor del av limpan blir varje del? Uppgift nr 2 Hur många tiondelar behövs för att det skall räcka till en hel? Uppgift nr Hur läser man ut bråket
Matematik. Bedömningsanvisningar. Vårterminen 2009 ÄMNESPROV. Delprov B ÅRSKURS
 ÄMNESPROV Matematik ÅRSKURS 9 Prov som ska återanvändas omfattas av sekretess enligt 4 kap. 3 sekretesslagen. Avsikten är att detta prov ska kunna återanvändas t.o.m. 2009-06-30. Vid sekretessbedömning
ÄMNESPROV Matematik ÅRSKURS 9 Prov som ska återanvändas omfattas av sekretess enligt 4 kap. 3 sekretesslagen. Avsikten är att detta prov ska kunna återanvändas t.o.m. 2009-06-30. Vid sekretessbedömning
Stockholms Tekniska Gymnasium 2014-11-19. Prov Fysik 2 Mekanik
 Prov Fysik 2 Mekanik För samtliga uppgifter krävs om inte annat står antingen en tydlig och klar motivering eller fullständig lösning och att det går att följa lösningsgången. Fråga 1: Keplers tredje lag
Prov Fysik 2 Mekanik För samtliga uppgifter krävs om inte annat står antingen en tydlig och klar motivering eller fullständig lösning och att det går att följa lösningsgången. Fråga 1: Keplers tredje lag
Statistik, sannolikhet, algebra och funktioner, 3 hp. Studenter i lärarprogrammet F-3 III
 Grundläggande matematik II 7,5 högskolepoäng Provmoment: Ladokkod: Tentamen ges för: Statistik, sannolikhet, algebra och funktioner, 3 hp Studenter i lärarprogrammet F-3 III TentamensKod: Tentamensdatum:
Grundläggande matematik II 7,5 högskolepoäng Provmoment: Ladokkod: Tentamen ges för: Statistik, sannolikhet, algebra och funktioner, 3 hp Studenter i lärarprogrammet F-3 III TentamensKod: Tentamensdatum:
Får nyanlända samma chans i den svenska skolan?
 Får nyanlända samma chans i den svenska skolan? Sammanställning oktober 2015 De nyanlända eleverna (varit här högst fyra år) klarar den svenska skolan sämre än andra elever. Ett tydligt tecken är att för
Får nyanlända samma chans i den svenska skolan? Sammanställning oktober 2015 De nyanlända eleverna (varit här högst fyra år) klarar den svenska skolan sämre än andra elever. Ett tydligt tecken är att för
Provet består av tre skriftliga delprov (Delprov B, C och D). Tillsammans kan de ge 55 poäng varav 22 E-, 19 C- och 14 A-poäng.
 Delprov D Provtid Hjälpmedel Uppgift 15-. Fullständiga lösningar krävs. 10 minuter. Digitala verktyg, formelblad och linjal. Kravgränser Provet består av tre skriftliga delprov (Delprov B, C och D). Tillsammans
Delprov D Provtid Hjälpmedel Uppgift 15-. Fullständiga lösningar krävs. 10 minuter. Digitala verktyg, formelblad och linjal. Kravgränser Provet består av tre skriftliga delprov (Delprov B, C och D). Tillsammans
Ekvationssystem - Övningar
 Ekvationssystem - Övningar Uppgift nr 1 y = 5x x + y = 54 Uppgift nr 2 y = 2x x + y = 12 Uppgift nr 3 y = 3x + 7 4x + y = 35 Uppgift nr 4 y = 4x - 18 3x + y = 38 Uppgift nr 5 2x - 2y = -4 x - 3y = 4 Uppgift
Ekvationssystem - Övningar Uppgift nr 1 y = 5x x + y = 54 Uppgift nr 2 y = 2x x + y = 12 Uppgift nr 3 y = 3x + 7 4x + y = 35 Uppgift nr 4 y = 4x - 18 3x + y = 38 Uppgift nr 5 2x - 2y = -4 x - 3y = 4 Uppgift
konstanterna a och b så att ekvationssystemet x 2y = 1 2x + ay = b 2 a b
 Tentamen i Inledande matematik för V och AT, (TMV25), 20-0-26. Till denna uppgift skulle endast lämnas svar, men här ges kortfattade lösningar. a) Bestäm { konstanterna a och b så att ekvationssystemet
Tentamen i Inledande matematik för V och AT, (TMV25), 20-0-26. Till denna uppgift skulle endast lämnas svar, men här ges kortfattade lösningar. a) Bestäm { konstanterna a och b så att ekvationssystemet
Subtraktion - Analys och bedömning av elevarbeten
 Analys och bedömning av elevarbete 1 Eleven anpassar sitt val av metoder efter de ingående talen genom att använda flera olika metoder för beräkningar; räknar uppåt när talen ligger nära varandra, räknar
Analys och bedömning av elevarbete 1 Eleven anpassar sitt val av metoder efter de ingående talen genom att använda flera olika metoder för beräkningar; räknar uppåt när talen ligger nära varandra, räknar
D A B A D B B D. Trepoängsproblem. Kängurutävlingen 2012 Benjamin
 Kängurutävlingen enjamin Trepoängsproblem. Skrivtavlan i klassrummet är 6 meter bred. Mittdelen är m bred. De båda yttre delarna är lika breda. Hur bred är den högra delen? A: m :,5 m C:,5 m D:,75 m E:
Kängurutävlingen enjamin Trepoängsproblem. Skrivtavlan i klassrummet är 6 meter bred. Mittdelen är m bred. De båda yttre delarna är lika breda. Hur bred är den högra delen? A: m :,5 m C:,5 m D:,75 m E:
Sammanfattning på lättläst svenska
 Sammanfattning på lättläst svenska Utredningen skulle utreda och lämna förslag i vissa frågor som handlar om svenskt medborgarskap. Svenskt medborgarskap i dag Vissa personer blir svenska medborgare när
Sammanfattning på lättläst svenska Utredningen skulle utreda och lämna förslag i vissa frågor som handlar om svenskt medborgarskap. Svenskt medborgarskap i dag Vissa personer blir svenska medborgare när
Läraren som moderator vid problemlösning i matematik
 Läraren som moderator vid problemlösning i matematik Cecilia Christiansen 9 oktober 2012 Kursplanen för matematik: matematisk verksamhet är till sin art en kreativ, reflekterande och problemlösande aktivitet
Läraren som moderator vid problemlösning i matematik Cecilia Christiansen 9 oktober 2012 Kursplanen för matematik: matematisk verksamhet är till sin art en kreativ, reflekterande och problemlösande aktivitet
c) 240/3 f) 1000 0,15
 1 Beräkna med huvudräkning a) 10-2,5 b) 2 4 7 d) 12+58 e) 45110 c) 240/3 f) 1000 0,15 2 Vilket tal är störst? a) 0,l9 eller 0,2 b) 1,9 eller 1,89 c) 0,7 eller 0,699 3 Vad kostar 8 liter mjölk, om priset
1 Beräkna med huvudräkning a) 10-2,5 b) 2 4 7 d) 12+58 e) 45110 c) 240/3 f) 1000 0,15 2 Vilket tal är störst? a) 0,l9 eller 0,2 b) 1,9 eller 1,89 c) 0,7 eller 0,699 3 Vad kostar 8 liter mjölk, om priset
Kapitel 6. f(x) = sin x. Figur 6.1: Funktionen sin x. 1 Oinas-Kukkonen m.fl. Kurs 6 kapitel 1
 Kapitel 6 Gränsvärde 6. Definition av gränsvärde När vi undersöker gränsvärdet av en funktion undersöker vi vad som händer med funktionsvärdet då variabeln, x, går mot ett visst värde. Frågeställningen
Kapitel 6 Gränsvärde 6. Definition av gränsvärde När vi undersöker gränsvärdet av en funktion undersöker vi vad som händer med funktionsvärdet då variabeln, x, går mot ett visst värde. Frågeställningen
PRÖVNINGSANVISNINGAR
 Prövning i Matematik 5 PRÖVNINGSANVISNINGAR Kurskod MATMAT05 Gymnasiepoäng 100 Läromedel Valfri aktuell lärobok för kurs Matematik 5 Skriftligt prov, 4h Teoretiskt prov Bifogas Provet består av två delar.
Prövning i Matematik 5 PRÖVNINGSANVISNINGAR Kurskod MATMAT05 Gymnasiepoäng 100 Läromedel Valfri aktuell lärobok för kurs Matematik 5 Skriftligt prov, 4h Teoretiskt prov Bifogas Provet består av två delar.
SKOGLIGA TILLÄMPNINGAR
 STUDIEAVSNITT 3 SKOGLIGA TILLÄMPNINGAR I detta avsnitt ska vi titta på några av de skogliga tillämpningar på geometri som finns. SKOGSKARTAN EN MODELL AV VERKLIGHETEN Arbetar man i skogen klarar man sig
STUDIEAVSNITT 3 SKOGLIGA TILLÄMPNINGAR I detta avsnitt ska vi titta på några av de skogliga tillämpningar på geometri som finns. SKOGSKARTAN EN MODELL AV VERKLIGHETEN Arbetar man i skogen klarar man sig
PROTOKOLL 2015-12-07. Svar på motion 2015:07 från Christer Johansson (V) om allmän visstidsanställning KS-2015/516
 Kommunstyrelsen Utdrag ur PROTOKOLL 2015-12-07 245 Svar på motion 2015:07 från Christer Johansson (V) om allmän visstidsanställning KS-2015/516 Beslut Kommunstyrelsen förslår kommunfullmäktige att avslå
Kommunstyrelsen Utdrag ur PROTOKOLL 2015-12-07 245 Svar på motion 2015:07 från Christer Johansson (V) om allmän visstidsanställning KS-2015/516 Beslut Kommunstyrelsen förslår kommunfullmäktige att avslå
OBSERVERA ATT DETTA EXEMPELMATERIAL INTE MOTSVARAR ETT HELT KURSPROV I OMFATTNING OCH INNEHÅLL.
 Matematik kurs b och c - Exempeluppgifter OBSERVERA ATT DETTA EXEMPELMATERIAL INTE MOTSVARAR ETT HELT KURSPROV I OMFATTNING OCH INNEHÅLL. Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv
Matematik kurs b och c - Exempeluppgifter OBSERVERA ATT DETTA EXEMPELMATERIAL INTE MOTSVARAR ETT HELT KURSPROV I OMFATTNING OCH INNEHÅLL. Del I: Digitala verktyg är inte tillåtna. Endast svar krävs. Skriv
PB 186, 01531 VANDA, FINLAND, tel. 358 (0)9 4250 11, fax 358 (0)9 4250 2898
 OPS M2-1, Bilaga 1 21.12.2007 PB 186, 01531 VANDA, FINLAND, tel. 358 (0)9 4250 11, fax 358 (0)9 4250 2898 www.luftfartsforvaltningen.fi FLYGPLANSLJUS Anm. Se avsnitt 6. 1. DEFINITIONER Termer och begrepp
OPS M2-1, Bilaga 1 21.12.2007 PB 186, 01531 VANDA, FINLAND, tel. 358 (0)9 4250 11, fax 358 (0)9 4250 2898 www.luftfartsforvaltningen.fi FLYGPLANSLJUS Anm. Se avsnitt 6. 1. DEFINITIONER Termer och begrepp
Sammanfattning av kursdag 2, 2013-03-07 i Stra ngna s och 2013-03-12 Eskilstuna
 Sammanfattning av kursdag 2, 2013-03-07 i Stra ngna s och 2013-03-12 Eskilstuna Sammanfattning och genomgång av lektion 1 samt hemläxa. -Hur ta ut en position i sjökortet? Mät med Passaren mellan positionen
Sammanfattning av kursdag 2, 2013-03-07 i Stra ngna s och 2013-03-12 Eskilstuna Sammanfattning och genomgång av lektion 1 samt hemläxa. -Hur ta ut en position i sjökortet? Mät med Passaren mellan positionen
Partnerskapsförord. giftorättsgods görs till enskild egendom 1, 2. Parter 3. Partnerskapsförordets innehåll: 4
 Partnerskapsförord giftorättsgods görs till enskild egendom 1, 2 Parter 3 Namn Telefon Adress Namn Telefon Adress Partnerskapsförordets innehåll: 4 Vi skall ingå registrerat partnerskap har ingått registrerat
Partnerskapsförord giftorättsgods görs till enskild egendom 1, 2 Parter 3 Namn Telefon Adress Namn Telefon Adress Partnerskapsförordets innehåll: 4 Vi skall ingå registrerat partnerskap har ingått registrerat
Bedömning för lärande i matematik i praktiken. Per Berggren och Maria Lindroth 2012-11-29
 Bedömning för lärande i matematik i praktiken Per Berggren och Maria Lindroth 2012-11-29 Inlärningsnivåer i matematik 1. Intuitiv tänka, tala 2. Konkret göra och pröva 3. Representationsformer synliggöra
Bedömning för lärande i matematik i praktiken Per Berggren och Maria Lindroth 2012-11-29 Inlärningsnivåer i matematik 1. Intuitiv tänka, tala 2. Konkret göra och pröva 3. Representationsformer synliggöra
912 Läsförståelse och matematik behöver man lära sig läsa matematik?
 912 Läsförståelse och matematik behöver man lära sig läsa matematik? Med utgångspunkt från min egen forskning kring läsförståelse av matematiska texter kommer jag att diskutera olika aspekter av läsning
912 Läsförståelse och matematik behöver man lära sig läsa matematik? Med utgångspunkt från min egen forskning kring läsförståelse av matematiska texter kommer jag att diskutera olika aspekter av läsning
kostar en lägenhet i Helsingfors? Det varierar. ska köttet vara i ugnen? Ungefär en timme.
 ska köttet vara i ugnen? Ungefär en timme. kostar en lägenhet i Helsingfors? Det varierar. gammal är Tina? Tjugofyra år. gillar du ditt arbete? Bra! Jag har mycket ansvar och bra lön. länge har du varit
ska köttet vara i ugnen? Ungefär en timme. kostar en lägenhet i Helsingfors? Det varierar. gammal är Tina? Tjugofyra år. gillar du ditt arbete? Bra! Jag har mycket ansvar och bra lön. länge har du varit
Lokal kursplan för Ängkärrskolan år 9 Rev. 2009-09-22. -Positionssystemet. -Multiplikation och division. (utan miniräknare).
 Lokal kursplan för Ängkärrskolan år 9 Rev. 009-09- Matematik år 9 MOMENT MÅL KRITERIER/EXEMPELl Taluppfattning, aritmetik Repetition av: Skriv med siffror tolv -Positionssystemet. hundradelar. 0,, 0,7
Lokal kursplan för Ängkärrskolan år 9 Rev. 009-09- Matematik år 9 MOMENT MÅL KRITERIER/EXEMPELl Taluppfattning, aritmetik Repetition av: Skriv med siffror tolv -Positionssystemet. hundradelar. 0,, 0,7
Pesach Laksman är lärarutbildare i matematik och matematikdidaktik vid Malmö högskola.
 111a Geometri med snöre Pesach Laksman är lärarutbildare i matematik och matematikdidaktik vid Malmö högskola. Areabegreppet När elever får frågan vad area betyder ges mestadels svar som antyder hur man
111a Geometri med snöre Pesach Laksman är lärarutbildare i matematik och matematikdidaktik vid Malmö högskola. Areabegreppet När elever får frågan vad area betyder ges mestadels svar som antyder hur man
SEPARABLA DIFFERENTIALEKVATIONER
 SEPARABLA DIFFERENTIALEKVATIONER En differentialekvation (DE) av första ordningen sägs vara separabel om den kan skrivas på formen P ( y) Q( ) () Den allmänna lösningen till () erhålles genom att integrera
SEPARABLA DIFFERENTIALEKVATIONER En differentialekvation (DE) av första ordningen sägs vara separabel om den kan skrivas på formen P ( y) Q( ) () Den allmänna lösningen till () erhålles genom att integrera
NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN 1998 2
 freeleaks NpMaB ht1998 1(8) Innehåll Förord 1 NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN 1998 Förord Skolverket har endast publicerat ett kursprov till kursen Ma. Innehållet i den äldre kursen Ma B
freeleaks NpMaB ht1998 1(8) Innehåll Förord 1 NATIONELLT KURSPROV I MATEMATIK KURS B HÖSTEN 1998 Förord Skolverket har endast publicerat ett kursprov till kursen Ma. Innehållet i den äldre kursen Ma B
I den här delen används inte räknare. Motivera alltid din slutsats med matematiska uttryck, figurer, förklaring el.dyl.
 DEL 1 Tid 30 min Poängantal 20 I den här delen används inte räknare. Motivera alltid din slutsats med matematiska uttryck, figurer, förklaring el.dyl. 1. Vilket är det största heltalet, som uppfyller följande
DEL 1 Tid 30 min Poängantal 20 I den här delen används inte räknare. Motivera alltid din slutsats med matematiska uttryck, figurer, förklaring el.dyl. 1. Vilket är det största heltalet, som uppfyller följande
Uppgift 2 0 0.10 1 0.25 2 0.40 3 0.20 4 0.05
 Uppgift 1 En grönsaksgrossist har utvecklat ett test för att kontrollera kvaliteten hos tomater. Efter att ha inspekterat ett urval från ett parti tomater, accepteras eller förkastas partiet. Med detta
Uppgift 1 En grönsaksgrossist har utvecklat ett test för att kontrollera kvaliteten hos tomater. Efter att ha inspekterat ett urval från ett parti tomater, accepteras eller förkastas partiet. Med detta
LATIN SPRÅK OCH KULTUR
 LATIN SPRÅK OCH KULTUR Ämnet latin språk och kultur är till sin karaktär ett humanistiskt ämne som förenar språk- och kulturstudier. Latinet har varit modersmål och kommunikationsspråk för en stor del
LATIN SPRÅK OCH KULTUR Ämnet latin språk och kultur är till sin karaktär ett humanistiskt ämne som förenar språk- och kulturstudier. Latinet har varit modersmål och kommunikationsspråk för en stor del
Arbetsblad 4:1. Bråkform decimalform procentform. 1 Fyll i tabellen. 2 Fyll i tabellen. Bild Bråkform Decimalform Procentform 1 0,5 50 % 20 % 0,3 75 %
 Arbetsblad 4:1 sid 108, 120 Bråkform decimalform procentform 1 Fyll i tabellen Bild Bråkform Decimalform Procentform 1 0,5 50 % 2 4 20 % 0,3 75 % 2 Fyll i tabellen f) Uttryck Bråkform Decimalform Procentform
Arbetsblad 4:1 sid 108, 120 Bråkform decimalform procentform 1 Fyll i tabellen Bild Bråkform Decimalform Procentform 1 0,5 50 % 2 4 20 % 0,3 75 % 2 Fyll i tabellen f) Uttryck Bråkform Decimalform Procentform
Brister i kunskap vid gymnasieval
 Brister i kunskap vid gymnasieval En undersökning om hur niondeklassarna tänker inför sitt val av skola och program Gymnasium.se Hovslagargatan 3 SE 103 88 STOCKHOLM 08-50 91 06 00 1 Bakgrund och metod
Brister i kunskap vid gymnasieval En undersökning om hur niondeklassarna tänker inför sitt val av skola och program Gymnasium.se Hovslagargatan 3 SE 103 88 STOCKHOLM 08-50 91 06 00 1 Bakgrund och metod
Gissa det hemliga talet
 Laborationsanvisning Gissa det hemliga talet Steg 1, laborationsuppgift 1 Författare: Mats Loock Kurs: ASP.NET MVC Kurskod:1DV409 Innehåll Problem 4 Modell 4 Den uppräkningsbara typen Outcome 5 Strukturen
Laborationsanvisning Gissa det hemliga talet Steg 1, laborationsuppgift 1 Författare: Mats Loock Kurs: ASP.NET MVC Kurskod:1DV409 Innehåll Problem 4 Modell 4 Den uppräkningsbara typen Outcome 5 Strukturen
Innehållet i detta häfte är sekretessbelagt t o m den 9 juni 2006.
 Innehållet i detta häfte är sekretessbelagt t o m den 9 juni 2006. Efter varje uppgift anges maximala antalet poäng som du kan få för din lösning. T ex betyder (2/1) att uppgiften kan ge 2 g-poäng och
Innehållet i detta häfte är sekretessbelagt t o m den 9 juni 2006. Efter varje uppgift anges maximala antalet poäng som du kan få för din lösning. T ex betyder (2/1) att uppgiften kan ge 2 g-poäng och
Omvandla Vinklar. 1 Mattematiskt Tankesätt
 Omvandla Vinklar 1 Mattematiskt Tankesätt (Kan användas till mer än bara vinklar) 2 Omvandla med hjälp av Huvudräkning (Snabbmetod i slutet av punkt 2) 3 Omvandla med Miniräknare (Casio) Läs denna Först
Omvandla Vinklar 1 Mattematiskt Tankesätt (Kan användas till mer än bara vinklar) 2 Omvandla med hjälp av Huvudräkning (Snabbmetod i slutet av punkt 2) 3 Omvandla med Miniräknare (Casio) Läs denna Först
2005-01-31. Hävarmen. Peter Kock
 2005-01-31 Hävarmen Kurs: WT0010 Peter Kock Handledare: Jan Sandberg Sammanfattning Om man slår upp ordet hävarm i ett lexikon så kan man läsa att hävarm är avståndet mellan kraften och vridningspunkten.
2005-01-31 Hävarmen Kurs: WT0010 Peter Kock Handledare: Jan Sandberg Sammanfattning Om man slår upp ordet hävarm i ett lexikon så kan man läsa att hävarm är avståndet mellan kraften och vridningspunkten.
Sannolikhet och Odds
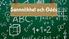 Sannolikhet och Odds Sannolikhet Tärning (Orange) och (Blå) 0 0 0 Om man satsat sina pengar på rätt summa multipliceras oddset med insatsen (pengarna man satsar) Odds Utfall (summan av två tärningar) Sannolikhet
Sannolikhet och Odds Sannolikhet Tärning (Orange) och (Blå) 0 0 0 Om man satsat sina pengar på rätt summa multipliceras oddset med insatsen (pengarna man satsar) Odds Utfall (summan av två tärningar) Sannolikhet
Institutionen för matematik Envariabelanalys 1. Jan Gelfgren Datum: Fredag 9/12, 2011 Tid: 9-15 Hjälpmedel: Inga (ej miniräknare)
 Umeå universitet Dugga i matematik Institutionen för matematik Envariabelanalys 1 och matematisk statistik IE, ÖI, Stat. och Frist. Jan Gelfgren Datum: Fredag 9/12, 2011 Tid: 9-15 Hjälpmedel: Inga (ej
Umeå universitet Dugga i matematik Institutionen för matematik Envariabelanalys 1 och matematisk statistik IE, ÖI, Stat. och Frist. Jan Gelfgren Datum: Fredag 9/12, 2011 Tid: 9-15 Hjälpmedel: Inga (ej
Skriva B gammalt nationellt prov
 Skriva B gammalt nationellt prov Skriva B.wma Då fortsätter vi skrivträningen. Detta avsnitt handlar om att anpassa sin text till en särskild situation, en speciell texttyp och särskilda läsare. Nu ska
Skriva B gammalt nationellt prov Skriva B.wma Då fortsätter vi skrivträningen. Detta avsnitt handlar om att anpassa sin text till en särskild situation, en speciell texttyp och särskilda läsare. Nu ska
4-3 Vinklar Namn: Inledning. Vad är en vinkel?
 4-3 Vinklar Namn: Inledning I det här kapitlet skall du lära dig allt om vinklar: spetsiga, trubbiga och räta vinklar. Och inte minst hur man mäter vinklar. Att mäta vinklar och sträckor är grundläggande
4-3 Vinklar Namn: Inledning I det här kapitlet skall du lära dig allt om vinklar: spetsiga, trubbiga och räta vinklar. Och inte minst hur man mäter vinklar. Att mäta vinklar och sträckor är grundläggande
Har vi lösningen för en bättre hemtjänst? Självklart.
 Har vi lösningen för en bättre hemtjänst? Självklart. Låt oss prata om Självklarhetsmetoden. Låt oss prata om Självklarhetsmetoden! 164 000 äldre är beroende av hemtjänsten i sin vardag. Och det är du
Har vi lösningen för en bättre hemtjänst? Självklart. Låt oss prata om Självklarhetsmetoden. Låt oss prata om Självklarhetsmetoden! 164 000 äldre är beroende av hemtjänsten i sin vardag. Och det är du
Fakta om Malala Yousafzai
 SIDAN 1 Elevmaterial Namn: Klicka HÄR för att skriva ut arbetsmaterialet. Klicka HÄR för att skicka ditt färdiga arbetsmaterial till din pedagog. LÄSFÖRSTÅELSE Skottet 1. Vart var Malala på väg när hon
SIDAN 1 Elevmaterial Namn: Klicka HÄR för att skriva ut arbetsmaterialet. Klicka HÄR för att skicka ditt färdiga arbetsmaterial till din pedagog. LÄSFÖRSTÅELSE Skottet 1. Vart var Malala på väg när hon
Skogsbruk på ren svenska Lektion 4: Mästare på både förnyelse och återvinning. Tema: Återvinning Ämne: Biologi, Kemi Årskurs: 7-9
 Skogsbruk på ren svenska Lektion 4: Mästare på både förnyelse och återvinning. Tema: Återvinning Ämne: Biologi, Kemi Årskurs: 7-9 Förord Sveaskog är landets största skogsägare. Det ger oss både mycket
Skogsbruk på ren svenska Lektion 4: Mästare på både förnyelse och återvinning. Tema: Återvinning Ämne: Biologi, Kemi Årskurs: 7-9 Förord Sveaskog är landets största skogsägare. Det ger oss både mycket
DEMOKRATI 3 DEMOKRATINS VILLKOR
 SIDA 1/8 WORKSHOP I KLASSRUMMET TEMA: DEMOKRATI LÄRARMANUAL I det här dokumentet finns allt du behöver veta för att hålla workshopen. Här ser du också tydligt i vilka moment du använder det arbets- och
SIDA 1/8 WORKSHOP I KLASSRUMMET TEMA: DEMOKRATI LÄRARMANUAL I det här dokumentet finns allt du behöver veta för att hålla workshopen. Här ser du också tydligt i vilka moment du använder det arbets- och
Tentamen. Makroekonomi NA0133. Juni 2016 Skrivtid 3 timmar.
 Jag har svarat på följande fyra frågor: 1 2 3 4 5 6 Min kod: Institutionen för ekonomi Rob Hart Tentamen Makroekonomi NA0133 Juni 2016 Skrivtid 3 timmar. Regler Svara på 4 frågor. (Vid svar på fler än
Jag har svarat på följande fyra frågor: 1 2 3 4 5 6 Min kod: Institutionen för ekonomi Rob Hart Tentamen Makroekonomi NA0133 Juni 2016 Skrivtid 3 timmar. Regler Svara på 4 frågor. (Vid svar på fler än
Sveriges Trafikskolors Riksförbund Film om körkort för nysvenskar Speakertext - Svensk
 Sveriges Trafikskolors Riksförbund Film om körkort för nysvenskar Speakertext - Svensk Vägen till svenskt körkort Funderar du på att skaffa svenskt körkort för personbil? I den här filmen får du reda på
Sveriges Trafikskolors Riksförbund Film om körkort för nysvenskar Speakertext - Svensk Vägen till svenskt körkort Funderar du på att skaffa svenskt körkort för personbil? I den här filmen får du reda på
Individuellt Mjukvaruutvecklingsprojekt
 Individuellt Mjukvaruutvecklingsprojekt RPG-spel med JavaScript Författare Robin Bertram Datum 2013 06 10 1 Abstrakt Den här rapporten är en post mortem -rapport som handlar om utvecklandet av ett RPG-spel
Individuellt Mjukvaruutvecklingsprojekt RPG-spel med JavaScript Författare Robin Bertram Datum 2013 06 10 1 Abstrakt Den här rapporten är en post mortem -rapport som handlar om utvecklandet av ett RPG-spel
a n = A2 n + B4 n. { 2 = A + B 6 = 2A + 4B, S(5, 2) = S(4, 1) + 2S(4, 2) = 1 + 2(S(3, 1) + 2S(3, 2)) = 3 + 4(S(2, 1) + 2S(2, 2)) = 7 + 8 = 15.
 1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D och F, SF161 och SF160, den juni 008 kl 08.00-1.00. DEL I 1. (p) Lös rekursionsekvationen
1 Matematiska Institutionen KTH Lösningar till tentamensskrivning på kursen Diskret Matematik, moment A, för D och F, SF161 och SF160, den juni 008 kl 08.00-1.00. DEL I 1. (p) Lös rekursionsekvationen
NpMa2a vt Provet består av tre skriftliga delprov (Delprov B, C och D). Tillsammans kan de ge 55 poäng varav 22 E-, 19 C- och 14 A-poäng.
 Delprov B Delprov C Provtid Hjälpmedel Uppgift 1-8. Endast svar krävs. Uppgift 9-14. Fullständiga lösningar krävs. 10 minuter för Delprov B och Delprov C tillsammans. Formelblad och linjal. Kravgränser
Delprov B Delprov C Provtid Hjälpmedel Uppgift 1-8. Endast svar krävs. Uppgift 9-14. Fullständiga lösningar krävs. 10 minuter för Delprov B och Delprov C tillsammans. Formelblad och linjal. Kravgränser
Kunskapskrav för godtagbara kunskaper i matematik - slutet av åk 3
 Kunskapskraven åk k 3 - matematik 20 Kunskapskrav för godtagbara kunskaper i matematik - slutet av åk 3 Eleven kan lösa enkla problem i elevnära situationer genom att välja och använda någon strategi med
Kunskapskraven åk k 3 - matematik 20 Kunskapskrav för godtagbara kunskaper i matematik - slutet av åk 3 Eleven kan lösa enkla problem i elevnära situationer genom att välja och använda någon strategi med
Steg 10. 6 a) 0,129 b) 1,72 c) 2,05 7 a) 960 kr b) 1600 kr c) 14 kr 8 30% 9 a) 32% b) 60% c) 12% 10 20% 11 a) b) c) 2. 12 a) 135 b) c) 6 ( )
 Bråk och procent Steg elever a) st b) st 0,, %,,,, 0 liter T ex och a) b) 0 a) 0, b) 0, c) 0, a) ( ) b) c) 00 0 a) b) c) a) ( 00) b) 0 ( 000) c) ( ) 000 a) 0, b) 0, c) 0, a) b) c) 0 a) b) a) > b) < c)
Bråk och procent Steg elever a) st b) st 0,, %,,,, 0 liter T ex och a) b) 0 a) 0, b) 0, c) 0, a) ( ) b) c) 00 0 a) b) c) a) ( 00) b) 0 ( 000) c) ( ) 000 a) 0, b) 0, c) 0, a) b) c) 0 a) b) a) > b) < c)
Det flippade klassrummet hur uppfattas det av eleverna?
 Det flippade klassrummet hur uppfattas det av eleverna? Vi och vår skola Undervisningslyftet Samarbete Karlskrona kommun och Högskolan i Jönköping Föreläsningar, seminarier, handledning Möjlighet att ta
Det flippade klassrummet hur uppfattas det av eleverna? Vi och vår skola Undervisningslyftet Samarbete Karlskrona kommun och Högskolan i Jönköping Föreläsningar, seminarier, handledning Möjlighet att ta
Del I. Miniräknare ej tillåten. Namn:... Klass/Grupp:... 1. Vilket tal är 0,1 större än 3,96? Svar: (1/0) 2. Vilket tal i decimalform ska stå i rutan?
 Miniräknare ej tillåten Namn:... Klass/Grupp:... Del I 1. Vilket tal är 0,1 större än 3,96? Svar: (1/0) 2. Vilket tal i decimalform ska stå i rutan? a 0 1 2 Svar: a = (1/0) 3. Vilka koordinater har punkten
Miniräknare ej tillåten Namn:... Klass/Grupp:... Del I 1. Vilket tal är 0,1 större än 3,96? Svar: (1/0) 2. Vilket tal i decimalform ska stå i rutan? a 0 1 2 Svar: a = (1/0) 3. Vilka koordinater har punkten
VÄRDERINGSÖVNINGAR. Vad är Svenskt?
 VÄRDERINGSÖVNINGAR Vad är Svenskt? Typ av övning: Avstamp till diskussion. Övningen belyser hur svårt det är att säga vad som är svenskt och att normen vad som anses vara svenskt ändras med tiden och utifrån
VÄRDERINGSÖVNINGAR Vad är Svenskt? Typ av övning: Avstamp till diskussion. Övningen belyser hur svårt det är att säga vad som är svenskt och att normen vad som anses vara svenskt ändras med tiden och utifrån
Kriterium Kvalitet 1 Kvalitet 2 Kvalitet 3 Kvalitet 4 Använda, Utveckla och uttrycka
 Matematik Enheter - Tid Utveckla och Känner till några enheter och enstaka mätinstrument. Utför enkla mätningar. Avläser analoga och digitala tider.använder både muntliga och skriftliga metoder samt tekniska
Matematik Enheter - Tid Utveckla och Känner till några enheter och enstaka mätinstrument. Utför enkla mätningar. Avläser analoga och digitala tider.använder både muntliga och skriftliga metoder samt tekniska
SF1620 Matematik och modeller
 KTH Teknikvetenskap, Institutionen för matematik 1 SF160 Matematik och modeller 007-09-10 Andra veckan Trigonometri De trigonometriska funktionerna och enhetscirkeln Redan vid förra veckans avsnitt var
KTH Teknikvetenskap, Institutionen för matematik 1 SF160 Matematik och modeller 007-09-10 Andra veckan Trigonometri De trigonometriska funktionerna och enhetscirkeln Redan vid förra veckans avsnitt var
Från min. klass INGER BJÖRNELOO
 Från min klass INGER BJÖRNELOO Vi har nu följt Inger Björneloos klass under två år. Klassen börjar i höst på sitt sista lågstadieår, åk 3. Denna årgång av NÄMNAREN kommer att följa upp vad de gör och hur
Från min klass INGER BJÖRNELOO Vi har nu följt Inger Björneloos klass under två år. Klassen börjar i höst på sitt sista lågstadieår, åk 3. Denna årgång av NÄMNAREN kommer att följa upp vad de gör och hur
Diskussionsfrågor till version 1 och 2
 Diskussionsfrågor till version 1 och 2 Version 1 Tillgång till internet i hemmet A. Vilken åldersgrupp har haft den största ökningen av tillgång till internet under perioden? B. Kan man med hjälp av de
Diskussionsfrågor till version 1 och 2 Version 1 Tillgång till internet i hemmet A. Vilken åldersgrupp har haft den största ökningen av tillgång till internet under perioden? B. Kan man med hjälp av de
Mamma Angelica: Vi saknar henne och vill att hon kommer hem. 1 av 5 2015-11-05 08:43. Textstorlek:
 Textstorlek: Johanssons dotter Nathalie har förts utomlands av sin pappa. har även tre barn tillsammans med Andreas Iversen. PERNILLA WAHLMAN Mamma : Vi saknar henne vill hon kommer hem SUNDSVALL. Nästan
Textstorlek: Johanssons dotter Nathalie har förts utomlands av sin pappa. har även tre barn tillsammans med Andreas Iversen. PERNILLA WAHLMAN Mamma : Vi saknar henne vill hon kommer hem SUNDSVALL. Nästan
Avgifter i skolan. Informationsblad
 Informationsblad 1 (8) Avgifter i skolan Här kan du läsa om hur Skolinspektionen bedömer avgifter i skolan i samband med tillsynen. Informationsbladet redogör för Skolinspektionens praxis. Här kan du även
Informationsblad 1 (8) Avgifter i skolan Här kan du läsa om hur Skolinspektionen bedömer avgifter i skolan i samband med tillsynen. Informationsbladet redogör för Skolinspektionens praxis. Här kan du även
Föreläsning 8: Räkning. Duvhålsprincipen. Kombinatorik
 Föreläsning 8: Räkning. Duvhålsprincipen. Kombinatorik Summaregeln Om och B är disjunkta mängder så B = + B, ty innehåller inga upprepningar Produktregeln Om och B är disjunkta mängder så är B = B Exempel:
Föreläsning 8: Räkning. Duvhålsprincipen. Kombinatorik Summaregeln Om och B är disjunkta mängder så B = + B, ty innehåller inga upprepningar Produktregeln Om och B är disjunkta mängder så är B = B Exempel:
Kvinnor som driver företag pensionssparar mindre än män
 Pressmeddelande 7 september 2016 Kvinnor som driver företag pensionssparar mindre än män Kvinnor som driver företag pensionssparar inte i lika hög utsträckning som män som driver företag, 56 respektive
Pressmeddelande 7 september 2016 Kvinnor som driver företag pensionssparar mindre än män Kvinnor som driver företag pensionssparar inte i lika hög utsträckning som män som driver företag, 56 respektive
Statsbidrag för läxhjälp till huvudmän 2016
 Statsbidragsenheten 1 (5) Statsbidrag för läxhjälp till huvudmän 2016 Skolverket lämnar statsbidrag enligt förordning (2014:144) om statsbidrag för hjälp med läxor eller annat skolarbete utanför ordinarie
Statsbidragsenheten 1 (5) Statsbidrag för läxhjälp till huvudmän 2016 Skolverket lämnar statsbidrag enligt förordning (2014:144) om statsbidrag för hjälp med läxor eller annat skolarbete utanför ordinarie
Affärsplan? Ett dokument där viktig information om ert företag samlas. Den ska förtydliga och visa era tankar kring hur ert företag ska drivas.
 Affärsplan Affärsplan? Ett dokument där viktig information om ert företag samlas. Den ska förtydliga och visa era tankar kring hur ert företag ska drivas. Berätta om den verksamhet ni tänker bygga upp.
Affärsplan Affärsplan? Ett dokument där viktig information om ert företag samlas. Den ska förtydliga och visa era tankar kring hur ert företag ska drivas. Berätta om den verksamhet ni tänker bygga upp.
FRÅN A TILL Ö LäraMera Ab / www.laramera.se och Allemansdata Ab / www.allemansdata.se FRÅN A TILL Ö
 I programmet finns 11 olika aktiviteter för att träna varje bokstav och på att känna igen ord. För varje bokstav kan olika övningsblad skrivas ut: Inledningsvis väljer du vilken bokstav du vill öva på.
I programmet finns 11 olika aktiviteter för att träna varje bokstav och på att känna igen ord. För varje bokstav kan olika övningsblad skrivas ut: Inledningsvis väljer du vilken bokstav du vill öva på.
Del 1, trepoängsproblem
 Del 1, trepoängsproblem 1 Lisa ska sätta in siffran 3 någonstans i talet 2014 så att hon får ett femsiffrigt tal. Det femsiffriga talet ska bli så litet som möjligt. Var ska hon sätta siffran 3? A: före
Del 1, trepoängsproblem 1 Lisa ska sätta in siffran 3 någonstans i talet 2014 så att hon får ett femsiffrigt tal. Det femsiffriga talet ska bli så litet som möjligt. Var ska hon sätta siffran 3? A: före
Friskoleurval med segregation som resultat
 Friskoleurval med segregation som resultat Rapport februari 2016 Sammanfattning och slutsatser Denna undersökning har tagits fram som en del av projektet Ge alla elever samma chans som är ett samarbete
Friskoleurval med segregation som resultat Rapport februari 2016 Sammanfattning och slutsatser Denna undersökning har tagits fram som en del av projektet Ge alla elever samma chans som är ett samarbete
e-cm Elektronisk Cash Management dygnet runt, världen över.
 e-cm Elektronisk Cash Management dygnet runt, världen över. Välkommen till gränslösa affärsmöjligheter. Goda affärer kräver rätt förutsättningar. Rätt information när du behöver det och möjligheten att
e-cm Elektronisk Cash Management dygnet runt, världen över. Välkommen till gränslösa affärsmöjligheter. Goda affärer kräver rätt förutsättningar. Rätt information när du behöver det och möjligheten att
[ÖVNINGSBANK] Sollentuna FK. Expressbollen
![[ÖVNINGSBANK] Sollentuna FK. Expressbollen [ÖVNINGSBANK] Sollentuna FK. Expressbollen](/thumbs/41/22376262.jpg) Expressbollen Övning nr. 1 Två lag på varje långlinje i en rektangel på 15x25 meter. o T.ex. Halv gympasal o Viktigt att vara tydlig med mitten, d.v.s. markera mitten med koner Varje spelare har en boll.
Expressbollen Övning nr. 1 Två lag på varje långlinje i en rektangel på 15x25 meter. o T.ex. Halv gympasal o Viktigt att vara tydlig med mitten, d.v.s. markera mitten med koner Varje spelare har en boll.
Tomi Alahelisten Lärare Idrott & Hälsa - Internationella Skolan Atlas i Linköping. Orientering
 Orientering 1. Inledning Orientering härstammar från Norden i slutet på 1800-talet. Ursprungligen var orientering en militär övning, men tidigt såg man nyttan med att sprida denna kunskap till allmänheten
Orientering 1. Inledning Orientering härstammar från Norden i slutet på 1800-talet. Ursprungligen var orientering en militär övning, men tidigt såg man nyttan med att sprida denna kunskap till allmänheten
