2. Lösning av elektrostatiska problem för ledare
|
|
|
- Lars Hermansson
- för 8 år sedan
- Visningar:
Transkript
1 2. Lösning av elektrostatiska problem för ledare [RMC] Elektrodynamik, vt 2008, Kai Nordlund 2.1
2 2.1. Poissons ekvation [RMC, Jackson] Från tidigare vet vi att E(r) = ρ(r) ε 0 (2.1) E(r) = ϕ(r) (2.2) Detta ger oss genast 2 ϕ(r) = ρ(r) ε 0 (2.3) som kallas Poissons ekvation. Laplace-operatorn är i Cartesiska koordinater (x, y, z), 2 ϕ = 2 x ϕ + 2 y ϕ + 2 z ϕ (2.4) Elektrodynamik, vt 2008, Kai Nordlund 2.2
3 2 ϕ(r) = 1 ρ ρ ρ ϕ(r) «+ 1 2 ϕ(r) ρ ρ 2 ψ ϕ(r) z 2 (2.5) i cylindriska koordinater (ρ, ψ, z), och 2 ϕ(r) = 1 r 2 r «r 2 ϕ(r) + 1 r r 2 sin θ θ sin θ ϕ(r) «+ θ 1 r 2 sin 2 θ 2 ϕ(r) φ 2 (2.6) i sfäriska koordinater (r, θ, ϕ), Om ρ(r) = 0 i de flesta punkter r, d.v.s. vi har ledare och bara ett fåtal externa laddningsfördelningar, så får vi Laplaces ekvation 2 ϕ(r) = 0 (2.7) Tidigare bestämde vi elfältet från en laddningsfördelning ρ(r) genom att integrera ett enda uttryck. I dessa fall var fördelningen ρ(r) bestämd på förhand. Elektrodynamik, vt 2008, Kai Nordlund 2.3
4 Vi kommer nu att granska allmänna system av laddningsfördelningar och ledare, och hur de ser ut vid statisk jämvikt. Situationen kompliceras nu av att laddnigar induceras på de ledande ytorna, och denna laddning är inte känd på förhand. Dylika system beskrivs i det allmänna fallet av Poissons ekvation, vars lösning ϕ(r) alltså ger oss systemets elektrostatiska tillstånd. För att lösa Laplaces ekvation (eller Poissons ekvation i allmänhet) för ett system av N st ledare behöver vi känna till randvillkoren, d.v.s. definierade värden på den sökta funktionen ϕ eller dess derivator i givna punkter. Om ϕ(r) är känd på ledarnas ytor, d.v.s. vi vet ϕ Ai, i = 1, 2,..., N, kallas randvillkoren för Dirichlet-randvillkor. Om istället ϕ/ n (potentialens normalderivata, d.v.s. elfältet) är känd på ledarnas ytor, d.v.s. vi vet ( ϕ/ n) Ai, i = 1, 2,..., N, kallas randvillkoren för Neumann-randvillkor. Med både ϕ Si och ( ϕ/ n) Ai specificerade kan en lösning inte garanteras existera. Detta för att Dirichlet- och Neumann-randvillkor kan leda till olika lösningar! Denna kombination av randvillkor kallas Cauchy-randvillkor. Om vi har bara en ledare och punkt-laddningar betecknar man ofta ledarens ytpotential med ϕ 0. Elektrodynamik, vt 2008, Kai Nordlund 2.4
5 Exempel 1: Två klot bredvid varandra. Exempel 2: Två cylindrar bredvid varandra. Exempel 3: Två plan bredvid varandra. Exempel 4: En punktladdning ovanför ett plan. Exempel 5: En punktladdning ovanför ett klot. Exempel 6: En punktladdning utanför en cylinder. O.s.v.! Vi kommer i de följande sektionerna att lösa Laplace-ekvationen explicit för olika högsymmetri-fall. Vi kommer också att se på en alternativ lättare teknik vid namn bildladdnings-metoden. Elektrodynamik, vt 2008, Kai Nordlund 2.5
6 2.2. Laplace-ekvationens egenskaper Superposition Låt ϕ i (r), i = 1,..., M vara lösningar till Laplaces ekvation. Då gäller att MX ϕ(r) = C i ϕ i (r) (2.8) i=1 där C i är godtyckliga konstanter också är en lösning. Bevis: Direkt insättning av ϕ(r) i Laplaces ekvation! Unikhet Låt ϕ 1 och ϕ 2 vara två lösningar till Laplaces ekvation, så att de uppfyller samma randvillkor på alla ledarnas ytor A 1, A 2,... i systemet. Då gäller att ϕ 1 och ϕ 2 kan skilja sig med högst en konstant term. Bevis: Definiera Φ = ϕ 1 ϕ 2. Eftersom båda löser Laplaces ekvation så gäller 2 Φ = 0. Dessutom, antingen gäller Φ = 0 eller bn Φ = 0 på ledarnas ytor. Elektrodynamik, vt 2008, Kai Nordlund 2.6
7 Välj nu ytan A i oändligheten, där potentialerna fösvinner: Enligt Gauss teorem har vi då att I A dabn Φ( Φ) = 0 (2.9) Expandera integranden: I V dv (Φ( Φ)) = 0 (2.10) (Φ( Φ)) = Φ 2 Φ + ( Φ) 2 = 0 + ( Φ) 2 (2.11) Vi har då I V dv ( Φ) 2 = 0 (2.12) Enda möjligheten är att ( Φ) 2 = 0 överallt inom V. Alltså, ϕ 1 ϕ 2 = 0, så att vi måste ha ϕ 2 = ϕ 1 + C 0, där C 0 är en konstant. Om vi alltså har randvillkoren givna så existerar det endast en unik lösning till Laplaces ekvation. Ifall vi har ett Neumann-problem kan vi addera en godtycklig konstant till lösningen för potentialen, men elfältet är fortfarande unikt. Elektrodynamik, vt 2008, Kai Nordlund 2.7
8 2.3. Laplace-ekvationen i en oberoende variabel Låt nu ϕ vara en funktion i endast en variabel. Laplace-ekvationen ger nu för reaktangulära koordinater d 2 ϕ dx 2 = 0 (2.13) Detta kan genast integreras till ϕ(x) = ax + b. Ett annat fall är att ϕ är sfäriskt symmetrisk, d.v.s. ϕ = ϕ(r). Laplace-ekvationen i sfäriska koordinater ger nu 1 d r 2 dr «r 2 dϕ dr = 0 (2.14) Detta ger efter en integrering Elektrodynamik, vt 2008, Kai Nordlund 2.8
9 så att r 2 dϕ dr = a (2.15) dϕ dr = a r 2 (2.16) Efter ytterligare en integrering: ϕ(r) = a r + b (2.17) Elektrodynamik, vt 2008, Kai Nordlund 2.9
10 2.4. Laplace-ekvationen i sfäriska koordinater [RMC, Jackson, Arfken] Azimutal symmetri Vi kommer i det följande att anta azimutal symmetri, d.v.s. att den potential som sökes är symmetrisk runt z-axeln. Då gäller att ϕ = ϕ(r, θ). Laplaces ekvation blir 1 r 2 r «r 2 ϕ + 1 r r 2 sin θ θ sin θ ϕ «θ = 0 (2.18) Enklaste lösningsmetoden är att anta att ϕ kan skrivas som en produkt av en-variabels funktioner: ϕ(r, θ) = Z(r)Q(θ). Insättning ger 1 r 2Q d dr «r 2 dz + 1 dr r 2 sin θ Z d dθ sin θ dq «dθ = 0 (2.19) Efter förenkling 1 d Z dr «r 2 dz + 1 dr sin θ 1 d Q dθ sin θ dq «dθ = 0 (2.20) Första termen beror bara på r medan andra beror bara på θ. För att dessa termer ska vara lika för Elektrodynamik, vt 2008, Kai Nordlund 2.10
11 alla värden på r och θ måste de vara en konstant. Kalla denna k: sin θ Q dθ d Z dr d r 2 dz dr sin θ dq dθ ««= k (2.21) = k (2.22) Detta är Legendres ekvation. Med en icketrivial matematisk betraktelse kan man visa att dessa differentialekvationer har fysikaliskt meningsfulla lösningar endast ifall k = m(m + 1) där m är ett heltal. Vi inför beteckningen P (x) P (cos θ) = Q(θ). = - k P Lösningarna är s.k. Legendre-polynom, av vilka de fem första är Elektrodynamik, vt 2008, Kai Nordlund 2.11
12 P 0 (x) = 1 (2.23) P 1 (x) = x (2.24) P 2 (x) = 1 2 (3x2 1) (2.25) P 3 (x) = 1 2 (5x3 3x) (2.26) P 4 (x) = 1 8 (35x4 30x 2 + 3) (2.27) där x = cos θ. Man kan visa [Arfken] att i allmänhet ges Legendre-polynomet m av uttrycket som kallas Rodrigues formel. P m (x) = 1 2 m m! d dx «m (x 2 1) m, (2.28) Elektrodynamik, vt 2008, Kai Nordlund 2.12
13 Då alltså vinkeldelen ger villkoret k = m(m + 1), gäller för den radiellea delen: 1 d Z dr «r 2 dz dr = m(m + 1) (2.29) Gör Ansatzen Z(r) = r p, där p bör bestämmas. Insättning ger m(m + 1) = r p d dr = pr p dr p+1 r 2 pr p 1 dr = p(p + 1)r p r p = p(p + 1) (2.30) Elektrodynamik, vt 2008, Kai Nordlund 2.13
14 Lös detta: p 2 + p + 1 = m 2 + m + 1 (2.31) 4 4 p = m + 2«1 2 (2.32) 2«p = ±(m ) (2.33) p = 1 2 ± (m ) (2.34) Vi får förutom triviallösningen p = m möjligheten p = (m + 1). Problemets lösning är alltså ϕ m (r, θ) = Ar m P m (cos θ) eller ϕ m (r, θ) = Br (m+1) P m (cos θ) (2.35) med m = 0, 1, 2,... och A, B konstanter. Dessa funktioner kallas zon-ytfunktioner (zonal harmonics). Elektrodynamik, vt 2008, Kai Nordlund 2.14
15 Den mest allmänna lösningen till problemet är dock ϕ(r, θ) = X A m r m P m (cos θ) + m=0 X B n r (n+1) P n (cos θ), SPH, (r, θ) (2.36) n=0 Exempel 1: m = 0. ϕ(r, θ) = A eller ϕ(r, θ) = A r 1. Den senare lösningen är ju en punktladdnings potential. Exempel 2: m = 1. ϕ(r, θ) = ArP 1 (cos θ) eller ϕ(r, θ) = A r 2 P 1 (cos θ). Den senare lösningen är ju en dipols potential. Elektrodynamik, vt 2008, Kai Nordlund 2.15
16 Exempel 3: Oladdad ledande sfär i ett konstant elfält. Låt elfältet vara i z-riktningen och sfärens mittpunkt i origo. Vi har samma potential ϕ(r = a, θ) ϕ 0 i ledarens inre som på dess yta. Elektrodynamik, vt 2008, Kai Nordlund 2.16
17 Lösningen är helt allmänt ϕ(r, θ) = A 0 + B 0 r 1 +A 1 r cos θ + B 1 r 2 cos θ A 2r 2 (3 cos 2 θ 1) B 2r 3 (3 cos 2 θ 1) +... (2.37) I oändligheten återfår vi det urprungliga fältet, E(r = ) = E 0 bz = dϕ/dz, så ϕ(r = ) = E 0 z + C, med C en konstant. ϕ(r =, θ) = E 0 z + C = E 0 r cos θ + C A 0 + A 1 r cos θ (2.38) Vi måste då ha att A n = 0, n 2 och A 1 = E 0. Då r = a gäller ϕ(r = a, θ) = konstant, så alla B n = 0 för n 2. Vi behåller B 1 för att ha möjlighet att kompensera A 1 -termens θ-beroende vid r = a. Elektrodynamik, vt 2008, Kai Nordlund 2.17
18 Vi har nu ϕ(r, θ) = A 0 + B 0 r 1 + A 1 r cos θ + B 1 r 2 cos θ, r > a. (2.39) Men B 0 -termen står för en punktladdning i origo. Dock har vi nu en neutral sfär, så B 0 = 0: ϕ(r, θ) = A 0 + A 1 r cos θ + B 1 r 2 cos θ, r > a (2.40) Då ϕ(r = a, θ) ϕ 0 : så att B 1 = a 3 A 1 = E 0 a 3. A 1 a cos θ + B 1 a 2 cos θ = 0 (2.41) Slutliga uttrycket är ϕ(r, θ) = ϕ 0 E 0 r cos θ + a 3 E 0 r 2 cos θ (2.42) Elektrodynamik, vt 2008, Kai Nordlund 2.18
19 Från detta kan vi bestämma elfältet och sfärens ytladdningsfördelning: E r = ϕ r = E 0 E θ = 1 r ϕ θ = E 0! a3 r 3 cos θ, r > a (2.43)! 1 a3 r 3 sin θ, r > a (2.44) σ = ε 0 E r (r = a) = 3ε 0 E 0 cos θ (2.45) Totala laddningen: Q = Z 2π Z π 0 0 = 3ε 0 E 0 2π, θ=π daσ = Z π 0 Z 2π Z π 0 0 dθ sin θ cos θ dφdθ sin θσ = 3 ε 0 E 0 2π 1 2 sin2 θ (2.46) θ=0 = 0. (2.47) Elektrodynamik, vt 2008, Kai Nordlund 2.19
20 Utan azimutal symmetri [Jackson, Arfken] Laplace-ekvationen är nu: 2 ϕ(r) = 1 r 2 r «r 2 ϕ(r) + 1 r r 2 sin θ θ sin θ ϕ(r) «+ θ 1 r 2 sin 2 θ 2 ϕ(r) φ 2 (2.48) Vi försöker igen med en produkt av en-variabels-funktioner: ϕ = Z(r)Q(θ)U(φ). Vi får efter insättning och multiplikation med sin 2 θ/(z(r)q(θ)u(φ):» 1 sin 2 d θ Z dr «r 2 dz + 1 dr Q sin θ d dθ sin θ dq «dθ + 1 U d 2 U dφ 2 = 0 (2.49) Elektrodynamik, vt 2008, Kai Nordlund 2.20
21 Den sista termen beror enbart på φ, medan de två första beror på r och θ. Inför separationskonstanten m 2 :» 1 sin 2 d θ Z dr «r 2 dz + 1 dr Q sin θ d dθ 1 d 2 U = m 2 (2.50) U dφ 2 sin θ dq «= m 2 (2.51) dθ Första ekvationens lösning är U(φ) = e ±imφ (2.52) Här måste vi kräva att m är ett heltal. Andra ekvationen blir: 1 d Z dr «r 2 dz + 1 dr Q sin θ d dθ sin θ dq «m 2 1 dθ sin 2 θ = 0 (2.53) Elektrodynamik, vt 2008, Kai Nordlund 2.21
22 Inför nu en ny separationskonstant, k: 1 d Q sin θ dθ sin θ dq dθ 1 d Z dr ««r 2 dz dr m 2 1 sin 2 θ = k (2.54) = k (2.55) I den andra ekvationen känner vi igen Legendres ekvation, men nu finns det en extra term medplockad. Enligt de tidigare resultaten kan vi genast identifiera k med l(l + 1), där l är ett heltal (tidigare: m): 1 d Q sin θ dθ sin θ dq dθ 1 d Z dr ««r 2 dz dr m 2 1 sin 2 θ = l(l + 1) (2.56) = l(l + 1) (2.57) I den första ekvationen kan vi försöka med Z(r) = r p : r p d dr r 2 pr p 1 =... = p(p + 1) = l(l + 1) (2.58) Elektrodynamik, vt 2008, Kai Nordlund 2.22
23 Lösningarna är Z(r) = r l, eller Z(r) = r l 1 (2.59) Ekvationen i θ är: 1 d Q sin θ dθ sin θ dq «m 2 1 dθ sin 2 θ = l(l + 1) (2.60) Detta är ekvationen för de associerade Legendre-polynomen P m l (cos θ) P m (x). l De associerade Legendre-polynomen är relaterade till de vanliga polynomen P l (x) via ekvationen För indexen m gäller P m l (x) = (1 x 2 ) m/2 d m dx mp l(x) (2.61) m = l,..., 0,..., l (2.62) Elektrodynamik, vt 2008, Kai Nordlund 2.23
24 Negativa m kan relateras till positiva värden: P m l = ( 1) m (l m)! (l + m)! P m l (x) (2.63) Den mest allmänna lösningen till problemet är nu: ϕ(r, θ, φ) = X l=0 lx m= l A lm r l + B lm r l 1 P m l (x)e imφ, SPH, (r, θ, φ) (2.64) Här står SP H för sfärisk symmetriskt system.. Ofta reducerar man de två sista faktorerna till en enda, och skriver lösningen som ϕ(r, θ, φ) = X l=0 lx m= l A lm rl + B lm r l 1 Y lm (θ, φ), SPH, (r, θ, φ) (2.65) där Y lm (θ, φ) är klotytfunktionerna (spherical harmonics). Elektrodynamik, vt 2008, Kai Nordlund 2.24
25 Klotytfunktionerna är Man kan visa att Y lm (θ, φ) = r 2l + 1 4π s (l m)! (l + m)! P m l (cos θ)e imφ (2.66) där betyder komplex-konjugering. Några klotytfunktioner: Y l, m (θ, φ) = ( 1) m Y lm (θ, φ), (2.67) Y 00 (θ, φ) = 1 4π (2.68) r 3 Y 1, 1 (θ, φ) = 8π sin θe iφ (2.69) r 3 Y 10 (θ, φ) = cos θ (2.70) 4π r 3 Y 11 (θ, φ) = 8π sin θeiφ (2.71) Elektrodynamik, vt 2008, Kai Nordlund 2.25
26 2.5. Cylindrisk symmetri Utan z-beroende [Jackson] Ifall vi har cylindrisk symmetri och inget beroende på z, blir Laplace-ekvationen 1 ρ ρ ρ ϕ «+ 1 2 ϕ ρ ρ 2 ψ = 0 (2.72) 2 Försök med den separabla ansatzen ϕ(ρ, ψ) = R(ρ)Ψ(ψ): ρ d R dρ ρ dr «+ 1 d 2 Ψ dρ Ψ dψ = 0 (2.73) 2 Vi får ρ d R dρ ρ dr «dρ = ν 2 (2.74) 1 Ψ d 2 Ψ dψ 2 = ν 2 (2.75) Elektrodynamik, vt 2008, Kai Nordlund 2.26
27 Lösningarna är R(ρ) = aρ ν + bρ ν (2.76) Ψ(ψ) = A sin(νψ) + B cos(νψ) A sin(νψ + B) (2.77) Vi måste nu kräva att ν är ett positivt eller negativt heltal. Om ν = 0 fås lösningarna R(ρ) = a 0 + b 0 ln ρ (2.78) Ψ(ψ) = A 0 + B 0 ψ (2.79) Vi måste dock sätta B 0 = 0 så att Ψ(0) = Ψ(2π)! Konstanten A 0 kan sedan inbakas i uttrycket för R. Elektrodynamik, vt 2008, Kai Nordlund 2.27
28 Den mest allmänna lösningen är nu X ϕ(ρ, ψ) = a 0 + b 0 ln ρ + a n ρ n sin(nψ + c n ) n=1 X + b n ρ n sin(nψ + d n ), CYL, (ρ, ψ) (2.80) n=1 Exempel : Betrakta de hopfogade ledande planen i figuren. Problemet är 2-dimensionellt, så låt oss använda polära koordinater ρ, ψ. Detta motsvarar cylindriska koordinater med inget z-beroende. Ifall β < π är det fråga om en inbuktning, ifall β > π om ett hörn, β 2π skarpt hörn. Potentialen vid planens yta är φ 0 (detta är ett randvillkor). Elektrodynamik, vt 2008, Kai Nordlund 2.28
29 Första randvillkoret för vårt specifika problem: ϕ 0 = ϕ(ρ, ψ = 0) = a 0 + X a n ρ n sin c n (2.81) För att undvika singulariteter i origo ρ = 0: b n = 0, för n 0. Dessutom måste ϕ 0 vara oberoende av ρ, så vi måste ha c n = 0. Uppenbarligen gäller a 0 = ϕ 0. n=1 Andra randvillkoret: ϕ 0 = ϕ(ρ, ψ = β) = a 0 + X a n ρ n sin(nβ) (2.82) n=1 Igen, detta ska gälla för godtyckligt värde på ρ, så vi måste ha sin(nβ) = 0. Detta ger nβ = mπ eller n = mπ/β där m är ett heltal. Det korrekta uttrycket för potentialen är alltså X ϕ(ρ, ψ) = ϕ 0 + a m ρ mπ/β sin(mπψ/β), m = 1, 2, 3,... (2.83) m=1 Men fortfarande är koefficienterna a m okända! Elektrodynamik, vt 2008, Kai Nordlund 2.29
30 Elfältets komponenter är: E ρ = ϕ ρ = X m=1 E ψ = 1 ϕ ρ ψ = mπ β a m sin(mπψ/β) (2.84) X m=1 mπ β a mρ mπ/β 1 cos(mπψ/β) (2.85) Ytladdningstätheten är (Gauss lag, jfr. pillerburken ). σ = ε 0 E ψ (ρ, ψ = 0) = ε 0 π β X a m ρ mπ/β 1 (2.86) m=1 För små ρ kan vi skära av serien efter första termen och får σ ε 0 π β a 1ρ π/β 1 (2.87) Elektrodynamik, vt 2008, Kai Nordlund 2.30
31 β = π/4 : σ ρ 3 β = π/2 : σ ρ 1 β = π : σ 1 β = 3π/2 : σ ρ 1/3 β = 2π : σ ρ 1/2 Vinkeln β = π motsvarar alltså en plan yta, β = 3π/2 ett vinkelrätt hörn, och β = 2π kanten av ett oändligt halvplan. Från detta ser vi att ju skarpare hörn (mindre vinkel) desto mindre laddningstäthet i hörnet! För hörn med en öppningsvinkel β > π blir laddningstätheten och elfältet ρ f, med f > 0. Då man låter ρ 0, d.v.s. då man närmar sig hörnet, blir elfältet allt starkare. I tre dimensioner kan man göra en motsvarande härledning också för en konisk spets (se Jackson kapitel 3.4) och får då ett kvalitativt liknande resultat. Elektrodynamik, vt 2008, Kai Nordlund 2.31
32 Det här kan man nyttja till sin fördel för att skydda sig mot åsknedslag: för att skapa goda förutsättningar i en viss punkt för en urladdning mellan åskmoln och mark är det bara att placera dit en mycket spetsig ledande stång. Kring åskledarens spets kommer även en svag laddningsfördelning på marken att ge upphov till ett starkt fält. Kring den här spetsen är det nu lättare för åskmolnen att övervinna luftens gränsvärde för elektriskt genomslag/urladdning. Med z-beroende Behandlas inte. Lösningarna för ρ-beroendet blir Bessel-funktioner. Elektrodynamik, vt 2008, Kai Nordlund 2.32
33 2.6. Bildladdningsmetoden I vissa situationer kommer man lättare undan genom att inte utgå från Laplace-ekvationen. Vi behandlar nu en grundläggande metod som handlar om att bygga upp en lösning med hjälp av enkla laddningsfördelningar, så kallade bild-laddningar. Potentialen utanför ett system av (o)laddade ledare och enkla laddningsfördelningar kan skrivas som ϕ(r) = X i ϕ i (r) + 1 4πε 0 X j Z da j σ j(r j ) r r j (2.88) Termerna i den första summeringen står för enkla laddningsfördelningar (punkter, linjer,... ). Termerna i den andra summeringen beaktar de inducerade laddningsfördelningarna på ledarnas ytor, och måste alltså erhållas som en explicit integrering över dessa fördelningar. Vi bör komma ihåg att ledarnas ytor är ekvipotentialytor, så att ϕ i på ledarnas ytor är kända. Inom bildladdningsmetoden inför man fiktiva punkt- och linjeladdningar placerade så att dessa ger uppphov till de kända ytpotentialerna. Detta betyder, att den andra summeringen i ekv. (2.88) ersätts med en summa som liknar den första. Elektrodynamik, vt 2008, Kai Nordlund 2.33
34 Platserna för de fiktiva laddningarna måste vara inom ledarna, och de är alltså bara ett hjälpmedel för att räkna fram totalpotentialen! Om bildladdningar förekommer utanför ledarna, i samma region där potentialen ska bestämmas, löser man ju inte längre Laplaces ekvation utans Poissons ekvation dessutom med fel laddningsfördelning (bildladdningen är ju inte verklig)! Elektrodynamik, vt 2008, Kai Nordlund 2.34
35 2.7. Punktvisa bildladdningar Exempel : Punktladdning q utanför ett ledande oändligt plan som sammanfaller med yz-planet. Låt punktladdningens position vara r 1 = (x 1, y 1, z 1 ) = (d, 0, 0). Punktladdningen q inducerar en laddningsfördelning σ(y, z) på ledarens plan. Totala potentialen utanför ledaren är då en summa av punktladdningens potential och den från den inducerade laddningen. Istället för att försöka räkna fram σ(y, z) tar vi fasta på faktumet att ledarens yta måste ha samma potential överallt. Elektrodynamik, vt 2008, Kai Nordlund 2.35
36 Totalpotentialen är ϕ(r) = ϕ 1 (r) + ϕ 2 (r) där φ 2 är potentialen för ytan, som för stunden är okänd. = = q 1 4πε 0 r r 1 + ϕ 2(r) q p 4πε 0 (x d)2 + y 2 + z + ϕ 2(r) (2.89) 2 På ledarens yta: ϕ(0, y, z) = q 4πε 0 p d2 + y 2 + z 2 + ϕ 2(0, y, z) 0 (2.90) Ett naturligt val för bildladdningen är nu ϕ 2 (x, y, z) = q 4πε 0 p (x + d)2 + y 2 + z 2 (2.91) Därav metodens namn! Elektrodynamik, vt 2008, Kai Nordlund 2.36
37 Totala potentialen är nu ϕ(x, y, z) = q 4πε 0 p (x d)2 + y 2 + z 2 q p x 0 (2.92) 4πε 0 (x + d)2 + y 2 + z2, Den inducerade ytladdningsfördelningen är ϕ σ(x, y, z) = ε 0 E x (x = 0) = ε 0 qd = (2.93) x x=0 2π(d 2 + y 2 + z 2 ) 3/2 Absolutbeloppet är maximalt då y = z = 0, då gäller σ = q/(2πd 2 ). Kraften på punktladdningen: F q = q ( ϕ 2 ) x=d,y=0,z=0 = q2 1 4πε 0 ((x + d) 2 + y 2 + z 2 ) 3/2(x + d, y, z) x=d,y=0,z=0 = q2 1 4πε 0 (2d) 3(2d, 0, 0) (2.94) Elektrodynamik, vt 2008, Kai Nordlund 2.37
38 Exempel : Punktladdning q utanför en ledande sfär med mittpunkten i origo. Låt punktladdningens position vara r 1 = dbr. Placera nu en bildladdning q inuti sfären, i punkten r 2 = bbr. Potentialen i en punkt r är nu ϕ(r, θ, φ) = = q 1 4πε 0 r 1 r + q 1 4πε 0 r 2 r q 1 4πε 0 r2 + d 2 2rd cos θ + q 1 4πε 0 r2 + b 2 2rb cos θ (2.95) Elektrodynamik, vt 2008, Kai Nordlund 2.38
39 Om vi har sfären vid noll potential: ϕ(r = a, θ, φ) = 0: a 2 + d 2 2ad cos θ = q2 Denna ekvation skall gälla för alla värden på θ. q 2(a2 + b 2 2ab cos θ) (2.96) Om θ = π/2: Om θ = 0: a 2 + d 2 = q2 q 2(a2 + b 2 ) (2.97) a 2 + d 2 2ad = q2 q 2(a2 + b 2 2ab) (2.98) Okända är b och q! Nu har vi 2 ekvationer och 2 obekanta, så vi kan söka en unik lösning för dessa. Elektrodynamik, vt 2008, Kai Nordlund 2.39
40 Subtrahera den senare ekvationen från den förra: Ins. i ekv. (2.97) ger d = q2 q 2b (2.99) a 2 + q4 q 4b2 = q2 q 2(a2 + b 2 ) (2.100) q 4 q q2 a2 4 q 2(1 + b ) + a2 (2.101) 2 b 2 q 2 q 2 = 1 2 = a2 b 2 ± + a2 b 2 ± s s a2 b + a4 2 b 4 4a2 A (2.102) b 2 (1 a2 b 2 )2 1 A (2.103) Elektrodynamik, vt 2008, Kai Nordlund 2.40
41 Lösningarna är q 2 /q 2 = 1 eller q 2 /q 2 = a 2 /b 2. Den senare ger q/q = ±a/b av vilkan vi väljer q/q = a/b. Vi har nu d = q2 q 2b (2.104) q = a (2.105) q b Detta ger b = a2 d (2.106) q = a d q (2.107) Elektrodynamik, vt 2008, Kai Nordlund 2.41
42 Om vi betecknar den verkliga punktladdningens position med r = r 1 = dbr så blir potentialen utanför sfären ϕ(r, θ, φ) = = = q 1 4πε 0 r r aq 1 4πε 0 q 4πε 0 q 4πε 0 br r " # 1 r r a d a2 br d r r r a d r a2 d 2r d a2 d 5 (2.108) Om vi önskar att sfären befinner sig på en potential ϕ 0 måste vi addera ytterligare en bildladdning q, denna gång i sfärens mitt: ϕ(r, θ, φ) = 1 4πε 0 «q + q + q r 1 r 2 r (2.109) Elektrodynamik, vt 2008, Kai Nordlund 2.42
43 Vi har nu att ϕ(r = a, θ, φ) = 1 4πε 0 «0 + q a = ϕ 0 (2.110) från vilket vi får q. Kraften på punktladdningen? Avståndet mellan laddningarna är så att h d b = d a2 d = d2 a 2 d (2.111) F q = q q 4πε 0 1 h 2 = a d q 2 d 2 4πε 0 (d 2 a 2 ) = q2 2 4πε 0 ad (d 2 a 2 ) 2 (2.112) Elektrodynamik, vt 2008, Kai Nordlund 2.43
44 Sfärens ytladdningstäthet är σ(θ, φ) = ε 0 ϕ r Sfärens totala laddning ges av Gauss lag tillämpad på sfärens yta: (2.113) r=a Q = q + q (2.114) Obs: Jordad sfär: ϕ(r = a) = 0, q = 0. Ickeladdad sfär: q = q = aq/d. Elektrodynamik, vt 2008, Kai Nordlund 2.44
45 2.8. Linjeformade bildladdningar Exempel : Laddad ledande cylinder utanför ett ledande plan. Låt ledaren ligga i yz-planet. Låt linjeladdningen vara längs med z-axeln, och ha koordinaterna x = d, y = 0. Uppenbarligen har vi inget z-beroende, förutsatt att planet och ledningen är oändligt långa inga kant-effekter! Om potentialen på planet är noll, bör vi ha en bildladdning i platsen x = d, y = 0, orienterad längs med z-axeln. Elektrodynamik, vt 2008, Kai Nordlund 2.45
46 Potentialen i en punkt (x, y) är ϕ(x, y) = λ ln r 1 + 2πε 0 Potentialen är noll på planet, d.v.s. för r 1 = r 2. λ ln r 2 = 2πε 0 λ ln r 1 (2.115) 2πε 0 r 2 Helt allmänt: r 2 1 = (x d) 2 + y 2 (2.116) r 2 2 = (x + d) 2 + y 2 (2.117) Konstant potential, som inte är noll, fås i punkterna (x, y) där r 1 /r 2 är konstant, säg M. M 2 = r2 1 r 2 2 = x2 2xd + d 2 + y 2 x 2 + 2xd + d 2 + y 2 (2.118) Elektrodynamik, vt 2008, Kai Nordlund 2.46
47 Efter förenkling fås x + d M! 2 2 «+ 1 + y 2 2M 2 = d (2.119) M 2 1 M 2 1 som är ekvationen för en cylinder med mittpunkten ( d(m 2 + 1)/(M 2 1), 0) och radien 2M R c = d M 2 1 (2.120) Med M < 1 fås en cylindrisk ekvipotentialyta som innestänger den högra linjeladdningen. Elektrodynamik, vt 2008, Kai Nordlund 2.47
48 2.9. Greens metod [Jackson, Arfken] Greens metoder hör inte till kärnmaterialet på denna kurs, men de behandlas kort för att de annars kan anses vara en del av en fysikers allmänbildning. Gauss teorem säger ju att Z V Greens I och II teorem dv F = I A da F I A dabn F (2.121) Låt nu vektorfältet F vara givet som produkten av en skalärfunktion med gradienten av en annan skalärfunktion: Vi har nu F = φ ψ (2.122) F = (φ ψ) = φ 2 ψ + φ ψ (2.123) Elektrodynamik, vt 2008, Kai Nordlund 2.48
49 bn F = φbn ψ φ ψ n (2.124) Elektrodynamik, vt 2008, Kai Nordlund 2.49
50 Insättning i Gauss teorem ger Greens I teorem Skriver vi istället Z V dv φ 2 ψ + φ ψ = I A daφ ψ n (2.125) F = ψ φ (2.126) får vi Z V dv ψ 2 φ + ψ φ = I A daψ φ n (2.127) Subtrahera denna från den tidigare: Z V dv φ 2 ψ ψ 2 φ = I A da φ ψ «n ψ φ n (2.128) Detta är Greens II teorem, som ibland också kallas bara Greens teorem.. Elektrodynamik, vt 2008, Kai Nordlund 2.50
51 Låt nu φ = ϕ(r) (den elektrostatiska potentialen) och ψ = G(r, r ), där funktionen G uppfyller följande villkor: Med detta villkor kan G skrivas som summan 2 G = 4πδ(r r ) (2.129) där F satisifierar Laplaces ekvation: G(r, r ) = 1 r r + F (r, r ), (2.130) 2 F (r, r ) = 0. (2.131) Greens II teorem ger nu Z V dv ϕ 2 G G 2 ϕ = = Z I V A «dv ϕ4πδ(r r ) + G ρ(r ) «da ϕ G n ϕ G n ε 0 (2.132) Elektrodynamik, vt 2008, Kai Nordlund 2.51
52 Detta ger med att utföra integralen över Diracs delta-funktion: ϕ(r) = 1 4πε 0 Z V dv ρ(r )G(r, r ) 1 4π I A da ϕ(r ) G(r, r ) G(r, r ) ϕ(r «) n n (2.133) Denna ekvation ger alltså inte en fysikaliskt vettig lösning till elektrostatiska randvärdesproblem, för den innehåller både Dirichlet- och Neumann-randvillkoren. Men iden är nu att denna form möjliggör att söka funktioner G som får nåndera randvillkorstermen att försvinna, och därmed leder till en fysikaliskt rimlig lösning för den andra typen av randvillkor! Detta är grundideen i den s.k. Greens-funktion-metoden. Om vi har ett Dirichlet-problem är ϕ(r ) känd på randytan, medan ϕ/ n är okänd. För att göra oss av med detta uttryck söker vi en s.k. Greens funktion G D (r, r ) = 0 då r är på randytan A! Potentialen ges då genast av uttrycket ϕ(r) = 1 4πε 0 Z V dv ρ(r )G D (r, r ) 1 4π I A da ϕ(r ) G D (r, r ) n (2.134) Om vi istället har ett Neumann-problem är ϕ(r )/ n känd på randytan. Vi söker en Greens funktion G N (r, r ) för vilken gäller att G N (r, r )/ n = 0 då r är på randytan A. Elektrodynamik, vt 2008, Kai Nordlund 2.52
53 Potentialen ges då av uttrycket ϕ(r) = 1 4πε 0 Z V dv ρ(r )G N (r, r ) + 1 4π I A da G N (r, r ) ϕ(r ) n (2.135) Elektrodynamik, vt 2008, Kai Nordlund 2.53
54 Från den första termen i dessa uttryck ser vi att Greens funktion kan väljas så att den motsvarar en potential, bara laddningsfördelningen har dividerats bort! Exempel 1: En Greens funktion för en punktladdning utanför ledande sfär. Antag potentialen på ytan är känd, så att vi har ett Dirichlet-problem. Vi ska då ha G(r, r ) = 0 för r på ledarens yta. Låt punktladdningen vara i r, och sfärens radie vara a. Vi löste detta problem tidigare, se ekv. (2.108). Vi kan nu försöka välja den erhållna potentialen (med laddningsfaktorn bortdividerad) som Greens funktion: G(r, r ) = 1 r r a d r a2 d 2r Här gäller att r är platsen för den reella punktladdningen. 1 r r a r r a2 r 2r (2.136) Vi observerar nu att r = a ger G = 0, som det bör vara för det här Dirichlet-problemet. Med sfäriska kordinater fås G(r, r ) = 1 p r2 + r 2 2rr cos γ 1 q r 2 r 2 a 2 + a 2 2rr cos γ (2.137) Elektrodynamik, vt 2008, Kai Nordlund 2.54
55 Normalderivatan på ytan, som separerar den externa volymen (där vi vill veta potentialen!) från ledarens inre, är G = G n r =a r = r =a r a r cos γ (r 2 + a 2 2ar cos γ) a r cos γ 3/2 (r 2 + a 2 2ar cos γ) 3/2 r 2 a 2 = (2.138) a(r 2 + a 2 2ar cos γ) 3/2 2 Elektrodynamik, vt 2008, Kai Nordlund 2.55
56 Exempel : En ledare bestående av två hemisfärer isolerade från varandra. Låt potentialen för den övre halvsfären vara +ϕ 0 och ϕ 0 för den undre. Dirichlet-problemets lösning med Greens metod ger oss ekvationen ϕ(r) = 1 4πε 0 Ingen laddning utanför ledaren! Z V dv 0 1 4π I A da ϕ(r ) G D (r, r ) n (2.139) Elektrodynamik, vt 2008, Kai Nordlund 2.56
57 Med Greens funktion vald som i föregående exempel: ϕ(r) = 1 4π + 1 4π Z 2π 0 Z 2π 0 dφ Z π/2 0 dφ Z π π/2 dθ sin θ ϕ 0 a 2 G D (r, r ) n dθ sin θ ϕ 0 a 2 G D (r, r ) n (2.140) ϕ(r) = ϕ 0 4π Z 2π 0 Z π/2 dφ dθ sin θ + 0 Z 2π 0 dφ Z π π/2 dθ sin θ! a 2 G D (r, r ) n (2.141) ϕ(r) = ϕ 0 4π Z 2π 0 Z π/2 dφ dθ sin θ + 0 Z 2π 0 dφ Z π π/2 dθ sin θ! a(a 2 r 2 ) (r 2 + a 2 2ar cos γ) 3/2 (2.142) Med u = cos θ, du = sin θ : ϕ(r) = ϕ 0 4π Z 2π 0 Z 0 dφ du 1 Z 2π 0 Z 1 «dφ du 0 a(a 2 r 2 ) (r 2 + a 2 2ar cos γ) 3/2 (2.143) Elektrodynamik, vt 2008, Kai Nordlund 2.57
58 ϕ(r) = ϕ 0 4π Z 2π 0 Z 1 dφ du 0 Z 2π 0 dφ Z 0 1 du «a(r 2 a 2 ) (r 2 + a 2 2ar cos γ) 3/2 (2.144) Denna integral är inte enkel att utföra, eftersom γ beror på alla vinklar φ, φ, θ, θ. Specialfall: r är på den positiva z-axeln. Då gäller cos γ br br = br bz = cos θ och r = z. ϕ(r) = ϕ 0 4π Z 2π 0 Z 1 dφ du 0 Z 2π 0 dφ Z 0 1 du «a(z 2 a 2 ) (z 2 + a 2 2az cos θ ) 3/2 (2.145) ϕ(r) = ϕ 0 2 Z 1 du 0 Z 0 1 du «a(z 2 a 2 ) (z 2 + a 2 2azu ) 3/2 (2.146) Slutsvaret ska bli ϕ(r) = ϕ 0 1 z2 a 2 z z 2 + a 2! (2.147) Obs: För z = a fås ϕ = ϕ 0 som väntat. Elektrodynamik, vt 2008, Kai Nordlund 2.58
59 2.10. Lösning av Poissons ekvation Poissons ekvation är ju Vi har två möjliga situationer. 2 ϕ(r) = ρ(r) ε 0 (2.148) Situation 1 Laddningstätheten ρ(r) ger den fullständiga fördelningen i volymen av intresse, d.v.s. givna laddningar och inducerade laddningar: Lösningen till Poissons ekvation är då ρ(r) = ρ ext (r) + ρ ind (r) (2.149) ϕ(r) = 1 4πε 0 Z V dv ρ(r ) r r (2.150) Elektrodynamik, vt 2008, Kai Nordlund 2.59
60 Exempel : Antag vi har en radiell symmetrisk laddningsfördelning, ρ = ρ(r). Vi har nu Poissons ekvation i den enkla formen Detta ger 1 d r 2 dr «r 2 dϕ dr = 1 ε 0 ρ(r) (2.151) ϕ(r) = 1 ε 0 Z r r 0 dr 1 r 2 Z r r 0 dr ρ(r )r 2 (2.152) Situation 2 I det andra faller innehåller ρ(r) inte inducerad laddning, utan enbart den externa laddningen, d.v.s. den som vi har kvar efter att alla ledare (innehållande inducerad laddning) har plockats bort: ρ(r) = ρ ext (r) (2.153) Vi söker nu två lösningar. Den första lösningen ϕ (r) ges av Poissons ekvation med laddningstätheten ρ ext (r). Vi löser alltså ekvationen 2 ϕ (r) = ρ ext(r) ε 0 (2.154) Elektrodynamik, vt 2008, Kai Nordlund 2.60
61 eller utför integralen ϕ (r) = 1 4πε 0 Z V dv ρ ext (r ) r r (2.155) Den andra lösningen ϕ (r) får vi med Laplaces ekvation: 2 ϕ (r) = 0 (2.156) Utifrån ϕ (r) kan vi ju bestämma den inducerade laddningen på ledarnas ytor. Den totala lösningen är nu ϕ(r) = ϕ (r) + ϕ (r) (2.157) Obs: Randvillkoren, t.ex. i ett Dirichlet-problem, är nu givna för ϕ Ai = ϕ A i + ϕ A i, så randvillkoren för ϕ A i (lösningen från Laplace-ekvationen) måste modifieras därefter! Elektrodynamik, vt 2008, Kai Nordlund 2.61
2. Lösning av elektrostatiska problem för ledare
 2. Lösning av elektrostatiska problem för ledare [RMC] Elektrodynamik, vt 2013, Kai Nordlund 2.1 2.1. Poissons ekvation [RMC, Jackson] Från tidigare vet vi att Er) = ρr) ε 0 2.1) Er) = ϕr) 2.2) Detta ger
2. Lösning av elektrostatiska problem för ledare [RMC] Elektrodynamik, vt 2013, Kai Nordlund 2.1 2.1. Poissons ekvation [RMC, Jackson] Från tidigare vet vi att Er) = ρr) ε 0 2.1) Er) = ϕr) 2.2) Detta ger
2. Lösning av elektrostatiska problem för ledare
 [RMC] 2. Lösning av elektrostatiska problem för leare 2 ϕr ρ ρ i cylinriska koorinater ρ, ψ, z, och ρ ϕr 2 ϕr + 2 ϕr 2.5 ρ ρ 2 ψ 2 z 2 2 ϕr r 2 ϕr r 2 r r r 2 sin θ θ sin θ ϕr + θ r 2 sin 2 θ 2 ϕr φ 2
[RMC] 2. Lösning av elektrostatiska problem för leare 2 ϕr ρ ρ i cylinriska koorinater ρ, ψ, z, och ρ ϕr 2 ϕr + 2 ϕr 2.5 ρ ρ 2 ψ 2 z 2 2 ϕr r 2 ϕr r 2 r r r 2 sin θ θ sin θ ϕr + θ r 2 sin 2 θ 2 ϕr φ 2
2. Lösning av elektrostatiska problem för ledare
 2. Lösning av elektrostatiska problem för leare [RMC] Elektroynamik, vt 23, Kai Norlun 2. 2.. Poissons ekvation [RMC, Jackson] Från tiigare vet vi att Er) = ρr) ε 2.) Er) = ϕr) 2.2) Detta ger oss genast
2. Lösning av elektrostatiska problem för leare [RMC] Elektroynamik, vt 23, Kai Norlun 2. 2.. Poissons ekvation [RMC, Jackson] Från tiigare vet vi att Er) = ρr) ε 2.) Er) = ϕr) 2.2) Detta ger oss genast
2. Lösning av elektrostatiska problem för ledare
 2. Lösning av elektrostatiska problem för leare [RMC] Elektroynamik, ht 25, Krister Henriksson 2. 2.. Poissons ekvation [RMC, Jackson] Från tiigare vet vi att E(r) = ρ(r) ε (2.) E(r) = ϕ(r) (2.2) Detta
2. Lösning av elektrostatiska problem för leare [RMC] Elektroynamik, ht 25, Krister Henriksson 2. 2.. Poissons ekvation [RMC, Jackson] Från tiigare vet vi att E(r) = ρ(r) ε (2.) E(r) = ϕ(r) (2.2) Detta
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 16, 2018 9. Lösningar av Poissons ekvation Vi vet att Poissons
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 16, 2018 9. Lösningar av Poissons ekvation Vi vet att Poissons
3. Lösning av elektrostatiska problem för dielektrika
 3. Lösning av elektrostatiska problem för dielektrika [RMC] Elektrodynamik, ht 2005, Krister Henriksson 3.1 3.1. Dielektrika Ett perfekt dielektrikum (isolator) är ett material som inte innehåller några
3. Lösning av elektrostatiska problem för dielektrika [RMC] Elektrodynamik, ht 2005, Krister Henriksson 3.1 3.1. Dielektrika Ett perfekt dielektrikum (isolator) är ett material som inte innehåller några
Repetition kapitel 21
 Repetition kapitel 21 Coulombs lag. Grundbulten! Definition av elektriskt fält. Fält från punktladdning När fältet är bestämt erhålls kraften ur : F qe Definition av elektrisk dipol. Moment och energi
Repetition kapitel 21 Coulombs lag. Grundbulten! Definition av elektriskt fält. Fält från punktladdning När fältet är bestämt erhålls kraften ur : F qe Definition av elektrisk dipol. Moment och energi
Elektrodynamik. Elektrostatik. 4πε. eller. F q. ekv
 1 Elektrodynamik I det allmänna fallet finns det tidsberoende källor för fälten, dvs. laddningar i rörelse och tidsberoende strömmar. Fälten blir då i allmänhet tidsberoende. Vi ser då att de elektriska
1 Elektrodynamik I det allmänna fallet finns det tidsberoende källor för fälten, dvs. laddningar i rörelse och tidsberoende strömmar. Fälten blir då i allmänhet tidsberoende. Vi ser då att de elektriska
3. Lösning av elektrostatiska problem för dielektrika
 3. Lösning av elektrostatiska problem för dielektrika [RMC] Elektrodynamik, vt 2013, Kai Nordlund 3.1 3.1. Dielektrika Ett perfekt dielektrikum (isolator) är ett material som inte innehåller några fria
3. Lösning av elektrostatiska problem för dielektrika [RMC] Elektrodynamik, vt 2013, Kai Nordlund 3.1 3.1. Dielektrika Ett perfekt dielektrikum (isolator) är ett material som inte innehåller några fria
3. Lösning av elektrostatiska problem för dielektrika
 3. Lösning av elektrostatiska problem för dielektrika [RMC] Elektrodynamik, vt 2013, Kai Nordlund 3.1 3.1. Dielektrika Ett perfekt dielektrikum (isolator) är ett material som inte innehåller några fria
3. Lösning av elektrostatiska problem för dielektrika [RMC] Elektrodynamik, vt 2013, Kai Nordlund 3.1 3.1. Dielektrika Ett perfekt dielektrikum (isolator) är ett material som inte innehåller några fria
14. Potentialer och fält
 4. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
4. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
14. Potentialer och fält
 14. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
14. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
Formelsamling. Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01
 Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
3. Lösning av elektrostatiska problem för dielektrika
 [RMC] 3. Lösning av elektrostatiska problem för dielektrika Eftersom de minsta beståndsdelarna i ett dielektrikum är molekyler kan man definiera ett molekylärt dipolmoment Nu gäller p m = mol dqr (3.3)
[RMC] 3. Lösning av elektrostatiska problem för dielektrika Eftersom de minsta beståndsdelarna i ett dielektrikum är molekyler kan man definiera ett molekylärt dipolmoment Nu gäller p m = mol dqr (3.3)
9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1
![9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1](/thumbs/61/46243221.jpg) 9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
9. Magnetisk energi [RMC 12] Elektrodynamik, vt 2013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
TATA44 Lösningar 26/10/2012.
 TATA44 Lösningar 6/1/1. 1. Lösning 1: Konen z x + y skär sfären x + y + (z 5 5 då 4z + (z 5 5 och enkla räkningar ger nu z z some ger z(z och vi ser att z eller z. Observera att punkter på sfären med z
TATA44 Lösningar 6/1/1. 1. Lösning 1: Konen z x + y skär sfären x + y + (z 5 5 då 4z + (z 5 5 och enkla räkningar ger nu z z some ger z(z och vi ser att z eller z. Observera att punkter på sfären med z
Poissons ekvation och potentialteori Mats Persson
 1 ärmeledning Föreläsning 21/9 Poissons ekvation och potentialteori Mats Persson i vet att värme strömmar från varmare till kallare. Det innebär att vi har ett flöde av värmeenergi i en riktning som är
1 ärmeledning Föreläsning 21/9 Poissons ekvation och potentialteori Mats Persson i vet att värme strömmar från varmare till kallare. Det innebär att vi har ett flöde av värmeenergi i en riktning som är
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Skriftlig tentamen i Elektromagnetisk fältteori för π3 (ETEF01) och F3 (ETE055)
 Skriftlig tentamen i Elektromagnetisk fältteori för π (ETEF01 och F (ETE055 1 Tid och plats: 6 oktober, 016, kl. 14.00 19.00, lokal: Gasquesalen. Kursansvarig lärare: Anders Karlsson, tel. 40 89 och 07-5958.
Skriftlig tentamen i Elektromagnetisk fältteori för π (ETEF01 och F (ETE055 1 Tid och plats: 6 oktober, 016, kl. 14.00 19.00, lokal: Gasquesalen. Kursansvarig lärare: Anders Karlsson, tel. 40 89 och 07-5958.
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
9. Magnetisk energi Magnetisk energi för en isolerad krets
 9. Magnetisk energi [RM] Elektrodynamik, vt 013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets anod
9. Magnetisk energi [RM] Elektrodynamik, vt 013, Kai Nordlund 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets anod
Tentamen i tmv036c och tmv035c, Analys och linjär algebra C för K, Kf och Bt A =, = det(a λi) = e 2t + c 2. x(t) = c 1. = c 1.
 Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
Institutionen för matematiska vetenskaper Chalmers tekniska högskola Niklas Eriksen Tentamen i tmv6c och tmv5c, Analys och linjär algebra C för K, Kf och Bt Lösningar 9--6. Lös initialvärdesproblemet x
9. Magnetisk energi Magnetisk energi för en isolerad krets
 9. Magnetisk energi [RMC] Elektrodynamik, ht 005, Krister Henriksson 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
9. Magnetisk energi [RMC] Elektrodynamik, ht 005, Krister Henriksson 9.1 9.1. Magnetisk energi för en isolerad krets Arbetet som ett batteri utför då det för en laddning dq runt en krets, från batteriets
ANDREAS REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se. Coulombs lag och Maxwells första ekvation
 ANDREA REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se oulombs lag och Maxwells första ekvation oulombs lag och Maxwells första ekvation Inledning Två punktladdningar q 1 samt q 2 i rymden
ANDREA REJBRAND 2007-11-03 Elektromagnetism http://www.rejbrand.se oulombs lag och Maxwells första ekvation oulombs lag och Maxwells första ekvation Inledning Två punktladdningar q 1 samt q 2 i rymden
TATA44 ösningar till tentamen 13/01/ ) Paraboloiden z = 2 x 2 y 2 skär konen z = x 2 + y 2 då x 2 + y 2 = 2 x 2 y 2. Med
 TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
15. Strålande system
 15. Strålande system [Griffiths,RMC] Elektrodynamik, vt 2013, Kai Nordlund 15.1 15.1. Introduktion Laddningar i vila eller i likformig rörelse skapar inte elektromagnetiska vågor för detta krävs att laddningarna
15. Strålande system [Griffiths,RMC] Elektrodynamik, vt 2013, Kai Nordlund 15.1 15.1. Introduktion Laddningar i vila eller i likformig rörelse skapar inte elektromagnetiska vågor för detta krävs att laddningarna
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen DEL A. r cos t + (r cos t) 2 + (r sin t) 2) rdrdt.
 1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
1 Potenitallösningen för strömningen kring en cylinder
 Föreläsning 9 1 Potenitallösningen för strömningen kring en cylinder I denna föreläsning ska vi kortfattat behandla potentialströmning, som traditionellt varit ett stort område inom aerodynamiken, men
Föreläsning 9 1 Potenitallösningen för strömningen kring en cylinder I denna föreläsning ska vi kortfattat behandla potentialströmning, som traditionellt varit ett stort område inom aerodynamiken, men
av envariabelfunktionen g(t) och flervariabelfunktionen t = h(x, y) = x 2 + e y.)
 Lösningsskisser till TATA69 Flervariabelanalys 16-1- 1 Stationära punkter ges av f (4x 3 + 4x, 3y + 6z, z + 6y (,,, dvs (x, y, z (,, eller (x, y, z (, 6, 18 Ur andraderivatorna fås de kvadratiska formerna
Lösningsskisser till TATA69 Flervariabelanalys 16-1- 1 Stationära punkter ges av f (4x 3 + 4x, 3y + 6z, z + 6y (,,, dvs (x, y, z (,, eller (x, y, z (, 6, 18 Ur andraderivatorna fås de kvadratiska formerna
15. Strålande system. Elektrodynamik, vt 2013, Kai Nordlund 15.1
 15. Strålande system [Griffiths,RMC] Elektrodynamik, vt 2013, Kai Nordlund 15.1 15.1. Introduktion Laddningar i vila eller i likformig rörelse skapar inte elektromagnetiska vågor för detta krävs att laddningarna
15. Strålande system [Griffiths,RMC] Elektrodynamik, vt 2013, Kai Nordlund 15.1 15.1. Introduktion Laddningar i vila eller i likformig rörelse skapar inte elektromagnetiska vågor för detta krävs att laddningarna
r 2 C Arbetet är alltså endast beroende av start- och slutpunkt. Det följer av att det elektriska fältet är konservativt ( E = 0).
 1 Föreläsning 2 Motsvarar avsnitten 2.4 2.5 i Griffiths. Arbete och potentiell energi (Kap. 2.4) r 1 r 2 C Låt W vara det arbete som måste utföras mot ett givet elektriskt fält E, då en laddning Q flyttas
1 Föreläsning 2 Motsvarar avsnitten 2.4 2.5 i Griffiths. Arbete och potentiell energi (Kap. 2.4) r 1 r 2 C Låt W vara det arbete som måste utföras mot ett givet elektriskt fält E, då en laddning Q flyttas
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232)
 ösningsskiss för tentamen Vektorfält och klassisk fysik FFM232) Tid och plats: ösningsskiss: Måndagen den 24 oktober 2016 klockan 14.00-18.00 i M-huset. Christian Forssén och Tobias Wenger Detta är enbart
ösningsskiss för tentamen Vektorfält och klassisk fysik FFM232) Tid och plats: ösningsskiss: Måndagen den 24 oktober 2016 klockan 14.00-18.00 i M-huset. Christian Forssén och Tobias Wenger Detta är enbart
Institutionen för matematik SF1626 Flervariabelanalys. Lösningsförslag till tentamen Måndagen den 5 juni 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Lösningar till seminarieuppgifter
 Lösningar till seminarieuppgifter 2018-09-26 Uppgift 1 z ρ P z = 0 ρ Introducera ett koordinatsystem så att det jordade planet sammanfaller med planet z = 0, oc skivans centrum med punkten (0,0,). a) Problemet
Lösningar till seminarieuppgifter 2018-09-26 Uppgift 1 z ρ P z = 0 ρ Introducera ett koordinatsystem så att det jordade planet sammanfaller med planet z = 0, oc skivans centrum med punkten (0,0,). a) Problemet
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM34, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct, 08 Repetition: Singulära fält Punktkälla i origo. Fältet i punkten
FFM34, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct, 08 Repetition: Singulära fält Punktkälla i origo. Fältet i punkten
LAPLACES OCH POISSONS EKVATIONER
 TH Matematik Olle tormark LAPLACE OCH POION EVATIONE Poissons ekvation φ(x) = (där ρ är en given funktion och φ söks) satisfieras till exempel av den elektrostatiska potentialen i ett område som innehåller
TH Matematik Olle tormark LAPLACE OCH POION EVATIONE Poissons ekvation φ(x) = (där ρ är en given funktion och φ söks) satisfieras till exempel av den elektrostatiska potentialen i ett område som innehåller
x ( f u 2y + f v 2x) xy = 24 och C = f
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Tentamen SF1626, Analys i flera variabler, Svar och lösningsförslag. 2. en punkt på randkurvan förutom hörnen, eller
 Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 24-8-2 DEL A. Bestäm och skissera definitionsmängden till funktionen fx, y) = x 2 + y 2 + 2x 4y + + x. Är definitionsmängden kompakt? 4 p) Lösning.
SF626 Flervariabelanalys Lösningsförslag till tentamen 24-8-2 DEL A. Bestäm och skissera definitionsmängden till funktionen fx, y) = x 2 + y 2 + 2x 4y + + x. Är definitionsmängden kompakt? 4 p) Lösning.
Appendix A: Differentialoperatorer i olika koordinatsystem
 Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A. 1. En svängningsrörelse beskrivs av
 SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
u av funktionen u = u(x, y, z) = xyz i punkten M o = (x o, y o, z o ) = (1, 1, 1) i riktningen mot punkten M 1 = (x 1, y 1, z 1 ) = (2, 3, 1)
 ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
TATA44 Lösningar 24/8/ ) Låt S vara den del av x 2 + y 2 + z 2 = 2 innanför cylindern x 2 + y 2 = 1. Inför cylinderkoordinater.
 TATA Lösningar /8/.. Låt vara den del av x + y + z innanför cylindern x + y. Inför cylinderkoordinater. Parametrisera med ortsvektorn r(ρ, φ (ρ cos φ, ρ sin φ, ρ som man kan skriva som r(ρ, φ ρ ˆρ + ρ
TATA Lösningar /8/.. Låt vara den del av x + y + z innanför cylindern x + y. Inför cylinderkoordinater. Parametrisera med ortsvektorn r(ρ, φ (ρ cos φ, ρ sin φ, ρ som man kan skriva som r(ρ, φ ρ ˆρ + ρ
Lösningsförslag Inlämningsuppgift 1 elstatikens grunder
 Inst. för fysik och astronomi 017-11-08 1 Lösningsförslag Inlämningsuppgift 1 elstatikens grunder Elektromagnetism I, 5 hp, för ES och W (1FA514) höstterminen 017 (1.1) Laddningen q 1 7,0 10 6 C placeras
Inst. för fysik och astronomi 017-11-08 1 Lösningsförslag Inlämningsuppgift 1 elstatikens grunder Elektromagnetism I, 5 hp, för ES och W (1FA514) höstterminen 017 (1.1) Laddningen q 1 7,0 10 6 C placeras
Vektoranalys I. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
r 2 Arbetet är alltså endast beroende av start- och slutpunkt. Det följer av att det elektriska fältet är konservativt ( E = 0).
 1 Föreläsning 2 Motsvarar avsnitten 2.4 2.5 i Griffiths. Arbete och potentiell energi (Kap. 2.4) r 1 r 2 C Låt W vara det arbete som måste utföras mot ett givet elektriskt fält E, då en laddning Q flyttas
1 Föreläsning 2 Motsvarar avsnitten 2.4 2.5 i Griffiths. Arbete och potentiell energi (Kap. 2.4) r 1 r 2 C Låt W vara det arbete som måste utföras mot ett givet elektriskt fält E, då en laddning Q flyttas
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM234 och FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
VIKTIGA TILLÄMPNINGAR AV GRUNDLÄGGANDE BEGREPP
 Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december Lösningsförslag. F n ds,
 Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 16-8-18 DEL A 1 Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x oc y = x Beräkna x-koordinaten
SF166 Flervariabelanalys Lösningsförslag till tentamen 16-8-18 DEL A 1 Låt D vara det område ovanför x-axeln i xy-planet som begränsas av cirkeln x + y = 1 samt linjerna y = x oc y = x Beräkna x-koordinaten
Tentamen i El- och vågrörelselära,
 Tentamen i El- och vågrörelselära, 05-0-05. Beräknastorlekochriktningpådetelektriskafältetipunkten(x,y) = (4,4)cm som orsakas av laddningarna q = Q i origo, q = Q i punkten (x,y) = (0,4) cm och q = Q i
Tentamen i El- och vågrörelselära, 05-0-05. Beräknastorlekochriktningpådetelektriskafältetipunkten(x,y) = (4,4)cm som orsakas av laddningarna q = Q i origo, q = Q i punkten (x,y) = (0,4) cm och q = Q i
SF1626 Flervariabelanalys Tentamen Torsdagen den 18 augusti 2016
 Institutionen för matematik SF166 Flervariabelanalys Tentamen Torsdagen den 18 augusti 16 Skrivtid: 8:-1: Tillåtna jälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF166 Flervariabelanalys Tentamen Torsdagen den 18 augusti 16 Skrivtid: 8:-1: Tillåtna jälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
Strålningsfält och fotoner. Våren 2016
 Strålningsfält och fotoner Våren 2016 1. Fält i rymden Vi har lärt oss att beräkna elektriska fält utgående från laddningarna som orsakar dem Kan vi härleda nånting åt andra hållet? 2 1.1 Gauss lag Låt
Strålningsfält och fotoner Våren 2016 1. Fält i rymden Vi har lärt oss att beräkna elektriska fält utgående från laddningarna som orsakar dem Kan vi härleda nånting åt andra hållet? 2 1.1 Gauss lag Låt
Tentamen i El- och vågrörelselära,
 Tentamen i El- och vågrörelselära, 23 2 8 Hjälpmedel: Physics Handbook, räknare. Ensfäriskkopparkulamedradie = 5mmharladdningenQ = 2.5 0 3 C. Beräkna det elektriska fältet som funktion av avståndet från
Tentamen i El- och vågrörelselära, 23 2 8 Hjälpmedel: Physics Handbook, räknare. Ensfäriskkopparkulamedradie = 5mmharladdningenQ = 2.5 0 3 C. Beräkna det elektriska fältet som funktion av avståndet från
f(x, y) = ln(x 2 + y 2 ) f(x, y, z) = (x 2 + yz, y 2 x ln x) 3. Beräkna en vektor som är tangent med skärningskurvan till de två cylindrarna
 ATM-Matematik Mikael Forsberg 734-41 3 31 För studenter i Flervariabelanalys Flervariabelanalys mk1b 13 8 Skrivtid: 9:-14:. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler
ATM-Matematik Mikael Forsberg 734-41 3 31 För studenter i Flervariabelanalys Flervariabelanalys mk1b 13 8 Skrivtid: 9:-14:. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler
(x 3 + y)dxdy. D. x y = x + y. + y2. x 2 z z
 UPPAA UNIVERITET Matematiska institutionen Abrahamsson, 4715, 7-57 (tyf, 47119, 77-517) Prov i matematik IT, K, X, W, EI, MI, NVP samt fristående kurs. Flerdimensionell analys och Analys MN 5-1-9 krivtid:
UPPAA UNIVERITET Matematiska institutionen Abrahamsson, 4715, 7-57 (tyf, 47119, 77-517) Prov i matematik IT, K, X, W, EI, MI, NVP samt fristående kurs. Flerdimensionell analys och Analys MN 5-1-9 krivtid:
Föreläsning 4 1. Den andra av Maxwells ekvationer i elektrostatiken
 Föreläsning 4 1 Potential Den andra av Maxwells ekvationer i elektrostatiken!" C E!dl = 0 eller # E = 0 innebär att E-fältet är konservativt. Det finns inga fältlinjer som bildar loopar. Alla fältlinjer
Föreläsning 4 1 Potential Den andra av Maxwells ekvationer i elektrostatiken!" C E!dl = 0 eller # E = 0 innebär att E-fältet är konservativt. Det finns inga fältlinjer som bildar loopar. Alla fältlinjer
(x + 1) dxdy där D är det ändliga område som begränsas av kurvorna
 UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik ES, W Flervariabelanalys 8 1 1 Skrivtid: 9-1. Inga hjälpmedel. Lösningarna skall åtföljas av förklarande text/figurer. Varje
UPPSALA UNIVERSITET Matematiska institutionen Anders Källström Prov i matematik ES, W Flervariabelanalys 8 1 1 Skrivtid: 9-1. Inga hjälpmedel. Lösningarna skall åtföljas av förklarande text/figurer. Varje
SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Lösningsförslag till tentamen Torsdag augusti 16, 2018 DEL A
 Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
0. Introduktion, matematisk bakgrund
 0. Introduktion, matematisk bakgrund Kai Nordlund vt. 2013. Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht. 2005. Vissa delar,
0. Introduktion, matematisk bakgrund Kai Nordlund vt. 2013. Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht. 2005. Vissa delar,
SF1646 Analys i flera variabler Tentamen 18 augusti 2011, Svar och lösningsförslag
 SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
Tentamen Modellering och simulering inom fältteori, 21 oktober, 2006
 Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, oktober, 006 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori Varje uppgift ger 0 poäng. Delbetyget
Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, oktober, 006 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori Varje uppgift ger 0 poäng. Delbetyget
Dubbelintegraler och volymberäkning
 ubbelintegraler och volymberäkning Volym och dubbelintegraler över en rektangel Alla funktioner nedan antas vara kontinuerliga. Om f (x) i intervallet [a, b], så är arean av mängden {(x, y) : y f (x),
ubbelintegraler och volymberäkning Volym och dubbelintegraler över en rektangel Alla funktioner nedan antas vara kontinuerliga. Om f (x) i intervallet [a, b], så är arean av mängden {(x, y) : y f (x),
Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum:
 Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum: 004-08- Observera Om tentamensuppgiften är densamma som på den nya kursen MTM3 är uppgiften löst med den metod som är vanligast i denna kurs.
Lösningar/svar till tentamen i MTM060 Kontinuumsmekanik Datum: 004-08- Observera Om tentamensuppgiften är densamma som på den nya kursen MTM3 är uppgiften löst med den metod som är vanligast i denna kurs.
Övning 6, FMM-Vektoranalys, SI1140
 Övning 6, FMM-ektoranalys, I114 ˆ 6. Beräkna integralen där A dr A x 2 ay + z) ) e x + y 2 az ) e y + z 2 ax + y) ) e z och är den kurva som utgör skärningslinjen mellan cylindern { x a) 2 + y 2 a 2 och
Övning 6, FMM-ektoranalys, I114 ˆ 6. Beräkna integralen där A dr A x 2 ay + z) ) e x + y 2 az ) e y + z 2 ax + y) ) e z och är den kurva som utgör skärningslinjen mellan cylindern { x a) 2 + y 2 a 2 och
SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 2016
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Lösningar till tentamen i Elektromagnetisk fältteori för Π3 & F3
 Lösningar till tentamen i Elektromagnetisk fältteori för Π3 & F3 Tid och plats: januari 2, kl. 4.9., i MA. Kursansvarig lärare: Christian Sohl, tel. 222 34 3. Tillåtna hjälpmedel: Formelsamling i elektromagnetisk
Lösningar till tentamen i Elektromagnetisk fältteori för Π3 & F3 Tid och plats: januari 2, kl. 4.9., i MA. Kursansvarig lärare: Christian Sohl, tel. 222 34 3. Tillåtna hjälpmedel: Formelsamling i elektromagnetisk
Tentamen: Lösningsförslag
 Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Visa att vektorfältet F har en potential och bestäm denna. a. F = (3x 2 y 2 + y, 2x 3 y + x) b. F = (2x + y, x + 2z, 2y 2z)
 Kap. 15.1 15.2, 15.4, 16.3. Vektorfält, integralkurva, konservativa fält, potential, linjeintegraler av vektorfält, enkelt sammanhängande område, oberoendet av vägen, Greens formel. A 1701. Undersök om
Kap. 15.1 15.2, 15.4, 16.3. Vektorfält, integralkurva, konservativa fält, potential, linjeintegraler av vektorfält, enkelt sammanhängande område, oberoendet av vägen, Greens formel. A 1701. Undersök om
SF1626 Flervariabelanalys Tentamen Torsdagen den 20 augusti 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
23 Konservativa fält i R 3 och rotation
 Nr 23, 7 maj -5, Amelia 2 23 Konservativa fält i R 3 och rotation 23. Potential 23.. Två dimensioner (2D) I två dimensioner definierade vi ett vektorfält som konservativt om kurvintegralen av fältet endast
Nr 23, 7 maj -5, Amelia 2 23 Konservativa fält i R 3 och rotation 23. Potential 23.. Två dimensioner (2D) I två dimensioner definierade vi ett vektorfält som konservativt om kurvintegralen av fältet endast
Strålningsfält och fotoner. Våren 2013
 Strålningsfält och fotoner Våren 2013 1. Fält i rymden Vi har lärt oss att beräkna elektriska fält utgående från laddningarna som orsakar dem Kan vi härleda nånting åt andra hållet? 2 1.1 Gauss lag Låt
Strålningsfält och fotoner Våren 2013 1. Fält i rymden Vi har lärt oss att beräkna elektriska fält utgående från laddningarna som orsakar dem Kan vi härleda nånting åt andra hållet? 2 1.1 Gauss lag Låt
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF66 Flervariabelanals Lösningsförslag till tentamen --9 EL A. En kulle beskrivs approximativt av funktionen 5 hx, ) + 3x + i lämpliga enheter där hx, ) är höjden. Om du befinner dig i punkten,, ) på kullen,
SF66 Flervariabelanals Lösningsförslag till tentamen --9 EL A. En kulle beskrivs approximativt av funktionen 5 hx, ) + 3x + i lämpliga enheter där hx, ) är höjden. Om du befinner dig i punkten,, ) på kullen,
Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum:
 Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum: 2004-08-21 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar
Lösningar/svar till tentamen i MTM113 Kontinuumsmekanik Datum: 2004-08-21 Observera att lösningarna inte alltid är av tentamenslösningskvalitet. De skulle inte ge full poäng vid tentamen. Motiveringar
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 2, 2017 10. Värmeledning, diffusionsekvation Betrakta ett temperaturfält
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 2, 2017 10. Värmeledning, diffusionsekvation Betrakta ett temperaturfält
6. Räkna ut integralen. z dx dy dz,
 Institutionen för Matematik, TH Flervariabelanalys SF626. Tentamen den 23 november 29 kl. 8-3 Tillåtet hjälpmedel är Beta Mathematics Handbook. Tydliga lösningar med fullständiga meningar och utförliga
Institutionen för Matematik, TH Flervariabelanalys SF626. Tentamen den 23 november 29 kl. 8-3 Tillåtet hjälpmedel är Beta Mathematics Handbook. Tydliga lösningar med fullständiga meningar och utförliga
Integraler av vektorfält Mats Persson
 Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
Rep. Kap. 27 som behandlade kraften på en laddningar från ett B-fält.
 Rep. Kap. 7 som behandlade kraften på en laddningar från ett -fält. Kraft på laddning i rörelse Kraft på ström i ledare Gauss sats för -fältet Inte så användbar som den för E-fältet, eftersom flödet här
Rep. Kap. 7 som behandlade kraften på en laddningar från ett -fält. Kraft på laddning i rörelse Kraft på ström i ledare Gauss sats för -fältet Inte så användbar som den för E-fältet, eftersom flödet här
FK Elektromagnetism och vågor, Fysikum, Stockholms Universitet Tentamensskrivning, måndag 21 mars 2016, kl 9:00-14:00
 FK5019 - Elektromagnetism och vågor, Fysikum, Stockholms Universitet Tentamensskrivning, måndag 21 mars 2016, kl 9:00-14:00 Läs noggrant igenom hela tentan först Tentan består av 5 olika uppgifter med
FK5019 - Elektromagnetism och vågor, Fysikum, Stockholms Universitet Tentamensskrivning, måndag 21 mars 2016, kl 9:00-14:00 Läs noggrant igenom hela tentan först Tentan består av 5 olika uppgifter med
) 2 = 1, där a 1. x + b 2. y + c 2
 ap 7 Användningar av multipelintegraler Arean av ett plant område 0 Beräkna arean av det område som begränsas av följande kurvor: A a (x y) 2 + x 2 = a 2 A b xy =, xy = 8, y = x och y = 2x (x > ) A c y
ap 7 Användningar av multipelintegraler Arean av ett plant område 0 Beräkna arean av det område som begränsas av följande kurvor: A a (x y) 2 + x 2 = a 2 A b xy =, xy = 8, y = x och y = 2x (x > ) A c y
SF1626 Flervariabelanalys Tentamen Måndagen den 21 mars 2016
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Måndagen den 2 mars 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF626 Flervariabelanalys Tentamen Måndagen den 2 mars 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Kroklinjiga koordinater och räkning med vektoroperatorer. Henrik Johanneson/(Mats Persson)
 Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Lösning till kontrollskrivning 1A
 KTH Matematik Olle Stormark Lösning till kontrollskrivning 1A i SF1626 Flervariabelanalys för E, vt 28. Varje uppgift ger maximalt 3 poäng. För godkänt krävs minst 5 poäng sammanlagt. 1. Funktionen f(x,
KTH Matematik Olle Stormark Lösning till kontrollskrivning 1A i SF1626 Flervariabelanalys för E, vt 28. Varje uppgift ger maximalt 3 poäng. För godkänt krävs minst 5 poäng sammanlagt. 1. Funktionen f(x,
Vektoranalys III. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
SF1626 Flervariabelanalys Tentamen Tisdagen den 10 januari 2017
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den januari 27 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF626 Flervariabelanalys Tentamen Tisdagen den januari 27 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
1.1 Gradienten i kroklinjiga koordinatsystem
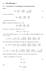 1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
Vecka 2 ELEKTRISK POTENTIAL OCH KAPACITANS (HRW 24-25) Inlärningsmål
 Vecka 2 ELEKTRISK POTENTIAL OCH KAPACITANS (HRW 24-25) Inlärningsmål Elektrisk potential Arbete och elektrisk potentialenergi Elektrisk potential Ekvipotentialytor Sambandet mellan elfält och elektrisk
Vecka 2 ELEKTRISK POTENTIAL OCH KAPACITANS (HRW 24-25) Inlärningsmål Elektrisk potential Arbete och elektrisk potentialenergi Elektrisk potential Ekvipotentialytor Sambandet mellan elfält och elektrisk
Tentamen TMA044 Flervariabelanalys E2
 Tentamen TMA44 Flervariabelanalys E 4--3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, halmers Telefonvakt: Elin Solberg, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan från
Tentamen TMA44 Flervariabelanalys E 4--3 kl. 8.3.3 Examinator: Peter Hegarty, Matematiska vetenskaper, halmers Telefonvakt: Elin Solberg, telefon: 73 88 34 Hjälpmedel: bifogat formelblad, ordlistan från
SF1626 Flervariabelanalys Tentamen Måndagen den 27 maj, 2013
 SF626 Flervariabelanalys Tentamen Måndagen den 27 maj, 23 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mattias Dahl Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. De tre
SF626 Flervariabelanalys Tentamen Måndagen den 27 maj, 23 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mattias Dahl Tentamen består av nio uppgifter som vardera ger maximalt fyra poäng. De tre
f(x, y) = ln(x 2 + y 2 + 1). 3. Hitta maximala arean för en rektangel inskriven i en ellips på formen x 2 a 2 + y2
 TM-Matematik Mikael Forsberg Matematik med datalogi, mfl. Flervariabelanalys mk12b Övningstenta vt213 nr1 Skrivtid: 5 timmar. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler
TM-Matematik Mikael Forsberg Matematik med datalogi, mfl. Flervariabelanalys mk12b Övningstenta vt213 nr1 Skrivtid: 5 timmar. Hjälpmedel är formelbladen från insidan av Pärmen i Adams Calculus, dessa formler
Fysik TFYA68. Föreläsning 2/14
 Fysik TFYA68 Föreläsning 2/14 1 Elektrostatik University Physics: Kapitel 21 & 22 2 Elektrisk laddning Två typer av elektrisk laddning: positiv + och negativ Atom Atomkärnan: Proton (+1), neutron (0) elekton
Fysik TFYA68 Föreläsning 2/14 1 Elektrostatik University Physics: Kapitel 21 & 22 2 Elektrisk laddning Två typer av elektrisk laddning: positiv + och negativ Atom Atomkärnan: Proton (+1), neutron (0) elekton
Lösningsförslag till tentamen Tisdagen den 10 januari 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Tisdagen den januari 7 DEL A. En partikel rör sig så att positionen efter starten ges av (x, y, z (t cos t, t sin t, t
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Tisdagen den januari 7 DEL A. En partikel rör sig så att positionen efter starten ges av (x, y, z (t cos t, t sin t, t
Föreläsning 13, SF1626 Flervariabelanalys
 Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
